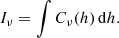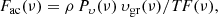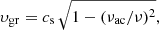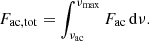| Issue |
A&A
Volume 642, October 2020
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 10 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202038559 | |
| Published online | 02 October 2020 | |
Observational study of chromospheric heating by acoustic waves
1
Astronomical Institute of the Czech Academy of Sciences (v.v.i.), Fričova 298, 25165 Ondřejov, Czech Republic
e-mail: vahid.abbasvand.azar@asu.cas.cz
2
Astronomical Institute of Charles University, Faculty of Mathematics and Physics, V Holešovičkách 2, 180 00 Praha 8, Czech Republic
3
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
4
Astronomical Institute, Slovak Academy of Sciences, 059 60, Tatranská, Lomnica, Slovakia
Received:
2
June
2020
Accepted:
5
August
2020
Aims. Our aim is to investigate the role of acoustic and magneto-acoustic waves in heating the solar chromosphere. Observations in strong chromospheric lines are analyzed by comparing the deposited acoustic-energy flux with the total integrated radiative losses.
Methods. Quiet-Sun and weak-plage regions were observed in the Ca II 854.2 nm and Hα lines with the Fast Imaging Solar Spectrograph (FISS) at the 1.6-m Goode Solar Telescope on 2019 October 3 and in the Hα and Hβ lines with the echelle spectrograph attached to the Vacuum Tower Telescope on 2018 December 11 and 2019 June 6. The deposited acoustic energy flux at frequencies up to 20 mHz was derived from Doppler velocities observed in line centers and wings. Radiative losses were computed by means of a set of scaled non-local thermodynamic equilibrium 1D hydrostatic semi-empirical models obtained by fitting synthetic to observed line profiles.
Results. In the middle chromosphere (h = 1000–1400 km), the radiative losses can be fully balanced by the deposited acoustic energy flux in a quiet-Sun region. In the upper chromosphere (h > 1400 km), the deposited acoustic flux is small compared to the radiative losses in quiet as well as in plage regions. The crucial parameter determining the amount of deposited acoustic flux is the gas density at a given height.
Conclusions. The acoustic energy flux is efficiently deposited in the middle chromosphere, where the density of gas is sufficiently high. About 90% of the available acoustic energy flux in the quiet-Sun region is deposited in these layers, and thus it is a major contributor to the radiative losses of the middle chromosphere. In the upper chromosphere, the deposited acoustic flux is too low, so that other heating mechanisms have to act to balance the radiative cooling.
Key words: Sun: chromosphere / Sun: oscillations / radiative transfer
© V. Abbasvand et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The solar chromosphere is hotter than the photosphere and the increase in temperature in semi-empirical models of the chromosphere cannot be explained by radiative heating. The strong spectral lines of neutral hydrogen, Ca II, and Mg II are the most important lines for studying the released radiative energy from the chromosphere (Carlsson et al. 2019). The cores of these spectral lines are formed under non-local thermodynamic equilibrium (non-LTE) conditions, where departures from the LTE are important. In the quiet Sun, Vernazza et al. (1981) integrated the radiative losses over the height of the chromosphere, obtaining 4600 W m−2. In active regions, these losses are higher by a factor of two to four (Withbroe & Noyes 1977). They have to be balanced by an energy input supplied by various heating mechanisms.
There are several candidates of chromospheric heating mechanisms, which can be classified into two main competitive groups (see Jess et al. 2015, for a review): (1) heat release related to two groups of magnetic field lines with opposite directions and their reconnection, which creates local electric current sheets to release the magnetic energy (Rabin & Moore 1984; Testa et al. 2014); (2) dissipation of the energy of upward-propagating magneto-acoustic waves. These waves stem from the acoustic waves generated in the upper convection zone because of turbulent motions (e.g., Aschwanden 2001; Zaqarashvili & Erdélyi 2009; Kayshap et al. 2018, and references therein). In this paper, we focus to the latter mechanism.
The magnetic field affects the propagation of acoustic waves. The acoustic waves undergo the mode conversion of magneto-acoustic waves on equipartition surfaces in the upper photosphere, where the Alfvén velocity is equal to the sound speed. The inclined magnetic field then also facilitates the propagation of the waves with frequencies below the acoustic cut-off frequency νac = 5.2 mHz (Bel & Leroy 1977) into the upper atmosphere through so-called magnetic portals (Jefferies et al. 2006; Stangalini et al. 2011; Kontogiannis et al. 2014, 2016).
The physical properties of the solar chromosphere, including its dynamics, energetics, and the formation of spectral-line features, have been explored with significant efforts, using both theoretical simulations and observational analysis. Theoretical evidence shows that acoustic waves can heat the intranetwork (i.e., non-magnetic) regions on the Sun (Ulmschneider & Musielak 2003). Based on simulations, Carlsson & Stein (1992) reported that when the acoustic wave dissipation is fully employed, the Ca II H line behavior is very similar to the observed one. Cuntz et al. (2007) discussed the physical nature of acoustic heating in the solar chromosphere using time-dependent 1D simulations to calculate wave energy fluxes. They claimed that high-frequency acoustic waves are sufficient to heat the intranetwork regions in the solar chromosphere.
According to the work of Bello González et al. (2010a, b), the total acoustic flux in quiet regions calculated from observed Doppler velocities at the height of 500–600 km is approximately 2000 W m−2, and in the photosphere (h = 250 km) it reaches 6500 W m−2. Its spatial distribution in the field of view is strongly inhomogeneous. Beck et al. (2009) estimated acoustic energy fluxes from velocity oscillations in the chromospheric Ca II H line core and in several photospheric lines blended in the wings of that line. They found that the acoustic flux of 1000 W m−2 at the heights 800–1200 km was insufficient to maintain the temperature stratification of chromospheric semi-empirical models above the temperature minimum.
The dissipation of (magneto)acoustic waves is generally time-dependent. Carlsson & Stein (1995, 1997) applied time-dependent 1D radiation-hydrodynamic models to compute the propagation of acoustic waves in the non-LTE regime. They found that acoustic shocks cause short time intervals of high temperature; however, the average temperature of the chromosphere continuously decreases with height. This result disagrees with the fact that emission in chromospheric lines exists everywhere and all the time (Carlsson & Stein 1997; Curdt & Heinzel 1998; Kalkofen et al. 1999). The discrepancy might be solved by a multi-dimensional approach, but the difficulties connected with multi-dimensional time-dependent non-LTE modeling, namely extremely high computational requirements, do not allow us to represent the observed chromospheric structures directly this way (Carlsson & Leenaarts 2012). A review on radiation-hydrodynamic models of the solar atmosphere was recently published by Leenaarts (2020).
An alternative is the stationary approach, which uses time-averaged atmospheric parameters of 1D semi-empirical hydrostatic models. The energy flux of (magneto)acoustic waves is calculated from power spectra of Doppler velocities obtained during a time interval of several tens of minutes. It is a time-averaged quantity, which cannot be compared with instantaneously radiated energy but with time-averaged radiative losses derived from the semi-empirical models. This approach was used by Sobotka et al. (2016, hereafter Paper I) who, analyzing the velocities measured from the Ca II 854.2 nm line, showed that the acoustic energy flux deposited in the middle chromosphere provides a remarkable source of energy required to balance the local radiative losses.
Abbasvand et al. (2020, hereafter Paper II) recently introduced a new grid of semi-empirical 1D hydrostatic models, which were obtained by scaling the temperature and column mass of six initial models VAL A–F (Vernazza et al. 1981). This grid describes most of the solar features at moderate spatial resolution (1″), including both the quiet and active Sun, and enables us to scrutinize the hypothesis of chromospheric heating by acoustic and magneto-acoustic waves. Using the data analyzed already in Paper I, they also demonstrated that in the middle chromosphere, the contribution of the deposited (magneto)acoustic flux energy to the released radiative energy in the quiet Sun is approximately 30–50%. In a weak plage, it is 50–90%, and values above 70% correspond to locations where the magnetic field is inclined more than 50° with respect to the solar surface normal. The cadence of observations was 52 s, limiting the maximum detectable wave frequency to 9.6 mHz.
In Papers I and II, a single region on the Sun was examined using only one spectral line formed in the middle chromosphere. More regions have to be studied in several chromospheric lines to expand the range of heights in the chromosphere, arrive at plausible results, and to validate the working hypothesis. Therefore, in the present work, we set out to estimate the contribution of (magneto)acoustic waves to chromospheric heating by means of observations of three different, quiet and active, regions in combinations of three chromospheric lines Hα, Hβ, and Ca II 854.2 nm with a raster scan time of about 25 s. This cadence provides a maximum detectable wave frequency of approximately 20 mHz, making it possible to include also high-frequency waves.
2. Observations and data processing
2.1. Data sets
The observations were performed during three campaigns at two different instruments, both being long-slit scanning spectrographs: (1) the echelle spectrograph attached to the 70-cm German Vacuum Tower Telescope (VTT, Schröter et al. 1985; von der Lühe 1998), operating at the Observatorio del Teide, Tenerife, Spain – data sets on 2018 December 11 and 2019 June 6; (2) the Fast Imaging Solar Spectrograph (FISS, Chae et al. 2013) attached to the 1.6-m Goode Solar Telescope (GST, Cao et al. 2010) at the Big Bear Solar Observatory (BBSO), California, USA – data set on 2019 October 3.
The most important data set was obtained with FISS at GST in a service mode, because simultaneous observations of the spectral lines Ca II 854.2 nm and Hα make it possible to measure the deposited acoustic flux in the middle and in the upper chromosphere. The target was a quiet-Sun area located exactly at the center of the solar disk. Some small magnetic elements were dispersed in this area. The advantage of FISS is its high spectral and spatial resolution combined with short exposure times that facilitate fast scanning of the observed area on the Sun. The seeing was good and stable during the 80-min period of observation that was selected for further analysis. With the aid of the adaptive-optics system installed at GST, high-order correction of atmospheric seeing was provided within an isoplanatic patch, with a gradual roll off of the correction at larger distances (Shumko et al. 2014). Additional observations were taken with the Near Infra-Red Imaging Spectropolarimeter (NIRIS, Cao et al. 2012) to obtain information about the magnetic field. Due to some calibration issues, it was not possible to invert the spectropolarimetric data.
Two other data sets, obtained using the echelle spectrograph at VTT, allowed us to study only the upper chromosphere. The first one was acquired on 2018 December 11 and the second on 2019 June 6. In both cases, weak magnetic regions near disk center were scanned where weak chromospheric plages and small pores were present. The spectra were recorded simultaneously in the Hβ and Hα lines of neutral hydrogen. The seeing conditions were average during the data-acquisition period of 25 min on December 11 and good and stable during the 83-min period on June 6. The Kiepenheuer Adaptive Optics System (KAOS, von der Lühe et al. 2003) working at a wavelength of 500 nm indicated a Fried parameter of 5–6 cm on December 11 and 7–9 cm on June 6.
The raw data were calibrated using standard dark- and flat-field procedures and the FISS data were compensated for image rotation in the coudé focal plane of the telescope. In the December 11 VTT data set, the spatial sampling along the spectrograph slit is finer than the scanning step, so that the spatial pixels are rectangular. The relevant characteristics of all data sets are summarized in Table 1. Regions of interest (ROI) of all data sets in the continuum and Hα line center are displayed in Fig. 1.
 |
Fig. 1. Maps of continuum intensity (top) and Hα line-center intensity (bottom) corresponding to data sets of 2018 December 11 (left), 2019 June 6 (middle), and 2019 October 3 (right). |
Parameters of the VTT and BBSO data sets.
Additional polarimetric observations in the photospheric line Fe I 1564.9 nm were acquired on December 11 with the GREGOR Infrared Spectrograph (GRIS, Collados et al. 2012) attached to the 1.5-m telescope GREGOR (Schmidt et al. 2012) at the Observatorio del Teide. These polarimetric data were inverted with the Stokes inversion code based on response functions (Ruiz Cobo & del Toro Iniesta 1992). The spatial resolution of the resulting magnetic-field vector map was 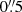 .
.
2.2. Data processing
The Doppler velocities were measured for two purposes: (1) to remove Doppler shifts from the spectroscopic observations to calculate time-averaged line profiles and (2) to obtain purely chromospheric Doppler velocities required for the calculation of acoustic fluxes. In both cases, we used the bisec_abs_lin.pro routine included in the Leibniz-Institut für Sonnenphysik (KIS) IDL library. This routine returns line shifts at pre-selected intensity levels in the line profile (a bisector calculation) and the shift of the line center, derived from a parabolic fit around the minimum intensity. The shifts were converted into the Doppler velocities assuming that the quiet-Sun regions within the field of view are at rest on average.
To remove Doppler shifts, we averaged bisector positions at five intensity levels from 40% to 70%, where 0% corresponded to the line-center intensity and 80% to the line-wing intensity near the continuum. The whole line profile was then moved back by the obtained average shift. To obtain the chromospheric velocities, we used the line-center shifts of Hα and Ca II 854.2 nm lines and bisector shifts of Hβ and Ca II at line-profile intensity levels corresponding respectively to wavelength distances of ±18 pm and ±13 pm from the line center, which were found from contribution functions (see Sect. 3.1).
Mean profiles of all spectral lines were obtained by time-averaging over the observing period of each series of the observed profiles with removed Doppler shifts. They were used to find the most appropriate semi-empirical models at each location in ROIs (Sect. 3.1).
The photospheric magnetic-field strength and inclination are necessary for the acoustic-flux calculation. Because this information was not available for two (June 6 and October 3) of the three data sets, we decided to retrieve it for all the data sets from an independent common source. The magnetic-field maps are a data product from the Helioseismic and Magnetic Imager (HMI, Schou et al. 2012) on board the Solar Dynamics Observatory (SDO, Pesnell et al. 2012). The HMI Vector Magnetic Field Pipeline (Hoeksema et al. 2014) obtains the magnetic-field vector from Stokes parameters. The Stokes parameters are measured at six wavelength positions across the Fe I 617.3 nm line for the full disk and are inverted using the Very Fast Inversion of the Stokes Vector code (VFISV, Borrero et al. 2011; Centeno et al. 2014). VFISV solves the radiative-transfer equation considering a Milne-Eddington atmosphere. The azimuth is disambiguated according to the existence of a strong field. In regions with strong magnetic field and their surroundings, a minimum-energy method is applied (Metcalf 1994; Leka et al. 2009). In regions with weak magnetic field, the azimuth that makes the magnetic-field vector more similar to the potential-field vector is selected. The inverted vector magnetic-field angular parameters, such as the azimuth and inclination, are referred to the line-of-sight (LOS) frame and they are converted to the local reference frame (LRF) using the AZAM code (Lites et al. 1995). The spatial resolution of HMI magnetic-field vector maps is 1″.
The HMI data sets were obtained on December 11 at 12:00 UT, June 6 at 11:24 UT, and October 3 at 18:12 UT and the full-disk maps of continuum intensity, magnetic-field strength, and inclination were cropped to match the ROIs. When the magnetic-field strength is low (|B| < 125 G in the case of HMI), the inversion code returns unreliable LOS inclinations θ ≈ 90° because of noisy Stokes Q and U signals. To remove these unreliable values, we applied a mask that set θ to zero in the regions where |B| was below this limit. Figure 2 shows the resulting masked maps of photospheric LRF inclination and maps of |B| in logarithmic scale for all data sets. The effect of masking was discussed in Paper II, where we showed that unreliable values of θ led to overestimated acoustic fluxes.
 |
Fig. 2. Maps of photospheric magnetic-field strength and inclination in the ROIs for December 11 (top), June 6 (middle), and October 3 (bottom). |
To align the spectroscopic observations with magnetic-field maps, we need to compare pores and granulation observed in VTT and GST continua (reference images) to those in HMI continuum images (transformed images). These features can be identified in both types of continuum images. The transformed an reference images are inputs for the following semi-automatic spatial alignment procedure.
First, a pair of co-temporal images is inspected visually by the routine setpts.pro (or setpts_roi.pro) implemented within the IDL SolarSoft System (SSW, Freeland & Handy 1998). The routine serves for an interactive definition of common points in two images. Then the set of reference points is used to calculate a linear transformation, which maps one image onto another, by the SSW function caltrans.pro. Finally, the initial transform parameters are entered into the SSW function auto_align_images.pro by T. Metcalf, which looks for the best spatial alignment of an image pair based on their cross-correlation. Five cross-alignment parameters, namely [x, y] shifts, [x, y] magnification factors, and rotation angle, which yield the maximum cross-correlation, are inferred in two subsequent calls of the function. In the first call, the downhill simplex method (Press et al. 1992), implemented as the amoeba.pro routine, is applied. Its results are used as initial parameters for the second call, using the more robust Powell method (Press et al. 1992). By this two-step procedure, a satisfactory spatial alignment between the co-temporal image pairs GST – HMI and VTT – HMI (June and December) are achieved with the cross-correlation coefficients of 0.90, 0.92 and 0.85, respectively.
3. The method
The applied method calculates the acoustic energy flux deposited in a chromospheric layer between two reference geometrical heights and compares it with radiative losses computed from model atmospheres and integrated over the same height range. The reference heights were determined with regard to typical formation heights of the observed spectral lines.
3.1. Model atmospheres
The initial semi-empirical models VAL A–F include the column mass m, optical depth τ500 at 500 nm, temperature T, microturbulent velocity υt, hydrogen density nH, electron density ne, total pressure Ptot, gas pressure Pg, and density ρ as a function of geometrical height h. To approximate the physical conditions in the ROIs, these initial models are scaled by changing two free parameters pT and pm that define the T and m stratifications (see Paper II, for details). These stratifications are used as inputs in the non-LTE radiative-transfer code based on the Multi-level Accelerated Lambda Iterations technique (MALI, Rybicki & Hummer 1991, 1992) with standard partial frequency redistribution (PRD). The hydrogen version of the code (with PRD in Lyman lines) computes the ionization structure and populations of hydrogen levels using a 5-level plus continuum atomic model. It re-computes the complete scaled atmospheric models and calculates synthetic profiles of the Hα and Hβ lines. As a next step, the calcium version of the MALI code (with PRD in the K and H lines) is used to get synthetic profiles of the Ca II 854.2 nm line. Again, a 5-level plus continuum atomic model is used. For each of the initial VAL models, a grid of 2806 scaled models is computed using a combination of 61 and 46 possible values of pT and pm, respectively. In total, a grid of 16836 models, parameterized by the initial model selection, pT, and pm, is available (Paper II).
The initial models were assigned to different areas in ROIs in accordance with the line-core intensity of the observed chromospheric lines. Then, a scaled model from the grid, which provided the best match of the synthetic to the local time-averaged observed profiles, was selected at each position within the ROIs. The best match means that the sum of squared differences between the synthetic and observed profiles of all lines under study (merit function) is at minimum.
The optimal selections of initial models for the ROIs of the December, June, and October data sets are VAL B–E, VAL C–F, and VAL C, respectively. Figure 3 shows the selection maps of the initial models in the ROIs of the December and June data sets. Finally, the December, June, and October ROIs are described by 482, 657, and 59 different scaled models, respectively.
 |
Fig. 3. Initial models for December 11 (left) and June 6 (right). The October 3 data set has only one initial model, VAL C. |
Physical quantities, which are used to calculate acoustic fluxes, are retrieved from the models at reference heights that are common for all models in a ROI. These heights also delimit integration ranges of radiative losses. The reference heights are selected with regard to formation heights of the observed spectral lines, properly speaking, formation heights of parts of line profiles utilized to measure Doppler velocities. The formation heights can be obtained from a contribution function Cν(h), which describes the contribution of different atmospheric layers to the emergent intensity of radiation Iν at the considered frequency ν (e.g., Gurtovenko et al. 1974),
In the scaled models, Cν(h) of Hα, Hβ and Ca II 854.2 nm lines were computed by the non-LTE radiative-transfer codes described above. Contribution functions computed from two typical models that characterize the quiet Sun (October data set) and bright chromospheric features (December and June data sets) are plotted for different wavelength distances Δλ from the line center and different heights h in Fig. 4. We can see that the central parts of line profiles are formed largely in the chromosphere, each of them in different ranges of heights.
 |
Fig. 4. Contribution functions of the Hα, Hβ, and Ca II 854.2 nm lines for two typical models derived from our observations – quiet Sun (left) and bright chromospheric features (right). The colors change from light orange to black with increasing values of the contribution function. Black lines show corresponding synthetic line profiles. |
The typical formation height can be calculated as a mean h weighted by Cν(h) at a given Δλ. We obtained typical formation heights using all models in each ROI and found the most frequent ones. The Hα line center is formed typically at 1800 km in the quiet-Sun atmosphere and at 1900 km in bright chromospheric features. For the Ca II 854.2 nm line in the quiet Sun, the typical formation height of the line center is 1400 km and the inner wings at Δλ = ±13 pm are formed at 1000 km. From contribution functions computed at this Δλ for each pixel in the October ROI we find that only 4% of pixels have a contribution from the photosphere, which, however, is smaller than 1%. The Hβ line is more problematic. Its inner wings at Δλ = ±18 pm are formed typically at 1600 km in bright chromospheric features (Fig. 4) but 18% of pixels in the December and June ROIs have photospheric contributions larger than 20% at this wavelength. The selection of Δλ for Hβ and Ca II was intended to reach the deepest possible chromospheric layers with a minimum contribution from the photosphere. The most frequent typical formation heights, stated above, were accepted as the reference heights for the calculation of radiative losses and deposited acoustic fluxes.
The scatter of typical formation heights around the reference height is characterized by standard deviations of 20 km in the middle and upper chromosphere of the quiet-Sun region (October 3 data set, Ca II and Hα) and 100 km in the upper chromosphere of weak active regions with a wide variety of models (December 11 and June 6 data sets, Hβ and Hα). Although the latter value is large, it does not introduce any error into physical quantities and radiative losses computed from the models, because they refer to fixed reference heights. The difficulty arises in Doppler velocities, which are sometimes measured at heights different from the reference ones. We analyzed root-mean-squared (rms) Doppler velocities συ measured at different Δλ, corresponding to the formation-height uncertainty of ±100 km, in the Hα and Hβ profiles of the December and June data sets. The relative difference Δσυ/συ was approximately of 7% in the central parts of profiles formed purely in the chromosphere and increased by a factor of two at Δλ with photospheric contribution. Because the acoustic energy flux is proportional to 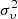 , its relative error was estimated to
, its relative error was estimated to 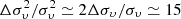 % and 30%, respectively. For the October 3 data set, the relative error of the acoustic flux is 3%.
% and 30%, respectively. For the October 3 data set, the relative error of the acoustic flux is 3%.
The net radiative cooling rates (radiative losses) characterize the energy released by radiation from the chromosphere. These also indicate the amount of non-radiative heating that maintains the semi-empirical temperature at a given height in the solar atmosphere. To calculate them, we used the scaled models assigned to each pixel in a ROI. For each model, they were computed for the main contributors in the solar chromosphere, namely, the lines Ca II H&K, the Ca II infrared triplet, Mg II h&k, hydrogen Lyman and Balmer lines, and hydrogen continua, using our non-LTE radiative transfer codes MALI. The total net radiative cooling rates, a sum of the main contributors, were integrated over the geometrical height in the range between the reference heights for each pixel in the ROIs.
3.2. Deposited acoustic flux
Oscillations at each position in the ROIs were studied using standard Fourier analysis of the time series of Doppler maps measured in the line centers of Hα and Ca II 854.2 nm and at Δλ = ±18 pm and Δλ = ±13 pm from the line centers of Hβ and Ca II 854.2 nm, respectively. The cadence of the time series was around 25 s and thus the maximum detectable frequency 20 mHz was sufficient to investigate the power spectra of velocity oscillations in the quiet-Sun and magnetic regions in the chromosphere. The method of power-spectra calculation and calibration in absolute units is described by Rieutord et al. (2010).
The acoustic-energy flux at a given height in the chromosphere was estimated following the method of Bello González et al. (2009), assuming that (i) the acoustic waves propagate upward and (ii) the inclination of magnetic field along the track of acoustic waves is equal to that measured in the photosphere. It can be formulated as
where ρ is the gas density at the given height, Pυ the spectral-power density derived from the Doppler velocities, and TF(ν) is a transfer function of the atmosphere. The transfer function relates to the transmission of the wave amplitudes by the solar atmosphere as a function of frequency. It is proportional to the ratio of the velocity amplitude observable as a Doppler shift of the given line to the true amplitude. Its value is unity if the entire wave signal is observed as the Doppler shift of the spectral line throughout the atmosphere at a given frequency, whereas values smaller than unity represent some loss of the signal because of the extent in height of the spectral-line contribution functions. In general, the most affected are short-period (small-scale) fluctuations. A detailed time-dependent model of the atmosphere is needed to derive this value. We set this function equal to unity for all frequencies, which means that the observed Doppler signal of all waves at a given frequency is detected throughout the solar atmosphere (see Paper I). This rough approximation may lead to underestimated acoustic-flux values at higher frequencies.
The group velocity for vertical energy transportation υgr is given by
where νac = γg cos θ/(4πcs) is the acoustic cut-off frequency and 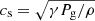 the sound speed. Here, γ is the adiabatic index equal to 5/3 for monoatomic gas, g the surface gravity, and θ the magnetic-field inclination in the photosphere, which reduces the acoustic cut-off frequency (Cally 2006). For νac we adopt the value 5.2 cos θ mHz. The total acoustic flux at all frequencies between νac and the maximum detectable frequency νmax is
the sound speed. Here, γ is the adiabatic index equal to 5/3 for monoatomic gas, g the surface gravity, and θ the magnetic-field inclination in the photosphere, which reduces the acoustic cut-off frequency (Cally 2006). For νac we adopt the value 5.2 cos θ mHz. The total acoustic flux at all frequencies between νac and the maximum detectable frequency νmax is
The values of gas pressure Pg and density ρ are taken in each pixel of the ROIs from the corresponding scaled model atmosphere at two reference heights h1 and h2. The deposited acoustic flux ΔFac is the difference between the incoming acoustic energy flux at the lower reference height h1 and the outgoing one at the upper reference height h2,
A part of the incoming energy flux is dissipated in the chromosphere between h1 and h2 and likely converted into radiation, while the outgoing part continues to propagate higher in the atmosphere.
4. Results
The best-matching semi-empirical models (see Sect. 3.1) were assigned to all positions in ROIs of all data sets. Then the deposited acoustic fluxes were calculated for each position. The most important input parameters for the ΔFac calculation are the Doppler velocity amplitudes, gas densities and pressures at the reference heights, and the magnetic-field inclination (Fig. 2). Table 2 gives an overview of the first three quantities, where the velocity magnitudes are represented by the rms Doppler velocity and the gas densities and pressures by their mean values and standard deviations obtained by averaging over the corresponding ROIs.
Reference heights href, rms Doppler velocities συ, mean densities ⟨ρ⟩, and mean gas pressures ⟨Pg⟩ at the reference heights.
4.1. October 3 data set – quiet Sun
The data set acquired on 2019 October 3 with the GST/FISS instrument includes a quiet-Sun region at the center of the solar disk. The lines Ca II 854.2 nm and Hα provide the information about two different ranges of heights, 1000–1400 km (middle chromosphere) and 1400–1800 km (upper chromosphere) – see Sect. 3.1. In the quiet-Sun atmosphere, the reference heights for the Ca II wing, Ca II center, and Hα center are 1000, 1400, and 1800 km, respectively. The deposited acoustic fluxes ΔFac and the total integrated radiative losses L are computed for those height ranges.
The frequency distribution of the deposited acoustic-flux density spatially averaged over the magnetic (|B|> 125 G, 11.6% of ROI) and non-magnetic (|B| < 125 G, magnetic inclination set to zero, 88.4% of ROI) areas is displayed in Fig. 5 for the two height ranges. The maximum contribution in non-magnetic areas is at 6–7 mHz and for frequencies higher than 14 mHz, the contribution is by an order of magnitude smaller than the maximum one. The presence of inclined magnetic fields adds a substantial contribution at frequencies below 5.2 mHz, increasing the total deposited acoustic fluxes in the middle and upper chromosphere by a factor of 2.3.
 |
Fig. 5. Frequency distribution of the deposited acoustic-flux density averaged over magnetic (red) and non-magnetic (black) areas of the October 3 data set. MC and UC lines correspond to the height ranges 1000–1400 km (middle chromosphere) and 1400–1800 km (upper chromosphere), respectively. |
The maps of the deposited acoustic flux and total integrated radiative losses are displayed in Fig. 6. The scatter and density (2D histogram) plots of the ΔFac to L pixel-by-pixel comparison are shown in Fig. 7. The spatial distribution of ΔFac is strongly intermittent, as already noted by Bello González et al. (2010b), and we observe a large scatter of ΔFac versus L. For this reason, we have to analyze the contribution of the deposited acoustic flux to radiative losses statistically, using the mean, median, and standard deviation of ΔFac. These statistical values were calculated in 100 W m−2 wide bins of the L histogram and each bin had to contain at least 50 points. In Fig. 7 left, the red and green solid lines represent the bin-averaged 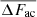 and median values, respectively, and the red dashed lines set the boundaries of the ±1σ range that characterize the scatter of individual points in each bin. In the density plots (Fig. 7 right), pixels of magnetic and non-magnetic areas are separated and their densities are normalized to the common histogram maximum of the two areas. The bin size of the 2D histogram is 30 W m−2 × 30 W m−2. Contours are plotted at four density levels with a step of one order of magnitude, beginning at 0.03% of the maximum.
and median values, respectively, and the red dashed lines set the boundaries of the ±1σ range that characterize the scatter of individual points in each bin. In the density plots (Fig. 7 right), pixels of magnetic and non-magnetic areas are separated and their densities are normalized to the common histogram maximum of the two areas. The bin size of the 2D histogram is 30 W m−2 × 30 W m−2. Contours are plotted at four density levels with a step of one order of magnitude, beginning at 0.03% of the maximum.
 |
Fig. 6. Deposited acoustic energy flux (left) and the total integrated radiative losses (right) in the ROI of the October 3 data set. Top: h = 1000–1400 km (middle chromosphere), bottom: h = 1400–1800 km (upper chromosphere). |
In the middle chromosphere, the total radiative losses integrated over the 400 km thick layer are 1000 < L < 2600 W m−2 in the quiet area and reach 4300 W m−2 in two bright points connected with magnetic elements (bottom panels in Fig. 2 and right panels in Fig. 6). The ratio of the mean deposited acoustic flux to the radiative losses 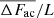 is between 0.9 and 1.3 in the quiet area, so that the acoustic energy flux balances the energy released by radiation (top panels in Fig. 7). However, the contribution of
is between 0.9 and 1.3 in the quiet area, so that the acoustic energy flux balances the energy released by radiation (top panels in Fig. 7). However, the contribution of  to L in the two bright points is only 60%.
to L in the two bright points is only 60%.
 |
Fig. 7. Left: scatter plots of total integrated radiative losses versus deposited acoustic flux in the ROI of the October 3 data set. Top: h = 1000–1400 km, bottom: h = 1400–1800 km. Solid lines show average (red) and median (green) values together with red dashed lines of ±1σ. Right: density contours of the scatter plots. Contours for magnetic (red) and non-magnetic (black) areas are plotted separately at density levels of 0.03, 0.3, 3, and 30% of a common density maximum. Straight dashed lines represent the full balance of radiative losses by acoustic-flux deposit. |
In the upper chromosphere at the heights 1400–1800 km, the radiative losses (400 < L < 1900 W m−2) are larger than the deposited acoustic flux for all the points in the scatter plot (bottom panels in Fig. 7) and 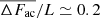 . This means that the deposited acoustic flux is insufficient to balance the radiative losses and maintain the semi-empirical temperature at these heights. Negative values of ΔFac appearing at some scarce locations in the ROI are caused by the limited accuracy of our method (see Sect. 3.1).
. This means that the deposited acoustic flux is insufficient to balance the radiative losses and maintain the semi-empirical temperature at these heights. Negative values of ΔFac appearing at some scarce locations in the ROI are caused by the limited accuracy of our method (see Sect. 3.1).
To estimate the fraction of the incoming acoustic energy flux Fh1 = Fac, tot(h1) deposited in a layer between the reference heights h1 and h2, we use spatially-averaged values of Fh1 and ΔFac in the magnetic and non-magnetic areas in the ROI. The results are shown in Table 3 together with the corresponding spatially averaged values L of the total integrated radiative losses and the ratio ΔFac/L. Standard deviations characterize a large scatter of values corresponding to individual pixels in these areas. The incoming acoustic flux at 1000 km is by a factor of 2.4 larger in the magnetic area than in the non-magnetic one. In both types of areas, 90% of the incoming flux is deposited between the heights 1000–1400 km, which is sufficient to balance the radiative losses. A fraction of 0.6–0.7 of the remaining 10% of the acoustic flux passing through the height of 1400 km is deposited below 1800 km, but its contribution to the radiative losses is small. Acoustic fluxes of 200 W m−2 in the magnetic area and 70 W m−2 in the non-magnetic one pass to layers above 1800 km.
October 3 data set: spatial averages of incoming acoustic flux Fh1, its part ΔFac deposited between the reference heights h1 and h2, and corresponding radiative losses L.
4.2. December 11 and June 6 data sets – weak active regions
Two weak active regions including plages and small pores were observed on 2018 December 11 and 2019 June 6 with the VTT echelle spectrograph in the hydrogen lines Hα and Hβ (see Sect. 2). The Doppler velocities observed in the line center of Hα (reference height 1900 km in active regions, see Sect. 3.1) and at the distance Δλ = ±18 pm from the line center of Hβ (reference height 1600 km) were used to calculate acoustic energy fluxes (Sect. 3.2).
The amplitudes of Hβ velocities are quite small in comparison with the other chromospheric lines (see Table 2). This results in very small mean incoming acoustic fluxes Fac, tot(1600 km), which, however, differ for the December and June data sets, being equal to 40 and 15 W m−2, respectively. This difference can be explained by different frequency distributions plotted in Fig. 8. On June 6, the shape of the frequency distribution is similar to that on October 3 (Fig. 5), while the December 11 data exhibit significant contributions at frequencies in the ranges 1–5 mHz (thanks to the large fraction of magnetised area) and 8–20 mHz, induced probably by seeing, which was not sufficiently good during the December 11 run.
 |
Fig. 8. Frequency distribution of the incoming acoustic-flux density at h1 = 1600 km averaged over the whole ROIs (magnetic plus non-magnetic areas) of December 11 (blue) and June 6 (black). |
The deposited acoustic fluxes ΔFac and total integrated radiative losses L are computed and integrated for the range h = 1600–1900 km in the upper chromosphere. The maps of ΔFac and L for both ROIs are displayed in Fig. 9. Enhanced radiative losses on the order of 104 W m−2 are observed in the central part of the plage on June 6. This area is characterized by hot atmospheric models, obtained by scaling the initial model VAL F (see Fig. 3), for which a strong contribution of hydrogen Lyman-α to L at h > 1800 km becomes important.
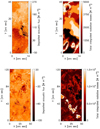 |
Fig. 9. Deposited acoustic energy flux (left) and the total integrated radiative losses (right) for the range h = 1600–1900 km (upper chromosphere) in the ROIs of December 11 (top) and June 6 (bottom). |
The scatter and density plots comparing ΔFac and L for both ROIs are shown in Fig. 10. The mean, median, and standard deviation of the deposited acoustic flux were calculated in the same way as in Sect. 4.1. For all plotted points, the deposited acoustic flux is mostly in the range from −50 W m−2 to 150 W m−2 and it is very small compared to the radiative losses. Its mean values are approximately 30 W m−2 for the December 11 data set and zero for the June 6 one. The small positive mean value of the December flux is a consequence of the high-frequency contribution induced probably by the seeing. In the density plots, magnetic and non-magnetic areas are distinguished. The densities were calculated and the contour levels were set in the same way as for the October 3 data set (Sect. 4.1). The magnetic areas of the December and June data sets include 33.0% and 3.9% of pixels in the ROIs, respectively.
 |
Fig. 10. Left: scatter plots of total integrated radiative losses versus deposited acoustic flux for the range h = 1600–1900 km in the ROIs of December 11 (top) and June 6 (bottom). Solid lines show average (red) and median (green) values together with red dashed lines of ±1σ. Right: density contours of the scatter plots. Contours for magnetic (red) and non-magnetic (black) areas are plotted separately at density levels of 0.03, 0.3, 3, and 30% of a common density maximum. |
A co-temporal measurement of the magnetic-field vector obtained with GRIS at the GREGOR telescope (Sect. 2.1) was used alternatively to re-compute the deposited acoustic fluxes of the December 11 data set. Because the spatial resolution of the GRIS magnetic-inclination map was by a factor of two better than that of HMI, the scatter of ΔFac values was reduced but the mean and median values did not change.
Thus, the contribution of the deposited acoustic flux to the radiative losses is practically zero in the layer between h = 1600–1900 km. This confirms the finding of Sect. 4.1 that ΔFac cannot balance L in the upper chromosphere. We expect that the scatter of deposited acoustic-flux values around zero in the December and June data sets is caused by a limited accuracy in the determination of incoming and outgoing acoustic fluxes. The fact that Doppler velocities are sometimes measured at heights different from the reference ones (Sect. 3.1), introduces the relative error of 15% in both quantities. Moreover, when the inner wings of Hβ are affected by a photospheric contribution, the error of the incoming acoustic flux increases to 30%.
5. Discussion and conclusions
We studied the dissipation of (magneto)acoustic waves through different layers of the solar chromosphere using the VTT/echelle spectrograph and GST/FISS multi-line observations in Hα, Hβ and Ca II 854.2 nm. The deposited acoustic energy fluxes were quantitatively compared with the total radiative losses in quiet-Sun and weak active regions in the central zone of the solar disk.
We utilized time series of Doppler velocities measured in the line centers and wings (see Sect. 3.2) to derive the deposited acoustic fluxes. The maximum detectable frequency of waves was 20 mHz. The calculation of radiative losses was based on a set of non-LTE 1D hydrostatic semi-empirical models assigned to different positions in the ROIs according to the best match of synthetic profiles to time-averaged observed profiles. The models were obtained by scaling the temperatures and column masses of the initial models VAL B–F.
We have demonstrated that the radiative losses can be fully balanced by the deposited acoustic energy flux in the middle chromosphere (h = 1000–1400 km) of a quiet-Sun region observed in the October 3 data set. Seemingly, this contradicts the result of Paper II, stating that the deposited acoustic flux contributes to the radiative losses only by 30–50% in quiet areas. The discrepancy can be explained by the fact that the area considered as quiet Sun in Paper II was close to a plage and fell within its extended canopy region. Thus, the effect of magnetic shadows (Vecchio et al. 2007; Kontogiannis et al. 2010), related to the elevated magnetic field of the canopy, reduced the oscillatory power and the deposited acoustic flux. The quiet-Sun region studied in the current work was far from any plage or pore, so that the propagation of waves in the chromosphere was less affected by canopy fields.
Radiative losses L > 4000 W m−2 in small bright chromospheric features related to magnetic elements in the quiet region were larger than the deposited acoustic flux by a factor of 1.7 on average. The enhancement of deposited acoustic flux at frequencies below 5.2 mHz in moderately inclined magnetic field of these features did not compensate the energy released by radiation.
We have also shown that in the upper chromosphere, the incoming and deposited acoustic fluxes are very small compared to the radiative losses. In quiet-Sun region, the acoustic-flux deposit contributes only by about 20% to the radiative losses between the heights 1400 km and 1800 km and in the weak active regions (data sets of December 11 and June 6), its contribution is practically equal to zero in the range 1600–1900 km.
This finding may be explained by the fact that the acoustic energy flux at a given height is proportional to the density of gas ρ, power density of Doppler velocities Pυ, and the group velocity υgr (Eq. (2)). Of these three quantities, the change of ρ with height is the most important one. Densities in the middle chromosphere are by an order of magnitude higher than those in the upper chromosphere, while 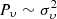 is approximately of the same order (see Table 2) and υgr (Eq. (3)) may change by a factor of three at maximum. Thus, it is mainly the density that determines the amounts of the incoming and deposited acoustic fluxes, which are considerable in the middle chromosphere (h = 1000–1400 km) but negligible in the upper layers.
is approximately of the same order (see Table 2) and υgr (Eq. (3)) may change by a factor of three at maximum. Thus, it is mainly the density that determines the amounts of the incoming and deposited acoustic fluxes, which are considerable in the middle chromosphere (h = 1000–1400 km) but negligible in the upper layers.
We can conclude that the acoustic energy flux is efficiently deposited in the middle chromosphere, where the density of gas is sufficiently high. The deposited acoustic flux is a major contributor to the radiative losses of this layer in quiet-Sun regions and in plages (see Paper II). However, the energy transported by (magneto)acoustic waves can be reduced by magnetic shadows of canopy regions around plages and pores. In the upper chromosphere, the incoming – and thus deposited – acoustic flux cannot balance the radiative losses, which can be large in active regions thanks to the radiation in the hydrogen Lyman-α line formed at the top of the chromosphere. This means that other heating mechanisms have to act in the upper chromosphere.
We would like to emphasize that our results are not inconsistent with the previous studies, where many (e.g., Fossum & Carlsson 2005; Beck et al. 2009, or see a thorough discussion in Sect. 4.1 of Jess et al. 2015) showed that the (magneto)acoustic waves are not sufficient to explain the heating of the chromosphere. In the present work we only studied two separate layers of the chromosphere available to us in our observations. We have no information about the relations between the deposited acoustic flux and radiative losses in the lower chromosphere. Thus, we do not attempt to draw any conclusions regarding the energy budget of the chromosphere as a whole. We point out that for some layers the heating by (magneto)acoustic waves may be sufficient, whereas in other layers it is insufficient. This fact itself draws a need for an additional source of energy. It is interesting to note that a similar conclusion was drawn by Fawzy et al. (2002) in the case of chromospheres of six late-type main-sequence stars, for which high-quality spectroscopic observations were available.
We are aware that our stationary approach (time-averaged acoustic fluxes and 1D semi-empirical models) is only a rough approximation to the real time-dependent physical conditions in the chromosphere. For this reason, we consider as meaningful just the statistical comparison of the deposited acoustic fluxes to the radiative losses, trying to provide a general estimate of the role of (magneto)acoustic waves in the heating of long-lived chromospheric structures.
Acknowledgments
We thank the anonymous referee for valuable comments and suggestions. This work was supported by the Czech Science Foundation and Deutsche Forschungsgemeinschaft under the common grant 18-08097J—DE 787/5-1 and the institutional support ASU:67985815 of the Czech Academy of Sciences. The observations were partly supported by the project SOLARNET that has received funding from the European Union Horizon 2020 research and innovation programme under grant agreement no. 824135 and by the Czech Science Foundation grant 18-06319S. J.K. acknowledges the project VEGA 2/0048/20, M.G.R. the Charles University project GA UK No. 204119, and D.K. the project GA UK No. 532217. BBSO operation is supported by the New Jersey Institute of Technology and US NSF AGS-1821294 grant. GST operation is partly supported by the Korea Astronomy and Space Science Institute, the Seoul National University, and the Key Laboratory of Solar Activities of Chinese Academy of Sciences (CAS) and the Operation, Maintenance and Upgrading Fund of CAS for Astronomical Telescopes and Facility Instruments. We are grateful to N. Gorceix, C. Plymate, J. Varsik, and the BBSO staff for operating the instrument, observing the data, and performing the basic data reduction. The 1.5-m GREGOR solar telescope was built by a German consortium under the leadership of the Leibniz-Institut für Sonnenphysik in Freiburg (KIS) with the Leibniz-Institut für Astrophysik Potsdam (AIP), the Institut für Astrophysik Göttingen, the Max-Planck-Institut für Sonnensystemforschung in Göttingen (MPS) as partners, and with contributions by the Instituto de Astrofísica de Canarias (IAC) and the Astronomical Institute of the Czech Academy of Sciences. The Vacuum Tower Telescope at the Spanish Observatorio del Teide of IAC is operated by the German consortium of KIS, AIP, and MPS.
References
- Abbasvand, V., Sobotka, M., Heinzel, P., et al. 2020, ApJ, 890, 22 [Google Scholar]
- Aschwanden, M. J. 2001, ApJ, 560, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, C., Khomenko, E., Rezaei, R., & Collados, M. 2009, A&A, 507, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bel, N., & Leroy, B. 1977, A&A, 55, 239 [NASA ADS] [Google Scholar]
- Bello González, N., Flores Soriano, M., Kneer, F., & Okunev, O. 2009, A&A, 508, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Flores Soriano, M., Kneer, F., Okunev, O., & Shchukina, N. 2010a, A&A, 522, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Franz, M., Martínez Pillet, V., et al. 2010b, ApJ, 723, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Borrero, J. M., Tomczyk, S., Kubo, M., et al. 2011, Sol. Phys., 273, 267 [Google Scholar]
- Cally, P. S. 2006, Phil. Trans. R. Soc. London Ser. A, 364, 333 [Google Scholar]
- Cao, W., Gorceix, N., Coulter, R., et al. 2010, Astron. Nachr., 331, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, W., Goode, P. R., Ahn, K., et al. 2012, ASP Conf. Ser., 463, 291 [Google Scholar]
- Carlsson, M., & Leenaarts, J. 2012, A&A, 539, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M., & Stein, R. F. 1992, ApJ, 397, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., & Stein, R. F. 1995, ApJ, 440, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., & Stein, R. F. 1997, ApJ, 481, 500 [Google Scholar]
- Carlsson, M., De Pontieu, B., & Hansteen, V. H. 2019, ARA&A, 57, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., Schou, J., Hayashi, K., et al. 2014, Sol. Phys., 289, 3531 [Google Scholar]
- Chae, J., Park, H.-M., Ahn, K., et al. 2013, Sol. Phys., 288, 1 [Google Scholar]
- Collados, M., López, R., Páez, E., et al. 2012, Astron. Nachr., 333, 872 [Google Scholar]
- Cuntz, M., Rammacher, W., & Musielak, Z. E. 2007, ApJ, 657, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Curdt, W., & Heinzel, P. 1998, ApJ, 503, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Fawzy, D., Ulmschneider, P., Stȩpień, K., Musielak, Z. E., & Rammacher, W. 2002, A&A, 386, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fossum, A., & Carlsson, M. 2005, Nature, 435, 919 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Freeland, S. L., & Handy, B. N. 1998, Sol. Phys., 182, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Gurtovenko, E., Ratnikova, V., & de Jager, C. 1974, Sol. Phys., 37, 43 [CrossRef] [Google Scholar]
- Hoeksema, J. T., Liu, Y., Hayashi, K., et al. 2014, Sol. Phys., 289, 3483 [Google Scholar]
- Jefferies, S. M., McIntosh, S. W., Armstrong, J. D., et al. 2006, ApJ, 648, L151 [Google Scholar]
- Jess, D. B., Morton, R. J., Verth, G., et al. 2015, Space Sci. Rev., 190, 103 [Google Scholar]
- Kalkofen, W., Ulmschneider, P., & Avrett, E. H. 1999, ApJ, 521, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Kayshap, P., Murawski, K., Srivastava, A. K., Musielak, Z. E., & Dwivedi, B. N. 2018, MNRAS, 479, 5512 [NASA ADS] [CrossRef] [Google Scholar]
- Kontogiannis, I., Tsiropoula, G., & Tziotziou, K. 2010, A&A, 510, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kontogiannis, I., Tsiropoula, G., & Tziotziou, K. 2014, A&A, 567, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kontogiannis, I., Tsiropoula, G., & Tziotziou, K. 2016, A&A, 585, A110 [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J. 2020, Liv. Rev. Sol. Phys., 17, 3 [CrossRef] [Google Scholar]
- Leka, K. D., Barnes, G., Crouch, A. D., et al. 2009, Sol. Phys., 260, 83 [Google Scholar]
- Lites, B. W., Low, B. C., Martinez Pillet, V., et al. 1995, ApJ, 446, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalf, T. R. 1994, Sol. Phys., 155, 235 [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN. The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Rabin, D., & Moore, R. 1984, ApJ, 285, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M., Roudier, T., Rincon, F., et al. 2010, A&A, 512, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1992, A&A, 262, 209 [NASA ADS] [Google Scholar]
- Schmidt, W., von der Lühe, O., Volkmer, R., et al. 2012, Astron. Nachr., 333, 796 [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Schröter, E. H., Soltau, D., & Wiehr, E. 1985, Vist. Astron., 28, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Shumko, S., Gorceix, N., Choi, S., et al. 2014, Proc. SPIE, 9148, 914835 [CrossRef] [Google Scholar]
- Sobotka, M., Heinzel, P., Švanda, M., et al. 2016, ApJ, 826, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Stangalini, M., Del Moro, D., Berrilli, F., & Jefferies, S. M. 2011, A&A, 534, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Testa, P., De Pontieu, B., Allred, J., et al. 2014, Science, 346, 1255724 [NASA ADS] [CrossRef] [Google Scholar]
- Ulmschneider, P., & Musielak, Z. 2003, ASP Conf. Ser., 286, 363 [Google Scholar]
- Vecchio, A., Cauzzi, G., Reardon, K. P., Janssen, K., & Rimmele, T. 2007, A&A, 461, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [Google Scholar]
- von der Lühe, O. 1998, New Astron. Rev., 42, 493 [Google Scholar]
- von der Lühe, O., Soltau, D., Berkefeld, T., & Schelenz, T. 2003, Proc. SPIE, 4853, 187 [Google Scholar]
- Withbroe, G. L., & Noyes, R. W. 1977, ARA&A, 15, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Zaqarashvili, T. V., & Erdélyi, R. 2009, Space Sci. Rev., 149, 355 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Reference heights href, rms Doppler velocities συ, mean densities ⟨ρ⟩, and mean gas pressures ⟨Pg⟩ at the reference heights.
October 3 data set: spatial averages of incoming acoustic flux Fh1, its part ΔFac deposited between the reference heights h1 and h2, and corresponding radiative losses L.
All Figures
 |
Fig. 1. Maps of continuum intensity (top) and Hα line-center intensity (bottom) corresponding to data sets of 2018 December 11 (left), 2019 June 6 (middle), and 2019 October 3 (right). |
| In the text | |
 |
Fig. 2. Maps of photospheric magnetic-field strength and inclination in the ROIs for December 11 (top), June 6 (middle), and October 3 (bottom). |
| In the text | |
 |
Fig. 3. Initial models for December 11 (left) and June 6 (right). The October 3 data set has only one initial model, VAL C. |
| In the text | |
 |
Fig. 4. Contribution functions of the Hα, Hβ, and Ca II 854.2 nm lines for two typical models derived from our observations – quiet Sun (left) and bright chromospheric features (right). The colors change from light orange to black with increasing values of the contribution function. Black lines show corresponding synthetic line profiles. |
| In the text | |
 |
Fig. 5. Frequency distribution of the deposited acoustic-flux density averaged over magnetic (red) and non-magnetic (black) areas of the October 3 data set. MC and UC lines correspond to the height ranges 1000–1400 km (middle chromosphere) and 1400–1800 km (upper chromosphere), respectively. |
| In the text | |
 |
Fig. 6. Deposited acoustic energy flux (left) and the total integrated radiative losses (right) in the ROI of the October 3 data set. Top: h = 1000–1400 km (middle chromosphere), bottom: h = 1400–1800 km (upper chromosphere). |
| In the text | |
 |
Fig. 7. Left: scatter plots of total integrated radiative losses versus deposited acoustic flux in the ROI of the October 3 data set. Top: h = 1000–1400 km, bottom: h = 1400–1800 km. Solid lines show average (red) and median (green) values together with red dashed lines of ±1σ. Right: density contours of the scatter plots. Contours for magnetic (red) and non-magnetic (black) areas are plotted separately at density levels of 0.03, 0.3, 3, and 30% of a common density maximum. Straight dashed lines represent the full balance of radiative losses by acoustic-flux deposit. |
| In the text | |
 |
Fig. 8. Frequency distribution of the incoming acoustic-flux density at h1 = 1600 km averaged over the whole ROIs (magnetic plus non-magnetic areas) of December 11 (blue) and June 6 (black). |
| In the text | |
 |
Fig. 9. Deposited acoustic energy flux (left) and the total integrated radiative losses (right) for the range h = 1600–1900 km (upper chromosphere) in the ROIs of December 11 (top) and June 6 (bottom). |
| In the text | |
 |
Fig. 10. Left: scatter plots of total integrated radiative losses versus deposited acoustic flux for the range h = 1600–1900 km in the ROIs of December 11 (top) and June 6 (bottom). Solid lines show average (red) and median (green) values together with red dashed lines of ±1σ. Right: density contours of the scatter plots. Contours for magnetic (red) and non-magnetic (black) areas are plotted separately at density levels of 0.03, 0.3, 3, and 30% of a common density maximum. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.