| Issue |
A&A
Volume 642, October 2020
|
|
|---|---|---|
| Article Number | A222 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202038216 | |
| Published online | 23 October 2020 | |
Sulphur and carbon isotopes towards Galactic centre clouds★
1
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
e-mail: phumire@mpifr-bonn.mpg.de
2
Department of Astronomy, King Abdulaziz University,
PO Box 80203,
Jeddah
21589, Saudi Arabia
3
Xinjiang Astronomical Observatory, Chinese Academy of Sciences,
830011
Urumqi,
PR China
4
Institut des Sciences Moléculaires (ISM), CNRS, Univ. Bordeaux, 351 cours de la Libération,
33400
Talence, France
5
Institute for Astrophysical Research, 725 Commonwealth Avenue, Boston University Boston,
MA
02215, USA
6
Laboratoire d’astrophysique de Bordeaux, CNRS, Univ. Bordeaux, B18N, allée Geoffroy Saint-Hilaire,
33615
Pessac, France
7
Argelander-Institut für Astronomie, Universität Bonn,
Auf dem Hügel 71,
53121
Bonn, Germany
Received:
20
April
2020
Accepted:
30
August
2020
Context. Measuring isotopic ratios is a sensitive technique used to obtain information on stellar nucleosynthesis and chemical evolution.
Aims. We present measurements of the carbon and sulphur abundances in the interstellar medium of the central region of our Galaxy. The selected targets are the +50 km s−1 Cloud and several line-of-sight clouds towards Sgr B2(N).
Methods. Towards the +50 km s−1 Cloud, we observed the J = 2–1 rotational transitions of 12C32S, 12C34S, 13C32S, 12C33S, and 13C34S, and the J = 3–2 transitions of 12C32S and 12C34S with the IRAM-30 m telescope, as well as the J = 6–5 transitions of 12C34S and 13C32S with the APEX 12 m telescope, all in emission. The J = 2–1 rotational transitions of 12C32S, 12C34S, 13C32S, and 13C34S were observed with ALMA in the envelope of Sgr B2(N), with those of 12C32S and 12C34S also observed in the line-of-sight clouds towards Sgr B2(N), all in absorption.
Results. In the +50 km s−1 Cloud we derive a 12C/13C isotopic ratio of 22.1−2.4+3.3, that leads, with the measured 13C32S/12C34S line intensity ratio, to a 32S/34S ratio of 16.3−2.4+3.0. We also derive the 32S/34S isotopic ratio more directly from the two isotopologues 13C32S and 13C34S, which leads to an independent 32S/34S estimation of 16.3−1.7+2.1 and 17.9 ± 5.0 for the +50 km s−1 Cloud and Sgr B2(N), respectively. We also obtain a 34S/33S ratio of 4.3 ± 0.2 in the +50 km s−1 Cloud.
Conclusions. Previous studies observed a decreasing trend in the 32S/34S isotopic ratios when approaching the Galactic centre. Our result indicates a termination of this tendency at least at a galactocentric distance of 130−30+60 pc. This is at variance with findings based on 12C/13C, 14N/15N, and 18O/17O isotope ratios, where the above-mentioned trend is observed to continue right to the central molecular zone. This can indicate a drop in the production of massive stars at the Galactic centre, in the same line as recent metallicity gradient ([Fe/H]) studies, and opens the work towards a comparison with Galactic and stellar evolution models.
Key words: Galaxy: centre / submillimetre: ISM / Galaxy: formation / Galaxy: evolution / stars: atmospheres / submillimetre: general
The reduced spectra and datacubes are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/642/A222
© P. K. Humire et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
Studying stellar nucleosynthesis and chemical enrichment of rare isotopes of a given element at optical wavelengths is difficult because the observed atomic isotope lines are usually affected by blending (e.g. Hawkins & Jura 1987; Levshakov et al. 2006; Ritchey et al. 2011). However, at radio and (sub)millimetre wavelengths, transitions from rare isotopic substitutions of a given molecular species, called isotopologues, are well separated in frequency from their main species, typically by a few percent of their rest frequency.
While the relative abundances of C, N, and O isotopes provide information on carbon–nitrogen–oxygen (CNO) and helium burning, sulphur isotopes allow us to probe late evolutionary stages of massive stars and supernovae (SNe) of Type Ib/c and II (oxygen-burning, neon-burning, and s-process nucleosynthesis) (Wilson & Rood 1994; Chin et al. 1996; Mauersberger et al. 1996), filling a basic gap in our understanding of stellar nucleosynthesis and the chemical evolution of the Universe (e.g. Wang et al. 2013).
In the interstellar medium (ISM), atomic sulphur is thought to freeze out on dust grain mantles and to be later released from the grains due to shocks, leading to the formation of several molecular species in the gas phase, such as OCS, SO2, H2S, and H2 CS (Millar & Herbst 1990), which serve as both shock and high-mass star formation tracers in starburst galaxies (Bayet et al. 2008).
Among the sulphur-bearing compounds, CS (carbon monosulfide) is the most accessible molecular species: its lines are ubiquitous in the dense ISM and tend to be strong at sites of massive star formation in the spiral arms of our Galaxy, in the Galactic centre (GC) region and in external galaxies (e.g. Linke & Goldsmith 1980; Mauersberger et al. 1989; Bayet et al. 2009; Kelly et al. 2015).
Sulphur has four stable isotopes: 32S, 33S, 34S, and 36S. Their solar system fractions are 95.018:0.750:4.215:0.017 (Lodders 2003), respectively. In the ISM, Chin et al. (1996) found a relation between 32S/34S isotope ratios and their galactocentric distance (DGC) of 32S/34S = (3.3 ± 0.5)(DGC/kpc) + (4.1 ± 3.1) by using a linear least-squares fit to the unweighted data, with a correlation coefficient of 0.84, while no correlation was obtained between 34S/33S ratios and DGC. However, most of the sources observed in that study are located within the galactocentric distance range 5.5 ≤ DGC ≤ 7.0 kpc, with the minimum distance at 2.9 kpc from the Galactic centre. Therefore, it is important to also cover the inner region of the Milky Way to find out whether the trend proposed by Chin et al. (1996) is also valid for the inner Galaxy as has been reported for the 12C/13C (see e.g. Yan et al. 2019), 14N/15N (Adande & Ziurys 2012) and 18O/17O (Wouterloot et al. 2008; Zhang et al. 2015) isotopic ratios.
The GC region harbours one of the most intense and luminous sites of massive star formation in the Galaxy, Sgr B2 (Molinari et al. 2014; Ginsburg et al. 2018). It provides an extreme environment in terms of pressure, turbulent Mach number, and gas temperature(Ginsburg et al. 2016) over a much more extended region than encountered in star-forming regions throughout the Galactic disc (Morris & Serabyn 1996; Ginsburg et al. 2016; Schwörer et al. 2019; Dale et al. 2019). These conditions are comparable to those in starburst galaxies (Belloche et al. 2013; Schwörer et al. 2019). We therefore expect unique results in this GC study from sulphur ratios, which are a tool for tracing stellar processing (see Sect. 6). For a compilation of sulphur ratios determined in our Milky Way, we refer to Tables 2 and 7 in Mauersberger et al. (2004) and Müller et al. (2006), respectively.
As is true for our Galaxy, detections of 34S in extragalactic objects remain scarce. Some observations, also accounting for 12C/13C ratios (using the double-isotope ratio method, Sect. 4.1.1) led to values of ~16–25 and 13.5 ± 2.5 for the 32S/34S ratio in the nuclear starbursts of NGC 253 and NGC 4945, respectively (Wang et al. 2004; Henkel et al. 2014), although the value for NGC 4945 might be underestimated due to saturation of the CS lines (Martín et al. 2010). A ratio of 20 ± 5 was obtained for N159 in the Large Magellanic Cloud (Johansson et al. 1994). At redshift z = 0.89, a 32S/34S ratio of 10 ± 1 has been derived using absorption lines from the spiral arm of a galaxy located along the line of sight (l.o.s.) towards a radio loud quasar (Müller et al. 2006).
In the present study we focus on the J = 2–1 transitions of 12C32S (hereafter CS), 12C34S (hereafter C34S), 13C32S (hereafter 13CS), 12C33S (hereafter C33S), and 13C34S, the J = 3–2 transitions of CS and C34S, and the J = 6–5 transitions of C34S and 13CS, all observed together towards the Sgr A Complex (see, e.g., Sandqvist et al. 2015). We have also studied absorption features caused by the envelope of Sgr B2(N) in the J = 2–1 rotational transition of CS, C34S, 13CS and 13C34S, as well as CS and C34S absorption features caused by l.o.s. clouds towards Sgr B2(N). These absorption and emission profiles allow us to obtain 12C/13C and the missing 32S/34S ratios close to the Galactic nucleus. Expanding the database for sulphur isotope ratios in the GC region is important in order to constrain models of stellar interiors as well as models of the chemical evolution of the Galaxy (e.g. Kobayashi et al. 2011).
The paper is organized as follows. In Sect. 2, we describe the observations. In Sect. 3, we describe in detail our targets. In Sect. 4, we present measured opacities and isotopologue ratios from CS species, the modelling of our Sgr B2(N) data, and a comprehensive study of CS fractionation. In Sect. 5, we compare our results with previous studies. In Sect. 6, we discuss the results in the context of trends with galactocentric distance and give some explanations for our findings, before summarizing and concluding in Sect. 7.
2 Observations
2.1 +50 km s−1 Cloud
The +50 km s−1 Cloud observations were conducted with the IRAM 30 m and the APEX 12 m telescopes over a period of 1.5 yr, from 2015 May to 2016 September, under varying weather conditions. The observed position was EQ J2000: 17h 45m50.20s, −28°59′ 41.1′′ for both telescopes, and the representative spectral resolution was 0.6 km s−1. With the IRAM 30 m telescope, three frequency set-ups were observed with the E090 and E150 receivers in combination with the Fast Fourier Transform Spectrometer (FFTS, at 195 kHz resolution mode1). For the observations presented in this paper, we covered the 93.2–100.98 GHz frequency range (CS, C34S, and C33S J = 2–1) in one set-up with the E090 receiver. In a separate E090 set-up, our tuning covered the frequency range 85.5–93.3 GHz (13CS and 13C34S J = 2–1), while simultaneously the E150 receiver covered the frequency range from 143.5 to 151.3 GHz (for CS and C34S J = 3–2). The observationswere conducted in total power position switching mode. No spectral contamination was found in our off-source reference position (17h 46m10.4s, −29°07′ 08′′). The main beam efficiencies for our IRAM 30 m measurements were computed using the Ruze formalism (Ruze 1966). Adopted values were 0.8 and 0.7 at 98 and 147 GHz, respectively2. We discarded data taken under poor weather conditions (precipitable water vapor content (pwv) > 7 mm) by discarding data taken with system temperatures > 500 K. The representative half-power beam widths (HPBW) values are about 25′′ at 98 GHz and 17′′ at 147 GHz for the IRAM 30 m observations.
The Atacama Pathfinder Experiment 12 m telescope (APEX) 12 m (Güsten et al. 2006) was used for observations of the J = 6–5 lines of the CS, 13CS, and 13C34S isotopologues at roughly 280 GHz. The measurements were conducted simultaneously using the FLASH345 (Klein et al. 2014) receiver connected to the extended FFTS (XFFTS) backend. These observations were also executed in total power position switching mode and the same off-source reference position, which was found to be clean. The HPBW was about 22′′ at the observed frequency and the adopted main beam efficiency was 0.7.
All line intensities are reported in main beam brightness temperature units (TMB). While the spectral resolution was instrument dependent (between 0.4 and 0.6 km s−1 for the IRAM and 0.08 km s−1 for the APEX data), all spectra were smoothed to a resolution of 3 km s−1 for analysis.
The data were reduced with the GILDAS package3 and required minimal flagging, followed by a baseline subtraction of order two.
2.2 Line-of-sight clouds towards Sgr B2(N)
For Sgr B2(N), we used the Exploring Molecular Complexity with ALMA (EMoCA) survey (Belloche et al. 2016) that was performed with the Atacama Large Millimetre/submillimetre Array (ALMA) in the direction of this source. The centre of the observed field (see Fig. 1) lies in the middle (EQ J2000: 17h 47m19.87s, −28°22′ 16′′) between the two main hot cores, N1 and N2, which are separated by 4. ′′9 along the north–south direction, or around 0.19 pc in projection assuming a distance to the Galactic centre, Sgr A*, of 8.122 kpc (Gravity Collaboration 2018). The survey covers the frequency range from 84.1 to 114.4 GHz, which includes carbon monosulfide J = 2–1 lines, with a spectral resolution of 488 kHz (1.7 to 1.3 km s−1) at a median angular resolution of 1. ′′6, or ~0.06 pc. The average noise level is ~3 mJy beam−1 per channel.Details of the calibration and deconvolution of the data are reported in Belloche et al. (2016, Sect. 2.2). For this work, we correctedthe data for primary beam attenuation. Several isotopologues of CS are detected in the EMoCA survey. To determine the 32S/34S and 12C/13C isotopic ratios, we use four isotopologues: CS, C34S, 13CS, and 13C34S.
A list of the observed transitions of CS isotopologues and some associated parameters is given in Table 1.
 |
Fig. 1 ALMA continuum map of Sgr B2(N) at 85 GHz. The black contour lines show the flux density levels at 3σ, 6σ, 12σ, and 24σ and the dotted lines indicate −3σ, where σ is the rms noise level of 5.4 mJy beam−1. The white crosses denote the positions of the two main hot cores, Sgr B2(N1) and Sgr B2(N2). The black cross, located between the white ones, indicates the phase centre. The green crosses show peaks of continuum emission selected for our absorption study. They label the ultra-compact H II region K4, two peaks in the shell of the H II region K6 and one peak in the shell of the H II region K5 (Gaume et al. 1995). The green ellipse in the lower left corner shows the size of the synthesized beam of ~1. ′′6 (see Table 1). |
3 Sources
The +50 km s−1 Cloud (also known as M–0.02–0.07, although the +50 km s−1 Cloud could include additional molecular knots on its positive-longitude side; Ferrière 2012), observed here with IRAM and APEX, is a giant molecular cloud (GMC) of hook or indented-sphere shape, considered to be one of the most prominent high-mass star formation sites in the GC. It has a mass of ~5 × 105 M⊙; a density of 104 –105 cm−3; a gas temperature of 80–100 K (from NH3, CH3CN, and CH3CCH; Güsten et al. 1985), ~190 K (from H2CO, Ao et al. 2013), or 410 ± 10 K (from NH3, Mills & Morris 2013); and a dust temperature of 20–30 K (Sandqvist et al. 2008). The energetics of at least a part of the +50 km s−1 Cloud are influenced by the supernova (SN) remnant Sgr A East (Ferrière 2012; Uehara et al. 2019). In CS emission, its dense core peaks at a l.o.s. distance of 3 ± 3 pc relative to the Galactic centre (Ferrière 2012), coincident with 1.2 mm observations (Vollmer et al. 2003, and references therein), and peaks at (Δα, Δδ) ≈ (3.′0, 1.′5) with respect to Sgr A*, corresponding to ≈7 ± 3 pc to the east along the Galactic plane and 4.5 ± 3 pc to the south from the Galactic plane (see the explanation for galactocentric Cartesian coordinates in Ferrière 2012, and their Table 1).
With ALMA we have observed Sgr B2(N)orth, one of the sites of massive star formation associated with Sgr B2, the most massive cloud in our Galaxy. The whole Sgr B2 complex has a total mass of 107 M⊙ (Goldsmith et al. 1990) and gas temperatures of at least 50 K (from p–H2CO in Ginsburg et al. 2016, their Sect. 5.8). Most of the mass in Sgr B2(N) (~73%) is contained in one single core (AN01) (Sánchez-Monge et al. 2017). The densities and column densities of the hot cores in Sgr B2(N) are high (>106 cm−3 and >1023 cm2; Sánchez-Monge et al. 2017; Bonfand et al. 2019).
Sgr B2(N) is located at a galactocentric distance of 130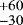 pc from Sgr A* (from Reid et al. 2009, considering the projected distance of 100 pc as lower limit) or ~8 kpc from us. Its diameter is ~0.8 pc (Lis & Goldsmith 1990; Schmiedeke et al. 2016). Several diffuse and translucent clouds are detected in absorption along the l.o.s. to Sgr B2(N) (see e.g. Greaves & Williams 1994; Thiel et al. 2019). The exact locations of the different velocity components of the l.o.s. clouds towards Sgr B2(N) are not yet fully constrained. In the case of our observations (see Table 4), we can only suggest that the lines with negative velocities arise from l.o.s. clouds between the Expanding Molecular Ring (with a galactocentric radius of 200–300 pc, Whiteoak & Gardner 1979) and the 1 kpc disc, while the lines with positive velocities arise from the envelope of Sgr B2(N) (Greaves & Williams 1994; Wirström et al. 2010; Thiel et al. 2019). Specifically, our lines in the range −105 to −70 km s−1 are believed to be located within 1 kpc of the GC (Corby et al. 2018, and references therein), and our lines with velocities around +60 km s−1 are associated with the envelope of Sgr B2(N) (Wirström et al. 2010).
pc from Sgr A* (from Reid et al. 2009, considering the projected distance of 100 pc as lower limit) or ~8 kpc from us. Its diameter is ~0.8 pc (Lis & Goldsmith 1990; Schmiedeke et al. 2016). Several diffuse and translucent clouds are detected in absorption along the l.o.s. to Sgr B2(N) (see e.g. Greaves & Williams 1994; Thiel et al. 2019). The exact locations of the different velocity components of the l.o.s. clouds towards Sgr B2(N) are not yet fully constrained. In the case of our observations (see Table 4), we can only suggest that the lines with negative velocities arise from l.o.s. clouds between the Expanding Molecular Ring (with a galactocentric radius of 200–300 pc, Whiteoak & Gardner 1979) and the 1 kpc disc, while the lines with positive velocities arise from the envelope of Sgr B2(N) (Greaves & Williams 1994; Wirström et al. 2010; Thiel et al. 2019). Specifically, our lines in the range −105 to −70 km s−1 are believed to be located within 1 kpc of the GC (Corby et al. 2018, and references therein), and our lines with velocities around +60 km s−1 are associated with the envelope of Sgr B2(N) (Wirström et al. 2010).
This massive star-forming region harbours five hot cores, namely Sgr B2(N1–N5), with kinetic temperatures ranging from ~130 to 150 K forN3–N5, between 150 and 200 K for N2, and between 160 and 200 K for N1, assuming LTE conditions in all these cases (Belloche et al. 2016, 2019; Bonfand et al. 2017). In addition, there are 20 ~1.3 mm continuum sources associated with dense clouds in Sgr B2(N) that exhibit a rich chemistry (Sánchez-Monge et al. 2017; Schwörer et al. 2019). Recently, Ginsburg et al. (2018) detected 271 compact continuum sources at ~3 mm in the extended Sgr B2 cloud, thought to be high-mass protostellar cores, representing the largest cluster of high-mass young stellar objects reported to date in the Galaxy.
4 Results
In the following we first discuss the measured profiles towards the +50 km s−1 Cloud, and provide the equations used to determine peak opacities and the carbon isotope ratio (Sect. 4.1). Then we determine the 32S/34S isotope ratio in two different ways (Sects. 4.1.1 and 4.1.2) from the J = 2–1 lines of the different detected CS isotopologues. The J = 3–2 opacities and the 34S/33S ratio are the topics of Sects. 4.1.3 and 4.1.4. Sgr B2(N) data are analysed in Sect. 4.2, while the relation between the 32S/34S isotoperatios from CS and the actual interstellar 32S/34S values is thetopic of Sect. 4.3. Generally, the analysis assumes that lines with the same rotational quantum numbers, related to different CS isotopologues, are co-spatial. We present a summary of our results in Table 3.
Some observational and physical parameters for the five measured CS isotopologue transitions in the +50 km s−1 Cloud and the four transitions from the l.o.s. clouds towards Sgr B2(N), which are also located in the Galactic centre region.
Line parameters for the nine measured CS isotopologue transitions in the +50 km s−1 Cloud.
4.1 Peak opacities and column density ratios in the +50 km s–1 Cloud
The CS emission lines observed towards the +50 km s−1 Cloud are presented in Fig. 2. All lines show peaks in agreement with the local standard of rest (LSR) velocity of the system, ~50 km s−1 (Sandqvist et al. 2008; Requena-Torres et al. 2008). In addition to the CS J = 2–1 isotopologue lines, there are probably weak features of cyanoformaldehyde (NCCHO) and ethanol (C2 H5OH) at 96.4260958 GHz and 96.4273380 GHz, respectively, on the blue-shifted side (~0 km s−1) of C34S; dimethyl ether (CH3OCH3) at 90.9375080 GHz or ~10 km s−1 on the blue-shifted side dominates the 13C34S spectrum. Those molecules have been observed already in Sgr B2 (Zuckerman et al. 1975; Nummelin et al. 1998; Martín-Pintado et al. 2001; Remijan et al. 2008; Belloche et al. 2013).
Moreover, the CS J = 2–1 and J = 3–2 line profiles show double-peaked profiles, which are readily explained by self-absorption, cantered at the systemic velocity of the cloud in the J = 2–1 transition and with a self-absorption marginally redshifted (by ~0.4 km s−1) in the J = 3–2 transition. The CS parameters allowed to vary freely and obtained from single- or double-component Gaussian fitting are summarized in Table 2. They were obtained using a series of Python codes, mainly within the lmfit package4.
As can be seen in Fig. 2, for the CS J = 2–1 and J = 3–2 lines, we have fitted a double Gaussian considering a positive (in blue) and a negative (in green) Gaussian component each. Their parameters are summarized in Table 2, where the uncertainties were taken directly from the lmfit package (for details see Appendix D).
Given that CS J = 2–1 and J = 3–2 show double-peaked profiles, while the rare isotopologues exhibit a single peak in between, the CS lines are likely optically thick. This was also suggested by Tsuboi et al. (1999) who find that CS J = 1–0 is moderately optically thick in this object, with an opacity (τ) of around 2.8. Then, we can further assume as a first approximation that C34S J = 2–1 is optically thin in the expected case that 32S/34S ≫ 3 (see Sect. 4.1.2 for a confirmation of this assumption; see also Frerking et al. 1980 and Corby et al. 2018). In this case 13C34S J = 2–1 is definitively optically thin.
In the following, we consider an excitation temperature range of 9.4–300 K for our column density computations in order to obtain conservative estimates. Our column density values were calculated using Eq. (80) in Mangum & Shirley (2015) assuming a filling factor of unity. We then deduce from the integrated line intensities of C34S J = 2–1 and 13C34S J = 2–1, converted to column densities, a 12C/13C ratio of 22.1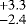 . This value is used in Eqs. (1) and (2) (denoted RC), and it agrees with previous observations in the GC within the uncertainties (~17–25; e.g. Frerking et al. 1980; Corby et al. 2018), and with the values derived from many transitions of complex organic molecules (COMs) in the hot core Sgr B2(N2) (Belloche et al. 2016; Müller et al. 2016), indicating that our approach is correct and confirming that C34S is indeed optically thin.
. This value is used in Eqs. (1) and (2) (denoted RC), and it agrees with previous observations in the GC within the uncertainties (~17–25; e.g. Frerking et al. 1980; Corby et al. 2018), and with the values derived from many transitions of complex organic molecules (COMs) in the hot core Sgr B2(N2) (Belloche et al. 2016; Müller et al. 2016), indicating that our approach is correct and confirming that C34S is indeed optically thin.
Assuming equal excitation temperatures (see Appendix B) and beam filling factors for 12CS and 13CS, the 13CS J = 2–1 peak opacity τ(13CS) can then be determined from
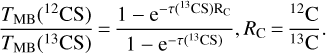 (1)
(1)
However, as there is a self-absorption feature at the centre of the 12CS J = 2–1 and J = 3–2 profiles, we measure the line temperatures of both 12CS and 13CS at a redshifted velocity, vr = 63 km s−1, where the line shape is not affected by self-absorption. We can then retrieve the opacity at the systemic velocity, assumed to be the 13CS J = 2–1 peak velocity, vsys = 46.94 km s−1, by considering a Gaussian distribution. First, we compute the opacities at vr in the following way:
 (2)
(2)
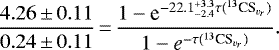 (3)
(3)
Here, T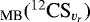 and T
and T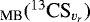 are the main-beam brightness temperatures of CS and 13CS J = 2–1 at vr. This results in
are the main-beam brightness temperatures of CS and 13CS J = 2–1 at vr. This results in 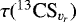 = 0.02 ± 0.01, considering the same uncertainties for the peak temperatures as those obtained by performing a single Gaussian fit in those lines. We can nowretrieve the opacity at the systemic velocity as
= 0.02 ± 0.01, considering the same uncertainties for the peak temperatures as those obtained by performing a single Gaussian fit in those lines. We can nowretrieve the opacity at the systemic velocity as
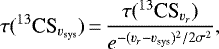 (4)
(4)
where σ is the full width at half maximum (FWHM) of 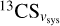 divided by
divided by 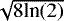 (FWHM/
(FWHM/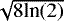 = 9.46 ± 0.12 km s−1) and vsys = 46.942 ± 0.118 km s−1. We obtain
= 9.46 ± 0.12 km s−1) and vsys = 46.942 ± 0.118 km s−1. We obtain 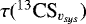 = 0.08
= 0.08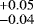 . Multiplying this by RC, we obtain
. Multiplying this by RC, we obtain 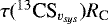 =
=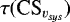 = 1.9
= 1.9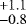 , consistent with previous observations (
, consistent with previous observations (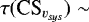 2.8; Tsuboi et al. 1999). The uncertainty on vsys corresponds to a 0.15% variation in the
2.8; Tsuboi et al. 1999). The uncertainty on vsys corresponds to a 0.15% variation in the 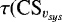 ) value in the worst case. Therefore, it is ignored in the following.
) value in the worst case. Therefore, it is ignored in the following.
 |
Fig. 2 From left to right and top to bottom: observed line profiles of the J = 2–1 transitions of CS, C34S, 13CS, C33S, and 13C34S, the J = 3–2 transitions of CS and C34S, and the J = 6–5 transitions of C34S and 13CS, in the +50 km s−1 Cloud (EQ J2000: 17h45m50.20s, −28°59′ 41.1′′). Measured profiles are shown in black; the resulting Gaussian fitting is presented in red. For the CS J = 2–1 and J = 3–2 lines, a double Gaussian fitting was performed to account for the self-absorbed component (in green) in an attempt to retrieve the undisturbed emission line (in blue) (see Sect. 4.1). All the other lines are well fitted by a single component. In the case of 13C34S J = 2–1, the companion line is subtracted because of its relatively strong emission and potential contamination. The dashed vertical linesdenote the 13CS J = 2–1 peak position (46.94 km s−1, see Table 2). Dash-dotted red lines denote the redshifted velocity (vr = 63 km s−1) at which the CS J = 2–1 and J = 3–2 transition lines are not affected by self-absorption (see Sect. 4.1). Nearby lineslikely observed are labelled. |
4.1.1 A 32S/34S ratio obtained through the double isotope method
As we have seen, CS must be moderately optically thick. Then, the 32S/34S isotope ratios cannot be determined from the observed N(12CS)/N(C34S) ratio. Instead, we can use the column densities of 13CS and C34S by realistically assuming that those lines are optically thin (see Sect. 4.1). Therefore, we have derived the values for 32S/34S making use of the carbon isotope ratio mentioned above, in the following way:
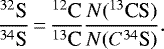 (5)
(5)
From Eq. (5) we obtain a 32S/34S J = 2–1 ratio of 16.3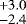 . By using the 13CS and C34S J = 6–5 transitions, we obtain a 32S/34S J = 6–5 ratio of 15.8
. By using the 13CS and C34S J = 6–5 transitions, we obtain a 32S/34S J = 6–5 ratio of 15.8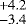 . This agreement within the uncertainties can be taken as another argument in favour of the low opacity of C34S and the subsequent validity of our assumptions and calculations. If some of the C34S lines in the rotational ladder were not optically thin, we would expect different N(13CS)/N(C34S) ratios in the J = 2–1 and 6–5 transitions due to photon trapping leading to higher excitation temperatures in the more abundant isotopologue, which is not observed.
. This agreement within the uncertainties can be taken as another argument in favour of the low opacity of C34S and the subsequent validity of our assumptions and calculations. If some of the C34S lines in the rotational ladder were not optically thin, we would expect different N(13CS)/N(C34S) ratios in the J = 2–1 and 6–5 transitions due to photon trapping leading to higher excitation temperatures in the more abundant isotopologue, which is not observed.
4.1.2 32S/34S ratio from direct observations
As we have measured the 13C34S J = 2–1 transition, we can also obtain the 32S/34S ratio directly from
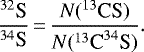 (6)
(6)
Using this we obtain a 32S/34S J = 2–1 ratio of 16.3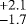 , consistent with the ratio obtained through the double-isotope method in Eq. (5) and again indicating that our initial assumptions concerning line saturation were correct. In the following, we use the latter value for our analysis because it was determined in the most direct way. In order to estimate the opacity of CS from C34S (see Sect. 4.1.3), we use this C32S/C34S J = 2–1 ratio of 16.3
, consistent with the ratio obtained through the double-isotope method in Eq. (5) and again indicating that our initial assumptions concerning line saturation were correct. In the following, we use the latter value for our analysis because it was determined in the most direct way. In order to estimate the opacity of CS from C34S (see Sect. 4.1.3), we use this C32S/C34S J = 2–1 ratio of 16.3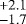 as the sulphur isotopic ratio 32S/34S and call it RS.
as the sulphur isotopic ratio 32S/34S and call it RS.
To compare our results with those of Chin et al. (1996), we also derived a sulphur ratio from the integrated intensities: 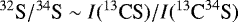 . This results in a 32S/34S value of 18.6
. This results in a 32S/34S value of 18.6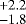 . The differences between the column density and integrated intensity ratios are due to the rotational partition functions, rotational constants, and Einstein A-coefficients for spontaneous emission of radiation that slightly differ for the different isotopologues.
. The differences between the column density and integrated intensity ratios are due to the rotational partition functions, rotational constants, and Einstein A-coefficients for spontaneous emission of radiation that slightly differ for the different isotopologues.
4.1.3 CS and C34S J = 3–2 opacities
Now we are able to determine the opacities of CS and C34S J = 3–2 by proceeding in the same way as in Eqs. (2) and (4), but considering this time the sulphur ratio. Here, as in Eq. (2), we also assume equal excitation temperatures (see Appendix B) and beam filling factors, this time for 12CS and C34S J = 3–2:
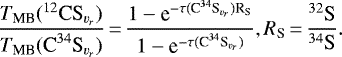 (7)
(7)
From Eq. (7), 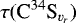 = 0.01–0.03. Following the formalism in Eq. (4), we obtain a
= 0.01–0.03. Following the formalism in Eq. (4), we obtain a 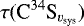 value of 0.05–0.15. Entering this value and replacing
value of 0.05–0.15. Entering this value and replacing 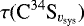 RS by
RS by 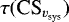 , the CS
, the CS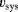 opacity results in a proper range of 1.0–2.8, considering throughout this calculation that this latter value cannot lie below unity, since CS shows clear signs of optical thickness (see Sect 4.1). This is consistent with previous observations (Tsuboi et al. 1999). All the derived opacities are summarized in Table 2.
opacity results in a proper range of 1.0–2.8, considering throughout this calculation that this latter value cannot lie below unity, since CS shows clear signs of optical thickness (see Sect 4.1). This is consistent with previous observations (Tsuboi et al. 1999). All the derived opacities are summarized in Table 2.
Summary for our carbon and sulphur column density ratio calculations in the +50 km s−1 Cloud.
4.1.4 34S/33S ratio from direct observations
The C33S J = 2–1 line was also observed. This offers the possibility of obtaining the 34S/33S ratio for the GC. Since C33S is less abundant than C34S, we can expect a clearly optically thin profile. This ratio is easily obtained by
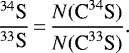 (8)
(8)
We obtain a 34S/33S ratio of 4.3 ± 0.2 for the +50 km s−1 Cloud. If we take the integrated intensities instead of the column densities, this ratio would be 4.2 ± 0.2, consistent with the lower end of the range of ratios obtained by Chin et al. (1996), who derived 34S/33S ratios between 4.38 and 7.53, irrespective of Galactic radius. Whether this is a first hint of a gradient remains to be seen. Better data from the Galactic disc are necessary to tackle this question.
4.2 Modelling the Sgr B2(N) data
Here, we rely on the modelling of the absorption profiles of the isotopologues of CS carried out by Thiel (2019) using the EMoCA survey, following the same method as Thiel et al. (2019). They used the software Weeds (Maret et al. 2011) to model the absorption profiles. Their work assumes that all transitions of a molecule have the same excitation temperature and that the beam filling factor is unity, which is a reasonable assumption given that most absorption features are extended on scales of 15′′ or beyond in the ALMA maps (see Thiel et al. 2019, their Sect. 5.4), while the beam size is 1. ′′ 6 (see Sect. 2.2, Fig. 1, and Table 1). The fitted parameters were the column density, line width, and the centroid velocity, under the assumption that the excitation temperature is equal to the temperature of the cosmic microwave background (2.73 K).
We selected four continuum peaks inside Sgr B2(N) (Fig. 1). We excluded the two strong continuum peaks at which the main hot cores N1 and N2 are located because at these positions the spectra are full of emission lines of organic molecules (e.g. Bonfand et al. 2017) contaminating the carbon monosulfide absorption features. The offsets to the centre of the observed field are (1. ′′ 8, 11. ′′ 1), (9. ′′ 3, 1. ′′ 8), (4. ′′ 8, 9. ′′ 3), and (6. ′′ 6, 3. ′′ 3) (see Fig. 1 and Table 4). The observed absorption profiles and the corresponding Weeds models for the four isotopologues and the four positions are shown in Fig. 3. Using their results for the column densities, we determined the isotopic ratios CS/C34S, 13CS/13C34S, and C34S/13C34S. We determined those ratios separately for the envelope of Sgr B2(N) and some GC clouds along the l.o.s. to Sgr B2(N), the latter with velocities lower than − 50 km s−1. We only determine the ratio CS/C34S in those cases where the absorption caused by CS is not optically thick.
The resulting unweighted average values of the isotopic ratios are listed in Table 4, namely a 32S/34S isotope ratioof 16.3 ± 3.8 in the GC l.o.s. clouds towards Sgr B2(N) and 17.9 ± 5.0 in the envelope of Sgr B2(N). For this envelope we obtain a 12C/13C ratio of 27.6 ± 6.5. It should benoted that our uncertainties correspond to the standard deviation for independent measurements, i.e. without dividing it by the square root of the number of studied spectral components.
Isotopic ratios determined in the envelope of Sgr B2(N) (13CS/13C34S and C34S/13C34S) and in GC clouds along the line of sight to Sgr B2(N) (CS/C34S) using absorption lines of CS isotopologues.
4.3 Discussion on the validity of using C32S/C34S as a proxy for 32S/34S
Chin et al. (1996) estimated that sulphur fractionation is marginal for CS isotopic ratios. If the bulk of the CS emission, which allows us to measure rare isotopes, arises from the densest parts of the molecular clouds only, the heating from the massive stars should inhibit significant fractionation (Chin et al. 1996). In that case, CS emission can be used directly to determine sulphur isotope ratios from such sources.
In their oxygen fractionation study, Loison et al. (2019) analyse sulphur fractionation including CS. Some sulphur fractionation is induced at low temperature by the 34S+ + CS → S+ + C34S reaction. To determine the potential fractionation of sulphur, we used the network from Loison et al. (2019) in the +50 km s−1 Cloud, the l.o.s. clouds towards Sgr B2(N) and the envelope of Sgr B2(N), with realistic physical conditions for these objects, in particular a much higher value of the cosmic-ray ionization rate (CRIR) than the usual value in more local dense molecular clouds. Some typical results are shown in Fig. 4 and are described below.
In the simulations, all elements with an ionization potential below the maximum energy of ambient UV photons (13.6 eV) are assumed to be initially in an atomic, singly ionized state. We considered all sulphur in the S+ form without depletion, and we performed some tests to quantify the effect of depletion, which is low (see below). Hydrogen, with its high degree of self-shielding, is taken to be entirely molecular. The initial abundances are similar to those in Table 1 of Hincelin et al. (2011), the C/O elemental ratio being equal to 0.7 in our study. We verified that the initial state of carbon and nitrogen (C+ versus CO and N versus N2) have very little influence on sulphur fractionation (less than 4% for the typical ages considered: 105−6 yr). The estimation of the dense cloud ages is deduced from clouds with similar density (104 to a few 105 cm−3) for which the age is given by the best agreement between calculations and observations for key species given by the so-called distance of disagreement (Wakelam et al. 2006). By key species we mean species typically encountered in molecular clouds such as HCN, HNC, CN, CH, C2H, c–C3H, c–C3H2, CO, H2 CO, CH3OH, NO, SO, CS, HCS+, and H2CS (see e.g. Wakelam et al. 2010; Agúndez & Wakelam 2013; Agúndez et al. 2019).
For Fig. 4a, which represents conditions in the +50 km s−1 Cloud, we adopted a density of 105 cm−3 and a CRIR of ζH2 = 7 × 10−16 s−1 based on measurements in hot cores of Sgr B2(N) by using COMs (Bonfand et al. 2019). For Figs. 4b and c, which represent the conditions for the envelope of Sgr B2(N) and the l.o.s. clouds towards Sgr B2(N), respectively, we chose a density of 104 cm−3, an upper limit for the volume density in those regions (see Thiel et al. 2019, their Table 12), in order to avoid possible UV heating in our models. Due to this high density, we have adopted a CRIR of ζH2 = 3 × 10−15 s−1, i.e. one order of magnitude lower than the value usually obtained in the l.o.s. of translucent and diffuse clouds towards the Galactic centre, but within the range obtained for the nuclear ~100 pc of our Galaxy (Indriolo et al. 2015; Le Petit et al. 2016). The 32S/34S isotope ratio chosen for each simulation is that obtained from our measurements, namely 16.3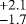 , 17.9 ± 5.0, and 16.3 ± 3.8 for Figs. 4a, b, and c, respectively.
, 17.9 ± 5.0, and 16.3 ± 3.8 for Figs. 4a, b, and c, respectively.
Despite the limited literature on the subject, according to models from Laas & Caselli (2019), the +50 km s−1 Cloud is the only object in this study that could show signs of sulphur depletion. However, for a depletion level of up to 90%, our models give results consistent with no sulphur depletion (which is the case for the results shown in Fig. 4) because of the high temperatures that prevent any efficient fractionation. It should be noted that if this cloud’s chemistry was determined in an earliercolder evolutionary period with possibly significant sulphur fractionation, CS, in contrast to CO, could not accumulate because it would have been destroyed by protonation as the dissociative recombination of HCS+ leads mainly to S + CH and not to CS + H (see Appendix A). Therefore, the memory effect for the CS fractionation of such a dense cloud is small. For the l.o.s. clouds towards Sgr B2(N) and the envelope of Sgr B2(N), some runs (those shown in Fig. 4) give some sulphur fractionation when the gas temperature is low. This is due to the combination of low density limiting the depletion of sulphur and a high CRIR (ζH2 = 3 × 10−15 s−1). These characteristics induce an elevated concentration of S+ in the gas phase and then a 34S enrichment through the 34S+ + CS → S+ + C34S reaction (see Table 2 in Loison et al. 2019). It should be noted that the cases with some 34S enrichment only concern low kinetic temperatures, and that this relatively low enrichment will be evenlower with some sulphur depletion. This depletion is not well constrained in the +50 km s−1 Cloud, the l.o.s. clouds towards Sgr B2(N), and the envelope of Sgr B2(N), but it is high for some cold dense molecular clouds (between 10 and 25 for the dark cloud L1544 Barnard 1b (Fuente et al. 2016) and even up to 200 for the dark cloud L1544 (Vastel et al. 2018).
The extremely low gas temperature cases in our models (black lines in Fig. 4) are shown to demonstrate the dependence of sulphur depletion on gas temperature. Since Galactic centre molecular cloud temperatures are higher (Ginsburg et al. 2016), CS shows likely very little fractionation in 34S for the purposes of this study and our measurements of the C32S/C34S ratio are a good approximation to the 32S/34S ratio (even if the values thus obtained may be slightly underestimated when considering the results of the models). We can then expect a ≲10% increase in the 32S/34S ratios obtained for the +50 km s−1 Cloud in Fig. 4a and slightly more for the l.o.s. clouds towards Sgr B(N) and its envelope (≲15%), considering the conditions labelled in red and blue in Figs. 4b and c.
Some measurements using the double-isotope ratio method (see Sect. 4.1.1), which take the 12C/13C ratio into account, may induce a bias since CS may show a non-negligible fractionation into 13C. There is no specific study of the 13C fractionation of CS, but the reactivity of C+ and C, in particular with CO and CN (but also with CS), can induce an enrichment or depletion in 13C of carbonaceous species including CS (Smith & Adams 1980; Roueff et al. 2015). In that case, the good agreement between the sulphur fractionation measurements using C32S/C34S and the values obtained using the double-isotope method also suggests a low 13C fractionation of CS. This result is interesting and could initiate future studies on the modelling of 13C fractionation in CS.
 |
Fig. 3 EMoCA absorption spectra of four isotopologues of CS towards four positions in Sgr B2(N). The offsets (in units of arcseconds, see Table 4 and Fig. 1) from the phase centre are indicated at the right of each row. The observed spectra are shown in black and the synthetic spectra in magenta, purple, green, and blue, depending on the position. The synthetic spectra were obtained by Thiel (2019). The dotted vertical lines indicate the velocities atwhich we determined the isotopic ratios using the corresponding isotopologue. The velocities are listed in Table 4. The grey horizontal lines show the continuum level. |
 |
Fig. 4 Calculated abundance ratios of gas phase species C32S/C34S as a functionof cloud age for conditions in (a) the +50 km s−1 Cloud, (b) the envelope of Sgr B2(N), and (c) l.o.s. cloudstowards Sgr B2(N) (see Sect. 4.2 for details). Low values for the gas temperatures were chosen to illustrate an upper limit for fractionation. The vertical grey loci represent values given by the most probable chemical age. The observational results from this study are illustrated as horizontal light grey rectangles (including the uncertainties). |
5 Our results in the light of previous studies
If we assume that the gradient proposed by Chin et al. (1996) would also be valid in the Galactic centre region, the 32S/34S ratio would decrease to values of 4.1 ± 3.1 at the centre of our Galaxy, i.e. to a very low value, only 1/4 of the solar system ratio. This value is lessthan one fourth of the value derived from integrated intensities in this work, 18.6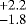 .
.
This difference can be explained in terms of the 12C/13C ratios assumed in Chin et al. (1996), required to obtain the 32S/34S ratio through the double-isotope method by using the formalism of Eq. (5) (although using intensities instead of column densities). The 12C/13C ratios were derived from the relation found by Wilson & Rood (1994) of 12C ∕13C = (7.5 ±1.9) (DGC∕kpc) + (7.6 ± 12.9) that gives a value of 7.6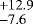 for the Galactic centre, although the authors claimed a value of ~20 near the Galactic nucleus (Wilson & Rood 1994, Sect 5.1). This provides an idea of the large uncertainty in this relation.
for the Galactic centre, although the authors claimed a value of ~20 near the Galactic nucleus (Wilson & Rood 1994, Sect 5.1). This provides an idea of the large uncertainty in this relation.
On the other hand, we are confident about our 12C/13C ratio of 22.1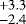 (Sect. 4.1) for two reasons: first, the agreement between the 32S/34S ratio obtained through the double-isotope method (Sect. 4.1.1), which makes use of the 12C/13C ratio, and the 32S/34S ratio obtained directly from 13CS/13C34S (Sect. 4.1.2), i.e. independently of the carbon ratio (this also indicates that the carbon fractionation is low, as described in Sect. 4.3) and second, its proximity to the ratio obtained through decades of observations in the nuclear regions of our Galaxy (12C/13C = 17–25, Frerking et al. 1980; Wilson & Rood 1994; Milam et al. 2005; Müller et al. 2008; Corby et al. 2018), including LTE modelling of complex organic molecules (Belloche et al. 2016; Müller et al. 2016). There is no abrupt redirection in the 12C/13C ratio (e.g. Henkel et al. 1985).
(Sect. 4.1) for two reasons: first, the agreement between the 32S/34S ratio obtained through the double-isotope method (Sect. 4.1.1), which makes use of the 12C/13C ratio, and the 32S/34S ratio obtained directly from 13CS/13C34S (Sect. 4.1.2), i.e. independently of the carbon ratio (this also indicates that the carbon fractionation is low, as described in Sect. 4.3) and second, its proximity to the ratio obtained through decades of observations in the nuclear regions of our Galaxy (12C/13C = 17–25, Frerking et al. 1980; Wilson & Rood 1994; Milam et al. 2005; Müller et al. 2008; Corby et al. 2018), including LTE modelling of complex organic molecules (Belloche et al. 2016; Müller et al. 2016). There is no abrupt redirection in the 12C/13C ratio (e.g. Henkel et al. 1985).
Recently, Corby et al. (2018) found 32S/34S ratios mostly in the 5–10 range, based on C32S and C34S J = 1–0 absorption lines from diffuse clouds near the GC, with a resolution of ~15′′. Considering their data in the –73 to –106 km s−1 velocity range, corresponding to our GC l.o.s. clouds towards Sgr B2(N), their observations reach values between 6.6 ± 6 and 29 ± 14, consistent with our values between 9.0 ± 1.0 and 21.0 ± 4.9 (Table 4, lower panel).
In addition, Armijos-Abendaño et al. (2015), with a resolution of ~30′′–38′′, found values of ≳22 and 8.7 ± 1.3 for 32S/34S isotope ratios in l.o.s. clouds towards Sgr A and Sgr B2, respectively, consistent with previous estimations (Frerking et al. 1980). However, their sulphur ratios were obtained from OCS/OC34S, with OCS being potentially optically thick and OC34S spectra being badly affected by band pass ripples, possibly providing only tentative detections. So we propose a more conservative lower limit for the l.o.s. clouds towards Sgr A of ~10 and we suggest that the uncertainty for their ratio in Sgr B2 was underestimated.
Both Corby et al. (2018) and Armijos-Abendaño et al. (2015) employed integrated column density ratios, so we should compare those measurements with our normal 32S/34S isotope ratioestimation, that is 16.3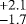 for the +50 km s−1 Cloud (as an approximation for their l.o.s. clouds towards Sgr A) and 16.3 ± 3.8 for the l.o.s.clouds towards Sgr B2 (see Table 4). Our data represent a significant improvement in terms of accuracy and precision with respect to those previous observations. In addition, our estimation of 17.9 ± 5.0 for the envelope of Sgr B2(N) agrees with both estimations for the +50 km s−1 Cloud and also with previous calculations for the whole Sgr B2 region: ~16, from the OCS/OC34S ratio, which is claimed to be derived from optically thin lines (Goldsmith & Linke 1981).
for the +50 km s−1 Cloud (as an approximation for their l.o.s. clouds towards Sgr A) and 16.3 ± 3.8 for the l.o.s.clouds towards Sgr B2 (see Table 4). Our data represent a significant improvement in terms of accuracy and precision with respect to those previous observations. In addition, our estimation of 17.9 ± 5.0 for the envelope of Sgr B2(N) agrees with both estimations for the +50 km s−1 Cloud and also with previous calculations for the whole Sgr B2 region: ~16, from the OCS/OC34S ratio, which is claimed to be derived from optically thin lines (Goldsmith & Linke 1981).
Cutting-edge model calculations performed by Kobayashi et al. (2011) relate sulphur isotope ratios (32S/33,34,36S) with metallicity ([Fe/H]5). We can use this relation in combination with a given metallicity gradient along the Milky Way ([Fe/H] versus DGC /kpc), to derive a 32S/34S versus DGC/kpc relation andcompare it with our measurements.
Table 3 of Kobayashi et al. (2011) gives values for the 32S/34S ratio as a function of [Fe/H] over the range –0.5 ≤ [Fe/H] ≤ 0.0. We can derive the following relation by interpolating their data:
![\begin{equation*}\frac{{^{32}\textrm{S}}}{{^{34}\textrm{S}}} \,{=}\,{-}19.8\times{\textrm{[Fe/H]}}+23.2. \end{equation*}](/articles/aa/full_html/2020/10/aa38216-20/aa38216-20-eq44.png) (9)
(9)
Extrapolating up to [Fe/H] ≤ 0.85, we can account for the inner part of our Galaxy. Then, to relate 32S/34S to the galactocentric distance, we can make use of the relations obtained by Bovy et al. (2014) and Genovali et al. (2014), valid for 5 ≤ DGC/kpc ≤ 14–19, respectively:
![\begin{equation*}\textrm{[Fe/H]}\,{=}\,(-0.09\,{\pm}\,0.01)\times(\textit{D}\textsubscript{GC}/kpc-8)+0.03\,{\pm}\,0.01, \end{equation*}](/articles/aa/full_html/2020/10/aa38216-20/aa38216-20-eq45.png) (10)
(10)
![\begin{equation*}\textrm{[Fe/H]}\,{=}\,(-0.06\,{\pm}\,0.002)\times\textit{D}\textsubscript{GC}/kpc+0.57\,{\pm}\,0.02, \end{equation*}](/articles/aa/full_html/2020/10/aa38216-20/aa38216-20-eq46.png) (11)
(11)
and combine them with Eq. (9), to obtain the following relations:
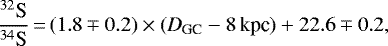 (12)
(12)
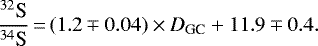 (13)
(13)
Equations (12) and (13) are plotted in Fig. 5 as hatched-shaded regions. As described in the legend, their extrapolations down to 2.53kpc, following Inno et al. (2019, their Fig. 11), for both Eqs. (10) and (11), are indicated as hatched regions only.
Additionally, we have accounted for iron abundances obtained from high-resolution near-infrared observations by Davies et al. (2009) and Najarro et al. (2009) in the inner 30 pc of the Galaxy (see also Kovtyukh et al. 2019). Their measurements are [Fe/H] = 0.1 ± 0.2 and − 0.06 ± 0.2, respectively, and we converted them to 32S/34S ratios of 21.2 ± 4 and 24.4 ± 4 by applying Eq. (9).
In summary, the relations of both Bovy et al. (2014) and Genovali et al. (2014), through Eq. (9), give results closer to those obtained from the double-isotope method (Eq. (5)), considering 12C/13C ratios by Yan et al. (2019) in combination with the 13C32S/C34S ratios from Chin et al. (1996), as can be seen in Fig. 5 (dotted blue line). In the nuclear region of the Galaxy the Davies et al. (2009) and Najarro et al. (2009) observations, when accounting for Eq. (9), are both consistent with our measurements for the +50 km s−1 Cloud and the envelope of Sgr B2(N).
6 Discussion
Among the four stable sulphur isotopes (32S, 33S, 34S, and 36S), 32S is a primary nucleus which could be synthesized in a single generation of massive stars. 32S is mostly formed during stages of hydrostatic and explosive oxygen-burning (Wilson & Matteucci 1992) either preceding a Type II supernova event or in a Type Ia supernova, where two 16O nuclei collide to form 28Si and 4He, with these products subsequently fusing to yield 32S. Type II supernovae synthesize around ten times more 32S than Type I supernovae, and occur roughly 5 times as often as those of Type I (Hughes et al. 2008). 33S is partly a secondary isotope because it can be formed by neutron capture from newly made 32S if the star not only has hydrogen and helium, but also carbon and oxygen in its initial composition (Clayton 2007). It is synthesized in hydrostatic and explosive oxygen- and neon-burning, also produced in massive stars. 34S is partly a secondary product because it can be formed from newly made 32S and 33S by neutron capture, but also during oxygen burning in supernovae like the primary isotope, 32S (Hughes et al. 2008, and references therein). While the comprehensive calculations of Woosley & Weaver (1995) identify 32S as a primary isotope, the same study also found that 34S is not a clean primary isotope; its yields decrease with decreasing metallicity. However, they identify 33S as a primary isotope, in contradiction with later findings (Clayton 2007). 36S is probably the only purely secondary sulphur isotope, being produced by s-process nucleosynthesis in massive stars (Thielemann & Arnett 1985; Mauersberger et al. 1996) and also by explosive C and He burning and via direct neutron capture from 34S, according to models (Pignatari et al. 2016). 36S could be theonly S isotope not only produced from massive stars but also, to a lesser extent, from AGB stars (Pignatari et al. 2016). However, lines from C36S are too weak to be detected in this study. Massive stars, as well as Type Ib/c and II supernovae, appear to slightly overproduce 34S and underproduce 33S compared to32S, relative to the solar vicinity (Timmes et al. 1995).
The main result of our study is that the previous trend observed by Chin et al. (1996) is broken near the centre of our Galaxy. In other words, the increase in 32S/34S with DGC is not valid in the Galactic centre region. The values of 16.3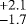 from the +50 km s−1 Cloud and 16.3 ± 3.8 and 17.9 ± 5.0 from the GC l.o.s. clouds towards Sgr B2(N) and its envelope, respectively, contrast with the expected ~5–10 regardless of the value of 12C/13C adopted (see Fig. 5) when accounting for the 13C32S/C34S ratios used in Chin et al. (1996). It is also worth mentioning that our 32S/34S isotope ratios derived from absorption lines from diffuse or translucent clouds (Sgr B2(N)) are consistent with values derived from emission lines from a prominent star-forming region with dense molecular gas (the +50 km s−1 Cloud), even though the chemistry for CS formation is completely different in those regions (see Appendix A).
from the +50 km s−1 Cloud and 16.3 ± 3.8 and 17.9 ± 5.0 from the GC l.o.s. clouds towards Sgr B2(N) and its envelope, respectively, contrast with the expected ~5–10 regardless of the value of 12C/13C adopted (see Fig. 5) when accounting for the 13C32S/C34S ratios used in Chin et al. (1996). It is also worth mentioning that our 32S/34S isotope ratios derived from absorption lines from diffuse or translucent clouds (Sgr B2(N)) are consistent with values derived from emission lines from a prominent star-forming region with dense molecular gas (the +50 km s−1 Cloud), even though the chemistry for CS formation is completely different in those regions (see Appendix A).
Frerking et al. (1980), even before the 32S/34S slope was found, suggested values for 32S/34S of ~22 for the Galactic centre. Therefore, the sulphur ratio seems to be constant, or even increases with decreasing DGC, within the inner 2.9 kpc of the Milky Way, in contrast to 12C/13C (e.g. Yan et al. 2019), 14N/15N (e.g. Adande & Ziurys 2012), and 18O/17O (Wouterloot et al. 2008; Zhang et al. 2015). Intriguingly, 32S/34S behaves in a similar way to 16O/18O (Polehampton et al. 2005), two nuclei with the bulk of their formation taking place in massive stars (≥ 10 M⊙) (Clayton 2007). This is surprising because 34S is a tracer of secondaryprocessing as 13C and 15N, and therefore its abundance is expected to increase in the same manner as observed for those isotopes.
The fact that sulphur traces late evolutionary stages of massive stars can give a clue to this difference in comparison to C and N, which give information on CNO and helium burning (Chin et al. 1996). Due to their short lives, the star formation rate of massive stars can be traced by their SN rate. Although the amount of 34S is related tometallicity, which decreases with increasing galactocentric radius especially in spiral galaxies (e.g. as observed from oxygen, Henry & Worthey 1999), leading to a trend similar to C and N, the production of 34S is mostly related to SNe II, which show a dip in the inner regions of our Galaxy and other spiral galaxies (Anderson & James 2009), in good agreement with our higher than expected 32S/34S ratios in theGalactic centre. However, these results are still under debate (see e.g. Hakobyan et al. 2009) and more observations are needed.
Another argument in favour of the above could be that metallicities traced by iron (Genovali et al. 2014; Kovtyukh et al. 2019) instead of oxygen (Henry & Worthey 1999) show a trend in good agreement with our observations (after converting [Fe/H] to DGC /kpc not only outside the central 2.53 kpc as in Fig. 5, but also in the GC region itself). This could also indicate a drop in the production of massive stars at the Galactic centre compared to the rest of the Galaxy and to less massive stars.
Our 32S/34S isotope ratioof 16.3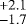 can constrain opacity estimates of sulphur-bearing molecules in the Galactic centre region and will considerably augment the confidence in theoretical modelling of dense molecular clouds (e.g. Loison et al. 2019). Such results can then be used as initial inputs to reproduce hot core conditions (Charnley 1997; Viti et al. 2004; Vidal et al. 2018).
can constrain opacity estimates of sulphur-bearing molecules in the Galactic centre region and will considerably augment the confidence in theoretical modelling of dense molecular clouds (e.g. Loison et al. 2019). Such results can then be used as initial inputs to reproduce hot core conditions (Charnley 1997; Viti et al. 2004; Vidal et al. 2018).
Our new value for this ratio can also improve synthetic spectral fitting and subsequent line identification, giving better estimations to sulphur-bearing molecules. As a prime example, we mention the recent work of Zakharenko et al. (2019): the canonical ratio of 32S/34S = 22.5 (Frerking et al. 1980) is insufficient to reproduce their data, as can be seen in their Fig. 4. Our value of 16.3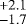 leads to an enhancement of the 34S isotopologue by a factor of 1.4 in their fit (red line), better reproducing the lines detected at 99.512 and 99.520 GHz, and thus increasing the confidence in the identification of CH3 34SH in the hot core Sgr B2(N2).
leads to an enhancement of the 34S isotopologue by a factor of 1.4 in their fit (red line), better reproducing the lines detected at 99.512 and 99.520 GHz, and thus increasing the confidence in the identification of CH3 34SH in the hot core Sgr B2(N2).
 |
Fig. 5 Sulphur isotope 32S/34S ratio variation when accounting for different carbon 12C/13C ratios as a function of galactocentric radius, DGC (e.g. Wilson & Rood 1994; Halfen et al. 2017; Milam et al. 2005; Yan et al. 2019) (for the implemented 13C32S/C34S ratios, see Chin et al. 1996). The 32S/34S to DGC relations obtained from a linear least-squares fit to weighted data (taken as 1/σ, see Sect. 5) are shown and plotted as lines with different styles (see legend). The 32S/34S ratios from this work are shown in orange, cyan, and light green. All ratios were gleaned from integrated intensity ratios except for Sgr B2(N) (see Fig. 3), where our derived integrated column density ratios are used. Possible differences between integrated column density ratios and line intensity ratios for the mean values in Sgr B2(N) fall inside the error bars. For the case of the GC l.o.s. clouds towards Sgr B2(N), their distances are uncertain and they are believed to be located within 1 kpc from the GC (see Sect. 3). As described in Sect. 5, the purple and yellow hatched-shaded loci are derived from [Fe/H] vs DGC relationsobtained by Bovy et al. (2014) and Genovali et al. (2014), after accounting for the models of Kobayashi et al. (2011); hatched-only loci correspond to an extrapolation of those relations, following Inno et al. (2019). Using the same models, two 32S/34S ratios are included. These ratios are derived from iron abundances measured in the central 30 pc of the Galaxy by Davies et al. (2009) and Najarro et al. (2009). A zoom on the results of our study displayed in the left part of the figure is shown in Fig. C.1. |
7 Summary and conclusions
From our analysis of the emission line profiles of CS, 13CS, C34S, 13C34S J = 2–1, of CS and C34S J = 3–2, and of 13CS and C34S J = 6–5 in the +50 km s−1 Cloud and CS, 13CS, C34S, 13C34S J = 2–1 observed in absorption towards Sgr B2(N), we obtain the following main results:
-
From measurements of the J = 2–1 lines of 12C34S J = 2–1 and 13C34S J = 2–1, we have obtained a 12C/13C isotope ratio of 22.1
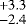 near the centre of our Galaxy, in good agreement with previous estimations.
near the centre of our Galaxy, in good agreement with previous estimations. -
For the +50 km s−1 Cloud we obtain a 34S/33S ratio of 4.3 ± 0.2, derived from C34S J = 2–1 and C33S J = 2–1 column densities. If we take the integrated intensities instead, this ratio would be 4.2 ± 0.2, consistent with the lower end of the range of ratios obtained by Chin et al. (1996), who derived 34S/33S ratios between 4.38 and 7.53, irrespective of Galactic radius. This might be a first indication of a gradient with rising ratios as a function of increasing galactocentric distance, but data from the Galactic disc have to become more precise for a definite result.
-
From theJ = 2–1 13CS and 13C34S emission lines in the +50 km s−1 Cloud, we derive, for the first time in a direct way, a 32S/34S column density ratio of 16.3
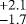 , which is consistent with the 32S/34S ratio derived from the J = 6–5 and J = 2–1 13CS and C34S isotopologues when accounting for the above-mentioned 12C/13C ratio. Due to possible CS fractionation, the above ratio might be underestimated by less than
~10%.
, which is consistent with the 32S/34S ratio derived from the J = 6–5 and J = 2–1 13CS and C34S isotopologues when accounting for the above-mentioned 12C/13C ratio. Due to possible CS fractionation, the above ratio might be underestimated by less than
~10%. -
We were able to directly obtain a 32S/34S ratio of 17.9 ± 5.0 for the envelope of Sgr B2(N), from the isotopologues 13CS and 13C34S in the J = 2–1 lines. Moreover, we have obtained a 32S/34S ratio of 16.3 ± 3.8 for the GC l.o.s. clouds towards Sgr B2(N) through the CS and C34S J = 2–1 isotopologue lines, when CS is not optically thick. Those ratios are prone to increase by up to ~15%, when taking CS fractionation effects into account.
-
Making use of the network presented in Loison et al. (2019), we significantly improved CS fractionation estimations under conditions similar to those taking place in massive molecular clouds, young stellar objects, and diffuse or translucent cold molecular clouds.
-
Comparing the sulphur ratios from this work with data available in the literature that were obtained from larger distances to Sgr A* and showed a decrease in 32S/34S towards the Galactic centre, we can confidently establish that this decrease terminates at least at a distance of 100 pc to Sgr A*, at the position of Sgr B2(N) (Reid et al. 2009). This is different from trends previously reported for 12C/13C, 14N/15N, and 18O/17O.
-
Our improved 32S/34S isotope ratio will considerably augment the confidence in theoretical modelling for hot cores and in synthetic spectral fitting and subsequent line identification, giving better constraints for the intensities of sulphur-bearing molecules.
Overall, our results suggest that processes occurring at late evolutionary stages of massive stars could be better traced by sulphur isotopologues instead of the most commonly studied CNO isotopes. Further observations targeting isotopologue ratios with distinct nucleogenesis like 32S/34S (i.e. primary species versus secondary isotopologues) produced in advanced massive stars and SNe II can lead to a better understanding of environmental discrepancies between the solar neighbourhood and the inner Galaxy. This will allow, for example, a connection between metallicity gradients traced by iron (Genovali et al. 2014; Kovtyukh et al. 2019) and observations of SNe II (Anderson & James 2009). The above could be also extrapolated to external galaxies, especially with the advent of a new generation of facilities.
Acknowledgements
We appreciate the important suggestions by the anonymous referee that helped to express this research in a clearer and more comprehensive way. PH is a member of and received financial support for this research from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne. This work makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00017.S, ADS/JAO.ALMA#2012.1.00012.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. The interferometric data are available in the ALMA archive at https://almascience.eso.org/aq/. This paper is partly based on data acquired with the Atacama PathfinderEXperiment (APEX). APEX is a collaboration between the Max Planck Institute for Radio Astronomy, the European Southern Observatory, and the Onsala Space Observatory. Part of this work is based on observations carried out with the IRAM 30-m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). We acknowledge the IRAM staff for the support and help offered during all the applicable observational runs.
Appendix A Chemical aspects
In diffuse clouds, it has been suggested that CS forms mainly by exothermic ion-molecule reactions of S+ with CH and C2 (Drdla et al. 1989; van Dishoeck & Blake 1998). However, these species require to be one order of magnitude more abundant than currently observed in order to reproduce the observed quantities of CS (Lucas & Liszt 2002). Currently, CS formation is believed to be dominated by the exothermic reaction (Drdla et al. 1989; Lucas & Liszt 2002; Montaigne et al. 2005; Laas & Caselli 2019)
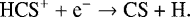 (A.1)
(A.1)
Subsequently, the dominant destruction route of CS is photodissociation, with destruction by He+ being only significant in denser clouds (Drdla et al. 1989).
At higher densities, CS is mainly produced through neutral–neutral reactions with atomic sulfur such as (Fuente et al. 2016; Vidal et al. 2018; Laas & Caselli 2019)
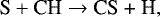 (A.2a)
(A.2a)
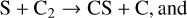 (A.2b)
(A.2b)
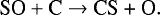 (A.2c)
(A.2c)
The dissociative recombination (DR) of HCS+ becomes the main path for CS destruction at low temperatures because HCS+ is mainly produced through protonation of CS and its DR leads mainly to S+CH and not to CS+H (Montaigne et al. 2005).
At higher temperatures, such as in hot cores and hot corinos for which recent models suggest some changes in sulfur chemistry (Vidal et al. 2018), CS is also destroyed by atomic oxygen:
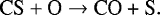 (A.3)
(A.3)
This reaction is supposed to be negligible at low temperature due to the presence of a barrier (Lilenfeld & Richardson 1977; González et al. 1996). However the value of the barrier is questionable (Adriaens et al. 2010) so that this reaction may not be completely negligible at low temperature. Apart from this reaction, and despite the recent advances in the investigation of sulfur species in the interstellar medium (Fuente et al. 2016; Vidal et al. 2018; Laas & Caselli 2019), there are still large uncertainties with respect to CS and HCS+ chemistry.
Recent studies agree with the above reactions, but indicate that the dominant mechanism also depends on the cosmic ray ionization rates (CRIR). At high CRIR, which may be typical of the central parts of giant spiral galaxies, reactions (A.2c) and (A.3) dominate CS formation and destruction, but at lower CRIR the following reaction (route (A.4)) becomes dominant for the destruction of CS (Kelly et al. 2015; Viti 2016):
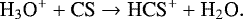 (A.4)
(A.4)
In hot cores and corinos, recent models suggest some deviations from the above-mentioned routes of sulfur chemistry (Vidal et al. 2018). Specifically for CS, the main paths for its formation and destruction continue being Eqs. (A.2c) and (A.3), respectively.CS is initially destroyed by atomic oxygen (Eq. (A.3)) both at 100 and 300 K, on timescales of 104 and 103 yr, respectively.Nevertheless, CS is then also produced by
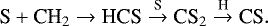 (A.5)
(A.5)
Appendix B Excitation temperatures
As mentioned in Sects. 4.1 and 4.1.3, we assumed the same excitation temperatures (Tex) in all our opacity calculations. This is argued by the low opacity of the isotopologues used to make such calculations.
 |
Fig. B.1 Excitation temperatures (Tex) as a functionof opacity (τ) for 13CS J = 2–1 (top) and C34S J = 3–2 (bottom). Molecular column densities range between 1011 and 1015 cm−2, and the kinetic temperature is 80, 200, and 400 K, represented by blue, green, and red lines, respectively. Δ(Tex) refers to the Tex maximum variation between τ = 0.04 and 0.15 (delineated by dashed vertical red lines). |
Let us take an opacity (τ) ranging between 0.04 and 0.15 (see Table 2) for both 13CS J = 2–1 and C34S J = 3–2 with which we obtained theopacity for 12CS J = 2–1 andJ = 3–2, respectively. As can be seen in Fig. B.1, the variations in Tex within this range falls below 0.64 K. Considering that this temperature will be inside an exponential as denominator of a fraction and, furthermore, multiplied by the Boltzmann constant (see Eq. (80) in Mangum & Shirley 2015), is reasonable to assume that Tex variations are negligible for the scope of this work.
Calculations were done with a python version6 of RADEX (van der Tak et al. 2007), a statistical equilibrium molecular radiative transfer code. Our inputs were a kinetic temperature of 80, 200, and 400 K; 100 equally spaced values for the column density from 1011 to 1015 cm−2; and a H2 volumetric density of 5 × 104 cm−3, in an attempt to emulate the conditions of the +50 km s−1 Cloud (see Sect. 3). 13CS and C34S collision rates were taken from the Leiden Atomic and Molecular Database (LAMDA, Schwörer et al. 2019), which in turn uses calculations made by Lique et al. (2006).
Appendix C Zoom in for Fig. 5
We plot ourown data from Fig. 5 in a magnified way. Data values for the l.o.s. clouds towards Sgr B2(N) and its envelope are given in Table 4. The integrated intensity 32S/34S ratio of the +50 km s−1 Cloud (18.6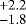 ) comes from Sect. 4.1.2.
) comes from Sect. 4.1.2.
 |
Fig. C.1 Sulphur isotope 32S/34S ratio for the new data presented in this paper as a function of galactocentric radius, DGC. |
Appendix D Gaussian fitting
We preferred to use the lmfit package instead of Gildas7, for example, because the former has some improvements related to uncertainty calculations. While both use minimization, Simplex and Gradient methods, because of the use of the Minimize package8, lmfit has additional functions and packages to ensure a proper uncertainty estimation “even in the most difficult cases”9. We compared the uncertainties from Gildas and lmfit; those derived based on Gildas are lower than those from lmfit by a small percentage (well within the uncertainties), and at the same time the use of Gildas results in a less successful fit in certain cases (not shown). Given the rich available documentation for lmfit, we opted for the lmfit-based fitting and associated uncertainty determination.
References
- Adande, G. R., & Ziurys, L. M. 2012, ApJ, 744, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Adriaens, D. A., Goumans, T. P. M., Catlow, C. R. A., & Brown, W. A. 2010, J. Phys. Chem. C, 114, 1892 [CrossRef] [Google Scholar]
- Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [Google Scholar]
- Agúndez, M., Marcelino, N., Cernicharo, J., Roueff, E., & Tafalla, M. 2019, A&A, 625, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, J. P., & James, P. A. 2009, MNRAS, 399, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Ao, Y., Henkel, C., Menten, K. M., et al. 2013, A&A, 550, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armijos-Abendaño, J., Martín-Pintado, J., Requena-Torres, M. A., Martín, S., & Rodríguez-Franco, A. 2015, MNRAS, 446, 3842 [NASA ADS] [CrossRef] [Google Scholar]
- Bayet, E., Viti, S., Williams, D. A., & Rawlings, J. M. C. 2008, ApJ, 676, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Bayet, E., Aladro, R., Martín, S., Viti, S., & Martín-Pintado, J. 2009, ApJ, 707, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Müller, H. S. P., Menten, K. M., Schilke, P., & Comito, C. 2013, A&A, 559, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Müller, H. S. P., Garrod, R. T., & Menten, K. M. 2016, A&A, 587, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2019, A&A, 628, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfand, M., Belloche, A., Menten, K. M., Garrod, R. T., & Müller, H. S. P. 2017, A&A, 604, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfand, M., Belloche, A., Garrod, R. T., et al. 2019, A&A, 628, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bovy, J., Nidever, D. L., Rix, H.-W., et al. 2014, ApJ, 790, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B. 1997, ApJ, 481, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Chin, Y. N., Henkel, C., Whiteoak, J. B., Langer, N., & Churchwell, E. B. 1996, A&A, 305, 960 [NASA ADS] [Google Scholar]
- Clayton, D. 2007, Handbook of Isotopes in the Cosmos (Cambridge: Cambridge University Press) [Google Scholar]
- Corby, J. F., McGuire, B. A., Herbst, E., & Remijan, A. J. 2018, A&A, 610, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dale, J. E., Kruijssen, J. M. D., & Longmore, S. N. 2019, MNRAS, 486, 3307 [CrossRef] [Google Scholar]
- Davies, B., Origlia, L., Kudritzki, R.-P., et al. 2009, ApJ, 694, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Drdla, K., Knapp, G. R., & van Dishoeck, E. F. 1989, ApJ, 345, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectr., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrière, K. 2012, A&A, 540, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frerking, M. A., Wilson, R. W., Linke, R. A., & Wannier, P. G. 1980, ApJ, 240, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Fuente, A., Cernicharo, J., Roueff, E., et al. 2016, A&A, 593, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaume, R. A., Claussen, M. J., de Pree, C. G., Goss, W. M., & Mehringer, D. M. 1995, ApJ, 449, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Genovali, K., Lemasle, B., Bono, G., et al. 2014, A&A, 566, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., Henkel, C., Ao, Y., et al. 2016, A&A, 586, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginsburg, A., Bally, J., Barnes, A., et al. 2018, ApJ, 853, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., & Linke, R. A. 1981, ApJ, 245, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., Lis, D. C., Hills, R., & Lasenby, J. 1990, ApJ, 350, 186 [NASA ADS] [CrossRef] [Google Scholar]
- González, M., Hijazo, J., Novoa, J. J., & Sayós, R. 1996, J. Chem. Phys., 105, 10999 [CrossRef] [Google Scholar]
- Gravity Collaboration (Abuter, R., et al.) 2018, A&A, 615, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greaves, J. S., & Williams, P. G. 1994, A&A, 290, 259 [NASA ADS] [Google Scholar]
- Güsten, R., Walmsley, C. M., Ungerechts, H., & Churchwell, E. 1985, A&A, 142, 381 [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hakobyan, A. A., Mamon, G. A., Petrosian, A. R., Kunth, D., & Turatto, M. 2009, A&A, 508, 1259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Halfen, D. T., Woolf, N. J., & Ziurys, L. M. 2017, ApJ, 845, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Hawkins, I., & Jura, M. 1987, ApJ, 317, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Henkel, C., Guesten, R., & Gardner, F. F. 1985, A&A, 143, 148 [Google Scholar]
- Henkel, C., Asiri, H., Ao, Y., et al. 2014, A&A, 565, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, R. B. C., & Worthey, G. 1999, PASP, 111, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Hincelin, U., Wakelam, V., Hersant, F., et al. 2011, A&A, 530, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hughes, G. L., Gibson, B. K., Carigi, L., et al. 2008, MNRAS, 390, 1710 [NASA ADS] [Google Scholar]
- Indriolo, N., Neufeld, D. A., Gerin, M., et al. 2015, ApJ, 800, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Inno, L., Urbaneja, M. A., Matsunaga, N., et al. 2019, MNRAS, 482, 83 [Google Scholar]
- Johansson, L. E. B., Olofsson, H., Hjalmarson, A., Gredel, R., & Black, J. H. 1994, A&A, 291, 89 [NASA ADS] [Google Scholar]
- Kelly, G., Viti, S., Bayet, E., Aladro, R., & Yates, J. 2015, A&A, 578, A70 [CrossRef] [EDP Sciences] [Google Scholar]
- Klein, T., Ciechanowicz, M., Leinz, C., et al. 2014, IEEE Trans. Terahertz Sci. Technol., 4, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Karakas, A. I., & Umeda, H. 2011, MNRAS, 414, 3231 [NASA ADS] [CrossRef] [Google Scholar]
- Kovtyukh, V. V., Andrievsky, S. M., Martin, R. P., et al. 2019, MNRAS, 489, 2254 [CrossRef] [Google Scholar]
- Laas, J. C., & Caselli, P. 2019, A&A, 624, A108 [CrossRef] [EDP Sciences] [Google Scholar]
- Le Petit, F., Ruaud, M., Bron, E., et al. 2016, A&A, 585, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levshakov, S. A., Centurión, M., Molaro, P., & Kostina, M. V. 2006, A&A, 447, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lilenfeld, H. V., & Richardson, R. J. 1977, J. Chem. Phys., 67, 3991 [CrossRef] [Google Scholar]
- Linke, R. A., & Goldsmith, P. F. 1980, ApJ, 235, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Lique, F., Spielfiedel, A., & Cernicharo, J. 2006, A&A, 451, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lis, D. C., & Goldsmith, P. F. 1990, ApJ, 356, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J.-C., Wakelam, V., Gratier, P., et al. 2019, MNRAS, 485, 5777 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, R., & Liszt, H. S. 2002, A&A, 384, 1054 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [Google Scholar]
- Maret, S., Hily-Blant, P., Pety, J., Bardeau, S., & Reynier, E. 2011, A&A, 526, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martín, S., Aladro, R., Martín-Pintado, J., & Mauersberger, R. 2010, A&A, 522, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martín-Pintado, J., Rizzo, J. R., de Vicente, P., Rodríguez-Fernández, N. J., & Fuente, A. 2001, ApJ, 548, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Mauersberger, R., Henkel, C., Wilson, T. L., & Harju, J. 1989, A&A, 226, L5 [NASA ADS] [Google Scholar]
- Mauersberger, R., Henkel, C., Langer, N., & Chin, Y. N. 1996, A&A, 313, L1 [Google Scholar]
- Mauersberger, R., Ott, U., Henkel, C., Cernicharo, J., & Gallino, R. 2004, A&A, 426, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, T. J., & Herbst, E. 1990, A&A, 231, 466 [NASA ADS] [Google Scholar]
- Mills, E. A. C., & Morris, M. R. 2013, ApJ, 772, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Bally, J., Glover, S., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 125 [Google Scholar]
- Montaigne, H., Geppert, W. D., Semaniak, J., et al. 2005, ApJ, 631, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M., & Serabyn, E. 1996, ARA&A, 34, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, S., Guélin, M., Dumke, M., Lucas, R., & Combes, F. 2006, A&A, 458, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Belloche, A., Menten, K. M., Comito, C., & Schilke, P. 2008, J. Mol. Spectr., 251, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Belloche, A., Xu, L.-H., et al. 2016, A&A, 587, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Najarro, F., Figer, D. F., Hillier, D. J., Geballe, T. R., & Kudritzki, R. P. 2009, ApJ, 691, 1816 [NASA ADS] [CrossRef] [Google Scholar]
- Nummelin, A., Bergman, P., Hjalmarson, Å., et al. 1998, ApJS, 117, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Pignatari, M., Herwig, F., Hirschi, R., et al. 2016, ApJS, 225, 24 [Google Scholar]
- Polehampton, E. T., Baluteau, J. P., & Swinyard, B. M. 2005, A&A, 437, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., Brunthaler, A., & Xu, Y. 2009, ApJ, 705, 1548 [NASA ADS] [CrossRef] [Google Scholar]
- Remijan, A. J., Hollis, J. M., Lovas, F. J., et al. 2008, ApJ, 675, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Requena-Torres, M. A., Martín-Pintado, J., Martín, S., & Morris, M. R. 2008, ApJ, 672, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Ritchey, A. M., Federman, S. R., & Lambert, D. L. 2011, ApJ, 728, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., Loison, J. C., & Hickson, K. M. 2015, A&A, 576, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruze, J. 1966, IEEE Proc., 54, 633 [Google Scholar]
- Sánchez-Monge, Á., Schilke, P., Schmiedeke, A., et al. 2017, A&A, 604, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandqvist, A., Larsson, B., Hjalmarson, Å., et al. 2008, A&A, 482, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandqvist, A., Larsson, B., Hjalmarson, Å., et al. 2015, A&A, 584, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmiedeke, A., Schilke, P., Möller, T., et al. 2016, A&A, 588, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwörer, A., Sánchez-Monge, Á., Schilke, P., et al. 2019, A&A, 628, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, D., & Adams, N. G. 1980, ApJ, 242, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Thiel, V. 2019, PhD thesis, University of Bonn, Germany [Google Scholar]
- Thiel, V., Belloche, A., Menten, K. M., et al. 2019, A&A, 623, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thielemann, F. K., & Arnett, W. D. 1985, ApJ, 295, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1995, ApJS, 98, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuboi, M., Handa, T., & Ukita, N. 1999, ApJS, 120, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Uehara, K., Tsuboi, M., Kitamura, Y., Miyawaki, R., & Miyazaki, A. 2019, ApJ, 872, 121 [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., & Blake, G. A. 1998, ARA&A, 36, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Quénard, D., Le Gal, R., et al. 2018, MNRAS, 478, 5519 [Google Scholar]
- Vidal, T. H. G., Loison, J.-C., Jaziri, A. Y., et al. 2018, MNRAS, 469, 435 [Google Scholar]
- Viti, S. 2016, IAU Symp., 17 [Google Scholar]
- Viti, S., Collings, M. P., Dever, J. W., McCoustra, M. R. S., & Williams, D. A. 2004, MNRAS, 354, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., Duschl, W. J., & Zylka, R. 2003, Astron. Nachr. Suppl., 324, 613 [CrossRef] [Google Scholar]
- Wakelam, V., Herbst, E., & Selsis, F. 2006, A&A, 451, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Smith, I. W. M., Herbst, E., et al. 2010, Space Sci. Rev., 156, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, M., Henkel, C., Chin, Y. N., et al. 2004, A&A, 422, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, K. S., Bourke, T. L., Hogerheijde, M. R., et al. 2013, A&A, 558, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whiteoak, J. B., & Gardner, F. F. 1979, MNRAS, 188, 445 [NASA ADS] [Google Scholar]
- Wilson, T. L.,& Matteucci, F. 1992, A&ARv, 4, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L.,& Rood, R. 1994, ARA&A, 32, 191 [Google Scholar]
- Wirström, E. S., Bergman, P., Black, J. H., et al. 2010, A&A, 522, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Wouterloot, J. G. A., Henkel, C., Brand, J., & Davis, G. R. 2008, A&A, 487, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, Y. T., Zhang, J. S., Henkel, C., et al. 2019, ApJ, 877, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Zakharenko, O., Lewen, F., Ilyushin, V. V., et al. 2019, A&A, 627, A41 [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, J. S., Sun, L. L., Riquelme, D., et al. 2015, ApJS, 219, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B., Turner, B. E., Johnson, D. R., et al. 1975, ApJ, 196, L99 [NASA ADS] [CrossRef] [Google Scholar]
Calculated following the table in https://www.iram.fr/GENERAL/calls/w08/w08/node20.html
See https://pypi.org/project/ndradex/ for a full description. We have used the Grid RADEX run option.
All Tables
Some observational and physical parameters for the five measured CS isotopologue transitions in the +50 km s−1 Cloud and the four transitions from the l.o.s. clouds towards Sgr B2(N), which are also located in the Galactic centre region.
Line parameters for the nine measured CS isotopologue transitions in the +50 km s−1 Cloud.
Summary for our carbon and sulphur column density ratio calculations in the +50 km s−1 Cloud.
Isotopic ratios determined in the envelope of Sgr B2(N) (13CS/13C34S and C34S/13C34S) and in GC clouds along the line of sight to Sgr B2(N) (CS/C34S) using absorption lines of CS isotopologues.
All Figures
 |
Fig. 1 ALMA continuum map of Sgr B2(N) at 85 GHz. The black contour lines show the flux density levels at 3σ, 6σ, 12σ, and 24σ and the dotted lines indicate −3σ, where σ is the rms noise level of 5.4 mJy beam−1. The white crosses denote the positions of the two main hot cores, Sgr B2(N1) and Sgr B2(N2). The black cross, located between the white ones, indicates the phase centre. The green crosses show peaks of continuum emission selected for our absorption study. They label the ultra-compact H II region K4, two peaks in the shell of the H II region K6 and one peak in the shell of the H II region K5 (Gaume et al. 1995). The green ellipse in the lower left corner shows the size of the synthesized beam of ~1. ′′6 (see Table 1). |
| In the text | |
 |
Fig. 2 From left to right and top to bottom: observed line profiles of the J = 2–1 transitions of CS, C34S, 13CS, C33S, and 13C34S, the J = 3–2 transitions of CS and C34S, and the J = 6–5 transitions of C34S and 13CS, in the +50 km s−1 Cloud (EQ J2000: 17h45m50.20s, −28°59′ 41.1′′). Measured profiles are shown in black; the resulting Gaussian fitting is presented in red. For the CS J = 2–1 and J = 3–2 lines, a double Gaussian fitting was performed to account for the self-absorbed component (in green) in an attempt to retrieve the undisturbed emission line (in blue) (see Sect. 4.1). All the other lines are well fitted by a single component. In the case of 13C34S J = 2–1, the companion line is subtracted because of its relatively strong emission and potential contamination. The dashed vertical linesdenote the 13CS J = 2–1 peak position (46.94 km s−1, see Table 2). Dash-dotted red lines denote the redshifted velocity (vr = 63 km s−1) at which the CS J = 2–1 and J = 3–2 transition lines are not affected by self-absorption (see Sect. 4.1). Nearby lineslikely observed are labelled. |
| In the text | |
 |
Fig. 3 EMoCA absorption spectra of four isotopologues of CS towards four positions in Sgr B2(N). The offsets (in units of arcseconds, see Table 4 and Fig. 1) from the phase centre are indicated at the right of each row. The observed spectra are shown in black and the synthetic spectra in magenta, purple, green, and blue, depending on the position. The synthetic spectra were obtained by Thiel (2019). The dotted vertical lines indicate the velocities atwhich we determined the isotopic ratios using the corresponding isotopologue. The velocities are listed in Table 4. The grey horizontal lines show the continuum level. |
| In the text | |
 |
Fig. 4 Calculated abundance ratios of gas phase species C32S/C34S as a functionof cloud age for conditions in (a) the +50 km s−1 Cloud, (b) the envelope of Sgr B2(N), and (c) l.o.s. cloudstowards Sgr B2(N) (see Sect. 4.2 for details). Low values for the gas temperatures were chosen to illustrate an upper limit for fractionation. The vertical grey loci represent values given by the most probable chemical age. The observational results from this study are illustrated as horizontal light grey rectangles (including the uncertainties). |
| In the text | |
 |
Fig. 5 Sulphur isotope 32S/34S ratio variation when accounting for different carbon 12C/13C ratios as a function of galactocentric radius, DGC (e.g. Wilson & Rood 1994; Halfen et al. 2017; Milam et al. 2005; Yan et al. 2019) (for the implemented 13C32S/C34S ratios, see Chin et al. 1996). The 32S/34S to DGC relations obtained from a linear least-squares fit to weighted data (taken as 1/σ, see Sect. 5) are shown and plotted as lines with different styles (see legend). The 32S/34S ratios from this work are shown in orange, cyan, and light green. All ratios were gleaned from integrated intensity ratios except for Sgr B2(N) (see Fig. 3), where our derived integrated column density ratios are used. Possible differences between integrated column density ratios and line intensity ratios for the mean values in Sgr B2(N) fall inside the error bars. For the case of the GC l.o.s. clouds towards Sgr B2(N), their distances are uncertain and they are believed to be located within 1 kpc from the GC (see Sect. 3). As described in Sect. 5, the purple and yellow hatched-shaded loci are derived from [Fe/H] vs DGC relationsobtained by Bovy et al. (2014) and Genovali et al. (2014), after accounting for the models of Kobayashi et al. (2011); hatched-only loci correspond to an extrapolation of those relations, following Inno et al. (2019). Using the same models, two 32S/34S ratios are included. These ratios are derived from iron abundances measured in the central 30 pc of the Galaxy by Davies et al. (2009) and Najarro et al. (2009). A zoom on the results of our study displayed in the left part of the figure is shown in Fig. C.1. |
| In the text | |
 |
Fig. B.1 Excitation temperatures (Tex) as a functionof opacity (τ) for 13CS J = 2–1 (top) and C34S J = 3–2 (bottom). Molecular column densities range between 1011 and 1015 cm−2, and the kinetic temperature is 80, 200, and 400 K, represented by blue, green, and red lines, respectively. Δ(Tex) refers to the Tex maximum variation between τ = 0.04 and 0.15 (delineated by dashed vertical red lines). |
| In the text | |
 |
Fig. C.1 Sulphur isotope 32S/34S ratio for the new data presented in this paper as a function of galactocentric radius, DGC. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


