| Issue |
A&A
Volume 641, September 2020
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201937232 | |
| Published online | 16 September 2020 | |
ALMA resolves molecular clouds in metal-poor Magellanic Bridge A★
1
Departamento de Astronomía, Universidad de Chile,
Santiago,
Chile
e-mail: maria.valdivia@ug.uchile.cl
2
University of Maryland,
MD,
USA
3
Observatorio Astronómico de Córdoba,
UNC,
Argentina
4
Joint Alma Observatory (JAO),
Alonso de Córdova 3107,
Vitacura,
Santiago,
Chile
Received:
2
December
2019
Accepted:
22
June
2020
Context. The Magellanic Bridge is a tidal feature located between the Magellanic Clouds, containing young stars formed in situ. Its proximity allows high-resolution studies of molecular gas, dust, and star formation in a tidal low-metallicity environment.
Aims. Our goal is to characterize gas and dust emission in Magellanic Bridge A, the source with the highest 870 μm excess of emission found in single-dish surveys.
Methods. Using the ALMA telescope including the Morita Array, we mapped a 3′ field of view centered on the Magellanic Bridge A molecular cloud, in 1.3 mm continuum emission and 12CO(2−1) line emission at subparsec resolution. This region was also mapped in continuum at 870 μm and in 12CO(2−1) line emission at ~6 pc resolution with the APEX telescope. To study its dust properties, we also use archival Herschel and Spitzer data. We combine the ALMA and APEX 12CO(2−1) line cubes to study the molecular gas emission.
Results. Magellanic Bridge A breaks up into two distinct molecular clouds in dust and 12CO(2−1) emission, which we call North and South. Dust emission in the North source, according to our best parameters from fitting the far-infrared fluxes, is ≈3 K colder than in the South source in correspondence to its less developed star formation. Both dust sources present large submillimeter excesses in LABOCA data: according to our best fits the excess over the modified blackbody (MBB) fit to the Spitzer/Herschel continuum is E(870 μm) ~ 7 and E(870 μm) ~ 3 for the North and South sources, respectively. Nonetheless, we do not detect the corresponding 1.3 mm continuum with ALMA. Our limits are compatible with the extrapolation of the MBB fits, and therefore we cannot independently confirm the excess at this longer wavelength. The 12CO(2−1) emission is concentrated in two parsec-sized clouds with virial masses of around 400 and 700 M⊙. Their bulk volume densities are n(H2) ~ 0.7−2.6 × 103 cm−3, higher than typical bulk densities of Galactic molecular clouds. The 12CO luminosity to H2 mass conversion factor αCO is 6.5 and 15.3 M⊙ (K km s−1 pc2)−1 for the North and South clouds, calculated using their respective virial masses and 12CO(2−1) luminosities. Gas mass estimates from our MBB fits to dust emission yields masses M ~ 1.3 × 103 M⊙ and 2.9 × 103 M⊙ for North and South, respectively, a factor of ~4 higher than the virial masses we infer from 12CO.
Key words: ISM: clouds / Magellanic Clouds / ISM: molecules / submillimeter: ISM
Reduced maps and images are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/641/A97
© ESO 2020
1 Introduction
The Magellanic Bridge was first described through neutral hydrogen (H I) observations as a gaseous bridge joining the Large Magellanic Cloud (LMC) and Small Magellanic Cloud (SMC; Hindman et al. 1963). It is a filamentary structure with lumps, holes, and shells, with an extent of 15 to 21 kpc, a total gas mass of ~ 1.5 × 108 M⊙, and an H I column density between 1020 and 1021 cm−2 (Staveley-Smith et al. 1998; Muller et al. 2003a). Simulations suggest that the Magellanic Bridge is the result of a close gravitational interaction between the LMC and SMC that happened around 200–300 Myrs ago (Murai & Fujimoto 1980; Gardiner et al. 1994; Besla et al. 2012). Star formation has and is taking placein the Magellanic Bridge: there are young stars and clusters of less than 100 Myr in age (Bica & Schmitt 1995; Harris 2007; Bica et al. 2015; Kalari et al. 2018) and evidence of current star formation in the form of Hα filamentary shells (Muller & Parker 2007) and young stellar objects (YSOs; Chen et al. 2014). Its metallicity is low and seems to present a gradient, from values similar to the SMC main body (Z ~1∕5 Z⊙, Lee et al. 2005) to about half (or even less) of the SMC metallicity (Z ~ 1∕10 Z⊙, Rolleston et al. 2003; Lehner et al. 2008). At a distance of almost 60 kpc, using the SMC as reference (Harries et al. 2003; Cioni et al. 2000), the Magellanic Bridge is the closest low-metallicity tidally influenced region outside of a dwarf galaxy; it allows detailed studies of star formation under unique physical conditions.
Stars form in molecular clouds, which are composed of molecular hydrogen gas (H2) and dust. Studying the molecular component of low-metallicity galaxies helps to understand the process of star formation in metal-poor environments, like those present in high-redshift galaxies. To this end, the molecular component of the Magellanic Bridge has been studied through carbon monoxide (CO) and dust emission, both tracers of H2 gas, but these emissions are weaker than in the SMC main body (Meixner et al. 2013; Muller et al. 2014), and are therefore harder to detect.
The first study that detected a molecular cloud in the Magellanic Bridge was done by Muller et al. (2003b), using 12 CO(1−0) observations. The detection was found in a region with an H I intensity peak and where the 60-to-100 μm intensity ratio S60μm∕S100μm < 0.2. Using a different criteria, matching H I and 100 μm intensity peaks, Mizuno et al. (2006) detected seven more 12CO clouds which, together with the Muller et al. (2003b) detected cloud, have 12CO(1−0) intensities between 30 and 140 mK km s−1 in a 2.′6 beam. These molecular clouds have narrow velocity widths (Δv ≲ 2 km s−1), similar to the clouds in the metal-poor far edges of our galaxy, and molecular masses derived from their CO luminosities between (1− 7) × 103 M⊙ (Mizuno et al. 2006), similar to the masses of nearby molecular clouds in the Milky Way (Mizuno et al. 1995, 2001). The eight clouds have been labeled from A to H, which is the naming convention that we use in this work. Mizuno et al. (2006) concluded that these clouds are a recent product of the Magellanic Bridge ISM and not remnants from the SMC. All of the clouds except for one are within a few tens of parsecs to the closest OB stellar association (Bica & Schmitt 1995). YSO candidates have been found towards all of these sources, except for cloud D (Chen et al. 2014), showing the correlation of these molecular clouds with local star formation.
Dust, which is heated by star radiation and emits continuum at far-infrared (FIR) and millimeter wavelengths, also traces H2 gas. Observations in the FIR and millimeter regime have been done in the part of the Magellanic Bridge that is closest to the SMC, a section usually referred to as the SMC Tail (Gordon et al. 2011; Meixner et al. 2013). These observations reveal that dust in the Magellanic Bridge has a lower brightness than the SMC dust and a gas-to-dust ratio of ~1200, similar to the SMC gas-to-dust ratio (Gordon et al. 2011). Gordon et al. (2009) determined that dust in the Mizuno et al. (2006) molecular clouds B and C have temperatures of around 16–17 K and a gas-to-dust ratio lower than the rest of the Bridge, between 250 and 440.
The focus of our work is Magellanic Bridge source A, the molecular cloud that is closest to the SMC (~ 3.5 kpc from the main body of the SMC; see Fig. 1). Magellanic Bridge A is one of the faintest of the eight molecular clouds detected by Mizuno et al. (2006), with a 12CO(1−0) intensity of 30 mK km s−1 and a molecular mass of 103 M⊙, estimated from its 12CO(1−0) emission. Magellanic Bridge A is located between two faint compact H II regions (Muller & Parker 2007) and is within a stellar association (Bica & Schmitt 1995). There is recent star formation in this region, revealed by two YSO candidates within the molecular cloud (Chen et al. 2014) and its proximity to H II regions and 24 μm bright sources (Muller et al. 2014). Verdugo (2012) found that Magellanic Bridge A has very high excess emission at 870 μm in comparison with other dust sources in the LMC and SMC.
The goal of this work is to characterize the gas and dust present in the Magellanic Bridge A molecular cloud at subparsec resolution. The Atacama Large Millimeter/Submillimeter Array (ALMA) telescope has the power to resolve gas and dust emission at the desired scales. With this characterization we can obtain the molecular gas properties in a region that is similar to low-metallicity galaxies at high redshift. In addition, we investigate the dust component of Magellanic Bridge A to characterize the submillimeter excess detected in this region (Verdugo 2012). To achieve our goal, we use high-resolution ALMA observations of Magellanic Bridge A together with observations from the Atacama Pathfinder Explorer (APEX) telescope, which reveal molecular gas and dust emission.
This article is organized as follows. In Sect. 2 we present new ALMA B6 continuum and 12CO(2−1) line observations and complementary APEX observations, together with details of their reduction and imaging. In Sect. 3 we describe the submillimeter and millimeter emission and characterize the dust emission through its spectral energy distribution. In Sect. 4 we describe the molecular gas emission using 12CO(2−1) and determine the physical properties of the detected 12CO(2−1) sources. In Sect. 5 we discuss the results obtained for molecular gas and dust and compare them with previous observations of the ISM in Magellanic Bridge A. We summarize our results in Sect. 6.
 |
Fig. 1 Herschel 160 μm map of the SMC from Meixner et al. (2013). White contours represent the H I column density map constructed using the Parkes Galactic All-Sky Survey (GASS) first data release (McClure-Griffiths et al. 2009). The contour levels are (1, 1.5, 2, 2.5, and 3) × 1021 cm−2. The yellow circular region gives the position of Magellanic Bridge A (labeled MagBridge A). |
2 Observations and data reduction
In the following section, we describe the observations used to study the millimeter and submillimeter emission from Magellanic Bridge A. We summarize the main properties of the observations and describe the reduction process for the new data presented in this work.
2.1 ALMA observations
Magellanic Bridge A was observed with ALMA, located at Llano de Chajnantor in Atacama, Chile. We used Band 6 observations taken with the 12m array and the 7m array (also known as the Morita Array), which include continuum emission observations and the 12CO(2−1) line emission data. In this paper we refer to the 12CO(2−1) line as CO(2−1). Observations were performed in separate cycles: we used 7m array data taken during Cycle 1 and 12m array observations taken in Cycle 2. The datasets belong to project 2012.1.00683.S (PI: M. Rubio). As the observations were obtained and reduced in different cycles, we decided to start from the raw data and completely reprocess both datasets, instead of using the delivered data products by ALMA.
The 12m observations were constructed with 33 antennas and consist of a mosaic of 93 pointings, with 13.′′ 7 spacing, and a total excecution time of 107 min. Uranus was used as flux calibrator, J0057−7040 as phase calibrator, and J2357−5311 as bandpass calibrator.
The 7m observations were conducted with ten antennas and consist of a mosaic of 34 pointings, with a distance of 23.′′ 4 between the center of each pointing, and a total integration time of 93.7 min. Uranus was also used as a flux calibrator for these observations. The phase calibrator was J0102−7546 and the bandpass calibrator was J2357−5311.
We reduced, combined, and imaged the data using the Common Astronomy Software Applications (CASA, McMullin et al. 2007) package version 4.7, with the consideration that the software was released later than the observations. We used the standard scripts provided by the ALMA Science Archive1 with the delivered raw data to recover the calibrated datasets. The 12m and 7m data were reduced separately.
We combined the calibrated 12m and 7m observations into one dataset. The observations were done using both the 12m and 7m array to have high-resolution data without losing extended emission: the 12m array configuration gives us observations at high resolution, yet it filters out diffuse emission on a scale that exceeds the maximum recoverable scale (MRS), which for our 12m observations is 18.′′ 3. The MRS increases to 30.′′9 after the 7m array data are combined with the 12m array observations. To combine data taken with two different arrays of antennas, it is crucial that the relative weights of each visibility are correct, as specified in the CASA guide2. We calculated the visibility weights of the 12m and 7m observations with the statwt task. After calculating the correct visibility weights, the 12m array and 7m array data were combined using the concat task with a frequency tolerance of 10 MHz (using the freqtol parameter).
We imaged the combined 12m and 7m data and generated a continuum emission image and a CO(2−1) line cube. We describe the imaging process for the continuum map in Sect. 2.1.1 and the procedure to generate the CO(2−1) line cube in Sect. 2.1.2. We also combined the ALMA CO(2−1) 12m and 7m data with single-dish CO(2−1) observations obtained with the APEX telescope to include the zero spacing emission. The combination of ALMA and APEX data is described in Sect. 2.3.
Properties of the resulting continuum at 1.3 mm (230 GHz).
2.1.1 1.3 mm continuum
We used the standard clean task on the 12m and 7m combined data to generate the 1.3 mm (230 GHz) continuum image, removing the spectral channels that containthe CO(2−1) line. We generate the image using both natural weight and Briggs weight. The natural weight lowers the noise and allows point sources to be detected more effectively, but degrades the angular resolution; on the other hand, Briggs weighting (also known as robust weighting) provides better resolution and smaller sidelobes of the beam, with a penalty in noise. The Briggs weighted image is generated with a robust parameter r = 0.5. The Briggs and natural weighted images resulted in nearly identical rms, 0.18 mJy beam−1 for Briggs weight and 0.17 mJy beam−1 for natural weight. We decided to use natural weight for this work as sensitivity tends to be higher for natural weighted images than Briggs weighted ones. The natural weighted continuum image is in Fig. 2. The continuum image has a field of view (FOV) of 3′ × 3′.
The continuum image we use for this work is generated using natural weight and a tapering in the u–v plane. The taper gives more weight to the shorter baselines, which might improve the sensitivity to extendedsources but degrades the resolution of the image. We applied a tapering of 5′′, which results in an image with a resolution of 5.′′9 × 4.′′ 7. To compare with the APEX LABOCA 870 μm image (see Sect. 2.2.1), we convolved the natural, uv-tapered image to reach a beam FWHM equal to 22′′. The beam size (described through the FWHM in the major and minor axes θmajor and θminor) and rms σ of the continuum images, before and after tapering and convolution, are summarized in Table 1. The tapered continuum images (convolved and not convolved to 22′′) are in Fig. 2.
2.1.2 CO(2–1) line
We performed the clean standard routine in the combined 12m and 7m data, using a mask based on the APEX CO(2−1) data described in Sect. 2.2.2. We used Briggs weighting with a robust parameter of 0.5. The reduced CO(2−1) cube has a FOV of 3′ × 3′, a velocity resolution of 0.5 km s−1, an angular resolution of 1.′′ 22 × 1.′′15 (PA = 42°), and variable rms throughout the line cube with values ranging from 22 and 36 mJy beam−1 per channel.
This ALMA CO(2−1) cube was combined with the CO(2−1) APEX line cube as described in Sect. 2.3.
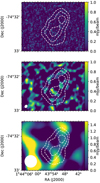 |
Fig. 2 ALMA continuum images at 1.3 mm of Magellanic Bridge A, generated using 12m and 7m data, where imaging is performed using natural weight. Top image: continuum without tapering in the visibility data. Middle image: continuum with its visibility data tapered using a Gaussian with an on-sky FWHM of 5′′. Bottom image: tapered continuum image convolved to reach a resolution of 22′′. The color scale for this last image is different from the other two images. The white ellipse in the bottom left corner of each image represents the beam size. Dashed contours correspond to continuum emission in the APEX 870 μm map at 25, 30, and 35 mJy beam−1. |
2.2 APEX observations
We used observations of Magellanic Bridge A performed with the APEX telescope3, a 12 m diameter telescope located in Llano de Chajnantor, Chile. These observations consist of an 870 μm continuum image, which we describe in Sect. 2.2.1, and a CO(2−1) line emission cube, described in Sect. 2.2.2.
2.2.1 0.87 mm continuum
We used 870 μm continuum observations of Magellanic Bridge A obtained with the Large APEX Bolometer Camera (LABOCA) on the APEX telescope. LABOCA is an array of bolometers with a central frequency of 345 GHz, a bandwidth of 60 GHz, and a total FOV of 11.′4 (Siringo et al. 2009).
We used the 870 μm continuum image of Magellanic Bridge A presented in Verdugo (2012). The Magellanic Bridge A data belongs to project C-086.F-0679A-2010 (PI: M. Rubio). The observations were done in August and October 2010, with a precipitable water vapor (pwv) content between 0.2 and 0.9 mm. The total integration time of the LABOCA observations was 3.94 h. The reduction of this continuum image was done with the Bolometric Array Analysis Software (BoA)4. The reduction required two calibrations: an opacity (τ) calibration, using the τ values obtained from pwv measurements done with the APEX radiometer, and a flux calibration based on Neptune and Uranus flux observations. The flux calibration has an estimated error of 20%. The final continuum image was generated through an iterative reduction process:
first reduction, with the standard BoA reduction script optimized for weak sources;
two iterations of the reduction code, flagging pixels with S/N over 2.5 to get rid of extra noise;
six repetitions of the reduction code using a mask to detect emission with S/N higher than 2.5, subtracting the emission, reducing the map without the source, and adding the source again before the beginning of the next iteration.
The final image is presented in the bottom right box of Fig. 3. It has a beam size of 22.′′ 4 (6.4 pc), a FOV of 11.′4 × 11.′4, and an rms of 5 mJy beam−1, which is consistent with the integration time and weather conditions at the time of observation.
2.2.2 CO(2–1) line
We use CO(2−1) line observations, performed using the on-the-fly mapping technique with the APEX−1 receiver of the Swedish Heterodyne Facility Instrument (SHeFI) at the APEX telescope. The receiver has a spectral range of 213–275 GHz. These observations were made in June 2014, under project C-093.F-9711A-2014 (PI: M. Rubio), with pwv between 1.0 and 1.6 mm. The total integration time towards Magellanic Bridge A was 1.28 h. The mapped area consists of a square of 5.′′ 9 × 5.′′9 covering thecentral region of the infrared emission detected by the Herschel telescope (see Fig. 3).
We reduced the APEX CO(2−1) line cube through the standard procedure of the CLASS software, Gildas5. The antenna temperature 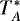 is delivered by APEX corrected for atmospheric attenuation6. We scaled
is delivered by APEX corrected for atmospheric attenuation6. We scaled 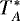 to the main beam brightness temperature using
to the main beam brightness temperature using 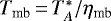 , with a main beam efficiency ηmb = 0.72 for APEX−1 (Vassilev et al. 2008). The resulting APEX CO(2−1) cube has a spatial resolution of 28.′′7, a velocity channel spacing of 0.125 km s−1, and an rms of 5.4 Jy beam−1 (150 mK) per channel. This line cube was combined with the resulting ALMA CO(2−1) line cube and described in Sect. 2.3.
, with a main beam efficiency ηmb = 0.72 for APEX−1 (Vassilev et al. 2008). The resulting APEX CO(2−1) cube has a spatial resolution of 28.′′7, a velocity channel spacing of 0.125 km s−1, and an rms of 5.4 Jy beam−1 (150 mK) per channel. This line cube was combined with the resulting ALMA CO(2−1) line cube and described in Sect. 2.3.
2.3 Combined ALMA–APEX CO(2–1) observations
We combined the 12m and 7m ALMA CO(2−1) line cube described in Sect. 2.1.2 with the single-dish APEX CO(2−1) line cube from Sect. 2.2.2. To combine the observations we used the feather task from the CASA software, which performs the combination in Fourier space. The final combined CO(2−1) datacube has a FOV of 3′ × 3′, a spatial resolution of 1.′′ 22 × 1.′′15 (≈ 0.3 pc) and spectral resolution of0.5 km s−1. This CO(2−1) line cube has a variable rms, with values between 30 and 36 mJy beam−1 per channel depending on position.
 |
Fig. 3 Herschel continuum images of Magellanic Bridge A at 100, 160, 250, 350, and 500 μm, together with the LABOCA continuum image at 870 μm. The cyan contours correspond to the LABOCA 870 μm continuum image at 25 (5σ), 30 (6σ), and 35 mJy beam−1 (7σ). The dashed circles indicate the beam sizes for each image, which correspond to a FWHM of 9′′ (100 μm), 14′′ (160 μm), 22′′ (250 μm), 30′′ (350 μm), 43′′ (500 μm), and 22.′′ 4 (870 μm). The scale bar in the bottom right panel indicates a 10 pc length. |
2.4 Complementary data
We used Herschel observations from the HERITAGE Herschel key project (Meixner et al. 2013), consisting of maps of the SMC at 100, 160, 250, 350, and 500 μm. We extract a square region of 11′ × 11′ from these maps, centered at α =1h43m50s, δ = –74°32′23′′ (FK5, J2000) to work with the continuum images centered at Magellanic Bridge A. The angular resolution of the 100, 160, 250, 350, and 500 μm images is 9′′, 14′′, 22′′, 30′′, and 43′′ and the rms noise of each image is 9, 6, 0.6, 0.3, and 0.2 MJy sr−1, respectively. The flux calibration of these images has an associated uncertainty of 10 and 20% for the 100 and 160 μm images, respectively, and ~8% for the 250, 350, and 500 μm images. We also use the 160 μm Spitzer image obtained from the Multiband Imaging Photometer for Spitzer (MIPS) for the SAGE-SMC Spitzer Legacy Program (Gordon et al. 2011), and extracted the region containing Magellanic Bridge A in the same way. The Spitzer image has a resolution of 40′′, an rms of 4 MJy sr−1, and flux calibration uncertainty of ~10%. All these images were taken from the NASA/IPAC Infrared Science Archive7.
We used an Hα image of the SMC from the Southern Hα Sky Survey Atlas (SHASSA; Gaustad et al. 2001), which contains the Magellanic Bridge. The survey covers 13° of the southern sky and has a resolution of about 0.′8. We extract the region containing the Magellanic Bridge A source in the same way as with the Hershel images.
3 Millimeter and submillimeter emission from Magellanic Bridge A
In this section we study the Magellanic Bridge A dust emission through the millimeter and submillimeter continuum images described in Sects. 2.1.1, 2.2.1, and 2.4. We first describe the sources present in the 870 μm continuum image. Then we present the spectral energy distribution (SED) of Magellanic Bridge A dust we constructed using the continuum images and subtracting all contributions that do not come from dust emission (Sect. 3.1). We obtained the dust properties of Magellanic Bridge A by adjusting a Modified Blackbody (MBB) model to the SED (Sect. 3.2). We compare the resulting MBB model with the dust emission derived from the LABOCA 870 μm and ALMA 1.3 mm continuum images (Sect. 3.3). Finally, we used the properties obtained from the model to calculate the total gas mass using dust emission (Sect. 3.4).
We present three different ALMA 1.3 mm continuum images using different weights and tapered as explained inSect. 2.1.1; no continuum source was detected in these ALMA continuum images, as seen in Fig. 2. There is a hint of emission in the uv-tapered ALMA image convolved to 22′′, but this emission is not coincident with Magellanic Bridge A in the continuum images from Herschel, Spitzer, or LABOCA, so it might be related to antenna noise generating some artifacts. We used the natural weighted uv-tapered image to obtain an upper limit for theflux density at 1.3 mm (see Sect. 3.1).
We detected continuum emission from Magellanic Bridge A at 870 μm. The APEX continuum image is shown in the bottom right panel of Fig. 3. The source was also detected in the Herschel 100, 160, 250, 350, and 500 μm images. There are two peaks with similar intensities (~40 mJy beam−1) and separated by ~27′′ (8 pc), which is near the limit of the APEX resolution. We identify these two sources as North and South throughout this paper. In the Herschel 100 and 160 μm images, the northern peak is not seen, while the southern source can be seen in all images. Unlike the APEX 870 μm continuum, the 350 and 500 μm lower resolution images do not separate well the northern component from the southern one, but it can be seen as an elongated structure. For comparison, we plot the APEX contours over the Herschel continuum images in Fig. 3. In the following section, we characterize the dust emission towards Magellanic Bridge A, and we also characterize the emission coming from the North and South sources found in the APEX 870 μm image.
Dust emission flux densities in Magellanic Bridge A North and South.
3.1 Spectral energy distribution of Magellanic Bridge A
We built the SED for Magellanic Bridge A using Herschel, Spitzer, APEX, and ALMA continuum images. We also built the SED for the North and South sources using Herschel emissions only at 100, 160 and 250 μm, together with the LABOCA and ALMA continuum images. To construct each SED, we performed aperture photometry at each wavelength where emission was detected to obtain the fluxes. Then, we subtracted the contributions that are not thermal emission. We determined an upper flux limit in the ALMA 1.3 mm continuum image, as no emission was detected.
In the following, we describe how we constructed the SED and how we determined the contribution from other emission mechanisms.
3.1.1 Flux measurements
We obtained the fluxes in the Herschel, Spitzer, and LABOCA continuum images of Magellanic Bridge A using aperture photometry. We first convolved all images to a common resolution of 43′′, which corresponds to the resolution of the Herschel 500 μm image, as it has the poorest resolution of all our images. Convolving results in a change in the rms of each image: the new rms are 2.0, 5.0, 0.5, and 0.3 MJy sr−1 for the Herschel 100, 160, 250, and 350 μm images, respectively. The convolved LABOCA image has an rms of 26 mJy beam−1. We measured the total emission coming from Magellanic Bridge A in an aperture with a radius r = 50′′, centered at α = 1h43m52.s68, δ = –74°32′20.′′23 (FK5, J2000). For all images, we subtracted the sky using an annulus centered at the same position as the aperture, with inner radius rin = 2.′5 and outer radius rout = 3.′0 for Magellanic Bridge A. We did not apply an aperture correction to the photometry results of Magellanic Bridge A because the aperture encloses the source completely and the aperture area is almost four times the beam size. The total flux error is the sum in quadrature of the flux calibration error for the measured flux and the photometric error ɛ:
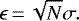 (1)
(1)
Here N is the number of beams inside the aperture and σ is the rms of the image in Jy beam−1. The fluxes measured for Magellanic Bridge A are given in the first row of Table 2. The 870 μm and 1.3 mm emission in this table have been corrected for free-free emission and CO(2−1) line contribution at the respective wavelength. These corrections are further explained in Sect. 3.1.2. In the Spitzer 160 μm image (not included in Table 2), we measured a flux density S160μm = 1009 ± 101 ± 386, where the first error corresponds to the flux calibration error and the second is the photometric error.
In the case of Magellanic Bridge A North and South, we only used the 100, 160, and 250 μm images from Herschel and the LABOCA 870 μm continuum. We did not use the 350 and 500 μm images because the North and South sources cannot be separated due to the resolution (their beam FWHM are larger than 22′′). We convolved the Herschel images to a common resolution of 22′′ to measure their fluxes. The rms after convolution are 2.2 and 5.5 MJy sr−1 for the Herschel 100 and 160 μm images, respectively. For the photometry, we used a circular aperture with a common radius r = 11′′, centered at α = 1h43m49.s0, δ = –74°32′00.′′2 (FK5, J2000) for source North and at α = 1h 43m53.s8, δ = –74°32′24.′′5 (FK5, J2000) for source South, which correspond to the peak positions in the LABOCA image. In this case, since the sources are not resolved andthe photometry is performed within the FWHM of the spatial beam, we applied an aperture correction factor of 2 in the flux measurements. The total flux error was also calculated as the sum in quadrature of the associated flux calibration error and photometric error.
Since there is no emission detected in the ALMA 1.3 mm image, we determined an upper limit for the flux at 1.3 mm for the source Magellanic Bridge A and sources North and South, based on the ALMA continuum image sensitivity. To do this we used a value of three times the photometric error ɛ. For Magellanic Bridge A we obtained a photometric error ɛ = 5.5 mJy inside an r = 50′′ circular aperture, which gives a 1.3 mm flux upper limit for Magellanic Bridge A of 16.5 mJy. The photometric error for the North and South sources is ɛ = 2.4 mJy in a r = 11′′ circular aperture, after applying an aperture correction of a factor of 2. This gives a 1.3 mm flux upper limit of 7.2 mJy for sources North and South.
The fluxes measured for each source and wavelength, together with the flux upper limit at 1.3 mm, are summarized in Table 2. The 1.3 mm and 870 μm fluxes listed correspond to dust emission only at these wavelengths as free-free emission and CO line contributions have been estimated and subtracted (see Sect. 3.1.2). Using these fluxes, we built the SED shown in Fig. 4.
 |
Fig. 4 SEDs for Magellanic Bridge A and the North and South sources. The points correspond to the energy νSν derived fromthe measured flux density Sλ, obtained using aperture photometry. Red points correspond to νSν obtained using Herschel data. Dark blue points correspond to the energy νSν obtained using the LABOCA image. The purple arrow corresponds to the νSν upper limit at 1.3 mm using the ALMA continuum image. Left panel: Magellanic Bridge A SED, for which were used the 100, 160, 250, 350, and 500 μm Herschel continuum images; the 160 μm Spitzer continuum image; and the 870 μm (LABOCA) and 1.3 mm (ALMA) continuum images, all with a common resolution of 43′′. The flux from Magellanic Bridge A was measured inside a circular aperture of radius r = 50′′. The North and South sources SEDs are shown in the last two panels, constructed with the Hershel 100, 160, and 250 μm continuum images, the 870 μm (LABOCA) and 1.3 mm (ALMA) continuum images at a common resolution of 22′′. The fluxes from sources North and South were measured in a circular aperture of radius r = 11′′. The MBB model that best fits the Herschel points for each source is shown as a black curve. The parameters of each curve are listed in Table 4. |
3.1.2 Free–free and CO(3–2) contribution
The flux measurement from the APEX 870 μm image contains emission of three different physical processes: (1) thermal dust continuum emission, (2) free–free (bremsstrahlung) emission from ionized gas, and (3) a contribution from molecular lines in the passband (12CO(3−2) in particular, which is the brightest). At 1.3 mm, there is also free–free emission and a molecular line (12CO(2−1)). We are interested in the dust continuum emission; therefore, we need to calculate and remove the other two contributions to the measured flux. The CO(2−1) line emission was already removed when the ALMA 1.3 mm continuum image is constructed (see Sect. 2.1.1), so we determined the contribution of free-free to both 870 μm and 1.3 mm continuum emission and the contribution of 12CO(3−2) line emission in the 870 μm continuum image.
We determined the free–free contribution to continuum emission using Hα emission as the intensity of the Hα line traces the warm ionized gas component of the ISM and, therefore, is proportional to the free-free emission (see the Appendix in Hunt et al. 2004). To convert Hα flux density into free-free emission 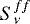 in mJy, we used the following formula:
in mJy, we used the following formula:
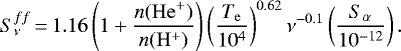 (2)
(2)
Here Sα is the intensity of Hα in erg cm−2 s−1; Te is the gas electron temperaturein K; n(He+) and n(H +) are the number density of helium and hydrogen ions, respectively; and ν is the frequency where we need to determine the free-free emission in GHz. To obtain the intensity of Hα emission in Magellanic Bridge A weused the Hα image from SHASSA (Gaustad et al. 2001), which is in decirayleighs (dR). We first transformed the map units to rayleighs (R) dividing by 10 and then to erg cm−2 s−1 sr−1 using 1R = hν × 106∕(4π) = 2.41 × 10−7 erg cm−2 s−1 sr−1, where ν is the frequency corresponding to the Hα line (4.57 × 1014 Hz). The Hα measurements obtained through aperture photometry in the same positions as in Sect. 3.1.1 are (1.2 ± 0.2) × 10−13 erg cm−2 s−1 for Magellanic Bridge A, and (2.3 ± 0.3) × 10−14 erg cm−2 s−1 and (2.4 ± 0.4) × 10−14 erg cm−2 s−1 for the North and South sources, respectively. These values consider an extinction AV = 0.140, obtained for the position of Magellanic Bridge A (Schlafly & Finkbeiner 2011). We used Te ~ 1.7 × 104 K, the upper limit for the gas temperature reported in Lehner et al. (2001), and n(He+)∕n(H+) ~ 0.08, which is the value estimated for low-metallicity sources like the Magellanic Clouds (Hunt et al. 2004).
After applying Eq. (2) using ν = 344.8 GHz (870 μm), we obtained a free–free contribution of 117 ± 22 μJy for Magellanic Bridge A, 22 ± 4 μJy for cloud North, and 23 ± 4 μJy for cloud South. These values represent ≲0.05% of the total continuum emission. When we used Eq. (2) with ν = 230.8 GHz (1.3 mm), we obtained a free–free contribution of 122 ± 23 μJy in Magellanic Bridge A, 23 ± 4 μJy in cloud North and 24 ± 4 μJy in cloud South. The values for each source and wavelength are listed in Table 3. The fluxes presented in Table 2 have these contributions subtracted.
We obtained the 12CO(3−2) molecular line contribution to the LABOCA continuum flux SCO(3−2) in Magellanic Bridge A using Eq. (5) of Drabek et al. (2012). We calculate the total flux density present in Magellanic Bridge A from the peak integrated intensity ICO(3−2) using
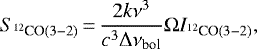 (3)
(3)
where ICO(3−2) is in K km s−1, Δνbol is the bandpass width in Hz, ν is the frequency of the 12CO(3−2) line in Hz, Ω is the source area in sr, and SCO(3−2) is in Jy. We approximated the LABOCA spectral response to a function that is constant over the LABOCA bandpass, so that 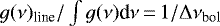 . We used
. We used 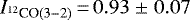 K km s−1, the value for the peak
K km s−1, the value for the peak 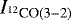 in Magellanic Bridge A given in Table 2 of Muller et al. (2014), and its area Ω corresponds to one single ASTE pointing, with FWHM = 22′′. The resultant 12CO(3−2) line contribution to the continuum emission at 870 μm is SCO(3−2) = 0.85 ± 0.06 mJy. This value is subtracted from the total flux in Magellanic Bridge A at 870 microns, but not from the North and South sources as there is only one source detected in 12CO(3−2). Nevertheless, the estimated 12CO(3−2) contribution is less than 2% of the 870 μm flux in sources North and South.
in Magellanic Bridge A given in Table 2 of Muller et al. (2014), and its area Ω corresponds to one single ASTE pointing, with FWHM = 22′′. The resultant 12CO(3−2) line contribution to the continuum emission at 870 μm is SCO(3−2) = 0.85 ± 0.06 mJy. This value is subtracted from the total flux in Magellanic Bridge A at 870 microns, but not from the North and South sources as there is only one source detected in 12CO(3−2). Nevertheless, the estimated 12CO(3−2) contribution is less than 2% of the 870 μm flux in sources North and South.
We used the APEX 870 μm flux measurement with the free–free and 12CO(3−2) line emission contribution subtracted, the ALMA 1.3 mm flux upper limit with free-free contribution subtracted, and the FIR flux densities obtained from Herschel and Spitzer images to construct the SED of Magellanic Bridge A and the North and South sources. The three SEDs are plotted in Fig. 4.
Free–free emission for each source at 870 μm and 1.3 mm, obtained through aperture photometry.
3.2 SED modeling
We used the SED constructed in Sect. 3.1.2 for Magellanic Bridge A to obtain the dust temperature and dust emissivity index of the region. We also used the SEDs of sources North and South to obtain their dust temperatures. Each SED was modeled assuming that the emission comes from an MBB, which consists of the Planck function multiplied by an emissivity that depends on frequency and dust properties. We derived the physical properties of these dust sources using the parameters of the MBB that best fit each source SED.
At millimeter and submillimeter wavelengths, we can assume that dust emission is optically thin, which means we can write the power per unit area, frequency, and solid angle as Iν = τνBν(Td), where τν is the dust optical depth and Bν is the Planck’s law value at the dust temperature Td. The optical depth can be defined through the dust absorption coefficient (in cm2 g−1) as τν = κd(ν)Σd, where Σd is the surface density of the source in g cm−2. Replacing τν and integrating Iν by the solid angle we obtain
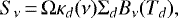 (4)
(4)
where Ω is the solid angle of the source.
In the MBB model we write the absorption coefficient κd (ν) as a function of the spectral emissivity index β as 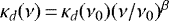 , where κd (ν0) is the absorption coefficient at the reference frequency ν0. Replacing κd(ν) and reorganizing the constant values Ω, Σd, κd (ν0), and ν0 as C, the flux density is a function of frequency ν, emissivity index β, and dust temperature Td (Hildebrand 1983):
, where κd (ν0) is the absorption coefficient at the reference frequency ν0. Replacing κd(ν) and reorganizing the constant values Ω, Σd, κd (ν0), and ν0 as C, the flux density is a function of frequency ν, emissivity index β, and dust temperature Td (Hildebrand 1983):
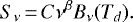 (5)
(5)
We fitted the MBB model described by Eq. (5) for Magellanic Bridge A using the 100, 160, 250, 350, and 500 μm fluxes, obtained from Herschel images in a r = 50′′ radius aperture (see Sect. 3.1.1). We assumed a single dust component and single β dust emissivity index. There are three free parameters in the model: C, β, and Td. We used χ2 minimization to determine C, β, and Td that best fit the SED, using the function curve_fit of the scipy.optimize package (Virtanen et al. 2020). The MBB that best fits the SED of Magellanic Bridge A has a dust temperature Td = 22.4 ± 3.4 K and an emissivity index β = 1.4 ± 0.5, listed in Table 4. In Fig. 4, the solid black line in the left panel represents the best fit MBB for the SED of Magellanic Bridge A.
We fitted the MBB model for the North and South sources only using the 100, 160, and 250 μm fluxes because the 350 and 500 μm beams do not resolve two sources and have poorer resolution than 22′′ (the 870 μm beam). For these sources, we assume that the dust emissivity is the same as that found for Magellanic Bridge A, and we therefore fixed β = 1.4 for both sources. We note that assuming a β value for these sources influences the dust temperature obtained, as there is an inverse correlation between β and Td (Shetty et al. 2009). We found the parameters C and Td that best fit the SEDs with χ2 minimization. The temperature obtained for source South is Td = 24.5.4 ± 2.2 K and source North Td = 21.7.4 ± 1.1 K; these parameters are listed in Table 4, and the best fit curves are plotted in Fig. 4 (black line). The best fit results indicate that the North source is colder than the South source by ~ 3 K.
3.3 Submillimeter excess
We define the submillimeter and millimeter excesses E(λ) as the ratioof the measured flux to the predicted flux from the SED model at λ = 870 μm and 1.3 mm. We calculate these excesses for each source and summarize our results in Table 5.
The submillimeter excess found at 870 μm for Magellanic Bridge A is E(870 μm) = 6.9 ± 1.6 inside an circular aperture with r = 50′′. When we separate Magellanic Bridge A into the North and South sources, this submillimeter excess is also present. For the North source, E(870 μm) = 6.7 ± 1.6, while in the South is E(870 μm) = 3.0 ± 1.4, both considering a photometry aperture radius r = 11′′. Excess emission at 870 μm has been detected in other low-metallicity galaxies using LABOCA (Galametz et al. 2009, 2014; Hermelo et al. 2016) and SCUBA observations (Galliano et al. 2003, 2005; Bendo et al. 2006).
Since we do not detect our sources in the 1.3 mm ALMA continuum, we calculate how much higher the flux upper limits calculated in Sect. 3.1.1 are than the predicted flux densities at 1.3 mm. We derive an expected flux using the MBB model that best fits the FIR SED (see Table 4). We obtain an expected flux density of 10.7 mJy for Magellanic Bridge A in an aperture radius r = 50′′, and 2.0 mJy for the North source and 5.3 mJy for the South source within an aperture of radius r = 11′′. The flux upper limit at 1.3 mm is 16.5 mJy, which is 1.5 times higher than the expected flux density using the MBB model fitted to the FIR fluxes for Magellanic Bridge A. For the individual North and South sources, the upper limits from the ALMA continuum image at 1.3 mm are 7.2 mJy (3.6 times higher than the expected flux density for source North) and 2.2 mJy (1.4 times higher for source South). These valuesare reported as E(1.3 mm) in Table 5. In summary, our ALMA 1.3 mm data are compatible, within the detection limit, with the MBB fit to the FIR observations, and show no excess at this wavelength. If the excess at 1.3 mm were similar to that at 870 μm, we would have detected the source.
The fact that we do not observe emission at 1.3 mm when there is notable excess emission at 870 μm in our sources is puzzling. The calibration of the LABOCA data was verified as correct by members of our team and the instrument support team, who performed independent reductions of the data that resulted in very similar images. In addition, we note that the morphology of the source at 870 μm in Fig. 3 is consistent with emission at 250 to 500 μm continuum images, and the noise of the map is consistent with that expected for the integration time. We would have only detected the South source at ~3σ in the complex if there were no excess. Therefore, we have every expectation that the 870 μm excess is real. If this is so, there are two possibilities to explain the lack of a 1.3 mm detection: either the anomalous emission at 870 μm is present only at that wavelength or the dust emission is too extended and resolved out in the ALMA 1.3 mm observation. We note that it is very difficult to explain the 870 μm excess as resulting from an additional very cold dust component, as the lack of an excess at 500 μm would require it to have a dust temperature Td ~ 3 K. Through the inclusion of the Morita Array our ALMA observations have a maximum recoverable scale (MRS) of 30.9′′, although our sensitivity substantially degrades close to that limit. We would expect to see continuum sources similar in size to the CO emitting clouds in this region (Fig. 5) if their 1.3 mm flux had an excess over the MBB fit similar to that measured at 870 μm. If the sources were larger than the 22′′ used for the photometry, however, they would be at least partially resolved out and undetectable. Clearly future ALMA observations determining the sizes of the sources at 870 μm or deeper observations at 1.3 mm would be extremely useful to establish the nature of the excess.
Gas masses and best fit MBB parameters to the cloud SEDs.
Submillimeter and millimeter excesses for Magellanic Bridge A and sources North and South.
 |
Fig. 5 Velocity integrated intensity image of the combined ALMA and APEX CO(2−1) cube of Magellanic Bridge A, integrated between 172 and 176.0 km s−1. The cyan contours correspond to 5 times the σ of the integrated image (σ = 48 mJy beam−1 km s−1). The white contours correspond to the LABOCA 870 μm continuum image at 25, 30, and 35 mJy beam−1, as in Fig. 3. The white ellipse in the lower left corner represents the beam FWHM (1.22′′ ×1.15′′). The scale bar in the lower right corner indicates a 2 pc length. |
3.4 Gas masses obtained from dust emission
We calculate the total gas masses associated with the 870 μm dust emission for Magellanic Bridge A predicted by the MBB model that best fits the FIR fluxes. We use the same method to obtain the gas mass from dust flux used in Bot et al. (2010) and Rubio et al. (2004). The dust flux Sν is related to the gas mass Mgas through
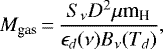 (6)
(6)
where Sν is the predicted flux at frequency ν by the MBB model that best fits the FIR data in Jy; D is the distance to the source in centimeters (we use the estimated distance to the SMC, 60 kpc; Harries et al. 2003); μmH is the gas weight per hydrogen atom in grams, including the contribution of helium8 ; ɛd (ν) is the emissivity of dust per hydrogen atom at frequency ν in cm2; and Bν (Td) is the spectral radiance at a dust temperature Td in Jy sr−1.
We use the ɛd(345GHz) value presented in Bot et al. (2010), ɛd(345GHz) = (3.94 ± 0.05) × 10−27 cm2, which assumes an absorption coefficient κ345GHz = 1.26 ± 0.02 cm2 g−1 and a dust-to-gas ratio that is 1/6 of the ratio in the solar neighborhood. This dust-to-gas ratio is similar to the ratios derived in Magellanic Bridge B and C (Gordon et al. 2009).
For Magellanic Bridge A source, North source, and South source, we use the dust temperatures Td = 22.4 ± 3.4 K, Td = 21.7 ± 2.2 K, and Td = 24.5 ± 1.1 K, respectively, obtained from the best fit MBB to the Magellanic Bridge A SED with β = 1.4, as derived in Sect. 3.2.
The total gas mass are calculated using the 870 μm flux predicted from the MBB fit. For Magellanic Bridge A, the gas mass is (6.8 ± 1.5) × 103 M⊙ and for the two separate clouds, North and South, their gas masses are (1.3 ± 0.5) × 103 M⊙ and (2.9 ± 0.5) × 103 M⊙, respectively.There is a difference between the sum of the gas masses of sources North and South and the gas mass of Magellanic Bridge A because dust measurements for the North and South sources are obtained in an aperture of radius r = 11′′, which only includes the peak emission of each cloud, while Magellanic Bridge A is measured inside an aperture of radius r = 50′′, which captures the complete emission from the source. We also estimated the gas masses using an absorption coefficient determined for dust emission at 160 μm by Gordon et al. (2014), κ160μm = 9.6 ± 2.5 cm2 g−1, as the gas masses are dependant on the chosen ɛd(ν), which depends on the calibration of κν. Using κ160μm and the same gas-to-dust ratio (1∕6 of the value in the solar neighborhood), we obtain a gas mass for Magellanic Bridge A of (9.6 ± 4.4) × 103 M⊙, while for source North it is (1.7 ± 0.8) × 103 M⊙ and for source South (3.9 ± 1.4) × 103 M⊙. These values are within the uncertainties of those obtained using the Bot et al. (2010) value. For the rest of this work, we use the total gas masses derived from the Bot et al. (2010) calibration, listed in the last column of Table 4.
4 Resolved CO(2–1) molecular clouds
In this section, we study the CO(2−1) molecular line emission in Magellanic Bridge A. We produced the velocity integrated intensity image between 172 and 176 km s−1 of the ALMA and APEX CO(2–1) line cube (see Fig. 5). We measured an rms of 48 mJy beam−1 km s−1 in this image, a value that is consistent with the calculated values of 42 and 50 mJy beam−1 km s−1 using the rms range of the velocity interval (see Sect. 2.3). We resolved two parsec-sized CO(2−1) clouds, which are located towards the North and South 870 μm continuum sources. We extracted the spectra of each of these molecular clouds (Sect. 4.1) and determined the physical properties of the molecular clouds in this region (Sect. 4.2).
4.1 CO(2–1) molecular clouds spectra
We identified the molecular clouds in the ALMA and APEX CO(2−1) line cube and extracted their spectra. We first identified potential sources in the velocity integrated intensity image as all emission greater than 3σ, being σ the rms of the integrated image. We define the area of each source as the number of pixels inside the 3σ contour. Then we measured the second moments of emission along the major and minor axes of each source in the CO(2−1) integrated emission image. We only kept those sources whose minor second moment is larger than the beam size. The only sources that met this criterion (survived this decimation) are the two brightest CO(2−1) sources seenin Fig. 5, which we call CO clouds from now on. These CO clouds spatially coincide with the dust sources characterized in Sect. 3, as seen in Fig. 5. The peak ICO(2−1) of these clumps in the CO(2−1) integrated image are 1.67 ± 0.05 Jy beam−1 km s−1 in the North CO cloud and 2.81 ± 0.05 Jy beam−1 km s−1 in the South CO cloud.
We obtained the integrated velocity spectra of each source, adding all spectra in the source area. The resulting spectra have an rms noise of σ = 0.30 Jy km s−1 for CO cloud North and σ = 0.25 Jy km s−1 for CO cloud South, in a velocity channel width 0.5 km s−1. We fitted a Gaussian profile to the velocity integrated spectra of clouds North and South to obtain the central velocity vLSR in km s−1, velocity dispersion σv in km s−1 and integrated flux density SCO(2−1)Δv in Jy km s−1. We adjusted the Gaussian model to the spectra through least-squares fitting. We corrected σv for broadening due to the finite spectral resolution, using Eq. (10) of Rosolowsky & Leroy (2006) to obtain the deconvolved velocity dispersion σv,dc, and report the velocity FWHM Δv calculated from σv,dc. We did not extrapolate σv to correct for a sensitivity bias (as stated in Rosolowsky & Leroy 2006), as the peak emission of the CO clouds North and South is detected with a S/N of 33 and 56, respectively.
The CO cloud North is centered at a velocity of 174.6 ± 0.6 km s−1 with a velocity FWHM of 1.33 ± 0.03 km s−1, and the CO cloud South is centered at 174.0 ± 0.9 km s−1 with a FWHM of 1.93 ± 0.05 km s−1. The clouds are centered at similar velocities and have similar velocity linewidths. The CO North cloud shows a peak ICO(2−1) emission of 1.67 ± 0.05 Jy beam−1 km s−1 and cloud South has a peak ICO(2−1) emission of 2.81 ± 0.05 Jy beam−1 km s−1. However, as CO cloud North covers an area of 8.1 pc2, while CO cloud South covers 5.8 pc2, the North cloud has a larger emission than the South, with a total flux density SCO(2−1)Δv of 30.67 ± 2.86 Jy km s−1 and 21.65 ± 2.05 Jy m s−1, respectively.
The results of these fits are summarized in Table 6.
4.2 Physical properties
We derived the sizes, CO(2−1) luminosities, and virial masses for the CO(2−1) clouds we found in Magellanic Bridge A using the parameters obtained from the integrated spectra for each cloud.
We calculated the radius using the second moments of emission, as suggested in Sect. 2.1 of Rosolowsky & Leroy (2006) using R = 1.91σrD, where σr is the geometric mean of the spatial second moments of emission in radians, corrected for the spatial broadening due to the beam as indicated by their Eq. (9), and D is the distance to the cloud in pc. We assumed that Magellanic Bridge A is at a distance of ~ 60 kpc, the same as the distance to the SMC (Harries et al. 2003). We did not extrapolate the radius σr as we do not expect a significant change in the size σr, for the same reason as wedid not do it for σv: both CO sources were detected with high S/N values as can be seen in Fig. 5. The radius obtained for the CO clouds are 1.29 ± 0.07 pc for cloud North and 1.04 ± 0.04 pc for cloud South.
We calculated the CO(2−1) luminosities in K km s−1 pc2 using LCO(2−1) = 611.5SCO(2−1)ΔvD2, where SCO(2−1)Δv is the CO(2−1) integrated flux density in Jy km s−1, obtained from the ALMA and APEX combined CO(2−1) line cube, and D is the distance to Magellanic Bridge in Mpc. The resulting luminosities are LCO(2−1) = 67.5 ± 6.3 K km s−1 pc2 for CO cloud North, and LCO(2−1) = 47.7 ± 4.5 K km s−1 pc2 for CO cloud South.
We compared the Magellanic Bridge A total luminosity measured by the single-dish APEX CO(2−1) observations and by the ALMA CO(2−1) observations to determine any missing diffuse emission. The total luminosity detected by APEX, measured inside a a 58′′ × 58′′ box centered at α =1h43m51.s3, δ = –74°32′09.′′2, is 134 ± 9 K km s−1 pc2. The luminosity of clouds North and South in the ALMA CO(2−1) line cube is 66.7 ± 6.0 and 48.4 ± 4.2 K km s−1 pc2, respectively. If we add the CO luminosities of the two clouds, we obtain a total luminosity for Magellanic Bridge A of 115 ± 10 K km s−1 pc2. Thus, ALMA recovers, within the uncertainties, almost all the luminosity measured in the APEX CO(2–1) line cube, implying that most of the emission in Magellanic Bridge A is concentrated in the two CO(2−1) clouds we characterize in this work.
We determined the virial masses Mvir of the clouds using Eq. (3) of MacLaren et al. (1988),
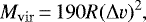 (7)
(7)
where R is the radius in pc, Δv is the FWHM of the line emission in km s−1, and Mvir is in M⊙. This equation assumes spherical-shaped gravitationally bound molecular clouds and a density profile ρ ∝ r−1. We used the deconvolved radii in Table 7 and the FWHM in Table 6. The virial mass for CO source North is 437.3 ± 26.1 M⊙ and for source South it is 732.9 ± 37.0 M⊙. Even though these clouds are parsec-sized, they contain ~ 5 × 102 M⊙, similar to the masses of the most massive molecular clumps in the Milky Way, which have typical radii of ~ 1 pc (see Bergin & Tafalla 2007, and references within).
We estimated the CO-to-H2 conversion factor αCO = Mvir∕LCO and the corresponding XCO, which is usually derived for the 12CO(1−0) emission. We did not attempt to correct for variations in the J = 2−1 to J = 1−0 ratio r21, and simply assumed r21 ~ 1 for the purposes of comparison, which is also a common result for SMC observations (e.g., Lequeux et al. 1994; Rubio et al. 1996). For CO cloud North the derived conversion factor is αCO = 6.5 ± 0.7 M⊙ (K kms−1 pc2)−1 (XCO = (3.0 ± 0.3) × 1020 cm−2 (K km s−1)−1) and for cloud South αCO = 15.3 ± 1.6 M⊙ (K km s−1 pc2)−1 (XCO = (7.1 ± 0.7) × 1020 cm−2 (K km s−1)−1). These values are 1.5 and 3.6 times the canonical value for the Milky Way αCO(MW) = 4.3 M⊙ (K km s−1 pc2)−1 (XCO = 2 × 1020 cm−2 (K km/s)−1).
The derived properties R, Mvir, LCO(2−1) and αCO are summarized in Table 7.
Characteristics of the clouds identified in the CO(2−1) line cube.
Physical properties of the emission found in the 12CO(2−1) line cube.
5 Discussion
In this section we discuss our results and compare them to previous observations of Magellanic Bridge A and other low-metallicity galaxies.
5.1 CO(2–1) in comparison with previous studies
The molecular clouds we found in CO(2−1) emission have spectral properties and masses similar to those inferred from previous unresolved CO measurements in Magellanic Bridge A. The central velocities of CO sources North and South, 174.6 ± 0.6 and 174.0 ± 0.9 km s−1, respectively, are close to the 174.7 km s−1 reported for Magellanic Bridge A by Mizuno et al. (2006) through 12CO(1−0) emission with NANTEN (beam FWHM = 2.6′). The linewidths of the CO clouds, 1.33 ± 0.03 km s−1 for cloud North and 1.93 ± 0.05 km s−1 for cloud South, are consistent with the 12CO(1−0) velocity FWHM of 1.6 km s−1 reported for Magellanic Bridge A in Mizuno et al. (2006) and with the 12CO(3−2) FWHM of 1.4 km s−1, reported in Muller et al. (2014) observed with ASTE Telescope (FWHM = 22′′). The sum of the virial masses of the CO clouds North and South, (1.17 ± 0.06) × 103 M⊙ is in agreement with the mass estimated for Magellanic Bridge A by Mizuno et al. (2006), 103 M⊙, using ICO(1−0) and a conversion factor of XCO = 1.4 × 1021 cm−2 (K km s−1)−1.
Comparing the CO luminosities found by previous studies of this source is not easy as they measure different rotational transitions with different resolutions and sensitivities. Nevertheless, by comparing the luminosities over matched areas, together with the similarities in velocity FWHM and virial mass, we estimate that the emission detected in previous observations is mainly associated with the two clouds we observed in this work. The 12CO(1−0) luminosity in the NANTEN detection of Magellanic Bridge A is LCO(1-0) = 70 ± 8 K km s−1 pc2 (Mizuno et al. 2006). The 12CO(3−2) luminosity in the ASTE detection is LCO(3−2) = 64 ± 8 K km s−1 pc2 (Muller et al. 2014). The total CO(2−1) luminosity we measured from both Magellanic Bridge A clouds is LCO(2−1) = 115 ± 11 K km s−1 pc2. The resulting 12CO (3−2)/(2−1) luminosity ratio is r32 = 0.56 ± 0.09, which is reasonable for a star-forming cloud. The 12CO (2−1)/(1−0) ratio is r21 = 1.64 ± 0.24, which is unusually high with respect to typical values observed in the Milky Way, the Magellanic Clouds, and other galaxies where r21 ~ 0.7−1.1 (e.g., Rubio et al. 1996; Sorai et al. 2001; Bolatto et al. 2003; Nikolić et al. 2007). Although in localized regions higher ratios can be observed, caused by effective optical depth (Bolatto et al. 2003), it is also possible that the NANTEN 12CO(1−0) luminosity is underestimated. Because of the similarities in velocity, FWHM, and luminosity, it seems that most (if not all) of the CO emission from Magellanic Bridge A detected in previous studies comes from the two compact clouds presented in this work.
The CO emission from the North and South clouds show interesting differences from parsec-sized CO sources present in the Milky Way. Their virial masses are one order of magnitude higher, implying higher densities in the gas. At radii between 1 and 2 pc, clouds in the Milky Way have masses between a few 10 M⊙ to a few 100 M⊙ (Miville-Deschênes et al. 2017), while the clouds found in Magellanic Bridge A have 400 M⊙ and 700 M⊙ for North and South, respectively. We note, however, that most of the clouds in the Miville-Deschênes et al. (2017) catalog have large virial parameters, and as a consequence are not self-gravitating and are unlikely to be forming stars. The assumption of virial or self-gravitating equilibrium in the Magellanic Bridge A clouds may not be strictly correct, but it is not unreasonable for star-forming clouds. Clouds that have an excess of kinetic energy with respect to their potential energy will be short-lived and very unlikely to locally collapse to form stars. If the CO-emitting cloud is embedded in a large envelope, part of the velocity dispersion may be associated with the external confining pressure associated with the weight of the envelope. In that case the virial mass estimate effectively includes part of the mass of the envelope. Using the virial mass estimate, the CO clouds North and South have surface densities Σmol ≈ 80 and 230 M⊙ pc−2, respectively, and corresponding bulk densities n(H2) ~ 700 and 2600 cm−3 assuming spherical geometry. The surface densities of Magellanic Bridge A clouds are similar to typical Σmol for star-forming clouds in the Milky Way disk (e.g., Heiderman et al. 2010; Evans et al. 2014), but their bulk volume densities are higher than commonly found bulk densities in our Galaxy, which is a reflection of the small size of the clouds in this work. Roman-Duval et al. (2010) find Σmol ~ 144 M⊙ pc−2 and n(H2) ~ 230 cm−3 as an average for Milky Way clouds in the Galactic Ring Survey, which tend to be star-forming clouds. The Magellanic Bridge clouds have volume densities that are similar to the densities of clumps in local star-forming molecular clouds (e.g., Evans et al. 2014). This supports the idea that what we see emitting brightly in CO at low metallicities corresponds to the denser regions of molecular clouds.
In other aspects, the Magellanic Bridge A clouds are similar to clouds found in the Magellanic System and other low-metallicity galaxies. Their CO(2−1) emission has similar velocity dispersion and luminosity to other CO clouds studied in the Magellanic Bridge. Molecular clouds with radii 0.3−1 pc, velocity FWHM 1− 2 km s−1 and CO luminosities 10− 100 K km s−1 pc2 have been found in Magellanic Bridge B (Saldaño et al. 2018). Magellanic Bridge C 12CO(1−0) emission is concentrated in clouds with radii 0.9−1.5 pc and velocity FWHM 0.5−1.4 km s−1 (Kalari et al. 2020), similar to the clouds we found in this work. The Magellanic Bridge A clouds have similar radii and slightly narrower linewidths and luminosities than regions in the LMC and SMC with active star formation, observed at similar (subparsec) resolution. For example, in 30 Doradus in the LMC, clouds with radii ≳ 0.5 pc show lines 1− 6 km s−1 wide and CO(2−1) luminosities ≳ 100 K km s−1 pc2 (Indebetouw et al. 2013). In N83 in the SMC, clouds with radii ~ 0.8 pc have linewidths of ~ 4 km s−1 and CO(2−1) luminosities 100−200 K km s−1 pc2 (Muraoka et al. 2017). The narrower linewidths in Magellanic Bridge A may be the consequence of lower cloud masses, or alternatively lower external pressures (Field et al. 2011). Small clouds (1− 3 pc radii) with linewidths around 2− 3 km s−1 and high densities (n(H2) ~ 103 cm−3) have been reported in dwarf galaxies like WLM (Rubio et al. 2015) and NGC6822 (Schruba et al. 2017). In general, our results support the idea that CO in low-metallicity galaxies traces dense regions of the molecular clouds, and is detected as compact dense CO clouds with narrow linewidths (Rubio et al. 2015).
The αCO CO-to-H2 conversion factor values estimated in this work using the virial masses are around 2–4 times larger than the standard Milky Way disk value αCO(MW) = 4.3 M⊙ (K kms−1 pc2)−1. Although large conversion factors are observed on large scales for low-metallicity galaxies, observations on small scales and in regions where CO is bright in low-metallicity cloud complexes frequently yield conversion factors αCO similar to the canonical value for theGalaxy (e.g., Rubio et al. 2015; Schruba et al. 2017; Wong et al. 2017; Jameson et al. 2018). Rubio et al. (1993) found that in the SMC, XCO decreases with cloud size as log XSMC = 0.7logR + 20.26 between 10 and 100 pc. Extending their relation for cloud sizes R ~ 1 pc, the resulting value of XCO is almost the canonical galactic value. For CO cloud North, αCO is in good agreement with the value obtained for clouds sizes of ~ 2 pc using the Rubio et al. (1993) relation. Therefore, the αCO values found in this work are consistent with αCO values found for other low-metallicity regions at similar resolution.
5.2 Gas and dust comparison
We compared the molecular gas and dust emission in Magellanic Bridge A by convolving the CO(2−1) ALMA and APEX combined cube to 22′′ resolution. We integrated the convolved CO(2−1) emission between 172 and 176 km s−1. The rms noise of the resultant image is σ = 1.8 Jy beam−1 km s−1. The CO(2−1) peaks can still be distinguished as separate sources at this resolution, but they share the same 3σ and 5σ contours (see Fig. 6).
At this common resolution we can characterize the relative sizes of the sources in dust and CO by fitting two-dimensional Gaussians. In CO(2−1), the FWHM of the Gaussians are (7.1 ± 0.2) pc × (6.6 ± 0.2) pc for cloud North, and (5.6 ± 0.4) pc × (4.9 ± 0.3) pc for cloud South. Sources North and South in the 870 μm continuum are described byGaussians with FWHM of (10.3 ± 0.6) pc × (10.0 ± 0.7) pc and (16.9 ± 1.1) pc × (16.5 ± 0.5) pc, respectively. The ratio of the continuum to CO spatial size for the cloud North source is 1.5 ± 0.1, while for cloud South it is 3.0 ± 0.3. This difference in size (in particular for cloud South) suggests the presence of an extended halo of cold material, possibly molecular, that is not bright in CO. The expectation from photodissociation region models is that at low metallicity the region of a cloud thatemits brightly in CO shrinks due to the diminished extinction caused by the lower dust-to-gas ratio (Bolatto et al. 2013).
It is interesting to note that not only is the size of the emission larger in the long-wavelength dust continuum, but the gas mass estimates from the FIR dust continuum MBB fit to sources North and South are also a factor of ~ 3−4 higher than virial masses from CO (see Tables 4 and 7). This result is along the lines of previous studies in the SMC, where the total gas mass derived using CO emission is substantially lower than the cold gas mass obtained from modeling the dust emission (Rubio et al. 2004; Leroy et al. 2007; Bot et al. 2007, 2010; Bolatto et al. 2011; Jameson et al. 2016). It is consistent with the idea that the CO-emitting regions of molecular clouds at low metallicity are encapsulated in a much larger cold gas envelope, likely molecular, that is not emitting in CO.
 |
Fig. 6 LABOCA continuum image at 870 μm, with black contours placed at 25, 30, and 35 mJy beam−1, as in Fig. 3. The white circle represents the beam size (beam FWHM = 22′′). Red contours correspond to the ALMA and APEX CO(2−1) combined line emission convolved to the APEX resolution of 22′′, integrated between 172 and 176 km s−1, at 5σ, 6σ, and 7σ, where σ is the rms of the integrated image (σ = 1.8 Jy beam−1 km s−1). The scalebar in the lower right corner represents a 5 pc length. |
5.3 Gas and dust in the context of star formation
The North and South clouds in Magellanic Bridge A show differences in the mid-infrared. In the 8 and 24 μm emission images of SAGE-SMC program, source North is detected with a flux of 0.9 ± 0.1 and 1.0 ± 0.1 mJy, respectively, whereas source South has a flux density of 7.1 ± 0.3 and 60.0 ± 0.7 mJy (Gordon et al. 2011). The 8 μm emission is associated with the presence of polycyclic aromatic hydrocarbons (PAHs), which are components of dust and are usually correlated with star formation activity (Chen et al. 2014). The 24 μm emission is a tracer of warm dust, which is associated with massive star formation. The difference in fluxes at 24 μm is consistent with the presence of a B-type star towards the South cloud.
The CO(2−1) clouds in Magellanic Bridge A have ongoing star formation, with associated YSOs. The North source coincides with a faint YSO candidate (J014349.20-743200.63) classified by Chen et al. (2014), while the South source coincides with a brighter YSO (J014353.94-743224.71) classified as an embedded source in the same work. The South source hosts a compact multiple system, where a B-type star dominates the far-ultraviolet (FUV) light, while the YSO in this location dominates the near-infrared and mid-infrared light (Chen et al. 2014). The dust temperature reflects this difference in stellar content: the South cloud is being heated by the multiple stars it hosts, in particular a B-type star, while the North cloud might be mostly heated by its fainter YSO. Therefore, it seems that the South molecular cloud has already had an episode of massive starformation, and indeed Chen et al. (2014) speculate that the formation of a group of early B stars 5− 10 Myr ago and the corresponding expansion of their H II regions (still visible in Hα) may have triggered the current star formation activity in Magellanic Bridge A.
6 Summary and conclusions
We characterized the molecular gas and dust emission from the Magellanic Bridge A molecular clouds using ALMA 1.3 mm continuum and CO(2−1) observations at subparsec resolution, together with APEX 870 μm continuum and CO(2−1) line observations at ~6 pc resolution and Spitzer and Herschel FIR archival data.
At this resolution, Magellanic Bridge A separates into two components, North and South. Their dust emission has temperatures of Td = 21.7 ± 2.2 K and Td = 24.5 ± 1.1 K, respectively, with an emissivity exponent β ≈ 1.4 obtained from the MBB fitting to the FIR emission of Magellanic Bridge A at λ ≤ 500 μm. The difference in temperature is consistent with the fact that the North source is not detected at 100 and 160 μm, and that its star formation activity seems to be weaker than that of the South source. Using the MBB model that best fits the FIR dust fluxes, we obtained total gas masses of (1.3 ± 0.3) × 103 M⊙ at source North and (2.9 ± 1.2) × 103 M⊙ at source South, and a total gas mass of (6.8 ± 1.5) × 103 M⊙ for the entire complex.
After removing possible contributions from free–free and CO line emission, the bolometer measurement at 870 μm from LABOCA shows a very significant submillimeter excess of a factor of ~ 6.7 for source North and 3.0 for source South over their FIR fits. The 870 μm image exhibits morphology consistent with that of the FIR images, peaking at the location of the CO clouds. The calibration of the data does not appear to be at fault, and the noise in the image is entirely consistent with a priori expectations: without the excess there would have been a marginal detection of the source. A similar excess, however, is not detected in the ALMA 12m and Morita Array imaging at 1.3 mm. The upper limits for flux density at 1.3 mm are consistent with the predicted fluxes by the MBB model. This requires that either emission is extended enough that it is filtered out by the interferometer or that the excess is caused by a process that peaks at 870 μm (perhaps similar to the Anomalous Microwave Emission detected at lower frequencies; Dickinson et al. 2018). High-resolution observations at 870 μm with ALMA will help to establish the nature of the excess.
We found dense molecular clouds in Magellanic Bridge A using ALMA+APEX combined CO(2−1) line emission, which spatially coincide with the North and South dust sources. These two clouds have radii ~ 1 pc, velocity FWHM of 1.3 and 1.9 km s−1 and virial masses of ~400 and 700 M⊙ for clouds North and South, respectively. Accordingly, their bulk volume densities are n(H2) ~ 700 and 2600 cm−3, significantly higher than the typical density of clouds in the Milky Way (n ~ 230 cm−3; Roman-Duval et al. 2010). The total interferometric LCO(2−1) of the complex is 85% of the luminosity LCO(2−1) measured with the APEX single dish, which suggests that most (if not all) CO(2−1) emission from Magellanic Bridge A comes from these two clouds. Using the virial mass, we find a CO-to-H2 conversionfactor αCO of 6.5 ± 1.2 M⊙ (K kms−1 pc2)−1 and 15.3 ± 1.6 M⊙ (K km s−1 pc2)−1 for the North and South clouds respectively, consistent with the trend of αCO approachingMilky Way values on the small spatial scales.
We compared the CO(2−1) and dust emissions at a common resolution of 22′′. We find that CO(2−1) emission covers a smaller area than continuum emission in the South cloud, whereas they have a similar spatial extent on the more quiescent North cloud. The total gas mass derived from the dust emission is ~ 4 times higherthan the sum of virial masses obtained for both clouds.
Acknowledgements
We thank the anonymous referee for very constructive feedback and comments which helped to improve the quality of this article. M.T.V. acknowledges financial support from CONICYT (Chile) through the scholarship CONICYT-PFCHA/ Magister Nacional 2018 – 22180279, Universidad de Chile VID grant ENL22/18 and FONDECYT grant No1190684. M.R. wishes to acknowledge support from Universidad de Chile VID grant ENL22/18, from CONICYT (CHILE) through FONDECYT grant No1190684, and partial support from CONICYT project Basal AFB-170002. H.P.S acknowledges financial support from a fellowship from Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), and from Secretaría de Ciencias y Técnicas (Secyt), Córdoba, Argentina. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2012.1.00683.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This publication is based on data acquired with the Atacama Pathfinder Experiment (APEX). This research made use of APLpy, an open-source plotting package for Python (Robitaille & Bressert 2012). This research made use of Astropy (http://www.astropy.org), a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018).
References
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bendo, G. J., Dale, D. A., Draine, B. T., et al. 2006, ApJ, 652, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Besla, G., Kallivayalil, N., Hernquist, L., et al. 2012, MNRAS, 421, 2109 [NASA ADS] [CrossRef] [Google Scholar]
- Bica, E. L. D., & Schmitt, H. R. 1995, ApJS, 101, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Bica, E., Santiago, B., Bonatto, C., et al. 2015, MNRAS, 453, 3190 [CrossRef] [Google Scholar]
- Bolatto, A. D., Leroy, A., Israel, F. P., & Jackson, J. M. 2003, ApJ, 595, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Leroy, A. K., Jameson, K., et al. 2011, ApJ, 741, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Bot, C., Boulanger, F., Rubio, M., & Rantakyro, F. 2007, A&A, 471, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bot, C., Rubio, M., Boulanger, F., et al. 2010, A&A, 524, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, C. H. R., Indebetouw, R., Muller, E., et al. 2014, ApJ, 785, 162 [CrossRef] [Google Scholar]
- Cioni, M. R. L., van der Marel, R. P., Loup, C., & Habing, H. J. 2000, A&A, 359, 601 [Google Scholar]
- Dickinson, C., Ali-Haïmoud, Y., Barr, A., et al. 2018, New Astron. Rev., 80, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Drabek, E., Hatchell, J., Friberg, P., et al. 2012, MNRAS, 426, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, Neal J. I., Heiderman, A., & Vutisalchavakul, N. 2014, ApJ, 782, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B., Blackman, E. G., & Keto, E. R. 2011, MNRAS, 416, 710 [NASA ADS] [Google Scholar]
- Galametz, M., Madden, S., Galliano, F., et al. 2009, A&A, 508, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galametz, M., Albrecht, M., Kennicutt, R., et al. 2014, MNRAS, 439, 2542 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Madden, S. C., Jones, A. P., et al. 2003, A&A, 407, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galliano, F., Madden, S. C., Jones, A. P., Wilson, C. D., & Bernard, J. P. 2005, A&A, 434, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gardiner, L. T., Sawa, T., & Fujimoto, M. 1994, MNRAS, 266, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Gaustad, J. E., McCullough, P. R., Rosing, W., & Van Buren, D. 2001, PASP, 113, 1326 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Bot, C., Muller, E., et al. 2009, ApJ, 690, L76 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Meixner, M., Meade, M. R., et al. 2011, AJ, 142, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Roman-Duval, J., Bot, C., et al. 2014, ApJ, 797, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Harries, T. J., Hilditch, R. W., & Howarth, I. D. 2003, MNRAS, 339, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, J. 2007, ApJ, 658, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Heiderman, A., Evans, Neal J. I., Allen, L. E., Huard, T., & Heyer, M. 2010, ApJ, 723, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Hermelo, I., Relaño, M., Lisenfeld, U., et al. 2016, A&A, 590, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hindman, J. V., Kerr, F. J., & X.McGee, R. 1963, Aust. J. Phys., 16, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., Dyer, K. K., Thuan, T. X., & Ulvestad, J. S. 2004, ApJ, 606, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Indebetouw, R., Brogan, C., Chen, C. H. R., et al. 2013, ApJ, 774, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Jameson, K. E., Bolatto, A. D., Leroy, A. K., et al. 2016, ApJ, 825, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Jameson, K. E., Bolatto, A. D., Wolfire, M., et al. 2018, ApJ, 853, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Kalari, V. M., Carraro, G., Evans, C. J., & Rubio, M. 2018, ApJ, 857, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Kalari, V. M., Rubio, M., Saldaño, H. P., & Bolatto, A. D. 2020 MNRAS, submitted [Google Scholar]
- Lee, J. K., Rolleston, W. R. J., Dufton, P. L., & Ryans, R. S. I. 2005, A&A, 429, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehner, N., Sembach, K. R., Dufton, P. L., Rolleston, W. R. J., & Keenan, F. P. 2001, ApJ, 551, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Lehner, N., Howk, J. C., Keenan, F. P., & Smoker, J. V. 2008, ApJ, 678, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Le Bourlot, J., Pineau des Forets, G., et al. 1994, A&A, 292, 371 [NASA ADS] [Google Scholar]
- Leroy, A., Bolatto, A., Stanimirovic, S., et al. 2007, ApJ, 658, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- MacLaren, I., Richardson, K. M., & Wolfendale, A. W. 1988, ApJ, 333, 821 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Pisano, D. J., Calabretta, M. R., et al. 2009, ApJS, 181, 398 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in ASP Conf. Ser., 376, 127 [Google Scholar]
- Meixner, M., Panuzzo, P., Roman-Duval, J., et al. 2013, AJ, 146, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Miville-Deschênes, M.-A., Murray, N., & Lee, E. J. 2017, ApJ, 834, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, A., Onishi, T., Yonekura, Y., et al. 1995, ApJ, 445, L161 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, A., Yamaguchi, R., Tachihara, K., et al. 2001, PASJ, 53, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, N., Muller, E., Maeda, H., et al. 2006, ApJ, 2, 107 [CrossRef] [Google Scholar]
- Muller, E., & Parker, Q. A. 2007, PASA, 24, 69 [CrossRef] [Google Scholar]
- Muller, E., Staveley-Smith, L., Zealey, W., & Stanimirovic, S. 2003a, MNRAS, 339, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Muller, E., Staveley-Smith, L., & Zealey, W. J. 2003b, MNRAS, 338, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Muller, E., Mizuno, N., Minamidani, T., et al. 2014, PASJ, 66, 4 [CrossRef] [Google Scholar]
- Murai, T., & Fujimoto, M. 1980, PASJ, 32, 581 [NASA ADS] [Google Scholar]
- Muraoka, K., Homma, A., Onishi, T., et al. 2017, ApJ, 844, 98 [CrossRef] [Google Scholar]
- Nikolić, S., Garay, G., Rubio, M., & Johansson, L. E. B. 2007, A&A, 471, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T., & Bressert, E. 2012, APLpy: Astronomical Plotting Library in Python [Google Scholar]
- Rolleston, W. R. J., Venn, K., Tolstoy, E., & Dufton, P. L. 2003, A&A, 400, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roman-Duval,J., Jackson, J. M., Heyer, M., Rathborne, J., & Simon, R. 2010, ApJ, 723, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E., & Leroy, A. 2006, PASP, 118, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Rubio, M., Lequeux, J., & Boulanger, F. 1993, A&A, 271, 9 [NASA ADS] [Google Scholar]
- Rubio, M., Lequeux, J., Boulanger, F., et al. 1996, A&AS, 118, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubio, M., Boulanger, F., Rantakyro, F., & Contursi, A. 2004, A&A, 425, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rubio, M., Elmegreen, B. G., Hunter, D. A., et al. 2015, Nature, 525, 218 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Saldaño, H. P., Rubio, M., Jameson, K., & Bolatto, A. D. 2018, Bol. Asoc. Argent. Astron. Plata Argent., 60, 192 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Kruijssen, J. M. D., et al. 2017, ApJ, 835, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Kauffmann, J., Schnee, S., & Goodman, A. A. 2009, ApJ, 696, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sorai, K., Hasegawa, T., Booth, R. S., et al. 2001, ApJ, 551, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Staveley-Smith, L., Kim, S., Putman, M., & Stanimirovic, S. 1998, RvMA, 11, 117 [Google Scholar]
- Vassilev, V., Meledin, D., Lapkin, I., & Belitsky, V. 2008, A&A, 490, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verdugo, C. 2012, Master’s thesis, Universidad de Chile, Chile [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wong, T., Hughes, A., Tokuda, K., et al. 2017, ApJ, 850, 139 [NASA ADS] [CrossRef] [Google Scholar]
http://www.apex-telescope.org/observing/ (APECS user manual, Revision 4.1 June 5, 2020).
All Tables
Free–free emission for each source at 870 μm and 1.3 mm, obtained through aperture photometry.
Submillimeter and millimeter excesses for Magellanic Bridge A and sources North and South.
All Figures
 |
Fig. 1 Herschel 160 μm map of the SMC from Meixner et al. (2013). White contours represent the H I column density map constructed using the Parkes Galactic All-Sky Survey (GASS) first data release (McClure-Griffiths et al. 2009). The contour levels are (1, 1.5, 2, 2.5, and 3) × 1021 cm−2. The yellow circular region gives the position of Magellanic Bridge A (labeled MagBridge A). |
| In the text | |
 |
Fig. 2 ALMA continuum images at 1.3 mm of Magellanic Bridge A, generated using 12m and 7m data, where imaging is performed using natural weight. Top image: continuum without tapering in the visibility data. Middle image: continuum with its visibility data tapered using a Gaussian with an on-sky FWHM of 5′′. Bottom image: tapered continuum image convolved to reach a resolution of 22′′. The color scale for this last image is different from the other two images. The white ellipse in the bottom left corner of each image represents the beam size. Dashed contours correspond to continuum emission in the APEX 870 μm map at 25, 30, and 35 mJy beam−1. |
| In the text | |
 |
Fig. 3 Herschel continuum images of Magellanic Bridge A at 100, 160, 250, 350, and 500 μm, together with the LABOCA continuum image at 870 μm. The cyan contours correspond to the LABOCA 870 μm continuum image at 25 (5σ), 30 (6σ), and 35 mJy beam−1 (7σ). The dashed circles indicate the beam sizes for each image, which correspond to a FWHM of 9′′ (100 μm), 14′′ (160 μm), 22′′ (250 μm), 30′′ (350 μm), 43′′ (500 μm), and 22.′′ 4 (870 μm). The scale bar in the bottom right panel indicates a 10 pc length. |
| In the text | |
 |
Fig. 4 SEDs for Magellanic Bridge A and the North and South sources. The points correspond to the energy νSν derived fromthe measured flux density Sλ, obtained using aperture photometry. Red points correspond to νSν obtained using Herschel data. Dark blue points correspond to the energy νSν obtained using the LABOCA image. The purple arrow corresponds to the νSν upper limit at 1.3 mm using the ALMA continuum image. Left panel: Magellanic Bridge A SED, for which were used the 100, 160, 250, 350, and 500 μm Herschel continuum images; the 160 μm Spitzer continuum image; and the 870 μm (LABOCA) and 1.3 mm (ALMA) continuum images, all with a common resolution of 43′′. The flux from Magellanic Bridge A was measured inside a circular aperture of radius r = 50′′. The North and South sources SEDs are shown in the last two panels, constructed with the Hershel 100, 160, and 250 μm continuum images, the 870 μm (LABOCA) and 1.3 mm (ALMA) continuum images at a common resolution of 22′′. The fluxes from sources North and South were measured in a circular aperture of radius r = 11′′. The MBB model that best fits the Herschel points for each source is shown as a black curve. The parameters of each curve are listed in Table 4. |
| In the text | |
 |
Fig. 5 Velocity integrated intensity image of the combined ALMA and APEX CO(2−1) cube of Magellanic Bridge A, integrated between 172 and 176.0 km s−1. The cyan contours correspond to 5 times the σ of the integrated image (σ = 48 mJy beam−1 km s−1). The white contours correspond to the LABOCA 870 μm continuum image at 25, 30, and 35 mJy beam−1, as in Fig. 3. The white ellipse in the lower left corner represents the beam FWHM (1.22′′ ×1.15′′). The scale bar in the lower right corner indicates a 2 pc length. |
| In the text | |
 |
Fig. 6 LABOCA continuum image at 870 μm, with black contours placed at 25, 30, and 35 mJy beam−1, as in Fig. 3. The white circle represents the beam size (beam FWHM = 22′′). Red contours correspond to the ALMA and APEX CO(2−1) combined line emission convolved to the APEX resolution of 22′′, integrated between 172 and 176 km s−1, at 5σ, 6σ, and 7σ, where σ is the rms of the integrated image (σ = 1.8 Jy beam−1 km s−1). The scalebar in the lower right corner represents a 5 pc length. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


