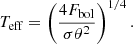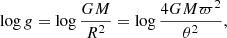EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 640 (August 2020) A&A, 640 (2020) A25 Full HTML
Free Access
Issue
A&A
Volume 640, August 2020
Article Number A25
Number of page(s) 12
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202037590
Published online 04 August 2020

© ESO 2020

1. Introduction

In the era of large stellar surveys, it is it essential to establish a method with which to reliably determine fundamental stellar parameters of the observed sources. Surveys such as Gaia (Perryman et al. 2001), APOGEE (Allende Prieto et al. 2008), Gaia-ESO Survey (Gilmore et al. 2012; Randich & Gilmore 2013), 4MOST (de Jong et al. 2012), WEAVE (Dalton et al. 2012), GALAH (De Silva et al. 2015) and many others are collecting extraordinary observational data. The surveys are covering millions of stars over the entire sky, allowing us to better understand stellar and Galactic structure and evolution. However, placing stars in a detailed evolutionary context is dependent on the accurate determination of fundamental stellar parameters of the stars such as: effective temperature (Teff), surface gravity (log(g)), metallicity [Fe/H], and stellar radius.

Each star observed by the survey must be analysed by using reliable stellar models which are tested and refined against a sample of reference stars: so-called benchmark stars (Jofré et al. 2014; Heiter et al. 2015). Those are stars with very well-defined fundamental stellar parameters that are determined independently of the survey. It is clear that it is crucial to establish such a set of benchmarks because robust stellar models allow the parameters of the rest of the stars in the survey to be mapped to the benchmark standard scale.

Ideally, the fundamental parameters of benchmark stars would be determined homogeneously, with both high accuracy and high precision, independently of each other, and directly (i.e. in a model-independent way). For the fundamental stellar parameter of Teff, the closest realisation of this ideal is with optical interferometry. Optical interferometry is a powerful technique that fulfills all these requirements because it allows an almost independent and rigorous estimate of Teff, it accurately and precisely measures the angular diameter, θ, and in combination with the bolometric flux, Fbol, which is weakly model-dependent via the adopted bolometric correction, the Teff can be determined directly by the Stefan-Boltzmann relation:

T eff = ( 4 F bol σ θ 2 ) 1 / 4 . $$ \begin{aligned} T_\mathrm{eff} = \left(\frac{4 F_\mathrm{bol} }{\sigma \theta ^2}\right)^{1/4}. \end{aligned} $$(1)

Unfortunately, direct, accurate and precise measurement of θ using optical interferometry is limited to a relatively small number of bright stars (V <  8 mag) with θ ≳ 0.3 mas. Therefore, the establishment of a consistent, homogeneous sample of benchmark stars is challenging. In an ideal case, stars in such a sample would cover a wide range of stellar parameters and abundances. Unfortunately, such a set of benchmarks is currently missing. The stars used in the Gaia-ESO survey as benchmarks (34 Gaia FGK benchmark stars in Jofré et al. 2014 and Heiter et al. 2015) are collected from unrelated individual, inconsistent observations reported in the literature. Although their effective temperatures were established directly (Mozurkewich et al. 2003; Thévenin et al. 2005; Wittkowski et al. 2006), the values were obtained using different interferometric instruments and methods (Mark III, CHARA, VINCI, etc.) and final results were obtained by applying inconsistent limb-darkening corrections from various model atmosphere grids, resulting in an inhomogeneous data set.

For metal-poor stars, it is particularly challenging to obtain a large set of reliable benchmark stars. This is due to the fact the stars with low metallicities are rare and there are only a few of them that can be observed using the state-of-the-art interferometric instrument at the CHARA array. Moreover, the few observable stars with low metallicities are also rather dim and their reliable observability is at the current brightness limit of the technique. Therefore, there are currently very few metal-poor stars for which angular diameters have been reliably measured, and thus their effective temperatures reliably inferred. To derive the Teff of metal-poor stars is nevertheless especially crucial, as metal-poor stars hold the information about the very early Universe and are of a special importance for Galactic archaeology (Frebel & Norris 2015; Silva Aguirre et al. 2018). Moreover, the demand for high-accuracy, high-precision stellar parameters of these stars is reflected in the need for metallicity-dependent surface brightness calibration for standard candles (Mould et al. 2019; Onozato et al. 2019), and reliable calibration of metallicity-dependent parameters for asteroseismology (Huber et al. 2012; Epstein et al. 2014).

Three very metal-poor stars HD 103095, HD 122563 and HD 140283 were previously interferomerically studied (Karovicova et al. 2018) using the same methods described in this paper. These metal-poor stars are Gaia FGK benchmarks, but two of them HD 103095 and HD 140283, were not recommended as benchmarks and were nominated for removal from the sample due to Teff discrepancies (see Heiter et al. 2015, and references therein for a detailed discussion). We resolved previously reported differences between Teff derived by spectroscopy, photometry and interferometry and this allowed the re-inclusion of these metal-poor stars in the benchmark stars sample. This demonstrates the robustness of our approach using the most interesting and challenging candidates.

Our overall goal is to determine fundamental stellar parameters of a new and updated set of benchmark stars measured with the highest possible accuracy and precision and determined by the best available stellar models. This paper is the first in a series of papers aiming to build a new robust sample of benchmark stars collected and analysed with a consistent approach. Here, special attention is paid to the part of our sample covering stars with low metallicities, as they are under-represented in benchmarks stars currently in use by large stellar surveys. In this study we present ten metal-poor stars that will be part of a larger sample of benchmarks. The consistent sample, both in observations and derived stellar parameters of the stars presented in this paper, will serve as validating standards for current and future large stellar surveys.

2. Observations

2.1. Science targets

The ten metal-poor stars considered in this work have metallicities between [Fe/H] = −0.7 and −2.6, these are HD 2665, HD 6755, HD 6833, HD 103095, HD 122563, HD 127243, HD 140283, HD 175305, HD 221170, and HD 224930. These stars are candidates for benchmarks used for validating large stellar surveys. The sample spans the entire evolutionary range of solar-mass metal-poor stars as seen in Fig. 1, and we list their astrometric parameters in Table 1.

thumbnail Fig. 1.

Stellar parameters of our ten metal-poor stars, colour-coded by metallicity, compared to theoretical Dartmouth isochrones of different ages (linestyles) and metallicities (colours). Formal 1σ uncertainties are shown by the error bars. The symbol size is proportional to the angular diameter of the star.

Table 1.

Astrometric parameters.

We selected the ten stars in consultation with the Gaia-ESO spectroscopic team. The stars have sizes and brightnesses such that their angular diameters can be measured reliably using the chosen interferometric instrument, and thus the Teff can be inferred reliably.

Three of the stars, HD 103095, HD 122563, and HD 140283, are currently used as Gaia FGK benchmark stars (Heiter et al. 2015). In the previous paper (Karovicova et al. 2018), the reliability of the approach was demonstrated on these three stars. They are again included here in order to present a homogeneous set of stellar parameters for all ten stars, and because the data reduction have been updated.

The other seven stars have not previously been used as benchmark stars. HD 175303 was discussed in an update to the Gaia FGK benchmarks (Hawkins et al. 2016). Four stars (HD 2665, HD 6755, HD 6833, HD 221170) were nominated as benchmarks by Heiter et al. (2015) on the basis of their inclusion in the catalogue of hydrogen line profiles from Huang et al. (2012). We moreover added two targets (HD 127243 and HD 224930) with slightly higher metallicities (−0.7 dex), which according to the PASTEL catalogue (Soubiran et al. 2010), are thought to be typical stars and serve to complete the sample.

2.2. Interferometric observations and data reduction

We observed the stars using the interferometric instrument PAVO (Ireland et al. 2008). The instrument is located at the CHARA array at Mt. Wilson Observatory, California (Ten Brummelaar et al. 2005). The PAVO instrument is operating in optical wavelengths between ∼600 and 900 nm, is a pupil-plane beam combiner, and is limited to observations of targets with magnitudes of mR ∼ 7.5. In the case of ideal weather conditions, it is possible to observe targets down to mR = 8, with recent improvements due to adaptive optics (Che et al. 2014). The CHARA array offers the longest available baselines in the optical wavelengths worldwide. The stars were observed using baselines between 107.9 m and 313.6 m. We collected the observations between 2009 Jul. 17 and 2016 Oct. 7. Table 2 summarises our dates of observations, telescope configuration and the projected baselines B.

Table 2.

Interferometric observations – metal-poor stars.

The data were reduced with the PAVO reduction software. The PAVO data-reduction software has been thoroughly tested and used in multiple studies (Bazot et al. 2011; Derekas et al. 2011; Huber et al. 2012; Maestro et al. 2013). In order to monitor the interferometric transfer function, a set of calibrating stars were observed. These calibrating stars were selected from a catalogue of CHARA calibrators and from the HIPPARCOS catalogue (ESA 1997). According to the location and size of an observed target, we selected unresolved or closely unresolved sources located close on the sky to the science target. The calibrating stars were observed immediately before and after the science target. We determined the angular diameters of the calibrators using the V − K relation of Boyajian et al. (2014) and corrected for limb darkening to determine the uniform disc diameter in R band. The V-band magnitudes were selected from the Tycho-2 catalogue (Høg et al. 2000) and converted into the Johnson system using the calibration by Bessell (2000). The K-band magnitudes were selected from the Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006). The reddening was estimated from the dust map of Green et al. (2015) and the reddening law of O’Donnell (1994) was applied. We set the relative uncertainty on calibrator diameters to 5% (Boyajian et al. 2014). The uncertainty is set in a way that it covers the uncertainty on the calibrator diameters as well as the uncertainty on the reddening. We also set the absolute uncertainty on the wavelength scale to 5 nm. We checked the literature for each calibrator to ensure they were not known binaries. According to Gaia DR2, both the proper motion anomaly (Kervella et al. 2019) and the phot_bp_rp_excess_factor (Evans et al. 2018) suggest that none of our calibrators have a companion that is large enough to affect our interferometric measurements or estimated calibrator sizes. We note that for the smallest science targets, such as HD 2665 and HD 6755, we have endeavored to choose the smallest calibrators that were practical, which in these cases were < 0.15 mas. For all the calibrating stars, their spectral type, magnitude in the V and R band, their expected angular diameter and the corresponding science targets are summarised in Table 3.

Table 3.

Calibrator stars used for interferometric observations – metal-poor stars.

3. Methods and analysis

In this section we describe the method delivering the stellar parameters, showing the connection between the interferometric, photometric and spectroscopic analysis. To obtain the angular diameter (see below), and hence the Teff, from the interferometric data requires a limb-darkening parameter. This depends on Teff, log(g), and [Fe/H]. The process of estimating the Teff is initiated by entering a first guess for the stellar parameters (from the literature), and linearly interpolating the limb-darkening coefficients from the STAGGER-grid (Magic et al. 2015).

The first limb-darkened angular diameter together with the bolometric flux allows us to directly compute the Teff (Eq. (1)). The log(g) and [Fe/H] were then refined by isochrone fitting and spectroscopic analysis: log(g) is sensitive to Teff and metallicity, and [Fe/H] is sensitive to Teff and log(g), therefore, these values are slightly refined with each iteration. The final values of fundamental stellar parameters of the benchmark stars were iterated between interferometric, photometric, and spectroscopic modelling, until convergence was reached.

We did not encounter any major convergence problems. Changing the initial guess parameters by 500 K in Teff, 0.2 dex in log(g), or 0.2 dex in [Fe/H] did not change the final converged angular diameter result (to within the 1σ errors).

3.1. Modelling of limb-darkened angular diameters

The determination of accurate angular diameters requires an estimate of an appropriate amount of limb-darkening derived from stellar model atmospheres. As a first step, we fitted an undarkened uniform disc to the visibility curves. For all our fits, both with and without limb-darkening, we used a least-squares fitting routine in IDL (MPFIT, Markwardt et al. 2009), with uncertainties being determined by Monte Carlo simulations that took into account the uncertainty in the visibility measurements, as well as the wavelength calibration (5 nm), calibrator sizes (5%) and, for the limb-darkened fits, the limb-darkening coefficients.

Our fitted uniform disk diameters are listed in Table 4. We also fitted the commonly used linear limb-darkening law from Claret & Bloemen (2011); these are grids of coefficients calculated for various model atmospheres and different photometric filters. For reference, we also present the resulting limb-darkened angular diameters in Table 4. However, we stress that our final Teff estimates are based on high-order limb-darkening coefficients from the STAGGER-grid. The 3D hydrodynamical models have been shown to better reproduce the solar limb darkening than both theoretical and semi-empirical 1D hydrostatic models (Pereira et al. 2013). For this reason, they are expected to give better overall results and are adopted in the present analysis. The final results based on the STAGGER-grid are presented in Table 5, and discussed below.

Table 4.

Angular diameters and linear limb-darkening coefficients.

Table 5.

Observed (ΘLD) and derived (Fbol, M, L, R) stellar parameters.

For robust estimates and accurate angular diameter we employed higher-order limb-darkening laws. The method used in this study generally follows the same procedure described in Sect. 2.2 in the previous study of the same topic in Karovicova et al. (2018). In short, we employed the four-parameter limb-darkening coefficients of Magic et al. (2015) that were calculated from 3D synthetic spectra from Chiavassa et al. (2018) for the STAGGER-grid of ab initio 3D hydrodynamic stellar atmosphere simulations (Magic et al. 2013). These coefficients are tabulated as functions of Teff, log(g), and [Fe/H]; we interpolated them based on our initial guesses, and refined them using our measurements of Teff based on the bolometric flux (Sect. 3.2), log(g) based on stellar evolution models (Sect. 3.3), and [Fe/H] based on spectroscopy (Section 3.4). We note that for one of our stars, HD 221170, its log(g) value places it outside the STAGGER-grid. For this star we therefore linearly extrapolated its coefficients from the STAGGER-grid, and confirmed that these provided reasonable values by comparing them with coefficients from the tables of Claret & Bloemen (2011). Using 3D models instead of 1D models generally has a very small effect on the determined limb-darkened angular diameters, compared to the error bars, indicating that the measurements are usually only mildly dependent on the model assumptions. However, in the worst case (HD 122563) the differences are 2%, which translates to 1% in Teff which is the targeted precision. We present the limb-darkening coefficients from the STAGGER-grid (in all 38 channels) in Tables 9–18 available at the CDS.

3.2. Bolometric flux

Many of the stars in the sample have saturated or unreliable 2MASS photometry, which prevents us from using the InfraRed Flux Method to derive bolometric fluxes (Casagrande et al. 2010). Hence, for all targets we use bolometric corrections from Casagrande & VandenBerg (2014, 2018a). We use Hipparcos Hp and Tycho2 BTVT magnitudes for all stars, and 2MASS JHKS only if it has quality flag “A”. We assumed no reddening for all stars closer than 100 pc; for stars further away we estimated E(B − V) using interstellar Na I D lines when possible, or the Green et al. (2015) map otherwise.

Tables of bolometric corrections1 were interpolated at the adopted reddening, and spectroscopic [Fe/H] and log(g). Spectroscopic Teff were used only as a starting point to interpolate bolometric corrections. The adopted bolometric corrections are listed in Table 6. An iterative procedure was adopted where the bolometric corrections were used together with the angular diameter to derive an updated Teff until convergence was reached to within a few Kelvin.

Table 6.

Bolometric corrections.

The bolometric flux was obtained using a weighted average of the bolometric flux from the bolometric correction in each band. Weights were given by the inverse of the estimated variance of the bolometric flux derived from each band. These were obtained for each photometric band by computing the mean square deviation using a Monte Carlo integration over four independent parameters (Teff, log(g), [Fe/H] and E(B − V)) and the photometric magnitude for that band. All five input parameter errors were modelled as independent normally distributed random variables. The uncertainties quoted for the bolometric flux are the square root of the weighted sample variance plus a 0.3% systematic error to account for the uncertainty in the adopted reference solar luminosity. The systematic uncertainties and inaccuracies stemming from the use of model fluxes are harder to quantify, but extensive comparison with absolute spectrophotometry in Casagrande & VandenBerg (2018b) indicates that bolometric fluxes are typically recovered at the percent level for FG stars. Our sample comprises cooler stars, for which the performances of our bolometric corrections are much less tested. Reassuringly, the comparison of our bolometric corrections with absolute spectrophotometry from White et al. (2018) also indicates good agreement for stars in the Teff range covered by the present work.

3.3. Stellar evolution models

We used the ELLI package2 (Lin et al. 2018) to estimate stellar masses based on comparisons to Dartmouth stellar evolution tracks (Dotter et al. 2008), computed with alpha enhancement. The comparison uses a Bayesian framework to estimate the stellar mass and age from Teff, log L/L⊙ and [Fe/H], taking into account their related (assumed independent) errors. An initial guess is produced from a maximum-likelihood estimate at our estimated metallicity, between the fundamental stellar parameters and those estimated on the isochrone. A Markov chain Monte Carlo (MCMC) method is then used to sample the posterior distribution, and we take the mean and dispersion on this distribution as our estimate for the mass and its uncertainty. Finally, we compute the surface gravity from its fundamental relation, rewritten to a form that directly utilises the measurements,

log g = log GM R 2 = log 4 G M ϖ 2 θ 2 , $$ \begin{aligned} \log g = \log \frac{G M}{R^2} = \log \frac{4 G M \varpi ^2}{\theta ^2}, \end{aligned} $$(2)

where G is the gravitational constant and ϖ the parallax.

As shown in Fig. 1, there are systematic offsets between the theoretical stellar isochrones and the parameters of metal-poor stars on the red giant branch. Our Bayesian sampling approach therefore does a poor job of predicting the properties of these stars. Instead, we adopted the turn-off mass at the relevant metallicity and assume an age > 10 Gyr. Since we did not use the Bayesian approach for these stars, we instead use a conservative uncertainty estimate on the stellar mass of 0.05 M⊙.

3.4. Spectroscopic analysis

High-resolution spectra for the stars were extracted from the ELODIE (R ≈ 42 000, Moultaka et al. 2004) and FIES (R ≈ 65 000, Telting et al. 2014) archives. We determined the stellar iron abundances using a custom pipeline based on the spectrum synthesis code SME (Piskunov & Valenti 2017) using MARCS model atmospheres (Gustafsson et al. 2008) and pre-computed non-local thermodynamic equilibrium (NLTE) departure coefficients for Fe (Amarsi et al. 2016).

We selected unblended lines of Fe I and Fe II between 4400 and 6800 Å with accurately known oscillator strengths from laboratory measurements. For saturated lines, we ensured that collisional broadening parameters were available from ABO theory (Barklem et al. 2000; Barklem & Aspelund-Johansson 2005). To obtain a differential [Fe/H], solar abundances were also measured from solar spectra recorded with the same spectrographs as our target stars, based on observations of light reflected off the Moon (ELODIE) and Vesta (FIES). We thereby produce solar-differential abundances, which mostly cancels uncertainties in oscillator strengths as well as potential systematic differences between the spectrographs. We estimated the iron abundance of each star from the outlier-resistant mean of the entire set of Fe I and Fe II lines, with 3σ clipping. We also computed the difference in abundance between lines of Fe I and Fe II, as an estimate of how closely our fundamental stellar parameters fulfill the ionisation equilibrium. Finally, we compute a systematic uncertainty on the metallicity, which we derive by perturbing the input parameters one at a time according to their formal errors, and add these differences in quadrature.

4. Results and discussion

4.1. Recommended stellar parameters

We present fundamental stellar parameters and angular diameters for a set of benchmark stars. Four of the ten stars are Gaia FGK benchmark stars (HD 12256, HD 103095, HD 140283, HD 175305) to which we add a further six stars (HD 2665, HD 6755, HD 6833, HD 221170, HD 127243, HD 224930) that we put forward as new benchmark stars. We plot the final visibility curves in Figs. 2–6. We estimate Teff, log g, [Fe/H] and θLD for all ten stars. All the values along with mass, luminosity and radii are summarised in Table 5.

thumbnail Fig. 2.

Squared visibility vs. spatial frequency for HD 2665 and HD 6755. The HD number is noted in the right upper corner in the each plot. The error bars have been scaled to the reduced χ2. For HD 2665 the reduced χ2 = 1.6 and for HD 6755 χ2 = 1.7. The grey dots are the individual PAVO measurements in each wavelength channel. For clarity, we show weighted averages of the PAVO measurements as red circles. The green line shows the fitted limb-darkened model to the PAVO data, with the light grey-shaded region indicating the 1-σ uncertainties. The lower panel shows the residuals from the fit.

thumbnail Fig. 3.

Squared visibility vs. spatial frequency for HD 6833 and HD 103095. Lower panel: residuals from the fit. The error bars have been scaled to the reduced χ2. For HD 6833 the reduced χ2 = 7.0 and for HD 103095 χ2 = 1.1. All lines and symbols are the same as for Fig. 2.

thumbnail Fig. 4.

Squared visibility vs. spatial frequency for HD 122563 and HD 127243. Lower panel: residuals from the fit. The error bars have been scaled to the reduced χ2. For HD 122563 the reduced χ2 = 3.0 and for HD 127243 χ2 = 1.6. All lines and symbols are the same as for Fig. 2.

thumbnail Fig. 5.

Squared visibility vs. spatial frequency for HD 140283 and HD 175305. Lower panel: residuals from the fit. The error bars have been scaled to the reduced χ2. For HD 140283 the reduced χ2 = 1.4 and for HD 175305 χ2 = 3.7. All lines and symbols are the same as for Fig. 2.

thumbnail Fig. 6.

Squared visibility vs. spatial frequency for HD 221170 and HD 224930. Lower panel: residuals from the fit. The error bars have been scaled to the reduced χ2. For HD 221170 the reduced χ2 = 2.1 and for HD 224930 χ2 = 8.4. All lines and symbols are the same as for Fig. 2.

4.2. Uncertainties

The final Teff uncertainties consist of uncertainties in the bolometric flux and the uncertainties in the angular diameter. Table 7 shows the contribution of each part. The third column shows the final Teff uncertainties, the fourth column the uncertainties arising from the bolometric flux if the ΘLD uncertainties are set to zero. The fifth column shows the Fbol uncertainties set to 0, with the uncertainties raising entirely from the angular diameter.

Table 7.

Uncertainties in Teff and how they propagate from the underlying measurements.

The statistical measurement uncertainties in log(g) and [Fe/H] from the isochrone fitting and spectroscopic analysis were folded into the uncertainties in the angular diameters and are therefore included in the final Teff error estimates. The median uncertainties in log(g) and [Fe/H] across our sample of stars are 0.03 dex and 0.09 dex, respectively (Table 8).

Table 8.

Derived stellar parameters (Teff , [Fe/H], log(g)).

For five of the stars, the final Teff uncertainties are less than around 50 K, or 1%. For these stars, the errors coming from the bolometric flux are less than or similar to those coming from the limb-darkened angular diameter. The final Teff uncertainties for the other five stars are somewhat larger: 100–150 K. This is driven by larger errors in the bolometric flux, rather than in the angular diameter. As mentioned above, the precision that is desired by the spectroscopic teams of surveys like Gaia-ESO or GALAH is around 1% (or around 40–60 K); we achieve this for half of our sample, and could achieve it for the full sample if more precise bolometric fluxes are available.

4.3. Comparison with literature values

Three of our ten targets (HD 103095, HD 122563 and HD 140283) were previously interferometrically studied by Creevey et al. (2012, 2015) and they are also a part of the previous interferometric study (Karovicova et al. 2018). These stars were used as Gaia FGK benchmark stars in the Gaia-ESO spectroscopic survey. However, the stars HD 103095 and HD 140283 had to be reconsidered as their Teff did not reconcile with spectroscopic studies, and the stars were not recommended as temperature standards pending resolution of these discrepancies (see Heiter et al. 2015). The issues were resolved by Karovicova et al. (2018) and the stars can be now again used as benchmarks.

HD 103095. This star was interferometrically observed by Creevey et al. (2012), who reported Teff = 4818 ± 54 K. This value is lower than a value estimated in a previous study (Karovicova et al. 2018) where Teff = 5140 ± 49 K was determined. Here with our improved reduction method we obtain Teff = 5174 ± 32, log g = 4.702 ± 0.015 dex and [Fe/H] = −1.26 ± 0.07 dex; we note that all the differences with the previous study are within the stipulated uncertainties.

HD 122563. This metal-poor star is well studied spectroscopically. It was included in the Gaia FGK benchmark sample with Teff = 4587 ± 60 K and log g = 1.61 ± 0.07 dex (Heiter et al. 2015). The star was also a part of the interferometric study by Creevey et al. (2012). The reported Teff = 4598 ± 41 K by Creevey et al. (2012) agrees within the uncertainties with our estimated value. The Teff value from Karovicova et al. (2018) is Teff = 4636 ± 37 K, and the updated value is Teff = 4635 ± 34 together with log g = 1.404 ± 0.035 dex and [Fe/H] = − 2.75 ± 0.12 dex. The Teff is in agreement with expected photometric and spectroscopic value.

HD 140283. This very metal-poor star was interferometrically measured by Creevey et al. (2015). There were two values reported for Teff based on two different reddenings and Teff is therefore between Teff = 5534 ± 103 K and 5647 ± 105 K. These values were in disagreement with spectroscopy and photometry. The Teff = 5787 ± 48 K determined by Karovicova et al. (2018) is in disagreement with those found by Creevey et al. (2015), namely 253 K and 140 K higher, respectively, bringing the interferometric values into disagreement also. The issues were resolved, putting the spectroscopic, photometric, and interferometric values into better agreement. The new Teff = 5792 ± 55 and other stellar parameters are: log g = 3.653 ± 0.024 dex and [Fe/H] = − 2.29 ± 0.10 dex. The differences between the interferometrically determined Teff of Creevey et al. (2012, 2015) and Karovicova et al. (2018) are the result of differences in the measured angular diameters of the stars. This points to systematic errors arising from the known difficult calibration of interferometric observations, especially of the smaller targets.

The remaining stars have not previously been interferometrically studied; however, for comparison we list various spectroscopic parameters as published in the PASTEL catalogue (Soubiran et al. 2010). Our values of Teff, log g, and [Fe/H] are listed in Table 8. We compare our values with spectroscopical studies executed after 2000 when high-resolution spectroscopic instruments were available. For details on uncertainties of our values, please see Tables 8 and 7 as well as Sect. 4.2.

HD 175305. Hawkins et al. (2016) proposed this star as a benchmark. They derived stellar parameters for it by averaging different values from the PASTEL catalogue, and arrived at Teff = 5085 ± 58 K, log g = 2.49 ± 0.25 dex and [Fe/H] = − 1.43 ± 0.07 dex (see Hawkins et al. 2016). The stellar parameters were compiled using the PASTEL database (Soubiran et al. 2010). We report Teff = 4850 ± 118 K, log g = 2.502 ± 0.031 dex and [Fe/H] = − 1.52 ± 0.08 dex. Our values point to a much cooler star.

HD 2665. According to the PASTEL catalogue, the Teff measurements range between 5000 and 5123 K, with log g between 2.20 and 2.35 and metallicity of −1.9. Our Teff of 4883 ± 95 K is significantly lower; our log g is within this latter range but we have a lower metallicity of −2.1 ± 0.09 dex.

HD 6755. In the PASTEL catalogue the Teff measurements range between 5011 and 5169 K, with only two values for log g;: 2.7 and 2.8 dex, and the same for [Fe/H]: −1.47 and −1.58 dex. Our value for Teff is again systematically much lower, 4888 ± 131 K, however with a rather large uncertainty of 131 K arising from the bolometric flux estimate. We also determine a slightly lower metallicity of −1.7 ± 0.10 dex in comparison to the literature values.

HD 6833. The PASTEL catalogue shows only two Teff values for this star of 4400 and 4450 K, log g values of 1 and 1.4 dex and [Fe/H] of −0.89 and −1.04 dex. Our values agree to some extent with Teff = 4438 ± 141 K and [Fe/H] = − 0.8 ± 0.07 dex, but we present higher log g:1.860 dex± 0.072.

HD 127243. According to the PASTEL catalogue, this subgiant has been studied spectroscopically four times, with Teff measurements ranging between 5000 and 5350 K, surface gravity between 2.2 and 3.5, and metallicity between −0.6 and −0.7. Our estimate of the Teff shows a value close to the lower range (4959 ± 21 K), while other stellar values are within the above ranges.

HD 221170. The literature values from the PASTEL catalogue show a slightly warmer star with higher metallicity than our estimated values. The PASTEL Teff is between 4425 and 4648 K, log g between 0.9 and 1.05 dex, and [Fe/H] between −2 and −2.190 dex. Our temperature is significantly lower, with Teff of 4248 ± 128 K. We present log g of 1.251 ± 0.042 dex and our results also show the star to be more metal poor with [Fe/H] of −2.4 ± 0.13 dex.

HD 224930. According to the PASTEL catalogue, this star has been studied spectroscopically several times and the reported Teff is widely spread between 5169 K and 5680 K, log g between 4.1 and 4.5 dex and [Fe/H] between −0.52 and −1. Our values lie in the middle of the spread with Teff of 5422 ± 28 K, log g of 4.337 ± 0.012 dex and [Fe/H] of −0.81 ± 0.05 dex.

4.4. Fe ionisation balance

The relative populations of different ionisation stages is a sensitive measure of atmospheric properties. The so-called ionisation balance involves matching the overall Fe elemental abundance as derived from Fe I and Fe II in order to determine a star’s surface gravity (Tsantaki et al. 2019). Conversely, when the surface gravity is already known, the ionisation balance can instead be used to infer an effective temperature (see, e.g., Bergemann et al. 2012), or to verify the consistency of the two.

We find that our iron abundance determinations generally yield acceptable agreement for lines of neutral and ionised iron. We illustrat ethese abundance differences in Fig. 7 as a function of the measured angular diameters and stellar parameters. The abundance differences are small for the dwarf stars in the sample, consistent with their statistical uncertainties. However, among the giant stars, we find a strong trend with Teff such that the coolest stars deviate strongly from ionisation equilibrium by upwards of 0.5 dex. However, we find that these discrepancies do not correlate with angular diameters, indicating that they are not driven by instrumental artefacts but rather by shortcomings in the spectroscopic analysis. We do however identify a trend between the abundance differences and the effective temperature, where the coolest stars in our sample show increasingly large deviations from ionisation balance exceeding 0.4 dex for HD 6833 (4438 K) and 0.6 dex for HD 221170 (4248 K).

thumbnail Fig. 7.

Deviations from ionisation balance, i.e. the difference between the abundances determined from lines of neutral and ionised iron, as a function of the measured stellar parameters. Vertical and horizontal lines represent the combined uncertainties from the two measurements. Each star is labelled, and colour-coded as red for red giants or blue for main sequence and subgiants.

Importantly, this indicates that a non-differential spectroscopic derivation of stellar parameters for cool, very metal-poor stars cannot accurately recover their surface gravity. 3D NLTE models could help to resolve this discrepancy (e.g. Amarsi et al. 2016, 2019).

The measurement of iron abundances from lines of the neutral species is sensitive to the adopted effective temperature, where a change of ±100 K will on average affect the measured abundance by ±0.07 dex. The corresponding effect on lines of ionised iron is of the order ±0.02 and ±0.05 dex for stars warmer and cooler than 5500 K, respectively. Conversely, a change in log(g) of ±0.1 dex will affect the abundance from lines of neutral iron by less than 0.01 dex. For ionised lines, the corresponding effect on the abundance difference is ±0.05 dex. An error in Teff of ±100 K will therefore typically affect the difference in iron abundances inferred from lines of Fe I relative to those inferred from lines of Fe II by approximately ±0.1 dex, and an error in log(g) of ±0.1 dex would have a corresponding effect of ±0.05 dex. Errors in [Fe/H] from Fe I and from Fe II could thereby partially cancel.

5. Conclusions

This project delivered fundamental stellar parameters for ten metal-poor stars. Stars with low metallicity are poorly represented in the benchmark sample used so far. Reliable angular diameters for metal-poor stars have been difficult to measure so far because these stars are faint for suitable interferometric instruments. We took this into consideration, observed the stars over various nights and with various baseline configurations, and tried to resolve the targets close to the first null of the visibility curve. We observed the stars using the high-angular-resolution instrument PAVO and the CHARA array and measured accurate angular diameters for the stars.

In order to estimate the limb-darkening diameters, we used the 3D radiation-hydrodynamical model atmospheres in the STAGGER-grid. The Teff were directly computed from the Stefan-Boltzmann relation using the measured angular diameters and bolometric flux. Bolometric fluxes were computed from multi-band photometry interpolating iteratively on a grid of synthetic stellar fluxes to ensure consistency with the final adopted stellar parameters. High-resolution-spectroscopy allowed us to determine [Fe/H], isochrone fitting to derive mass, and parallax measurements to constrain the absolute luminosity. After iterative refinement we derived the final fundamental parameters of Teff, log(g), and [Fe/H].

This allowed us to reach the desired precision of better than 1% in the Teff for five stars in our sample HD 103095, HD 122563, HD 127243, HD 140283 and HD 224930. A precision of 1% in Teff is essential for correct determination of the atmospheric parameters of the survey sources. For the remaining stars, for which the uncertainties in Teff are higher than 1%, the uncertainty in the bolometric flux significantly contributes to the final uncertainty in the effective temperature (∼2–3%). For all stars in our sample we determined log(g) and [Fe/H], with median uncertainties of 0.03 dex and 0.09 dex, respectively.

We present the first of a series of papers with which we aim to build a new robust sample of benchmark stars. The reliable interferometric stellar parameters presented here should be useful for testing and validating stellar analysis pipelines (Jofré et al. 2019), which typically rely on photometric and spectroscopic methods. Our consistent measurements and analysis will also help to cross-calibrate different large stellar surveys such as Gaia (Gaia Collaboration 2018), APOGEE (Allende Prieto et al. 2008), Gaia-ESO Survey (Gilmore et al. 2012; Randich & Gilmore 2013), 4MOST (de Jong et al. 2012), WEAVE (Dalton et al. 2012), and GALAH (De Silva et al. 2015). In turn, achieving these goals will help us to more robustly understand the physics of stars, and uncover the structure and evolution of our Galaxy.

2

Available online at https://github.com/dotbot2000/elli

Acknowledgments

I.K. acknowledges the German Deutsche Forschungsgemeinschaft, DFG project number KA4055 and by the European Science Foundation – GREAT Gaia Research for European Astronomy Training, award numbers 4652 and 4947. M.I. was the recipient of an Australian Research Council Future Fellowship (FT130100235) funded by the Australian Government. P.J. acknowledges FONDECYT Iniciación programme number 11170174. This work is based upon observations obtained with the Georgia State University Center for High Angular Resolution Astronomy Array at Mount Wilson Observatory. The CHARA Array is supported by the National Science Foundation under Grants No. AST-1211929 and AST-1411654. Institutional support has been provided from the GSU College of Arts and Sciences and the GSU Office of the Vice President for Research and Economic Development. This work is based on spectral data retrieved from the ELODIE archive at Observatoire de Haute-Provence (OHP), and on observations made with the Nordic Optical Telescope, operated by the Nordic Optical Telescope Scientific Association at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofisica de Canarias. Thanks to Prof. Gilmore for supporting observing and grant proposals through the whole project. Thanks to Dr. Thévenin for providing helpful comments and for his support of the project. Thanks to Dr. Creevey for her collaboration. Thanks to Dr. Lind for helpful discussions and for providing preliminary spectroscopic computations. Finally, we are extremely grateful to the anonymous referee for carefully reading the manuscript, and providing helpful comments.

References

  1. Allende Prieto, C., Majewski, S. R., Schiavon, R., et al. 2008, Astron. Nachr., 329, 1018 [Google Scholar]
  2. Amarsi, A. M., Lind, K., Asplund, M., Barklem, P. S., & Collet, R. 2016, MNRAS, 463, 1518 [NASA ADS] [CrossRef] [Google Scholar]
  3. Amarsi, A. M., Nissen, P. E., & Skúladóttir, Á. 2019, A&A, 630, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Barklem, P. S., & Aspelund-Johansson, J. 2005, A&A, 435, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&AS, 142, 467 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  6. Bazot, M., Ireland, M. J., Huber, D., et al. 2011, A&A, 526, L4 [Google Scholar]
  7. Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012, MNRAS, 427, 27 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bessell, M. S. 2000, PASP, 112, 961 [NASA ADS] [CrossRef] [Google Scholar]
  9. Boyajian, T. S., van Belle, G., & von Braun, K. 2014, AJ, 147, 47 [NASA ADS] [CrossRef] [Google Scholar]
  10. Casagrande, L., & VandenBerg, D. A. 2014, MNRAS, 444, 392 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  11. Casagrande, L., & VandenBerg, D. A. 2018a, MNRAS, 475, 5023 [NASA ADS] [CrossRef] [Google Scholar]
  12. Casagrande, L., & VandenBerg, D. A. 2018b, MNRAS, 479, L102 [NASA ADS] [CrossRef] [Google Scholar]
  13. Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Che, X., Sturmann, L., Monnier, J. D., et al. 2014, The CHARA Array Adaptive Optics I: Common-path Optical and Mechanical Design, and Preliminary On-sky Results, SPIE Conf. Ser., 9148, 914830 [Google Scholar]
  15. Chiavassa, A., Casagrande, L., Collet, R., et al. 2018, A&A, 611, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Creevey, O. L., Thévenin, F., Boyajian, T. S., et al. 2012, A&A, 545, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Creevey, O. L., Thévenin, F., Berio, P., et al. 2015, A&A, 575, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Dalton, G., Trager, S. C., Abrams, D. C., et al. 2012, in WEAVE: the next generation wide-field spectroscopy facility for the William Herschel Telescope, SPIE Conf. Ser., 8446, 84460P [Google Scholar]
  20. de Jong, R. S., Bellido-Tirado, O., Chiappini, C., et al. 2012, in 4MOST: 4-metre Multi-object Spectroscopic Telescope, SPIE Conf. Ser., 8446, 84460T [Google Scholar]
  21. De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., et al. 2015, MNRAS, 449, 2604 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  22. Derekas, A., Kiss, L. L., Borkovits, T., et al. 2011, Science, 332, 216 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  23. Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
  24. Epstein, C. R., Elsworth, Y. P., Johnson, J. A., et al. 2014, ApJ, 785, L28 [NASA ADS] [CrossRef] [Google Scholar]
  25. ESA 1997, in The HIPPARCOS and TYCHO catalogues, ESA SP, 1200 [Google Scholar]
  26. Evans, D. W., Riello, M., De Angeli, F., et al. 2018, A&A, 616, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Frebel, A., & Norris, J. E. 2015, ARA&A, 53, 631 [NASA ADS] [CrossRef] [Google Scholar]
  28. Gaia Collaboration 2018, VizieR Online Data Catalog: I/345 [Google Scholar]
  29. Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
  30. Green, G. M., Schlafly, E. F., Finkbeiner, D. P., et al. 2015, ApJ, 810, 25 [NASA ADS] [CrossRef] [Google Scholar]
  31. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Hawkins, K., Jofré, P., Heiter, U., et al. 2016, A&A, 592, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
  34. Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [Google Scholar]
  35. Huang, W., Wallerstein, G., & Stone, M. 2012, A&A, 547, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Huber, D., Ireland, M. J., Bedding, T. R., et al. 2012, ApJ, 760, 32 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ireland, M. J., Mérand, A., ten Brummelaar, T. A., et al. 2008. Optical and Infrared Interferometry, Proc. SPIE,, 7013, 701324 [CrossRef] [Google Scholar]
  38. Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Jofré, P., Heiter, U., & Soubiran, C. 2019, ARA&A, 57, 571 [Google Scholar]
  40. Karovicova, I., White, T. R., Nordlander, T., et al. 2018, MNRAS, 475, L81 [NASA ADS] [CrossRef] [Google Scholar]
  41. Kervella, P., Arenou, F., Mignard, F., & Thévenin, F. 2019, A&A, 623, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Lin, J., Dotter, A., Ting, Y.-S., & Asplund, M. 2018, MNRAS, 477, 2966 [NASA ADS] [CrossRef] [Google Scholar]
  43. Maestro, V., Che, X., Huber, D., et al. 2013, MNRAS, 434, 1321 [NASA ADS] [CrossRef] [Google Scholar]
  44. Magic, Z., Collet, R., Asplund, M., et al. 2013, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Magic, Z., Chiavassa, A., Collet, R., & Asplund, M. 2015, A&A, 573, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Markwardt, C. B. 2009, in Non-linear Least-squares Fitting in IDL with MPFIT, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
  47. Mould, J., Clementini, G., & Da Costa, G. 2019, PASA, 36, e001 [CrossRef] [Google Scholar]
  48. Moultaka, J., Ilovaisky, S. A., Prugniel, P., & Soubiran, C. 2004, PASP, 116, 693 [NASA ADS] [CrossRef] [Google Scholar]
  49. Mozurkewich, D., Armstrong, J. T., Hindsley, R. B., et al. 2003, AJ, 126, 2502 [NASA ADS] [CrossRef] [Google Scholar]
  50. O’Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
  51. Onozato, H., Ita, Y., Nakada, Y., & Nishiyama, S. 2019, MNRAS, 486, 5600 [CrossRef] [Google Scholar]
  52. Pereira, T. M. D., Asplund, M., Collet, R., et al. 2013, A&A, 554, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Randich, S., Gilmore, G., & Gaia-ESO Consortium 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
  56. Silva Aguirre, V., Bojsen-Hansen, M., Slumstrup, D., et al. 2018, MNRAS, 475, 5487 [NASA ADS] [Google Scholar]
  57. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  58. Soubiran, C., Le Campion, J. F., Cayrel de Strobel, G., & Caillo, A. 2010, A&A, 515, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Telting, J. H., Avila, G., Buchhave, L., et al. 2014, Astron. Nachr., 335, 41 [NASA ADS] [CrossRef] [Google Scholar]
  60. Ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
  61. Thévenin, F., Kervella, P., Pichon, B., et al. 2005, A&A, 436, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Tsantaki, M., Santos, N. C., Sousa, S. G., et al. 2019, MNRAS, 485, 2772 [NASA ADS] [CrossRef] [Google Scholar]
  63. White, T. R., Huber, D., Mann, A. W., et al. 2018, MNRAS, 477, 4403 [NASA ADS] [CrossRef] [Google Scholar]
  64. Wittkowski, M., Hummel, C. A., Aufdenberg, J. P., & Roccatagliata, V. 2006, A&A, 460, 843 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1.

Astrometric parameters.

In the text
Table 2.

Interferometric observations – metal-poor stars.

In the text
Table 3.

Calibrator stars used for interferometric observations – metal-poor stars.

In the text
Table 4.

Angular diameters and linear limb-darkening coefficients.

In the text
Table 5.

Observed (ΘLD) and derived (Fbol, M, L, R) stellar parameters.

In the text
Table 6.

Bolometric corrections.

In the text
Table 7.

Uncertainties in Teff and how they propagate from the underlying measurements.

In the text
Table 8.

Derived stellar parameters (Teff , [Fe/H], log(g)).

In the text

All Figures

thumbnail Fig. 1.

Stellar parameters of our ten metal-poor stars, colour-coded by metallicity, compared to theoretical Dartmouth isochrones of different ages (linestyles) and metallicities (colours). Formal 1σ uncertainties are shown by the error bars. The symbol size is proportional to the angular diameter of the star.
In the text
thumbnail Fig. 2.

Squared visibility vs. spatial frequency for HD 2665 and HD 6755. The HD number is noted in the right upper corner in the each plot. The error bars have been scaled to the reduced χ2. For HD 2665 the reduced χ2 = 1.6 and for HD 6755 χ2 = 1.7. The grey dots are the individual PAVO measurements in each wavelength channel. For clarity, we show weighted averages of the PAVO measurements as red circles. The green line shows the fitted limb-darkened model to the PAVO data, with the light grey-shaded region indicating the 1-σ uncertainties. The lower panel shows the residuals from the fit.
In the text
thumbnail Fig. 3.

Squared visibility vs. spatial frequency for HD 6833 and HD 103095. Lower panel: residuals from the fit. The error bars have been scaled to the reduced χ2. For HD 6833 the reduced χ2 = 7.0 and for HD 103095 χ2 = 1.1. All lines and symbols are the same as for Fig. 2.
In the text
thumbnail Fig. 4.

Squared visibility vs. spatial frequency for HD 122563 and HD 127243. Lower panel: residuals from the fit. The error bars have been scaled to the reduced χ2. For HD 122563 the reduced χ2 = 3.0 and for HD 127243 χ2 = 1.6. All lines and symbols are the same as for Fig. 2.
In the text
thumbnail Fig. 5.

Squared visibility vs. spatial frequency for HD 140283 and HD 175305. Lower panel: residuals from the fit. The error bars have been scaled to the reduced χ2. For HD 140283 the reduced χ2 = 1.4 and for HD 175305 χ2 = 3.7. All lines and symbols are the same as for Fig. 2.
In the text
thumbnail Fig. 6.

Squared visibility vs. spatial frequency for HD 221170 and HD 224930. Lower panel: residuals from the fit. The error bars have been scaled to the reduced χ2. For HD 221170 the reduced χ2 = 2.1 and for HD 224930 χ2 = 8.4. All lines and symbols are the same as for Fig. 2.
In the text
thumbnail Fig. 7.

Deviations from ionisation balance, i.e. the difference between the abundances determined from lines of neutral and ionised iron, as a function of the measured stellar parameters. Vertical and horizontal lines represent the combined uncertainties from the two measurements. Each star is labelled, and colour-coded as red for red giants or blue for main sequence and subgiants.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.