EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 637 (May 2020) A&A, 637 (2020) A80 Full HTML
Free Access
Issue
A&A
Volume 637, May 2020
Article Number A80
Number of page(s) 17
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201937054
Published online 19 May 2020

© ESO 2020

1 Introduction

The determination of chemical abundances in stars relies on the comparison with physical models of stellar atmospheres, which involves a number of approximations. One of these, the assumption that the gas is in local thermodynamic equilibrium (LTE), that is, finding the atomic populations using the Saha and Boltzmann equations from the local temperature and electron density, is known to be one if not the main factor that limits the determination of accurate abundances. One of the difficulties in relaxing the LTE assumption, performing non-LTE (NLTE) calculations, is the need for detailed data on the radiative and collisional processes that affect the atoms of interest. Over the past decade, much progress has been made in this direction, and substantial effort has been made to implement NLTE in the analysis of stellar spectra (Allende Prieto 2016; Asplund 2005).

Implementing NLTE is particularly hard for very large spectroscopic samples with high-resolution and wide spectral coverage because it requires collecting all the necessary data for many ions and performing time-consuming calculations. Surveys such as the galactic archeology with HERMES (GALAH) have started to provide NLTE abundances for a few elements (Buder et al. 2018), and we are about to do the same for the Apache Point Observatory galactic evolution experiment APOGEE (Majewski et al. 2017). In this paper we address the important question of whether NLTE calculations can be performed for a chemical element at a time, or if NLTE effects from one element affect others significantly.

In contrast to NLTE radiative transfer calculations for hot stars, where H and other elements must be considered in NLTE in order to obtain a reliable atmospheric structure and spectrum (Auer & Mihalas 1969a,b, 1970), NLTE radiative transfer calculations in cool stars are performed using the trace element approach, where the effects of the NLTE populations on the atmospheric structure and background opacities are neglected. The justification for this approach lies in the argument that the abundance of the element under study, and the differences between the LTE and NLTE populations, are small enough that they do not affect other elements or the stellar atmospheric structure.

In the calculations described in this paper we do not allow the atmospheric structure to change, that is, temperatureand electron and density distributions are kept fixed. In this case, interactions between the NLTE populations for different elements in our calculations take place through the opacity. In the specific case of Mg and Ca, the broad resonance lines of their first ions provide an important contribution to the opacities between ~2700 and 4000 Å in solar-type stars, and NLTE populations of the excited levels of those ions can also affect the opacity that is “seen” by other elements, and thus modify their NLTE populations. Elements with small contributions to the opacity will then have a negligible effect on other elements that are calculated simultaneously in NLTE.

Section 2 describes the model atoms and the reference observations against which we tested our models. Section 3 provides an overview of the basics of our NLTE calculations. Section 4 compares calculations for a single element with two different NLTE codes: MULTI and TLUSTY. Section 5 describes our multi-element calculations, and in Sect. 6 we compare them with observations. We focus on the most relevant results for the APOGEE survey in Sect. 7, and give our conclusions in Sect. 8.

2 Model atoms and reference stars

We used four different atomic elements: Na I, Mg I & II, K I, and Ca I & II. The atomic data were drawn from different sources. The Mg andCa model atoms were basically the same as in Osorio et al. (2015, 2019), while the model atoms for Na and K were created from scratch for this work. Three reference stars with observational data of exceptional quality and well-determined stellar parameters were adopted: Procyon, the Sun, and Arcturus. The observational data and the synthetic model atmosphereswere the same as in Osorio et al. (2019). A description of these data is given in Sect. 2.4.

2.1 Mg and Ca

Energy levels were taken mostly from the national institute of standards and technology NIST database (Ralchenko et al. 2014), line data were taken from the Vienna atomic line database VALD (Kupka et al. 2000; Ryabchikova et al. 2015), NIST, and in the case of Ca I, from Yu & Derevianko (2018). Continuum data were taken from the opacity project database TOPBASE (Cunto & Mendoza 1992). Hydrogen collisions (Belyaev et al. 2012; Barklem 2016, 2017a) and electron collisions (Meléndez et al. 2007; Zatsarinny et al. 2019; Barklem et al. 2017) were included in the NLTE calculations, and when no data were available, approximation formulas were used. Our Mg model atoms have 96 levels of Mg I, 29 levels of Mg II, and the ground level of Mg III. The Ca atoms we used have 66 levels of Cai, 24 levels of Ca II, and the ground level of Ca III. A detailed description of the atomic data used for Mg and Ca is given in Osorio et al. (2015, 2019). There are only two differences between the Mg and Ca data from the works mentioned above and this study: (1) Because the Van der Waals broadening parameter accepted by TLUSTY is Γ6, we computed these parameters from the Anstee-Barklem-O’mara (ABO) theory (Barklem et al. 1998). (2) The photo-ionisation cross sections in this work where resonance-averaged photo-ionisation cross sections (Allende Prieto et al. 2003) based on TOPBASE data, while the same data without smoothing were used for Mg and Ca in Osorio et al. (2015, 2019).

thumbnail Fig. 1

Grotrian diagram of Na (upper panel) and K (lower panel) model atoms. The red lines correspond to transitions in the H-band.

2.2 Na and K

The final model atom of Na Has 42 levels of Na I and the ground level of Na II, and a total of 190 radiative transitions, while for K we used 31 levels of K I, the ground level of K II, and a total of 219 radiative transitions. Figure 1 shows the Grotrian diagram with the levels and the transitions of the K and Na model atoms.

2.2.1 Energy levels and radiative data

Energy levels for Na I and K I were adopted from NIST. Fine-structure components were ignored, and the allowed angular momentum components lower than l = 6 for a given principal quantum number n were taken as separated levels up to n = 8 for Na and n = 6 for K. n super levels were included up to n = 20 for Na and K in order to ensure coupling between the highest level of the neutral species and the ground level of their first ion.

Photo-ionisation cross sections of Na I were taken from the TOPBASE data base. K I photo-ionisation data were taken from Zatsarinny & Tayal (2010). When bound-free data were not available, photo-ionisation cross sections were calculated using the hydrogenic formula implemented in TLUSTY (Hubeny & Lanz 1995, for recent upgrades, detailed description, and user manual, see Hubeny & Lanz 2017a,b,c).

Oscillator strengths (f-values) come from various sources collected in the NIST and VALD data bases. TOPBASE (Cunto & Mendoza 1992) provides the atomic data (f-values, photo-ionisation cross sections) from the Opacity Project calculations (Seaton 1996). For Na, VALD lists the experimental f-values provided by NIST, therefore the Na f-values from VALD have priority over those from NIST. For the remaining bound–bound transitions, TOPBASE data were used when available. Inthe case of K, data from VALD come from Kurucz (2012), and data from NIST are mostly from Sansonetti (2008). When for the same transition the f-values from different sources differed, preference was given to NIST over VALD in this case. VALD also provides collisional broadening parameters from Kurucz (2012) and Barklem et al. (2000) where available. Line broadening data were taken from Barklem et al. (2000) from VALD when available. Otherwise, we adopted the formula from Unsöld (1955) with an enhancement factor of 2, as suggested by Mashonkina et al. (2000) in their Na NLTE studies on the Sun. Radiative bound–bound data for the most important transitions of Na and K (including those in the APOGEE window) are presented in Table 1.

Table 1

Data adopted for the NLTE calculations for characteristic lines of Na and K.

2.2.2 Collisional data

Electron collisions

The formula from Park (1971), which is an empirical adjustment of the Born approximation that is only applicable to neutral alkali atoms, has shown to be a good approximation for NLTE calculations of Li and Na in cool stars when compared with more sophisticated data (Osorio et al. 2011; Lind et al. 2011). For Na, the convergent close coupling (CCC) calculations from Igenbergs et al. (2008) cover all transitions for the levels up to 4f, and those where included in our model atom. Regarding K, very recent calculations from Reggiani et al. (2019) suggest that the Park formula tends to overestimate the K collisional rates. They performed CCC and B-spline R-matrix (BSR) calculations (both agree extremely well) for electron collisional excitation between all levels up to 6d; we decided to adopt their BSR data.

We filled the missing transitions of Na in Lind et al. (2011) and of K in Reggiani et al. (2019) with the Park formula. It covers all the transitions between levels up to n = 7 for Na and n = 6 for K. For higher levels, it provides data for transitions between the 16 closest levels with nupper ≤ 20. For the remaining transitions, the formula from Seaton (1962) was implemented.

Electron collisional ionisation was described via the hydrogenic approximation as presented in Cox (2000, Sect 3.6.1) for low-lying levels, and the formula from Vrinceanu (2005) for levels with principal quantum number n ≥ 5 for Na and n ≥ 6 for K.

Hydrogen collisions

For collisional excitation of Na and K we adopted data from Barklem et al. (2012) and Barklem (2016, 2017a), respectively. These works cover the transitions between all levels from the ground state up to 5p for Na and 4f for K. For the missing one-electron transitions in these works, the hydrogen collisional excitation was calculated using the code from Barklem (2017b) based on the free electron model of Kaulakys (1985, 1986).

Charge transfer processes such as A + H ↔A+ + H− were calculated by Barklem et al. (2012) and Barklem (2016, 2017a) for Na and K, respectively, and are included in this work.

Figure 2 shows the rate coefficients obtained at 5000 K for the different collisional processes described above for the Na and K atoms. We recall that the rate coefficients are an estimate of the transition efficiency, and the actual rate of a transition is obtained by multiplying by the population of the projectile. For solar metallicities the population of hydrogen is higher by about four orders of magnitude than the population of free electrons, and even if the rate coefficients for the electron collisional excitation are one or two orders of magnitude higher than their hydrogen counterpart, the contributionto the total collisional excitation rate from hydrogen collisions can therefore be more important than the contribution from electron collisions. At lower metallicities, fewer free electrons are available, which weakens their contribution to the total collisional rate even more and thus makes the hydrogen contribution even more important.

2.3 APOGEE spectral window

The NLTE effects are different for different lines, and when the atomic lines that are to be observed are from transitions that involve higher levels, it is important to have high-quality collisional data for the low-lying levels (which are the most populated). However, particular attention must also be paid to the collisional data for transitions associated with the lines of interest. For this reason, the study of the H-band (where mostof the atomic transitions are between high-excitation levels) requires that the model atoms of the elements under study have enough high-lying levels and that the collisional data for transitions involving these levels are as good as possible. Unfortunately, modern calculations of collisional excitation and ionisation usually do not cover these transitions.

We have built our model atoms with these concerns in mind. The levels used in the final model atom are such that the lines in the H-band do not involve transitions between super levels, which are required to keep the size of the model atom manageable, and at the same time have a realistic coupling with the continuum (Mashonkina 2010; Asplund 2005). Most of the collisional (de-) excitation data for the transitions in the H-band and the collisional ionisation data for levels involved in those transitions are beyond modern detailed quantum-mechanical calculations.Recent studies (and some older but not commonly used studies) give us better alternatives to previous traditional approximations methods. These considerations demonstrate that we put considerable effort in the adoption of the best data available for transitions involving high-lying levels, as is the case for many of the lines in the H-band.

thumbnail Fig. 2

Rate coefficients of the electron related collisions (excitation and ionisation, top) and hydrogen related collisions (excitation and charge-exchange, bottom) for Na (left) and K (right). Initial levels of the transitions are labelled in rows and final levels are labelled in columns. The arrows point towards the transition that separates the hydrogen collisional excitation data from Barklem et al. (2012) and the data calculated using the formula from Kaulakys (1985). The colour scale at the left is for the Na Rates and the colour scale at the right is for the K rates.

2.4 Reference stars

We decided to use the Sun, Arcturus, and Procyon for the comparison between observations and our synthetic spectra. The observational data used in this work are the same as those described in Osorio et al. (2019). Here, we can mention that our selection was based on the excellent quality of the data and on the reliability of the atmospheric parameters, together with the wide wavelength coverage of the observations.

For Procyon, we used the observations from the Postdam Echelle Polarimetric and Spectroscopic Instrument PEPSI (Strassmeier et al. 2018). Its wavelength coverage is (3800–9100 Å) at R ~ 220 000. The solar observations we used were the 2005 version of the flux atlas from Kurucz et al. (1984); it covers from 3000 to 10 000 Å, with a full width at half-maximum reducing power R ~ 400 000. For Arcturus we adopted the atlas from Hinkle et al. (2000), which spans from 3727 to 9300 Å and has R ~ 150 000. A more detailed description of the observations and a comparison with other atlases can be found in Osorio et al. (2019). The atmospheric parameters are listed in Table 2. For more details regarding the observational data, we refer to Osorio et al. (2019).

Table 2

Parameters of the model atmospheres used to construct the synthetic spectra.

3 Computations

Two sets of computations were made here: in the first set we used the results of the well-established NLTE radiative transfer code for cool stars, MULTI (Carlsson 1986, 1992), and compared its results with the last version of TLUSTY (Hubeny & Lanz 1995, 2017a,b,c), which now allows calculating NLTE populations in cool stellar atmospheres. Because TLUSTY was created for the study of early-type stars and accretion discs, it allows for the treatment of multiple species in NLTE at the same time; this has long been known to be necessary for NLTE studies in hot stars (Auer & Mihalas 1969a). We obtained Mg and Ca LTE and NLTE populations with the two codes using the same input atomic data and a configuration that was as similar as possible. The results and analysis of these calculations are given in Sect. 4.

The second set of computations were performed exclusively with TLUSTY (to calculate the LTE and NLTE populations) and SYNSPEC (to calculate the detailed spectra). We compared observations against the results of two different NLTE calculations: the traditional (for cool stars) trace-element, single-species NLTE calculation, referred to as NLTE-s, and calculations where multiple species weresimultaneously treated in NLTE, still within the trace-element framework. We refer to this as NLTE-m. We used Arcturus, the Sun, and Procyon to calculate the LTE, NLTE-s, and NLTE-m populations and spectra of Na, Mg, K, and Ca on these stars. From Sect. 5 on, this paper is dedicated to the second set of computations.

The NLTE-m calculations are a better approximation than the NLTE-s calculations from the physical point of view: the effects of the NLTE radiation of one atomic species on the NLTE populations of other species is included in the NLTE-m and ignored in the NLTE-s calculations. The relevance of these effects in cool stars is studied for the first time in this work (see Sect. 5.1).

In order to obtain the NLTE populations, we ran TLUSTY v.207 in the opacity table mode. The opacity tables were constructed using SYNSPEC v.531. After experimentation with different numbers of wavelengths, temperatures, and densities, the table for the second set of calculations had 100 000 wavelength points that were equally distributed in a logarithmic scale from 900 to 100 000 Å. The table also had tentemperature grid points and ten density grid points. The element abundances used in the opacity tables are the appropriate for the metallicity of each star. In each NLTE calculation, the opacity table excludes the contribution from the elements treated in NLTE.

The detailed synthetic spectra (in LTE and NLTE) were calculated using the same code as in the opacity tables SYNSPEC v.53, adopting the same atomic and molecular line-list as in Mészáros et al. (2012), but with log gf and broadening parameters of the Nai, Mg I & II, K I, and Ca I & II lines replaced by the lines used in the NLTE calculations with TLUSTY. The stellar model atmospheres are the same as in Osorio et al. (2019): Kurucz model atmospheres computed with ATLAS9 (Kurucz 1993), using the setup described in Mészáros et al. (2012).

4 Comparison between TLUSTY and MULTI

The last updates of TLUSTY include the possibility of using the code for NLTE calculations for a subset of species, while the remaining atomic as well as molecular species are treated through pre-calculated opacity tables. We can therefore compare this with other NLTE radiative transfer codes that are used in the study of cool stars.

Our first goal was to reproduce the results obtained in previous works, more precisely, the solar departure coefficients obtained for Mg (Osorio et al. 2015) and Ca (Osorio et al. 2019). In both cases the calculations were performed with the NLTE radiative transfer code MULTI (Carlsson 1986) version 2.3; and now we repeated the calculations with TLUSTY. The results of this comparison are shown in this section.

The same solar model atmosphere as used in Osorio et al. (2019) was adopted here for both Mg and Ca. The input data for Mg and Ca used in both MULTI and TLUSTY were adapted for each code, and this adaptation led to the differences described in Sects. 4.2, 4.3, and 4.4.

4.1 Background opacity

We here use the term background opacity to refer to all the sources of opacity that do not involve the elements under study. In TLUSTY, these are stored in pre-calculated opacity tables. In MULTI, the continuous opacities are calculated on the fly, while only line opacities are stored in a read-in file (line-opacity table).

For MULTI, we used a line-opacity table based on the background opacities presented in Gustafsson et al. (2008) re-sampled to 10 300 frequency points between 900 and 200 000 Å. The bound-free (b-f) and free-free (f-f) contribution from the most important atomic elements, and the b-f and f-f contribution from several molecules are also calculated by the code.

Unlike previous versions, the latest version of TLUSTY allows the use of opacity tables. These tables also include the bound-bound (b-b) contribution from atoms and some mole- cules. In order to facilitate the comparison, the opacity tables used in TLUSTY for this test have the same number of frequency points and wavelength coverage as those adopted for the MULTI calculations. The atoms and molecules that contribute to the background opacities are listed in Table 3. A sample of the background opacities used for the Mg NLTE calculations in MULTI and TLUSTY is presented in Fig. 3.

Table 3

Components of the background opacities used for the comparison calculations between MULTI(*) and TLUSTY.

4.2 Photo-ionisation

The source of the data for Mg and Ca is the TOPBASE database (Cunto & Mendoza 1992). For the MULTI calculations, the data were used directly with the exclusion of some values. A maximum of 500 points per b-f transition (starting from threshold) were used. When for a given level the cross section extended to energies higher than 13.6 eV (corresponding to 911 Å), those data points were removed because the lowest wavelength in the line-opacity table used by MULTI is 900 Å. This applies to all photo-ionisation cross sections, except for that of the ground level of Mg II because its threshold is at 14.3 eV (870 Å, see Fig. 4) and according tothe above criteria, the whole cross section for this level would have been removed in the MULTI calculations. Having the b-f taken directly enables us to have the resonances present in the data fully resolved for photon energies near the threshold.

For TLUSTY, the original TOPBASE data were smoothed and re-sampled using the resonance-averaged photo-ionisation cross-sections method presented by Bautista et al. (1998). This smoothing is physically justified given the uncertain in the atomic structure calculations, but it also brings a benefit by reducing the number of frequencies required to describe the cross sections. For these calculations, we used the full wavelength range provided by the sources for all the b-f transitions. Figure 4 shows the photo-ionisation data used for two levels of Mg I in the TLUSTY (symbols in black) and MULTI (red lines) codes.

4.3 Van der Waals broadening

When available, MULTI uses the ABO theory directly by having the van der Walls broadening input data in the “σ.α” format. TLUSTY, on the other hand, uses the van der Waals broadening coefficient Γ6 at 10 000 K. When available, the values adopted for TLUSTY are the equivalent Γ6 at 10 000 K obtained from the ABO theory. This difference in the treatment of the spectral lines does not affect the derived NLTE populations, but it affects the line profiles. We have compared two MULTI calculations: one using the ABO theory, and the other treating van der Waals damping with the Unsöld method (Unsöld 1955) with anΓ6 at T = 10 000 K derived from the ABO theory, and found no differences in the NLTE populations, although the wings of line profiles are clearly different (see Fig. 5). Therefore, the differences between the line profiles of MULTI and TLUSTY/SYNSPEC for lines with ABO format data lie in the line-profile calculations between MULTI and SYNSPEC, and not in the NLTE populations derived by MULTI and TLUSTY. This is easy to understand because possible departures form LTE a driven by radiative rates, which in turn are dominated by the line cores.

4.4 Collisional data

MULTI requires upward rate coefficients for transitions resulting in ionisation and downward rate coefficients for transitions resulting in excitation, while TLUSTY demands upward collisional rate coefficients in all cases. We used detailed balance relations in order to convert upward into downward rate coefficients, and vice versa (see Hubeny & Mihalas 2014, Sect. 9.3).

4.5 Results of the comparison

The most direct comparison between these two codes is done by comparing the NLTE populations through the departure b coefficients2 as a function of the column mass. Traditionally, departure coefficients as shown as a function of optical depth τ, but because τ depends more on the background opacities (which is not exactly the same in TLUSTY and MULTI) than on the column mass, and because the calculations in both codes are performed in the column mass scale, a more direct comparison between the two codes can be made using column mass as abscissae. Figure 6 compares the obtained departure coefficients of some levels of Mg and Ca against column mass for a solar model. The behaviour is very similar for the two codes (see the top panel of Fig. 6). The small discrepancies are due mainly to the differences in the background opacities. Figure 6 gives us confidence that the new version of TLUSTY can perform NLTE calculations in late-type stars.

Our experiments show that a certain level of detail in the background opacities is required to calculate reliable NLTE populations. It is also important to ensure that the adopted background opacities cover the wavelengths associated with the most important b-b and b-f transitions of the species computed in NLTE. A more detailed comparison between TLUSTY and other NLTE-trace-element radiative transfer codes will be presented in a future paper.

thumbnail Fig. 3

Sample of the background opacities from the opacity tables in the UV region used in the NLTE calculation of Mg (i.e. removing the contribution of Mg) by MULTI (red) and TLUSTY (black) at two different points of the solar atmosphere.

5 Multi-element NLTE radiative transfer

In what follows, we call NLTE-s the traditional single-element NLTE calculations (i.e. where only one atomic element was calculatedin NLTE while all the other elements were kept in LTE) and NLTE-m are the simultaneous multi-element NLTE calculations. We performed NLTE-s calculations for Na, Mg, K, and Ca. We also performed NLTEm calculations with all possible combination of two, three, and the four elements in NLTE. As a result, we found that departures from LTE in Mg mainly affect the Ca populations, but does not have significant effects on Na or K. Ca has a marginal effect on Mg, especially in Arcturus, but in this star, NLTE effects in Mg have a diminished influence on the NLTE Ca populations.Na and K do not affect the populations of each other, Mg, or Ca in any of the stars investigated in this work.

We emphasise that all the calculations described were performed with exactly the same atomic data: the opacity tables used for the different NLTE-s and NLTE-m calculations were constructed exactly in the same fashion with the exact same b-b and b-f data, and only the contribution to the opacity of the elements to be calculated in NLTE was removed. The model atoms of Mg I & II and Ca I & II for MULTI have the same radiative and collisional sources as those used for TLUSTY (the differences in the data implemented in the two codes are described in Sect. 4). The same Na I, Mg I & II, KI, and Ca I & II model atoms were used in all the NLTE calculations in TLUSTY and SYNSPEC. Thus, the differences found in the NLTE-s and NLTE-m populations and spectra are due only to inter-element NLTE effects.

In all the calculations we kept the atmospheric structure fixed, that is, we are still within the trace-element approach framework, therefore the influence of one NLTE element on the others is its contribution to the opacity. A comparison of the NLTE departure coefficients b between the NLTE-s and NLTE-m cases can give us information on the importance of inter-element NLTE effects (see below).

thumbnail Fig. 4

Photo-ionisation cross-section data used in the MULTI (red lines) and TLUSTY (black symbols) calculations for two b-f transitions of Mg I and the one from the ground level of Mg II. The red lines are the values taken from the TOPBASE database without the cross sections below 911 Å (except for the Mg II b-f transition). The symbols are the resonance-averaged photo-ionisation cross sections of the TOPBASE data (see Allende Prieto et al. 2003). The b-f cross section of the Mg II 3s(2S) and the Mg I 3p(3P) levels are vertically shifted by 4 and 2 log units, respectively, for visualisation.
thumbnail Fig. 5

Comparison between MULTI NLTE solar line profile and departure coefficients (inner figure) of the levels involved for the Ca I transition 4p1P–4s1S (4227 Å) when the van der Waals broadening is treated using the ABO theory (solid lines) and when the formulation from Unsöld (1955), with a Γ6 value derived from the ABO theory, is used (dashed lines).

5.1 Inter-element NLTE effects

Our experiments show that the Ca NLTE populations are sensitive to Mg NLTE opacities, but the Mg NLTE populations are not significantly affected by Ca NLTE opacities. This raises the question of how strongly the effect of Fe NLTE opacities is on the NLTE effects of other elements, considering that Fe is the metal that contributes the most to background opacities at solar metallicities, in particular in the UV region. We now proceed to interpret the behaviour of NLTE-m with respect to NLTE-s in the stars and atomic elements studied in this work.

thumbnail Fig. 6

Departure coefficients for some levels of Mg I (upper panel) and Ca I (lower panel) obtained with TLUSTY (red) and MULTI (black) for the same solar model atmosphere and the same atomic data. The grey vertical lines denote the depths at τross = 0.01 (left) and τross = 1.0 (right).

5.1.1 Procyon

In the case of Procyon, the interplay between Mg and Ca leads to an increase in NLTE flux in the ~2000–2300 Å region, which is the location of the photo-ionisation threshold of the ground level of Ca I (2028 Å). Thus, the resulting background UV opacity seen by Ca is different between the NLTE-s:Ca and the NLTE-m calculations. Photon loss competes with over-ionisation, but at a column mass of about − 1, the overpopulation of the Mg I lower levels in NLTE with respect to LTE reduces the UV flux in these layers, giving advantage to photo losses of the resonance Ca I lines (~2500 and 4226.7 Å). This results in an increase in the population of the lowest levels of Ca in NLTE-m with respect to NLTE-s:Ca (i.e. when Mg is treated in LTE). In contrast, Mg seems to be affected very little by Ca, and its NLTE populations are almost identical in the NLTE-s and NLTE-m calculations. Because the main NLTE mechanism driving the statistical balance of Na and K is photon-suction, the alkali elements are unaffected by the changes in the UV flux due to the Mg NLTE populations. The 3s(2 S) and 5p(2 P1∕2, 3∕2) are the levels involved in the 2852 Å Na lines, as described above. Their departure coefficients change due to differences in the background opacity because these lines are in the red wings of the 2852 Å Mg I line, whose formation in NLTE is not the same as in LTE.

thumbnail Fig. 7

Ultraviolet fluxes obtained for Procyon (top), the Sun (middle), and Arcturus (bottom) calculated in LTE (black), NLTE-m (red), NLTE-s:Mg (pink), and NLTE-s:Ca (blue). For each star, the Eddington flux (upper panel) and the difference inpercent between the LTE and the NLTE fluxes (lower panel) are plotted. The units of the Eddington flux Hλ are erg cm−2s−1Å−1.

5.1.2 Sun

As in the case of Procyon, the UV flux in the NLTE-m calculations is very similar to the NLTE-s:Mg calculations, which means that again, Ca is much more sensitive to Mg than Mg to Ca. The main difference in departure coefficients between NLTE-s:Ca and NLTE-m results are on the ground level of Ca I because a similar process to the process that occurs on Procyon also takes place on the Sun, and in this case, it is enhanced because the lines are broader, which favours photon losses. The UV synthetic spectra show that the fluxes of the NLTE-s:Mg and NLTE-m are very similar (middle panel of Fig. 7), and the departure coefficients of Mg in the two cases are therefore almost identical. The NLTE effects of Na and K are driven by photo-suction, which makes their departure coefficients of the NLTE-s and NLTE-m calculations almost identical.

5.1.3 Arcturus

Mg I is no longer a minority species in the atmosphere of Arcturus; at a column-mass ≲ 1, the population of Mg I is larger than the population of Mg II, as illustrated in Fig. 8. Because Arcturus no longer has a Mg II reservoir, photo-ionisation of the 3p(1P*) level is not efficient compared with the photon pumping that occurs in the 3p(1P)-3s(1S) Mg I line at 2850 Å. This causes b > 1 in the atmosphere at this level (see Mg in the Arcturus panel in Fig. 9).

Figure 7 shows that the NLTE-m UV fluxes are now more influenced by Ca than by Mg in some regions (e.g. the 1700–2000 Å). The UV flux in Arcturus is three to four orders of magnitude weaker than in the Sun, however, thus the absolute changes in the UV fluxes due to the NLTE populations of Ca and Mg are not large enough to significantly affect the NLTE-m populations of the four atomic elements with respect to their NLTE-s populations. On the other hand, the lower gravity of Arcturus means that metallic lines broaden, so that lines with different NLTE and LTE behaviour in the wings (mostly resonance lines) will also affect a larger part of the spectrum than in the case of dwarfs. This explains why the departure b coefficient of the ground level of K has an small but noticeable difference in NLTE-m and NLTE-s in Arcturus and no difference in the Sun and Procyon.

Ca I, on the other hand, is still a minority species in Arcturus, and thus UV over-ionisation still dominates. Because the UV is much weaker than in the other two stars, the effects of NLTE Mg opacities on the NLTE Ca populations is not as strong as in the solar and Procyon cases (see Fig. 9), however.

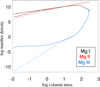thumbnail Fig. 8

Mg number densities of different ionisation stages in Arcturus. The solid lines represent the NLTE populations, and the dashed lines represent the LTE populations.

5.2 Physics of the inter-element effects

Na and K are not affected by any of the other elements. We note, however, that the Na I levels 3s(2 S) and 5p(2 P) have slightly differentdeparture b coefficients between the NLTE-s and NLTE-m calculations, in particular for Procyon. The transition between these levels produces the 2852.8 and 2853.0 Å lines, which lie in the red wing of the Mg I 2852 Å line. This is an illustration of the effect of NLTE opacities of some elements on the statistical balance of other elements: the background opacity at around 2853 Å is dominated by the red wing of the Mg I 2852 line, which has a different strength in the stellar atmosphere when Mg is treated in NLTE and in LTE (see Fig. 10). The differences observed between the red (NLTE-s) and black lines (NLTE-m) in Fig. 9 are the result of the combination of the overlap between b-b and b-f transitions of the different elements treated in NLTE, as we described.

The main NLTE mechanism that affects the Ca and Mg populations is UV over-ionisation, therefore the differences between the NLTE-s and NLTE-m populations for both Ca and Mg come mostly from their effects on the radiation field of that region. Figure 7 helps understand the differences between the departure coefficients b shown in Fig. 9. The figure shows three panels (one for each star) with the absolute flux obtained in LTE, NLTE-m, and NLTE-s for Mg and Ca at the top and the percentage difference between the LTE flux and the three NLTE fluxes (single and multi-element) at the bottom of each panel. Broad lines with wings affected by NLTE affect lines of other elements with lines formed in the wings because their background opacity receives a contribution of the NLTE wings. For the Sun and hotter stars, the UV flux is strong enough to affect species that are sensitive to over-ionisation in NLTE-m if there are other species in the calculations that affect the continuum fluxes through NLTE effects. Our results also show that NLTE effects on broad lines will result in different background opacities perceived by lines of other elements in the same region. This might affect the NLTE results of those other elements.

The fundamental effect of NLTE calculations is the redistribution of the population of different levels in the different ions of a given element, with respect to LTE. As a consequence, for an element X the spectral lines and the continuum contribution is different in LTE and NLTE for an atmosphere with the same X abundance. Even though the derived LTE and NLTE Mg solar abundance is the same, the derived NLTE-s and NLTE-m abundances of Ca are therefore different. Figure 10 illustrates this. The Mg abundance in the three profiles is the same (A(Mg) = 7.42 dex), and the LTE and NLTE-s:Na calculations provide the same profile of the broad 2852 Å Mg I line, but the NLTE core and wings of this line differ in the NLTE-m calculations because Mg is now in NLTE with the same A(Mg). The reason for the different profiles in LTE and NLTE is the redistribution of the population of the levels involving that transition (3p 1 P–3s 1 S), which leads to a deeper core and weaker wings of the Mg NLTE profile with respect to the Mg LTE line profile.

6 Comparison with observations

Finally, we derived Na, Mg, K, and Ca abundances for Procyon, the Sun, and Arcturus in LTE, NLTE-s, and NLTE-m. The derived abundances and macro-turbulent velocities are presented in Table 4.

We used the all-lines method described in Osorio et al. (2019), where all the lines of the spectrum were analysed simultaneously; therefore a single abundance and macro-turbulent velocity was used for all the lines of a given element simultaneously. In order to determine the error associated with the derived abundances and macro-turbulent velocities, we used the method described by Piskunov & Valenti (2017), where the model errors are prioritised. For all the three stars and the four elements, the residuals (χ2) of the best fit in NLTE are reduced relative to the LTE analysis, except for Ca in Arcturus (we found the same anomaly in Osorio et al. 2019). The χ2 of the NLTE-m calculations is either lower than or the same as the χ2 of NLTE-s calculation. The case of Ca in the Sun is particularly interesting: while its NLTE-s abundance correction is marginally positive (0.02), the NLTE-m abundance correction is negative (−0.05), and the NLTE-m abundance agrees excellently with the meteoritic value. A more detailed description is given below.

The closest comparison of our results and previous works are for Na from Lind et al. (2011), for Mg from Osorio et al. (2015), for K from Reggiani et al. (2019), and for Ca from Osorio et al. (2019). The LTE and NLTE-s results generally agree very well with these studies considering the differences in method (equivalent width versus line profile fitting, line-by-line abundancedetermination versus all-lines at once, etc.) and the input data used (different model atmospheres, background opacities, synthetic spectra calculations, radiative transfer codes, etc.)

6.1 Na

Lind et al. (2011) used the MULTI code to calculate LTE and NLTE-s equivalent widths in order to derive Na abundance corrections for a grid of MARCS model atmospheres. Using their Fig. 4, their abundance corrections for Procyon, the Sun, and Arcturus are approximately −0.15, −0.1, and − 0.2, respectively, while our corrections are − 0.22(9), − 0.14(5), and − 0.11(5) for the three stars. As expected from the departure coefficients in Fig. 9, we find the derived NLTE-s to be the same as the NLTE-m abundances. Figure 11 shows selected lines of Na in a comparison between observations of Procyon and synthetic spectra in LTE and NLTE. Because the NLTE-s and NLTE-m synthetic spectra are indistinguishable, we plot only one of them. The residuals between observations and the best fit of the synthetic spectra are lower in NLTE than in LTE. For Procyon, the best fit in NLTE is 73% better than the best fit in LTE, while for the Sun and Arcturus, the best fit is 46% and only 5% better, respectively. Our derived solar abundance becomes slightly lower than the value found in CI carbonaceous chondrites, after scaling through several well-determined refractory elements (Asplund et al. 2009; Lodders 2019).

thumbnail Fig. 9

Departure coefficients for some levels of Na, Mg, K and Ca obtained calculated in single-element mode (NLTE-s, in red) and in multiple-elements mode (NLTE-m, in black) for Procyon, the Sun and Arcturus. For each star, the same element abundances were used in all the LTE, NLTE-s and NLTE-m calculations. The fact that the b coefficient for the Mg II ground state increases toward the surface (due to NLTE effects in the Mg II h & k lines) inArcturus, but stays closely to 1 for the other two stars, follows from Mg II being the dominant stage of ionisation, and its ground state the most populated state, for Sun and Procyon, but not for the cooler starArcturus. The two grey vertical lines in each figure mark the depths in the atmospheres where τross = 0.01 (left) and 1.0 (right).

6.2 Mg

Osorio et al. (2015) also used the MULTI code to determine LTE and NLTE-s Mg abundances. Our absolute LTE and NLTE-s abundances agree very well. The NLTE best fits are 10, 24, and 7% better than the LTE best fit for Procyon, the Sun, and Arcturus, respectively. As in the case of Na, the effects of the other elements calculated in NLTE are negligible, and therefore the NLTE-s and NLTE-m results for Mg are almost identical.

In this case, our derived solar abundance agrees better with the meteoritic value. This solves the 2σ inconsistency shown in previous determinations (Asplund 2009).

Table 4

Na, Mg, K, and Ca abundances derived for the LTE, NLTE-s, and NLTE-m calculations.

thumbnail Fig. 10

Local thermal equilibrium (black), NLTE-m (red), and NLTE-s:Na (blue) normalised synthetic fluxes of Procyon around the red wing of the 2852 Å Mg I line. The atomic species of some lines are marked together with their LTE equivalent width in mÅ.

6.3 K

Reggiani et al. (2019) presented LTE and NLTE abundances for the Sun, Procyon, and other stars by fitting the synthetic equivalent widths with the observed ones. The NLTE abundance derived for the Sun agrees excellently with ours. Line profiles of our best fit is in excellent agreement with the high resolution solar spectrum (see Fig. 12). In the case of Procyon, although the abundance correction is the same (0.68 by Reggiani et al. 2019 and 0.66 by us), our LTE and NLTE abundances are higher by 0.19 dex. In Arcturus, the LTE and NLTE residuals of the best fit are same: we found an abundance correction of 0.44 dex.

thumbnail Fig. 11

Top: selected lines of Na Observed in Procyon (black) and the best fit for the LTE (red) and NLTE (blue) calculations with the parameters in derived in Table 4. Bottom: difference between observations and the synthetic spectrum in LTE (red) and in NLTE (blue).

6.4 Ca

The most interesting case is Ca, whose NLTE populations are affected most by the NLTE populations of the other elements, specifically by Mg. Osorio et al. (2019) presented NLTE-s abundance corrections of Ca for the three stars studied in this work. In order to make a cleaner comparison, we used the same masks as were used in the all-lines calculation in Osorio et al. (2019).

For Procyon, Osorio et al. (2019) found an abundance correction of Δnlte,s(Ca) = −0.08 dex, while in this work we found Δnlte,s(Ca) = −0.05 dex, although our new LTE Ca abundance is higher than that in Osorio et al. (2019). A possible explanation of the discrepancy is that MULTI calculates line profiles only of the element under study, while SYNSPEC computes synthetic spectra that include the contribution from several atomic and molecular species. The effects in Procyon of having a more realistic synthetic spectrum probably affect the derived abundances more than in the Sun or in Arcturus. A similar phenomenon occurs with K in Procyon when compared with Reggiani et al. (2019), who also used MULTI to calculate the synthetic spectral lines. Our multi-element calculation decreases the derived NLTE-m abundance by 0.03 dex with respect to the NLTE-s results. The top panel of Fig. 13 shows the region around 6165 Å that includes several lines of Ca. It is clear that the core of the 6162 Å line is the weakest in LTE (blue line), then in NLTE-s the core of this line matches the observations quite well, and the NLTE-m calculations strengthen the core slightly more. When only the 6162 Å line is considered, the fit with observations is better in NLTE-s than in NLTE-m, but by checking the other lines in the window, we note that the other NLTE-s Ca lines have weaker cores than the LTE profiles and the observations. The NLTE-m spectra have similar line profiles to the LTE for four of the Ca lines (6161.4, 6163.7, 6166.5, and 6169.1). The 6169.6 Å line has an NLTE-m profile that matches the observations better than the LTE and NLTE-s cases. We found that our NLTE-s best fit is 20% and our NLTE-m best fit is 18% better than the LTE best fit.

For the Sun, Osorio et al. (2019) derived an LTE Ca abundance that agrees with ours, but we found a negligible abundance correction of 0.02 dex, while the NLTE-m results show a correction of − 0.05 dex. The central panel in Fig. 13 shows solar observations and the synthetic spectra in the region around 6162 Å, where three Ca lines are clearly visible. There is also a Na line that has a NLTE line profile in the NLTE-m spectra. The NLTE calculations show that while the core of the 6162 Å line matches the observations better in the NLTE-s and NLTE-m cases than in LTE, the wings of the NLTE-s and the other two Ca lines in the figure suggest that the NLTE-s abundance must increase in order to fit the observations (as the results in Table 4 show). The LTE spectrum is unable to reproduce the core and the wings of the 6162 Å line, while the 6161.3 and 6163.7 Ca lines are reproduced better in LTE than in NLTE-s. The NLTE-m 6161.3 and 6163.7 Å lines are similar to the LTE lines, and with the same abundance, the core and the profile of the 6162 Å can be reproduced. The results of this sort of balance show that our NLTE-s best fit is 20% better than the best fit in LTE and our NLTE-m best fit is 34% better than the best fit in LTE. We also point out that the NLTE-m Ca abundance we found agrees excellently with the meteoritic value.

Like the other atomic elements studied in this work, Ca in Arcturus seems to be unaffected by NLTE multi-element effects. The LTE and NLTE-s abundances found by Osorio et al. (2019) agree with ours and the small NLTE corrections are in the same direction (− 0.02 in this work and − 0.01 dex in Osorio et al. 2019). As in the work from Osorio et al. (2019), the NLTE-s best fit is worse than the LTE best fit (32% in that work and 12% in this work). The questions remain whether the addition of iron to NLTE-m calculations will improve the situation of Ca in NLTE for Arcturus, and if the NLTE ionisation balance of the important electron donors affects the total electron populations and therefore the atmospheric structure in Arcturus in a sensitive manner. Further investigations will answer these questions.

thumbnail Fig. 12

Top: lines of K used in the solar observations (black) compared with the best fit of the LTE (red) and NLTE (blue) calculations with the parameters derived in Table 4. Bottom: difference between observations and the synthetic spectrum in LTE (red) and in NLTE (blue).

7 APOGEE spectral window

The only difference between the analysis of the observations of the Sun and Arcturus in the APOGEE window and the previous comparison in the optical are the b-b data adopted for SYNSPEC: we adopted the ASPCAP atomic line-list (Shetrone et al. 2015) formatted for SYNSPEC. The molecular b-b data use isotopic ratios suited to the Sun and Arcturus.

The solar observations in the H-band we adopted correspond to the centre-of-disc intensity spectrum from Livingston & Wallace (1991). For Na, K, and Ca there are no significant NLTE effects in the line profiles, and the derived abundances in LTE and NLTE are therefore the same. There are only two useful lines of Na in the H-band solar spectrum. The 15 992 Å line can be reproduced with A(Na) = 6.12 dex, which agrees well with the NLTE Na solar abundance we derived in the optical. The Na 16 388.8 Å line is weaker than the observations using the same abundance, but it is difficult to determine the continuum location around this line: it lies in the blue wing of an H-Brackett line (nl, nu] = [4,12] at 1.6398 Å) and has Fe, Ni and Ti blends. The Mg abundance found using the spectra in the APOGEE region is A(Mg) = 7.55 dex, which excellently agrees with our derived abundance from the optical transitions. Like in the optical, we found that the Mg abundances that correspond to the best fittings in NLTE and LTE are the same, but Fig. 14 shows that the LTE line profile is unable to reproduce the core of the strong Mg lines. The observed K lines in the H-band are insensitive to NLTE effects. The derived abundance in the Sun is A(K) = 5.05 dex, which also agrees well with our NLTE results for the optical lines. The derived abundance of Ca found from the five lines that were considered useful in the H-band is A(Ca) = 6.30 dex, which excellently agrees with our NLTE results for the optical. As described before, the LTE and NLTE line profiles for the transitions observed in the H-band do not differsignificantly, and therefore the derived abundance is the same.

In the case of Arcturus, we adopted the observations from Hinkle et al. (1995). For Na, the 15 992 Å line has an strong blend with two CN lines, and the other visible line (16 389 Å) is rather weak, but has NLTE effects. The derived abundances are therefore A(Nanlte) = 5.82 and A(Na) = 5.87 dex, and both results are consistent with our results in the optical. For Mg, abundances of the best fit in LTE and NLTE are A(Mg) = 7.55 and 7.40 dex. Like for the Sun, the core of the strong lines cannot be reproduced in LTE. K has two relatively strong lines at 15 170 Å. We found no significant NLTE effects for these two lines, and the derived abundance is A(K) = 4.80 dex, an intermediate value between the LTE and the NLTE abundances we found in the optical. There are some changes in the Ca line profiles observed in Arcturus. The derived abundances were A(Canlte) = 5.96 and A(Calte) = 6.00 dex, which both agree welt with the derived abundance from optical transitions. However, in this case, our best fit in NLTE is 12% better than the best fit in LTE. Figure 15 shows the results of the best fit in LTE and NLTE compared with the observationsfor the selected Ca lines. The redistribution of the Ca populations in NLTE shows that for some lines, the core of the NLTE profile is deeper than the core of the LTE profile, while for other lines, the opposite is true. Because the NLTE profile is closer to theobservations, the line-by-line analysis will present higher dispersion in the abundances derived in LTE than in NLTE.

thumbnail Fig. 13

Comparison between synthetic spectra and observations of the section around 6162 Å for Procyon (top), the Sun (middle), and Arcturus (bottom), where several Ca lines can be observed. The black lines represent the observations; and blue, pink, and red are the synthetic spectra in LTE, NLTE-s[Ca], and NLTE-m, respectively. Bellow each spectrum we plot the residuals (synthetic-observed). The Ca Abundance and Vmac adoptedfor the LTE, NLTE-s [Ca], and NLTE-m synthetic spectra are [A(Ca), Vmac (Km s−1)] = [6.10, 5.1] for Procyon, [6.30, 1.0] for the Sun, and [5.99, 3.6] for Arcturus.
thumbnail Fig. 14

Comparison between synthetic spectra and th centre-of-disc solar intensity observations of Mg lines in the APOGEE window. The black lines represent the observations, and red and blue are the synthetic spectra in LTE and NLTE, respectively. Below each spectrum we plot the residuals (synthetic-observed). The Mg abundance adopted for the two synthetic spectra is A(Mg) = 7.55 dex. The label of each line represents the wavelength (in Å).
thumbnail Fig. 15

Comparison of Ca lines in the APOGEE window between synthetic spectra and the observations of Arcturus. The black lines represent the observations, and red and blue are the best-fit synthetic spectra in LTE and NLTE, respectively. The lower panel shows the residuals (synthetic-observed).

7.1 Effects of resolution in NLTE corrections

Regarding the Mg I triplet in the H-band, we should stress that the effect of the inability of the LTE calculations to match the observed cores is minimised when the abundance determination is performed by fitting line profiles at high resolution, as we did here. The cores of the lines span only a few frequencies, the remaining line profile is reproduced well, and an abundance increase to improve the fitting in the core will necessarily ruin the match in the wings of the line profile. Therefore the best-fitting abundance is fairly insensitive to the NLTE changes in the line core. If the analysis is carried out by fitting line profiles at lower resolution or using equivalent widths, the NLTE abundance corrections will be enhanced. This implies that the abundance corrections expected for these lines in the APOGEE spectra will be significantly augmented compared to our estimates derived for very high-resolution data. We used the NLTE line profile of the 15 748 Å Mg I line as a test case. In both stars the NLTE cores are stronger than the LTE cores, but in the Sun, this line has broad wings and in Arcturus its wings are narrow. We fixed the NLTE abundance and determined the LTE value that minimises the residuals between the two profiles. This experiment was performed at different spectral resolutions by performing a Gaussian convolution with increasing full width at half-maximum in both LTE and NLTE spectra. Table 5 shows that at increasing resolution, the LTE and NLTE profiles become more similar, and the abundance correction increases simultaneously.

Table 5

NLTE abundance corrections at different resolutions for our test case: the Mg I 15 748 Å line in the Sun and Arcturus.

7.2 Other NLTE work in the APOGEE window

Other NLTE studies in the H-band spectra for the atoms we studied are those from Zhang et al. (2017) for Mg and Zhou et al. (2019) for Ca. Zhang et al. (2017) adopted for the Sun A(Mg) = 7.53 dex and calibrated the oscillator strength of the 15750 Å lines in order to fit the observations. Their Fig. 2 does not show a deeper NLTE core compared with the LTE line profile, a feature we see in our synthetic spectra (see Fig. 14). We believe the reason for this particular discrepancy is the collisional data adopted for the high-lying levels. Hydrogen collisional excitation were ignored for the high-lying levels of Mg I, while we used the formula from Kaulakys (1986). Electron collisional ionisation were taken from Seaton (1962), while we used the formula from Vrinceanu (2005) and electron collisional excitation for the high-lying levels were taken from van Regemorter (1962), while we used the BSR results of Barklem et al. (2017). The derived NLTE populations of the high-lying levels depend directly on the collisional rates that involve those levels. They also derived LTE and NLTE abundances for Arcturus and found an abundance correction of ΔA(Mg)nlte-lte = −0.03 dex, which is consistent with our results.

Zhou et al. (2019) studied the optical and the H-band spectra for Ca. The derived LTE abundances agree with ours for the Sun, but for Arcturus, they are ~0.1 dex lower than ours. The reason for this discrepancy might be differences in the abundance adopted and the radiative data (they used astrophysical f-values by setting the solar A(Ca) = 6.31 dex, while we adopted f-values based on Yu & Derevianko 2018, see Table 6).

For Arcturus, they found in the optical an abundance correction of 0.01 dex, which agrees excellently with our NLTE-s results. For the H-band, Zhou et al. (2019) found no abundance correction for Arcturus, while we found −0.04 dex. This discrepancy might again be due to differences in the collisional data adopted for the high-lying levels. In this work, hydrogen collisional excitations for the high-lying levels of Ca I were ignored, while we used the formula from Kaulakys (1986). For the electron collisional ionisation, Zhou et al. (2019) used the formula from Seaton (1962), while we adopted the formula from Vrinceanu (2005). Finally, electron collisional data involving the levels producing the Ca I lines that are visible in the H-band are from Seaton (1962), while we used an extension of the data presented in Zatsarinny et al. (2019).

Table 6

log(gf) values adopted for the Ca I lines visible in the H-band in Zhou et al. (2019) and in this work (taken from Yu & Derevianko 2018).

8 Conclusions

Traditional (1D and 3D) NLTE calculations in cool stars adopt the trace-element approximation, where all the atmospheric parameters are kept fixed while the populations of a single atomic element are allowed to change. With the aim of removing this approximation, we performed for the first time NLTE radiative transfer calculations in cool stars including several atomic elements simultaneously, still within the trace-element approximation, but including the inter-element effects through the background opacities.

Atomic elements in ionisation stages where over-ionisation is an important NLTE mechanism are most likely affected by Mg NLTE effects. For late-type stars at about solar temperature and hotter, there is enough change in the UV flux due to Mg-NLTE effects that it can affect the statistical balance of Ca, but not K or Na.

Because the NLTE results are sensitive to a particular radiative transition on the collisional data of the levels associated with that transition, particular care must be taken when NLTE calculations of spectral lines are made that involve high-lying levels, for which accurate collisional data are usually lacking.

As found in previous studies (Osorio et al. 2019), the best fit for Ca in Arcturus in LTE is better than the best fit for Ca in NLTE-s[Ca] and NLTE-m. Perhaps the calcium NLTE populations in Arcturus are sensitive to other elements than those we studied here; iron is the obvious candidate. Future calculations expanding the elements to calculate in the NLTE-m mode will help to clarify this issue.

Observations at lower resolution will cause the derived LTE abundances to increase because the LTE line profiles cannot match the cores of strong lines (e.g. the Mg I triplet in the H-band).

The derived NLTE abundance corrections in the optical and in the H-band differ, but the NLTE abundances we derived are consistent between the two spectral regions.

The goal of this effort is to update the synthetic spectral library that will be used by ASPCAP in DR17, which will include inter-element NLTE effects for Na, Mg, K, and Ca in the analysis of APOGEE spectra.

This work demonstrates that in cool stars, inter-element NLTE effects (via background opacities) can have an impact on the derived abundances on the same order as traditional NLTE effects. We expect the inter-element NLTE effects to increase with temperature (because of the increased radiative fluxes) and higher surface gravities (because of the wider lines). This is a step towards full NLTE stellar atmospheric modelling of cool stars. Our next step in this line will be to include more elements that contribute opacity in the next NLTE-m calculations and study its effects on the NLTE results derived for other species.

Asplund (2005) pointed out the lack of studies on effects of NLTE and 3D on the structure of cool stars, and the possible implications on parameters that are determined based on stellar spectra, such as Teff and log g, which are derived from ionisation balance and line broadening. More recently, Asplund et al. (2009) pointed out that even though we have had great progress in the quality and quantity of available atomic data, we still need to go beyond LTE in order to attain the desired 1% level of precision in derived solar abundances that are fundamental for the whole astrophysics community. Works regarding the effects of the trace element approach on the NLTE results in cool stars is still an area to explore, and this is our first effort on this front.

Acknowledgements

We want to thank the referee for the careful reading of the manuscript and for giving such constructive comments and suggestions which helped improving the quality and readability of the paper. We thank P. S. Barklem, M. Bautista, S. Nahar, J. Holtzman and O. Zatsarinny for providing assistance. I.H. is thankful for funding for his visit to the IAC by the Severo Ochoa program, awarded by the Government of Spain to the IAC to recognise, reward and promote outstanding scientific research in Spanish centres and units with a high level of excellence in the international arena. The research of Y.O. and C.A.P. is partially funded by the Spanish MINECO under grant AYA2014-56359-P. This research has made use of NASA’s Astrophysics Data System Bibliographic Services, TOPBASE, the NORAD-Atomic-Data web-page, and the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna. We build on software and data written, collected, maintained, and made publicly available by R. L. Kurucz and F. Castelli. S.M. has been supported by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences, by the Hungarian NKFI Grants K-119517 and GINOP-2.3.2-15-2016-00003 of the Hungarian National Research, Development and Innovation Office. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the US Department of Energy Office of Science, and the Participating Institutions. SDSS acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is www.sdss.org. SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU) / University of Tokyo, the Korean Participation Group, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatório Nacional / MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.

References

  1. Allende Prieto, C. 2016, Liv. Rev. Sol. Phys., 13, 1 [CrossRef] [Google Scholar]
  2. Allende Prieto, C., Asplund, M., García López, R. J., & Lambert, D. L. 2002, ApJ, 567, 544 [NASA ADS] [CrossRef] [Google Scholar]
  3. Allende Prieto, C., Lambert, D. L., Hubeny, I., & Lanz, T. 2003, ApJS, 147, 363 [NASA ADS] [CrossRef] [Google Scholar]
  4. Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
  5. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  6. Auer, L. H., & Mihalas, D. 1969a, ApJ, 156, 157 [NASA ADS] [CrossRef] [Google Scholar]
  7. Auer, L. H., & Mihalas, D. 1969b, ApJ, 156, 681 [NASA ADS] [CrossRef] [Google Scholar]
  8. Auer, L. H., & Mihalas, D. 1970, ApJ, 160, 233 [NASA ADS] [CrossRef] [Google Scholar]
  9. Barklem, P. S. 2016, Phys. Rev. A, 93, 042705 [NASA ADS] [CrossRef] [Google Scholar]
  10. Barklem, P. S. 2017a, Phys. Rev. A, 95, 069906 [NASA ADS] [CrossRef] [Google Scholar]
  11. Barklem, P. S. 2017b, KAULAKYS: Inelastic collisions between hydrogen atoms and Rydberg atoms [Google Scholar]
  12. Barklem, P. S., Anstee, S. D., & O’Mara, B. J. 1998, PASA, 15, 336 [NASA ADS] [CrossRef] [Google Scholar]
  13. Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&AS, 142, 467 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  14. Barklem, P. S., Belyaev, A. K., Spielfiedel, A., Guitou, M., & Feautrier, N. 2012, A&A, 541, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Barklem, P. S., Osorio, Y., Fursa, D. V., et al. 2017, A&A, 606, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bautista, M. A., Romano, P., & Pradhan, A. K. 1998, ApJS, 118, 259 [NASA ADS] [CrossRef] [Google Scholar]
  17. Belyaev, A. K., Barklem, P. S., Spielfiedel, A., et al. 2012, Phys. Rev. A, 85, 032704 [NASA ADS] [CrossRef] [Google Scholar]
  18. Buder, S., Asplund, M., Duong, L., et al. 2018, MNRAS, 478, 4513 [NASA ADS] [CrossRef] [Google Scholar]
  19. Carlsson, M. 1986, Upps. Astron. Obs. Rep., 33, 2 [Google Scholar]
  20. Carlsson, M. 1992, ASP Conf. Ser., 26, 499 [NASA ADS] [Google Scholar]
  21. Cox, A. N. 2000, Allen’s Astrophysical Quantities (Berlin: Springer) [Google Scholar]
  22. Cunto, W., & Mendoza, C. 1992, Rev. Mex. Astron. Astrofis., 23. 107 [NASA ADS] [Google Scholar]
  23. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Hinkle, K., Wallace, L., & Livingston, W. 1995, PASP, 107, 1042 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727–9300 A (San Francisco: Astronomical society of the Pacific) [Google Scholar]
  26. Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
  27. Hubeny, I., & Lanz, T. 2017a, ArXiv e-prints [arXiv:1706.01859] [Google Scholar]
  28. Hubeny, I., & Lanz, T. 2017b, ArXiv e-prints [arXiv:1706.01935] [Google Scholar]
  29. Hubeny, I., & Lanz, T. 2017c, ArXiv e-prints [arXiv:1706.01937] [Google Scholar]
  30. Hubeny, I., & Mihalas, D. 2014, Theory of Stellar Atmospheres (Princeton: Princeton University Press) [Google Scholar]
  31. Hubeny, I., Hummer, D. G., & Lanz, T. 1994, A&A, 282, 151 [NASA ADS] [Google Scholar]
  32. Igenbergs, K., Schweinzer, J., Bray, I., Bridi, D., & Aumayr, F. 2008, At. Data Nucl. Data Tables, 94, 981 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kaulakys, B. 1985, J. Phys. B At., 18, L167 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kaulakys, B. P. 1986, J. Exp. Theor. Phys., 91, 391 [Google Scholar]
  35. Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Balt. Astron., 9, 590 [NASA ADS] [Google Scholar]
  36. Kurucz, R. L. 1993, Phys. Scr. T, 47, 110 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kurucz, R. L. 2012, Robert L. Kurucz on-line database of observed and predicted atomic transitions (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
  38. Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar Flux Atlas from 296 to 1300 nm (New Mexico: National Solar Observatory) [Google Scholar]
  39. Lodders, K. 2019, ArXiv e-prints [arXiv:1912.00844] [Google Scholar]
  40. Lind, K., Asplund, M., Barklem, P. S., & Belyaev, A. K. 2011, A&A, 528, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Livingston, W. C., & Wallace, L. 1991, An Atlas of the Solar Spectrum in the Infrared from 1850 to 9000 cm-1 (1.1 to 5.4 [mu]m) with Decomposition into Solar and Atmospheric Components and Identifications of the Main Solar Features (Tucson: National Solar Observatory) [Google Scholar]
  42. Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
  43. Mashonkina, L. 2010, EAS Pub. Ser., 43, 189 [Google Scholar]
  44. Mashonkina, L. I., Shimanskiĭ, V. V., & Sakhibullin, N. A. 2000, Astron. Rep., 44, 790 [NASA ADS] [CrossRef] [Google Scholar]
  45. Meléndez, M., Bautista, M. A., & Badnell, N. R. 2007, A&A, 469, 1203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Mészáros, S., Allende Prieto, C., Edvardsson, B., et al. 2012, AJ, 144, 120 [NASA ADS] [CrossRef] [Google Scholar]
  47. Osorio, Y., Barklem, P. S., Lind, K., & Asplund, M. 2011, A&A, 529, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Osorio, Y., Barklem, P. S., Lind, K., et al. 2015, A&A, 579, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Osorio, Y., Lind, K., Barklem, P., Allende-Prieto, C., & Zatsarinny, O. 2019, A&A, 623, A17 [CrossRef] [EDP Sciences] [Google Scholar]
  50. Park, C. 1971, J. Quant. Spectr. Rad. Transf., 11, 7 [NASA ADS] [CrossRef] [Google Scholar]
  51. Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Ralchenko, Y., Kramida, A., Reader, J., & NIST ASD Team 2014, NIST Atomic Spectra Database (version 5.0) [online] available: http://physics.nist.gov/asd [2015, September 1] [Google Scholar]
  53. Ramírez, I., & Allende Prieto, C. 2011, ApJ, 743, 135 [NASA ADS] [CrossRef] [Google Scholar]
  54. Reggiani, H., Amarsi, A. M., Lind, K., et al. 2019, A&A, 627, A177 [EDP Sciences] [Google Scholar]
  55. Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr., 90, 054005 [NASA ADS] [CrossRef] [Google Scholar]
  56. Sansonetti, J. E. 2008, J. Phys. Chem. Ref. Data, 37, 7 [NASA ADS] [CrossRef] [Google Scholar]
  57. Seaton, M. J. 1962, Atomic and Molecular Processes, ed. D. R. Bates, Library of Congress Catalog Card Number 62-13122, (Cambridge: Academic Press), 375 [Google Scholar]
  58. Seaton, M. 1996, The Observatory, 116, 177 [NASA ADS] [Google Scholar]
  59. Shetrone, M., Bizyaev, D., Lawler, J. E., et al. 2015, ApJS, 221, 24 [NASA ADS] [CrossRef] [Google Scholar]
  60. Strassmeier, K. G., Ilyin, I., & Weber, M. 2018, A&A, 612, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Unsöld, A. 1955, Physik der Sternatmospharen, MIT besonderer Berucksichtigung der Sonne (Berlin: Springer) [Google Scholar]
  62. van Regemorter, H. 1962, ApJ, 136, 906 [NASA ADS] [CrossRef] [Google Scholar]
  63. Vrinceanu, D. 2005, Phys. Rev. A, 72 [Google Scholar]
  64. Yu, Y., & Derevianko, A. 2018, At. Data Nucl. Data Tables, 119, 263 [NASA ADS] [CrossRef] [Google Scholar]
  65. Zatsarinny, O., & Tayal, S. S. 2010, Phys. Rev. A, 81, 043423 [NASA ADS] [CrossRef] [Google Scholar]
  66. Zatsarinny, O., Parker, H., & Bartschat, K. 2019, Phys. Rev. A, 99, 012706 [NASA ADS] [CrossRef] [Google Scholar]
  67. Zhang, J., Shi, J., Pan, K., Allende Prieto, C., & Liu, C. 2017, ApJ, 835, 90 [NASA ADS] [CrossRef] [Google Scholar]
  68. Zhou, Z.-M., Pan, K., Shi, J.-R., Zhang, J.-B., & Liu, C. 2019, ApJ, 881, 77 [NASA ADS] [CrossRef] [Google Scholar]
1

The code can be found at https://owncloud.iac.es/index.php/s/WkFWNie5U6y3Nzh. A description of the code and an operation manual are found in Hubeny & Lanz (2017a,b,c).

2

The departure coefficient b of level i is defined as 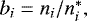bi=ni/ni*,$b_{i}=n_{i}/n_{i}^*, $ where ni is the number density of level i and the asterisk means LTE, so that 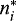ni*$n_i^*$ is the absolute LTE population of level i, that is, a population obtained by solving the set of LTE kinetic equations for all levels of all ionisation stages considered and not by the usual definition 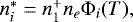ni*=n1+neΦi(T),$n_i^*=n_1^+ n_e \Phi_i(T),$ where n1+$n_1^+$ 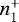is the actual population of the ground state of the next higher ion, ne the electron density and Φi the Saha-Boltzmann factor. See Hubeny & Mihalas (2014, Chap. 9, Sect. 9.1).

All Tables

Table 1

Data adopted for the NLTE calculations for characteristic lines of Na and K.

In the text
Table 2

Parameters of the model atmospheres used to construct the synthetic spectra.

In the text
Table 3

Components of the background opacities used for the comparison calculations between MULTI(*) and TLUSTY.

In the text
Table 4

Na, Mg, K, and Ca abundances derived for the LTE, NLTE-s, and NLTE-m calculations.

In the text
Table 5

NLTE abundance corrections at different resolutions for our test case: the Mg I 15 748 Å line in the Sun and Arcturus.

In the text
Table 6

log(gf) values adopted for the Ca I lines visible in the H-band in Zhou et al. (2019) and in this work (taken from Yu & Derevianko 2018).

In the text

All Figures

thumbnail Fig. 1

Grotrian diagram of Na (upper panel) and K (lower panel) model atoms. The red lines correspond to transitions in the H-band.
In the text
thumbnail Fig. 2

Rate coefficients of the electron related collisions (excitation and ionisation, top) and hydrogen related collisions (excitation and charge-exchange, bottom) for Na (left) and K (right). Initial levels of the transitions are labelled in rows and final levels are labelled in columns. The arrows point towards the transition that separates the hydrogen collisional excitation data from Barklem et al. (2012) and the data calculated using the formula from Kaulakys (1985). The colour scale at the left is for the Na Rates and the colour scale at the right is for the K rates.
In the text
thumbnail Fig. 3

Sample of the background opacities from the opacity tables in the UV region used in the NLTE calculation of Mg (i.e. removing the contribution of Mg) by MULTI (red) and TLUSTY (black) at two different points of the solar atmosphere.
In the text
thumbnail Fig. 4

Photo-ionisation cross-section data used in the MULTI (red lines) and TLUSTY (black symbols) calculations for two b-f transitions of Mg I and the one from the ground level of Mg II. The red lines are the values taken from the TOPBASE database without the cross sections below 911 Å (except for the Mg II b-f transition). The symbols are the resonance-averaged photo-ionisation cross sections of the TOPBASE data (see Allende Prieto et al. 2003). The b-f cross section of the Mg II 3s(2S) and the Mg I 3p(3P) levels are vertically shifted by 4 and 2 log units, respectively, for visualisation.
In the text
thumbnail Fig. 5

Comparison between MULTI NLTE solar line profile and departure coefficients (inner figure) of the levels involved for the Ca I transition 4p1P–4s1S (4227 Å) when the van der Waals broadening is treated using the ABO theory (solid lines) and when the formulation from Unsöld (1955), with a Γ6 value derived from the ABO theory, is used (dashed lines).
In the text
thumbnail Fig. 6

Departure coefficients for some levels of Mg I (upper panel) and Ca I (lower panel) obtained with TLUSTY (red) and MULTI (black) for the same solar model atmosphere and the same atomic data. The grey vertical lines denote the depths at τross = 0.01 (left) and τross = 1.0 (right).
In the text
thumbnail Fig. 7

Ultraviolet fluxes obtained for Procyon (top), the Sun (middle), and Arcturus (bottom) calculated in LTE (black), NLTE-m (red), NLTE-s:Mg (pink), and NLTE-s:Ca (blue). For each star, the Eddington flux (upper panel) and the difference inpercent between the LTE and the NLTE fluxes (lower panel) are plotted. The units of the Eddington flux Hλ are erg cm−2s−1Å−1.
In the text
thumbnail Fig. 8

Mg number densities of different ionisation stages in Arcturus. The solid lines represent the NLTE populations, and the dashed lines represent the LTE populations.
In the text
thumbnail Fig. 9

Departure coefficients for some levels of Na, Mg, K and Ca obtained calculated in single-element mode (NLTE-s, in red) and in multiple-elements mode (NLTE-m, in black) for Procyon, the Sun and Arcturus. For each star, the same element abundances were used in all the LTE, NLTE-s and NLTE-m calculations. The fact that the b coefficient for the Mg II ground state increases toward the surface (due to NLTE effects in the Mg II h & k lines) inArcturus, but stays closely to 1 for the other two stars, follows from Mg II being the dominant stage of ionisation, and its ground state the most populated state, for Sun and Procyon, but not for the cooler starArcturus. The two grey vertical lines in each figure mark the depths in the atmospheres where τross = 0.01 (left) and 1.0 (right).
In the text
thumbnail Fig. 10

Local thermal equilibrium (black), NLTE-m (red), and NLTE-s:Na (blue) normalised synthetic fluxes of Procyon around the red wing of the 2852 Å Mg I line. The atomic species of some lines are marked together with their LTE equivalent width in mÅ.
In the text
thumbnail Fig. 11

Top: selected lines of Na Observed in Procyon (black) and the best fit for the LTE (red) and NLTE (blue) calculations with the parameters in derived in Table 4. Bottom: difference between observations and the synthetic spectrum in LTE (red) and in NLTE (blue).
In the text
thumbnail Fig. 12

Top: lines of K used in the solar observations (black) compared with the best fit of the LTE (red) and NLTE (blue) calculations with the parameters derived in Table 4. Bottom: difference between observations and the synthetic spectrum in LTE (red) and in NLTE (blue).
In the text
thumbnail Fig. 13

Comparison between synthetic spectra and observations of the section around 6162 Å for Procyon (top), the Sun (middle), and Arcturus (bottom), where several Ca lines can be observed. The black lines represent the observations; and blue, pink, and red are the synthetic spectra in LTE, NLTE-s[Ca], and NLTE-m, respectively. Bellow each spectrum we plot the residuals (synthetic-observed). The Ca Abundance and Vmac adoptedfor the LTE, NLTE-s [Ca], and NLTE-m synthetic spectra are [A(Ca), Vmac (Km s−1)] = [6.10, 5.1] for Procyon, [6.30, 1.0] for the Sun, and [5.99, 3.6] for Arcturus.
In the text
thumbnail Fig. 14

Comparison between synthetic spectra and th centre-of-disc solar intensity observations of Mg lines in the APOGEE window. The black lines represent the observations, and red and blue are the synthetic spectra in LTE and NLTE, respectively. Below each spectrum we plot the residuals (synthetic-observed). The Mg abundance adopted for the two synthetic spectra is A(Mg) = 7.55 dex. The label of each line represents the wavelength (in Å).
In the text
thumbnail Fig. 15

Comparison of Ca lines in the APOGEE window between synthetic spectra and the observations of Arcturus. The black lines represent the observations, and red and blue are the best-fit synthetic spectra in LTE and NLTE, respectively. The lower panel shows the residuals (synthetic-observed).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.