| Issue |
A&A
Volume 635, March 2020
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 10 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201937416 | |
| Published online | 17 March 2020 | |
Revisiting astrometric parameters of quasars in Gaia-CRF2
School of Astronomy and Space Science, Key Laboratory of Modern Astronomy and Astrophysics (Ministry of Education), Nanjing University, 163 Xianlin Avenue, 210023 Nanjing, PR China
e-mail: zhuzi@nju.edu.cn, jcliu@nju.edu.cn
Received:
26
December
2019
Accepted:
9
February
2020
Aims. In order to check the astrometric solution quality, dependences of parallaxes and proper motions on precision, reliability, and consistency of sample solutions are studied for the quasars in the celestial reference frame of the second release of Gaia data (Gaia-CRF2).
Methods. Astrometric statistics (the number of visibility periods, the semi-major axis of the astrometric five-dimensional error ellipse σ5d, max, the unit weight error u, the correlation coefficients ρμα*, ϖ and ρμδ, ϖ) were selected to serve as indicators of the solution qualities of quasars. The dependences of the astrometric parameters, parallaxes and proper motions, on these indicators are evaluated. We also investigated mean values of astrometric statistics in equal-area spherical cells to study the impact of the scanning law.
Results. The astrometric parameters of quasars with fewer than 9 or more than 18 visibility periods show a departure from the global average. Moreover, the mean values of astrometric parameters of the most precise sources deviate from the others. Astrometric parameters are stable for those quasars fitting the five-parameter model well. The correlation coefficients, ρμα*, ϖ and ρμδ, ϖ obtained from the astrometric solutions show a generally ideal distribution for the full sample. Spherical-cell mean values of these correlation coefficients are found to have a centrally asymmetric distribution. Distributions of two correlation coefficients are found to correlate with the number of visibility periods. The quasars with visibility periods in the domain [13, 16], with ρμα*, ϖ and ρμδ, ϖ generally well-distributed have more reliable astrometric parameters. Magnitudes and colours are found to have little influence on the irregular patterns of the correlation coefficients.
Key words: astrometry / parallaxes / proper motions
© ESO 2020
1. Introduction
The Gaia celestial reference frame (Gaia-CRF) is a rotation-free celestial reference frame in the visible wavelengths built by the European Space Agency’s Gaia mission (Gaia Collaboration 2016) with its axes fixed with respect to distant extragalactic objects like quasars. The second release of data from Gaia (Gaia DR2, Gaia Collaboration 2018a) contains the entire astrometric data for more than half a million quasars (Gaia Collaboration 2018b). These sources and their positions in Gaia DR2 are a version of the Gaia-CRF called Gaia-CRF2. Gaia Collaboration (2018b) found that the accuracy of Gaia-CRF2 matches the current radio frame of the International Celestial Reference Frame (ICRF).
Astrometric properties of Gaia-CRF2 are crucial for the Gaia mission. Quasars with extremely small parallaxes are ideal for checking astrometric properties. Meanwhile, proper motions of quasars are nominally zero if the global pattern from the Galactic aberration is not considered. By “Galactic aberration”, we mean the change in aberration over decade time scales due to the rotation of our Galaxy (MacMillan et al. 2019; Liu et al. 2012; Kovalevsky 2003). It is necessary to take the Galactic aberration into consideration while checking quasar proper motions.
Lindegren et al. (2018) listed the selection criteria of these quasars. They analysed the parallaxes of these quasars and found −0.029 mas as the global zero point of the parallaxes. Spatial correlations of parallax uncertainties as well as proper motions on different scales were also estimated. They also introduced many quality indicators in Gaia DR2 to provide us with information on the precision, reliability, and consistency of these quasars.
Petrov et al. (2019) analysed systematic differences in the positions and proper motions of a group of these quasars with respect to very long baseline interferometry (VLBI) and found that nine percent of matched sources have significant position offsets. They explained proper motions of outliers as a manifestation of the source position jitter caused by flares. These outliers are more likely to associate with a high chi square per degree of freedom.
Main concerns of this work are systematic dependences of the astrometric parameters, parallaxes, and proper motions associated with various quality indicators. We analysed the spatial distributions of quality indicators differently. Common structures in spatial distributions of indicators were explored.
2. Quality indicator for reliability
Gaia Collaboration (2018b) selected a sample containing 556869 Gaia DR2 sources that they called Gaia-CRF2 (see also, Lindegren et al. 2018). The selection criteria are listed in Sect. 5.2, Eq. (14) of Lindegren et al. (2018). In the following sections, we systematically use this quasar sample or its subset.
The first selection criterion of Lindegren et al. (2018) puts a constraint on astrometric_matched_observations (number of field-of-view transits of the source used in the astrometric solution) to remove these astrometrically poorly observed sources. Compared to this statistic, visibility_periods_used (number of visibility periods of the source) is a better indicator of an astrometrically well-observed source (Lindegren et al. 2018). The relation between these two parameters for a random subset of about 2.5 million sources was presented in Fig. 2 of Lindegren et al. (2018). For all quasars in Gaia-CRF2, the relation is illustrated in Fig. 1. The median values in the plot are roughly equal to 1.8 times the visibility period. This fact just tells us that an average sequence of observations during a visibility period comprises, in general, almost two observations, one in the preceding field of view (FOV), and one in the following FOV. There are many sources with more than 10 transits concentrated in a few visibility periods. The statistic, astrometric_matched_observations, is thus not suitable as an indicator of the solution reliability. We studied the variation of the astrometric parameters of quasars with respect to the number of visibility periods.
 |
Fig. 1. Relation between the number of visibility periods and field-of-view transits (matched observations) per quasar in Gaia-CRF2. Like Fig. 2 of Lindegren et al. (2018), a small random number was added to the integer number of visibility periods to widen the vertical bars. The black line through each bar shows the location of the median. The red solid line is equal to 1.8 times the visibility periods. |
2.1. Astrometric parameters to be investigated
The full quasar sample was divided into several subsets according to the quality indicator value. For each subset, we studied the properties of astrometric parameters, parallaxes, and proper motions of the featured quasars.
2.1.1. Parallaxes
Given that quasars have nominally zero parallaxes, we investigated the mean parallax of each subset, 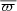 . The standard deviations of the normalised debiased parallaxes,
. The standard deviations of the normalised debiased parallaxes, 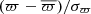 , were also calculated to trace systematic dependences.
, were also calculated to trace systematic dependences.
2.1.2. Normalised proper motion difference Xpm
The basic idea of the normalised proper motion difference Xpm is inspired by Mignard et al. (2016; see their Eq. (4) and Appendix B). Proper motions of quasars, μα* and μδ, are nominally zero due to their extremely small parallaxes. The normalised proper motion difference Xpm describes the difference between proper motions given in Gaia DR2 and the nominally zero proper motions. For a group of quasars with Gaussian errors, the theoretical distribution of this quantity depends on the standard deviation of proper motion, σμα* and σμδ, as well as the degree of correlation between μα* and μδ. Taking the correlation coefficient ρμα*, μδ into consideration, we have the statistic 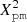 written as:
written as:
where the vector
The apparent proper motion μapparent is nominally 0 for every quasar. We expect X2 to follow the chi-squared distribution with two degrees of freedom for Gaussian errors. Therefore, the normalised proper motion difference Xpm is expected to have a standard Rayleigh distribution. Furthermore, we can accept that the apparent proper motions μapparent are affected by the global pattern from the Galactic aberration. Then, we have:
where (G1, G2, G3) are components of the glide vector in the ICRS (see their Eq. (64) and (65) Mignard & Klioner 2012). A typical glide vector directed towards the Galactic centre with a magnitude of 5.8 μas yr−1, or ( − 0.32, −5.07, −2.81) μas yr−1 is used hereinafter (MacMillan et al. 2019; Titov & Krásná 2018; Titov & Lambert 2013). The standard deviation of 1.09 for μα* (1.11 for μδ) is used to correct the given uncertainty in Gaia DR2 (see their Fig. 10 Gaia Collaboration 2018b).
As mentioned above, the normalised proper motion difference Xpm should follow a standard Rayleigh distribution for quasars with Gaussian errors. For a subset of quasars, the proper motions are more likely to be non-zero if the mean value of Xpm is larger than 1.253 (the mean value of a standard Rayleigh distribution), considering the deviation. The proper motions of these quasars are probably under-estimated if the mean value is less than 1.253.
The actual distribution of the normalised proper motion difference Xpm for the full sample is plotted in Fig. 2. The distribution follows, very closely, a standard Rayleigh distribution up to Xpm values of 3.5. As indicated by the distribution of Xpm, the magnitude effect is almost fully absorbed by the normalisation. This leads to a similar conclusion that for the full quasar sample, the Gaia accuracy is dominated by the photon noise (Gaia Collaboration 2018b).
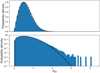 |
Fig. 2. Distribution of normalised proper motion difference Xpm for all Gaia-CRF quasars in linear scale (top) and logarithmic scale (bottom). The black curve is a standard Rayleigh distribution. |
Table 1 presents some statistics concerning three distributions. Distribution A stands for the distribution of the normalised proper motion difference Xpm between the given proper motions and the nominally zero proper motions, while distribution B represents the distribution of Xpm between the given proper motions and the proper motions affected by the Galactic aberration. Relatively large variances of distributions A and B might be caused by quasars with the extremely large Xpm. Mean values of distributions A and B coincide well with the standard Rayleigh distribution. We find that the distribution is almost the same if the global pattern from the Galactic aberration is taken into consideration. Hereinafter, we used the mean value of the normalised proper motion difference Xpm between the given proper motions and the nominally zero proper motions of each subset to trace systematic dependences.
Statistic parameters of different distributions.
2.2. Astrometric parameters against quality indicators
The astrometric parameters, with respect to the number of visibility periods, are plotted in Fig. 3. Mean values of the normalised proper motion difference Xpm with the number of visibility periods greater than 18 deviate from the mean of the full sample. The mean values of parallaxes also show a slight departure from the global parallax zero point, −0.029 mas (Gaia Collaboration 2018b). Meanwhile, the standard deviations of the normalised parallax of the same subsets depart from the global standard deviation of formal uncertainties, 1.081 (Gaia Collaboration 2018b). This departure may be caused by the decrease in numbers of quasars in these subsets as plotted in Fig. 4. A small subset size can also lead to the departure found in the subsets with fewer than 9 visibility periods.
 |
Fig. 3. Top: mean values of parallaxes plotted against number of visibility periods. Middle: standard deviations of the normalised centred parallaxes plotted against the number of visibility periods. Bottom: mean values of normalised proper motion difference Xpm plotted against the number of visibility periods. Dashed lines represent the mean values of the full sample. |
 |
Fig. 4. Sample sizes plotted against number of visibility periods. |
3. Quality indicator for precision
Quasars with enormous errors in parallax and proper motion are excluded by conditions (iii)-(iv) (Lindegren et al. 2018). Uncertainties in positions, parallaxes, and proper motions directly affect the measured precision of quasars. Subsets with different levels of precision may have different astrometric properties, which should be carefully investigated. Since the five-parameter solution gives the five astrometric parameters as a whole, we selected astrometric_sigma5d_max (the semi-major axis of the astrometric five-dimensional error ellipse, hereinafter denoted as σ5d, max) as the main quality indicator of precision.
Dependences of astrometric parameters on various levels of precision are illustrated in Fig. 5. Quasars are sorted by σ5d, max and divided into 56 subsets. Each dot is calculated in bins of 10 000 quasars, except for the last one containing 6869 quasars. In the top panel of Fig. 5, mean values of parallaxes of sources with σ5d, max less than 0.75 mas show a slight oscillation around the global parallax zero point, −0.029 mas. The mean parallax of 10 000 most precise sources deviates from others to some degree. An extremely large deviation of these precise sources can also be found in the middle panel. The standard deviation of centred parallaxes of this subset reaches 1.140, much greater than 1.081. In the bottom panel of Fig. 5, large departures from the global mean can be clearly found in subsets with high precisions (σ5d, max less than 0.3 mas). The mean value of the normalised proper motion difference Xpm of 10 000 most precise sources is 1.381 and beyond the frame. Dependences of these parameters are similar if we adopt the semi-major axes of the error ellipses in position or proper motion (see Eqs. (B.1) and (B.2) in Lindegren et al. 2018) as the indicator.
 |
Fig. 5. Top: mean values of parallaxes plotted against σ5d, max. Middle: standard deviations of the normalised centred parallaxes plotted against σ5d, max. Bottom: mean values of normalised proper motion difference Xpm plotted against σ5d, max. Dashed lines represent the mean values of the full sample. Horizontal error bar represents the standard deviation of σ5d, max in subsets. Sources are sorted by σ5d, max and divided into subsets. Each dot above is calculated in bins of 10 000 sources, except for the last one containing 6869 quasars. |
4. Quality indicator for consistency
Lindegren et al. (2018) proposed that an increased chi-square can be a good signal of those observations which do not fit the single-star parallax model very well. Considering that the sample consists of distant and dim quasars, the unit weight error u = (χ2/ν)1/2 is qualified for the goodness-of-fit to the five-parameter model. The unit weight error can be selected as an indicator of the consistency.
Investigation of subsets with the similar unit weight errors can reveal the relationship between astrometric parameters and the goodness of fit to the five-parameter model, as shown in Fig. 6. Parameters are relatively stable for those quasars well-fitted to the five-parameter model in the domain [1.0, 1.08]. Some fluctuations can be seen in these panels. For sources fitting the model poorly (unit weight errors greater than 1.25), mean values of parallaxes depart from the global parallax zero point, −0.029 mas. The standard deviations of the normalised centred parallax and mean values of the normalised proper motion difference Xpm also show similar departures. Quasars with the unit weight errors under 0.9 have the mean value of parallaxes greater than the global parallax zero point, and the mean value of Xpm smaller than the global mean. It should be noted that the mean value of the unit weight error of the 10 000 most precise quasars (the point at the far left in Fig. 5) is 1.078, indicating that most of these quasars fit the five-parameter model well. However, mean values of the parallaxes and Xpm largely deviate from the global means.
 |
Fig. 6. Top: mean values of parallaxes plotted against unit weight error. Middle: standard deviations of the normalised centred parallaxes plotted against the unit weight error. Bottom: mean values of normalised proper motion difference Xpm plotted against the unit weight error. Dashed lines represent the mean values of the full sample. Horizontal error bar represents the standard deviation of the unit weight error in subsets. Sources are sorted by the unit weight error u and divided into subsets. Each dot above is calculated in bins of 10 000 sources. The greatest 16 869 sources are not displayed due to the axis range. |
5. Spatial distribution of indicators
Detailed spatial distributions of quality indicators can reveal systematic patterns as function of position on the celestial sphere. The non-uniform sampling owing to the scanning law can be reflected by the spatial distribution of the number of visibility periods, as shown in the top panel of Fig. 7. The middle and bottom panels of Fig. 7 illustrate the spatial distribution of σ5d, max and the unit weight error. Some common large-scale patterns like arcs can be identified in these panels at the same area on the celestial sphere. The Gaia Collaboration (2018b) presented similar spatial distributions of the parallaxes and proper motions of the quasars in their Fig. 11. Exploring common structures in spatial distributions of the indicators can help us to learn more about astrometric properties over the celestial sphere.
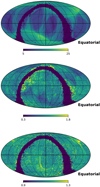 |
Fig. 7. Summary statistics for full quasar sample. Top: number of visibility periods used. Middle: σ5d, max. Bottom: unit weight error u. These maps use a Mollweide projection in equatorial (ICRS) coordinates, with origin α = δ = 0 at the centre, and α increasing from right to left. The values are calculated in spherical cells of about 1.8 × 1.8 deg2. Empty cells as well as cells with sources no more higher than ten are shown in dark blue. |
5.1. Spherical division
With the help of HEALPix (Górski et al. 2005), the celestial sphere is divided into 12288 equal-area spherical cells of about 1.8 × 1.8 deg2. Spherical cells are numbered and quasars are assigned to these cells according to their coordinates. Figure 8 shows the distribution of the quasar count in spherical cells. There are 11 170 spherical cells containing quasars, with 10 409 spherical cells with more than 10 quasars. The average quasar number for a spherical cell containing quasars is about 50. Considering statistical stability, spherical cells with more than 10 quasars are investigated in the following section.
 |
Fig. 8. Distribution of quasar density in 11170 spherical cells. There are 12288 spherical cells overall, with 11170 cells containing quasars, 10409 cells with more than 10 quasars. |
Various spherical-cell sizes of 0.9 × 0.9 deg2 and 3.6 × 3.6 deg2 had been set to repeat the procedure below. We found that so long as a spherical cell contains enough quasars (more than 10 quasars per cell on average), the choice of spherical-cell sizes hardly effects the outcomes.
5.2. Indicators in a spherical cell
Quasars in a given spherical cell have their own magnitudes, colour indices, and other physical properties. For a number of quasars, quality indicators are mainly obtained from the astrometric observations. Under the hypothesis that quasars with various physical properties have an isotropic and homogeneous distribution over the celestial sphere, influence on mean values of indicators produced by physical properties of quasars is expected to vary slightly from cell to cell. However, spherical cells are not observed uniformly due to the scanning law. Differences between the indicator averages from two spherical cells are more likely ruled by the scanning law.
For every spherical cell with more than 10 quasars, the standard deviation of the number of visibility periods is calculated and illustrated in Fig. 9. The standard deviation of visibility_periods_used for the full sample is 3.5. For 8977 spherical cells, about 86% of spherical cells analysed, standard deviations are smaller than 1.5. Thus the observation frequencies of quasars in a spherical cell are in a comparable situation. After simple calculations, we found that other indicators in most spherical cells also have much smaller deviations than the standard deviation of the full sample. We found that other indicators in most spherical cells also have much smaller deviations than the standard deviation of the full sample. This is a consequence of the spherical division. Within each small HEALPix pixel, there is no longer the large scatter coming from the sampling. Then mean values of indicators in a spherical cell are used to trace the systematic effects caused by the scanning law. Common structures between spatial distributions of two indicators can be demonstrated by the relationships between the spherical-cell mean values of these indicators.
 |
Fig. 9. Distribution of standard deviation of visibility_periods_used in 10409 spherical cells. For 8977 cells, about 86% of cells analysed, standard deviations are smaller than 1.5. |
6. Correlation coefficients ρμα*, ϖ and ρμδ, ϖ
The five-parameter solution provides us with the correlation coefficient between each pair of parameters. The correlations between these parameters also play a crucial role in checking the overall quality of these quasars. Usually, abnormal correlations between the astrometric parameters could lead to unreliable solutions. As the parallax and the proper motions are the focus of this paper, the correlation coefficients parallax_pmra_corr and parallax_pmdec_corr (hereinafter denoted as ρμα*, ϖ and ρμδ, ϖ) are thus chosen as additional quality indicators.
Holl et al. (2010) found that astrometric errors in the Gaia Catalogue can be separated into a star and a spacecraft attitude part, due to the estimation of the star and attitude parameters, respectively. Hence, the covariances between the estimated astrometric parameters can be separated in a star, a spacecraft attitude, and a cross term. The effect caused by the spacecraft attitude is expected to fall off, since quasars are generally uniformly distributed over the sky and have similar magnitudes (see their Eq. (3.5) Holl et al. 2010). Besides the spacecraft attitude, the non-uniform coverage in the scanning directions for a given source over the different visibility periods can result in the correlation between astrometric parameters. The spatial distributions of ρμα*, ϖ and ρμδ, ϖ in ecliptic coordinates are illustrated in Fig. 10. The effect of the scanning law is more pronounced at lower ecliptic latitudes. If a group of quasars are well-observed and solved in the global astrometric solution, it is natural to expect that the correlation coefficients, ρμα*, ϖ and ρμδ, ϖ, are generally independent and identically distributed from a common distribution function. Conversely, it is reasonable to infer the quality of the astrometric solutions from the distribution of these two coefficients.
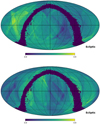 |
Fig. 10. Summary statistics for the full quasar sample. Top: ρμα*, ϖ. Bottom: ρμδ, ϖ. These maps use a Mollweide projection in Ecliptic coordinates. The values are calculated in spherical cells of about 1.8 × 1.8 deg2. Empty cells as well as cells with sources no more than 10 are shown in dark blue. |
6.1. Distributions of ρμα*, ϖ and ρμδ, ϖ
Figure 11 shows the distribution of ρμα*, ϖ and ρμδ, ϖ for the whole sample where these two coefficients are generally well-distributed in the parameter space. Slight radial asymmetries can be found away from the centre of the figure where there are only a few quasars. The coefficient ρμδ, ϖ is slightly biased towards −0.06 (mean value). The histograms of ρμα*, ϖ and ρμδ, ϖ present good distributions of both parameters. These distributions demonstrate that these two coefficients show no sign of significant correlation.
 |
Fig. 11. Top and right: probability density histograms of ρμα*, ϖ and ρμδ, ϖ of the full quasar sample, respectively. Bottom: density map of the full quasar sample. The colour bar represents the number of quasars in a pixel. The black curve represents the curve fitting with a Gaussian model. |
Figure 12 displays the density map of mean values of ρμα*, ϖ and ρμδ, ϖ calculated in spherical cells of 1.8 × 1.8 deg2. As seen in the right panel, the coefficient ρμδ, ϖ has a bimodal distribution. Compared with Fig. 11, the density map of spherical cells shows an odd pattern. There are few spherical cells around (0, −0.1), and spherical cells are more widely dispersed in the lower part of the panel. This is a hint that astrometric parameters of quasars in some sky areas may not be well-solved.
 |
Fig. 12. Top and right: histograms of mean values of ρμα*, ϖ and ρμδ, ϖ of the spherical cells, respectively. Bottom: the density map of mean values of two correlation coefficients, ρμα*, ϖ and ρμδ, ϖ, calculated in spherical cells of 1.8 × 1.8 deg2. The colour bar represents the number of spherical cells in a pixel. |
6.2. Correlation coefficients against other quality indicators
Density maps of spherical-cell mean values of these correlation coefficients against the parameter σ5d, max, the main quality indicator of precision, is illustrated in Fig. 13. An obvious symmetry between the upper and lower parts can be found in the top panel. More interestingly, the density map of ρμδ, ϖ with respect to σ5d, max for these spherical cells is asymmetric, and obviously biased towards a negative value. For spherical cells with good precision (mean values of σ5d, max less than 0.8), few spherical cells gather around the averages of these two coefficients. These patterns provide us with a clue towards the large deviation of mean parallax found for the 10 000 most precise sources (see Fig. 5). The density map of the correlation coefficients is displayed in Fig. 14 for two subsets. The top panel gives a centrally asymmetric distribution for the 10 000 most precise sources, while the bottom one shows that these two correlation coefficients are generally independent and identically distributed for the top 100 001–110 000 precise sources. The irregular distribution in the top panel of Fig. 14 suggests parallaxes of these top precise sources are less credible.
 |
Fig. 13. Density maps of mean values. Top: ρμα*, ϖ against σ5d, max. Bottom: ρμδ, ϖ against σ5d, max, calculated in spherical cells of 1.8 × 1.8 deg2. The colour bar represents the number of spherical cells in a pixel. |
 |
Fig. 14. Density map of correlation coefficients, ρμα*, ϖ and ρμδ, ϖ. Top: 10 000 most precise sources. Bottom: top 100 001–110 000 precise sources. The colour bar represents the number of quasars in a pixel. |
Considering the scanning law, we also checked the relationship between the number of visibility periods and these correlation coefficients. The diagram in Fig. 15 presents the density map of mean values of correlation coefficients against the number of visibility periods for 10 409 spherical cells. Similar symmetry is discovered in the distribution of the parameter, ρμα*, ϖ, against the number of visibility periods. For the spherical cells with fewer than eight visibility periods, the parameter ρμδ, ϖ are strongly biased to a negative value. The parameter, ρμα*, ϖ, although symmetrically distributed, has a fairly large deviation from zero. Patterns for spherical cells with the number of visibility periods greater than 18 are similar to those described above. Dense zones with mean values of the number of visibility periods of about 9 can be seen in both panels. Since the dense zone in the bottom panel is located in a region of positive correlations, astrometric solutions in these spherical cells are less stable. Patterns found in Fig. 15 can explain the dependence of astrometric parameters against the number of visibility periods plotted in Fig. 3. Besides sample sizes of these subsets shown in Fig. 4, the deviation in Fig. 3 may also be related to the irregular distribution of ρμδ, ϖ. The density map of the correlation coefficients, ρμα*, ϖ and ρμδ, ϖ, is displayed in Fig. 16 for three subsets with different numbers of visibility periods. Sources with visibility periods in the domain [13, 16] are more likely to be better solved than sources of the rest subsets under the assumption that the correlation coefficients are independent and identically distributed for a group of well-solved solutions.
 |
Fig. 15. Density maps of mean values. Top: ρμα*, ϖ against visibility_periods_used. Bottom: ρμδ, ϖ against visibility_periods_used, calculated in spherical cells of 1.8 × 1.8 deg2. The colour bar represents the number of spherical cells in a pixel. |
 |
Fig. 16. Density map of correlation coefficients, ρμα*, ϖ and ρμδ, ϖ. Top: 232 318 sources with the number of visibility periods under 12. Middle: 169 745 sources with the number of visibility periods in the domain [13, 16]. Bottom: 67 296 sources with the number of visibility periods over 17. The colour bar represents the number of quasars in a pixel. |
6.3. Examination of asymmetric distributions
We checked whether the centrally asymmetric distributions shown in Fig. 16 would bias the astrometric parameters of quasars. Mean values of the normalised proper motion difference Xpm are more precise than mean values of the parallaxes, since Xpm is obtained from two astrometric parameters. Thus, we investigated Xpm of these subsets. Here, we introduced a new variable
where −0.06 represents the mean value of ρμδ, ϖ of the full sample. The variable ρμ, ϖ describes the difference between a quasar and the centre of the density map (see Fig. 11). Then a set of quasars is divided into two new sets according to ρμ, ϖ. If the asymmetric distributions have little influence on the astrometric parameters, mean values of Xpm in all three sets should be coincident with the theoretical mean value of a standard Rayleigh distribution.
Mean values, as well as their standard deviations of Xpm, are presented in Table 2. Sample A represents the full sample. Remaining samples are divided by the number of visibility periods. Sample B contains 232 318 sources with fewer than 12 visibility periods, while sample C has 169 745 sources with the number of visibility periods in the domain [13, 16]. Sample D consists of 67 296 sources with the number of visibility periods more than 17. It is obvious that for well-distributed samples (A and C), the mean values of Xpm are stable and close to 1.2533, the mean value of a standard Rayleigh distribution. Two subsets of sample B have two distinct mean values of Xpm, while subsets of sample D have mean values close to each other. However, the mean values of subsets of sample D are not consistent with the theoretical value considering the uncertainties. Table 2 illustrates that sources with visibility periods in the domain [13, 16] are better solved.
Statistic parameters of different samples.
6.4. Magnitude and colour dependences
Here, we presented a simple examination on physical properties, magnitudes, and colours. The parameter phot_g_mean_mag is adopted as the magnitude Gmag. The density maps of correlation coefficients, ρμα*, ϖ and ρμδ, ϖ, against different magnitudes, are plotted in Fig. 17. Then, we adopted the parameter bp_rp as the colour index GBP − GRP (for the definition of these passbands, see Riello et al. 2018) and plotted density maps of correlation coefficients against the colour index in Fig. 18. All panels in these two figures present similar patterns to those we found in Fig. 16. In the top-right panel of Fig. 17, even if there are a few quasars around the panel centre, most of the quasars gather around the lower part of the panel. It is obvious that sources with visibility periods in the domain [13, 16] are generally well-distributed regardless of magnitude or colour.
 |
Fig. 17. Density map of correlation coefficients, ρμα*, ϖ and ρμδ, ϖ. Left: sources with the number of visibility periods under 12. Middle: sources with the number of visibility periods in the domain [13, 16]. Right: sources with the number of visibility periods over 17. The colour bar represents the number of quasars in a pixel. Top panels and bottom panels: subsets divided by the magnitude, respectively. |
 |
Fig. 18. Density map of correlation coefficients, ρμα*, ϖ and ρμδ, ϖ. Left: sources with the number of visibility periods under 12. Middle: sources with the number of visibility periods in the domain [13, 16]. Right: sources with the number of visibility periods over 17. The colour bar represents the number of quasars in a pixel. Top panels and bottom panels: subsets divided by the colour, respectively. |
7. Discussion and conclusion
Dependences of the astrometric parameters on different quality indicators are described through the mean parallax, the standard deviations of the normalised debiased parallaxes, and the normalised proper motion difference Xpm. Some departures of the astrometric parameters against various indicators are found. The astrometric parameters of quasars with the number of visibility periods under 9 or over 18 show a departure from the global average. Moreover, the mean values of astrometric parameters of the most precise sources analysed show an obvious deviation from those of the full sample.
The correlation coefficients, ρμα*, ϖ and ρμδ, ϖ, show a generally ideal distribution for the full sample. Spherical-cell averages of ρμα*, ϖ and ρμδ, ϖ show a centrally asymmetric distribution. Distributions of ρμα*, ϖ and ρμδ, ϖ with respect to different quality indicators are studied. These centrally asymmetric distributions give a probable interpretation on departures of the astrometric parameters against different indicators. The scanning law brings an important effect that quasars with the number of visibility periods in the domain [13, 16], with ρμα*, ϖ and ρμδ, ϖ well distributed, have more reliable astrometric parameters. Thus, it is preferable to check the distribution of the correlation coefficients if the astrometric solutions of a group of quasars are investigated. Magnitudes and colours of quasars have little influence on the centrally asymmetric patterns of the correlation coefficients found.
Due to the limit of the sample, spherical cells near the galactic plane and Magellanic clouds are not investigated. Results obtained are valid for the quasars and spherical cells analysed. Besides parallaxes and proper motions, the celestial coordinates may also be affected by the centrally asymmetric distributions of the correlation coefficients. In the absence of a reliable external reference for the positions of all quasars, the possibility of examining the true errors in position is limited. Given that the positions are derived from the same data as the other parameters, we expect the situation of the positions to be similar to the other parameters (Gaia Collaboration 2018b). More work needs to be done on the declinations and right ascensions of these quasars with the help of VLBI (Charlot 2019) in the future.
Acknowledgments
We thank the anonymous referee for constructive comments on the original version of the manuscript. This work has made use of data from the European Space Agency (ESA) mission Gaia (http://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, http://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This work is funded by the National Natural Science Foundation of China (NSFC) under grant No. 11833004.
References
- Charlot, P. 2019, 30th IAU General Assembly [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018a, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Mignard, F., et al.) 2018b, A&A, 616, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Holl, B., Lindegren, L., & Hobbs, D. 2010, EAS Pub. Ser., 45, 117 [CrossRef] [Google Scholar]
- Kovalevsky, J. 2003, A&A, 404, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, J. C., Capitaine, N., Lambert, S. B., Malkin, Z., & Zhu, Z. 2012, A&A, 548, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacMillan, D. S., Fey, A., Gipson, J. M., et al. 2019, A&A, 630, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignard, F., & Klioner, S. 2012, A&A, 547, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignard, F., Klioner, S., Lindegren, L., et al. 2016, A&A, 595, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrov, L., Kovalev, Y. Y., & Plavin, A. V. 2019, MNRAS, 482, 3023 [NASA ADS] [CrossRef] [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2018, A&A, 616, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titov, O., & Lambert, S. 2013, A&A, 559, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titov, O., & Krásná, H. 2018, A&A, 610, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Relation between the number of visibility periods and field-of-view transits (matched observations) per quasar in Gaia-CRF2. Like Fig. 2 of Lindegren et al. (2018), a small random number was added to the integer number of visibility periods to widen the vertical bars. The black line through each bar shows the location of the median. The red solid line is equal to 1.8 times the visibility periods. |
| In the text | |
 |
Fig. 2. Distribution of normalised proper motion difference Xpm for all Gaia-CRF quasars in linear scale (top) and logarithmic scale (bottom). The black curve is a standard Rayleigh distribution. |
| In the text | |
 |
Fig. 3. Top: mean values of parallaxes plotted against number of visibility periods. Middle: standard deviations of the normalised centred parallaxes plotted against the number of visibility periods. Bottom: mean values of normalised proper motion difference Xpm plotted against the number of visibility periods. Dashed lines represent the mean values of the full sample. |
| In the text | |
 |
Fig. 4. Sample sizes plotted against number of visibility periods. |
| In the text | |
 |
Fig. 5. Top: mean values of parallaxes plotted against σ5d, max. Middle: standard deviations of the normalised centred parallaxes plotted against σ5d, max. Bottom: mean values of normalised proper motion difference Xpm plotted against σ5d, max. Dashed lines represent the mean values of the full sample. Horizontal error bar represents the standard deviation of σ5d, max in subsets. Sources are sorted by σ5d, max and divided into subsets. Each dot above is calculated in bins of 10 000 sources, except for the last one containing 6869 quasars. |
| In the text | |
 |
Fig. 6. Top: mean values of parallaxes plotted against unit weight error. Middle: standard deviations of the normalised centred parallaxes plotted against the unit weight error. Bottom: mean values of normalised proper motion difference Xpm plotted against the unit weight error. Dashed lines represent the mean values of the full sample. Horizontal error bar represents the standard deviation of the unit weight error in subsets. Sources are sorted by the unit weight error u and divided into subsets. Each dot above is calculated in bins of 10 000 sources. The greatest 16 869 sources are not displayed due to the axis range. |
| In the text | |
 |
Fig. 7. Summary statistics for full quasar sample. Top: number of visibility periods used. Middle: σ5d, max. Bottom: unit weight error u. These maps use a Mollweide projection in equatorial (ICRS) coordinates, with origin α = δ = 0 at the centre, and α increasing from right to left. The values are calculated in spherical cells of about 1.8 × 1.8 deg2. Empty cells as well as cells with sources no more higher than ten are shown in dark blue. |
| In the text | |
 |
Fig. 8. Distribution of quasar density in 11170 spherical cells. There are 12288 spherical cells overall, with 11170 cells containing quasars, 10409 cells with more than 10 quasars. |
| In the text | |
 |
Fig. 9. Distribution of standard deviation of visibility_periods_used in 10409 spherical cells. For 8977 cells, about 86% of cells analysed, standard deviations are smaller than 1.5. |
| In the text | |
 |
Fig. 10. Summary statistics for the full quasar sample. Top: ρμα*, ϖ. Bottom: ρμδ, ϖ. These maps use a Mollweide projection in Ecliptic coordinates. The values are calculated in spherical cells of about 1.8 × 1.8 deg2. Empty cells as well as cells with sources no more than 10 are shown in dark blue. |
| In the text | |
 |
Fig. 11. Top and right: probability density histograms of ρμα*, ϖ and ρμδ, ϖ of the full quasar sample, respectively. Bottom: density map of the full quasar sample. The colour bar represents the number of quasars in a pixel. The black curve represents the curve fitting with a Gaussian model. |
| In the text | |
 |
Fig. 12. Top and right: histograms of mean values of ρμα*, ϖ and ρμδ, ϖ of the spherical cells, respectively. Bottom: the density map of mean values of two correlation coefficients, ρμα*, ϖ and ρμδ, ϖ, calculated in spherical cells of 1.8 × 1.8 deg2. The colour bar represents the number of spherical cells in a pixel. |
| In the text | |
 |
Fig. 13. Density maps of mean values. Top: ρμα*, ϖ against σ5d, max. Bottom: ρμδ, ϖ against σ5d, max, calculated in spherical cells of 1.8 × 1.8 deg2. The colour bar represents the number of spherical cells in a pixel. |
| In the text | |
 |
Fig. 14. Density map of correlation coefficients, ρμα*, ϖ and ρμδ, ϖ. Top: 10 000 most precise sources. Bottom: top 100 001–110 000 precise sources. The colour bar represents the number of quasars in a pixel. |
| In the text | |
 |
Fig. 15. Density maps of mean values. Top: ρμα*, ϖ against visibility_periods_used. Bottom: ρμδ, ϖ against visibility_periods_used, calculated in spherical cells of 1.8 × 1.8 deg2. The colour bar represents the number of spherical cells in a pixel. |
| In the text | |
 |
Fig. 16. Density map of correlation coefficients, ρμα*, ϖ and ρμδ, ϖ. Top: 232 318 sources with the number of visibility periods under 12. Middle: 169 745 sources with the number of visibility periods in the domain [13, 16]. Bottom: 67 296 sources with the number of visibility periods over 17. The colour bar represents the number of quasars in a pixel. |
| In the text | |
 |
Fig. 17. Density map of correlation coefficients, ρμα*, ϖ and ρμδ, ϖ. Left: sources with the number of visibility periods under 12. Middle: sources with the number of visibility periods in the domain [13, 16]. Right: sources with the number of visibility periods over 17. The colour bar represents the number of quasars in a pixel. Top panels and bottom panels: subsets divided by the magnitude, respectively. |
| In the text | |
 |
Fig. 18. Density map of correlation coefficients, ρμα*, ϖ and ρμδ, ϖ. Left: sources with the number of visibility periods under 12. Middle: sources with the number of visibility periods in the domain [13, 16]. Right: sources with the number of visibility periods over 17. The colour bar represents the number of quasars in a pixel. Top panels and bottom panels: subsets divided by the colour, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \begin{aligned} X^2_\mathtt{pm}&= \boldsymbol{\Delta \mu }^\mathrm{T} \ \boldsymbol{\Sigma }^{-1} \ \boldsymbol{\Delta \mu }\\&=\left[ \begin{matrix} \Delta \mu _{\alpha ^*} \\ \Delta \mu _{\delta } \end{matrix} \right]^\mathrm{T} \left[ \begin{matrix} \sigma _{ \mu _{\alpha ^*}}^2&\rho _{\mu _{\alpha ^*},\ \mu _{\delta }} \sigma _{ \mu _{\alpha ^*}} \sigma _{ \mu _{\delta }} \\ \rho _{\mu _{\alpha ^*},\ \mu _{\delta }} \sigma _{ \mu _{\alpha ^*}} \sigma _{ \mu _{\delta }}&\sigma _{ \mu _{\delta }}^2 \end{matrix} \right]^{-1} \left[ \begin{matrix} \Delta \mu _{\alpha ^*} \\ \Delta \mu _{\delta } \end{matrix} \right] , \end{aligned} \end{aligned} $$](/articles/aa/full_html/2020/03/aa37416-19/aa37416-19-eq4.gif)
![$$ \begin{aligned} \begin{aligned} \boldsymbol{\Delta \mu }&=\left[ \begin{matrix} \Delta \mu _{\alpha ^*} \\ \Delta \mu _{\delta } \end{matrix} \right] = \boldsymbol{\mu }_{ Gaia} - \boldsymbol{\mu }_{\rm apparent} = \left[ \begin{matrix} \mu _{\alpha ^*, Gaia} - \mu _{\alpha ^*, \mathrm{apparent}} \\ \mu _{\delta , { Gaia}} - \mu _{\delta , \mathrm{apparent}} \end{matrix} \right] . \end{aligned} \end{aligned} $$](/articles/aa/full_html/2020/03/aa37416-19/aa37416-19-eq5.gif)
![$$ \begin{aligned} \begin{aligned} \boldsymbol{\mu }_{\rm apparent}&=\left[ \begin{matrix} \mu _{\alpha ^*, \mathrm{apparent}} \\ \mu _{\delta , \mathrm{apparent}} \end{matrix} \right] \\&=\left[ \begin{matrix} -\sin \alpha&\cos \alpha&0 \\ -\cos \alpha \sin \delta&-\sin \alpha \sin \delta&\cos \delta \end{matrix} \right] \left[ \begin{matrix} G_1 \\ G_2 \\ G_3 \end{matrix} \right] , \end{aligned} \end{aligned} $$](/articles/aa/full_html/2020/03/aa37416-19/aa37416-19-eq6.gif)
![$$ \begin{aligned} \begin{aligned} \rho _{\mu ,\ \varpi } = [ \rho ^2_{\mu _{\alpha ^*},\ \varpi } + (\rho _{\mu _{\delta },\ \varpi } - (- 0.06) )^2]^{1/2} , \end{aligned} \end{aligned} $$](/articles/aa/full_html/2020/03/aa37416-19/aa37416-19-eq7.gif)