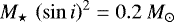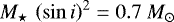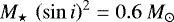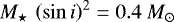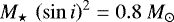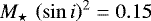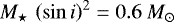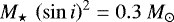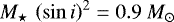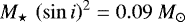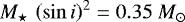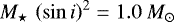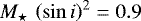| Issue |
A&A
Volume 635, March 2020
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 24 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201936798 | |
| Published online | 02 March 2020 | |
Searching for kinematic evidence of Keplerian disks around Class 0 protostars with CALYPSO
1
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
e-mail: sebastien.maret@univ-grenoble-alpes.fr
2
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris Diderot,
Sorbonne Paris Cité,
91191
Gif-sur-Yvette,
France
3
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
4
LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Université, UPMC Université Paris 06,
75014
Paris, France
5
INAF – Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5,
50125
Firenze, Italy
6
Institut de Radioastronomie Millimétrique (IRAM),
38406
Saint-Martin-d’Hères, France
Received:
27
September
2019
Accepted:
6
January
2020
The formation of protoplanetary disks is not well understood. To understand how and when these disks are formed, it is crucial to characterize the kinematics of the youngest protostars at a high angular resolution. Here we study a sample of 16 Class 0 protostars to measure their rotation profile at scales from 50 to 500 au and search for Keplerian rotation. We used high-angular-resolution line observations obtained with the Plateau de Bure Interferometer as part of the CALYPSO large program. From 13CO (J = 2−1), C18O (J = 2−1) and SO (Nj = 56−45) moment maps, we find that seven sources show rotation about the jet axis at a few hundred au scales: SerpS-MM18, L1448-C, L1448-NB, L1527, NGC 1333-IRAS 2A, NGC 1333-IRAS 4B, and SVS13-B. We analyzed the kinematics of these sources in the uv plane to derive the rotation profiles down to 50 au scales. We find evidence for Keplerian rotation in only two sources, L1527 and L1448-C. Overall, this suggests that Keplerian disks larger than 50 au are uncommon around Class 0 protostars. However, in some of the sources, the line emission could be optically thick and dominated by the envelope emission. Due to the optical thickness of these envelopes, some of the disks could have remained undetected in our observations.
Key words: protoplanetary disks / stars: formation / stars: protostars
© S. Maret et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Protoplanetary disks are the birth site of planetary systems. Determining how and when these disks are formed is, therefore, important for understanding the formation of planetary systems. Protoplanetary disks are ubiquitous around Class II young stellar objects. Continuum observations at millimeter to infrared wavelengths indicate that their radii comprise between a few tens and a few hundreds of au (see Williams & Cieza 2011, for a review), but recent ALMA surveys also find disks with smaller radii (e.g., Long et al. 2019). Millimeter line observations show that the gas around these disks is in Keplerian motion (e.g., Simon et al. 2000) and, therefore, these disks are rotationally supported. Disks are also common around Class I protostars (e.g., Brinch et al. 2007; Takakuwa et al. 2012; Lee et al. 2016). However, disks around the youngest Class 0 protostars are more difficult to observe. Because these objects are the youngest accreting protostars, most of their mass is still in the form of an envelope (André et al. 1993, 2000; Dunham et al. 2014), which makes the detection of a disk challenging. Yet the observation and the characterization of disks around young embedded protostars are key to understanding the formation of disks.
In the absence of magnetic fields, disks are expected to form and to grow quickly as a consequence of angular momentum conservation during the rotating collapse of the protostellar envelope (Terebey et al. 1984; Yorke & Bodenheimer 1999). However, magnetic fields can redistribute angular momentum from small to large scales efficiently (through so-called magnetic braking). Early magneto-hydrodynamical (MHD) simulations (in the ideal limit) have shown that the disk formation is hampered, even for modest values of the magnetic flux (Allen et al. 2003; Galli et al. 2006; Hennebelle & Fromang 2008; Mellon & Li 2008). More recent simulations that consider non-ideal MHD effects, radiative transfer, turbulence, and different initial conditions (such as the misalignment between the magnetic field and the rotation axis) now predict the formation of small (with a radius of a few tens of au) disks during the Class 0 phase (e.g., Hennebelle et al. 2016).
Observational evidence for disks around Class 0 protostars is still scarce. Jørgensen et al. (2009) observed a sub-millimeter continuum emission excess, mostly unresolved within the Submillimeter Array (SMA) beam, in a sample of Class 0 protostars that they attributed to disk emission. Yen et al. (2015a) used SMA observations to derive the rotation of a sample of 17 protostars on 1000 au scales. Assuming that the specific angular momentum was conserved during the collapse, they derived centrifugal radii comprised between 5 and 500 au. However, the spatial resolution of their observations is not sufficient for the detection of Keplerian rotation within the centrifugal radius. So far, direct evidence of Keplerian motions has only been found in a few Class 0 protostars and that is thanks to high resolution (sub-)millimeter interferometric observations: L1527, a border-line Class 0 object (Tobin et al. 2012b; Ohashi et al. 2014; Aso et al. 2017, disk radius of 74 au), VLA1623, the prototypical Class 0 protostar (Murillo et al. 2013, disk radius of 150 au), HH212 (Codella et al. 2014; Lee et al. 2014, disk radius of 90–120 au), L1448-IRS3 (Tobin et al. 2016a, disk radius of ~400 au), Lupus 3 MMS (Yen et al. 2017, disk radius of 100 au), and IRAS 16253-2429 (Hsieh et al. 2019, disk radius of 8–32 au). On the other hand, no disks have been detected at scales larger than 100 au in NGC 1333-IRAS 2A (Maret et al. 2014) and 10 au in B335 (Yen et al. 2015b). Therefore, it is still unclear if Keplerian disks are common around Class 0 protostars.
In this paper, we present high-angular millimeter line interferometric observations of a sample of 16 Class 0 protostars obtained with the IRAM Plateau de Bure interferometer (hereafter PdBI) as part of the CALYPSO (Continuum and Line from Young Protostellar Objects) survey. CALYPSO is an IRAM Large Program (PI: Philippe André) that consists of line and continuum observations towards a large sample of nearby (d < 436 pc) Class 0 protostars that aims to understand the angular momentum problem1. Here we use line observations to measure the rotation at scales between 50 and 500 au and to determine whether Keplerian disks are present in these objects. In a recent paper, Maury et al. (2019) study the continuum emission in the same sample to determine if disk-like structures are present. A companion paper focuses on the rotation of the envelopes on scales up to 5000 au (Gaudel et al. 2020).
Source sample.
2 Observations
Observations were carried out with the PdBI between September 2010 and March 2013 as part of CALYPSO2. We observed a sample of 16 Class 0 protostars located in the Taurus, Perseus, Serpens, and Aquila molecular cloud complexes at distances between 140 and 436 pc. Table 1 gives the continuum peak positions, distances, internal luminosities, envelope masses, and flux densities at 1.4 mm of the sources. Our sample covers a wide range of internal luminosities and envelope masses and should, therefore, be representative of the whole population of Class 0 protostars.
We used the configurations A and C of the array, which provide baselines3 between 15 and 760 m. In this study, we focus on the 13CO (2−1) (220.398 684 GHz), C18O (2−1) (219.560 354 GHz) and SO (56−45) (219.949 442 GHz) line emission. Previous studies have shown that these lines are good tracers of disks in Class 0 protostars (Tobin et al. 2012b; Murillo et al. 2013; Ohashi et al. 2014; Sakai et al. 2014). These three lines were observed simultaneously using the 1.3 mm receivers connected to the narrow-band backend with a bandwidth of 512 channels of 39 kHz (0.05 km s−1) each.
The data were calibrated and reduced using the GILDAS software package (Gildas Team 2013). For sources with a continuum peak flux density higher than 80 mJy, the line observations were self-calibrated using the continuum visibilities4. Other sources were calibrated using strong quasars only. To improve the signal-to-noise ratio (S/N), all line observations were re-sampled to a spectral resolution of 0.2 km s−1. Imaging was done using robust weighting with a robust parameter of 1. Typical synthesized beam sizes are 0.7″ (HPBW), which corresponds to linear scales between 100 and 300 au, depending on the source distance. The sensitivity of the line observations is between 10 and 24 mJy per 0.2 km s−1 channel depending on the source. Synthesized beams and sensitivities for each line are given in Appendix A.1.
3 Results
3.1 Overview of the sample
Figure 1 shows the zeroth-order moment (integrated intensity) and first-order moment (mean velocity) maps of the 13CO (2−1), C18O (2−1) and SO (56−45) lines, together with the 1.4 mm continuum emission maps from Maury et al. (2019) in L1448-NB, L1448-C, NGC 1333-IRAS 2A, and L1527. The same figures for the other sources of the sample are shown in Appendix B (Figs. B.1–B.3). The moments are computed using all spectral channels with emission above 5σ. In these figures, we also show for each source, the jet axis as derived from CALYPSO observations (Podio et al., in prep.). As seen in the zeroth-order moment maps, 13CO (2−1) emission is detected in all sources except L1521F, which is, together with IRAM 04191, the lowest luminosity source of our sample. C18O (2−1) is also detected in most sources, except IRAM 04191, L1521F, and GF9-2. Finally, we detect SO (56−45) emission in five sources: NGC 1333-IRAS 2A, NGC 1333-IRAS 4A, NGC 1333-IRAS 4B, L1527, and SerpS-MM18. The morphology of the emission varies from one source and line to the other and can be classified into three broad categories: (1) extended emission with respect to the continuum emission (e.g., the C18O (2−1) emission in NGC 1333-IRAS 2A), (2) compact emission centered on continuum emission (e.g., the 13CO (2−1) emission in L1527), and (3) bi-polar emission from the outflow (e.g., SO (56−45) in NGC 1333-IRAS 2A). For most sources, the 13CO (2−1) and C18O (2−1) line emissions fall into the first two categories. On the other hand, the SO (56−45) emission, when detected, falls into the third category for most sources, with the notable exception of L1527.
Most lines and sources show clear velocity gradients (as seen from the first-order moment maps), which could be due to the rotation of the envelope or a disk, or to the radial motion of the bipolar outflow. In order to determine the origin of these gradients, we fit the first-order moment map of each line with a linear gradient (Goodman et al. 1993):
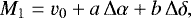 (1)
(1)
where M1 is the first-order moment, Δα and Δδ are the RA and declination offsets from the continuum peak position, and v0, a and b are the fitted parameters. A linear gradient is expected for a spherical envelope rotating as a solid body. Although solid-body rotation may be a crude approximation, such a fit provides a rough estimate of the velocity gradient amplitude and its orientation, and it is useful to determine the origin of the emission (see, e.g., Yen et al. 2015a). To perform these fits, we compute, for each pixel of in the image plane, the first-order moment and its uncertainty (see Belloche 2013, Eq. (2.3)), ignoring channels with emission lower than 5σ. Because the datacubes produced by the interferometer are over-sampled spatially, only two points per synthesized beam are fitted to ensure Nyquist sampling. Since we are interested in measuring the rotation of the innermost regions of the protostar (and in turn to determine if a disk is present), we consider pixels within a radius of 2″ from the continuum peak. This corresponds to a maximum radius from 300 to 1000 au depending on the source distance. The velocity gradient amplitude is given by:
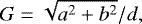 (2)
(2)
where d is the source distance. The position angle of the gradient, measured from north to east, is:
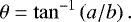 (3)
(3)
Table 2 gives the values of G, v0 and θ that we obtain. The gradient orientations are also shown in Figs. 1 and B.1–B.3. In Table 2 we also report the difference between the velocity gradient orientation and the direction perpendicular to the jet, which we note as Δθ. A value close to 0° is expected if the velocity gradient is due to the rotation of the envelope or a disk, while a value close to 90° indicates that the gradient is mostly due to the outflow, or infall in a flattened geometry. Based on these values, we selected a sample of disk candidates in which Δθ < 45° for at least one line5. According to this criterion, we find seven disk candidates: L1448-NB, L1448-C, NGC 1333-IRAS 2A, SVS13B, NGC 1333-IRAS 4B, L1527 and SerpS-MM18. In the following, we analyze the line kinematics of these sources to derive rotation curves down to 50 au scales. The results for L1527, L1448-NB, and L1448-C are presented in Sect. 3.2. The results for the other disk candidates are presented in Appendix C.
3.2 Disk candidates
3.2.1 L1527
L1527 is a border-line Class 0 protostar (Ladd et al. 1991; André et al. 2000) located in the Taurus molecular cloud at a distance of 140 pc (Loinard et al. 2007)6. The protostar internal luminosity is0.9 L⊙ (Ladjelate et al., in prep.) and its envelope mass is 1.2 M⊙ (Motte & André 2001). The blue-shifted lobe PA of L1527 jet is 90° (Podio et al., in prep.). L1527 is the first Class 0 protostar in which a Keplerian disk was claimed. Tobin et al. (2012b) observed the 13CO (2−1) line emission with the CARMA interferometer and suggest that the rotation profile of the inner envelope is consistent with Keplerian rotation (v ∝ r−0.5). Yen et al. (2013)
observed the C18O (2−1) line emission using the SMA interferometer and find that the rotation profile is best-fitted with v ∝ r−1 suggesting rotation andinfall with conservation of the angular momentum. Sakai et al. (2014) used ALMA cycle 0 observations of SO and cyclic-C3H2 line emission to find that SO is only present inside a 100 au region in radius, while the cyclic-C3H2 is present only outside. They interpret these observations as a change of the gas chemical composition at the centrifugal barrier, where the transition between the rotating and infalling envelope and the disk is expected to occur. Ohashi et al. (2014) used ALMA cycle 0 observations of the C18O (2−1) line emission to study the envelope or disk kinematics. They find a rotation profile of v ∝ r−1.2 from the C18O (2−1) line down to 50 au scales but suggest a possible transition to Keplerian rotation at smaller scales. Using ALMA cycle 1 observations, Aso et al. (2017) have recently confirmed Keplerian rotation at r < 56 au. The disk of L1527 is nearly edge-on (Tobin et al. 2008; Oya et al. 2015).
The bottom row of Fig. 1 shows the 1.4 mm continuum emission map together with the 13CO (2−1), C18O (2−1) and SO (56−45) zeroth and first-order moment maps in L1527. The continuum emission is resolved spatially, and it appears to be slightly elongated along a north-south axis. The 13CO (2−1), C18O (2−1), and SO (56−45) line emissions are all well detected and are spatially coincident with the continuum emission. The C18O (2−1) emission is more extended than the 13CO (2−1) emission. The 13CO (2−1) is more extended than the SO (56−45) emission. The emission of each line is extended along a north-south axis and has a well-defined velocity gradient. For all lines, the gradients are oriented along an axis roughly orthogonal to the red-shifted lobe of the jet, with Δθ of 5°, 36°, and 12° for the 13CO (2−1), C18O (2−1) and SO (56−45) lines, respectively.
The orientation of the gradients suggests that these lines probe the rotation of the envelope or the disk. To better quantify this rotation, we build a rotation curve from each line. Because the size of SO (56−45) emission is only slightly larger than the size of the synthesized beam, we construct the rotation curves from the measured visibilities rather than the image cubes or the PV diagrams (as done, e.g., by Yen et al. 2015a). This technique, which was also used by Codella et al. (2014) in their study of HH212 (see also Lindberg et al. 2014), allows us to constrain the velocity curve at scales smaller than the synthesized beam and it is also insensitive to potential deconvolution artifacts. A test of the robustness of this technique in recovering accurate velocity profiles is presented in Appendix D. In practice, we fit the position of the line emission in the uv plane with a circular Gaussian7. Because we are interested inthe disk emission rather than the emission of the envelope or the outflow, we ignore channels where the FWHM emission size is greater than 2″ and channels with a centroid position that is farther away than 1.5″ from the continuum peak. In addition, we ignore channels with centroid positions that are not along the assumed disk major axis, within 3σ. For this source, we assume a disk majoraxis PA of 1.5° (Aso et al. 2017).
Figure 2 shows for each line the centroid position in each channel, together with the zeroth-order moment map. We see that the centroid positions for each line are relatively well aligned with the assumed disk major axis. The velocity gradient is also apparent in this figure: for all lines, the centroids of the blue-shifted channels arelocated south of the continuum peak position, while the centroids of the red-shifted channels are located north of it. To determine the rotation curves for each line, we compute the offset from the source center by projecting the centroid position in each channel onto the assumed disk axis. Figure 3 shows the positionoffset as a function of the absolute value of the velocity difference from the systemic velocity vsys. For the latter, we adopt the same value as Ohashi et al. (2014), i.e., 5.9 km s−1. In this figure, we see that for both the 13CO (2−1) and C18O (2−1) lines, the position offset from the continuum peak decreases while |v −vsys| increases, indicating that the gas probed by these lines rotates faster as it gets closer to the continuum peak. The SO (56−45) line shows the same trend for high-velocity channels. For low-velocity channels, the position offset increases roughly linearly as |v −vsys| increases, asalso observed by Ohashi et al. (2014).
Then, we fit the velocities as a function of position with a power-law:
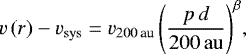 (4)
(4)
where p is the position offset in arcseconds (counted as positive on the red-shifted side of the emission, and as negative on the other side), d is the source distance in pc, β is the power-law exponent, and v200 au is the projected velocity at 200 au from the center. Both β and v200 au are left as free parameters. For the SO (56−45) fit, we ignore channels between 4.8 and 7.2 km s−1 because, as mentioned above, the low-velocity channels cannot be fitted with the same velocity curve as the high-velocity channels.
The best-fit results are shown as solid lines in Fig. 3. The best-fit values of v200 au and β, and the reduced χ2, are given in Table 3. The best-fit value of β is − 1.11 ± 0.07, − 1.88 ± 0.17, and − 0.57 ± 0.12 for the 13CO (2−1), C18O (2−1), and SO (56−45) lines, respectively. Therefore, the velocity curve we derive from the SO (56−45) line emission is consistent with Keplerian rotation (β = −0.5). Fitting the SO (56−45) position in each channel with a Keplerian law:
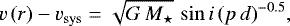 (5)
(5)
where G is the gravitational constant, M⋆ is the central mass and i is the disk inclination, we obtain 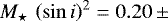 0.01 M⊙.
0.01 M⊙.
In Fig. 3, we also show the velocity curve obtained by Aso et al. (2017) from C18O (2−1) observations. These authors derive a power-law exponent of −0.50 at radii smaller than 56 au, and −1.22 beyond. The double power-law agrees well with our 13CO (2−1) and C18O (2−1) observations. However, our SO (56−45) observations are better reproduced with a single power law or a Keplerian law for a central mass of 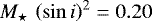 M⊙. The lowest velocity channel that is consistent with the Keplerian velocity curve is at a position offset of about 0.65″, that is, a radius of 90 au.
M⊙. The lowest velocity channel that is consistent with the Keplerian velocity curve is at a position offset of about 0.65″, that is, a radius of 90 au.
In Fig. 4, we show position-velocity (PV) cuts through the position of the L1527 continuum peak along the assumed disk axis, for the 13CO (2−1), C18O (2−1), and SO (56−45) lines. The PV diagrams for the 13CO (2−1) and C18O (2−1) lines indicate both infall and rotation (see, e.g., Tobin et al. 2012a). On the other hand, the PV diagram for the SO (56−45) is consistent with rotation alone. On these diagrams, we also show the power-law velocity curves we obtain for each of these lines with a fit in the uv plane. We see that the velocity curves provide a good fit to the emission peak in each velocity channel. For each diagram, we also plot the outermost Keplerian curve that is tangential to the first emission contour, with a 6σ threshold8 (see Seifried et al. 2016; Ginsburg et al. 2018, for a justification of the method). We obtain 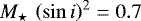 M⊙, 0.6 M⊙ and 0.4 M⊙ for the 13CO (2−1), C18O (2−1), and SO (56−45) lines, respectively.
M⊙, 0.6 M⊙ and 0.4 M⊙ for the 13CO (2−1), C18O (2−1), and SO (56−45) lines, respectively.
To summarize our findings for this source, we find evidence for Keplerian rotation, but with the SO (56−45) line only. Both the 13CO (2−1) and C18O (2−1) line emission appear to be dominated by the rotation and infall of the envelope. Keplerian rotation is observed with the SO (56−45) line at r ≤ 90 au. As discussed in Appendix D, a Keplerian fit in the uv plane gives a lower limit on the mass M⋆ of the central object, while a fit of the first contours in PV diagrams gives an upper limit. By combining these two techniques and assuming a disk inclination of 85° (Tobin et al. 2008), we obtain 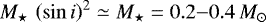 .
.
 |
Fig. 1 1.4 mm continuum emission, integrated intensities and mean velocities of the 13CO (2−1), C18O (2−1) and SO (56−45) lines in L1448-NB, L1448-C, NGC 1333-IRAS 2A, and L1527. Left panels: the 1.4 mm continuum emission. Other panels: the line mean velocities (first-order moment; background image), together with theline integrated intensities (zeroth-order moment; black contours). Contours are drawn at −3σ (dotted lines) 3σ, 6σ, 12σ and so on (solid lines). In each panel, the black crosses show the position of the main continuum peak(s). The blue and red lines in the left panels indicate the direction of the blue- and red-shifted lobes of the jet(s), respectively. The arrows in other panels indicate the direction of the velocity gradient, as determined from a linear fit of the mean velocity within 2″ of the continuum peak position. The gray sectors around each arrow show the 1σ uncertainty on the direction of the velocity gradient. The ellipse in each panel shows the synthesized beam. All coordinates are relative to the positions of the brightest continuum peak of each source (see Table 1). |
Results of linear fit of the mean velocity for each line.
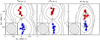 |
Fig. 2 Results of the fits in the uv plane for each spectral channel (circles with error bars) superimposed on zeroth-order moment map (black contours) in L1527 for the 13CO (2−1) (left panel), C18O (2−1) (middle panel), and SO (56−45) (right panel)lines. Contours are drawn at 3σ, 6σ, 12σ, and so on. Blue and red points show the centroid positions of the blue-shifted and red-shifted channels, respectively. Only filled points are considered when constructing the velocity curves; open points are ignored. The thick black lines connect the centroids that correspond to adjacent velocity channels. Black crosses show the position of the continuum peak, while the dashed line shows the assumed disk major axis. |
 |
Fig. 3 Position offset derived in the uv
plane along the disk major axis as a function of the velocity channel in L1527 for panel). In each panel the blue and red points with the error bars show the observations, the solid line shows the result of a power-law fit. The dashed line in the right panel shows the result of a fit with a Keplerian law with
|
Results of the rotation curve fits for the disk candidates.
 |
Fig. 4 Position velocity cuts in the image plane through the L1527 continuum peak along the assumed disk major axis for the 13 CO (2−1) (left panel), C18O (2−1) (middle panel), and SO (56−45) (right panel)lines. Contours are drawn at −3σ, 3σ, 6σ, 12σ
and so on. Black crosses correspond to the continuum peak. Black solid curves show the results of the velocity fit in the
uv
plane with a power-law function. Dashed lines show the result of the fit of the 6σ
contours with a Keplerian law with |
3.2.2 L1448-NB
L1448-NB (also known as L1448-IRS3B and Per-emb-33) is a Class 0 protostar (Curiel et al. 1990) located in the L1448-N complex in Perseus, at a distance of 293 pc (Ortiz-León et al. 2018). This source is a triple system, composed of L1448-NB1 (Per-emb-33 A) and a close binary, L1448-NB2. These two are separated by 260 au (0.9″; Tobin et al. 2015, 2016a; Maury et al. 2019). The two components of the binary (Per-emb-33 B and Per-emb-33 C) are separated by 80 au (0.26″; Tobin et al. 2016b) and they are unresolved with our observations. The internal luminosity of the triple system is 3.9 L⊙ (Ladejate et al., in prep.) and it is surrounded by a 4.8 M⊙ envelope (Sadavoy et al. 2014). The jet position angle is −80° (Podio et al., in prep.). Yen et al. (2015a) observed a large velocity gradient in this source orthogonal to the jet. They attribute this gradient to rotational and infall motions and derive a centrifugal radius between 410 and 900 au, that is, 1.4 and 3″. Recent ALMA 1.3 mm continuum observations have suggested the presence of one or two spiral arms that appear to originate from NB2 and extend to NB1 (Tobin et al. 2016a). The same authors observed a rotation pattern in the C18O (2−1) line emission that they interpret as Keplerian rotation of a disk around NB2, implying a central stellar mass9 of ~ 1 M⊙. In their scenario, NB1 would be the result of the gravitational fragmentation of the disk. However, Maury et al. (2019) find no evidence of continuum emission tracing a disk centered on NB2, and they suggest that the spiral structures observed by Tobin et al. trace tidal arms due to the gravitational interaction between the two components of the binary.
First-order moment maps of the 13CO (2−1), C18O (2−1), and SO (56−45) emission in L1448-NB are shown in Fig. 1. Both the 13CO (2−1) and C18O (2−1) line emissions are centered around NB2 and are elongated approximately along an axis orthogonal to the jet direction, with a well-defined velocity gradient. No SO (56−45) emission is detected in this source at a 3σ level. Fitting the first-order moment maps, we measure a gradient PA of (59 ± 7)° and (44 ± 5)° for the 13CO (2−1), and C18O (2−1) lines respectively. These correspond to angles with respect to the direction perpendicular to the jet of 49° and 34°, respectively.
Figure 5 shows the centroid positions in each velocity channel, together with the zeroth-order moment maps for the 13CO (2−1) and C18O (2−1) lines. In this figure, we also show the disk orientation measured by Tobin et al. (2016a, PA = 29.5°). The disk is assumed to be centered on NB2 because the line emission is centered on this source. The centroids of the 13CO (2−1) line are not aligned with the assumed disk axis, probably because of contamination by the outflow. On the contrary, the C18O (2−1) centroids are located close to the disk axis. The corresponding rotation curves are shown in Fig. 6. To build the rotation curves, we adopt a systemic velocity10 of 4.5 km s−1. The best-fit parameters for the rotation curve are given in Table 3. We find that the 13CO (2−1) emission is best fitted with β = −1.25 ± 1.48. This fit is uncertain because it is based on four channels only; other channels (marked with open symbols in Figs. 5and 6) are not considered in the fit because their centroids are not aligned with the assumed disk axis. Using the C18O (2−1) line emission, we find a best-fit β =−1.15 ± 0.20 for position offsets greater than ~ 0.6″, that is, r > 175 au.
PV diagrams along the assumed disk axis are shown in Fig. 7. The PV diagram for the 13CO (2−1) emission has a low S/N and, therefore, it is difficult to interpret. The PV diagram for the C18O (2−1) emission has a higher S/N and it is consistent with rotation alone (i.e., with no infall). Fitting the first contour of the C18O (2−1) emission with a Keplerian curve, we find 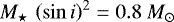 , i.e., M⋆ = 1.4 M⊙, assuming i = 45.4° (Tobin et al. 2016a). We note that the curve fits the first contour of red-shifted C18O (2−1) emission quite well, but not that of the blue-shifted emission.
, i.e., M⋆ = 1.4 M⊙, assuming i = 45.4° (Tobin et al. 2016a). We note that the curve fits the first contour of red-shifted C18O (2−1) emission quite well, but not that of the blue-shifted emission.
To summarize, we find no evidence of Keplerian rotation in this source. Instead, the rotation profile derived from the C18O (2−1) line is consistent with β = 1 for r > 175 au. We conclude that if a Keplerian disk is present in this source, its radius is smaller than 175 au.
 |
Fig. 5 Same as in Fig. 2 for L1448-NB. Black crosses show the positions of the NB1 and NB2 continuum peaks. |
3.2.3 L1448-C
L1448-C (also known as L1448-mm or Per-emb-26) is another Class 0 protostar (Anglada et al. 1989) located in the L1448-N complex in Perseus. This source is a multiple system, but with a large separation: its companion, L1448-C S (Per-emb-42), is located 8″ to the southeast (Jørgensen et al. 2006; Tobin et al. 2007; Maury et al. 2019). L1448-C itself appears as a single source at scales down to 50 au (Maury et al. 2019). Its internal luminosity is 10.9 L⊙ and its envelope mass is 2.0 M⊙ (Ladejate etal. in prep.; Sadavoy et al. 2014). L1448-C drives a prominent outflow with multiple high-velocity knots seen in CO, SO and H2O lines (Hirano et al. 2010; Kristensen et al. 2011). The blue-shifted lobe of the jet has a position angle of −17° (Podio et al., in prep.) and an inclination with respect to the plane of the sky of 21° (Girart & Acord 2001). From CARMA 1.3 mm observations, Tobin et al. (2015) find that the L1448-C continuum is elongated along a direction perpendicular to the jet, perhaps indicative of a disk-like structure. Yen et al. (2013, 2015a) measure a velocity gradient with a PA of 200°, dominated by the outflow component. Fitting only the component perpendicular to the jet, they find that the rotation profile was consistent with rotation with conservation of the angular momentum and they derive a centrifugal radius of 170–200 au.
In our maps, both the 13CO (2−1) and C18O (2−1) line emissions are extended along an axis close to the normal direction of the jet (see Fig. 1). No SO (56−45) emission is detected in the observed velocity range. Clear velocity gradients are observed in 13CO (2−1) and C18O (2−1) line mean velocity maps, and the fitted PA are 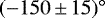 and (−111 ± 6)° for the 13CO (2−1) and C18O (2−1) lines, respectively. The corresponding values of Δθ are 43 and 4° for the 13CO (2−1) and C18O (2−1) lines, respectively.
and (−111 ± 6)° for the 13CO (2−1) and C18O (2−1) lines, respectively. The corresponding values of Δθ are 43 and 4° for the 13CO (2−1) and C18O (2−1) lines, respectively.
The results of the uv fit for these two lines are shown in Fig. 8, and the corresponding rotation curves are shown in Fig. 9. Here we use a systemic velocity11 of 5.2 km s−1 and a disk position angle of −107°, meaning that it is orthogonal to the jet axis. For the 13CO (2−1) emission, we measure the centroid positions only in a few blue-shifted channels; red-shifted channels are contaminated by the outflow emission. Only two channels have centroids that are located along the disk axis. For the C18O (2−1) emission, wemeasure the centroid positions of 9 channels, but several blue-shifted channels have centroids that are not aligned with the disk axis. For the 13CO (2−1) emission, wefind that the best-fit β value is − 0.44 ± 0.75, while for the C18O (2−1), we find β = −0.67 ± 0.09. Both rotation curves are consistent with Keplerian rotation, but the uncertainty on the β index for the 13CO (2−1) line is quite large because the fit is based on two channels only. The rotation curve we derive with the C18O (2−1) line is much better constrained, and the best-fit value of β is close to the value expected for Keplerian rotation (−0.5). From a fit with a Keplerian law, we obtain  M⊙ and
M⊙ and  M⊙ for the 13CO (2−1) and C18O (2−1) rotation curves, respectively.
M⊙ for the 13CO (2−1) and C18O (2−1) rotation curves, respectively.
Figure 10 shows the PV diagrams along the assumed disk axis. Both diagrams are consistent with rotation alone. Fitting the first emission contour with a Keplerian law, we obtain 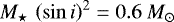 and
and 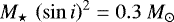 for the 13CO (2−1) and C18O (2−1) lines, respectively.
for the 13CO (2−1) and C18O (2−1) lines, respectively.
To summarize our finding for this source, we derive a velocity curve with the C18O (2−1) line that is close to Keplerian rotation. The velocity profile we derive with the 13CO (2−1) line is also consistent with Keplerian rotation, but it has a large uncertainly. Keplerian rotation is observed with the C18O (2−1) line at r < 0.7′′, that is, < 200 au. Combining the central mass obtained from the fit in the uv plane and from the PV diagram of the C18O (2−1) line, we find 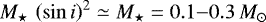 . Assuming that the disk has the same inclination as the jet (i = 21° Girart & Acord 2001), this gives M⋆ = 0.8−2.3 M⊙.
. Assuming that the disk has the same inclination as the jet (i = 21° Girart & Acord 2001), this gives M⋆ = 0.8−2.3 M⊙.
 |
Fig. 7 Same as in Fig. 4 for L1448-NB. Dashed curve shows a Keplerian curve for
|
 |
Fig. 9 Sameas in Fig. 3 for L1448-C. The dashed lines show the result of a Keplerian fit with
|
 |
Fig. 10 Same as in Fig. 4 for L1448-C. The dashed curves shows Keplerian velocity profiles with
|
4 Discussion
4.1 Evidence for disks in the CALYPSO sample
Our observations and analysis show that about half of the protostars of our sample (7 out of 16) have velocity gradients oriented close to the normal direction of the jet axis, at a few hundred au scales. These gradients are interpreted as rotation of the envelope or the disk about the jet axis. Among these sources, we detect Keplerian rotation in two sources, L1527 and L1448-C. In a third source, SVS13B, the rotation curve we derive is also consistent with Keplerian rotation, but as noted in Appendix C.2, the rotation curve for this source is very uncertain and we do not discuss it further. In L1527 and L1448-C, we estimate Keplerian radii of 90 and 200 au, and central object masses of 0.2−0.4 and 0.8−2.3 M⊙, respectively.
Our results are summarized in Table 4. In this Table we also report the results from Maury et al. (2019), who have recently used CALYPSO observations of the continuum emission at 93 GHz and 230 GHz to determine if disk-like structures are present in Class 0 protostars of the sample. For this, they have modeled the visibilities with a Plummer-like envelope density profile and an additional Gaussian component to mimic the disk emission. They find that a Gaussian component is needed in 12 protostars of the sample, but these disk-like components are spatially resolved in only six of these. The FWHM size of resolved disk-like components varies between 50 and 300 au. We also report the results from Gaudel et al. (2020) who have studied the specific angular momentum profile in CALYPSO protostellar envelopes using N2 H+ (1–0) and C18O (2−1) line observations. They find that the specific angular momentum at scales between 50 and 1200 au is conserved in eight protostars. In these protostars, the mean value of the specific angular momentum at scales < 100 au (noted as ⟨j100 au⟩) is (2− 16) × 10−4 km s−1 pc.
As seen in Table 4, all sources with a velocity gradient orth- ogonal to the jet also exhibit disk-like continuum components, except L1448-NB. However, this source is a binary and it is embedded in a 200 au circumbinary structure (Maury et al. 2019). All the sources in which we detect a velocity gradient orthogonal to the jet also have a constant specific angular momentum between 50 and 1200 au, with the exception of SerpS-MM18. Interestingly, L1527 and L1448-C, where we detect Keplerian rotation, are also among the sources with the highest ⟨j100 au⟩ values. The only source with a higher ⟨j100 au⟩ value than L1527 and L1448-C is L1448-NB, but as has already been mentioned, this source is peculiar. The Keplerian radii we derive here for L1527 and L1448-C are, respectively, ~2 and ~4 times larger than the compact continuum sources measured by Maury et al. (2019). As discussed by Maury et al. (2019), their analysis of the continuum emission is sensitive to deviation from the protostar envelope density profile, which is presumably due to the disk. Our results suggest that the gaseous disk may extend further away than the compact continuum emission. Indeed, protoplanetary disks around Class II protostars are also larger in gas emission than in millimeter continuum emission (by a factor 2 on average; Ansdell et al. 2018).
Overview of evidence of the presence of disks in the CALYPSO sample of Class 0 objects.
4.2 Rotation curves of L1527, L1448-C and L1448-NB
In L1527, we detect Keplerian rotation with the SO (56−45) line only. Both the 13CO (2−1) and C18O (2−1) lines indicate steeper velocity profiles, with β = −1.1 ± 0.1 and β = −1.9 ± 0.2, respectively.The velocity profiles we obtain with these two lines are in reasonable agreement with Aso et al. (2017), who derived a β =−1.22 at radii larger than 56 au (0.4″) and β = −0.5 at a smaller radius. Although the sensitivity and the spatial resolution of our observations are not sufficient to detect the “kink” in the velocity profile at 56 au, our observations are consistent with it, as seen in Fig. 3. Aso et al. (2017) interpreted this kink as a transition region between the infalling envelope and the Keplerian disk at r = 74 au12. Our observations and analysis of the SO (56−45) emission show that Keplerian rotation extends up to 0.7″ from the continuum peak, that is, r ~ 100 au (see Fig. 3). Sakai et al. (2014) studied the kinematics of L1527 using C3 H2 and SO (56−45) line observations. From this analysis, they estimate that the radius of the centrifugal barrier13 is 100 au. The Keplerian radius we derive from our SO (56−45) observations and analysis is in agreement with this value. Sakai et al. (2014) and Ohashi et al. (2014) argue that the SO (56−45) emission originates in a ring at the position of the centrifugal barrier. However, observations at higher angular resolution show that SO is also present inside the centrifugal barrier (Sakai et al. 2017).
A possible explanation for the differences between the disk radius derived by Aso et al. (2017) from C18O (2−1) line observations and the radius we derive from SO (56−45) line observations is the different spatial resolution of the observations. The synthesized beam size of the C18O (2−1) line observations of Aso et al. is 0.50′′× 0.40′′, while the synthesized beam size of our SO (56−45) observations is 0.72′′× 0.64′′. In principle, if the SO (56−45) line was not sufficiently resolved spatially, the transition between the two power-law regimes of the velocity profile could be blurred. However, we show in Appendix D that we can recover the velocity profile of a disk with a radius of 100 au at a distance of 293 pc, which corresponds to an apparent radius of 0.34″. This is smaller than the disk radius derived by Aso et al. (74 au at 140 pc, i.e., 0.53″). Another possible explanation is the opacity of the C18O (2−1) line. If this line is optically thick close to the systemic velocity, the Keplerian disk, which rotates faster than the envelope, would be seen only in the line wings. Closer to the source systemic velocity, the disk would be masked by the optically thick envelope. In this scenario, the change in the velocity profile at r = 56 au would be due to a change in the C18O (2−1) line opacity: optically thick for |v −vsys| < 2 km s−1, and optically thin for |v −vsys|≥ 2 km s−1. The SO (56−45) line is less affected because its critical density is higher than the critical density of the C18O (2−1) line and it is therefore excited only in the densest part of the envelope and the disk. Indeed, the opacity of the C18O (2−1) line was estimated by van ’t Hoff et al. (2018) from the 13CO (2−1) to C18O (2−1) line intensity ratio. They find that the C18O (2−1) line is optically thick in the mid-plane (see their Fig. 2). Confirming that the change in power-law index of the velocity profile at 56 au is due to the opacity of the C18O (2−1) line would require detailed modeling of the line radiative transfer, which is beyond the scope of the present paper.
In L1448-C, we detect Keplerian rotation with the C18O (2−1) line. This is the first detection of the Keplerian disk in this source. Although the rotation curve we derive with the 13CO (2−1) line is consistent with Keplerian rotation, the value of the velocity profile index β derived with this line has a large uncertainty. We estimate a Keplerian radius of 200 au and a central stellar mass between 0.8 and 2.3 M⊙. L1448-C’s disk is twice larger than L1527’s disk, and the central stellar mass is also significantly higher. Unfortunately, the disk is only marginally resolved by our observations. Higher-angular resolution are needed to better characterize this disk and, in turn, to compare its properties with that of other disks around Class 0 protostars.
Although we do not detect Keplerian rotation in L1448-NB, we briefly discuss the rotation profile in this source, in which the presence of a unstable disk with a radius of ~400 au has recently been claimed by Tobin et al. (2016a). In this source, our C18O (2−1) observations and modeling suggest a rotation profile with β = −1.15 ± 0.15 down to 0.6″ (175 au) from the continuum peak. The rotation profile we derive with 13CO (2−1) is steeper, but the line is affected by outflow emission (see Fig. 5). Our analysis suggests that the disk observed by Tobin et al. (2016a) is not in Keplerian rotation at r > 175 au, although it is possible that Keplerian rotation is present on smaller scales.
4.3 Could we have missed some of the disks?
Our observations and analysis of the gas kinematics in the CALYPSO sample reveal the presence of Keplerian disks in only two protostars, with disk radii of 90 and 200 au. Taken at face value, this suggests that Keplerian disks larger than 50 au (the typical scale probed by our observations) are present around 10–20% of the Class 0 protostars only. On the other hand, we cannot exclude that some of these protostars harbor disks with radii larger than 50 au that remain undetected in our observations. For example, Keplerian rotation is not detected in L1527 with the C18O (2−1) line at r > 74 au, but we detect Keplerian rotation at r < 90 au with the SO (56−45) line. We argue that this is because the C18O (2−1) line emission is dominated by the envelope and it is optically thick, whereas the SO (56−45) is less affected by the envelope and it is optically thin. In some other sources, the C18O (2−1) may also be too optically thick to reveal the Keplerian disk, as it is dominated by infalling gas. Unless the Keplerian disk is detected with another tracer, the disk would remain undetected. Unfortunately, in most sources the SO (56−45) line is dominated by the outflow emission, while in many others it is not detected on-source above our detection limit. Therefore, it cannot beused to constrain the envelope and disk kinematics. For this reason, we cannot exclude that more sources of our sample harbor a disk larger than 50 au.
5 Conclusions
We presented Plateau de Bure observations of the 13CO (J = 2−1), C18O (J = 2−1) and SO (Nj = 56−45) line emission in a sample of 16 Class 0 protostars at sub-arcsecond resolution. These observations were used to constrain the rotation of the protostars on scales between 50 and 500 au and to search for Keplerian disks. Our conclusions are the following:
-
Seven Class 0 sources out of 16 (SerpS-MM18, L1448-C, L1448-NB, L1527, NGC 1333-IRAS 2A, NGC 1333-IRAS 4B, and SVS13-B) show a velocity gradient oriented along the direction perpendicular to the jet axis (within ± 45°) in at least one line at a few hundred au scales. In other sources, the velocity gradients at these scales are mostly due to outflow emission.
-
Among the sources with a gradient approximately orthogonal to the jet axis, we detect Keplerian rotation in only two protostars: L1527 and L1448-C. Both sources are among the sources of the sample with the largest specific angular momentum at 100 au. They are also associated with compact continuum emission.
-
In L1527, we detect Keplerian rotation up to a radius of 0.7″ from the continuum peak (~90 au) with the SO (56−45) line. This is larger than the radius derived by Aso et al. (2017, 74 au) from the analysis of the C18O (2−1) rotation profile, but consistent with the radius of the centrifugal barrier obtained by Sakai et al. (2014, 2017) from several other molecular tracers. We argue that the difference between the disk radius derived with C18O (2−1) and SO (56−45) lines could be explained by the C18O (2−1) opacity, but a detailed radiative transfer model would be needed to confirm this scenario.
-
In L1448-C, we detect Keplerian rotation with the 13CO (2−1) and C18O (2−1) lines up to radii of 0.7″ (~200 au) from the continuum peak. This is the first detection of Keplerian rotation in this source.
-
On the contrary, we do not detect Keplerian rotation in L1448-NB. Our observations and analysis of the C18O (2−1) emission shows that the velocity profile is proportional to r−1 down to 0.5″ (175 au) from the continuum peak.
-
The detection rate of Keplerian disks in the CALYPSO sample of Class 0 objects is 10%. However, we argue that the 13CO (2−1) and C18O (2−1) emission could be optically thick in some of the sources as it remains dominated by the envelope emission. Unless the disk is seen with the SO (56−45) line, some of the disks could remain undetected by our observations.
This study shows that large (r > 50 au) Keplerian disks are rare in Class 0 protostars. However, the presence of jets or outflows (Podio et al., in prep.) and disk-like dust continuum components (Maury et al. 2019) strongly suggests that Class 0 protostars have disks. Therefore, most of these disks are smaller than 50 au, which is consistent with MHD simulations that predict radii on the order of a few tens of au (Hennebelle et al. 2016). Finding and characterizing Keplerian disks around Class 0 protostars will require a new survey of a sample of Class 0 protostars with a spatial resolution of 0.1″ or better. This can only be achieved by ALMA.
Acknowledgements
We would like to thank Nagayoshi Ohashi, Nami Sakai and John Tobin for fruitful discussions on the interpretation of the observations presented in this paper. We also thank the referee for his/her detailed report that helped us to improve the paper. This work is based on observations carried out under project number U052 with the IRAM NOEMA Interferometer. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain). This work has benefited from the support of the European Research Council under the European Union’s Seventh Framework Programme (Advanced Grant ORISTARS with grant agreement No. 291294 and Starting Grant MagneticYSOs with grant agreement No. 679937), and from the French Agence Nationale de la Recherche (ANR), under reference ANR-12-JS05-0005.
Appendix A Synthesized beam sizes and sensitivities
Synthesized beam sizes and sensitivities for each line are given in Tables A.1–A.3.
Beam sizes and noise per channel for the 13CO (2−1) line observations.
Beam sizes and noise per channel for the C18O (2−1) line observations.
Beam sizes and noise per channel for the SO (56−45) line observations.
Appendix B Moment maps
Figures B.1–B.3 show zeroth-order moment and first-order moment (mean velocity) maps of the 13CO (2−1), C18O (2−1) and SO (56−45) lines, together with the 1.4 mm continuum emission maps from Maury et al. (2019) in L1448-2A, SVS13B, NGC 1333-IRAS 4A, NGC 1333-IRAS 4B, IRAM 04191, L1521F, SerpM-S68N, SerpM-SMM4, SerpS-MM18, SerpS- MM22, L1157, and GF9-2.
Appendix C Other disk candidates
C.1 NGC 1333-IRAS 2A
NGC 1333-IRAS 2A (hereafter IRAS 2A) is a Class 0 protostar located in the NGC 1333 region, within the Perseus cloud. It is the most luminous source of our sample, with an internal luminosity of 47 L⊙ (Ladejate et al., in prep.). Its envelope mass is 7.9 M⊙ (Karska et al. 2013). The PA of the main jet is −155° (Podio et al., in prep.). A second jet originates from a few arcseconds south of IRAS 2A, and has a PA of −65° (Codella et al. 2014; Podio et al., in prep.). Brinch et al. (2009) studied the kinematics of the IRAS 2A envelope using interferometric observationsat 1″ resolution and find that the gas kinematics is dominated by infall, with very little rotation. Using CH3OH line observationswith a 0.8″ resolution, Maret et al. (2014) measured a small velocity gradient orthogonal to the jet axis (PA 107°). They argue that the methanol emission originates from the infalling and slowly rotating envelope around a central mass of 0.1–0.2 M⊙.
First-order moment maps for the 13CO (2−1), C18O (2−1), and SO (56−45) lines are shown in Fig. 1. The 13CO (2−1) emission peaks at the same position as the continuum peak. The mean velocity at this position is 4.5 km s−1, blueshifted from the source systemic velocity (~7.5 km s−1)14. This suggests that the 13CO (2−1) emission is optically thick and possibly in part filtered out by the interferometer. The mean velocity increases to ~12 km s−1 toward the north-east, in the direction of the red-shifted lobe of the jet. West of the continuum peak, the mean velocity is comparable to the systemic velocity. The C18O (2−1) line also peaks close to the continuum peak and shows a velocity gradient along an east-west axis. The SO (56−45) line indicates a velocity gradient along a north-south axis and appears to probe the outflow. Fitting the first order moment maps, we measure a gradient PA of (−29 ± 12)°, (60 ± 4)° and (−1 ± 6)° for the 13CO (2−1), C18O (2−1) and SO (56−45) lines, respectively. The corresponding values of Δθ are 36°, 55°, and 64°, respectively. Only the 13CO (2−1) line fulfills the Δθ < 45° criterion, and it could, in principle, probe the inner envelope or the disk. However, it is unlikely to be the case because the orientation of the gradient we measure with this line (PA = (−29 ± 12)°) is inconsistent with that measured by Maret et al. (2014) from CH3OH line observations (PA = 107°).
Figure C.1 shows the centroid positions together with the zeroth-order moment maps. For consistency with Maret et al. (2014), we assume that the disk major axis has a PA = 107°, slightly different from the direction orthogonal to the main jet (PA = 115°). For the 13CO (2−1) emission, several blue-shifted channels can be fitted, and their centroid positions are close to the continuum peak. These channels correspond to large velocities (|v − vsys| > 2 km s−1), so it is possible that they are due to outflow emission. For the SO (56−45) emission, the centroids are located along the jet axis. For the C18O (2−1) line, we canfit the position of four channels. The centroids of the two blue-shifted channels are roughly consistent with the gradient orientation measured by Maret et al. (2014). However, the centroids of the two red-shifted channels are not aligned with the gradient orientation. The centroids of the SO (56−45) line are aligned withthe jet. The corresponding rotation curves are shown in Fig. C.2. We do not attempt to fit the data points for the 13CO (2−1) and SO (56−45) line, because the emission of these two lines is most likely due to outflow emission. For the C18O (2−1) line, we obtain a best-fit β = −0.18 ± 0.09. However thefit is uncertain since it is based on two channels only. In Fig. C.3, we show PV diagrams obtained along the same axis. The C18O (2−1) emission diagram is consistent with infall and rotation along this axis, in agreement with the results of Maret et al. (2014). Fitting the first emission contour with a Keplerian law gives 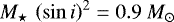 . The diagrams for the 13CO (2−1) and SO (56−45) lines indicates the presence high-velocity gas close to the central object, which is likely due to the outflow.
. The diagrams for the 13CO (2−1) and SO (56−45) lines indicates the presence high-velocity gas close to the central object, which is likely due to the outflow.
In summary, we find evidence for rotation and infall in this source from the C18O (2−1) line observations. The rotation profile we derive with this line is uncertain, but it does not appear to be consistent with Keplerian rotation.
C.2 SVS13B
SVS13B is a Class 0 protostar also located in NGC 1333. This source is part of a wide triple system (Lefèvre et al. 2017). SVS13A is a Class I protostar located 4400 au (15″) from SVS13B, while SVS13C, a Class 0 protostar, is located 5600 au (19″) from SVS13B (Tobin et al. 2016b; Maury et al. 2019). The internal luminosity of SVS13B is 3 ± 2 L⊙ (Ladejate et al., in prep.) and its envelope mass is 1.9 M⊙ (Chini et al. 1997). It drives a collimated outflow seen in high velocity SiO (Bachiller et al. 1998), with a PA of 167° (Podio et al., in prep.). Based on VLA observations and modeling, Segura-Cox et al. (2016) argue that SVS13B harbors a disk with a radius of ~ 40 au (0.13″).
Our observations of the 13CO (2−1), C18O (2−1) and SO (56−45) line emission in SVS13B are shown in Fig. B.1. Only C18O (2−1) emission is detected towards the continuum peak. The emission is compact, with a size of about 2″. The first-order moment map shows a velocity gradient, with the mean velocity increasing from 8 km s−1 west of the continuum peak up to 9 km s−1 east of it. Fitting the first-order moment map, we find a gradient position angle 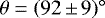 , close to the disk orientation expected from the jet axis (Δθ = 15°). The gradient orientation is roughly consistent with the disk PA derived by Segura-Cox et al. (2016, PA = 71°).
, close to the disk orientation expected from the jet axis (Δθ = 15°). The gradient orientation is roughly consistent with the disk PA derived by Segura-Cox et al. (2016, PA = 71°).
Figure C.4 shows the positions of the centroids we obtain from a fit in the uv plane, together with the zeroth-order moment. Only two red-shifted channels can be fitted in the uv plane. The centroids of both channels are located east of the continuum peak, in agreement with the velocity gradient orientation we measure in this source. The rotation curve we obtain is shown in Fig. C.5. For this source, we adopt a systemic velocity of 8.4 km s−1 (Chen et al. 2009) and we assume that the disk is orthogonal to the jet axis (PA 77°). From a fit with a power law, we obtain a best-fit β = −0.49 ± 0.28 for r < 0.5′′ (150 au), consistent with Keplerian rotation. However, we caution that the rotation curve for this source is very uncertain, because it is based on two velocity channels only. The lowest velocity channel we fit is a position offset of 0.5″, i.e., a radius of 150 au. From a fit with a Keplerian law, we find a best-fit  M⊙.
M⊙.
Figure C.6 shows the PV diagram we obtain along the assumed disk axis, together with the best-fit power-law rotation curve. The PV diagram appears to be symmetric around the adopted value of vsys and it is consistent with rotation. However, the emission is at the limit of the spatial resolution of our observations. Fitting the first emission contour with a Keplerian law gives  M⊙.
M⊙.
To summarize, we tentatively detect Keplerian rotation at r < 150 au in this source. From a fit in the uv plane and the PV diagram, we estimate that  M⊙, that is, M⋆ = 0.05 − 0.12 M⊙, assuming a disk inclination of 61° (Segura-Coxet al. 2016). Observations at higher angular resolution are needed to confirm this detection.
M⊙, that is, M⋆ = 0.05 − 0.12 M⊙, assuming a disk inclination of 61° (Segura-Coxet al. 2016). Observations at higher angular resolution are needed to confirm this detection.
C.3 NGC 1333-IRAS 4B
NGC 1333-IRAS 4B (hereafter IRAS 4B) is a Class 0 protostar also located in NGC 1333. This source is a wide binary whose secondary component, IRAS 4B2, is located 11″ (3200 au) to the east of the main component (Jørgensen et al. 2007; Maury et al. 2019). The internal luminosity of IRAS 4B is 2.3 L⊙ (Ladejate et al., in prep.), and it is surrounded by a 4.7 M⊙ envelope (Sadavoy et al. 2014). IRAS 4B drives a jet oriented along a north-south axis (PA = 167°; Podio et al., in prep.). Using C18O (2−1) observations, Yen et al. (2013, 2015a) measured a velocity gradient with a PA of − 14°, which is dominated by the outflow. Fitting only the component orthogonal to the outflow, they find little rotation of the envelope and derive a centrifugal radius <5 au.
Our observations of IRAS 4B are shown in Fig. B.1. The 13CO (2−1) emission is elongated along the jet direction, and shows a velocity gradient that is consistent with the jet orientation. SO (56−45) emission is detected close to the continuum peak, as well as in a few spots along the jet axis. The C18O (2−1) emission is centered close to the continuum emission, and its size is ~ 6″ in the north-south direction, and ~ 4″ in the east-west direction. The C18O (2−1) first-order moment map hints at a small velocity gradient along the east-west direction: the mean velocity to the east of the source is about 6.5 km s−1, while it is 7.0 km s−1 west of it. This gradient is confirmed by the fit of the first-order moment map, which gives a PA of − 79 ± 6° and Δθ = 24°. For the 13CO (2−1) line, we find a velocity gradient with θ = (−7 ± 19)° and Δθ = 84°. This confirms that the line is mostly due to outflow emission. For the SO (56−45), we find θ = (74 ± 6)° and Δθ = 3°. Although the orientation of the gradient we derive for this line is almost orthogonal to the jet, it is unlikely to be due to envelope rotation given the morphology of the SO (56−45) emission on larger scales. In addition, the orientation of the gradient measured with the SO (56−45) line is in a direction opposite to the C18O (2−1) line velocity gradient.
Figure C.7 shows the results of the fit in the uv plane. We assume that the disk major axis is orthogonal to the jet (PA − 103°), and we adopt a systemic velocity of 6.7 km s−1, consistent with the PV diagram of the C18O (2−1) emission (see below). For both the 13CO (2−1) and SO (56−45) lines, the centroids for the blue-shifted channels are located to the south, while the centroids for red-shifted channels are oriented to the north. This is consistent with the jet orientation. For the C18O (2−1) lines, the centroids of the red-shifted channels are located west of the source, along the expected disk axis. The centroids for the blue-shifted channels are roughly aligned along a north-south axis, and are probably contaminated by the outflow. Figure C.8 shows the position offset along the assumed disk axis as a function of velocity. We do not attempt to fit a rotation curve for the 13CO (2−1) and SO (56−45) lines, because these two lines are dominated by the outflow. For the C18O (2−1) line, we fit a rotation curve considering only two red-shifted channels. We obtain a best fit β =−2.09 ± 1.78. The fit for this source is uncertain, because it is based on two points only.
 |
Fig. C.3 Same as in Fig. 4 for IRAS 2A. The dashed curve in the middle panel shows the Keplerian velocity for |
Figure C.9 shows the PV diagrams along the assumed disk axis. The PV diagram for the 13CO (2−1) line shows negative emission at vLSR > vsys. This is likely due to spatial filtering and/or absorption by a foreground component. Emission is detected on several spots at vLSR < vsys which are probably due to shocked gas. The diagram for the SO (56−45) shows a similar pattern. On the other hand, The emission contours for the C18O (2−1) line peak close to a velocity of about 6.7 km s−1, and appear to be consistent with envelope rotation. From a fit of the first contour, we obtain 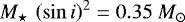 .
.
To summarize, we find evidence for rotation from our C18O (2−1) line observations. The velocity curve we derive is uncertain, so we cannot determine if the rotation is Keplerian.
C.4 SerpS-MM18
SerpS-MM18 is a Class 0 protostar located in the Serpens-South region of the Serpens/Aquila complex, at a distance of 350 pc (Palmeirim et al., in prep.). This protostar is part of a wide binary system, SerpS-MM18 and SerpS-MM18’, separated by 3600 au (Maury et al. 2019). The internal luminosity of SerpS-MM18 is 29 L⊙ and its envelope mass is 5 M⊙ (Ladejate et al., in prep.; Maury et al. 2011). The source drives a jet with a PA of − 172° (Podio et al., in prep.).
 |
Fig. C.6 Same as in Fig. 4 for SVS13B. Dashed curve in the right panel shows the Keplerian velocity for
|
 |
Fig. C.9 Same as in Fig. 4 for IRAS 4B. Dashed curve in the middle panel shows the Keplerian velocity for
|
Our observations of this source are shown in Fig. B.3. We detect 13CO (2−1) emission towards the continuum peak position that extends towards the south-west, along the direction of the blue-shifted lobe of the jet. We also detect SO (56−45) emission along both lobes of the jet. On the contrary, the C18O (2−1) emission appears to originate mostly in the envelope around the protostar. The C18O (2−1) emission peaks at the same position as the continuum and it is extended along an east-west axis. We observe a velocity gradient along southeast-northwest axis, with a mean velocity of 6.5 km s−1 to the southeast of the continuum peak, increasing up to 8.5 km s−1 to the northwest. From a fit of the first-order moment map, we obtain 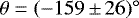 ,
, 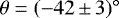 , and
, and 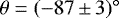 for the 13CO (2−1), C18O (2−1), and SO (56−45) lines, respectively. The corresponding values of Δθ are 77°, 40° and 5°, respectively. The gradient orientation we obtain for 13CO (2−1) is consistent with the jet orientation. However, the gradient for the SO (56−45) line is almost perpendicular to jet, although the emission of this line is clearly dominated by the outflow. Indeed, a careful examination of the first-order moment map for that line shows that the eastern part of the blue-shifted jet lobe has a lower mean velocity than the western part, suggesting rotation of the outflow cavities. The gradient we measure for the C 18O (2−1) line is consistent with envelope or disk rotation, although the value of Δθ we measure is close to the 45° threshold.
for the 13CO (2−1), C18O (2−1), and SO (56−45) lines, respectively. The corresponding values of Δθ are 77°, 40° and 5°, respectively. The gradient orientation we obtain for 13CO (2−1) is consistent with the jet orientation. However, the gradient for the SO (56−45) line is almost perpendicular to jet, although the emission of this line is clearly dominated by the outflow. Indeed, a careful examination of the first-order moment map for that line shows that the eastern part of the blue-shifted jet lobe has a lower mean velocity than the western part, suggesting rotation of the outflow cavities. The gradient we measure for the C 18O (2−1) line is consistent with envelope or disk rotation, although the value of Δθ we measure is close to the 45° threshold.
Figure C.10 shows the results of the fit of centroids of the emission in each channel, together with the assumed disk major axis (PA − 42°, orthogonal to the jet axis). No centroids can be fitted for the 13CO (2−1) and SO (56−45) lines. For the C 18O (2−1) line, we fit the centroids in 5 channels. Surprisingly, the centroids for the blue shifted and red-shifted channels are all located east of the continuum peak15. Because of this, we cannot fit a velocity curve for this source. The PV diagrams along the assumed disk axis are shown on Fig. C.11. The PV diagram for the C 18O (2−1) emission is consistent with rotation and perhaps infall. Fitting the first contour with a Keplerian law gives 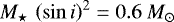 .
.
 |
Fig. C.11 Same as in Fig. 4 for SerpS-MM18. The dashed curve shows a Keplerian velocity profile for
|
To summarize the results for this source, the C 18O (2−1) PV diagramindicates the rotation of the envelope in the direction perpendicular to the jet. Because of outflow emission, we cannot fit a velocity profile and we therefore have no evidence for Keplerian rotation in this source.
Appendix D Test of the rotation curve determination from the visibilities
In this section, we test the technique we use in Sect. 3.2 to derive the rotation curves for the disk candidates from the visibilities. For this, we use the thindisk code (Maret 2019) to compute the line emission of a geometrically thin Keplerian disk. The disk line surface brightness distribution is assumed to follow a tapered power-law distribution (Andrews et al. 2009):
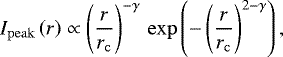 (D.1)
(D.1)
where r is the radius, rc is the disk characteristic radius16, and γ is the power-law exponent. We assume that rc = 100 au and γ = 0.8 (de Gregorio-Monsalvo et al. 2013). We also assume that the disk inclination is 45°, and that the disk major axis PA is 0°. The disk is assumed to be in Keplerian rotation around a central mass M⋆ = 0.3 M⊙. Finally, we adopt a distance of 293 pc (the same distance as L1448-C) and a systemic velocity of vsys = 5 km s−1. The model does not include artificial noise.
The thindisk code produces a synthetic data cube that we process with GILDAS to simulate the observations with the interferometer. First we use the UV_FMODEL task to compute synthetic visibilities, assuming the same uv coverage as our L1448-C observations. Then the visibilities are imaged using robust weighting and deconvolved. Finally, we analyze the synthetic observations using the technique outlined in Sect. 3.2.1.
Figure D.1 shows the results of the fit of the centroid position in the uv plane for each spectral channel superimposed on the zeroth-order moment contours for the model. In this figure, we see that the centroid positions are located onto the disk major axis, with the blue-shifted and red-shifted channels located in the south and north of the disk central position, respectively. The zeroth-order moment contours have an ellipsoidal shape with a major axis orientation that appears to be slightly tilted with respect to the north-south axis. This is an effect of the synthetic beam, whose FWHM size is 0.65′′× 0.41′′ and PA is 32°. The fit in the uv plane is obviously insensitive to the synthetic beam orientation and shape, which explains why the centroid positions in each channel are well aligned with the true disk major axis.
Figure D.2 shows the offset along the disk major axis for each velocity channel, as a function of the velocity offset. This plot shows a similar pattern than the L1527 plot for SO (see Fig. 3): a linear increase17 position offset as a function of the velocity offset between 0 < |v − vsys|≤ 0.8 km s−1, and a power-law decrease at higher velocity offset. Fitting the points at |v − vsys| > 0.8 km s−1 with a power law, we find a best-fit β = −0.58 ± 0.13, consistent with a Keplerian profile. With a Keplerian law, we obtain a best fit  M⊙, that is, M⋆ = 0.20 ± 0.02 M⊙ after correcting for the inclination. This is about 30% lower than the model central mass18. We can estimate the size of the disk from the centroid with the largest position offset that is consistent with the Keplerian velocity curve, within the error bars. On Fig. D.2 we see that Keplerian rotation is detected up to position offset of ~ 0.3′′. This gives a disk radius of 88 au for the assumed distance. This radius is comparable to the characteristic radius adopted in our model.
M⊙, that is, M⋆ = 0.20 ± 0.02 M⊙ after correcting for the inclination. This is about 30% lower than the model central mass18. We can estimate the size of the disk from the centroid with the largest position offset that is consistent with the Keplerian velocity curve, within the error bars. On Fig. D.2 we see that Keplerian rotation is detected up to position offset of ~ 0.3′′. This gives a disk radius of 88 au for the assumed distance. This radius is comparable to the characteristic radius adopted in our model.
Figure D.3 shows the PV diagram along the disk major axis, together with the best-fit rotation curve. Because the rotation curve is based on fits of the centroid position in each velocity channel, it follows the position of peak intensity in the PV diagram. Therefore, it tends to underestimate the velocity of the disk at each position, and in turn the mass of the central object. The mass of the disk can also be estimated by a fit of the first emission contour in the PV diagram. Using this technique, we find M⋆ = 0.7 M⊙. This is about a factor of two larger than the assumed central mass19. To summarize, we show that our rotation curve technique provides a good estimate of the power-law index of the rotation curve, even for a marginally spatially resolved disk. However, it underestimates the mass of the central object by about 30% for the adopted model. On the other hand, a fit of the first contour in the PV diagram overestimates the mass of the central object by about a factor of two. By combining these two techniques, we can obtain lower and upper limits on the mass of the central object. In addition, our technique can be used to estimate the disk’s characteristic radius.
 |
Fig. D.1 Same as in Fig. 2 for the synthetic disk model. The model assumes a disk characteristic radius rc = 100 au, a disk inclination of 45°, a disk major axis PA of 0°, a central mass M⋆ = 0.3 M⊙ and a distance of 293 pc. The right panel is a zoom on the central region of the plot in the left panel. |
 |
Fig. D.3 PVdiagram along the disk major axis for the synthetic disk model. The solid line shows the velocity curve obtained from a fit in the uv
plane (see the solid curve in Fig. D.2). The dashed line shows a fit of the first emission contour with a Keplerian law for |
References
- Allen, A., Li, Z.-Y., & Shu, F. H. 2003, ApJ, 599, 363 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Motte, F., & Bacmann, A. 1999, ApJ, 513, L57 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Ward-Thompson, D., & Barsony, M. 2000, Protostars and Planets IV (Tucson: University of Arizona Press), 59 [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada, G., Rodriguez, L. F., Torrelles, J. M., et al. 1989, ApJ, 341, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Ansdell, M., Williams, J. P., Trapman, L., et al. 2018, ApJ, 859, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Aso, Y., Ohashi, N., Saigo, K., et al. 2015, ApJ, 812, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Aso, Y., Ohashi, N., Aikawa, Y., et al. 2017, ApJ, 849, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Bachiller, R., Guilloteau, S., Gueth, F., et al. 1998, A&A, 339, L49 [Google Scholar]
- Belloche, A. 2013, EAS Pub. Ser., 62, 25 [CrossRef] [EDP Sciences] [Google Scholar]
- Brinch, C., Crapsi, A., Jørgensen, J. K., Hogerheijde, M. R., & Hill, T. 2007, A&A, 475, 915 [Google Scholar]
- Brinch, C., Jørgensen, J. K., & Hogerheijde, M. R. 2009, A&A, 502, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casali, M. M., Eiroa, C., & Duncan, W. D. 1993, A&A, 275, 195 [NASA ADS] [Google Scholar]
- Chen, X., Launhardt, R., & Henning, T. 2009, ApJ, 691, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Chini, R., Reipurth, B., Sievers, A., et al. 1997, A&A, 325, 542 [NASA ADS] [Google Scholar]
- Codella, C., Cabrit, S., Gueth, F., et al. 2014, A&A, 568, L5 [Google Scholar]
- Curiel, S., Raymond, J. C., Rodriguez, L. F., Canto, J., & Moran, J. M. 1990, ApJ, 365, L85 [NASA ADS] [CrossRef] [Google Scholar]
- de Gregorio-Monsalvo, I., Ménard, F., Dent, W., et al. 2013, A&A, 557, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunham, M. M., Stutz, A. M., Allen, L. E., et al. 2014, Protostars and Planets VI (Tucson: University of Arizona press), 195 [Google Scholar]
- Enoch, M. L., Evans, II, N. J., Sargent, A. I., & Glenn, J. 2009, ApJ, 692, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, D., Lizano, S., Shu, F. H., & Allen, A. 2006, ApJ, 647, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, P. A. B., Loinard, L., Ortiz-Léon, G. N., et al. 2018, ApJ, 859, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Gaudel, M., Maury, A., Belloche, A., et al. 2020, A&A, in press, https://doi.org/10.1051/0004-6361/201936364 [Google Scholar]
- Gildas Team 2013, Astrophysics Source Code Library [record ascl:1305.010] [Google Scholar]
- Ginsburg, A., Bally, J., Goddi, C., Plambeck, R., & Wright, M. 2018, ApJ, 860, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Girart, J. M., & Acord, J. M. P. 2001, ApJ, 552, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Benson, P. J., A., F. G., & Myers, P. C. 1993, ApJ, 406, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Grossman, E. N., Masson, C. R., Sargent, A. I., et al. 1987, ApJ, 320, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., Commerçon, B., Chabrier, G., & Marchand, P. 2016, ApJ, 830, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirano, N., Ho, P. P. T., Liu, S.-Y., et al. 2010, ApJ, 717, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Hirota, T., Bushimata, T., Choi, Y. K., et al. 2008, PASJ, 60, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Hsieh, T.-H., Hirano, N., Belloche, A., et al. 2019, ApJ, 871, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Jennings, R. E., Cameron, D. H. M., Cudlip, W., & Hirst, C. J. 1987, MNRAS, 226, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Harvey, P. M., Evans, II, N. J., et al. 2006, ApJ, 645, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Bourke, T. L., Myers, P. C., et al. 2007, ApJ, 659, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., van Dishoeck, E. F., Visser, R., et al. 2009, A&A, 507, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaas, A. A., Olofsson, G., Bontemps, S., et al. 2004, A&A, 421, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karska, A., Herczeg, G. J., van Dishoeck, E. F., et al. 2013, A&A, 552, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kristensen, L. E., van Dishoeck, E. F., Tafalla, M., et al. 2011, A&A, 531, L1 [Google Scholar]
- Ladd, E. F., Adams, F. C., Casey, S., et al. 1991, ApJ, 382, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C.-F., Hirano, N., Zhang, Q., et al. 2014, ApJ, 786, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C.-F., Hwang, H.-C., & Li, Z.-Y. 2016, ApJ, 826, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Lefèvre, C., Cabrit, S., Maury, A. J., et al. 2017, A&A, 604, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindberg, J. E., Jørgensen, J. K., Brinch, C., et al. 2014, A&A, 566, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loinard, L., Torres, R. M., Mioduszewski, A. J., et al. 2007, ApJ, 671, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Long, F., Herczeg, G. J., Harsono, D., et al. 2019, ApJ, 882, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S. 2019, https://doi.org/10.5281/zenodo.3244265 [Google Scholar]
- Maret, S., Belloche, A., Maury, A. J., et al. 2014, A&A, 563, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maury, A. J., André, P., Men’shchikov, A., Könyves, V., & Bontemps, S. 2011, A&A, 535, A77 [Google Scholar]
- Maury, A. J., André, P., Testi, L., et al. 2019, A&A, 621, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mellon, R. R., & Li, Z.-Y. 2008, ApJ, 681, 1356 [NASA ADS] [CrossRef] [Google Scholar]
- Mizuno, A., Onishi, T., Hayashi, M., et al. 1994, Nature, 368, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., & André, P. 2001, A&A, 365, 440 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murillo, N. M., Lai, S.-P., Bruderer, S., Harsono, D., & van Dishoeck E. F. 2013, A&A, 560, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohashi, N., Saigo, K., Aso, Y., et al. 2014, ApJ, 796, 131 [NASA ADS] [CrossRef] [Google Scholar]
- O’Linger, J., Wolf-Chase, G., Barsony, M., & Ward-Thompson, D. 1999, ApJ, 515, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz-León, G. N., Dzib, S. A., Kounkel, M. A., et al. 2017, ApJ, 834, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz-León, G. N., Loinard, L., Dzib, S. A., et al. 2018, ApJ, 865, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Oya, Y., Sakai, N., Lefloch, B., et al. 2015, ApJ, 812, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Podio, L., Codella, C., Gueth, F., et al. 2016, A&A, 593, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadavoy, S. I., Di Francesco, J., André, P., et al. 2014, ApJ, 787, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., et al. 2014, Nature, 507, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, N., Oya, Y., Higuchi, A. E., et al. 2017, MNRAS, 467, L76 [NASA ADS] [Google Scholar]
- Santangelo, G., Codella, C., Cabrit, S., et al. 2015, A&A, 584, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, S., & Elmegreen, B. G. 1979, ApJS, 41, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Segura-Cox, D. M., Harris, R. J., Tobin, J. J., et al. 2016, ApJ, 817, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Seifried, D., Sánchez-Monge, Á., Walch, S., & Banerjee, R. 2016, MNRAS, 459, 1892 [Google Scholar]
- Simon, M., Dutrey, A., & Guilloteau, S. 2000, ApJ, 545, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Takakuwa, S., Saito, M., Lim, J., et al. 2012, ApJ, 754, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Terebey, S., Shu, F. H., & Cassen, P. 1984, ApJ, 286, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Tobin, J. J., Looney, L. W., Mundy, L. G., Kwon, W., & Hamidouche, M. 2007, ApJ, 659, 1404 [NASA ADS] [CrossRef] [Google Scholar]
- Tobin, J. J., Hartmann, L., N., C., & D’Alessio, P. 2008, ApJ, 679, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Tobin, J. J., Hartmann, L., Bergin, E., et al. 2012a, ApJ, 748, 16 [Google Scholar]
- Tobin, J. J., Hartmann, L., Chiang, H.-F., et al. 2012b, Nature, 492, 83 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tobin, J. J., Looney, L. W., Wilner, D. J., et al. 2015, ApJ, 805, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Tobin, J. J., Kratter, K. M., Persson, M. V., et al. 2016a, Nature, 538, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Tobin, J. J., Looney, L. W., Li, Z.-Y., et al. 2016b, ApJ, 818, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Tokuda, K., Onishi, T., Saigo, K., et al. 2014, ApJ, 789, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Tokuda, K., Onishi, T., Matsumoto, T., et al. 2016, ApJ, 826, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Umemoto, T., Iwata, T., Fukui, Y., et al. 1992, ApJ, 392, L83 [NASA ADS] [CrossRef] [Google Scholar]
- van ’t Hoff, M. L. R., Tobin, J. J., Harsono, D., & van Dishoeck E. F. 2018, A&A, 615, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiesemeyer, H., Guesten, R., Wink, J. E., & Yorke, H. W. 1997, A&A, 320, 287 [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Yen, H.-W., Takakuwa, S., Ohashi, N., & Ho, P. T. P. 2013, ApJ, 772, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Yen, H.-W., Koch, P. M., Takakuwa, S., et al. 2015a, ApJ, 799, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Yen, H.-W., Takakuwa, S., Koch, P. M., et al. 2015b, ApJ, 812, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Yen, H.-W., Koch, P. M., Takakuwa, S., et al. 2017, ApJ, 834, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Yorke, H. W., & Bodenheimer, P. 1999, ApJ, 525, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, C., Speagle, J. S., Schlafly, E. F., et al. 2019, ApJ, 879, 125 [NASA ADS] [CrossRef] [Google Scholar]
See http://irfu.cea.fr/Projets/Calypso for more details.
CALYPSO data are available from http://www.iram.fr/ILPA/LP010/.
We refer the reader to Maury et al. (2019) for details on the calibration of the continuum observations.
A recent study gives a slightly closer distance (130 pc; Galli et al. 2018). Here we adopt a distance of 140 pc for consistency with previous studies of L1527.
Tobin et al. (2016a) assumed a distance of 235 pc (Hirota et al. 2008). For the distance adopted here (293 pc), the central stellar mass is ~1.2 M⊙
The choice of the systemic velocity is justified a posteriori by the red and blue points in the right panel of Fig. 6, which are consistent with a single rotation curve. If the assumed systemic velocity were incorrect, the blue and red points would not overlap, and they could not be fitted with a rotation curve.
The systemic velocity is estimated from the 13CO (2−1) and C18O (2−1) PV diagrams (see Fig. 10) which are centered around 5.2 km s−1.
The difference between the apparent position of the kink and the Keplerian disk radius is due to the limited angular resolution and the close to edge-on geometry, which makes the kink to appear closer to the central object than the actual Keplerian disk radius (Aso et al. 2015).
The radius of the centrifugal barrier is half the centrifugal radius (Sakai et al. 2014).
The P.V. diagram for the C18O (2−1) emission, which appears to trace the rotation in the envelope, is peaked around vLSR = 7.5 km s−1 (see Fig. C.3). We therefore adopt a systemic velocity of 7.5 km s−1 for this source.
The characteristic radius (defined in Eq. (D.1)) does not mean the disk-envelope boundary, because our model assumes Keplerian rotation outside the characteristic radius.
We note that because of the finite spatial resolution, the model predicts a linear variation although the velocity profile is a power law. This demonstrates that a linear variation in the rotation curve does not necessarily mean that the line arises from a ring in the disk (see, e.g., Ohashi et al. 2014). This conclusion is not specific to the uv plane fitting technique: a fit of peak emission as a function of velocity in the PV diagram shown in Fig. D.3 would also give a linear variation for velocities between 4 and 6 km s −1.
This is an effect of the spatial resolution: because the disk is marginally resolved, the emission contours are broaden by the synthetic beam along the position offset axis. This makes the first contour to appear further away from the central object than it would if the disk was resolved spatially. In turn, this tends to overestimate the mass.
All Tables
Overview of evidence of the presence of disks in the CALYPSO sample of Class 0 objects.
All Figures
 |
Fig. 1 1.4 mm continuum emission, integrated intensities and mean velocities of the 13CO (2−1), C18O (2−1) and SO (56−45) lines in L1448-NB, L1448-C, NGC 1333-IRAS 2A, and L1527. Left panels: the 1.4 mm continuum emission. Other panels: the line mean velocities (first-order moment; background image), together with theline integrated intensities (zeroth-order moment; black contours). Contours are drawn at −3σ (dotted lines) 3σ, 6σ, 12σ and so on (solid lines). In each panel, the black crosses show the position of the main continuum peak(s). The blue and red lines in the left panels indicate the direction of the blue- and red-shifted lobes of the jet(s), respectively. The arrows in other panels indicate the direction of the velocity gradient, as determined from a linear fit of the mean velocity within 2″ of the continuum peak position. The gray sectors around each arrow show the 1σ uncertainty on the direction of the velocity gradient. The ellipse in each panel shows the synthesized beam. All coordinates are relative to the positions of the brightest continuum peak of each source (see Table 1). |
| In the text | |
 |
Fig. 2 Results of the fits in the uv plane for each spectral channel (circles with error bars) superimposed on zeroth-order moment map (black contours) in L1527 for the 13CO (2−1) (left panel), C18O (2−1) (middle panel), and SO (56−45) (right panel)lines. Contours are drawn at 3σ, 6σ, 12σ, and so on. Blue and red points show the centroid positions of the blue-shifted and red-shifted channels, respectively. Only filled points are considered when constructing the velocity curves; open points are ignored. The thick black lines connect the centroids that correspond to adjacent velocity channels. Black crosses show the position of the continuum peak, while the dashed line shows the assumed disk major axis. |
| In the text | |
 |
Fig. 3 Position offset derived in the uv
plane along the disk major axis as a function of the velocity channel in L1527 for panel). In each panel the blue and red points with the error bars show the observations, the solid line shows the result of a power-law fit. The dashed line in the right panel shows the result of a fit with a Keplerian law with
|
| In the text | |
 |
Fig. 4 Position velocity cuts in the image plane through the L1527 continuum peak along the assumed disk major axis for the 13 CO (2−1) (left panel), C18O (2−1) (middle panel), and SO (56−45) (right panel)lines. Contours are drawn at −3σ, 3σ, 6σ, 12σ
and so on. Black crosses correspond to the continuum peak. Black solid curves show the results of the velocity fit in the
uv
plane with a power-law function. Dashed lines show the result of the fit of the 6σ
contours with a Keplerian law with |
| In the text | |
 |
Fig. 5 Same as in Fig. 2 for L1448-NB. Black crosses show the positions of the NB1 and NB2 continuum peaks. |
| In the text | |
 |
Fig. 6 Same as in Fig. 3 for L1448-NB. The reference position is NB2. |
| In the text | |
 |
Fig. 7 Same as in Fig. 4 for L1448-NB. Dashed curve shows a Keplerian curve for
|
| In the text | |
 |
Fig. 8 Same as in Fig. 2 for L1448-C. |
| In the text | |
 |
Fig. 9 Sameas in Fig. 3 for L1448-C. The dashed lines show the result of a Keplerian fit with
|
| In the text | |
 |
Fig. 10 Same as in Fig. 4 for L1448-C. The dashed curves shows Keplerian velocity profiles with
|
| In the text | |
 |
Fig. B.1 Same as in Fig. 1 for L1448-2A, SVS13B NGC 1333-IRAS 4A and NGC 1333-IRAS 4B. |
| In the text | |
 |
Fig. B.2 Same as in Fig. 1 for IRAM 04191, L1521F, SerpM-S68N, and SerpM-SMM4. |
| In the text | |
 |
Fig. B.3 Same as in Fig. 1 for SerpS-MM18, SerpS-MM22, L1157, and GF9-2. |
| In the text | |
 |
Fig. C.1 Same as in Fig. 2 for IRAS 2A. |
| In the text | |
 |
Fig. C.2 Same as in Fig. 3 for IRAS 2A. |
| In the text | |
 |
Fig. C.3 Same as in Fig. 4 for IRAS 2A. The dashed curve in the middle panel shows the Keplerian velocity for |
| In the text | |
 |
Fig. C.4 Same as in Fig. 2 for SVS13B. |
| In the text | |
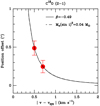 |
Fig. C.5 Same as in Fig. 3 for SVS13B. |
| In the text | |
 |
Fig. C.6 Same as in Fig. 4 for SVS13B. Dashed curve in the right panel shows the Keplerian velocity for
|
| In the text | |
 |
Fig. C.7 Same as in Fig. 2 for IRAS 4B. |
| In the text | |
 |
Fig. C.8 Same as in Fig. 3 for IRAS 4B. |
| In the text | |
 |
Fig. C.9 Same as in Fig. 4 for IRAS 4B. Dashed curve in the middle panel shows the Keplerian velocity for
|
| In the text | |
 |
Fig. C.10 Same as in Fig. 2 for SerpS-MM18. |
| In the text | |
 |
Fig. C.11 Same as in Fig. 4 for SerpS-MM18. The dashed curve shows a Keplerian velocity profile for
|
| In the text | |
 |
Fig. D.1 Same as in Fig. 2 for the synthetic disk model. The model assumes a disk characteristic radius rc = 100 au, a disk inclination of 45°, a disk major axis PA of 0°, a central mass M⋆ = 0.3 M⊙ and a distance of 293 pc. The right panel is a zoom on the central region of the plot in the left panel. |
| In the text | |
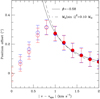 |
Fig. D.2 Same as in Fig. 3 for the synthetic disk model. |
| In the text | |
 |
Fig. D.3 PVdiagram along the disk major axis for the synthetic disk model. The solid line shows the velocity curve obtained from a fit in the uv
plane (see the solid curve in Fig. D.2). The dashed line shows a fit of the first emission contour with a Keplerian law for |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.