| Issue |
A&A
Volume 634, February 2020
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201936693 | |
| Published online | 29 January 2020 | |
Measuring galaxy-galaxy-galaxy-lensing with higher precision and accuracy
1
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: llinke@astro.uni-bonn.de
2
Excellenzcluster Universe, Boltzmannstr. 2, 85748 Garching, Germany
3
Ludwig-Maximilians-Universität, Universitäts-Sternwarte, Scheinerstr.1, 81679 München, Germany
Received:
13
September
2019
Accepted:
7
December
2019
Context. Galaxy-galaxy-galaxy lensing (G3L) is a powerful tool for constraining the three-point correlation between the galaxy and matter distribution and thereby models of galaxy evolution.
Aims. We propose three improvements to current measurements of G3L: (i) a weighting of lens galaxies according to their redshift difference, (ii) adaptive binning of the three-point correlation function, and (iii) accounting for the effect of lens magnification by the cosmic large-scale structure. Improvement (i) is designed to improve the precision of the G3L measurement, whereas improvements (ii) and (iii) remove biases of the estimator. We further show how the G3L signal can be converted from angular into physical scales.
Methods. The improvements were tested on simple mock data and simulated data based on the Millennium Run with an implemented semi-analytic galaxy model.
Results. Our improvements increase the signal-to-noise ratio by 35% on average at angular scales between 0.′1 and 10′ and physical scales between 0.02 and 2 h−1 Mpc. They also remove the bias of the G3L estimator at angular scales below 1′, which was originally up to 40%. The signal due to lens magnification is approximately 10% of the total signal.
Key words: gravitational lensing: weak / galaxies: evolution / cosmology: observations / large-scale structure of Universe / methods: numerical
© ESO 2020
1. Introduction
In the current standard model of cosmology the majority of matter in the Universe is dark and only interacts gravitationally (Planck Collaboration XIII 2016; Hildebrandt et al. 2017). While the formation of dark matter halos and the cosmic large-scale structure (LSS) has been successfully modelled by N-body simulations (see e.g. Springel et al. 2005), the interplay between dark and baryonic matter is still not well understood. Observational tools are needed to distinguish between various semi-analytic models of galaxy evolution (SAMs; see e.g. Henriques et al. 2015; Lacey et al. 2016) and to test the predictions of hydrodynamical simulations (see e.g. Crain et al. 2015; Vogelsberger et al. 2014).
One promising tool is galaxy-galaxy-galaxy-lensing (G3L), first proposed by Schneider & Watts (2005). It involves measuring the connected three-point correlation function between the galaxy and matter distribution by either evaluating the gravitational lensing shear of background galaxies around foreground galaxy pairs (lens-lens-shear correlation) or the lensing shear of background galaxy pairs around single foreground galaxies (lens-shear-shear correlation).
Here, we concentrate on the lens-lens-shear correlation function on small sub-megaparsec scales, where it is most sensitive to galaxy pairs residing in the same matter halo. This function is a powerful discriminator between models of galaxy formation and evolution. In particular, Saghiha et al. (2017) showed that it can better distinguish between galaxy evolution models than galaxy-galaxy-lensing (GGL), where the average shear of individual source galaxies around individual lens galaxies is measured (e.g. Mandelbaum et al. 2006).
The G3L correlation function on small scales was measured successfully by Simon et al. (2008) in the Red Cluster Sequence Lensing Survey and by Simon et al. (2013) in the Canada-France-Hawaii Telescope Lensing Survey (CFHTLenS). However, these measurements were based on photometric data without precise redshift estimates. Consequently, pairs of lens galaxies that are physically close and therefore highly correlated were treated with the same weight as galaxy pairs that are separated along the line of sight and have little to no correlation. As discussed by Simon et al. (2019), these separated galaxies decrease the signal and lower the signal-to-noise ratio (S/N).
Related measurements of the correlation of galaxy pairs and the matter distribution were also undertaken on larger scales, with galaxy pairs separated by several megaparsec, to detect inter-cluster filaments (Mead et al. 2010; Clampitt et al. 2016; Epps & Hudson 2017; Kondo et al. 2019; Xia et al. 2020). These studies relied on precise galaxy redshift estimates provided by spectroscopic surveys. This paper investigates how similarly precise redshift information can be used to enhance the S/N of G3L at smaller scales.
Additionally, G3L is affected by the magnification of lens galaxies caused by the LSS in front of the lenses (Bartelmann & Schneider 2001). This magnification affects the selection function and thereby the number density of lens galaxies in a survey. Because source galaxies are also lensed by the LSS, the shear of sources is correlated with the lens magnification, and an additional correlation signal arises. This signal has not yet been quantified for G3L, but was found to affect GGL by up to 5% in CFHTLenS (Simon & Hilbert 2018).
We introduce three improvements to the G3L estimator used by Simon et al. (2008, 2013): (i) weighting the lens galaxy pairs according to their redshift difference, (ii) using a new, adaptive binning method for the correlation function to reduce biases, and (iii) estimating the magnification bias with lens galaxies that are separated along the line of sight. We also show how the correlation can be measured in terms of physical instead of angular separation and weight the signal by the critical surface mass density Σcrit, as is common for GGL (e.g. Mandelbaum et al. 2006). Thereby, the signal no longer depends on the redshift distribution of source galaxies. To test the effect of our improvements, we apply the new estimator to simple mock data, for which we can directly calculate the expected aperture statistics, and to simulated data based on the Millennium Run (Springel et al. 2005, MR) with the SAM by Henriques et al. (2015, H15).
This paper is structured as follows: Sect. 2 defines the fundamental quantities of G3L, and gives the estimator for the three-point correlation function by Simon et al. (2008). Section 3 explains our new estimator with redshift weighting and the new binning scheme, as well as how the estimator can be converted into physical units and the effect of lens magnification can be estimated. We describe our simulated data set from the MR in Sect. 4. The results of applying our improved measurement scheme to the data are given in Sect. 5, and they are discussed in Sect. 6.
2. Fundamentals of galaxy-galaxy-galaxy-lensing
The G3L is a weak gravitational lensing effect, first discussed by Schneider & Watts (2005, for a review on weak lensing, see Bartelmann & Schneider 2001). We concentrate on systems of two lens and one source galaxy, whose geometric configuration projected onto the sky is shown in Fig. 1. The main observable of G3L in these systems is the three-point correlation function 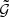 of the projected lens galaxy number density N(ϑ) and tangential gravitational lensing shear γt, given by
of the projected lens galaxy number density N(ϑ) and tangential gravitational lensing shear γt, given by
 |
Fig. 1. Geometry of a G3L configuration with one source and two lens galaxies; adapted from Schneider & Watts (2005). |
The tangential shear is measured with respect to the bisector of the angle ϕ between the lens positions θ + ϑ1 and θ + ϑ2. Because of the isotropy and homogeneity of the matter density field,  only depends on the lens-source separations ϑ1 and ϑ2 and on the opening angle ϕ, so we write
only depends on the lens-source separations ϑ1 and ϑ2 and on the opening angle ϕ, so we write
We can estimate  by averaging the tangential ellipticities of all lens-lens-source triplets where ϑ1 (ϑ2) is the separation between the first (second) lens and the source. As discussed by Simon et al. (2008), this average is an estimator of
by averaging the tangential ellipticities of all lens-lens-source triplets where ϑ1 (ϑ2) is the separation between the first (second) lens and the source. As discussed by Simon et al. (2008), this average is an estimator of
with the angular two-point correlation function ω of lens galaxies. When the complex ellipticity ϵk of source galaxies is used as estimator of their complex lensing shears, Eq. (3) implies that 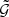 can be estimated for each bin b of ϑ1, ϑ2 and ϕ by a triple sum over all Nd lenses and Ns sources by
can be estimated for each bin b of ϑ1, ϑ2 and ϕ by a triple sum over all Nd lenses and Ns sources by
with
The angle φik(φjk) is the polar angle of the lens-source separation vector θi − θk (θj − θk), and ϕijk is the opening angle between θi − θk and θj − θk (see Fig. 1; θi − θk and θj − θk correspond to ϑ1 and ϑ2, ϕijk corresponds to ϕ). The wk are weights of the measured ellipticities. To apply the estimator to observational data, a higher weight should be assigned to sources with more precise shape measurements, whereas sources with less precise shapes should be down-weighted. Because we apply the estimator to simulated data, we set wk ≡ 1 throughout this work. The phase factor and minus sign in Eq. (4) are due to the definition of tangential and cross shear in terms of the Cartesian shear components.
In order to estimate ω, we use “randoms”. These are mock galaxies that are distributed unclustered on the sky, but obey the same selection function as the lens galaxies. With these randoms, we estimate ω with the Landy–Szalay estimator (Landy & Szalay 1993)
Here, DD(θ) is the pair-count of the Nd lens galaxies, RR(θ) is the pair-count of the Nr randoms and DR(θ) is the cross pair-count of lenses and randoms at separation θ.
The correlation function 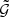 mixes second- and third-order statistics. This becomes evident when we rewrite
mixes second- and third-order statistics. This becomes evident when we rewrite 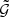 , using the galaxy density contrast κg = N/N̄ − 1, as
, using the galaxy density contrast κg = N/N̄ − 1, as
The second and third term in Eq. (8) are the GGL signals around individual lenses, while only the first term encompasses the G3L signal, which is the additional correlation 𝒢 around lens pairs.
To remove the contribution due to GGL, we convert 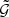 into aperture statistics. Aperture statistics are expectation values of products of the aperture number count 𝒩θ and the aperture mass Map, θ. These are defined as (Bartelmann & Schneider 2001)
into aperture statistics. Aperture statistics are expectation values of products of the aperture number count 𝒩θ and the aperture mass Map, θ. These are defined as (Bartelmann & Schneider 2001)
and
with the projected galaxy number density N(ϑ), the lensing convergence κ(ϑ), and the filter function Uθ(ϑ) with characteristic scale θ. This filter function needs to be compensated for, that is, 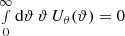 . Because of this property, the aperture number count can be written in terms of the galaxy number density contrast as
. Because of this property, the aperture number count can be written in terms of the galaxy number density contrast as
For each Uθ, an associated filter function Qθ can be defined by
With this filter Qθ,
where M⊥, θ is the B-mode of the aperture mass.
With the lens-lens-shear correlation function, we study the aperture statistics ⟨𝒩2Map⟩ and ⟨𝒩2M⊥⟩, given by
These aperture statistics can be related to 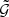 for a chosen filter function Uθ. Provided the exponential filter function,
for a chosen filter function Uθ. Provided the exponential filter function,
Schneider & Watts (2005) found
with the kernel function A𝒩𝒩M(ϑ1, ϑ2, ϕ|θ1, θ2, θ3) in the appendix of Schneider & Watts (2005).
Due to Eq. (12), Eq. (15) can also be written as
which leads to
with the same kernel function as Eq. (17). Consequently, the aperture statistics depend only on the additional correlation due to G3L, while the impact of GGL is removed by the compensated filter function.
As discussed in Schneider (2003), the imaginary part of the integral in Eq. (17), the B-mode ⟨𝒩2M⊥⟩, is expected to vanish unless systematic effects cause a parity violation. We do not expect such a violation by any physical process; even the occurrence of B-modes for the gravitational shear, which might be due to intrinsic alignments or clustering of source galaxies (Schneider et al. 2002), cannot induce a non-zero ⟨𝒩2M⊥⟩. We nevertheless measure ⟨𝒩2M⊥⟩, as a consistency check alongside the E-mode ⟨𝒩2Map⟩ with 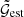 . We only measure the aperture statistics for equal aperture scale radii θ and use the short-hand notations ⟨𝒩2Map⟩(θ, θ, θ) = : ⟨𝒩2Map⟩(θ) and ⟨𝒩2M⊥⟩(θ, θ, θ) = : ⟨𝒩2M⊥⟩(θ).
. We only measure the aperture statistics for equal aperture scale radii θ and use the short-hand notations ⟨𝒩2Map⟩(θ, θ, θ) = : ⟨𝒩2Map⟩(θ) and ⟨𝒩2M⊥⟩(θ, θ, θ) = : ⟨𝒩2M⊥⟩(θ).
3. Methods
3.1. Redshift weighting
To reduce the signal degradation by uncorrelated lens pairs, we define a redshift-weighted correlation function  , for which lens pairs are weighted according to their redshift difference δz. To this end, we introduce the redshift-weighting function Z(δz), for which we choose a Gaussian,
, for which lens pairs are weighted according to their redshift difference δz. To this end, we introduce the redshift-weighting function Z(δz), for which we choose a Gaussian,
The width σZ is a free parameter that should correspond to the typical redshift difference of correlated lens pairs. The weighting function is normalized such that it is unity if the galaxies have the same redshift. Averaging over the tangential ellipticities of lens-lens-source triplets weighted with Z leads to an estimate of
where N(ϑ, z) is the number density of lens galaxies at angular position ϑ and redshift z, and Δz12 = z1 − z2. Equation (21) defines the redshift-weighted correlation function 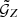 and uses the redshift-weighted two-point angular correlation function ωZ. We estimate
and uses the redshift-weighted two-point angular correlation function ωZ. We estimate 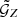 with
with
To estimate the redshift-weighted two-point correlation ωZ, we use the Nr randoms, located at 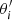 , the Nd lenses at the positions θi, and the estimator
, the Nd lenses at the positions θi, and the estimator
with the modified pair-counts
and
Here, ΘH is the Heaviside step function and Δθ is the bin size for which ωZ is estimated. For Z ≡ 1, this estimator reduces to the standard Landy–Szalay estimator in Eq. (7).
The aperture statistics from the redshift-weighted correlation function 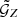 are expected to have a higher S/N than the aperture statistics from the original
are expected to have a higher S/N than the aperture statistics from the original 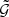 . This expected improvement can be estimated with simplified assumptions. For this, we assume that the Ntot lens-lens-source triplets can be split into Ntrue physical triplets, each carrying the signal s, and Ntot − Ntrue triplets carrying no signal. We further assume that all triplets carry the same uncorrelated noise n. Then, the measured total signal S, noise N and S/N are
. This expected improvement can be estimated with simplified assumptions. For this, we assume that the Ntot lens-lens-source triplets can be split into Ntrue physical triplets, each carrying the signal s, and Ntot − Ntrue triplets carrying no signal. We further assume that all triplets carry the same uncorrelated noise n. Then, the measured total signal S, noise N and S/N are
With redshift weighting we decrease the effective number of triplets from Ntot to Ñtot, while retaining the same number of physical triplets Ntrue. The signal S̃, the noise Ñ and the new S/N S̃/Ñ are then
Consequently, redshift weighting increases the noise by a factor of (Ntot/Ñtot)1/2. Nonetheless, the S/N improves by (Ntot/Ñtot)1/2 because the signal increases by Ntot/Ñtot. Accordingly, we expect the S/N to increase approximately by the square root of the signal increase.
The critical parameter for the redshift weighting is the width σz of the weighting function. For our application on the observational and simulated data described in Sect. 4, we choose σz = 0.01. Because lens pairs that carry signal and those that do not are not clearly divided, the choice of this parameter needs to remain somewhat arbitrary. However, three arguments can be made to motivate our choice.
The first argument considers the galaxy correlation length. Farrow et al. (2015) measured the two-point correlation function of galaxies in the Galaxy and Mass Assembly survey (GAMA) and found correlation lengths between 3.28 ± 0.42 h−1 Mpc and 38.17 ± 0.47 h−1 Mpc, depending on the stellar masses of the galaxies. The same function was measured by Zehavi et al. (2011) in the Sloan Digital Sky Survey (SDSS). They found similar correlation lengths between 4.2 h−1 Mpc and 10.5 h−1 Mpc. These correlation lengths correspond to redshift differences between 0.001 and 0.005 at the median redshift of GAMA of z = 0.21. We assume that galaxies separated by more than twice the correlation length are only weakly correlated, and therefore our choice of σz = 0.01 seems appropriate.
The second argument relates to the distribution of lens galaxy pairs with their redshift difference. The blue histogram in Fig. 2 shows the number of galaxy pairs per redshift difference δz with fixed angular separation between 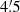 and
and 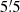 in our lens sample from the MR (see Sect. 4). This distribution has a prominent peak for small δz and a broad background distribution. Thus, most galaxy pairs that appear close on the sky are also close in redshift space. These physical pairs make up the peak. However, the background distribution shows that there are also many galaxy pairs with small angular separation whose redshift difference is large. The redshift weighting function should now be chosen in such a way that pairs inside the peak are preserved, while the background is suppressed.
in our lens sample from the MR (see Sect. 4). This distribution has a prominent peak for small δz and a broad background distribution. Thus, most galaxy pairs that appear close on the sky are also close in redshift space. These physical pairs make up the peak. However, the background distribution shows that there are also many galaxy pairs with small angular separation whose redshift difference is large. The redshift weighting function should now be chosen in such a way that pairs inside the peak are preserved, while the background is suppressed.
 |
Fig. 2. Weighted number of lens galaxy pairs in our sample from the MR with fixed angular separation between |
The other histograms in Fig. 2 show different weighted distributions, where the number of galaxy pairs is multiplied by the redshift-weighting function from Eq. (20). This gives the effective number of galaxy pairs per redshift difference bin that are considered for the improved 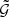 estimator. Here, the effect of different σz is visible. The peak is preserved when we use σz = 0.1 and 0.05, but a high percentage of the background is still present in the weighted distribution. For σz = 0.005 and σz = 0.001, the background is removed, but parts of the peak are also suppressed. A middle ground is found for σz = 0.01. Here, the tails of the peak still contribute, whereas most of the background galaxy pairs are suppressed. Consequently, we adopt this value for the measurement of
estimator. Here, the effect of different σz is visible. The peak is preserved when we use σz = 0.1 and 0.05, but a high percentage of the background is still present in the weighted distribution. For σz = 0.005 and σz = 0.001, the background is removed, but parts of the peak are also suppressed. A middle ground is found for σz = 0.01. Here, the tails of the peak still contribute, whereas most of the background galaxy pairs are suppressed. Consequently, we adopt this value for the measurement of 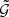 and subsequently ⟨𝒩2Map⟩.
and subsequently ⟨𝒩2Map⟩.
The third argument for our choice of σz considers the peculiar velocities of galaxies in clusters, which can cause redshift differences of correlated galaxy pairs inside the same halo. The weighting function Z needs to be broad enough to avoid discarding galaxy pairs whose redshift differences are induced simply by their peculiar motion. Velocities of galaxies inside halos can reach up to 1000 km s−1, leading to redshift differences of up to 0.006. This is a lower bound for σz, therefore choosing σz = 0.01 appears valid.
3.2. New binning scheme
In previous work (Simon et al. 2008, 2013), 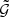 was measured on a regular grid with logarithmic spacing in the lens-source separations ϑ1 and ϑ2 and linear spacing in the opening angle ϕ. The aperture statistics were then calculated by summing over this grid.
was measured on a regular grid with logarithmic spacing in the lens-source separations ϑ1 and ϑ2 and linear spacing in the opening angle ϕ. The aperture statistics were then calculated by summing over this grid.
However, in this approach, the estimator for 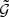 is undefined in any bin for which no triplet was found. In previous work,
is undefined in any bin for which no triplet was found. In previous work, 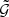 was therefore set to zero in these empty bins. As a result ⟨𝒩2Map⟩, which is obtained by integrating over the estimated
was therefore set to zero in these empty bins. As a result ⟨𝒩2Map⟩, which is obtained by integrating over the estimated 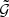 , was underestimated (Simon et al. 2008). This bias occurs for both small and large scales: At small scales, the bins for ϑ1 and ϑ2 are small because of the logarithmic binning, therefore many bins remain empty. At large scales, certain bins automatically remain empty because the opening angle ϕ cannot assume all values between 0 and 2π if ϑ1 or ϑ2 are larger than the side length of the field of view.
, was underestimated (Simon et al. 2008). This bias occurs for both small and large scales: At small scales, the bins for ϑ1 and ϑ2 are small because of the logarithmic binning, therefore many bins remain empty. At large scales, certain bins automatically remain empty because the opening angle ϕ cannot assume all values between 0 and 2π if ϑ1 or ϑ2 are larger than the side length of the field of view.
The bin sizes and number of lens-lens-source triplets affect by how much ⟨𝒩2Map⟩ is underestimated. If the bins are smaller, the probability of encountering empty bins is higher and the bias is stronger. If the number of triplets increases, there are fewer empty bins and the bias decreases.
To account for this effect, we introduce an adaptive binning scheme, illustrated in Fig. 3. In this new scheme, bins are defined such that they contain at least one triplet, and therefore the estimator for 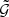 is always well defined. For this,
is always well defined. For this, 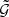 is first estimated on a regular grid, together with the average side lengths of the triplets in each bin. Then, in all bins for which triplets are found, the measured
is first estimated on a regular grid, together with the average side lengths of the triplets in each bin. Then, in all bins for which triplets are found, the measured 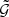 is associated with the average ϑ1, ϑ2 and ϕ of the corresponding bin. We use the averages of the triplets in filled bins as seeds to divide the parameter space by a Voronoi tessellation, using the library voro++ by Rycroft (2009). Each Voronoi cell is then considered as a new bin for which
is associated with the average ϑ1, ϑ2 and ϕ of the corresponding bin. We use the averages of the triplets in filled bins as seeds to divide the parameter space by a Voronoi tessellation, using the library voro++ by Rycroft (2009). Each Voronoi cell is then considered as a new bin for which 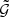 is estimated. These bins by definition contain at least one triplet. The aperture statistics are obtained by integrating over the Nbin new bins, using the numerical approximation of Eq. (17),
is estimated. These bins by definition contain at least one triplet. The aperture statistics are obtained by integrating over the Nbin new bins, using the numerical approximation of Eq. (17),
where bi is the ith bin, V(bi) is the volume of this bin, and ANNM(bi|θ) is the kernel function of Eq. (17) evaluated at the seed of bi. We estimate 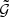 on a grid with 128 × 128 × 128 bins with ϑ1 and ϑ2 between
on a grid with 128 × 128 × 128 bins with ϑ1 and ϑ2 between 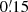 and 320′ for the data based on the MR (see Sect. 4.1) and between
and 320′ for the data based on the MR (see Sect. 4.1) and between 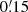 and 200′ for the simple mock data (see Sect. 4.2). The tessellation reduces the number of bins by approximately 3% in both cases.
and 200′ for the simple mock data (see Sect. 4.2). The tessellation reduces the number of bins by approximately 3% in both cases.
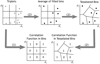 |
Fig. 3. Illustration of the old (1) and new (2) binning scheme for the calculation of |
3.3. Conversion into physical units
With the lens redshifts z1 and z2, we can transform the projected angular separation vectors ϑ1 and ϑ2 into physical separations r1 and r2 on a plane midway between the two lenses, using
with the angular diameter distance DA(za, zb) between redshifts za and zb and the average lens redshift z12 = (z1 + z2)/2.
The correlation function 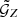 can therefore be estimated in physical scales in the bin b of r1, r2 and ϕ as
can therefore be estimated in physical scales in the bin b of r1, r2 and ϕ as
with
This 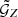 still depends on the redshift distribution of sources because the gravitational shear γt depends on the lensing efficiency, which in turn depends on the distances between observer and source and lens and source. To compare the measurements of different surveys with varying source redshift distributions, it is therefore useful to correlate the galaxy number density not with the tangential shear γt, but instead with the projected excess mass density ΔΣ, given by
still depends on the redshift distribution of sources because the gravitational shear γt depends on the lensing efficiency, which in turn depends on the distances between observer and source and lens and source. To compare the measurements of different surveys with varying source redshift distributions, it is therefore useful to correlate the galaxy number density not with the tangential shear γt, but instead with the projected excess mass density ΔΣ, given by
with the inverse critical surface mass density
Thus, we are interested in the correlation function 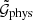 , defined by
, defined by
To estimate this quantity with a maximum likelihood estimator, we need to multiply the weight wk of each source galaxy with 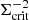 (Sheldon et al. 2004). This leads to the estimator
(Sheldon et al. 2004). This leads to the estimator
with Σcrit ijk = Σcrit(zij, zk).
This estimator requires a precise knowledge of the source redshifts. For the application to real data, however, only photometric redshift estimates are often available for source galaxies. Therefore, we do not use the exact 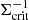 for each triplet, but instead
for each triplet, but instead 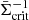 , which is averaged over the source distribution ps(zs) as
, which is averaged over the source distribution ps(zs) as
Consequently, we estimate  with
with
We convert this physical three-point correlation function into physical aperture statistics with
These aperture statistics are in units of mass over area.
3.4. Magnification of lens galaxies
Magnification of lens galaxies by the LSS affects G3L because the apparent magnitude and number density of lenses is changed (Bartelmann & Schneider 2001). In the weak-lensing limit, the number density of lens galaxies at angular position ϑ and redshift z is changed from the intrinsic number density N0(ϑ, z) to
where κ(ϑ, z) is the convergence caused by all matter in front of redshift z, and α(z) is the negative slope of the luminosity function Φ(S, z) at the flux limit Slim of lens galaxies. We define α by
Consequently, the correlation function 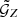 with the effect of lens magnification is
with the effect of lens magnification is
With the intrinsic aperture number count
and Map, θ as defined in Eq. (11), the aperture statistics are
Thus, the measured aperture statistics do not only include the intrinsic first term, but three additional terms that are due to lens magnification. These lens magnification terms, however, can be measured using as redshift-weighting function Z not a Gaussian, but a step function,
This means that only lens pairs with a redshift difference larger than Δz and z2 > z1 are counted in the estimator in Eq. (22). As explained in Sect. 3.1, we expect lens pairs with redshift differences larger than 0.01 to be intrinsically uncorrelated. When we choose Δz = 0.01, the first term in Eq. (44), which contains only the correlation of intrinsic number densities, should vanish. The measured ⟨𝒩2Map⟩ is then purely the correlation due to the lens magnification. We measure this ⟨𝒩2Map⟩ with the estimator in Eq. (22), using the step function weighting. If this signal is then subtracted from the measured ⟨𝒩2Map⟩ of all lenses, we obtain the intrinsic aperture statistics.
Because we tested our approach on simulated data from the MR, for which both the number density and convergence are available at different redshift planes, we can also use another approach to measure the terms due to lens magnification. In this approach we use the relation of the observed aperture number count 𝒩θ to the intrinsic aperture number count 𝒩0, θ and aperture mass Map, θ through
Consequently, Eq. (44) with the step function weighting in Eq. (45) leads to
where the terms due to lens magnification are given by the observed instead of by the intrinsic aperture number count. For a numerical evaluation, the integrals can be converted into sums over M redshift slices, so
Using Eq. (50), we measure the lens magnification terms Lℳℳℳ, Lℳ𝒩ℳ and L𝒩ℳℳ directly in the simulated data based on the MR for zj < 0.5 and zi < zj.
For this, we first convolve the number density and convergence maps at each redshift plane with the filter function Uθ to obtain 𝒩θ(ϑ, zi) and Map, θ(ϑ, zj). We then multiply the aperture statistics for each combination of zi and zj and spatially average the products to obtain ⟨𝒩θ(ϑ, zi) Map, θ(ϑ, zj) Map, θ(ϑ)⟩ and ⟨Map, θ(ϑ, zi) Map, θ(ϑ, zj) Map, θ(ϑ)⟩. These averages are then multiplied by the appropriate α and summed over. We repeat this procedure for different aperture scale radii θ between 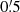 and 8′.
and 8′.
For this calculation, the slope α(z) of the lens luminosity function needs to be known. To obtain α(z), we extract the luminosity function Φ(S, z) at each redshift plane of the MR, with S measured in the r-band filter. We then fit a power law to Φ(S, z) in the proximity of the limiting flux. This flux is given in our case by the limiting r-band magnitude, chosen to be rlim = 19.8 mag. The slopes for each redshift z are the α(z) given in Table 1.
Slopes α(z) of the luminosity function at different redshifts z in the MR.
4. Data
4.1. Simulated data based on the MR
We tested our new estimator with simulated data sets from the MR. The MR (Springel et al. 2005) is a dark matter-only cosmological N-body-simulation. It traces the evolution of 21603 dark matter particles of mass m = 8.6 × 108 h−1 M⊙ from redshift z = 127 to today in a cubic region with co-moving side length 500 h−1 Mpc. For this, a flat ΛCDM cosmology was assumed, with matter density Ωm = 0.25, baryon density Ωb = 0.045, dark energy density ΩΛ = 0.75, Hubble constant H0 = 73 km s−1 Mpc−1, and power spectrum normalization σ8 = 0.9.
Using the multiple-lens-plane ray-tracing algorithm by Hilbert et al. (2009), we created maps of the complex gravitational shear γ caused by the matter distribution for a set of source redshift planes. For each redshift, 64 maps of γ on a regular mesh with 40962 pixels, corresponding to 4 × 4 deg2, were obtained. We combined the shear of nine different redshifts between z = 0.5082 and z = 1.1734 by summing γ weighted by an assumed source redshift distribution ps(z). This redshift distribution, shown in Fig. 4, was modelled after the redshift distribution of galaxies in the Kilo-Degree Survey (KiDS; Wright et al. 2019; Hildebrandt et al. 2020). To mimic the shape noise in observational data, we added a random number drawn from a Gaussian probability distribution with standard deviation 0.3 to both shear components at each pixel. This gave us 64 maps of mock source galaxies.
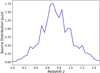 |
Fig. 4. Assumed source redshift distribution. This distribution is used to weigh the shear maps at different redshifts in the MR. It is modelled after the redshift distribution of galaxies in Hildebrandt et al. (2020). |
Lens galaxies in the simulation were created by using the SAM by H15. It is one of various SAMs that have been implemented on the MR (see e.g. Guo et al. 2011; Bower et al. 2006), but as Saghiha et al. (2017) have shown, this model agrees particularly well with measurements of GGL and G3L in CFHTLenS. To simulate the selection function of observations, we applied a redshift and flux limit on our lens samples. We used lenses with z ≤ 0.5 and SDSS r-band magnitude brighter than 19.8 mag. With these limits, we obtained a number density of lenses of 0.282 arcmin−2.
To mitigate possible biases induced by uneven galaxy pair numbers and matter distributions between the 64 lens galaxy maps, we subtracted the lensing signal around random points. This is similar to GGL studies, where the shear around random positions is measured and subtracted from the original measurement (Singh et al. 2017). However, for G3L, this task is in general more difficult because it requires a catalogue of unclustered galaxy pairs. Creating such a catalogue is in general non-trivial because the number of galaxy pairs depends on the selection function of individual galaxies in the survey. Nevertheless, we created a map of unclustered galaxies, similar to GGL, for each simulated lens map by distributing the same number of galaxies as on the lens map at random points on a 4 × 4 deg2 area. We measured the correlation function 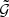 for each of these random maps and subtracted it from the correlation function measured for the actual lens map.
for each of these random maps and subtracted it from the correlation function measured for the actual lens map.
The total number of triplets to consider for our measurement of 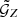 and
and 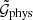 is 5 × 1012. This makes the evaluation of the sums in Eqs. (22) and (38) computationally involved. Because of this computational complexity, third-order correlation functions are usually computed involving some approximation, such as kd-Tree codes (Simon et al. 2013), where galaxy triplets with similar ϑ1, ϑ2 and ϕ are averaged. However, we implemented the estimator brute force and calculated it with graphics processing units (GPUs). This approach has two advantages compared to the usual methods. First, if is exact, even at the smallest scales. Second, due to the highly parallelized execution on a GPU, which allows for several thousand simultaneous calculations, the computing time is drastically reduced. In our case, the computational time to process the MR decreased from 200 h with a kd-Tree code executed on 8 CPU cores to just 9 h with the brute-force code on a single GPU. Details for our computational implementation are given in Appendix B.
is 5 × 1012. This makes the evaluation of the sums in Eqs. (22) and (38) computationally involved. Because of this computational complexity, third-order correlation functions are usually computed involving some approximation, such as kd-Tree codes (Simon et al. 2013), where galaxy triplets with similar ϑ1, ϑ2 and ϕ are averaged. However, we implemented the estimator brute force and calculated it with graphics processing units (GPUs). This approach has two advantages compared to the usual methods. First, if is exact, even at the smallest scales. Second, due to the highly parallelized execution on a GPU, which allows for several thousand simultaneous calculations, the computing time is drastically reduced. In our case, the computational time to process the MR decreased from 200 h with a kd-Tree code executed on 8 CPU cores to just 9 h with the brute-force code on a single GPU. Details for our computational implementation are given in Appendix B.
The covariance matrices of the measured ⟨𝒩2Map⟩ and ⟨𝒩2Map⟩phys were computed with jackknifing. For this, we assumed that each of the 64 fields is an independent realization and combined these fields to a total ⟨𝒩2Map⟩(θ) and 64 jackknife samples ⟨𝒩2Map⟩k(θ), where all but the kth tile were combined. The covariance matrix is then
where 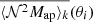 is the average of all ⟨𝒩2Map⟩k(θi). The statistical uncertainty of ⟨𝒩2Map⟩(θi) is
is the average of all ⟨𝒩2Map⟩k(θi). The statistical uncertainty of ⟨𝒩2Map⟩(θi) is 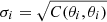 . We define the S/N at each scale radius θi as
. We define the S/N at each scale radius θi as
4.2. Simple mock data
Some of our tests also employed simple mock data. These were chosen such that it was easy to create them and to calculate their expected aperture statistics theoretically. For this we used the following assumptions:
-
A.
All matter and galaxies are distributed inside Nh halos over an area A.
-
B.
All halos are situated on the same lens plane.
-
C.
All halos have the same axisymmetric convergence profile κ(ϑ) = K u(ϑ), where ∫ dϑ ϑ u(ϑ) = 1, and also the same number of galaxies Ngal.
-
D.
There is no galaxy bias, so the discrete galaxy distribution follows the matter distribution up to Poisson shot-noise.
-
E.
Halo centres are distributed randomly within A.
With these assumptions and the calculations in Appendix A, the theoretical expectation for the aperture statistics using the exponential filter function in Eq. (16) is
with fn(x) = In(x) e−x and the modified Bessel functions of the first kind In(x). We evaluated the integrals numerically with a Monte Carlo integration using the monte-vegas-routine of the GNU Scientific Library (Gough 2009).
We used the Brainerd-Blandford-Smail (BBS) profile (Brainerd et al. 1996) as halo convergence profile κ(ϑ), which is
The BBS profile corresponds to a singular isothermal sphere (SIS) for ϑ much smaller than the scale radius θs that smoothly drops outside the sphere. In contrast to the SIS profile, it has a finite total mass. We chose K = 1 arcmin2 and θs = 5′.
We created mock lens galaxies following assumptions A to E in a circular area with a radius of 700′. The lens galaxies were distributed in 2170 halos with 200 galaxies each. These numbers were chosen such that the average number density of lens galaxies was N̅d = 0.287 arcmin−2, the lens number density in our lens sample from the MR. We distributed 3 × 106 source galaxies, whose shear was computed from the halo convergence profiles, in the central 750 × 750 arcmin2 area. We only considered lens-lens-source triplets in this area to ensure that the shear of each source was affeted by halos from all directions. No shape noise was added to the shears because our aim was not to create a realistic simulation, but only a simple test case. Because 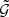 is linear in the ellipticities, any shape noise would not bias its estimate and only lead to a larger uncertainty of the measurement. The central area was cut into quadratic tiles with a side length of 150′, so that finally 25 maps of source and lens galaxies were used.
is linear in the ellipticities, any shape noise would not bias its estimate and only lead to a larger uncertainty of the measurement. The central area was cut into quadratic tiles with a side length of 150′, so that finally 25 maps of source and lens galaxies were used.
5. Results
5.1. Effect of the new binning scheme
Before measuring the aperture statistics in the data based on the MR, we estimated the effect of the new binning scheme by measuring the aperture statistics for equal-scale radii θ in the simple mock data, described in Sect. 4.2. The aperture statistics measured in this mock data are displayed in Fig. 5. The theoretically expected ⟨𝒩2Map⟩ follows a power law for scale radii above 2′ and steepens for larger scales. The ⟨𝒩2Map⟩ measured with the old and the new binning scheme both show the same steepening for θ larger than 2′, but the slope of the ⟨𝒩2Map⟩ measured with the old binning scheme is considerably shallower for scales between 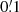 and
and 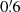 than the one measured with the new binning scheme. We confirm that the measurement with the new binning scheme agrees with the theoretical expectation within its statistical uncertainty. This agreement of the measured aperture statistics with the theoretical prediction validates our code for estimating
than the one measured with the new binning scheme. We confirm that the measurement with the new binning scheme agrees with the theoretical expectation within its statistical uncertainty. This agreement of the measured aperture statistics with the theoretical prediction validates our code for estimating 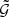 and for converting
and for converting 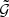 to ⟨𝒩2Map⟩.
to ⟨𝒩2Map⟩.
 |
Fig. 5. Aperture statistics measured in the simple mock data with the old binning scheme (blue dots) and the new binning scheme (red crosses), as well as the theoretical expectation (black line) given by Eq. (53). Upper plot: E-mode ⟨𝒩2Map⟩. Lower plot: ratio of the B-mode ⟨𝒩2M⊥⟩ and the E-mode. Uncertainties are the statistical error estimated with jackknifing. |
To quantify the effect of the new binning scheme, Fig. 6 shows the difference of the measured ⟨𝒩2Map⟩ to the theoretical prediction for both binning schemes, normalized by the theoretical prediction. While the ⟨𝒩2Map⟩ from the old method has no bias at scales between 1′ and 5′, it underestimates ⟨𝒩2Map⟩ both above and below these scales. At large scales, this bias grows to 10% at θ = 10′, whereas at small scales, the bias increases with decreasing scale to 40% at 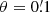 . The new binning scheme does not show this behaviour. Instead, the bias of the ⟨𝒩2Map⟩ measured with the new method is consistent with zero at all considered scales.
. The new binning scheme does not show this behaviour. Instead, the bias of the ⟨𝒩2Map⟩ measured with the new method is consistent with zero at all considered scales.
 |
Fig. 6. Fractional difference of the measured ⟨𝒩2Map⟩ relative to the theoretical prediction in the mock data. Blue dots show the measurement with the old binning scheme; red crosses show the measurement with the new binning scheme. |
5.2. Effect of lens magnification
As outlined in Sect. 3.4, the redshift weighting enables us to measure the impact of lens magnification on G3L. We estimated this effect in the data based on the MR with the two different methods outlined in Sect. 3.4. In the following, the terms “first” and “second” lens plane refer to the redshift plane in which the lens galaxy lies closer to the observer and closer to the source, respectively.
The result for the first method, using the step function weighting in the estimation of 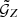 , is shown in Figs. 7 and 8 for ⟨𝒩2Map⟩ and ⟨𝒩2Map⟩phys, respectively. The figures show the aperture statistics measured for lens pairs with redshift differences larger than 0.01. If there were no lens magnification, this signal should vanish. The figures also show the aperture statistics measured when all lens pairs are taken into account, as well as the intrinsic aperture statistics “corrected” for the effect of lens magnification by subtracting the signal of physically distant lens pairs from the total measured aperture statistics.
, is shown in Figs. 7 and 8 for ⟨𝒩2Map⟩ and ⟨𝒩2Map⟩phys, respectively. The figures show the aperture statistics measured for lens pairs with redshift differences larger than 0.01. If there were no lens magnification, this signal should vanish. The figures also show the aperture statistics measured when all lens pairs are taken into account, as well as the intrinsic aperture statistics “corrected” for the effect of lens magnification by subtracting the signal of physically distant lens pairs from the total measured aperture statistics.
 |
Fig. 7. Effect of lens magnification on aperture statistics in the data based on the MR. The green dash-dotted line shows the signal measured for lens pairs with redshift differences larger than 0.01, which corresponds to the magnification terms in Eq. (44). The blue solid line is the aperture statistics for all lens pairs. The red dashed line is the intrinsic signal, which is corrected for lens magnification by subtracting the signal of separated lens pairs. Shaded regions are the 1σ uncertainties from jackknifing. |
For both ⟨𝒩2Map⟩ and ⟨𝒩2Map⟩phys, the signal of physically separated lens pairs is non-zero. We attribute this signal to the three magnification terms in Eq. (44). For ⟨𝒩2Map⟩ this signal is approximately 10% of the signal of all lens pairs. For ⟨𝒩2Map⟩phys, the magnification leads to a slightly weaker additional signal at scales below 0.1 h−1 Mpc and approximately 10% at larger scales.
At angular scales smaller than 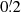 , the signal due to lens magnification for ⟨𝒩2Map⟩ decreases. This is probably due to smoothing in the simulation, which is no longer accurate at these small angular scales. Smoothing flattens the centre of halo convergence profiles in the simulation. If the aperture statistics are measured at scale radii smaller than the smoothing lengths, the flattened profile then leads to a smaller measured signal.
, the signal due to lens magnification for ⟨𝒩2Map⟩ decreases. This is probably due to smoothing in the simulation, which is no longer accurate at these small angular scales. Smoothing flattens the centre of halo convergence profiles in the simulation. If the aperture statistics are measured at scale radii smaller than the smoothing lengths, the flattened profile then leads to a smaller measured signal.
To verify that the measured signal for distant lens pairs is indeed related to lens magnification, Fig. 9 shows the magnification terms measured with the second method from Sect. 3.4, using the convolution of the aperture filter function with the convergence and number density maps. For comparison, the measured ⟨𝒩2Map⟩ from the first method is also shown.
 |
Fig. 9. Individual lens magnification terms in the MR. Green stars depict the term due to correlation between the convergence maps at the two lens planes and at the source plane, red dots are the term due to correlation of the galaxy number density at the first lens plane to the convergence maps at the second lens and the source plane, brown crosses are the term due to correlation of the convergence maps at the first lens and the source plane to the galaxy number density at the second lens plane. The blue line is the measured ⟨𝒩2Map⟩ for separated lens pairs, which should correspond to the total lens magnification signal. |
The figure shows that L𝒩ℳℳ(θ), which is due to the correlation of the number density of galaxies at smaller redshift to the convergence measured at higher redshifts, is the dominating term. It is larger than Lℳℳℳ and Lℳ𝒩ℳ by three orders of magnitude. Furthermore, the correlation of three convergence maps Lℳℳℳ and the correlation of foreground convergence maps to background galaxies Lℳ𝒩ℳ are almost identical. Consequently, the total lens magnification signal is approximately L𝒩ℳℳ.
This indicates that the lens magnification signal is driven mainly by the correlation of matter and the galaxy distribution at the first lens plane. This matter affects the convergence at the second lens and the source plane and thereby causes a significant L𝒩ℳℳ. Neither Lℳ𝒩ℳ nor Lℳℳℳ depend on the correlation between matter and galaxies at the same plane, and they are mainly caused by the LSS in front of the first lens plane. This LSS influences 𝒩θ and Map, θ at the lens planes and the source plane and thereby induces the non-zero Lℳ𝒩ℳ and Lℳℳℳ. However, as shown in Fig. 9, this effect is secondary, and the LSS in front of the lenses does not have a strong effect on the overall signal.
The total lens magnification signal is of the same order of magnitude as the ⟨𝒩2Map⟩ measured with separated lens pairs. At scales above 1′, it indeed agrees with the measured ⟨𝒩2Map⟩ for separated lens pairs within its statistical uncertainty. At smaller scales, the difference between the two quantities is still smaller than twice the statistical uncertainty. According to Eq. (48), the intrinsic aperture statistics are
where ⟨𝒩2Map⟩ are the measured aperture statistics for separated lens pairs. Therefore, the intrinsic aperture statistics for separated lens pairs vanishes, as expected.
5.3. Effect of redshift weighting
The results for ⟨𝒩2Map⟩ for the data based on the MR with and without redshift weighting are shown in Fig. 10a. The measured ⟨𝒩2M⊥⟩ is consistent with zero, both with and without redshift weighting. This signifies that no indication of parity violation and B-modes is found in the simulation.
 |
Fig. 10. Aperture statistics measured in the mock data based on the MR, in (a) with angular and in (b) with physical units. Upper plots: E-modes ⟨𝒩2Map⟩ and ⟨𝒩2Map⟩phys. Middle plots: ratio of the B-modes ⟨𝒩2M⊥⟩ and ⟨𝒩2M⊥⟩phys to ⟨𝒩2Map⟩ and ⟨𝒩2Map⟩phys. Lower plots: S/N of ⟨𝒩2Map⟩ and ⟨𝒩2Map⟩phys. The red dashed line depicts ⟨𝒩2Map⟩ taken with a redshift weighting function with width σz = 0.01. Shaded regions show the 1σ uncertainties from jackknifing. The blue solid line denotes the measurements without redshift weighting. |
Redshift-weighting increases the S/N, as indicated by the decreasing error region in Fig. 10a. Simultaneously, the measured ⟨𝒩2Map⟩ is increased by a factor of approximately two. This is expected because redshift weighting is assumed to increase both signal and S/N, as discussed in Sect. 3.1. The lower plot in Fig. 10a shows the S/N of ⟨𝒩2Map⟩ with and without redshift weighting as function of the aperture scale radius θ. Redshift weighting increases the S/N on all scales. On average, the S/N of ⟨𝒩2Map⟩ with redshift weighting is 1.35 times the S/N of ⟨𝒩2Map⟩ without redshift weighting.
The measured physical aperture statistics ⟨𝒩2Map⟩phys are displayed in Fig. 10b. Again, the B-mode is consistent with zero at all scales. Redshift weighting increases the signal by a factor of two, similar to the increase of ⟨𝒩2Map⟩, whereas the error region decreases. The increase of the S/N of ⟨𝒩2Map⟩phys, shown in the lower plot of Fig. 10b, is at the same level as for ⟨𝒩2Map⟩; on average, the S/N increases by 34%. In Fig. 10 the S/N of ⟨𝒩2Map⟩phys is higher than the S/N of ⟨𝒩2Map⟩, both with and without redshift weighting.
6. Discussion
We proposed three improvements to the measurement of the G3L signal: Using a redshift weighting of lens galaxies to improve the precision, removing biases on the estimator with a new binning scheme, and accounting for the impact of lens magnification. We furthermore showed how the G3L signal can be measured in physical units.
The effect of the improved binning scheme can be seen by comparing our measurement on the simple mock data with the theoretical expectation. The original binning leads to a discrepancy between the theoretical expectation and the measurement both for aperture scale radii below 1′ and above 5′, whereas the aperture statistics measured with the improved binning agrees with the expectation at all scales. At 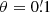 , the original binning underestimates ⟨𝒩2Map⟩ by 40%, whereas the result of the new binning scheme agrees with the theoretical expectation. Thus, our new method extends the reliability of the measurement. This is achieved by the tessellation because now the three-point correlation function is not incorrectly set to zero in bins for which no lens-lens-source triplet is found.
, the original binning underestimates ⟨𝒩2Map⟩ by 40%, whereas the result of the new binning scheme agrees with the theoretical expectation. Thus, our new method extends the reliability of the measurement. This is achieved by the tessellation because now the three-point correlation function is not incorrectly set to zero in bins for which no lens-lens-source triplet is found.
The signal due to the magnification of lens galaxies is approximately 10% of the total G3L signal and can therefore not be neglected in theoretical modelling of the G3L signal. Previous studies (Simon et al. 2008, 2013) did not account for lens magnification. Nonetheless, even though it has a significant effect on the measured G3L signal, the conclusions of Saghiha et al. (2017), who found good agreement between the G3L measured in CFHTLenS and the MR with the SAM by H15, are not impaired by this because the observational data and the simulations both included lens magnification.
We also demonstrated how the effect of lens magnification can be corrected for. The additional signal due to this effect can be measured with our redshift weighting by considering only lens pairs that are sufficiently far separated along the line of sight. The resulting signal matches the expectation for lens magnification from the convergence and number density maps at different redshift slices. We therefore conclude that the lens magnification signal can indeed be measured using physically separated lens pairs that have no intrinsic correlation. Because lens magnification only causes an additive signal, the intrinsic correlation can be found by subtracting the additional component from the overall measurement.
By directly measuring the different terms due to lens magnification, we found that the dominating term because galaxies at the closer lens plane are correlated to the convergence measured at the second lens plane and the convergence measured at the source plane, whereas the other terms are three orders of magnitude smaller. This finding explains why we measure a significant signal due to lens magnification, even though previous studies (e.g. Simon et al. 2013) expected this effect to be negligible: In these evaluations, only the 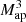 term was considered, which is indeed much smaller than any ⟨𝒩2Map⟩ signal. However, as we have shown here, it is not the dominant term for lens magnification.
term was considered, which is indeed much smaller than any ⟨𝒩2Map⟩ signal. However, as we have shown here, it is not the dominant term for lens magnification.
The magnification signal is mainly due to correlation of galaxies with matter at the first lens plane, which influences the convergence at the second lens and the source plane. Matter in front of both lenses, which influences the observed lens number density and the convergence at both lens and the source plane, also contributes to the magnification signal, although its measured contribution is minor. Nonetheless, because our lens sample has a low median redshift of 0.2, the effect of foreground matter might be stronger for lens samples at higher redshifts.
Using redshift weighting, we increased the S/N of both ⟨𝒩2Map⟩ and ⟨𝒩2Map⟩phys by approximately 35% between 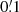 and 10′ and 0.1 h−1 Mpc and 2 h−1 Mpc. Simultaneously, the signal was increased by a factor of approximately two. This meets our expectation that the signal increases by the square of the increase in S/N.
and 10′ and 0.1 h−1 Mpc and 2 h−1 Mpc. Simultaneously, the signal was increased by a factor of approximately two. This meets our expectation that the signal increases by the square of the increase in S/N.
Our choice of σz was motivated by the correlation length between galaxies, the redshift distribution of galaxy pairs, and the typical peculiar velocities of galaxies in clusters. Choosing a different σz will lead to a different measured signal and to a different increase in S/N. However, the choice of σz does not affect the physical interpretation of the aperture statistics as long as the same σz is chosen in the theoretical modelling. Moreover, for each survey, different values of σz can be chosen, and the value that provides the highest S/N increase can be retained.
For the redshift-weighting scheme in the MR, we could use exact redshifts for all lens galaxies. This is generally not possible for observations. Although the redshift weighting with a broad weighting function might be possible for lens galaxies with photometric redshift estimates, we expect that redshift weighting is most useful for data sets that include spectroscopic redshifts. The uncertainties of spectroscopic redshifts are much smaller than of those photometric redshifts, so that a narrow weighting function, such as the one chosen for this work, can be used.
At first glance, the measurement of the aperture statistics in physical units ⟨𝒩2Map⟩phys does not appear to provide additional information to the measurement in angular units. However, in contrast to ⟨𝒩2Map⟩, ⟨𝒩2Map⟩phys is independent of the source redshift distribution. Direct comparisons of ⟨𝒩2Map⟩phys between surveys with different galaxy distributions are possible. Furthermore, the S/N of ⟨𝒩2Map⟩phys is slightly higher than for ⟨𝒩2Map⟩, independent of the redshift weighting. This is because for ⟨𝒩2Map⟩phys, triplets are weighted according to their lensing efficiency.
We only applied our improvements on the lens-lens-shear correlation function and the aperture statistics ⟨𝒩2Map⟩ here. However, the new binning scheme can also be applied to measurements of the lens-shear-shear correlation and 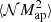 . We expect that this might extend the accuracy of measurement of this aperture statistics to scales below 1′, which were not taken into account in previous measurements (Simon et al. 2013). The transformation into physical units can also be applied to
. We expect that this might extend the accuracy of measurement of this aperture statistics to scales below 1′, which were not taken into account in previous measurements (Simon et al. 2013). The transformation into physical units can also be applied to 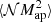 .
.
Acknowledgments
We are grateful to the anonymous referee for providing helpful comments. We thank Sandra Unruh for providing code for the slopes of the galaxy luminosity function in the MR. LL is a member of and received financial support for this research from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne.
References
- Bard, D., Bellis, M., Allen, M. T., Yepremyan, H., & Kratochvil, J. M. 2013, Astron. Comput., 1, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rev., 340, 291 [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Brainerd, T. G., Blandford, R. D., & Smail, I. 1996, ApJ, 466, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Cárdenas-Montes, M., Rodríguez-Vázquez, J. J., Vega-Rodríguez, M. A., Sevilla-Noarbe, I., & Alvaro, E. S. 2014, Comput. Phys. Commun., 185, 2558 [NASA ADS] [CrossRef] [Google Scholar]
- Clampitt, J., Miyatake, H., Jain, B., & Takada, M. 2016, MNRAS, 457, 2391 [NASA ADS] [CrossRef] [Google Scholar]
- Crain, R. A., Schaye, J., Bower, R. G., et al. 2015, MNRAS, 450, 1937 [NASA ADS] [CrossRef] [Google Scholar]
- Epps, S. D., & Hudson, M. J. 2017, MNRAS, 468, 2605 [NASA ADS] [CrossRef] [Google Scholar]
- Farrow, D. J., Cole, S., Norberg, P., et al. 2015, MNRAS, 454, 2120 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, B. 2009, GNU Scientific Library Reference Manual – Third Edition, 3rd edn. (Network Theory Ltd.) [Google Scholar]
- Guo, Q., White, S., Boylan-Kolchin, M., et al. 2011, MNRAS, 413, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Henriques, B. M. B., White, S. D. M., Thomas, P. A., et al. 2015, MNRAS, 451, 2663 [NASA ADS] [CrossRef] [Google Scholar]
- Hilbert, S., Hartlap, J., White, S. D. M., & Schneider, P. 2009, A&A, 499, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hildebrandt, H., Viola, M., Heymans, C., et al. 2017, MNRAS, 465, 1454 [Google Scholar]
- Hildebrandt, H., Köhlinger, F., van den Busch, J. L., et al. 2020, A&A, 633, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kondo, H., Miyatake, H., Shirasaki, M., Sugiyama, N., & Nishizawa, A. J. 2019, ArXiv e-prints [arXiv:1905.08991] [Google Scholar]
- Lacey, C. G., Baugh, C. M., Frenk, C. S., et al. 2016, MNRAS, 462, 3854 [NASA ADS] [CrossRef] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Hirata, C. M., Broderick, T., Seljak, U., & Brinkmann, J. 2006, MNRAS, 370, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Mead, J. M. G., King, L. J., & McCarthy, I. G. 2010, MNRAS, 401, 2257 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rycroft, C. H. 2009, J. Nonlinear Sci., 19, 041111 [Google Scholar]
- Saghiha, H., Simon, P., Schneider, P., & Hilbert, S. 2017, A&A, 601, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P. 2003, A&A, 408, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P., & Watts, P. 2005, A&A, 432, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P., van Waerbeke, L., & Mellier, Y. 2002, A&A, 389, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sheldon, E. S., Johnston, D. E., Frieman, J. A., et al. 2004, AJ, 127, 2544 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, P., & Hilbert, S. 2018, A&A, 613, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, P., Watts, P., Schneider, P., et al. 2008, A&A, 479, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, P., Erben, T., Schneider, P., et al. 2013, MNRAS, 430, 2476 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, P., Saghiha, H., Hilbert, S., et al. 2019, A&A, 622, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Singh, S., Mandelbaum, R., Seljak, U., Slosar, A., & Vazquez Gonzalez, J. 2017, MNRAS, 471, 3827 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vogelsberger, M., Genel, S., Springel, V., et al. 2014, MNRAS, 444, 1518 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, A. H., Hildebrandt, H., Kuijken, K., et al. 2019, A&A, 632, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xia, Q., Robertson, N., Heymans, C., et al. 2020, A&A, 633, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2011, ApJ, 736, 59 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Calculation of aperture statistics for mock data
Averages in the halo model are given by
Using assumption B in Sect. 5.1, we can reduce this integration to two spatial dimensions and use the projected halo centres ϑi and the projected separation Δϑij of the jth galaxy to the ith halo centre instead of xi and Δxij. Furthermore, due to assumption C, the mass integrals are trivial. Assumption D leads to
Assumption E means that
so that the average of a quantity is given by
Consequently, the correlation function ⟨N(θ1) N(θ2) κ(θ3)⟩ of the galaxy number density N(θ) and the projected matter density κ is
The matter density κ is the sum of the convergence profiles of all halos,
We treat galaxies as discrete objects, therefore their number density is
Inserting Eqs. (A.6) and (A.7) into Eq. (A.8) leads to
The delta “functions” reduce the integrals, therefore the expression simplifies to
We can split this triple sum into a one-halo term with i = j = k, three two-halo terms with i = j ≠ k, i = k ≠ k and j = k ≠ i, and a three-halo term with i ≠ j ≠ k. When we use ∫A d2ϑ = A and ∫ d2ϑu(ϑ) = 1, this leads to
From this, we can infer ⟨𝒩2Map⟩ with Eq. (15). Because the filter function Uθ is compensated for, the integrals over constant terms vanish and only the first term in the sum remains. Therefore, with the exponential filter function from Eq. (16) and N̅ = Nh Ngal/A leads to Eq. (15),
We can now use that
with the modified Bessel functions of the first kind In. We also introduce the scaled Bessel functions fn(x) = In(x)exp(−x), so that the aperture statistics are finally
Appendix B: Computational implementation with graphics processing units
Our estimates of 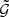 are computed by calculating the sums in Eqs. (4), (22), and (38) brutecforce on a GPU. Our algorithm (see Algorithm 1) for the estimation of
are computed by calculating the sums in Eqs. (4), (22), and (38) brutecforce on a GPU. Our algorithm (see Algorithm 1) for the estimation of 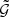 works similar to the procedures proposed by Bard et al. (2013) for the calculation of the galaxy two-point correlation and by Cárdenas-Montes et al. (2014) for the calculation of the galaxy two- and three-point function and the shear-shear correlation. It can be used for calculating the correlation between lenses from the same and from different samples.
works similar to the procedures proposed by Bard et al. (2013) for the calculation of the galaxy two-point correlation and by Cárdenas-Montes et al. (2014) for the calculation of the galaxy two- and three-point function and the shear-shear correlation. It can be used for calculating the correlation between lenses from the same and from different samples.
Algorithm for computing 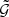
Read in lens and source galaxy positions and source ellipticities
into main memory (RAM)
Copy galaxy positions and ellipticities from RAM to the GPU
Initialize container for 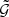 with Nbins bins on RAM
with Nbins bins on RAM
Initialize container for 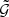 with Nbins bins on GPU
with Nbins bins on GPU
Initialize Nth threads on GPU
In each thread i do
for all sources j with j ∈ [i, i + Nth, i + 2Nth, … Ns] do
for all lenses do
for all lenses do
Get index of 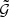 bin for this galaxy triplet
bin for this galaxy triplet
Add contribution of this triplet to 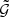 on GPU
on GPU
end for
end for
end for
end thread
Copy  from GPU to RAM
from GPU to RAM
Write 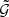 to file
to file
This algorithm is implemented in CUDA 10 using double floating point precision. For the calculation we used an NVIDIA RTX 2080 Ti GPU, which has CUDA capability 7.5 and therefore enables 46 × 1024 parallel threads. Data were read from and written to ASCII files on an SSD hard drive, enabling fast data transfer.
All Tables
All Figures
 |
Fig. 1. Geometry of a G3L configuration with one source and two lens galaxies; adapted from Schneider & Watts (2005). |
| In the text | |
 |
Fig. 2. Weighted number of lens galaxy pairs in our sample from the MR with fixed angular separation between |
| In the text | |
 |
Fig. 3. Illustration of the old (1) and new (2) binning scheme for the calculation of |
| In the text | |
 |
Fig. 4. Assumed source redshift distribution. This distribution is used to weigh the shear maps at different redshifts in the MR. It is modelled after the redshift distribution of galaxies in Hildebrandt et al. (2020). |
| In the text | |
 |
Fig. 5. Aperture statistics measured in the simple mock data with the old binning scheme (blue dots) and the new binning scheme (red crosses), as well as the theoretical expectation (black line) given by Eq. (53). Upper plot: E-mode ⟨𝒩2Map⟩. Lower plot: ratio of the B-mode ⟨𝒩2M⊥⟩ and the E-mode. Uncertainties are the statistical error estimated with jackknifing. |
| In the text | |
 |
Fig. 6. Fractional difference of the measured ⟨𝒩2Map⟩ relative to the theoretical prediction in the mock data. Blue dots show the measurement with the old binning scheme; red crosses show the measurement with the new binning scheme. |
| In the text | |
 |
Fig. 7. Effect of lens magnification on aperture statistics in the data based on the MR. The green dash-dotted line shows the signal measured for lens pairs with redshift differences larger than 0.01, which corresponds to the magnification terms in Eq. (44). The blue solid line is the aperture statistics for all lens pairs. The red dashed line is the intrinsic signal, which is corrected for lens magnification by subtracting the signal of separated lens pairs. Shaded regions are the 1σ uncertainties from jackknifing. |
| In the text | |
 |
Fig. 8. Same as Fig. 7, but for physical aperture statistics. |
| In the text | |
 |
Fig. 9. Individual lens magnification terms in the MR. Green stars depict the term due to correlation between the convergence maps at the two lens planes and at the source plane, red dots are the term due to correlation of the galaxy number density at the first lens plane to the convergence maps at the second lens and the source plane, brown crosses are the term due to correlation of the convergence maps at the first lens and the source plane to the galaxy number density at the second lens plane. The blue line is the measured ⟨𝒩2Map⟩ for separated lens pairs, which should correspond to the total lens magnification signal. |
| In the text | |
 |
Fig. 10. Aperture statistics measured in the mock data based on the MR, in (a) with angular and in (b) with physical units. Upper plots: E-modes ⟨𝒩2Map⟩ and ⟨𝒩2Map⟩phys. Middle plots: ratio of the B-modes ⟨𝒩2M⊥⟩ and ⟨𝒩2M⊥⟩phys to ⟨𝒩2Map⟩ and ⟨𝒩2Map⟩phys. Lower plots: S/N of ⟨𝒩2Map⟩ and ⟨𝒩2Map⟩phys. The red dashed line depicts ⟨𝒩2Map⟩ taken with a redshift weighting function with width σz = 0.01. Shaded regions show the 1σ uncertainties from jackknifing. The blue solid line denotes the measurements without redshift weighting. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



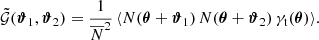
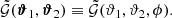
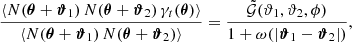
![$$ \begin{aligned}&\tilde{\mathcal{G} }_\mathrm{est} (b) \nonumber \\&\quad = -\dfrac{\sum _{i,j=1}^{N_\mathrm{d} }\sum _{k=1}^{N_\mathrm{s} } w_k \, \epsilon _k \, \mathrm{e} ^{-\mathrm{i}(\varphi _{ik}+\varphi _{jk})} \, \left[1+\omega (|\boldsymbol{\theta }_i -\boldsymbol{\theta }_j|)\right] \, { \Delta }_{ijk}(b)}{\sum _{i,j=1}^{N_\mathrm{d} }\sum _{k=1}^{N_\mathrm{s} } \, w_k \, \Delta _{ijk}(b)}\end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq9.gif)
![$$ \begin{aligned}&\quad =: -\dfrac{\sum _{ijk} w_k \, \epsilon _k \, \mathrm{e} ^{-\mathrm{i}(\varphi _{ik}+\varphi _{jk})} \, \left[1+\omega (|\boldsymbol{\theta }_i -\boldsymbol{\theta }_j|)\right] \, \Delta _{ijk}(b)}{\sum _{ijk} \, w_k \, \Delta _{ijk}(b)}, \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq10.gif)
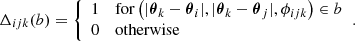
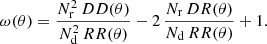
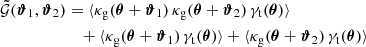
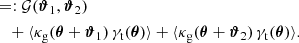
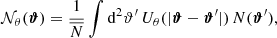
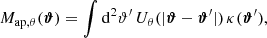
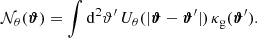
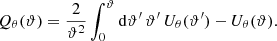
![$$ \begin{aligned}&{M}_{\rm ap, \theta }(\boldsymbol{\vartheta }) + \mathrm{i}\, M_{\perp , \theta }(\boldsymbol{\vartheta }) \nonumber \\&\quad = \int \mathrm{d}^{2}{\vartheta ^{\prime }} \,Q_\theta (|\boldsymbol{\vartheta }-\boldsymbol{\vartheta }^{\prime }|)\, \left[\gamma _\mathrm{t} (\boldsymbol{\vartheta }^{\prime }) + \mathrm{i}\,\gamma _\times (\boldsymbol{\vartheta }^{\prime })\right], \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq23.gif)
![$$ \begin{aligned}&\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle (\theta _1, \theta _2, \theta _3) + \mathrm{i} \langle {\mathcal{N} ^2 M_\perp }\rangle (\theta _1, \theta _2, \theta _3) \nonumber \\&\quad = \frac{1}{\overline{N}^2}\int \mathrm{d}^{2}{\vartheta _1}\, \int \mathrm{d}^{2}{\vartheta _2} \,\int \mathrm{d}^{2}{\vartheta _3}\, U_{\theta _1}( \vartheta _1) \,U_{\theta _2}({\vartheta _2})\, Q_{\theta _3}(\vartheta _3)\, \nonumber \\&\quad \times \left\langle {N(\boldsymbol{\vartheta }_1)\, N(\boldsymbol{\vartheta }_2)\, \left[\gamma _\mathrm{t} (\boldsymbol{\vartheta }_3)+\mathrm{i}\, \gamma _\times (\boldsymbol{\vartheta }_3)\right]}\right\rangle . \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq24.gif)
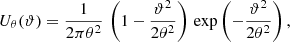
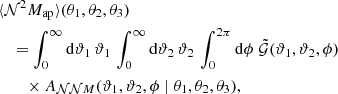
![$$ \begin{aligned}&\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle (\theta _1, \theta _2, \theta _3) + \mathrm{i} \langle {\mathcal{N} ^2 M_\perp }\rangle (\theta _1, \theta _2, \theta _3)\nonumber \\&\quad = \int \mathrm{d}^{2}{\vartheta _1}\, \int \mathrm{d}^{2}{\vartheta _2} \,\int \mathrm{d}^{2}{\vartheta _3}\, U_{\theta _1}\left( \vartheta _1 \right) \,U_{\theta _2}\left( {\vartheta _2}\right)\, Q_{\theta _3}\left(\vartheta _3\right)\, \nonumber \\&\qquad \times \left\langle {\kappa _\mathrm{g} (\boldsymbol{\vartheta }_1)\, \kappa _\mathrm{g} (\boldsymbol{\vartheta }_2)\, \left[\gamma _\mathrm{t} (\boldsymbol{\vartheta }_3)+\mathrm{i}\, \gamma _\times (\boldsymbol{\vartheta }_3)\right]}\right\rangle , \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq28.gif)
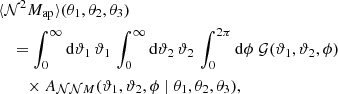
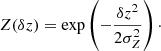
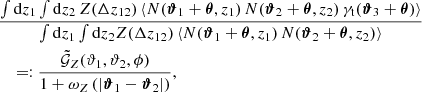
![$$ \begin{aligned}&\tilde{\mathcal{G} }_{Z, \mathrm{est} }(b) \nonumber \\&\quad =-\dfrac{\sum _{ijk} \, w_k \, \epsilon _k \, \mathrm{e} ^{-\mathrm{i}(\varphi _{ik}+\varphi _{jk})} \,\left[1+\omega _Z\left(|\boldsymbol{\theta }_i - \boldsymbol{\theta }_j|\right)\right]\, Z(\Delta z_{ij}) \, \Delta _{ijk}(b)}{\sum _{ijk} w_k \,Z(\Delta z_{ij}) \,\Delta _{ijk}(b)}\cdot \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq36.gif)
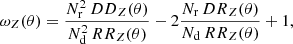
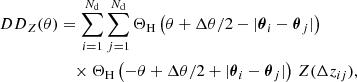
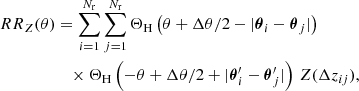
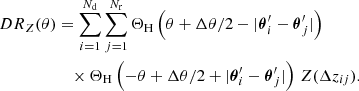
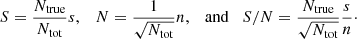
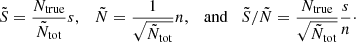
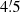
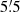
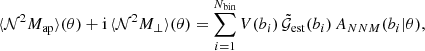
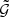
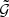
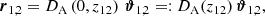
![$$ \begin{aligned}&\tilde{\mathcal{G} }_{Z, \mathrm{est} }(b) \nonumber \\&\quad =-\frac{\sum _{ijk} w_k \, \epsilon _k \, \mathrm{e} ^{-\mathrm{i} (\varphi _{ik} + \varphi _{jk})}\, \left[1 + \omega \left(|\boldsymbol{\theta }_i - \boldsymbol{\theta }_j|\right)\right] Z(\Delta z_{ij}) \Delta _{ijk}^{\mathrm{ph} }(b)}{\sum _{ijk} w_k \, Z(\Delta z_{ij})\, \Delta _{ijk}^{\mathrm{ph} }(b)}, \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq69.gif)
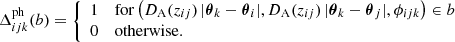
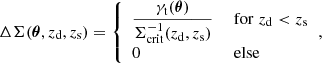
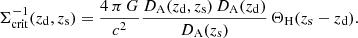
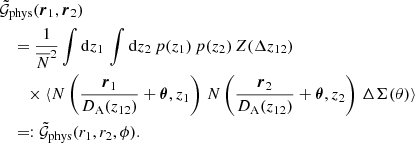
![$$ \begin{aligned}&\tilde{\mathcal{G} }_\mathrm{est,phys} (b)=\nonumber \\&\quad -\dfrac{\sum \limits _{ijk} w_k\, \epsilon _k \, \mathrm{e} ^{-\mathrm{i}(\varphi _{ik}+\varphi _{jk})}\left[1 + \omega \left(|\boldsymbol{\theta }_i - \boldsymbol{\theta }_j|\right)\right]Z(\Delta z_{ij})\,{\Sigma _{\mathrm{crit} }^{-1}}_{ijk}\,\Delta _{ijk}^{\mathrm{ph} }(b)}{\sum \limits _{ijk} w_k \, \Sigma _{\mathrm{crit} }^{-2}(z_\mathrm{d} , z_\mathrm{s} )\, Z(\Delta z_{ij})\, \Delta _{ijk}^{\mathrm{ph} }(b)}, \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq77.gif)
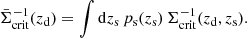
![$$ \begin{aligned}&\tilde{\mathcal{G} }_\mathrm{est,phys} (b)\nonumber \\&\quad =- \dfrac{\sum \limits _{ijk} w_k \, \epsilon _k \, \mathrm{e} ^{-\mathrm{i}(\varphi _{ik}+\varphi _{jk})}\left[1 + \omega \left(|\boldsymbol{\theta }_i - \boldsymbol{\theta }_j|\right)\right] Z(\Delta z_{ij})\, \bar{\Sigma }_{\mathrm{crit} }^{-1}(z_{ij})\, \Delta _{ijk}^{\mathrm{ph} }(b)}{\sum \limits _{ijk} w_k \, \bar{\Sigma }_{\mathrm{crit} }^{-2}(z_{ij})\, Z(\Delta z_{ij})\, \Delta _{ijk}^{\mathrm{ph} }(b)}\cdot \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq82.gif)
![$$ \begin{aligned}&\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle _\mathrm{phys} (R) + \mathrm{i}\, \langle {\mathcal{N} ^2 M_\perp }\rangle _\mathrm{phys} (R)\nonumber \\&\quad = \int _0^{\infty }\mathrm{d}{r_1}\, r_1\, \int _0^{\infty }\mathrm{d}{r_2}\, r_2\, \int _0^{2\pi } \mathrm{d}{\phi }\, \tilde{\mathcal{G} }_\mathrm{phys} (r_1, r_2, \phi ) \nonumber \\&\qquad \times {A}_{\mathcal{N} \mathcal{N} M}\left[D_{\rm A}^{-1}(z_{12})\,r_1, D_{\rm A}^{-1}(z_{12})\,r_2,\phi \; |\; D_{\rm A}^{-1}(z_{12})\,R\right]. \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq83.gif)
![$$ \begin{aligned} N(\boldsymbol{\vartheta }, z) = N_0(\boldsymbol{\vartheta }, z) + 2\,[\alpha (z) - 1]\, \overline{N} \, \kappa (\boldsymbol{\vartheta }, z), \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq84.gif)
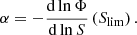
![$$ \begin{aligned}&\tilde{\mathcal{G} }_Z(\vartheta _1, \vartheta _2, \phi )\nonumber \\&\quad =\int \mathrm{d}{z_1}\, \int \mathrm{d}{z_2}\, Z(z_1-z_2) \nonumber \\&\qquad \times \Biggl \{ \frac{1}{\overline{N}^2}\,\langle {N_0(\boldsymbol{\vartheta }_1+\boldsymbol{\theta }, z_1)\,N_0(\boldsymbol{\vartheta }_2+\boldsymbol{\theta }, z_2)\,\gamma _\mathrm{t} (\boldsymbol{\theta })}\rangle \nonumber \\&\qquad \left. + \frac{2 [\alpha (z_2) - 1]}{\overline{N}}\, \langle {N_0(\boldsymbol{\vartheta }_1+\boldsymbol{\theta }, z_1)\,\kappa (\boldsymbol{\vartheta }_2+\boldsymbol{\theta }, z_2)\,\gamma _\mathrm{t} (\boldsymbol{\theta })}\rangle \right. \nonumber \\&\qquad \left. + \frac{2[\alpha (z_1) - 1]}{\overline{N}}\, \langle {\kappa (\boldsymbol{\vartheta }_1+\boldsymbol{\theta }, z_1)\,N_0(\boldsymbol{\vartheta }_2+\boldsymbol{\theta }, z_2)\,\gamma _\mathrm{t} (\boldsymbol{\theta })}\rangle \right.\nonumber \\&\qquad + \frac{4[\alpha (z_1) - 1][\alpha (z_2)-1]}{\overline{N}}\, \langle {\kappa (\boldsymbol{\vartheta }_1+\boldsymbol{\theta }, z_1)\,\kappa (\boldsymbol{\vartheta }_2+\boldsymbol{\theta }, z_2)\,\gamma _\mathrm{t} (\boldsymbol{\theta })}\rangle \Biggr \} . \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq87.gif)
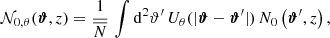
![$$ \begin{aligned}&\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle (\theta )\nonumber \\&\quad =\int \mathrm{d}{z_1}\, \int \mathrm{d}{z_2}\, Z(z_1-z_2) \nonumber \\&\qquad \times \Bigl \{ \langle {\mathcal{N} _{0,\theta }(\boldsymbol{\vartheta }, z_1)\, \mathcal{N} _{0,\theta }(\boldsymbol{\vartheta }, z_2)\, M_{\mathrm{ap} ,\theta }(\boldsymbol{\vartheta })}\rangle \nonumber \\&\qquad \left. + 2[\alpha (z_2)-1]\, \langle {\mathcal{N} _{0,\theta }(\boldsymbol{\vartheta }, z_1)\, M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_2) \, M_{\mathrm{ap} ,\theta }(\boldsymbol{\vartheta })}\rangle \right. \nonumber \\&\qquad \left. + 2[\alpha (z_1)-1]\, \langle {M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_1) \,\mathcal{N} _{0,\theta }(\boldsymbol{\vartheta }, z_2)\, M_{\mathrm{ap} ,\theta }(\boldsymbol{\vartheta })}\rangle \right. \nonumber \\&\qquad + 4[\alpha (z_1)-1][\alpha (z_2)-1]\langle {M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_1)\,M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_2)\, M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }) }\rangle \Bigr \} . \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq89.gif)
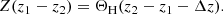
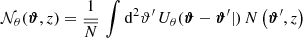
![$$ \begin{aligned}&= \mathcal{N} _{0, \theta } + 2\,[\alpha (z)-1]\, M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z). \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq92.gif)
![$$ \begin{aligned}&\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle (\theta )\nonumber \\&\quad =\int _0^{z_{\rm max}}\, \mathrm{d}{z_1} \int _{z_1+\Delta z}^{z_{\rm max}} \mathrm{d}{z_2}\, \left\{ \langle {\mathcal{N} _{0,\theta }(\boldsymbol{\vartheta }, z_1)\, \mathcal{N} _{0,\theta }(\boldsymbol{\vartheta }, z_2)\, M_{\mathrm{ap} ,\theta }(\boldsymbol{\vartheta })}\rangle \right.\nonumber \\&\qquad \left. + 2\,[\alpha (z_2)-1]\, \langle {\mathcal{N} _{\theta }(\boldsymbol{\vartheta }, z_1)\, M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_2) \, M_{\mathrm{ap} ,\theta }(\boldsymbol{\vartheta })}\rangle \right. \nonumber \\&\qquad \left. + 2\,[\alpha (z_1)-1]\, \langle {M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_1) \,\mathcal{N} _{\theta }(\boldsymbol{\vartheta }, z_2)\, M_{\mathrm{ap} ,\theta }(\boldsymbol{\vartheta })}\rangle \right. \nonumber \\&\qquad \left. - 4\,[\alpha (z_1)-1]\,[\alpha (z_2)-1] \langle {M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_1)\,M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_2)\, M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta })}\rangle \right\} , \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq93.gif)
![$$ \begin{aligned}&\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle (\theta ) \nonumber \\&\quad =\sum _{i=0}^{M}\sum _{j=i+1}^M \Delta z_i \, \Delta z_j \left\{ \langle {\mathcal{N} _{0,\theta }(\boldsymbol{\vartheta }, z_i)\, \mathcal{N} _{0,\theta }(\boldsymbol{\vartheta }, z_j)\, M_{\mathrm{ap} ,\theta }(\boldsymbol{\vartheta })}\rangle \right. \\&\qquad \left. + 2\,[\alpha (z_j)-1]\, \langle {\mathcal{N} _{\theta }(\boldsymbol{\vartheta }, z_i)\, M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_j) \, M_{\mathrm{ap} ,\theta }(\boldsymbol{\vartheta })}\rangle \right. \nonumber \\&\qquad \left. + 2\,[\alpha (z_i)-1] \, \langle {M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_i) \,\mathcal{N} _{\theta }(\boldsymbol{\vartheta }, z_j)\, M_{\mathrm{ap} ,\theta }(\boldsymbol{\vartheta })}\rangle \right. \nonumber \\&\qquad \left. - 4\,[\alpha (z_i)-1][\alpha (z_j)-1]\, \langle {M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_i)M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }, z_j)\, M_{\mathrm{ap} , \theta }(\boldsymbol{\vartheta }) }\rangle \right\} \nonumber \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq94.gif)
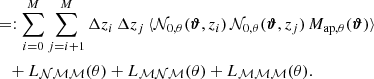
![$$ \begin{aligned} C(\theta _i, \theta _j)&= \frac{64}{64-1}\sum _{k=1}^{64} \left[\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle _k(\theta _i)-\overline{\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle _k}(\theta _i)\right] \nonumber \\&\quad \times \left[\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle _k(\theta _j)-\overline{\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle _k}(\theta _j)\right], \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq100.gif)
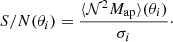
![$$ \begin{aligned}&\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle (\theta _1, \theta _2, \theta _3)\nonumber \\&\quad =\frac{2\pi \,A\,K}{N_\mathrm{h} }\int _0^{\infty }\mathrm{d}{\vartheta }\, \vartheta \, \prod _{i=1}^3 \int _0^{\infty } \mathrm{d}{y_i}\, \dfrac{y_i\, u(y_i)}{\theta _i^2}\, \exp \left[-\dfrac{(y_i-\vartheta )^2}{2\theta _i^2}\right] \nonumber \\&\qquad \times \left[\left(1-\frac{y_i^2+\vartheta ^2}{2\theta _i^2}\right)\,f_0\left(\dfrac{y_i\,\vartheta }{\theta _i^2}\right) +\dfrac{y_i\vartheta }{\theta _i^2}\,f_1\left(\dfrac{y_i\,\vartheta }{\theta _i^2}\right)\right], \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq104.gif)
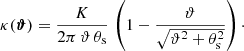
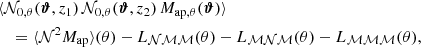

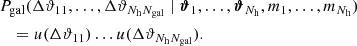
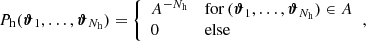
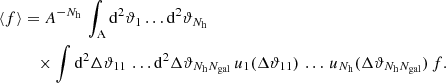
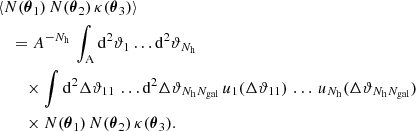
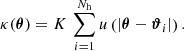
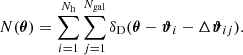
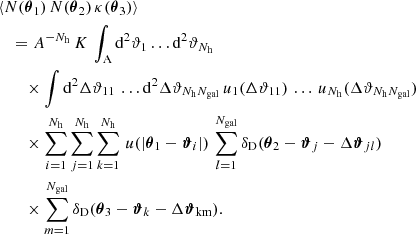
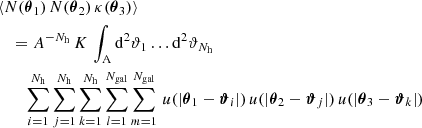
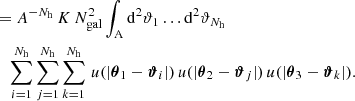
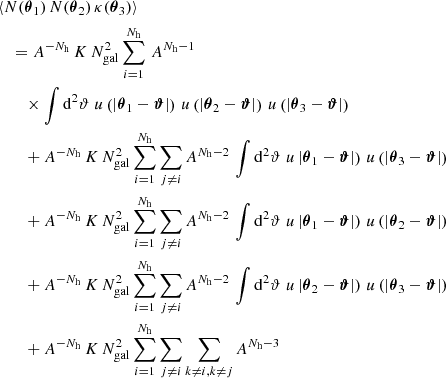
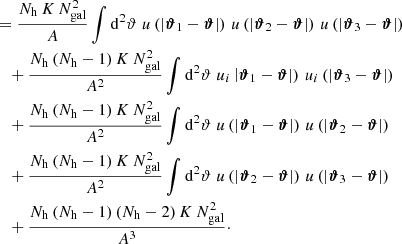
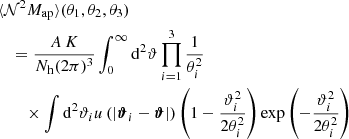
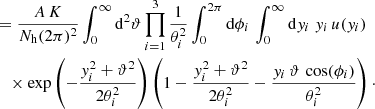
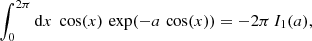
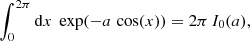
![$$ \begin{aligned}&\langle {\mathcal{N} ^2 M_\mathrm{ap} }\rangle (\theta _1, \theta _2, \theta _3)\nonumber \\&\quad =\frac{2\pi \,A\,K}{N_\mathrm{h} }\int _0^{\infty }\mathrm{d}{\vartheta }\; \vartheta \, \prod _{i=1}^3 \int _0^{\infty } \mathrm{d}{y_i}\; \dfrac{y_i\, u(y_i)}{\theta _i^2}\, \exp \left[-\dfrac{(y_i-\vartheta )^2}{2\theta _i^2}\right] \nonumber \\&\qquad \; \times \left[\left(1-\frac{y_i^2+\vartheta ^2}{2\theta _i^2}\right)f_0\left(\dfrac{y_i\,\vartheta }{\theta _i^2}\right) +\dfrac{y_i\vartheta }{\theta _i^2}f_1\left(\dfrac{y_i\,\vartheta }{\theta _i^2}\right)\right]\cdot \end{aligned} $$](/articles/aa/full_html/2020/02/aa36693-19/aa36693-19-eq136.gif)