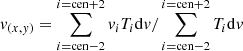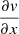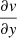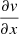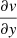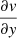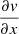| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201834613 | |
| Published online | 23 December 2019 | |
Rotation of molecular clouds in M 51
1
Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N, Allée Geoffroy Saint-Hilaire, 33615 Pessac, France
e-mail: jonathan.braine@u-bordeaux.fr
2
Institut de Recherche en Astrophysique et Planétologie (IRAP), Université Paul Sabatier, Toulouse cedex 4, France
3
Department of Physics, University of Alberta, 4-183 CCIS, Edmonton, AB T6G 2E1, Canada
4
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
5
Max-Planck-Institut for Astronomy, Konigstuhl 17, 69117 Heidelberg, Germany
Received:
9
November
2018
Accepted:
18
November
2019
The grand-design spiral galaxy M 51 was observed at 40 pc resolution in CO(1–0) by the PAWS project. A large number of molecular clouds were identified and we search for velocity gradients in two high signal-to-noise subsamples, containing 682 and 376 clouds. The velocity gradients are found to be systematically prograde oriented, as was previously found for the rather flocculent spiral M 33. This strongly supports the idea that the velocity gradients reflect cloud rotation, rather than more random dynamical forces, such as turbulence. Not only are the gradients prograde, but their ∂v/∂x and ∂v/∂y coefficients follow galactic shear in sign, although with a lower amplitude. No link is found between the orientation of the gradient and the orientation of the cloud. The values of the cloud angular momenta appear to be an extension of the values noted for galactic clouds despite the orders of magnitude difference in cloud mass. Roughly 30% of the clouds show retrograde velocity gradients. For a strictly rising rotation curve, as in M 51, gravitational contraction would be expected to yield strictly prograde rotators within an axisymmetric potential. In M 51, the fraction of retrograde rotators is found to be higher in the spiral arms than in the disk as a whole. Along the leading edge of the spiral arms, a majority of the clouds are retrograde rotators. While this work should be continued on other nearby galaxies, the M 33 and M 51 studies have shown that clouds rotate and that they rotate mostly prograde, although the amplitudes are not such that rotational energy is a significant support mechanism against gravitation. In this work, we show that retrograde rotation is linked to the presence of a spiral gravitational potential.
Key words: galaxies: individual: M 51 / galaxies: spiral / galaxies: ISM / ISM: clouds / ISM: molecules / stars: formation
© J. Braine et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Assuming giant molecular clouds (GMCs) form from the gravitational contraction of a more diffuse medium, their angular momenta should reflect the dynamics (angular momentum in particular) of the medium from which they formed. Despite the importance of measuring cloud rotation (thus angular momentum) to understand the formation mechanism of GMCs, relatively little work has appeared. The initial work was done by Kutner et al. (1977), followed by Blitz (1993) and works cited therein, all for molecular clouds in the Milky Way. These authors used velocity gradients as a measure of cloud rotation. From these studies, it was difficult to determine whether molecular clouds rotated in a systematic way or not. Bally (1989) argued that at least some velocity gradients may be due to pressure from stellar winds generated by massive star formation. Burkert & Bodenheimer (2000) found that turbulence could also produce velocity gradients similar to those observed. Most Galactic clouds have quite weak velocity gradients (Blitz 1993). In their compilation, Phillips (1999) found that clouds tend to have angular momentum vectors oriented perpendicular to the plane of the Galaxy. However, the number of clouds was quite small (48 in their Fig. 1a). Any systematic effects would tend to support the idea that velocity gradients generally trace rotation rather than more random effects, such as cloud-star interactions. Neither Blitz (1993) nor Phillips (1999) identifed a pro- or retrograde orientation of the velocity gradients observed in the Galaxy. “Pro-” or “retro”-grade rotation is defined with respect to the sense of rotation of the galaxy (prograde being in the same direction as galactic rotation), rather than a local gravitational potential.
It is now possible to observe molecular clouds in nearby galaxies. The first to look at cloud rotation in nearby galaxies were Rosolowsky et al. (2003), followed by Imara et al. (2011), from their observations of M 33. The velocity gradients were weak in their sample of 45 clouds. The deep CO(2–1) survey with the Institut de Radioastronomie Millimétrique (IRAM) 30 m telescope (Druard et al. 2014; Gratier et al. 2010) and the identification of a large sample of molecular clouds (Corbelli et al. 2017; Gratier et al. 2012) enabled Braine et al. (2018, hereafter B18) to measure velocity gradients. B18 show that the velocity gradients of the clouds are systematically in the prograde direction, lending support to the idea that the gradients are due to rotation. The rotational energy is, however, very low and not a significant source of support.
Here we use the high-resolution CO(1–0) PAWS observations of M 51 (PdBI Arcsecond Whirlpool Survey, Schinnerer et al. 2013) and the cloud identifications from Colombo et al. (2014a) to explore cloud rotation. The datacubes and images are available from the MPIA and IRAM websites1 and the cloud catalog in Colombo et al. (2014a) and via ApJ. The published and publicly available cloud catalog provides (among other quantities) cloud sizes, linewidths, and an indicative signal-to-noise ratio (S/N). The latter provides a good indication of the quality of the gradient calculation and is used to define our two cloud samples. M 51 is often thought of as a face-on spiral but the observed rotation curve reaches about 100 km s−1 so in-plane rotation is visible. The inclination is about 22° (Colombo et al. 2014b), but with significant uncertainty (Hu et al. 2013). Despite the velocity resolution of 5 km s−1, the clouds are detected in several adjacent channels. The situation is similar to M 33 where the velocity resolution was 2.6 km s−1, but cloud linewidths in M 51 are roughly twice as broad for an equivalent cloud size (see B18 Fig. 3 for a comparison).
Coincidentally similar to M 33, the major axis is oriented close to N-S and the northern side is approaching, such that the velocity gradient is positive toward the south. The observed velocities are also similar, reaching approximately ±90 km s−1 over the regions observed.
Colombo et al. (2014a) used CPROPS (Rosolowsky & Leroy 2006) to identify 1507 clouds. Each cloud has an estimated S/N and they define a high-quality cloud sample to have few or no false identifications. Because high S/N is critical to detecting rotation, we define two restrictive samples within their samples. The samples contain 682 clouds with S/N > 7 and 376 clouds with S/N > 10, respectively. The value of S/N is given in Col. 6 of Table 1 of Colombo et al. (2014a).
2. Velocity gradients and method to obtain them
We follow the method used by previous authors, and described in B18 Figs. 1 and 2, and Sect. 3. Each cloud is defined as a set of pixels in position-position-velocity space (i.e., a datacube) and the cloud velocity centroid is determined by CPROPS. For each of the spatial pixels occupied by the cloud, we calculate the first moment velocity using
where cen represents the central channel number. Five velocity channels are used to calculate the velocity; the channel corresponding to the cloud velocity calculated by CPROPS and two channels to either side so that a total of 25 km s−1 is covered. The lines of the M 51 clouds are quite broad, significantly broader than those of M 33 (see Fig. 3 of B18), so five channels are necessary. Including velocities further from that of the cloud simply adds noise to the calculation. Once the velocity for each pixel of a cloud is known, we fit a plane to the velocities, such that the velocity gradients 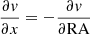 and
and 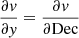 are determined. Figure 1 illustrates the procedure. The top panel shows the result of the first moment calculation (i.e., the representative velocity of each pixel), the middle panel shows the gradient deduced by our procedure, and the bottom panel shows the residuals. Cloud 1417 is a large cloud with a large gradient and, unlike smaller clouds, there is structure to be seen in the residual. The pattern of the residual image shows that rigid rotation is not appropriate as the true gradient is steeper near the cloud center and flattens somewhat. Figure 2 shows a smaller cloud with a smaller gradient. In both cases, the values of the residual image, which can be taken as indicative of the uncertainties, are far below the total velocity gradient.
are determined. Figure 1 illustrates the procedure. The top panel shows the result of the first moment calculation (i.e., the representative velocity of each pixel), the middle panel shows the gradient deduced by our procedure, and the bottom panel shows the residuals. Cloud 1417 is a large cloud with a large gradient and, unlike smaller clouds, there is structure to be seen in the residual. The pattern of the residual image shows that rigid rotation is not appropriate as the true gradient is steeper near the cloud center and flattens somewhat. Figure 2 shows a smaller cloud with a smaller gradient. In both cases, the values of the residual image, which can be taken as indicative of the uncertainties, are far below the total velocity gradient.
Given the ∼40 pc and 5 km s−1 resolution of the observations, we have not attempted to fit nonlinear velocity gradients. The velocity gradients are presented in Fig. 3, showing the two samples separately. As for M 33, the prograde orientation of the high S/N sample is stronger, confirming the prograde predominance. Due to the orientation of M 51, with a velocity increasing toward the south, prograde rotation is shown with a negative sign. The prograde orientation is highly significant (8σ for the 682 cloud sample and 9σ for the 376 S/N > 10 clouds).
Only a fraction of the velocity width can be explained via the observed velocity gradient. 0.05 km s−1 pc−1, a reasonable value from Fig. 3, over a diameter of 60 pc, only corresponds to 3 km s−1 whereas the typical velocity width for clouds of that size in M 51 is about ΔVFWHM = 14 km s−1. Some of the clouds are quite large; 26 of the 376 clouds of the S/N > 10 sample have radii of 100 pc or slightly greater. When inspecting morphologies, clearly some of these could potentially be agglomerations of smaller clouds, whether real agglomerations or simply line-of-sight associations, and approximately 1/4 are filamentary (axis ratios are given in Colombo et al. 2014a).
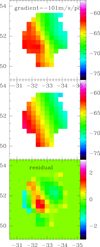 |
Fig. 1. First moment velocities (top panel) followed by the calculated gradient and the residual image. The color wedges show the velocities in km s−1 and the x and y axes show the position of the cloud in arcseconds. |
 |
Fig. 3. Histogram of velocity gradients measured for M 51 clouds. The black histogram is for the subsample S/N ≥ 7 and the red for the subsample S/N ≥ 10. The gradients in the higher S/N subsample are better defined (more prograde and with a more significant gradient). |
2.1. Rotational versus binding energy
Since velocity gradients expressed as km s−1 pc−1 are akin to an angular frequency, we can calculate rotation periods and compare rotational and gravitational potential energy. From Fig. 3, we see that the vast majority of the gradients are below 0.1 km s−1 pc−1 in absolute value although we only measure a projected gradient. The rotational energy is E = αMR2Ω2 where α takes values of 1/4 for a homogeneous disk, 1/6 for a disk whose surface density declines as r−1, 1/5 for a homogeneous sphere and less for more centrally concentrated spheres. Adopting R = 45 pc and M = 106 M⊙ as typical values, we obtain rotational energies of 6 − 10 × 1048 ergs and gravitational binding energies of 1.1 − 1.9 × 1051 ergs (U = βM2/R with β ∼ 0.6 − 1. It is unlikely that the gradients are underestimated by a factor 4 or more so the rotational energy is well below the binding energy. This is particularly true for centrally concentrated clouds.
Phillips (1999) proposed the ratio of the rotational and turbulent virial terms as a measure of the importance of rotation: 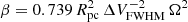 (his Eq. (1) converted to the units used here). For representative values of R = 45 pc, Ω = 0.1 km s−1 pc−1 (after correction for the beam-smearing below), and ΔVFWHM = 14 km s−1 (slightly below average for M 51 clouds – see Fig. 3 of B18), we obtain β ≈ 0.076. As also found by Phillips (1999), this is considerably below unity, even allowing for projection effects.
(his Eq. (1) converted to the units used here). For representative values of R = 45 pc, Ω = 0.1 km s−1 pc−1 (after correction for the beam-smearing below), and ΔVFWHM = 14 km s−1 (slightly below average for M 51 clouds – see Fig. 3 of B18), we obtain β ≈ 0.076. As also found by Phillips (1999), this is considerably below unity, even allowing for projection effects.
If Ω = 0.1 km s−1 pc−1 is an appropriate gradient, then the rotation period is T = 2π/Ω = 61 Myr. Even allowing for projection effects and the correction below, the rotation period is greater than typical GMC lifetimes of ∼15 Myr (e.g., Corbelli et al. 2017).
2.2. Angular momenta
Figure 4 shows the specific angular momenta of the clouds as a histogram. To calculate the angular momentum, we have assumed that the clouds can be represented as a disk with a linearly decreasing surface density, such that j = (Ω/0.59) R2 /3 where the factor 0.59 corrects for the underestimate in the velocity gradient due to beam smearing (see B18). Blitz (1993) takes j = ΩR2/2, which is appropriate for a constant surface density. Neither approximation is ideal but these expressions give an idea of the uncertainties.
 |
Fig. 4. Histogram of angular momenta for M 51 clouds. In black for the subsample S/N ≥ 7 and in red for the subsample S/N ≥ 10. Note that the gradients in the higher S/N subsample are better defined (more prograde and with a more significant gradient). We have included a correction for beam-smearing as in B18. The angular momenta of the M 51 clouds are substantially higher than in M 33 (see middle panel of next figure). |
The M 51 clouds have specific angular momenta three times those found in M 33 (Fig. 4 and top of Fig. 12 in B18). However, the angular momenta are similar for a given cloud mass (Fig. 5) and there is a large dispersion in all cases. The M 51 clouds are more massive, with both higher CO luminosities and CO linewidths than the M 33 clouds. The specific angular momentum of the M 51 clouds appears to increase with mass only as j(M) ∝ M0.4 whereas the slope is steeper for M 33 j(M) ∝ M0.68 (selecting the high S/N clouds). The uncertainties on the slopes of the fits of j(M) are 0.09 and 0.08 such that the difference is only 1.5σ, which we do not consider significant. For a cloud mass of 106 M⊙, the fits yield 50 km s−1 pc for M 51 and 45 km s−1 pc for M 33.
 |
Fig. 5. Top: specific angular momentum as a function of cloud mass. The trends from B18 for M 33 and from Phillips (1999) are indicated. This figure can be directly compared with B18 and with Dobbs (2008). Middle: here we show the strong M 33 clouds along with the M 51 clouds, without showing the distinctions between pro/retrograde and S/N level. While the values are lower for the M 33 clouds, the M 51 clouds follow a similar trend. Bottom: specific angular momentum as a function of cloud radius. The trend from Phillips (1999) is indicated. The cloud radii are from Colombo et al. (2014a) and the accumulation at 32 pc is due to a limit set by Colombo et al. (2014a). The fit results for M 33 and M 51 for both the high S/N and full samples are given in Table 1. The scatter about the fits is a factor 2–3 (precise values given in Table 1). |
The specific angular momentum in the M51 clouds varies sublinearly (0.4) with cloud mass but the distribution shows a lot of scatter. In the M 33 clouds, the variation, again with a scatter of a factor of several, is also slightly sublinear (0.68). This is in excellent agreement with Fig. 5 of Phillips (1999) for Galactic clouds (slope of 0.72) despite the absence of overlap in cloud masses (the Phillips clouds are smaller and less massive). It is also worth noting that the extragalactic clouds (M 51 and M 33, here and in B18) are an extension of the values of specific angular momentum found by Phillips (1999). The trends found by Phillips (1999) and by B18 for M 33 are shown as thick solid or dashed green lines. Extending the Phillips (1999) trend to 106 M⊙ yields j = 79 km s−1 pc, higher but well within the scatter of the extragalactic values.
The bottom plot of Fig. 5 shows how the specific angular momentum varies with cloud size. While the slope of j(M) was slightly steeper for Galactic clouds (Phillips 1999) than M 51 (although similar to M 33), the reverse is true for j(R) where Phillips (1999) found 1.3 but the slope is 1.6 for M 51 and ∼1.8 for M 33. Although the slopes of j(R) are not significantly different between M 33 and M 51, the angular momentum for a given cloud size is higher (significance > 3σ) in the M 51 clouds. It is more difficult to compare with the Galactic clouds because they are smaller and the (Phillips 1999) sample is quite inhomogeneous so the definition of “radius” may not correspond exactly to what CPROPS measures. In a situation where the galactic differential rotation contributes at the large scales, it is not surprising that we find a steeper j(R) compared to the smaller scales in Phillips (1999). Alternatively, the steepening at large (full GMC) scales suggests that galactic scale dynamics has an influence.
All of these features argue in favor of rotation. However, there is no obviously preferred orientation for the rotation axis with respect to the cloud major axis determined by CPROPS. In fact, the difference between the rotation and morphological axes appears to be distributed randomly.
It is quite remarkable that over several orders of magnitude in mass and a factor ∼100 in size, similar specific angular momentum trends are observed. The similar scaling relationships likely point to a driving physical origin. Any systematic cloud rotation should be driven by the galaxy and a signature of cloud rotation would be the alignment of the cloud angular momenta with the overall angular momentum of the galaxy (i.e., prograde cloud rotation). A turbulent velocity field of the molecular medium with a steep power-law power spectrum could lead to the largest-scale velocity modes having the most power, which could manifest itself as a gradient (Burkert & Bodenheimer 2000), although not necessarily prograde. The two explanations could be linked as galactic rotation could drive rotational motions in the molecular medium that exhibit common properties across a range of scales from a turbulent velocity cascade.
From Table 1 and Fig. 5 it is apparent that the j(M) relations for M 33 and M 51 are similar and both below the Phillips (1999) values for the Galaxy. However, one can also see that the j(R) is higher for M 51, presumably due to the higher gradient in gravitational potential.
Scaling relations for the specific angular momentum j as a function of cloud mass and size.
3. Link between velocity gradients and rotation
Figure 6 shows the observed and modeled velocities in the upper panels. The central part is not well reproduced because there is an apparent change in the position angle whereas the model is axisymmetric. The model is used to calculate how the observed velocity due to galactic rotation changes when moving along the RA or Dec axes. In other words, the 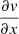 and
and 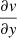 coefficients are calculated for each position in the galaxy due to rotation based on the model. The
coefficients are calculated for each position in the galaxy due to rotation based on the model. The 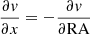 and
and 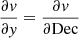 are given in the lower panels.
are given in the lower panels.
 |
Fig. 6. First panel: PAWS first moment (velocity) from the CO(1–0) observations by Schinnerer et al. (2013) and upper right panel: analytical velocity field designed to approximate the observations but with purely circular rotation and a constant position angle and inclination. Lower panels: (left) velocity gradient |
To further investigate the link between galactic rotation and the cloud velocity gradients, which only cover a very small fraction of the surface of M 51, we calculate the average cloud 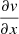 where the corresponding galactic coefficient is positive or negative (lower left panel). The cloud
where the corresponding galactic coefficient is positive or negative (lower left panel). The cloud 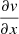 follows the galactic rotation as the average cloud
follows the galactic rotation as the average cloud 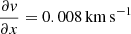 pc−1 where the galactic
pc−1 where the galactic 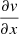 is positive and
is positive and 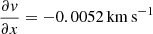 pc−1 where the galactic
pc−1 where the galactic 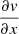 is negative. Along the Declination axis, all galactic values are negative because the velocity gradient of M 51 is positive toward the south (see bottom right panel). Taking regions where
is negative. Along the Declination axis, all galactic values are negative because the velocity gradient of M 51 is positive toward the south (see bottom right panel). Taking regions where 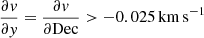 pc−1, the average of the clouds is
pc−1, the average of the clouds is 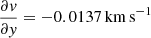 pc−1. Where the galactic
pc−1. Where the galactic 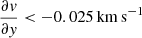 pc−1, the clouds have on average
pc−1, the clouds have on average 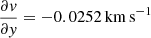 pc−1. These values are for the S/N ≥ 10 sample but similar values are found for lower S/N samples. Thus, in all cases the average rotation is prograde but lower than the galactic gradient or shear. Our measurements are in a frame not rotating with the galaxy – an inertial frame. When a cloud becomes gravitationally bound, it feels the shear but is not torn apart by it, meaning that the cloud rotation is below that of the shear (as observed here and in M 33). The average galactic shear at the positions of the clouds is
pc−1. These values are for the S/N ≥ 10 sample but similar values are found for lower S/N samples. Thus, in all cases the average rotation is prograde but lower than the galactic gradient or shear. Our measurements are in a frame not rotating with the galaxy – an inertial frame. When a cloud becomes gravitationally bound, it feels the shear but is not torn apart by it, meaning that the cloud rotation is below that of the shear (as observed here and in M 33). The average galactic shear at the positions of the clouds is 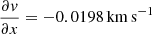 pc−1 for the region with
pc−1 for the region with 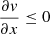 ,
, 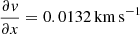 pc−1 for the region with
pc−1 for the region with 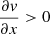 ,
, 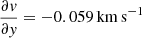 pc−1 for the region with
pc−1 for the region with 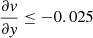 , and
, and 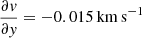 pc−1 for the region with
pc−1 for the region with 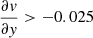 . In all cases, this is higher (in absolute value) than the cloud gradients calculated in the same way (−0.0052, 0.0080, −0.0252, and −0.0137 km s−1 pc−1, respectively). Thus, the cloud velocity gradients are on average slightly less than half what is provided by shear, showing (if need be) the effect of the cloud self-gravity.
. In all cases, this is higher (in absolute value) than the cloud gradients calculated in the same way (−0.0052, 0.0080, −0.0252, and −0.0137 km s−1 pc−1, respectively). Thus, the cloud velocity gradients are on average slightly less than half what is provided by shear, showing (if need be) the effect of the cloud self-gravity.
Throughout the region where these clouds are found, the rotation curve is rising (see Fig. 10 of Meidt et al. 2013). Mestel (1966) showed that throughout the rising part of a rotation curve, conservation of angular momentum implies that the rotation will be prograde. Clearly this does not include cloud-cloud collisions or winds or other pressure of any origin (i.e., the other possible sources of velocity gradients) and in fact these effects may explain why nearly 1/3 of the strong clouds (S/N ≳ 10) show retrograde gradients. We have shown that the sign and amplitude of the velocity gradients follow the sign and amplitude of the shear, as expected from gravitational contraction in a rotating disk. M 33 also has a rising rotation curve and all the same features were seen by B18, so the present results suggest that these are general features, at least for the rising parts of rotation curves. In the case of M 51, the strong local spiral arm potential may affect the angular momenta of some clouds.
4. Link between velocity gradients and spiral arms
A rather simple test was applied to see whether the spiral potential modified the pro/retrograde orientation of the cloud velocity gradients. Colombo et al. (2014a, Fig. 1) provide a mask defining different environments. Since the rotation curve is rising everywhere, only the nonaxisymmetric potential of the spiral arms could cause retrograde rotation in clouds formed through gravitational condensation. Comparing the arm and “not-arm” regions, we find that retrograde rotation is indeed considerably higher in the arm regions. For the S/N ≥ 7 sample, retrograde rotation represents 40% in the arms vs 30% in the not-arm regions. For the S/N ≥ 10 sample, retrograde rotation represents 36% in the arms but only 27% in the not-arm regions. The average velocity gradient amplitudes are similar at about 0.05 km s−1 pc−1 for the 4 categories (arm-retro, arm-pro, notarm-retro, and notarm-pro). Thus, while a majority of the clouds show prograde rotation, the fraction of retrograde rotators is higher where there is a strong nonaxisymmetric component to the gravitational potential. The results of the comparison of the regions of M 51 are summarized in Table 2.
Comparison of rotation in regions of M 51, showing the results for both samples.
The corotation radius of M 51 is at about 100″ from the center (Querejeta et al. 2016), so the clouds discussed here are within corotation. Being within corotation means that the stars and clouds go around the center more quickly than the arm pattern. Clouds enter the concave side of the arms and exit through the convex leading edge. They are accelerated when entering and slowed down upon leaving the arms. This explains the coherently red and blue shifted regions around the arms seen in Fig. 7.
 |
Fig. 7. Residual velocity field as in Colombo et al. (2014b), with annotations to clarify text. Note how each arm has a red-shifted and a blue-shifted side; this is used to separate the two sides of the arms. |
We took the residual velocity map from Fig. 1(top) of Colombo et al. (2014b) in which streaming motions are clearly visible and tested for the number of pro and retrograde rotators in the leading and trailing parts of the arms. In the western spiral arm (Arm 1 in Fig. 7), mostly on the far side of M 51, the leading edge is blue-shifted and the trailing (concave) edge is red-shifted compared to the large-scale rotation curve. In the eastern spiral arm (Arm 2), the situation is reversed. This can be seen in Fig. 7. We identified three regions: arm leading, arm trailing, and “not-arm” as a control sample. The majority of the clouds in the leading parts of the spiral arms are retrograde rotators! This is true for both the S/N ≥ 10 and S/N ≥ 7 samples. Less than 25% of the clouds on the trailing edges are retrograde rotators. About 30% of the not-arm clouds are retrograde rotators and these are distributed equally among regions where the velocity residual is red or blue-shifted.
Figure 8 shows this more graphically by focussing on Arm 1. The clouds, whose positions are indicated by the numbers (Colombo et al. 2014a), enter the arms as prograde rotators (red numbers) but exit as retrograde (black numbers) rotators! Presumably this is due to the nonaxisymmetric gravitational potential of the spiral arm or to cloud destruction-formation mechanisms within the arm. The stellar arm-interarm contrast is about 3 in M 51 (Elmegreen et al. 2011; Rix & Rieke 1993) as compared to probably 1.6 in M 33 (Elmegreen et al. 2011), so it is not surprising to see spiral-arm related features in M 51 while not in M 33. Meidt et al. (2018) show how GMCs can have internally driven motions (turbulence) in the interarm region but their kinematics could be driven (partially) by the large-scale potential upon arrival in the arms. This systematic behavior is yet further evidence that the velocity gradients are not due to random effects.
 |
Fig. 8. Residual velocity field as before but only for Arm 1. Printed in red and black are respectively the prograde and retrograde rotators from the S/N ≥ 10 sample. The contours give the cloud sizes and shapes. As can be seen, most clouds enter the arm (redshifted side for Arm 1) as prograde rotators and come out as retrograde rotators. The same is seen in Arm 2 and in the lower S/N sample (see last part of Table 2) but there are too many clouds for a simple visualization. |
5. Conclusions
Cloud velocity gradients are seen within the PAWS sample of clouds. Dominantly prograde velocity gradients are observed in the Colombo et al. (2014a) cloud sample. This in itself, coupled with the similar results found by Braine et al. (2018) for M 33, is evidence that velocity gradients are chiefly due to cloud rotation. 30% of the clouds show retrograde rotation. As in M 33, the rotational energy is not sufficient to support the cloud against gravity, at least at the GMC-scale observed here.
The gradients follow – but with lower amplitude – the shear in the disk, which is expected for gravitational contraction within an axisymmetric differentially rotating disk. Strictly prograde rotation would be expected in M 51 and M 33 for perfect measurements with only gravity in an axisymmetric potential. Thus, the presence in both galaxies of retrograde gradients indicates that other processes also play a role in creating the observed gradients, in addition to measurement uncertainties. The nonaxisymmetric potential of the spiral arm regions is one of the causes of retrograde rotation. Retrograde rotation is more common along the spiral arms than in the disk of M 51 as a whole. In particular, the leading (i.e., outer) edge of the spiral arms actually shows a majority of retrograde rotators, such that clouds apparently enter as prograde rotators and leave the arms as dominantly retrograde rotators.
References
- Bally, J. 1989, in European Southern Observatory Conference and Workshop Proceedings, eds. B. Reipurth, 33, 1 [Google Scholar]
- Blitz, L. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 125 [Google Scholar]
- Braine, J., Rosolowsky, E., Gratier, P., Corbelli, E., & Schuster, K.-F. 2018, A&A, 612, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burkert, A., & Bodenheimer, P. 2000, ApJ, 543, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Colombo, D., Hughes, A., Schinnerer, E., et al. 2014a, ApJ, 784, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Colombo, D., Meidt, S. E., Schinnerer, E., et al. 2014b, ApJ, 784, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Corbelli, E., Braine, J., Bandiera, R., et al. 2017, A&A, 601, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobbs, C. L. 2008, MNRAS, 391, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Druard, C., Braine, J., Schuster, K. F., et al. 2014, A&A, 567, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, D. M., Elmegreen, B. G., Yau, A., et al. 2011, ApJ, 737, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Gratier, P., Braine, J., Rodriguez-Fernandez, N. J., et al. 2012, A&A, 542, 108 [Google Scholar]
- Gratier, P., Braine, J., Rodriguez-Fernandez, N. J., et al. 2010, A&A, 522, 3 [Google Scholar]
- Hu, T., Shao, Z., & Peng, Q. 2013, ApJ, 762, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Imara, N., Bigiel, F., & Blitz, L. 2011, ApJ, 732, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Kutner, M. L., Tucker, K. D., Chin, G., & Thaddeus, P. 1977, ApJ, 215, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Leroy, A. K., Rosolowsky, E., et al. 2018, ApJ, 854, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Schinnerer, E., García-Burillo, S., et al. 2013, ApJ, 779, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L. 1966, MNRAS, 131, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, J. P. 1999, A&AS, 134, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Querejeta, M., Meidt, S. E., Schinnerer, E., et al. 2016, A&A, 588, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rix, H.-W., & Rieke, M. J. 1993, ApJ, 418, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E., Engargiola, G., Plambeck, R., & Blitz, L. 2003, ApJ, 599, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E., & Leroy, A. 2006, PASP, 118, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Meidt, S. E., Pety, J., et al. 2013, ApJ, 779, 42 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Scaling relations for the specific angular momentum j as a function of cloud mass and size.
Comparison of rotation in regions of M 51, showing the results for both samples.
All Figures
 |
Fig. 1. First moment velocities (top panel) followed by the calculated gradient and the residual image. The color wedges show the velocities in km s−1 and the x and y axes show the position of the cloud in arcseconds. |
| In the text | |
 |
Fig. 2. Same as Fig. 1 but for a smaller cloud with a smaller gradient. |
| In the text | |
 |
Fig. 3. Histogram of velocity gradients measured for M 51 clouds. The black histogram is for the subsample S/N ≥ 7 and the red for the subsample S/N ≥ 10. The gradients in the higher S/N subsample are better defined (more prograde and with a more significant gradient). |
| In the text | |
 |
Fig. 4. Histogram of angular momenta for M 51 clouds. In black for the subsample S/N ≥ 7 and in red for the subsample S/N ≥ 10. Note that the gradients in the higher S/N subsample are better defined (more prograde and with a more significant gradient). We have included a correction for beam-smearing as in B18. The angular momenta of the M 51 clouds are substantially higher than in M 33 (see middle panel of next figure). |
| In the text | |
 |
Fig. 5. Top: specific angular momentum as a function of cloud mass. The trends from B18 for M 33 and from Phillips (1999) are indicated. This figure can be directly compared with B18 and with Dobbs (2008). Middle: here we show the strong M 33 clouds along with the M 51 clouds, without showing the distinctions between pro/retrograde and S/N level. While the values are lower for the M 33 clouds, the M 51 clouds follow a similar trend. Bottom: specific angular momentum as a function of cloud radius. The trend from Phillips (1999) is indicated. The cloud radii are from Colombo et al. (2014a) and the accumulation at 32 pc is due to a limit set by Colombo et al. (2014a). The fit results for M 33 and M 51 for both the high S/N and full samples are given in Table 1. The scatter about the fits is a factor 2–3 (precise values given in Table 1). |
| In the text | |
 |
Fig. 6. First panel: PAWS first moment (velocity) from the CO(1–0) observations by Schinnerer et al. (2013) and upper right panel: analytical velocity field designed to approximate the observations but with purely circular rotation and a constant position angle and inclination. Lower panels: (left) velocity gradient |
| In the text | |
 |
Fig. 7. Residual velocity field as in Colombo et al. (2014b), with annotations to clarify text. Note how each arm has a red-shifted and a blue-shifted side; this is used to separate the two sides of the arms. |
| In the text | |
 |
Fig. 8. Residual velocity field as before but only for Arm 1. Printed in red and black are respectively the prograde and retrograde rotators from the S/N ≥ 10 sample. The contours give the cloud sizes and shapes. As can be seen, most clouds enter the arm (redshifted side for Arm 1) as prograde rotators and come out as retrograde rotators. The same is seen in Arm 2 and in the lower S/N sample (see last part of Table 2) but there are too many clouds for a simple visualization. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.