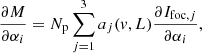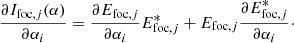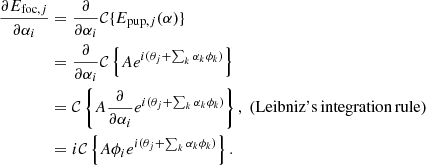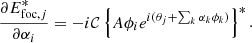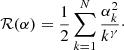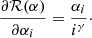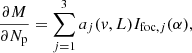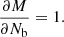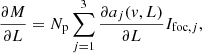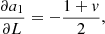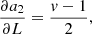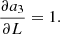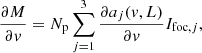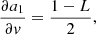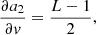| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 19 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201936062 | |
| Published online | 26 November 2019 | |
Focal-plane wavefront sensing with the vector-Apodizing Phase Plate
1
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: stevenbos@strw.leidenuniv.nl
2
National Astronomical Observatory of Japan, Subaru Telescope, National Institute of Natural Sciences, Hilo, HI 96720, USA
3
Steward Observatory, University of Arizona, 933 N. Cherry Ave, Tucson, AZ 85721, USA
4
College of Optical Sciences, University of Arizona, 1630 E. University Blvd., Tucson, AZ 85721, USA
5
Astrobiology Center, National Institutes of Natural Sciences, 2-21-1 Osawa Mitaka, Tokyo, Japan
6
Department of Astronomy, California Institute of Technology, 1200 E. California Blvd., Pasadena, CA 91125, USA
7
Observatoire de la Cote d’Azur, Boulevard de l’Observatoire, 06304 Nice, France
Received:
11
June
2019
Accepted:
10
September
2019
Context. One of the key limitations of the direct imaging of exoplanets at small angular separations are quasi-static speckles that originate from evolving non-common path aberrations (NCPA) in the optical train downstream of the instrument’s main wavefront sensor split-off.
Aims. In this article we show that the vector-Apodizing Phase Plate (vAPP) coronagraph can be designed such that the coronagraphic point spread functions (PSFs) can act as wavefront sensors to measure and correct the (quasi-)static aberrations without dedicated wavefront sensing holograms or modulation by the deformable mirror. The absolute wavefront retrieval is performed with a non-linear algorithm.
Methods. The focal-plane wavefront sensing (FPWFS) performance of the vAPP and the algorithm are evaluated via numerical simulations to test various photon and read noise levels, the sensitivity to the 100 lowest Zernike modes, and the maximum wavefront error (WFE) that can be accurately estimated in one iteration. We apply these methods to the vAPP within SCExAO, first with the internal source and subsequently on-sky.
Results. In idealized simulations we show that for 107 photons the root mean square (rms) WFE can be reduced to ∼λ/1000, which is 1 nm rms in the context of the SCExAO system. We find that the maximum WFE that can be corrected in one iteration is ∼λ/8 rms or ∼200 nm rms (SCExAO). Furthermore, we demonstrate the SCExAO vAPP capabilities by measuring and controlling the 30 lowest Zernike modes with the internal source and on-sky. On-sky, we report a raw contrast improvement of a factor ∼2 between 2 and 4 λ/D after five iterations of closed-loop correction. When artificially introducing 150 nm rms WFE, the algorithm corrects it within five iterations of closed-loop operation.
Conclusions. FPWFS with the vAPP coronagraphic PSFs is a powerful technique since it integrates coronagraphy and wavefront sensing, eliminating the need for additional probes and thus resulting in a 100% science duty cycle and maximum throughput for the target.
Key words: instrumentation: adaptive optics / instrumentation: high angular resolution
© ESO 2019
1. Introduction
The exploration of circumstellar environments at small angular separations by means of direct imaging is crucial for the detection and characterization of exoplanets. The challenges that need to be overcome are that of high contrast and small angular separation. For example the angular separation and contrast between the Earth and the Sun at 10 pc in the visible (∼0.3−1 μm) is respectively ∼100 milliarcseconds (mas) and ∼10−10 (Traub & Oppenheimer 2010).
The current generation of ground-based high-contrast imaging instruments SPHERE (Beuzit et al. 2019), GPI (Macintosh et al. 2014), the upcoming MagAO-X (Males et al. 2018; Close et al. 2018), and Subaru Coronagraphic Extreme Adaptive Optics (SCExAO; Jovanovic et al. 2015) are pushing towards contrasts of ∼10−6 at angular separations of 200 mas after post-processing in the near-infrared (0.95−2.3 μm; Vigan et al. 2015). These instruments are equipped with extreme adaptive optics systems to flatten the wavefront after the turbulent atmosphere, coronagraphs to suppress the star light and contrast-enhancing post-processing techniques that employ some form of diversity such as angular differential imaging (Marois et al. 2006), reference star differential imaging (Ruane et al. 2019), spectral differential imaging (Sparks & Ford 2002), and polarimetric differential imaging (Snik & Keller 2013). The latter two techniques can also be used as a characterization diagnostic. Medium- and high-resolution integral-field spectroscopy can be used to detect atomic and molecular lines from a planet’s atmosphere (e.g., Haffert et al. 2019; Hoeijmakers et al. 2018), while polarimetry can be used to detect cloud structures (Stam et al. 2004; De Kok et al. 2011; van Holstein et al. 2017).
The coronagraph relevant for the present work is the vector-Apodizing Phase Plate (vAPP; Snik et al. 2012; Otten et al. 2017), which manipulates the phase in the pupil-plane such that in selected regions in the focal plane the starlight is cancelled; these areas are referred to as dark holes. The phase is induced through the achromatic geometric phase (Pancharatnam 1956; Berry 1987) on the circular polarization states by a half-wave liquid-crystal layer with a varying fast-axis orientation. The two circular polarization states both receive equal but opposite phases, resulting in two coronagraphic point spread functions (PSFs) with opposite dark holes, as shown in Fig. 1. The geometric phase is inherently achromatic as it depends on geometric effects, but the efficiency with which the light acquires the phase is determined by the retardance of the liquid-crystal layer. Retardance offsets from half-wave result in leakage; light that has not acquired the desired phase will form a non-coronagraphic PSF based on the aperture geometry. Generally, vAPP coronagraphs are designed to have minimal leakage over a broad wavelength range. High leakage will affect coronagraphic performance as light from the leaked PSF will contaminate the dark hole. In the simplest and most common implementation the two coronagraphic PSFs are spatially separated with a polarization-sensitive grating (Oh & Escuti 2008) that is integrated in the phase design. These coronagraphs are known as grating-vAPPs (Otten et al. 2014) and are mainly used for operation with narrowband filters or integral-field spectrographs to prevent smearing by the grating. In this article the grating-vAPP is referred to as a vAPP. The vAPP has been put on-sky with several instruments: CHARIS/SCExAO (Doelman et al. 2017), MagAO/Clio2 (Otten et al. 2017), LMIRCAM/LBT (Doelman et al. 2017), and LEXI (Haffert et al. 2018). Furthermore, vAPPs have been designed for the following instruments: HiCIBaS (Côté et al. 2018), MagAO-X (Miller et al. 2018), ERIS (Boehle et al. 2018), METIS (Kenworthy et al. 2018), and MICADO (Davies et al. 2018).
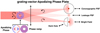 |
Fig. 1. Working principle of the grating-vector-Apodizing Phase Plate. The grating-vAPP is a half-wave retarder pupil-plane optic with a spatially varying fast-axis orientation. The varying fast-axis orientation induces the phase through the geometric phase on the circular polarization states. These polarization states receive the opposite phase and therefore have flipped coronagraphic point spread functions (PSFs). The PSFs are spatially separated by adding a phase ramp to the design. Any offsets from half-wave retardance within the optic reduces the efficiency with which the light will be transferred to the coronagraphic PSFs and results in a leakage PSF. |
One of the key limitations of the current high-contrast imaging instruments that limit them to contrasts above ∼10−6 within 300 mas are quasi-static speckles that originate from slowly evolving instrumental aberrations caused by changing temperature, humidity, and gravity vector during observations (Martinez et al. 2012, 2013; N’Diaye et al. 2016; Vigan et al. 2018). When these aberrations occur in the optical train downstream of the main wavefront sensor split-off, they are not be sensed and therefore cannot be corrected. Additional focal-plane wavefront sensing (FPWFS) with the science detector is a highly desirable solution to these non-common path aberrations (NCPA). In addition to eliminating the NCPAs, a FPWS can also address chromatic errors between the main sensing and science channels. Another advantage of FPWFS is that it has been shown by Guyon (2005) that it is able to reach high sensitivities for all spatial frequencies, only being surpassed in sensitivity by the Zernike wavefront sensor (N’Diaye et al. 2013; Doelman et al. 2019). A notable FPWFS is the Self-Coherent Camera (SCC; Baudoz et al. 2005; Galicher et al. 2008; Mazoyer et al. 2013). This is a WFS that is combined with a coronagraph, which uses focal-plane optics to block starlight. It operates by placing a small hole in the pupil-plane Lyot stop outside of the geometric pupil where the scattered starlight is located. This hole creates a reference beam that generates high spatial frequency fringes in the focal-plane image, which can be used to determine the full electric field. The SCC has a 100% science duty cycle, but requires a high focal-plane sampling to resolve the fringes, and optics of a sufficient size to accommodate the reference beam. FPWS has also been conducted by using vAPPs. Previous work focused on adding additional holograms in the focal plane that either encode wavefront information (Wilby et al. 2017) or directly probe the electric field (Por & Keller 2016); these will not be considered here.
An overview of FPWFS techniques can be found in Jovanovic et al. (2018). There are three FPWFS and control methods that are particularly relevant: The COronagraphic Focal-plane waveFront Estimation for Exoplanet detection (COFFEE; Sauvage et al. 2012; Paul et al. 2013a) wavefront sensor is an extension of classical phase diversity (Gonsalves 1982; Paxman et al. 1992) to coronagraphic imaging. Aberrations in a physical model of the coronagraphic system are fitted to two focal-plane images, one of which has a known phase diversity (e.g., defocus). The method has been demonstrated in the lab (Paul et al. 2013b) and on the SPHERE system using the internal calibration source (Paul et al. 2014). Recent extensions enable COFFEE to measure phase in long-exposure images affected by residual turbulence (Herscovici-Schiller et al. 2017), and measure both phase and amplitude (Herscovici-Schiller et al. 2018).
An interferometric approach to FPWFS is the Asymmetric Pupil Fourier Wavefront Sensor (APF-WFS; Martinache 2013). The APF-WFS assumes the small aberration regime enabling a Fourier analysis of focal-plane images to determine pupil-plane phase aberrations. The image is formed by an asymmetric pupil, which enables the full phase determination. The theory behind this technique is more extensively discussed in Sect. 2. The wavefront sensor has been demonstrated on-sky in closed-loop operation controlling the lowest-order Zernike modes (Martinache et al. 2016), also in the context of controlling the “island effect” (N’Diaye et al. 2018).
Linear dark-field control (LDFC; Guyon et al. 2017) and more specifically the spatial LDFC variant (Miller et al. 2017). The idea behind spatial LDFC is to measure and control small aberrations that pollute the dark hole (created by the vAPP or other techniques) by measuring the response of the bright field (see Fig. 1) relative to a reference state. This response is approximately linear for small aberrations. In Miller et al. (2017) it was shown to work for one-sided dark holes and modes that have a response in the bright field and the dark hole, but in this case there is also a spatial null-space consisting of the modes that do not have a response in the bright field but do pollute the dark hole. The authors overcame this problem by using the vAPP (Miller et al. 2018), where the bright field of one coronagraphic PSF covers the dark hole of the other. This has been shown to work in the laboratory (Miller 2018), but there is still a significant null space for most vAPP designs; it is insensitive to the even pupil phase modes (see Sect. 2).
COFFEE and the APF-WFS both suffer from low duty cycles as the science observations have to be stopped for the phase diversity probes or moving the asymmetric mask in and out the beam. LDFC, on the other hand, has a 100% duty cycle, but has currently only been considered for vAPPs with a significant null space (the even pupil phase modes), it only works in the small aberration regime, and does not perform an absolute phase measurement. In Sect. 2 we combine the APF-WFS and LDFC with vAPPs, eliminating the null space and improving the duty cycle to 100%. In Sect. 3 we present a non-linear algorithm similar to COFFEE that can perform absolute phase retrieval. In Sect. 4 we explore the theoretical FPWFS performance of the vAPP and the non-linear algorithm with simulations for the vAPP installed at SCExAO. In Sect. 5 we demonstrate the method first with the internal source and subsequently on-sky. In Sect. 6 we discuss the results and present the conclusions.
2. Theory
2.1. Phase retrieval
Phase retrieval techniques in astronomy deal with sensing pupil-plane phase aberrations by analyzing focal-plane images. These techniques require a unique response in the focal-plane intensity for every phase mode and sign of its modal coefficient (the amount of wavefront error in the specific phase mode). For symmetric pupils such a unique response does not exist for the sign of the modal coefficients of even phase modes. For example, it is easy to determine how an optic needs to be moved to correct for tip and/or tilt (odd Zernike mode). But when the PSF is defocused (even Zernike mode), it is not immediately clear in which direction the optic needs to be moved to bring the PSF back into focus. In this section we demonstrate the origin of this well-known sign ambiguity (Gonsalves 1982; Paxman et al. 1992).
The electric field in the pupil-plane consists of an amplitude component A(r) and a phase component θ(r):
Here the electric field Epup and its constituents, A and θ, are 2D entities where the position vector r, defined from the center of the pupil, is omitted from here on. The focal-plane electric field Efoc(x) is formed by propagating Epup using the Fraunhofer propagation operator 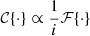 (Goodman 2005). We use the Fraunhofer propagator, instead of just the Fourier transform because it is the physically correct propagator:
(Goodman 2005). We use the Fraunhofer propagator, instead of just the Fourier transform because it is the physically correct propagator:
Here a(x) and b(x) are the real and imaginary components of Efoc(x), respectively, and generally contain a mixture of 𝒞{Acos(θ)} and 𝒞{iAsin(θ)}. The focal-plane coordinates are denoted by x and are omitted from here on as well. The focal-plane intensity Ifoc or PSF is subsequently given by
Before we continue with an example of even phase aberrations, we recall the following:
1. The decomposition of a function f(r) into even and odd functions:
An example of a symmetry decomposition of phase and amplitude in the context of the APP coronagraph is shown in Fig. 4.
2. The multiplication and composition properties of even and odd functions:
3. The symmetry properties of Fraunhofer propagation (see Table 1).
4. The Hermitian properties of the Fraunhofer propagation, which say that a conjugated pupil-plane electric field 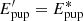 (i.e., a phase sign flip; * denotes the conjugation) will result in a flipped and conjugated focal-plane electric field
(i.e., a phase sign flip; * denotes the conjugation) will result in a flipped and conjugated focal-plane electric field 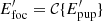 :
:
Fraunhofer propagation symmetry properties (Goodman 2005).
The reason that the symmetry decomposition, combined with the decomposition of Epup in its real and imaginary components (Eq. (2)), is important, is that the Fraunhofer propagation maps combinations of these decompositions into either real or imaginary components of Efoc, as shown in Table 1. We show below that these properties of the Fraunhofer propagation determine what kind of symmetry has to be introduced in the pupil-plane to determine the sign of even phase aberrations.
Let us assume that A is even, which is true for most instrument pupils. If an even phase aberration (e.g., astigmatism) is added, the terms A cos (θ) and iA sin (θ) will both be even. We note that only the imaginary term contains sign information on the aberration. In this example, when they are propagated to the focal plane, Acos(θ) will go to ib and iA sin (θ) to a (respectively shown in the first and third row of Table 1). These terms are still even and the sign information on the aberration is encoded in the real part of the focal-plane electric field. The resulting PSF recorded by the detector is even. These steps are shown in the top row of Fig. 2a. If the sign of the aberration flips (i.e., a conjugation of the pupil-plane electric field), the PSF flips, but as the PSF is even, there is no morphology change recorded and thus the sign information cannot be retrieved (see Fig. 2a, bottom row). We can only hope to determine the sign by measuring the real electric field as that is where the sign information is encoded. For odd phase aberrations the sign flip will result in a morphology change and can therefore be measured.
 |
Fig. 2. Focal- and pupil-plane quantities of an even phase aberration (astigmatism) through a symmetric pupil (a) and an asymmetric pupil (b). The two rows show opposite signs for the phase aberration. The columns in the pupil-plane box show (from left to right) the amplitude, phase, and real and imaginary electric fields. In the focal-plane box the columns show the real and imaginary electric fields, the power in the real and imaginary electric fields, and the total power. |
If the same exercise is performed with a pupil amplitude asymmetry, there will be a morphology change. This is shown in the top and bottom rows of Fig. 2b. The reason is that an even pupil amplitude, as shown in the top row of Fig. 3a, will only generate an imaginary electric field and therefore will not interfere with sign information containing a real electric field caused by even aberrations. This is not the case for an asymmetric pupil amplitude as it also generates a real electric field due to odd pupil amplitude (second row of Table 1). This real electric field interferes with the aberration’s real electric field and thus enables the sign determination. The electric field of an asymmetric pupil is shown in the bottom row of Fig. 3a. More examples of pupil-plane phase retrieval with focal-plane images can be found in Appendix A.
 |
Fig. 3. Focal- and pupil-plane quantities for (a) a symmetric and asymmetric pupil, and (b) vAPPs designed for these pupils. The columns in the pupil-plane box show (from left to right) the amplitude, phase, and real and imaginary electric fields. In the focal-plane box the columns show the real and imaginary electric fields, the power in the real and imaginary electric fields, and the total power. |
This is the working principle of the Asymmetric Pupil Fourier Wavefront Sensor (Martinache 2013). Interestingly, other focal-plane wavefront sensing methods such as the differential Optical Transfer Function (Codona & Doble 2012) and Self-Coherent Camera (Baudoz et al. 2005) also rely on pupil asymmetries, even though they use other reconstruction algorithms. Classical phase diversity techniques (Gonsalves 1982; Paxman et al. 1992) come to a similar result by introducing a known even phase aberration (e.g., defocus; odd phase modes can never be used; see top row of Fig. 3b). This is the only other way of probing the real part of the focal-plane electric field (Table 1). Therefore, all these methods can now be understood as one family that probes the real focal-plane electric field by manipulating either pupil-plane phase or the pupil-plane amplitude. In the context of FPWFS with the vAPP, it is undesirable to use an even pupil-plane phase to break the sign ambiguity because it fills up the dark-hole of the coronagraph and therefore prevents simultaneous science observations and wavefront measurements. On the other hand, vAPPs can be designed for pupils with an amplitude asymmetry, this will be shown in the next subsection, and therefore can combine science observations and wavefront sensing. This result also applies to other FPWFS techniques; for example, it affects spatial LDFC (see Appendix B).
2.2. vAPP design for phase retrieval
Our framework of describing how pupil-plane phase and amplitude symmetries map to the focal-plane electric field also helps us understand some of the aspects of APP design and the requirements for turning an APP into an FPWFS. The optimization method that guarantees optimal APP designs, which are phase-only solutions, is detailed in Por (2017) and is not discussed here. The APPs considered in this section are all designed to have a one-sided D-shaped dark hole from 1.8 λ/D to 10 λ/D with a raw contrast of < 10−5. The dark hole is defined as the area in the focal plane where the raw contrast meets the requirement.
Let us suppose that we want to design an APP with a one-sided dark hole (=PSF with odd symmetry) for a symmetric aperture (Aeven). Such an aperture will yield a completely imaginary focal-plane electric field with even symmetry (top row of Fig. 3). As the APP manipulates phase, this imaginary electric field needs to be cancelled on one side using pupil-plane phase. The last row of Table 1 indicates that the only way of removing an odd part of the imaginary focal-plane electric field (ib) for an even aperture (Aeven) is by introducing a purely odd pupil-plane phase. This indeed results from the optimization method (top row of Figs. 3b and 4a).
 |
Fig. 4. Decomposition of the pupil-plane phase and amplitude into their even and odd constituents for the two APP designs in Fig. 3b. (a): APP designed for a symmetric aperture. (b): APP designed for an asymmetric aperture. |
An asymmetric aperture (bottom row of Fig. 3a) yields a focal-plane electric field with real and imaginary components. The asymmetric aperture consists of a central obscuration that is 10% of the aperture diameter and a bar with the same width that connects the central obscuration with the edge of the aperture. Cancelling the focal-plane electric field on one side to create the dark hole requires an odd pupil phase to cancel the imaginary focal-plane electric field (last row of Table 1), and an even pupil-plane phase for the real part (third row of Table 1). Again, this is the solution the optimization method comes up with (see bottom rows of Figs. 3b and 4b). Crucially for FPWFS with the APP, the real focal-plane electric field originating from the odd pupil amplitude component cannot be completely removed by the even pupil-plane phase, but is enhanced on the bright side of the APP coronagraphic PSF, as shown in the bottom row of Fig. 3b.
To summarize, FPWFS capabilities of the vAPP are fundamentally enabled by the pupil amplitude asymmetry. This asymmetry introduces a real focal-plane electric field that interferes with the even pupil-plane phase aberrations and enables their sign determination. The vAPP allows for simultaneous science observations by removing the real electric field from the dark hole and moving it to the bright field (see Appendix A for figures that demonstrate this).
3. Aberration estimation algorithm
3.1. Maximum a posteriori estimation
We developed an algorithm that gives a maximum a posteriori estimation of the phase aberrations by maximizing the posterior likelihood p(α, Np, Nb, v, L|D). It takes into account a physical, non-linear model of the vAPP (shown in the next subsection), noise statistics, and prior knowledge of the estimated parameters. Given an image D the algorithm estimates α, a vector containing the amplitudes of the phase aberration modes of interest. There is the option to additionally estimate the following parameters: the number of source photons in the image Np, the background level Nb, the fractional degree of circular polarization v, and the fractional strength of the leakage PSF integrated over the spectral band L. These parameters are summarized in Table 2. The estimation of the phase aberrations is more conveniently performed by minimizing ℒ(α, Np, Nb, v, L|D), which is the negative logarithm of the likelihood function (ℒ(α, Np, Nb, v, L|D) = − ln[p(α, Np, Nb, v, L|D)]:
Parameters of ℒ that have been estimated are denoted with a hat. The objective function ℒ is given by
with D(x) the 2D image containing the data and M(α, Np, Nb, V, L) the 2D model of the vAPP PSF, which is discussed in the next subsection. The algorithm fits the model to the entire image and thus does not exclude any regions in D(x). The sum over x is over all spatial pixels. The algorithm is be applied to long-exposure images that have high photon numbers, which can be approximated to contribute spatially changing Gaussian noise (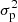 ), and detector noise (
), and detector noise (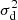 ), assumed to be white Gaussian noise. Therefore, the total noise is Gaussian and the variance is the sum of variances of the two independent processes (
), assumed to be white Gaussian noise. Therefore, the total noise is Gaussian and the variance is the sum of variances of the two independent processes (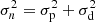 ). Prior information on the phase aberrations is taken into account explicitly by adding a term ℛ(α) to the objective function, which is given by
). Prior information on the phase aberrations is taken into account explicitly by adding a term ℛ(α) to the objective function, which is given by
with αk the modal coefficients and γ the assumed power spectrum. This term penalizes high spatial frequency modes according to assumptions on or measurements of the spatial power spectrum. Implicitly, we also regularize by using a truncated mode basis.
We minimize ℒ using the bounded limited-memory Broyden-Fletcher-Goldfarb-Shanno algorithm (L-BFGS-B; Byrd et al. 1995), which is a quasi-Newton optimization algorithm that assumes a differentiable scalar objective function. The algorithm accepts analytically calculated gradients to increase the speed and accuracy. The analytical expressions of the gradients of Eq. (20) are given in Appendix C. The algorithm also requires a start position for the estimated parameters. Generally, Np, Nb, v, and L can be easily estimated from the data, as is shown in Sect. 5. From experience, setting α = 0 (i.e., no aberration) works best when there is no initial guess available for the aberrated wavefront.
3.2. Coronagraph model
The vAPP is a half-wave retarder with a spatially varying fast-axis; these spatial variations induce geometric phase on the circular polarization states. Opposite circular polarizations receive the opposite phase, creating two similar but mirror-imaged coronagraphic PSFs (see Fig. 1). Additionally, as the optic is not perfectly half-wave, part of the light does not receive the desired phase and creates an extra non-coronagraphic PSF; we refer to this PSF as the leakage. The relative intensity of the coronagraphic PSFs depends on the fractional degree of circular polarization v (normalized to the total intensity) and the amount of leakage. In the model we assume a single point source and therefore the image plane is given by
with Np the total number of photons in the image, Nb the background level (sky background, dark current, or bias), Ifoc, j the image from either left- (j = 1) or right-handed (j = 2) circular polarization or from leakage (j = 3). The aj(v, L) terms describe the relative intensities of these PSFs and are given by
The PSFs are normalized such that the sum over all pixels in the image is one: ∑rIfoc, j = 1. We note that we can incoherently add the leakage term and the coronagraphic PSFs because orthogonal polarization states emitted by blackbody sources are incoherent, even when they are transformed to the same polarization state (Fresnel-Arago laws; Kanseri et al. 2008; Mujat et al. 2004). The Ifoc, j is given by
with A the amplitude of the aperture, θj = ±θapp for j = 1, 2 and θj = 0 for j = 3. The phase aberration is expanded in the mode basis {ϕi}, with αi being the estimated coefficients. This last equation shows the non-linearity of the model: (1) we estimate phase, which is contained in the complex exponent, and (2) the estimation is performed on intensity images, which are the square of the electric field.
4. Simulations
In this section we explore the performance of the algorithm in idealized circumstances by numerical simulations. Performance will be reported in absolute units (nm) in the context of the SCExAO vAPP and in relative units (fractional λ) to allow comparison with other methods.
The design of the SCExAO vAPP is detailed in Doelman et al. (2017); here we only discuss the most relevant details. The D-shaped dark holes have a raw contrast of 10−5 with respect to the peak flux of the coronagraphic PSF and extend from 2 to 11 λ/D. In addition to the two coronagraphic PSFs and the central leakage PSF, two more phase diversity PSFs were added. These PSFs have opposite defocus aberration and can be used for classical phase diversity, but are not considered in this work. The top row of Fig. 5 shows the pupil-plane amplitude for which the vAPP was designed, the subsequent phase design, and the focal-plane intensity. As detailed in the bottom row of the figure, there is a clear amplitude asymmetry due to the blocking of dead deformable mirror (DM) actuators. This odd amplitude component Aodd, combined with the even phase θeven that cancels the effect of the asymmetry in the dark holes, results in the real focal-plane electric field that is used to probe even pupil-plane phase aberrations. Approximately 3.5% of the focal-plane power is in the real electric field, and is therefore available to sense even phase aberrations.
 |
Fig. 5. Amplitude and phase design of the SCExAO vAPP (Doelman et al. 2017) and its resulting PSF. The pupil-plane quantities are decomposed into their even and odd constituents, while the focal-plane PSF is decomposed into the power in the real and imaginary parts of the electric field. |
Simulations are performed with the HCIPy package (Por et al. 2018), an open-source software for high-contrast imaging simulations that is available on GitHub1. The simulations are monochromatic (λ = 1550 nm). They sample the pupil-plane with 256 × 256 pixels and use the Fraunhofer approximation to propagate the electric field to the focal plane, which is sampled with 150 × 150 pixels for 3 pixels per λ/D. The aberration estimation algorithm is Python-based, uses the HCIPy package for the coronagraph model and the Scipy library (Jones et al. 2014) to minimize the objective function.
4.1. Photon and read noise sensitivity
Figure 6 presents the sensitivity of the algorithm and the SCExAO vAPP when considering varying levels of photon and read noise. The modal basis set used for these tests consists of the first 30 Zernike modes, starting at defocus. All induced aberrations were a linear sum of these modes. The aberrated phase screen is created by first calculating a phase screen following a spatial power spectrum with a slope of −2.5. This slope is steeper than a slope of −2, usually considered for the power spectrum of NCPA, but was chosen to put more power in the low-order modes as we focus on measuring them. Subsequently, this phase screen is projected onto the 30 Zernike modes, which were added together and scaled to a ∼λ/16 (100 nm) root mean square (rms) wavefront error (WFE). The algorithm estimated the same Zernike modes as were used to generate the phase screen. For every photon number Np (103 − 109 photons) we generated ten different phase screens and, for each phase screen, ten photon noise realizations. Furthermore, four levels of read noise were tested: 0 e−, 0.1 e−, 1 e−, and 10 e−. The results of the simulations are plotted in Fig. 6, where the dots denote the mean rms WFE per photon number and read noise level, and the error bars denote the 1σ deviation. The dotted line is a fit of a 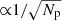 function to the pure photon noise simulations, confirming that the performance scales with the photon noise. The algorithm therefore is photon noise limited (i.e., no algorithmic effects limit the performance). For the photon-limited case, a < λ/1000 residual rms WFE is reached with 107 photons. In the context of the SCExAO system (Sect. 5) this would be a 1 nm residual WFE for a ∼5 s integration on a mH = 8 star. The simulations also show that increasing the read noise to 0.1 e− or 1 e− does not significantly impact the performance of the algorithm (i.e., the error is still dominated by photon noise). For a read noise level of 10 e− and photon numbers < 106, the read noise starts to dominate the error and decreases the performance by a factor of ∼2 − 3.
function to the pure photon noise simulations, confirming that the performance scales with the photon noise. The algorithm therefore is photon noise limited (i.e., no algorithmic effects limit the performance). For the photon-limited case, a < λ/1000 residual rms WFE is reached with 107 photons. In the context of the SCExAO system (Sect. 5) this would be a 1 nm residual WFE for a ∼5 s integration on a mH = 8 star. The simulations also show that increasing the read noise to 0.1 e− or 1 e− does not significantly impact the performance of the algorithm (i.e., the error is still dominated by photon noise). For a read noise level of 10 e− and photon numbers < 106, the read noise starts to dominate the error and decreases the performance by a factor of ∼2 − 3.
 |
Fig. 6. Residual rms WFE as a function of photon number Np for the SCExAO vAPP. Different colors denote various read noise levels. The dotted line shows a |
4.2. Mode photon noise sensitivity
In Guyon (2005) the photon noise sensitivity βp of a WFS to a single mode m is defined as
with σm the reconstruction error for mode m and Np the number of photons in the image. According to Guyon (2005), the ideal WFS will have βp = 1 for all reconstructed modes. Here we explore the sensitivity of the SCExAO vAPP to the first 100 Zernike modes (starting with defocus as the vAPP is tip/tilt insensitive), expecting that the vAPP has a lower sensitivity (resulting in a higher βp) for the even modes than for the odd modes (see discussion in Sect. 2). The reconstruction error σm was determined by calculating the standard deviation of the 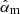 distribution, obtained after simulating 100 different photon noise realizations per photon number (107, 108, and 109) and estimating only
distribution, obtained after simulating 100 different photon noise realizations per photon number (107, 108, and 109) and estimating only 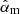 (no other modes were estimated simultaneously). This resulted in three βp values (one for each tested photon number), which were subsequently averaged to obtain the final result. The results are shown in Fig. 7, with the ideal WFS (βp = 1) shown as the horizontal gray dotted line. The gray boxes denote the even modes, and the white boxes the odd modes. The first thing to note is that the even modes perform a factor ∼4 − 10 worse than the odd modes. This occurs because, as discussed in Sect. 2, the real part of the focal-plane electric field probes the even modes, and in the case of the SCExAO vAPP is relatively weak: ∼3.5% of the total power is in the real electric field. Therefore, it is expected that βp is
(no other modes were estimated simultaneously). This resulted in three βp values (one for each tested photon number), which were subsequently averaged to obtain the final result. The results are shown in Fig. 7, with the ideal WFS (βp = 1) shown as the horizontal gray dotted line. The gray boxes denote the even modes, and the white boxes the odd modes. The first thing to note is that the even modes perform a factor ∼4 − 10 worse than the odd modes. This occurs because, as discussed in Sect. 2, the real part of the focal-plane electric field probes the even modes, and in the case of the SCExAO vAPP is relatively weak: ∼3.5% of the total power is in the real electric field. Therefore, it is expected that βp is 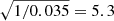 times higher for even modes compared to the odd modes, which is approximately observed. Furthermore, it should be noted that the spatial frequency content of the Zernike modes increases with the Noll index. Therefore, due to lower S/N at higher frequencies, sensitivity to both even and odd modes decreases with increasing mode number. The sensitivity to even modes decreases faster than the odd mode sensitivity because the real part of the focal-plane electric field is limited in extent compared to the imaginary part (shown in Fig. 5). We note that this analysis does not include any cross-talk effects, which are taken into account in the next section.
times higher for even modes compared to the odd modes, which is approximately observed. Furthermore, it should be noted that the spatial frequency content of the Zernike modes increases with the Noll index. Therefore, due to lower S/N at higher frequencies, sensitivity to both even and odd modes decreases with increasing mode number. The sensitivity to even modes decreases faster than the odd mode sensitivity because the real part of the focal-plane electric field is limited in extent compared to the imaginary part (shown in Fig. 5). We note that this analysis does not include any cross-talk effects, which are taken into account in the next section.
 |
Fig. 7. Photon noise sensitivity of the SCExAO vAPP to the first 100 Zernike modes, starting at defocus. The gray boxes denote the even Zernike modes, and the white boxes the odd Zernike modes. |
4.3. Dynamic range algorithm
Here we explore the maximum rms WFE for which the algorithm can accurately recover estimates for each modal coefficient in a single step. This limitation is mainly driven by modal cross-talk and determines the WFE for which the algorithm can converge to a low (∼λ/1000 − λ/100 or 1−10 nm) residual rms WFE in one iteration, assuming that the estimation is perfectly applied by the DM. We simulated phase screens consisting of 30 Zernike modes (starting with defocus), following a spatial power spectrum with a −2.5 slope, with increasing WFE. For rms WFE values between 0 and ∼λ/4 (400 nm) we simulated ten wavefronts, with either no photon noise (Np = ∞) or high photon numbers (Np = 106, 108). For the simulations with photon noise, we simulated ten photon-noise realizations per phase screen. The algorithm estimated the same Zernike modes. The residual rms WFE was determined by subtracting the estimation from the initial, aberrated wavefront. The mean residual rms WFEs are shown in Fig. 8. The performance of the algorithm does not significantly vary between the different photon number realizations. The algorithm converges in one iteration with an input aberration rms of up to ∼λ/8 or 200 nm. For WFE between λ/8 and λ/5 (200−300 nm), the algorithm still improves the wavefront, but there is significant residual WFE after one iteration. In this regime the algorithm converges to < λ/1000 or 1 nm rms WFE within two or three iterations in closed-loop operation. A WFE larger than λ/5 (300 nm) rms does not significantly improve after one iteration. We note that this performance is very similar to the non-coronagraphic results reported by Martinache et al. (2016) for the Asymmetric Pupil Fourier Wavefront Sensor.
 |
Fig. 8. Residual rms WFE as function of introduced rms WFE for the SCExAO vAPP. The colors denote various photon numbers. The dashed, gray line separates the regions where the wavefront improves or deteriorates. The wavelength is 1550 nm. |
5. Demonstration at SCExAO
5.1. SCExAO
The Subaru Coronagraphic Extreme Adaptive Optics (SCExAO) instrument (Jovanovic et al. 2015) is a high-contrast imaging instrument at the Subaru Telescope. It operates downstream of the AO188 system (Minowa et al. 2010), which gives an initial low-order correction. SCExAO drives a 2000-actuator DM based on wavefront measurements from a pyramid wavefront sensor (PYWFS) from the optical to near-IR (NIR) (in the range 600−900 nm) that can run at 3.5 kHz, but most often runs at 2 kHz. There are 45 actuators across the pupil, giving the system the ability to correct out to 22.5 λ/D. The real-time control of SCExAO is handled by the compute and control for adaptive optics (cacao) package (Guyon et al. 2018). Cacao allows NCPA corrections to be handled by a separate DM channel, where the software automatically sends offsets to the PYWFS. These offsets ensure that the PYWFS does not sense and attempt to control the NCPA corrections. The instrument routinely achieves Strehl ratios > 80% in the H band on-sky. SCExAO feeds the post-AO JHK bands to the integral field spectrograph CHARIS (Peters-Limbach et al. 2013; Groff et al. 2014). The ultimate goal is to operate the vAPP FPWFS with the CHARIS data; however, the tests were performed with the internal NIR camera for ease of operation. The NIR camera has recently (Lozi et al. 2018) been upgraded to a C-RED 2 detector (Feautrier et al. 2017), which has a 640 × 512 pixel InGaAs sensor that is cooled to −40°C.
5.2. Algorithm implementation in SCExAO
The algorithm has to be adapted to the SCExAO parameters and the vAPP design. To calibrate the model of the vAPP we had to take into account the following:
1. Pupil undersizing. To account for pupil misalignments the design of the vAPP was undersized by 1.5% (Doelman et al. 2017) with respect to the nominal SCExAO pupil.
2. Pupil rotation. To optimally block dead actuators in the DM, the SCExAO pupil was rotated by −6.25°, affecting the orientation of the PSF on the detector.
3. Detector pixel scale. For accurate propagation to the focal plane of the NIR camera, the pixel scale was determined manually (which was deemed sufficient for low-order Zernike mode measurement and correction) to be 15.6 mas per pixel at 1550 nm.
The coronagraph model described in Sect. 3 assumes a monochromatic light source, and the closest available option, in terms of bandwidth, for the NIR camera in SCExAO is the Δλ = 25 nm filter centered around λ = 1550 nm. For this filter, a 128 × 128 pixel sub-window in the NIR internal camera is sufficient to contain the vAPP PSFs. The image fed to the algorithm consists of the sum of 1000 unsaturated images (either of the internal source or the star; individual exposure times are on the order of 1−10 milliseconds) that are dark-subtracted, aligned with a reference PSF generated with the coronagraph model and subsequently stacked and calibrated for the camera system gain (2.33 e−/ADU; Feautrier et al. 2017). The large number of stacked images should generally bring the algorithm into the 1 nm residual rms WFE regime (Fig. 6) in ideal circumstances and is the best performance we can expect. After image acquisition and before running the algorithm, the parameters Np, Nb, v, and L have to be estimated. Nb is estimated first by selecting the corners in the image where there is no light from the vAPP. Np is estimated by subtracting Nb from the image and summing the values in all pixels. The grating in the vAPP acts as a circularly polarized beam-splitter, thus v is determined by aperture photometry on the two coronagraphic PSFs. From these intensity measurements, I1 and I2, the fractional degree of circular polarization can be determined by
The amount of leakage L is similarly calculated by aperture photometry on the two coronagraphic (I1 and I2) and the leakage PSFs (I3):
After this initial estimation, the estimation of these parameters can also be improved by the algorithm. This is generally not done for Nb, v, and L as it has not been found to improve the wavefront estimation. On the other hand, we find that estimating Np using the algorithm does improve the estimation. Another concern is that estimating some of these parameters could induce cross-talk with the aberration coefficients. An example of such cross-talk would be between the wavefront aberration coma and v, as both parameters result in relative brightness changes between the two coronagraphic PSFs. Therefore, the algorithm could tune either parameter to fit a relative brightness change and arrive at the wrong result. We did not extensively study the effects of this cross-talk.
The closed-loop correction is performed by phase conjugation, where the DM command θDM, i at iteration i is calculated as
with g the closed-loop gain that can be freely chosen, the factor 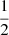 to account for the reflective nature of the DM, αj the estimated modal coefficients, and {ϕj} the mode basis.
to account for the reflective nature of the DM, αj the estimated modal coefficients, and {ϕj} the mode basis.
When estimating 30 Zernike modes with the SCExAO implementation of the algorithm, the computation time per iteration is ∼30 − 50 s. Generally, the convergence time increases when sensing more modes and larger wavefront errors. The convergence time is mainly limited by the Python library versions installed at SCExAO, and more fundamentally by the implementation in Python.
5.3. Internal source demonstration
We performed FPWFS tests with the SCExAO vAPP using the internal source in November and December 2018. The goal was to demonstrate the principle of FPWFS with the vAPP coronagraphic PSFs, and we therefore focused on measuring and correcting low-order modes (30−50 Zernike modes, starting with defocus). Figure 9 shows these results, where the 1σ raw contrast was determined by calculating the standard deviation of 1 λ/D wide annuli covering both PSFs that were normalized by the maximum number of counts in the image. The top row in the figure presents the pre- and post-correction PSFs and the radial averaged contrast improvements (panels a, b, and c, respectively) for the nominal SCExAO system using 30 Zernike modes, after one iteration with the algorithm (g = 1). The estimated wavefront is shown in Fig. 10a, and the measured WFE in the 30 Zernike modes is ∼100 nm rms. The dominant mode is astigmatism at ∼86 nm rms. The next three largest aberrations were coma, quadrafoil, and secondary astigmatism at respectively ∼28 nm, ∼24 nm, and ∼23 nm rms. Qualitatively, the wavefront improvement can be observed in the more symmetric leakage and phase diversity PSFs, and the dark hole better defined as an aberrated structure at a few λ/D was removed. Quantitatively, the peak flux of the leakage increased by ∼10%, and the raw contrast at 2.5 λ/D improved from ∼2 × 10−3 to ∼6 × 10−4 (solid lines in Fig. 9c). Only the lowest Zernike modes (both even and odd) were corrected, which is clearly visible as the contrast improvement decreases with λ/D. The dash-dotted lines in Fig. 9c show the results of a similar correction performed at another moment in time, but here the images used for the raw contrast determination were saturated such that the raw contrast was speckle-noise limited, instead of read noise limited as with the solid lines. The bottom row shows the result of a closed-loop correction where we introduced and estimated a 300 nm rms WFE with 50 Zernike modes, which should be correctable according to Fig. 8. Panels b and c show the pre- and post-correction after five iterations of closed-loop correction. The total duration of these corrections was around 4 min. These figures show that the algorithm can correct large WFE, recovering a PSF that is qualitatively very similar to what is shown in Fig. 9b. As shown in Fig. 9f, we recover similar or deeper raw contrasts compared to the nominal system after correction, Fig. 9c. In Figs. 10b and c, the introduced and estimated wavefronts are shown. The WFE for these figures are respectively ∼293 nm and ∼311 nm. We note that the estimated wavefront also includes WFE already present in the system before adding the known aberration, as this was not corrected before the test. Tests conducted on another day suggest that the remaining WFE after correction is on the order of ∼59 nm rms. These tests consist of sequential measurements of the nominal wavefront and a 150 nm rms introduced wavefront error. These measurements were then compared to find a residual WFE. This error consists of evolved NCPA between measurements, DM calibration errors, and algorithm errors. We did not investigate the amplitude of the individual error terms.
 |
Fig. 9. Focal-plane images and 1σ raw contrast curves pre- and post-correction with the internal source within SCExAO. (a) pre- and (b) post-correction images for the nominal SCExAO system. (c) 1σ raw contrast curves for the correction of the nominal system. The solid lines relate to (panels a and b) and are read noise limited beyond 7.5 λ/D, which is shown by the horizontal dashed line. The dot-dashed lines show a similar correction performed at a different time. For these lines the images for raw contrast determination were saturated such that they were speckle noise limited (instead of read noise limited), reaching deeper contrasts in the dark holes. (d) pre- and (e) post-correction images for an introduced wavefront of 300 nm rms. (f) 1σ raw contrast curves for the correction of the system with the introduced 300 nm rms wavefront, with again the horizontal dashed line denoting the read noise. |
 |
Fig. 10. (a) estimated wavefront of the nominal SCExAO system using the internal source and reconstructed by combining the estimated modal coefficients of the 30 Zernike modes. The estimated WFE is ∼100 nm rms. (b) introduced and (c) estimated wavefront from closed-loop tests with the internal source. The introduced wavefront (b), consisting of 50 Zernike modes, has a rms WFE of ∼293 nm. The estimated wavefront (c), using the same 50 Zernike modes, with an rms WFE of ∼311 nm. The estimated wavefront also includes other WFE already present in the system. |
5.4. On-sky demonstration
On 11 January 2019 we observed Regulus (mH = 1.57; Ducati 2002) during a SCExAO engineering night to test the vAPP FPWFS on-sky, to evaluate the performance with an incoherent background due to residual turbulence and long exposure images, and to demonstrate the true end-to-end optical system. Observing conditions were good (the seeing was ∼0.2″ − 0.4″) and predictive control was running during the tests (Guyon & Males 2017). We conducted tests similar to those with the internal source. The top row of Fig. 11 shows the results after five iterations of closed-loop with a gain = 0.5 with the nominal SCExAO system when estimating 30 Zernike modes. The five iterations took approximately 4 min. Qualitatively, the first Airy ring of the leakage PSF becomes more rounded and symmetric, the coronagraphic PSFs are more similar, the edge of the dark hole becomes better defined, and some speckles in the dark hole are removed. The gain in peak flux of the leakage PSF is 6%. In Fig. 11c the contrast gain is moderate, improving by a factor ∼2 between 2.5 and 4 λ/D. The estimated wavefront is shown in Fig. 12a and the WFE is ∼187 nm rms. A notable structure in this estimated wavefront is the sharp increase in phase at the edges of the pupil. It is thought that this phase ring is a relatively static and real structure that originates from the upstream AO188 system; the PYWFS reference offset contains a similar structure as well. The bottom row shows the correction of low-order quasi-static errors from the instrument on-sky plus and additional 150 nm rms WFE that was added to the DM consisting of 30 Zernike modes. After five iterations (gain = 0.5), shown in Fig. 11e, the algorithm recovers a similar PSF in a time similar to that for the correction of the nominal system (Fig. 11c), both in morphology and in achieved raw contrast (see Fig. 11f). In Figs. 12b–d the introduced, estimated, and residual wavefronts are shown, with the WFE being respectively ∼146 nm, ∼244 nm, and ∼78 nm rms. The residual wavefront was determined by subtracting the introduced and initial wavefronts from the estimated wavefront. This gives an estimate of the remaining wavefront error in the system. As discussed with the internal source results, the residual wavefront consists of evolved NCPA between measurements, DM calibration errors and algorithm errors. We note that the reported raw contrasts in Figs. 11c and f are worse than in Figs. 9c and f due to the incoherent speckle background created by the uncorrected residual atmospheric wavefront errors.
 |
Fig. 11. Focal-plane images and 1σ raw contrast curves pre- and post-correction during on-sky observations. (a) pre- and (b) post-correction images for the nominal SCExAO system. (c) 1σ raw contrast curves for the correction of the nominal system. The horizontal dashed line denotes the read noise level. (d) pre- and (e) post-correction images for an additional wavefront error of 150 nm rms. (f) 1σ raw contrast curves for the correction of the system with the additional 150 nm rms wavefront error, with again the horizontal dashed line denoting the read noise. |
 |
Fig. 12. (a) estimated wavefront of the nominal SCExAO system during on-sky observations and reconstructed by combining the estimated modal coefficients of the 30 Zernike modes. The estimated WFE is ∼187 nm rms. (b) introduced, (c) estimated, and (d) residual wavefront from closed-loop tests during on-sky observations. (b) introduced wavefront, consisting of 30 Zernike modes, with an rms WFE of ∼146 nm. (c) estimated wavefront, using the same 30 Zernike modes, with an rms WFE of ∼244 nm. (d) residual wavefront (introduced minus estimated and nominal wavefronts); the rms WFE is ∼78 nm. |
6. Discussion and conclusion
We showed in Sect. 2 that an asymmetry in the pupil amplitude enables the vAPP coronagraphic PSFs to measure both even and odd pupil phase modes, generalizing the Asymmetric Pupil Fourier Wavefront Sensor (APF-WFS; Martinache 2013) with spatial Linear Dark Field Control (LDFC; Miller et al. 2017) in the vAPP. The physical model for non-linear wavefront estimation developed in Sect. 3 was tested in idealized simulations (Sect. 4), confirming that the vAPP currently installed at SCExAO can sense the even modes, but is more sensitive to odd modes. Simulations suggest that the algorithm should be able to reach one-shot correction resulting in a < λ/1000 nm rms WFE with approximately 107 photons, and that with one iteration it should be able to correct up to ∼λ/8 of rms WFE. In Sect. 5, we demonstrated the principle with the vAPP in SCExAO, both with the internal source and on-sky, by measuring and controlling the 30 lowest Zernike modes and improving the raw contrast between 2.5 and 4 λ/D by a factor ∼2. Furthermore, we showed that the algorithm can correct WFEs of 300 nm and 150 nm rms with the internal source and on-sky, respectively. Although the contrast gains, both with the internal source and on-sky, are moderate, it does demonstrate that the coronagraphic PSFs of the vAPP can be used for wavefront sensing.
The FPWFS performance of the SCExAO vAPP can be improved in various ways: (1) better model calibration to increase the contrast gain, (2) measuring more and higher spatial frequency modes to increase the area of correction, and (3) improving the convergence speed of the algorithm. For this demonstration the model was calibrated ad hoc by tuning the pupil undersizing, rotation, and the detector pixel scale by hand. These parameters should be more accurately measured or be part of the fitted parameters. To measure more and higher spatial frequency modes we want to replace the current Zernike mode basis with a pixel-mode basis (Paul et al. 2013a). This should also reduce the effect of unsensed modes on the estimation, when estimating a truncated mode basis (Paul et al. 2013b). Improving the convergence speed of the algorithm would result in a higher correction cadence or the correction of a larger mode basis in a similar time. A relatively simple improvement would be to use the multi-processing capabilities in the latest python libraries not yet available on SCExAO, this would enable multi-core processing and give a maximum speed improvement of a factor of 40. Theoretically, the best possible performance we can then expect is a wavefront estimation with sub 1 nm WFE every six seconds for targets down to a mH = 8 (five seconds of integration and one second for estimation). Other coronagraph model improvements include the integral field spectrograph CHARIS, an accurate model of the focal-plane filter and the incoherent background due to residual turbulence effects. This is because science observations with the SCExAO vAPP are done with CHARIS. Preventing detector saturation due to bright fields of the vAPP requires a focal-plane neutral density filter that attenuates the bright fields. Therefore, exposures with the focal-plane filter in place will have a larger dynamic range. This increase in dynamic range will make the incoherent background, which is due to uncorrected atmospheric turbulence, a more prominent feature in the image compared to the current on-sky results. Thus, the incoherent background needs to be included within the coronagraph model as well (Herscovici-Schiller et al. 2017), also including any asymmetries in this background (Cantalloube et al. 2018).
In this article we focused on a FPWFS based on a grating-vAPP. We operated it only in narrowband mode or in an integral field spectrograph. Therefore, the FPWFS algorithm does not have to operate over broad wavelength ranges and the current coronagraph model would suffice. However, there are broadband imaging vAPP implementations foreseen, as is detailed in Bos et al. (2018). These coronagraphs are more complicated in their optical design and therefore require a more advanced coronagraph model. For such broadband coronagraphs, the coronagraph model also needs to be extended to handle broadband FPWFS to take full advantage of the coronagraph. This can be done by evaluating the model at multiple wavelengths (Seldin et al. 2000) and would come at an increased computational cost. Operating in broadband mode would increase the sensitivity as there is more light available, but speckles at larger λ/D would be washed out and therefore higher frequency aberrations would be harder to measure.
In this paper we discussed only FPWFS for vAPPs that generate asymmetric dark holes. But FPWFS with pupil-plane coronagraphs that create symmetric dark holes such as the 360° vAPP (Otten et al. 2014) and the shaped pupil (Kasdin et al. 2007) are desirable as well. Optimal designs of vAPPs with symmetric dark holes consist of only 0 and π phase structures (Por 2017). This results in a purely real pupil-plane electric field (Eq. (2)), and thus if the aperture is symmetric the focal-plane electric field of such a vAPP will be completely imaginary (Table 1) and will not support a FPWFS. Therefore, similar to one-sided dark holes, FPWFSing is enabled when an amplitude asymmetry is introduced. A similar argument can be given for shaped pupil coronagraphs, as these manipulate pupil-plane amplitude and thus only have a real pupil-plane electric field. A more important difference with one-sided dark hole PSFs is that such coronagraphs will not have a bright field in the other polarization that covers the dark hole of the coronagraph and thus does not directly probe the region of interest.
Future work will investigate optimization of the aperture asymmetry to enhance the wavefront sensing capabilities of the coronagraph. This also has implications for the APF-WFS and spatial LDFC controlling dark holes dug with other methods than the vAPP. With the current implementation of the vAPP and algorithm we can only sense phase aberrations. Uncorrected amplitude errors due to the atmosphere and instrumental errors will limit the raw contrast to ∼10−5 (Guyon 2018). This is at a level that is not yet reached by the vAPP, and therefore only sensing phase aberrations is sufficient for now. When this raw contrast is met it would be necessary to sense both pupil amplitude and phase aberrations. It is expected that the two coronagraphic PSFs alone do not contain sufficient diversity to estimate both in one image. For the current SCExAO vAPP design, an additional classical phase diversity image will likely provide the required diversity to enable amplitude estimation (Herscovici-Schiller et al. 2018), but will lower the science duty cycle. A better solution for future FPWFS vAPPs would be the addition of two strong phase diversity holograms, which would keep the science duty cycle at 100% at the cost of science throughput. Another use of FPWFS with the vAPP could be the fine co-phasing of multi-mirror telescopes from the image plane (Pope et al. 2014), such as for the upcoming Giant Magellan Telescope.
Integration of FPWFS with coronagraphy is a crucial step in the system wide integration of all optical modalities (e.g., spectroscopy and polarimetry) to get the best possible performance of high-contrast imaging instruments. The major advantages are that NCPA can be measured up to the science focal plane and a 100% science duty cycle as science observations do not have to be interrupted to probe the dark hole. The vAPP has now shown that it is able to combine both FPWFS and coronagraphy in one optic.
Acknowledgments
The authors thank the referee for comments on the manuscript that significantly improved the presentation of the work. The authors warmly thank S. Y. Haffert and E. H. Por for useful discussion on focal-plane wavefront sensing. The research of Steven P. Bos, David S. Doelman, and Frans Snik leading to these results has received funding from the European Research Council under ERC Starting Grant agreement 678194 (FALCONER). The development of SCExAO was supported by the JSPS (Grant-in-Aid for Research #23340051, #26220704, #23103002); the Astrobiology Center (ABC) of the National Institutes of Natural Sciences, Japan; the Mt Cuba Foundation; and the directors contingency fund at Subaru Telescope. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Maunakea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain. This research made use of HCIPy, an open-source object-oriented framework written in Python for performing end-to-end simulations of high-contrast imaging instruments (Por et al. 2018). This research used the following Python libraries: Scipy (Jones et al. 2014), Numpy (Walt et al. 2011), and Matplotlib (Hunter 2007).
References
- Baudoz, P., Boccaletti, A., Baudrand, J., & Rouan, D. 2005, Proc. Int. Astron. Union, 1, 553 [CrossRef] [Google Scholar]
- Berry, M. V. 1987, J. Mod. Opt., 34, 1401 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boehle, A., Glauser, A. M., Kenworthy, M. A., et al. 2018, in Ground-based and Airborne Instrumentation for Astronomy VII, Int. Soc. Opt. Photon., 10702, 107023Y [Google Scholar]
- Bordé, P. J., & Traub, W. A. 2006, ApJ, 638, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Bos, S. P., Doelman, D. S., de Boer, J., et al. 2018, in Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation III, Int. Soc. Opt. Photon., 10706, 107065M [Google Scholar]
- Byrd, R. H., Lu, P., Nocedal, J., & Zhu, C. 1995, SIAM J. Sci. Comput., 16, 1190 [Google Scholar]
- Cantalloube, F., Por, E., Dohlen, K., et al. 2018, A&A, 620, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Close, L. M., Males, J. R., Durney, O., et al. 2018, Proc. SPIE, 10703, 107034Y [Google Scholar]
- Codona, J. L., & Doble, N. 2012, in Adaptive Optics Systems III, Int. Soc. Opt. Photon., 8447, 84476R [CrossRef] [Google Scholar]
- Côté, O., Allain, G., Brousseau, D., et al. 2018, in Ground-based and Airborne Instrumentation for Astronomy VII, Int. Soc. Opt. Photon., 10702, 1070248 [Google Scholar]
- Davies, R., Alves, J., Clénet, Y., et al. 2018, in Ground-based and Airborne Instrumentation for Astronomy VII, Int. Soc. Opt. Photon., 10702, 107021S [Google Scholar]
- De Kok, R., Stam, D., & Karalidi, T. 2011, ApJ, 741, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Doelman, D. S., Snik, F., Warriner, N. Z., & Escuti, M. J. 2017, in Techniques and Instrumentation for Detection of Exoplanets VIII, Int. Soc. Opt. Photon., 10400, 104000U [Google Scholar]
- Doelman, D. S., Auer, F. F., Escuti, M. J., & Snik, F. 2019, Opt. Lett., 44, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Ducati, J. 2002, VizieR Online Data Catalog: II/237 [Google Scholar]
- Feautrier, P., Gach, J. L., Greffe, T., et al. 2017, in Image Sensing Technologies: Materials, Devices, Systems, and Applications IV, Int. Soc. Opt. Photon., 10209, 102090G [Google Scholar]
- Galicher, R., Baudoz, P., & Rousset, G. 2008, A&A, 488, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonsalves, R. A. 1982, Opt. Eng., 21, 215829 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J. W. 2005, Introduction to Fourier Optics (Roberts and Company Publishers) [Google Scholar]
- Groff, T. D., Kasdin, N. J., Limbach, M. A., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Int. Soc. Opt. Photon., 9147, 91471W [Google Scholar]
- Groff, T. D., Riggs, A. E., Kern, B., & Kasdin, N. J. 2015, J. Astron. Telesc. Instrum. Syst., 2, 011009 [NASA ADS] [CrossRef] [Google Scholar]
- Guyon, O. 2005, ApJ, 629, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Guyon, O. 2018, Annu. Rev. Astron. Astrophys., 56, 315 [Google Scholar]
- Guyon, O., & Males, J. 2017, AJ, accepted [arXiv:1707.00570] [Google Scholar]
- Guyon, O., Miller, K., Males, J., Belikov, R., & Kern, B. 2017, PASP, submitted [arXiv:1706.07377] [Google Scholar]
- Guyon, O., Sevin, A., Ltaief, H., et al. 2018, in Adaptive Optics Systems VI, Int. Soc. Opt. Photon., 10703, 107031E [Google Scholar]
- Haffert, S., Wilby, M., Keller, C., et al. 2018, in Adaptive Optics Systems VI, Int. Soc. Opt. Photon., 10703, 1070323 [Google Scholar]
- Haffert, S., Bohn, A., de Boer, J., et al. 2019, Nat. Astron., 3, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herscovici-Schiller, O., Mugnier, L. M., & Sauvage, J.-F. 2017, MNRAS, 467, L105 [Google Scholar]
- Herscovici-Schiller, O., Mugnier, L. M., Baudoz, P., et al. 2018, A&A, 614, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoeijmakers, H., Schwarz, H., Snellen, I., et al. 2018, A&A, 617, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, E., Oliphant, T., & Peterson, P. 2014, SciPy: Open Source Scientific Tools for Python [Google Scholar]
- Jovanovic, N., Martinache, F., Guyon, O., et al. 2015, PASP, 127, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Jovanovic, N., Absil, O., Baudoz, P., et al. 2018, in Adaptive Optics Systems VI, Proc. SPIE, 10703 [Google Scholar]
- Kanseri, B., Bisht, N. S., Kandpal, H., & Rath, S. 2008, Am. J. Phys., 76, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Kasdin, N. J., Vanderbei, R. J., & Belikov, R. 2007, Comptes Rendus Physique, 8, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Kenworthy, M. A., Absil, O., Carlomagno, B., et al. 2018, in Ground-based and Airborne Instrumentation for Astronomy VII, Int. Soc. Opt. Photon., 10702, 10702A3 [Google Scholar]
- Lozi, J., Guyon, O., Jovanovic, N., et al. 2018, in Adaptive Optics Systems VI, Int. Soc. Opt. Photon., 10703 [Google Scholar]
- Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, Proc. Natl. Acad. Sci., 111, 12661 [Google Scholar]
- Males, J. R., Close, L. M., Miller, K., et al. 2018, in Adaptive Optics Systems VI, Int. Soc. Opt. Photon., 10703, 1070309 [Google Scholar]
- Marois, C., Lafreniere, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Martinache, F. 2013, PASP, 125, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Martinache, F., Jovanovic, N., & Guyon, O. 2016, A&A, 593, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinez, P., Loose, C., Carpentier, E. A., & Kasper, M. 2012, A&A, 541, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinez, P., Kasper, M., Costille, A., et al. 2013, A&A, 554, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mazoyer, J., Baudoz, P., Galicher, R., Mas, M., & Rousset, G. 2013, A&A, 557, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, K. L. 2018, PhD Thesis, The University of Arizona [Google Scholar]
- Miller, K., Guyon, O., & Males, J. 2017, J. Astron. Telesc. Instrum. Syst., 3, 049002 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, K., Males, J. R., Guyon, O., et al. 2018, in Adaptive Optics Systems VI, Int. Soc. Opt. Photon., 10703, 107031T [Google Scholar]
- Minowa, Y., Hayano, Y., Oya, S., et al. 2010, in Adaptive Optics Systems II, Int. Soc. Opt. Photon., 7736, 77363N [CrossRef] [Google Scholar]
- Mujat, M., Dogariu, A., & Wolf, E. 2004, J. Opt. Soc. Am. A, 21, 2414 [NASA ADS] [CrossRef] [Google Scholar]
- N’Diaye, M., Dohlen, K., Fusco, T., & Paul, B. 2013, A&A, 555, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- N’Diaye, M., Vigan, A., Dohlen, K., et al. 2016, in Adaptive Optics Systems V, Int. Soc. Opt. Photon., 9909, 99096S [CrossRef] [Google Scholar]
- N’Diaye, M., Martinache, F., Jovanovic, N., et al. 2018, A&A, 610, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oh, C., & Escuti, M. J. 2008, Opt. Lett., 33, 2287 [NASA ADS] [CrossRef] [Google Scholar]
- Otten, G. P., Snik, F., Kenworthy, M. A., et al. 2014, in Advances in Optical and Mechanical Technologies for Telescopes and Instrumentation, Int. Soc. Opt. Photon., 9151, 91511R [CrossRef] [Google Scholar]
- Otten, G. P., Snik, F., Kenworthy, M. A., et al. 2017, ApJ, 834, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Pancharatnam, S. 1956, Proceedings of the Indian Academy of Sciences-Section A (Springer), 44, 398 [Google Scholar]
- Paul, B., Mugnier, L., Sauvage, J.-F., Dohlen, K., & Ferrari, M. 2013a, Opt. Exp., 21, 31751 [NASA ADS] [CrossRef] [Google Scholar]
- Paul, B., Sauvage, J.-F., & Mugnier, L. 2013b, A&A, 552, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paul, B., Sauvage, J.-F., Mugnier, L., et al. 2014, A&A, 572, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paxman, R. G., Schulz, T. J., & Fienup, J. R. 1992, J. Opt. Soc. Am. A, 9, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Peters-Limbach, M. A., Groff, T. D., Kasdin, N. J., et al. 2013, in Techniques and Instrumentation for Detection of Exoplanets VI, Int. Soc. Opt. Photon., 8864, 88641N [CrossRef] [Google Scholar]
- Pope, B., Cvetojevic, N., Cheetham, A., et al. 2014, MNRAS, 440, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Por, E. H. 2017, in Techniques and Instrumentation for Detection of Exoplanets VIII, Int. Soc. Opt. Photon., 10400, 104000V [Google Scholar]
- Por, E. H., & Keller, C. U. 2016, in Adaptive Optics Systems V, Int. Soc. Opt. Photon., 9909, 990959 [CrossRef] [Google Scholar]
- Por, E. H., Haffert, S. Y., Radhakrishnan, V. M., et al. 2018, in Adaptive Optics Systems VI, Proc. SPIE, 10703 [Google Scholar]
- Ruane, G., Ngo, H., Mawet, D., et al. 2019, AJ, 157, 118 [Google Scholar]
- Sauvage, J.-F., Mugnier, L., Paul, B., & Villecroze, R. 2012, Opt. Lett., 37, 4808 [NASA ADS] [CrossRef] [Google Scholar]
- Seldin, J. H., Paxman, R. G., Zarifis, V. G., Benson, L., & Stone, R. E. 2000, in Imaging Technology and Telescopes, Int. Soc. Opt. Photon., 4091, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Snik, F., & Keller, C. U. 2013, Planets, Stars and Stellar Systems (Springer), 175 [CrossRef] [Google Scholar]
- Snik, F., Otten, G., Kenworthy, M., et al. 2012, in Modern Technologies in Space-and Ground-based Telescopes and Instrumentation II, Int. Soc. Opt. Photon., 8450, 84500M [CrossRef] [Google Scholar]
- Sparks, W. B., & Ford, H. C. 2002, ApJ, 578, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Stam, D., Hovenier, J., & Waters, L. 2004, A&A, 428, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Traub, W. A., & Oppenheimer, B. R. 2010, Exoplanets (Tucson: University of Arizona Press), 111 [Google Scholar]
- van Holstein, R. G., Snik, F., Girard, J. H., et al. 2017, in Techniques and Instrumentation for Detection of Exoplanets VIII, Int. Soc. Opt. Photon., 10400, 1040015 [Google Scholar]
- Vigan, A., Gry, C., Salter, G., et al. 2015, MNRAS, 454, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Vigan, A., N’Diaye, M., Dohlen, K., et al. 2018, in Adaptive Optics Systems VI, Int. Soc. Opt. Photon., 10703, 107035O [Google Scholar]
- Walt, S. V. D., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Wilby, M. J., Keller, C. U., Snik, F., Korkiakoski, V., & Pietrow, A. G. 2017, A&A, 597, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Phase retrieval examples
In Sect. 2 we explained how the sign of even phase aberrations can be retrieved using an asymmetric pupil amplitude. In this appendix we give a more complete set of examples of how pupil symmetries, and APPs designed for them, respond to even and odd aberrations.
In the top row of Fig. A.2a we visually present Eqs. (1)–(7) for an even aperture (A = Aeven) and the odd coma aberration (θ = θodd). The real part of the pupil-plane electric field, Acos(θ), is completely even and contains no sign information due to cos(−θ) = cos(θ); the imaginary part, iAsin(θ), is completely odd. Therefore, propagation to the focal plane will result in a fully imaginary electric field ib (see Table 1) that has even and odd components. The bottom row of Fig. A.2a shows the same images but for a flipped sign of the phase (θ = −θodd), equivalent to conjugating the pupil-plane electric field. Thus the phase conjugation results in a flipped PSF, and due to the odd component of Efoc, it results in a morphological change that can be measured, which is clearly visible in Fig. A.2a.
Figure A.2b shows similar figures, but for the even astigmatism aberration (θ = θeven) and again, the top and bottom rows show opposite signs of the aberration. As expected, both the real and imaginary parts of the pupil-plane electric field, Acos(θ) and iAsin(θ), are even. Again, the sign information is encoded in the imaginary pupil electric field term iAsin(θ). This term propagates, in contrast to the odd phase aberration, to the real part of the focal-plane electric field a. Therefore, all sign information of the even phase aberration in encoded in the real focal-plane electric field. Because the aberration is even, this does not result in morphological changes in the total intensity measurement Ifoc, and thus sign information of the even aberration cannot be measured.
This well-known sign ambiguity (Gonsalves 1982; Paxman et al. 1992) is often broken by introducing a static, known diversity phase that results in a known real focal-plane electric field. This real electric field can interfere with the sign information carrying real electric fields resulting from the even phase aberrations, which enables unique intensity changes for sign changes. Figure A.1 shows the case of defocus as a static phase diversity and the even astigmatism aberration used in Fig. A.1. It shows a significant morphology change in both the real and imaginary focal-plane power |a|2 and |b|2 that can be used to determine sign changes.
 |
Fig. A.1. Focal- and pupil-plane quantities for a static diversity phase (defocus) with an even phase aberration (astigmatism) that has an alternating sign between the rows. The columns in the pupil-plane box show (from left to right) the amplitude, phase, and real and imaginary electric fields. In the focal-plane box, the columns show the real and imaginary electric fields, the power in the real and imaginary electric fields, and the total power. |
In Sect. 2 we explained how the Asymmetric Pupil Fourier Wavefront Sensor (Martinache 2013) breaks the sign ambiguity in a similar way using odd pupil amplitude. In Fig. A.2c the response of an asymmetric aperture to sign changes in odd phase aberrations is shown. It shows that, as expected, the ability of measuring odd phase modes is not affected. Figure A.2d has an even phase aberration, again the top and bottom rows differ in the sign. In contrast to Fig. A.2b, the PSF for an asymmetric aperture does show a morphological change when the sign of the even aberration changes, and therefore allows the retrieval of the complete pupil-plane phase.
 |
Fig. A.2. Focal- and pupil-plane quantities for different combinations of pupil symmetries and phase aberrations with alternating signs. (a) symmetric aperture with odd aberration coma. (b) symmetric aperture with even aberration astigmatism. (c) asymmetric aperture with odd aberration coma. (d) asymmetric aperture with even aberration astigmatism. The columns in the pupil-plane box show (from left to right) the amplitude, phase, and the real and imaginary electric fields. In the focal-plane box the columns show the real and imaginary electric fields, the power in the real and imaginary electric fields, and the total power. |
Now we show that wavefront sensing with APPs will give similar results. In Figs. A.3a and b the focal-plane intensity responses are shown to an odd and even pupil-plane phase aberration for an APP designed for a symmetric aperture. As in Fig. A.2, the APP shows an intensity morphology change for a sign change in the odd phase aberration (Fig. A.3a), but for a sign change in the even phase aberration there is no intensity morphology change (Fig. A.3b).
 |
Fig. A.3. Focal- and pupil-plane quantities for APPs designed for different pupil symmetries subjected to phase aberrations with alternating sign. (a) symmetric aperture with odd aberration coma. (b) symmetric aperture with even aberration astigmatism. (c) asymmetric aperture with odd aberration coma. (d) asymmetric aperture with even aberration astigmatism. The columns in the pupil-plane box show (from left to right) the amplitude, phase, and real and imaginary electric fields. In the focal-plane box, the columns show the real and imaginary electric fields, the power in the real and imaginary electric fields, and the total power. |
This changes for an APP designed for an asymmetric aperture, as shown in Figs. A.3c and d. Figure A.3d shows the focal-plane intensity response to an odd pupil-plane phase aberration and Fig. A.3d the response to an even pupil phase aberration. For both phase aberrations there is an intensity morphology change when the sign of the aberration changes.
Appendix B: Implications for spatial LDFC
Above we discussed the principle behind FPWFS in the context of the coronagraphic PSFs of the APP, but the same principle applies to maintaining the contrast in the dark hole, such as electric field conjugation (Groff et al. 2015), speckle nulling (Bordé & Traub 2006), or spatial Linear Dark Field Control (LDFC; Miller et al. 2017). Spatial LDFC maintains the contrast in the dark hole by monitoring the intensity of the bright field, which can be shown to have a linear response to small phase aberrations. Suppose the focal-plane electric field Efoc consists of the nominal electric field in the bright field E0 disturbed by the electric field of the aberration Eab:
Assuming that |E0|2 ≫ |Eab|2, we can write the intensity change ΔI, compared to the reference image I0 = |E0|2, due to the aberration as
Writing the electric fields as their real and imaginary components, E0 = a + ib and Eab = c + id, shows that in order to have a response to the complete electric field of the aberration, the bright field of the PSF should have real and imaginary components:
As discussed above, the real component a can be provided by either a known, even phase aberration such as defocus or by an amplitude asymmetry.
In Miller (2018) spatial LDFC was tested, both in simulation and in the lab, with a vAPP designed for an even aperture (a = 0). It was indeed observed that the LDFC loop was more stable when the vAPP image was defocused (a ≠ 0), compared to a focused image (a = 0). Therefore, adding a pupil amplitude asymmetry, generating a non-zero a, would allow the LDFC loop to run with a focused vAPP image, having a comparable stability to the defocused image.
Appendix C: Derivatives objective function
The phase estimation is performed by minimizing the objective function ℒ defined in Eq. (20). The convergence speed and accuracy of the minimization algorithm are improved when it is provided with the gradients of the parameters it is estimating. For the estimation the phase is expanded on a truncated mode basis {ϕi} with αi the estimated coefficients, and thus the gradient ∂ℒ/∂αi needs to be derived. In addition to the phase estimation, the algorithm can also estimate the photon number Np, the background level Nb, the fractional degree of circular polarization v, and the amount of leakage L. Therefore, the gradients ∂ℒ/∂Np, ∂ℒ/∂Nb, ∂ℒ/∂v, and ∂ℒ/∂L also need to be derived.
The gradient of ℒ to X (X = {αi, Np, Nb, v, L}) is given by
with M the model of the system given by Eq. (22). Here the dependency of ℒ and M on (α, Np, Nb, v, L) is omitted for readability. The term ℛ(α)/∂X is only non-zero for X = αi.
We start with the gradient ∂ℒ/∂αi; with the first step already shown in Eq. (C.1), the derivative of M is
where the sum is over the two coronagraphic PSFs and the non-coronagraphic leakage PSF, and Ifoc, j is given in Eq. (26). The derivative ∂Ifoc, j(α)/∂αi is
The partial derivatives to the focal-plane electric field Efoc are
The partial derivatives to the focal-plane electric field  is then simply
is then simply
Combining these results, we find for ∂Ifoc, j(α)/∂αi:
The regularization term ℛ(α) that we adopted is fairly simple:
Here γ is a power that matches the known or assumed power-law distribution of the aberrations in the system. The derivative with respect to αi is given by
Combining the results in Eqs. (C.1), (C.2), (C.6), and (C.8) gives the final expression for ∂ℒ/∂αi.
Next, the derivatives of M to Np and Nb are
The derivative of M to the leakage L is
with the derivatives ∂aj(v, L)/∂L given by
Finally, the derivative of M to v is
with the derivatives ∂aj(v, L)/∂v given by
All Tables
All Figures
 |
Fig. 1. Working principle of the grating-vector-Apodizing Phase Plate. The grating-vAPP is a half-wave retarder pupil-plane optic with a spatially varying fast-axis orientation. The varying fast-axis orientation induces the phase through the geometric phase on the circular polarization states. These polarization states receive the opposite phase and therefore have flipped coronagraphic point spread functions (PSFs). The PSFs are spatially separated by adding a phase ramp to the design. Any offsets from half-wave retardance within the optic reduces the efficiency with which the light will be transferred to the coronagraphic PSFs and results in a leakage PSF. |
| In the text | |
 |
Fig. 2. Focal- and pupil-plane quantities of an even phase aberration (astigmatism) through a symmetric pupil (a) and an asymmetric pupil (b). The two rows show opposite signs for the phase aberration. The columns in the pupil-plane box show (from left to right) the amplitude, phase, and real and imaginary electric fields. In the focal-plane box the columns show the real and imaginary electric fields, the power in the real and imaginary electric fields, and the total power. |
| In the text | |
 |
Fig. 3. Focal- and pupil-plane quantities for (a) a symmetric and asymmetric pupil, and (b) vAPPs designed for these pupils. The columns in the pupil-plane box show (from left to right) the amplitude, phase, and real and imaginary electric fields. In the focal-plane box the columns show the real and imaginary electric fields, the power in the real and imaginary electric fields, and the total power. |
| In the text | |
 |
Fig. 4. Decomposition of the pupil-plane phase and amplitude into their even and odd constituents for the two APP designs in Fig. 3b. (a): APP designed for a symmetric aperture. (b): APP designed for an asymmetric aperture. |
| In the text | |
 |
Fig. 5. Amplitude and phase design of the SCExAO vAPP (Doelman et al. 2017) and its resulting PSF. The pupil-plane quantities are decomposed into their even and odd constituents, while the focal-plane PSF is decomposed into the power in the real and imaginary parts of the electric field. |
| In the text | |
 |
Fig. 6. Residual rms WFE as a function of photon number Np for the SCExAO vAPP. Different colors denote various read noise levels. The dotted line shows a |
| In the text | |
 |
Fig. 7. Photon noise sensitivity of the SCExAO vAPP to the first 100 Zernike modes, starting at defocus. The gray boxes denote the even Zernike modes, and the white boxes the odd Zernike modes. |
| In the text | |
 |
Fig. 8. Residual rms WFE as function of introduced rms WFE for the SCExAO vAPP. The colors denote various photon numbers. The dashed, gray line separates the regions where the wavefront improves or deteriorates. The wavelength is 1550 nm. |
| In the text | |
 |
Fig. 9. Focal-plane images and 1σ raw contrast curves pre- and post-correction with the internal source within SCExAO. (a) pre- and (b) post-correction images for the nominal SCExAO system. (c) 1σ raw contrast curves for the correction of the nominal system. The solid lines relate to (panels a and b) and are read noise limited beyond 7.5 λ/D, which is shown by the horizontal dashed line. The dot-dashed lines show a similar correction performed at a different time. For these lines the images for raw contrast determination were saturated such that they were speckle noise limited (instead of read noise limited), reaching deeper contrasts in the dark holes. (d) pre- and (e) post-correction images for an introduced wavefront of 300 nm rms. (f) 1σ raw contrast curves for the correction of the system with the introduced 300 nm rms wavefront, with again the horizontal dashed line denoting the read noise. |
| In the text | |
 |
Fig. 10. (a) estimated wavefront of the nominal SCExAO system using the internal source and reconstructed by combining the estimated modal coefficients of the 30 Zernike modes. The estimated WFE is ∼100 nm rms. (b) introduced and (c) estimated wavefront from closed-loop tests with the internal source. The introduced wavefront (b), consisting of 50 Zernike modes, has a rms WFE of ∼293 nm. The estimated wavefront (c), using the same 50 Zernike modes, with an rms WFE of ∼311 nm. The estimated wavefront also includes other WFE already present in the system. |
| In the text | |
 |
Fig. 11. Focal-plane images and 1σ raw contrast curves pre- and post-correction during on-sky observations. (a) pre- and (b) post-correction images for the nominal SCExAO system. (c) 1σ raw contrast curves for the correction of the nominal system. The horizontal dashed line denotes the read noise level. (d) pre- and (e) post-correction images for an additional wavefront error of 150 nm rms. (f) 1σ raw contrast curves for the correction of the system with the additional 150 nm rms wavefront error, with again the horizontal dashed line denoting the read noise. |
| In the text | |
 |
Fig. 12. (a) estimated wavefront of the nominal SCExAO system during on-sky observations and reconstructed by combining the estimated modal coefficients of the 30 Zernike modes. The estimated WFE is ∼187 nm rms. (b) introduced, (c) estimated, and (d) residual wavefront from closed-loop tests during on-sky observations. (b) introduced wavefront, consisting of 30 Zernike modes, with an rms WFE of ∼146 nm. (c) estimated wavefront, using the same 30 Zernike modes, with an rms WFE of ∼244 nm. (d) residual wavefront (introduced minus estimated and nominal wavefronts); the rms WFE is ∼78 nm. |
| In the text | |
 |
Fig. A.1. Focal- and pupil-plane quantities for a static diversity phase (defocus) with an even phase aberration (astigmatism) that has an alternating sign between the rows. The columns in the pupil-plane box show (from left to right) the amplitude, phase, and real and imaginary electric fields. In the focal-plane box, the columns show the real and imaginary electric fields, the power in the real and imaginary electric fields, and the total power. |
| In the text | |
 |
Fig. A.2. Focal- and pupil-plane quantities for different combinations of pupil symmetries and phase aberrations with alternating signs. (a) symmetric aperture with odd aberration coma. (b) symmetric aperture with even aberration astigmatism. (c) asymmetric aperture with odd aberration coma. (d) asymmetric aperture with even aberration astigmatism. The columns in the pupil-plane box show (from left to right) the amplitude, phase, and the real and imaginary electric fields. In the focal-plane box the columns show the real and imaginary electric fields, the power in the real and imaginary electric fields, and the total power. |
| In the text | |
 |
Fig. A.3. Focal- and pupil-plane quantities for APPs designed for different pupil symmetries subjected to phase aberrations with alternating sign. (a) symmetric aperture with odd aberration coma. (b) symmetric aperture with even aberration astigmatism. (c) asymmetric aperture with odd aberration coma. (d) asymmetric aperture with even aberration astigmatism. The columns in the pupil-plane box show (from left to right) the amplitude, phase, and real and imaginary electric fields. In the focal-plane box, the columns show the real and imaginary electric fields, the power in the real and imaginary electric fields, and the total power. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



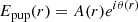
![$$ \begin{aligned}&= A(r)\cos [\theta (r)] + i A\sin [\theta (r)]. \end{aligned} $$](/articles/aa/full_html/2019/12/aa36062-19/aa36062-19-eq2.gif)
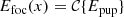
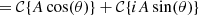
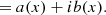
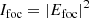
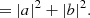
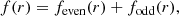
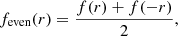
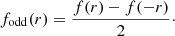
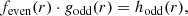
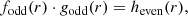
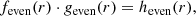
![$$ \begin{aligned}&f_{\mathrm{even} }[ g_{\mathrm{odd} }(r)] = h_{\mathrm{even} }(r), \end{aligned} $$](/articles/aa/full_html/2019/12/aa36062-19/aa36062-19-eq15.gif)
![$$ \begin{aligned}&f_{\mathrm{odd} }[g_{\mathrm{odd} }(r)] = h_{\mathrm{odd} }(r), \end{aligned} $$](/articles/aa/full_html/2019/12/aa36062-19/aa36062-19-eq16.gif)
![$$ \begin{aligned}&f_{\mathrm{odd} }[g_{\mathrm{even} }(r)] = h_{\mathrm{even} }(r), \end{aligned} $$](/articles/aa/full_html/2019/12/aa36062-19/aa36062-19-eq17.gif)
![$$ \begin{aligned}&f_{\mathrm{even} }[ g_{\mathrm{even} }(r)] = h_{\mathrm{even} }(r). \end{aligned} $$](/articles/aa/full_html/2019/12/aa36062-19/aa36062-19-eq18.gif)
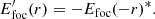
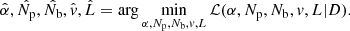
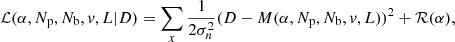
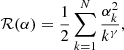
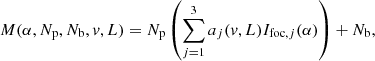
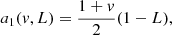
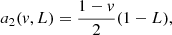
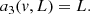
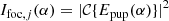
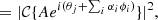
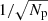
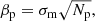
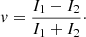
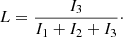
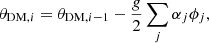
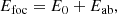
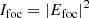
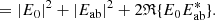
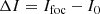
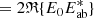
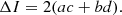
![$$ \begin{aligned} \frac{\partial \mathcal{L} }{\partial X} = \sum _{{x}} \frac{1}{\sigma _n^2} [{D} - {M}] \frac{\partial {M}}{\partial X} + \frac{\partial \mathcal{R} (\alpha )}{\partial X}, \end{aligned} $$](/articles/aa/full_html/2019/12/aa36062-19/aa36062-19-eq60.gif)