| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 20 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201935837 | |
| Published online | 22 November 2019 | |
The Araucaria project: High-precision orbital parallax and masses of eclipsing binaries from infrared interferometry⋆
1
European Southern Observatory, Alonso de Córdova 3107, Casilla 19001 Santiago, Chile
e-mail: agallenn@eso.org, alexandre.gallenne@gmail.com
2
Laboratoire Lagrange, UMR7293, Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte dAzur, Nice, France
3
Nicolaus Copernicus Astronomical Centre, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
4
Universidad de Concepción, Departamento de Astronomía, Casilla 160-C, Concepción, Chile
5
Millenium Institute of Astrophysics, Av. Vicuña Mackenna 4860, Santiago, Chile
6
Centrum Astronomiczne im. Mikołaja Kopernika, PAN, Rabiańska 8, 87-100 Toruń, Poland
7
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
8
Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
9
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
10
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
Received:
3
May
2019
Accepted:
8
October
2019
Context. The precise determinations of stellar mass at ≲1% provide important constraints on stellar evolution models. Accurate parallax measurements can also serve as independent benchmarks for the next Gaia data release.
Aims. We measured the masses and distance of binary systems with a precision level better than 1% using a fully geometrical and empirical method.
Methods. We obtained the first interferometric observations for the eclipsing systems AI Phe, AL Dor, KW Hya, NN Del, ψ Cen and V4090 Sgr with the VLTI/PIONIER combiner, which we combined with radial velocity measurements to derive their three-dimensional orbit, masses, and distance.
Results. We determined very precise stellar masses for all systems, ranging in precision from 0.04% to 3.3%. We combined these measurements with the stellar effective temperature and linear radius to fit stellar isochrones models and determined the age of the systems. We also derived the distance to the systems with a precision level of 0.4%.
Conclusions. The comparison of theoretical models with stellar parameters shows that stellar models are still deficient in simultaneously fitting the stellar parameters (Teff, R and M) with this level of precision on individual masses. This stresses the importance of precisely measuring the stellar parameters to better calibrate stellar evolution models. The precision of our model-independent orbital parallaxes varies from 24 μas as to 70 μas and the parallaxes provide a unique opportunity to verify whether the future Gaia measurements have systematic errors.
Key words: stars: fundamental parameters / instrumentation: high angular resolution / techniques: interferometric / techniques: spectroscopic / binaries : close / binaries: eclipsing
Based on observations made with ESO telescopes at Paranal and La Silla observatory under program IDs 087.C-0012(A), 087.C-0012(B), 089.C-0415(A), 089.C-0415(B), 092.C-0454(A), 093.C-0417(A), 094.C-0428(A), 094.D-0056(A), 096.C-0417(A), 096.D-0299(A), 097.D-0025(A), 097.C-0571(B), 098.C-0292(A), 0100.D-0024(A), 0100.D-0339(B).
© ESO 2019
1. Introduction
In the course of the Araucaria project, different techniques are applied to measure distances in order to track down the influence of the population effects on the most important standard candles such as Cepheids, RR Lyrae stars, red clump stars, and the tip of the red-giant branch (Gieren et al. 2005a,b). Binary systems are of particular importance in our project, as demonstrated in our works with eclipsing binary systems, which have provided the most accurate distance of the Large and Small Magellanic Clouds (Pietrzyński et al. 2019, 2013; Graczyk et al. 2014).
Binary stars are the only tool enabling direct and accurate distance and stellar mass measurements. When they are double-lined spectroscopic binaries, the geometric distance can be measured, which provides an independent benchmark to other measurements, for instance, the future Gaia parallax measurements (Gaia Collaboration 2016). The mass is a fundamental parameter for understanding the structure and evolution of stars, and precise measurements are necessary to determine the consistency with theoretical models and to tighten the constraints. Stellar parameters (e.g. the effective temperature and radius) predicted from different stellar evolution codes can currently lead to discrepancies with the empirical values, and therefore provide a wide range of possible ages for a given system (see, e.g., Torres et al. 2010; Gallenne et al. 2016). Models of the stellar interior differ in various ways, for instance in the input physics, the initial chemical compositions, the treatment of convective-core overshooting, the rotational mixing or the mixing length parameter (Marigo et al. 2017; Bressan et al. 2012; Dotter et al. 2008; Pietrinferni et al. 2004). With high-precision measurements, evolutionary models can be tightly constrained and provide a better understanding of the stellar interior physics (Higl et al. 2018; Claret & Torres 2018; Valle et al. 2017).
The precision on stellar parameters (Teff, R and M) gradually improved with the years through eclipsing binary systems and ground- and space-based large photometric surveys (e.g. the Optical Gravitational Lensing Experiment, the Wide Angle Search for Planets, Kepler, the Large Synoptic Survey Telescope, and the Transiting Exoplanet Survey Satellite). By combining radial velocities data with photometric observations during the eclipses, measurements at a ∼1−3% precision level are routinely achieved (e.g., Pilecki et al. 2013, 2015, 2018; Pribulla et al. 2018; Kirkby-Kent et al. 2016; Graczyk et al. 2015; Gieren et al. 2015), but recent work shows that a precision on the stellar mass ≪1% is necessary to obtain reliable determinations of the stellar interior model parameters (overshooting, initial helium abundance, etc.; Higl et al. 2018; Valle et al. 2017).
Another model-independent approach to measuring stellar masses and geometrical distances with binary systems at < 1% accuracy is to combine spectroscopic and astrometric observations (see, e.g., Pribulla et al. 2018; Gallenne et al. 2016; Torres et al. 2009; Zwahlen et al. 2004; Morbey 1975; Herbison-Evans et al. 1971). This method does not require any assumptions. This has recently been applied to a Galactic binary Cepheid and has provided the most accurate distance and mass for a Milky Way Cepheid (Gallenne et al. 2018a). However, the systems need to be spatially resolved to enable astrometric measurements, which is not always the case with single-dish telescope observations where the components are too close. A higher angular resolution is provided from optical long-baseline interferometry (LBI), where close-in binary systems (< 20 mas) can be detected. LBI has proved its efficiency in terms of angular resolution and accuracy for close-in binary stars (see, e.g., Pribulla et al. 2018; Gallenne et al. 2018a, 2016, 2015, 2014, 2013; Le Bouquin et al. 2013; Baron et al. 2012).
Recent work using LBI with eclipsing systems provided the most precise distances and masses for such systems, that is, < 0.4% and < 0.1%, respectively (Pribulla et al. 2018; Gallenne et al. 2018b, 2016). Valle et al. (2017) demonstrated that these very precise mass determinations are required to obtain reliable determinations of stellar parameters such as convective core overshooting, initial helium abundance, and age of the system.
In this paper, we report new observations with LBI of six eclipsing systems. The first goal of this interferometric observing program is to investigate the calibration of surface brightness-color (SBC) relations based only on eclipsing binary stars (see Graczyk et al. 2017). This will be published in a forthcoming dedicated paper. Here we focus on the precise measurement of mass and distance. Our sample is presented in Sect. 2. Section 3 contains details about our interferometric observations, the data reduction process, and the radial velocities data we used. Our model-fitting method is explained in Sect. 4 and the results for all systems are detailed in Sect. 5. The evolutionary status is discussed in Sect. 6. In this section, we also compare our derived orbital parallaxes with the parallaxes from the second Gaia data release (Gaia DR2). We then conclude in Sect. 7.
2. Our sample
We present here a brief background of our targets which are reported in this paper. They are bright eclipsing binaries (H < 7.5 mag) with short orbital periods (< 100 d).
AI Phoenicis. This 24.6 d binary system is composed of a subgiant star (K0IV) that is eclipsed by a main-sequence companion (F7V). This double-lined eclipsing system was discovered by Strohmeier (1972), and has been extensively studied in spectroscopy and photometry over the years (see e.g., Imbert 1979; Andersen et al. 1988; Hełminiak et al. 2009; Kanjanascul et al. 2012; Sybilski et al. 2018). Recently, variations in the systemic velocity seem to indicate that there might be a wider component in the system (M. Konacki, priv. comm.), but no orbital parameters have been derived so far.
Kirkby-Kent et al. (2016) provided precise mass measurements (∼0.3%) that have enabled testing stellar evolution models, constraining the mixing length and the helium abundance, and deriving an age of 4.39 ± 0.32 Gyr. The most recent results of Sybilski et al. (2018) gave masses precise to ∼0.08%, but there is no additional information about the stellar evolution. A third visual component located at about 11″ was thought to be also bound to the AI Phe system, but Kirkby-Kent et al. (2016) concluded that it is not physically associated.
From spectroscopic and photometric observations, Andersen et al. (1988) derived the parallax to be 6.17 ± 0.23 mas, consistent with the 5.94 ± 0.24 mas from Graczyk et al. (2017) using the same method and the 5.98 ± 0.31 mas from Stassun & Torres (2016) from absolute stellar luminosity and bolometric flux fitting. The value from HIPPARCOS (van Leeuwen 2007, assuming a single star) is ∼2σ away from the more recent estimate (Graczyk et al. 2017), but the Gaia measurement is within 1σ with 5.8336 ± 0.0262 mas (Gaia Collaboration et al. 2018).
AL Doradus. This eclipsing system has two identical main-sequence stars orbiting each other with a period of 14.9 d (G0V+F9V Graczyk et al. 2019). It was identified to be eclipsing by Kazarovets et al. (1999) and has been poorly monitored in the past. The orbital parameters where only recently derived by Graczyk et al. (2019) by combining new photometric and spectroscopic observations, but they did not provide estimates of the masses and the distance. The parallax from Gaia is 15.1292 ± 0.0286 mas, which corresponds to a distance of 66.97 ± 0.13 pc, while the HIPPARCOS measurement (van Leeuwen 2007) has a lower accuracy with 16.07 ± 0.43 mas, but the two measurements roughly agree with each other.
KW Hydrae. The primary star is a chemically peculiar post-main-sequence A-type star (A5m, with metallic lines) and was discovered to be a double-lined spectroscopic binary by Chauville (1975). She also determined the orbital parameters, and measured a period of 7.75 days and a mass ratio of 1.14. The eclipsing nature of the system was later revealed by Reipurth (1981). The secondary is a main-sequence star of spectral type F0V (Hillenbrand & White 2004). From new light curves and spectroscopic observations, Andersen & Vaz (1984) redetermined the orbital parameters and provided the absolute dimensions of the system. They estimated masses with a precision of 1.5% and the distance to the system to be 86 ± 4 pc (π = 11.63 ± 0.54). From the absolute stellar luminosity and bolometric flux, Stassun & Torres (2016) derived a parallax of 11.75 ± 0.62 mas, consistent with Andersen’s value and the HIPPARCOS estimate (11.53 ± 0.42 mas, assuming a single star). These values all agree with the Gaia measurement of 11.6744 ± 0.0891 mas.
NN Delphini. This star was first detected as variable by Makarov et al. (1994) and was later identified to be eclipsing by Kazarovets et al. (1999). The first estimate of the orbital period of 99.3 days was derived by Gómez-Forrellad et al. (2003) from photometric observations. Later work that combined spectroscopy and photometry was performed by Griffin (2014) who derived the full orbital parameters and mass of both components to a precision level of ∼1.7%. Recent works of Sybilski et al. (2018) refined the masses to a precision of ∼0.9%, also by combining spectroscopy and photometry. The parallax of this system was determined with the HIPPARCOS satellite to be 6.28 ± 0.89 mas (van Leeuwen 2007), and was recently refined with Gaia to 5.6393 ± 0.0636 mas.
ψ Centauri. This A0IV star was recently discovered to be a 38.8 d eclipsing system by Bruntt et al. (2006) from photometric measurements. They inferred the effective temperature of both components which, combined with isochrone models, provided the approximate masses M1 = 3.1 ± 0.3 M⊙ and M2 = 2.0 ± 0.2 M⊙. Spectroscopic measurements were later obtained by Mantegazza et al. (2010), and they separated the spectra of the two components. They independently estimated the spectroscopic orbital solutions, and combined them with the parameters derived from the light curve by Bruntt et al. (2006) to determine the physical parameters of this system, such as the masses M1 = 3.084 ± 0.016 M⊙ and M2 = 1.891 ± 0.030 M⊙. These parameters have not been updated since then.
The parallax π = 12.60 ± 0.20 mas was provided by the HIPPARCOS mission (van Leeuwen 2007, assuming a single star), consistent with the prediction of Stassun & Torres (2016 12.99 ± 1.35 mas) from fitting the absolute stellar luminosity and bolometric flux. The Gaia DR2 gives a parallax 14.458 ± 0.467 mas, which is at 3.7σ from the HIPPARCOS value, probably for the same reasons as listed before.
V4090 Sagittarii. The eclipsing nature of this system was discovered by Waelkens & Rufener (1983) from photometric light-curve measurements. The authors reported a likely A5m spectral type for the primary and derived an orbital period of 11.415 days. The spectral type was independently confirmed from spectroscopic lines to be between A1mA6-F0 (Houk 1982), which is also in agreement with the earlier work of Andersen & Nordstrom (1977), who derived an A2m spectral type. The first photometric orbital solution of this eclipsing system was determined by Giuricin et al. (1984) by analyzing the data of Waelkens & Rufener (1983). They determined an early-G spectral type for the secondary star and concluded that both components are on the main sequence. They also inferred M1 = 2.1 M⊙ and M2 = 1.0 M⊙ from their spectral type. North et al. (1997) performed a more complete light-curve analysis by combining additional observations in different photometric bands. They combined them with the few available radial velocities (RVs) from the literature (Nordstrom & Andersen 1985; Catchpole et al. 1982) to update the physical properties of the system. Using evolutionary tracks, they derived M1 = 1.81 ± 0.18 M⊙ and inferred M2 = 0.95 ± 0.08 M⊙ from the mass function. They also estimated a distance of 85 ± 10 pc, in agreement with HIPPARCOS (84.5 ± 7.0 pc) and Gaia (92.46 ± 0.71 pc).
3. Observations
3.1. Astrometry
Astrometric measurements were performed using near-IR LBI. We used the Very Large Telescope Interferometer (VLTI; Woillez et al. 2018) with the four-telescope combiner PIONIER (Le Bouquin et al. 2011) to measure the squared visibilities and the closure phases. PIONIER combines the light coming from four telescopes in the H band, either in a broadband mode or with a low spectral resolution, where the light is dispersed into six spectral channels. The recombination from all four telescopes simultaneously provides six visibility and four closure-phase measurements across a range of spectral channels.
Our observations were carried out from 2016 to 2017 using the 1.8 m Auxiliary Telescopes with various configurations, providing six projected baselines ranging from 40 to 140 m. Data were dispersed over six spectral channels across the H band (1.50−1.80 μm). To monitor the instrumental and atmospheric contributions, we used the standard observational procedure, which consists of interleaving the science target by reference stars. The calibrators, listed in Table 1 and detailed in Table B.1, were selected using the SearchCal1 software (Bonneau et al. 2006, 2011) provided by the Jean-Marie Mariotti Center (JMMC).
Relative astrometric position of the secondary component for all systems.
The data were reduced with the pndrs package described in Le Bouquin et al. (2011). The main procedure is to compute squared visibilities and triple products for each baseline and spectral channel, and to correct for photon and readout noises. The calibrated data are available at the Optical Interferometry DataBase2 In Fig. 2, we present an example of the squared visibilities and closure phases for the last observation of AI Phe. The binary nature of the system is clearly detected.
For each epoch, we proceeded to a grid search to find the global minimum and the location of the companion. For this we used the interferometric tool CANDID3 (Gallenne et al. 2015) to search for the companion using all available observables. CANDID allows a systematic search for point-source companions performing an N × N grid of fit, whose minimum required grid resolution is estimated a posteriori. The tool delivers the binary parameters, that is, the flux ratio f and the relative astrometric separation (Δα, Δδ). CANDID can also fit the angular diameter of both components, but in our cases, we kept them fixed during the fitting process as the VLTI baselines do not allow reliable measurements of such small diameters. For each epoch, CANDID found the global best-fit separation vector. The final astrometric positions for all epochs of all systems are listed in Table 1. We estimated the uncertainties from the bootstrapping technique (with replacement) and 10 000 bootstrap samples (also included in the CANDID tool). For the flux ratio, we took from the distributions the median value and the maximum value between the 16th and 84th percentiles as uncertainty. For the astrometry, the 1σ error region of each position (Δα, Δδ) is defined with an error ellipse parameterized with the semimajor axis σmaj, the semiminor axis σmin, and the position angle σPA measured from north through east. We also quadratically added to (σmaj, σmin) the systematic uncertainty of 0.35% from the precision of the PIONIER wavelength calibration (Gallenne et al. 2018b; Kervella et al. 2017). This systematic error is one of the fundamental limitation of our analysis: it limits the final accuracy on the apparent semi-major axis in the orbital fit (“a (mas)” in Table 2). Because the distance is inversely proportional to apparent semimajor axis, the accuracy on the distance is limited by the same amount of 0.35%.
Best-fit orbital elements and parameters for our binary systems.
As mentioned, the angular diameters of some of the stars are too small to be spatially resolved by the VLTI. We therefore kept them fixed during the grid search. For AI Phe, we fixed the values to θLD1 = 0.102 ± 0.004 mas and θLD2 = 0.161 ± 0.007 mas, as estimated by Graczyk et al. (2017, hereafter Gr17). For AL Dor, we adopted the values θLD1 = θLD2 = 0.156 ± 0.001 mas from Graczyk et al. (2019). We adopted θLD1 = 0.228 ± 0.008 mas and θLD2 = 0.159 ± 0.006 mas from Gr17 for KW Hya. For ψ Cen we used θLD1 = 0.424 ± 0.007 mas and θLD2 = 0.211 ± 0.007 mas (Mantegazza et al. 2010). We adopted θLD1 = 0.227 ± 0.030 mas and θLD2 = 0.106 ± 0.026 mas from North et al. (1997) for V4090 Sgr. Finally, for NN Del we used θLD1 = 0.115 ± 0.001 mas and θLD2 = 0.084 ± 0.001 mas from Sybilski et al. (2018). Except for AI Phe and KW Hya, the angular diameters were determined from the combination of the linear radius and the Gaia parallax. We note that angular diameters do not affect the measured astrometry.
Finally, we also investigated the effect of fitting or fixing the flux ratio in deriving our astrometric positions for very nearby components (i.e., < λ/2B). For this we used the star AI Phe, which has a component with the closest orbit. We repeated the process with CANDID (i.e., the grid search and then the bootstrapping) by keeping the flux ratio to the average value f = 49.7%. The differences for our 12 astrometric positions (Δα, Δδ) with and without fitting the flux ratio are displayed in Fig. 1. We note that removing f from the fitted parameters does not affect the agreement within 1σ.
 |
Fig. 1. Difference in number of sigmas of the astrometric positions (Δα, Δδ) for a fitted and fixed flux ratio. This is calculated as |
 |
Fig. 2. Closure phase and squared visibility measurements of the last measurements of AI Phe. The data are plotted in blue, and the red dots represent the fitted binary model for this epoch. The residuals (in number of sigmas) are also shown in the bottom panels. |
3.2. Radial velocities
We present here the radial velocities we used for our analysis. They are mostly from the literature, but new measurements are also reported.
AI Phe. We used radial velocity measurements from Sybilski et al. (2018) and Hełminiak et al. (2009) only, which are the most precise. In addition, we retrieved 33 HARPS spectra (Mayor et al. 2003) from the ESO archive. Thirty spectra were taken in full-resolution mode, and three in EGGS mode, covering the spectral range 3900–6900 Å. HARPS data were processed with the standard ESO/HARPS pipeline reduction package. To extract the RVs we used the broadening function (BF) formalism (Rucinski 1992) implemented in the RaveSpan software4 (Pilecki et al. 2017, see also e.g., Pilecki et al. 2018, 2013; Gallenne et al. 2016; Graczyk et al. 2015). The measurement errors were estimated using the uncertainties of the broadening profiles fits. The velocities are listed in Table A.1.
AL Dor. We used the radial velocity measurements from Graczyk et al. (2019). No other data are available in the literature.
KW Hya. For our analysis, we used the radial velocity measurements of Andersen & Vaz (1984).
NN Del. We collected the velocity measurements from Griffin (2014) and Sybilski et al. (2018). We also completed the sample of RVs with new observations from the STELLA echelle spectrograph (SES, Strassmeier et al. 2010). It is mounted on the robotic 1.2 m STELLA-II telescope in Tenerife, Spain, and provides high-resolution spectra in the wavelength range 3900–8700 Å (R ∼ 55 000). The spectra were reduced using the STELLA data-reduction pipeline (Weber et al. 2008). To extract the RVs we used the RaveSpan software as explained previously for the AI Phe system. The velocities are listed in Table A.2.
ψ Cen. The only spectroscopic observations of this system in the literature are those from Mantegazza et al. (2010), but in the method they used (spectral disentangling) individual RVs are not calculated and thus are not provided. Because we need them for our analysis, we collected their reduced spectra (kindly provided by M. Rainer) and extracted RVs using our own method. These data were supplemented by our own spectra taken with the HARPS spectrograph (Mayor et al. 2003) in a much more recent epoch. Spectra were reduced using the ESO data-reduction pipeline. To extract the RVs we used the RaveSpan software, as explained previously for the AI Phe system. The use of the BF method was crucial to obtain reliable RV measurements for ψ Cen because the lines show very high rotational broadening and blending of the profiles, especially at phases where the separation of orbital velocities are small. If individual RVs were not needed, the only other method that could give similar results in this case would be spectral disentangling as used by Mantegazza et al. (2010). The velocities are listed in Table A.3.
V4090 Sgr. Unfortunately, no velocity measurements of the secondary component are available because spectral disentangling is difficult. We used the only three RVs of the primary estimated by Nordstrom & Andersen (1985). The authors also used six additional velocities from Catchpole et al. (1982), but unfortunately it was not possible to retrieve them as they are not listed anywhere.
4. Fitting method
To determine the best-fit parameters we simultaneously fit the radial velocities and astrometric positions using a Markov chain Monte Carlo (MCMC) routine5, whose the log-likelihood function is given as
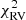 defines the radial velocity measurements with
defines the radial velocity measurements with
in which Vi and σVi denotes the measured radial velocities and uncertainties for the component i. Error bars are often underestimated in the literature, therefore all of them were rescaled according to the average scatter of the fit. (V1m, V2m) are the Keplerian velocity models of both components, defined by (Heintz 1978)
where γ is the systemic velocity, e the eccentricity, ω the argument of periastron, ν the true anomaly, E the eccentric anomaly, t the observing date, Porb the orbital period, and Tp the time of periastron passage. The parameters K1 and K2 are the RV amplitude of both stars.
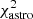 defines the astrometric measurements such as
defines the astrometric measurements such as
in which Δα, Δδ, σPA, σmaj and σmin denote the relative astrometric measurements with the corresponding error ellipses, and Δαm and Δδm the astrometric model which defined with:
where Ω is the longitude of ascending node, i the orbital inclination, and a the angular semimajor axis.
As a starting point for our 100 MCMC walkers, we performed a least-squares fit using orbital values from the literature as first guesses. We then ran 100 initialization steps to explore the parameter space well and settled into a stationary distribution. For all cases, the chain converged before 50 steps. Finally, we used the last position of the walkers to generate our full production run of 1000 steps, discarding the initial 50 steps. All the orbital elements, that is, Porb, Tp, e, ω, Ω, K1, K2, γ, a and i, are estimated from the distribution taking the median value and the maximum value between the 16th and 84th percentiles as uncertainty (although the distributions were roughly symmetrical).
From these distributions, we derive the distributions of the mass of both components and the distance to the system with (Torres et al. 2010)
where the masses are expressed in solar units, the distance in parsec, K1 and K2 in km s−1, P in days, and a in arcsecond. The parameter aAU is the linear semimajor axis expressed in astronomical units (the constant value of Torres et al. 2010 is expressed in solar radii, and was converted using the astronomical constants R⊙ = 695.658 ± 0.140 × 106 m from Haberreiter et al. 2008 and AU = 149 597 870 700 ± 3 m from Pitjeva & Standish 2009). As previously, we then took the median value and the maximum value between the 16th and 84th percentiles as uncertainty. The fitting results are presented in the next section for all systems. For the angular size of the orbit (and so the distance), we additionally took into account the systematic uncertainty from the interferometric wavelength calibration, that is, we also quadratically added 0.35% to the final uncertainty.
5. Results for individual systems
5.1. AI Phoenicis
We first fit our astrometric measurements with radial velocities from Hełminiak et al. (2009) only. The rms of the velocity residuals is similar to Hełminiak et al. (2009): we have 54 and 21 m s−1 for the primary and secondary, respectively. The orbital elements are agree well with the latest published values (Kirkby-Kent et al. 2016; Sybilski et al. 2018), except for the inclination, for which we found the symmetric value with respect to 90°. All previous works made use of photometric measurements (instead of astrometry as in our case), but photometry does not allow us to obtain the true inclination, and by convention the value < 90° is always adopted. The masses we obtained agree very well with the published values (within 1σ), with a precision level of ∼0.11%. The accuracy of the distance is also improved to 0.48%. We then performed the same fit with the velocities of Sybilski et al. (2018) only. The rms of the velocity residuals is slightly larger with 88 and 40 m s−1 for the primary and secondary, respectively. Except for the systemic velocity, all derived parameters agree (within 1σ) with our previous estimates, including the inclination. Because there are more velocity measurements, the precision is slightly better at ∼0.09% for the masses, and 0.43% for the distance. We only note a shift of 4.14 km s−1 of the systemic velocity, but it does not affect the precision on the other parameters (which may come from the orbital motion of the inner binary system (studied here) around the common center of mass in this tertiary system). We note that the methods used to derive the RVs by Hełminiak et al. (2009) and Sybilski et al. (2018) are different, but the masses agree with each other at < 0.4σ. Hełminiak et al. (2009) derived the RVs from the two-dimensional cross-correlation technique (TODCOR), while Sybilski et al. (2018) used both TODCOR and the BF function, outside and during eclipses respectively. Sybilski et al. (2018) also compared both methods and found the RVs to agree very well. This shows that the methods used to derive the RVs are robust and have no significant effect on the measured masses.
Our HARPS dataset spans a longer time range (7 yr) than Helminiak and Sybilski’s observations (six months and one months respectively), therefore we are more sensitive to the effect of the third component. The same fit was performed with our HARPS data and our astrometry. Clear offsets are detected for each data point, and this is related to the third component (rms ∼ 1.3 km s−1). As our dataset is limited, we manually searched for the best orbital period and eccentricity of a third component that gave the lowest residuals for the inner binary component. We found that a period around 109 yr with an eccentricity of ∼0.8 provided the lowest residuals. We then corrected the velocities of the inner binary for the third component which we simultaneously fit with our astrometry. The result is displayed in Fig. 3. We obtained a final rms of 32 m s−1 for the primary and 26 m s−1 for the secondary. Our measured masses have a precision of 0.06%, and the distance is precise at 0.41%. We adopted these results as our final values and list them in Table 2. We did not combine them with the other datasets because the determination of the RVs was different and may lead to biases in the correction of the third component. However, it is worth mentioning that our masses agree very well with our independent fit of Helminiak and Sybilski’s data we previously performed with our astrometry, at < 0.7σ and 0.5σ respectively. This again shows the robustness of the methods in determining RVs.
 |
Fig. 3. Left: radial velocities of the primary (red) and the secondary (blue) in the AI Phe system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
Our geometrical parallax is in agreement at ∼1.2σ with the parallax from Gaia DR2. We note that we took into account the parallax offset of 0.029 mas (Lindegren et al. 2018). This slight disagreement might be explained by the fact that the Gaia DR2 astrometric pipeline processing does not yet take the binarity of stars into account. Compared with previous distance estimates (162 ± 6 pc from Andersen et al. 1988, 168.4 ± 6.8 pc from Gr17), our value is within 1σ, but we have a much better precision. We also note that the HIPPARCOS parallax of 3.50 ± 1.04 mas also disagrees with our value, but the astrometric solutions also assumed a single star (probably reflected in the 30% precision).
5.2. AL Doradus
We fit our astrometric positions with RVs taken from Graczyk et al. (2019). We have an rms for the residual of the velocities of 30 m s−1 and 39 m s−1 for the primary and secondary, respectively. Our orbital fit is displayed in Fig. 4 and the resulting parameters are listed in Table 2. For this system, the Gaia DR2 parallax is consistent with our value at a 0.6σ level (taking into account the 0.029 mas parallax offset). Although our precision on the distance is slightly lower than the Gaia precision, our 0.37% precision is still good enough to provide a value to compare measurements of the next Gaia data release because it includes all known systematics.
We also precisely measured the mass of both components with a precision of 0.04%. We found that both stars have the same mass, which is expected because the stars have similar spectral type.
5.3. KW Hydrae
Our simultaneous fit is displayed in Fig. 5 and our adopted parameters are listed in Table 2. The rms scatter in velocity of the secondary is not that good with 2.7 km s−1, but it is better for the primary with 0.7 km s−1, and similar to the values from Andersen & Vaz (1984). We note that the velocities of the secondary are shifted by about 2.5 km s−1, therefore here we allowed fitting a separate systemic velocity. This large shift is probably not due to convective blueshift, as is sometimes observed (see e.g. Pilecki et al. 2018; Gallenne et al. 2016), but is probably due to the determination of the RV. Our orbital parameters are consistent with the estimates of Andersen & Vaz (1984), except for the orbital inclination, where we found the solution > 90° for the same reason as we explained before for AI Phe. Our derived masses are agree also very well, but we have a slightly better precision of lower than 1% for both stars.
 |
Fig. 4. Left: radial velocities of the primary (red) and the secondary (blue) star in the AL Dor system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
 |
Fig. 5. Left: radial velocities of the primary (red) and the secondary (blue) star in the KW Hya system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
We also obtained an orbital parallax with a precision of 0.7%. The Gaia parallax is ∼2.1σ higher than our value (taking into account the parallax offset), probably because of the binarity as previously explained. However, the parallaxes from HIPPARCOS (11.53 ± 0.42 mas, assuming astrometric solutions for a single star) and Andersen & Vaz (1984, 11.63 ± 0.54 mas) are consistent within 1σ with our value.
5.4. NN Delphini
We first fit our astrometry with RVs of Griffin (2014). We obtained a velocity rms of 0.48 km s−1 and 0.87 km s−1, for the primary and secondary respectively. We obtained masses precise to ∼0.9% that agree very well with the estimates of Griffin (2014), within 0.4σ. The estimated distance with these RVs alone is 167.92 ± 0.90 pc, in agreement with the HIPPARCOS value, but not with Gaia. We then fit RVs of Sybilski et al. (2018) only. We obtained a better velocity rms of 17 m s−1 and 130 m s−1 , for the primary and secondary respectively (although there are only seven measurements). All parameters agree with our previous fit (within 1σ, except for the systemic velocity). The precision on the masses is ∼0.9%, and is consistent with Sybilski’s values at ∼1.5σ. The slight disagreement arises because we rescaled the error bars to the average scatter. The distance also agrees at a level of 0.3σ with our previous estimate. We only note a velocity zero-point difference of −1.235 km s−1 with the first dataset. Because this system is not known to be tertiary, the shift may come from the use of a different instrument or a template with some intrinsic non-zero radial velocity. We also fit our STELLA spectra alone. The velocity rms obtained is 0.10 km s−1 and 0.18 km s−1, for the primary and secondary respectively. Our fitted masses and distance are well within 1σ with the two previous analyses, except that the precision is much better. We derived masses precise to ∼0.18% and the distance is precise to 0.4%. A combination with Griffin’s data degrades the precision because of the scatter, while the use with Sybilski measurements only slightly improves the precision (by 0.01%), therefore we decided to use only our STELLA RVs. Our final fitted parameters are listed in Table 2, and the orbit is displayed in Fig. 6. We derived the mass of both components precise to ∼0.2%. Our derived final parallax is precise to 0.4%, and is 4.2σ higher than the Gaia parallax (parallax offset included), but agrees with the HIPPARCOS estimate (measured assuming a single star).
 |
Fig. 6. Left: radial velocities of the primary (red) and the secondary (blue) star in the NN Del system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
5.5. ψ Centauri
We display our combined fit in Fig. 7 and our final adopted parameters in Table 2. We obtained an rms on the velocities of 0.64 km s−1 for the primary and 1.57 km s−1 for the secondary. We measured precise masses at a ∼0.9% level, which agrees with the estimates of Bruntt et al. (2006). However, they are higher by ∼2−3σ than the estimates of Mantegazza et al. (2010). This difference probably comes from our different and more adapted way of extracting the radial velocities from the spectra. This is noticeable in our estimates of K1 and K2 which are different by 2.6σ and 1.6σ, respectively.
 |
Fig. 7. Left: radial velocities of the primary (red) and the secondary (blue) star in the ψ Cen system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
We derived a distance accurate to 0.5%, which is larger by 2.1σ than the HIPPARCOS value. This is possibly due to the astrometric solutions of HIPPARCOS, which assumed a single star. The Gaia parallax is 3.1σ higher than our value (parallax offset included), and probably also because the pipeline assumed a single star for this system.
5.6. V4090 Sagittarii
Because this system is still a single-line spectroscopic binary, our astrometric positions were fit with the radial velocities of the primary star alone (Nordstrom & Andersen 1985). Our final fit is displayed in Fig. 8 and the resulting parameters are listed in Table 2. To estimate the masses from a single-line binary, we must assume the distance to the system. We adopted the Gaia distance because it agrees to within 1σ with the HIPPARCOS value. In our MCMC procedure, we included the parallax uncertainty using a normal distribution centered on 10.8450 mas with a standard deviation of 0.083 mas. Our derived masses are reported in Table 2 and have a precision of ∼3%. They agree (within 2σ) with the estimates of North et al. (1997), but here we measured the dynamical masses instead of inferring it from evolution models.
 |
Fig. 8. Left: radial velocities of the primary in the V4090 Sgr system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
6. Discussion
6.1. Mass comparison with the literature
In Fig. 9 we compare of our mass measurements with previous estimates from the literature, except for AL Dor, for which no measurements exist. We note that all literature data are based on the combination of RVs and photometric light curves which are more dependent on atmospheric models.
 |
Fig. 9. Comparison of our mass measurements (colored area) with the literature (black dots). The red (left) and blue (right) shaded areas represent the 1σ, 2σ, and 3σ combined uncertainties of the primary and secondary, respectively. References are Sy18 for Sybilski et al. (2018), Gr17 for Graczyk et al. (2017), Ki16 for Kirkby-Kent et al. (2016), He09 for Hełminiak et al. (2009), Mi92 for Milone et al. (1992), An88 for Andersen et al. (1988), An84 for Andersen & Vaz (1984), Gr14 for Griffin (2014), Ma10 for Mantegazza et al. (2010), Br06 for Bruntt et al. (2006), No97 for North et al. (1997) and Gi84 for Giuricin et al. (1984). |
Most previous measurements agree within 1−2σ with ours, but we note a few discrepancies > 2σ. The masses of the AI Phe components estimated by Hełminiak et al. (2009) are more than 3σ away. In Sect. 5.1 we fit our astrometry with their RVs alone and found masses that agreed with our final values at < 0.7σ. We therefore conclude that the discrepancy might come from the fit of the photometric light curves and the fact that they only have eight velocity measurements. The masses estimated by Mantegazza et al. (2010) for the ψ Cen system also agree within > 2σ with our values and the estimate from Bruntt et al. (2006, estimated from isochrone fitting). As explained previously in Sect. 3, in the method used by Mantegazza et al. (2010), individual RVs are not calculated, and as they stated, they did not completely disentangle the components, which probably adds some errors. We also note that they did not perform a combined fit with photometric light curves.
6.2. Evolutionary state
We employed the same fitting method as in Gallenne et al. (2018b, 2016), that is, we fit the PAdova and TRieste Stellar Evolution Code (PARSEC, Bressan et al. 2012), Bag of Stellar Tracks and Isochrones (BaSTI, Pietrinferni et al. 2004) and Mesa Isochrones and Stellar Tracks (MIST, Choi et al. 2016) isochrone models to estimate the stellar age of our systems. These models are well suited because they include the horizontal and asymptotic giant branch evolutionary phases and contain a wide range of initial masses and metallicities. In addition, it enables us to test the uncertainty of the age induced by different stellar models.
PARSEC models are computed for a scaled-solar composition with Z⊙ = 0.0152, and follow an initial helium content relation Y = 0.2485 + 1.78Z with a mixing length parameter αMLT = 1.74. They include convective core overshooting during the main-sequence phase, parameterized with the strength of convective overshooting in units of the pressure scale height lov = αovHp. The overshooting parameter αov is set depending on the mass of the star, that is, αov = 0 for M ≲ 1.1 M⊙, αov ∼ 0.25 for M ≳ 1.4 M⊙, and linearly ramps with the mass in between. The BaSTI models are computed for a scaled-solar composition with Z⊙ = 0.0198, following the relation Y = 0.245 + 1.4Z with αMLT = 1.913. They also include convective core overshooting with the same parameterization, but with the conditions αov = 0 for M ≲ 1.1 M⊙, αov = 0.20 for M ≳ 1.7 M⊙, and (M − 0.9 M⊙)/4 in between. The MIST models used a scaled-solar composition with Z⊙ = 0.0142, with the relation Y = 0.2703 + 1.5Z and αMLT = 1.82. They used an alternate prescription of the core overshooting with a diffusion coefficient Dov = D0exp( − 2z/Hν), where z is the distance from the edge of the convective zone, D0 is the coefficient at z = 0, and Hν is defined with the overshooting parameter fov such that Hν = fovHp. MIST models adopted a fixed value fov = 0.016 for all stellar masses, which would be approximatively converted into αov ∼ 0.18 (Claret & Torres 2017).
We retrieved several isochrones from the PARSEC database tool6, with ages ranging from logt = 6.6 to 10 in steps of 0.05 (i.e., ∼0.1–13 Gyr), and metallicities from Z = 0.003 to 0.06 (i.e., −0.7 ≤ [Fe/H] ≤ +0.6, using [Fe/H]∼log(Z/Z⊙)), in steps of 0.001 (fine enough to avoid re-interpolation). The BaSTI isochrones are pre-computed in their database7, we downloaded models for t = 0.1−9.5 Gyr in steps of ∼0.2 Myr and Z = 0.002, 0.004, 0.008, 0.01, 0.0198, 0.03, and 0.04 (i.e., −1.0 ≤ Fe/H ≤ 0.3). For fitting purpose, we created an interpolated grid of the BaSTI isochrones in Z, from 0.002 to 0.04 in steps of 0.001. We also computed MIST isochrones from their database tool8 using the standard age grid from 0.1 Myr to 20 Gyr in steps of ∼1 Myr, and for metallicities in the range 0.002 ≤ Z ≤ 0.04 (i.e., −0.85 ≤ Fe/H ≤ 0.45) in steps of 0.001.
When possible, we searched for the best-fit age in stellar effective temperature, radius and mass for both components simultaneously, assuming coeval stars and following a χ2 statistics
where the sum is over both components (i = 1, 2) and the Δ symbol represents the difference between the predicted and observed quantities. The effective temperature and the radii are measured quantities and were taken from the literature. They are listed in Table 3. The masses are also measured from this work and are reported in Table 2. We took care to rescale the retrieved linear radii according to our own estimate of the linear semimajor axis. In our isochrone plots we also display the stellar luminosity estimated from the Stefan–Boltzmann law, but this parameter was not included in the fit because this is not an independent measurement.
Stellar parameters used for the age determinations, together with our fitted and adopted age of the systems.
The stellar metallicity was kept fixed in this process to a value from the literature (listed in Table 3). Our fitting procedure was the following: For all isochrone models, we first chose the closest grid in Z for a given metallicity. Then, we searched for the global χ2 minimum in age by fitting all isochrones for that given metallicity. A second fit was then performed around that global minimum value, and the grid was interpolated in age at each iteration. To assess the uncertainties on the three isochrone models (i.e. PARSEC, BaSTI and MIST), we repeated the process with Z ± σ. Our final adopted age corresponds to the average and standard deviation between the three models.
AI Phoenicis. We adopted the metallicity from Andersen et al. (1988) and the stellar parameters listed in Table 3. All fitted isochrones are consistent and give a similar age within 1σ (see Table 3). They are displayed in Fig. 10. We found an average age of this system of t = 4.20 ± 0.19 Gyr. This value agrees well with previous estimates of Kirkby-Kent et al. (2016, 4.39 ± 0.32 Gyr), Kanjanascul et al. (2012, 4.3 Gyr), and Hełminiak et al. (2009, 4 Gyr) Andersen et al. (1988, 4.1 ± 0.4 Gyr), who used different stellar evolution models. The more evolved component particularly agrees very well for all models, while the other component located at the turn-off point disagrees at > 3σ with the PARSEC model. This might be linked to differences in the implementation of overshooting, helium content or the mixing length in the models. We note, however, that the strength of convective core overshooting rapidly starts increasing from ∼1.2 M⊙ (Claret & Torres 2016, 2017, 2018), which means that for this system with masses < 1.25 M⊙ the effect of overshooting should be negligible.
 |
Fig. 10. Fitted PARSEC, BaSTI, and MIST isochrones for the AI Phe system. We note that the luminosity is not fitted and is estimated from the Stefan-Boltzmann law. |
AL Doradus. We first used the metallicity [Fe/H] = −0.21 dex derived by Graczyk et al. (2019) with the stellar parameters listed in Table 3. We found that both stars are in a similar main-sequence phase, but the best-fit isochrones are not satisfactory for all models, as shown in Fig. 11 in gray. The corresponding average age is t = 1.28 ± 0.89 Gyr. The metallicity does not seem consistent, and the value ∼0.10 dex would be more appropriate to reconcile the observables with the isochrones, as plotted in Fig. 11 in black. This value is consistent with the 0.15 ± 0.15 dex derived by Ammons et al. (2006) from a metallicity-color calibration. All isochrone models locate the stars near the main-sequence turn-off with an average age tavg = 2.97 ± 0.23 Gyr. This can be compared to Casagrande et al. (2011) who performed a Bayesian analysis of the primary star with the PARSEC and BaSTI isochrones to derive t = 4.30 ± 0.85 Gyr and t = 3.90 ± 0.90 Gyr, respectively. Although they used a ∼100 K hotter temperature and a metallicity of −0.10 dex, their estimates are consistent with ours at < 1.5σ.
 |
Fig. 11. Fitted PARSEC, BaSTI and MIST isochrones for the AL Dor system. The gray isochrones correspond to a metallicity of [Fe/H] = −0.21 dex, and the black isochrones are for 0.10 dex. We note that the luminosity is not fitted and is estimated from the Stefan–Boltzmann law. |
Radii agree at ∼1σ with all models, while the masses disagree at more than 2.5σ, the PARSEC model showing the largest discrepancy. A better estimate of the metallicity and more precise temperatures are needed for further conclusions.
KW Hydrae. No measurement of the metallicity for this system is available in the literature. We therefore manually searched for a [Fe/H] value giving the lowest χ2 for all models. We found that [Fe/H] = 0.25 dex provided a satisfactory fit for all models with the stellar parameters listed in Table 3. We conservatively chose an uncertainty of ±0.10 dex to derive our age uncertainty. The isochrones are displayed in Fig. 12, and are all consistent with each other. They show two components located on the main sequence, with the more evolved one being near the turn-off point. The age of all model agrees and we adopted an average age for the KW Hya system of tavg = 0.54 ± 0.05 Gyr. This is consistent with the 0.5 Gyr derived by Andersen & Vaz (1984) with Z = 0.02 and other isochrones models using old opacity data.
 |
Fig. 12. Fitted PARSEC, BaSTI, and MIST isochrones for the KW Hya system. We note that the luminosity is not fitted and is estimated from the Stefan–Boltzmann law. |
However, we note that the more evolved component (the primary) is better fit than the less evolved star (the secondary). More particularly, the fit of the radius of the secondary is not fully satisfactory. Removing the mass measurements from the fitted parameters slightly improved the agreement in radius, which might mean that the M − R calibration of the models is still not optimal for this level of precision. Finally, it is worth mentioning that fitting each component independently provides a similar age for the primary (within 1σ), while the secondary is ∼7σ younger.
NN Delphini. No estimate of the metallicity is available for this system. We therefore proceeded in the same way as for KW Hya, that is, we manually searched for a value giving the lowest χ2 for all models, given the parameters listed in Table 3. We found that [Fe/H] = −0.10 dex provided a satisfactory fit for all models. We also conservatively chose an uncertainty of ±0.10 dex to derive our age uncertainty for each models. The isochrones are displayed in Fig. 13 and agree with each other. All isochrones give the same evolutionary phase, that is, both components are at the main-sequence turn-off point. The age between the PARSEC and MIST models are very similar, while the BaSTI model gives a younger system. They are reported in Table 3. We adopted the average tavg = 2.21 ± 0.18 Gyr.
 |
Fig. 13. Fitted PARSEC, BaSTI, and MIST isochrones for the NN Del system. We note that the luminosity is not fitted and is estimated from the Stefan–Boltzmann law. |
We also note that our secondary mass measurement is ∼9σ away from the BaSTI isochrones. Again, this might be linked to the calibrations of the models, but further analyses are still necessary, particularly a measurement of the metallicity.
ψ Centauri. The metallicity of ψ Cen is also unknown, therefore we proceeded as for our previous systems and manually searched for a value giving the lowest χ2 for all models, according to the parameters listed in Table 3. We found that [Fe/H] = 0.2 dex provided a satisfactory fit for all models. We also conservatively chose an uncertainty of ±0.10 dex to derive our age uncertainty. The isochrones are displayed in Fig. 14. We found that the secondary is on the main sequence and the primary entered the main-sequence turn-off. We estimated an average age of 0.28 ± 0.01 Gyr, consistent with the estimate of Bruntt et al. (2006, 290 Myr), who used Yonsei-Yale model isochrones and a metallicity Z = 0.01812. While all models give a similar age, the PARSEC model gives a better fit with the measurements. We note that the less evolved component agrees better with the tracks than the primary star located at the turn-off point. Changing the metallicity value does not reconcile the tracks, and the slight disagreement may be due to the internal physics used in the models. The difference in the parameterization of the core overshooting may be a lead to explore. For instance, we note that the PARSEC model, which has the largest overshooting parameter (αov = 0.25), provides a slightly better agreement than the other models. However, the MIST model with the lowest parameter (αov ∼ 0.18) is in between, but they also used a alternate prescription of the core overshooting.
 |
Fig. 14. Fitted PARSEC, BaSTI, and MIST isochrones for the ψ Cen system. The gray isochrones correspond to a metallicity of [Fe/H] = 0.1 dex, and the black isochrones are for 0.05 dex. We note that the luminosity is not fitted and is estimated from the Stefan–Boltzmann law. |
V4090 Sagittarii. We adopted the metallicity of 0.36 ± 0.07 estimated by North et al. (1997) for the primary, as well as the effective temperature and radii. We note that their temperatures were estimated from average color indices and not from spectroscopy. Here we only fit the PARSEC and MIST isochrones because we are beyond the BaSTI metallicity range with this system. The isochrones displayed in Fig. 15 show that both components are in the main-sequence phase, with the primary star approaching the turn-off point. Both models provide a similar age (within 1σ), although the MIST models give a younger system. We estimated tavg = 0.44 ± 0.13 Gyr. We note that the observables of the secondary star are within 1σ with the isochrones, but this is not the case for the more evolved component. The models predict a hotter component with a larger radius for this given mass, which might be linked to the core overshooting or the calibration of isochrones. The disagreement could also be due to a bias in the Gaia parallax. To reconcile the isochrones to ∼1σ, we would need to correct the Gaia measurements by +0.25 mas. We note that the HIPPARCOS parallax has a low accuracy of ∼8%, providing a primary mass precise to ∼30%, which does not help in constraining the models. Finally, the lack of radial velocities likely affects a reliable estimates of the semi-amplitude parameters, and therefore of the masses.
 |
Fig. 15. Fitted PARSEC and MIST isochrones for the V4090 Sgr system. We note that the luminosity is not fitted and is estimated from the Stefan–Boltzmann law. |
In general, for all our systems we see that the models cannot properly reproduce all observables, especially the radii and masses. We do not see a general trend related to the metallicity, although we still lack precise measurements to conclude reliably. We note, however, that the stars located at the main-sequence stage are generally better fit than the star that is located at the turn-off point. A possible explanation would be the parameterization of the convective core overshooting. For instance for KW Hya and ψ Cen which have stars at a similar evolution stage, we note that the model with the largest core overshooting parameterization (PARSEC) better matches both stars to all observables (assuming a metallicity of 0.05 dex for ψ Cen). Unfortunately, for a finer analysis, we require metallicity measurements with a higher precision, and require entering the models to change specific internal stellar parameters to better compare between models instead of pre-computed isochrones.
6.3. Distance comparison with Gaia parallaxes
We display in Fig. 16 the comparison between our derived orbital parallaxes and those from the Gaia DR2. Only one system (AL Dor) agrees within 1σ. AI Phe is at 1.2σ, while the other systems are > 2σ. We note that we took into account the +29 μas astrometric offset suggested by Lindegren et al. (2018). As stated previously, this is to be expected because the Gaia DR2 astrometric pipeline processing does not yet take the binarity of stars into account. However, it is worth mentioning that the Gaia bias indicators (the renormalized unit weight error and the astrometric excess noise) do not show strong evidence of possible biased measurements.
 |
Fig. 16. Comparison between our derived orbital parallaxes and the Gaia DR2. Bottom panel: difference in number of σ, with the gray area representing 1σ. |
We also examined the proper motion (PM) of these systems by comparing the HIPPARCOS and Gaia measurements following the approach developed by Kervella et al. (2019a, see also Kervella et al. 2019b). The long time-baseline of 24.25 years between the two missions allows us to compare the mean long-term PM vectors with the individual measurements. Any difference (or anomaly) between the vectors indicates the presence of an orbiting third component. The detection is quantified using the signal-to-noise ratio (S/N) of the PM anomalies with respect to the mean PM as defined by Kervella et al. (2019b). We found strong evidence of a third orbiting component for the AI Phe and KW Hya systems, with an S/N of 14.8 and 36.4, respectively. We note that this is consistent with our analysis in Sect. 5 for a third component of AI Phe. Moderately compelling evidence is found for V4090 Sgr and NN Del (S/N ∼ 3), while there is no sign of an additional component around ψ Cen and AL Dor.
7. Conclusion
We reported the first interferometric observations of the eclipsing binary systems AI Phe, AL Dor, KW Hya, NN Del, ψ Cen, and V4090 Sgr using the VLTI/PIONIER combiner. We performed a simultaneous fit of our precise astrometric positions provided by interferometry with RV measurements to measure all the orbital elements, accurate dynamical masses, and orbital parallaxes. For some systems we obtained a precision down to 0.04% on the masses and 0.4% on the orbital parallaxes. The accuracy on the orbital parallaxes is dominated by the systematic uncertainty of 0.35% on the interferometric separation measurements, limited by the knowledge of the effective wavelength of the PIONIER instrument. For our next targets of our observing program, this limitation will be overcome with the use of the VLTI/GRAVITY instrument (Eisenhauer et al. 2011), which has a dedicated internal reference laser source providing a wavelength accuracy of ∼0.01%. Improving the precision on the astrometric and radial velocity measurements is expected to also improve the precision on the masses.
We compared our precisely measured masses to stellar evolution models, together with stellar effective temperatures and radii retrieved from the literature. While our combined fits are satisfactory to derive the age of the systems, the high accuracy level on the masses of some systems showed that stellar evolution theory is still deficient in fitting all parameters simultaneously, with the radii or masses in marginal agreement with the models. This stresses the importance of precise stellar measurements for stellar evolution modeling and their calibration. Unfortunately, with precomputed isochrones (and predefined evolution parameters) and without precise measurements of the metallicity and temperature, it is impossible to conclude which specific evolution model is more appropriate.
With a median accuracy of ∼55 μas, our parallax measurements shows that the Gaia parallaxes still suffer from large systematic errors. However, this is expected because the last data release did not take the effect of binarity in the astrometric solutions into account. Precise and accurate measurements like this provide a unique benchmark on which to test the next Gaia parallaxes.
Available at http://www.jmmc.fr/searchcal
Available at https://github.com/amerand/CANDID
With the Python package emcee developed by Foreman-Mackey et al. (2013).
Acknowledgments
The authors would like to thank all the people involved in the VLTI project. A.G. acknowledges support from FONDECYT grant 3130361. We acknowledge the support of the French Agence Nationale de la Recherche (ANR-15-CE31-0012-01, project Unlock-Cepheids). WG and GP gratefully acknowledge financial support from the BASAL Centro de Astrofisica y Tecnologias Afines (CATA, AFB-170002). WG also acknowledges financial support from the Millenium Institute of Astrophysics (MAS) of the Iniciativa Cientifica Milenio del Ministerio de Economia, Fomento y Turismo de Chile (project IC120009). We acknowledge financial support from the Programme National de Physique Stellaire (PNPS) of CNRS/INSU, France. Support from the Polish National Science Centre grants MAESTRO UMO-2017/26/A/ST9/00446 and from the IdP II 2015 0002 64 grant of the Polish Ministry of Science and Higher Education is also acknowledged. The research leading to these results has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement N°695099, 639889 and 670519). BP acknowledges financial support from the Polish National Science Center grant SONATA 2014/15/D/ST9/02248. MT acknowledges financial support from the Polish National Science Center grant PRELUDIUM 2016/21/N/ST9/03310. We also thank Monica Reiner for kindly providing the reduced FEROS spectra of ψ Cen. The research leading to these results has (partially) received funding from the KU Leuven Research Council (grant C16/18/005: PARADISE), from the Research Foundation Flanders (FWO) under grant agreement G0H5416N (ERC Runner Up Project), as well as from the BELgian federal Science Policy Office (BELSPO) through PRODEX grant PLATO.
References
- Ammons, S. M., Robinson, S. E., Strader, J., et al. 2006, ApJ, 638, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Andersen, J., & Nordstrom, B. 1977, A&AS, 29, 309 [NASA ADS] [Google Scholar]
- Andersen, J., & Vaz, L. P. R. 1984, A&A, 130, 102 [NASA ADS] [Google Scholar]
- Andersen, J., Clausen, J. V., Nordstrom, B., Gustafsson, B., & Vandenberg, D. A. 1988, A&A, 196, 128 [NASA ADS] [Google Scholar]
- Baron, F., Monnier, J. D., Pedretti, E., et al. 2012, ApJ, 752, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Bonneau, D., Clausse, J.-M., Delfosse, X., et al. 2006, A&A, 456, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonneau, D., Delfosse, X., Mourard, D., et al. 2011, A&A, 535, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bruntt, H., Southworth, J., Torres, G., et al. 2006, A&A, 456, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catchpole, R. M., Evans, D. S., Jones, D. H. P., King, D. L., & Wallis, R. E. 1982, R. Greenwich Obs. Bull., 188 [Google Scholar]
- Chauville, M.-T. 1975, A&A, 40, 207 [NASA ADS] [Google Scholar]
- Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Torres, G. 2016, A&A, 592, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Torres, G. 2017, ApJ, 849, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Torres, G. 2018, ApJ, 859, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenhauer, F., Perrin, G., Brandner, W., et al. 2011, The Messenger, 143, 16 [NASA ADS] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Monnier, J. D., Mérand, A., et al. 2013, A&A, 552, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Mérand, A., Kervella, P., et al. 2014, A&A, 561, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Mérand, A., Kervella, P., et al. 2015, A&A, 579, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Pietrzyński, G., Graczyk, D., et al. 2016, A&A, 586, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Kervella, P., Evans, N. R., et al. 2018a, ApJ, 867, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Gallenne, A., Pietrzyński, G., Graczyk, D., et al. 2018b, A&A, 616, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieren, W., Pietrzynski, G., Bresolin, F., et al. 2005a, The Messenger, 121, 23 [NASA ADS] [Google Scholar]
- Gieren, W., Pietrzyński, G., Soszyński, I., et al. 2005b, ApJ, 628, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Gieren, W., Pilecki, B., Pietrzyński, G., et al. 2015, ApJ, 815, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Giuricin, G., Mardirossian, F., & Mezzetti, M. 1984, A&A, 135, 194 [NASA ADS] [Google Scholar]
- Gómez-Forrellad, J. M., Sánchez-Bajo, F., Corbera-Subirana, M., García-Melendo, E., & Vidal-Sainz, J. 2003, Ap&SS, 283, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Graczyk, D., Pietrzyński, G., Thompson, I. B., et al. 2014, ApJ, 780, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Graczyk, D., Maxted, P. F. L., Pietrzyński, G., et al. 2015, A&A, 581, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graczyk, D., Konorski, P., Pietrzyński, G., et al. 2017, ApJ, 837, 7 [Google Scholar]
- Graczyk, D., Pietrzyński, G., Gieren, W., et al. 2019, ApJ, 872, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, R. F. 2014, The Observatory, 134, 109 [NASA ADS] [Google Scholar]
- Haberreiter, M., Schmutz, W., & Kosovichev, A. G. 2008, ApJ, 675, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Heintz, W. D. 1978, Double Stars (Reidel: Dordrecht) [CrossRef] [Google Scholar]
- Hełminiak, K. G., Konacki, M., Ratajczak, M., & Muterspaugh, M. W. 2009, MNRAS, 400, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Herbison-Evans, D., Hanbury Brown, R., Davis, J., & Allen, L. R. 1971, MNRAS, 151, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Higl, J., Siess, L., Weiss, A., & Ritter, H. 2018, A&A, 617, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillenbrand, L. A., & White, R. J. 2004, ApJ, 604, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Houk, N. 1982, Michigan Catalogue of Two-dimensional Spectral Types for the HD stars (Ann Arbor, MI: Univ. of Michigan), 3 [Google Scholar]
- Imbert, M. 1979, A&AS, 36, 453 [NASA ADS] [Google Scholar]
- Kanjanascul, C., Bach, K.-H., Hong, K.-S., et al. 2012, J. Astron. Space Sci., 29, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Kazarovets, E. V., Samus, N. N., Durlevich, O. V., et al. 1999, IBVS, 4659 [Google Scholar]
- Kervella, P., Bigot, L., Gallenne, A., & Thévenin, F. 2017, A&A, 597, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Gallenne, A., Remage Evans, N., et al. 2019a, A&A, 623, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Arenou, F., Mignard, F., & Thévenin, F. 2019b, A&A, 623, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirkby-Kent, J. A., Maxted, P. F. L., Serenelli, A. M., et al. 2016, A&A, 591, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Bouquin, J.-B., Berger, J.-P., Lazareff, B., et al. 2011, A&A, 535, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Bouquin, J.-B., Beust, H., Duvert, G., et al. 2013, A&A, 551, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Makarov, V., Bastian, U., Hoeg, E., Grossmann, V., & Wicenec, A. 1994, IBVS, 4118 [Google Scholar]
- Mantegazza, L., Rainer, M., & Antonello, E. 2010, A&A, 512, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2017, ApJ, 835, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Milone, E. F., Stagg, C. R., & Kurucz, R. L. 1992, ApJS, 79, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Morbey, C. L. 1975, PASP, 87, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Nordstrom, B., & Andersen, J. 1985, A&AS, 61, 53 [NASA ADS] [Google Scholar]
- North, P., Studer, M., & Kunzli, M. 1997, A&A, 324, 137 [NASA ADS] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gieren, W., et al. 2013, Nature, 495, 76 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gallenne, A., et al. 2019, Nature, 567, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Pilecki, B., Graczyk, D., Pietrzyński, G., et al. 2013, MNRAS, 436, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Pilecki, B., Graczyk, D., Gieren, W., et al. 2015, ApJ, 806, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Pilecki, B., Gieren, W., Smolec, R., et al. 2017, ApJ, 842, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Pilecki, B., Gieren, W., Pietrzyński, G., et al. 2018, ApJ, 862, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Pitjeva, E. V., & Standish, E. M. 2009, Celest. Mech. Dyn. Astron., 103, 365 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pribulla, T., Mérand, A., Kervella, P., et al. 2018, A&A, 616, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reipurth, B. 1981, IBVS, 2015 [Google Scholar]
- Rucinski, S. M. 1992, AJ, 104, 1968 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., & Torres, G. 2016, AJ, 152, 180 [Google Scholar]
- Strassmeier, K. G., Granzer, T., Weber, M., et al. 2010, Adv. Astron., 2010, 970306 [Google Scholar]
- Strohmeier, W. 1972, IBVS, 665 [Google Scholar]
- Sybilski, P., Pawłaszek, R. K., Sybilska, A., et al. 2018, MNRAS, 478, 1942 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Claret, A., & Young, P. A. 2009, ApJ, 700, 1349 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Valle, G., Dell’Omodarme, M., Prada Moroni, P. G., & Degl’Innocenti, S. 2017, A&A, 600, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Waelkens, C., & Rufener, F. 1983, A&AS, 52, 13 [NASA ADS] [Google Scholar]
- Weber, M., Granzer, T., Strassmeier, K. G., & Woche, M. 2008, in Advanced Software and Control for Astronomy II, Proc. SPIE, 7019, 70190L [NASA ADS] [CrossRef] [Google Scholar]
- Woillez, J., Darré, P., Egner, S., et al. 2018, in Optical and Infrared Interferometry and Imaging VI, SPIE Conf. Ser., 10701, 1070103 [Google Scholar]
- Zwahlen, N., North, P., Debernardi, Y., et al. 2004, A&A, 425, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Radial velocities
Radial velocities of the AI Phe system from the HARPS echelle spectrograph.
Radial velocities of the NN Del system from the STELLA echelle spectrograph.
Radial velocities of the ψ Cen system.
Appendix B: Parameters of the calibrators used for the PIONIER interferometric observations
Calibrators used for our observations for all systems.
All Tables
Stellar parameters used for the age determinations, together with our fitted and adopted age of the systems.
All Figures
 |
Fig. 1. Difference in number of sigmas of the astrometric positions (Δα, Δδ) for a fitted and fixed flux ratio. This is calculated as |
| In the text | |
 |
Fig. 2. Closure phase and squared visibility measurements of the last measurements of AI Phe. The data are plotted in blue, and the red dots represent the fitted binary model for this epoch. The residuals (in number of sigmas) are also shown in the bottom panels. |
| In the text | |
 |
Fig. 3. Left: radial velocities of the primary (red) and the secondary (blue) in the AI Phe system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
| In the text | |
 |
Fig. 4. Left: radial velocities of the primary (red) and the secondary (blue) star in the AL Dor system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
| In the text | |
 |
Fig. 5. Left: radial velocities of the primary (red) and the secondary (blue) star in the KW Hya system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
| In the text | |
 |
Fig. 6. Left: radial velocities of the primary (red) and the secondary (blue) star in the NN Del system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
| In the text | |
 |
Fig. 7. Left: radial velocities of the primary (red) and the secondary (blue) star in the ψ Cen system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
| In the text | |
 |
Fig. 8. Left: radial velocities of the primary in the V4090 Sgr system. Right: PIONIER astrometric orbit. The shaded gray area represents the 1σ orbit. |
| In the text | |
 |
Fig. 9. Comparison of our mass measurements (colored area) with the literature (black dots). The red (left) and blue (right) shaded areas represent the 1σ, 2σ, and 3σ combined uncertainties of the primary and secondary, respectively. References are Sy18 for Sybilski et al. (2018), Gr17 for Graczyk et al. (2017), Ki16 for Kirkby-Kent et al. (2016), He09 for Hełminiak et al. (2009), Mi92 for Milone et al. (1992), An88 for Andersen et al. (1988), An84 for Andersen & Vaz (1984), Gr14 for Griffin (2014), Ma10 for Mantegazza et al. (2010), Br06 for Bruntt et al. (2006), No97 for North et al. (1997) and Gi84 for Giuricin et al. (1984). |
| In the text | |
 |
Fig. 10. Fitted PARSEC, BaSTI, and MIST isochrones for the AI Phe system. We note that the luminosity is not fitted and is estimated from the Stefan-Boltzmann law. |
| In the text | |
 |
Fig. 11. Fitted PARSEC, BaSTI and MIST isochrones for the AL Dor system. The gray isochrones correspond to a metallicity of [Fe/H] = −0.21 dex, and the black isochrones are for 0.10 dex. We note that the luminosity is not fitted and is estimated from the Stefan–Boltzmann law. |
| In the text | |
 |
Fig. 12. Fitted PARSEC, BaSTI, and MIST isochrones for the KW Hya system. We note that the luminosity is not fitted and is estimated from the Stefan–Boltzmann law. |
| In the text | |
 |
Fig. 13. Fitted PARSEC, BaSTI, and MIST isochrones for the NN Del system. We note that the luminosity is not fitted and is estimated from the Stefan–Boltzmann law. |
| In the text | |
 |
Fig. 14. Fitted PARSEC, BaSTI, and MIST isochrones for the ψ Cen system. The gray isochrones correspond to a metallicity of [Fe/H] = 0.1 dex, and the black isochrones are for 0.05 dex. We note that the luminosity is not fitted and is estimated from the Stefan–Boltzmann law. |
| In the text | |
 |
Fig. 15. Fitted PARSEC and MIST isochrones for the V4090 Sgr system. We note that the luminosity is not fitted and is estimated from the Stefan–Boltzmann law. |
| In the text | |
 |
Fig. 16. Comparison between our derived orbital parallaxes and the Gaia DR2. Bottom panel: difference in number of σ, with the gray area representing 1σ. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



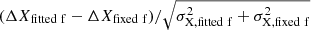
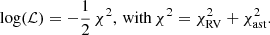
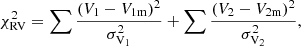
![$$ \begin{aligned}&V_\mathrm{1m} = \gamma + K_1\,[\cos (\omega + \nu ) + e\cos {\omega }], \\&V_\mathrm{2m} = \gamma + K_2\,[\cos (\omega + \nu ) + e\cos {\omega }], \\&\tan \dfrac{\nu }{2} = \sqrt{\dfrac{1 + e}{1 - e}} \tan \dfrac{E}{2}, \\&E - e \sin E = \dfrac{2\pi (t - T_\mathrm{p} )}{P_\mathrm{orb} }, \end{aligned} $$](/articles/aa/full_html/2019/12/aa35837-19/aa35837-19-eq5.gif)
![$$ \begin{aligned}&\chi ^2_\mathrm{ast} = \chi ^2_\mathrm{a} + \chi ^2_\mathrm{b} , \\&\chi ^2_\mathrm{a} = \sum \frac{[ (\Delta \alpha - \Delta \alpha _\mathrm{m} ) \sin \sigma _\mathrm{PA} + (\Delta \delta - \Delta \delta _\mathrm{m} ) \cos \sigma _\mathrm{PA} ]^2}{\sigma ^2_\mathrm{maj} }, \\&\chi ^2_\mathrm{b} = \sum \frac{[ -(\Delta \alpha - \Delta \alpha _\mathrm{m} ) \cos \sigma _\mathrm{PA} + (\Delta \delta - \Delta \delta _\mathrm{m} ) \sin \sigma _\mathrm{PA} ]^2}{\sigma ^2_\mathrm{min} }, \end{aligned} $$](/articles/aa/full_html/2019/12/aa35837-19/aa35837-19-eq7.gif)
![$$ \begin{aligned} \Delta \alpha _\mathrm{m}&= r \,[ \sin \Omega \cos (\omega + \nu ) + \cos i \cos \Omega \sin (\omega + \nu ) ], \\ \Delta \delta _\mathrm{m}&= r \,[ \cos \Omega \cos (\omega + \nu ) - \cos i \sin \Omega \sin (\omega + \nu ) ], \\ r&= \dfrac{a (1 - e^2)}{1 + e\cos \nu }, \end{aligned} $$](/articles/aa/full_html/2019/12/aa35837-19/aa35837-19-eq8.gif)
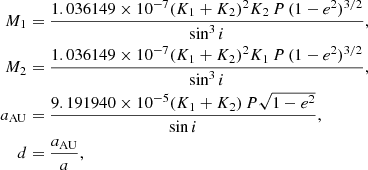
![$$ \begin{aligned} \chi ^{2} = \sum _{i=1}^{2} \left[ \left(\frac{\Delta T_{\mathrm{eff}}}{\sigma _{{T}_{\mathrm{eff}}}}\right)_i^2 + \left(\frac{\Delta R}{\sigma _{R}}\right)_{i}^{2} + \left(\dfrac{\Delta M}{\sigma _{M}}\right)_{i}^{2} \right] \end{aligned} $$](/articles/aa/full_html/2019/12/aa35837-19/aa35837-19-eq10.gif)