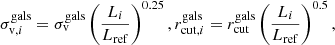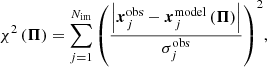| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 27 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201935454 | |
| Published online | 25 November 2019 | |
Strong lensing models of eight CLASH clusters from extensive spectroscopy: Accurate total mass reconstructions in the cores⋆
1
Kapteyn Astronomical Institute, University of Groningen, Postbus 800, 9700 AV Groningen, The Netherlands
e-mail: caminha@astro.rug.nl
2
Dipartimento di Fisica e Scienze della Terra, Università degli Studi di Ferrara, Via Saragat 1, 44122 Ferrara, Italy
3
INAF – Osservatorio Astronomico di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
4
Dipartimento di Fisica, Università degli Studi di Milano, Via Celoria 16, 20133 Milano, Italy
5
Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
6
The Cosmic Dawn Center, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
7
INFN – Sezione di Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
8
INAF – Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Napoli, Italy
9
University Observatory Munich, Scheinerstrasse 1, 81679 Munich, Germany
10
Dipartimento di Fisica e Astronomia “G. Galilei”, Università degli Studi di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
11
INAF – Osservatorio Astronomico di Trieste, Via G. B. Tiepolo 11, 34143 Trieste, Italy
12
Academia Sinica Institute of Astronomy and Astrophysics (ASIAA), No. 1, Section 4, Roosevelt Road, Taipei 10617, Taiwan
13
Physics Department, Tufts University, 574 Boston Ave., Medford 02155, MA, USA
14
Department of Theoretical Physics, University of the Basque Country UPV/EHU, Bilbao, Spain
15
Donostia International Physics Center (DIPC), 20018 Donostia-San Sebastian, Gipuzkoa, Spain
16
IKERBASQUE, Basque Foundation for Science, Bilbao, Spain
17
Departamento de Astronomía, Facultad de Ciencias Físicas y Matemáticas, Universidad de Concepción, Concepción, Chile
18
Space Telescope Science Institute, 3700 San Martin Dr., Baltimore, MD 21218, USA
19
University of Vienna, Department of Astrophysics, Tuerkenschanzstrasse 17, 1180 Vienna, Austria
20
Physics Department, Ben-Gurion University of the Negev, PO Box 653, Be’er-Sheva 84105, Israel
Received:
12
March
2019
Accepted:
17
July
2019
We carried out a detailed strong lensing analysis of a sub-sample of eight galaxy clusters of the Cluster Lensing And Supernova survey with Hubble (CLASH) in the redshift range of zcluster = [0.23 − 0.59] using extensive spectroscopic information, primarily from the Multi Unit Spectroscopic Explorer (MUSE) archival data and complemented with CLASH-VLT redshift measurements. The observed positions of the multiple images of strongly lensed background sources were used to constrain parametric models describing the cluster total mass distributions. Different models were tested in each cluster depending on the complexity of its mass distribution and on the number of detected multiple images. Four clusters show more than five spectroscopically confirmed multiple image families. In this sample, we did not make use of families that are only photometrically identified in order to reduce model degeneracies between the values of the total mass of a cluster source redshifts, in addition to systematics due to the potential misidentifications of multiple images. For the remaining four clusters, we used additional families without any spectroscopic confirmation to increase the number of strong lensing constraints up to the number of free parameters in our parametric models. We present spectroscopic confirmation of 27 multiply lensed sources, with no previous spectroscopic measurements, spanning over the redshift range of zsrc = [0.7 − 6.1]. Moreover, we confirm an average of 48 galaxy members in the core of each cluster thanks to the high efficiency and large field of view of MUSE. We used this information to derive precise strong lensing models, projected total mass distributions, and magnification maps. We show that, despite having different properties (i.e. number of mass components, total mass, redshift, etc.), the projected total mass and mass density profiles of all clusters have very similar shapes when rescaled by independent measurements of M200c and R200c. Specifically, we measured the mean value of the projected total mass of our cluster sample within 10 (20)% of R200c to be 0.13 (0.32) of M200c, with a remarkably small scatter of 5 (6)%. Furthermore, the large number of high-z sources and the precise magnification maps derived in this work for four clusters add up to the sample of high-quality gravitational telescopes to be used to study the faint and distant Universe.
Key words: galaxies: clusters: general / gravitational lensing: strong / dark matter
The full redshift catalogue from the MUSE observations (Table 2) is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/632/A36
© ESO 2019
1. Introduction
The importance of galaxy cluster strong lensing in cosmological studies has increased significantly in recent years thanks to high quality data from extensive observational programmes, using photometry and spectroscopy. Strong lenses can be used for different purposes, such as to study the details of the total mass distribution in galaxy clusters, to identify and characterise intrinsically faint but highly magnified sources at high-redshifts, and to probe the background geometry of the Universe (for a review see Kneib & Natarajan 2011). For instance, gravitational lensing studies (e.g. Sand et al. 2004; Newman et al. 2013a,b) have indicated that the inner slope of the dark-matter mass density profile of massive clusters is flatter than the canonical Navarro-Frenk-White profile (NFW, Navarro et al. 1996, 1997; Moore et al. 1998; Gao et al. 2012). On the other hand, hydrodynamical simulations have shown contrasting results, whether baryonic processes produce a shallow dark matter profile (Martizzi et al. 2012) or whether they are in agreement with the NFW model (Schaller et al. 2015). To clarify observationally this discrepancy found in simulations, it is necessary to perform accurate strong lensing analyses using a large sample of spectroscopically confirmed multiple image families, that is, strong lensing constraints, in order to provide reliable measurements of the inner total mass density.
Moreover, the gravitational lensing magnification effect produced by clusters across a relatively large area of the sky has been used to select candidates of the most distant galaxies in the Universe (z ≳ 9, Coe et al. 2013; Bouwens et al. 2014; Zitrin et al. 2014; Salmon et al. 2018). Therefore, lensing fields are good targets to push the detection limits of current instrumentation towards the faint and far population of galaxies (Atek et al. 2015, 2018; Bouwens et al. 2017). Studies of background faint galaxies at lower redshifts z ≈ 3 − 6 (Caminha et al. 2016a; Patrício et al. 2016; Hernán-Caballero et al. 2017; Smit et al. 2017; Vanzella et al. 2017a,b, 2019) have also greatly benefited from the enhanced spatial resolution and amplified flux produced by the gravitational lensing effect. This all leads to some important insights on the evolution and characterization of galaxies, indicating that this faint population might be important for the reionisation of the Universe (Yue et al. 2014; Bouwens et al. 2015; Robertson et al. 2015). In pursuing this large variety of applications, several observational efforts, such as the Cluster Lensing And Supernova survey with Hubble (CLASH, Postman et al. 2012), the Hubble Frontier Fields (HFF, Lotz et al. 2017) and, more recently, the REionisation Lensing Cluster Survey (RELICS, Salmon et al. 2017; Coe et al. 2019), have spent a total of ≈1300 orbits of the Hubble Space Telescope (HST). This then provides homogeneous photometry in optical and near infra-red filters with limiting magnitudes in the range of magF160W = 27.5 − 28.7 (5σ detection for point sources within  radius) for 68 lens galaxy clusters. However, it is crucial to have extensive spectroscopic information about multiple image families and cluster members to build precise and high-resolution mass and magnification maps in order to probe the total mass distribution of lens clusters and the physical properties of lensed background sources in detail (see e.g. Grillo et al. 2015; Caminha et al. 2016b; Johnson & Sharon 2016). Therefore, different spectroscopic campaigns have targeted sub-samples of these clusters confirming high-redshift candidates, multiple images and cluster members. Using HST, the Grism Lens-Amplified Survey from Space (GLASS, Treu et al. 2015) has obtained relatively low resolution grism spectroscopy in the inner core (≈5 arcmin2) of ten clusters. The CLASH-VLT ESO Large programme carried out a panoramic spectroscopic campaign of 13 southern CLASH clusters using the VIsible Multi-Object Spectrograph (VIMOS), covering ≈0.1 deg2 in each cluster (Rosati et al., in prep.; Grillo et al. 2015; Balestra et al. 2016; Monna et al. 2017).
radius) for 68 lens galaxy clusters. However, it is crucial to have extensive spectroscopic information about multiple image families and cluster members to build precise and high-resolution mass and magnification maps in order to probe the total mass distribution of lens clusters and the physical properties of lensed background sources in detail (see e.g. Grillo et al. 2015; Caminha et al. 2016b; Johnson & Sharon 2016). Therefore, different spectroscopic campaigns have targeted sub-samples of these clusters confirming high-redshift candidates, multiple images and cluster members. Using HST, the Grism Lens-Amplified Survey from Space (GLASS, Treu et al. 2015) has obtained relatively low resolution grism spectroscopy in the inner core (≈5 arcmin2) of ten clusters. The CLASH-VLT ESO Large programme carried out a panoramic spectroscopic campaign of 13 southern CLASH clusters using the VIsible Multi-Object Spectrograph (VIMOS), covering ≈0.1 deg2 in each cluster (Rosati et al., in prep.; Grillo et al. 2015; Balestra et al. 2016; Monna et al. 2017).
The Multi Unit Spectroscopic Explorer (MUSE, Bacon et al. 2014) has driven a revolution in strong lens studies of galaxy clusters. Its efficiency, field of view of 1 arcmin2, and capability of detecting faint emission lines out to z ≈ 6.5 without any source pre-selection are being exploited to expand significantly the spectroscopic confirmation of multiply lensed sources and cluster members that are then used to constrain lens models (see e.g. Grillo et al. 2016; Caminha et al. 2017a,b; Lagattuta et al. 2017; Mahler et al. 2018; Jauzac et al. 2019). The spectroscopic confirmation of many multiple images is essential to remove some degeneracies between the source redshifts and the cluster total mass. Moreover, this information avoids wrong identifications of counterimages that can significantly limit the accuracy and precision with which the cluster mass and magnification maps are reconstructed.
In this work, we selected a sub-sample of eight CLASH clusters with MUSE observations in order to carry out detailed strong lensing analyses and improve their total mass distribution measurements in the cores. The cluster extended names are listed in Table 1 and hereafter we will use their abbreviated names, namely RX J2129, MACS J1931, MACS J0329, MACS J2129, MACS J1115, MACS J0429, RX J1347 and MACS J1311. We also incorporated a relatively small set of CLASH-VLT spectroscopic redshifts to cover the regions external to the MUSE field of view (Rosati et al., in prep.). Our cluster sample spans the redshift and virial mass ranges of zcluster = 0.234 − 0.587 and 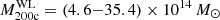 , respectively (these last values were obtained from weak lensing measurements, Merten et al. 2015; Umetsu et al. 2018). With the exception of MACS J2129, these clusters were selected within the CLASH survey to be dynamically relaxed, based on Chandra X-ray observations (Postman et al. 2012). The combination of these eight clusters with previous works on MACS J0416, MACS J1206 and Abell 1063 (Caminha et al. 2016b, 2017a,b) constitutes the sample of all CLASH clusters with available MUSE spectroscopy to date.
, respectively (these last values were obtained from weak lensing measurements, Merten et al. 2015; Umetsu et al. 2018). With the exception of MACS J2129, these clusters were selected within the CLASH survey to be dynamically relaxed, based on Chandra X-ray observations (Postman et al. 2012). The combination of these eight clusters with previous works on MACS J0416, MACS J1206 and Abell 1063 (Caminha et al. 2016b, 2017a,b) constitutes the sample of all CLASH clusters with available MUSE spectroscopy to date.
MUSE observation summary.
Previous studies have carried out strong lensing analyses on this cluster sample. To mention some recent works, Monna et al. (2017) and Ueda et al. (2018) studied the specific clusters MACS J2129 and RX J1347, respectively. Moreover, the full CLASH 25 cluster sample has been strong (and weak-)-lens analysed by Zitrin et al. (2015). Our work, using the MUSE spectroscopic data, adds a significant number of new confirmed multiple images used to constrain the lens models.
This paper is organised as follows. In Sect. 2, we present the data used in this work and describe the MUSE observations and redshift measurements. The methodology used in our strong lens modelling is explained in Sect. 3, and in Sect. 4 we discuss the results on the total mass distribution of the clusters. Finally, in Sect. 5, we summarise our conclusions.
Throughout this work, we adopt the a flat ΛCDM cosmological model, with Ωm = 0.3 and H0 = 70 km s−1 Mpc−1. The images are oriented with north at top and east to the left, and the angles are measured from the west and oriented counterclockwise.
2. Data
2.1. HST-CLASH
The cluster sample presented in this work has been observed by the CLASH survey, using the ACS and WFC3 cameras onboard HST, in 16 filters from the UV through the NIR (Postman et al. 2012). The data has been reduced using the Mosaicdrizzle pipeline (Koekemoer et al. 2011) and the final co-added science imaging is made publicly available1 with two different spatial resolutions of 30 mas and 65 mas per pixel. In Fig. 1, we show the colour composite images of the eight clusters studied in this work, produced from the combination of optical and near IR filters by using the Trilogy code (Coe et al. 2012).
 |
Fig. 1. Colour composite images of the eight clusters in our sample created from the combination of the HST/ACS and WFC3 imaging. Circles show the multiple image positions used as model constraints in our strong lens modelling. We identify in white the families with spectroscopic redshift measurements and in green those for which the redshift value is a free parameter in our models (considered only in our silver sample, see Sect. 3 for more details). Blue boxes indicate the BCG positions. |
2.2. Spectroscopic data
Up to now, a total of 11 CLASH clusters have been observed by MUSE in different programmes. In previous works, we have used deep observations on three targets, MACS J1206, Abell 1063 and MACS J0416 (Caminha et al. 2016b, 2017a,b), where the last two clusters are also part of the HFF initiative. In this work, we made use of archival MUSE data from the ESO programme IDs 095.A-0525, 096.A-0105, 097.A-0909 and 098.A-0590 (P.I. J.-P. Kneib) on the remaining eight clusters. The observations were carried out during the period between 2015-June and 2017-January, with observation blocks (OBs) consisting of two exposures of ≈1465 s. The fields of view of RX J2129, MACS J2129 and MACS J0429 are composed of two pointings with overlapping areas of ≈0.29 arcmin2, ≈0.12 arcmin2 and zero arcmin2, respectively. The remaining five clusters were observed with one single pointing, of which MACS J1115 and RX J1347 observations are off-centred by ≈30″ from the corresponding brightest cluster galaxies (BCGs). Although having similar exposure times, the dither and rotation pattern of each OB is slightly different in each cluster.
Final exposure times on target of each pointing vary from shallow 0.8 h to 3.2 h and the overlapping regions in RX J2129 and MACS J2129 reach ≈5.6 h depth. The summary of MUSE observations is presented in Table 1 and the final fields of view in Figs. 2 and 3. For all exposures, a small dither pattern and 90° rotations with respect to the original position angle (PA) were applied. We note that for the clusters MACS J2129 and MACS J1931, although they include more than two exposures, only two different rotation angles were used, the original PA and PA + 90°. For the other clusters with more than two exposures, all four 90° rotations were applied. Because of that, in some final MUSE data-cubes the instrumental features were not optimally removed, in particular in the regions between single instrument IFUs.
 |
Fig. 2. Cluster member selection. White and magenta circles show the position of the cluster members with MUSE spectroscopic confirmation and selected from photometry, respectively. Red boxes show the cluster members spectroscopically confirmed by CLASH-VLT and thus included in the final member catalogue, but not selected by our criteria. The green regions show the area covered by the MUSE observations. |
 |
Fig. 3. Same as in Fig. 2 but for the silver sample of galaxy clusters. Red regions indicate MUSE exposures with less than one hour on target. We note that MACS J0429 is not a CLASH-VLT cluster. |
We followed the standard MUSE reduction procedure, similarly to our previous analyses of other clusters (Karman et al. 2015, 2017; Grillo et al. 2016; Caminha et al. 2017a,b). We used the MUSE pipeline version 2.4.1 (Weilbacher et al. 2014) to process all raw exposures. Each object exposure is corrected using BIAS and FLAT calibrations of the corresponding night, as well as ILLUMINATION exposures. Moreover, wavelength and flux calibration are applied in order to create the PIXELTABLEs and data-cubes of each exposure. We inspected the wavelength collapsed (white) images and the data-cubes of each exposure, finding no large variations between the observational conditions of most pointings. Two object exposures on RX J2129 presented technical problems and were not used in the final stacks (they are not included in the numbers presented in Table 1). For the same cluster, one exposure shows a bright satellite track across the field of view, which we mask out by removing the affected slices in order not to contaminate the final stack. After that, we combined the PIXELTABLEs into a final data-cube with the final depth and covering the entire field of view of each cluster (see Figs. 2 and 3). Since the standard reduction pipeline does not have an optimal sky subtraction, we applied the ZAP tool (version 2.1, Soto et al. 2016) to remove remaining sky residuals. To do that, we defined the sky regions using a combination of the MUSE white images and HST data. The MUSE data-cubes extend from 4750 Å to 9350 Å in wavelength, with an almost constant dispersion of ≈1.25 Å, and spatial sampling of 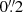 . The final seeing varies from
. The final seeing varies from 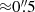 to
to 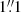 in the final stacked data-cubes (see Table 1). The final fields of view of all observations are shown in Figs. 2 and 3.
in the final stacked data-cubes (see Table 1). The final fields of view of all observations are shown in Figs. 2 and 3.
Since MUSE does not cover the entire HST field of view, we also used a small subset of redshifts from the ESO large programme CLASH-VLT (ID 186.A-0798, P.I.: Rosati) that has observed seven of the eight clusters analysed in this work, using VIMOS high-multiplexing capabilities (Le Fèvre et al. 2003). MACS J0429 is the only cluster in our sample not included in that programme. We refer to the spectroscopic campaign of MACS J0416 (Balestra et al. 2016) as an example of CLASH-VLT observations, which typically extend to approximately two virial radii. A full description of all observations and data processing of the 13 CLASH-VLT clusters will be presented in Rosati et al. (in prep.).
While VIMOS provides an efficient coverage of the entire cluster volume, over a field of view of ≈25′ across, the central ≈1 − 2′ is not adequately sampled with the standard multi-slit strategy due to the rapid increase of targets in the cluster cores (multiple images and cluster galaxies). To this respect, MUSE integral field spectroscopy represents an ideal complement to the VIMOS observations in the cluster cores. Finally, we also incorporated redshifts from the GLASS (Treu et al. 2015) survey that has observed RX J1347 and MACS J2129.
2.3. MUSE redshift measurements
Following our previous works, we identify and measure source redshifts in two different manners. Firstly, we use HST detections as a prior to extract spectra centred on these positions and with an aperture radius of 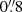 from the data-cubes. This aperture value is similar to the observational seeing of the observations and found to be a good compromise to reduce the contamination from nearby sources and maximise the signal to noise. In the case of some extended sources and objects with large lensing distortion and with low surface brightness, for which we could not estimate a secure redshift with the previously mentioned apertures, we use a customised extraction that takes into account the extent of the emission observed in the MUSE data. Secondly, a continuum subtracted data-cube is created by subtracting a median kernel (with 151 spectral pixel width) in the wavelength axis from each spaxel. The result is a data-cube where continuum emission is removed and emission lines are more easily identified. We visually inspect these continuum subtracted data-cubes in order to identify emission lines from sources with no HST continuum detection and to disentangle emission from nearby sources in projection.
from the data-cubes. This aperture value is similar to the observational seeing of the observations and found to be a good compromise to reduce the contamination from nearby sources and maximise the signal to noise. In the case of some extended sources and objects with large lensing distortion and with low surface brightness, for which we could not estimate a secure redshift with the previously mentioned apertures, we use a customised extraction that takes into account the extent of the emission observed in the MUSE data. Secondly, a continuum subtracted data-cube is created by subtracting a median kernel (with 151 spectral pixel width) in the wavelength axis from each spaxel. The result is a data-cube where continuum emission is removed and emission lines are more easily identified. We visually inspect these continuum subtracted data-cubes in order to identify emission lines from sources with no HST continuum detection and to disentangle emission from nearby sources in projection.
To measure redshifts, we used the one-dimension (spatially averaged) and pseudo two-dimension (in two perpendicular directions) spectra. Similarly to our previous works (see e.g., Caminha et al. 2017a,b), we analysed the data in order to identify spectral features to measure redshifts, such as emission or absorptions lines. In the cases of sources with continuum emission but no evident features, we used a template matching to help with the identification of faint spectral features. To each redshift, we attributed a quality flag that is related to the reliability of the measurement. The quality flag system has four different categories: QF = 1, the measurement is not reliable; QF = 2, the redshift value is based on a faint, but clearly detected, feature and is likely to be correct; QF = 3, secure measurement from more than one absorption and/or emission lines; QF = 9, redshift based on a single narrow emission. Cases of objects having a single emission line with clear features that allow us to identify its nature (for instance the Lyman-α profile or O II doublet) are considered to have secure (QF = 3) redshift measurements. The full sample of all fields presented in this work contains ≈900 secure (i.e., QF > 1) redshift measurements, of which 114 are stars, 62 are foreground galaxies, 390 are cluster members and 395 are background galaxies. Regarding high redshift sources with z > 2.9, where the Lyman-α line falls within the MUSE wavelength range, the number of unique detections (i.e. accounting for the lensing multiplicity) is 116. The first entries of the full catalogue are presented in Table 2 and the entire catalogue is available in the electronic version of the paper.
Full redshift catalogue.
3. Strong lensing models
To perform the strong lensing modelling, we adopted the same methodology applied in our previous studies of the galaxy clusters Abell 1063, MACS J0416 and MACS J1206. In this work we use the software lenstool (Kneib et al. 1996; Jullo et al. 2007). We adopted parametric models to describe the different components of the total mass distribution of each cluster. Moreover, the multiple image positions of the lensed sources were used as constraints to estimate the best-fitting values of the model parameters. In the next subsections, we provide a short description of our methodology and refer to Caminha et al. (2016b, 2017a,b) for more details.
3.1. Overall description
For the smooth mass components (i.e., dark matter, intracluster light and hot gas), we used a pseudo-isothermal elliptical mass distribution (PIEMD, Kassiola & Kovner 1993), that has been shown to describe well such component in previous studies (e.g. Grillo et al. 2015; Caminha et al. 2017b). A PIEMD profile is characterised by a total of six parameters: the central velocity dispersion (σv) and core radius (rcore); the orientation angle (θ) and ellipticity (ε); and the position of the centre (x, y). The ellipticity is given by ε ≡ 1 − b/a, where a and b are the major and minor axis, respectively. The orientation angle θ is defined to be zero in the east-west direction and increases counterclockwise.
In order to test possible systematic effects related to the adopted cluster mass parametrization, we also used a generalised NFW profile (gNFW, Zhao 1996; Jing & Suto 2000; Wyithe et al. 2001) for the cluster smooth mass component. This model has the value of the central 3-dimensional slope γgNFW, besides those of the concentration c and scale radius rs, as free parameters. In this model, the total number of free parameters is seven (including the position of the centre and the values of ellipticity and orientation angle). A value of γgNFW equal to one translates into the standard NFW model. We remark that this model has a pseudo-elliptical implementation in the lenstool software, in which the ellipticity is introduced in the projected lens potential and not in the projected mass density profile. This approximation enables a faster solution of the ray-tracing equation. However, for high values of ellipticity (ε ≳ 0.5) it is known to create nonphysical dumbbell shaped projected mass density distributions (Golse & Kneib 2002; Dúmet-Montoya et al. 2012). We remark here that we used this profile only to compare with our reference PIEMD parametrization.
For the total mass profiles of the galaxy members, we adopted the dual pseudoisothermal mass distribution (dPIE, Elíasdóttir et al. 2007; Suyu & Halkola 2010) with zero ellipticity and core radius. Moreover, the centres of the profiles were fixed to the centroids of the light distribution of the selected galaxy members (see Sect. 3.2). Therefore, each galaxy member has two free parameters, its central velocity dispersion (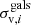 ) and truncation radius (
) and truncation radius (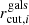 ). Since the total number of observables does not allow us to have two free parameters for each galaxy member, in our models we assumed a constant total mass-to-light ratio with the following scaling relations:
). Since the total number of observables does not allow us to have two free parameters for each galaxy member, in our models we assumed a constant total mass-to-light ratio with the following scaling relations:
where Li is the value of the luminosity of each member in the HST filter F160W and Lref is the reference luminosity. Hence, all galaxy members are described by the two parameters 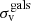 and
and 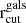 . We choose as reference luminosity the value corresponding to the rest-frame magnitude of MF160W = −23 in each cluster, which is close to L* for cluster galaxies at z = 0.4 (see e.g. Connor et al. 2017; Bergamini et al. 2019). This choice does not affect the lens modelling and the values of the normalization parameters (i.e.
. We choose as reference luminosity the value corresponding to the rest-frame magnitude of MF160W = −23 in each cluster, which is close to L* for cluster galaxies at z = 0.4 (see e.g. Connor et al. 2017; Bergamini et al. 2019). This choice does not affect the lens modelling and the values of the normalization parameters (i.e. 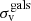 and
and 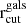 ) can be rescaled to any other reference luminosity by using Eq. (1).
) can be rescaled to any other reference luminosity by using Eq. (1).
By starting from the observed positions of the multiple images, we used the software lenstool to obtain the best-fitting values of the free parameters of each model. The software uses a χ2 function defined as
where 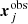 and
and 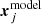 are the observed and model predicted positions of multiple images, respectively. The positional errors are given by
are the observed and model predicted positions of multiple images, respectively. The positional errors are given by 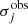 and Π is the vector containing the values of all model free parameters. We used flat priors for all model free parameters (Π) in every model. The set of parameter values that minimises the χ2 function (
and Π is the vector containing the values of all model free parameters. We used flat priors for all model free parameters (Π) in every model. The set of parameter values that minimises the χ2 function (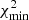 ) is called the best fit solution. In addition to the
) is called the best fit solution. In addition to the 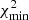 value, we also used the root-mean-square difference between the model predicted and observed positions (Δrms) of the multiple images to quantify the goodness of the fit of each model.
value, we also used the root-mean-square difference between the model predicted and observed positions (Δrms) of the multiple images to quantify the goodness of the fit of each model.
Given the different characteristics of the galaxy clusters in our sample, we explored a range of different models for each of them, from simple unimodal mass distributions to combinations of many different components in order to find the best fit solution. First, we minimised the χ2 function for a single smooth mass component plus the galaxy members. However, it is known that that in merging clusters, such as MACS J0416 (Caminha et al. 2017a), Abell 2744 (Mahler et al. 2018) and Abell 370 (Lagattuta et al. 2017), multiple smooth mass components are necessary to reproduce well the positions of all multiple images. Therefore, we also optimised models with one and two extra smooth mass components, as well as models with an external shear component. Since the BCG of a cluster undergoes formation and evolution processes that are different from those of the other galaxy members, we also tested models where the BCG parameters are free to vary and are not attached to those of the overall scaling relations described by Eq. (1). We present the results of our lensing analyses in Sect. 4.
3.2. Membership selection
The cluster member selection is strongly based on our redshift measurements from MUSE in the very central regions and complemented with the CLASH-VLT spectroscopy and CLASH photometry in the outer regions. For the photometric measurements, we used the CLASH public catalogues (Postman et al. 2012; Molino et al. 2017). Firstly, we selected all sources from the MUSE spectroscopic catalogue located within ±4000 km s−1 from the cluster redshift (see Table 3, column 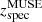 ). In Fig. 4, we show the colour-magnitude diagrams for the HST filters F814W−F160W (except for RX J2129 that has a low redshift value and for which we used F435W−F814W), where the cluster red sequences are well defined. In order to select members with no spectroscopic confirmation (mainly outside the MUSE field of view), we used two criteria based on the empiric distribution of colours and photometric redshifts of confirmed members. For the first criterion, we computed standard deviation of the colours in the aforementioned filters for each cluster, see the grey region in Fig. 4. The differences in the colour intervals observed in our cluster sample depend on the cluster redshift, the different regions covered by the MUSE pointings and cluster-to-cluster variance in the galaxy population in these small regions. Moreover, the number of late-type galaxies is different in each cluster. Specifically, RX J2129, MACS J1931, MACS J2129, MACS J0429 and MACS J1311 have around 7%−10% of late-type galaxies in the sample of spectroscopically confirmed members, whereas the other clusters have around 3%.
). In Fig. 4, we show the colour-magnitude diagrams for the HST filters F814W−F160W (except for RX J2129 that has a low redshift value and for which we used F435W−F814W), where the cluster red sequences are well defined. In order to select members with no spectroscopic confirmation (mainly outside the MUSE field of view), we used two criteria based on the empiric distribution of colours and photometric redshifts of confirmed members. For the first criterion, we computed standard deviation of the colours in the aforementioned filters for each cluster, see the grey region in Fig. 4. The differences in the colour intervals observed in our cluster sample depend on the cluster redshift, the different regions covered by the MUSE pointings and cluster-to-cluster variance in the galaxy population in these small regions. Moreover, the number of late-type galaxies is different in each cluster. Specifically, RX J2129, MACS J1931, MACS J2129, MACS J0429 and MACS J1311 have around 7%−10% of late-type galaxies in the sample of spectroscopically confirmed members, whereas the other clusters have around 3%.
Summary of cluster member selection with F160W photometry.
 |
Fig. 4. Colour-magnitude diagrams showing the red-sequence for all clusters analysed in this work. Only for RX J2129 we use the filters F435W and F814W because of its low redshift, for all remaining clusters we use the F814W and F160W bands. Orange circles indicate the spectroscopically confirmed members. The grey region shows our colour cut and the photometric redshift range used to select photometric members is quoted in the legend (see Sect. 3.2 for more details). Both criteria are used to select the photometric members that are indicated by magenta circles. A summary of the membership selection is shown in Table 3. |
For the second criterion, we used the photometric redshift distribution of spectroscopically confirmed members. Since such distributions are fairly asymmetric and present some outliers, we used the 68% confidence levels (after applying a sigma clipping) to define the lower and upper values of zphot for members with no spectroscopic confirmation. Therefore, we selected members with no MUSE measurements that are encompassed by both criteria (colour and zphot limits) and are brighter than magF160W = 24. We note that the distribution of photometrically selected galaxies in Fig. 4 closely follows the distribution of spectroscopic members, that is, the so called red-sequence. A summary of the membership is presented in Table 3, where we quote the number of spectroscopically confirmed members by MUSE and the total number of members in our final selection.
To estimate the contamination and completeness of this selection, we used the available CLASH-VLT measurements (besides MACS J0429 that was not included in this programme) in the regions outside the MUSE field of view. Such comparison yields important information about missing members and provide lower limits for the number of interlopers. In Table 3, we quote the number of photometric members wrongly identified and galaxies with CLASH-VLT redshifts that belong to the cluster (i.e. are within ±4000 km s−1 from the cluster redshift), but were not selected by our criteria. The completeness of our sample is relatively high, around ≈80%−90% thanks to the large number of spectroscopic confirmations of galaxy members. We remark that members with CLASH-VLT confirmation, but not selected with our photometric criteria, are included in the strong lensing models. Likewise, spectroscopic interlopers are removed from the final membership samples. While VIMOS incomplete spectroscopic coverage always leads to some possible membership contamination, MUSE integral field spectroscopy ensures highly pure samples of cluster galaxies in its field of view.
In Figs. 2 and 3, we show the selected galaxy members used in our strong lens models. We indicate the members with MUSE confirmation and galaxies selected using the colour – photo-z cuts (see Fig. 4). Members with spectroscopic confirmation from CLASH-VLT but not selected by our photometric criteria are also marked. We note that within the MUSE field of view only a very small fraction of members does not have spectroscopic confirmation. These galaxies are usually very faint or the contamination or confusion with nearby bright sources (caused by the atmospheric seeing) makes a secure spectroscopic confirmation difficult.
3.3. Multiple-image identification
In order to build reliable lensing models, we based our identification of multiple image families on spectroscopic confirmations. To identify multiple images of the same source, we selected entries in our MUSE and VIMOS (Rosati et al., in prep.) catalogues with similar redshifts (considering only measurements with QF greater than one) and inspected the HST images to verify if their positions, colours and parities are in agreement with what we expect from strong lensing theory. We note that some Lyman-α emitters have no clear detection in the CLASH photometry, but their line profile, position and, in some cases, their spatial morphologies ensure a secure identification of a multiple image family. In these cases, we used the centroid positions of the MUSE detections in the lens modelling. With this first set of spectroscopic constraints, we built a preliminary version of strong lensing models and compute the model predicted positions of all other sources with measured redshifts behind the clusters.
When a model predicts that a source is multiply imaged, we checked the HST images for possible photometric counterparts near the model predicted positions. In this step, we added to our set of multiple images only those with unambiguous photometric identification and with correct parity and colours. This allowed us to include multiple images that are outside the MUSE field of view or too faint (given the different lensing magnification of each multiple image) to be spectroscopically confirmed. The images selected in this way always belong to a family with measured redshift and are considered secure identifications. In Fig. 1, we show the positions of all multiple images used in our models and in Table A.2 we list their positions, MUSE redshifts and previous measurements from the literature, when present. Moreover, in Fig. A.1, we show the spectral features used to measure the multiple image redshifts from the MUSE spectra.
We were able to confirm all previously published redshift measurements of the multiple images within the MUSE field of views, except for family 11 behind MACS J2129. This system was confirmed at z = 6.85 by Huang et al. (2016) using HST grism and Keck/DEIMOS data. At this redshift, the Lyman-α line is outside the MUSE wavelength range, that extends out to 9350 Å, corresponding to a maximum limit of z ≈ 6.69 to detect this line. Moreover, for family 9 behind MACS J0329 (see also Zitrin et al. 2012), we make use of archival ESO/FORS2 data to support our MUSE measurement of z ≈ 6.1, using the Lyman-break detection, and assign to this redshift a QFMUSE = 2. The ESO/FORS2 observations were obtained under the ESO programme ID 096.A-0650 (P.I. Vanzella) and we used the reduction methodology described in Vanzella et al. (2011, 2014). The multiple images 9b, 9c, and 9d were observed with an exposure time of 11 hours each, totalling 33 hours on the same source. In Fig. 5, we show the stacked one-dimensional spectrum and the two-dimensional signal to noise ratio and sky emission. The spectrum shows a clear feature around 8720 Å that we associate to the break at 1215.7 Å rest-frame. This break is in very good agreement with the MUSE data (see Fig. A.1) and supports our measurement. In total, we present 27 new spectroscopic measurements of multiple image families and confirm other ten with previous redshift determinations.
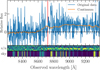 |
Fig. 5. Top panel: ESO/FORS2 stacked spectrum of the multiple images belonging to family 9 in MACS J0329 in arbitrary units, totaling 33 h of exposure time on target. The original data and continuum are shown in blue and orange, respectively. The vertical red line indicates the Lyman-break position around ≈8720 Å and the dashed horizontal line shows the zero level. Middle and bottom panels: two-dimensional signal-to-noise ratio of the data and the sky emission. |
We note that there are four clusters with a large number of spectroscopically confirmed families (Nspec > 5, namely RX J2129, MACS J1931, MACS J0329, and MACS J2129), and four with a smaller number of strong lensing constraints (MACS J1115, MACS J0429, RX J1347 and MACS J1311). For the second group, in order to have a larger number of observables to constrain the values of the free parameters of the models, we also included multiple image families without spectroscopic confirmation. To do that, we inspected previous identifications available in the literature (see e.g. Zitrin et al. 2015, and references therein) and again select multiple images based on their positions, colours and parities. For these families, we used the photometric redshift estimates from Molino et al. (2017) to build priors for the strong lensing models. We assumed flat priors for the redshift values, where the lower and upper limits were taken as the minimum and maximum of the 68% confidence levels of all images of each source (excluding the cases where there is clear contamination from bright nearby objects). In Table A.2, within brackets, we show the allowed redshift range of each family, that we used in the model optimization and sampling.
Because of this difference between the number of spectroscopic confirmations and the use of multiple image families selected from the photometric data only, we treated the two sample of clusters separately. We refer to the sample of clusters with good constraints as “gold” sample and explore a variety of parametrizations with increasing complexity. Conversely, the small number of multiple images of the second sample, called “silver”, did not allow us to test models with a large number of free parameters. Therefore, we considered only a unimodal smooth mass component, except for RX 1347 that has two very bright central galaxies and is known to be a merging system (see e.g. Schwarz et al. 1992; Allen et al. 2002; Ueda et al. 2018).
4. Strong lensing model results
As mentioned in Sect. 3.1, we used a bottom-to-top approach in order to find the mass model that better reproduces the positions of all multiple images. We first considered simple models with one smooth PIEMD mass component plus galaxy members. Since merging clusters or systems with high asymmetries in their mass distributions cannot reproduce the observed positions of all multiple images with only one smooth component (see e.g. Lagattuta et al. 2017; Caminha et al. 2017b), we gradually increased the complexity of our models by including additional smooth mass components and allowing values of the BCG parameters to vary independently from those of the other cluster members. These different models are tested for our gold sample of clusters, whereas in the silver sample we do not have enough constraints. Therefore, in these last four clusters we considered only simple models.
For each model, we computed the values of the best fitting Δrms and 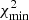 , considering a positional error
, considering a positional error 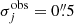 for all multiple images. We used this value of the positional errors to account for mass perturbers along the line of sight and limitations of parametric models. This is in agreement with some theoretical predictions (Host 2012) and estimates obtained from real data (Chirivì et al. 2018). In Table 5, we summarise all models we optimised in our sample and give the numbers of free parameters (Npar) and degrees of freedom (d.o.f. ≡ number of constraints–Npar). Moreover, we also show the values of the Bayesian information criterion (BIC, Schwarz 1978) and of the Akaike information criterion (AIC, Akaike 1974). These two quantities are particularly important to select the best model, balancing between the goodness of the fit and the number of free parameters. Therefore, the models with smaller BIC and AIC values were selected to be our reference models. We note that both BIC and AIC values select the same reference model for each cluster.
for all multiple images. We used this value of the positional errors to account for mass perturbers along the line of sight and limitations of parametric models. This is in agreement with some theoretical predictions (Host 2012) and estimates obtained from real data (Chirivì et al. 2018). In Table 5, we summarise all models we optimised in our sample and give the numbers of free parameters (Npar) and degrees of freedom (d.o.f. ≡ number of constraints–Npar). Moreover, we also show the values of the Bayesian information criterion (BIC, Schwarz 1978) and of the Akaike information criterion (AIC, Akaike 1974). These two quantities are particularly important to select the best model, balancing between the goodness of the fit and the number of free parameters. Therefore, the models with smaller BIC and AIC values were selected to be our reference models. We note that both BIC and AIC values select the same reference model for each cluster.
For the reference models (indicated in bold in Table 5), we have run lenstool also in the sampling mode to obtain the posterior distribution of each model parameter. Although the values of the 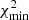 are already close to those of the number of d.o.f., we rescaled the values of
are already close to those of the number of d.o.f., we rescaled the values of 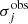 in order to have
in order to have 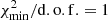 and obtain more realistic statistical uncertainties for the model parameters. For each model, ten different sets of Markov chain Monte Carlo (MCMC) are run until they reach a value of the so-called Gelman-Rubin test (Brooks & Gelman 1998) lower than 1.2 for all model parameters, thus indicating the convergence of the chains. We quote the median values and the 68%, 95% and 99.7% confidence level intervals of all model free parameters in Table A.1.
and obtain more realistic statistical uncertainties for the model parameters. For each model, ten different sets of Markov chain Monte Carlo (MCMC) are run until they reach a value of the so-called Gelman-Rubin test (Brooks & Gelman 1998) lower than 1.2 for all model parameters, thus indicating the convergence of the chains. We quote the median values and the 68%, 95% and 99.7% confidence level intervals of all model free parameters in Table A.1.
In addition to the best PIEMD models, we also sampled a model with a gNFW profile for the main smooth mass component, to quantify the dependence of the reconstructed total mass distribution on the specific choice of the smooth mass profile. We remark that the pseudo-elliptical implementation of the gNFW profile in lenstool might lead to unphysical projected mass density distributions (see Sect. 3.1). We used these models only for the sake of comparison with our reference models. In the following subsections, we briefly discuss the details of the strong lensing models of all eight clusters.
4.1. RX J2129
The multiple images of RX J2129 are located within ≈100 kpc from the cluster centre and out to zsrc = 3.43, the smallest redshift range for our gold lenses. The positions of the galaxy members and of the multiple images (see Figs. 2 and 1) suggest a fairly regular total mass distribution, although some asymmetry in the intracluster light (ICL) towards the south-west region can be noted.
The observed positions of all 22 multiple images are well reproduced, with 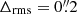 , by a single smooth mass component plus the galaxy members. The inclusion of extra smooth mass components reduces further the value of Δrms, but the increased values of the BIC and AIC do not justify these extra free parameters. RX J2129 is also the least massive cluster in our full sample, with MSL(< 200 kpc) ≈ 1.2 × 1014 M⊙. We note that in previous strong lensing analysis, presented in Zitrin et al. (2015), one multiple image belonging to family ID 2 was wrongly assigned. Multiple image 2a here (with zMUSE = 0.916, see Table A.2; their image ID 5.3) was wrongly assigned to a nearby foreground object, located ≈4″ from the correct one, and with zMUSE = 0.671.
, by a single smooth mass component plus the galaxy members. The inclusion of extra smooth mass components reduces further the value of Δrms, but the increased values of the BIC and AIC do not justify these extra free parameters. RX J2129 is also the least massive cluster in our full sample, with MSL(< 200 kpc) ≈ 1.2 × 1014 M⊙. We note that in previous strong lensing analysis, presented in Zitrin et al. (2015), one multiple image belonging to family ID 2 was wrongly assigned. Multiple image 2a here (with zMUSE = 0.916, see Table A.2; their image ID 5.3) was wrongly assigned to a nearby foreground object, located ≈4″ from the correct one, and with zMUSE = 0.671.
4.2. MACS J1931
MACS J1931 shows a strong BCG activity and an indication of a current infalling process of some galaxy members. However, its multiple image positions and X-rays emission indicate a regular total mass distribution. Our strong lens model is composed of two smooth mass components in addition to the galaxy members. The first smooth component is located very close to the BCG centre and has a fairly low ellipticity value (ε ≈ 0.56, see Table A.1). A second smooth mass component with circular symmetry reduces significantly the best fitting Δrms and is favoured by the information criteria. This component is located relatively far (≈300 kpc) from the cluster centre, however its position is not well determined by the available strong lensing constraints alone.
We remark that in previous works on HFF clusters the addition of extra smooth mass components within 500 kpc from the cluster centre (Mahler et al. 2018, for Abell 2744) or an external shear component (Lagattuta et al. 2019, for Abell 370) was used in order to obtain better models and lower final multiple image Δrms. In the case of Abell 2744, a detection of possible extra smooth components was discussed in Jauzac et al. (2016), using weak lensing information. We argue that the reduced values of the BIC and AIC parameters obtained with the inclusion of a second mass component in the model of MACS J1931 might be an indication of the presence of an extra mass concentration. However, a detailed weak lensing study in the corresponding region is not possible with the data currently available.
4.3. MACS J0329
In this cluster, all multiple images are located around the south-east BCG (see Fig. 1), however the second bright galaxy located in the north-west indicates that the cluster is possibly undergoing a merging event. In order to reproduce well the positions of all multiple images, a second smooth mass component must be included around this galaxy (indicated as NW in the top-right panel of Fig. 1). This model improves significantly the final Δrms and is accepted by the BIC and AIC criteria. We note that no secure multiple image systems or photometrically selected candidates are present around the north-west BCG, making our strong lensing constraints weaker in that region. Although an elongated gravitational arc is visible near the north-west BCG, this is not multiply lensed and does not add constraints to our models.
The BIC and AIC information criteria do not show clear preference between the parametrizations with and without an external shear term (model IDs MACSJ0329-P2 and MACS J0329-P2-shear in Table 5). We note that despite the differences in the two parametrizations, the final total mass and density profiles are nearly identical, therefore the specific choice between these two models will not affect our conclusions in this work. Because of the lower values of the reduced χ2 and final Δrms, we select here as reference the model with the presence of an external shear term.
4.4. MACS J2129
MACS J2129 is the cluster with the largest set of multiple images (i.e. strong lensing constraints) in our sample. Although the spectroscopic data have qualities similar to those of other clusters in this work, its higher redshift (z ≈ 0.6) and total mass probably make it a more efficient gravitational lens. The most recent strong lensing model, presented in Monna et al. (2017), made use of eight multiple image families, for which six were spectroscopically confirmed by CLASH-VLT and GLASS. The five new confirmations of multiple image families presented in this work highlights the high efficiency of MUSE over previous surveys in the cores of galaxy clusters.
The best-fit model is composed of two smooth mass components, one centred near the BCG and the other located ≈38″ (≈250 kpc) south from the cluster centre. Interestingly, the position of this second smooth mass component lies close to a group of cluster members and an arclet (not multiply lensed) candidate.
In the gold sample, MACS J2129 is the cluster with the highest value of Δrms. Despite that, the reduced χ2 is 1.18, indicating a good fit. The relatively high value of Δrms (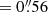 ) can be explained by the limitations of simple parametric models to reproduce an increasingly large number of multiple images. For instance, the cluster MACS J0416 is the cluster with the largest number of spectroscopically confirmed multiple images to date (Caminha et al. 2017a) and has the largest Δrms in the full sample of this work (see Table 5).
) can be explained by the limitations of simple parametric models to reproduce an increasingly large number of multiple images. For instance, the cluster MACS J0416 is the cluster with the largest number of spectroscopically confirmed multiple images to date (Caminha et al. 2017a) and has the largest Δrms in the full sample of this work (see Table 5).
4.5. MACS J1115
As discussed in Sect. 3.3, four clusters have a small number (< 5) of spectroscopic multiple image families. These clusters form our silver sample and MACS J1115 belongs to it. MUSE observations were carried out off-centred with respect to the BCG and located ≈40″ towards the north-west direction, see Fig. 3. In addition to the two spectroscopic families (one confirmed by MUSE and the other by CLASH-VLT), we included a family with three multiple images with secure identification from the HST data (see Fig. 1). The positions of all multiple images is recovered by one single smooth mass component with 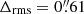 . The low number of constraints does not allow us to test more complex mass model.
. The low number of constraints does not allow us to test more complex mass model.
4.6. MACS J0429
To model MACS J0429, we used the constrains from three multiple image families, two of which have spectroscopic confirmation from MUSE. The third family shows an Einstein Cross configuration with four clear detections in the HST images. Three multiple images (IDs 3.b, 3.c and 3.d) have a relatively secure photometric redshift value in the range [1.64 − 1.79], whereas the fourth (ID 3.a) is strongly contaminated by the BCG. Our model with one smooth mass component can reproduce well the positions of all multiple images, with 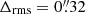 .
.
4.7. RX J1347
RX J1347 is a very massive cluster at zcluster = 0.451 with M200crit = (3.54 ± 0.51) × 1015 M⊙ from weak lensing only measurements (see Table 4), and shows two bright central galaxies. For the membership selection of this cluster we have also included five redshifts from Cohen & Kneib (2002) and two from Verdugo et al. (2012), in addition to the CLASH-VLT and GLASS measurements, in our spectroscopic sample. By using X-ray and Sunyaev–Zel’dovich observations, Ueda et al. (2018) argues that this cluster is likely to be undergoing the first passage of a major merging event and shows that the intra cluster medium has been perturbed by this event. In Ueda et al. (2018), the most recent strong lensing model of this cluster is presented, using the software GLAFIC (Oguri 2010). The authors consider a set of strong lensing constraints very similar to that in Zitrin et al. (2015). Moreover, they include a family containing six multiple images (family ID 3 of Ueda et al. 2018). This family has no spectroscopic confirmation and for some images the lensing effect is dominated by the mass distribution on the scale of galaxy members. Since the identification of some images cannot be considered secure due to significant differences between the model-predicted values of magnification and parity from the strong lensing model and those observable in the HST data, we decide not to include this family in our model. In addition, we removed multiple images with dubious photometric identification. As a result, we used 11 multiple images with photometric identification only (belonging to four families) in addition to the six multiple images with MUSE redshifts (three families) and one family (with three multiple images) with previous spectroscopy (Bradač et al. 2008; Halkola et al. 2008). We note that further deep and wide MUSE observations will become available in the near future and will likely provide a larger number of strong lensing constraints, that will clarify any apparent inconsistency in the models.
Strong lensing model general information.
As in the previous strong lensing models of this cluster, we have to consider two smooth mass components in order to reproduce the positions of all multiple images. Moreover, we show that an external shear component improves significantly the best fitting model with no penalty to the BIC and AIC factors. Although the final 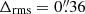 is relatively small, the low number of d.o.f. of this model suggests that the total mass distribution of this cluster might not be accurately described with the current data.
is relatively small, the low number of d.o.f. of this model suggests that the total mass distribution of this cluster might not be accurately described with the current data.
4.8. MACS J1311
MACS J1311 is the cluster with the smallest number of strong lensing constraints presented in this work, having spectroscopic confirmation for only one multiple image family. The other two photometrically selected families show two and three multiple images. Even in the simplest mass model composed of one smooth component plus galaxy members, the number of free parameters (eight for the mass distribution and two free redsfhits) is equal to the number of constraints. This strong lensing model has 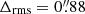 , the highest value in our sample.
, the highest value in our sample.
4.9. Cluster sample mass distribution
In Table 5, we see that three out of four of the gold clusters prefer a secondary smooth mass component and/or an external shear term. Particularly two clusters, MACS J1931 and MACS J2129, have secondary smooth mass components relatively far from their luminosity centres and with no obvious association to bright galaxy members. Although the inclusion of these extra components is supported by the information criteria, we cannot reconstruct their physical properties very accurately, given the strong lensing data presented here. Unfortunately, both clusters lack detailed and deep weak lensing analyses. In the case of MACS J2129, this is not possible due the presence of a strong galactic cirrus in the field of view, and MACS J1931 has the second smallest surface number density of back ground sources in the CLASH sample (see Table 3 in Umetsu et al. 2016). Therefore, possible detections of substructures using weak lensing, similarly to the work by Jauzac et al. (2016, 2018), is very difficult in these two clusters. We remark that in this work we focus on the inner total mass distribution of these clusters, that is, R < 200 kpc, where the contribution of these secondary mass components represents only a very small fraction of the total. Moreover, we notice that the information criteria favour always cluster mass models where the BCG profiles are scaled according to the relations valid for all other cluster members.
Models summary.
In addition to the intrinsic limitations of parametric models to represent complex mass distributions in some irregular or merging clusters, mass concentrations along the line-of-sight might introduce extra deflections to the light of background sources and these are not taken into account in our work. However, in Chirivì et al. (2018), the detailed study of the effect of these extra perturbers in MACS J0416 shows that, for a realistic case, the projected total mass density profile of the cluster is not significantly affected (see e.g. their Fig. 18). Another possible source of systematics in our modelling is some deviation of the adopted mass-to-light scaling relations of cluster members. This effect has been also recently addressed in Bergamini et al. (2019) by using robust stellar kinematics information of the cluster members. When comparing our previous lens models of MACS J1206, MACS J0416 and Abell 1063 to the new models using prior information from the member kinematics, the authors show that the differences in the total mass distribution is of the order of a few percent and within the statistical errors, in the region where the multiple images are observed. Therefore, although our modelling might be subject to some intrinsic systematics, their effect on the total mass profiles of the cluster sample should be very small.
In Figs. 6 and 7, we show the circularly averaged projected total mass (cumulative) and mass density profiles for each cluster for both the gold and silver samples. For the gold sample, we also show the gNFW models, in addition to the reference PIEMD ones. Remarkably, the different mass models provide very similar results in the regions where the multiple images are located. This indicates that, given our good sample of strong lensing constraints, the recovered total mass distribution is mildly sensitive to the specific parametrization of the smooth mass component. Moreover, we show for comparison the total mass distributions obtained by Zitrin et al. (2015) with the PIEMDeNFW and light-traces-mass (LTM) methods. The differences between the results obtained with these last two methods and those presented in this work might be ascribed primarily to the different sets of strong lensing constraints: Zitrin et al. (2015) only had very small number of spectroscopically confirmed multiple images available. The discrepancies between our and previous results are more evident in the very inner regions (i.e. at R < 30 kpc) and become less pronounced at large radii (i.e. at R > 250 kpc). Finally, the smaller number of strong lensing constraints of the silver sample (Fig. 7) yields larger statistical errors on the recovered total mass distribution. We were able to measure the total mass profiles of the clusters in this sample with a ≈2%−10% statistical uncertainties within 200 kpc from the cluster centres (see Table 4). However, these measurements of the silver sample are less precise and more likely to be biased than the ones of the gold clusters.
 |
Fig. 6. Top row: cumulative projected total mass profile out to R = 470 kpc from our reference lensing models using the PIEMD (blue) and gNFW (magenta) profiles for the main smooth mass component. Red and green regions show the models from Zitrin et al. (2015) with the two parametrizations NFW and LTM, respectively. Bottom row: same for the total surface mass density profile. The areas correspond to the 95% confidence level regions from 1000 random realizations of our models and 100 for the NFW and LTM models. Vertical lines indicate the distances from the BCG of the multiple images used to constraint the cluster total mass model in this work (black) and in Zitrin et al. (2015) (red, mainly with no spectroscopic measurements). The position of the centre used to compute the profiles in each realization is given by the centre of mass estimated within a circle of 10″ radius from the BCG. We remark that the external smooth components of MACS J1931 and MACS J2129 do not affect the total mass distributions over the radial distances considered here. |
 |
Fig. 7. Same as in Fig. 6, but for the silver sample, i.e. the four clusters with lower number of strong lensing constraints. |
In order to compare the total mass profiles of the clusters in our gold sample, we used the values of M200c and R200c from independent weak lensing measurements (Umetsu et al. 2018) to rescale our total mass and mass density profiles. We remark that weak lensing studies probe the outer regions of the clusters, with the innermost meaningful constraints typically located at R ≈ 300 kpc. In Fig. 8, we show the projected total mass and density profiles of clusters in our sample, after rescaling the mass and physical scale of clusters by these two quantities. We also include in this comparative analysis Abell 1063, MACS J1206 and MACS J0416 from Caminha et al. (2016b, Caminha et al. (2017a,b). Since the cluster MACS J2129 does not have weak lensing measurements, we use an empirical scaling relation between MSL(R < 200 kpc) and 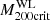 obtained using the other six clusters to rescale its mass profiles. All clusters have a relatively large number of strong lensing constraints in the region 10−2 ≲ R/R200c ≲ 10−1 and we find that the shape of the one dimensional averaged projected total mass and mass density profiles are remarkably similar. Even MACS J0416, which is a highly asymmetric merging cluster, does not deviate significantly from the overall homologous profiles. Within 10% and 20% of R200c, we measure a mean projected total mass value for our seven clusters of 0.13 and 0.32 × M200c, respectively, finding a remarkably small scatter of 5−6%. At these same radii, for the projected total mass density profiles, we find a mean value of 9.0 and
obtained using the other six clusters to rescale its mass profiles. All clusters have a relatively large number of strong lensing constraints in the region 10−2 ≲ R/R200c ≲ 10−1 and we find that the shape of the one dimensional averaged projected total mass and mass density profiles are remarkably similar. Even MACS J0416, which is a highly asymmetric merging cluster, does not deviate significantly from the overall homologous profiles. Within 10% and 20% of R200c, we measure a mean projected total mass value for our seven clusters of 0.13 and 0.32 × M200c, respectively, finding a remarkably small scatter of 5−6%. At these same radii, for the projected total mass density profiles, we find a mean value of 9.0 and 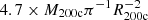 , with a slightly larger scatter of 7% and 9%. The observed trend is consistent with the predictions by Diemer & Kravtsov (2014), according to which dark-matter halos reveal a self-similar behaviour in their inner (or outer) structure when their mass profiles are expressed in units of spherical overdensity radii defined with respect to the critical (or mean) density of the Universe, especially R200c (or R200m, see also Umetsu & Diemer 2017). Since the cluster total mass profiles reconstructed with a gNFW or a PIEMD main mass component are very similar (see Fig. 6), we conclude that the observed self-similarity does not depend on the specific modelling details.
, with a slightly larger scatter of 7% and 9%. The observed trend is consistent with the predictions by Diemer & Kravtsov (2014), according to which dark-matter halos reveal a self-similar behaviour in their inner (or outer) structure when their mass profiles are expressed in units of spherical overdensity radii defined with respect to the critical (or mean) density of the Universe, especially R200c (or R200m, see also Umetsu & Diemer 2017). Since the cluster total mass profiles reconstructed with a gNFW or a PIEMD main mass component are very similar (see Fig. 6), we conclude that the observed self-similarity does not depend on the specific modelling details.
 |
Fig. 8. Projected total mass (cumulative, left panel) and mass density (right panel) profiles rescaled by the quantities M200c and R200c from independent weak lensing measurements. In addition to the four galaxy clusters with the best strong lensing models presented in this work (i.e., the gold sample), we also show the profiles of MACS J1206, Abell 1063 and MACS J0416, the last one is known to be a prominent merging cluster. The vertical lines indicate the distances from the cluster centers of the multiple images belonging to the spectroscopically confirmed families. |
5. Conclusions
In this work, we have performed a detailed strong lensing analysis of eight CLASH galaxy clusters, making use of extensive spectroscopic information from MUSE and complemented with CLASH-VLT. Our cluster sample spans a range of masses of ![$ M_{\mathrm{200c}}^{\mathrm{WL}} = [5{-}35] \times 10^{14}\,{M_{\odot}} $](/articles/aa/full_html/2019/12/aa35454-19/aa35454-19-eq45.gif) (from weak lensing measurements, Merten et al. 2015; Umetsu et al. 2018) and redshifts zcluster = 0.23 − 0.59. We used primarily MUSE spectroscopy to build a bona-fide set of strong lensing constraints (i.e. multiple image families), and to have a clean selection of galaxy cluster members. Four lens clusters in our sample have spectroscopic confirmation of more than five multiple image families, defining our gold sample, whereas the other four clusters have a limited number of constraints (see Table 4). For the gold sample, we investigated different mass models with increased complexity and use the BIC and AIK information criteria in order to select our reference models. Given the small number of strong lensing constraints for the silver sample, we used there only simple models to describe the cluster total mass distributions. Although we can constrain the total mass profiles of these clusters with ≈2%−10% statistical errors, these last lens models are less precise and more likely to be biased. Therefore, our conclusions on the total mass distributions of the clusters studied in this work are focused only on the gold sample. The main results can be summarised as follows:
(from weak lensing measurements, Merten et al. 2015; Umetsu et al. 2018) and redshifts zcluster = 0.23 − 0.59. We used primarily MUSE spectroscopy to build a bona-fide set of strong lensing constraints (i.e. multiple image families), and to have a clean selection of galaxy cluster members. Four lens clusters in our sample have spectroscopic confirmation of more than five multiple image families, defining our gold sample, whereas the other four clusters have a limited number of constraints (see Table 4). For the gold sample, we investigated different mass models with increased complexity and use the BIC and AIK information criteria in order to select our reference models. Given the small number of strong lensing constraints for the silver sample, we used there only simple models to describe the cluster total mass distributions. Although we can constrain the total mass profiles of these clusters with ≈2%−10% statistical errors, these last lens models are less precise and more likely to be biased. Therefore, our conclusions on the total mass distributions of the clusters studied in this work are focused only on the gold sample. The main results can be summarised as follows:
-
We built strong lensing models with a bottom-to-top approach, where we have first considered simple unimodal parametrizations and have gradually increased their complexity. In order to choose the reference models with PIEMD profiles for the smooth components, we used the BIC and AIK criteria to balance the goodness of a fit and the number of free parameters of a model. In our gold sample, the models can reproduce well the positions of all multiple images, with values of Δrms in the range of
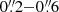 .
. -
When testing a pseudo-elliptical gNFW profile for the main smooth mass components, we found that the overall shapes of the reconstructed total mass and mass density profiles are similar to those obtained with a PIEMD profile. This indicates that, with a sufficiently large number of strong lensing constraints, modelling details do not affect the general conclusions on the cluster total mass distributions, supporting the robustness of our results.
-
When comparing our cluster total mass profiles with those obtained in previous strong lensing analyses, we found some differences in the very inner regions (R < 30 kpc). This might be explained by the smaller sets of strong lensing constraints used in the past, based on a very limited number of spectroscopically confirmed multiple images.
-
Three out of four clusters in our gold sample require a secondary smooth mass component and/or an external shear term. Although the strong lensing constraints cannot provide detailed information on these components, because they are located in the cluster external regions (R ≳ 200 kpc) where only a few multiple images are present, their inclusion in the models is favoured by the BIC and AIK criteria. Given their projected distances from the cluster centres, these components do not affect significantly the inner total mass distributions of the clusters in our sample.
-
In order to compare the total mass profiles of the different clusters in our gold sample and in some of our previous analyses, we rescaled them using independent weak lensing measurements. Remarkably, we found that all clusters have very similar one-dimensional projected total mass profiles with a small scatter of 5% at R = 0.1R200c, including MACS J0416 that is a clear merging cluster. This is a noteworthy observational confirmation of the self-similarity of cluster-size halos predicted by cosmological simulations.
The high-quality strong lensing modelling presented in this work adds up to the sample of clusters with accurate total mass measurements in their inner regions (i.e. R < 200 kpc) and constitutes an optimal sample to be compared to N-body and hydrodynamical simulations of clusters. Investigations of the separate dark matter and baryonic mass components (hot-gas and stars, see e.g., Annunziatella et al. 2017; Bonamigo et al. 2017, 2018) in a statistically significant sample of clusters might lead to interesting constraints on the physical nature of dark matter. Moreover, the MUSE data presented in this work and the magnification maps produced by our analyses increase the number of gravitational telescopes with accurate lens models that can be used to study the very faint galaxy population at high redshift.
Finally, we make publicly available all MUSE spectroscopic redshift measurements in electronic form at the CDS. The convergence, shear and magnification maps, as well as the lenstool configuration files of the strong lensing models, are also available online2 and at the CDS.
Acknowledgments
We thank the anonymous referee for the useful comments and suggestions that improved the manuscript. G.B.C, G.R. and K.I.C. acknowledge funding from the European Research Council through the award of the Consolidator Grant ID 681627-BUILDUP. C.G. acknowledges support by VILLUM FONDEN Young Investigator programme grant 10123. A.M. acknowledges funding from the INAF PRIN-SKA 2017 programme 1.05.01.88.04. K.U. acknowledges support from the Ministry of Science and Technology of Taiwan (grant MOST 106-2628-M-001-003-MY3) and from Academia Sinica (grant AS-IA-107-M01). R.D. gratefully acknowledges support from the Chilean Centro de Excelencia en Astrofísica y Tecnologías Afines (CATA) BASAL grant AFB-170002 This research made use of Astropy, (http://www.astropy.org) a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018). This work made use of the CHE cluster, managed and funded by ICRA/CBPF/MCTI, with financial support from FINEP (grant 01.07.0515.00 from CT-INFRA – 01/2006) and FAPERJ (grants E-26/171.206/2006 and E-26/110.516/2012). This work made use of data taken under the ESO programme IDs 186.A-0798, 095.A-0525, 096.A-0105, 096.A-0650, 097.A-0909 and 098.A-0590.
References
- Akaike, H. 1974, IEEE Trans. Autom. Control, 19, 716 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Allen, S. W., Schmidt, R. W., & Fabian, A. C. 2002, MNRAS, 335, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Annunziatella, M., Bonamigo, M., Grillo, C., et al. 2017, ApJ, 851, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Atek, H., Richard, J., Kneib, J.-P., et al. 2015, ApJ, 800, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Atek, H., Richard, J., Kneib, J.-P., & Schaerer, D. 2018, MNRAS, 479, 5184 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Vernet, J., Borisova, E., et al. 2014, The Messenger, 157, 13 [NASA ADS] [Google Scholar]
- Balestra, I., Mercurio, A., Sartoris, B., et al. 2016, ApJS, 224, 33 [Google Scholar]
- Belli, S., Jones, T., Ellis, R. S., & Richard, J. 2013, ApJ, 772, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Bergamini, P., Rosati, P., Mercurio, A., et al. 2019, A&A, 631, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonamigo, M., Grillo, C., Ettori, S., et al. 2017, ApJ, 842, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bonamigo, M., Grillo, C., Ettori, S., et al. 2018, ApJ, 864, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Bradley, L., Zitrin, A., et al. 2014, ApJ, 795, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 811, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R. J., Oesch, P. A., Illingworth, G. D., Ellis, R. S., & Stefanon, M. 2017, ApJ, 843, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Bradač, M., Schrabback, T., Erben, T., et al. 2008, ApJ, 681, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, S. P., & Gelman, A. 1998, J. Comput. Gr. Stat., 7, 434 [Google Scholar]
- Caminha, G. B., Karman, W., Rosati, P., et al. 2016a, A&A, 595, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2016b, A&A, 587, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2017a, A&A, 600, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caminha, G. B., Grillo, C., Rosati, P., et al. 2017b, A&A, 607, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chirivì, G., Suyu, S. H., Grillo, C., et al. 2018, A&A, 614, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coe, D., Umetsu, K., Zitrin, A., et al. 2012, ApJ, 757, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, D., Zitrin, A., Carrasco, M., et al. 2013, ApJ, 762, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, D., Salmon, B., Bradac, M., et al. 2019, ApJ, 884, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., & Kneib, J.-P. 2002, ApJ, 573, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Connor, T., Donahue, M., Kelson, D. D., et al. 2017, ApJ, 848, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Diemer, B., & Kravtsov, A. V. 2014, ApJ, 789, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dúmet-Montoya, H. S., Caminha, G. B., & Makler, M. 2012, A&A, 544, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elíasdóttir, A., Limousin, M., Richard, J., et al. 2007, ArXiv e-prints [arXiv:0710.5636] [Google Scholar]
- Gao, L., Navarro, J. F., Frenk, C. S., et al. 2012, MNRAS, 425, 2169 [NASA ADS] [CrossRef] [Google Scholar]
- Golse, G., & Kneib, J.-P. 2002, A&A, 390, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grillo, C., Suyu, S. H., Rosati, P., et al. 2015, ApJ, 800, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Grillo, C., Karman, W., Suyu, S. H., et al. 2016, ApJ, 822, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Halkola, A., Hildebrandt, H., Schrabback, T., et al. 2008, A&A, 481, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernán-Caballero, A., Pérez-González, P. G., Diego, J. M., et al. 2017, ApJ, 849, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Host, O. 2012, MNRAS, 420, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, K.-H., Lemaux, B. C., Schmidt, K. B., et al. 2016, ApJ, 823, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Jauzac, M., Eckert, D., Schwinn, J., et al. 2016, MNRAS, 463, 3876 [NASA ADS] [CrossRef] [Google Scholar]
- Jauzac, M., Eckert, D., Schaller, M., et al. 2018, MNRAS, 481, 2901 [NASA ADS] [CrossRef] [Google Scholar]
- Jauzac, M., Mahler, G., Edge, A. C., et al. 2019, MNRAS, 483, 3082 [NASA ADS] [CrossRef] [Google Scholar]
- Jing, Y. P., & Suto, Y. 2000, ApJ, 529, L69 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Johnson, T. L., & Sharon, K. 2016, ApJ, 832, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Jullo, E., Kneib, J.-P., Limousin, M., et al. 2007, New J. Phys., 9, 447 [Google Scholar]
- Karman, W., Caputi, K. I., Grillo, C., et al. 2015, A&A, 574, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karman, W., Caputi, K. I., Caminha, G. B., et al. 2017, A&A, 599, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kassiola, A., & Kovner, I. 1993, ApJ, 417, 450 [NASA ADS] [CrossRef] [Google Scholar]
- Kneib, J.-P., & Natarajan, P. 2011, A&ARv, 19, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Kneib, J.-P., Ellis, R. S., Smail, I., Couch, W. J., & Sharples, R. M. 1996, ApJ, 471, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Faber, S. M., Ferguson, H. C., et al. 2011, ApJS, 197, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Lagattuta, D. J., Richard, J., Clément, B., et al. 2017, MNRAS, 469, 3946 [Google Scholar]
- Lagattuta, D. J., Richard, J., Bauer, F. E., et al. 2019, MNRAS, 485, 3738 [NASA ADS] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, Proc. SPIE, 4841, 1670 [CrossRef] [Google Scholar]
- Lotz, J. M., Koekemoer, A., Coe, D., et al. 2017, ApJ, 837, 97 [Google Scholar]
- Mahler, G., Richard, J., Clément, B., et al. 2018, MNRAS, 473, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Martizzi, D., Teyssier, R., Moore, B., & Wentz, T. 2012, MNRAS, 422, 3081 [NASA ADS] [CrossRef] [Google Scholar]
- Merten, J., Meneghetti, M., Postman, M., et al. 2015, ApJ, 806, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Molino, A., Benítez, N., Ascaso, B., et al. 2017, MNRAS, 470, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Monna, A., Seitz, S., Balestra, I., et al. 2017, MNRAS, 466, 4094 [NASA ADS] [Google Scholar]
- Moore, B., Governato, F., Quinn, T., Stadel, J., & Lake, G. 1998, ApJ, 499, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Treu, T., Ellis, R. S., & Sand, D. J. 2013a, ApJ, 765, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Treu, T., Ellis, R. S., et al. 2013b, ApJ, 765, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M. 2010, PASJ, 62, 1017 [NASA ADS] [Google Scholar]
- Patrício, V., Richard, J., Verhamme, A., et al. 2016, MNRAS, 456, 4191 [NASA ADS] [CrossRef] [Google Scholar]
- Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Ravindranath, S., & Ho, L. C. 2002, ApJ, 577, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B. E., Ellis, R. S., Furlanetto, S. R., & Dunlop, J. S. 2015, ApJ, 802, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Salmon, B., Coe, D., Bradley, L., et al. 2017, ApJ, submitted [arXiv:1710.08930] [Google Scholar]
- Salmon, B., Coe, D., Bradley, L., et al. 2018, ApJ, 864, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Sand, D. J., Treu, T., Smith, G. P., & Ellis, R. S. 2004, ApJ, 604, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Schaller, M., Frenk, C. S., Bower, R. G., et al. 2015, MNRAS, 452, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [Google Scholar]
- Schwarz, R. A., Edge, A. C., Voges, W., et al. 1992, A&A, 256, L11 [NASA ADS] [Google Scholar]
- Smit, R., Swinbank, A. M., Massey, R., et al. 2017, MNRAS, 467, 3306 [NASA ADS] [Google Scholar]
- Soto, K. T., Lilly, S. J., Bacon, R., Richard, J., & Conseil, S. 2016, MNRAS, 458, 3210 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., & Halkola, A. 2010, A&A, 524, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Treu, T., Schmidt, K. B., Brammer, G. B., et al. 2015, ApJ, 812, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, S., Kitayama, T., Oguri, M., et al. 2018, ApJ, 866, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., & Diemer, B. 2017, ApJ, 836, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Zitrin, A., Gruen, D., et al. 2016, ApJ, 821, 116 [Google Scholar]
- Umetsu, K., Sereno, M., Tam, S.-I., et al. 2018, ApJ, 860, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Pentericci, L., Fontana, A., et al. 2011, ApJ, 730, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Fontana, A., Pentericci, L., et al. 2014, A&A, 569, A78 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Vanzella, E., Balestra, I., Gronke, M., et al. 2017a, MNRAS, 465, 3803 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Calura, F., Meneghetti, M., et al. 2017b, MNRAS, 467, 4304 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Calura, F., Meneghetti, M., et al. 2019, MNRAS, 483, 3618 [NASA ADS] [CrossRef] [Google Scholar]
- Verdugo, M., Lerchster, M., Böhringer, H., et al. 2012, MNRAS, 421, 1949 [NASA ADS] [CrossRef] [Google Scholar]
- Weilbacher, P. M., Streicher, O., Urrutia, T., et al. 2014, in Astronomical Data Analysis Software and Systems XXIII, eds. N. Manset, & P. Forshay, 485, 451 [NASA ADS] [Google Scholar]
- Wyithe, J. S. B., Turner, E. L., & Spergel, D. N. 2001, ApJ, 555, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Yue, B., Ferrara, A., Vanzella, E., & Salvaterra, R. 2014, MNRAS, 443, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, H. 1996, MNRAS, 278, 488 [Google Scholar]
- Zitrin, A., Moustakas, J., Bradley, L., et al. 2012, ApJ, 747, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Zheng, W., Broadhurst, T., et al. 2014, ApJ, 793, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Zitrin, A., Fabris, A., Merten, J., et al. 2015, ApJ, 801, 44 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Multiple images and reconstructed model parameters
Median values and confidence levels of the cluster total mass distribution parameters from the MCMC analyses of the reference strong lensing models (see Table 5).
Information on the spectroscopically identified multiple images.
 |
Fig. A.1. MUSE spectra of multiply lensed background sources. Vertical black lines indicate the positions of spectral features used to estimate the redshifts. The grey area shows the rescaled variance obtained from the data reduction pipeline; the flux is given in units of 10−20 erg s−1 cm−2 Å−1. The image boxes are extracted from the CLASH colour images and have 2″ side. The white circles show the HST counterparts and, for the cases with no apparent photometric counterparts, they are centred at the position of the MUSE peak emission. We remark that multiple image MACS J0329-9c has an independent redshift measurement from Vanzella et al. (in prep.). |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
All Tables
Median values and confidence levels of the cluster total mass distribution parameters from the MCMC analyses of the reference strong lensing models (see Table 5).
All Figures
 |
Fig. 1. Colour composite images of the eight clusters in our sample created from the combination of the HST/ACS and WFC3 imaging. Circles show the multiple image positions used as model constraints in our strong lens modelling. We identify in white the families with spectroscopic redshift measurements and in green those for which the redshift value is a free parameter in our models (considered only in our silver sample, see Sect. 3 for more details). Blue boxes indicate the BCG positions. |
| In the text | |
 |
Fig. 2. Cluster member selection. White and magenta circles show the position of the cluster members with MUSE spectroscopic confirmation and selected from photometry, respectively. Red boxes show the cluster members spectroscopically confirmed by CLASH-VLT and thus included in the final member catalogue, but not selected by our criteria. The green regions show the area covered by the MUSE observations. |
| In the text | |
 |
Fig. 3. Same as in Fig. 2 but for the silver sample of galaxy clusters. Red regions indicate MUSE exposures with less than one hour on target. We note that MACS J0429 is not a CLASH-VLT cluster. |
| In the text | |
 |
Fig. 4. Colour-magnitude diagrams showing the red-sequence for all clusters analysed in this work. Only for RX J2129 we use the filters F435W and F814W because of its low redshift, for all remaining clusters we use the F814W and F160W bands. Orange circles indicate the spectroscopically confirmed members. The grey region shows our colour cut and the photometric redshift range used to select photometric members is quoted in the legend (see Sect. 3.2 for more details). Both criteria are used to select the photometric members that are indicated by magenta circles. A summary of the membership selection is shown in Table 3. |
| In the text | |
 |
Fig. 5. Top panel: ESO/FORS2 stacked spectrum of the multiple images belonging to family 9 in MACS J0329 in arbitrary units, totaling 33 h of exposure time on target. The original data and continuum are shown in blue and orange, respectively. The vertical red line indicates the Lyman-break position around ≈8720 Å and the dashed horizontal line shows the zero level. Middle and bottom panels: two-dimensional signal-to-noise ratio of the data and the sky emission. |
| In the text | |
 |
Fig. 6. Top row: cumulative projected total mass profile out to R = 470 kpc from our reference lensing models using the PIEMD (blue) and gNFW (magenta) profiles for the main smooth mass component. Red and green regions show the models from Zitrin et al. (2015) with the two parametrizations NFW and LTM, respectively. Bottom row: same for the total surface mass density profile. The areas correspond to the 95% confidence level regions from 1000 random realizations of our models and 100 for the NFW and LTM models. Vertical lines indicate the distances from the BCG of the multiple images used to constraint the cluster total mass model in this work (black) and in Zitrin et al. (2015) (red, mainly with no spectroscopic measurements). The position of the centre used to compute the profiles in each realization is given by the centre of mass estimated within a circle of 10″ radius from the BCG. We remark that the external smooth components of MACS J1931 and MACS J2129 do not affect the total mass distributions over the radial distances considered here. |
| In the text | |
 |
Fig. 7. Same as in Fig. 6, but for the silver sample, i.e. the four clusters with lower number of strong lensing constraints. |
| In the text | |
 |
Fig. 8. Projected total mass (cumulative, left panel) and mass density (right panel) profiles rescaled by the quantities M200c and R200c from independent weak lensing measurements. In addition to the four galaxy clusters with the best strong lensing models presented in this work (i.e., the gold sample), we also show the profiles of MACS J1206, Abell 1063 and MACS J0416, the last one is known to be a prominent merging cluster. The vertical lines indicate the distances from the cluster centers of the multiple images belonging to the spectroscopically confirmed families. |
| In the text | |
 |
Fig. A.1. MUSE spectra of multiply lensed background sources. Vertical black lines indicate the positions of spectral features used to estimate the redshifts. The grey area shows the rescaled variance obtained from the data reduction pipeline; the flux is given in units of 10−20 erg s−1 cm−2 Å−1. The image boxes are extracted from the CLASH colour images and have 2″ side. The white circles show the HST counterparts and, for the cases with no apparent photometric counterparts, they are centred at the position of the MUSE peak emission. We remark that multiple image MACS J0329-9c has an independent redshift measurement from Vanzella et al. (in prep.). |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.