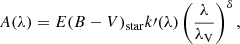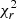| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935975 | |
| Published online | 05 November 2019 | |
Properties of LBGs with [OIII] detection at z ∼ 3.5
The importance of including nebular emission data in SED fitting
1
Shanghai Astronomical Observatory, CAS, Nandan Road 80, 200030 Shanghai, PR China
e-mail: yuanft@shao.ac.cn
2
Aix Marseille Université, CNRS, LAM (Laboratoire d’astrophysique de Marseille) UMR 7326, 13388 Marseille, France
3
Centro de Astronomía (CITEVA), Universidad de Antofagasta, Avenida Angamos 601, Antofagasta, Chile
Received:
28
May
2019
Accepted:
28
September
2019
Context. Nebular emission lines are critical to measure physical properties in the ionized gas (e.g., metallicity, the star formation rate, or dust attenuation). They also account for a significant fraction of broadband fluxes, in particular at the highest redshifts, and therefore can strongly affect the determination of other physical properties, such as the stellar mass, which are crucial in shaping our understanding of galaxy formation and evolution.
Aims. We investigate a sample of 51 Lyman break galaxies at 3.0 < zspec < 3.8 with detected [OIII] line emissions and estimated the physical properties of these galaxies to examine the impact of including nebular emission data in the Spectral energy distribution (SED) fitting.
Methods. We used the Code Investigating GALaxy Emission (CIGALE) to fit the rest-frame ultraviolet-to-near-infrared SEDs of these galaxies and their emission line data simultaneously. We ran CIGALE with and without the nebular model or the emission line data, and compare the results to show the importance of including the nebular emission line data in the SED fitting.
Results. We find that without the nebular model, the SED fitting overestimates the stellar mass due to the strong [OIII] lines that are redshifted to the Ks-band, which is consistent with previous results. The emission line data are necessary to constrain the nebular model in the SED fitting. We examine the Ks-band excess, which is mostly used to estimate the emissions of the [OIII]+Hβ lines when there is no spectral data, and we find that the estimation and observation are statistically consistent. However, the difference can reach up to more than 1 dex in some catastrophic cases, which shows the importance of obtaining spectroscopic measurements for these lines. We also estimate the equivalent width of the Hβ absorption and find it negligible compared to the Hβ emission.
Conclusions. Line emission is important to constrain the nebular models and to obtain reliable estimates of the physical properties of galaxies. These data should be taken into account in the SED fitting.
Key words: galaxies: evolution / galaxies: high-redshift
© ESO 2019
1. Introduction
The Lyman break technique is commonly used to select high redshift galaxies. It was first used extensively by Steidel et al. (1996) as the selection of U-band dropouts to detect galaxies at z ∼ 3. The galaxies selected with the Lyman break technique, that is, Lyman Break Galaxies (LBGs), are found to be star forming galaxies with relatively low dust attenuation. As shown by Madau & Dickinson (2014), these galaxies are important tracers for measuring the cosmic star formation rate (SFR) at z > 3.
However, deriving the physical properties of LBGs can be very uncertain. First of all, the lack of spectroscopic redshift can lead to difficulties when estimating galaxy properties because the photometric redshift degenerates with properties, such as SFRs, age, metallicity, and reddening in the SED fitting. Second, at higher redshifts, the contribution of the nebular emission lines to broadband fluxes becomes greater than typically observed at intermediate redshifts. Third, the dust attenuation at high redshift is not well understood. The attenuation law is uncertain for high redshift galaxies (Kriek & Conroy 2013; Buat et al. 2018), and the data (especially infrared (IR) data) are not sufficient to constrain the dust attenuation. Furthermore, there are degeneracies between different parameters. For example, the age, metallicity, and dust attenuation degenerate with each other.
In this work, we focus on the effect of the nebular emission on the spectral energy distribution (SED) fitting. Nebular emission is found to be quite common in LBGs; de Barros et al. (2014) show that about 65% of LBGs present detectable signs of emission lines. These LBGs are more actively star forming and play an important role in estimating the cosmic SFR density as compared to the other 35% of LBGs that have weak or no emission lines. However, the strong emission lines presented in these LBGs can contaminate the broadband photometry due to their larger equivalent width (EW). Stark et al. (2013) show that [OIII]5007, Hβ, and Hα contaminate K-band and Spitzer’s IRAC warm bands at 3.6 μm and 4.5 μm from redshift ∼3. Therefore, it is essential to constrain emission lines by spectroscopic observation.
Spectroscopic emission line data not only enable us to remove the contamination from broadband photometry, but also give additional constraints for properties such as SFR, stellar mass, and dust attenuation. Schaerer et al. (2013) suggest that observational emission line data may help constrain the star formation history (SFH). Buat et al. (2018) show that including Hα data in the fitting could provide constraints on the dust attenuation law.
Detecting emission lines at high redshift, however, is not trivial. It requires deep near infrared (NIR) spectroscopy with sufficient spectral resolution. When spectroscopic data are not available, emission lines are estimated from narrow band photometry or broadband SED fitting. A commonly used approach is to calculate the excess of the observed broadband fluxes relative to the SED modeled fluxes, assuming that the excess in K(Ks) or IRAC bands is due to the line emission redshifted to the band (e.g., Stark et al. 2013; Forrest et al. 2017; Malkan et al. 2017). This method provides a rough estimation for the emission lines, but its accuracy should be examined more carefully.
To examine the contamination from nebular emission lines and to constrain the properties of LBGs more accurately, we investigate a sample of LBGs with detected emission lines ([OII], [NeIII], Hβ, [OIII]4959,5007) at 3.0 < z < 3.8. We analyze the properties of these galaxies using an SED fitting method by considering the data from both the broadband photometry and emission line observations. We attempt to determine the effect of including nebular emission data in the SED fitting, and whether and to what degree the nebular emission data can help constrain the physical parameters.
We introduce the data used in this work in Sect. 2 and describe the SED fitting method in Sect. 3. In Sect. 4, we present the fitting results and discuss the impact of including emission line data in the SED fitting. We further discuss the properties of the LBGs in our sample and the constraints of the data on the SED models in Sect. 5. Finally, we conclude this work in Sect. 6.
2. Data
We aim to build a sample of LBGs that have both photometric and spectroscopic data. First, we collected a sample of LBGs with emission line data from the literature, including the following three works:
Schenker et al. (2013; hereafter S13) present the fluxes of Hβ and [OIII] lines for a sample of 20 galaxies at z ∼ 3.5 in the GOODS-North field. The NIR spectra were observed by Keck I MOSFIRE, and the fluxes were measured by fitting these lines with Gaussian profiles. For [OIII] doublet, only the total fluxes of [OIII]λ4959 and [OIII]λ5007 are presented.
Holden et al. (2016; hereafter H16) present the fluxes of Hβ, [OIII]λ4959, and [OIII]λ5007 lines for 24 star forming galaxies at z ∼ 3.2–3.7 in the GOODS-South field. Similar to S13, these spectra are observed by MOSFIRE on the Keck I telescope. The line fluxes are extracted by fitting the Gaussian-Hermite model to the observed maps.
Troncoso et al. (2014; hereafter T14) present the fluxes of [OIII]λ5007, Hβ, [OII]λ3727, and [NeIII]λ3869 lines for a sample of 34 galaxies. These galaxies were observed with the Assessing the Mass-Abundance redshift[Z] Evolution (AMAZE) and the Lyman-break galaxies Stellar population and Dynamics (LSD) projects (Maiolino et al. 2008; Mannucci et al. 2009). The line fluxes were measured by fitting a Gaussian profile to the lines. The continua of the lines were estimated by linear interpolation and then subtracted from the spectra.
From the above selection, we obtain 78 galaxies that have emission line data. We note that these galaxies are shown to have little or no sign of AGN activities, so we ignore the effect of AGN in this work.
We then collected the photometric data of these galaxies from public available multiwavelength catalogs, including the GOODS-MUSIC catalog (CDFS field; Grazian et al. 2006; Santini et al. 2009), the 3D-HST catalog (GOODS-S and GOODS-N field, Brammer et al. 2012; Skelton et al. 2014), and a catalog constructed by Magdis et al. (2010) (Table 1). In CDFS or GOODS-S field, a source may be found in both the GOODS-MUSIC catalog and the 3D-HST catalog. For such sources, we choose to use the measurements in the GOODS-MUSIC catalog, because it provides additional photometry for Spitzer’s MIPS 24 μm band. We also compared the measured fluxes at each photometric band given by these two catalogs and confirm that the values agree when their uncertainties are considered. Therefore, which catalog to use does not affect our conclusion.
Photometric data of sample.
We matched the photometric data to the line data using a radius of 5″. The closest match was used if there are multiple matches. We also compared the redshifts given by the photometric catalog, zphot, with those from the line catalog, zline. The matches with Δz/zline > 0.1 were removed from our sample, where Δz is the difference between zphot and zline. In total, there are 51 galaxies whose matches are found in the photometric catalogs.
The photometric bands used in this work are summarized in Table 1. These bands were selected to obtain a good sampling of the SED from the ultraviolet (UV) to the IR. The wavelength and response of these bands are shown in Fig. 1. To examine the contamination of optical emission lines, we plot in Fig. 1 the wavelength ranges of five main optical emission lines at redshift 3.0 < z < 3.8. It can be observed that, at this redshift range, the Ks-band is contaminated by [OIII]λλ4959, 5007 and Hβ lines. H-band is contaminated by [OII]λ3727 and [NeIII]λ3869 lines.
 |
Fig. 1. Response of each filter used in this work. The shaded regions show the observed wavelengths of optical emission lines at 3.0 < z < 3.8. The dotted line shows an example of the SED for a galaxy at z ∼ 3.5 in arbitrary scale. |
Since the sample and data are collected from different works and catalogs, the quality of the data needs to be carefully controlled. The remaining 51 galaxies are further classified into “Sample-A” and “Sample-B” to better describe the quality of the data. Sample-A galaxies must satisfy the following criteria: First, the galaxy must be detected in at least five bands at an signal-to-noise ratio (S/N) higher than 3; Secondly, the galaxy must be detected in at least one of the four IRAC bands at an S/N higher than 3; Finally, the galaxy must have at least one emission line detection that has an S/N > 3.
The galaxies not satisfying these criteria are classified into Sample-B. Galaxies in sample-A (26 galaxies) have better data quality than those in Sample-B (25 galaxies), and thus their properties should be better constrained by the SED fitting. Although galaxies in Sample-B have a poorer data quality than those in Sample-A, all these Sample-B galaxies are detected in at least three photometric bands. In both Sample-A and Sample-B, the upper limit data are included additionally. These upper limits are treated in the SED fitting using the method presented by Sawicki (2012) and Boquien et al. (2019) (see also Sect. 3).
3. Method
3.1. SED modeling with CIGALE
The SED fitting is performed with Code Investigating GALaxy Emission (CIGALE)1. Detailed descriptions of the code CIGALE can be found in Burgarella et al. (2005), Noll et al. (2009), and Boquien et al. (2019), as well as on the website. This code adopts the energy balance strategy which assumes that the energy absorbed by dust is re-emitted at IR wavelengths so that it can fit the star and dust emission simultaneously. For this study, we make use of a particular feature of CIGALE that it can fit the photometric data and the nebular emission data simultaneously.
We use the Salpeter (1955) initial mass function (IMF) and the stellar populations from Bruzual & Charlot (2003). The SFH is assumed to follow the delayed form: SFR ∝ t/τ2exp(−t/τ), where t is the age from the onset of star formation, and τ is the star formation time-scale. This functional form is more flexible and more physical than the simple exponentially increasing or decreasing SFH. It removes the discontinuity in SFR at t = 0 and can mimic an increasing SFR when τ is large (Hirashita et al. 2017; Carnall et al. 2019). More discussion of the SFH models is presented in Sect. 5.
We assume that the dust attenuation for the stellar part obeys the modified Calzetti Law (Noll et al. 2009), which modifies the original Calzetti attenuation curve (Calzetti et al. 2000; hereafter C00) by adding a UV bump and by adjusting the slope. In this work, we adopt the form of the attenuation law assuming there is no bump:
where k′(λ) is from C00, and δ indicates the modification to the slope. The input value of δ is taken as free, in the range of −0.6 to 0.4. We assume there is no bump because our broadband data are unable to constrain the bump. Further observation with better spectral resolution are required to provide a better constraint.
The nebular emission is modeled based on the templates of Inoue (2011) using the CLOUDY code. The input parameters include the metallicity, radiation strength U, the dust attenuation, and the escape fraction of the Lyman continuum photons, fesc. The metallicity is assumed to be the same as that of stars. The radiation strength U is fixed to logU = −2.5. The dust obscuration for the nebular emission is assumed to follow a simple screen model and a Milky Way extinction curve (Cardelli et al. 1989). Since our emission line data are at optical wavelengths, other “standard” extinction curves (e.g., LMC, SMC) produce similar extinction values (Fitzpatrick 1986; Calzetti 1997). The fesc is fixed to 0.2 (e.g., Stark et al. 2013). In our SED fitting, we estimate the model fluxes of the emission lines using a linear interpolated continuum obtained from the synthetic model spectrum in order to be consistent with what has been measured from the observations. CIGALE also allows to use the theoretical fluxes of the emission lines (given by CLOUDY) as the model fluxes. We find little difference between the results of these two methods.
The nebular emission and stellar emission are connected through fesc and febv. With the escape fraction fesc, there are (1 − fesc) of Lyman continuum photons to ionize the gas and power the nebular emission. The total number of Lyman continuum photons, which determines the absolute strength of both the continuous and line emission of nebula, is computed from the stellar SED (e.g., Schaerer & de Barros 2009; Castellano et al. 2014). The parameter febv is the ratio of the E(B − V)star to the E(B − V)gas. Although febv = 0.44 given by Calzetti (1997) is commonly adopted in the works on the nearby galaxies, many recent studies have found that this factor can vary up to 1 (e.g., Puglisi et al. 2016; Yuan et al. 2018; Buat et al. 2018). In this work, we take this parameter as free and find that the fitting is improved compared to that using a fixed value.
CIGALE is also able to fit the dust emission. However, the SED shape of dust emission is not constrained in this study because of the lack of rest-frame far-IR data. We model the dust emission using the templates from Dale et al. (2014) (without AGN component) with a single parameter α that represents the exponent of the distribution of the heating intensities over dust masses. We adopt the SED template with α = 2.0. The input values of the model parameters are listed in Table 2.
Parameters in SED fitting.
The output parameters are estimated through a Bayesian approach. For each model, the χ2 is calculated by comparing the model fluxes and the observed fluxes. Including the nebular emission data, the χ2 is thus the sum of 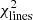 for emission lines and
for emission lines and 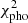 for photometric fluxes. For upper limits, the error function is used to calculate the χ2 (see Eq. (15) in Boquien et al. 2019). The probability distribution function (PDF) of each parameter is then calculated from the likelihood, which is proportional to exp(−χ2). The parameters and the corresponding uncertainties are thus estimated from the PDF by taking the likelihood-weighted mean and the standard deviation of all models.
for photometric fluxes. For upper limits, the error function is used to calculate the χ2 (see Eq. (15) in Boquien et al. 2019). The probability distribution function (PDF) of each parameter is then calculated from the likelihood, which is proportional to exp(−χ2). The parameters and the corresponding uncertainties are thus estimated from the PDF by taking the likelihood-weighted mean and the standard deviation of all models.
The global quality of the fit is estimated using a reduced χ2 of the best model (that is, the model with the smallest χ2), 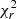 = χ2/(N − 1), where N is the number of input fluxes. In this fitting, only one galaxy has
= χ2/(N − 1), where N is the number of input fluxes. In this fitting, only one galaxy has 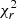 > 5.0. The galaxy has large measurement errors in the IRAC bands and an abnormal shape of SED (Fig. 2, right panel). It is probably mismatched between the IR bands and the optical bands in the photometric catalog. Therefore, we removed it from our sample. Figure 2 shows three examples of the SED fitting with different value of
> 5.0. The galaxy has large measurement errors in the IRAC bands and an abnormal shape of SED (Fig. 2, right panel). It is probably mismatched between the IR bands and the optical bands in the photometric catalog. Therefore, we removed it from our sample. Figure 2 shows three examples of the SED fitting with different value of 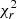 . For the fit with χ2 > 5, which was already removed from our sample, the best model deviates significantly from the observation.
. For the fit with χ2 > 5, which was already removed from our sample, the best model deviates significantly from the observation.
3.2. Reliability of the output parameters
We test the reliability of the parameters using the method developed by Giovannoli et al. (2011) and widely used among CIGALE users (e.g., Buat et al. 2012; Boquien et al. 2012; Yuan et al. 2018). The mock catalog is based on the fitting described in Sect. 3.1. The mock spectra of each galaxy are created from the best-fit model. The fluxes of the photometric bands are then generated by deviating the flux of the best-fit model in each band with a random error σ, which follows a Gaussian distribution with a standard deviation of the observed error in that band. On these simulated data, we run the SED fitting code and compare the “accurate” values known from the best-fit model and the values estimated by the code.
 |
Fig. 2. Examples of SED fit with |
Figure 3 shows the comparison result. Values of the linear Pearson correlation coefficient (r) are also indicated in the plots. We find very good correlations for M* and SFR with r > 0.9. The parameters febv, age, and metallicity Z are also well constrained (r > 0.8). The estimations of V-band attenuation AV and δ are less satisfying but still marginally constrained, with 0.7 < r < 0.8. The parameter τmain is not constrained at all, with r ∼ 0.
 |
Fig. 3. Results of SED fitting of the mock catalog. Each plot corresponds to an output parameter considered in this work. The model values are plotted on the x-axis, the results applying the SED fitting method to the mock data are plotted on the y-axis, and the standard error given by the Bayesian analysis is over-plotted as an error bar for each value. The linear Pearson correlation coefficient (r) is indicated above each plot. |
The Bayesian approach allows one to transparently test how well the data constrain certain parameters according to the shape of the resulting PDF. If a parameter is poorly constrained, we will obtain PDFs with large width which give large errors for the estimation (Salim et al. 2007). The potential dependency and degeneracy of the parameters can be examined using the 2D PDF for each object. We show in Fig. 4 an example of the 1D and 2D PDF of one mock galaxy with 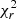 = 1.34, slightly above the average
= 1.34, slightly above the average 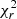 for our sample, which is ∼1.25. The figure shows that the model values are consistent with the estimated values considering the uncertainties. No severe degeneracy is found between these parameters. We also find that τmain is not constrained given the almost flat PDF, meaning that the probability for each value of τmain is the same. The estimated τmain thus depends on the input values. The 2D PDFs also show that although the parameters are estimated independently from each other, the global set of parameters (except the unconstrained ones) correspond to a self-consistent realization of the models, because the estimated parameters are all taken from models with high likelihood.
for our sample, which is ∼1.25. The figure shows that the model values are consistent with the estimated values considering the uncertainties. No severe degeneracy is found between these parameters. We also find that τmain is not constrained given the almost flat PDF, meaning that the probability for each value of τmain is the same. The estimated τmain thus depends on the input values. The 2D PDFs also show that although the parameters are estimated independently from each other, the global set of parameters (except the unconstrained ones) correspond to a self-consistent realization of the models, because the estimated parameters are all taken from models with high likelihood.
According to the above analysis which was also confirmed by that of the Bayesian error distribution Noll et al. (2009), we conclude that the reliable parameters are M*, SFR, Z, febv and age. In the following, we mainly use these parameters and also give some discussion about AV, and δ. We ignore τmain since it cannot be constrained.
 |
Fig. 4. PDF corner plot for a mock galaxy with χ2 = 1.34, showing the 1D and 2D marginalized posteriors for each parameters using our Bayesian approach. The blue lines represent the true values used to generate the mock photometry. For the 1D histogram, the red dashed lines show the estimated values and the shaded regions indicate 1σ uncertainties. For the 2D plot, the different contours correspond to 1, 2, 3σ. |
3.3. Fitting to the SEDs
First, we fit the SED using both the stellar and nebular models on both the photometric and line data. The models and input parameters for this fit have been described in Sect. 3.1, and we refer it as the “Withline” fit. In order to investigate the impact of the emission lines on the SED fitting, we additionally run two other fits, referred to as the “Noline” and “Nonebular” fits, respectively. In the Noline run, we use both the stellar and nebular models, which are exactly the same as in the Withline run, but only fit the photometric data. In the Nonebular run, we use only the stellar model, and fit for the photometric data. The three fits are summarized in Table 3. We discuss the influence of including nebular emission model and data in the fitting by comparing the results of these three runs.
Models and data used for the Withline, Noline and Nonebular runs of CIGALE carried out in this work.
4. Results
4.1. Impact of including line emission in SED fitting on the output parameters
Figure 5 compares the stellar masses derived from the Withline, Noline and Nonebular runs. We use the Withline run as a reference because this run included more data than the other two runs. Then we compare the other two runs to this reference run. First, compared with the Withline run, the Nonebular run overestimates the stellar mass by 0.22 dex, with a scatter of 0.21 dex. In the Noline run, with the nebular model included in the SED fitting, the consistency with the Withline run is improved: The average discrepancy is reduced to 0.11 dex, with a scatter of 0.14 dex. The difference between the Nonebular and Noline estimated stellar masses are 0.11 dex on average. This is consistent with the results of Grazian et al. (2015), who found that the stellar masses computed with and without the nebular contribution are less than 0.1–0.2 dex. For Sample-A and Sample-B, the conclusion seems quite similar, implying that the data quality affects insignificantly in estimating the stellar masses.
 |
Fig. 5. Left: comparison of stellar masses derived from Withline and Nonebular runs. Right: comparison of the stellar masses derived from the Withline and Noline runs. Orange dots are galaxies in Sample-A. Blue circles are galaxies in Sample-B. Sample-A has better data quality than Sample-B, as defined in Sect. 3.3. The dotted line is the 1:1 line. The dashed line shows the average difference between the two runs in each panel. |
We then compare the SFRs derived from the three runs (Fig. 6). The Nonebular run gives very similar SFRs compared with the Withline run. The average difference is only 0.01 dex, with a scatter of 0.22 dex. The average difference between the Noline run and Withline run is also small, about 0.02 dex, with a scatter of 0.18 dex. It seems that the SFRs derived from the SED fitting are not affected significantly by including either the nebular model or the emission line data. The possible reason is that since we do not have Hα data, the SFR derived from the SED fitting is heavily determined by UV fluxes, which has little contamination by emission lines. We also find that for Sample-A and Sample-B, the average difference between these runs is quite similar. The scatter of Sample-A is slightly smaller (by 0.04 dex) than Sample-B, for both the Withline-Nonebular and the Withline- Noline comparison.
 |
Fig. 6. Left: comparison of the SFRs derived from the Withline and Nonebular runs. Right: comparison of the SFRs derived from the Withline and Noline runs. Orange dots are galaxies in Sample-A. Blue circles are galaxies in Sample-B. Sample-A has better data quality than Sample-B, as defined in Sect. 3.3. The dotted line is the 1:1 line. The dashed line shows the average difference between the two runs in each panel. |
We also compare the metallicity Z, the dust attenuation AV, the age of the stellar population t, and δ derived from these three runs, as shown in Fig. 7. The Noline fit provides similar results compared with the Withline runs for these parameters. It slightly underestimates the metallicity and overestimates the age. The Nonebular run, however, obtains lower metallicity, lower dust attenuation, and older age compared with the Withline run, for both Sample-A and Sample-B galaxies. For the modification of the C00 slope δ, the three runs show little difference. It is not surprising because δ is not well constrained. As shown in Sect. 3.2, the correlation between the model values and the estimation of δ is only 0.77 for the Withline fit.
 |
Fig. 7. Top: comparison of the metallicity, dust attenuation, age, and δ derived from the Withline and Noline runs. Bottom: comparison of the metallicity, dust attenuation, age, and δ derived from the Withline and Nonebular runs. Orange dots are galaxies in Sample-A. Blue circles are galaxies in Sample-B. Sample-A has a better data quality than Sample-B, as defined in Sect. 3.3. The dotted line are the 1:1 line. |
The different outputs of these three runs can be explained by the effect of the Ks-band excess caused by the strong line emission. In the Nonebular run, without any consideration of the nebular emission, the Ks-band fluxes are fully attributed to the stellar emission, and therefore the fit overestimates the amount of old stellar populations. The older ages then leads to a redder slope of the unobscured stellar models and to lower AV derived from the fit. The result is consistent with what was found by de Barros et al. (2014) for galaxies with strong emission lines.
By adding the nebular model, the Noline run improves the results. However, due to the lack of constraints on the nebular models, the Noline fit still has some discrepancies with the Withline fit because in the Withline fit the emission line data provide additional constraints on the parameters.
4.2. Impact on the parameter uncertainties
As mentioned in Sect. 4.1, although the Withline and Noline fits output similar M*, SFR, and AV for our sample, the Withline fit has more constraints on the outputs since it includes more information provided by the line emission data. We find that the uncertainties of the parameters are reduced by including the emission line data. On average, the uncertainties are reduced by 0.05 dex, 0.06 dex, and 0.05 dex for M*, SFR, and AV, respectively. For some galaxies (∼30% of the sample), the reduction is larger than 0.1 dex. Figure 8 shows an example of the pdf of the output parameters. From the comparison of the pdf derived from the Withline and Noline fits, we can see clearly that the inclusion of the emission line data improves the constraints on these parameters.
 |
Fig. 8. PDFs of M*, SFR and AV for a galaxy in our sample. Top: PDFs estimated from the Noline fit. Bottom: PDFs estimated from the Withline fit. |
4.3. Improvement of the line flux estimation
Besides of the output parameters discussed in Sect. 4.1, we also find that without emission line data, the Noline fit cannot predict line fluxes consistent with the observation. Figure 9 shows the comparison of the line fluxes obtained by the Withline and Noline fit with the observation. The line fluxes obtained by the Withline fit are consistent with the observation, while those obtained by the Noline fit are not, implying the importance of including the emission line observation data in the fitting procedure.
 |
Fig. 9. Comparison of the observed and CIGALE modeled line fluxes. Circles show the fluxes obtained from the Withline run. Triangles show the fluxes obtained from the Noline run. |
4.4. Reliability of the line fluxes estimated from the Ks-band excess
Stark et al. (2013) found that the broadband flux excesses can be used to infer line strengths in carefully selected spectroscopic samples at higher redshifts where direct spectroscopic measurements of nebular line fluxes are not yet available. They examined the SEDs of a sample of nebular line emitters at 1.3 < z < 2.3 with spectroscopically measured [OIII] line fluxes from WFC3 grism observations of the Hubble Ultra Deep Field (UDF; Trump et al. 2011). By comparing the observed broadband flux (in the contaminated filter, J125 or H160) to the stellar continuum flux expected from the best-fitting population synthesis models, they characterized the strength of the emission lines and found that the results were consistent with those measured spectroscopically. Based on this method, the Ks-band excess is used to indicate the [OIII] fluxes for galaxies at z ∼ 3 (e.g., Forrest et al. 2017; Malkan et al. 2017). However, since the direct comparison of this estimation to the spectroscopic data made by Stark et al. (2013) is only for galaxies at z < 2.3, with the photometric and spectroscopic data of our galaxies, we further examine the reliability of this estimation for galaxies at higher redshifts (z ∼ 3.5).
Taking advantage of the spectroscopic data of our sample, we compare the Ks-band excess with the observed f([OIII]+Hβ) to test this method. We use only galaxies in Sample-A for this test because they have more data points to constrain the fluxes. The Ks-band excess is calculated by fK, obs − fK, mod, where fK, obs is the observed fluxes, and fK, mod is the model fluxes derived from the Nonebular fit. As described in Sect. 3, the Nonebular fit is a simple stellar population synthesis, which is consistent with the models that have been used in other works (e.g., Stark et al. 2013; Malkan et al. 2017). The excess of the observed flux to the continuum flux expected from the model in Ks-band is then interpreted as the [OIII]+Hβ line contamination. The results are shown in Fig. 10.
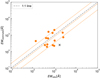 |
Fig. 10. Comparison of Ks-band excess and [OIII]+Hβ fluxes for Sample-A galaxies. The cross shows the catastrophic case. The three dotted lines indicate the mean and standard deviations of the ΔEW, where ΔEW = logEWobs − logEWmodel. |
Figure 10 shows that the EWs estimated from the Ks-band excess correlates well with the observations except for one catastrophic case (marked as the cross in the figure). We check the fitting results of this galaxy and find that the χ2 value is too small (∼0.2), meaning that the data for this galaxy have large uncertainties so that the fit cannot detect the excess due to the emission lines.
Excluding this case, we find that the mean EWmodel is 759 Å, and the mean EWobs is 908 Å. Both have large scatters (∼711 Å). We calculate the difference ΔEW between logEWobs and logEWmodel, and find that the mean ΔEW is −0.09 dex, with a standard deviation of 0.37 dex. The results confirm that the estimation of line fluxes from the Ks-band excess is statistically consistent with the observation. However, there are large uncertainties in the estimation for individual galaxies.
In the above analysis, we include the contaminated filters in the fitting process. We further examine the stellar models excluding the contaminated bandpass and find that the inferred line flux is typically two times greater than the spectroscopic measurement. This result agrees with what has been found by Stark et al. (2013). As explained by Stark et al. (2013), since the SEDs are quite poorly sampled in the wavelength range around the D4000 break, without the contaminated filter, the fitting process will take prior to fit the adjacent filters but underpredict the D4000 break and thus the continuum in the vicinity of the emission line of interest.
4.5. Balmer absorption
In the works of S13, T14, and H16, the fluxes of emission lines are calculated without considering the underline absorption of the stellar continuum. The continuum is subtracted simply using linear interpolation. However, for Balmer lines, such as Hβ, the absorption from stellar continuum can be strong, and thus the measured line fluxes can be quite different from the flux of the nebular model because the measurement is the sum of the absorption and the emission.
From the best model of the SED fitting, we can estimate the contribution of the stellar absorption to the measured line fluxes. From the best fitting model of each galaxy, we calculate the EW of the Hβ absorption, 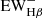 , from the stellar model. Then we calculate the EW of the Hβ emission,
, from the stellar model. Then we calculate the EW of the Hβ emission, 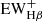 , from the nebular model. In both calculations, the continuum is estimated from the mean of 4 nm spectrum each on the blue and red side of the Hβ line from the best fitting model spectrum.
, from the nebular model. In both calculations, the continuum is estimated from the mean of 4 nm spectrum each on the blue and red side of the Hβ line from the best fitting model spectrum.
The mean 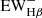 of our sample, ⟨
of our sample, ⟨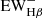 ⟩, is 4.4 Å for our sample in the observational frame, and ∼1 Å in the rest-frame. This result is smaller than the estimation given in Brinchmann et al. (2004), where the ⟨
⟩, is 4.4 Å for our sample in the observational frame, and ∼1 Å in the rest-frame. This result is smaller than the estimation given in Brinchmann et al. (2004), where the ⟨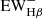 ⟩ is estimated as ∼3.3 Å (assuming ⟨
⟩ is estimated as ∼3.3 Å (assuming ⟨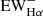 ⟩=0.6⟨
⟩=0.6⟨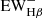 ⟩). The smaller
⟩). The smaller 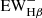 means that the stellar populations in these galaxies are so young that the absorption features produced by older stellar populations are not significant. The mean EW of the Hβ emission ⟨
means that the stellar populations in these galaxies are so young that the absorption features produced by older stellar populations are not significant. The mean EW of the Hβ emission ⟨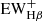 ⟩ is 236.3 Å in the observational frame, and 56.3 Å in the rest-frame. We also calculated the ratio of the absorption to the emission,
⟩ is 236.3 Å in the observational frame, and 56.3 Å in the rest-frame. We also calculated the ratio of the absorption to the emission, 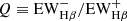 , and find that the average is about 0.04, indicating that the absorption from the stellar continuum is insignificant in the study of the line fluxes.
, and find that the average is about 0.04, indicating that the absorption from the stellar continuum is insignificant in the study of the line fluxes.
5. Discussion
5.1. Properties of LBGs with detected emission lines at z ∼ 3.5
The LBGs in our sample have detected emission lines, indicating that they are more actively star forming than LBGs with no or weak emission lines. To examine how representative our galaxies are for typical z ∼ 3.5 galaxies, we compare the average specific star formation rate (SSFR) of our galaxies with those derived from other studies, as shown in Fig. 11. We use the compilation from González et al. (2010) and de Barros et al. (2014), including the results from Noeske et al. (2007), Daddi et al. (2007), Reddy et al. (2012), and de Barros et al. (2014). Among them, de Barros et al. (2014) provide results from different models. The REF, Dec and RIS models assume constant SFH, exponentially declined SFH, and rising SFH, respectively. The “+NEB” model includes the nebular emission. The median mass of our galaxies is 109.7 M⊙, which is close to the results given by the REF model in de Barros et al. (2014).
 |
Fig. 11. Median SSFR as a function of redshift with a 68% confidence limit based on the whole PDF with comparison of results from different studies (Noeske et al. 2007; Daddi et al. 2007; Reddy et al. 2012) and results from the study of de Barros et al. (2014, DB14) for four different models. The dashed line shows the relation expected from Bouché et al. (2010) for an exponentially increasing star formation at a fixed stellar mass, 109.5 M⊙. |
We find that the median SSFR of our galaxy sample is higher than the median SSFRs estimated in Reddy et al. (2012) and de Barros et al. (2014) except for the RIS+NEB model. The higher median SSFR can be explained by the fact that the galaxies with emission lines are more actively forming stars than those with weak or no emission lines, as concluded by de Barros et al. (2014). However, the comparison is also dependent on the model used in the SED fitting. Compared to the result using a rising SFH (RIS+NEB) in de Barros et al. (2014), our galaxies have lower median SSFR. Moreover, both samples in the work of de Barros et al. (2014) and this work are incomplete. Due to the incompleteness, the results can be considered as a lower limit considering the trend of increasing SSFR with decreasing stellar mass (de Barros et al. 2014). A more detailed study on the SSFRs for galaxies at this redshift range requires a more statistically complete sample.
5.2. Composite SED
We further investigate the properties of our galaxies with the stacking method. We aim to compare the composite SED of our galaxies with the template SED given by Álvarez-Márquez et al. (2019), who selected more than 10 000 LBGs in the COSMOS field and obtained empirical UV-to-IR SED templates of LBG templates at z ∼ 3.5 by stacking the images at multiple wavelengths. For this comparison, we use galaxies with logM* > 9.75 (24 galaxies) because in Álvarez-Márquez et al. (2019), the mass range is from logM* > 9.75. We check the distribution of the stellar mass of these 24 galaxies and find that the shape of the distribution is similar to that in Álvarez-Márquez et al. (2019).
We adopt the same method described in Hirashita et al. (2017) to stack the SEDs of these galaxies. First, we redshift the SEDs of these galaxies into the same redshift (z = 3.5). Second, we normalize the SED of each galaxy to the flux at rest 0.2 μm (i.e., observed wavelength is 0.9 μm), in order to extract the information on the SED shape. Then we divide the data into 15 bins with a logarithmically equal width. We take the median values of the normalized data points in each bin to obtain the composite SED. Finally, the normalized flux is multiplied by the logarithmically averaged rest 0.2 μm (0.71 μJy) to obtain the absolute level of the flux. The composite SED is shown in Fig. 12.
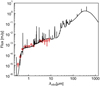 |
Fig. 12. SEDs of LBG galaxies shifted to z = 3.5 and normalized to the flux at rest 0.2 μm (0.9 μm in this figure). Red circles show the composite SED with the errorbars corresponding to the dispersion of the data. The normalization of the composite SED at 0.9 μm is 0.71 μJy. The line is the SED template given by Álvarez-Márquez et al. (2019). |
The template SED given by Álvarez-Márquez et al. (2019) is plotted in Fig. 12 for comparison (re-scaled to the same stellar mass as our composite SED). We find that the composite SED of our galaxies with [OIII] detections has a similar shape to galaxies in Álvarez-Márquez et al. (2019). However, we can see that our composite SED is slightly bluer, which may suggest that the galaxies with emission lines have a higher sSFR, or they are with less dust. Further investigation of the dust attenuation properties of these galaxies requires data from far-IR.
5.3. Constraints on the models
We examine whether the photometric and line data used in this work could put some constraints on different star formation and dust attenuation models. First, we compare four different SFH models, including the delayed SFH (used in the above sections), exponentially decreasing SFH, exponentially rising SFH, and the delay+burst SFH. The functional forms of these models are listed in Table 4. In these models, t is the stellar age from the onset of the star formation, and τ is the star formation time-scale. The delay+burst model is more complicated than the other three models. It allows for an second exponential burst representing the latest episode of star formation (Małek et al. 2018; Boquien et al. 2019). In the model, t0 and t1 are the time of the onset of the first and the second episodes of star formation, respectively, τ1 is the e-folding time of the burst, and k the relative amplitude of the burst component.
SFH models used for comparison.
The comparison shows that the four models result in similar χ2 values (see Table 4). Furthermore, we compare the Bayesian information criterion (BIC) which accounts for the increase of free parameters. We calculated the BIC values using a simplified form, BIC = χ2 + k × ln(n), where χ2 is the non-reduced of the best-fit model, k the number of free parameters, and n the number of data fit (Buat et al. 2018; Ciesla et al. 2018). The BIC values for these four different models are quite similar. For most galaxies (∼85%), the difference between BIC(delayed SFH) and BIC(rising or decreasing SFH) is smaller than 2, meaning that the evidence against the model with the higher BIC is not worth more than a bare mention. The difference between BIC(delay+burst) and BIC(delay) is higher than 2 for 80% of our galaxies, indicating positive evidence against the delay+burst model, which has two more free parameters than the other models. However, the difference is larger than 6 for only nine galaxies, i.e., the evidence is not strong for most galaxies in our sample. The BIC analysis for these models suggests that our data are not sufficient to discriminate these SFHs.
We also compare different attenuation curves. We compare the Calzetti Law and the modified Calzetti Law and find that the average 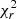 for the fit using the Calzetti law is 1.52, about ∼20% larger than that with the modified Calzetti law. Considering the different number of the input parameters, we compare the values of the BIC. The difference between BIC(Calzetti) and BIC(modified-Calzetti) is found higher than 6 (corresponding to a strong evidence against the model with the higher BIC) only for three galaxies (∼6% of the sample), meaning that the photometric and line data used in our work cannot discriminate these attenuation curves for most of our galaxies.
for the fit using the Calzetti law is 1.52, about ∼20% larger than that with the modified Calzetti law. Considering the different number of the input parameters, we compare the values of the BIC. The difference between BIC(Calzetti) and BIC(modified-Calzetti) is found higher than 6 (corresponding to a strong evidence against the model with the higher BIC) only for three galaxies (∼6% of the sample), meaning that the photometric and line data used in our work cannot discriminate these attenuation curves for most of our galaxies.
Providing additional data may improve the constraints on the models. First, it is essential to obtain Hα data for these galaxies. The [OIII] and [OII] data can provide some constraints on the nebular models, but they depend strongly on the metallicity, and therefore cannot entirely break the degeneracy between the metallicity and the dust attenuation. As shown in Buat et al. (2018), the Hα data have helped constrain the dust attenuation curves. With Hα and Hβ data, the derived Balmer decrement can add a strong constraint on the dust attenuation in the ISM. Second, restframe mid-to-far IR data can also help improve the constraints on the dust attenuation. We note that using different models does not affect our conclusion obtained in Sect. 4.
6. Summary and conclusion
We collected a sample of LBGs with emission line data at z ∼ 3.5. To investigate the impact of including emission line data in the SED fitting, we compare three different fits. The Withline fit uses the nebular and stellar population models on both the line and photometry data. The Noline fit uses the nebular and stellar population models, but only fit the photometry data. The Nonebular fit does not consider the nebular model. It fit the photometry data using the stellar population model only. By comparing the output of these fits, we conclude as follows:
The Nonebular fit overestimates the old stellar populations and thus overestimates the stellar masses because it does not take into account the contribution of the emission lines (such as [OIII] and Hβ) to the broadband fluxes. The Noline fit can give similar results of M*, SFR and AV compared to the Withline fit. However, in the Noline fit the uncertainties of these parameters are considerably larger than in the Withline fit. Also, without the emission line data, the Noline fit cannot predict the line fluxes reliably.
By comparing the line fluxes estimated from models to the observed line fluxes, we find that it is risky to predict line fluxes using photometric data alone. The method of the Ks-band excess is statistically right, but it may cause significant errors if used for individual galaxies. We also find that Balmer absorption plays an insignificant role in measuring the line fluxes, consistent with the fact that the stellar populations in these galaxies are not old enough to produce deep absorption features.
Our UV-to-NIR SED and the emission line data ([OII], [OIII], Hβ, etc.) together still cannot constrain dust attenuation law and SFH very well. The Hα emission line data provided by future observations (e.g., JWST) may help anchor dust attenuation and thus better constrain the properties of these galaxies.
Acknowledgments
We thank the anonymous referee for helpful and constructive comments that improve the paper. This work is partly supported by the National Natural Science Foundation of China (NSFC) under grant nos. 11433003, 11573050, and by a China-Chile joint grant from CASSACA. FTY acknowledges support from the Natural Science Foundation of Shanghai (Project Number: 17ZR1435900). MB acknowledges the FONDECYT regular grant 1170618. This work is based on observations taken by the 3D-HST Treasury Program (GO 12177 and 12328) with the NASA/ESA HST, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555.
References
- Álvarez-Márquez, J., Burgarella, D., Buat, V., Ilbert, O., & Pŕez-González, P. G. 2019, A&A, 630, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Buat, V., Boselli, A., et al. 2012, A&A, 539, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouché, N., Dekel, A., Genzel, R., et al. 2010, ApJ, 718, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., Franx, M., et al. 2012, ApJS, 200, 13 [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buat, V., Noll, S., Burgarella, D., et al. 2012, A&A, 545, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buat, V., Boquien, M., Małek, K., et al. 2018, A&A, 619, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgarella, D., Buat, V., & Iglesias-Páramo, J. 2005, MNRAS, 360, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 1997, in AIP Conf. Ser., ed. W. H. Waller, 408, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carnall, A. C., Leja, J., Johnson, B. D., et al. 2019, ApJ, 873, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Castellano, M., Sommariva, V., Fontana, A., et al. 2014, A&A, 566, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciesla, L., Elbaz, D., Schreiber, C., Daddi, E., & Wang, T. 2018, A&A, 615, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Helou, G., Magdis, G. E., et al. 2014, ApJ, 784, 83 [NASA ADS] [CrossRef] [Google Scholar]
- de Barros, S., Schaerer, D., & Stark, D. P. 2014, A&A, 563, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzpatrick, E. L. 1986, AJ, 92, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Forrest, B., Tran, K.-V. H., Broussard, A., et al. 2017, ApJ, 838, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannoli, E., Buat, V., Noll, S., Burgarella, D., & Magnelli, B. 2011, A&A, 525, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González, V., Labbé, I., Bouwens, R. J., et al. 2010, ApJ, 713, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Grazian, A., Fontana, A., de Santis, C., et al. 2006, A&A, 449, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grazian, A., Fontana, A., Santini, P., et al. 2015, A&A, 575, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirashita, H., Burgarella, D., & Bouwens, R. J. 2017, MNRAS, 472, 4587 [NASA ADS] [CrossRef] [Google Scholar]
- Holden, B. P., Oesch, P. A., González, V. G., et al. 2016, ApJ, 820, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K. 2011, MNRAS, 415, 2920 [NASA ADS] [CrossRef] [Google Scholar]
- Kriek, M., & Conroy, C. 2013, ApJ, 775, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Magdis, G. E., Rigopoulou, D., Huang, J. S., & Fazio, G. G. 2010, MNRAS, 401, 1521 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Małek, K., Buat, V., Roehlly, Y., et al. 2018, A&A, 620, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malkan, M. A., Cohen, D. P., Maruyama, M., et al. 2017, ApJ, 850, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., et al. 2009, MNRAS, 398, 1915 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [Google Scholar]
- Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puglisi, A., Rodighiero, G., Franceschini, A., et al. 2016, A&A, 586, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reddy, N. A., Pettini, M., Steidel, C. C., et al. 2012, ApJ, 754, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Santini, P., Fontana, A., Grazian, A., et al. 2009, A&A, 504, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sawicki, M. 2012, PASP, 124, 1208 [Google Scholar]
- Schaerer, D., & de Barros, S. 2009, A&A, 502, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., de Barros, S., & Sklias, P. 2013, A&A, 549, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schenker, M. A., Ellis, R. S., Konidaris, N. P., & Stark, D. P. 2013, ApJ, 777, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Skelton, R. E., Whitaker, K. E., Momcheva, I. G., et al. 2014, ApJS, 214, 24 [Google Scholar]
- Stark, D. P., Schenker, M. A., Ellis, R., et al. 2013, ApJ, 763, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Giavalisco, M., Pettini, M., Dickinson, M., & Adelberger, K. L. 1996, ApJ, 462, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Troncoso, P., Maiolino, R., Sommariva, V., et al. 2014, A&A, 563, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trump, J. R., Weiner, B. J., Scarlata, C., et al. 2011, ApJ, 743, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F.-T., Argudo-Fernández, M., Shen, S., et al. 2018, A&A, 613, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Models and data used for the Withline, Noline and Nonebular runs of CIGALE carried out in this work.
All Figures
 |
Fig. 1. Response of each filter used in this work. The shaded regions show the observed wavelengths of optical emission lines at 3.0 < z < 3.8. The dotted line shows an example of the SED for a galaxy at z ∼ 3.5 in arbitrary scale. |
| In the text | |
 |
Fig. 2. Examples of SED fit with |
| In the text | |
 |
Fig. 3. Results of SED fitting of the mock catalog. Each plot corresponds to an output parameter considered in this work. The model values are plotted on the x-axis, the results applying the SED fitting method to the mock data are plotted on the y-axis, and the standard error given by the Bayesian analysis is over-plotted as an error bar for each value. The linear Pearson correlation coefficient (r) is indicated above each plot. |
| In the text | |
 |
Fig. 4. PDF corner plot for a mock galaxy with χ2 = 1.34, showing the 1D and 2D marginalized posteriors for each parameters using our Bayesian approach. The blue lines represent the true values used to generate the mock photometry. For the 1D histogram, the red dashed lines show the estimated values and the shaded regions indicate 1σ uncertainties. For the 2D plot, the different contours correspond to 1, 2, 3σ. |
| In the text | |
 |
Fig. 5. Left: comparison of stellar masses derived from Withline and Nonebular runs. Right: comparison of the stellar masses derived from the Withline and Noline runs. Orange dots are galaxies in Sample-A. Blue circles are galaxies in Sample-B. Sample-A has better data quality than Sample-B, as defined in Sect. 3.3. The dotted line is the 1:1 line. The dashed line shows the average difference between the two runs in each panel. |
| In the text | |
 |
Fig. 6. Left: comparison of the SFRs derived from the Withline and Nonebular runs. Right: comparison of the SFRs derived from the Withline and Noline runs. Orange dots are galaxies in Sample-A. Blue circles are galaxies in Sample-B. Sample-A has better data quality than Sample-B, as defined in Sect. 3.3. The dotted line is the 1:1 line. The dashed line shows the average difference between the two runs in each panel. |
| In the text | |
 |
Fig. 7. Top: comparison of the metallicity, dust attenuation, age, and δ derived from the Withline and Noline runs. Bottom: comparison of the metallicity, dust attenuation, age, and δ derived from the Withline and Nonebular runs. Orange dots are galaxies in Sample-A. Blue circles are galaxies in Sample-B. Sample-A has a better data quality than Sample-B, as defined in Sect. 3.3. The dotted line are the 1:1 line. |
| In the text | |
 |
Fig. 8. PDFs of M*, SFR and AV for a galaxy in our sample. Top: PDFs estimated from the Noline fit. Bottom: PDFs estimated from the Withline fit. |
| In the text | |
 |
Fig. 9. Comparison of the observed and CIGALE modeled line fluxes. Circles show the fluxes obtained from the Withline run. Triangles show the fluxes obtained from the Noline run. |
| In the text | |
 |
Fig. 10. Comparison of Ks-band excess and [OIII]+Hβ fluxes for Sample-A galaxies. The cross shows the catastrophic case. The three dotted lines indicate the mean and standard deviations of the ΔEW, where ΔEW = logEWobs − logEWmodel. |
| In the text | |
 |
Fig. 11. Median SSFR as a function of redshift with a 68% confidence limit based on the whole PDF with comparison of results from different studies (Noeske et al. 2007; Daddi et al. 2007; Reddy et al. 2012) and results from the study of de Barros et al. (2014, DB14) for four different models. The dashed line shows the relation expected from Bouché et al. (2010) for an exponentially increasing star formation at a fixed stellar mass, 109.5 M⊙. |
| In the text | |
 |
Fig. 12. SEDs of LBG galaxies shifted to z = 3.5 and normalized to the flux at rest 0.2 μm (0.9 μm in this figure). Red circles show the composite SED with the errorbars corresponding to the dispersion of the data. The normalization of the composite SED at 0.9 μm is 0.71 μJy. The line is the SED template given by Álvarez-Márquez et al. (2019). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.