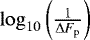| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 23 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201935742 | |
| Published online | 01 October 2019 | |
Simulations of starspot anomalies within TESS exoplanetary transit light curves
I. Detection limits of starspot anomalies in TESS light curves★
Centro de Astronomía (CITEVA), Universidad de Antofagasta,
Avenida U. de Antofagasta
02800,
Antofagasta,
Chile
e-mail: jeremy.tregloanreed@uantof.cl
Received:
19
April
2019
Accepted:
14
August
2019
Context. The primary targets of the NASA Transiting Exoplanet Survey Satellite (TESS) are K and M dwarf stars within our solar neighbourhood. Young K and M dwarf stars are known to exhibit a high starspot coverage (≈50%), however, older stars are known to show fewer starspots. This implies that TESS transit light curves at 2 min cadence may contain starspot anomalies, and if so, will require transit-starspot models to determine accurately the properties of the system.
Aims. The goals are to determine if starspot anomalies can manifest in TESS transit light curves, to determine the detection limits of the starspot anomalies, and to examine the relationship between the change in flux caused by the starspot anomaly and the planetary transit.
Methods. We conducted 20 573 simulations of planetary transits around spotted stars using the transit-starspot model, PRISM. In total 3888 different scenarios were considered using three different host star spectral types, M4V, M1V, and K5V. The mean amplitude of the starspot anomaly was measured and compared to the photometric precision of the light curve to determine if the characteristic “blip” of the starspot anomaly was noticeable in the light curve.
Results. The simulations show that starspot anomalies are observable in TESS 2 min cadence data. The smallest starspot detectable in TESS transit light curves has a radius of ≈ 1900 km. The starspot detection limits for the three host stars are 4900 ± 1700 km (M4V), 13 800 ± 6000 km (M1V), and 15 900 ± 6800 km (K5V). The smallest change in flux of the starspot (ΔFspot = 0.00015 ± 0.00001) can be detected when the ratio of planetary to stellar radii k = 0.082 ± 0.004.
Conclusions. The results confirm known dependencies between the amplitude of the starspot anomaly and the photometric parameters of the light curve. The results facilitated the characterisation of the relationship between the change in flux of the starspot anomaly and the change in flux of the planetary transit for TESS transit light curves.
Key words: stars: late-type / stars: activity / starspots / planets and satellites: general / methods: numerical / techniques: photometric
Simulated light curves are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/630/A114
© ESO 2019
1 Introduction
The next generation of transit planet hunters (e.g. Next Generation Transit Survey, NGTS: Wheatley et al. 2013; NASA Transiting Exoplanet Survey Satellite, TESS: Ricker et al. 2009, 2014, 2015) have been observing transiting planets orbiting both K and M dwarf stars within the solar neighbourhood; these surveys have an emphasis on super-Earth: 1.25 R⊕ to 2 R⊕; sub-Neptune: 2 R⊕ to 4 R⊕; Neptune: 4 R⊕ to 6 R⊕ class planets. TiO absorption bands show that young K dwarfs can have 20–40% starspot coverage (O’Neal et al. 2004), while young M dwarfs can have a starspot coverage of 40 ± 10% (Jackson & Jeffries 2013). Older stars are known to show fewer starspots, however, the dependence on age has not been reliably quantified. This leads to the potential of an increased likelihood that the transits observed by these new planet hunters contain starspot anomalies.
Late-type stars (G, K, M) have magnetic fields which often manifest themselves as dark spots on the stellar surface. When a transiting planet passes in front of a starspot, a short-term increase in the brightness of the star is seen because the planet is temporarily blocking a fainter part of the surface of the star (Silva 2003). This “blip” in the light curve can be modelled to determine the size and position of the starspot (e.g. WASP-19: Tregloan-Reed et al. 2013; Mancini et al. 2013; WASP-6: Tregloan-Reed et al. 2015; CoRoT-2: Silva-Valio et al. 2010; WASP-4: Sanchis-Ojeda et al. 2011; HAT-P-11: Sanchis-Ojeda & Winn 2011; Kepler-30: Sanchis-Ojeda et al. 2012; Kepler-63: Sanchis-Ojeda et al. 2013; HATS-2: Mohler-Fischer et al. 2013; Qatar-2: Mancini et al. 2014; WASP-41: Southworth et al. 2016; WASP-52: Mancini et al. 2017; GJ 3470: Chen et al. 2017: Kepler-17: Valio et al. 2017).
Starspots can affect the shape of the light curve (Silva-Válio 2010) and if not correctly modelled can lead to biased measurements of the system parameters (e.g. planetary radius: Nikolov et al. 2013; limb darkening coefficients: Ballerini et al. 2012; time of minimum light: Sanchis-Ojeda et al. 2011). However, an accurate measurement of the planetary radius is achievable ifthe perturbations are accounted for, thereby improving investigations into the atmosphere, structure, and evolution of a planet (Fortney et al. 2007).
When two closely spaced transit light curves, both of which contain a starspot anomaly (due to the same starspot), are accuratelymodelled, the position of the starspot can be determined at two distinct points in time, allowing for an extra- ction of the latitudinal stellar rotation period (P*) and sky-projected orbital obliquity (the sky projection of the angle between the orbit of the planet and the spin of the host star), i.e. λ from the transit light curves (e.g. Sanchis-Ojeda et al. 2011; Sanchis-Ojeda & Winn 2011; Tregloan-Reed et al. 2013, 2015; Southworth et al. 2016; Mancini et al. 2017).
Over the years there have been multiple transit-starspot models developed both by the eclipsing binary star community (e.g. Wilson-Devinney code: Wilson & Devinney 1971; Wilson 1979, 1990, 2008, 2012; PHEOBE: Prša & Zwitter 2005; Prša et al. 2016) and the exoplanet community (e.g. PRISM: Tregloan-Reed et al. 2013, 2015, 2018; SOAP-T: Oshagh et al. 2013; spotrod: Béky et al. 2014; KSint: Montalto et al. 2014; ellc: Maxted 2016; StarSim: Herrero et al. 2016; PyTranSpot: Juvan et al. 2018). With a large variety of models readily available to the community, the treatment of starspot anomalies and their associated effects on light curves no longer cause difficulties or delays in the analysis of the exoplanetary light curves.
Locating starspot anomalies in light curves of smaller planets requires a significantly higher precision in the light curve because the size of the starspot anomaly scales linearly with the area of the planetary disc (Tregloan-Reed et al. 2013). This precludes the use of ground-based data for small planets, but the remarkable quality of the light curves from dedicated space missions such as the Kepler satellite (Borucki et al. 2010) makes this work viable. Whilst the temporal sampling of Kepler data (30 min cadence) is too low to resolve starspot anomalies for the vast majority of the stars observed, the NASA’s TESS will observe ≥200 000 stars at a 2 min cadence (Stassun et al. 2018) and provide a large set of light curves suitable for detecting and measuring starspots.
The TESS instrument is spending 2018 and 2019 looking for super-Earth planets (< 2 R⊕) transiting between 200 000 and 400 000 pre-selected stars at a 2 min cadence (Stassun et al. 2018) with a particular emphasis on M dwarf stars. Recent simulations for TESS indicate the potential to detect 1700 planets from the smallest selection of pre-selected stars (Sullivan et al. 2015, 2017). With 1100 of these planets predicted to be sub-Neptune (2 R⊕ to 4 R⊕) class planets, while, 419 super-Earth or smaller (< 2 R⊕) planets are expected to be found orbiting M dwarfs. With a further 137 super-Earth or smaller planets orbiting F, G, K stars (Sullivan et al. 2015, 2017). TESS is already exceeding early expectations with 21 confirmed planets (e.g. Pi Mensae c: Huang et al. 2018: LHS 3884 b; Vanderspek et al. 2019: HD 21749 b; Dragomir et al. 2019: HD 202772A b; Wang et al. 2019) with a further 336 TESS Objects of Interest (ToIs)1.
The objective of this work is to determine the detection limits of starspot anomalies in TESS exoplanetary transit light curves. This is accomplished by varying the variables that directly or indirectly alter the duration and/or amplitude of the starspot anomaly in the light curve and comparing the results against the photometric noise of the light curve: starspot size (rspot) and temperature (Tspot), host star radius (R*) and effective temperature (Teff), planetary radius (Rp), semi-major axis (a), orbital period (P), orbital inclination (i), observing cadence, and the frequency (ν) of the observation. Through this, it is possible to determine the physical properties of starspots at the detection limits for TESS transit light curves.
The outline of this paper is as follows. Section 2 describes how the contrast of the starspots was calculated in the TESS passband for use in the simulations and describes which parameters influence the size and shape of the starspot anomalies. The section then describes how the simulations were designed using the PRISM model to produce the simulated light curves. Section 3 presents the results, separated into three host star spectral types: K5V dwarf, M1V, and M4V dwarf stars. Section 4 discusses the results and gives the overall conclusions to the simulations.
2 Simulating starspot anomalies with PRISM
We used thetransit-starspot model PRISM (Tregloan-Reed et al. 2013, 2015, 2018) to perform the simulations in this work. The PRISM2 model is written in IDL3 (Interactive Data Language) and uses a pixellation approach to model the stellar disc in a 2D array by subdividing the star into many individual elements. These elements can then be described by a 2D vector in Cartesian coordinates. Each element is then assigned an intensity value based on whether a stellar feature is present at that location and then the quadratic limb darkening law is applied over the entire stellar disc. The planet is then set to transit the star. For each data point in the transit light curve, the total received intensity is calculated based on which elements of the star are visible. The pixellation method is an ideal method to introduce stellar features to the stellar disc becausethe model allows individual intensities to be assigned to individual elements at specific coordinates (see Tregloan-Reed et al. 2013). This allows researchers to use PRISM to model both occulted and unocculted starspots and thus help “rule out” starspot trends when examining wavelength dependent transit depth (planetary radii) variations.
The original version of PRISM used six parameters to model the light curve: the ratio of the planetary to stellar radii (k), the sum of the fractional (rp = Rp∕a and r* = R*∕a) planetary and stellar radii (rp + r*), linear and quadratic coefficients of the quadratic limb darkening law (u1 and u2), orbital inclination (i), and time of minimum light (T0). These were combined with four additional parameters for each starspot: the longitude of the centre of the spot (θ), the co-latitude of the centre of the spot (ϕ), the angular size (rspot) and contrast (ρspot) (Tregloan-Reed et al. 2013). Since its publication, PRISM has had two major updates. The first added two orbital parameters: orbital eccentricity (e) and argument of periastron (ω) (Tregloan-Reed et al. 2015). The second major update included a third light parameter and the out-of-transit detrending polynomial coefficients (Tregloan-Reed et al. 2018).
During its development the ability of PRISM to model the stellar disc and transit was tested via JKTEBOP (Southworth et al. 2004, 2005, 2007, 2009; Southworth 2008, 2010, 2011, 2013) as a benchmark transit modelling program. To accomplish this, a series of light curves were generated by both PRISM and JKTEBOP using the same transit parameter values. The average difference between the two models for all the tests was ~ 10 ppm, which is six times lower than the expected noise floor in TESS data (see Sullivan et al. 2015).
Since the development of PRISM other researchers have used the model to ascertain the photometric parameters of a transiting system and to derive the parameters of the detected starspots observed in transit light curves (e.g. Mancini et al. 2013, 2014; Mohler-Fischer et al. 2013; Chen et al. 2017). The PRISM model has also been used to help calibrate and benchmark other transit-starspot models (e.g. spotrod: Béky et al. 2014; PyTranSpot: Juvan et al. 2018).
The PRISM model measures rspot in units of angular radius (°). Consequently, an n° starspot maintains a constant ratio of the stellar to starspot surfaces for all values of R*. The simulations in this work use three different host stars, and as such, three different R*. To avoid the projection effects on the spherical surface of the star we quote the starspot stellar surface radius in units of R*, i.e.,
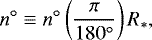 (1)
(1)
where a starspot with an angular radius of 1° has a stellar surface radius of 0.017 R*
2.1 Typical starspot contrast in the TESS passband
While the temperature of the starspot (Tspot) is fixed across all wavelengths, ρspot is not, it is dependent on the frequency of the observation, ν. At bluer wavelengths ρspot decreases (higher contrast), increasing the amplitude of the starspot anomaly. This is because a starspot is cooler than the surrounding photosphere and both the starspot and photosphere can be treated as black bodies (Rabus et al. 2009; Sanchis-Ojeda & Winn 2011). When the observation wavelength shifts towards a redder wavelength, ρspot increases (lower contrast) and therefore the amplitude of the starspot anomaly can potentially fade into the observational noise.
Assuming that both the starspot and surrounding photosphere radiate as black bodies, Silva (2003) used the ratio of the intensities of the starspot to the surrounding photosphere to give an equation to find ρspot from the stellar effective temperature (Teff), Tspot and ν. By doing so, Silva (2003) incorporated the spectral signature of the starspot into ρspot,
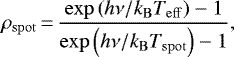 (2)
(2)
where h is Planck’s constant and kB is Boltzmann constant.
The TESS instrument uses its own T (TESS) passband with a spectral response between 600–1000 nm with the Johnson-Cousins IC passband lying near the centre of the T passband (Sullivan et al. 2015). The effective wavelength midpoint of the IC passband lies approximately at 785 nm. We used Eq. (2) to calculate the contrast for a typical starspot on a cool M dwarf at 600, 785, and 1000 nm because a large proportion of the emitted flux from an M dwarf lies within the optical red infrared, potentially engulfing the starspot signal owing to the redder observational wavelengths. Using a Teff = 3200 K (transit detection limit in T passband; Sullivan et al. 2015) and setting Tspot to be 200 K cooler than the photosphere (i.e. Tspot = 3000 K), in line with starspot temperatures of fully convective M dwarf stars (e.g. Barnes et al. 2015), ρspot was calculated to be ρspot = 0.60, ρspot = 0.68, and ρspot = 0.74 for the three respective wavelengths. The amplitude of a starspot anomaly is primarily dependent on rspot and ρspot. However, there is a critical threshold for ρspot at which the starspot anomaly is no longer detected, irrespective of rspot. Previous works using ground-based telescopes have found starspot anomalies with ρspot > 0.74 (e.g. HAT-P-36, ρspot = 0.92: Mancini et al. 2015; WASP-41, ρspot = 0.90: Southworth et al. 2016; WASP-6, ρspot = 0.80: Tregloan-Reed et al. 2015; WASP-19, ρspot = 0.78: Tregloan-Reed et al. 2013). This indicates that ρspot of a typical starspot anomaly lying within the photosphere of a M dwarf star, observed in the T passband, isbelow the critical threshold to be detected by ground-based telescopes and implies that starspot anomalies should be detected in TESS transit light curves.
2.2 Parameter impact on the shape of a starspot anomaly
Before we begin simulating starspot anomalies in transit light curves, we need to examine the parameters which directly or indirectly influence the size (amplitude) and shape (duration) of the anomaly. The parameters can be divided into four groups: starspot parameters, stellar and planetary parameters, orbital parameters, and observing constraints.
The first group of parameters belong to the starspot itself θ, ϕ, rspot, and ρspot (or Tspot). The amplitude of a starspot anomaly is directly proportional to ρspot and the surface area of the starspot (Tregloan-Reed et al. 2013). As ρspot decreases (i.e. the starspot darkens and cools), rspot must be reduced, to maintain the amplitude of the starspot anomaly. In essence, a small starspot needs a large ratio of Tspot to Teff to be detected (see Eq. (2)). The location of the starspot, θ and ϕ have an indirect effect on the amplitude and duration of the anomaly. When the position of the starspot approaches the limb of the star, there is a reduction in the 2D projection of the surface area of the spot as a consequence of foreshortening along the radial vector, i.e. the vector between the centres of the stellar disc and starspot. Hence, this reduces the amplitude of the starspot anomaly. As the radial vector rotates (by altering the Azimuth angle) to being parallel with the transit cord, the duration of the anomaly is reduced too.
The next group of parameters are related to the host star; Teff, R*, and the planet; Rp. It was shown in both Sect. 2.1 and Eq. (2) how Teff directly alters ρspot thereby indirectly influencing the amplitude of the anomaly. The amplitude of a starspot anomaly is also directly proportional to k, the ratio of Rp to R* (Tregloan-Reed et al. 2013). If k is too small in relation to the noise then the change in flux due to the planet occulting the starspot will not be detectable over the noise in the light curve.
The orbital parameters i, a, and P all indirectly impact the amplitude and duration of the starspot anomaly. The parameter i controls the impact parameter (b) and therefore i controls the stellar latitude at which the transit cord crosses. Because occulted starspots must lie on the transit chord to be observed then as i decreases, the position of the starspot moves towards the stellar pole (i.e. the limb of the stellar disc). By doing so, the 2D projection of the surface area of the starspot decreases owing to foreshortening. The parameter b is also controlled by a combined with the orbital eccentricity (e) and the argument of periastron (ω) (e.g. Winn 2010), i.e.
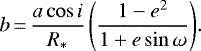 (3)
(3)
Because P is related to a via Kepler’s third law and directly controls the transit duration (e.g. Winn 2010), it becomes apparent how a and P can both directly control the duration and indirectly influence the amplitude of the starspot anomaly.
The final group consists of just two parameters, ν and the observing cadence. In Sect. 2.1 it was shown how ν alters the amplitude of the starspot anomaly. Where the amplitude of the starspot anomaly increases towards bluer wavelengths and reduces towards redder wavelengths. The observing cadence however does not physically affect the size or shape of the starspot anomaly. However, it does alter our perception of the size and shape. When the cadence decreases (from high to low cadence), the number of data points that describe the starspot anomaly decreases, altering our perception of the true shape of the anomaly. This increases the uncertainty in the duration of the anomaly and thus increases the uncertainty in the measured parameters which influence the duration of the starspot anomaly.
Because these simulations are based on TESS transit light curves, the observational cadence is fixed at 2 min (Stassun et al. 2018) and ν is fixed at 600, 785, and 1000 nm (Sullivan et al. 2015). Consequently both the cadence and ν are considered as constraints and are used in the simulations at fixed values.
2.3 Simulating starspots in TESS transit light curves
The primary goal of this work is to find the detection limits of starspot anomalies appearing within TESS exoplanet light curves. The TESS instrument was developed to find small planets (< 6 R⊕) orbiting local K and M dwarf stars (Ricker et al. 2009). As a result of this, the host star and planetary properties used in these simulations were based on the selections used by Sullivan et al. (2015, 2017), covering K and M late-type stars with small planets, < 6 R⊕.
When predicting the planetary yields of TESS Sullivan et al. (2015) calculated that TESS would have a photometric sensitivity of 200 ppm for an IC 10th magnitude star. Because of this, the light curves generated by PRISM had added Gaussian noise of 60 ± 34, 100 ± 5, 150 ± 7.5, and 200 ± 10 ppm. This approach allows us to simulate the photometric sensitivity of light curves for host stars brighter than IC = 10, after undergoing the TESS data processing pipeline and known systematics removal (see Jenkins et al. 2016).
With the TESS observations being performed in the T passband (600–1000 nm; Sullivan et al. 2015) the simulations were run at three wavelengths: 600, 785, and 1000 nm. These wavelengths were selected to give a good average approximation to the T passband (785 nm) and to obtain results at the bluest (600 nm) and reddest (1000 nm) edge of the T-passband spectral response, thereby producing the largest and smallest amplitudes for the starspot anomalies.
Examining the range of parameters described in Sect. 2.2 it becomes apparent that the parameter space which controls the amplitude and duration of a starspot anomaly is large and complex due to multiple degeneracies between the parameters (e.g. rspot ↔ ρspot, ϕ ↔ i, P ↔ a, and ϕ ↔ P). However, for this work we are only interested in the detection limits of starspot anomalies found within TESS light curves (i.e. smallest rspot for a given scenario). Therefore, we can streamline the parameter space by using a mixture of predetermined key parameter values and scenarios (e.g. setting R* and Teff for typical K and M dwarf stars) and search for the smallest detectable rspot.
In the simulations the position of the starspot was set at the centre of the stellar disc, therefore minimising the effect from foreshortening. As discussed in Sect. 2.2 foreshortening reduces the amplitude of the starspot anomaly. Therefore, owing to the geometric nature of spherical foreshortening, the smallest detectable rspot is for starspots lying at the centre of the stellar disc. This is because when the starspot moves closer to the limb, rspot needs to increase so as to maintain the same 2D projected surface area of the starspot. Because we want to detect the smallest starspot for a given set of circumstances placing the starspot at the centre of the stellar disc achieves this result.
To determine TESS planetary yields Sullivan et al. (2015, 2017) used an M4V dwarf with Teff = 3200 K, a radius of R* = 0.155 R⊙, a solar metallicity, and an age of 1 Gyr (in keeping with the Dartmouth Stellar Evolution Database; Dotter et al. 2008). The Teff was selected because M dwarfs cooler than 3200 K are too faint for planetary transit detection in the T passband (Sullivan et al. 2015). For this work it was therefore natural to start with an M4V dwarf star. The smaller value for R* and by association, larger k, meant that a 1 R⊕ radius could be used in the M4V dwarf simulations. The planetary radii used ranged from 1 to 3 R⊕ in 0.25 R⊕ increments. An upper limit of 3 R⊕ was used because of the rare occurrence of close in (< 50 d), large (> 3 R⊕) planets orbiting M dwarf stars, determined from population studies using Kepler and K2 data (Dressing & Charbonneau 2013, 2015; Morton & Swift 2014). Although the recent discovery of NGTS-1 b, an ≈ 15 R⊕, hot Jupiter transiting an M 0.5 dwarf star with a 2.65 d orbital period (Bayliss et al. 2018) along with two previously known close-in large planets transiting M dwarfs (Kepler-45 b; Johnson et al. 2012: HATS-6 b; Hartman et al. 2015) appears to be lifting this limit.
A key objective of TESS is to find suitable planets for further study within the habitable zone of the host star. A planet orbiting an M4V dwarf star with a relative insolation (S∕S⊕) set at the inner (S∕S⊕ = 1.0), mean (S∕S⊕ = 0.6), and outer edge (S∕S⊕ = 0.2) of the habitable zone (Kopparapu et al. 2013) has an orbital period between 12 and 40 days (Eq. (13) Sullivan et al. 2015). The difficulty in detecting starspot anomalies at these orbital periods is that the transit duration, is less than 10 min (see Fig. 1). This results in the duration of a starspot anomaly being less than a minute, which is not favourable when using 2 min cadence data. Unlike transit detections, which can use phase-folded light curves to increase the number of data points within the transit and therefore aid in the transit detection, a starspot anomaly can generally only be detected using a single transit. This is the result of the rotation of the host star smearing the different positions of the starspot anomaly when viewing multiple phase-folded light curves. Because of this, the orbital period in the M4V dwarf simulations was set at 1, 2, and 3 days to allow sufficient sampling in the single light curves to detect a starspot anomaly. It should be stated however that a subset of TESS data will be made available with a cadence of less than two minutes (20 s) for the asteroseismology community (Ricker et al. 2015).
Kepler’s third law was used to calculate a from P using a stellar mass, M* = 0.1 M⊙ these are given in Table 1. The stellar mass was determined using R* = 0.155 R⊙ combined with Eq. (10) (second order polynomial) from Boyajian et al. (2012), which was derived from interferometric measurements of M and K dwarfs. We then calculated logg = 5.06 for the M4V dwarf and combined this value with Teff = 3200 K; we determined the quadratic limb darkening coefficients u1 and u2 (Table 2) with grids developed by Claret (2017) using stellar atmosphere models that are designed for use in the TESS passband.
Barnes et al. (2015) looked at starspot distributions of two fully convective M dwarfs, M4.5V: GJ 791.2 A, and M9V: LP 944-20 and found starspot temperatures around 200–300 K cooler than the surrounding photosphere. In line with this, we selected four equidistant starspot temperatures 3000, 3050, 3100, and 3150 K for the 3200 K M4V dwarf simulations.
We used 1296 different scenarios for the M4V dwarf star simulations. Each scenario was derived from alternating the nine Rp, three orbital periods, three observational wavelengths (600, 785, and 1000 nm), four starspot temperatures, and four noise levels (60, 100, 150, and 200 ppm). We then varied the rspot to find the detection limit for each of the 1296 scenarios. Figure 2 shows an example light curve and stellar disc from PRISM for one of the simulations.
Owing to the small radius (R* = 0.155 R⊙) of the initial host star, the second host star used in the simulations was a larger M1V dwarf star, where Teff = 3700 K (Table 1, Sullivan et al. 2015). This allowed the simulations to examine the detection limit of starspot anomalies at the two ends of the range of R* and Teff of M dwarfs observed by TESS. The R* and M* of the M1V dwarf were extrapolated using the polynomials derived from interferometric measurements of M and K dwarfs (Eqs. (8) and (10), Boyajian et al. 2012)using Teff = 3700 K. The results5 are given in Table 2 along with the extrapolated properties of the M4V and K5V dwarf host stars. We employed the same procedure that was used for the M4V dwarf in determining u1 and u2 from Claret (2017) with the results reported in Table 2.
As a consequence of a threefold increase in the stellar radius, the planetary radii used in the M1V simulations ranged from 2 to 4 R⊕ in 0.25 R⊕ increments. Three orbital periods were selected at 2, 3, and 4 days and the corresponding values for a were calculated using Kepler’s third law using a stellar mass of 0.52 M⊙ (see Table 2) and are given in Table 1. Adopting Teff = 3700 K for the M1V dwarf star, we selected four equidistant starspot temperatures, 3400, 3475, 3550, and 3625 K, giving a further 1296 different scenarios using an M1V dwarf host star; we used the same three observational wavelengthsand four noise levels that were used in the M4V dwarf simulations. The same procedure that was used in the M4V simulations was used for the M1V simulations in that for each of the 1296 scenarios, rspot was varied to find the detection limit in each scenario.
For the third host star, a K5V dwarf star was selected. Using an Teff = 4100 K (Table 1, Sullivan et al. 2015), the R* and M* was extrapolated from the two polynomials presented by Boyajian et al. (2012); these values are given in Table 2. We determined u1 and u2 from Claret (2017), for the K5V dwarf; these values are given in Table 2.
Because of the larger R* the K5V simulations probed the detection limits of starspot anomalies for larger planets, 3–7 R⊕ (sub-Neptune to sub-Saturn class planets) in 0.5 R⊕ increments. Owing to the larger R* and Rp the three values of P were selected at 2, 4, and 6 days with the corresponding values for a calculated using Kepler’s third law with a stellar mass of 0.65 M⊙ (see Table 2); these values are given in Table 1. With Teff = 4100 K four temperatures were selected for the starspot 3700, 3800, 3900, and 4000 K. Combining the three observational wavelengths and four noise levels meant that a further 1296 scenarios were generated using a K5V dwarf host star.
 |
Fig. 1 Simulated 2 min cadence TESS light curve of a 1 R⊕ planet orbiting an M4V dwarf star with P = 12 d and an rms scatter of 104 ppm (generated by PRISM). The transit duration is approximately 8 min and only 3 data points lie within the transit. |
Calculated values of a for each value of P for the three simulated host stars.
Extrapolated values of R* and M* using Teff from polynomials derived from interferometric measurements of M and K dwarf stars (Eqs. (8) and (10), Boyajian et al. 2012), for the three simulated host stars combined with the calculated log g and u1 and u2 for the quadratic limb darkening law from Claret (2017).
 |
Fig. 2 Example light curve (left) and stellar disc (right) generated by PRISM. Light curve: the solid line represents the noise-free synthetic light curve containing the starspot anomaly, while, the filled circles represent the spot-free synthetic light curve (see Sect. 3) with added Gaussian noise. Stellar disc: the central solid line represents the stellar equator (assuming orbital alignment) and the upper and lower solid linesrepresent the upper and lower boundaries of the transit cord. These were generated with a 1.5 R⊕ super-Earth planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0° and P = 1 d. The starspotproperties are: θ = 0°, ϕ = 90°, rspot = 0.035R* and Tspot = 3000 K. The observational wavelength and rms scatter for the simulated data were set at 785 nm and 150 ± 7.5 ppm, respectively. |
3 Simulation results
For all 3888 different scenarios a total of 20 573 simulated transits were generated. All 20 573 simulated transit light curves are available at the CDS. The number of simulated transits per scenario was dependent on the detection of rspot and ranged from 2 to 40 simulations per scenario, where rspot started at 0.0087R* and was increased in 0.0087R* steps up to 0.35R*. The simulations were stopped when the starspot anomaly was deemed detectable. The starspot anomaly was considered “detected” in the simulated transits, if the characteristic blip was visible in the simulated light curve (e.g. Fig. 2). This was accomplished by comparing the amplitude of the anomaly to the photometric precision (rms scatter) of the data. The amplitude of the starspot anomaly was measured by creating two transit light curves. The first had the centre of the starspot within the transit cord while the second light curve had the starspot latitude shifted so that it was no longer within the transit cord. Because both occulted and non-occulted starspots affect the shape of the light curve (Silva-Válio 2010) and in particular the transit depth (Nikolov et al. 2013) it was important that the stellar disc of the “spot-free” light curve model still contained a starspot of equal properties. To reduce the impact fromforeshortening, the starspot was positioned so that only a gap of one pixel separated the starspot and transit cord boundaries. We compared the resulting light curves to determine the amount of systematic error the approximation would generate and found a mean divergence of ≈ 1 ppm, which is 60 times smaller than the TESS mission specified noise floor. Therefore, we conclude that this approximation is suitable for this work.
The light curve plots produced in this work show two synthetic light curves represented by a solid line and filled circles. The light curves represented by a solid line are the synthetic light curves containing the starspot anomaly and these do not have added noise. The light curves represented by filled circles are the synthetic light curves of the spot-free model and have added Gaussian noise. By comparing the two synthetic light curves it is possible to determine if the amplitude of the starspot anomaly is larger than the rms scatter.
To determine the most efficient set of detection conditions, tests were performed on the synthetic data. After the additionof noise to the synthetic light curve, PRISM was fitted to the synthetic light curve in an attempt to recover the starspot parameters. The amplitude of the starspot anomaly was determined by the data points which described the starspot anomaly and the mean change in flux was calculated. The mean change in flux was then divided by the rms scatter of the light curve to give the amplitude of the starspot anomaly in units of rms (σ). Different amplitudes were considered from 1σ to 3σ. In all cases where the amplitude was greater than 2.0σ, the best fitting starspot parameters of the synthetic light curves were close to the original values and agreed within their 1σ parameter uncertainties. However, when the amplitude of the starspot anomaly was between 1.5σ and 2σ, the 1σ uncertainty in the starspot parameters was non-physical. For example in one test the starspot radius was found to be 0.047R*± 1.700R*, indicating that the starspot covered the entire visible hemisphere of the stellar disc, and in another test the latitude of the starspot was found to be 0.17° ± 97.39°; this indicated that a spot-free solution, i.e. the starspot was no longer on the transit cord, was an acceptable solution. These tests showed that when the amplitude of the starspot anomaly was between 1.5σ and 2σ the anomaly could be detected but it was not possible to constrain the starspot parameters, thereby confirming the presence of a starspot. Therefore, the optimal cutoff point for the amplitude of the starspot anomaly was set at the 2σ limit to differentiate between a detection and non-detection.
3.1 M4V dwarf host star results
A total of 6870 simulations were conducted for the 1296 scenarios using an M4V dwarf host star; the results are presented in Table A.1. It was found that the starspot detection limit in TESS transit light curves of an M4V dwarf host star was rspot = 0.045R*± 0.016R* (4900 ± 1700 km), where the uncertainty is the 1σ standard deviation from the 1296 scenarios of the M4V host star simulations. The smallest rspot detected in the M4V simulations (under optimal parameter conditions) was rspot = 0.017R* or 1900 km (see Fig. 3) and was detected in 7 of the 1296 scenarios (0.5%).
It was found that for three scenarios, it was not possible to resolve the starspot size (see Fig. 4). These scenarios involved a 3150 K starspot with a photometric precision of 200 ppm observed at 1000 nm with a 1 R⊕ transiting planet. When examining the stellar disc output for the 0.093R* starspot in Fig. 4, the area of the 2D projection of the starspot is larger than the planetary disc. Therefore, increasing rspot further, would no longer increase the amplitude of the starspot anomaly because it would not affect the amount of flux blockedby the planet. However, it increases the duration because the planet spends longer occulting the starspot. This can be seen when examining the three simulated light curves in Fig. 4. Therefore, for these scenarios, the amplitude of the starspot anomaly never became larger than the rms scatter of the synthetic data.
Hence, the simulations show that it is not possible to observe a 3150 K starspot on the surface of a 3200 K M4V dwarf, using a 1.0 R⊕ Earth-sized planet, when observed at the reddest edge of the T passband (i.e. 1000 nm) with an rms scatter of 200 ppm. However, by either increasing the planetary radius (+ 0.25 R⊕), reducing therms scatter (− 50 ppm), or shifting to a bluer wavelength, it would be possible to detect these starspots down to 0.035R* (3800 km) (see Table A.1).
3.2 M1V dwarf host star results
A total of 7769 simulations were conducted for the 1296 scenarios using an M1V dwarf host star; these results are presented in Table A.2. It was found that the starspot detection limit in TESS transit light curves of an M1V dwarf host star was rspot = 0.040R*± 0.017R* (13800 ± 6000 km). The smallest rspot detected in the M1V simulations (under optimal parameter conditions) was rspot = 0.017R* or 6000 km (see Fig. 5), which was detected in 85 of the 1296 scenarios (6.6%).
To allow for a direct comparison between the starspots on the M1V and M4V dwarf stars requires the M1V dwarf star, rspot to be multiplied by 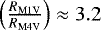 . From this itcan be seen that while the smallest starspot detected in the M1V dwarf simulations had rspot = 0.017R*, this is the equivalent to rspot ≈ 0.056R* for a M4V dwarf star.
. From this itcan be seen that while the smallest starspot detected in the M1V dwarf simulations had rspot = 0.017R*, this is the equivalent to rspot ≈ 0.056R* for a M4V dwarf star.
Similar to the M4V host star results, the M1V host star results show that it is not possible to detect the hottest starspots when small planets (e.g. < 2.75 R⊕) are transiting the star if the photometric precision is > 100 ppm.
3.3 K5V dwarf host star results
A total of 5934 simulations were conducted for the 1296 scenarios using a K5V dwarf host star; these results are presented in Table A.3. It was found that the starspot detection limit in TESS transit light curves of a K5V dwarf host star was rspot = 0.038R*± 0.016R* (15 900 ± 6800 km). The smallest rspot detected in the K5V simulations (under optimal parameter conditions) was rspot = 0.017R* or 7600 km (see Fig. 6) and was detected in 102 of the 1296 scenarios (7.9%).
We used the same process described in Sect. 3.2 to compare the starspot sizes on the K5V and M4V dwarf stars. We find that for the K5V dwarf star, rspot should be multiplied by 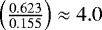 . The smallest starspot detections for the K5V host star simulations were when rspot = 0.017R*, which would equate to a detection with rspot ≈ 0.07R* if the starspots were on a M4V dwarf instead.
. The smallest starspot detections for the K5V host star simulations were when rspot = 0.017R*, which would equate to a detection with rspot ≈ 0.07R* if the starspots were on a M4V dwarf instead.
It was found that it was not possible to resolve the starspot for only 15 (1.2%) scenarios. These scenarios followed the same pattern as found with the previous host stars. The scenarios involving a high temperature starspot, small planet, and that were observed at redder wavelengths with low photometric precision tended to prevent the detection of the starspot.
 |
Fig. 3 Two simulated transit light curves generated by PRISM. These were both generated using a 1.0 R⊕ Earth-sized planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0° and P = 1 d. The starspotproperties are θ = 0°, ϕ = 90°, rspot = 0.009R* (left), rspot = 0.017R* (right), and Tspot = 3000 K. The observational wavelength and rms scatter for the simulated transits were set at 600 nm and 60 ppm, respectively. The starspot anomaly becomes visible over the simulated noise when rspot is increased from 0.009R* to 0.017R*. The solid lines represents the noise-free synthetic light curves containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. |
 |
Fig. 4 Three simulated transit light curves (top panels) and stellar disc outputs (bottom panels), generated by PRISM. Light curves: the solid lines represent the noise-free synthetic light curves containing the starspot anomaly, while, the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. Stellar discs: the central solid lines represents the stellar equator (assuming orbital alignment) and the upper and lower solid lines represent the upper and lower boundaries of the transit cords. Because the high ρspot, the starspot boundary is highlighted with a black circular boarder. The observational wavelength and rms scatter for the simulated transits are set at 1000 nm and 200 ppm, respectively. These were generated using a 1.0 R⊕ Earth-sized planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0° and P = 1 d. The starspotproperties were set at θ = 0°, ϕ = 90° and Tspot = 3150 K (ρspot = 0.93). Left panels: rspot = 0.087R*, middle panels: rspot = 0.175R*, right panels: rspot = 0.262R*. |
 |
Fig. 5 Two simulated transit light curves generated by PRISM. These were both generated using a 2.75 R⊕ sub-Neptune planet transiting a 3700 K, 0.493 R⊙ M1V dwarf star with i = 90.0° and P = 3 d. The starspot properties are θ = 0°, ϕ = 90°, rspot = 0.009R* (left), rspot = 0.017R* (right), and Tspot = 3400 K. The observational wavelength and rms scatter for the simulated transits were set at 785 nm and 60 ppm, respectively. The starspot anomaly becomes visible over the simulated noise when rspot is increased from 0.009R* to 0.017R*. The solid lines represent the noise-free synthetic light curves containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. |
 |
Fig. 6 Two simulated transit light curves generated by PRISM. These were both generated using a 4.5 R⊕ Neptune-sized planet transiting a 4100 K, 0.623 R⊙ K5V dwarf star with i = 90.0° and P = 4 d. The starspotproperties are θ = 0°, ϕ = 90°, rspot = 0.009R* (red), rspot = 0.017R* (blue), and Tspot = 3700 K. The observational wavelength and rms scatter for the simulated transits were set at 785 nm and 60 ppm, respectively. The starspot anomaly becomes visible over the simulated noise when rspot is increased from 0.009R* to 0.017R*. The solid lines represents the noise-free synthetic light curves containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. |
 |
Fig. 7 Four simulated transit light curves generated by PRISM. The observational wavelength of the simulated transits was 785 nm. These were generated using a 3.0 R⊕ sub-Neptune planet transiting a 3700 K, 0.493 R⊙ M1V dwarf star with i = 90.0° and P = 2 d. The starspotproperties were set at θ = 0°, ϕ = 90° and Tspot = 3475 K. The rms scatter of the light curves from left to right are 60, 100, 150, and 200 ppm. Each light curve shows the smallest detectable starspot size for the scenarios, 0.017R* (red), 0.026R* (blue), 0.035R* (green), and 0.044R* (purple), which increases with increasing noise. The solid lines represents the noise-free synthetic light curves containing the starspotanomaly, while the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. |
3.4 Expected trends
By examining the results from the 20 573 simulated transits (see Tables A.1–A.3), known trends (described in Sect. 2.2) in the starspot detection limits are seen.
The simulations confirmed that increasing the photometric precision (decrease in noise) in the observations allowed smaller starspots to be detected (e.g. Fig. 7). The simulations also confirm that the starspot detection limit is dependent on Tspot, observational wavelength, and orbital period (e.g. Fig. 8). It is easier to detect a small cool starspot than a small hot starspot(top row, Fig. 8). Likewise, a shorter orbital period allows the detection of smaller starspots (bottom row, Fig. 8). This is because of a longer transit duration and, by association, a longer starspot anomaly duration, thereby increasing the number of data points describing both the transit and starspot anomaly becuase of fixed 2 min cadence of TESS data.
The simulations help support the predicted and known trends given in Sect. 2.2 and highlights which parameters the detection limit is strongly or weakly dependent on. Examining Fig. 8, we see that by doubling the orbital period (P), the minimum detected rspot increases by20%, while shifting the observed wavelength from 600 to 1000 nm, the minimum detected rspot increases by 50%. However increasing Tspot by 100 K increases the minimum detected rspot by 67%6, indicating that the detection limit is primarily influenced by Tspot and λobs; this is expected because the amplitude of a starspot anomaly is directly proportional to ρspot (see Tregloan-Reed et al. 2013), which in turn is proportional to Tspot and λobs (see Eq. (2)).
The amplitude of the starspot anomaly is proportional to 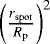 when rspot ≤ Rp. Therefore, smaller planets can detect smaller starspots. The results from the simulations agree with this when dealing with cool starspots. However, the simulations depict a different trend when dealing with the hotter starspots in that larger planets are able to detect smaller starspots. For example in Table A.1 we can see that a 1.25 R⊕ planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0°, P = 2 d, λobs = 785 nm, and Tspot = 3150 K, where the rms scatter is 150 ± 7.5 ppm, the smallest detected rspot is rspot = 0.070R* While for a 1.5 R⊕ and 1.75 R⊕ planet the smallest detected rspot becomes rspot = 0.061R* and rspot = 0.052R*, respectively.
when rspot ≤ Rp. Therefore, smaller planets can detect smaller starspots. The results from the simulations agree with this when dealing with cool starspots. However, the simulations depict a different trend when dealing with the hotter starspots in that larger planets are able to detect smaller starspots. For example in Table A.1 we can see that a 1.25 R⊕ planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0°, P = 2 d, λobs = 785 nm, and Tspot = 3150 K, where the rms scatter is 150 ± 7.5 ppm, the smallest detected rspot is rspot = 0.070R* While for a 1.5 R⊕ and 1.75 R⊕ planet the smallest detected rspot becomes rspot = 0.061R* and rspot = 0.052R*, respectively.
3.5 Unexpected trend
Table 3 shows the comparison between Rp and the statistical mean of the starspot detection limit (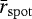 ), including its 1σ uncertainty. At first glance, Table 3 seems to be in contradiction with the statement small planets are needed to detect small starspots. However, looking at the top row of Table 3, we see that when the 1σ uncertainty in
), including its 1σ uncertainty. At first glance, Table 3 seems to be in contradiction with the statement small planets are needed to detect small starspots. However, looking at the top row of Table 3, we see that when the 1σ uncertainty in 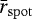 is taken into account, we see that the smallest planet (e.g. Rp = 1 R⊕) can detect the smallest starspot (e.g.
is taken into account, we see that the smallest planet (e.g. Rp = 1 R⊕) can detect the smallest starspot (e.g. 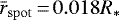 ). The results in Table 3 also indicate that the range of values for
). The results in Table 3 also indicate that the range of values for 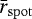 decreases with increasing Rp.
decreases with increasing Rp.
When examining Tables A.1–A.3, we can see an unexpected trend emerging: starspots that are small and hot can be detected by large planets, however, they cannot be detected by smaller planets. This unexpected and counter-intuitive trend, however, is a manifestation, from using a fixed cadence combined with the methodology used to detect starspot anomalies in transit light curves.
Increasing Rp not only increases the transit duration, it also increases the duration of the starspot anomaly. This is because a larger planetary disc spends longer occulting the starspot. For a fixed cadence (2 min for TESS) this equates to an increase in the number of data points which describe the starspot anomaly. As mentioned in Sect. 3 the mean flux of the data points within the starspot anomaly was used to determine if the starspot had been detected. This is in principle the same method used to detect starspot anomalies in observed light curves. In the case when a single data point describes the apex of a starspot anomaly (i.e. the 2D projection of rspot equals Rp ; Fig. 9) the data points which lie within the ingress and egress of the starspot anomaly reduce the mean flux. For a starspot anomaly that is described by multiple data points which form a plateau – i.e. the 2D projection of rspot is either larger or smaller than Rp (Fig. 10) – the mean flux increases because the data points lying on the starspot ingress and egress have a weaker impact. Because of this, a starspot with an apex requires a larger amplitude to be detected. This is correct as a single data point should require a larger amplitude (compared to multiple data points) to allow a confirmed starspot detection. However, this creates an unavoidable detection bias.
Figures 9 and 10 depict two identical scenarios except that they have two different Rp, Rp = 1.0 R⊕ (Fig. 9) and Rp = 1.75 R⊕ (Fig. 10). The starspot (rspot = 0.061R*) is not detected in Fig. 9, however by increasing the duration of the starspot anomaly and therefore the number of data points which describe this anomaly, the starspot is then detected (Fig. 10).
The mean amplitude of the starspot anomalies are 205 ppm (Fig. 9) and 394 ppm (Fig. 10). This shows how increasing the duration of starspot anomaly can allow for its detection and explains why large planets are needed to detect starspots which are both small and hot in TESS transit light curves.
 |
Fig. 8 Ninesimulated transit light curves generated by PRISM, showing the smallest detected starspot for 3 trends, Teff: top row; λobs: middle row; P: bottom row. Top row: simulations of a 1.5 R⊕ super-Earth planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0°, P = 1 d, λobs = 600 nm, and rms scatter 150 ± 7.5 ppm. Each column on the top row shows a different Tspot, where Tspot = 3000, 3050, and 3100 K (left to right). The smallest detected rspot are rspot = 0.026R* (red), rspot = 0.035R* (blue), and rspot = 0.044R* (green). Middle row: simulations of a 3.0 R⊕ Neptune-sized planet transiting a 4100 K, 0.623 R⊙ K5V dwarf star with i = 90.0°, P = 4 d, Tspot = 3900 K, and rms scatter 200 ± 10 ppm. Each column on the middle row shows a different λobs, where λobs = 600, 785, and 1000 nm (left to right). The smallest detected rspot values are rspot = 0.052R* (red), rspot = 0.061R* (blue), and rspot = 0.079R* (green). Bottom row: simulations of a 2.25 R⊕ sub-Neptune planet transiting a 3700 K, 0.493 R⊙ M1V dwarf star with i = 90.0°, Tspot = 3550 K, λobs = 1000 nm and rms scatter 100 ± 5 ppm. Each column on the bottom row shows a different P, where P = 2 d, 3 d and 4 d (left to right). The smallest detected rspot are rspot = 0.044R* (red), rspot = 0.044R* (blue), and rspot = 0.052R* (green). The solid lines represent the noise-free synthetic light curves containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. |
 |
Fig. 9 Example of a single data point describing the apex of a starspot anomaly. Using a 1.0 R⊕ Earth-sized planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0° and P = 2 d. The starspotproperties are θ = 0°, ϕ = 90°, rspot = 0.061R*, and Tspot = 3150 K. The observational wavelength and rms scatter for the simulated data were set at 785 nm and 200 ± 10 ppm, respectively. The solid line represents the noise-free synthetic light curve containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curve (see Sect. 3) with added Gaussian noise. |
 |
Fig. 10 Example of multiple data points describing the plateau of a starspot anomaly. Using a 1.75 R⊕ super-Earth planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0° and P = 2 d. The starspot properties are θ = 0°, ϕ = 90°, rspot = 0.061R*, and Tspot = 3150 K. The observational wavelength and rms scatter for the simulated data were set at 785 nm and 200 ± 10 ppm, respectively. The solid line represents the noise-free synthetic light curve containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curve (see Sect. 3) with added Gaussian noise. |
Comparison between Rp and 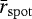 for the M4V, M1V and K5V host stars.
for the M4V, M1V and K5V host stars.
Thirty-six values of ρspot used in the simulations and the 3 calculated 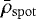 for the M4V, M1V, and K5V host star simulations (highlighted in bold).
for the M4V, M1V, and K5V host star simulations (highlighted in bold).
3.6 Comparing the change in flux between the planet and starspot
While the values of Rp and 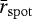 given in Table 3 are valuable they do not allow for a direct comparison between the three host star spectral types. To allow a direct comparison, Rp and
given in Table 3 are valuable they do not allow for a direct comparison between the three host star spectral types. To allow a direct comparison, Rp and 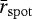 need to be converted into change in flux (ΔF). Rp can be converted to ΔFp using k2, where
need to be converted into change in flux (ΔF). Rp can be converted to ΔFp using k2, where
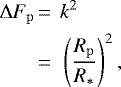 (4)
(4)
which gives the area of the planetary disc in units of a uniform stellar disc. Because the simulations used in this work examined starspot occultations when the starspot was at the centre of the stellar disc, we can use this approximation of ΔFp in the absence of limb darkening.
The surface area of the starspot is the solid angle, Ω, and can be determined from rspot (in units of angular radius) using
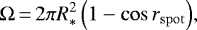 (5)
(5)
which in units of the stellar hemisphere (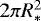 ) becomes
) becomes
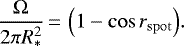 (6)
(6)
However, unlike the planet, the starspot emits a flux which means that the flux deficit caused by the starspot, ΔFspot, is related to rspot by ρspot using the following relation:
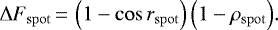 (7)
(7)
For the simulations in this work 36 different values of ρspot were used. These were derived using Eq. (2) using three values of Teff, four Tspot, and three λobs. This equates to 12 different values of ρspot for each stellar spectral class. To determine ΔFspot, the mean starspot contrast (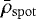 ) was calculated for each spectral class and are given in Table 4.
) was calculated for each spectral class and are given in Table 4.
Therefore ΔFspot was calculated for the nine 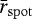 (Table 3) for each spectral class using the associated
(Table 3) for each spectral class using the associated 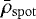 (Table 4). The resultant calculated values of ΔFp (Eq. (4)) and ΔFspot (Eq. (7)) are given in Figs. 11 and 12.
(Table 4). The resultant calculated values of ΔFp (Eq. (4)) and ΔFspot (Eq. (7)) are given in Figs. 11 and 12.
Figure 11 shows that the results for each of the three host stars are in excellent agreement with each other in terms of the smallest ΔFspot that can be detected. The simulation results indicate that when k ≥ 0.10 a starspot needs a larger ΔFspot to be detected, either by increasing rspot or by decreasing ρspot. The positive gradient towards larger ΔFp represents that larger planets can only detect larger or cooler starspots. The steep negative gradient towards smaller ΔFp shows that the effect from using a fixed cadence, combined with the method that is used to detect starspot anomalies, has a stronger influence on the size of starspot which can be detected in TESS transit light curves.
To determine which ΔFp allows for the smallest ΔFspot to be detected, we fitted a parametrised second order polynomial to the results. This was accomplished by parametrising ΔFp to a logarithmic scale given by
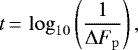 (8)
(8)
where t is the logarithmic parametrisation of ΔFp.
Figure 12 shows the comparison between t and ΔFspot, which indicates a quadratic relation between the two quantities. We used Markov chain Monte Carlo to fit a quadratic relation as follows:
![\begin{align*}\Delta F_{\mathrm{spot}} \,{=}&\, \left(0.00028\,{\pm}\,0.00001\right)t^2 \nonumber\\[2pt] &- \left(0.00121\,{\pm}\,0.00001\right)t \nonumber\\[2pt] &+ \left(0.00147\,{\pm}\,0.00002\right). \end{align*}](/articles/aa/full_html/2019/10/aa35742-19/aa35742-19-eq22.png) (9)
(9)
Using Eq. (9) and setting 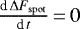 we find that the smallest detectable ΔFspot = 0.00015 ± 0.00001, when ΔFp = 0.0067 ± 0.0006 (k = 0.082 ± 0.004). This allows us to determine that for a 1 R⊕ planet, a host star with R* = 0.112 ± 0.005 R⊙ is required to detect starspots with ΔFspot = 0.00015 ± 0.00001. While for a 3 R⊕ sub-Neptune planet, a host star with R* = 0.335 ± 0.015 R⊙ is required to find starspots with ΔFspot = 0.00015 ± 0.00001.
we find that the smallest detectable ΔFspot = 0.00015 ± 0.00001, when ΔFp = 0.0067 ± 0.0006 (k = 0.082 ± 0.004). This allows us to determine that for a 1 R⊕ planet, a host star with R* = 0.112 ± 0.005 R⊙ is required to detect starspots with ΔFspot = 0.00015 ± 0.00001. While for a 3 R⊕ sub-Neptune planet, a host star with R* = 0.335 ± 0.015 R⊙ is required to find starspots with ΔFspot = 0.00015 ± 0.00001.
In Sect. 2.2 we describe how a degeneracy exists between rspot and ρspot. For the simulations performed in this work,the smallest rspot was determined for sets of fixed parameter values, which included ρspot (calculated from Tspot, Teff, and λobs using Eq. (2)). Table 4 gives the range of ρspot used in the simulations (0.53–0.93) and when combined with the results given in Tables A.1–A.3 allows an extrapolation to determine the largest ρspot for a fixed rspot.
However, Eq. (9) can be used to determine the largest average detectable ρspot for a fixed rspot. For a 1 RJup planet, transiting a 1 R⊙ star, the change in flux caused by the transiting planet is ΔFp ≈ 0.01. When parametrised using Eq. (8) gives t = 2. Equation (9) then calculates the smallest detectable ΔFspot for the system, ΔFspot = 0.000166 ± 0.00006. Using Eq. (7) with a given starspot angular radius, rspot = 5° (rspot = 0.087R*) we can determine the lowest contrast detectable in TESS transit light curves for the starspot, ρspot = 0.96 ± 0.02. While for a rspot = 2° (rspot = 0.035R*) we find the lowest contrast detectable to be ρspot = 0.73 ± 0.10. For a rspot = 1° (rspot = 0.017R*) Eq. (7) gives a negative value for ρspot, indicating that it is not possible for a rspot = 0.017R* starspot to be detected in TESS transit data of a 1 RJup planet that is transiting a 1 R⊙ star.
 |
Fig. 11 Plot of ΔFp and ΔFspot calculated from Eq. (4) and (7) combined with the best fitting model (solid black line). The blue data points represent the M4V host star results. The red data points represent the M1V host star results, while the green data points represent the K5V host star results. |
 |
Fig. 12 Plot of |
4 Discussion and conclusions
The key result from the simulations performed in this work indicates that when TESS observes a transiting planet that occults a starspot on the stellar disc, the characteristic blip of the starspot anomaly is seen in the resulting light curve. This removes any doubt that starspot anomalies are present in TESS light curves because the TESS primary targets are cooler (redder) host stars with shorter transit durations. It also opens the possibility of using the starspot tracking technique (e.g. Tregloan-Reed et al. 2013, 2015; Mohler-Fischer et al. 2013; Southworth et al. 2016; Mancini et al. 2017) to measure the orbital obliquity of TESS planetary systems. Particularly for targets where the conventional Rossiter-McLaughlin technique (Rossiter 1924; McLaughlin 1924; Schlesinger 1910, 1916; Holt 1893) is not viable (e.g. slow-rotators, small k, and active stars). The simulations then go further in determining the detection limits for a variety of starspot temperatures, planetary and stellar radii, photometric precision, orbital periods, and observational wavelengths. It was found that the starspot detection limits in TESS light curves for M4V, M1V, and K5V host stars were 4900 ± 1700, 13 800 ± 6000, and 15 900 ± 6800 km, respectively.
The simulations confirmed expected trends in the detection limits of starspot anomalies, including the photometric parameter dependencies of the amplitude of the starspot anomaly. The results confirmed that the amplitude of a starspot anomaly is strongly dependent on rspot and ρspot, and therefore, by association with ρspot, strongly dependent on Teff and λobs. While, the amplitude of the starspot anomaly is less dependent on P. The simulations then show that overall the detection limit of a starspot anomaly is dependent on Rp (Table 3) and is therefore dependent on ΔFplanet. However, the simulations uncovered an unexpected trend: starspots that are small and hot can be detected by large planets, however, they cannot be detected by smaller planets.
From our investigations of the synthetic light curves, we uncovered that the unexpected trend was a detection bias generated by the fixed 2 min cadence of TESS combined with the method used to determine if the starspot anomaly was detectable, by comparing the mean amplitude of a starspot anomaly to the observational noise. This detection method is in agreement with fitting starspot anomalies in transit light curves. If the mean amplitude of the starspot anomaly is not large enough, it is not possible to constrain the starspot properties (see Sect. 3). It was found that for anomalies with a short maximum duration (apex shape) the data points lying on the ingress and egress of the starspot anomaly reduced the mean amplitude. As a consequence for the starspot to be detected either rspot or Rp needed to be increased to increase the mean amplitude. Although as in the case depicted in Fig. 4, if the maximum amplitude of the starspot anomaly is below the detection threshold, then increasing rspot further did not allow a detection. If the maximum amplitude was tested against the rms scatter in the data instead of using the mean amplitude, this would allow starspot anomalies described by a single data point (i.e. apex shape) to be considered detected when in reality these anomalies would be dismissed as noise (e.g. Fig. 9). Using the mean amplitude of the starspot anomaly effectively mimics what happens when a transit-starspot model fits a starspot anomaly. Hence, the unexpected trend that smaller hot starspots are detected by larger planets will be seen when analysing TESS transit light curves. To counter this would require a reduction in the observational cadence, which would increase the number of data points that describe the starspot anomaly. However, this is not practical when analysing TESS transit data and would require further follow-up photometric observations using a different telescope.
By separating the simulations into three groups for each of the three host stars and then converting Rp and 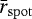 into ΔFplanet and ΔFspot, a direct comparison between the planets and starspots for the three host stars was made. The resultant comparison between ΔFplanet and ΔFspot shows excellent agreement of the simulations between the three host stars and indicates that the smallest and hottest starspots detected in TESS transit light curves are when k = 0.082 ± 0.004. By fitting a parametrised second order polynomial to the results, we are able to determine the minimum size and lowest contrast (highest intensity) that can be detected for a given value of k in the TESS exoplanetary transit data. The comparison also revealed that the effect from using a fixed 2 min cadence combined with the mean flux of a starspot anomaly to determine its detection had a larger impact on ΔFspot than Rp.
into ΔFplanet and ΔFspot, a direct comparison between the planets and starspots for the three host stars was made. The resultant comparison between ΔFplanet and ΔFspot shows excellent agreement of the simulations between the three host stars and indicates that the smallest and hottest starspots detected in TESS transit light curves are when k = 0.082 ± 0.004. By fitting a parametrised second order polynomial to the results, we are able to determine the minimum size and lowest contrast (highest intensity) that can be detected for a given value of k in the TESS exoplanetary transit data. The comparison also revealed that the effect from using a fixed 2 min cadence combined with the mean flux of a starspot anomaly to determine its detection had a larger impact on ΔFspot than Rp.
Young K and M dwarf stars are known to have a high starspot surface coverage (e.g. O’Neal et al. 2004; Jackson & Jeffries 2013). However, the activity-age relationship is still unknown. This leads to the question of how many TESS transit light curves will contain starspot anomalies. The simulations presented in this work are the starting point of answering this question in that the simulations show that starspot anomalies are observable in TESS transit light curves. The starspot distribution on the stellar disc is also an important factor in this question. Barnes et al. (2015) used high resolution Doppler images of two M dwarfs (GJ 791.2 A; M4.5: LP 944-20; M9) to determine the overall starspot filling factors ≈ 3 and ≈ 1.5% for the two M dwarfs. However, Barnes et al. (2015) found maximum starspot filling factors 82.3 and 76.6% at high latitudes (polar). If the starspot distributions of GJ 791.2 A and LP 944-20 can be considered typical of M dwarf stars that will be observed by TESS, then a polar biased starspot distribution will affect the total number of TESS transit light curves which contain a starspot anomaly. Determining the smallest detectable starspot size for a range of planetary sizes, starspot temperatures, orbital periods, and noise levels is an essential first step in beginning to forecast the number of TESS transit light curves which will be affected by starspot anomalies. Therefore, these studies will gauge the importance and the future reliance by the community on transit-starspot models.
Acknowledgements
We would like to thank the anonymous referee and the editor for their helpful comments, which improved the quality of this manuscript. This work was supported by a CONICYT/FONDECYT 2018 Postdoctoral research grant, project number: 3180071. J.T.R. thanks the Centro de Astronomía (CITEVA), Universidad de Antofagasta for hosting the CONICYT/FONDECYT 2018 Postdoctoral research grant. The following internet-based resources were used in the research for this paper: the NASA Astrophysics Data System; the SIMBAD database and VizieR catalogue access tool operated at CDS, Strasbourg, France, and the arXiv scientific paper preprint service operated by Cornell University.
Appendix A Full results of all simulations
Smallest detectable value of rspot determined from the 6718 simulations of the 1296 scenarios that used an M4V dwarf host star.
Smallest detectable value of rspot determined from the 7812 simulations of the 1296 scenarios that used an M1V dwarf host star.
Smallest detectable value of rspot determined from the 6737 simulations of the 1296 scenarios that used an K5V dwarf host star.
References
- Ballerini, P., Micela, G., Lanza, A. F., & Pagano, I. 2012, A&A, 539, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, J. R., Jeffers, S. V., Jones, H. R. A., et al. 2015, ApJ, 812, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Bayliss, D., Gillen, E., Eigmüller, P., et al. 2018, MNRAS, 475, 4467 [NASA ADS] [CrossRef] [Google Scholar]
- Béky, B., Kipping, D. M., & Holman, M. J. 2014, MNRAS, 442, 3686 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G., Guenther, E. W., Pallé, E., et al. 2017, A&A, 600, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2017, A&A, 600, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Dragomir, D., Teske, J., Gunther, M. N., et al. 2019, ApJ, 875, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Dressing, C. D., & Charbonneau, D. 2013, ApJ, 767, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Dressing, C. D., & Charbonneau, D. 2015, ApJ, 807, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bayliss, D., Brahm, R., et al. 2015, AJ, 149, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, E., Ribas, I., Jordi, C., et al. 2016, A&A, 586, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holt, J. R. 1893, Astronomy and Astro-Physics, 12, 646 [Google Scholar]
- Huang, C. X., Burt, J., Vanderburg, A., et al. 2018, ApJ, 868, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, R. J., & Jeffries, R. D. 2013, MNRAS, 431, 1883 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, Proc. SPIE, 9913, 99133E [Google Scholar]
- Johnson, J. A., Gazak, J. Z., Apps, K., et al. 2012, AJ, 143, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Juvan, I. G., Lendl, M., Cubillos, P. E., et al. 2018, A&A, 610, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kopparapu, R. K., Ramirez, R., Kasting, J. F., et al. 2013, ApJ, 765, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, L., Ciceri, S., Chen, G., et al. 2013, MNRAS, 436, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, L., Southworth, J., Ciceri, S., et al. 2014, MNRAS, 443, 2391 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, L., Esposito, M., Covino, E., et al. 2015, A&A, 579, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mancini, L., Southworth, J., Raia, G., et al. 2017, MNRAS, 465, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L. 2016, A&A, 591, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, D. B. 1924, ApJ, 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Mohler-Fischer, M., Mancini, L., Hartman, J. D., et al. 2013, A&A, 558, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montalto, M., Boué, G., Oshagh, M., et al. 2014, MNRAS, 444, 1721 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, T. D., & Swift, J. 2014, ApJ, 791, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Nikolov, N., Chen, G., Fortney, J. J., et al. 2013, A&A, 553, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Neal, D., Neff, J. E., Saar, S. H., & Cuntz, M. 2004, AJ, 128, 1802 [NASA ADS] [CrossRef] [Google Scholar]
- Oshagh, M., Boisse, I., Boué, G., et al. 2013, A&A, 549, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., Conroy, K. E., Horvat, M., et al. 2016, ApJS, 227, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Rabus, M., Alonso, R., Belmonte, J. A., et al. 2009, A&A, 494, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Latham, D. W., Vanderspek, R. K., et al. 2009, BAAS, 41, 193 [NASA ADS] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, Proc. SPIE, 9143, 914320 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., & Winn, J. N. 2011, ApJ, 743, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., Winn, J. N., Holman, M. J., et al. 2011, ApJ, 733, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., Fabrycky, D. C., Winn, J. N., et al. 2012, Nature, 487, 449 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sanchis-Ojeda, R., Winn, J. N., Marcy, G. W., et al. 2013, ApJ, 775, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Schlesinger, F. 1910, Publications of the Allegheny Observatory of the University of Pittsburgh (Charleston: Nabu Press), 1, 123 [NASA ADS] [Google Scholar]
- Schlesinger, F. 1916, Publications of the Allegheny Observatory of the University of Pittsburgh (Charleston: Nabu Press), 3, 23 [NASA ADS] [Google Scholar]
- Silva, A. V. R. 2003, ApJ, 585, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Silva-Válio, A. 2010, IAU Symp., 264, 440 [NASA ADS] [Google Scholar]
- Silva-Valio, A., Lanza, A. F., Alonso, R., & Barge, P. 2010, A&A, 510, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J. 2008, MNRAS, 386, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2010, MNRAS, 408, 1689 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2011, MNRAS, 417, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2013, A&A, 557, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J., Maxted, P. F. L., & Smalley, B. 2004, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Smalley, B., Maxted, P. F. L., Claret, A., & Etzel, P. B. 2005, MNRAS, 363, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Bruntt, H., & Buzasi, D. L. 2007, A&A, 467, 1215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Southworth, J., Hinse, T. C., Dominik, M., et al. 2009, ApJ, 707, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Tregloan-Reed, J., Andersen, M. I., et al. 2016, MNRAS, 457, 4205 [NASA ADS] [CrossRef] [Google Scholar]
- Stassun, K. G., Oelkers, R. J., Pepper, J., et al. 2018, AJ, 156, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, P. W., Winn, J. N., Berta-Thompson, Z. K., et al. 2015, ApJ, 809, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, P. W., Winn, J. N., Berta-Thompson, Z. K., et al. 2017, ApJ, 837, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Tregloan-Reed, J., Southworth, J., & Tappert, C. 2013, MNRAS, 428, 3671 [NASA ADS] [CrossRef] [Google Scholar]
- Tregloan-Reed, J., Southworth, J., Burgdorf, M., et al. 2015, MNRAS, 450, 1760 [NASA ADS] [CrossRef] [Google Scholar]
- Tregloan-Reed, J., Southworth, J., Mancini, L., et al. 2018, MNRAS, 474, 5485 [NASA ADS] [CrossRef] [Google Scholar]
- Valio, A., Estrela, R., Netto, Y., Bravo, J. P., & de Medeiros, J. R. 2017, ApJ, 835, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderspek, R., Huang, C. X., Vanderburg, A., et al. 2019, ApJ, 871, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., Jones, M., Shporer, A., et al. 2019, AJ, 157, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Wheatley, P. J., Pollacco, D. L., Queloz, D., et al. 2013, Eur. Phys. J. Web Conf., 47, 13002 [CrossRef] [Google Scholar]
- Wilson, R. E. 1979, ApJ, 234, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E. 1990, ApJ, 356, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E. 2008, ApJ, 672, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E. 2012, AJ, 144, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N. 2010, Exoplanet Transits and Occultations, ed. S. Seager (Tucson, AZ: University of Arizona Press), 55 [Google Scholar]
From TESS data MAST page; accessed 2019-06-24.
The latest version of PRISM is available from GitHub
For further details see http://www.harrisgeospatial.com/ ProductsandTechnology/Software/IDL.aspx
Mission specified noise floor at 60 ppm hr1∕2 (see Sullivan et al. 2015).
We ignore the coefficient uncertainties in the polynomials presented by Boyajian et al. (2012) as we are generating hypothetical host stars, whose physical properties are consistent with the physical properties of observed stars of the same spectral type.
All Tables
Extrapolated values of R* and M* using Teff from polynomials derived from interferometric measurements of M and K dwarf stars (Eqs. (8) and (10), Boyajian et al. 2012), for the three simulated host stars combined with the calculated log g and u1 and u2 for the quadratic limb darkening law from Claret (2017).
Thirty-six values of ρspot used in the simulations and the 3 calculated 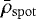 for the M4V, M1V, and K5V host star simulations (highlighted in bold).
for the M4V, M1V, and K5V host star simulations (highlighted in bold).
Smallest detectable value of rspot determined from the 6718 simulations of the 1296 scenarios that used an M4V dwarf host star.
Smallest detectable value of rspot determined from the 7812 simulations of the 1296 scenarios that used an M1V dwarf host star.
Smallest detectable value of rspot determined from the 6737 simulations of the 1296 scenarios that used an K5V dwarf host star.
All Figures
 |
Fig. 1 Simulated 2 min cadence TESS light curve of a 1 R⊕ planet orbiting an M4V dwarf star with P = 12 d and an rms scatter of 104 ppm (generated by PRISM). The transit duration is approximately 8 min and only 3 data points lie within the transit. |
| In the text | |
 |
Fig. 2 Example light curve (left) and stellar disc (right) generated by PRISM. Light curve: the solid line represents the noise-free synthetic light curve containing the starspot anomaly, while, the filled circles represent the spot-free synthetic light curve (see Sect. 3) with added Gaussian noise. Stellar disc: the central solid line represents the stellar equator (assuming orbital alignment) and the upper and lower solid linesrepresent the upper and lower boundaries of the transit cord. These were generated with a 1.5 R⊕ super-Earth planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0° and P = 1 d. The starspotproperties are: θ = 0°, ϕ = 90°, rspot = 0.035R* and Tspot = 3000 K. The observational wavelength and rms scatter for the simulated data were set at 785 nm and 150 ± 7.5 ppm, respectively. |
| In the text | |
 |
Fig. 3 Two simulated transit light curves generated by PRISM. These were both generated using a 1.0 R⊕ Earth-sized planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0° and P = 1 d. The starspotproperties are θ = 0°, ϕ = 90°, rspot = 0.009R* (left), rspot = 0.017R* (right), and Tspot = 3000 K. The observational wavelength and rms scatter for the simulated transits were set at 600 nm and 60 ppm, respectively. The starspot anomaly becomes visible over the simulated noise when rspot is increased from 0.009R* to 0.017R*. The solid lines represents the noise-free synthetic light curves containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. |
| In the text | |
 |
Fig. 4 Three simulated transit light curves (top panels) and stellar disc outputs (bottom panels), generated by PRISM. Light curves: the solid lines represent the noise-free synthetic light curves containing the starspot anomaly, while, the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. Stellar discs: the central solid lines represents the stellar equator (assuming orbital alignment) and the upper and lower solid lines represent the upper and lower boundaries of the transit cords. Because the high ρspot, the starspot boundary is highlighted with a black circular boarder. The observational wavelength and rms scatter for the simulated transits are set at 1000 nm and 200 ppm, respectively. These were generated using a 1.0 R⊕ Earth-sized planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0° and P = 1 d. The starspotproperties were set at θ = 0°, ϕ = 90° and Tspot = 3150 K (ρspot = 0.93). Left panels: rspot = 0.087R*, middle panels: rspot = 0.175R*, right panels: rspot = 0.262R*. |
| In the text | |
 |
Fig. 5 Two simulated transit light curves generated by PRISM. These were both generated using a 2.75 R⊕ sub-Neptune planet transiting a 3700 K, 0.493 R⊙ M1V dwarf star with i = 90.0° and P = 3 d. The starspot properties are θ = 0°, ϕ = 90°, rspot = 0.009R* (left), rspot = 0.017R* (right), and Tspot = 3400 K. The observational wavelength and rms scatter for the simulated transits were set at 785 nm and 60 ppm, respectively. The starspot anomaly becomes visible over the simulated noise when rspot is increased from 0.009R* to 0.017R*. The solid lines represent the noise-free synthetic light curves containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. |
| In the text | |
 |
Fig. 6 Two simulated transit light curves generated by PRISM. These were both generated using a 4.5 R⊕ Neptune-sized planet transiting a 4100 K, 0.623 R⊙ K5V dwarf star with i = 90.0° and P = 4 d. The starspotproperties are θ = 0°, ϕ = 90°, rspot = 0.009R* (red), rspot = 0.017R* (blue), and Tspot = 3700 K. The observational wavelength and rms scatter for the simulated transits were set at 785 nm and 60 ppm, respectively. The starspot anomaly becomes visible over the simulated noise when rspot is increased from 0.009R* to 0.017R*. The solid lines represents the noise-free synthetic light curves containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. |
| In the text | |
 |
Fig. 7 Four simulated transit light curves generated by PRISM. The observational wavelength of the simulated transits was 785 nm. These were generated using a 3.0 R⊕ sub-Neptune planet transiting a 3700 K, 0.493 R⊙ M1V dwarf star with i = 90.0° and P = 2 d. The starspotproperties were set at θ = 0°, ϕ = 90° and Tspot = 3475 K. The rms scatter of the light curves from left to right are 60, 100, 150, and 200 ppm. Each light curve shows the smallest detectable starspot size for the scenarios, 0.017R* (red), 0.026R* (blue), 0.035R* (green), and 0.044R* (purple), which increases with increasing noise. The solid lines represents the noise-free synthetic light curves containing the starspotanomaly, while the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. |
| In the text | |
 |
Fig. 8 Ninesimulated transit light curves generated by PRISM, showing the smallest detected starspot for 3 trends, Teff: top row; λobs: middle row; P: bottom row. Top row: simulations of a 1.5 R⊕ super-Earth planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0°, P = 1 d, λobs = 600 nm, and rms scatter 150 ± 7.5 ppm. Each column on the top row shows a different Tspot, where Tspot = 3000, 3050, and 3100 K (left to right). The smallest detected rspot are rspot = 0.026R* (red), rspot = 0.035R* (blue), and rspot = 0.044R* (green). Middle row: simulations of a 3.0 R⊕ Neptune-sized planet transiting a 4100 K, 0.623 R⊙ K5V dwarf star with i = 90.0°, P = 4 d, Tspot = 3900 K, and rms scatter 200 ± 10 ppm. Each column on the middle row shows a different λobs, where λobs = 600, 785, and 1000 nm (left to right). The smallest detected rspot values are rspot = 0.052R* (red), rspot = 0.061R* (blue), and rspot = 0.079R* (green). Bottom row: simulations of a 2.25 R⊕ sub-Neptune planet transiting a 3700 K, 0.493 R⊙ M1V dwarf star with i = 90.0°, Tspot = 3550 K, λobs = 1000 nm and rms scatter 100 ± 5 ppm. Each column on the bottom row shows a different P, where P = 2 d, 3 d and 4 d (left to right). The smallest detected rspot are rspot = 0.044R* (red), rspot = 0.044R* (blue), and rspot = 0.052R* (green). The solid lines represent the noise-free synthetic light curves containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curves (see Sect. 3) with added Gaussian noise. |
| In the text | |
 |
Fig. 9 Example of a single data point describing the apex of a starspot anomaly. Using a 1.0 R⊕ Earth-sized planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0° and P = 2 d. The starspotproperties are θ = 0°, ϕ = 90°, rspot = 0.061R*, and Tspot = 3150 K. The observational wavelength and rms scatter for the simulated data were set at 785 nm and 200 ± 10 ppm, respectively. The solid line represents the noise-free synthetic light curve containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curve (see Sect. 3) with added Gaussian noise. |
| In the text | |
 |
Fig. 10 Example of multiple data points describing the plateau of a starspot anomaly. Using a 1.75 R⊕ super-Earth planet transiting a 3200 K, 0.155 R⊙ M4V dwarf star with i = 90.0° and P = 2 d. The starspot properties are θ = 0°, ϕ = 90°, rspot = 0.061R*, and Tspot = 3150 K. The observational wavelength and rms scatter for the simulated data were set at 785 nm and 200 ± 10 ppm, respectively. The solid line represents the noise-free synthetic light curve containing the starspot anomaly, while the filled circles represent the spot-free synthetic light curve (see Sect. 3) with added Gaussian noise. |
| In the text | |
 |
Fig. 11 Plot of ΔFp and ΔFspot calculated from Eq. (4) and (7) combined with the best fitting model (solid black line). The blue data points represent the M4V host star results. The red data points represent the M1V host star results, while the green data points represent the K5V host star results. |
| In the text | |
 |
Fig. 12 Plot of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.