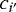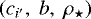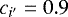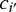| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201935709 | |
| Published online | 25 September 2019 | |
Multicolour photometry for exoplanet candidate validation★
1
Instituto de Astrofísica de Canarias (IAC),
38200 La Laguna,
Tenerife,
Spain
e-mail: hannu@iac.es
2
Department Astrofísica, Universidad de La Laguna (ULL),
38206 La Laguna,
Tenerife,
Spain
3
Bøggildsvej 14,
8530 Hjortshøj,
Denmark
4
Department of Astronomy, The University of Tokyo,
7-3-1 Hongo,
Bunkyo-ku,
Tokyo 113-0033,
Japan
5
Astrobiology Center,
2-21-1 Osawa,
Mitaka,
Tokyo 181-8588,
Japan
6
Japan Science and Technology Agency, PRESTO,
2-21-1 Osawa,
Mitaka,
Tokyo 181-8588,
Japan
7
National Astronomical Observatory of Japan,
2-21-1 Osawa,
Mitaka,
Tokyo 181-8588,
Japan
8
Department of Earth and Planetary Science, Graduate School of Science, The University of Tokyo,
7-3-1 Hongo,
Bunkyo-ku,
Tokyo 113-0033,
Japan
9
Optical and Infrared Astronomy Division, National Astronomical Observatory,
Mitaka, Tokyo, Japan
10
Department of Astronomical Science, SOKENDAI (The Graduate University of Advanced Studies), Mitaka, Tokyo, Japan
11
Department of Physics, Kyoto Sangyo University, Motoyama, Kamigamo, Kita-ku,
Kyoto
603-8555, Japan
12
European Space Agency, European Space Research and Technology Centre,
Keplerlaan 1,
2201 AZ Noordwijk,
The Netherlands
Received:
16
April
2019
Accepted:
22
July
2019
Context. The TESS and PLATO missions are expected to find vast numbers of new transiting planet candidates. However, only a fraction of these candidates will be legitimate planets, and the candidate validation will require a significant amount of follow-up resources. Radial velocity (RV) follow-up study can be carried out only for the most promising candidates around bright, slowly rotating, stars. Thus, before devoting RV resources to candidates, they need to be vetted using cheaper methods, and, in the cases for which an RV confirmation is not feasible, the candidate’s true nature needs to be determined based on these alternative methods alone.
Aims. We study the applicability of multicolour transit photometry in the validation of transiting planet candidates when the candidate signal arises from a real astrophysical source (transiting planet, eclipsing binary, etc.), and not from an instrumental artefact. Particularly, we aim to answer how securely we can estimate the true uncontaminated star-planet radius ratio when the light curve may contain contamination from unresolved light sources inside the photometry aperture when combining multicolour transit observations with a physics-based contamination model in a Bayesian parameter estimation setting. More generally, we study how the contamination level, colour differences between the planet host and contaminant stars, transit signal-to-noise ratio, and available prior information affect the contamination and true radius ratio estimates.
Methods. The study is based on simulations and ground-based multicolour transit observations. The contamination analyses were carried out with a contamination model integrated into the PYTRANSIT v2 transit modelling package, and the observations were carried out with the MuSCAT2 multicolour imager installed in the 1.5 m Telescopio Carlos Sanchez in the Teide Observatory, in Tenerife.
Results. We show that multicolour transit photometry can be used to estimate the amount of flux contamination and the true radius ratio. Combining the true radius ratio with an estimate for the stellar radius yields the true absolute radius of the transiting object, which is a valuable quantity in statistical candidate validation, and enough in itself to validate a candidate whose radius falls below the theoretical lower limit for a brown dwarf.
Key words: planetary systems / planets and satellites: detection / methods: statistical / methods: numerical / methods: data analysis / techniques: photometric
The MuSCAT lightcurve data are also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/630/A89
© ESO 2019
1 Introduction
Both the currently operational TESS and the upcoming PLATO mission are expected to find vast numbers of new exoplanet candidates (Ricker et al. 2014; Rauer et al. 2014), while the current ground-based surveys, such as WASP (Pollacco et al. 2006), continue producing new discoveries at a steady pace. However, as with the previous CoRoT, Kepler, and K2 missions, only a fraction of these candidates will be legitimate planets (Moutou et al. 2009; Almenara et al. 2009; Santerne et al. 2012; Fressin et al. 2013). Several astrophysical phenomena, such as eclipsing binaries (EBs), blended eclipsing binaries (BEBs), and transiting brown dwarfs, can lead to a photometric signal that mimics an exoplanet transit (Brown 2003; Cameron 2012), and most of the candidates require follow-up observations to clarify the nature of the object causing the observed transit-like signal (e.g. Cabrera et al. 2017; Mullally et al. 2018).
Measuring the mass of a transiting object using radial velocity (RV) observations is considered to be the most reliable technique for the confirmation of transiting exoplanet candidates. However, RV observations can be carried out only with a small number of specialised instruments installed in high-demand telescopes, and the observations are restricted to candidates with a relatively high planet-star mass ratio orbiting bright host stars. Moreover, RVs can be difficult to measure for certain types of stars (for example fast rotators, hot stars, or very metal-poor stars) due to the absence or broadening of the absorption lines on which the cross-correlation is used to measure the RV depends.
While the methods available for candidate planet vetting and validation1 have diversified during the last decade2, there is still a strong demand for observationally economical approaches to reduce the amount of false positives reaching the RV follow-up phase. Additionally, methods that can reliably identify false positives are required in candidate validation for cases where the RV follow-up is not viable, such as with rapidly rotating host stars.
Eclipsing binaries, and in particular BEBs, where the light of an unresolved EB contaminates an otherwise constant star (Brown 2003; Mandushev et al. 2005; Cameron 2012), can closely resemble exoplanet transits. BEBs are a common source of false positive transit signals, and can be problematic for RV analysis. For example, a faint EB blended with a bright star may not show any detectable RV signal since the bright star dominates the spectrum. Another (although rarer) case is that of a BEB where all the stars have approximately the same colour. This happened with WASP-9b, where the system exhibited strong radial velocity variations consistent with a planet with a mass of 2.3 MJup, showed no sign of any bisector variation, yet still proved to be a false positive. When the WASP team attempted to detect the Rossiter-McLaughlin effect for this previously announced exoplanet, they noticed highly rotationally-broadened spectral lines shifting back and forth with the same period as their proposed exoplanet. The only possible explanation for this phenomena was that WASP-9b was actually not a planet, but a BEB with little colour difference between the stars. Generally, the presence of a transit combined with a mass from RV measurements that exhibit no bisector variations is considered enough for confirmation, yet the case of WASP-9b shows that these criteria may not be sufficient in all cases.
Both TESS and PLATO have large pixel sizes (21′′ and 15′′, respectively), which leads to blending being a more significant issue than with either CoRoT or Kepler with pixel sizes of 2.32′′ and 3.98′′, respectively. Thus, even while point spread function (PSF) centroid variations can be used to identify many of the blending cases (Bryson et al. 2013), the TESS and PLATO candidate vetting will rely heavily on ground-based photometric follow-up study.
This paper explores the use of multicolour transit photometry in transiting exoplanet candidate vetting and validation, continuing the ideas presented originally by Rosenblatt (1971), developed further by Drake (2003) and Tingley (2004), and applied in practice by Tingley et al. (2014).
While the mass of a planet obtained from the RV observations is an important quantity, it is not strictly necessary for the validation of a planet candidate. Restricting the radius of the transiting body to planetary size is an equally viable option. This may proceed by establishing a radius less than the smallest brown dwarfs (~0.8 RJup, Burrows et al. 2011) or a radius consistent with a hot Jupiter and an upper mass limit (via RV) less than a brown dwarf (~ 13 MJup, Chabrier & Baraffe 2000). The radius of a transiting body can be measured in two different ways, either using the Rossiter-McLaughlin effect (Worek 2000; Giménez 2006) or through the analysis of transit photometry. The latter yields an estimate for the (apparent) planet-star radius ratio based on the transit depth, 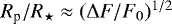 . However, this ratio is valid only if we can assure that the occulting body is not performing a grazing eclipse or that the light curve does not contain any relevant flux from a third body (flux contamination, from now on). If the light curve is contaminated, the measured apparent radius ratio is smaller than the true radius ratio (that is, the transit appears shallower than it truly is), and a radius ratio estimate that has been derived with a model that does not include contamination can not be trusted.
. However, this ratio is valid only if we can assure that the occulting body is not performing a grazing eclipse or that the light curve does not contain any relevant flux from a third body (flux contamination, from now on). If the light curve is contaminated, the measured apparent radius ratio is smaller than the true radius ratio (that is, the transit appears shallower than it truly is), and a radius ratio estimate that has been derived with a model that does not include contamination can not be trusted.
Multicolour photometry has already been used in the vetting of space-based transit candidates, both from Kepler; for example in combination with data from Spitzer (Ballard et al. 2011) or from precise ground-based photometry (Colón & Ford 2011; Tingley et al. 2014), as well as in data from CoRoT, where colour differences among its three-channel data were routinely used to reject planet candidates (Carone et al. 2012). However, multicolour transit photometry can be utilised further than what is currently done. For candidate vetting purposes, it allows one to estimate the true radius ratio that accounts for possible flux contamination from unresolved sources, including the transiting object itself, using relatively small (possibly automatised) ground-based telescopes, thus revealing blends. The true radius ratio estimate can then be combined with the stellar radius estimate to produce an estimate for the absolute planet radius, which can be used in the candidate validation. As an additional benefit, the observations improve the candidate’s ephemeris, which can be crucial when following up candidates from missions consisting of relatively short stares, such as TESS (Deeg & Tingley 2017).
In this paper, we study the applicability of multicolour transit photometry in transiting planet candidate validation, assuming that the candidate signal arises from a real astrophysical event (such as a planetary transit or binary eclipse), and is not from an instrumental source. Particularly, we aim to answer how accurately can the true radius ratio be estimated, and how the contamination level, host-contaminant colour difference, transit signal-to-noise ratio (S/N), and available prior information affect the contamination and true radius ratio estimates.
Most previous work involving multicolour photometry of planetary transits has interpreted the different passbands individually; for example by fitting a transit model on each passband individually. In this work, we combine a physics-based contamination model with a Bayesian parameter estimation approach where all passbands are modelled jointly. This allows us to break the degeneracies between the impact parameter, radius ratio, stellar limb darkening, and possible flux contamination, yielding improved orbital parameter estimates, an estimate for the level of contamination, and a robust true planet-star radius ratio estimate.
The simulation and light curve analysis codes developed for this paper are publicly available from GitHub. The contamination model is detailed in Appendix A, and included in the transit modelling package PYTRANSIT v2, which is also publicly available from GitHub3.
2 Transit colour signatures
Flux contamination (blending) decreases the observed transit depth and leads to incorrect transit – and thus planetary – parameters (Daemgen et al. 2009). The effects from contamination on a single passband are degenerate with the effects from orbital geometry, stellar limb darkening, and radius ratio, which means single colour observations cannot generally be used to constrain contamination.
Two separate colour-dependent effects yield information about the degree of contamination and the true radius ratio of the transiting object:
- 1.
Colour differences between the stars contributing flux to the observed light curve will lead to variations in the transit depth observed in different passbands (Drake 2003; Tingley 2004). This makes identifying EBs and BEBs relatively easy, since the variations in transit depth can be significant if the stars have very different colours.
- 2.
The transit itself produces a colour-dependent signal where the shape of the signal depends on the size of the transiting object. As originally noted by Rosenblatt (1971) and elaborated in more detail by Tingley (2004), systems with ratio of radii genuinely consistent with exoplanets exhibit a distinctive, double-horned colourimetric signature during transit that increases in prominence relative to the transit depth as the radius ratio decreases. This effect does not depend on the colour differences between the host and the contaminant(s), and can be used to estimate blending even when all the components have the same colour.
Contamination measures based on the analysis of multicolour photometric time series can reveal all contaminating sources, regardless of proximity in the sky – including those that are actually gravitationally bound to the host star, and therefore extremely hard to resolve.
The first effect, colour-dependent transit depth variations due to contamination from a star of a different spectral type (colour) than the host star, is well known and has been used in planet candidate validation (O’Donovan et al. 2006, 2007; Ballard et al. 2011; Cochran et al. 2011; Tingley et al. 2011; Colón & Ford 2011). Figure 1 demonstrates the colour-dependent transit depth variations when the host and contaminant stars have different colours. Panel a shows an uncontaminated transit by a planet with a true planet-star radius ratio (ktrue) of 0.1 observed in the i′ band, and panel b an M-dwarf eclipsed by an object with a true radius ratio of 0.32 blended with a G-star so that 90% of the total flux comes from the contaminant (c = 0.9) leading to an apparent radius ratio (kapp) of 0.1 in the i′ band. Panel c shows the same contaminated transit in g′, r′, i′, and z′, where the strong transit depth variations make the significant contamination evident. Figure 2 demonstrates the transit depth variations further as a function of impact parameter. Since the variations are due to the changing contamination (i.e. the relative brightness of the stars vary as a function of wavelength), the effect is not dependent on the geometric properties of the transiting object’s orbit.
The second effect is less well known, and is illustrated in Fig. 3. Rosenblatt (1971) was the first to propose to use the distinctive signature that appears in multicolour time series photometry of the parent star during an exoplanet transit to discriminatebetween eclipsing binaries and transiting exoplanets. This signature arises from the interplay between the relatively small size of a planet compared to its parent star and differential limb darkening. Qualitatively speaking, the light coming from a stellar disc is bluer in its centre than near its limb. Therefore, at the beginning of all uncontaminated eclipses and transits, the integrated light from the stellar disc becomes bluer, as the redder light at the limb is occulted. What follows depends primarily on the radius-ratio of the system (see Tingley 2004, for details). At one extreme, if the transiting object is much smaller than the transited one, the redder light at the limb is revealed and the bluer light at the centre of the disc is occulted as the transit proceeds, causing a red-ward shift in the integrated light. This reaches a maximum at transit centre, after which the entire process is repeated in reverse during egress. This results in a sharp blue spike in the colourimetry at both ingress and egress, with a red-ward bulge near the transit centre, the details of which depend on the impact parameter. The situation at the other extreme – two bodies approximately the same size – is markedly different, as the redder light at the limb remains occulted for most or all of the transit, resulting in a distinct absence of sharp features of any sort – whether or not light from any third star is included.
In practice, these two effects can be included in the transit model used to model the multicolour photometry. Including a passband dependent contamination into a transit model takes both effects into account naturally, and allows for the per-passband contamination and the true radius ratio to be estimated directly from the multicolour observations.
 |
Fig. 1 Comparison between a planetary transit and blended eclipsing binary. Panel a: uncontaminated transit by a planet with radius ratio of 0.1 observed in the i′ band, panelb: faint M-dwarf transited by an object with a radius ratio of 0.32 strongly contaminated by a G star (c = 0.9, i.e. 10% of the total flux comes from the M dwarf, and 90% from the G star) leading to an apparent radius ratio of 0.1 in the i′ band, and panel c: same contaminated transit observed in g′, r′, i′, and z′ bands. |
3 Numerical methods
We developed a physics-based contamination model that is used to carry out the analyses presented in this paper, and included it in PYTRANSIT v2 (Parviainen 2015). The model uses synthetic stellar spectra calculated with PHOENIX by Husser et al. (2013), and is detailed in Appendix A.
The analysis of simulations and observations is carried out with PYTHON code utilising SCIPY, NUMPY (van der Walt et al. 2011), ASTROPY (Astropy Collaboration 2013), IPYTHON (Perez & Granger 2007), PANDAS (Mckinney 2010), MATPLOTLIB (Hunter 2007), SEABORN 4, and F2PY (Peterson 2009). The limb darkening computations were carried out with LDTK 5 (Parviainen & Aigrain 2015), global optimisation was carried out with PYDE 6, the Markov chain Monte Carlo (MCMC) sampling was carried out with EMCEE (Foreman-Mackey et al. 2013; Goodman & Weare 2010), and the Gaussian processes (GPs) were computed using GEORGE7 (Ambikasaran et al. 2015).
 |
Fig. 2 Effect of varying impact parameter on transit depth colour differences when host and contaminant stars are of different spectral types (M and G). The setup is the same as in Fig. 1c, but the impact parameter varies from panel to panel. The colour differences between the stars lead to differences in the relative contamination from one passband to another, which leads to variations in the observed transit depths. |
 |
Fig. 3 Examples of the transit colour differences when the host and contaminant are of same spectral type for three contamination values and three impact parameters. The smaller the transiting object is, the sharper the differential features are. |
4 Simulations
4.1 Overview
Before studying real observations, we study the practical applicability of the multicolour validation method using simulated transit light curves. The simulations mimic observations by an instrument observing four passbands simultaneously (g′, r′, i′, z′), installed in a (~1.5 m) ground-based telescope located in an observatory with good observing conditions. The simulations were designed to match closely the instrument and telescope setup used for the observational study presented in Sect. 5, that is, MuSCAT2 multicolour imager installed in the 1.5 m Telescopio Carlos Sanchez in the Teide Observatory (Narita et al. 2018). The noise level, 1000 ppm over an exposure of 60 s, is also based on existing observations for a V = 12 star with this setup. However, we consider only white noise, and leave the effects from correlated noise for a later study.
The simulations are divided into separate sets of illustrative scenarios. For each scenario, the computations are repeated for combinations of apparent radius ratio (kapp = {0.07, 0.10, 0.15}), impact parameter (b = {0.0, 0.5, 0.85}), number of observed transits (nn = {1, 2, 4}), and transit duration (T14 ~ {1 h, 2 h}), leading to 54 simulations per scenario.
We parametrise the planet candidate orbit by the zero epoch (t0), period (p), stellar density (ρ⋆), and impact parameter (b), and assume zero eccentricity for simplicity. The planet and the contamination are parametrised by the effective temperatures of the host (TEff,H) and contaminant (TEff,C), the true uncontaminated planet-star area ratio (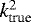 ), and the apparent area ratio in the i′ passband (
), and the apparent area ratio in the i′ passband (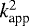 ). The contamination in the reference i′ band is calculated from the true and contaminated area ratios, and PYTRANSIT’s contamination module is used to calculate the contamination in the rest of the passbands.
). The contamination in the reference i′ band is calculated from the true and contaminated area ratios, and PYTRANSIT’s contamination module is used to calculate the contamination in the rest of the passbands.
We carry out most of the simulations both with and without an informative prior on TEff,H, where the informative prior is set to constrain TEff,H close to the true value of the dominant component TEff (that is, we also study cases where the contaminant dominates and we misidentify the host star). We set an uninformative prior on t0, and a tight normal prior on p (which usually can be assumed to be known well). The two orbital parameters, ρ⋆ and b, have either uninformative priors or tight informative priors to study the effects of having prior knowledge on the planet candidate orbit. Thesetwo options represent extreme cases. Many of the orbital parameters are degenerate in low S/N scenarios, and the uninformative-priors-cases are used to study how the contamination posterior behaves in a poorly constrained situation. In practise, especially when following up candidates found by space-based transit surveys, we can obtain informative priors for ρ⋆ and b based on the existing photometry (as long as we remember to use a transit model that includes contamination also in the analysis of the existing photometry), or model the existing photometry jointly with the multicolour photometry. Informative priors based on high S/N photometry can help to reduce the degeneracies and improve the reliability of the contamination estimate.
Finally, limb darkening is also degenerate with the impact parameter, radius ratio, and contamination, and constraining limb darkening could help to reduce the degeneracies. However, since in a real situation we do not know if the host is the dominant source or not, we choose a conservative approach and marginalise (average) over the whole limb darkening coefficient space.
4.2 M-dwarf without contamination
We begin by considering an uncontaminated (TEff = 3600 K, ρ⋆ = 5 g cm-3) M dwarf planet host with and without an informative prior set on the host star effective temperature (TEff,H), and with and without informative priors on the stellar density and impact parameter. An estimate for TEff,H derived from spectroscopy (or from the same multicolour photometry used in the contamination analysis) helps to constrain the parameter space, as do estimates for the orbital parameters derived from existing transit photometry. However, if the contaminant is brighter than the host, the TEff,H estimate can be erroneous. Also, the orbital parameter estimates used as priors need to be derived using a model that allows for contamination (or the prior photometry needs to be modelled jointly with the multicolour observations). If the orbital parameter priors are based on an analysis with a model that does not include contamination, they will most likely be biased and unrealistically narrow, leading to biased contamination estimates from the multicolour analysis.
Figure 4 collects the results from the uncontaminated simulations. The first two sub-figures (from the top) show the simulations with an informative prior on the orbital parameters, and the last two without (basically, the amount of prior information decreases from top to bottom). The columns separate the three different apparent radius ratios, and each sub-figure is divided vertically by the impact parameter, and further by the number of transits observed.
When the orbit is constrained by a prior, the marginal reference passband contamination (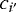 ) posteriors are also well-constrained and have their modes at (or close-to) 0 for all impact parameters, no matter whether we set a prior on TEff,H or not. This shows that significant contamination, when there is none, can be ruled out using a relatively small amount of ground-based photometry if we have reliable constraints on the orbital parameters.
) posteriors are also well-constrained and have their modes at (or close-to) 0 for all impact parameters, no matter whether we set a prior on TEff,H or not. This shows that significant contamination, when there is none, can be ruled out using a relatively small amount of ground-based photometry if we have reliable constraints on the orbital parameters.
When the orbit is unconstrained, the marginal contamination becomes less constrained as the impact parameter increases, and the posterior mode moves towards higher values of contamination. This effect becomes increasingly prominent when we set an uninformative prior on TEff,H.
When we look at the 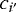 , TEff,H, TEff,C, b, and ρ⋆ joint distributions, shown in Fig. 5 for kapp = 0.1, b = 0.9, we find patterns that help us to understand what is happening. With the orbit and TEff,H unconstrained (1st row in Fig. 5), the stellar density, impact parameter, and contamination are increasingly degenerate for higher impact parameter values, and orbits with low impact parameter, high stellar density, and high contamination are favoured when the orbit is constrained only by the ground-based photometry. Constraining the host TEff (2nd row inFig. 5) reduces the degeneracy and leads to bimodal marginal b, ρ⋆, and
, TEff,H, TEff,C, b, and ρ⋆ joint distributions, shown in Fig. 5 for kapp = 0.1, b = 0.9, we find patterns that help us to understand what is happening. With the orbit and TEff,H unconstrained (1st row in Fig. 5), the stellar density, impact parameter, and contamination are increasingly degenerate for higher impact parameter values, and orbits with low impact parameter, high stellar density, and high contamination are favoured when the orbit is constrained only by the ground-based photometry. Constraining the host TEff (2nd row inFig. 5) reduces the degeneracy and leads to bimodal marginal b, ρ⋆, and 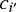 distributions, where the weaker mode corresponds to the true configuration. When we set tight priors on b and ρ⋆, but assume no information about TEff,H (3rd row in Fig. 5), the degeneracy between the orbital parameters and contamination disappears. When we add constraints on TEff,H (4th row in Fig. 5), the allowed contamination space decreases further. Now the maximumamount of contamination is constrained strongly, and any significant differences between TEff,C and TEff,H are rejected.
distributions, where the weaker mode corresponds to the true configuration. When we set tight priors on b and ρ⋆, but assume no information about TEff,H (3rd row in Fig. 5), the degeneracy between the orbital parameters and contamination disappears. When we add constraints on TEff,H (4th row in Fig. 5), the allowed contamination space decreases further. Now the maximumamount of contamination is constrained strongly, and any significant differences between TEff,C and TEff,H are rejected.
Even in the least-constrained case the joint distributions yield useful information that can be used together with other planet candidate vetting methods. First, the TEff,C and TEff,H distribution tells that if the photometry is contaminated, the contamination is from source(s) with a similar TEff as the host (or that the combined spectrum from multiple sources matches closely the host star’s spectrum). Further, the stellar density distribution can be used with external information to assess how likely the host star is to be of the predicted density.
 |
Fig. 4 50 and 95% posterior limits (darker and lighter colouring, respectively) for the estimated contamination in the i′ band for an uncontaminated M dwarf with either informative or uninformative priors on ρ⋆ and b, and either informative or uninformative prior on TEff,H. The results are shown for three impact parameters (b), three apparent radius ratios in the i′ band (kapp), three dataset sizes (n, number of observed transits), and two transit durations, as detailed in Sect. 4.1. Blue colour corresponds to short (1 h) transit duration, and orange to long (2 h) transit duration. |
 |
Fig. 5 Joint posterior distributions for TEff,H, TEff,C, b, ρ⋆, and |
4.3 M-dwarf slightly contaminated by a G-star
Next, we study the same M dwarf as in Sect. 4.2, but now slightly contaminated (10% of the total flux) by a TEff = 5800 K G star. This should be an easy-to-identify scenario since the colour difference between the two stars leads to significant transit depth variations across passbands. Again, we consider the effect of setting informative priors on TEff,H and the orbital parameters, and we assume that the prior on TEff,H corresponds to the true TEff,H since the host dominates the total flux.
Figure 6 collects the results from the low-contamination simulations with host-contaminant colour difference. Now, the most constrained case (where we set informative priors on TEff,H, b, and ρ⋆) yields reliable contamination estimates for all the simulation scenarios, whereas the least constrained case still yields reliable estimates for the high S/N transit light curves with centric transits. Having information about the orbital parameters allows us to again estimate the high-impact-parameter candidates, but does not significantly affect the low-impact-parameter estimates. Finally, setting a prior on TEff,H significantly improves the contamination estimates for all cases, even for b = 0.9. Specially, unconstrained TEff,H with low S/N leads to a bias towards high contamination values. This can be explained by the nonlinear relation between the contamination, apparent radius ratio, and true radius ratio. Contamination scales as 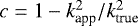 , so a small increase in the range of values the true radius ratio can have can lead to a significant increase in the contamination values (see Appendix A for details).
, so a small increase in the range of values the true radius ratio can have can lead to a significant increase in the contamination values (see Appendix A for details).
In most cases, having reliable information about TEff,H is more important than being able to constrain the orbit. The TEff,H estimate can be obtained either from spectroscopy, or roughly from the multicolour photometry itself. However, this estimate may be erroneous if the contaminant dominates the total observed flux. This case is the topic of the next section.
4.4 M-dwarf heavily contaminated by a G-star
Considering that even a slight contamination by a star with significantly different TEff is relatively easy to measure, we can expect the detection of heavy contamination to be easy as well. Now, the main issue of interest is what happens if we mistake the contaminant as the candidate host star, and set an informative prior on TEff,H that actually corresponds to TEff,C.
Figure 7 collects the results from the high-contamination (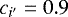 ) simulations with host-contaminant colour difference, and Fig. 8 shows the joint posteriors for a single simulation case with short (1 h) transit duration, uninformative priors on TEff,H and orbital parameters, kapp = 0.07, and b = 0.5 for one observed transit. As expected, we recover accurate TEff,H, TEff,C, and contamination estimates in the case of uninformative prior on TEff,H, even with low S/N observations. Surprisingly, setting a (wrong) informative prior on TEff,H has a relatively small effect on the final contamination estimate. This can be explained by degeneracies in the relative fluxes in the (TEff,C, TEff,H)-space. Even when forcing TEff,H close to 5800 K, we can discover a solution with TEff,C ~ 12 000 K (at the boundary of the contamination model space) that sufficiently explains the transit depth differences (that is, the relative colour differences between the two cases are similar enough to yield a reliable contamination estimate.) However, this result cannot be generalised, since the situation will likely be different for a hotter host star. Thus, as expected, significant contamination from a contaminant with TEff,C ≪ TEff,H or TEff,C ≫ TEff,H can be estimated reliably without imposing an informative prior on TEff,H due to the transit depth differences.
) simulations with host-contaminant colour difference, and Fig. 8 shows the joint posteriors for a single simulation case with short (1 h) transit duration, uninformative priors on TEff,H and orbital parameters, kapp = 0.07, and b = 0.5 for one observed transit. As expected, we recover accurate TEff,H, TEff,C, and contamination estimates in the case of uninformative prior on TEff,H, even with low S/N observations. Surprisingly, setting a (wrong) informative prior on TEff,H has a relatively small effect on the final contamination estimate. This can be explained by degeneracies in the relative fluxes in the (TEff,C, TEff,H)-space. Even when forcing TEff,H close to 5800 K, we can discover a solution with TEff,C ~ 12 000 K (at the boundary of the contamination model space) that sufficiently explains the transit depth differences (that is, the relative colour differences between the two cases are similar enough to yield a reliable contamination estimate.) However, this result cannot be generalised, since the situation will likely be different for a hotter host star. Thus, as expected, significant contamination from a contaminant with TEff,C ≪ TEff,H or TEff,C ≫ TEff,H can be estimated reliably without imposing an informative prior on TEff,H due to the transit depth differences.
 |
Fig. 6 50 and 95% posterior limits for the estimated contamination in the i′ band for an M dwarf slightly contaminated by a G2 star (10% of the total flux) with or without an informative prior on ρ⋆ and b (first two rows from the top and the last two rows from the top, respectively), and either informative or uninformative prior on TEff,H (first and third, and second and fourth rows, respectively). The results are shown for three impact parameters (b), three apparent radius ratios in the i′ band (kapp), three dataset sizes (n), and two transit durations, as detailed in Sect. 4.1. Blue colour corresponds to short (1 h) transit duration, and orange to long (2 h) transit duration. |
 |
Fig. 7 50 and 95% posterior limits for the estimated contamination in the i′ band for an M dwarf strongly contaminated by a G2 star (90% of the total flux) with or without an informative prior on ρ⋆ and b (first two rows from the top and the last two rows from the top, respectively), and either informative or uninformative prior on TEff,H (first and third, and second and fourth rows, respectively). The results are shown for three impact parameters (b), three apparent radius ratios in the i′ band (kapp), three dataset sizes (n), and two transit durations, as detailed in Sect. 4.1. Blue colour corresponds to short (1 h) transit duration, and orange to long (2 h) transit duration. |
4.5 M-dwarf contaminated by an M-dwarf
We next focus our attention to the case of contamination when TEff,C ~ TEff,H. Now the lack of colour difference means that contamination does not lead to transit depth variations across passbands, and all of the information about it is in the chromatic variations in the curvature of the transit light curve. We change the simulation setup slightly, and study contamination factors 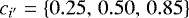 , since the
, since the 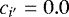 case was already studied in Sect. 4.2.
case was already studied in Sect. 4.2.
We show the result in Fig. 9 for three contamination levels, informative prior on TEff,H, and either with or without informative priors on b and ρ⋆. Constraining TEff,H does not affect parameter posteriors other than TEff,H and TEff,C, since the second colour signature does not depend on the absolute TEff,H (we carried out the simulations for cases without an informative prior on TEff,H to ensure this is the case). Thus, in the following we focus only on the cases with an informative prior on TEff,H.
Because of the degeneracies, except for the largest planets and highest contamination levels, the contamination is poorly constrained when we do not have informative priors on the orbital parameters. However, constraining b and ρ⋆ constrains the contamination estimates significantly.
Further constraints could be obtained by constraining the stellar limb darkening. This however goes outside the scope of the simulation study, but is done in the analysis of real observations in Sect. 5.
4.6 Scaling to small planets and low S/N
We carry out a separate set of simulations to study how the approach extends to small planet candidates observed with large telescopes. We choose kapp = 0.02 corresponding to an Earth-sized planet around an M-star and run the simulations for 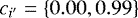 without host-contaminant colour difference, and for
without host-contaminant colour difference, and for 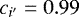 with an G2 contaminant, as before. The true radius ratio, ktrue, for the contaminated case (
with an G2 contaminant, as before. The true radius ratio, ktrue, for the contaminated case (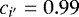 ) is now 0.2. We repeat the simulations for two white noise levels, 100 and 200 ppm over an exposure of 1 min, and three sets of observed transits (nn = {1, 2, 4}), but restrict to b = 0, a short transit duration with T14 ~ 1 h, and uninformative priors on TEff,C, ρ⋆, and b. We do not show the results here, but they are available from the paper’s GitHub repository.
) is now 0.2. We repeat the simulations for two white noise levels, 100 and 200 ppm over an exposure of 1 min, and three sets of observed transits (nn = {1, 2, 4}), but restrict to b = 0, a short transit duration with T14 ~ 1 h, and uninformative priors on TEff,C, ρ⋆, and b. We do not show the results here, but they are available from the paper’s GitHub repository.
All the high-contamination cases are identified correctly, even without host-contaminant colour difference. However, the contamination estimates for the no-contamination cases are biased towards high contamination values. This is because of the low S/N and thenonlinear relationship between the contamination, apparent radius ratio, and true radius ratio. Contamination from sources withcolour difference is still ruled out, but the transit shape cannot constrain contamination from sources without a colour difference.
More than four transits are needed to rule out significant contamination from a source with TEff,C = TEff,H when σ = 200 ppm over a one minute exposure. However, a single transit is sufficient with σ = 100 ppm to ensure that the true radius ratio is no more than 2–3 times the apparent radius ratio, which is sufficient to validate a super-Earth (this corresponds to maximum contamination of 0.9, see Appendix A for details).
While the required precision is high, it may be achievable from the ground with the currently existing large telescopes, such as the 10.3 m Gran Telescopio Canarias (GTC). It may possibly be also reached with the smaller telescopes with the aid of a photometric diffuser (Stefansson et al. 2017; von Essen et al. 2019).
 |
Fig. 8 As in Fig. 5, but for an M dwarf heavily contaminated by a G star ( |
 |
Fig. 9 50 and 95% posterior limits for the estimated contamination in the i′ band for an M dwarf contaminated by an identical M dwarf with an informative prior on TEff,H (see the text why this has no impact), with or without an informative prior on ρ⋆ and b (left and right columns, respectively), and 25, 50, and 85% of contamination in the i′ band, from top to bottom. The results are shown for three impact parameters (b), three apparent radius ratios in the i′ band (kapp), three dataset sizes (n), and two transit durations, as detailed in Sect. 4.1. Blue colour corresponds to short (1 h) transit duration, and orange to long (2 h) transit duration. |
5 Application to real data
5.1 MuSCAT2 observations
We use transit observations of WASP-43b and WASP-12b to study the contamination estimation in practice. The observations were carried out with MuSCAT2, a new four-colour imager installed in the 1.5 m Carlos Sanchez Telescope (TCS) in the Teide Observatory (OT), Tenerife (Narita et al. 2018). The instrument has the capability of simultaneous imaging in g′ (400–550 nm), r′ (550–700 nm), i′ (700–820 nm), and zs (820–920 nm) bands, which closely match our simulations.
 |
Fig. 10 Two full and one partial transits of WASP-43b observed with MuSCAT2 in g′, r′, i′, and z′ with a transit model corresponding to the median of the model parameter posteriors. The systematics have been modelled using a Gaussian process, and the GP mean has been removed from the observed data for visualisation purposes. |
5.2 Datareduction and analysis
The photometry was carried out with a dedicated MuSCAT2 photometry pipeline based on NUMPY, SCIPY, ASTROPY (Astropy Collaboration 2013), PHOTUTILS (Bradley et al. 2019), and ASTROMETRY.NET (Lang et al. 2010). The contamination analysis wascarried out using MuSCAT2 transit analysis pipeline relying on PYTRANSIT, GEORGE, EMCEE, and PYDE.
The light curve modelling was carried out with a MuSCAT2 transit analysis pipeline that uses PYTRANSIT v2 for blending simulation and LDTK to constrain limb darkening. We first modelled each night separately to test for possible night-to-night variations in any of the parameters of interest, and then carried out a joint modelling using all the nights simultaneously. The analysis starts by fitting a transit to the data with a linear baseline model. Next, we repeat the analysis with a GP-based systematics model where the GP hyperparameters are fixed to values optimised to the light curves with the best-fitting linear-baseline-model transit removed. The initial fitting is carried out using a Differential Evolution global optimisation method that results with a population of parameter vectors clumped close to the global posterior mode. We use this parameter vector population as a starting population for the MCMC sampling with emcee, and carry out the sampling until the we obtain a reliable posterior sample (Parviainen 2018).
The MCMC sampling was repeated both for the linear and GP systematics models to test for possible differences in the inference due to the different systematics modelling approaches. The posteriors from the two approaches agreed with each other, and we adopted the GP-based posteriors for the rest of the study.
5.3 WASP-43b
WASP-43b is a short-period hot Jupiter transiting a TEff = 4400 K K7V star every 0.81 d (Hellier et al. 2011; Gillon et al. 2012). The planet is well-studied (Murgas et al. 2014; Chen et al. 2014), and is a good example case of an easy target for contamination estimation.
The observations cover two full and one partial transit of WASP-43b on nights 9.1.2018, 18.1.2018, and 18.2.2018, shown in Fig. 10. We first carry out the analysis for original observations, and then repeat the analysis for cases with 10 and20% of injected contamination from a 3600 K star. The results are shown in Fig. 11.
In the first case (no injected colour-dependent contamination) the observations allow us to reject any significant differences between the host and a possible contaminant effective temperatures. The contamination is also constrained to relatively low values, and could be constrained further by setting a prior on stellar density. In the two cases with small levels of injected contamination from a 3600 K star, the contaminant properties and the level of contamination are retrieved faithfully.
5.4 WASP-12b
WASP-12b is an inflated hot Jupiter orbiting the TEff = 6300 K primary of ahierarchical triple star system (Bechter et al. 2014). The existence of two close-in M-star companions was originally missed (Hebb et al. 2009), and the two companion stars were first identified as a single M star by Crossfield et al. (2012) with TEff = 3660 ± 70 K, and combined primary-companion flux ratios of 0.08 in the H band, and 0.03 in the i′ band. The presence of well-characterised contaminating stars makes WASP-12b an interesting target to test the contamination estimation in practise. The two companions are of same type, which allows us to carry out a simple simulation with one contaminant.
We observed two full and two partial four-colour transits of WASP-12b with MuSCAT2 on nights 15.11.2017, 16.11.2017, 14.1.2018, and 25.1.2018, shown in Fig. 12. LDTK was used to constrain the limb darkening assuming TEff = 6300 ± 50 K, log g = 4.38 ± 0.1, and Z = 0.3 ± 0.1 (Hebb et al. 2009), with an uncertainty multiplier of 2 (used to inflate the stellar limb darkening profile uncertainty estimates).
The blending analysis results are shown in Fig. 13. The marginal contamination posterior mode agrees with the true reference passband contamination value of 4%, but contamination levels up to ~25% are allowed. However, looking at the joint distributions, it is clear that significant contamination from sources with TEff,H≠TEff,C is excluded. Interestingly, also the low-contamination solutions by a contaminant without a colour difference are ruled out, and a correct lower-temperature contaminant is favoured instead.
 |
Fig. 11 WASP-43b blending analysis using the MuSCAT2-observed light curves without injected contamination (above), with 10% contamination from a 3600 K star (middle), and with 20% contamination from a 3600 K star (bottom). The dotted lines show the 65, 75, 85, and 95% percentiles for the posterior contamination. |
6 Discussion and conclusions
Multicolour transit photometry combined with a physics-based contamination model can be used to estimate the true radius ratio of the transiting object in the presence of possible flux contamination from unresolved sources, even from the transiting object itself. The true radius ratio combined with a stellar radius estimate results in an absolute radius estimate that can be used to validate a transiting object as a planet if its radius is smaller than 0.8 RJup, the lower limit of what is expected for brown dwarfs (Burrows et al. 2011; Chabrier & Baraffe 2000).
The visualisation of the results from the analyses (simulations and observations) presented in this paper focused on showing the estimated contamination level in an arbitrarily chosen reference passband. However, the true radius ratio, and especially its upper limit, is the main quantity of interest in planet candidate validation.
The apparent radius ratio is generally well-constrained by the observations (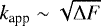 ), but the true radius ratio posterior depends also on how well the photometry can constrain the contamination space. As detailed in Appendix B, (and visible in the simulations) decreasing S/N (increasing uncertainty in kapp) leads to a contamination posterior with an increasingly non-zero mode. However, the contamination posterior should always be considered in the context of the whole parameter space (as illustrated in the joint-parameter plots), and the maximum contamination allowed by the observations (giving the maximum ktrue) should be considered as the main output of the analysis.
), but the true radius ratio posterior depends also on how well the photometry can constrain the contamination space. As detailed in Appendix B, (and visible in the simulations) decreasing S/N (increasing uncertainty in kapp) leads to a contamination posterior with an increasingly non-zero mode. However, the contamination posterior should always be considered in the context of the whole parameter space (as illustrated in the joint-parameter plots), and the maximum contamination allowed by the observations (giving the maximum ktrue) should be considered as the main output of the analysis.
The required photometric precision for multicolour transit photometry to be used efficiently in planet candidate validation can be reached with small (~1 m) ground-based telescopes. Further, the current developments in ground-based photometry, such as the use of diffusers (Stefansson et al. 2017), can improve the achievable precision to level where only a few transits are required for candidate validation.
In practice, the analysis can be made more robust by comparing the results with analyses of simulations mimicking the observations. This is feasible since a single analysis of multiple transits observed in multiple colours (real observations or simulations) takes minutes, and can give insight into the possible biases arising from the S/N or observing geometry.
In some cases, this technique can confirm candidates with less telescope time than the RV technique, particularly for long period systems. While the mass is certainly a desirable parameter to possess, when in a situation with a large backlog of candidates requiring verification, the less time needed on “premium” telescope facilities for confirmation, the better. Moreover, the intrinsic RV noise in stars, orbital eccentricity, and the presence of unknown planets can complicate attempts to confirm candidates with RV. From space, it should be possible to confirm low-mass, long period planets that would be enormously difficult to impossible to confirm with RV.
The method does have limitations: it cannot separate grazing exoplanets from grazing binary stars (unless blended, in which case different depths in different colours are still likely), nor can it distinguish between red dwarfs, brown dwarfs and giant planets – in these cases, an upper mass limit from RV is necessary. However, this is not necessarily a severe problem. Transiting exoplanet surveys have found that the red and brown dwarfs seem to be much more rare than transiting exoplanets despite the fact that they induced much stronger RV variations – for example, out of the 22 announced CoRoT exoplanets, only two (CoRoT-3b, CoRoT-15b) seem to be brown dwarfs. On the other hand, Santerne et al. (2012) found that approximately 35% of close-in giant planet candidates are non-planetary false positives. Half of these were found to be CEBs after extensive RV follow-up and likely would have been more easily identified as such with multicolour photometry.
Further, transits with high impact parameters (not necessarily grazing) lead to overestimated contamination. This is connected to the fact that increasing uncertainty in the true radius ratio leads to a bias in the contamination, as detailed in Appendix B. For a high impact parameter, even the apparent radius ratio can be poorly constrained, and the true radius ratio even more so, which leads to systematically high contamination estimates.
The approach is very good at identifying CEBs (O’Donovan et al. 2006, 2007), which are the most problematic cases for the RV technique; indeed, many hours of very valuable telescope time have been wasted on fruitless efforts to detect the RV signal of a possible planet which was actually a CEB. In some cases, multicolour photometry may actually be the best technique for follow-up – not only for relatively deep transits (≳ 0.8%) with long periods or faint V ≳ 15 host stars using ground-based photometry but also for earth-size candidates using space telescopes. One practical application of this technique would be a systematic effort to follow up TESS candidates. Combining these observations with the TESS light curves would allow relatively efficient characterisation of such systems.
Naturally, the method is applicable only when the candidate signal is due to a real astrophysical phenomenon, such as transiting planet or eclipsing binary, and not due to an instrumental artefact (also a source of false candidates). However, these candidates can be directly rejected based on the lack of a transit in the follow-up photometry.
The strength of the colour difference depends not only on limb darkening and transit parameters, but also on the colour difference between the light sources, arising from temperature differences and interstellar reddening. Despite this, it would be eminently practical for future satellite missions dedicated to have the capability to observe in multiple colours. At the cost of some photons, a large fraction of the telescope resources committed to the follow-up effort would be spared, as RV follow up would only be necessary in case when the planetary mass was of particular scientific interest.
 |
Fig. 12 Two full and two partial transits of WASP-12b observed with MuSCAT2 in g′, r′, i′, and z′. The light curves have been detrended using a GP with a conservative kernel for visualisation purposes. |
 |
Fig. 13 WASP-12b blending analysis using the MuSCAT2-observed light curves shown in Fig. 12. WASP-12 is a hierarchical triple system with the planet transiting a TEff = 6300 K primary. The photometry is contaminated by two unresolved M-star companions contributing ~ 4% of flux in the i′ band. |
Acknowledgements
We thank the anonymous referee for their helpful comments. H.D. acknowledges support by grants ESP2015-65 712-C5-4-R and ESP2017-87 676-C5-4-R, and F.M., R.A., and E.P. by grant ESP2016-80 435-C2-2-R, all from the Spanish Ministry of Economy and Competitiveness (MINECO/MICINN). V.J.S.B. acknowledges support by grant AYA2015- 69 350-C3-2-P. N.N. acknowledges supports by JSPS KAKENHI Grant Numbers JP17H04574, JP18H01265 and JP18H05439, and JST PRESTO Grant Number JPMJPR1775. This article is partly based on observations made with the MuSCAT2 instrument, developed by ABC, at Telescopio Carlos Sánchez operated on the island of Tenerife by the IAC in the Spanish Observatorio del Teide. The authors wish to acknowledge the contribution of Teide High-Performance Computing facilities to the results of this research. TeideHPC facilities are provided by the Instituto Tecnológico y de Energías Renovables (ITER, SA); http://teidehpc.iter.es. The authors thankfully acknowledge the technical expertise and assistance provided by the Spanish Supercomputing Network (Red Española de Supercomputación), as well as the computer resources used: the LaPalma Supercomputer, located at the Instituto de Astrofísica de Canarias.
Appendix A Contaminated transit model
The light contamination model in PYTRANSIT v2 depicts the observed flux as a combination of the host star flux and the contaminantflux (possibly from multiple contaminating sources). The contamination is calculated for a set of passbands given the passband transmission functions, host and contaminant effective temperatures, and the level of contamination in some reference passband.
PYTRANSIT offers two contamination models: a simple black body model where the stars are approximated as black bodies, and a more realistic model using PHOENIX-calculated stellar spectra by Husser et al. (2013). In the latter, the spectra calculated for a (TEff, Z, log g) grid are downsampled to a lower spectral resolution, and averaged over Z and log g. The set of averaged downsampled spectra is stored as a single 2D array, from which the stellar fluxes can be interpolated for 2300 K < TEff < 12 000 K and 300 nm < λ < 1000 nm.
The observed flux is a linear combination of host and contaminant star fluxes, possibly from several contaminating stars. The contaminated model flux, Fc, for a single passband normalised to the out-of-transit flux level is
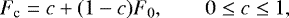 (A.1)
(A.1)
where c is the contamination fraction, and F0 the (uncontaminated) host-star flux. The transit depth scales linearly with the contamination factor, ΔFc = ΔF0(1 − c), so the apparent and true planet-star radius ratios are
 (A.2)
(A.2)
respectively.
The relative host and contaminant fluxes (FH and FC, respectively) for wavelength λ are
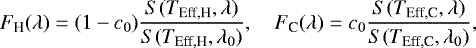 (A.3)
(A.3)
where S is the flux model, λ0 is a reference wavelength, c0 is the contamination level in this reference wavelength, and TEff,H and TEff,C are the hostand contaminant effective temperatures, respectively. Now, contamination for any given wavelength is
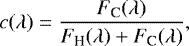 (A.4)
(A.4)
as illustrated in Fig. A.1.
The relative fluxes integrated over a set of passbands defined by transmission functions 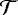 , are obtained by multiplying the flux model by the transmission function and integrating over the wavelength, as
, are obtained by multiplying the flux model by the transmission function and integrating over the wavelength, as
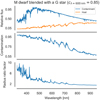 |
Fig. A.1 A TEff = 3600 K M dwarf strongly contaminated (cλ=600 nm = 0.85) by a TEff = 5800 K G star. Upper panel: relative stellar fluxes as a function of wavelength; middle panel: contamination factor as a function of wavelength; bottom panel: radius ratio factor (ktrue ∕kapp) as a function of wavelength. |
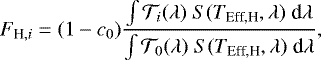 (A.5)
(A.5)
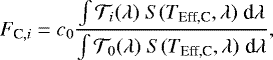 (A.6)
(A.6)
where c0 is now the amount of contamination in the reference passband. The contamination for passband i is now
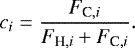 (A.7)
(A.7)
The main science case for the contamination model is in multicolour transit candidate analysis, as detailed earlier in this paper. Combining the contamination model with a transit model allows one to estimate the true, uncontaminated, radius ratio of a transiting exoplanet. The model has been integrated into PYTRANSIT v2, and an IPYTHON notebook tutorial on how to use the model in practical analysis can be found online8.
Appendix B True radius ratio and contamination
The flux contamination can be derived from the apparent and true radius ratios as 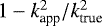 . Earlier in Sect. 4 we noticed that the contamination estimates are biased towards high values with low S/N observations. Not only does the higher contamination posterior limit increase as the S/N level decreases, but also the contamination mode moves from zero towards higher values. This is due to the nonlinear relation between the contamination and the true radius ratio. When ktrue ~ kapp, a small change in ktrue leads to a large change in contamination. Keeping the ktrue posterior mode constant, but increasing its width, moves the contamination posterior mode towards unity, as illustrated in Fig. B.1. Moving the ktrue posterior mode away from kapp but keeping its width constant leads to the contamination posterior mode moving towards higher values with the width of the distribution decreasing, as illustrated in Fig. B.2.
. Earlier in Sect. 4 we noticed that the contamination estimates are biased towards high values with low S/N observations. Not only does the higher contamination posterior limit increase as the S/N level decreases, but also the contamination mode moves from zero towards higher values. This is due to the nonlinear relation between the contamination and the true radius ratio. When ktrue ~ kapp, a small change in ktrue leads to a large change in contamination. Keeping the ktrue posterior mode constant, but increasing its width, moves the contamination posterior mode towards unity, as illustrated in Fig. B.1. Moving the ktrue posterior mode away from kapp but keeping its width constant leads to the contamination posterior mode moving towards higher values with the width of the distribution decreasing, as illustrated in Fig. B.2.
 |
Fig. B.1 Effect of widening true radius ratio posterior distribution on the contamination posterior distribution. We assume a constant apparent radius ratio of 0.04, and model the true radius ratio posterior as a half-normal distribution with the mode at 0.04, and four values for the standard deviation. Right panels: contamination distribution corresponding to the true radius ratio distribution on the left panel. |
Thus, when interpreting the contamination posterior distribution, a high mode but long tail means that the observations cannot constrain the true radius ratio well, while a high sharply peaked mode means that the observations support strong contamination.
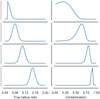 |
Fig. B.2 Effect of changing mode of ktrue posterior on the contamination posterior distribution. Apparent radius ratio is again assumed constant, kapp =0.04, and the ktrue posterior ismodelled as concatenated normal distribution with a lower limit of 0.04. Right panels: contamination distribution corresponding to the true radius ratio distribution on the left panel. |
References
- Almenara, J. M., Deeg, H. J., Aigrain, S., et al. 2009, A&A, 506, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ambikasaran, S., Foreman-Mackey, D., Greengard, L., Hogg, D. W., & O’Neil, M. 2015, IEEE Trans. Pattern Anal. Mach. Intell., 38, 2 [Google Scholar]
- Armstrong, D. J., Pollacco, D., & Santerne, A. 2017, MNRAS, 465, 2634 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 33, A1 [Google Scholar]
- Ballard, S., Fabrycky, D., Fressin, F., et al. 2011, ApJ, 743, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Gilliland, R. L., et al. 2010, ApJ, 713, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Bechter, E. B., Crepp, J. R., Ngo, H., et al. 2014, ApJ, 788, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, L., Sipocz, B., Robitaille, T., et al. 2019, https://doi.org/10.5281/ZENODO.2533376 [Google Scholar]
- Brown, T. M. 2003, ApJ, 593, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Bryson, S. T., Jenkins, J. M., Gilliland, R. L., et al. 2013, PASP, 125, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A. S., Heng, K., & Nampaisarn, T. 2011, ApJ, 736, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera, J., Barros, S. C. C., Armstrong, D., et al. 2017, A&A, 606, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, A. C. 2012, Nature, 492, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Carone, L., Gandolfi, D., Cabrera, J., et al. 2012, A&A, 538, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2000, ARA&A, 38, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G., van Boekel, R., Wang, H., et al. 2014, A&A, 563, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cochran, W. D., Fabrycky, D. C., Torres, G., et al. 2011, ApJS, 197, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Colón, K. D., & Ford, E. B. 2011, PASP, 123, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Coughlin, J. L., Thompson, S. E., Bryson, S. T., et al. 2014, AJ, 147, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Crossfield, I. J. M., Hansen, B. M. S., & Barman, T. 2012, ApJ, 746, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Daemgen, S., Hormuth, F., Brandner, W., et al. 2009, A&A, 498, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deeg, H. J., & Tingley, B. 2017, A&A, 599, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deeg, H. J., Gillon, M., Shporer, A., et al. 2009, A&A, 506, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, R. F., Almenara, J. M., Santerne, A., et al. 2014, MNRAS, 441, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, A. J. 2003, ApJ, 589, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fressin, F., Torres, G., Charbonneau, D., et al. 2013, ApJ, 766, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Fortney, J. J., et al. 2012, A&A, 542, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giménez, A. 2006, ApJ, 650, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Guenther, E. W., Fridlund, M., Alonso, R., et al. 2013, A&A, 556, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hebb, L., Collier-Cameron, A., Loeillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
- Hellier, C., Anderson, D. R., Cameron, A. C., et al. 2011, A&A, 535, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lang, D., Hogg, D. W., Mierle, K., Blanton, M., & Roweis, S. 2010, AJ, 139, 1782 [Google Scholar]
- Mandushev, G., Torres, G., Latham, D. W., et al. 2005, ApJ, 621, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Mckinney, W. 2010, Proceedng of the 9th Python Science Conference, 51 [Google Scholar]
- Morton, T. D., Bryson, S. T., Coughlin, J. L., et al. 2016, ApJ, 822, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Moutou, C., Pont, F., Bouchy, F., et al. 2009, A&A, 506, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mullally, F., Coughlin, J. L., Thompson, S. E., et al. 2016, PASP, 128, 074502 [NASA ADS] [CrossRef] [Google Scholar]
- Mullally, F., Thompson, S. E., Coughlin, J. L., Burke, C. J., & Rowe, J. F. 2018, AJ, 155, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Murgas, F., Pallé, E., Zapatero Osorio, M. R., et al. 2014, A&A, 563, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narita, N., Fukui, A., Kusakabe, N., et al. 2018, J. Astron. Telesc. Instrum. Syst., 5, 1 [CrossRef] [Google Scholar]
- O’Donovan, F. T., Charbonneau, D., Torres, G., et al. 2006, ApJ, 644, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- O’Donovan, F. T., Charbonneau, D., Alonso, R., et al. 2007, ApJ, 662, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Parviainen, H. 2015, MNRAS, 450, 3233 [NASA ADS] [CrossRef] [Google Scholar]
- Parviainen, H. 2018, in Handbook of Exoplanest (Cham: Springer International Publishing), 1 [Google Scholar]
- Parviainen, H., & Aigrain, S. 2015, MNRAS, 453, 3822 [NASA ADS] [CrossRef] [Google Scholar]
- Perez, F., & Granger, B. 2007, Comput. Sci. Eng., 21 [Google Scholar]
- Peterson, P. 2009, Int. J. Comput. Sci. Eng., 4, 296 [Google Scholar]
- Pollacco, D. L., Skillen, I., Cameron, A. C., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Quintana, E. V., Rowe, J. F., Barclay, T. S., et al. 2013, ApJ, 767, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Rosenblatt, F. 1971, Icarus, 14, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Santerne, A., Díaz, R. F., Moutou, C., et al. 2012, A&A, 545, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santerne, A., Díaz, R. F., Almenara, J.-M., et al. 2015, MNRAS, 451, 2337 [NASA ADS] [CrossRef] [Google Scholar]
- Stefansson, G., Mahadevan, S., Hebb, L., et al. 2017, ApJ, 848, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tingley, B. 2004, A&A, 425, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tingley, B., Palle, E., Parviainen, H., et al. 2011, Astron. Astrophys. Lett., 536, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Tingley, B., Parviainen, H., Gandolfi, D., et al. 2014, A&A, 567, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torres, G., Fressin, F., Batalha, N. M., et al. 2011, ApJ, 727, 24 [NASA ADS] [CrossRef] [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- von Essen, C., Stefansson, G., Mallonn, M., et al. 2019, A&A, 628, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Worek, T. 2000, Inf. Bull. Var. Stars, 1 [Google Scholar]
Current standard methods include the use of the original space-based photometry (Batalha et al. 2010; Quintana et al. 2013; Bryson et al. 2013; Coughlin et al. 2014; Mullally et al. 2016; Armstrong et al. 2017), ground-based photometry and high-resolution imaging (Deeg et al. 2009; Guenther et al. 2013), and statistical candidate validation using evidence from multiple information sources, such as BLENDER (Torres et al. 2011), PASTIS (Díaz et al. 2014; Santerne et al. 2015), and VESPA (Morton et al. 2016).
All Figures
 |
Fig. 1 Comparison between a planetary transit and blended eclipsing binary. Panel a: uncontaminated transit by a planet with radius ratio of 0.1 observed in the i′ band, panelb: faint M-dwarf transited by an object with a radius ratio of 0.32 strongly contaminated by a G star (c = 0.9, i.e. 10% of the total flux comes from the M dwarf, and 90% from the G star) leading to an apparent radius ratio of 0.1 in the i′ band, and panel c: same contaminated transit observed in g′, r′, i′, and z′ bands. |
| In the text | |
 |
Fig. 2 Effect of varying impact parameter on transit depth colour differences when host and contaminant stars are of different spectral types (M and G). The setup is the same as in Fig. 1c, but the impact parameter varies from panel to panel. The colour differences between the stars lead to differences in the relative contamination from one passband to another, which leads to variations in the observed transit depths. |
| In the text | |
 |
Fig. 3 Examples of the transit colour differences when the host and contaminant are of same spectral type for three contamination values and three impact parameters. The smaller the transiting object is, the sharper the differential features are. |
| In the text | |
 |
Fig. 4 50 and 95% posterior limits (darker and lighter colouring, respectively) for the estimated contamination in the i′ band for an uncontaminated M dwarf with either informative or uninformative priors on ρ⋆ and b, and either informative or uninformative prior on TEff,H. The results are shown for three impact parameters (b), three apparent radius ratios in the i′ band (kapp), three dataset sizes (n, number of observed transits), and two transit durations, as detailed in Sect. 4.1. Blue colour corresponds to short (1 h) transit duration, and orange to long (2 h) transit duration. |
| In the text | |
 |
Fig. 5 Joint posterior distributions for TEff,H, TEff,C, b, ρ⋆, and |
| In the text | |
 |
Fig. 6 50 and 95% posterior limits for the estimated contamination in the i′ band for an M dwarf slightly contaminated by a G2 star (10% of the total flux) with or without an informative prior on ρ⋆ and b (first two rows from the top and the last two rows from the top, respectively), and either informative or uninformative prior on TEff,H (first and third, and second and fourth rows, respectively). The results are shown for three impact parameters (b), three apparent radius ratios in the i′ band (kapp), three dataset sizes (n), and two transit durations, as detailed in Sect. 4.1. Blue colour corresponds to short (1 h) transit duration, and orange to long (2 h) transit duration. |
| In the text | |
 |
Fig. 7 50 and 95% posterior limits for the estimated contamination in the i′ band for an M dwarf strongly contaminated by a G2 star (90% of the total flux) with or without an informative prior on ρ⋆ and b (first two rows from the top and the last two rows from the top, respectively), and either informative or uninformative prior on TEff,H (first and third, and second and fourth rows, respectively). The results are shown for three impact parameters (b), three apparent radius ratios in the i′ band (kapp), three dataset sizes (n), and two transit durations, as detailed in Sect. 4.1. Blue colour corresponds to short (1 h) transit duration, and orange to long (2 h) transit duration. |
| In the text | |
 |
Fig. 8 As in Fig. 5, but for an M dwarf heavily contaminated by a G star ( |
| In the text | |
 |
Fig. 9 50 and 95% posterior limits for the estimated contamination in the i′ band for an M dwarf contaminated by an identical M dwarf with an informative prior on TEff,H (see the text why this has no impact), with or without an informative prior on ρ⋆ and b (left and right columns, respectively), and 25, 50, and 85% of contamination in the i′ band, from top to bottom. The results are shown for three impact parameters (b), three apparent radius ratios in the i′ band (kapp), three dataset sizes (n), and two transit durations, as detailed in Sect. 4.1. Blue colour corresponds to short (1 h) transit duration, and orange to long (2 h) transit duration. |
| In the text | |
 |
Fig. 10 Two full and one partial transits of WASP-43b observed with MuSCAT2 in g′, r′, i′, and z′ with a transit model corresponding to the median of the model parameter posteriors. The systematics have been modelled using a Gaussian process, and the GP mean has been removed from the observed data for visualisation purposes. |
| In the text | |
 |
Fig. 11 WASP-43b blending analysis using the MuSCAT2-observed light curves without injected contamination (above), with 10% contamination from a 3600 K star (middle), and with 20% contamination from a 3600 K star (bottom). The dotted lines show the 65, 75, 85, and 95% percentiles for the posterior contamination. |
| In the text | |
 |
Fig. 12 Two full and two partial transits of WASP-12b observed with MuSCAT2 in g′, r′, i′, and z′. The light curves have been detrended using a GP with a conservative kernel for visualisation purposes. |
| In the text | |
 |
Fig. 13 WASP-12b blending analysis using the MuSCAT2-observed light curves shown in Fig. 12. WASP-12 is a hierarchical triple system with the planet transiting a TEff = 6300 K primary. The photometry is contaminated by two unresolved M-star companions contributing ~ 4% of flux in the i′ band. |
| In the text | |
 |
Fig. A.1 A TEff = 3600 K M dwarf strongly contaminated (cλ=600 nm = 0.85) by a TEff = 5800 K G star. Upper panel: relative stellar fluxes as a function of wavelength; middle panel: contamination factor as a function of wavelength; bottom panel: radius ratio factor (ktrue ∕kapp) as a function of wavelength. |
| In the text | |
 |
Fig. B.1 Effect of widening true radius ratio posterior distribution on the contamination posterior distribution. We assume a constant apparent radius ratio of 0.04, and model the true radius ratio posterior as a half-normal distribution with the mode at 0.04, and four values for the standard deviation. Right panels: contamination distribution corresponding to the true radius ratio distribution on the left panel. |
| In the text | |
 |
Fig. B.2 Effect of changing mode of ktrue posterior on the contamination posterior distribution. Apparent radius ratio is again assumed constant, kapp =0.04, and the ktrue posterior ismodelled as concatenated normal distribution with a lower limit of 0.04. Right panels: contamination distribution corresponding to the true radius ratio distribution on the left panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.