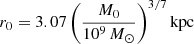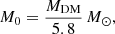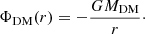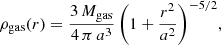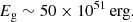| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A140 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935328 | |
| Published online | 08 October 2019 | |
High-resolution three-dimensional simulations of gas removal from ultrafaint dwarf galaxies
I. Stellar feedback
1
INAF, Astrophysics and Space Science Observatory, Via Gobetti 93/3, 40129 Bologna, Italy
e-mail: donatella.romano@inaf.it
2
E.A. Milne Centre for Astrophysics, University of Hull, Cottingham Road, Kingston Upon Hull HU6 7RX, UK
3
Joint Institute for Nuclear Astrophysics–Center for the Evolution of the Elements (JINA–CEE), USA
Received:
21
February
2019
Accepted:
4
September
2019
Context. The faintest Local Group galaxies found lurking in and around the Milky Way halo provide a unique test bed for theories of structure formation and evolution on small scales. Deep Subaru and Hubble Space Telescope photometry demonstrates that the stellar populations of these galaxies are old and that the star formation activity did not last longer than 2 Gyr in these systems. A few mechanisms that may lead to such a rapid quenching have been investigated by means of hydrodynamic simulations, but these have not provided any final assessment so far.
Aims. This is the first in a series of papers aimed at analyzing the roles of stellar feedback, ram pressure stripping, host-satellite tidal interactions, and reionization in cleaning the lowest mass Milky Way companions of their cold gas using high-resolution, three-dimensional hydrodynamic simulations.
Methods. We simulated an isolated ultrafaint dwarf galaxy loosely modeled after Boötes I, and examined whether or not stellar feedback alone could drive a substantial fraction of the ambient gas out from the shallow potential well.
Results. In contrast to simple analytical estimates, but in agreement with previous hydrodynamical studies, we find that most of the cold gas reservoir is retained. Conversely, a significant amount of the metal-enriched stellar ejecta crosses the boundaries of the computational box with velocities exceeding the local escape velocity and is, thus, likely lost from the system.
Conclusions. Although the total energy output from multiple supernova explosions exceeds the binding energy of the gas, no galactic-scale outflow develops in our simulations and as such, most of the ambient medium remains trapped within the weak potential well of the model galaxy. It seems thus unavoidable that to explain the dearth of gas in ultrafaint dwarf galaxies, we will have to resort to environmental effects. This will be the subject of a forthcoming paper.
Key words: galaxies: dwarf / galaxies: evolution / ISM: bubbles / methods: numerical / hydrodynamics
© ESO 2019
1. Introduction
In the Λ cold dark matter concordance cosmology, large halos form from the merging and accretion of small building blocks (White & Rees 1978). A large number of subhalos, however, are predicted to survive this digestion process and inhabit the current main galaxy halos. The mismatch between theoretical expectations and observed Galactic satellites gave rise to a highly debated issue, the so-called missing satellite problem (MSP; Klypin et al. 1999; Moore et al. 1999). In the past dozen years, however, the number of known Milky Way (MW) companions has increased apace, thanks to the commitment of hundreds of scientists around the world to deep large-area sky imaging surveys, such as the Sloan Digital Sky Survey (York et al. 2000), the VLT Survey Telescope ATLAS Survey (Shanks et al. 2015), the Dark Energy Survey (DES Collaboration 2016), the Pan-STARRS1 3 π Survey (Chambers et al. 2016), and the Hyper Suprime-Cam Subaru Strategic Program Survey (Aihara et al. 2018). A new class of galaxy has been discovered that is made of extremely faint, dark-matter dominated, scarcely evolved stellar systems, which have been named ultrafaint dwarf galaxies (UFDs; see, e.g., Willman et al. 2005; Belokurov et al. 2006, 2007, 2014; Bechtol et al. 2015; Laevens et al. 2015; Homma et al. 2016, 2018). Deep Hubble Space Telescope observations of six UFDs, reaching below the main-sequence turnoff, are best fit by ancient stellar populations (11.6 Gyr old; Brown et al. 2014). From deep images obtained with the Suprime-Cam on the Subaru Telescope, Okamoto et al. (2012) concluded that most stars in Boötes I, one of the best studied UFDs, are consistent with a single-epoch, short burst of star formation.
All of this has dramatically impacted our understanding of the way the halo of our Galaxy came into being. The continuous discovery of more and more UFDs, even at the detectability limits of the surveys (see Torrealba et al. 2016, their Fig. 9), considerably alleviates the need to resort to alternative dark matter scenarios to address the MSP (see Tollerud et al. 2008, and references therein), and moves the focus to studies aimed at establishing how star formation and chemical enrichment proceed in smaller and smaller dark matter halos.
Semi-analytical and pure chemical evolution models were initially used to follow the evolution of different elements in the interstellar medium (ISM) of systems with structural properties resembling those of UFDs. By introducing simple, heuristic (yet physically motivated) recipes to treat complex processes, such as accretion, cooling, star formation, and radiative feedback, these models can efficiently (in terms of computational costs) explore a wide range of parameter space. It has been concluded that UFDs formed stars very inefficiently; they converted less than 1–3% of their baryons into stars. However, there is no consensus about the dominant mechanism that truncates star formation, in which either reionization (Salvadori & Ferrara 2009), galactic winds (Vincenzo et al. 2014), or tidal stripping (Romano et al. 2015) are preferred. Chemical evolution models have been very successful in explaining many observed properties of galaxies but, when moving to stellar systems with lower and lower dynamical masses, the parameterizations adopted to treat the thermal feedback from stars, the conditions imposed on the onset of galactic-scale outflows, and the assumed mass loading factors introduce severe degeneracies in the proposed solutions. Furthermore, there are important limitations in the treatment of spatial inhomogeneities. That is why pure chemical evolution models cannot put firm constraints on the physical processes regulating the evolution of the lowest mass systems (see, e.g., a discussion in Romano et al. 2015). The natural outcome is to turn to hydrodynamical simulations.
There are not that many such studies devoted to UFDs in the literature. Bland-Hawthorn et al. (2015) adopted the three-dimensional hydro-ionization code Fyris Alpha (Sutherland 2010) to track the response of adiabatic and cooling models, with clumpy or smooth gas distributions, to a single supernova (SN) explosion, occurring either at the center or off-center of isolated UFD-sized halos. Building on this work, Webster et al. (2015) evolved Mvir = 107 M⊙ systems in isolation with extended star formation to fit the stellar metallicity distribution functions and [α/Fe] ratios observed in six UFDs. Their main conclusion is that UFDs form in low-mass halos, rather than being remnants of larger systems.
High-resolution studies of the coevolution of a UFD with a MW-like galaxy over a Hubble time remain out of reach of present computational capabilities (Faucher-Giguère 2018). Jeon et al. (2017) used a customized version of the N-body/TreePM smoothed particle hydrodynamics code GADGET (Springel et al. 2001) to perform zoom-in simulations of relatively isolated systems outside of the virial radius of a MW-like host halo. This choice allows these authors to minimize the computational cost by excluding processes such as tidal interactions and ram pressure stripping1. They found that halos with virial mass Mvir ≤ 2 × 109 M⊙ form the bulk of their stellar populations before reionization and confirm that the combined effect of reionization and SN feedback is responsible for quenching the star formation in these systems (see also Wheeler et al. 2015; Sawala et al. 2016). They also found that accretion and mergers may play an important role in the assembly history of UFDs. More recently, Corlies et al. (2018) studied the formation and evolution of UFDs in the context of the cosmological, adaptive mesh refinement (AMR) radiation hydrodynamics simulations discussed by Wise et al. (2012). The maximum comoving resolution is 1 pc, at the forefront of current cosmological simulations. Although some important observational properties of Local Group UFDs are recovered, some limitations remain. For instance, the authors acknowledge that the stellar metallicity distribution functions in the simulation are too narrow and metal-rich.
This paper is the first in a series that aims to analyze the roles of internal processes, such as stellar feedback, and external processes, such as ram pressure stripping, host-satellite tidal interactions, and reionization, in the evolution of the lowest mass MW satellites, paying particular attention to the way they lose their cold (T < 104 K) gas. We perform three-dimensional adiabatic and radiative simulations for an isolated system loosely resembling the UFD Boötes I, and examine whether or not stellar feedback alone is able to drive a significant amount of gas out from the simulation volume. The paper is organized as follows. In Sect. 2, we describe the adopted numerical setup. In Sect. 3, we present the results from our fiducial high-resolution runs, with and without radiative cooling; a suite of lower resolution simulations is analyzed in Appendix A. We demonstrate that the neutral ambient medium is mostly unaffected by the SN events, even when their effect is maximized in the simulation. However, the newly produced metals efficiently escape the galaxy potential well. In Sect. 4, we discuss our results and compare them to the expectations from analytic computations and to previous work in the literature. Finally, in Sect. 5 we draw our conclusions.
2. Numerical setup
We ran our simulations with a customized version of the AMR code RAMSES (Teyssier 2002), which solves the Euler equations of gravitohydrodynamics with a second-order, unsplit Godunov scheme. The fluid follows the adiabatic equation of state for an ideal monatomic gas with adiabatic index γ = 5/3.
The initial configuration is designed to mimic the Boötes I UFD, for which extensive observational work has been published elsewhere (see Romano et al. 2015, and references therein), and foresees a nonrotating distribution of gas and stars embedded in an isolated dark matter halo. The theoretical initial baryonic and dark masses are Mgas = 6 × 106 M⊙ and MDM = 3.5 × 107 M⊙, which follow a Plummer (1911) density profile, with characteristic radius a ≃ 200 pc, and a Burkert’s (1995) profile, with cut-off radius Rc ≃ 1.2 kpc, respectively. The gas is assumed to follow a smooth, single-phase distribution reflecting that observed nowadays for long-lived stars in Boötes I. The dark matter component is modeled as a static external potential and added to the solution of the Poisson equation; owing to the dark matter dominance, the self-gravity of the gas is neglected, for simplicity. The initial pressure profile is set by solving the hydrostatic equilibrium2 equation. The initial temperature profile is pretty flat, and ranges from ∼4400 K in the central region to ∼3900 K in the outer zones.
A population of coeval stars with mass Mstars = 105 M⊙ is set in place at the beginning of the simulation. In this work, we considered an instantaneous star formation episode. We made this choice to maximize the effects of stellar feedback and to obtain the highest synergy among the stellar-wind and SN-driven bubbles. In the framework of the integrated galactic initial mass function (IGIMF) theory (Yan et al. 2017; Jeřábková et al. 2018, and references therein), a star formation lasting a few tens to hundreds of megayears, or longer, would imply that the stars form in small embedded clusters, thus leading to far fewer SN events than expected for a canonical stellar initial mass function (IMF) as that adopted in this work (Kroupa 2001). Assuming a canonical stellar IMF that has lower and upper mass limits of 0.1 and 100 M⊙, respectively, we assigned initial masses in excess of 8 M⊙ to 650 of the stars. These massive stars were grouped in ten OB associations 2 rOB wide (see next paragraph) scattered across the computational volume, following the procedure outlined in Calura et al. (2015). We note that, because of our idealized setup, some OB associations may fall in regions of very low gas density (see previous paragraph). The implicit assumption can be made that the OB associations formed in small overdense regions – a few spots with the right characteristics to collapse and form stars. However, de los Reyes & Kennicutt (2019) have recently shown that in local dwarf galaxies the Schmidt law for star formation (Schmidt 1959) does not seem to exhibit any threshold, as even the lowest surface brightness regions show the presence of very young stars. An even more extreme confirmation of this is represented by an utterly low density (n ∼ 0.01 cm−3) – yet, star-forming – galaxy recently found in the Virgo cluster (Bellazzini et al. 2018). All in all, since UFDs are thought to represent the extreme limit of the galaxy formation process (Simon 2019), the assumed gas and star distributions for our model Boötes I galaxy may well be not quite so unreasonable. More details about the sampling procedure and a discussion of the dependence of the results on the particular setup choice are deferred to Appendix A.
We allowed each association to inject mass and energy in its surroundings at a constant rate for an uninterrupted period of 30 Myr (roughly corresponding to the lifetime of a 8 M⊙ star) through both stellar winds and SN explosions. The energy input from discrete SNe can be reasonably approximated as a continuous luminosity as long as the blast waves become subsonic before cooling radiatively. This condition is usually met for SNe exploding in a superbubble inflated by previous stellar wind activity (see Mac Low & McCray 1988, their Sect. 3). Following Leitherer et al. (2014), during the pre-SN phase (lasting 3 Myr) an OB association containing N high-mass stars injects N (5 × 10−8) M⊙ yr−1 and N (3 × 1035) erg s−1, while during the SN phase (i.e., from 3 to 30 Myr) these quantities rise to N (4 × 10−7) M⊙ yr−1 and N (7 × 1035) erg s−1. Mass and energy are spread on the volume occupied by the OB association, that is 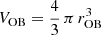 , with rOB = 4 pc for our high-resolution simulations. We modeled the massive star feedback through thermal energy deposition and included no other mechanism, such as radiation pressure. Unlike other authors (e.g., Scannapieco & Brüggen 2010), we did not include any subgrid turbulence model.
, with rOB = 4 pc for our high-resolution simulations. We modeled the massive star feedback through thermal energy deposition and included no other mechanism, such as radiation pressure. Unlike other authors (e.g., Scannapieco & Brüggen 2010), we did not include any subgrid turbulence model.
The computational box is L = 2 kpc on a side, with a maximum refinement level of ℓmax = 11, corresponding to a minimum cell size of Δxmin = 0.95 pc; the lower resolution simulations discussed in Appendix A have ℓmax = 9 and Δxmin = 3.80 pc. The refinement strategy is geometry- and discontinuity-based. In particular, at each time step a number of cells at the highest refinement level is set up to cover the regions occupied by the OB associations. This assures us that every OB association is adequately spatially resolved; stellar ejecta and SN energy are added to the gas within a sphere that is four grid cells in radius, which prevents the occurrence of square-shaped shock fronts. With the introduction of a discontinuity-based criterion for refinement, in addition, we made sure that growing dynamical instabilities at the front of the bubbles, as well as their interactions and merging, are followed at the highest refinement level.
According to Kim & Ostriker (2015), for a discrete SN event occurring in a uniform, unmagnetized medium consistent convergence of the results is obtained for Δxmin, rinit < rsf/3, where rinit is the initial size of the SN remnant and rsf = 21 pc (nH/1 cm−3)−0.46 is its size at shell formation. In our simulations, nH = 0.76 (ρgas/mp)≲7 cm−3 and rsf ≳ 9 pc everywhere, thus our choice of Δxmin ≃ 1 pc for the high-resolution runs satisfies the first convergence criterion. As for the second criterion, we have rOB ∼ rsf/2 at the center (considering OB associations rather than single SNe). Although this leads to evolutionary history and internal profiles of the innermost bubbles that differ from the converged solutions, the momentum and kinetic energy are expected to be not too far from the correct values (see Sect. 4.2 in Kim & Ostriker 2015). Caution is urged, however, in that the study of Kim & Ostriker (2015) refers to discrete sources. A new study including the effects of the preceding action of low-luminosity stellar winds would be very helpful to clarify how this works for a continuous energy injection. It could be that any initial numerical overcooling would be negligible once the densities around the OB associations have dropped slightly owing to pre-SN feedback, but this still needs to be quantified in detail.
We used free outflow boundary conditions and created a passive scalar, Z = ρZ/ρgas, to trace the evolution of the metallicity of the gas in each cell, starting from a primordial (zero) metallicity value. The simulation outputs have a time resolution of 1 Myr.
We ran both adiabatic and cooling models. While the adiabatic simulations run from 0 to 30 Myr, the cooling model is truncated at 20 Myr for computational reasons3. We used RAMSES built-in cooling rates, namely, for temperatures T > 104 K gas cooling follows the cooling function of Sutherland & Dopita (1993) involving hydrogen, helium, and metals. Below such temperature threshold, only fine-structure metal cooling was considered by adopting the cooling function of Rosen & Bregman (1995). In accordance with the idealized nature of our simulations, we set a temperature floor (Tmin = 3900 K), which mimics the effects of several heating mechanisms – for instance, photoionization and photoelectric heating from stars, and heating from the galactic ultraviolet (UV) background radiation – within the model galaxy.
3. Results
In this section, we discuss the results of high-resolution simulations with 650 SN precursors sorted in 10 OB associations placed at different radii. In Appendix A, we provide a general overview of the dependence of the results on the particular configuration chosen for the OB associations. To this aim, we make use of a suite of lower resolution simulations.
3.1. Hydrodynamic evolution driven by stellar activity
Radiative losses are fairly ineffective at the beginning of the simulation because of the relatively low densities, i.e., nH ≃ 7 cm−3 at the center and ∼1 cm−3 at the Plummer radius. Therefore, large cavities filled with tenuous, hot (T ≥ 108 K) gas are already carved out around the OB associations during the pre-SN phase (0–3 Myr), both in the adiabatic and cooling models (Figs. 1 and 2, upper panels); there is no need to switch off cooling artificially in the radiative simulation. In the presence of radiative cooling, during the SN phase (3–30 Myr) multiple SN explosions dig superbubbles smaller than those molded in the adiabatic limit and filled with hot (T > 107 K), rarefied gas (cf. in particular, the middle and lower panels in Figs. 1 and 2, respectively, referring to the t = 20 Myr snapshots). These bubbles also take more time to lose their individuality, disrupt, and merge. We note that in spite of the growth of Rayleigh-Taylor instabilities at the borders, the bubbles preserve ovoid shapes delimited by thin, dense, cold shells, until they do not interact with each other. The largest holes are created in the outskirts of the galaxy, where the ISM is less dense and, thus, less resilient and less reluctant to being pulled away. Given the low SN rate, however, the filling factor of the superbubbles is overall small and the OB associations fail to produce a large-scale, coherent action of gas removal. Undoubtedly, the adopted geometry of the system, distribution of OB associations, and static implementation of stellar feedback play a role in determining the exact amount of gas that is expelled from the system. We briefly touch upon this in Sect. 4.3. The issue of the dependence of the results on variations in the number and position of (static) OB associations is discussed in more detail in Appendix A.
 |
Fig. 1. Gas density (left), temperature (middle), and metallicity (right) maps for the Boötes I-like galaxy in the z = 0 plane at five representative times, i.e., t = 3, 13, 20, 25, and 30 Myr. The projected positions of the OB associations are shown on the metallicity maps as gray circles, with sizes proportional to the number of massive stars. The snapshots refer to the galaxy simulated in the adiabatic limit at high resolution. |
 |
Fig. 2. Same as Fig. 1, for t = 3, 13, 17, and 20 Myr for the high-resolution simulation with radiative cooling. |
Figures 3 and 4 depict the gas radial velocity field at t = 20 Myr for the adiabatic and radiative simulations and t = 30 Myr only for the adiabatic simulation, respectively. Pockets of tenuous, heated gas around individual OB associations expand at supersonic velocity. Supernova debris are channelled in hot structures that resemble chimneys and fountains and can either be entrained in an outflow or ‘rain back’ to the galaxy center with velocities up to several hundreds of kilometers per second. The cooler ambient medium is largely unaffected by the SN activity and remains bound in both the radiative and adiabatic regimes; however, in the latter case a fraction of the gas, mostly in the outermost regions, is swept up and steadily moves outward with velocities that exceed the local escape velocity4 (see insets in Figs. 3 and 4).
 |
Fig. 3. Gas radial velocity field, in the z = 0 plane, at t = 20 Myr. The maps on the left refer to the galaxy simulated in the adiabatic limit, while the maps on the right indicate the run with radiative cooling. The black cells in the inset maps on the bottom left of each panel highlight regions where the gas moves with velocities lower than the local escape velocity. |
The maps in Figs. 3–4 capture a limited portion of the simulation volume. A comprehensive view of the total gas mass participating in the outflow is provided in Fig. 5, where we show the mass fraction of gas normalized to the total gas mass in the simulation volume per velocity (upper panels) and density bin (middle panels) for the adiabatic and radiative runs (left-hand and right-hand panels, respectively) at t = 20 Myr. The distribution for all gas is divided into the contribution from a cold/warm (T < 105 K) and a hot phase (T ≥ 105 K). While most of the outflowing material is in a hot phase with velocities in excess of a few hundred kilometers per second, the cold/warm component peaks at low ( < 50 km s−1) velocities. In the radiative case, the hot gas is characterized by a considerably narrower velocity distribution with the absence of a tail at very high ( > 500 km s−1) velocities.
 |
Fig. 5. Mass-weighted distributions of gas radial velocity (upper panels) and density (middle panels) at t = 20 Myr, for the runs with (right-hand panels) and without radiative losses (left-hand panels). The distribution of metals in radial velocity bins at the same time for the two runs (lower panels) is also shown. The red (green) lines on the left (right) panels show all the gas and metals in the simulation volume. The yellow solid and blue dotted lines in all panels show the hot (T ≥ 105 K) and cold/warm (T < 105 K) components, respectively. The integrals of the red and green lines are normalized to unity. |
The majority of the gas in the simulation volume does not contribute to the mass carried away by the wind: contrary to conventional wisdom (see Sect. 4.1), even in the adiabatic limit we find that after 30 Myr the system has lost less than 20% of its initial gaseous mass (see Fig. 6, lower panel).
 |
Fig. 6. Cumulative mass (upper panel) and metals (middle panel) ejected by massive stars (m > 8 M⊙) and recycled in the simulation volume, at different times. The (red) empty stars refer to the adiabatic run; the (green) filled stars indicate the run with radiative cooling. The quantities computed using injection rates from Leitherer et al. (2014) are shown as dashed (black) lines in all panels, and would be recovered in the case of a closed system. In the lower panel, the total gas masses, normalized to the initial gas mass of the system, are shown as solid lines; SN ejecta, normalized to the corresponding quantities computed with Leitherer et al. (2014) mass return rate at each time are indicated as stars joined by dotted lines; these shown in the system at different times for the adiabatic (red lines and symbols) and radiative models (green lines and symbols). |
As already stressed elsewhere (e.g., Mori et al. 2002), there are two main reasons why the energy deposition, even though it is higher than the gas binding energy, does not produce a complete blow-away of the gas, even in the adiabatic regime. In real galaxies, the explosion sites are scattered, rather than all closely packed at the center. The energy released in the outer, low-density regions tends to escape the galactic potential well without much coupling with the ambient medium, while off-nuclear explosions in the inner regions tend to compress the gas at the center through inward-propagating shocks, which enhances the radiative losses in the cooling model. In Appendix A we show that the system can get rid of a higher fraction of gas if the OB associations are more concentrated; we do not force all the OB associations to lie at the center of the system, however, because this would produce a nuclear star cluster, which is not observed in local UFDs. Overall, from our simulations we conclude that to sweep the galaxy clean of its gas some external force or event must likely be considered.
3.2. Metal enrichment
Even if the galaxy does not get rid of its cold gas, most of the mass and energy injected by massive stars in the ISM escape the system. The upper and middle panels of Fig. 5 show that, at t = 20 Myr, most of the gas is in the cold/warm component and has relatively high densities (> 10−2 cm−3). The same is not true for the metals. The majority of the metals reside in the hot component (Fig. 5, lower panels). In particular, in the adiabatic case their velocity distribution is much broader than that of the gas without any substantial dominance of the low-velocity component. This implies that the metals are not mixed with the cold, dense pristine gas. As can be seen from the lower panel of Fig. 6, for the adiabatic run at t = 20 Myr only 40% of the ejecta from massive stars is trapped within the simulation volume, and this percentage drops to 20% at 30 Myr5. For the run with radiative cooling, 55% of the stellar ejecta is still present in the simulation box at t = 20 Myr, but this percentage is likely to decrease at later times.
The metal-rich, hot SN ejecta is clearly more easily removed from the system than the cold ambient medium. For the sake of completeness, in the upper and middle panels of Fig. 6 we show the total SN ejecta and the metals (not-normalized quantities) that are retained in the simulation volume at different times for the adiabatic and cooling models, respectively. These can be directly compared to the corresponding quantities computed using the mass injection rates from Leitherer et al. (2014), to be recovered in the case of a closed system.
3.3. Radial profiles
The evolution of the gas density profile is shown in Fig. 7. For the simulation with radiative cooling, the profile at t = 20 Myr is undistinguishable from the initial profile, which means that to a large extent the ambient medium is unaffected by the mass return from SNe. On the other hand, the density profiles for the galaxy simulated in the adiabatic regime at t = 20 Myr and 30 Myr deviate considerably from the initial density profile: in particular, the final profile displays densities three orders of magnitude lower at the center (i.e., within the innermost 10 pc) and slightly higher beyond 500 pc. The pressure profiles clearly show that the hot pressurized SN ejecta is expanding to cross the simulation box boundaries at late times (Fig. 8).
 |
Fig. 7. Initial (black line) and final density profiles for the adiabatic simulation (t = 30 Myr; thin red line) and for the run with radiative cooling (t = 20 Myr; thick green line). The density profile for the adiabatic simulation at t = 20 Myr (thick red line) is also shown. The vertical lines on the bottom indicate the location of the OB associations. |
Owing to the larger filling factor of the superbubbles (cf. Figs. 1 and 2) and to the more efficient loss of metals (Fig. 6, bottom panel), at t = 20 Myr the metallicity profile predicted in the adiabatic limit is flatter than that predicted with the cooling model (Fig. 9) and fewer metals are found beyond the innermost 10 pc (Fig. 10). In the radiative regime, the metals tend to remain close to the regions where they are injected by dying stars, which explains the rise from the inner regions; we remind the note that for the high-resolution runs discussed in this section the OB associations are randomly distributed following a Plummer’s mass profile with a ≃ 200 pc (see Sect. 2). The decrease of the metal density profile at large radii is due to the leakage of metals from the simulation box. At later times (t = 30 Myr), a low-density, metal-rich blob occupies the central regions of the adiabatic model, that is when and where the filling factor of the bubbles approaches unity.
 |
Fig. 9. Metallicity profiles, for the Boötes I-like UFD simulated in the adiabatic limit (red lines) and with radiative cooling (green line). The thick lines delineate t = 20 Myr; the thin line delineates t = 30 Myr. |
4. Discussion
In general, the smallest MW satellites nowadays appear gas-free. Understanding the physical processes that caused the removal of their gas is therefore necessary to explain their present-day properties. In pure chemical evolution models, it is often taken for granted that the injection of energy by SNe regulates the onset of galactic-scale outflows. Consequently, the timescales for gas removal, star formation quenching and, ultimately, chemical enrichment are dictated by uncertain prescriptions on stellar feedback.
By means of our three-dimensional hydrodynamical simulations, we have shown that in realistic conditions, it appears difficult to explain the removal of the bulk of the cold gas by means of stellar feedback alone. This is at variance with results purely based on analytical calculations, which implicitly assume an idealized configuration with all SNe at the center and full energy coupling with the gas. We pick up on this point further in the coming paragraphs.
4.1. Supernova-driven outflows: Analytic model expectations versus simulations
In this section, we contrast the expectations about SN-driven outflows from an analytic model for Böotes I with the results of our hydrodynamical simulations performed in the adiabatic regime. The analytic model rests on the original setup described in Sect. 2. The binding energy of the gas is given by
We assume that the density distribution of the dark matter halo is represented by Burkert (1995) profile, and calculate the potential by integrating Poisson’s equation as
where G is the gravitational constant, r0 is the core radius of the dark matter distribution, and M0 is the total dark mass inside r0. The observed scaling relation derived by Burkert (1995) yields
and
where MDM = 3.5 × 107 M⊙ (Wolf et al. 2010). Beyond the dark matter cutoff radius, Rc, the potential simply reads
For the gas, we use a Plummer (1911) density distribution,
with a characteristic radius a ≃ 200 pc and Mgas = fb MDM = 6 × 106 M⊙, where fb is the cosmic baryon fraction (Komatsu et al. 2009). By integrating Eq. (1) with these assumptions, it turns out that
By assuming an average SN energy of 1051 erg, it is concluded that in adiabatic conditions ∼50 SNe suffice to remove the gas from the galaxy completely. Our adiabatic simulations, however, tell us a different story. From an inspection of Figs. 1, 3, and 4, it is clear that the energy release from SNe clustered in associations is highly spatially inhomogeneous. The SN ejecta are channelled outward through different funnels. If the OB associations are located at large radii, the rarefied gas crosses the boundaries of the computational box and is lost from the system. If, instead, the hot gas originates from the innermost OB associations, it not may receive enough energy to become unbound and, eventually, it may fall to the center (see Fig. 4, bottom right). The more concentrated the OB associations, the higher the gas fraction that is lost from the system (see Appendix A), but we never predict a complete blow-away of the gas.
In summary, under our specific premises on the initial distributions of gas and stars we show that, although the number of SNe that explode in the simulated galaxy is one order of magnitude larger than required to blow away the entire gas reservoir according to the analytical estimate, a global wind is unlikely to develop (see also Mori et al. 2002). Although the outflow may entrain a non-negligible fraction of the ambient ISM, the galaxy is not swept clean of its gas in our simulations.
4.2. Role of stellar feedback in the evolution of dwarf galaxies
In principle, our results may pose a problem for the evolution of dwarf galaxies on a larger perspective. One crucial aspect concerns the capability of the stellar feedback of blowing away the gas and regulating star formation in small systems. In semi-analytic and pure chemical evolution models, a simple criterion for star formation regulation by stellar feedback is commonly assumed, i.e., that the ISM might be ejected from a galaxy when the cumulative energy injected by all the SNe that ever exploded exceeds the binding energy of the remaining gas (e.g., Larson 1974; Ferguson & Binggeli 1994). Our results strengthen previous findings in the literature (e.g., Marcolini et al. 2006; Caproni et al. 2015) that such a criterion could be too simplistic, and that perhaps the role of stellar feedback in the regulation of star formation in dwarf galaxies needs to be reconsidered.
In the past, it has been also pointed out that the compression due to a large accumulation of energy from nearby OB associations might lead to very high gas densities, with very rapid cooling and dissipation of such energy and consequently inefficient effects of feedback (e.g., Vader 1986). Our simulations have clearly shown that radiative cooling does not play a major role in the failure of the removal of the gas by stellar feedback. Based on our assumptions, even in adiabatic conditions, i.e., in the complete absence of radiative cooling, stellar winds and SNe are unable to power a massive wind capable of removing the bulk of the cold gas from a Boötes I-like galaxy. Indeed, the energy injected in the ISM tends to escape the system along privileged paths, rather than uniformly spread and heat the gas all over the simulation volume.
One major future development of our study will be a direct assessment of the effects of stellar feedback in star-forming UFDs, simulated at very high spatial resolution. A relevant previous attempt to simulate isolated gas-rich dwarf galaxies taking into account their star formation history, which also includes a halo in the UFD domain, has been carried out by Read et al. (2016); this work resolves the interactions of the bubbles created by individual SN explosions (for high-resolution cosmological simulations, see Wheeler et al. 2018). The authors of that work state that their lowest mass halo forms virtually no stars, so they refrain from further analysis, but this could perhaps imply that it clears enough gas to quench the star formation in the system. Detailed high-resolution, three-dimensional simulations of UFDs including both SN feedback and star formation history are necessary to investigate further these crucial aspects of dwarf galaxy evolution at the lowest mass end, as well as to gain a broader understanding of such a disparate class of objects.
4.3. Galactic winds in dwarf galaxies and massive star clusters
For a long time, energetic feedback from stellar winds and SNe have been known to be able to drive vast superbubbles. A direct observational confirmation of the presence of superbubbles in a local system was possible thanks to spectacular, high-spatial resolution Chandra X-ray images of the 30 Doradus star-forming complex in the Large Magellanic Cloud (Townsley et al. 2006). This study provided a clear view of the complex network generated by interacting stellar winds and SNe, working together to create large cavities filled with hot X-ray emitting plasma. On the theoretical side, the true impact of such powerful events on the evolution of the smallest stellar systems, such as dwarf galaxies and stellar clusters, is still an open question.
Because of their shallow potential wells and in some cases low surface brightness, which implies low stellar and gas densities, dwarf galaxies should in principle be highly vulnerable to the effects of stellar winds and SN feedback. Several previous studies have already pointed out that the smallest systems (i.e., those with total mass lower than about 107 M⊙) should more easily have most of their natal gas removed by SN-driven large-scale outflows (e.g., Mac Low & Ferrara 1999; Recchi & Hensler 2013).
A recent numerical study of metal-rich winds in dwarf galaxies by Robles-Valdez et al. (2017), based on three-dimensional N-body and smoothed particle hydrodynamics, focuses on important parameters such as the galaxy concentration index, gas fraction, shape of the mass distribution, and the position of the starburst inside the system. These authors found that an off-center starburst in dwarf galaxies is the most effective mechanism to produce a significant loss of metals. In their comprehensive survey of models characterized by different parameters, they found that most winds produced by starbursts in dwarf galaxies have a high metal content, but that in general the winds are not well-mixed, in that the metals ejected by the massive stars are unable to mix efficiently with the gas of the galaxy.
In other studies, the shape of the galaxy seems to be key in gas expulsion. For instance, Silich & Tenorio-Tagle (2001) concluded that the ejection of enriched gas from a flat galaxy is facilitated with respect to a spherical galaxy (see also Recchi & Hensler 2013). From such studies, it was concluded that the fate of the pristine gas is generally more dependent on the total mass, including a dark matter halo, and that smaller galaxies develop larger outflows; in these systems the fractions of the ejected gas tend to be higher.
It is interesting to note that in massive stellar clusters the capability of superbubbles to drive outflows is a controversial issue as well, in particular in systems with baryonic mass comparable to that of Boötes I. Massive clusters with total mass 107 M⊙ are much more compact than a dwarf galaxy, are not dark matter dominated, and have generally a factor of ten more massive stars than Boötes I. In principle, such stars could contribute simultaneously to the creation of a large-scale outflow; in the work of Baumgardt et al. (2008), these conditions were sufficient to unbind the gas only in systems with mass lower than 107 M⊙ (see also Dopita & Smith 1986; Krause et al. 2016).
On the other hand, in Calura et al. (2015) the evolution of a massive cluster with total mass 107 M⊙ was studied by means of three-dimensional hydro-simulations very similar to those carried out in this work. These authors took a distribution of OB associations scattered in the cluster into account and concluded that according to their thermal modeling of the ISM, which included both heating by stellar winds and SNe and radiative cooling, the entire initial gas content is blown away already after 15 Myr of evolution. Other studies are needed to investigate the fate of the gas in such system if different implementations of stellar feedback are taken into account, to test, for example, the effects of the injection of momentum or of a combination of thermal energy and momentum. In Calura et al. (2015), the coherence of concentrated associations, which causes the hot gas to cover a significant amount of the volume in a short time (a few million years) is key for the ejection of gas. This seems to be the condition to drive a steady wind, as other studies have shown (e.g., Yadav et al. 2017), and in which a sufficiently large (104, or more) number of SNe acting simultaneously seems to be required. In the light of these findings, and also following the insight provided by the lower resolution simulations presented in Appendix A of this paper, it seems that one major cause of the failure of stellar feeback in driving a steady mass outflow might be the relative isolation of the OB associations.
Finally, a few considerations are in order concerning our static implementation of stellar feedback. In principle, these conditions should maximize the effects of stellar feedback with respect to particle-like (i.e., free to move) energy sources. In a medium already heated and diluted by previous activity of stellar winds such as that of our simulation, the action of the SN feedback should be enhanced because the energy released by both sources can accumulate around their fixed positions. If OB associations were free to move and if their dynamics were followed in detail, it is likely that their effect on the system would be less pronounced (Vorobyov et al. 2015).
4.4. Other numerical issues
In a simulated high-density gas, the energy deposited by massive stars in the pre-SN and SN phases can be radiated away very quickly, which renders the stellar feedback highly inefficient (Katz 1992). This implies that other assumptions are needed to have an appreciable effect of stellar winds and SNe on the ISM (see, e.g., Thacker & Couchman 2000; Agertz et al. 2013), for example, by injecting momentum in fully radiative conditions or by switching off cooling in an appropriate and hopefully realistic fashion (e.g., in some spheres of influence around OB associations). This problem seems to be related to our poor understanding of the physical processes associated with stellar feedback which, to be described realistically, would require several ingredients particularly complex to implement, including magnetic fields, turbulence, and other nonthermal processes such as cosmic rays and stellar radiation (see Teyssier et al. 2013).
In this work, we have shown that tenuous, hot bubbles are also created in our radiative simulation; this confirms that at high resolution, the effects of stellar feedback tend to be insensitive to the details of the subgrid physics (Read et al. 2016). Our results strengthen and confirm recent findings of other authors who have shown that, if the cooling radius of the interstellar bubbles is resolved well enough, the momentum that accompanies the fast ejecta of the OB association is correctly recovered before the deposited energy is radiated away (Kim & Ostriker 2015; Martizzi et al. 2015; Simpson et al. 2015).
It is important to note that there are well-known numerical difficulties in studies such as this one. The fast fluid injected by stellar winds and SNe, with typical velocities of a few 103 km s−1, is particularly difficult to treat computationally. This occurs mostly because, in order to satisfy the Courant-Friedrichs-Lewy condition, very small time steps are generally required (for our high-resolution simulations, dt is on the order of 100–400 yr). Some authors have chosen to overcome this difficulty by artificially decreasing the wind velocity (e.g., Emerick et al. 2019). In our simulations, the wind velocity has not been altered, and we have been able to complete our high-resolution adiabatic run up to 30 Myr. However, we have been unable to follow the entire evolution of our galaxy in the high-resolution radiative simulation because of computational constraints that are too demanding. At subparsec resolution the radiative simulation is significantly slowed down: a considerable portion of the domain is refined to the maximum level, hence, at each time step the implicit algorithm for radiative cooling used within RAMSES has to run an extremely large number of times (on the order of 200 million times, corresponding to the number of grids with the highest refinement level). This, however, was not an impediment, since our aim was to study the effects of stellar feeback in an UFD and, in a conservative fashion, we have been able to show that, even in a maximal case of feedback efficiency (i.e., without radiative losses), it is pretty hard to remove the bulk of the gas from the system for a realistic distribution of OB associations (see also the results of our lower resolution numerical experiments in Appendix A). A scattered distribution of the OB associations makes stellar feedback less efficient than expected from simple energetic arguments: cold gas may pile up in some regions, and it is relatively easy to carve tunnels and chimneys along which massive star energy is vented out of the system, rather than being used to accelerate the ambient gas (see also Mori et al. 2002).
5. Conclusions
This paper is the first in a series aimed at studying the evolution of the ISM in UFDs. In particular, our aim is to understand which physical process ultimately caused the removal of gas from a system resembling Boötes I.
By means of idealized three-dimensional grid-based numerical simulations we studied the effects of an internal process, i.e., the stellar feedback, taking into account both stellar winds and SN explosions, on the early evolution of Boötes I. We fully account for the fast fluid injected by stellar winds and SNe, which has typical velocities of a few 103 km s−1 and is particularly difficult to treat computationally.
We assumed an instantaneously born stellar population and that massive stars are grouped in OB associations scattered across the computational volume. Each association was allowed to inject mass and energy in its surroundings at a constant pace for an uninterrupted period of 30 Myr (roughly corresponding to the lifetime of a 8 M⊙ star).
We ran adiabatic simulations in which radiative cooling was switched off as well as a radiative simulation. We ran high-resolution and lower resolution simulations. The results of the high-resolution simulations are presented in Sect. 3, while a suite of lower resolution simulations is discussed in Appendix A. Our findings can be summarized as follows:
-
In the adiabatic case, the effects of stellar feedback are to be regarded as maximal as, in principle, the energy injected by OB associations is entirely used to heat the ISM. Nevertheless, once the OB associations are randomly distributed over the simulation volume (following the density profile of the gas, or a more concentrated density profile), the results of the simulations fall short of the expectations from simple energetic arguments. In these conditions, the energy injected by stellar winds and SNe is not fully coupled to the cold gas present in the system. After 30 Myr, the system has lost less than 20–30% of its initial gaseous mass in our simulations; the exact figure depends on the location of the OB associations more than on their number. However, in this time interval the radial distribution of gas is subject to substantial evolution. At the end of the high-resolution simulation, the density decreases by three orders of magnitude at the center and increases in the outskirts. At the same time, the hot, pressurized gas expands to cross the simulation box boundaries. For computational reasons, the radiative high-resolution run was only followed for 20 Myr. In this case, the cold, initial gas is even less affected by stellar feedback.
-
In both the adiabatic and radiative cases, a substantial amount of the hot ejecta provided by OB associations is lost from the system. In the adiabatic case, at 20 Myr (30 Myr) from 30 to 60% (70–80%) of the ejecta has left the system; the exact amount depends on the specific location of the OB associations. As for the radiative simulation, at 20 Myr nearly 50% of the ejecta is expelled. Consistent with previous results from the literature, at the end of the simulation the hot, metal-enriched tenuous gas driven by OB associations is not well-mixed with the cold, pristine gas.
-
Interstellar bubbles are rapidly and efficiently created in both the adiabatic and radiative simulations. This occurs because of the high resolution of the simulations, which renders the effects of stellar feedback insensitive to the details of the subgrid physics (Read et al. 2016). This confirms the results from other recent studies, which have shown that if the cooling radius of interstellar bubbles is resolved well enough, momentum happens to be correctly deposited in the medium (e.g., Kim & Ostriker 2015).
Finally, we note that these results have to be interpreted with caution, always bearing in mind the approximations introduced in the underlying model.
If OB associations fail to cause the removal of the bulk of the cold gas, environmental processes need to be invoked for the model UFD to evolve to a gas-free system, which is a conclusion already drawn for more massive dwarf spheroidal galaxies (e.g., Marcolini et al. 2006; Caproni et al. 2015). Together with a more realistic modeling of star formation, these external processes will be addressed in a forthcoming paper. As we already stressed in Sect. 2, in the framework of the IGIMF theory a prolonged star formation in UFDs should result in fewer SN explosions, and we plan to implement this theory in our simulations.
A remarkable attempt to consider the role of stripping on the evolution of the lowest mass MW satellites was made by Emerick et al. (2016). Although their ∼10 pc resolution simulations cannot be considered fully converged (see Emerick et al. 2016, their Fig. 7), these authors can conclude that other mechanisms besides stellar feedback and ram pressure stripping must be at play to reconcile the theoretical quenching timescales with those deduced from observations.
Following Ni et al. (2018, their Eq. (1)), the escape velocity is computed by taking into account both the energy required to escape from the “surface” of the halo and that needed to reach the surface from inner regions.
Acknowledgments
We acknowledge the CINECA awards under the ISCRA initiative and under the MoU INAF-CINECA for the availability of high performance computing resources and support. We acknowledge the computing center of INAF, Osservatorio Astronomico di Catania, under the coordination of the CHIPP project, for the availability of computing resources and support. CGF would like to acknowledgethe Viper HPC facility at the University of Hull. DR and FC are grateful for financial support from INAF PRIN-SKA “Empowering SKA as a Probe of galaxy Evolution with H I (ESKAPE-HI)” program 1.05.01.88.04 (PI L. K. Hunt). This work also benefited from the International Space Science Institute (ISSI) in Bern, CH, thanks to the funding of the team “The Formation and Evolution of the Galactic Halo” (PI D. Romano). Last but not least, the authors are indebted to the anonymous referee for an extremely thorough report, which helped to improve the manuscript significantly, and to Pavel Kroupa, who commented on an earlier version of this paper.
References
- Abel, T., Bryan, G. L., & Norman, M. L. 2000, ApJ, 540, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Agertz, O., Kravtsov, A. V., Leitner, S. N., & Gnedin, N. Y. 2013, ApJ, 770, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Aihara, H., Arimoto, N., Armstrong, R., et al. 2018, PASJ, 70, S4 [NASA ADS] [Google Scholar]
- Baumgardt, H., Kroupa, P., & Parmentier, G. 2008, MNRAS, 384, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Bechtol, K., Drlica-Wagner, A., Balbinot, E., et al. 2015, ApJ, 807, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M., Armillotta, L., Perina, S., et al. 2018, MNRAS, 476, 4565 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Zucker, D. B., Evans, N. W., et al. 2006, ApJ, 647, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Zucker, D. B., Evans, N. W., et al. 2007, ApJ, 654, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Irwin, M. J., Koposov, S. E., et al. 2014, MNRAS, 441, 2124 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., Sutherland, R., & Webster, D. 2015, ApJ, 807, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Tumlinson, J., Geha, M., et al. 2014, ApJ, 796, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Burkert, A. 1995, ApJ, 447, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Calura, F., Few, C. G., Romano, D., & D’Ercole, A. 2015, ApJ, 814, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Caproni, A., Lanfranchi, G. A., da Silva, A. L., & Falceta-Gonçalves, D. 2015, ApJ, 805, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Corlies, L., Johnston, K. V., & Wise, J. H. 2018, MNRAS, 475, 4868 [NASA ADS] [CrossRef] [Google Scholar]
- de los Reyes, M. A. C., & Kennicutt, Jr., R. C. 2019, ApJ, 872, 16 [NASA ADS] [CrossRef] [Google Scholar]
- DES Collaboration 2016, MNRAS, 460, 1270 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., & Smith, G. H. 1986, ApJ, 304, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Emerick, A., Mac Low, M.-M., Grcevich, J., & Gatto, A. 2016, ApJ, 826, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Emerick, A., Bryan, G. L., & Mac Low, M.-M. 2019, MNRAS, 482, 1304 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A. 2018, Nat. Astron., 2, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, H. C., & Binggeli, B. 1994, A&ARv, 6, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Homma, D., Chiba, M., Okamoto, S., et al. 2016, ApJ, 832, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Homma, D., Chiba, M., Okamoto, S., et al. 2018, PASJ, 70, S18 [NASA ADS] [CrossRef] [Google Scholar]
- Jeon, M., Besla, G., & Bromm, V. 2017, ApJ, 848, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Jeřábková, T., Hasani Zonoozi, A., Kroupa, P., et al. 2018, A&A, 620, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, N. 1992, ApJ, 391, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, C.-G., & Ostriker, E. C. 2015, ApJ, 802, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Gottlöber, S., Kravtsov, A. V., & Khokhlov, A. M. 1999, ApJ, 516, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M. G. H., Charbonnel, C., Bastian, N., & Diehl, R. 2016, A&A, 587, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Laevens, B. P. M., Martin, N. F., Bernard, E. J., et al. 2015, ApJ, 813, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1974, MNRAS, 169, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Ekström, S., Meynet, G., et al. 2014, ApJS, 212, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., & Ferrara, A. 1999, ApJ, 513, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., & McCray, R. 1988, ApJ, 324, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Marcolini, A., D’Ercole, A., Brighenti, F., & Recchi, S. 2006, MNRAS, 371, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Martizzi, D., Faucher-Giguère, C.-A., & Quataert, E. 2015, MNRAS, 450, 504 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Williams, J. P. 1997, ApJ, 476, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Ghigna, S., Governato, F., et al. 1999, ApJ, 524, L19 [Google Scholar]
- Mori, M., Ferrara, A., & Madau, P. 2002, ApJ, 571, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Ni, Y., Di Matteo, T., Feng, Y., Croft, R. A. C., & Tenneti, A. 2018, MNRAS, 481, 4877 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, S., Arimoto, N., Yamada, Y., & Onodera, M. 2012, ApJ, 744, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [CrossRef] [Google Scholar]
- Read, J. I., Agertz, O., & Collins, M. L. M. 2016, MNRAS, 459, 2573 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., & Hensler, G. 2013, A&A, 551, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, M. S. 1957, PASP, 69, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Robles-Valdez, F., Rodríguez-González, A., Hernández-Martínez, L., & Esquivel, A. 2017, ApJ, 835, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Bellazzini, M., Starkenburg, E., & Leaman, R. 2015, MNRAS, 446, 4220 [NASA ADS] [CrossRef] [Google Scholar]
- Rosen, A., & Bregman, J. N. 1995, ApJ, 440, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Salvadori, S., & Ferrara, A. 2009, MNRAS, 395, L6 [NASA ADS] [Google Scholar]
- Sawala, T., Frenk, C. S., Fattahi, A., et al. 2016, MNRAS, 456, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, E., & Brüggen, M. 2010, MNRAS, 405, 1634 [NASA ADS] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Shanks, T., Metcalfe, N., Chehade, B., et al. 2015, MNRAS, 451, 4238 [NASA ADS] [CrossRef] [Google Scholar]
- Silich, S., & Tenorio-Tagle, G. 2001, ApJ, 552, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. D. 2019, ARA&A, 57, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, C. M., Bryan, G. L., Hummels, C., & Ostriker, J. P. 2015, ApJ, 809, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New Astron., 6, 79 [Google Scholar]
- Sutherland, R. S. 2010, Ap&SS, 327, 173 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teyssier, R., Pontzen, A., Dubois, Y., & Read, J. I. 2013, MNRAS, 429, 3068 [NASA ADS] [CrossRef] [Google Scholar]
- Thacker, R. J., & Couchman, H. M. P. 2000, ApJ, 545, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Tollerud, E. J., Bullock, J. S., Strigari, L. E., & Willman, B. 2008, ApJ, 688, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Torrealba, G., Koposov, S. E., Belokurov, V., et al. 2016, MNRAS, 463, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Townsley, L. K., Broos, P. S., Feigelson, E. D., et al. 2006, AJ, 131, 2140 [NASA ADS] [CrossRef] [Google Scholar]
- Vader, J. P. 1986, ApJ, 305, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Vincenzo, F., Matteucci, F., Vattakunnel, S., & Lanfranchi, G. A. 2014, MNRAS, 441, 2815 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., Recchi, S., & Hensler, G. 2015, A&A, 579, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Webster, D., Bland-Hawthorn, J., & Sutherland, R. 2015, ApJ, 799, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Wheeler, C., Oñorbe, J., Bullock, J. S., et al. 2015, MNRAS, 453, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Wheeler, C., Hopkins, P. F., Pace, A. B., et al. 2018, MNRAS, submitted [arXiv:1812.02749] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Willman, B., Blanton, M. R., West, A. A., et al. 2005, AJ, 129, 2692 [NASA ADS] [CrossRef] [Google Scholar]
- Wise, J. H., Abel, T., Turk, M. J., Norman, M. L., & Smith, B. D. 2012, MNRAS, 427, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, J., Martinez, G. D., Bullock, J. S., et al. 2010, MNRAS, 406, 1220 [NASA ADS] [Google Scholar]
- Yadav, N., Mukherjee, D., Sharma, P., & Nath, B. B. 2017, MNRAS, 465, 1720 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, Z., Jerabkova, T., & Kroupa, P. 2017, A&A, 607, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
Appendix A: Distribution of OB associations and convergence test
To assess the ability of stellar feedback to lift the gas left over from the star formation process out of the potential well of an isolated, low-mass dark matter halo (MDM = 3.5 × 107 M⊙), we adopt an idealized setup.
Massive stars are assumed to be coeval (i.e., born on a timescale that is short compared to their lifetimes) and grouped in OB associations. It has long been recognized that most stars originate in associations (Roberts 1957; Lada & Lada 2003). The probability for an OB association to contain N SNe is set to f(N)∝N−2 (see McKee & Williams 1997; Calura et al. 2015, and references therein), where 30 ≤ N ≤ 650; the upper limit is dictated by the total number of SNe that are expected in the system under scrutiny (see Sect. 2). By applying a grouping procedure and using the above power-law distribution, we end up with a number 𝒩OB of associations, each containing a variable number of massive stars such that the total number of SN progenitors comes to 650.
Figure A.1 shows the frequency distribution of 𝒩OB for 1000 random realizations. The distribution has a peak around 𝒩OB ≃ 6–9, with values lower than 3 and higher than 11 largely disadvantaged. We then need to locate spatially the 𝒩OB associations, which is clearly an extremely noisy procedure. Figure A.2 shows the relative numbers of OB associations that fall in ten galactocentric distance bins (r < 10 pc, r = 10 − 100 pc, r = 100 − 200 pc, r = 200 − 300 pc, r = 300 − 400 pc, ..., r = 700 − 800 pc, r > 800 pc) after 1000 random placements of 𝒩OB = 4 or 10 associations drawn from a Plummer density profile with characteristic radius a ≃ 200 pc or sensibly (70%) lower. The distribution depends strongly on the assumed Plummer radius, in which second-order effects are due to the actual number of associations.
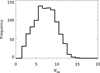 |
Fig. A.1. Occurrence rate of configurations with 650 SNe distributed in 𝒩OB associations for 1000 random realizations. |
 |
Fig. A.2. Relative numbers of OB associations in different radial bins for 1000 random placements of 4 (dashed lines) and 10 (solid lines) associations following a Plummer density profile with either a ≃ 200 (black lines) or 60 pc (red lines). |
In the high-resolution simulations discussed in Sect. 3, ten OB associations are disseminated randomly across the simulation volume, according to the same smooth, low-density, single-phase profile (Plummer 1911, with a ≃ 200 pc) used to describe the gas distribution. With these assumptions, some SN progenitors turn out to be placed in very low-density regions (see Fig. 7), but we note that there is observational evidence that some extreme systems may form stars notwithstanding their utterly low densities (Bellazzini et al. 2018). OB associations located away of the bulk of the ambient medium are clearly unable to affect it. On the other hand, the denser the surrounding gas, the less efficient the stellar feedback. We perform a series of lower resolution adiabatic simulations, in which the number and location of OB associations are let to vary, to ascertain the dependence of the overall results and conclusions reported in this paper on the particular setup choice. In particular, in one simulation we suppose that the OB associations form closer to the halo center (a ≃ 60 pc) from the early collapse and fragmentation of primordial molecular clouds (Abel et al. 2000). We did not investigate more compact configurations, since this would essentially results in handling a proto-globular cluster (see Calura et al. 2015).
In Table A.1 we specify the number and location of the OB associations for the different simulations discussed in this paper. We also give the number of SNe for each association. A particular simulation is identified with the notation X-yy-zz-ww-V, where X indicates if the simulation is adiabatic (A) or radiative (R), yy is the number of OB associations, zz refers to their size (in pc), ww is the maximum spatial resolution (in pc) and V tells if the associations are drawn from the same, shallow profile used for the gas (P) or if they are more concentrated in the central regions (C).
Characteristics of OB associations for different simulations.
The results are summarized in Figs. A.3 and A.4, where we show the fractions of the initial gaseous mass and of the SN ejecta that are retained by the model UFD in the course of different simulations. The quantities from the high-resolution runs are shown as solid lines, while those from the lower resolution numerical experiments show up as dotted lines. The lower resolution run A-10-20-04-P meets only partially the convergence criteria by Kim & Ostriker (2015, see Sect. 2). Nevertheless, it tracks pretty well the results of the corresponding high-resolution simulation A-10-04-01-P (cf. red dotted and red solid lines in Figs. A.3 and A.4, respectively).
 |
Fig. A.3. Evolution of the gas fraction retained by the system (normalized to the initial gas mass), for different resolutions and OB association distributions (see bottom left corner and Table A.1). |
 |
Fig. A.4. Same as Fig. A.3, for the SN ejecta, normalized to the expected theoretical value at each time according to Leitherer et al. (2014). |
Overall, it appears that both changing the number of the OB associations and their position within the simulation volume does not change our main conclusion that stellar feedback alone does not suffice to vent the bulk of the neutral ISM out of the model galaxy. However, it must be stressed that we adopt an idealized setup, which lacks a structured, multiphase ISM. Furthermore, we consider a stellar population already in place at the beginning of the simulation. In principle, however, according to the IGIMF theory a prolonged star formation in UFDs should result in less massive stars available to heat the gas (Yan et al. 2017; Jeřábková et al. 2018), leading to a reduced feedback. Yet, before jumping to conclusions it is mandatory to include a self-consistent recipe for star formation in the simulations, and this will be part of a forthcoming work.
Appendix B: Three-dimensional visualization
Figures B.1 and B.2 show the projections of the three-dimensional distributions of gas and metallicity within the simulation box, at two different times, for our high-resolution simulations. Translucent rendering of the volume is performed by using IDL post-processing utils distributed with the source code.
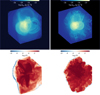 |
Fig. B.1. Three-dimensional structure of gas (top images) and metals (bottom images) in the simulation box at t = 20 Myr. The images on the left refer to the high-resolution adiabatic run, while those on the right are for the run with cooling. |
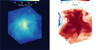 |
Fig. B.2. Three-dimensional structure of gas (left-hand image) and metals (right-hand image) in the simulation box at t = 30 Myr, for the adiabatic run. |
All Tables
All Figures
 |
Fig. 1. Gas density (left), temperature (middle), and metallicity (right) maps for the Boötes I-like galaxy in the z = 0 plane at five representative times, i.e., t = 3, 13, 20, 25, and 30 Myr. The projected positions of the OB associations are shown on the metallicity maps as gray circles, with sizes proportional to the number of massive stars. The snapshots refer to the galaxy simulated in the adiabatic limit at high resolution. |
| In the text | |
 |
Fig. 2. Same as Fig. 1, for t = 3, 13, 17, and 20 Myr for the high-resolution simulation with radiative cooling. |
| In the text | |
 |
Fig. 3. Gas radial velocity field, in the z = 0 plane, at t = 20 Myr. The maps on the left refer to the galaxy simulated in the adiabatic limit, while the maps on the right indicate the run with radiative cooling. The black cells in the inset maps on the bottom left of each panel highlight regions where the gas moves with velocities lower than the local escape velocity. |
| In the text | |
 |
Fig. 4. Same as Fig. 3, for t = 30 Myr for the adiabatic simulation only. |
| In the text | |
 |
Fig. 5. Mass-weighted distributions of gas radial velocity (upper panels) and density (middle panels) at t = 20 Myr, for the runs with (right-hand panels) and without radiative losses (left-hand panels). The distribution of metals in radial velocity bins at the same time for the two runs (lower panels) is also shown. The red (green) lines on the left (right) panels show all the gas and metals in the simulation volume. The yellow solid and blue dotted lines in all panels show the hot (T ≥ 105 K) and cold/warm (T < 105 K) components, respectively. The integrals of the red and green lines are normalized to unity. |
| In the text | |
 |
Fig. 6. Cumulative mass (upper panel) and metals (middle panel) ejected by massive stars (m > 8 M⊙) and recycled in the simulation volume, at different times. The (red) empty stars refer to the adiabatic run; the (green) filled stars indicate the run with radiative cooling. The quantities computed using injection rates from Leitherer et al. (2014) are shown as dashed (black) lines in all panels, and would be recovered in the case of a closed system. In the lower panel, the total gas masses, normalized to the initial gas mass of the system, are shown as solid lines; SN ejecta, normalized to the corresponding quantities computed with Leitherer et al. (2014) mass return rate at each time are indicated as stars joined by dotted lines; these shown in the system at different times for the adiabatic (red lines and symbols) and radiative models (green lines and symbols). |
| In the text | |
 |
Fig. 7. Initial (black line) and final density profiles for the adiabatic simulation (t = 30 Myr; thin red line) and for the run with radiative cooling (t = 20 Myr; thick green line). The density profile for the adiabatic simulation at t = 20 Myr (thick red line) is also shown. The vertical lines on the bottom indicate the location of the OB associations. |
| In the text | |
 |
Fig. 8. Same as Fig. 7, but for the pressure profiles. |
| In the text | |
 |
Fig. 9. Metallicity profiles, for the Boötes I-like UFD simulated in the adiabatic limit (red lines) and with radiative cooling (green line). The thick lines delineate t = 20 Myr; the thin line delineates t = 30 Myr. |
| In the text | |
 |
Fig. 10. Same as Fig. 9, but the profiles refer to the metal density, ρZ = Z ρgas. |
| In the text | |
 |
Fig. A.1. Occurrence rate of configurations with 650 SNe distributed in 𝒩OB associations for 1000 random realizations. |
| In the text | |
 |
Fig. A.2. Relative numbers of OB associations in different radial bins for 1000 random placements of 4 (dashed lines) and 10 (solid lines) associations following a Plummer density profile with either a ≃ 200 (black lines) or 60 pc (red lines). |
| In the text | |
 |
Fig. A.3. Evolution of the gas fraction retained by the system (normalized to the initial gas mass), for different resolutions and OB association distributions (see bottom left corner and Table A.1). |
| In the text | |
 |
Fig. A.4. Same as Fig. A.3, for the SN ejecta, normalized to the expected theoretical value at each time according to Leitherer et al. (2014). |
| In the text | |
 |
Fig. B.1. Three-dimensional structure of gas (top images) and metals (bottom images) in the simulation box at t = 20 Myr. The images on the left refer to the high-resolution adiabatic run, while those on the right are for the run with cooling. |
| In the text | |
 |
Fig. B.2. Three-dimensional structure of gas (left-hand image) and metals (right-hand image) in the simulation box at t = 30 Myr, for the adiabatic run. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



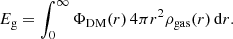
![$$ \begin{aligned} \Phi _{\rm DM}(r) =&-\!1.96\, \frac{G M_0}{r_0} \, \bigg \{ \pi - 2 \, \bigg ( 1 + \frac{r_0}{r} \bigg ) \, \mathrm{arctan}\frac{r}{r_0}\nonumber \\&+\!2 \, \bigg ( 1 + \frac{r_0}{r} \bigg ) \, \mathrm{ln}\bigg ( 1 + \frac{r}{r_0} \bigg )\\&- \bigg ( 1 - \frac{r_0}{r} \bigg ) \, \mathrm{ln}\bigg [ 1 + \bigg ( \frac{r}{r_0} \bigg )^2 \bigg ] \bigg \},\nonumber \end{aligned} $$](/articles/aa/full_html/2019/10/aa35328-19/aa35328-19-eq3.gif)