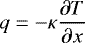| Issue |
A&A
Volume 630, October 2019
Rosetta mission full comet phase results
|
|
|---|---|---|
| Article Number | A5 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834631 | |
| Published online | 20 September 2019 | |
Effect of radiative heat transfer in porous comet nuclei: case study of 67P/Churyumov-Gerasimenko
1
Institut für Geodäsie und Geoinformationstechnik, Technische Universität Berlin,
Straße des 17. Juni 135,
10623
Berlin, Germany
e-mail: hu@tu-berlin.de
2
Institut für Geophysik und extraterrestrische Physik, Technische Universität Braunschweig,
Mendelssohnstraße 3,
38106
Braunschweig, Germany
3
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37077
Göttingen, Germany
Received:
12
November
2018
Accepted:
4
April
2019
Context. Radiative heat transfer occurs in a porous medium, such as regolith on planetary bodies. Radiation enhances the efficiency of heat transport through the subsurface, effecting a strong temperature dependence of thermal conductivity. However, this effect has been omitted in many studies of comet 67P/Churyumov-Gerasimenko (67P).
Aims. We concisely review the method for characterizing radiative heat transfer and present a generic treatment in thermal modeling. In particular, we study the impact of radiative heat transfer on 67P subject to both diurnal and seasonal variations of insolation.
Methods. We adapted a numerical model based on the Crank–Nicolson scheme to estimate the subsurface temperatures and water production rate of 67P, where conductivity may vary with depth.
Results. Radiative heat transfer is efficient during the day near the surface but it dicreases at night, which means that more energy is deposited underneath the diurnal thermal skin. The effect increases with pore size and accordingly, with the size of the constituent aggregates of the nucleus. It also intensifies with decreasing heliocentric distance. Close to perihelion, within 2 au, for example, radiation may raise the temperature by more than 20 K at a depth of 5 cm, compared with a purely conductive nucleus. If the nucleus is desiccated and composed of centimeter-sized aggregates, the subsurface at 0.5 m may be warmed to above 180 K.
Conclusions. Radiative heat transfer is not negligible if the nucleus of 67P consists of aggregates that measure millimeters or larger. To distinguish its role and ascertain the pore size of the subsurface, measurements of temperatures from a depth of ~1 cm down to several decimeters are most diagnostic. The water production rate of the nucleus, on the other hand, does not provide a useful constraint.
Key words: radiation mechanisms: thermal / methods: numerical / comets: general / minor planets, asteroids: general / comets: individual: 67P/Churyumov-Gerasimenko
© ESO 2019
1 Introduction
The gas coma of comet 67P/Churyumov-Gerasimenko (hereafter 67P) was dominated by water vapor throughout its last perihelion passage in August 2015 (Fougere et al. 2016a,b). At least over the northern hemisphere, which was illuminated protractedly until the Fall equinox in May, the dust activity was decidedly driven by water outgassing in response to solar illumination over irregular landscape (Shi et al. 2018). Water ice must have been present from some shallow depths, for example, a few millimeters, from the nucleus surface, where the temperature rises sufficiently during daytime to invigorate ice sublimation and in turn induce dust emission.
Even when only the topmost layer of the nucleus is considered, the thermo-physical processes governing the water outgassing and dust activities remain to be resolved (Fulle et al. 2016). This resolution depends on a proper parameterization of the physical, structural, and compositional properties of the nucleus, such as material strengths, porosity, and ice content. It also relies on a valid characterization of heat transport, mass transfer of gas diffusion, and dust mobilization through the subsurface (Prialnik et al. 2004; Huebner et al. 2006). Understanding the activity mechanisms is further compounded by the constant resurfacing of the nucleus, whereby the interior is excavated. Intuitively, the breakup and subsequent removal of the surface layers discontinues the heat transport in the subsurface and exposes the icy interior to direct solar radiation (Gortsas et al. 2011).
Cometary nuclei in general are porous. In the case of 67P, this is evidenced by the low bulk density of ρ ≈ 500 kg m−3 (Sierks et al. 2015; Pätzold et al. 2016). The prevalent occurrence of dust activity and surface changes can only be explained by low material strengths of the nucleus, which is prone to destabilization (Groussin et al. 2015; Shi et al. 2016). The dominant role of diurnal water outgassing in driving dust activity in response to insolation is in accordance with the insulating nature of the surface layer, as inferred from the measured low thermal inertias, 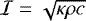 , up to about 100 W m−2K−1s1∕2 (Gulkis et al. 2015; Choukroun et al. 2015; Schloerb et al. 2015; Spohn et al. 2015). Within uncertainties in the density estimate and for commonly adopted values for specific heat capacity, for instance, 500 < c < 1500 J K−1, such a thermal inertia indicates a low heat conductivity of κ ~ 0.001 W m−1K−1 that certainly does not far exceed 0.01 W m−1K−1, in good agreement with laboratory results (Krause et al. 2011). The findings mentioned above constitute a line of persuasive if incomplete arguments that the nucleus of 67P is a weak agglomerate of dust and ice mixtures, most likely formed (or reorganized) through the gentle accretion of aggregates or “pebbles” under self-gravitation (Blum et al. 2014, 2017).
, up to about 100 W m−2K−1s1∕2 (Gulkis et al. 2015; Choukroun et al. 2015; Schloerb et al. 2015; Spohn et al. 2015). Within uncertainties in the density estimate and for commonly adopted values for specific heat capacity, for instance, 500 < c < 1500 J K−1, such a thermal inertia indicates a low heat conductivity of κ ~ 0.001 W m−1K−1 that certainly does not far exceed 0.01 W m−1K−1, in good agreement with laboratory results (Krause et al. 2011). The findings mentioned above constitute a line of persuasive if incomplete arguments that the nucleus of 67P is a weak agglomerate of dust and ice mixtures, most likely formed (or reorganized) through the gentle accretion of aggregates or “pebbles” under self-gravitation (Blum et al. 2014, 2017).
The heat transport in porous media differs from that in solids in that energy may be radiated through voids (Fig. 1). The bulk effect of radiative heat transfer cannot easily be separated from that of conduction through contacting solid grains. The efficiency of the radiative heat transfer increases with the size of the pores, which is determined by the size and the packing structure of the constituent aggregates. Radiation always enhances the efficiency of heat transfer compared with pure heat conduction through contacting grains. In other words, neglecting radiation always causes an underestimation of instant heat flux (for the same temperature distribution). This problem may be tolerable in the case of small voids, but it must become more challenging as the pore size increases.
Heat transport is admittedly also affected by other factors. The heat conductivity of ice is dependent on temperature(Klinger 1980). The conductivity of dust and ice mixtures then varies with material composition, such as the dust-to-ice ratio (Orosei et al. 1995; Davidsson & Skorov 2002) and grain structure (Haruyama et al. 1993). The sublimation and recondensation of ices in the porous interior require the conservation of mass of the system to be characterized; these phenomena also affect the energy of the system in a complex manner (Squyres et al. 1985; Mekler et al. 1990; Spohn & Benkhoff 1990; Orosei et al. 1995; De Sanctis et al. 1999; Kossacki, Szutowicz & Leliwa-Kopystyński 1999; Skorov et al. 1999; Capria et al. 2000). Depending on the pressure, gas diffusion through pores may yield a non-negligible contribution to heat transport (Piqueux & Christensen 2009). Steiner & Kömle (1991) found that the effects of phase changes of materials and mass flows on the energy distribution can be assimilated by a temperature-dependent “effective” conductivity when the heat equation is solved. This result was subsequently refined by Kossacki et al. (1994). The specific heat capacity likewise exhibits a temperature dependence (Klinger 1980), which in turn complicates the behavior of thermal inertia (Ferrari & Lucas 2016; Ferrari 2018).
The aim of this study is to cast some light on the thermal behavior of the porous nucleus where radiative heat transfer likely plays a role. Radiative heat transfer is a classic problem of thermal modeling and was proved to be an important mechanism to consider in the case of the Moon (Linsky 1966; Winter & Saari 1969) and asteroids (Gundlach & Blum 2013). So far, however, it has been largely ignored in the studies of 67P, with only few exceptions such as the analysis by Blum et al. (2017). As a part of their comprehensive investigation, the thermal model developed by Hu et al. (2017a) has been applied for some benchmark calculations. In particular, the model has been adapted in order to treat the heat equation in the case of temperature-dependent heat conductivity. Hence, it is also an objective to recapitulate the general concept of radiative heat transfer, as discussed by many precedent studies, and to introduce our treatment of the topic (Sect. 2). The difference between the nucleus with constant conductivity and one with radiative heat transfer can be easily recognized in their distinct subsurface temperatures (Sect. 3). We also illustrate the effect of radiative heat transfer on the water production rate of the nucleus of 67P (Sect. 4).
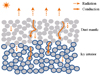 |
Fig. 1 Schematic illustration of heat transfer through the granular, porous subsurface of a comet nucleus under solar illumination. The outermost layer is desiccated, leaving behind a dust mantle that lies above the mixture of dust and ice aggregates. Conduction takes place through the aggregates that are in contact. Radiation occurs inside the pores; porosity of the individual aggregates is neglected. |
2 Statement of the problem
Because of low thermal inertia, only the topmost centimeters of the subsurface respond perceptibly to insolation over a nucleus rotation. Insolation over an orbit of 67P (Table 1) probably affects less than one meter below the surface (Capria et al. 2017). This is insignificant compared with the resolution of most remote-sensing observations of the nucleus of 67P. It is therefore justified to adopt the plane-parallel assumption and consider heat transfer in 1D,
![\begin{equation*}c\rho \frac{\partial T}{\partial t} = \frac{\partial}{\partial x}\left[ \kappa(T) \frac{\partial T}{\partial x} \right], \end{equation*}](/articles/aa/full_html/2019/10/aa34631-18/aa34631-18-eq2.png) (1)
(1)
where T is the temperature of the medium at depth x from the surface. The mass density, ρ, the specific heat capacity, c, and conductivity, κ, are introduced in Sect. 1.
2.1 Heat conductivity
The heat conductivity of a granular, porous medium accounts for two distinct mechanisms: (1) the heat conduction through the “network” aggregates that are in contact, and (2) the transport through thermal radiation inside the pores (Watson 1964; Clegg et al. 1966; Linsky 1966; Winter & Saari 1969; Cremers & Birkebak 1971; Mendis & Brin 1977; Brin & Mendis 1979; Fanale & Salvail 1984; Squyres et al. 1985; Kömle and Steiner 1992; Orosei et al. 1995; Krause et al. 2011; Gundlach & Blum 2012). Accordingly, we let
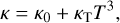 (2)
(2)
where the constant κ0 and the temperature-dependent component, κTT3, measure theefficiency of heat transfer through the contacting grains and that of radiation through pores, respectively.
2.1.1 Conductive component
The nucleus of 67P, and most probably, the nuclei of comets in general, is composed of aggregates. The conductivity through the contacting aggregates is given by (Gundlach & Blum 2012; Blum et al. 2017)
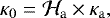 (3)
(3)
which depends on the conductivity of the individual aggregates, κa, as well as on the contact areas between them, which are measured by the Hertz factor, 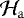 . The Hertz factor is given by
. The Hertz factor is given by
![\begin{equation*}\mathcal{H}_{\mathrm{a}} = \left[ \frac{9 \pi}{4} \left(\frac{1-\mu^2_{\mathrm{a}}}{\mathcal{Y}_{\mathrm{a}}}\right) \frac{\gamma_{\mathrm{a}}}{r_{\mathrm{a}}} \right]^{\frac{1}{3}} h_1 \exp(h_2 \phi_0), \end{equation*}](/articles/aa/full_html/2019/10/aa34631-18/aa34631-18-eq6.png) (4)
(4)
where μa, 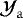 , γa, and ra denote the Poisson ratio, Young’s modulus, the specific surface energy, and the radius of the aggregates, respectively. ϕ0 is the volume filling factor of the aggregate pack that depends on their packing structure (i.e. neglecting the filling factor inside the aggregates; see ϕa in Eq. (5)). h1 and h2 are experimentally fitted constants that account for the influence of the packing structure of the aggregates on their contact areas as a function of the volume filling factor (Gundlach & Blum 2012).
, γa, and ra denote the Poisson ratio, Young’s modulus, the specific surface energy, and the radius of the aggregates, respectively. ϕ0 is the volume filling factor of the aggregate pack that depends on their packing structure (i.e. neglecting the filling factor inside the aggregates; see ϕa in Eq. (5)). h1 and h2 are experimentally fitted constants that account for the influence of the packing structure of the aggregates on their contact areas as a function of the volume filling factor (Gundlach & Blum 2012).
The conductivity of the individual aggregate analogously depends on the contact between the (solid) constituent monomers, that is (Gundlach & Blum 2012),
![\begin{equation*}\kappa_{\mathrm{a}} = \mathcal{H}_{\mathrm{m}} \times \kappa_{\mathrm{m}} = \left[ \frac{9 \pi}{4} \left(\frac{1-\mu^2_{\mathrm{m}}}{\mathcal{Y}_{\mathrm{m}}}\right) \frac{\gamma_{\mathrm{m}}}{r_{\mathrm{m}}} \right]^{\frac{1}{3}} h_1 \exp(h_2 \phi_{\mathrm{a}}) \times \kappa_{\mathrm{m}}, \end{equation*}](/articles/aa/full_html/2019/10/aa34631-18/aa34631-18-eq8.png) (5)
(5)
with 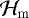 and κm denoting the Hertz factor and conductivity of the monomers, respectively. μm,
and κm denoting the Hertz factor and conductivity of the monomers, respectively. μm, 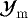 , γm, and rm are as defined for Eq. (4), but all refer to the monomers. ϕa is the volume fraction of the aggregate that is filled by monomers (compared to ϕ0 for the nucleus).
, γm, and rm are as defined for Eq. (4), but all refer to the monomers. ϕa is the volume fraction of the aggregate that is filled by monomers (compared to ϕ0 for the nucleus).
The specific energy of the aggregate (in Eq. (4)) can be evaluated as
![\begin{equation*}\gamma_{\mathrm{a}} = \phi_{\mathrm{a}} \gamma_{\mathrm{m}} \left[ 9 \pi \left(\frac{1-\mu^2_{\mathrm{a}}}{\mathcal{Y}_{\mathrm{m}}}\right) \frac{\gamma_{\mathrm{m}}}{r_{\mathrm{m}}} \right]^{\frac{2}{3}}. \end{equation*}](/articles/aa/full_html/2019/10/aa34631-18/aa34631-18-eq11.png) (6)
(6)
Orbital and rotation parameters of 67P for the orbital solution.
 |
Fig. 2 Effective thermal conductivity as functions of aggregate size and temperature. The conductivity consists of a contact and a radiative component, as indicated by Eq. (2). The radius and (color-scaled) conductivity are of logarithmic scales. The contours for 0.0001, 0.001, 0.01, and 0.1 W m−1K−1 are indicated. |
2.1.2 Radiative component
The second term on the right-hand side of Eq. (2) accounts for the contribution due to radiative heat transfer. Gundlach & Blum (2012) suggested using the formula by Merrill (1969) to evaluate κT as follows:
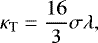 (7)
(7)
where σ is the Stefan–Boltzmann constant. λ is a characteristic length of the pores through which radiation occurs that is linear to the aggregate size. Gundlach & Blum (2012) found that it can be approximated by
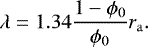 (8)
(8)
Hereafter we only consider a homogenous medium consisting of uniform grains and therefore of constant pore size, in which case, λ and κT are constants.
The dependence of the effective conductivity on aggregate size and temperature is demonstrated in Fig. 2. At low temperatures, below 100 K, for instance, the influence of the radiative component is only noticeable for aggregates larger than about one millimeter (as suggested by the increase in conductivity with size). For aggregates smaller than one millimeter, this conductivity decreases with size, indicating that the contact component dominates. Generally speaking, the radiative component hardly exceeds the order of 10−3 W m−1K−1 for temperature up to 300 K, and can be neglected for a nucleus that is composed of aggregates smaller than 0.1 mm. If the object is composed of larger aggregates, for example, several millimeters in diameters in the case of 67P, the radiative component likely dominates heat transport (Blum et al. 2017). The conductivity may thus be strongly dependent on temperature.
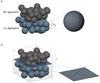 |
Fig. 3 Nucleus subsurface comprising uniform spherical dust aggregates. The topmost few layers of aggregates are desiccated, and water ice is present underneath in addition to the dust aggregates (panel a). The aggregate radius is ra and is independent of the ice content. We also assume for simplification that sublimation occurs from a fixed depth of X (panel b). |
2.1.3 Note on simplifications
Other mechanisms or conditions may contribute to heat transport but are neglected in our study. The conductive component of the solid mixture of dust and ice is given by (Orosei et al. 1995)
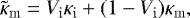 (9)
(9)
where Vi is the volumetric fraction of ice and where κi = 567∕T W m−1K−1 is the conductivity of water ice (Klinger 1980). As in Blum et al. (2017), we envision the nucleus structure to be made of aggregates, where ice grains adhere to the dust aggregates (Fig. 3). In view of the complex aggregate structure of the nucleus, the expression of conductivity is sophisticated (Ferrari & Lucas 2016; Ferrari 2018). However, at least over the northern hemi-nucleus of 67P, the ice abundance in the subsurface is low, that is, below 10% (in volume and mass). Assuming κm and κi are both on the order of 1 W m−1K−1 in Eq. (9), as is the case for silicate dust (Gundlach & Blum 2012), we may neglect the component due to water ice and thereby assume 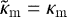 , which enters Eq. (5).
, which enters Eq. (5).
Diffusing gas in the pore space transports heat. The efficiency depends on the density or pressure of gas in the pores (Piqueux & Christensen 2009). The Knudsen number, 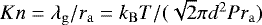 , which is the ratio between the mean free path and the pore dimension, may be considered. Here, kB is the Boltzman constant, d ≈ 6 × 10−10 m is the diameter of a water molecule, and P is the gas pressure. For example, the gas pressure of 1 Pa1 in millimeter-sized pores results in Kn ≈ 3 at a temperature of ~200 K. According to Piqueux & Christensen (2009), this corresponds to an effective conductivity of ~0.001 W m−1K−1. The gas pressure in the subsurface is lower, so that the diffusion occurs consistently in the free molecular regime (i.e. with Kn ≫ 1). Consequently, the contribution to conductivity is smaller than 0.001 W m−1K−1 and can therefore be neglected. This conclusion was also drawn by Steiner & Kömle (1991).
, which is the ratio between the mean free path and the pore dimension, may be considered. Here, kB is the Boltzman constant, d ≈ 6 × 10−10 m is the diameter of a water molecule, and P is the gas pressure. For example, the gas pressure of 1 Pa1 in millimeter-sized pores results in Kn ≈ 3 at a temperature of ~200 K. According to Piqueux & Christensen (2009), this corresponds to an effective conductivity of ~0.001 W m−1K−1. The gas pressure in the subsurface is lower, so that the diffusion occurs consistently in the free molecular regime (i.e. with Kn ≫ 1). Consequently, the contribution to conductivity is smaller than 0.001 W m−1K−1 and can therefore be neglected. This conclusion was also drawn by Steiner & Kömle (1991).
2.2 Boundary conditions
2.2.1 Surface
Most generally, the energy input to the system is the flux of solar irradiation that is absorbed by the nucleus surface,
![\begin{eqnarray*}Q_{(0)}(t) &=& Q_{\odot}(t) = \frac{C_{\odot}}{r_{\odot} (t)^2} (1-\mathcal{A}) \nonumber\\ && \times\; \delta \left[\alpha_{\odot}(t),\varphi_{\odot}(t)\right] \sin \left[\varphi_{\odot}(t)\right]\quad ({\textrm{W\,m}^{-2}}), \end{eqnarray*}](/articles/aa/full_html/2019/10/aa34631-18/aa34631-18-eq17.png) (10)
(10)
where C⊙ = 1361 W m−2 is the solar constant, r⊙ is the heliocentric distance of the objectin units of au, and δ is the Kronecker operator describing the illuminability of the local surface, which depends on the angles of solar azimuth and elevation, α⊙, φ⊙. Namely, δ = 1 if the surface is illuminated and δ = 0 if the surface is in shadow, for example, when the Sun is below the horizon or obstructed by surrounding topography. 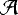 is the bolometric Bond albedo that measures the fraction of sunlight that is reflected off the surface. We note that more realistically, sunlight could penetrate several grain layers (Davidsson & Skorov 2002). When we assume that the aggregates are composed of micron-sized monomers, the energy absorption occurs in a thin layer down to the depth of a few micron. The microscopic surface roughness, which also affects energy deposition, is neglected.
is the bolometric Bond albedo that measures the fraction of sunlight that is reflected off the surface. We note that more realistically, sunlight could penetrate several grain layers (Davidsson & Skorov 2002). When we assume that the aggregates are composed of micron-sized monomers, the energy absorption occurs in a thin layer down to the depth of a few micron. The microscopic surface roughness, which also affects energy deposition, is neglected.
The angles α⊙, φ⊙, and r⊙ in Eq. (10) were evaluated from the rotational and orbital parameters of 67P (Table 1). The rotation state of 67P, in particular, exhibits considerable variability due to activity (Preusker et al. 2015). The parameters have been closely monitored over the span of the Rosetta mission. We used the SPICE kernels to retrieve the position of the Sun in the body-fixed coordinate system of 67P at any given epoch within the mission span (Costa 2018). α⊙, φ⊙ at a certain location on the nucleus were subsequently derived through a transformation of the solar position into the local horizontal system. To determine the obstruction of sunlight by the surroundings, δ, we used the Landscape database for 67P described in Hu et al. (2017a). The Horizon component is useful here for tabulating the panoramic view of the skyline at all locations (corresponding polyhedral facets) of the nucleus. When it is necessary to evaluate Q(0) outside the mission span, for instance, over a full orbit, we evaluated r⊙ assuming Keplerian (elliptic) motion of 67P around the Sun. We also assumed fixed orientation of the rotation axis and constant rotation rate to calculate the solar position in the body-fixed coordinate system of 67P for each epoch.
Then, the heat flux transported into the nucleus results from the solar irradiation offset by heat dissipation through thermal radiation from the surface,
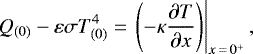 (11)
(11)
where ε is the emissivity of the surface and T(0) is the surface temperature.
Nucleus parameter properties for thermal modeling.
2.2.2 Ice front
To model water outgassing from the nucleus, we assumed that the nucleus consists of a desiccated layer, or mantle, packed by spherical dust aggregates of radius, ra. A mixture of dust and (crystalline) water-ice aggregates lies underneath with a random areal mixing. For the sake of simplicity, the gas diffusion through the pores of the icy interior was neglected. In other words, the sublimation was assumed to occur from a uniform solid plane below the dust mantle (see Fig. 3).
Let X denote the thickness of the mantle. The energy balance at the ice front can be expressed as (Kührt & Keller 1994)
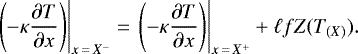 (12)
(12)
Depending on the temperature of the ice front, T(X), the mass flux of sublimation from the subsurface of pure ice is given by (Gundlach et al. 2011)
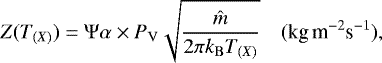 (13)
(13)
where PV = p0 exp(p1∕T) Pa is the saturation vapor pressure of water for some constants p0, p1, 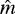 is the mass of a water molecule, and kB is the Boltzmann constant.
is the mass of a water molecule, and kB is the Boltzmann constant. ![$\alpha = \alpha_0 + \alpha_1/\left[1+ \exp (\alpha_2 - \alpha_3/T)\right]$](/articles/aa/full_html/2019/10/aa34631-18/aa34631-18-eq23.png) is an empirical sublimation coefficient accommodating the (experimentally observed) overestimation of sublimation flux by kinetic theory due to complex mechanisms, such as non-negligible vapor pressure of non-escaping molecules relative to the saturation pressure and deposition of impinging molecules onto pores.
is an empirical sublimation coefficient accommodating the (experimentally observed) overestimation of sublimation flux by kinetic theory due to complex mechanisms, such as non-negligible vapor pressure of non-escaping molecules relative to the saturation pressure and deposition of impinging molecules onto pores. 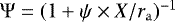 is a permeability coefficient of the mantle that quantifies the reduction of the sublimation flux as a function of mantle thickness and aggregate size. The constants in the expressions introduced above are listed in Table 2.
is a permeability coefficient of the mantle that quantifies the reduction of the sublimation flux as a function of mantle thickness and aggregate size. The constants in the expressions introduced above are listed in Table 2.
Z(T(X)) will overestimate the sublimation flux if the subsurface contains dust impurities. We introduce the factor f ∈ [0, 1] indicating the icy area fraction of the (plane of) ice front from which sublimation occurs (Crifo 1997). For a dusty nucleus (e.g. composed dominantly of dust or nonvolatile materials), this factor is approximately inversely proportional to the dust-to-ice mass ratio. For instance, a dust-to-ice ratio of ~10 corresponds to a uniform microscopic icy area fraction of 10% at all depths below the dust mantle. ℓ is the latent heat of water ice.
The behavior of Z(T) is dominated by an exponential trend (assuming sublimation from the surface, i.e. Ψ = 1, Fig. 4). In the case of 67P, whose heliocentric distance varies between about 1.24 and 5.7 au, the temperaturerange of interest is roughly between 150 and 350 K. This is a crude estimate based on surface energy balance of a dry nucleus as a limiting case. We considered the equilibrium surface temperature of 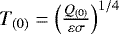 (Eq. (11)), where heat conduction is neglected and where the energy input is simplified as
(Eq. (11)), where heat conduction is neglected and where the energy input is simplified as 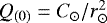 (Eq. (10)). This simplification is only justified if the nucleus is nearly dry. In reality, the energy consumption by sublimation of ice, such as activity from below the surface rather than directly from the surface, and heat conduction into the nucleus all reduce the surface temperature. The actual temperature of ice sublimation is therefore lower than indicated in Fig. 4, especially toward perihelion.
(Eq. (10)). This simplification is only justified if the nucleus is nearly dry. In reality, the energy consumption by sublimation of ice, such as activity from below the surface rather than directly from the surface, and heat conduction into the nucleus all reduce the surface temperature. The actual temperature of ice sublimation is therefore lower than indicated in Fig. 4, especially toward perihelion.
While not always realistic, it is usually imposed that heat flux effectively vanishes from a certain depth. The nucleus becomes isothermal underneath. We denote the isothermal depth by 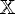 . Here, the boundary condition is expressed as
. Here, the boundary condition is expressed as 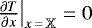 .
.
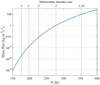 |
Fig. 4 Mass flux of water-ice sublimation as a function of temperature (Gundlach et al. 2011). We also indicate the range of heliocentric distance of interest. The perihelion distance is 1.24 au. |
2.3 Modeling parameters
The contribution of thermal radiation to the effective heat conductivity is the chief interst here. For this reason, other parameters of the thermal model are treated as constants. We justify the parameterization below.
Becausewe lack evidence that the density of the subsurface deviates from that of the bulk nucleus, we adopted ρ = 500 kg m−3. Likewise, little is known about the heat capacity of material on 67P. We refer to Orosei et al. (1995), who used ci =7.49T + 90 J kg−1K−1 for water ice and cd = 1200 J kg−1K−1 for dust; Davidsson & Skorov (2002) cited another expression of cd = 3T J kg−1K−1. In either case, the temperature dependence of the expressions is linear and thus indistinct compared with the effective heat conductivity. Therefore, we adopted a constant of c = 1000 J kg−1K−1 for the bulk capacity. The Bond albedo is 0.01, according to Fornasier et al. (2015).
The nucleus of 67P is probably overlaid by a dust mantle that conceals water ice underneath.An estimate of the mantle thickness is provided by Shi et al. (2016), who measured the durationof dust jet activities after local sunset. The timescale of heat transport from the surface to the ice front is given by (Huebner et al. 2006)
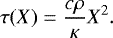 (14)
(14)
When we attribute the hour-long continuation of activity after dark to thermal lag in the subsurface, we find that the ice front is at the depth of 6 mm. Following this analysis, which is the sole estimate of mantle thickness on 67P, we adopted X = 5 or 6 mm in this study.
While it is confirmed that little water ice was exposed on the surface of 67P (Capaccioni et al. 2015), no direct measurement of the ice abundance in the subsurface is available. Depending on model interpretations, a dust mantle ranging in thickness between 5 and 10 mm, together with an underlying icy area fraction between 1 and 10%, yields consistent estimates for the accumulated water-ice loss at numerous locations over the northern hemi-nucleus of 67P, which underwent meter-deep erosion up to ~2 au before perihelion (Hu et al. 2017b). This in turn provides a constraint on the ice abundance of probably on the order of a few percent. Hereafter, we consider f = 0.1 for the icy nucleus (and f = 0 for a desiccated nucleus).
The structural parameters of the nucleus also affect heat transport. Above all, the size of the constituent aggregates determines the efficiency of thermal radiation. The nucleus of 67P is probably made of millimeter- to centimeter-sized pebbles (Blum et al. 2017). We assumed here that the radius of the constituent aggregates is 0.5 or 5 mm. Because of low ice content, the change in radius due to ice loss is neglected. According to Eqs. (3)–(6), the contact component of the conductivity is κ0 = 10−4 W m−1K−1. The effective conductivity is thus dominated by the radiative component, that is, κT T3, which ranges between 0.001 and 0.01 W m−1K−1 for temperature below 300 K (see also Fig. 2). The parameters of the thermal model are summarized and grouped in Table 2.
2.4 Numerical solution
We resorted to numerical methods to model the temperatures of the object for generic time-varying energy input, such as solar irradiation over the surface of an asteroid or comet nucleus. The numerical structure is as described by Hu et al. (2017a), where the heat Eq. (1) is solved through the Crank–Nicolson method. A revision is needed for the present problem, which involves temperature-dependent and hence time-varying conductivity. Equation (1) is expressed in the more convenient form of a continuity equation,
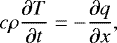 (15)
(15)
is the heat flux through the subsurface. Equations (15) and (16) are then discretized in depth and time, and approximated through the central difference scheme. This results in a tri-diagonal system of linear equations that are implicit functions of the future temperature, that is, T(t + Δt) with t and Δt denoting the current epoch and time step of discretization, respectively. In order to apply the existing solver for Eq. (15) based on the Crank–Nicolson method, the temperature-dependent conductivity, ![$\kappa\left[T(t+\Delta t)\right]$](/articles/aa/full_html/2019/10/aa34631-18/aa34631-18-eq32.png) , has to be predicted. This was accomplished by forecasting the temperature by
, has to be predicted. This was accomplished by forecasting the temperature by 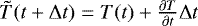 .
.
When the energy input varies periodically, the periodicity of the solution is imposed. The numerical solution needs to be iterated such that the temperature profiles one period apart (nearly) coincide, namely, T(t) = T(t ± tP), where tP is the period of the energy input.
We distinguished between two periodicities and the respective spatial scales. The diurnal thermal skin is the depth at which the temperature variation attenuates by a factor of e−1 with respect to the surface temperatures (with no risk of confusion with the italicized symbol of orbital eccentricity defined in Table 1). The skin depth can be approximated by 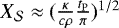 , where tP ≈ 12.4 h is the rotation period of the nucleus. Depending on the effective conductivity, the top centimeters of the subsurface can be sensitive to the diurnal insolation. The solution over a diurnal cycle was performed to resolve the temperatures here that repeat over each nucleus rotation. The temperature in deeper layers is affected by energy accumulated over longer time. For instance, the thermal lag at the depth of0.5 m is several months (Eq. (14), assuming the temperature beneath the diurnal skin depth is lower than 200 K),in which case the orbital variation in insolation must be considered. The energy input involves the orbital period tP ≈ 6.4 yr in Eq. (10).
, where tP ≈ 12.4 h is the rotation period of the nucleus. Depending on the effective conductivity, the top centimeters of the subsurface can be sensitive to the diurnal insolation. The solution over a diurnal cycle was performed to resolve the temperatures here that repeat over each nucleus rotation. The temperature in deeper layers is affected by energy accumulated over longer time. For instance, the thermal lag at the depth of0.5 m is several months (Eq. (14), assuming the temperature beneath the diurnal skin depth is lower than 200 K),in which case the orbital variation in insolation must be considered. The energy input involves the orbital period tP ≈ 6.4 yr in Eq. (10).
The convergence of the numerical solution is measured by the root-mean-square of the deviation between the (discrete) temperatureprofiles one period apart. The iterations are ended once the deviation falls below the threshold of tolerance. For instance, the convergence of a diurnal solution typically requires no more than 20 iterations for a threshold of 1 K.
To ensure numerical stability, that is, avoid artificial oscillations in the solution, the discretization must satisfy Δt∕Δx2 ≤ cρ∕(2κ). A fine spatial resolution, Δx, therefore demands high temporal resolution. We used a multi-resolution spatial grid whose resolution decreased with depth. Specifically, the top 2 decimeters were divided into 200 layers, that is, Δx = 1 mm, underlaid by 30 layers of 1 cm in thickness. The deeper subsurface was discretized more coarsely into decimeter layers down to the depth of 20 m. This depth is far below the isothermal depth, 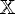 (see Sect. 2.2), which is found to be a few meters at most (as shown later in Fig. 8). The temporal resolution was variable along a full orbit depending on the heliocentric distance. The longest time step was 60 s, while it was reduced to 1 s near perihelion to accommodate an effective conductivity up to 0.1 W m−1K−1. Equations (11) and (12) are implicit functions of T(X) and can be solved with the Newton–Raphson method.
(see Sect. 2.2), which is found to be a few meters at most (as shown later in Fig. 8). The temporal resolution was variable along a full orbit depending on the heliocentric distance. The longest time step was 60 s, while it was reduced to 1 s near perihelion to accommodate an effective conductivity up to 0.1 W m−1K−1. Equations (11) and (12) are implicit functions of T(X) and can be solved with the Newton–Raphson method.
3 Influence of radiative heat transfer on subsurface temperatures
In this section, we consider the effect of radiative heat transfer on the temperatures of the subsurface. The following discussion is based on results obtained for a point located at 25°N on the nucleus of 67P. 67P is in a distinctly eccentric orbit around the Sun. The nucleus currently has an obliquity of about 52° (Preusker et al. 2015). Therefore, the chosen location at mid-latitudes experiences both diurnal and seasonal heating episodes, the latter of which arises from the variations of the subsolar latitude and of the heliocentric distance. We note that Blum et al. (2017) modeled the subsurface temperatures at the same location to interpret the measurements of the Microwave Instrument for the Rosetta Orbiter (MIRO), which were collected at roughly the same heliocentric distance.
In the following discussion, we always distinguish between the nucleus with constant heat conductivity, that is, κ = κ0, and a nucleus in which radiation offers the dominant mechanism of heat transport, κ ≈ κTT3. In the former case, we fixed κ0 = 0.002 W m−1K−1, as used in Hu et al. (2017a); we considered two aggregate sizes for the radiative case, that is, ra = 0.5 or 5 mm. For the sake of brevity, we hereafter refer to the two types of media as a (purely) conductive nucleus and a radiative nucleus, respectively.
3.1 Diurnal cycle: temperature distribution in shallow subsurface
We first analyze the variation of subsurface temperature over one rotation of the nucleus. For comets such as 67P, the diurnal solution is of special interest because the sublimation of water ice, usually the most abundant source of outgassing, occurs above the diurnal skin depth. We examined the solutions for two dates, 2014 September 30 and 2015 June 30, when 67P was inbound at 3.27 and 1.35 au, respectively. The starting time of the simulations was set at 00:00:00 UTC on both dates; this choice is arbitrary, however, and does not affect the results of periodic solutions. In each case, we distinguish between the radiative and conductive nuclei.
3.1.1 Desiccated subsurface
Figure 5 shows the temperature evolution as a function of depth over one nucleus rotation. The nucleus was assumed to be dry and consist of millimeter-sized aggregates. We observe a clear repeatability of the temperatureprofiles one rotation apart (by about 12.4 h). At the larger heliocentric distance, the temperature from the surface down to about 10 mm fluctuates from below 100 up to 200 K, which reflects the energization by (or absence of) insolation (Figs. 5a and b). As depth increases, the temperature variation lags steadily behind insolation and eventually starts to trail off in amplitude. This visualizes the progression of the “thermal wave”.
There isa notable difference at depths above 10 mm, mostly on the nightside (e.g. from about 4 to 8 h), between the two types of media (Figs. 5a and b). With efficient radiative heat transfer, the subsurface is warmer. The steep drop in temperatureto below 120 K was restricted to above the depth of 3 mm, whereas the interior stayed warmer than about 160 K. This insulating behavior can be attributed to the temperature-dependent heat conductivity that must decrease at night. The surface temperature of the radiative nucleus during the day reaches 200 K, giving rise to an effective conductivity on the order of 0.001 W m−1K−1, similar to that in a conductive nucleus (see Fig. 2). When the surface cools down to about 100 K at night, the conductivity decreases to a minimum of about 0.0001 W m−1K−1, thus inhibiting the loss of heat from the interior upwards.
The deeper penetration of the heat wave in the radiative nucleus is more evident closer to perihelion (Figs. 5c and d). This is reflected by the swathe of maximum dayside temperature beyond 200 K dipping as far as 20 mm (from 2 to 9 h). In comparison, only the top 10 mm of the conductive nucleus shows strong diurnal fluctuations (Fig. 5c). The maximum temperature at 20 mm is lower than 180 K. On the nightside, we observe again that the lowest temperatures in the radiative nucleus are confined to the more shallow depth than in the conductive nucleus. It is also notable that more heat is deposited beneath the diurnal skin depth. For instance, the temperature below 30 mm is below 160 K in a conductive nucleus (Fig. 5c), whereas that in a radiative nucleus remains at about 180K at the depth of 40 mm (Fig. 5d). At these depths, the conductivity in the radiative nucleus approaches a steady level of 0.1 W m−1K−1 and therefore exceeds the adopted constant conductivity by two orders of magnitude.
The subsurface in a nucleus composed of larger, centimeter-sized aggregates is warmer as a result of more efficient radiative heat transfer (Fig. 6). The diurnal heat wave penetrates deeper and faster than in a nucleus of millimeter-sized aggregates (in comparison with Figs. 5b and d). Especially at closer heliocentric distance, the temperature at the depth of 50 mm exhibits perceptible diurnal fluctuation (Fig. 6b). In comparison, the temperatures from a nucleus of millimeter-sized aggregates are homogenized at a more shallow depth of about 30 mm (Fig. 5d). We note that the heat transport is faster through the pores between larger aggregates because the temperature fluctuation at the depth of 50 mm trails the surface variation by about 4 h, while a similar delay occurs at around 30 mm through millimeter aggregates.
 |
Fig. 5 Diurnal variation in subsurface temperature as a function of depth in a conductive or radiative nucleus. The temperatures are graded in color scale and contoured between 100 and 220 K at an interval of 20 K. The results are for the latitude of 25°N on the nucleus of 67P with an unobstructed horizon (as on a spherical nucleus). The simulation parameters are listed in Table 2. The nucleus is assumed to be dry and to consist of aggregates 0.5 mm in radius. Results are obtained for the heliocentric distances of 3.27 au (panels a and b) and 1.35 au (panels c and d). The temperatures for constant conductivity are shown in panels a and c, and those for the radiative nucleus are plotted in panels b and d. |
3.1.2 Icy subsurface with dust mantle
It is desirable to examine the temperature evolution of the nucleus in the presence of water ice as well. We adopted the simplification that the sublimation occurs from an ice front below the dust mantle (Fig. 3). The thickness of the mantle was assumed to be 5 mm. The sublimation always consumes part of the heat flux across the ice front, causing a difference in the temperature gradient (Eq. (12)) and lowering the interior temperature. We assumed that the icy area fraction is 10%.
At a heliocentric distance of 3.27 au, the ice sublimation has an insignificant effect on the interior temperatures, which show a similar pattern to that for a desiccated nucleus (Figs. 7a and b in comparison with Figs. 5a and b, respectively). At a depth of about 10 mm, the temperature in the radiative nucleus is higher. In the case of constant heat conductivity, the diurnal skin depth decreases and the temperature underneath attenuates when sublimation occurs (comparing Figs. 5a and 7a). This is an expected result because the ice front regulates the heat transport and thus the temperature variation underneath.
The same is true when the nucleus approaches perihelion (Figs. 7c and d). We note a marked discontinuity in temperature at the depth of 5 mm. The temperature drops off at the ice front, evidently due to enhanced heat consumption by intensifying water sublimation close to perihelion. The temperature variation below the ice front is smoothed out in contrast. The interior temperatures in both radiative and conductive nuclei are lower by more than 20 K when ice sublimation occurs. The influence of radiative heat transfer on the strength of activity is also discussed in Sect. 4.
3.2 Orbital cycle: temperature distribution in deeper layers
For an aggregate nucleus, radiation deepens the diurnal skin depth and transports more heat underneath than a purely conductive nucleus. It is desirable to investigate the extent of this temperature enhancement in the interior. The temperaturebelow the diurnal skin depth, no more than a few centimeters, is no longer governed by the energy input over afew nucleus rotations, but is rather strongly influenced by the heat flux that accumulated over longer periods.
The evolution of subsurface temperatures between the depth of 5 cm and 2 m over a full orbit of 67P is shown in Fig. 8. Starting with a uniform temperature of 15 K, assumed to reflect the initial condition when 67P first entered the inner solar system, the solution comprises ten iterations, which approximately correspond to the number of orbits 67P had completed. For a constant conductivity of 0.002 W m−1K−1, the temperatures down to 1.5 m are increased to above 100 K (Fig. 8a). The maximum temperature occurs at shallow depths close to perihelion. The deeper layers respond more slowly to varying insolation, as is inferred from the skewed profile of the temperature enhancement. The maximum temperature does not exceed 200 K. The peak warmth does not coincide with but slightly predates perihelion because the point is located at the latitude of 25°N, which experiences peak insolation before perihelion when the subsolar point has moved to the southern hemi-nucleus. This also readily explains the appearance of another less strongly pronounced rise shortly after perihelion, when the Sun returned to the northern hemi-nucleus (around 200 days).
The pattern of the temperature evolution in the case of the radiative nucleus differs in several aspects. The subsurface, composed ofmillimeter-sized aggregates, has reached a temperature of 150 K down to the depth of 0.5 m (Fig. 8b). The maximum temperature at 0.1 m downward exceeds 200 K, which is an enhancement of almost 20 K from that in the nucleus with a constant conductivity. On the other hand, the temperatures exhibit a sharp decrease at about 1 m, and the interior underneath has not been warmed above 100 K. The steeper decrease in temperature in the radiative nucleus results from the inefficient radiative heat transfer. The conductivity of the subsurface, comprising millimeter-sized aggregates, is on the order of 10−4 W m−1K−1 at temperatures below 100 K (Fig. 2), which impedes warming of the interior. In the nucleus of centimeter-sized aggregates, the radiative heat transfer is more efficient. This is reflected by the stronger temperature variation close to the surface. We note that the temperature may reach 200 K at 0.2 m and 180 K as far as 0.5 m below the surface around perihelion. The subsurface down to about 3 m has reached 100 K (Fig. 8c).
 |
Fig. 6 Diurnal variation in subsurface temperature in a radiative dry nucleus comprising aggregates of 5 mm in radius, at the heliocentric distances of 3.27 au (panel a) and 1.35 au (panel b). The results are compared with Figs. 5b and d, respectively, which show a nucleus consisting of aggregates 0.5 mm in radius. |
3.3 Average diurnal temperature in full equilibrium
It provides insight to examine the end case where the subsurface temperatures are fully equilibrated and the average temperaturegradient vanishes, such that there is no net heat flux through the nucleus, over one nucleus rotation:
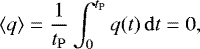 (17)
(17)
where q is given by Eq. (16). It follows that
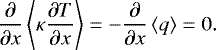 (18)
(18)
The assumption for establishing Eqs. (17) and (18) is that the diurnal average of energy input to the nucleus does not vary, that is, 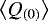 is a constant according to Eq. (11) (so is
is a constant according to Eq. (11) (so is 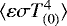 therein). This condition is nearly satisfied for objects at unvarying heliocentric distance and with negligible obliquity (with respect to the ecliptic), for instance, the Moon (Linsky 1966, 1973). However, it does not hold for the nucleus of 67P in an elliptic orbit and with strong obliquity (Table 1).
therein). This condition is nearly satisfied for objects at unvarying heliocentric distance and with negligible obliquity (with respect to the ecliptic), for instance, the Moon (Linsky 1966, 1973). However, it does not hold for the nucleus of 67P in an elliptic orbit and with strong obliquity (Table 1).
While the solution of fully equilibrated temperatures may not be entirely feasible, it is instructive on the effect of the radiative heat transfer This problem has been analyzed in depth, for example, by Linsky (1966), who presented a general treatment for estimating the temperature distribution inside a body with depth- and temperature-dependent heat conductivity. Hereafter, we apply his analysis to examine the subsurface temperatures governed by the conductivity κ proportional to T3 in comparison with the case of constant conductivity.
Substituting the expression of κ by Eq. (2) into Eq. (18), we find
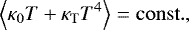 (19)
(19)
for all depths. We adopted the expression of the subsurface temperature in terms of a Fourier series used by Linsky (1966),
![\begin{equation*}T(x,t) = \sum^{\infty}_{n=0} A_n(x) \cos\left[ n \omega t - \phi_n(x) \right], \end{equation*}](/articles/aa/full_html/2019/10/aa34631-18/aa34631-18-eq41.png) (20)
(20)
where n is some non-negative integer and where ω = 2π∕tP is the rotation rate of the body. ϕn is the depth-dependent phase lag of the temperature wave. An is the amplitude of temperature variation that attenuates with depth. A0 indicates the average temperature at each depth.
If the conductivity is dominated by radiation, or κ ≈ κTT3, Eq. (19) indicates that 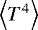 is independent of depth. The expression of
is independent of depth. The expression of 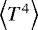 can be found by averaging out the periodic components (Appendix A),
can be found by averaging out the periodic components (Appendix A),
![\begin{equation*}\left< T^4 \right> = \left[ A_0(x) + \alpha(x) \right]^2 + \beta(x) = \mathrm{const.}, \end{equation*}](/articles/aa/full_html/2019/10/aa34631-18/aa34631-18-eq44.png) (21)
(21)
where α and β take real positive values dependent on An(x) and thus decrease with depth. Hence, the average temperature, A0(x), increases with depth.
This phenomenon is evident in our numerical solution. Figure 9 shows the average temperature of the subsurface over a full nucleus rotation on 2014 September 30 at the heliocentric distance of 3.27 au. When the conductivity is dominated by the radiative component, κ ≈ κTT3, we observe a steady increase in average temperature, 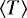 , from about 159 K at the surface to around 170 K at 10 mm. The increase in average temperature is correlated with the attenuation of the temperature variation with depth, a consequence of Eq. (21).
, from about 159 K at the surface to around 170 K at 10 mm. The increase in average temperature is correlated with the attenuation of the temperature variation with depth, a consequence of Eq. (21). 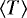 becomes nearly constant from the depth of 10 mm, suggesting that the temperature variation becomes negligible underneath. The diurnal skin is not far from 10 mm. In contrast,
becomes nearly constant from the depth of 10 mm, suggesting that the temperature variation becomes negligible underneath. The diurnal skin is not far from 10 mm. In contrast, 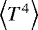 is nearly constant at all depths, as mandated by Eq. (19). The maximum deviation of no greater than 0.5 K probably indicates the errors of the solution.
is nearly constant at all depths, as mandated by Eq. (19). The maximum deviation of no greater than 0.5 K probably indicates the errors of the solution.
In the case of constant conductivity, κ0, the equilibrium temperature is about 10 K lower than the temperature of a radiative subsurface. A nearly constant 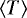 is observed, which is a necessary consequence according to Eq. (19). This is distinct from the behavior of a radiative subsurface where the
is observed, which is a necessary consequence according to Eq. (19). This is distinct from the behavior of a radiative subsurface where the 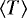 increases steadily with depth.
increases steadily with depth.
The distinct behavior of the average temperature is best explained by the conservation of heat fluxes if the body is in diurnal thermal equilibrium (Linsky 1966). The temperature-dependent heat conductivity is higher in the daytime, which must result in a steeper temperature gradient at night such that there is no net average flux over a nucleus rotation. The average temperature gradient must therefore be governed by the gradient at night, when the temperature decreases toward the cooling surface. On the other hand, when the heat conductivity is constant, the average temperature gradient must vanish and the average temperature should be constant.
 |
Fig. 7 Diurnal variation in subsurface temperature in the radiative icy nucleus. The results are for the same locations on 67P and thesame dates as in Fig. 5. Results are obtained for the heliocentric distances of 3.27 au (panels a and b) and 1.35 au (panels c and d). The nucleus is assumed to consist of an icy interior overlaid by a dry dust mantle of 5 mm in thickness. The icy area fraction is 10%. Panels a and c show the temperature distribution in a conductive nucleus, andpanels b and d correspond to a radiative nucleus consisting of aggregates with 0.5 mm radius. |
4 Influence of radiative heat transfer on the water production of comet 67P
When perihelion is approached, the subsurface temperature of the nucleus steadily increases, more so in the case of the radiative nucleus. It is perhaps not yet evident that the outgassing activity must also intensify as a result of increasing insolation. Attempts have been made to model the evolution of water outgassing of 67P through its perihelion passage and have been reported in several studies, both before and after the beginning of the Rosetta rendezvous with 67P (see, e.g. Davidsson & Gutiérrez 2005; Fulle et al. 2010; Keller et al. 2015; Hu et al. 2017a; Blum et al. 2017). We concern ourselves with the effect of radiative heat conductivity on the total water production of 67P, defined by
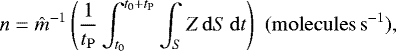 (22)
(22)
integrated over the total surface area of the nucleus, S, and averaged over one comet rotation, tP. 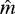 is the molecular mass of water (Eq. (13)). We adopted a polyhedral shape model of the nucleus of 67P (Preusker et al. 2017), down-sampled to about 1000 facets. Numerical tests suggest that the effect of the resolution of the shape model on the calculated water production is minimal.
is the molecular mass of water (Eq. (13)). We adopted a polyhedral shape model of the nucleus of 67P (Preusker et al. 2017), down-sampled to about 1000 facets. Numerical tests suggest that the effect of the resolution of the shape model on the calculated water production is minimal.
We onlyconsidered sublimation of water ice located above the diurnal skin depth, no deeper than a few centimeters. Diurnal solutions apply in this case (see Sect. 3.1). The initial temperatures were assumed to be uniform at 100 K. Varying the initial condition does not affect the final results, which must converge after a number of iterations.
The input and output of the thermal model are visualized in Fig. 10. The energy input of insolation over the nucleus (polyhedral shape) on early 2015 June 4 is represented in gray scale in comparison with a context image showing the instantaneous illumination acquired by the Navigation Camera (NAVCAM) on board Rosetta (Figs. 10a and b). For illustration, we first adopted a constant conductivity of κ = 0.002 W m−1K−1 and assumed a dust mantle thickness of X = 6 mm. Underneath, the icy area fraction was assumed to be 10%. The temperatures at this depth govern the sublimation flux (Eq. (13)) and correspond to the insolation pattern at the time (Figs. 10c and d).
We performed calculations from 2014 July 1 until the end of December 2015. This period of time encompasses the perihelion passage of 67P. The water production rate defined by Eq. (22) was evaluated at an interval of ten (terrestrial) days, except around perihelion on 2015 August 13, when results were obtained every day (about two nucleus rotations). The evolution of the modeled water production rate is plotted as a function of heliocentric distance in Fig. 11. We also provide the production rates determined by Fougere et al. (2016b) based on in situ measurements obtained with the Rosetta Orbiter Spectrometer for Ion and Neutral Analysis (ROSINA) of the gas density in conjunction with a direct simulation Monte Carlo of the global coma structure.
It is therefore expected that the overall trend of the global production can be reasonably well if not exclusively ascribed to a global dust mantle of the same thickness. This is true regardless of the nature of the heat conductivity of the nucleus. The effect of the radiative heat transfer is manifested in an increase in the slope of the production curve compared to that in the case of a constant conductivity. The two curves intersect at the inbound heliocentric distance of about 2.7 au, most likely because the temperature near the ice front effects a conductivity near the assumed constant value of 0.002 W m−1K−1. From there on, the conductivity in a radiative nucleus steadily increases due to rising (dayside) temperatures. From about 2 au inward, however, the two curves stop diverging and the respective enhancements are nearly proportional.
The production of the radiative nucleus surpasses that of the conductive nucleus by about 50%. Both tend to underestimate the water production from shortly before perihelion until beyond 1.5 au outbound; the radiative model is less strongly biased. However, both models seem to overestimate the water production outside 1.5 au before perihelion, that is, they roughly trace the upper bound of the measured rates.
Blum et al. (2017) found that the water production from a nucleus consisting of centimeter-sized aggregates and with one desiccated layer of aggregates could account for the observed trend by ROSINA until at least ~1.5 au inbound. The thermal model for deriving the water production differs from the model used here in that it includes bulk sublimation from the interior. It is beyond the scope of this work to treat this phenomenon. While radiative heat transfer will undoubtedly enhance water activity, our results show that it is not a requisite mechanism for explaining the evolution of the water production. Other observational constraints will have to be introduced to resolve the effect of radiative heat transfer.
 |
Fig. 8 Evolution of subsurface temperature over one orbit of 67P. The temperatures are for the same location on the nucleus as inFigs. 5 and 7. The simulation parameters for the orbit and orientation of 67P are listed in Table 1. The nucleus is assumed to be dry. Results are shown for a conductive nucleus with κ = 0.002 W m−1K−1 (panel a), aradiative nucleus consisting of 1 mm aggregates (panel b), and 1 cm aggregates (panel c). In panel c, the contours are only indicated below 0.1 m because the temperatures in the upper layers display diurnal variations that clutter the contour lines. |
 |
Fig. 9 Average temperature of the subsurface over one comet rotation. The solid blue curve corresponds to a constant heat conductivityof κ = κ0 = 0.002 W m−1K−1. The solid red curve corresponds to purely radiative conductivity, κ = κTT3. The dotted red curve indicates the average of T4 in a quartic root. In the case of radiative conductivity, the average temperature increases with depth, while the average of T4 is nearly constant. The average temperature in the subsurface with constant conductivity is nearly constant. |
 |
Fig. 10 Estimate of the water production of 67P using the thermal model. The results here are for 1:04:26 UTC on 2015 June 4, when NAVCAM on Rosetta took an image of the nucleus (panel a). The energy input of insolation over the nucleus was estimated using a 1000-facet shape model with an orientation and emphemeris of the nucleus provided by the SPICE kernels for the Rosetta mission (panel b). The temperature pattern at the ice front, or the bottom of the dry dust mantle, at the depth of 6 mm differs from that of insolation on the surface (panel c) because of the insulation effect of the mantle. The sublimation or outgassing flux is controlled by the temperature at 6 mm (panel d). Image credit (panel a): ESA/Rosetta/NAVCAM, CC BY-SA IGO 3.0. |
 |
Fig. 11 Modeled water production rate of 67P as a function of heliocentric distance. The red and blue solid lines correspond to the production rates from the radiative and conductive nuclei, respectively. In both cases, the aggregate size was assumed to be 1 mm. The constant heat conductivity was 0.002 Wm−1K−1. The water production rates derived by Fougere et al. (2016b) using ROSINA coma density measurements are plotted as gray squares for comparison. |
5 Conclusion
The conclusions of our investigation are summarized below.
- 1.
Radiative heat transfer plays a fundamental role in accumulating energy into the subsurface, doing so by enhancing heat flux inward on the dayside while reducing heat loss outward at night (Linsky 1966, 1973).
- 2.
The penetration depth of the diurnal heat wave increases with conductivity, which is temperature dependent. Close to perihelion, the subsurface comprising centimeter-sized aggregates, the probable size of building blocks of 67P (Blum et al. 2017), may reach a steady temperature of 200 K at a depth of 5 cm, while diurnal variations may persist down to a depth of 3 cm.
- 3.
Even if the nucleus consists of millimeter-sized aggregates, radiative heat transfer can sustain a temperature of about 140 K down to 0.5 m in the subsurface for more than a year after perihelion. On the other hand, the deeper, colder interior is insulated from warming up because of the low conductivity.
- 4.
Radiative heat transfer may enhance water production of 67P near perihelion. However, its role is ambiguous and it is certainly not required for interpreting the measured production rates of the comet during the last perihelion passage. Other measurements, of the subsurface temperature, for example, will provide stronger constraints on the effect of radiative heat transfer, such as MIRO data (Gulkis et al. 2015; Schloerb et al. 2015).
- 5.
From a modeling standpoint, a consistent characterization of cometary activity in the presence of radiative heat transfer likely requires more sophisticated approaches that properly treat mass transfer, for instance. Fortunately, these alternatives are available and at our disposal. Depending on the efficiency of radiation, the diurnal skin depth is highly variable along an elliptic orbit. If only for modeling water activity, which arises dominantly from above the diurnal skin, it may be advantageous to resolve the thermo-physical states of deeper layers.
Acknowledgments
We thank an anonymous referee for critically reading the manuscript and providing numerous suggestions for improvement. I.v.B. thanks the Deutsches Zentrum für Luft- und Raumfahrt for support under grants 50WM1536 and 50WM1846.
Appendix A Increase in average temperature with depth in the radiative subsurface
We followed the derivation by Linsky (1966) and illustrate that the average temperature of the subsurface increases with depth if the conductivity satisfies κ ~ T3 and if there is no internal heat source. Referring to Eq. (20), we find that
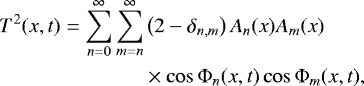 (A.1)
(A.1)
with the shorthand notation Φn(x, t) = nωt − ϕn(x). δn,m is the Kronecker delta. Hereafter, we omit the notations for the dependence of An, Φn on depth and time. Taking the time-average of T2 and substituting the resultant expression into Eq. (19), we obtain
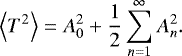 (A.2)
(A.2)
Thus, the second-order temperature moment can be rewritten as
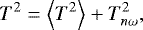 (A.3)
(A.3)
where the periodic variations are given by
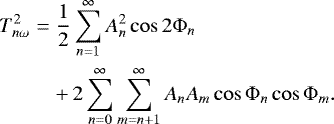 (A.4)
(A.4)
In the same fashion, the fourth-order moment is found as
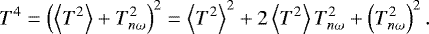 (A.5)
(A.5)
The second term on the right-hand side is periodic. Thus, the time-averaged moment consists of 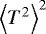 and a constant component from
and a constant component from 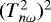 . We recall Eq. (A.2), based on which the expression is of the form
. We recall Eq. (A.2), based on which the expression is of the form
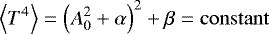 (A.6)
(A.6)
for some positive constants α and β, the latter of which results from 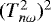 . In the absence of an internal heat source, the temperature amplitudes, An for n > 0, attenuate with depth. Accordingly, α and β decrease with depth. Therefore, the average temperature, A0, must increase with depth.
. In the absence of an internal heat source, the temperature amplitudes, An for n > 0, attenuate with depth. Accordingly, α and β decrease with depth. Therefore, the average temperature, A0, must increase with depth.
References
- Blum, J., Gundlach, B., Mühle, S., et al. 2014, Icarus, 235, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., Gundlach, B., Krause, M., et al. 2017, MNRAS, 469, S755 [CrossRef] [Google Scholar]
- Brin, G. D., & Mendis, D. A. 1979, ApJ, 229, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Capaccioni, F., Coradini, A., Filacchione, G., et al. 2015, Science, 347, aaa0628 [Google Scholar]
- Capria, M. T., Coradini, A., De Sanctis, M. C., & Orosei, R. 2000, AJ, 119, 3112 [NASA ADS] [CrossRef] [Google Scholar]
- Capria, M. T., Capaccioni, F., Filacchione, G., et al. 2017, MNRAS, 469, S685 [Google Scholar]
- Choukroun, M., Keihm, S., Schloerb, F. P., et al. 2015, A&A, 583, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clegg, P. E., Bastin, F. A., & Gear, A.-E. 1966, MNRAS, 133, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, M. 2018, Proceedings of 2018 SpaceOps Conference (Marseille, France: AIAA), 2018 [Google Scholar]
- Cremers, C. J., & Birkebak, R. C. 1971, Lunar Planet. Sci. Conf. Proc., 2, 2311 [NASA ADS] [Google Scholar]
- Crifo, J. F. 1997, Icarus, 130, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J. R., & Gutiérrez, P. J. 2005, Icarus, 176, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Davidsson, B. J. R., & Skorov, Y. V. 2002, Icarus, 159, 239 [NASA ADS] [CrossRef] [Google Scholar]
- De Sanctis, M. C., Capaccioni, F., Capria, M. T., et al. 1999, Planet. Space Sci., 47, 855 [Google Scholar]
- Fanale, F. P., & Salvail, J. R. 1984, Icarus, 60, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrari, C. 2016, Soc. Sci. Rep., 214, 111 [NASA ADS] [Google Scholar]
- Ferrari, C., & Lucas, A. 2016, A&A, 588, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fornasier, S., Hasselmann, P. H., Barucci, M.-A., et al. 2015, A&A, 583, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fougere, N., Altwegg, K., Berthelier, J.-J., et al. 2016a, A&A, 588, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fougere, N., Altwegg, K., Berthelier, J.-J., et al. 2016b, MNRAS, 462, S156 [CrossRef] [Google Scholar]
- Fulle, M., Colangeli, L., Agarwal, J., et al. 2010, A&A, 522, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulle, M., Altobelli, N., Buratti, B., et al. 2016, MNRAS, 462, S2 [CrossRef] [Google Scholar]
- Gortsas, N., Kührt, E., Motschmann, U., et al. 2011, Icarus, 212, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Groussin, O., Jorda, L., Auger, A.-T., et al. 2015, A&A, 583, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, aaa0709 [Google Scholar]
- Gundlach, B., & Blum, J. 2012, Icarus, 219, 618 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gundlach, B., & Blum, J. 2013, Icarus, 223, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Gundlach, B., Skorov, Y. V., & Blum, J. 2011, Icarus, 213, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Haruyama, J., Yamamoto, T., Mizutani, H., & Greenberg, J. M. 1993, J. Geophys. Res., 98, 93JE01325 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, X., Shi, X., Sierks, H., et al. 2017a, MNRAS, 469, S295 [CrossRef] [Google Scholar]
- Hu, X., Shi, X., Sierks, H., et al. 2017b, A&A, 604, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huebner, W. F., Benkhoff, J., Capria, M. T., et al. 2006, Heat and Gas Diffusion in Comet Nuclei (Bern: International Space Science Institute) [Google Scholar]
- Keller, H. U., Mottola, S., Davidsson, B., et al. 2015, A&A, 583, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klinger, J. 1980, Science, 209, 271 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kömle, N., & Steiner, G. 1992, Icarus, 96, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Kossacki, K. J., Koemle, N. I., Kargl, G., & Steiner, G. 1994, Planet. Space Sci., 42, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Kossacki, K. J., Szutowicz, S. Ł., & Leliwa-Kopystyński, J. 1999, Icarus, 142, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M., Blum, J., Skorov, Y. V., & Trieloff, M. 2011, Icarus, 214, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Kührt, E., & Keller, H. U. 1994, Icarus, 109, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Linsky, J. L. 1966, Icarus, 5, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Linsky, J. L. 1973, ApJS, 25, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Mekler, Y., Prialnik, D., & Podolak, M. 1990, ApJ, 356, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Mendis, D. A., & Brin, G. D. 1977, Moon, 17, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Merrill, R. B. 1969, Thermal Conduction through an Evacuated Idealized Powder over the Temperature Range of 100° to 500° K, NASA Tech. Note, D-5063 [Google Scholar]
- Orosei, R., Capaccioni, F., Capria, M. T., et al. 1995, A&A, 301, 613 [NASA ADS] [Google Scholar]
- Pätzold, M., Andert, T., Hahn, M., et al. 2016, Nature, 530, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Piqueux, S., & Christensen, P. R. 2009, J. Geophys. Res. Planets, 114, E09005 [NASA ADS] [Google Scholar]
- Preusker, F., Scholten, F., Matz, K.-D., et al. 2015, A&A, 583, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preusker, F., Scholten, F., Matz, K.-D., et al. 2017, A&A, 607, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prialnik, D., Benkhoff, J., & Podolak, M. 2004, Comets II (Tucson: University of Arizona Press), 359 [Google Scholar]
- Schloerb, F. P., Keihm, S., von Allmen, P., et al. 2015, A&A, 583, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skorov, Y. V., Kömle, N. I., Markiewicz, W. J., & Keller, H. U. 1999, Icarus, 140, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, X., Hu, X., Sierks, H., et al. 2016, A&A, 586, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shi, X., Hu, X., Mottola, S., et al. 2018, Nat. Astron., 2, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Sierks, H., Barbieri, C., Lamy, P. L., et al. 2015, Science, 347, aaa1044 [Google Scholar]
- Spohn, T., & Benkhoff, J. 1990, Icarus, 87, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Spohn, T., Knollenberg, J., Ball, A. J., et al. 2015, Science, 349, aab0464ss [NASA ADS] [CrossRef] [Google Scholar]
- Squyres, S. W., McKay, C. P., & Reynolds, R. T. 1985, J. Geophys. Res., 90, 12381 [Google Scholar]
- Steiner, G., & Kömle, N. I. 1991, J. Geophys. Res., 96, 18 [CrossRef] [Google Scholar]
- Watson, K. 1964, Ph.D. Dissertation, Caltech, Pasadena, California [Google Scholar]
- Winter, D. F., & Saari, J. M. 1969, ApJ, 156, 1135 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Schematic illustration of heat transfer through the granular, porous subsurface of a comet nucleus under solar illumination. The outermost layer is desiccated, leaving behind a dust mantle that lies above the mixture of dust and ice aggregates. Conduction takes place through the aggregates that are in contact. Radiation occurs inside the pores; porosity of the individual aggregates is neglected. |
| In the text | |
 |
Fig. 2 Effective thermal conductivity as functions of aggregate size and temperature. The conductivity consists of a contact and a radiative component, as indicated by Eq. (2). The radius and (color-scaled) conductivity are of logarithmic scales. The contours for 0.0001, 0.001, 0.01, and 0.1 W m−1K−1 are indicated. |
| In the text | |
 |
Fig. 3 Nucleus subsurface comprising uniform spherical dust aggregates. The topmost few layers of aggregates are desiccated, and water ice is present underneath in addition to the dust aggregates (panel a). The aggregate radius is ra and is independent of the ice content. We also assume for simplification that sublimation occurs from a fixed depth of X (panel b). |
| In the text | |
 |
Fig. 4 Mass flux of water-ice sublimation as a function of temperature (Gundlach et al. 2011). We also indicate the range of heliocentric distance of interest. The perihelion distance is 1.24 au. |
| In the text | |
 |
Fig. 5 Diurnal variation in subsurface temperature as a function of depth in a conductive or radiative nucleus. The temperatures are graded in color scale and contoured between 100 and 220 K at an interval of 20 K. The results are for the latitude of 25°N on the nucleus of 67P with an unobstructed horizon (as on a spherical nucleus). The simulation parameters are listed in Table 2. The nucleus is assumed to be dry and to consist of aggregates 0.5 mm in radius. Results are obtained for the heliocentric distances of 3.27 au (panels a and b) and 1.35 au (panels c and d). The temperatures for constant conductivity are shown in panels a and c, and those for the radiative nucleus are plotted in panels b and d. |
| In the text | |
 |
Fig. 6 Diurnal variation in subsurface temperature in a radiative dry nucleus comprising aggregates of 5 mm in radius, at the heliocentric distances of 3.27 au (panel a) and 1.35 au (panel b). The results are compared with Figs. 5b and d, respectively, which show a nucleus consisting of aggregates 0.5 mm in radius. |
| In the text | |
 |
Fig. 7 Diurnal variation in subsurface temperature in the radiative icy nucleus. The results are for the same locations on 67P and thesame dates as in Fig. 5. Results are obtained for the heliocentric distances of 3.27 au (panels a and b) and 1.35 au (panels c and d). The nucleus is assumed to consist of an icy interior overlaid by a dry dust mantle of 5 mm in thickness. The icy area fraction is 10%. Panels a and c show the temperature distribution in a conductive nucleus, andpanels b and d correspond to a radiative nucleus consisting of aggregates with 0.5 mm radius. |
| In the text | |
 |
Fig. 8 Evolution of subsurface temperature over one orbit of 67P. The temperatures are for the same location on the nucleus as inFigs. 5 and 7. The simulation parameters for the orbit and orientation of 67P are listed in Table 1. The nucleus is assumed to be dry. Results are shown for a conductive nucleus with κ = 0.002 W m−1K−1 (panel a), aradiative nucleus consisting of 1 mm aggregates (panel b), and 1 cm aggregates (panel c). In panel c, the contours are only indicated below 0.1 m because the temperatures in the upper layers display diurnal variations that clutter the contour lines. |
| In the text | |
 |
Fig. 9 Average temperature of the subsurface over one comet rotation. The solid blue curve corresponds to a constant heat conductivityof κ = κ0 = 0.002 W m−1K−1. The solid red curve corresponds to purely radiative conductivity, κ = κTT3. The dotted red curve indicates the average of T4 in a quartic root. In the case of radiative conductivity, the average temperature increases with depth, while the average of T4 is nearly constant. The average temperature in the subsurface with constant conductivity is nearly constant. |
| In the text | |
 |
Fig. 10 Estimate of the water production of 67P using the thermal model. The results here are for 1:04:26 UTC on 2015 June 4, when NAVCAM on Rosetta took an image of the nucleus (panel a). The energy input of insolation over the nucleus was estimated using a 1000-facet shape model with an orientation and emphemeris of the nucleus provided by the SPICE kernels for the Rosetta mission (panel b). The temperature pattern at the ice front, or the bottom of the dry dust mantle, at the depth of 6 mm differs from that of insolation on the surface (panel c) because of the insulation effect of the mantle. The sublimation or outgassing flux is controlled by the temperature at 6 mm (panel d). Image credit (panel a): ESA/Rosetta/NAVCAM, CC BY-SA IGO 3.0. |
| In the text | |
 |
Fig. 11 Modeled water production rate of 67P as a function of heliocentric distance. The red and blue solid lines correspond to the production rates from the radiative and conductive nuclei, respectively. In both cases, the aggregate size was assumed to be 1 mm. The constant heat conductivity was 0.002 Wm−1K−1. The water production rates derived by Fougere et al. (2016b) using ROSINA coma density measurements are plotted as gray squares for comparison. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.