| Issue |
A&A
Volume 629, September 2019
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 16 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201936029 | |
| Published online | 10 September 2019 | |
Chemical evolution of elliptical galaxies with a variable IMF
A publicly available code⋆
1
Helmholtz-Institut für Strahlen- und Kernphysik (HISKP), Universität Bonn, Nussallee 14–16, 53115 Bonn, Germany
e-mail: yan@astro.uni-bonn.de, pkroupa@uni-bonn.de
2
Charles University in Prague, Faculty of Mathematics and Physics, Astronomical Institute, V Holešovičkách 2, 180 00 Praha 8, Czech Republic
3
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching bei München, Germany
e-mail: tereza.jerabkova@eso.org
4
Instituto de Astrofisica de Canarias, 38200 La Laguna, Tenerife, Spain
Received:
5
June
2019
Accepted:
23
July
2019
Growing evidence in recent years suggests a systematic variation of the stellar initial mass function (IMF), being top-heavy for starburst galaxies and possibly bottom-heavy for massive ellipticals. Galaxy chemical evolution simulations adopting an invariant canonical IMF face difficulty in simultaneously reproducing the metallicity and α-enhancement of the massive elliptical galaxies. Applying a variable IMF that changes with time is a promising solution, however, it is non-trivial to couple a variable IMF theory with the existing galaxy evolution codes. Here we present the first open source simulation code which recalculates the galaxy-wide IMF at each time step according to the integrated galactic IMF (IGIMF) theory where the galaxy-wide IMF depends on the galactic star formation rate and metallicity. The resulting galaxy-wide IMF and metal abundance evolve with time. With this pilot work, we explore the effect of the IGIMF theory on galaxy chemical evolution in comparison with an invariant IMF.
Key words: galaxies: stellar content / galaxies: ISM / galaxies: abundances / galaxies: evolution / methods: numerical / galaxies: starburst
© ESO 2019
1. Introduction
The evolution of galaxies sensitively depends on the stellar initial mass function (IMF). The understanding of the IMF has changed rapidly in the past decade. Despite a direct conflict (Kroupa et al. 2013) with the theoretical expectation that the IMF should vary as the star-forming environment alters (e.g. ambient gas temperature, metallicity, density, and pressure dependence, as argued by Adams & Fatuzzo 1996; Larson 1998; Elmegreen 2004; Dib et al. 2007; Papadopoulos 2010) the observed IMFs of star clusters in the local Universe are consistent with no variation (Kroupa 2001, 2002; Bastian et al. 2010; Offner et al. 2014; Hopkins 2018). Thus, the universal and invariant canonical IMF assumption was widely applied. The more recent observations, which are able to probe physical regimes further from the solar and Galactic neighbourhood, have been consistently suggesting a variation of the galaxy-wide IMF (gwIMF1). For the distribution of low-mass stars, a bottom-heavy IMF (excess in the number of low-mass stars) in the inner regions of massive metal-rich elliptical galaxies is indicated by the galaxy mass-to-light ratio (Li et al. 2017), spectral analysis of stellar-mass sensitive features (Vazdekis et al. 1997, 2003; Cenarro et al. 2003; van Dokkum & Conroy 2010; Conroy & van Dokkum 2012; Ferreras et al. 2013; Martín-Navarro et al. 2015; La Barbera et al. 2017; Parikh et al. 2018) and lensing studies (Auger et al. 2010; Oldham & Auger 2018)2. For the distribution of massive stars, independent evidence strongly indicates a systematically varying IMF (galaxy photometry: Hoversten & Glazebrook 2008; Meurer et al. 2009; Lee et al. 2009; Gunawardhana et al. 2011, metal abundance of galaxy clusters: Renzini & Andreon 2014; Urban et al. 2017, isotope abundance: Romano et al. 2017; Zhang et al. 2018), being top-heavy (more massive stars than predicted when assuming the canonical IMF) when the SFR is high and/or when the metallicity is low, as summarized by Kroupa et al. (2013), Yan et al. (2017), and Jeřábková et al. (2018). We note that the IMF can be bottom-heavy and top-heavy at the same time (see Jeřábková et al. 2018).
If the IMF is universal and invariant, the observed α-enhancement of massive ellipticals indicate that they should have a short star formation timescale (e.g. Matteucci 1994; Thomas et al. 2005; de La Rosa et al. 2011). However, in the case of the most massive ellipticals, the required timescale for reproducing the α-enhancement is too short, and the galaxy does not have enough time to recycle the metal-rich gas and enrich its stellar population (De Lucia et al. 2017; Okamoto et al. 2017). The difficulty in simultaneously reproducing the total metallicity and α-enhancement of massive elliptical galaxies indicates the necessity of introducing at least one new degree of freedom, for example a varying and top-heavy gwIMF (Arrigoni et al. 2010; Martín-Navarro et al. 2018).
The IMF measurements in the local universe that are consistent with no variation and the apparent necessity of a variable extragalactic IMFs suggest that the IMF may vary in a complicated manner (Guszejnov et al. 2019). Motivated by the notion that stars form as groups in molecular cloud cores (i.e. in embedded clusters such that the gwIMF is the sum of all individual IMFs of all embedded clusters), the integrated galaxy-wide IMF (IGIMF) theory has been developed gradually by Kroupa & Weidner (2003), Weidner et al. (2004, 2011, 2013a), Weidner & Kroupa (2005), Kroupa et al. (2013), and Jeřábková et al. (2018). The IGIMF theory suggests that the shape of the gwIMF should depend on the galactic properties at the time of the star formation and is able to explain/predict3 the apparent gwIMF variation based on the molecular cloud core density- and metallicity-dependent IMF as empirically deduced by Dabringhausen et al. (2009, 2012), and Marks et al. (2012) from an analysis of observed open and globular cluster and ultra-compact dwarf galaxies. We note that we distinguish in this paper between the modern and the earlier IGIMF formulation according to whether it includes the metallicity- and density-dependent star cluster IMF variation suggested by Marks et al. (2012) or not. A milestone is the self-consistency of the IGIMF theory considering the independent observational constraints for both the star cluster IMF variation and the gwIMF variation, as demonstrated in Weidner et al. (2013a), Yan et al. (2017), and Jeřábková et al. (2018).
When the gwIMF varies for different galaxies and at different times, galactic chemical evolution and the time-integrated gwIMF (TIgwIMF, see Table 1) will differ from the canonical estimate. Since interpretations of galaxy observations (e.g. stellar mass, metal abundance, star formation activity) depend on the assumption of their IMF and element composition, it is important to apply the IGIMF theory to galaxy evolution simulations. However, current publicly available galaxy evolution simulation codes assume an invariant IMF (e.g. NuPyCEE, Ritter & Côté 2016), and it is difficult to modify the codes to allow for a varying gwIMF. A few semi-analytical models have adopted the modern IGIMF theory formulation that includes a star cluster IMF variation (e.g. Gargiulo et al. 2015; Fontanot et al. 2017, but without the metallicity dependence of the IMF; see Sect. 5.2 below)4; however, their codes are not publicly available.
Abbreviations applied in this paper.
This contribution makes available a public version of a galaxy chemical evolution code, which allows for a constantly updated gwIMF that evolves with the galaxy metal abundance. The instantaneous gas-phase metallicity (as well as galaxy-wide SFR) determines the gwIMF of the forming stellar population, while the change of the gwIMF modifies the later metal enrichment process. To be able to explore the effect of the variable gwIMF on the chemical evolution of a galaxy, our code applies a fixed star formation history (SFH) and varies only the gwIMF. A full-scale hydrodynamical simulation is not necessary for this pilot study on the effect of the IGIMF theory. The aim of the present work is to demonstrate the mechanism of how the IMF variation influences the galaxy chemical evolution and to give the reader an idea of what kind of impact can be caused by such a variation. A more complicated gas-flow model without adequate observational constraints does not necessarily improve the reliability of our results.
The paper is organized as follows. The IGIMF theory is outlined in Sect. 2. The publicly available code of our galaxy evolution model is introduced in Sect. 3. The assumptions applied in the model are described in Sect. 4, and the systematic uncertainties of the model are discussed in Sect. 5. Example runs of the model assuming a given SFH and gwIMF formulation are shown in Sect. 6 and Appendix A resulting in the mass composition, supernova rate, and evolution of the chemical composition. Our conclusions follow in Sect. 7.
2. The IGIMF theory
The fundamental insight underlying the IGIMF theory is that the systematic variation of the gwIMF, which appears to correlate with galactic SFR and metallicity, has its origin in the variation of the IMF on a molecular cloud core (i.e. embedded star cluster) scale. In other words, there exists a universal law of the star cluster scale IMF shape which leads to the various IMF shapes of different composite systems.
Here the core ideas and assumptions of the IGIMF theory are outlined:
1. Stars always form in the dense region of the pre-star cluster molecular cloud core with their initial masses following the IMF, thus all the stars belong to a star cluster (whether this star cluster survives or unbinds at a later time is a different issue; see Yan et al. 2017, and references therein). This simple assumption leads to a straightforward mathematical formulation and fruitful predictions that have been proved to be successful (see footnote 3).
2. The initial mass distribution of the stars in a star cluster strictly follows an IMF5 where the slope of the IMF varies with the pre-star cluster cloud core density (which is correlated with the star cluster mass) and metallicity of the gas cloud. This IMF formulation is adopted from Marks et al. (2012), which is currently the only comprehensive observational study that gives an empirical IMF shape dependence on both the star cluster mass and metallicity.
3. The stellar masses of the embedded star clusters are distributed by strictly following the embedded star cluster mass function (ECMF; see footnote 5). The ECMF is estimated from observations to be consistent with a single power-law function (Kroupa & Weidner 2003, and references therein) with a power-law index β ≈ 2 (Calura et al. 2010)6.
4. The shortest time, δt, for a galaxy to form enough star clusters that fully populate (saturate) the observed ECMF is defined as a star formation epoch. The length of the star formation epoch is likely to be in the range from a few Myr to several tens of Myr (Yan et al. 2017, and references therein). We adopt δt = 10 Myr following Weidner et al. (2004) and Schulz et al. (2015) 7. This timescale is the key that relates the galaxy-wide SFR to the total mass of stars that populate a gwIMF (see Sect. 4.1).
With the above axioms, it is possible to calculate the gwIMF by integrating over the IMFs of all embedded star clusters assembled in the star formation epoch, δt, in the galaxy. We note that by basing the gwIMF calculation on the empirically constrained IMF variation, most of the implicit possible physical drivers for the variation, such as the cosmic-ray flux (Papadopoulos 2010), are largely incorporated. Thus, the IGIMF theory provides a mathematical framework that could reproduce the variety of extragalactic observations and be consistent with the local star cluster scale IMF measurements in so far as tests have been made (Pflamm-Altenburg & Kroupa 2008; Weidner et al. 2013a; Yan et al. 2017; Jeřábková et al. 2018).
We refer the readers to Yan et al. (2017), Jeřábková et al. (2018) for a more detailed description of the IGIMF theory, its modern mathematical formulation, and for a comprehensive demonstration of the resulting gwIMFs under different circumstances.
3. Open source code
The gwIMF predicted by the IGIMF theory can be computed by the publicly available galimf.py code in the Python3 programming language (Yan et al. 2017)8. The current contribution adds to the same repository a galaxy evolution module, galevo.py, which integrates the galimf.py code as is shown in Fig. 1. The main inputs and outputs are shown in the plot, while the details can be found in the online code description.
 |
Fig. 1. Interaction between the newly developed galaxy evolution module and the previously published IGIMF calculation module (Yan et al. 2017), which returns the gwIMF at any given time ti, and the input/output of each module. The main inputs are shown in the black text while the default settings are shown in the grey text. |
We note that the gwIMF calculation module and the Galaxy evolution module, shown as the two grey blocks in Fig. 1, work independently. Thus, it is possible to substitute the gwIMF model assuming the IGIMF theory with another variable IMF theory or to adopt the IGIMF theory into another galaxy evolution model.
Both galimf.py and galevo.py are publicly available and are maintained on GitHub9 with detailed description, instruction, and example files.
4. Galaxy chemical evolution model
Recent research points to a two-phase galaxy formation stage, with the inner regions of present-day massive ellipticals being formed at a redshift greater than two, mostly in situ through a quick dissipative event. This phase leads to a rather compact relic galaxy core (Trujillo et al. 2014), which resembles the so-called red nuggets found at high redshifts (Buitrago et al. 2008; Ferré-Mateu et al. 2017). This phase is followed by a significant growth in size (Holwerda et al. 2015), and to a lesser extent in mass from ex situ contributions, in a process that extends over cosmic time. These findings are recently being supported by some numerical simulations (Oser et al. 2010; Navarro-González et al. 2013). Such a scenario can be approached by a monolithic collapse that particularly applies to the central regions of giant ellipticals (Renzini 2006).
In this pilot study presenting the chemical-evolution code, we do not apply in- and outflows for our default model. The influence of baryon physics has large uncertainties and a weak predictive power (Naab & Ostriker 2017; Andrews et al. 2017). To simulate the influence of a varying gwIMF using the IGIMF theory on galaxy evolution, we minimize the number of free parameters and therefore do not involve the hydrodynamic physics. Baryonic behaviour such as inflow, cooling, mixing, selective mixing, galactic fountain, and galactic wind are not considered (but see Sect. 5.1 below for a discussion, notably that for our studied cases in- and outflows do not play significant roles) and the gas in our model is always well-mixed. All the matter is initially presented as primordial gas and the SFH is pre-specified (see Sect. 4.2 below).
A star transformation fraction (fst) parameter is applied, being the total initial mass of stars formed over the entire galaxy formation history per unit mass of primordial gas provided. The fst can be adjusted to give the right metallicity of a typical galaxy and is invariant for all simulations in this paper. A higher (lower) fst leads to a higher (lower) final metallicity of the simulated galaxies. Thus, a good fit on the metallicity of a single galaxy does not give a simulation much credit, but the ability to fit the metallicity–galaxy-mass relation can constrain the choice of the gwIMF theory.
We do not modify the metal yield table given by the stellar evolution and explosion studies10. Different stellar yield tables are available in the code, while the applied yield for this paper is specified in Sect. 4.4 below.
The basic components of our galaxy chemical evolution model are described below.
4.1. Simulation time step
Our aim was to simulate a continuous star formation activity. The shortest age difference between different stars is set to be 10 Myr, about 1% of the nominal galaxy formation timescale of the massive elliptical galaxies. The value of 10 Myr is preferred as it is the characteristic timescale of the formation of a star cluster population applied by the IGIMF theory (see Weidner et al. 2004; Yan et al. 2017, and Sect. 2 above). Thus, all stars formed within a δt = 10 Myr time grid are assigned the same age.
We note that we do not perform a dynamical simulation, and the chemical abundance at any time is determined solely by the former stellar populations. Thus, it is not necessary to do the calculation at each 10 Myr during the time period without star formation activity. Other than the time span that has star formation, only a few additional time steps are inserted manually since we want the galaxy evolution outcomes to extend to about 13 Gyr even if the star formation quenches within the first billion years.
At a new time step, ti, without star formation activity, the gas-phase element abundances are calculated according to the values at the nearest previous time step, ti − 1, and all the ejections from dying stars and type Ia supernovae (SNIa) during time ti − 1 to ti. If there is star formation at time ti, the new stellar population is stamped with the current gas-phase metallicity as its initial stellar metallicity. The total mass of the stellar population is given by the galaxy-wide SFR specified for this epoch (in units of M⊙ yr−1) times the 10 Myr; and the gwIMF of this star formation epoch is given by the IGIMF theory that depends on the galaxy-wide SFR and the gas-phase metallicity at ti (see Sect. 2). Thus a new stellar population is generated and the amount of mass for every element transformed into stars is deducted from the gas phase. Such a calculation is performed for every time step that has star formation and at additional time steps, if specified, that do not have star formation.
4.2. Star formation history
In our code there are two different ways to determine the SFH, either by a relation between the SFR with the instantaneous gas-mass or by using a specified SFH. The two modes require different input parameters; this paper only demonstrates the latter mode11.
The SFH is set up before the simulation starts where the SFR for each time step, SFR, is specified. For example, the boxy and log-normal distributions applied for this contribution are shown in Fig. 2.
 |
Fig. 2. Adopted SFHs. The galaxy evolution simulation comparing different IMF assumptions (Sect. 6) adopts the boxy SFH (orange dashed line) with a constant SFR = 103M⊙ yr−1 and a tsf of 1 Gyr. The simulation adopting the log-normal SFH (solid red line) finishes its 50%, 75%, and 90% star formation (in mass fraction) in 0.5, 0.98, and 1.8 Gyr, respectively. A comparison of the galaxy chemical evolution results adopting these two different SFHs are shown in Appendix A. |
Previous studies assuming a boxy SFH (or applying a galactic wind which assumes no star formation activity after a certain time) and taking into consideration the age and metallicity dependence on the stellar luminosity in the observations have concluded that there is no notable difference between the luminosity- and mass-weighted metal abundance (Matteucci et al. 1998; Thomas et al. 1999; Recchi et al. 2009). This claim may no longer be valid under an extended SFH with recent star formation activity. As is discussed in Sect. 5.5 below, the luminosity-weighted abundances can be significantly different from the mass-weighted results even if the SFR at late time is much lower than the SFR of the initial starburst in the case of our log-normal SFH model.
An important aspect of the SFH is the timescale over which the burst or galaxy formation occurs (tsf, see Table 1). The tsf is understood to be shorter for more massive elliptical galaxies with a tsf of about 1 Gyr for the most massive ellipticals with the strongest indication come from their α-enhancement (Pipino & Matteucci 2004; Pipino et al. 2009; Thomas et al. 2005, 2010). This relation is referred to as the downsizing of the star formation timescale. However, we note that the estimation of tsf according to the observed [Mg/Fe] value would be different with a different IMF assumption (Matteucci 1994; Thomas et al. 1999; Recchi et al. 2009; Martín-Navarro 2016). In this first contribution, we discuss only the influence of the different IMF assumptions on the chemical evolution of massive elliptical galaxies and assume tsf to be 1 Gyr. An analysis of the possible variation of tsf will be covered in our next paper.
4.3. Gas-, star-, and remnant-mass evolution
The mass of different elements in gas, living stars, and the total stellar remnants mass are updated at each time step in our galaxy evolution model. The mass in gas transforms into stars according to the assumed SFH. The lifetime of a star and the mass of its stellar remnant is taken from the stellar evolution tables of Portinari et al. (1998) and Marigo (2001) as a function of stellar initial mass and metallicity12. The living stars eject gas and become stellar remnants after exhausting their lifetime. The gas reservoir and the stellar ejected gas are instantaneously mixed at the time of ejection.
Following Ritter et al. (2018), a smoothing spline fit on the logarithmic scale is applied to the adopted relation of the stellar lifetime and remnant-mass versus stellar initial mass. As is shown in Fig. 3, massive stars have shorter lifetimes and metal-rich stars have lower remnant masses. The fitted lifetime instead of the original values given by the stellar evolution model is applied in our galaxy evolution model. This treatment not only prevents the galaxy evolution model from being sensitive to the non-monotonic fluctuations of the stellar lifetime and remnant-mass given by the stellar model with large uncertainties, but also unites (and smooths the transition between) the values of intermediate-mass stars given by Marigo (2001) and the values of massive stars given by Portinari et al. (1998). We note that the spline fitted remnant mass (Fig. 3, lower panel) is only used to estimate the remnant mass (shown by the dashed “all remnants” line in Fig. 6 below) and does not modify the amount of mass ejection of the dying stars from their original values. The mass difference between the stellar initial and final mass is considered as ejected gas at the time the star dies, while all SNIa are assumed to increase the gas-phase mass (and decrease the remnant mass) by 1.15 M⊙, as is given by Thielemann et al. (1993) 13. Stellar mass loss due to the stellar wind is accounted for when the star dies. The current total mass of living stars (the solid lines in Fig. 6 below) is approximated by the sum of all the stellar initial masses of the stars that are still living.
 |
Fig. 3. Lifetime (upper panel) and remnant mass, M*, final (lower panel), of a star as a function of its initial mass, M*, initial, and metal mass fraction, Z (or [Z] as defined in Eq. (5)). The shown relations are one-dimensional smoothing spline fits to the stellar evolution tables given by Marigo (2001) and Portinari et al. (1998) for AGB and massive stars, respectively. The colour-coding is the same as in Figs. 5 and A.1. |
4.4. Metal enrichment
The gas-phase metallicity is set to have a primordial composition initially following the element abundances given by Cyburt et al. (2016) 14 and then the gas phase is enriched by the ejected gas from dying stars and SNIa events. The metal-rich gas forms stars and elevates the average stellar metallicity.
Since the formation scenario of the SNIa event is still unsettled, we assume all SNIa have the same yield (as is also assumed in other studies, e.g. De Lucia et al. 2014) given by Gibson et al. (1997, their TNH93 dataset). That is, the SNIa yield does not depend on the progenitor mass or on the metallicity.
The mass of the elements returned to the gas phase by a star over its entire lifetime is accounted for when it dies, and the amount of the ejection is given by the stellar yield table according to the stellar initial mass and metallicity. There are a limited number of stellar initial metallicity values available in the yield table (adopted from the NuPyCEE program, see footnote 12), Z = 0.0127, 0.008, 0.004, and 0.0004, as is shown in Fig. 4 below. We interpolate the yield as a function of stellar mass for the same initial metallicity but apply the yield with the closest initial Z without interpolation (i.e. the yield of a star with given mass switches according to its metallicity at Z = 0.01035, 0.006, and 0.0022). This treatment is reasonable as the applied stellar yields have large systematic uncertainties. A more complicated interpolation treatment would not necessarily increase the reliability of the results. However, it does make the slope of the chemical evolution plots discontinuous at these switch values, as highlighted by the dash-dotted lines in Fig. 8.
 |
Fig. 4. Metallicity [Z] (as defined in Eq. (5)), helium mass fraction Y, and α-enhancement [Mg/Fe] of the ejected gas from a dying star (or supernova event) as a function of the stellar initial metal mass fraction Z and the stellar initial mass M*, initial (or the initial mass of the possible SNIa progenitor, i.e. 3 to 8 M⊙ shown by the dashed line). The thin dotted lines indicate the solar value (the solar value of Y = 0.273 is adopted from Serenelli & Basu 2010). The relation is interpolated from the stellar total yield table given by Marigo (2001) and Portinari et al. (1998) where a solar value stellar initial helium abundance is assumed for the stellar evolution model. The values are different from those in the original paper because of the difference between the “net yield” and the “total yield” (see text). The colour-coding is the same as in Figs. 5 and A.1. |
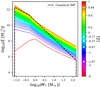 |
Fig. 5. Evolution of the TIgwIMF for a galaxy with the boxy SFH shown in Fig. 2, where ξ is the total number of stars within a unit mass range. The assumed lowest and highest possible stellar mass is 0.08 M⊙ and 150 M⊙, respectively, following Yan et al. (2017). The solid lines represent the TIgwIMF after 10, 20, ..., and 1000 Myr since the beginning of the star formation (from bottom to top). The colour of the lines indicates the metallicity [Z] (as defined in Eq. (5)) in gas at the time. The colour-coding is the same as in Figs. 3 and 4; the white dots in the colour bar indicate the available initial metallicity values of the stellar yield table (see Sect. 4.4) and the white line indicates the initial metallicity of the last stellar population (i.e. the most metal-rich population). The dashed line is the canonical IMF given by Kroupa (2001), normalized to have the same ξ as the final TIgwIMF at M* = 1. |
We note the difference between the “net yield”, which is the mass of an element added or destroyed by a star from the gas phase, and the “total yield”, which is the mass of ejected elements. The total yield is always positive, but the net yield can be negative. We adopt the total yield table. The element ejection in our code depends only on the stellar initial mass and metallicity, but not on its metal composition. This approximation is only valid for the stars with solar composition and leads to errors in general situations. Simply applying the net yield cannot solve this problem as the difficulty lies in there being no yield table using stellar models with extremely non-solar initial abundances (especially for helium, see Sect. 6 below) that can be applied for the massive elliptical galaxies.
The mass of the most abundant elements H, He, C, N, O, Ne, Mg, Si, S, Ca, Fe, and the sum of all the elements heavier than helium are traced separately15. For low- and intermediate-mass stars, we apply the AGB yields given by Marigo (2001). For massive stars, we apply the yield given by Portinari et al. (1998). The metallicity [Z] (defined in Eq. (5)), helium mass fraction Y, and α-enhancement [Mg/Fe] of the ejected gas from a single dying star (or supernova event) as a function of the stellar initial mass and metallicity are shown in Fig. 4. Massive stars exhibit higher yields and α-enhancement while almost all stars generate ejections with a higher helium fraction than the Sun.
The total metal ejection of dying stars, Mmetal, is calculated as Mmetal = Mini − Mrem − Mej, H − Mej, He, with the symbols on the right-hand side being the stellar initial mass, final remnant mass16, ejected hydrogen mass, and ejected helium mass, respectively, instead of adding up the ejected mass of every element (Mmetal = Mej, Li + Mej, Be + …) since not all the elements are computed in the simulation.
The metal evolution is traced by three metal indicators: (i) the gas-phase metallicity (i.e. the mass fraction of metals in gas), (ii) the stellar mass-weighted metallicity, and (iii) the approximated stellar luminosity-weighted metallicity. Element gravitational settling in the star is not considered and the stellar initial metallicity is adopted for the calculations as it has a minor effect (see Sect. 5.6 below).
The calculation of stellar luminosity-weighted results are as follows.
First we consider the luminosity of a single star, which is simplified by adopting only the main-sequence luminosity and because there is no dependence on the stellar metallicity. We note that the luminosity variation during the AGB phase may not have a significant influence on the result since the average element abundance of the AGB stars should be a representation of the entire stellar population. Following Duric (2004, their chapter 1.3.8) for the low-mass stars and Salaris & Cassisi (2006, their Chap. 5.7) for the stars more massive than about 2 M⊙, the empirically determined mass–luminosity relation is approximated in our calculation to be
where M*, initial is the stellar initial mass (same as the M*, initial in Figs. 3 and 4). While the detailed shape of the mass-luminosity relation is important for understanding the shape of the stellar luminosity function (Kroupa et al. 1990, 1993, 2013), the approximation used here suffices for the present purpose. Then the luminosity-weighted metallicity, Zlw, of all the living stars at time tn is calculated as
where ξ(t) is the gwIMF for the stellar population formed at time t (see ξIGIMF in Yan et al. 2017 for definition), Z(t) is the metallicity (or mass fraction for a given element) of the stellar population formed at time t, mmax is the mass of the most massive star that is still living at time tn for the stellar population formed at time t, and mmin is the lowest possible stellar mass. The luminosity-weighted element ratio ([Fe/H]lw) is calculated by a similar equation given in Appendix B.
4.5. Modelling the rate of type Ia supernova
Type Ia supernovae are generally thought to originate in binary systems containing degenerate stellar remnants (Maoz & Mannucci 2012). As a consequence, the SNIa rate should depend on the spatial density of the potential progenitors of the binary stellar system (i.e. the dynamical encounter rate in star cluster; cf. Shara & Hurley 2002). Since we do not have spacial modelling in our simulation, we simplify the consideration with the following assumptions:
1. The stellar density is similar for different stellar systems such that the rate of SNIa depends only on the star formation rate (SFR) and the delay time distribution (DTD) function but not on the density of the stellar system. This is not a good assumption (see Sect. 5.4 below), but it is commonly implied in galaxy evolution models17.
2. The SNIa progenitors and their companion stars are born in the same star cluster. This is reasonable because, although stars and white dwarfs do leave their birth star cluster, the chance that they will meet and form a binary system outside their birth star cluster can be neglected. Under this consideration, the SNIa rate of a stellar population formed in a star formation epoch, δt, is not correlated with any earlier or later star formation epoch.
Given the above assumptions, the standard number of SNIa for a canonical IMF is calculated individually for each stellar population according to its age.
The estimation of the SNIa rate that begins with a theoretical consideration of a specific SNIa formation model, and thus the SNIa progenitor number, suffers from the fact that the nature of the companion star is still under discussion (but see Tucker et al. 2019). Modern galaxy evolution studies avoid this problem by applying the DTD function that is observationally constrained (Greggio 2005). Our contribution applies such a recently constrained DTD function, but deals simultaneously with the variable gwIMF that affects the SNIa number by re-normalizing the result.
The DTD function of the SNIa is assumed to be a power law following Maoz & Mannucci (2012),
where NSNIa, < t(t) is the number of exploded SNIa for a stellar population with age t, and k is a normalization parameter such that the DTD integral over 10 Gyr is 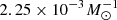 (i.e. about 2 SNIa for every 1000 M⊙ of stars formed). The value
(i.e. about 2 SNIa for every 1000 M⊙ of stars formed). The value 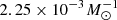 is suggested by observation and has an error of roughly ±1 × 10−3
is suggested by observation and has an error of roughly ±1 × 10−3 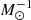 (Maoz & Mannucci 2012), where the error is not considered in our code.
(Maoz & Mannucci 2012), where the error is not considered in our code.
Since we are dealing with a non-canonical IMF and the number of SNIa depends on the number of potential SNIa progenitors, that is, stars with initial mass between about 1.5 and 8 M⊙ 18, NSNIa, < t(t) needs to be re-normalized accordingly with the new number of potential SNIa progenitors per stellar mass formed times the possibility of also having its companion in the correct mass range:
Here NSNIa, < t, nor(t) is the re-normalized number of SNIa and p is the normalization parameter depending on the assumed IMF. Thus, the number of SNIa is adjusted by the p value assuming any given gwIMF over the p value assuming the “diet-Salpeter IMF”, which is the assumed gwIMF for the empirical measurements of the SNIa rate and it differs from the Salpeter IMF by having a flat slope below 0.35 M⊙, as is defined in Bell & de Jong (2001). Parameter n is the number of stars within the mass range given by its subscript (in units of M⊙), and M is the corresponding total mass of the stars in the given mass range. 0.08 M⊙ and 150 M⊙ are the assumed lowest and highest possible stellar mass in our model following Yan et al. (2017). Thus, the normalization parameter p stands for the number of stars in the correct mass range to be the primary star in the progenitor system of SNIa for a stellar population with known total mass, times the possibility that its companion star is also in the correct mass range19. We note that the possibility of any star being in a binary system is absent in Eq. (4) as this possibility will be cancelled in the term pgwIMF/pdiet − Salpeter according to assumption 1 in Sect. 4.5. Considering the possible variation of the stellar dynamical encounter rate, and thus of the fraction of hard binaries, it may be possible that more SNIa occur at high SFRs, and thus in massive galaxies.
4.6. The definition of the metallicity
Throughout the study we adopt an earlier solar metal20 mass fraction measurement of Z⊙ = 0.01886 from Anders & Grevesse (1989) to make it easier to compare our study with earlier galaxy evolution simulations (see Sect. 5.6 below). Thus, the metallicity is defined as
where Z is the metal mass fraction of the target.
When comparing the relative metal and hydrogen abundances, this paper uses [Z/X], where X is the hydrogen mass fraction of the target, instead of [Z/H] to highlight the definition of this symbol,
where X⊙ = 0.70683 is the solar mass fraction of hydrogen adopted from Anders & Grevesse (1989). The values of [Z] and [Z/X] gradually deviate from each other as stellar helium abundance increase to super-solar values.
On the other hand, the symbols written with the name of the element (e.g. [Fe/H] and [Mg/Fe]) follow the canonical definition calculated by the atom number ratio.
5. Uncertainties
The different input components that a galaxy chemical evolution simulation is most sensitive to and that are not well constrained are briefly reviewed to get an idea of the reliability of our simulation. The following factors are able to significantly affect the galaxy chemical evolution via changing, for example the relative influence of SNIa and type II supernovae (SNII). The input parameters typically have an uncertainty larger than 0.2 decimal exponent (dex) in the logarithmic scale (which is an error of about 50%). This section evaluates the influence of these uncertainties.
5.1. Gas flow and efficiency of star formation
Here we discuss whether the applied simplifications of instant gas mixing and no gas flows are good approximations.
Lelli et al. (2014), Concas et al. (2017), and Berg et al. (2018) find a lack of outflows driven by star formation in observed low-mass and low- to intermediate-redshift galaxies. Outflows in more massive elliptical galaxies would be more difficult since they have a deeper potential well, consistent with the suggestion from X-ray (Kim & Pellegrini 2012) and chemical evolution studies (Ferreras & Silk 2000). In principle, with the violent star formation activity of massive galaxies, the galaxy gas can be heated to a high temperature (O’Sullivan et al. 2001), and may escape the galaxy and enrich the intercluster medium (ICM; Renzini & Andreon 2014; Mernier et al. 2017), and/or it can be locked up in the hot corona around the galaxy, thereby having a significantly long cooling time and thus not being available for further recycling (Hirschmann et al. 2016). A positive correlation between the gas velocity and the galaxy-wide SFR is indeed evident in observations (Sugahara et al. 2017, 2019), but it is unclear if such an outflowing gas is a galactic fountain, which can be recycled, or galactic wind, which cannot (see Matteucci 2012 for definition).
For the inflow, since the star formation and galaxy assembly of the massive elliptical galaxies are accomplished within a Gyr timescale (Renzini 2006), their formation can be approximated as an initial rapid collapse during which gas inflow from afar would not have played a significant role.
We discuss the hydrodynamic considerations employed by other simulation studies and their possible effects:
– The primordial gas inflow regulates when and how much gas is accreted to the galaxy and thus the SFH. An exponentially decreasing gas-inflow rate is often assumed in semi-analytical simulations to simulate the SFH of the starburst (see e.g. Calura et al. 2009; Pipino & Matteucci 2011; Vincenzo et al. 2015). Our model achieves a similar SFH by specifying it.
The amount of gas infall is usually used as a free parameter to adjust the final metallicity of a galaxy21. Our model does not have gas flows and use the initial gas mass as a free parameter to adjusts the final metallicity.
– The galactic fountain refers to the gas flows within the galaxy. The general effect is to delay the gas mixing between the SN ejecta and the ISM, and thus the recycling of the elements, which appears to have a limited effect on the chemical evolution of disc galaxies (Spitoni et al. 2009). For the simulation of high-mass ellipticals that have a high SFR and supernova explosion rate (see Fig. 7 below), gas-mixing should be more efficient and we consider the instantaneous mixing of gas to be a good approximation.
– A galactic wind can be included in our model. It would move the enriched gas out of the galaxy thereby reducing the final total gas mass and metallicity of the simulated galaxy.
A uniform galactic wind, where element ratios of the ejected gas are the same as in the well-mixed gas phase, is often applied in galaxy evolution studies22. For massive ellipticals, we test with our model that if the mass of the galactic wind is the same as the mass of stars being formed at the time, as suggested for dwarf irregular galaxies (Matteucci 2012), the metal abundance of the galaxy at t = 13 Gyr would decrease by about 0.1 dex, and the metal abundance ratios would change less than 0.05 dex. A significant influence on the simulated chemical evolution results would require a strong galactic wind scenario with an outflow-mass–star-formation-mass ratio much higher than 1. According to Sugahara et al. (2017, 2019), the estimated total mass of outflows for high-redshift galaxies should be less than about five times the total stellar mass. This amount of outflow would not affect significantly our simulation results even if all the outflow becomes a galactic wind. The effect of galactic wind may not be significant for lower mass galaxies either, as suggested by Köppen et al. (2007). Since there is no direct observational evidence supporting the strong galactic wind scenario, we decided to demonstrate only the simulations without a galactic wind.
Other than the uniform galactic wind, the wind may contain more metals (i.e. a selective outflow, Pagel 2009), as metal elements experience higher radiation pressure (Recchi et al. 2008); or the wind may be largely composed of the α-element-rich supernova ejections (Lian et al. 2018) probably under strong starburst circumstances (Yates et al. 2013). The enriched wind taking away the metals more efficiently and selectively is used to explain anomalous observations (Matteucci 2012, their Eq. (2.36)). A time-dependent galactic wind might be necessary to explain the metal abundance of gas and stars together as suggested by Lian et al. (2018). These selective treatments have large uncertainties and are not applied in our model. They will result in a lower metallicity and [α/Fe] if applied.
– The efficiency of star formation (the parameter ν in unit of Gyr−1 as defined in Matteucci 1994) strongly affects the metallicity. It depends on baryonic physics that influences the gas recycling process such as gas expulsion, mixing, and cooling processes. In some studies, the efficiency of star formation is assumed to be a constant for galaxies with order of magnitude differences in mass or SFR. In others, especially those trying to reproduce the downsizing of the star formation timescale, the efficiency of star formation is assumed to be higher in more massive galaxies (Matteucci 1994; Calura et al. 2009). The uncertainty of the efficiency of star formation is about 0.2 dex and leads to an uncertainty on the chemical evolution simulation results larger than 0.2 dex. Since we aim to apply a fixed SFH and vary only the IMF assumption, our model does not involve the parameter ν. Instead, we use the parameter fst (Table 1) to specify how many stars are formed relative to the initial gas mass.
We note that the necessity of the gas-flow model depends on the galaxy type and assumptions about the IMF. Gas flows were initially introduced to explain the metal distribution of the stars in the solar neighbourhood and the Galactic disc (e.g. the G-dwarf problem of the Milky Way). For an elliptical galaxy with a variable gwIMF, we need to re-evaluate the situation. Only when the simpler mode without gas flows fails should we introduce more free parameters to describe the gas flow (as Martinelli & Matteucci 2000 do to explore for disc galaxies).
As noted in Pagel (2009, their Sect. 11.2.1), a constraint on any modelling parameter requires an independent observable. This is difficult when we consider distant elliptical galaxies that cannot be resolved into single stars and are likely to have a non-canonical TIgwIMF23. Without proper constraints, the gas in- and outflow models are not reliable and only complicate the analysis.
Essentially, the formation of elliptical galaxies occurs on a much shorter timescale than the disc galaxies that apart from the initial infall the most star formation is finished before additional gas accretion or galaxy wind can play a role (cf. Thomas et al. 1999 their “fast clumpy collapse model”). Models without gas-flow are thus likely good and in particular computationally efficient approximations to describe the formation and evolution of elliptical galaxies (especially for the central region where most of the star formation and metal enrichment happens, cf. Afruni et al. 2019).
5.2. Initial gas metallicity
Most massive elliptical galaxies are thought to be formed at the earliest time (Renzini 2006; Thomas et al. 2010; Estrada-Carpenter et al. 2019) when the gas is not pre-enriched. The effect of pre-enrichment, if it occurs, is to eliminate the very metal-poor stars and it may raise the final metallicity of the galaxy.
In our simulation, the metallicity dependence of the gwIMF leads to a feedback effect since a low-metallicity environment results in a more top-heavy gwIMF (Yan et al. 2017, their Fig. B.1) leading to a higher IMF-weighted metal yield (Recchi & Kroupa 2015). This effect makes the final metallicity of the galaxy insensitive to its initial value.
The initial gas metallicity, as well as the metal-dependence of the IGIMF formulation, mainly affects the property of the very first generations of stars polluted by massive star ejections, which is beyond the scope of the current study. Later stages of the chemical evolution depend far more on the details of the SFH and IMF slope than on the initial metallicity.
5.3. Type II supernovae
The stellar evolution models give different SNII yields. Thomas et al. (1998), Karlsson & Gustafsson (2005), and Philcox et al. (2018) show that the IMF averaged [Mg/Fe] yield between two tables may differ by as much as 0.3 dex. This uncertainty is inherited by the final metallicity of the galaxy and modifies the element abundance ratios (Thomas et al. 1998; Andrews et al. 2017, their Sect. 4.2). Considering the rotation of pre-supernova star in the stellar evolution model gives even larger yield uncertainties, especially for isotopes (Hirschi et al. 2005; Choplin et al. 2018).
In addition, not all high-mass stars will end up as a SNII. Direct black hole formation without supernova (Smartt 2015) and different types of core-collapse supernovae due to initial mass, metallicity, and angular momentum differences of the supernova progenitors (Heger et al. 2003; Sukhbold et al. 2016), kilonovae (supposed merger events of two neutron stars, or a neutron star and a black hole), as well as other cosmic selection effects that may modify the SNII rate (Horiuchi et al. 2011) or favour contributions from supernovae in a certain mass range or favour the recycling of certain elements (Karlsson & Gustafsson 2005) are currently not considered by most galaxy evolution simulations.
These concerns mean that the yield of a stellar population is uncertain even with a known IMF.
5.4. Type Ia supernovae
The SNIa yields also show large uncertainties. For example, the ejecta from a single SNIa event have a [O/Mg] ranging in different references from about −0.43 (Nomoto et al. 1984; Seitenzahl et al. 2013) and about −0.25 (Thielemann et al. 1986, 2003) to about 0.05 in Iwamoto et al. (1999) and Gibson et al. (1997), which is our applied SNIa yield. Thus, applying a different SNIa yield table and considering different α element certainly affect the resulting [α/Fe]. We note that dying stars give a [O/Mg] yield ranging from about 0 dex to as high as 1.6 dex depending on the stellar initial mass and metallicity, which leads to an oxygen overproduction relative to magnesium in galaxy evolution simulation relative to observations. Choosing a higher SNIa Mg yield could in principle be helpful (cf. François et al. 2004; Pipino & Matteucci 2011) but this discussion is beyond the scope of the current publication. The ejected iron mass shows more consistency between different references, typically being 0.663 ± 0.066 M⊙ per SNIa event. The applied Fe yield in the current simulations is 0.744 M⊙ per SNIa event (Gibson et al. 1997).
A different shape of the SNIa DTD can have a significant effect on the abundance ratio between the α elements and iron peak elements of a galaxy. A single power law, a broken power law, and a bivariate DTD have been proposed (Mannucci et al. 2006; Matteucci et al. 2009; Maoz et al. 2010; Yates et al. 2013). The estimated power index, assuming a single power-law shape, ranges from 0.9 to 1.3. The time delay between the formation of a single age stellar population and the peak of its SNIa rate (40 Myr in Eq. (3)) has an uncertainty of several dozens megayears. However, it does not have a notable affect on the SNIa history of a galaxy where SNIa rate peaks on a billion year timescale since the SNIa explosion history is a convolution of Eq. (3) with the billion year timescale SFH. Thus, the uncertainty of the 40 Myr applied in Eq. (3) can be ignored for the present purpose.
The largest uncertainty introduced by Eq. (3) to the galaxy chemical evolution is from the normalization parameter, 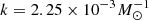 . The empirical measurements of the parameter k not only have a large scatter of about ±1 SNIa per 1000 M⊙, but also tensions between different measures. Studies of the iron abundance in the ICM have shown that the parameter k should be higher than 3.4 (Maoz et al. 2010)24, being inconsistent with other direct measurement methods. This suggests a systematic error possibly relating to the intrinsic variation due to environmental differences.
. The empirical measurements of the parameter k not only have a large scatter of about ±1 SNIa per 1000 M⊙, but also tensions between different measures. Studies of the iron abundance in the ICM have shown that the parameter k should be higher than 3.4 (Maoz et al. 2010)24, being inconsistent with other direct measurement methods. This suggests a systematic error possibly relating to the intrinsic variation due to environmental differences.
5.5. Recent star formation activity
Later star formation after the primary star burst is likely (Chauke et al. 2018; Morishita et al. 2019). A SFH with a long tail of low SFR after the starburst, or a later second smaller starburst that contributes a decent portion of stars (10%, e.g. Tojeiro et al. 2013) formed from metal-enriched gas may not influence the stellar mass-weighted metallicity, but can alter the luminosity–weighted metallicity significantly, as is shown in Appendix A. The luminosity-weighted metal abundances are closer to the metal abundance of the gas phase, which is higher than the stellar mass-weighted metallicity. The different SFH of galaxies and especially the difference in recent star formation activity will introduce an intrinsic scatter on the interpreted galaxy properties.
5.6. Adopted solar metallicity value
The solar metal mass fraction, Z⊙ (i.e. the mass fraction of the elements heavier than helium) have been declining continuously over the past decades, from 1.89% in Anders & Grevesse (1989) to about 1.34% in Asplund et al. (2009). Thus, the application of a different solar metallicity can lead to a 0.15 dex difference in the resulting [Z]. However, many observational papers do not explicitly define the solar metallicity they applied. Following Woosley & Weaver (1995), this paper adopts the earlier solar metallicity measurement of Z⊙ = 0.01886 from Anders & Grevesse (1989) as mentioned in Sect. 4.6. We avoid the involvement of the solar metallicity when adopting the stellar evolution yield table by applying Z instead of [Z]. Finally, the present-day photosphere metallicity of the Sun is similar to its bulk or protosolar metallicity with a difference in log10(Z) smaller than 0.03 dex according to Asplund et al. (2009). The difference in abundance ratio, e.g. [Mg/Fe] could be even smaller (Dotter et al. 2017). Thus, we do not distinguish the two as other parameters introduce far larger uncertainties.
6. Simulation results
In this section, the effect of applying different IMF assumptions is shown. Two simulations with exactly the same set-up (e.g. SFH and initial gas mass), except for the assumption on the gwIMF, are carried out, one assuming the gwIMF is the invariant canonical two-part power-law IMF (Kroupa 2001), the other assuming the gwIMF is metallicity- and SFR-dependent according to the latest IGIMF theory formulation (Jeřábková et al. 2018, their IGIMF3 model). The fst is set to be 100% (i.e. the sum of the initial stellar masses of all the stars ever formed throughout the galaxy formation history is the same as the initial gas mass25). The boxy SFH in Fig. 2 is assumed, where the SFR is fixed at 1000 M⊙ yr−1 and lasts for tsf = 1 Gyr. We simulate the chemical evolution of a galaxy for 13 Gyr (the nominal age of the Universe) and result in the stellar-mass-weighted, the gas-mass-weighted, and a stellar-luminosity-weighted (approximated, see Sect. 4.4) element abundance evolution, the evolution of total gas, living star, and stellar remnant mass, the evolution of the TIgwIMF, and the evolution of SN rates.
In addition, we compare the galaxy evolution assuming different SFHs (the boxy and log-normal SFH shown in Fig. 2) under the IGIMF theory. The results are shown in Appendix A.
6.1. Evolution of the TIgwIMF
Under the IGIMF theory framework, the TIgwIMF changes gradually from top-heavy bottom-light to top-heavy bottom-heavy26 (see Fig. 5), in conformity with the pioneering variable-IMF suggestion for producing the old and metal-rich stellar population of ellipticals (Vazdekis et al. 1996, their Sect. 4.2.1).
We note that the TIgwIMF shown in Fig. 5 combines all gwIMFs over the formation history of the galaxy (i.e. it comprises all stars ever formed). The TIgwIMF shown here does not resemble the gwIMF of the Milky Way, which has a different SFH.
The IMF is top-heavy due to the high SFR in the assumed starburst SFH. Consistent with Bekki (2013), there is a lack of low-mass stars at early times when the environment is metal poor; while the low-mass end evolves to a bottom-heavy form as the metallicity increases. The time-dependent TIgwIMF variation at the low-mass end may be relevant for the bottom-heavy TIgwIMF determined by some observations (see the generated bottom-heavy gwIMF and a more in-depth discussion in Jeřábková et al. 2018).
We note that the massive stars have a short lifetime and would not be observable in the present day. The observations on the still living low-mass stars do not give information about the high-mass IMF slope except for their observed metallicity which can be compared with the prediction given by the galaxy chemical evolution simulation assuming a certain IMF theory.
6.2. Gas, living star, and stellar remnant mass evolution
The difference in the mass evolution of gas, living stars, and stellar remnants as a function of time assuming the IGIMF theory and invariant canonical IMF are shown in Fig. 6.
 |
Fig. 6. Mass evolution of gas, living stars, and stellar remnants as a function of time for the boxy SFH shown in Fig. 2. The orange and blue lines are, respectively, the results obtained assuming the gwIMF is given by the IGIMF theory and the invariant canonical IMF. The same colour-coding is applied from Figs. 6–11. The “all gas” includes gas outside the galaxy that is constrained by the galactic potential (see Sect. 5.1 above). Different from Fig. 5, here the simulated values at 10, 19, 20, 29... Myr are demonstrated, where star formation happens at 10, 20... Myr (see Sect. 4.1). The death of stars with a lifetime shorter than the star formation time step (10 Myr) causes the serrated shape of the lines. |
We note that the total gas shown includes the circumgalactic medium that is trapped in the galactic potential. As our model assumes no galactic wind, all the gas is considered as trapped gas. The total gas mass is reduced less significantly in the IGIMF theory as the massive stars return most of their mass to the gas phase quickly after their formation (Loewenstein 2006, their Fig. 1). We consider that the star formation is not truncated due to a lack of gas, but because the gas is heated to a high temperature; in other words, the apparent high gas mass in our simulation is the mass of a hot gas halo with a significantly long cooling time, precluding it from forming new stars (cf. Hirschmann et al. 2016).
The stellar remnant mass is comparable to the mass of living stars in the IGIMF theory framework, while the canonical result is that the remnant mass is much lower than the stellar mass. Thus, the dynamical mass-to-light ratio of the studied massive elliptical galaxy would increase by about a factor of two under the IGIMF theory in comparison with applying the canonical IMF, in line with the IMF mismatch parameter of about 2 for massive ellipticals in most27 of the cases as evident in Cappellari et al. (2012), Li et al. (2017), and Oldham & Auger (2018).
6.3. Number of supernovae
The time evolution of the number of SNIa and SNII adopting different IMF assumptions is plotted in Fig. 7.
 |
Fig. 7. Number of SNIa and SNII per century as a function of time for the boxy SFH shown in Fig. 2. As in Fig. 6, the orange lines are the results applying the IGIMF theory, while the blue lines apply the invariant canonical IMF. The thick lines below and the thin lines above are the rates for SNIa and SNII, respectively. The serrated shape is caused by the simplification that all the stars formed in a 10 Myr star formation epoch have an identical age. |
The high SNII rate is a direct result of the assumed SFH. With the commonly assumed relation that more massive galaxies have a shorter tsf (see Sect. 4.2 above), the starburst has to be extremely violent. Thus, the galaxy produces a large number of SNII at early times with about 0.5 and 1 SNII event per day under the assumption of the invariant canonical IMF and the IGIMF theory, respectively (for a similar discussion in the context of the formation of ultra-compact dwarf galaxies see Jeřábková et al. 2017). This seems to be consistent with the stronger emission lines observed for higher redshift galaxies (Labbé et al. 2013; Stark et al. 2015).
On the other hand, the number of SNIa per stellar mass formed is reduced for the simulated high-SFR galaxy as the variation of the gwIMF changes the pgwIMF in Eq. (4). As is shown in Fig. 7, the resulting SNIa rate applying the IGIMF theory is about one-third of the simulation applying the canonical IMF (cf. Loewenstein & Davis 2010). Since SNIa produce more than half of the iron in galaxies, this suggests that using iron as a tracer may underestimate the metallicity (see Sect. 6.4.3 below).
6.4. Element abundances
The mass- or luminosity-averaged [Z/X], Y, [Fe/H], and [Mg/Fe] evolution for stars and gas comparing different IMF assumptions are shown in Figs. 8–11.
 |
Fig. 8. Evolution of gas- and mass-averaged stellar [Z/X] for the boxy SFH shown in Fig. 2, where [Z/X] is defined in Sect. 5.6. Simulations applying the IGIMF theory and fixed canonical IMF are shown as the orange and blue lines, respectively. The solid, dashed, and dotted lines represent the value calculated for gas phase, mass average, and luminosity average (approximation, see text), respectively. The horizontal dash-dotted lines mark the boundaries where the stellar yield table is changed (at [Z/X] ≈ [Z] = −0.26, −0.497, −0.933, see Sect. 4.4 for explanation), which causes a change in the speed of enrichment (but with a 10 Myr delay). The serrated shape is caused by our simplification that all the stars formed in a 10 Myr star formation epoch have an identical age. |
We note that our gas-phase element abundances are mass averaged, which may differ from the emission-weighted observations that depend on the local gas temperature and density. We also note that the observed stellar luminosity-weighted metallicity should be lower than our estimate which adopts the luminosity without the metallicity dependence (see Sect. 4.4 above) since metal-poor stars are more luminous.
The behaviour of the evolution for different elements shown in the following sections is similar. The stellar luminosity-weighted results are close to the gas-phase results during the star formation and quickly recover to the stellar mass-weighted results as the luminous massive stars die out on a hundred million or billion year timescale.
6.4.1. Metallicity
Figure 8 shows that the metal enrichment happens at an earlier time under the IGIMF theory relative to the invariant canonical IMF. It follows that the IGIMF theory results in earlier metal enrichment and higher final metallicity. The metal abundances of galaxies during the first few hundred million years are difficult to constrain, but the next generation James Webb Space Telescope may allow observations of this kind of the high-redshift universe.
We note that the stars only form at 10 Myr time steps. The temporary decrease in the mass- and luminosity-weighted stellar metallicity during the 10 Myr epoch is caused by the death of the most recently formed metal-rich massive stars.
6.4.2. Helium abundance
Figure 9 shows the enrichment of helium under different IMF assumptions and the helium-enrich is more prominent under the IGIMF theory. This is a natural outcome of the high helium yield of the massive stars according to the adopted stellar yield table (see Fig. 4).
 |
Fig. 9. Same as Fig. 8, but for helium mass fraction Y. The solar value of 0.273 is adopted from Serenelli & Basu (2010). |
It is important to self-consistently consider the helium abundance in galaxy chemical evolution models because the abundance of carbon, nitrogen, and oxygen is highly influenced by the hydrogen burning process and the amount of hydrogen is different for the stars with the same mass but different helium abundance. When the galactic helium abundance changes, the stellar yield of the newly formed stars must come from a stellar evolution simulation assuming that changed helium abundance.
6.4.3. Iron abundance
The iron evolution is shown in Fig. 10. We highlight three features of the result obtained using the IGIMF theory due to a larger fraction of iron produced by SNII relative to SNIa.
– The resulting [Fe/H] is lower than the [Z/X] (compared to the IGIMF line in Fig. 8), consistent with the α-enhanced characteristic of massive elliptical galaxies (see Sect. 6.4.4 below).
– The iron production is faster at earlier times thanks to the enhanced number of SNII but slower at later times (see Fig. 7 above). The earlier production of iron is in line with the suggestion from the abundance profiles of the ICM (Mernier et al. 2017).
– The iron abundance difference at 13 Gyr between the gas phase and stellar phase is smaller compared to the models resting on the canonical IMF assumption, alleviating the difficulty in explaining the observed equality of stellar and gas-phase iron abundance (see Pipino & Matteucci 2011).
6.4.4. Alpha element enhancement
Figure 11 shows that IGIMF-applied galaxy evolution results in a higher [Mg/Fe], in line with the results obtained by Recchi et al. (2009).
 |
Fig. 11. Same as Fig. 8, but for [Mg/Fe]. The discontinuous change in slope of the curves (e.g. the blue curves near 108.4 yr) is explained in Fig. 8 with the horizontal “Yield Switch” lines. |
We note that Recchi et al. (2009) applied an early version of the IGIMF theory where the IMF variation of individual star clusters was not applied. The modern IGIMF prescription used here with a possible top-heavy gwIMF further increases the resulting [Mg/Fe] value.
7. Conclusions
This contribution publishes an open source galaxy evolution code that is able to vary the gwIMF according to the IGIMF theory (or any other variable IMF theory) at each time step, yielding the mass composition, supernova rate, and chemical composition evolution of the galaxy. Following Yan et al. (2017) and Jeřábková et al. (2018),
where the gwIMF for a single star formation epoch is derived according to the IGIMF theory, the newly developed code published here enables us, for the first time, to perform a comprehensive and detailed examination of the effect of applying a different IMF theory in the context of galaxy chemical evolution assuming an identical SFH.
Our preliminary result of a high-mass starburst galaxy assuming different IMFs and the same SFH is shown in Sect. 6; the result assuming the same gwIMF (the IGIMF theory) but different SFHs is shown in Appendix A. A systematically varying gwIMF leads to a strong modification of the element composition of a galaxy (naturally reproducing the observed higher metallicity and α-enhancement of the massive elliptical galaxies), while the difference in SFH and recent star formation activity influences the interpreted property of a galaxy due to a difference in the luminosity-weighted observation.
The star formation environment of massive ellipticals in the early Universe is very different from the local Universe where we calibrate the IGIMF theory. There is no guarantee that such an extrapolation of the theory would work, but it is certainly an inspiring step. We will use this open source code for more comprehensive and detailed studies for galaxies with different masses and SFHs and also develop a spatially resolved IGIMF formulation.
See Table 1 for a list of abbreviations applied in our galaxy chemical evolution model. Following Jeřábková et al. (2018) we distinguish the IMF (as resulting in a star-forming event over about 1 Myr in a molecular cloud core) from the galaxy-wide IMF, gwIMF.
The bottom-heaviness of the TIgwIMF (Table 1) in the central region of massive elliptical galaxies is still under debate. See also the evidence against the bottom-heavy TIgwIMF from the latest spectral energy distribution fitting study (Alton et al. 2018) and strong lensing studies (Smith & Lucey 2013; Collier et al. 2018; Smith et al. 2018) suggesting that the current spectral analysis procedure may have unaccounted systematic uncertainties or the spectral features have a different origin.
Verified predictions include: a non-trivial relation between the mass of an embedded or a very young star cluster and the mass of the most massive star formed in this cluster (Weidner & Kroupa 2006; Weidner et al. 2010, 2013b, 2014); all the apparent isolated massive stars being back-traceable to a parent star cluster (Gvaramadze et al. 2012; Stephens et al. 2017); integrating the observed star cluster IMFs results in the observed gwIMF (Weidner et al. 2013a; Yan et al. 2017; Jeřábková et al. 2018); a deficit of the Hα/UV signal from dwarf galaxies (Meurer et al. 2009; Pflamm-Altenburg et al. 2009; Lee et al. 2009).
There are other galaxy evolution works adopting a specified star cluster IMF variation, but not following Marks et al. (2012). Such a modification of the IGIMF formulation is plausible as long as the proposed formulation is well calibrated with observation. We adopt Marks et al. (2012) as it is comprehensively calibrated, but the research on star cluster scale IMF variation is not settled.
The “strictly” refers to the observed lack of Poisson scatter of the stellar mass distribution as summarized in Kroupa et al. (2013). This highly self-regulated star formation behaviour implies a significant relation between the mass of stars in a star cluster and the star cluster mass (Kroupa & Weidner 2003; Kroupa et al. 2013; Yan et al. 2017).
The power-law index, β, for the ECMF is defined in Yan et al. (2017, their Eq. (9), where the Salpeter index in the same equation would be 2.35). In addition, the power-law index is likely to depend on the galaxy-wide SFR with massive clusters forming more frequently in galaxies with a higher SFR (Weidner et al. 2013a; Recchi & Kroupa 2015). However, the influence of having a variable β assumption on the galaxy chemical evolution may not be significant since it is a second-order effect.
The deduced timescale of about 10 Myr is related to the luminosity-weighted stellar age of the observed galaxies, and thus its SFH. The dim lower mass stars are not well represented in such estimations, but they also contribute less to the chemical evolution and the ISM returned mass budget because they have a long lifetime.
There is also an equivalent code in the FORTRAN programming language (Zonoozi et al. 2019) available at https://github.com/ahzonoozi/gwIMF
Earlier galaxy chemical evolution studies suggest a modification of the literature yield table in order to fit the observation, but they lack independent support (Pipino & Matteucci 2004; Recchi et al. 2009).
With a top-heavy IMF, a new stellar population returns most of its mass to the gas phase shortly after its formation. In this case, the gas mass is hardly depleted. In order to quench the star formation in the former mode, one has to introduce other considerations and assumptions, such as the energy produced by supernovae and the binding energy of a galaxy, which is beyond the scope of the current contribution.
Data pre-processing done by Christian, 25 Feb 2016, for the Public NuGrid Python Chemical Evolution Environment (NuPyCEE, https://github.com/NuGrid/NuPyCEE). The data given by the NuPyCEE program is adopted and shown in our Figs. 3 and 4. The net yield from Marigo (2001) is converted to total yield by NuGrid initial composition files and it has been updated. The newest version updated on May 2018 shows no significant difference compared with the old version we applied. We keep using the old version since it covers wider mass and metallicity ranges.
The value is adopted from Gibson et al. (1997, their TNH93 dataset). The 1.15 M⊙ comes from summing over the Fe, Si, O, S, Mg, and Ne element ejections.
This is the case not only for all the studies applying a DTD function, e.g. Yates et al. (2013) and De Lucia et al. (2014), but also those considering a specific SNIa formation model, e.g. Pipino & Matteucci (2004).
It is commonly assumed that the maximum stellar mass able to produce a degenerate C/O white dwarf is 8 M⊙ (Greggio & Renzini 1983). The minimum possible binary mass ensuring that the smallest possible white dwarf can accrete enough mass from the secondary star to reach the Chandrasekhar mass is about 2 or 3 M⊙. Here we assume that all stars with a initial mass from 1.5 M⊙ to 8 M⊙ has the same chance to be part of a SNIa event. It may not be the best approximation (cf. Loewenstein 2006), but the chemical evolution results of massive galaxies are not sensitive to the choice of 1.5 M⊙ limit (see footnote 19 below).
The correct mass range of the companion star should depend on the primary star, but since the SNIa progenitor model is still uncertain and other uncertainties of the SNIa model are larger, a more detailed consideration does not improve the accuracy of our estimation. In addition, the average level of the SNIa rate is determined mostly by the empirical parameter k in Eq. (3), while the re-normalization procedure is only used as a secondary adjustment to compensate for the non-canonical IMF effect instead of trying to calculate the SNIa rate directly. Thus, the re-normalized SNIa rate is not sensitive to the exact mass boundary we chose in Eq. (4) as long as the gwIMF is not top-light. This is confirmed when we apply a different lower boundary of 3 M⊙. Thus, it is reasonable to apply the same mass range of 1.5−8 M⊙ in Eq. (4) for both the primary and secondary star to reduce the computational cost.
The infall model increases the metal production of a galaxy and ends up with less metal-poor stars, thus is a solution of the G-dwarf problem (Pagel 2001, 2009; Matteucci 2012).
The lockup of gas by low-mass stars has the same effect as a uniform galactic wind. The mass fraction in brown dwarfs and planets is smaller than about 4% (Kroupa et al. 2013), thus has a negligible effect and will not be considered.
Maoz et al. (2010) assumes a diet-Salpeter IMF. The conclusion for other Milky Way-like IMFs will be similar. The conclusion for a top-heavy IMF would require an even larger normalization parameter as the relative number of SNIa precursors is reduced in a top-heavy IMF.
Acknowledgments
ZY acknowledges financial support from the China Scholarship Council (CSC). TJ acknowledges support through an ESO studentship. We acknowledge the open source NuPyCEE project from which we adopted the digital stellar yield tables. This work also benefited from the International Space Science Institute (ISSI/ISSI-BJ) in Bern and Beijing, thanks to the funding of the team “Chemical abundances in the ISM: the litmus test of stellar IMF variations in galaxies across cosmic time” (Principal Investigators Donatella Romano and Zhi-Yu Zhang). We thank especially Donatella Romano for reading our manuscript and providing important comments. Last but not least, we thank Daniel Thomas for the helpful comments that improved our paper.
References
- Adams, F. C., & Fatuzzo, M. 1996, ApJ, 464, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Afruni, A., Fraternali, F., & Pezzulli, G. 2019, A&A, 625, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alton, P. D., Smith, R. J., & Lucey, J. R. 2018, MNRAS, 478, 4464 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Andrews, B. H., Weinberg, D. H., Schönrich, R., & Johnson, J. A. 2017, ApJ, 835, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Arrigoni, M., Trager, S. C., Somerville, R. S., & Gibson, B. K. 2010, MNRAS, 402, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Auger, M. W., Treu, T., Gavazzi, R., et al. 2010, ApJ, 721, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., Covey, K. R., & Meyer, M. R. 2010, ARA&A, 48, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K. 2013, ApJ, 779, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Berg, D. A., Erb, D. K., Auger, M. W., Pettini, M., & Brammer, G. B. 2018, ApJ, 859, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Buitrago, F., Trujillo, I., Conselice, C. J., et al. 2008, ApJ, 687, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Calura, F., Pipino, A., Chiappini, C., Matteucci, F., & Maiolino, R. 2009, A&A, 504, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calura, F., Recchi, S., Matteucci, F., & Kroupa, P. 2010, MNRAS, 406, 1985 [NASA ADS] [Google Scholar]
- Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2012, Nature, 484, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Cenarro, A. J., Gorgas, J., Vazdekis, A., Cardiel, N., & Peletier, R. F. 2003, MNRAS, 339, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Chauke, P., van der Wel, A., Pacifici, C., et al. 2018, ApJ, 861, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Choplin, A., Hirschi, R., Meynet, G., et al. 2018, A&A, 618, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collier, W. P., Smith, R. J., & Lucey, J. R. 2018, MNRAS, 478, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- Concas, A., Popesso, P., Brusa, M., et al. 2017, A&A, 606, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conroy, C., & van Dokkum, P. G. 2012, ApJ, 760, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Fields, B. D., Olive, K. A., & Yeh, T.-H. 2016, Rev. Mod. Phys., 88, 015004 [NASA ADS] [CrossRef] [Google Scholar]
- Dabringhausen, J., Kroupa, P., & Baumgardt, H. 2009, MNRAS, 394, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- Dabringhausen, J., Kroupa, P., Pflamm-Altenburg, J., & Mieske, S. 2012, ApJ, 747, 72 [NASA ADS] [CrossRef] [Google Scholar]
- de La Rosa, I. G., La Barbera, F., Ferreras, I., & de Carvalho, R. R. 2011, MNRAS, 418, L74 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Tornatore, L., Frenk, C. S., et al. 2014, MNRAS, 445, 970 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Fontanot, F., & Hirschmann, M. 2017, MNRAS, 466, L88 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Kim, J., & Shadmehri, M. 2007, MNRAS, 381, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Conroy, C., Cargile, P., & Asplund, M. 2017, ApJ, 840, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Duric, N. 2004, Advanced Astrophysics (Cambridge: Cambridge University Press) [Google Scholar]
- Elmegreen, B. G. 2004, MNRAS, 354, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Estrada-Carpenter, V., Papovich, C., Momcheva, I., et al. 2019, ApJ, 870, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Ferré-Mateu, A., Trujillo, I., Martín-Navarro, I., et al. 2017, MNRAS, 467, 1929 [NASA ADS] [Google Scholar]
- Ferreras, I., & Silk, J. 2000, MNRAS, 316, 786 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., La Barbera, F., de la Rosa, I. G., et al. 2013, MNRAS, 429, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., Weidner, C., Vazdekis, A., & La Barbera, F. 2015, MNRAS, 448, L82 [NASA ADS] [CrossRef] [Google Scholar]
- Fontanot, F., De Lucia, G., Hirschmann, M., et al. 2017, MNRAS, 464, 3812 [NASA ADS] [CrossRef] [Google Scholar]
- François, P., Matteucci, F., Cayrel, R., et al. 2004, A&A, 421, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gargiulo, I. D., Cora, S. A., Padilla, N. D., et al. 2015, MNRAS, 446, 3820 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, B. K., Loewenstein, M., & Mushotzky, R. F. 1997, MNRAS, 290, 623 [NASA ADS] [Google Scholar]
- Greggio, L. 2005, A&A, 441, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greggio, L., & Renzini, A. 1983, A&A, 118, 217 [NASA ADS] [Google Scholar]
- Gunawardhana, M. L. P., Hopkins, A. M., Sharp, R. G., et al. 2011, MNRAS, 415, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Guszejnov, D., Hopkins, P. F., & Graus, A. S. 2019, MNRAS, 485, 4852 [NASA ADS] [CrossRef] [Google Scholar]
- Gvaramadze, V. V., Weidner, C., Kroupa, P., & Pflamm-Altenburg, J. 2012, MNRAS, 424, 3037 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2005, A&A, 433, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirschmann, M., De Lucia, G., & Fontanot, F. 2016, MNRAS, 461, 1760 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. W., Bouwens, R., Oesch, P., et al. 2015, ApJ, 808, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M. 2018, PASA, 35, e039 [Google Scholar]
- Horiuchi, S., Beacom, J. F., Kochanek, C. S., et al. 2011, ApJ, 738, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Hoversten, E. A., & Glazebrook, K. 2008, ApJ, 675, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Iwamoto, K., Brachwitz, F., Nomoto, K., et al. 1999, ApJS, 125, 439 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jeřábková, T., Kroupa, P., Dabringhausen, J., Hilker, M., & Bekki, K. 2017, A&A, 608, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeřábková, T., Hasani Zonoozi, A., Kroupa, P., et al. 2018, A&A, 620, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karlsson, T., & Gustafsson, B. 2005, A&A, 436, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, D. W., & Pellegrini, S. 2012, in Hot Interstellar Matter in Elliptical Galaxies, Astrophys. Space Sci. Lib., 378 [CrossRef] [Google Scholar]
- Köppen, J., Weidner, C., & Kroupa, P. 2007, MNRAS, 375, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kroupa, P., & Weidner, C. 2003, ApJ, 598, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1990, MNRAS, 244, 76 [NASA ADS] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Weidner, C., Pflamm-Altenburg, J., et al. 2013, The Stellar and Sub-Stellar Initial Mass Function of Simple and Composite Populations (Springer Science + Business Media Dordrecht), 115 [Google Scholar]
- La Barbera, F., Vazdekis, A., Ferreras, I., et al. 2017, MNRAS, 464, 3597 [NASA ADS] [CrossRef] [Google Scholar]
- Labbé, I., Oesch, P. A., Bouwens, R. J., et al. 2013, ApJ, 777, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C. G., Baugh, C. M., Frenk, C. S., et al. 2016, MNRAS, 462, 3854 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1998, MNRAS, 301, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Gil de Paz, A., Tremonti, C., et al. 2009, ApJ, 706, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., Verheijen, M., & Fraternali, F. 2014, A&A, 566, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H., Ge, J., Mao, S., et al. 2017, ApJ, 838, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Lian, J., Thomas, D., Maraston, C., et al. 2018, MNRAS, 474, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Loewenstein, M. 2006, ApJ, 648, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Loewenstein, M., & Davis, D. S. 2010, ApJ, 716, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Della Valle, M., & Panagia, N. 2006, MNRAS, 370, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., & Mannucci, F. 2012, PASA, 29, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Sharon, K., & Gal-Yam, A. 2010, ApJ, 722, 1879 [Google Scholar]
- Marigo, P. 2001, A&A, 370, 194 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marks, M., Kroupa, P., Dabringhausen, J., & Pawlowski, M. S. 2012, MNRAS, 422, 2246 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Navarro, I. 2016, MNRAS, 456, L104 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Navarro, I., Vazdekis, A., La Barbera, F., et al. 2015, ApJ, 806, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Navarro, I., Vazdekis, A., Falcón-Barroso, J., et al. 2018, MNRAS, 475, 3700 [NASA ADS] [CrossRef] [Google Scholar]
- Martinelli, A., & Matteucci, F. 2000, A&A, 353, 269 [NASA ADS] [Google Scholar]
- Matteucci, F. 1994, A&A, 288, 57 [NASA ADS] [Google Scholar]
- Matteucci, F. 2012, Chemical Evolution of Galaxies (Berlin Heidelberg: Springer-Verlag) [CrossRef] [Google Scholar]
- Matteucci, F., Ponzone, R., & Gibson, B. K. 1998, A&A, 335, 855 [NASA ADS] [Google Scholar]
- Matteucci, F., Spitoni, E., Recchi, S., & Valiante, R. 2009, A&A, 501, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mernier, F., de Plaa, J., Kaastra, J. S., et al. 2017, A&A, 603, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meurer, G. R., Wong, O. I., Kim, J. H., et al. 2009, ApJ, 695, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Morishita, T., Abramson, L. E., Treu, T., et al. 2019, ApJ, 877, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., & Ostriker, J. P. 2017, ARA&A, 55, 59 [Google Scholar]
- Narayanan, D., & Davé, R. 2013, MNRAS, 436, 2892 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro-González, J., Ricciardelli, E., Quilis, V., & Vazdekis, A. 2013, MNRAS, 436, 3507 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Thielemann, F.-K., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
- Offner, S. S. R., Clark, P. C., Hennebelle, P., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 53 [Google Scholar]
- Okamoto, T., Nagashima, M., Lacey, C. G., & Frenk, C. S. 2017, MNRAS, 464, 4866 [NASA ADS] [CrossRef] [Google Scholar]
- Oldham, L. J., & Auger, M. W. 2018, MNRAS, 476, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Oser, L., Ostriker, J. P., Naab, T., Johansson, P. H., & Burkert, A. 2010, ApJ, 725, 2312 [NASA ADS] [CrossRef] [Google Scholar]
- O’Sullivan, E., Forbes, D. A., & Ponman, T. J. 2001, MNRAS, 328, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J. 2001, PASP, 113, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J. 2009, Nucleosynthesis and Chemical Evolution of Galaxies (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Papadopoulos, P. P. 2010, ApJ, 720, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Parikh, T., Thomas, D., Maraston, C., et al. 2018, MNRAS, 477, 3954 [NASA ADS] [CrossRef] [Google Scholar]
- Pflamm-Altenburg, J., & Kroupa, P. 2008, Nature, 455, 641 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pflamm-Altenburg, J., Weidner, C., & Kroupa, P. 2009, MNRAS, 395, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Philcox, O., Rybizki, J., & Gutcke, T. A. 2018, ApJ, 861, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Pipino, A., & Matteucci, F. 2004, MNRAS, 347, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Pipino, A., & Matteucci, F. 2011, A&A, 530, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pipino, A., Devriendt, J. E. G., Thomas, D., Silk, J., & Kaviraj, S. 2009, A&A, 505, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Portinari, L., Chiosi, C., & Bressan, A. 1998, A&A, 334, 505 [NASA ADS] [Google Scholar]
- Recchi, S., & Kroupa, P. 2015, MNRAS, 446, 4168 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., Calura, F., & Kroupa, P. 2009, A&A, 499, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recchi, S., Spitoni, E., Matteucci, F., & Lanfranchi, G. A. 2008, A&A, 489, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renzini, A. 2006, ARA&A, 44, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Renzini, A., & Andreon, S. 2014, MNRAS, 444, 3581 [NASA ADS] [CrossRef] [Google Scholar]
- Ritter, C., & Côté, B. 2016, Astrophysics Source Code Library [record ascl:1610.015] [Google Scholar]
- Ritter, C., Côté, B., Herwig, F., Navarro, J. F., & Fryer, C. L. 2018, ApJS, 237, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Matteucci, F., Zhang, Z.-Y., Papadopoulos, P. P., & Ivison, R. J. 2017, MNRAS, 470, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Cassisi, S. 2006, Evolution of Stars and Stellar Populations (Wiley) [Google Scholar]
- Schulz, C., Pflamm-Altenburg, J., & Kroupa, P. 2015, A&A, 582, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seitenzahl, I. R., Ciaraldi-Schoolmann, F., Röpke, F. K., et al. 2013, MNRAS, 429, 1156 [Google Scholar]
- Serenelli, A. M., & Basu, S. 2010, ApJ, 719, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M., & Hurley, J. R. 2002, ApJ, 571, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J. 2015, PASA, 32, e016 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., & Lucey, J. R. 2013, MNRAS, 434, 1964 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Lucey, J. R., & Collier, W. P. 2018, MNRAS, 481, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., Matteucci, F., Recchi, S., Cescutti, G., & Pipino, A. 2009, A&A, 504, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stark, D. P., Walth, G., Charlot, S., et al. 2015, MNRAS, 454, 1393 [Google Scholar]
- Stephens, I. W., Gouliermis, D., Looney, L. W., et al. 2017, ApJ, 834, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Sugahara, Y., Ouchi, M., Lin, L., et al. 2017, ApJ, 850, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Sugahara, Y., Ouchi, M., Harikane, Y., et al. 2019, ApJ, submitted [arXiv:1904.03106] [Google Scholar]
- Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H.-T. 2016, ApJ, 821, 38 [Google Scholar]
- Thielemann, F.-K., Nomoto, K., & Yokoi, K. 1986, A&A, 158, 17 [NASA ADS] [Google Scholar]
- Thielemann, F. K., Nomoto, K., & Hashimoto, M. 1993, in Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse, 297 [Google Scholar]
- Thielemann, F. K., Argast, D., Brachwitz, F., et al. 2003, in From Twilight to Highlight: The Physics of Supernovae, eds. W. Hillebrandt, & B. Leibundgut, 331 [Google Scholar]
- Thomas, D., Greggio, L., & Bender, R. 1998, MNRAS, 296, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Greggio, L., & Bender, R. 1999, MNRAS, 302, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Bender, R., & Mendes de Oliveira, C. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Schawinski, K., Sarzi, M., & Silk, J. 2010, MNRAS, 404, 1775 [NASA ADS] [Google Scholar]
- Tojeiro, R., Masters, K. L., Richards, J., et al. 2013, MNRAS, 432, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Ferré-Mateu, A., Balcells, M., Vazdekis, A., & Sánchez-Blázquez, P. 2014, ApJ, 780, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Tucker, M. A., Shappee, B. J., Vallely, P. J., et al. 2019, MNRAS, submitted [arXiv:1903.05115] [Google Scholar]
- Urban, O., Werner, N., Allen, S. W., Simionescu, A., & Mantz, A. 2017, MNRAS, 470, 4583 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., & Conroy, C. 2010, Nature, 468, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Casuso, E., Peletier, R. F., & Beckman, J. E. 1996, ApJS, 106, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Peletier, R. F., Beckman, J. E., & Casuso, E. 1997, ApJS, 111, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Cenarro, A. J., Gorgas, J., Cardiel, N., & Peletier, R. F. 2003, MNRAS, 340, 1317 [NASA ADS] [CrossRef] [Google Scholar]
- Vincenzo, F., Matteucci, F., Recchi, S., et al. 2015, MNRAS, 449, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2005, ApJ, 625, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2006, MNRAS, 365, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Larsen, S. S. 2004, MNRAS, 350, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Bonnell, I. A. D. 2010, MNRAS, 401, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Pflamm-Altenburg, J. 2011, MNRAS, 412, 979 [NASA ADS] [Google Scholar]
- Weidner, C., Kroupa, P., Pflamm-Altenburg, J., & Vazdekis, A. 2013a, MNRAS, 436, 3309 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Pflamm-Altenburg, J. 2013b, MNRAS, 434, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Ferreras, I., Vazdekis, A., & La Barbera, F. 2013c, MNRAS, 435, 2274 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Pflamm-Altenburg, J. 2014, MNRAS, 441, 3348 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, Z., Jerabkova, T., & Kroupa, P. 2017, A&A, 607, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yates, R. M., Henriques, B., Thomas, P. A., et al. 2013, MNRAS, 435, 3500 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Z.-Y., Romano, D., Ivison, R. J., Papadopoulos, P. P., & Matteucci, F. 2018, Nature, 558, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Zonoozi, A. H., Mahani, H., & Kroupa, P. 2019, MNRAS, 483, 46 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Results for a log-normal SFH
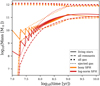 |
Fig. A.2. Same as Fig. 6, but comparing different SFHs instead of different IMF assumptions. The orange lines apply the boxy SFH and the red lines apply the log-normal SFH, both shown in Fig. 2. The same colour-coding is applied from Figs. A.2–A.7. The serrated shape is caused by the dying stars with a lifetime shorter than 10 Myr (see Sect. 6.2). We note that the orange lines are the same as the orange lines in Fig. 6. |
This section compares the simulation results applying the IGIMF theory, but with the two different SFHs shown in Fig. 2. The log-normal SFH forms the same stellar mass, but on a more extended timescale. The tail of the SFH with a low SFR leads to a stellar population that receives a contribution every δt = 10 Myr from a top-light gwIMF, which does not exist in the box-shaped SFH model described in the main text. Thus, a more realistic and extended SFH naturally leads to a time-varying gwIMF suggested qualitatively already by Vazdekis et al. (1996, 1997), Weidner et al. (2013c), Narayanan & Davé (2013), Ferreras et al. (2015), and Lacey et al. (2016), with a top-heavy gwIMF at the beginning and a bottom-heavy (and top-light) gwIMF at later times.
Figure A.1 shows the resulting TIgwIMF for the log-normal SFH. The variation of the low-mass part of the TIgwIMF is smoother than the boxy SFH case (Fig. 5) because the metal enrichment is slower, as is shown in Fig. A.4.
Figures A.2–A.7 apply the same colour-coding as in Fig. 2. The orange lines labelled “boxy SFH” are the same as the orange lines in Figs. 6–11 labelled “IGIMF”. The luminosity-weighted stellar element abundance becomes closer to the gas-phase value as the log-normal SFH has a more recent star formation activity. The luminosity-weighted result depends on the SFH and fluctuates for different galaxies that have different SFHs.
Appendix B: Luminosity-weighted element ratio
The luminosity-weighted element ratio (e.g. [Fe/H]lw) is not weighted with the [Fe/H] of each star, but with the element mass Mi, mw of the stars, where i is Fe or H and
We then calculate the abundance ratio as
where Ai = log10(Ni/NH)+12 is the solar photospheric abundance of element i adopted from Anders & Grevesse (1989, their Table 2).
All Tables
All Figures
 |
Fig. 1. Interaction between the newly developed galaxy evolution module and the previously published IGIMF calculation module (Yan et al. 2017), which returns the gwIMF at any given time ti, and the input/output of each module. The main inputs are shown in the black text while the default settings are shown in the grey text. |
| In the text | |
 |
Fig. 2. Adopted SFHs. The galaxy evolution simulation comparing different IMF assumptions (Sect. 6) adopts the boxy SFH (orange dashed line) with a constant SFR = 103M⊙ yr−1 and a tsf of 1 Gyr. The simulation adopting the log-normal SFH (solid red line) finishes its 50%, 75%, and 90% star formation (in mass fraction) in 0.5, 0.98, and 1.8 Gyr, respectively. A comparison of the galaxy chemical evolution results adopting these two different SFHs are shown in Appendix A. |
| In the text | |
 |
Fig. 3. Lifetime (upper panel) and remnant mass, M*, final (lower panel), of a star as a function of its initial mass, M*, initial, and metal mass fraction, Z (or [Z] as defined in Eq. (5)). The shown relations are one-dimensional smoothing spline fits to the stellar evolution tables given by Marigo (2001) and Portinari et al. (1998) for AGB and massive stars, respectively. The colour-coding is the same as in Figs. 5 and A.1. |
| In the text | |
 |
Fig. 4. Metallicity [Z] (as defined in Eq. (5)), helium mass fraction Y, and α-enhancement [Mg/Fe] of the ejected gas from a dying star (or supernova event) as a function of the stellar initial metal mass fraction Z and the stellar initial mass M*, initial (or the initial mass of the possible SNIa progenitor, i.e. 3 to 8 M⊙ shown by the dashed line). The thin dotted lines indicate the solar value (the solar value of Y = 0.273 is adopted from Serenelli & Basu 2010). The relation is interpolated from the stellar total yield table given by Marigo (2001) and Portinari et al. (1998) where a solar value stellar initial helium abundance is assumed for the stellar evolution model. The values are different from those in the original paper because of the difference between the “net yield” and the “total yield” (see text). The colour-coding is the same as in Figs. 5 and A.1. |
| In the text | |
 |
Fig. 5. Evolution of the TIgwIMF for a galaxy with the boxy SFH shown in Fig. 2, where ξ is the total number of stars within a unit mass range. The assumed lowest and highest possible stellar mass is 0.08 M⊙ and 150 M⊙, respectively, following Yan et al. (2017). The solid lines represent the TIgwIMF after 10, 20, ..., and 1000 Myr since the beginning of the star formation (from bottom to top). The colour of the lines indicates the metallicity [Z] (as defined in Eq. (5)) in gas at the time. The colour-coding is the same as in Figs. 3 and 4; the white dots in the colour bar indicate the available initial metallicity values of the stellar yield table (see Sect. 4.4) and the white line indicates the initial metallicity of the last stellar population (i.e. the most metal-rich population). The dashed line is the canonical IMF given by Kroupa (2001), normalized to have the same ξ as the final TIgwIMF at M* = 1. |
| In the text | |
 |
Fig. 6. Mass evolution of gas, living stars, and stellar remnants as a function of time for the boxy SFH shown in Fig. 2. The orange and blue lines are, respectively, the results obtained assuming the gwIMF is given by the IGIMF theory and the invariant canonical IMF. The same colour-coding is applied from Figs. 6–11. The “all gas” includes gas outside the galaxy that is constrained by the galactic potential (see Sect. 5.1 above). Different from Fig. 5, here the simulated values at 10, 19, 20, 29... Myr are demonstrated, where star formation happens at 10, 20... Myr (see Sect. 4.1). The death of stars with a lifetime shorter than the star formation time step (10 Myr) causes the serrated shape of the lines. |
| In the text | |
 |
Fig. 7. Number of SNIa and SNII per century as a function of time for the boxy SFH shown in Fig. 2. As in Fig. 6, the orange lines are the results applying the IGIMF theory, while the blue lines apply the invariant canonical IMF. The thick lines below and the thin lines above are the rates for SNIa and SNII, respectively. The serrated shape is caused by the simplification that all the stars formed in a 10 Myr star formation epoch have an identical age. |
| In the text | |
 |
Fig. 8. Evolution of gas- and mass-averaged stellar [Z/X] for the boxy SFH shown in Fig. 2, where [Z/X] is defined in Sect. 5.6. Simulations applying the IGIMF theory and fixed canonical IMF are shown as the orange and blue lines, respectively. The solid, dashed, and dotted lines represent the value calculated for gas phase, mass average, and luminosity average (approximation, see text), respectively. The horizontal dash-dotted lines mark the boundaries where the stellar yield table is changed (at [Z/X] ≈ [Z] = −0.26, −0.497, −0.933, see Sect. 4.4 for explanation), which causes a change in the speed of enrichment (but with a 10 Myr delay). The serrated shape is caused by our simplification that all the stars formed in a 10 Myr star formation epoch have an identical age. |
| In the text | |
 |
Fig. 9. Same as Fig. 8, but for helium mass fraction Y. The solar value of 0.273 is adopted from Serenelli & Basu (2010). |
| In the text | |
 |
Fig. 10. Same as Fig. 8, but for [Fe/H]. |
| In the text | |
 |
Fig. 11. Same as Fig. 8, but for [Mg/Fe]. The discontinuous change in slope of the curves (e.g. the blue curves near 108.4 yr) is explained in Fig. 8 with the horizontal “Yield Switch” lines. |
| In the text | |
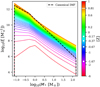 |
Fig. A.1. Same as Fig. 5, but for the log-normal SFH shown in Fig. 2 that extends for 13 Gyr. |
| In the text | |
 |
Fig. A.2. Same as Fig. 6, but comparing different SFHs instead of different IMF assumptions. The orange lines apply the boxy SFH and the red lines apply the log-normal SFH, both shown in Fig. 2. The same colour-coding is applied from Figs. A.2–A.7. The serrated shape is caused by the dying stars with a lifetime shorter than 10 Myr (see Sect. 6.2). We note that the orange lines are the same as the orange lines in Fig. 6. |
| In the text | |
 |
Fig. A.3. Same as Figs. A.2 and 7. The orange lines are the same as the orange lines in Fig. 7. |
| In the text | |
 |
Fig. A.4. Same as Figs. A.2 and 8. The orange lines are the same as the orange lines in Fig. 8. |
| In the text | |
 |
Fig. A.5. Same as Figs. A.2 and 9. The orange lines are the same as the orange lines in Fig. 9. |
| In the text | |
 |
Fig. A.6. Same as Figs. A.2 and 10. The orange lines are the same as the orange lines in Fig. 10. |
| In the text | |
 |
Fig. A.7. Same as Figs. A.2 and 11. The orange lines are the same as the orange lines in Fig. 11. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



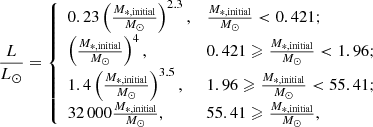
![$$ \begin{aligned} Z_{\rm lw}(t_n) = \frac{\sum \limits _{t=t_1}^{t_n} \left[ \int _{m=m_{\rm min}}^{m_{\rm max}(t_n-t)} \xi (t,M_{*,\mathrm{initial}})L(M_{*,\mathrm{initial}})\mathrm{d}m \cdot Z(t) \right]}{\sum \limits _{t=t_1}^{t_n} \left[ \int _{m=m_{\mathrm{min}}}^{m_{\rm max}(t_n-t)} \xi (t,M_{*,\mathrm{initial}})L(M_{*,\mathrm{initial}})\mathrm{d}m \right]}, \end{aligned} $$](/articles/aa/full_html/2019/09/aa36029-19/aa36029-19-eq2.gif)
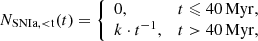
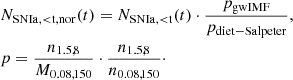
![$$ \begin{aligned} {[Z]}=\mathrm{log}_{10}({Z}/0.01886), \end{aligned} $$](/articles/aa/full_html/2019/09/aa36029-19/aa36029-19-eq8.gif)
![$$ \begin{aligned} \mathrm{[Z/X]} = \log _{10}(\mathrm{Z/X}) - \mathrm{\log }_{10}({Z}_\odot /{X}_\odot ), \end{aligned} $$](/articles/aa/full_html/2019/09/aa36029-19/aa36029-19-eq9.gif)
![$$ \begin{aligned} M_{i, \mathrm{mw}}(t_n) = \frac{\sum \limits _{t=t_1}^{t_n} \left[ \int _{m=m_{\rm min}}^{m_{\rm max}(t_n-t)} \xi (t,M_{*,\mathrm{initial}})L(M_{*,\mathrm{initial}})\mathrm{d}m \cdot M_{i}(t) \right]}{\sum \limits _{t=t_1}^{t_n} \left[ \int _{m=m_{\rm min}}^{m_{\rm max}(t_n-t)} \xi (t,M_{*,\mathrm{initial}})L(M_{*,\mathrm{initial}})\mathrm{d}m \right]}\cdot \end{aligned} $$](/articles/aa/full_html/2019/09/aa36029-19/aa36029-19-eq11.gif)
![$$ \begin{aligned} \mathrm{[Fe/H]} _{\rm mw}(t_n) =&\mathrm{log} _{10}\left[(M_{\rm Fe, mw}(t_n)/W_{\rm Fe}) / (M_{\rm H, mw}(t_n)/W_{\rm H})\right] \nonumber \\&- \mathrm{log} _{10}(A_{\rm Fe} / A_{\rm H}), \end{aligned} $$](/articles/aa/full_html/2019/09/aa36029-19/aa36029-19-eq12.gif)