| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201834787 | |
| Published online | 01 July 2019 | |
Non-thermal desorption of complex organic molecules
Efficient CH3OH and CH3COOCH3 sputtering by cosmic rays★
1
Institut des Sciences Moléculaires d’Orsay (ISMO), UMR8214, CNRS – Université de Paris-Sud, Université Paris-Saclay,
Bât 520, Rue André Rivière,
91405 Orsay,
France
e-mail: emmanuel.dartois@u-psud.fr
2
Institut de Physique Nucléaire d’Orsay (IPNO), CNRS-IN2P3, Université de Paris-Sud, Université Paris-Saclay,
91406 Orsay, France
3
Centre de Recherche sur les Ions, les Matériaux et la Photonique, CIMAP-CIRIL-GANIL, Normandie Université, ENSICAEN, UNICAEN, CEA, CNRS,
14000 Caen, France
4
Centre de Sciences Nucléaires et de Sciences de la Matière (CSNSM), CNRS/IN2P3, Université de Paris-Sud, Université Paris-Saclay,
91405 Orsay, France
5
Department of Physics, Indian Institute of Technology, Hauz Khas,
New Delhi 110016, India
Received:
6
December
2018
Accepted:
25
May
2019
Context. The occurrence of complex organic molecules (COMs) in the gas phase at low temperature in the dense phases of the interstellar medium suggests that a non-thermal desorption mechanism is at work because otherwise, COMs should condense within a short timescale onto dust grains. Vacuum ultraviolet (VUV) photodesorption has been shown to be much less efficient for complex organic molecules, such as methanol, because mostly photoproducts are ejected. The induced photolysis competes with photodesorption for large COMs, which considerably lowers the efficiency to desorb intact molecules.
Aims. We pursue an experimental work that has already shown that water molecules, the dominant ice mantle species, can be efficiently sputtered by cosmic rays. We investigate the sputtering efficiency of complex organic molecules that are observed either in the ice mantles of interstellar dense clouds directly by infrared spectroscopy (CH3OH), or that are observed in the gas phase by millimeter telescopes (CH3COOCH3) and that could be released from interstellar grain surfaces.
Methods. We irradiated ice films containing complex organic molecules (methanol and methyl acetate) and water with swift heavy ions in the electronic sputtering regime. We monitored the infrared spectra of the film as well as the species released to the gas phase with a mass spectrometer.
Results. We demonstrate that when methanol or methyl acetate is embedded in a water-ice mantle exposed to cosmic rays, a large portion is sputtered as an intact molecule, with a sputtering yield close to that of the main water-ice matrix. This must be even more true for the case of more volatile ice matrices, such as those that are embedded in carbon monoxide.
Conclusions. Cosmic rays penetrating deep into dense clouds provide an efficient mechanism to desorb complex organic molecules. Compared to the VUV photons, which are induced by the interaction of cosmic rays, a large portion desorb as intact molecules with a proportion corresponding to the time-dependent bulk composition of the ice mantle, the latter evolving with time as a function of fluence due to the radiolysis of the bulk.
Key words: astrochemistry / cosmic rays / molecular processes / ISM: lines and bands / solid state: volatile / ISM: abundances
© E. Dartois et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The observed relatively high abundance of complex organic molecules in dense and pre-stellar phases of the interstellar medium (ISM) is puzzling (e.g. Lefloch et al. 2018; Soma et al. 2018; Ceccarelli et al. 2017; López-Sepulcre et al. 2017; Jørgensen et al. 2016; Jiménez-Serra et al. 2016; Öberg et al. 2014; Vasyunina et al. 2014; Bacmann et al. 2012, and references therein). If these molecules are formed on the surface of dust grains, an effective desorption mechanism must be invoked for their release in the gas phase. As shown in laboratory experiments, many of the desorption mechanisms working effectively on small icy molecules such as CO and N2 become much less relevant for large molecular systems comprising about six or more atoms, the complex organic molecules (COM)s. In addition, the source of energy required for the desorption in the case of vacuum ultraviolet (VUV) photons easily photolyses large molecules such as methanol (e.g. Cruz-Diaz et al. 2016; Bertin et al. 2016). Thermal desorption of COMs is also much less efficient for large molecular systems because of the out-diffusion of the most volatile species without efficient transport of COMs (e.g. Ligterink et al. 2018). Competition with other channels during formation (e.g. Minissale et al. 2016) is also of consequence at the surface of the grains in the desorption of the smaller species.
This article reports the experimental measurement of the desorption of COMs by sputtering following the impact of cosmic rays on ice mantles. The focus is on the most abundant well-known 6-atom ice mantle COM, methanol (CH3OH). We also investigate an even larger COM with 11 atoms, methyl acetate (CH3COOCH3), which has been detected quite recently in Orion (Tercero et al. 2013). The experiments are described in Sect. 2. Section 3 presents the results of a combined IR and mass spectrometer analysis of the products in the experimentally simulated ice mantles that are ejected upon the swift interaction of heavy ions with thin ice films that are deposited at low temperature. Radiolysis and sputtering are examined together within a simple model framework. In the last section the observed astronomical occurrence and variations with respect to water ice and carbon monoxide ices of methanol in interstellar ice mantles are considered. Before we conclude, we discuss the destruction cross-section dependency on stopping-power. and the astrophysical implications of sputtering rates for COMs.
2 Experiments
Swift ion-irradiation experiments were performed at the heavy-ion accelerator Grand Accélérateur National d’Ions Lourds (GANIL, Caen, France). Heavy-ion projectiles were delivered on the IRRSUD beam line1. The Irradiation de GLaces d’Intérêt AStrophysique (IGLIAS) facility, a vacuum chamber (10−9 mbar under our experimental conditions) that holds an IR-transmitting substrate that can be cryocooled down to about 10 K,was coupled to the beam line. The ice films were produced by placing the cold window substrate in front of adosing needle that was connected to the deposition line. Ice films were condensed at 10 K on the window from the vapour phase and were kept at this temperature during the irradiations. Methanol was rectapur grade, and methyl acetate (99.5% purity) was purchased from Sigma Aldrich; both were used as received. Details of the experimental setup are given in Augé et al. (2018). The stopping power of the projectiles (136 Xe 23+ at 0.7 MeV u−1) in the electronic regime is close to 8 keV nm−1 for a pure H2O ice film when we adopt an ice density of 0.93 g cm−3. For pure methanol, the stopping power is slightly higher, about 9.4 keV nm−1 for a density of pure ice of 1.013 g cm−3 (e.g. Maté et al. 2009), and is about 7.5–8.3 keV nm−1 for methyl acetate when a pure ice density of between 0.9 and 1.0 g cm−3 is assumed. This stopping-power value lies in a range close to previous thick-film experiments (Dartois et al. 2015, 2018, and references therein). The determination of the semi-infinite sputtering yield was discussed in Dartois et al. (2018), using the same projectiles. This previously determined yield-dependency on the stopping power for pure water ice predicts a total sputtering yield for intact plus radiolysed molecules of 2.0 ± 0.2 × 104 sputtered H2O/ion; this yield is dominated by intact molecules. The ion flux, set between 107 and 109 ions cm−2 s−1, was monitored online using the current measured on the beam entrance-slits that define the aperture. The relation between the current at different slit apertures and the flux was calibrated before the experiments. We used a Faraday cup that was inserted in front of the sample chamber to do this. The deposited ice-film thicknesses allow the ion beam to pass through the film with an almost constant energy loss per unit path length. A Bruker FTIR spectrometer (Vertex 70v) with a spectral resolution of 1 cm−1 was used to monitor the IR film transmittance. The evolution of the IR spectra was recorded as a function of the ion fluence. The irradiation was performed at normal incidence, whereas the IR transmittance spectra were recorded simultaneously at 12o of incidence (a correction factor of ≈0.978 was therefore applied to determine the normal column densities). A sweeping device allows for uniform and homogeneous ion irradiation over the target surface. Mass measurements were performed simultaneously using a microvision2 mks quadrupole mass-spectrometer (QMS). The QMS signals were noise-filtered to smooth out high-frequency temporal fluctuations using a Lee filter algorithm with a typical box size of five to seven points. The mass ranges that we scanned were varied for the different experiments in order to optimise the integration time. The masses we used to follow a given species were selected in order to avoid overlap with masses that are dominated by contamination and avoid confusion with a byproduct of the radiolysis. For water, masses 17 and 18 were used. For methanol, mass 31 was used preferentially, especially when the signal was low. It is the strongest signal in the high-mass fragmentation pattern for methanol and was recorded for pure methanol during injection, as shown in Fig. 1. Mass 32 can also be used, but it will be contaminated by radiolytically produced oxygen in the mixtures that contain high proportions of H2O. Masses 28, 29, and 30 contain significant fractions of CO and H2CO fragments, which are the main products of methanol radiolysis at the surface and/or in the bulk of the ice (see the summary Table 6 in de Barros et al. 2011). Mass 31 can contain small amounts of methanol radiolysis products such as metoxy or hydroxymethyl radicals (CH3O, CH2OH), but as shown in Fig. 1 for the first steps of irradiation and also in the methanol experiments figures, the m = 32/m = 31 ratio is almost constant and close to the pure methanol value that is recorded systematically with the QMS before irradiation. In these experiments, the direct contributions of the metoxy or hydroxymethyl radical should therefore be considered as low. When only selected optimum masses are used, a correction factor needs to be applied to estimate the abundance of a species so that the mass fragmentation pattern following electron impact ionisation can be taken into account. The experimental fragmentation pattern within our QMS for a species X was monitored during the injection of the gas mixture, that is, when the ice film was deposited. A self-calibration of the QMS for the mass-fragmentation pattern of species X was then obtained at mass m as follows:
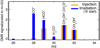 |
Fig. 1 Average of the mass spectra that were recorded during the methanol injection that was meant to form the ice film (orangehistogram), tracing the QMS mass-fragmentation pattern of pure methanol; average of a few spectra that were recorded at the beginning of the ice-film irradiation (blue histogram). Both mass spectra are scaled to mass 32 for comparison.This shows that masses 32 and 31 can be used to monitor methanol because the radiolysis with the ion mainly contributes to peaks at lower masses. See text for details. |
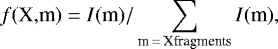 (1)
(1)
where only the expected masses from possible (major) fragments (Xfragments) were included, for instance, masses 16, 17, and 18 for H2O. Therefore, the sum of the chosen masses were used and divided by their relative fragmentation-pattern percentage to retrieve the total number of species X. The spectra were also corrected for the total electron-impact ionisation cross section σimpact(X) at 70 eV (energy of the QMS electron ionisation source) for each molecule: H2O (2.275 Å2, NIST database), CH3OH (4.8 Å2, Vinodkumar et al. 2011), and CH3OOCH3 (11.2 Å2, Kaur et al. 2015), to compensate for the higher ionisation efficiency of larger species (which carry more electrons).
The abundance ratios of species X and Y were thus evaluated with
![\begin{equation*} \!\frac{\textrm{[X]}}{\textrm{[Y]}}{=}\frac{\sum_{\textrm{m\,{=}\,Xfragments}}{{I}(\textrm{m})}}{\sum_{\textrm{m\,{=}\,Xfragments}}{{f}(\textrm{X,m})}}\times \frac{\sum_{\textrm{m\,{=}\,Yfragments}}{{f}(\textrm{Y,m})}}{\sum_{\textrm{m\,{=}\,Yfragments}}{{I}(\textrm{m})}} \times \frac{\sigma^{\textrm{impact}}\textrm{(Y)}}{\sigma^{\textrm{impact}}\textrm{(X)}} ,\end{equation*}](/articles/aa/full_html/2019/07/aa34787-18/aa34787-18-eq2.png) (2)
(2)
with the fragments chosen so that they have a significant signal-to-noise ratio (S/N) and do not overlap with other dominant species and/or potential residual gas masses.
For each of the pure methanol and methyl acetate experiments, the measured QMS mass signals are hereafter displayed multiplied by an arbitrary global factor (i.e. scaled to span a unit range). In the mixture experiments, in order to establish the relative abundance of species, the QMS signals are presented corrected for the relative mass-fragmentation pattern for a given mass or group of masses that is attributed to a dominant species, normalised by its electron-impact ionisation cross section, as discussed above. The signals are then scaled by a global factor. During the experiments, the ion beam was regularly stopped during a few cycles in order to record and follow the evolution of the QMS and chamber background signal. The QMS spectra we present are background subtracted. A summary of the ice-film parameters such as ice mixture, deposition, and irradiation temperatures, and the scanned QMS masses is given in Table 1. A summary of the integrated band strengths from the literature that we used in the IR spectra analysis to determine ice-film column densities is listed in Table 2.
Summary of experiment parameters.
3 Results
3.1 Pure CH3OH, thin and thick films
Before we investigated potentially more relevant astrophysical methanol/ice abundance mixtures, we performed pure methanol ice-irradiation experiments for which we varied the film thicknesses to determine among other parameters the methanol destruction cross section under fixed ion-beam conditions. Three ice films with different thicknesses were irradiated. The evolution of the CH3OH IR spectra, ice column densities, and QMS intensities as a function of fluence is displayed in Fig. 2. The sputtering is unambiguously detected in the three experiments, and its contribution is negligible to the IR signal evolution compared to the radiolysed molecules for the two thicker ice experiments. This allows a direct determination of the radiolysis cross section. For the two thicker ice films, a fit of the destruction cross section of methanol for the considered ion leads to two independent determinations of 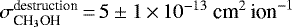 and 5.9 ± 1 × 10−13 cm2 ion−1. The deviation from the apparent pure destruction evolution measured for thick films, that is, when the number of molecules that is removed by sputtering becomes comparable or higher in importance than the bulk destruction of methanol, is best observed when the film becomes thinner, here for column densities below a few 1016 cm−2, as shown in the lower panel of Fig. 2. The methanol sputtering yield can be calculated with the thinner ice experiment using a model similar to those used in Dartois et al. (2015, 2018). An estimate is obtained by adjusting a fit that includes the electronic sputtering for the thinner film and setting the previously determined destruction cross section to 5.45 ± 1.5 × 10−13 cm2 ion−1. We obtain
and 5.9 ± 1 × 10−13 cm2 ion−1. The deviation from the apparent pure destruction evolution measured for thick films, that is, when the number of molecules that is removed by sputtering becomes comparable or higher in importance than the bulk destruction of methanol, is best observed when the film becomes thinner, here for column densities below a few 1016 cm−2, as shown in the lower panel of Fig. 2. The methanol sputtering yield can be calculated with the thinner ice experiment using a model similar to those used in Dartois et al. (2015, 2018). An estimate is obtained by adjusting a fit that includes the electronic sputtering for the thinner film and setting the previously determined destruction cross section to 5.45 ± 1.5 × 10−13 cm2 ion−1. We obtain 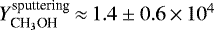 sputtered CH3OH/ion. The QMS intensities are shown, scaled by a global factor, at selected masses that we used to follow carbon dioxide m = 44, methanol m = 32, m = 31, and m = 28 (mainly CO with lower contributions from H2CO, CO2) upon irradiation. The ratio of the m = 32 to m = 31 masses is shown as a function of the fluence. This ratio (grey) is almost constant and is compared to the mass-pattern ratio of pure methanol during the preparation of the ice film by injection of methanol in the chamber (dotted line) for each experiment. This constancy tells us that the contribution of the direct desorption of metoxy and/or hydroxymethyl radical species (CH3O, CH2OH) from the ice is at most a small contribution to the signal because it would imply a marked decrease in this ratio. The relative intensities of the CO to CH3OH masses from the QMS at a given fluence change with the initial ice thickness because CO is produced by the radiolysis and is also more mobile. Measured gaseous CO can arise from a greater depth than CH3OH, and the CO to CH3OH gaseous ratio at comparable fluences therefore decreases with the initial thickness of the film. This can also be inferred from the IR spectra because in the case of the thinner film, the radiolytically produced CO does not accumulate in the film, but desorbes almost entirely immediately from the film.
sputtered CH3OH/ion. The QMS intensities are shown, scaled by a global factor, at selected masses that we used to follow carbon dioxide m = 44, methanol m = 32, m = 31, and m = 28 (mainly CO with lower contributions from H2CO, CO2) upon irradiation. The ratio of the m = 32 to m = 31 masses is shown as a function of the fluence. This ratio (grey) is almost constant and is compared to the mass-pattern ratio of pure methanol during the preparation of the ice film by injection of methanol in the chamber (dotted line) for each experiment. This constancy tells us that the contribution of the direct desorption of metoxy and/or hydroxymethyl radical species (CH3O, CH2OH) from the ice is at most a small contribution to the signal because it would imply a marked decrease in this ratio. The relative intensities of the CO to CH3OH masses from the QMS at a given fluence change with the initial ice thickness because CO is produced by the radiolysis and is also more mobile. Measured gaseous CO can arise from a greater depth than CH3OH, and the CO to CH3OH gaseous ratio at comparable fluences therefore decreases with the initial thickness of the film. This can also be inferred from the IR spectra because in the case of the thinner film, the radiolytically produced CO does not accumulate in the film, but desorbes almost entirely immediately from the film.
Integrated band strengths used in the analysis.
3.2 CH3OH:H2O
H2O:CH3O (100:122)
A mixture of methanol and water-ice with equivalent proportions (H2O:CH3OH-100:122) was irradiated. The recorded IR spectra and their evolution as a function of the ion fluence are shown in Fig. 3. Using the C-O stretching mode of methanol and the OH stretch of water ice (corrected for the methanol OH contribution), we report the column density of these molecules in the ice. The abundance ratio of gaseous methanol to water measured with the QMS duringthe ice deposition (blue star in Fig. 3, lower right panel) gives, within uncertainties, the same value as the ratio measured after deposition for the ice film in the IR (thus providing an independent measurement of the expected deposited ice-mixture ratio). The abundance ratios of gas- and solid-phase methanol to water evolve in parallel during irradiation. The measured abundance ratio is lower than the bulk of the ice film, showing that the methanol sputtering yield is influenced both by its sputtering and by radiolysis efficiencies. The mass spectra in Fig. 3 show that water and methanol are desorbed as soon as the ion irradiation begins (middle panel) and only decrease, whereas the m = 28 (gas-phase CO, CO2, and H2CO) intensity is lower at the beginning of irradiation, then rises, and finally decreases. The observed gaseous CO arises partly as a direct sputtered CH3OH radiolytic product and partly from the bulk of the ice at later times. In addition, because it is much more highly volatile, the desorbing CO can come from deeper layers of the ice film than water and methanol. This is shown by the amount of m = 28 that desorbs with respect to methanol, whereas the mean bulk ratio of these ices is lower (upper panel of Fig. 3) than what the QMS sees. The extent of the radiolysis of methanol with respect to the sputtering of intact molecules is discussed in the next section.
Water-rich methanol ice, H2O:CH3OH (100:6)
An experiment with an ice methanol water mixture was performed on a water-rich mixture, an H2O:CH3OH (100:6) ice film. This mixture, which is dominated by water ice, was chosen for two reasons: (i) to represent a typical integrated abundance ratio of methanol to water ice, as is observed along many lines of sights, when methanol is detected. (ii) We expect the sputtering behaviour to be dominated by the main matrix component, water. For this, the previous pure water-ice sputtering experiments can provide a good anchor point from which to start (Dartois et al. 2018). The recorded IR spectra and their evolution as a function of the ion fluence are shown in Fig. 4. Selected QMS mass intensities are also shown, which allows us to monitor the gas-phase evolutions. For water, m = 17 and m = 18 were used. For methanol, only the m = 31 mass was used. In contrast to the previous experiment, m = 32 cannot be used because it is higher than expected from methanol fragmentation and its trend is flatter, closer to the trend of gas-phase water. This suggests that the m = 32 mass is dominated by an O2 (or H2O2 fragments) contribution that arises from the radiolysis of the main component of the ice, water. The other masses of the methanol fragmentation pattern are affected by other species (m = 30, 29: H2CO and fragments, m = 28: CO and H2CO fragments). Mass m = 28 was also followed to monitor the contribution of CO (main contributor, it also contains less important contributions from the H2CO and CH3OH fragmentation pattern). The abundance ratio of gaseous methanol to water measured with the QMS during the ice deposition (blue star in Fig. 4, lower right panel) gives, within uncertainties, a slightly higher value than the ratio measured after deposition for the ice film in the IR. The abundance ratios of gas- and solid-phase methanol towater evolve in parallel during the irradiation, as for the richer mixture, showing that the sputtering reflects a direct fraction of the ice abundance evolution of these species. The ratio seems slightly higher than for the mixture with equal proportions of methanol and water in the ice. This measurement suggests that with a lower abundance of methanol with respect to water ice, more intact molecules are sputtered. However, based on a single mass m = 31 and given the low S/N of the QMS measurement, the QMS uncertainty on this methanol ice mixture is high and needs to be better constrained by additional measurements in the future.
 |
Fig. 2 Pure methanol ice-film experiments with various initial film thicknesses (thick to thin from top to bottom). Left panels: evolution of the CH3OH IR spectra as a function of fluence. Right, top panels: ice column density measurements from IR spectra (circles). The column densities are estimated using the integrated cross sections from Table 2. The purple dashed line is the fit to the destruction cross section of methanol (top 5 ± 1 × 10−13 cm2 ion−1, middle 5.9 ± 1 × 10−13 cm2 ion−1). For the thinner film (bottom panels), the onset of dominant sputtering appears for a column density lower than ≈ 1016 cm−2. Right, lower panels: QMS scaled intensities at selected masses that were used to follow carbon dioxide m = 44, methanol m = 32, m = 31, and m = 28 (CO, H2CO, and CO2) during irradiation. The mass-pattern ratio for methanol m = 32/m = 31 (grey curves) is compared to the ratio measured for pure methanol during the ice-film preparation (dotted line). See text for details. |
 |
Fig. 3 Left: H2O:CH3OH (100:122) ice film. Evolution of the IR spectra as a function of fluence. Right, top panel: ice column density measurements from IR spectra. The black dashed lines represent the fits to the destruction cross section of water and methanol. Middle panel: QMS-normalised signals we used to follow the relative abundance of water (m = 17+m = 18), methanol (m = 32 and m = 31), and carbon monoxide (m = 28) upon irradiation. See text for details. m = 28 increases atthe beginning because it is mainly composed of fragments from the radiolytic products of the initial ice mixture. Lower panel: CH3OH/H2O abundance ratio deduced from the IR spectra of the ice film as a function of fluence (red dots, the uncertainty is filled in in red). Comparison with the QMS-determined abundance ratio of the same desorbed molecules (dark blue line, from m = 32+m = 31 for methanoland m = 17+m = 18 for water). The blue and cyan star indicates the gas ratio measurement with the QMS during the ice film deposition. The dashed blue and cyan line represents Eq. (6); the uncertainty is filled in blue. |
3.3 Radiolysis versus sputtering
For semi-infinite thick ice films, the evolution with the fluence (F) of the species column densities (N) in the ice film (monitored with the IR measurements) satisfies the following differential equation:
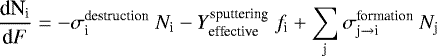 (3)
(3)
for species i, where 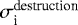 is the radiolytic destruction cross section.
is the radiolytic destruction cross section. 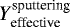 is the semi-infinite thickness effective-sputtering yield for the ice mixture we considered. It corresponds to the total number of sputtered molecules per ion, including the intact and the radiolysed ions. fi is the fraction of species i in the ice surface layers that are involved in the sputtering, and
is the semi-infinite thickness effective-sputtering yield for the ice mixture we considered. It corresponds to the total number of sputtered molecules per ion, including the intact and the radiolysed ions. fi is the fraction of species i in the ice surface layers that are involved in the sputtering, and 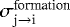 is the induced radiolytic production of species i from another species j in the ice film.
is the induced radiolytic production of species i from another species j in the ice film.
For i = CH3OH, the induced radiolytic production from the daughter products is of lesser importance, and Eq. (3) can be approximated by
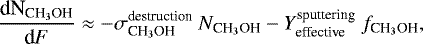 (4)
(4)
where 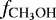 is the fraction of methanol molecules in the sputtered ice layers (i.e. the fraction in the ice composition).
is the fraction of methanol molecules in the sputtered ice layers (i.e. the fraction in the ice composition).
Adopting a cylindrical geometry for the sputtered volume (e.g. Dartois et al. 2018, Fig. 1), we define Nd as the column density of molecules in the ice film that corresponds to the depth of desorption (i.e. the height of the cylinder). For methanol molecules mixed in a water matrix, 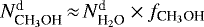 . The sputtering efficiency, that is, the observed yield in the electronic regime of stopping power, therefore depends on the fraction of molecules radiolytically processed during the ion interaction within this volume of ice with respect to the net amount of molecules contained in this (“ejected”) volume. We consider the product
. The sputtering efficiency, that is, the observed yield in the electronic regime of stopping power, therefore depends on the fraction of molecules radiolytically processed during the ion interaction within this volume of ice with respect to the net amount of molecules contained in this (“ejected”) volume. We consider the product 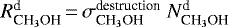 .
.
It is obvious that if 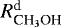 approaches the value of
approaches the value of 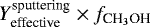 , most sputtered species should come out as fragments from the radiolysis.
, most sputtered species should come out as fragments from the radiolysis.
The QMS abundance ratio measurements, which allow us to access the fraction of intact sputtered molecules χ in the gas phase, should reflect this, and to first order,
 (5)
(5)
The radiolytic destruction cross sections 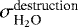 of water and
of water and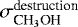 of methanol were obtained to first order by fitting the IR measurement when the film is thick enough for the sputtering to not contribute significantly to the IR evolution. Equation (5) may overestimate the radiolysis because the processes at the surface are not fully symmetrical with respect to the surface interface (e.g. secondary electrons produced close to the surface may escape before to act radiolytically on neihbouring species).
of methanol were obtained to first order by fitting the IR measurement when the film is thick enough for the sputtering to not contribute significantly to the IR evolution. Equation (5) may overestimate the radiolysis because the processes at the surface are not fully symmetrical with respect to the surface interface (e.g. secondary electrons produced close to the surface may escape before to act radiolytically on neihbouring species).
For theice-mixture experiment shown in Fig. 3, the fitted CH3OH cross section is 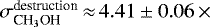 10−13 cm2 ion−1 (i.e. close to the pure CH3OH cross section of
10−13 cm2 ion−1 (i.e. close to the pure CH3OH cross section of 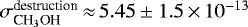 cm2 ion−1 fitted for thepure CH3OH irradiations shown in Fig. 2). The
cm2 ion−1 fitted for thepure CH3OH irradiations shown in Fig. 2). The 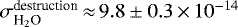 cm2/ion. The two fitted cross-section curves are shown overlaid as dashed lines in the right upper panel of Fig. 3.
cm2/ion. The two fitted cross-section curves are shown overlaid as dashed lines in the right upper panel of Fig. 3.
In the case of a water-rich ice mantle, the sputtering yield should be close to the yield of water ice. The water-ice sputtering yield is 2 ± 0.2 × 104 for this ion. The number of sputtered layers at this energy is about 30 ice monolayers, which corresponds to a column density of Nd ≈ 3 ± 0.6 × 1016 cm−2 (Dartois et al. 2018).
For this experiment, Eq. (5) reads
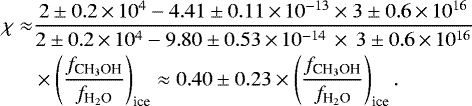 (6)
(6)
The expected percentage of intact methanol molecules that are ejected for this experiment is about 40%. The calculated evolution with time is represented by the blue dashed line in the right lower panel of Fig. 3, compared to the QMS measurement, which is shown as the solid blue line.
For theice-mixture experiment shown in Fig. 4, the fitted CH3OH cross section is 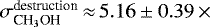 10−13 cm2 ion−1 (i.e. close to the pure CH3OH cross section of
10−13 cm2 ion−1 (i.e. close to the pure CH3OH cross section of 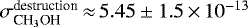 cm2 ion−1 fitted for thepure CH3OH irradiations shown in Fig. 2). The
cm2 ion−1 fitted for thepure CH3OH irradiations shown in Fig. 2). The 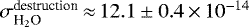 cm2/ion. The two fitted cross-section curves are shown overlaid as dashed lines in Fig. 4.
cm2/ion. The two fitted cross-section curves are shown overlaid as dashed lines in Fig. 4.
For this experiment, Eq. (5) reads
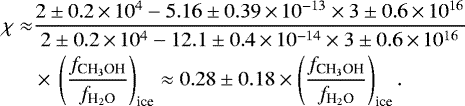 (7)
(7)
The expected percentage of intact methanol molecules that are ejected for this experiment is about 30% with respect to the bulk ice composition, with a higher relative uncertainty than for the previous experiment. The calculated evolution with irradiation time is represented by the blue dashed line in the right lower panel of Fig. 4. The QMS measurements are above this calculation, closer to 65%, which would mean that more methanol is preserved when it is less abundant and more diluted in the ice matrix.
 |
Fig. 4 Left: H2O:CH3OH (100:6) ice-film evolution of the IR spectra as a function of fluence. Right: H2O:CH3OH 100:6 ice-film experiment. Top panel: ice column density measurements from IR spectra. The black dashed lines represent the fits to the destruction cross section of water and methanol. Middle panel: QMS-normalised signals we used to follow the relative abundance of water (m = 17+m = 18), methanol (m = 31), and carbon monoxide (m = 28) upon irradiation. See text for details. CO increases initially because it is a radiolytic product of the ice mixture. Lower panel: CH3OH/H2O abundance ratio deduced from the IR spectra of the ice film as a function of fluence (red dots). Comparison with the QMS-determined abundance ratio of the same desorbed molecules (dark blue line). The blue and cyan star indicates the gas ratio measurement with the QMS during the ice-film deposition. The dashed blue and cyan line represents Eq. (7); the uncertainty is filled in blue. |
 |
Fig. 5 Average of the mass spectra that were recorded during the methyl acetate injection to form the ice film (orange histogram), which trace the QMS mass fragmentation pattern of pure methyl acetate. We also show the average of a few spectra thatwere recorded at the beginning of the ice-film irradiation (blue histogram). Both mass spectra are scaled to mass 74, which corresponds to ionised methyl acetate for comparison. This shows that masses 74, 59, and 43 can be used to monitor methyl acetate because the radiolysis with the ion produces most contributions to peaks at lower masses. See text for details. |
3.4 CH3 COOCH3
In order to explore the sputtering for an even larger COM, we performed an irradiation experiment with methyl acetate. The evolution of the C2H6O2 IR spectra, ice column densities, and QMS intensities as a function of fluence are displayed in Fig. 6. As for the methanol case, this pure measurement allows us to fit the bulk destruction cross section of methyl acetate from IR data for the considered ion, yielding 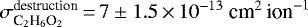 . We show in Fig. 5 the mass spectra recorded for methyl acetate (during the injection to form the ice film), which traces the QMS mass fragmentation pattern of pure methyl acetate, and the comparison with the average of a few spectra that were recorded at the beginning of the ice-film irradiation. The two mass spectra are scaled to mass 74, which corresponds to ionised methyl acetate, for comparison. This shows that masses 74, 59, and 43 can be used to monitor methyl acetate because the radiolysis with the ion mostly contributes to peaks at lower masses. The different QMS signals for the main mass pattern-fragments at masses 74, 59, and 43 for the experiment are displayed in the middle right panel of Fig. 6. The ratio between the largest fragment signals at masses 59 (CH3COO) and 43 (CH3CO) to the pure ionised species recorded at mass 74 are displayed as a function of irradiation (full lines) in the lower panel. The value measured at injection is added for comparison (dashed lines). The mass fragmentation pattern during irradiation for these higher mass fragments evolves close to the pattern that is measured during the gas-phase injection (i.e. without irradiation), thus showing that mostly intact CH3COOCH3 molecules dominate for these signals.
. We show in Fig. 5 the mass spectra recorded for methyl acetate (during the injection to form the ice film), which traces the QMS mass fragmentation pattern of pure methyl acetate, and the comparison with the average of a few spectra that were recorded at the beginning of the ice-film irradiation. The two mass spectra are scaled to mass 74, which corresponds to ionised methyl acetate, for comparison. This shows that masses 74, 59, and 43 can be used to monitor methyl acetate because the radiolysis with the ion mostly contributes to peaks at lower masses. The different QMS signals for the main mass pattern-fragments at masses 74, 59, and 43 for the experiment are displayed in the middle right panel of Fig. 6. The ratio between the largest fragment signals at masses 59 (CH3COO) and 43 (CH3CO) to the pure ionised species recorded at mass 74 are displayed as a function of irradiation (full lines) in the lower panel. The value measured at injection is added for comparison (dashed lines). The mass fragmentation pattern during irradiation for these higher mass fragments evolves close to the pattern that is measured during the gas-phase injection (i.e. without irradiation), thus showing that mostly intact CH3COOCH3 molecules dominate for these signals.
3.5 CH3 COOCH3:H2O
The methyl acetate mixed experiment was performed on a water-rich mixture, an H2O:CH3COOCH3 (100:13) ice film. This mixture is dominated by water ice and was chosen for the same reasons as explained previously for methanol, in particular, because we expect such large COMs to be minor components with respect to water ice (and this mixture is already quite rich for such a large COM in astrophysics). The recorded IR spectra and their evolution as a function of the ion fluence are shown in Fig. 7. We report the column density of these molecules in the ice using a C-O stretching mode of methyl acetate and the OH stretch of water ice. The selected QMS mass intensities are shown, which allows us to monitor the gas-phase evolution of water (m = 17+ m = 18) and methyl acetate (m = 74, 59, and 43 masses are identified as stable in the methyl acetate fragmentation pattern during deposition and at the beginning of irradiation). Mass m = 28 was also followed to monitor the contribution of CO (main contributing species that also contains less important contributions from the CH3CO, CH3CO2, CH3COOCH3 fragmentation pattern). The destruction cross section of CH3COOCH3 obtained for this mixture from the IR is evaluated to 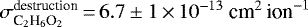 . The observed QMS abundance ratio of CH3COOCH3/H2O in experiment 29W1BIS (Fig. 7, panel with the abundance ratios) evolves in parallel with the species ratio of the ice film thatis observed in the IR at any time of the irradiation. The bulk composition of the ice evolves with the fluence because of the radiolytic processes that occur inside, but the sputtering, which is a surface process, probes the ice composition.
. The observed QMS abundance ratio of CH3COOCH3/H2O in experiment 29W1BIS (Fig. 7, panel with the abundance ratios) evolves in parallel with the species ratio of the ice film thatis observed in the IR at any time of the irradiation. The bulk composition of the ice evolves with the fluence because of the radiolytic processes that occur inside, but the sputtering, which is a surface process, probes the ice composition.
4 Discussion
4.1 Methanol in interstellar ices
Observationally, no strong generic correlation exists between the column densities of CO ice and CH3OH (e.g. Whittet et al. 2011). Because of this lack of correlation, it is difficult if not problematic for an observer to predict a priori the observed methanol column density from the observed ice-mantle water, carbon dioxide, and carbon monoxide column densities for a given line of sight. This absence of a strong correlation is shown in Fig. 8, where we report the column densities of CH3OH/H2O versus H2O, CH3OH/CO versus CO, and theCH3OH versus CO for sources investigated in Whittet et al. (2011). After analysing this large dataset of CH3OH observations, the authors conclude that its concentration in the ices towards embedded stars show order-of-magnitude object-to-object variations. The observations seem to show that the occurrence of methanol ice requires high column densities of matter, which generally corresponds to a (possibly anterior) very cold or deeply protected environment phase (with AV > 15, see Fig. 7 of Boogert et al. 2015). This is a necessary but maybe not sufficient condition because some lines of sight show stringent upper limits even at AV > 30. The launch of the James Webb Space Telescope (JWST) is expected to help push these upper limit constraints towards detections, to properly quantify source-to-source variations.
It has long been hypothesised that methanol ice forms from the direct hydrogenation of CO ice. In which phase the methanol is observed in interstellar ice is debated through comparisons to laboratory data (e.g., Penteado et al. 2015; Cuppen et al. 2011, and references therein). Definite observational proof of the statement that this is the unique (or at least the by far dominant) pathway to methanol formation is still lacking. Furthermore, the observed interstellar profiles of the carbon dioxide bending mode in some lines of sight can be reproduced in the laboratory and explained by the formation of methanol-carbon dioxide intermolecular complexes, which would suggest that CO2 is also part of the methanol environment. The formation of such complexes is affected by a dominant fraction of water ice, in which case the water molecules control the structure of the ice and inhibit the formation of such complexes (Dartois et al. 1999; Ehrenfreund et al. 1999; Klotz et al. 2004).
CH3OH has been investigated with Spitzer space telescope observations in dense regions (Bottinelli et al. 2010). Botinelli and coworkers show in their Fig. 12 that most of the observed methanol C-O stretching-mode position versus full width at half-maximum (FWHM) is in a mantle whose composition is neither dominated by a H2O-rich nor by a CO-rich matrix. The methanol C-O stretching-mode position versus FWHM diagram for our experiments is reported in such a diagram in Fig. 9, together with these previous measurements and other laboratory data. This diagram shows that different ice-mantle mixtures are still compatible with the positions we observed, which encourages us to explore several alternatives to the ice-mantle composition in laboratory experiments.
 |
Fig. 6 Left: CH3COOCH3 ice-film experiment. Right, top panel: ice column density measurements from IR spectra. Middle panel: QMS-scaled intensities at selected masses we used to follow carbon dioxide (m = 44), methyl acetate (m = 74, 59, 43, 29, 15), and CO (m = 28) during irradiation. Lower panel: QMS signal ratios of the m = 43 (CH3CO) and m = 59 (CH3COO) biggest fragments to the m = 74 (ionised CH3COOCH3) are shown as a function of irradiation (full lines). The ratios stay reasonably constant, with a value close to the pre-irradiation value (dotted lines). See text for details. |
4.2 Stopping-power destruction cross-section dependency
Destruction cross sections for methanol ice have been reported for different stopping powers (Fig. 8, de Barros et al. 2011, and references therein). The dependency of this ice on the electronic stopping power follows a power law, σ ∝Sen. We used the data of this article and reanalysed some of the data. We excluded from the analysis the previously included 3 keV He+ measurement for which the nuclear stopping power (Sn) is of the same order of magnitude as the electron stopping power (Se, this point therefore mixes two different regimes), as well as the proton irradiation at 0.8 MeV value (Gerakines et al. 2001) because the cross section was not measured for a pure CH3OH ice but in a mixture that also contained H2O and CO2. We reanalysed the data reported in Baratta et al. (2002) for 30 keV He+ (because the authors did not provide a destruction cross section) by fitting the data presented in their Fig. 7. This provided a cross section 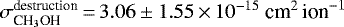 . We used the stopping power in the electron regime calculated for this ion using the SRIM software package (Ziegler et al. 2010, The stopping and range of ions in matter), leading to 39.5 × 10−15 eV molecules−1 cm2. We added the mean destruction cross section for the 16 K measurements of two methanol near-IR transitions with a 200 keV H+ projectile by Brunetto et al. (2005), which provided a mean cross section of
. We used the stopping power in the electron regime calculated for this ion using the SRIM software package (Ziegler et al. 2010, The stopping and range of ions in matter), leading to 39.5 × 10−15 eV molecules−1 cm2. We added the mean destruction cross section for the 16 K measurements of two methanol near-IR transitions with a 200 keV H+ projectile by Brunetto et al. (2005), which provided a mean cross section of 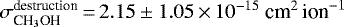 . We used the electron stopping power calculated with the SRIM package, that is, 39.4 × 10−15 eV molecules−1 cm2. The resulting regression fit on the data gives a dependency of
. We used the electron stopping power calculated with the SRIM package, that is, 39.4 × 10−15 eV molecules−1 cm2. The resulting regression fit on the data gives a dependency of 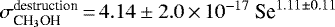 , which we show in the upper panel of Fig. 10. The methanol destruction radiochemical yield
, which we show in the upper panel of Fig. 10. The methanol destruction radiochemical yield 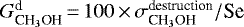 , that is, the number of methanol molecules that are destroyed by radiation per 100 eV of absorbed energy, and its evolution, can be derived from the previous fit. We show this in the lower panel of Fig. 10. Its evolution shows that at lower stopping power in the electron regime, a higher fraction of methanol is preserved, and the fraction of mean sputtered intact molecules integrated over the cosmic-ray distribution should therefore be higher.
, that is, the number of methanol molecules that are destroyed by radiation per 100 eV of absorbed energy, and its evolution, can be derived from the previous fit. We show this in the lower panel of Fig. 10. Its evolution shows that at lower stopping power in the electron regime, a higher fraction of methanol is preserved, and the fraction of mean sputtered intact molecules integrated over the cosmic-ray distribution should therefore be higher.
 |
Fig. 7 Left: H2O:CH3COOCH3 100:13 ice-film experiment. Right, top panel: ice column density measurements from IR spectra. The black dashed lines represent the fits to the destruction cross section of water and CH3COOCH3. Middle panel: QMS-normalised masses we used to follow water, methanol, and m = 28 (CO, H2CO, and CO2) upon irradiation. m = 28 increases atthe beginning because it is mainly composed of fragments from the radiolytic products of the initial ice mixture. Lower panel: CH3COOCH3/H2O abundance ratio deduced from the IR spectra of the ice film as a function of fluence (red dots). Comparison with the QMS-determined abundance ratio of the same desorbed molecules (dark blue line). The blue and cyan star indicates the gas ratio measurement with the QMS during the ice-film deposition. |
 |
Fig. 8 Correlation plots for the ice column density for CH3OH/H2O vs. H2O, CH3OH/CO vs. CO, and the CH3OH vs. CO for the sources presented in Whittet et al. (2011, red squares) and Bottinelli et al. (2010, green circles). |
4.3 Radiolytic destruction versus sputtering dependency as a function of energy and stopping power
The dependency of our results on the stopping power is an important question for a large distribution of energies in cosmic-ray particles. The relevant astrophysical criterion is the fraction of intact molecules that are sputtered from an interstellar ice mantle, or in other words, the radiolytic to sputtering efficiency as a function of energy. As discussed above, to first order, the number of molecules that are dissociated in the sputtered volume for a species X is
 |
Fig. 9 Methanol C-O stretching-mode position–FWHM diagram of the experiments performed in this work, compared to ISM measurements presented in Bottinelli et al. (2010) (yellow squares), as well as the CO-rich point given in this article, and position FWHM from ice spectra of various compositions from the Leiden ice database, extracted in the same way as for our irradiation measurements. |
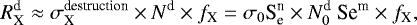
where Nd is the column density of molecules in the ice film, which corresponds to the depth of the desorption when we assume that all the molecules come from the same sputtered volume. σ0 Sen is the dependency of the destruction cross section with the stopping power in the electron regime, as shown and discussed in the previous section. We also expect the depth dependency to follow a power law, with a power-law index m. The sputtered molecule yield is
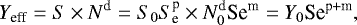
where S is the surface (cm2) of a sputtering “cylinder”.
The fraction of dissociated to total sputtered molecules in the sputtered volume is then
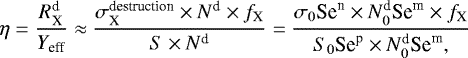 (8)
(8)
where the dependency of the different parameters with the stopping power in the electronic regime is specified. Thus,
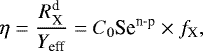 (9)
(9)
where C0 is a constant. From previous measurements, we know that the sputtering yield evolves quadratically with respect to the stopping power in the electron regime for a large majority of molecular cryogenic solids (e.g. H2O, CO2, and CO, Rothard et al. 2017), thus p + m ≈ 2, then p ≈ 2 − m.
In general, the measured and adjusted destruction cross sections for ices at low temperature show a power-law dependency with 1 < n < 1.5, for example, CH3OH, n = 1.1, this work; CO2 (n = 1.1, Fig. 5, Mejía et al. 2015) as a function of the electronic stopping power. As discussed in Dartois et al. (2018), experiments and thermal spike models of the phase transformation induced by the ion track in insulators predict a dependency of the radius r of the cross section that evolves as 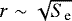 , where Se = dE∕dx is the deposited energy per unit path length (e.g. Lang et al. 2015; Toulemonde et al. 2000; Szenes 1997), and with a threshold in
, where Se = dE∕dx is the deposited energy per unit path length (e.g. Lang et al. 2015; Toulemonde et al. 2000; Szenes 1997), and with a threshold in 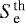 to be determined. In this case, this implies that m ≈ 1. When we combine these arguments, we find
to be determined. In this case, this implies that m ≈ 1. When we combine these arguments, we find
![\begin{align*} \eta = \frac{{R}^{\textrm{d}}_{\textrm{X}}}{{Y}_{\textrm{eff}}} = {C}_{0} \textrm{Se}^{[0-0.5]} \times {f}_{\textrm{X.}} \end{align*}](/articles/aa/full_html/2019/07/aa34787-18/aa34787-18-eq38.png) (10)
(10)
Within this regime, the fraction of dissociated molecules in the sputtered volume will therefore not strongly depend on the stopping power and will decrease at lower stopping power in the electron regime, as shown in the lower panel of Fig. 10. The majority of the molecules, even for COMs, should be sputtered intact, in contrast to VUV photodesorption.
4.4 Sputtering rates
Methanol in water ice
Assuming that the fraction of dissociated molecules does not depend on the stopping power, we calculated the astrophysical sputtering rate in the same way as discussed in Dartois et al. (2015), using Eq. (5). The result is shown in Fig. 11 for the measured fractional methanol abundances in a water-dominated ice mantle as a function of different ionisation rates. The filled regions give the extent of the rate, including the measured uncertainties. We added to this figure an estimate of the relation between the expected secondary VUV photon flux and the ionisation rate, as discussed in Shen et al. (2004), under dense-cloud conditions when the external UV field is fully attenuated. We show a photodesorption rate of ~ 10−5/VUV photon, which approximately corresponds to the estimated pure methanol-ice desorption in Bertin et al. (2016), whereas Cruz-Diaz et al. (2016) obtained an upper limit of about < 3 × 10−5/VUV photon.
Methanol in carbon monoxide ice
When methanol is mixed with CO ice, the photodesorption rate is considerably lower than for pure methanol, with fewer than ~ 10−6/VUV photon (Bertin et al. 2016). In thermal desorption studies of mixtures with a temperature-programmed desorption (TPD) technique, with heating rates of about 10 K min−1 (e.g. Ligterink et al. 2018), methanol does not desorb efficiently, while CO sublimates easily. Unlike TPDexperiments, the rate of the heating spike that is induced by cosmic rays may reach 1012 –1014 K s−1, and most of the embedded methanol molecules may be driven by the sudden sputtering of the main ice constituents. To estimate the expected sputtering magnitude if methanol were embedded in a CO matrix and driven by the thermal spike, we therefore replaced H2O by CO in Eq. (5). The effective yield for a pure CO ice can be estimated from the equation in Fig. 6 of Seperuelo Duarte et al. (2010), Y = 0.033 ×Se2, with an Se of about 2920 × 10−15 eV∕(CO/cm2) which was estimated with the SRIM package for a density of CO ice of 0.8 g cm−3 (Roux et al. 1980; Bouilloud et al. 2015). This led to about 2.8 × 105 CO/ion. In the absence of constraints and when we assume an aspect ratio close to 1 for the sputtered volume, this corresponds to about 66 CO layers, or about 4.4 × 1016 cm−2 in equivalent column density for the sputtered depth. The CO destruction cross section can be evaluated to lie between 1.7 and 2.3 × 10−13 cm2 from previous measurements when we assume a dependency between Se1 and Se3∕2 based on the previous 50 MeV Ni experiment reported by Seperuelo Duarte et al. (2010). As reported in Eq. (5), we expect 95% of the bulk ice CH3OH/CO to be sputtered intact. Even with an aspect ratio of 5, which favours methanol radiolysis more, the factor decreases only to 70%. The global rates are therefore about a factor 40 higher than for a water-ice matrix. Following the arguments we discussed above, the sputtering rates by cosmic rays for methanol that is embedded in a CO or a CO2 matrix will be order(s) of magnitude higher than our measurements in water ice.
 |
Fig. 10 Upper panel: methanol destruction cross section as a function of stopping power in the electron regime. Red diamonds show data from de Barros et al. (2011), the magenta triangle represents 30 keV He+ (Baratta et al. 2002), the green circle shows 200 keV H+ (Brunetto et al. 2005), and the blue square shows data from this work. The dashed line represent the best least-squares fit to the cross section, and the filled region delineates the 95% interval confidence. See text for details. Lower panel: corresponding methanol radiochemical destruction yield. |
Larger species
As discussed in Sect. 3.3, if 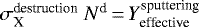 , most sputtered species are expected to come out as fragments from the radiolysis. The limiting destruction cross section from this equality and the ion we used in our experiments for a water rich mixture should be
, most sputtered species are expected to come out as fragments from the radiolysis. The limiting destruction cross section from this equality and the ion we used in our experiments for a water rich mixture should be 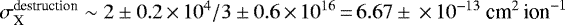 , which is close to the cross sectionthat was evaluated for methyl acetate. However, the measurements displayed in Fig. 7 show that a large portion of CH3COOCH3 molecules are sputtered intact, that is, the radiolysis of molecules that are ejected from the surface seems less efficient. The sputtering process of intact molecules when the COM is diluted in the ice also seem higher than expected from Eq. (5).
, which is close to the cross sectionthat was evaluated for methyl acetate. However, the measurements displayed in Fig. 7 show that a large portion of CH3COOCH3 molecules are sputtered intact, that is, the radiolysis of molecules that are ejected from the surface seems less efficient. The sputtering process of intact molecules when the COM is diluted in the ice also seem higher than expected from Eq. (5).
Simple physical assumptions were made in the calculations we presented in Sect. 3.3 for instance for the adopted constant effective sputtering yield, the constant depth of desorption for the mixtures, the cylindrical shape for the sputtered volume, or that the cylindric radius assumed for the sputtered volume is the same for the radiolysis radius. For the latter, it hasall reasons to be different. The ejected fragments that are observed can occur in the direct excitation process in the core of the track (infratrack), or they may be partly the result of some of the secondary (delta-) electron processing, but the sputtering of intact molecules likely occurs from a much larger radius. These assumptions are of first order and too simple to represent the complexity of these mixtures. The calculations presented in Sect. 3.3 explain the order of magnitude of intact sputtered molecules. They also follow the decrease in measured ratio from QMS data of the gas phase for intact species that are sputtered upon irradiation, in agreement with the ice compositionin the bulk, as monitored by the IR measurements. However, they probably underestimate the sputtering of intact species because even larger COMs molecules can be sputtered intact by swift heavy ions (e.g. leucine, M = 131 u, ergosterol, M = 393 u, and even larger, Hedin et al. 1987; Håkansson et al. 1982; Håkansson & Sundqvist 1989), and calls for the development of a more advanced model.
 |
Fig. 11 Methanol in a water-ice matrix sputtering rate as a function of the cosmic-ray ionisation rate. The different curves correspond to the methanol fraction with respect to the water ice that we measured here. This range covers most of the observational dispersion. This sputtering rate must formally be multiplied by two because the cosmic-ray projectiles move through the interstellar grains. The upper axis gives an estimate of the evolution of the corresponding secondary VUV photon flux (e.g. Shen et al. 2004; Prasad & Tarafdar 1983), given for comparison with photodesortion rates. The rate corresponding to ~ 10−5 CH3OH/VUV photon for a pure methanol-ice film is shown in green. This is the order of magnitude measured by Bertin et al. (2016), whereas Cruz-Diaz et al. (2016) obtained an upper limit that is three times higher. Cosmic-ray sputtering rates for methanol that is embedded in a CO matrix would be orders of magnitude higher because CO desorbs more efficiently. |
5 Conclusions
We have measured the electron sputtering yield of ice mixtures including COMs that are observed in the solid phase or in the gas phase in the ISM by simulating methanol and methyl acetate embedded in water-rich ice mantles at 10 K exposed to interstellar cosmic rays. We conclude that for COMs, whose abundance is generally a small fraction of the main ice-matrix component, a large portion of intact molecules are desorbed by cosmic rays and with a sputtering efficiency that is close to that of the ice matrix.
Our measurements were performed at a single electron stopping power, but because COMs are in most cases a minor component with respect to the water-ice dominating mantle, the measured quadratic water-ice sputtering-yield dependency on the stopping power can be used to extrapolate the effective yield in a distribution of cosmic rays in an astrophysical medium, as was previously done for pure water ice. The investigation made in this article is a step in the development of a more systematic study of the sputtering efficiency of COMs (methanol and larger molecules) in various ice matrices that are relevant for interstellar contexts. The next experiments will probe mixtures of methanol-CO2 and methanol-CO. Based on the experiments performed in this work, we expect the same qualitative behaviour, that is, that the sputtering yield is dominated by the effective yield of the matrix, which is higher (more efficient by up to orders of magnitude for CO) than for H2O, and that a large portion will be ejected intact. Measurement campaigns are also scheduled to explore the composition and depth dependency parameters in order to refine the energy dependency of the parameters on this process.
The calculations indicate that cosmic-ray sputtering dominates secondary photons for CH3OH desorption. This is most probably a general case for larger COMs as well.
Acknowledgements
This work was supported by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES, by the P2IO LabEx program: “Evolution de la matière du milieu interstellaire aux exoplanètes avec le JWST” and the ANR IGLIAS, grant ANR-13-BS05-0004 of the French Agence Nationale de la Recherche. Experiments performed at GANIL. We thank T. Madi, T. Been, J.-M. Ramillon, F. Ropars and P. Voivenel for their invaluable technical assistance. A.N.A. acknowledges funding from INSERM-INCA (Grant BIORAD) and Région Normandie fonds Européen de développement régional-FEDER Programmation 2014–2020. We would like to acknowledge the anonymous referee for very constructive comments that significantly improved the content of our article, as well as the editor M. Tafalla and language editor A. Peters.
References
- Augé, B., Been, T., Boduch, P., et al. 2018, Rev. Sci. Instrum., 89, 075105 [NASA ADS] [CrossRef] [Google Scholar]
- Bacmann, A., Taquet, V., Faure, A., Kahane, C., & Ceccarelli, C. 2012, A&A, 541, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baratta, G. A., Leto, G., & Palumbo, M. E. 2002, A&A, 384, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, M., Romanzin, C., Doronin, M., et al. 2016, ApJ, 817, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Boogert, A. C. A., Gerakines, P. A., & Whittet, D. C. B. 2015, ARA&A, 53, 541 [Google Scholar]
- Bottinelli, S., Boogert, A. C. A., Bouwman, J., et al. 2010, ApJ, 718, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Bouilloud, M., Fray, N., Bénilan, Y., et al. 2015, MNRAS, 451, 2145 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetto, R., Baratta, G. A., Domingo, M., & Strazzulla, G. 2005, Icarus, 175, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, C., Caselli, P., Fontani, F., et al. 2017, ApJ, 850, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Cruz-Diaz, G. A., Martín-Doménech, R., Muñoz Caro, G. M., & Chen, Y.-J. 2016, A&A, 592, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuppen, H. M., Penteado, E. M., Isokoski, K., van der Marel, N., & Linnartz, H. 2011, MNRAS, 417, 2809 [NASA ADS] [CrossRef] [Google Scholar]
- Dartois, E., Demyk, K., d’Hendecourt, L., & Ehrenfreund, P. 1999, A&A, 351, 1066 [NASA ADS] [Google Scholar]
- Dartois, E., Augé, B., Boduch, P., et al. 2015, A&A, 576, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dartois, E., Chabot, M., Id Barkach, T., et al. 2018, A&A, 618, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Barros, A. L. F., Domaracka, A., Andrade, D. P. P., et al. 2011, MNRAS, 418, 1363 [NASA ADS] [CrossRef] [Google Scholar]
- D’Hendecourt,L. B., & Allamandola, L. J. 1986, A&AS, 64, 453 [Google Scholar]
- Ehrenfreund, P., Kerkhof, O., Schutte, W. A., et al. 1999, A&A, 350, 240 [NASA ADS] [Google Scholar]
- Gerakines, P. A., Schutte, W. A., Greenberg, J. M., & van Dishoeck, E. F. 1995, A&A, 296, 810 [NASA ADS] [Google Scholar]
- Gerakines, P. A., Moore, M. H., & Hudson, R. L. 2001, J. Geophys. Res., 106, 33381 [NASA ADS] [CrossRef] [Google Scholar]
- Håkansson, P.,& Sundqvist, B. U. R. 1989, Vacuum, 39, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Håkansson, P., Kamensky, I., & Sundqvist, B. 1982, Nucl. Instrum. Methods Phys. Res., 198, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Hedin, A., Hkansson, P., Salehpour, M., & Sundqvist, B. U. R. 1987, Phys. Rev. B, 35, 7377 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, G. J., Person, W. B., & Brown, K. G. 1975, J. Chem. Phys., 62, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Vasyunin, A. I., Caselli, P., et al. 2016, ApJ, 830, L6 [Google Scholar]
- Jørgensen, J. K., van der Wiel, M. H. D., Coutens, A., et al. 2016, A&A, 595, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaur, J., Naghmaa, R., & Bobby, A. 2015, RSC Adv., 5, 20090 [CrossRef] [Google Scholar]
- Klotz, A., Ward, T., & Dartois, E. 2004, A&A, 416, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lang, M., Devanathan, R., Toulemonde, M., & Trautmann, C. 2015, Curr. Opin. Solid State Mater. Sci., 19, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Lefloch, B., Bachiller, R., Ceccarelli, C., et al. 2018, MNRAS, 477, 4792 [NASA ADS] [CrossRef] [Google Scholar]
- Ligterink, N. F. W., Walsh, C., Bhuin, R. G., et al. 2018, A&A, 612, A88 [Google Scholar]
- López-Sepulcre, A., Sakai, N., Neri, R., et al. 2017, A&A, 606, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maté, B., Gálvez, Ó., Herrero, V. J., & Escribano, R. 2009, ApJ, 690, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Mejía, C., Bender, M., Severin, D., et al. 2015, Nucl. Instrum. Methods Phys. Res. B, 365, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Minissale, M., Moudens, A., Baouche, S., Chaabouni, H., & Dulieu, F. 2016, MNRAS, 458, 2953 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Lauck, T., & Graninger, D. 2014, ApJ, 788, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Palumbo, M. E., Castorina, A. C., & Strazzulla, G. 1999, A&A, 342, 551 [NASA ADS] [Google Scholar]
- Penteado, E. M., Boogert, A. C. A., Pontoppidan, K. M., et al. 2015, MNRAS, 454, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Prasad, S. S., & Tarafdar, S. P. 1983, ApJ, 267, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Rothard, H., Domaracka, A., Boduch, P., et al. 2017, J. Phys. B At. Mol. Phys., 50, 062001 [Google Scholar]
- Roux, J. A., Wood, B. E., Smith, A. M., & Plyer, R. R. 1980, Final Report, 1 Oct. 1978–1 Sep. 1979 ARO, Inc., Arnold Air Force Station, TN, USA [Google Scholar]
- Sandford, S. A., & Allamandola, L. J. 1993, ApJ, 417, 815 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Seperuelo Duarte, E., Domaracka, A., Boduch, E., et al. 2010, A&A, 512, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, C. J., Greenberg, J. M., Schutte, W. A., & van Dishoeck, E. F. 2004, A&A, 415, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soma, T., Sakai, N., Watanabe, Y., & Yamamoto, S. 2018, ApJ, 854, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Szenes, G. 1997, Nucl. Instrum. Methods Phys. Res. B, 122, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Tercero, B., Kleiner, I., Cernicharo, J., et al. 2013, ApJ, 770, L13 [Google Scholar]
- Toulemonde, M., Dufour, C., Meftah, A., & Paumier, E. 2000, Nucl. Instrum. Methods Phys. Res. B, 166, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyunina, T., Vasyunin, A. I., Herbst, E., et al. 2014, ApJ, 780, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Vinodkumar, M., Korot, K., & Vinodkumar, P. C. 2011, Int. J. Mass Spectrom., 305, 26 [CrossRef] [Google Scholar]
- Whittet, D. C. B., Cook, A. M., Herbst, E., Chiar, J. E., & Shenoy, S. S. 2011, ApJ, 742, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Ziegler, J. F., Ziegler, M. D., & Biersack, J. P. 2010, Nucl. Instrum. Methods Phys. Res. B, 268, 1818 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Average of the mass spectra that were recorded during the methanol injection that was meant to form the ice film (orangehistogram), tracing the QMS mass-fragmentation pattern of pure methanol; average of a few spectra that were recorded at the beginning of the ice-film irradiation (blue histogram). Both mass spectra are scaled to mass 32 for comparison.This shows that masses 32 and 31 can be used to monitor methanol because the radiolysis with the ion mainly contributes to peaks at lower masses. See text for details. |
| In the text | |
 |
Fig. 2 Pure methanol ice-film experiments with various initial film thicknesses (thick to thin from top to bottom). Left panels: evolution of the CH3OH IR spectra as a function of fluence. Right, top panels: ice column density measurements from IR spectra (circles). The column densities are estimated using the integrated cross sections from Table 2. The purple dashed line is the fit to the destruction cross section of methanol (top 5 ± 1 × 10−13 cm2 ion−1, middle 5.9 ± 1 × 10−13 cm2 ion−1). For the thinner film (bottom panels), the onset of dominant sputtering appears for a column density lower than ≈ 1016 cm−2. Right, lower panels: QMS scaled intensities at selected masses that were used to follow carbon dioxide m = 44, methanol m = 32, m = 31, and m = 28 (CO, H2CO, and CO2) during irradiation. The mass-pattern ratio for methanol m = 32/m = 31 (grey curves) is compared to the ratio measured for pure methanol during the ice-film preparation (dotted line). See text for details. |
| In the text | |
 |
Fig. 3 Left: H2O:CH3OH (100:122) ice film. Evolution of the IR spectra as a function of fluence. Right, top panel: ice column density measurements from IR spectra. The black dashed lines represent the fits to the destruction cross section of water and methanol. Middle panel: QMS-normalised signals we used to follow the relative abundance of water (m = 17+m = 18), methanol (m = 32 and m = 31), and carbon monoxide (m = 28) upon irradiation. See text for details. m = 28 increases atthe beginning because it is mainly composed of fragments from the radiolytic products of the initial ice mixture. Lower panel: CH3OH/H2O abundance ratio deduced from the IR spectra of the ice film as a function of fluence (red dots, the uncertainty is filled in in red). Comparison with the QMS-determined abundance ratio of the same desorbed molecules (dark blue line, from m = 32+m = 31 for methanoland m = 17+m = 18 for water). The blue and cyan star indicates the gas ratio measurement with the QMS during the ice film deposition. The dashed blue and cyan line represents Eq. (6); the uncertainty is filled in blue. |
| In the text | |
 |
Fig. 4 Left: H2O:CH3OH (100:6) ice-film evolution of the IR spectra as a function of fluence. Right: H2O:CH3OH 100:6 ice-film experiment. Top panel: ice column density measurements from IR spectra. The black dashed lines represent the fits to the destruction cross section of water and methanol. Middle panel: QMS-normalised signals we used to follow the relative abundance of water (m = 17+m = 18), methanol (m = 31), and carbon monoxide (m = 28) upon irradiation. See text for details. CO increases initially because it is a radiolytic product of the ice mixture. Lower panel: CH3OH/H2O abundance ratio deduced from the IR spectra of the ice film as a function of fluence (red dots). Comparison with the QMS-determined abundance ratio of the same desorbed molecules (dark blue line). The blue and cyan star indicates the gas ratio measurement with the QMS during the ice-film deposition. The dashed blue and cyan line represents Eq. (7); the uncertainty is filled in blue. |
| In the text | |
 |
Fig. 5 Average of the mass spectra that were recorded during the methyl acetate injection to form the ice film (orange histogram), which trace the QMS mass fragmentation pattern of pure methyl acetate. We also show the average of a few spectra thatwere recorded at the beginning of the ice-film irradiation (blue histogram). Both mass spectra are scaled to mass 74, which corresponds to ionised methyl acetate for comparison. This shows that masses 74, 59, and 43 can be used to monitor methyl acetate because the radiolysis with the ion produces most contributions to peaks at lower masses. See text for details. |
| In the text | |
 |
Fig. 6 Left: CH3COOCH3 ice-film experiment. Right, top panel: ice column density measurements from IR spectra. Middle panel: QMS-scaled intensities at selected masses we used to follow carbon dioxide (m = 44), methyl acetate (m = 74, 59, 43, 29, 15), and CO (m = 28) during irradiation. Lower panel: QMS signal ratios of the m = 43 (CH3CO) and m = 59 (CH3COO) biggest fragments to the m = 74 (ionised CH3COOCH3) are shown as a function of irradiation (full lines). The ratios stay reasonably constant, with a value close to the pre-irradiation value (dotted lines). See text for details. |
| In the text | |
 |
Fig. 7 Left: H2O:CH3COOCH3 100:13 ice-film experiment. Right, top panel: ice column density measurements from IR spectra. The black dashed lines represent the fits to the destruction cross section of water and CH3COOCH3. Middle panel: QMS-normalised masses we used to follow water, methanol, and m = 28 (CO, H2CO, and CO2) upon irradiation. m = 28 increases atthe beginning because it is mainly composed of fragments from the radiolytic products of the initial ice mixture. Lower panel: CH3COOCH3/H2O abundance ratio deduced from the IR spectra of the ice film as a function of fluence (red dots). Comparison with the QMS-determined abundance ratio of the same desorbed molecules (dark blue line). The blue and cyan star indicates the gas ratio measurement with the QMS during the ice-film deposition. |
| In the text | |
 |
Fig. 8 Correlation plots for the ice column density for CH3OH/H2O vs. H2O, CH3OH/CO vs. CO, and the CH3OH vs. CO for the sources presented in Whittet et al. (2011, red squares) and Bottinelli et al. (2010, green circles). |
| In the text | |
 |
Fig. 9 Methanol C-O stretching-mode position–FWHM diagram of the experiments performed in this work, compared to ISM measurements presented in Bottinelli et al. (2010) (yellow squares), as well as the CO-rich point given in this article, and position FWHM from ice spectra of various compositions from the Leiden ice database, extracted in the same way as for our irradiation measurements. |
| In the text | |
 |
Fig. 10 Upper panel: methanol destruction cross section as a function of stopping power in the electron regime. Red diamonds show data from de Barros et al. (2011), the magenta triangle represents 30 keV He+ (Baratta et al. 2002), the green circle shows 200 keV H+ (Brunetto et al. 2005), and the blue square shows data from this work. The dashed line represent the best least-squares fit to the cross section, and the filled region delineates the 95% interval confidence. See text for details. Lower panel: corresponding methanol radiochemical destruction yield. |
| In the text | |
 |
Fig. 11 Methanol in a water-ice matrix sputtering rate as a function of the cosmic-ray ionisation rate. The different curves correspond to the methanol fraction with respect to the water ice that we measured here. This range covers most of the observational dispersion. This sputtering rate must formally be multiplied by two because the cosmic-ray projectiles move through the interstellar grains. The upper axis gives an estimate of the evolution of the corresponding secondary VUV photon flux (e.g. Shen et al. 2004; Prasad & Tarafdar 1983), given for comparison with photodesortion rates. The rate corresponding to ~ 10−5 CH3OH/VUV photon for a pure methanol-ice film is shown in green. This is the order of magnitude measured by Bertin et al. (2016), whereas Cruz-Diaz et al. (2016) obtained an upper limit that is three times higher. Cosmic-ray sputtering rates for methanol that is embedded in a CO matrix would be orders of magnitude higher because CO desorbs more efficiently. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


