| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A174 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834389 | |
| Published online | 19 July 2019 | |
Discovery and progenitor constraints on the Type Ia supernova 2013gy⋆
1
Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
e-mail: simonholmbo@phys.au.dk; max@phys.au.dk
2
Institute for Astronomy, University of Hawai’i, 2680 Woodlawn Drive, Honolulu, HI 96822, USA
3
Department of Astronomy, University of California, Berkeley, CA 94720-3411, USA
4
Department of Physics, Florida State University, 77 Chieftain Way, Tallahassee, FL 32306, USA
5
Carnegie Observatories, Las Campanas Observatory, Casilla 601, La Serena, Chile
6
Miller Institute for Basic Research in Science, University of California, Berkeley, CA 94720, USA
7
Observatories of the Carnegie Institution for Science, 813 Santa Barbara St., Pasadena, CA 91101, USA
8
Physics Department and Tsinghua Center for Astrophysics (THCA), Tsinghua University, Beijing, 100084, PR China
9
Yunnan Observatories, Chinese Academy of Sciences, Kunming 650216, PR China
10
Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, Kunming 650216, PR China
11
Homer L. Dodge Department of Physics and Astronomy, University of Oklahoma, 440 W. Brooks, Rm 100, Norman, OK 73019-2061, USA
12
Visiting Astronomer, Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
13
Cerro Tololo Inter-American Observatory, National Optical Astronomy Observatory, Casilla 603 La Serena, Chile
14
George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, Department of Physics and Astronomy, Texas A&M University, College Station, TX 77843, USA
15
The Oskar Klein Centre, Department of Astronomy, Stockholm University, AlbaNova, 10691 Stockholm, Sweden
16
INAF, Osservatorio Astronomico di Padova, 35122 Padova, Italy
17
National Astronomical Observatories of China, Beijing 100012, PR China
18
School of Science, Tianjin University of Technology, Tianjin 300384, PR China
Received:
5
October
2018
Accepted:
30
January
2019
We present an early-phase g-band light curve and visual-wavelength spectra of the normal Type Ia supernova (SN) 2013gy. The light curve is constructed by determining the appropriate S-corrections to transform KAIT natural-system B- and V-band photometry and Carnegie Supernova Project natural-system g-band photometry to the Pan-STARRS1 g-band natural photometric system. A Markov chain Monte Carlo calculation provides a best-fit single power-law function to the first ten epochs of photometry described by an exponent of 2.16+0.06−0.06 and a time of first light of MJD 56629.4+0.1−0.1, which is 1.93+0.12−0.13 days (i.e., < 48 h) before the discovery date (2013 December 4.84 UT) and −19.10+0.12−0.13 days before the time of B-band maximum (MJD 56648.5 ± 0.1). The estimate of the time of first light is consistent with the explosion time inferred from the evolution of the Si IIλ6355 Doppler velocity. Furthermore, discovery photometry and previous nondetection limits enable us to constrain the companion radius down to Rc ≤ 4 R⊙. In addition to our early-time constraints, we used a deep +235 day nebular-phase spectrum from Magellan/IMACS to place a stripped H-mass limit of < 0.018 M⊙. Combined, these limits effectively rule out H-rich nondegenerate companions.
Key words: supernovae: general / supernovae: individual SN 2013gy
The spectra are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/627/A174.
© ESO 2019
1. Introduction
Today, Type Ia supernova (SN Ia) cosmology is limited by a subtle matrix of systematic errors. Although significant effort is being placed to reduce known systematics in order to improve upon the accuracy of measuring their peak luminosities (see Phillips et al. 2019), obtaining distances accurate to the percent level will likely require a better understanding of their progenitors and explosion physics. Although SNe Ia are generally agreed to originate from the thermonuclear disruption of a carbon-oxygen white dwarf (Hoyle & Fowler 1960), progenitor scenarios which give rise to SNe Ia and explosion processes involved remain critical questions to answer. With the growth of wide field surveys, these questions can be addressed better than ever before. In particular, the discovery of SNe Ia shortly after explosion can provide new information through their early light curves, such as shock cooling of the white dwarf surface (Piro et al. 2010; Rabinak et al. 2012), collision with the companion star (Kasen 2010), evidence for shallow radioactive nickel (Piro & Morozova 2016; Maeda et al. 2018; Polin et al. 2019), and interaction with circumstellar material (Piro & Morozova 2016; Noebauer et al. 2016; Maeda et al. 2018; Tucker et al. 2019).
The current sample of SNe Ia with early-time observations exhibit at least two different morphologies (Stritzinger et al. 2018). In one case, the early light curves are well fit with a single power-law function. Objects exhibiting such a behavior include SN 2011fe (Zhang et al. 2016), KSN 2011b (Olling et al. 2015; Shappee et al. 2019), KSN 2012a (Olling et al. 2015; Shappee et al. 2019), ASASSN-14lp (Shappee et al. 2016), and SN 2015F (Im et al. 2015; Cartier et al. 2017). On the other hand, some SNe Ia exhibit a two-phase morphology. In such cases the first phase consists of a linear increase in flux typically extending over three to five days past the time of first light (tfirst), followed by an abrupt increase in flux (power law) as the light curve rises to maximum brightness. Objects exhibiting a two-phase morphology include SN 2012cg, (Marion et al. 2016; Shappee et al. 2018), SN 2012fr (Contreras et al. 2018), SN 2013dy (Zheng et al. 2013; Pan et al. 2015), SN 2014J (Zheng et al. 2014; Siverd et al. 2015; Goobar et al. 2015), iPTF 16abc (Miller et al. 2018), and SN 2017cbv (Hosseinzadeh et al. 2017). A two-component power-law function (or broken power-law function; Zheng et al. 2017) provides superior fits to the early light curves of these objects and more accurate estimates of both tfirst and the rise time (trise) to maximum (tmax).
Aside from four SNe Ia located in Kepler fields (Olling et al. 2015; Brown et al. 2018; Cornect et al. 2018), the current sample of objects studied at early times consists of low-cadence coverage, and it may be possible that a two-component emission structure has been misinterpreted as a single power law. For example, Foley et al. (2012) fit the early light curve of SN 2009ig with a single power law; however, when photometry computed from an open-filter discovery image is included, a two-component power law may indeed provide a superior fit (see Contreras et al. 2018). Taken together with the recent observations of MUSSES1604D (also known as SN 2016jhr; Jiang et al. 2017) a SN 2006bt-like event (Foley et al. 2010; Stritzinger et al. 2011) that exhibited clear departures from a single and double power-law rise, the early-phase observational parameter space of SNe Ia is far from fully explored.
Currently there are < 20 SNe Ia in the literature discovered within approximately three days of tfirst, and the addition of more objects to the sample is crucial to fully map out the early-time parameter space. Here we present an early g-band light curve of the normal SN 2013gy (also known as PS1-13ejo) based on photometry calibrated to one well-understood photometric system. Specifically, Pan-STARRS1 (PS1; Tonry et al. 2012; Chambers et al. 2016) first g-band detection images are combined with follow-up imaging obtained by the Carnegie Supernova Project-II (CSP-II; Phillips et al. 2019) and the Lick Observatory Supernova Search (LOSS; Filippenko et al. 2001). In addition to the light curve, a comprehensive set of visual-wavelength spectra is also presented.
Kim et al. (2013) announce the discovery of SN 2013gy in open-filter images obtained with the 0.76 m Katzman Automatic Imaging Telescope (KAIT) at Lick Observatory on 2013 December 6.33 (UT dates are used throughout this paper). An open-filter image taken the previous day provides a nondetection limit of 19.3 mag. SN 2013gy was also recovered in PS1 images obtained on 2013 December 5.34 with an apparent g-band (hereafter gPS1) magnitude of 19.48 ± 0.09. The previous PS1 nondetection image was obtained 5.95 days earlier on 2013 November 29.39 with a limiting gPS1 magnitude of 20.54. An optical spectrum obtained by Tomasella et al. (2013) on 2013 December 7.5 indicated the object was a young SN Ia.
With J2000 coordinates of 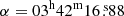 and δ = −04 ° 43′18″52, SN 2013gy was located 32″ north and 11″ east from the center of the SB(s)b host galaxy NGC 1418. A color image of NGC 1418 with the position of SN 2013gy indicated is provided in Fig. A.1. The redshift of NGC 1418 is z = 0.014023 (Catinella et al. 2005) and its Tully Fisher (TF) distance ranges from 43.8 Mpc (Springob et al. 2007) to 88.8 Mpc (Theureau et al. 2007). Given the high dispersion of the TF distances, in the following we adopt the redshift distance, which after correcting for a Virgo, Great Attractor, and Shapley infall model and adopting H0 = 73 km s−1 Mpc−1 corresponds to a distance of 55.9 ± 3.9 Mpc (i.e., μ = 33.75 ± 0.15 mag). This is fully consistent with the distance derived from the comprehensive set of optical and near-infrared (NIR) light curves obtained by the CSP-II, which provides μ = 33.68 ± 0.09 mag (see Sect. 2.3).
and δ = −04 ° 43′18″52, SN 2013gy was located 32″ north and 11″ east from the center of the SB(s)b host galaxy NGC 1418. A color image of NGC 1418 with the position of SN 2013gy indicated is provided in Fig. A.1. The redshift of NGC 1418 is z = 0.014023 (Catinella et al. 2005) and its Tully Fisher (TF) distance ranges from 43.8 Mpc (Springob et al. 2007) to 88.8 Mpc (Theureau et al. 2007). Given the high dispersion of the TF distances, in the following we adopt the redshift distance, which after correcting for a Virgo, Great Attractor, and Shapley infall model and adopting H0 = 73 km s−1 Mpc−1 corresponds to a distance of 55.9 ± 3.9 Mpc (i.e., μ = 33.75 ± 0.15 mag). This is fully consistent with the distance derived from the comprehensive set of optical and near-infrared (NIR) light curves obtained by the CSP-II, which provides μ = 33.68 ± 0.09 mag (see Sect. 2.3).
2. Early-time observations of SN 2013gy
2.1. Photometry and visual-wavelength spectroscopy
Our early-phase gPS1-band light curve of SN 2013gy is constructed using data from three different facilities. This includes two epochs of gPS1 separated by ∼20 min, 52 epochs of g-band photometry obtained by the CSP-II (hereafter gCSP) extending from −15.3 d1 to +59.4 d, and 37 epochs of B- and V-band photometry from KAIT extending from −16.2 d to +53.6 d. To facilitate our analysis presented below, in the following the KAIT B- and V-band photometry is summed together (in flux space) and then multiplied by one half, creating what we refer to as BV.5-band photometry (see below). Reduced gPS1-band photometry was downloaded from the PS1 webpage2, while CSP-II and KAIT images were reduced in the standard manner following the techniques described by Krisciunas et al. (2017) and Zheng et al. (2013), respectively. Natural-system photometry of the supernova was computed for each set of science images relative to local sequences of stars. These local sequences of stars were calibrated to the natural system of each setup using standard-star photometry converted to the natural systems through the use of color terms obtained from multiple observations of the standard fields (see Contreras et al. 2018, for details). The resulting gPS1-, gCSP-, and KAIT BV.5-band photometry is listed in Table A.1, along with the S-corrections (see below) that transform their photometry to the gPS1 natural system.
Table A.2 contains the journal of spectroscopic observations. These include 18 epochs of unpublished early optical spectra, five published spectra (Graham et al. 2017), and a late-phase spectrum taken with the Magellan Baade telescope. The spectra were reduced following standard procedures (see, e.g., Hamuy et al. 2006), were color-matched to multiband photometry, and are plotted in the rest frame in Fig. A.2.
2.2. S-correction and a definitive gPS1 light curve
Here we describe how the gCSP- and BV.5-band photometry was transformed to the gPS1 natural system. We transform to the gPS1 natural system to avoid S-correcting the earliest observations where the S-corrections are more uncertain. To compute accurate S-corrections requires system response functions and a spectrum, and/or a spectral template (Stritzinger et al. 2002). The left panel of Fig. 1 contains the gPS1-, gCSP-, and KAIT BV.5-band response functions, along with early-phase optical spectra. The BV.5 response function is obtained by summing together the KAIT B- and V- response functions and multiplying the product by one half. The motivation for doing this is that the S-corrections computed for the KAIT B and V bands are found to be very similar (on the order of ±0.6 mag), but with opposite signs. So, by combining their photometry into a BV.5 system, the required S-corrections to transform the KAIT photometry to the gPS system are minimized and found to lie between −0.1 to 0.2 mag out to +60 d.
 |
Fig. 1. System response functions and S-correction results. Left: comparison of the normalized gPS1 (dashed line), the gCSP (dotted line), and BV.5 (solid line) system response functions. Also plotted are seven visual-wavelength spectra of SN 2013gy ranging between −16.1 d and −13.4 d as indicated by the color bar. Right, top panel: S-corrections as a function of phase using observed (dark circles) spectra and Hsiao et al. (2007) template spectra (light circles). The smoothing splines of those S-corrections (red and blue lines for gCSP and BV.5, respectively) enable us to accurately transform gCSP-band and BV.5-band natural-system photometry to the gPS1 natural system at any phase. Right, bottom panel: gCSP- (red squares) and BV.5-band (blue triangles) natural-system photometry, and the S-corrected versions (green squares and green triangles) transformed to the gPS1 natural system (offset by +1 mag). |
 |
Fig. 2. Left: early-time gPS1-band light curve of SN 2013gy based on photometry measured from PS1, CSP-II, and KAIT images, plotted along with the best-fit, single power-law function characterized by an index α = 2.16 (solid curve), the “fireball” model (α = 2, dash-dot curve), and a linear rise for the first ∼3 d (dashed curve). The KAIT open-filter nondetection obtained 1 d prior to discovery is plotted as a black filled triangle. The solid vertical black line indicates tfirst with its width corresponding to the 1σ uncertainty (gray region), and the vertical dashed line corresponds to the epoch of the first spectrum. Right, top: residuals between the best-fit model and the data (horizontal dashed white line); black lines correspond to models sampled from below (right, bottom panel), which contains 1σ, 2σ, and 3σ error ellipses indicating the uncertainties in the model fit parameters α and tfirst. |
To compute an S-correction at a specific epoch, the observed and template spectra are first color-matched to CSP-II broad-band photometry. The S-correction that transforms gCSP-band natural-system photometry to the gPS1-band natural system is computed by taking the difference between synthetic photometry computed using the two different passbands and the spectrum – that is, m(gPS1) = m(gCSP)−ΔS. Given that the spectral energy distribution of SNe Ia is time dependent, S-corrections are computed for each epoch and then a smoothing spline is derived to give S-corrections at all times. Imaging was obtained using both the observed spectra and the Hsiao et al. spectral template. The S-corrections transforming our gCSP- and BV.5-band photometry to the gPS1 natural system are plotted in Fig. 1 (right, top panel) and listed in Table A.1. The observed gCSP and BV.5 photometry is also plotted (right, bottom panel) with and without the S-corrections.
2.3. Light-curve parameters and reddening
Basic light-curve parameters were computed using the light-curve fitter SNooPy (Burns et al. 2011), and key results are listed in Table A.3. SNooPy fits provide an estimate of the time and magnitude of peak brightness, the light-curve decline-rate parameter Δm15(B), and the color-stretch parameter sBV (Burns et al. 2014), as well as host-galaxy reddening. Using the SNooPy “max model” tB, max is found to have occurred on MJD = 56648.5 ± 0.1 with mB = 14.699 ± 0.013 mag, and Δm15(B) = 1.234 ± 0.060 mag. Fitting the entire suite of CSP-II optical/NIR light curves3 with SNooPy’s “EBV method2”, we obtain an sBV = 0.892 ± 0.05 mag, a host-galaxy color excess of E(B − V)host = 0.106 ± 0.004stat ± 0.060sys mag, and a distance modulus μ = 33.68 ± 0.09 mag. Combining E(B − V)host with the Milky Way component of E(B − V)MW = 0.049 mag (Schlafly & Finkbeiner 2011; Schlegel et al. 1998), we obtain E(B − V)tot = 0.155 ± 0.060 mag, which is adopted throughout. Adjusting mB for reddening and K-corrections, and assuming our adopted distance to the host, we find that SN 2013gy reached a peak absolute B-band magnitude MB = −19.32 ± 0.16 mag.
3. Results
3.1. Early gPS1 light curve and constraints on tfirst
Plotted in the left panel of Fig. 2 is the early-time gPS1-band light curve of SN 2013gy. Overplotted on the light curve is the best-fit single power-law function (i.e., f(t) = A(t−tfirst)α), a single power-law function with an index of two, and a linear function. The right, top panel shows the residuals between the best-fit model and the photometry. Finally, the bottom right panel of Fig. 2 contains the estimated error in the fit parameters and their correlation. Fitting was performed using the Markov chain Monte Carlo (MCMC) Python package PyMC3
4 (Salvatier et al. 2016) and the No-U-Turn Sampler (NUTS; Hoffman & Gelman 2011). When fitting we considered only data obtained prior to −10 d (Conley et al. 2006; Ganeshalingam et al. 2011), and α was a free parameter with priors defined using the results of Firth et al. (2015). The best-fit power law corresponds to 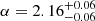 and
and 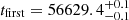 MJD. We note that from examination of the right, bottom panel of Fig. 2, a value of α = 2.0 is found to be within 2σ of the best-fit value. Assuming α = 2.0 would imply a tfirst value that is 7 h later than our inferred best-fit value. We also note that because the first 3 epochs span more than three days and the uncertainty of the first KAIT measurement is relatively large, we cannot rule out a linear rise prior to ∼15 d before tB, max. The best fit to a linear rise implies a value of tfirst that is 1.3 d later and only 14 h before the PS1 images. Comparison of the best-fit trise to the first PS1 detection indicates that SN 2013gy was discovered
MJD. We note that from examination of the right, bottom panel of Fig. 2, a value of α = 2.0 is found to be within 2σ of the best-fit value. Assuming α = 2.0 would imply a tfirst value that is 7 h later than our inferred best-fit value. We also note that because the first 3 epochs span more than three days and the uncertainty of the first KAIT measurement is relatively large, we cannot rule out a linear rise prior to ∼15 d before tB, max. The best fit to a linear rise implies a value of tfirst that is 1.3 d later and only 14 h before the PS1 images. Comparison of the best-fit trise to the first PS1 detection indicates that SN 2013gy was discovered 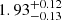 d past tfirst, and when compared to tB, max, one obtains
d past tfirst, and when compared to tB, max, one obtains 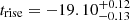 days.
days.
3.2. Spectroscopy and an estimate of texplosion
Spectra of SN 2013gy taken around maximum light resemble those of normal SNe Ia. Pseudo-equivalent-width (pEW) measurements of the Si IIλ5972 anda superior fit and implies λ6355 features indicate that it is “core normal” (CN) according to Branch et al. (2006). Moreover, the position of the absorption minimum of the Si IIλ6355 feature in the −0.8 d spectrum indicates a Doppler velocity at maximum absorption of −νabs = 10 180 ± 90 km s−1, consistent with a normal object in the Wang et al. (2009) system.
Piro & Nakar (2013) suggest that an estimate of the explosion time (texplosion) can be obtained through the evolution of Si IIλ6355. This is achieved by fitting the early-time velocity evolution with an appropriate power law. Following Piro & Nakar, we fit a ν ∝ tβ power law with β = −0.20, −0.22, and −0.24. The resulting goodness-of-fit parameter χ2 per degree of freedom ( χ2/d.o.f.) is plotted in the top-left panel of Fig. 3 for each power-law index. A constant systematic error is added to get a best fit with χ2/d.o.f. = 1. We find that β = −0.20 provides a superior fit and implies  MJD. Comparison of tfirst and texplosion reveals that SN 2013gy likely experienced minimal to no dark phase.
MJD. Comparison of tfirst and texplosion reveals that SN 2013gy likely experienced minimal to no dark phase.
3.3. Constraints on interaction with a nondegenerate companion
Companion radius (Rc) limits are computed following the methodology of Shappee et al. (2018), which is based on comparing the observations to the analytical model predictions of Kasen (2010). Taking a conservative explosion time to be ∼2 d before discovery, mass of the companion to be 1 M⊙ and assuming a favorable viewing angle of 15°, we compute Rc limits using both the discovery gPS1 photometry and the previous KAIT nondetection. Our limits on Rc are plotted vs. days relative to the epoch of discovery in the top-right panel of Fig. 3. Combined limits indicate Rc ≲ 4 R⊙ in the case of a favorable viewing angle. Adopting the TF distances as upper and lower bounds on the distance, results in 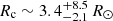 for the estimated value of tfirst. The same analysis has been done a number of times for other SNe, yielding possible companion radii limits ranging between a fraction of R⊙ and tens of R⊙ (Bloom et al. 2012; Foley et al. 2012; Silverman et al. 2012; Goobar et al. 2015; Olling et al. 2015; Im et al. 2015; Marion et al. 2016; Shappee et al. 2016, 2018; Hosseinzadeh et al. 2017; Miller et al. 2018).
for the estimated value of tfirst. The same analysis has been done a number of times for other SNe, yielding possible companion radii limits ranging between a fraction of R⊙ and tens of R⊙ (Bloom et al. 2012; Foley et al. 2012; Silverman et al. 2012; Goobar et al. 2015; Olling et al. 2015; Im et al. 2015; Marion et al. 2016; Shappee et al. 2016, 2018; Hosseinzadeh et al. 2017; Miller et al. 2018).
3.4. Limits on the presence of companion material
Hydrodynamic simulations of ejecta-companion interactions indicate that > 0.15 M⊙ of material could be removed from hydrogen-rich (H-rich) Roche-lobe overflow (RLOF) companions via stripping and/or momentum-transfer or ablation and/or heating and is expected to have a velocity dispersion of ν ≈ 1000 km s−1 (e.g., Marietta et al. 2000; Pan et al. 2012; Boehner et al. 2018). This unbound material should be visible during the nebular phase – when the ejecta become optically thin – and lead to a prominent emission signature.
To place a limit on the Hα emission we have followed conventional techniques in the literature (e.g., Leonard 2007; Shappee et al. 2013). Briefly, the late-phase (+235 d) spectrum of SN 2013gy was flux calibrated to match photometry computed from PS1 stars (Flewelling et al. 2016) located in an R-band acquisition image. Next, the continuum was fitted in the vicinity of Hα and subtracted from the spectrum, yielding no statistical evidence for Hα emission as demonstrated in the bottom panel of Fig. 3. Following Leonard (2007), we obtain a 3σ statistical flux limit of 4.5 × 10−16 ergs s−1 cm−2 Å−1. For our adopted distance and using the models of Botyánszki et al. (2018), this corresponds to an H-mass limit of < 0.018 M⊙. This limit is an order of magnitude lower than all estimates of unbound mass values for normal SNe Ia, effectively ruling out H-rich RLOF companions. This finding is consistent with similar constraints of a number of other SNe Ia discovered soon after explosion (Mattila et al. 2005; Leonard 2007; Lundqvist et al. 2013, 2015; Shappee et al. 2013, 2018; Maguire et al. 2016; Graham et al. 2017; Sand et al. 2018; Dimitriadis et al. 2019). This leaves only a small parameter space of subdwarfs and He stars whose signatures could remain undetected in the spectrum. We note that inspection of an unpublished early-phase NIR spectral time-series of SN 2013gy obtained by the CSP-II yields no indication of He lines, and unfortunately, no late-phase NIR spectrum was obtained.
 |
Fig. 3. Left: estimate of texplosion based upon functional fits to the velocity evolution of Si IIλ6355. Right: maximum allowed radius of a companion star as a function of explosion time as inferred from the discovery gPS1 photometry and the previous KAIT nondetection limit plotted vs. days since discovery. The vertical black line in the left and right panels corresponds to the best-fit tfirst, accompanied by a shaded gray region corresponding to its 1σ uncertainty. Bottom: rest-frame-corrected nebular spectrum of SN 2013gy (black line), the continuum fit (red), and our 3σ Hα flux limit (blue line). The shaded area extends over the expected location of Hα ± 1000 km s−1. |
4. Discussion
We have presented discovery and follow-up photometry of the normal SN Ia 2013gy. Photometry obtained from different facilities was carefully calibrated to the gPS1 system. The early rise of the light curve is well fit with a single power-law function, indicating that SN 2013gy was discovered within 48 h of tfirst. The corresponding tfirst value is consistent with a texplosion estimate based on the Doppler velocity evolution of the Si IIλ6355 feature, suggesting minimal to no dark phase for SN 2013gy. A short dark phase has been inferred from the study of several other supernovae including SN 2009ig, SN 2011fe, SN 2012cg (Piro & Nakar 2014), and iPTF 16abc (Miller et al. 2018). In contrast, the transitional iPTF 13ebh may have experienced an approximately four-day dark phase (see Hsiao et al. 2015).
Examination of the pEW values of the Si IIλ5972 and λ6355 doublets shows that SN 2013gy is core normal (Branch et al. 2006, 2009), while its Si IIλ6355 Doppler velocity makes it a normal object according to the classification scheme of Wang et al. (2009). Moreover, as discussed by Stritzinger et al. (2018), the early intrinsic (B − V)0 colors reveal it to be a red and rapidly evolving object, similar to SN 2011fe. In summary, SN 2013gy displays all of the characteristics of a normal SN Ia.
Making use of the early discovery of SN 2013gy, limits were placed on the radius of any companion star of R ≤ 4 M⊙. Combined with our stripped H-mass limit of ≲0.018 M⊙ obtained from a nebular-phase Magellan spectrum, our analysis effectively rules out H-rich RLOF companions. This result highlights that it is possible to constrain existing SN Ia progenitor models with the use of both early and late-phase observations.
Acknowledgments
A special thanks to the referee for detailed comments to the submitted manuscript. We thank P. Massey and M. Kasliwal for obtaining a spectrum each with the Magellan telescopes. S. Holmbo and M. D. Stritzinger are supported by a research grant (13261) from the VILLUM FONDEN. A. V. Filippenko’s supernova group is grateful for financial assistance from USA National Science Foundation (NSF) grant AST-1211916, the TABASGO Foundation, the Christopher R. Redlich Fund, and the Miller Institute for Basic Research in Science (U. C. Berkeley). Research at Lick Observatory is partially supported by a generous gift from Google. P. Höflich acknowledges NSF grants AST-1715133 and AST-1613472. L. Tomasella is partially supported by the PRIN-INAF 2016 with the project “Towards the SKA and CTA era: discovery, localisation, and physics of transient sources” (P.I. M. Giroletti). The CSP-II has been funded by the USA NSF under grants AST-0306969, AST-0607438, AST-1008343, AST-1613426, AST-1613455, and AST-1613472, and in part by a Sapere Aude Level 2 grant funded by the Danish Agency for Science and Technology and Innovation (PI Stritzinger). J.-J. Zhang is supported by the National Natural Science Foundation of China (NSFC, grants 11403096 and 11773067), the Key Research Program of the CAS (grant KJZD-EW-M06), the Youth Innovation Promotion Association of the CAS (grant 2018081), and the CAS Light of West China Program. X. Wang is supported by the National Natural Science Foundation of China (NSFC grants 11325313 and 11633002), and the National Program on Key Research and Development Project (grant 2016YFA0400803). Based in part on observations made with the Nordic Optical Telescope (P49-017; PI Stritzinger), operated by the Nordic Optical Telescope Scientific Association at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofisica de Canarias. This paper includes data gathered with the 6.5 m Magellan telescopes located at Las Campanas Observatory, Chile. We acknowledge the support of the staff of Lijiang 2.4 m and the Xinglong 2.16 m telescopes. Partially based on observations made with the Copernico 1.8 m telescope (Asiago, Italy) operated by INAF Osservatorio Astronomico di Padova. This paper made use of discovery images obtained by the Pan-STARRS1 Survey (PS1), which was made possible through contributions of the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max-Planck Society and its participating institutes, the Max Planck Institute for Astronomy, Heidelberg and the Max Planck Institute for Extraterrestrial Physics, Garching, The Johns Hopkins University, Durham University, the University of Edinburgh, Queen’s University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network Incorporated, the National Central University of Taiwan, the Space Telescope Science Institute, the National Aeronautics and Space Administration (NASA) under grant NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate, the NSF under grant AST-1238877, the University of Maryland, and Eotvos Lorand University (ELTE).
References
- Bloom, J. S., Kasen, D., Shen, K. J., et al. 2012, ApJ, 744, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Boehner, P., Plewa, T., & Langer, N. 2018, MNRAS, 465, 2060 [NASA ADS] [CrossRef] [Google Scholar]
- Botyánszki, J., Kasen, D., & Plewa, T. 2018, ApJ, 852L, 6 [Google Scholar]
- Branch, D., Dang, L. C., & Hall, N. 2006, PASP, 118, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., Dang, L. C., & Baron, E. 2009, PASP, 121, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. S., Stanek, K. Z., Vallely, P., et al. 2018, ATel, 11253, 00 [NASA ADS] [Google Scholar]
- Burns, C. R., Stritzinger, M. D., Phillips, M. M., et al. 2011, AJ, 141, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, C. R., Stritzinger, M. D., Phillips, M. M., et al. 2014, ApJ, 789, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Cartier, R., Sullivan, M., Firth, R. E., et al. 2017, MNRAS, 464, 4476 [NASA ADS] [CrossRef] [Google Scholar]
- Catinella, B., Haynes, M. P., & Giovanelli, R. 2005, AJ, 130, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, K. C., Magnier, E. A., & Metcalfe, N. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Conley, A., Howell, D. A., Howes, A., et al. 2006, AJ, 132, 1707 [NASA ADS] [CrossRef] [Google Scholar]
- Contreras, C., Phillips, M. M., Burns, C. R., et al. 2018, ApJ, 859, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Cornect, R., Brimacombe, J., Stone, G., et al. 2018, ATel, 11259 [Google Scholar]
- Dimitriadis, G., Rojas-Bravo, C., Kilpatrick, C. D., et al. 2019, ApJ, 870, L14 [Google Scholar]
- Filippenko, A. V., Li, W. D., Treffers, R. R., & Modjaz, M. 2001, in Small Telescope Astronomy on Global Scales, eds. W. P. Chen, C. Lemme, & B. Paczyński (San Francisco: ASP), 246, 121 [NASA ADS] [Google Scholar]
- Firth, R. E., Sullivan, M., Gal-Yam, A., et al. 2015, MNRAS, 446, 3895 [NASA ADS] [CrossRef] [Google Scholar]
- Flewelling, H. A., Magnier, E. A., & Chambers, K. C. 2016, ArXiv e-prints [arXiv:1612.05243] [Google Scholar]
- Foley, R. J., Narayan, G., Challis, P. J., et al. 2010, ApJ, 708, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Challis, P. J., Filippenko, A. V., et al. 2012, ApJ, 744, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Ganeshalingam, M., Li, W., & Filippenko, A. V. 2011, MNRAS, 416, 2607 [NASA ADS] [CrossRef] [Google Scholar]
- Goobar, A., Kromer, M., Siverd, R., et al. 2015, ApJ, 799, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, M. L., Kumar, S., Hosseinzadeh, G., et al. 2017, MNRAS, 472, 3437 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Folatelli, G., Morrell, N. I., et al. 2006, PASP, 118, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, M. D., & Gelman, A. 2011, ArXiv e-prints [arXiv:1111.4246] [Google Scholar]
- Hosseinzadeh, G., Sand, D. J., Valenti, S., et al. 2017, ApJ, 845, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., & Fowler, W. A. 1960, ApJ, 132, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hsiao, E. Y., Conley, A., Howell, D. A., et al. 2007, ApJ, 663, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Hsiao, E. Y., Burns, C. R., Contreras, C., et al. 2015, A&A, 578, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Im, M., Choi, C., Yoon, S.-C., et al. 2015, ApJS, 221, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Doi, M., Maeda, K., et al. 2017, Nature, 550, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D. 2010, ApJ, 708, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, H., Zheng, W. K., Li, W., et al. 2013, CBET, 3743, 1 [NASA ADS] [Google Scholar]
- Krisciunas, K., Contreras, C., Burns, C. R., et al. 2017, AJ, 154, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, D. C. 2007, ApJ, 670, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Lundqvist, P., Mattila, S., Sollerman, J., et al. 2013, MNRAS, 435, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lundqvist, P., Nyholm, A., Taddia, F., et al. 2015, A&A, 577, A39 [Google Scholar]
- Maeda, K., Jiang, J.-A., Shigeyama, T., & Doi, M. 2018, ApJ, 861, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Maguire, K., Taubenberger, S., Sullivan, M., & Mazzali, P. A. 2016, MNRAS, 457, 3254 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marietta, E., Burrows, A., & Fryxell, B. 2000, ApJS, 128, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Marion, G. H., Brown, P. J., Vinkó, J., et al. 2016, ApJ, 820, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, S., Lundqvist, P., Sollerman, J., et al. 2005, A&A, 443, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, A. A., Cao, Y., Piro, A. L., et al. 2018, ApJ, 852, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Noebauer, U. M., Taubenberger, S., Blinnikov, S., Sorokina, E., & Hillebrandt, W. 2016, MNRAS, 463, 2972 [NASA ADS] [CrossRef] [Google Scholar]
- Olling, R. P., Mushotzky, R., Shaya, E. J., et al. 2015, Nature, 521, 332 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pan, K.-C., Ricker, P. M., & Taam, R. E. 2012, ApJ, 760, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, Y.-C., Foley, R. J., Kromer, M., et al. 2015, MNRAS, 452, 4307 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Contreras, C., Hsiao, E. Y., et al. 2019, PASP, 131, 014001 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Morozova, V. S. 2016, ApJ, 826, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Nakar, E. 2013, ApJ, 769, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., & Nakar, E. 2014, ApJ, 784, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L., Chang, P., & Weinberg, N. N. 2010, ApJ, 708, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Polin, A., Nugent, P., & Kasen, D. 2019, ApJ, 873, 1 [Google Scholar]
- Rabinak, I., Livne, E., & Waxman, E. 2012, ApJ, 757, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Salvatier, J., Wiecki, T. V., & Fonnesbeck, C. 2016, Astrophysics Source Code Library [record ascl:1610.016] [Google Scholar]
- Sand, D. J., Graham, M. L., Botyánszki, J., et al. 2018, ApJ, 863, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., Stanek, K. Z., Pogge, R. W., & Garnavich, P. M. 2013, ApJ, 762, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., Piro, A. L., Holoien, T. W.-S., et al. 2016, ApJ, 826, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., Piro, A. L., Stanek, K. Z., et al. 2018, ApJ, 855, 6 [Google Scholar]
- Shappee, B. J., Holoien, T. W.-S., Drout, M. R., et al. 2019, ApJ, 870, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. M., Ganeshalingam, M., Cenko, S. B., et al. 2012, ApJ, 756, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Siverd, R. J., Goobar, A., Stassun, K. G., et al. 2015, ApJ, 799, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S., Smith, K. W., & Wright, D. 2014, ATel, 5850 [Google Scholar]
- Springob, C. M., Masters, K. L., Haynes, M. P., Giovanelli, R., & Marinoni, C. 2007, ApJS, 172, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Hamuy, M., Suntzeff, N. B., et al. 2002, AJ, 124, 2100 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M. D., Phillips, M. M., Boldt, L. N., et al. 2011, AJ, 142, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M. D., Shappee, B. J., Piro, A., et al. 2018, ApJ, 864, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Theureau, G., Hanski, M. O., Courdreau, N., Hallet, N., & Martin, J.-M. 2007, A&A, 465, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tomasella, L., Benetti, S., & Tartaglia, L. 2013, ATel, 5638 [Google Scholar]
- Tonry, J. L., Stubbs, C. W., Lykke, K. R., et al. 2012, ApJ, 750, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Tucker, M. A., Shappee, B. J., & Wisniewski, J. P. 2019, ApJ, 872, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X., Filippenko, A. V., Ganeshalingam, M., et al. 2009, ApJ, 699, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, K., Wang, X., Zhang, J.-J., et al. 2016, ApJ, 820, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., Silverman, J., Filippenko, A. V., et al. 2013, ApJ, 778, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., Shivvers, I., Filippenko, A. V., et al. 2014, ApJ, 783, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., Kelly, P. L., & Filippenko, A. V. 2017, ApJ, 848, 66 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional material
Photometry of SN 2013gy and S-corrections.
Journal of spectroscopic observations.
Key parameters of SN 2013gy.
 |
Fig. A.1. Composite image of NGC 1418 (north up and east left) constructed from multiband images obtained with the Swope telescope. The inset contains a close-up view of the position of SN 2013gy, highlighting its position in the outer region of the host. |
 |
Fig. A.2. Spectroscopic time series of SN 2013gy used to compute S-corrections, enabling us to transform natural-system gCSP- and BV.5-band photometry to the gPS1 natural system. |
All Tables
All Figures
 |
Fig. 1. System response functions and S-correction results. Left: comparison of the normalized gPS1 (dashed line), the gCSP (dotted line), and BV.5 (solid line) system response functions. Also plotted are seven visual-wavelength spectra of SN 2013gy ranging between −16.1 d and −13.4 d as indicated by the color bar. Right, top panel: S-corrections as a function of phase using observed (dark circles) spectra and Hsiao et al. (2007) template spectra (light circles). The smoothing splines of those S-corrections (red and blue lines for gCSP and BV.5, respectively) enable us to accurately transform gCSP-band and BV.5-band natural-system photometry to the gPS1 natural system at any phase. Right, bottom panel: gCSP- (red squares) and BV.5-band (blue triangles) natural-system photometry, and the S-corrected versions (green squares and green triangles) transformed to the gPS1 natural system (offset by +1 mag). |
| In the text | |
 |
Fig. 2. Left: early-time gPS1-band light curve of SN 2013gy based on photometry measured from PS1, CSP-II, and KAIT images, plotted along with the best-fit, single power-law function characterized by an index α = 2.16 (solid curve), the “fireball” model (α = 2, dash-dot curve), and a linear rise for the first ∼3 d (dashed curve). The KAIT open-filter nondetection obtained 1 d prior to discovery is plotted as a black filled triangle. The solid vertical black line indicates tfirst with its width corresponding to the 1σ uncertainty (gray region), and the vertical dashed line corresponds to the epoch of the first spectrum. Right, top: residuals between the best-fit model and the data (horizontal dashed white line); black lines correspond to models sampled from below (right, bottom panel), which contains 1σ, 2σ, and 3σ error ellipses indicating the uncertainties in the model fit parameters α and tfirst. |
| In the text | |
 |
Fig. 3. Left: estimate of texplosion based upon functional fits to the velocity evolution of Si IIλ6355. Right: maximum allowed radius of a companion star as a function of explosion time as inferred from the discovery gPS1 photometry and the previous KAIT nondetection limit plotted vs. days since discovery. The vertical black line in the left and right panels corresponds to the best-fit tfirst, accompanied by a shaded gray region corresponding to its 1σ uncertainty. Bottom: rest-frame-corrected nebular spectrum of SN 2013gy (black line), the continuum fit (red), and our 3σ Hα flux limit (blue line). The shaded area extends over the expected location of Hα ± 1000 km s−1. |
| In the text | |
 |
Fig. A.1. Composite image of NGC 1418 (north up and east left) constructed from multiband images obtained with the Swope telescope. The inset contains a close-up view of the position of SN 2013gy, highlighting its position in the outer region of the host. |
| In the text | |
 |
Fig. A.2. Spectroscopic time series of SN 2013gy used to compute S-corrections, enabling us to transform natural-system gCSP- and BV.5-band photometry to the gPS1 natural system. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


