| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 17 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834506 | |
| Published online | 30 April 2019 | |
Reclassification of Cepheids in the Gaia Data Release 2
Period-luminosity and period-Wesenheit relations in the Gaia passbands⋆
1
INAF-Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Naples, Italy
e-mail: ripepi@oacn.inaf.it
2
Department of Astronomy, University of Geneva, Ch. des Maillettes 51, 1290 Versoix, Switzerland
Received:
24
October
2018
Accepted:
28
February
2019
Context. Classical Cepheids are the most important primary indicators for the extragalactic distance scale. Establishing the precise zero points of their period-luminosity and period-Wesenheit (PL/PW) relations has profound consequences on the estimate of H0. Type II Cepheids are also important distance indicators and tracers of old stellar populations.
Aims. The recent Data Release 2 (DR2) of the Gaia spacecraft includes photometry and parallaxes for thousands of classical and Type II Cepheids. We seek to review the classification of Gaia DR2 Cepheids and to derive precise PL/PW for the Magellanic Clouds (MCs) and Galactic Cepheids.
Methods. We adopted information from the literature and the Gaia astrometry and photometry to assign DR2 Galactic Cepheids to the classical, anomalous, and Type II Cepheids classes.
Results. We reclassified the DR2 Galactic Cepheids and derived new precise PL/PW relations in the Gaia passbands for the MCs and Milky Way Cepheids. We investigated for the first time the dependence on metallicity of the PW relation for classical Cepheids in the Gaia bands, finding inconclusive results.
Conclusions. According to our analysis, the zero point of the Gaia DR2 parallaxes as estimated from classical and Type II Cepheids seems likely to be underestimated by ∼0.07 mas, which agrees with recent literature. The next Gaia data releases are expected to fix this zero point offset to allow eventually a determination of H0 to less than 1%.
Key words: stars: distances / stars: variables: Cepheids / distance scale
Full Tables 2, 5, 7 and 8 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/625/A14
© ESO 2019
1. Introduction
Classical Cepheids (DCEPs) are the most important primary distance indicators for the cosmic distance scale (see e.g. Riess et al. 2016, 2018a) because of their characteristic period-luminosity (PL) and period-Wesenheit (PW) relations (Leavitt & Pickering 1912; Madore 1982; Caputo et al. 2000).
In conjunction with secondary distance indicators such as SNIa, the DCEPs provide an estimate of H0 ∼ 73.48 ± 1.66 km s−1 Mpc−1 with 2.3% of claimed uncertainty (Riess et al. 2018b). However, there is a tension at 3.4–3.7σ with H0 ∼ 66.93 ± 0.62 km s−1 Mpc−1 obtained from the analysis of the cosmic microwave background plus ΛCDM (Planck Collaboration Int. XLVI 2016; Riess et al. 2018a,b).
To reconcile the inconsistency between these values, we need more accurate calibrations of the different steps of the cosmic distance ladder. In first place we have to check the calibration of slopes/zero points of the PL/PW relations used for DCEPs, which currently rely on a handful of objects with accurate Hubble Space Telescope (HST) parallaxes (Riess et al. 2018a). In this context, measurements of the astrometric spacecraft Gaia (Gaia Collaboration 2016), which is collecting repeated multi-band photometric and astrometric data of sources over the entire sky to a limiting magnitude of about G ∼ 20.7 mag, can help significantly. The Gaia Data Release 2 (DR2) (see Gaia Collaboration 2018, for a detailed description of the content of the release) has published photometry in the three Gaia passbands G, GBP, and GRP, as well as astrometry and radial velocity data obtained during the initial 22 months of data collection.
The multi-epoch Gaia data have permitted the study of an unprecedented number of variable stars of different types (for details see Holl et al. 2018). In particular, Clementini et al. (2019) discussed the pipeline of the Cepheid&RRLyrae Specific Object Studies (SOS) used to measure period(s), intensity-averaged G, GBP, and GRP magnitudes and amplitudes of pulsation for a sample of 140 784 RR Lyrae, and 9575 Cepheids. Among the latter, 3767, 3692, and 2116 are Cepheids belonging to the Large Magellanic Cloud (LMC), Small Magellanic Cloud (SMC), and all sky sample, respectively. The latter sample, consists essentially in candidate Cepheids belonging to our Galaxy. In the following we refer to these stars as the Milky Way (MW) sample. As a result of a complex concomitant factors, such as the automatic procedure and inaccurate parallaxes, the MW sample is thought to be significantly contaminated by non-cepheid types of variable stars (see Clementini et al. 2019, for details). Therefore, the main scope of this paper is to provide a detailed reclassification of the objects classified as Cepheids (of different types, see below) in Clementini et al. (2019), providing a comparison with the classification in the literature. We also aim at calculating empirical PL/PW relations in the Gaia passbands for the LMC/SMC and MW for future uses.
Before proceeding, we distinguish three types of cepheid variables: DCEPs, anomalous Cepheids (ACEPs), and Type II Cepheids (T2CEPs). The latter type is usually subdivided into three subclasses, BL Her (BLHER), W Vir (WVIR), and RV Tau (RVTAU), in order of increasing periods. The DCEPs and ACEPs types are known to pulsate in different modes. In this paper we consider DCEPs pulsating in the fundamental, first overtone, second overtone1, and multiple mode: we name these variables DCEP_F, DCEP_1O, DCEP_2O, DCEP_MULTI, respectively. Similarly, for ACEPs we distinguish objects pulsating in the fundamental (ACEP_F) and first overtone modes (ACEP_1O). For a detailed description of these classes of variability and their evolutionary status, see the recent textbook by Catelan & Smith (2015).
The manuscript is organised as follows: in Sect. 2 we derive empirical PL/PW relations for all type of Cepheids in the LMC/SMC; in Sect. 3 we present the results of the literature search and carry out the reclassification of the MW Cepheids; in Sect. 4 we calculate the PL/PW relations for the MW sample; and a brief summary closes the paper.
2. Gaia DR2 Cepheids in the magellanic clouds
Before facing the task of reclassifying the MW Cepheids in DR2, it is first useful to analyse the DR2 output for the MCs Cepheids.
In Clementini et al. (2016, 2019), i.e. for DR1 and DR2, respectively, we used PL/PW relations derived from OGLE-III2 (Optical Gravitational Lensing Experiment) V, I photometry transformed in G, GRP bands on the basis of Jordi et al. (2010) predicted colour transformations. It is then important to derive accurate PL/PW relations for the different types of Cepheids in the Gaia passbands directly from the actual data.
In DR2, 3767 and 3692 Cepheids of all types in the LMC and SMC were released, respectively (see Table 2 of Clementini et al. 2019, for full details). These samples were complemented with 61 and 73 Cepheids coming from the MW sample, but actually belonging to the LMC and SMC, respectively, as shown in Sect. 3.2.1 (see also Table 7). For DCEPs we first discarded multiple pulsators and used only objects with reliable values of the three G, GBP, GRP bands. We were then left with 1624 and 1207 DCEP_F and DCEP_1O pulsators in the LMC, as well as 1772 and 1368 DCEP_F and DCEP_1O pulsators in the SMC, respectively. We did not attempt to correct the classification of these objects because it had been already demonstrated that it is very accurate (see Fig. 41 in Clementini et al. 2019).
Secondly, we decided to use a different formulation of the Wesenheit magnitude with respect to that used in Gaia DR1 and DR2, involving only G and GRP bands (see Clementini et al. 2016, 2019, for details). The new formulation is the following:
where λ = A(G)/E(GBP − GRP). Empirically, it is known that the value of λ is of the order of 2 over a wide range of effective temperatures, including those typically spanned by Cepheids (Andrae et al. 2018). To obtain a more precise value, we adopted the synthetic photometry by Jordi et al. (2010), which provides the value of λ as a function of effective temperature, gravity, and metallicity. We selected the ranges of these parameters typical for Cepheids (i.e. 4500 < Teff < 7000 K; 0.5 < log g < 3.5 dex; −1 < [Fe/H]< + 0.5 dex) and then averaged out the selected values, obtaining λ = 1.95 ± 0.05, which is very close to the Andrae et al. (2018) result.
We tested this Wesenheit magnitude on DCEPs in the LMC, which are known to show very tight PW relations in all bands (see e.g. Soszyński et al. 2017a; Ripepi et al. 2012, in the optical and near-infrared, respectively). After a few experiments, we realised that the least-squares fit to the data gave a tighter PW relation (smaller scatter) if the λ value was slightly decreased to 1.90; the uncertainty was estimated of the order of 0.05, by looking at the value of λ that produced an increase in the dispersion. Hence, in the following we decided to use the ensuing Wesenheit magnitude:
where G, GBP, GRP are the magnitudes in the Gaia bands. In comparison to that used in Clementini et al. (2016, 2019), the new formulation has the advantage to be linear in the colour term and to provide smaller dispersions in the PW relations.
Apart from the PW relation, we also derived individual PLs for the G, GBP, GRP bands. We did not attempt to correct for extinction because no reliable individual reddening estimate is present in the literature (see e.g. Gieren et al. 2018, for a discussion on the uncertainties in the individual reddening value for DCEPs). In any case, the average foreground reddening values in LMC and SMC are known to be small, of the order of E(B − V)≈0.08 and 0.04 mag, respectively (see e.g. the values from NASA/IPAC Extragalactic Database; NED3) so that extinction only affects the zero points of the PL relations, whereas the slope values are solid.
Operatively, to derive the relevant PL/PW relationships, we adopted a standard least-squares fitting procedure with σ clipping at 2.5–3σ level; typically 3 and 2.5 is used for PW and PL, respectively, because of the larger scatter in PL relations. The number of outliers is small because, as recalled above, the contamination of Cepheids in LMC and SMC is very small. It is important to note that for the DCEP_F in the SMC, we fitted two different lines in different period regimes characterised by values shorter or longer than ∼2.95 days. This break in the PL/PW relations is well documented in the literature at all the wavelengths (see e.g. Subramanian & Subramaniam 2015; Ripepi et al. 2016, 2017). The result of the fitting procedure is shown in Table 1 and in Figs. 1 and 2. An inspection of Table 1 reveals that the PL and especially the PW relations for the LMC are less dispersed than those for the SMC. This is due to a depth effect generated by the well-known elongation of the SMC along the line of sight (see Ripepi et al. 2017, and references therein). We also note that the PW for the LMC is much less dispersed than the PLs both because the PW is not affected by reddening and because the colour term in the Wesenheit magnitude takes partially into account the intrinsic width of the instability strip. In the SMC there is less difference between the dispersion of PW and PLs because the dominant effect on the dispersion is the elongation along the line of sight.
 |
Fig. 1. For the LMC, PL/PW relations in the form mag = α + β log P. From top to bottom panels, mag is represented by the apparent W, G, GBP, and GRP magnitudes, respectively. Orange filled circles: DCEP_F; cyan filled circles: DECP_1O; magenta four-starred symbols: ACEP_F; dark green four-starred symbols: ACEP_1O; green open triangles: BLHER; violet open triangles: WVIR; and magenta open triangles: RVTAU. |
As for the T2CEP variables, because of the paucity of the sample, we decided to use also objects without the GBP, GRP magnitudes to derive the PL relations in G. After some experiments, we decided to exclude RVTAU stars from the fits because they are too scattered and show a different slope of PL/PW with respect to BLHER and WVIR stars; this effect is well documented in the literature (see e.g. Soszyński et al. 2008; Matsunaga et al. 2009, 2011; Ripepi et al. 2015). The results of the above procedure are listed in Table 1 and in Figs. 1 and 2. The T2CEP PL relations in the SMC for GBP, GRP bands were not calculated as the shortage of stars (only 15 usable objects) coupled with the large errors resulted in unreliable relationships.
We were also able to fit reasonable PL/PW relations for the ACEP_F and ACEP_1O variables in both the MCs. Also these results are presented in Table 1 and in Figs. 1 and 2. As a final remark, we underline that the PW and PL relations calculated in this paper (especially those in the G band) will be used in the SOS pipeline (Clementini et al. 2019) for the cepheid classification in the next Gaia Data Release 3.
3. Reclassification of Gaia MW DR2 Cepheids
3.1. Comparison with the literature
As anticipated in the introduction, the sample of MW Cepheids presented in the Gaia DR2 is most likely significantly contaminated and one of the purposes of this work is to clean it. To this aim, the first step consisted in a massive search for alternative classification in the literature. The largest databases of variable stars in the MW available are Simbad (Wenger et al. 2000) and VSX (The International Variable Star Index; Watson et al. 2006 4). These sources have been complemented and completed by several additional literature works whose complete list is reported in the notes of Table 2. This table reports the source identification, equatorial coordinates, and variability classification given in Gaia DR2, as well as the literature name of the object, literature type(s) of variability, period(s) and source of this information. The acronyms for the variability types used in the table are listed in Table A.1. The analysis of periods in the literature is particularly important, as one cause of misclassification in DR2 is the wrong period found by the Cepheids&RRLyrae SOS pipeline, caused by the low number of epochs available for a consistent sample of objects; Clementini et al. (2019) analysed objects with more than 12 epochs.
Table with the literature classification for 1416 objects among the 2116 candidate Cepheids in the MW by Clementini et al. (2019).
Among the 2116 candidate Cepheids in the MW, 1416 have some mention in the literature. About 1008 of these have been classified in at least one of the cepheid subclasses, whereas 50 objects have a generic classification as “variables”. The rest of the sample is composed by a disparate collection of variability types (see Tables 2 and A.1), even if a significant portion is represented by 121 variables classified as RR Lyrae. As expected, the cepheid sample in the MW from Gaia DR2 is actually contaminated by different variability types. The literature classification is also useful as a base for the specific reclassification, which is discussed in the next section.
3.2. Detailed reclassification
The procedure adopted for the reclassification relies on the visual inspection of each light curve (LC) and comparison with a reliable atlas of LCs such as that by the OGLE group5 for the classical pulsating stars. The visual inspection of LCs was complemented by the analysis of the location of the stars in period-absolute Wesenheit magnitude, or astrometry-based luminosity, ABL, in case of negative parallaxes (see e.g. Arenou & Luri 1999, and Eq. (7) in the next section) and period-Fourier parameters (R21, R31, ϕ21, ϕ31) diagrams (for a definition of the Fourier parameters and their use in the Gaia Cepheids&RRLyrae SOS pipeline, see Clementini et al. 2016, 2019, and references therein). Additionally, we took into account the peak-to-peak amplitude ratio Amp(GBP)/Amp(GRP) which, for the different types of Cepheids assumes characteristic values as shown in Table 4. The amplitude ratio is particularly useful to separate non-pulsating from pulsating variables, as the former type generally assumes values lower (∼1.0–1.2) than the latter (∼1.3–1.6).
Average peak-to-peak amplitude ratio Amp(GBP)/Amp(GRP) for the different types of Cepheids considered in this work.
We note that in building the PW/P−ABL diagrams we corrected the parallax zero point by adding 0.046 mas according to Riess et al. (2018b) (see also Schönrich & Eyer 2019, for a recent discussion on the zero point offset). This operation has little importance for the purpose of reclassifying the Cepheids, but is important for the determination of the absolute PW relations performed in the next section. The reclassification also made use of the literature classification, which was especially useful in the most doubtful cases. In particular, the use of periods from the literature helped to reclassify more than 140 objects whose LC shape clearly revealed the wrong period from Gaia DR2, which is generally caused by the low number of epochs available for these objects. In several of these cases, when sufficient data were available, we used the Gaia photometry to recalculate the periods using the literature values as a starting point and refining these values using Period04 package (Lenz & Breger 2005). In this context, particularly useful was the work by Lemasle et al. (2018), who analysed in detail the multimode DCEPs in DR2, providing a list of reliable new multimode candidates.
As for the types of variability, our reclassification is restricted to all subtypes of cepheid variables that are the main target of the present work. Apart from these objects, we only classified in detail RR Lyrae and ACEP stars. We classified the former because their characteristic LCs make these sources relatively easy to identify and because they are analysed together with Cepheids in the Gaia Cepheids&RRLyrae SOS pipeline. As for the ACEPs, they were absent in the Cepheids&RRLyrae SOS pipeline (see Clementini et al. 2019), but several literature works reported their presence in the MW (e.g. OGLE group). Moreover during the process of reclassification, we realised that the LC shape for some short (1–2 days) period Cepheids did not fit completely neither with DCEPs nor with BLHERs. Therefore, we adopted the usual classification scheme for ACEPs in terms of ACEP_F and ACEP_1O. We note that in the absence of very precise distances (the candidate ACEPs are in general faint), the distinction between ACEP_1O and DCEP_1O on the basis of the LC shapes is very difficult because at fixed period the LCs of these two classes are very similar. Similarly, ACEP_Fs with periods shorter or longer than one day can be confused with RRABs or DCEP_Fs, respectively. The distinction between ACEPs and DCEPs is favoured by the position of the object in the MW; high Galactic latitude DCEPs are unlikely. However RRABs are ubiquitous in the Galaxy and a similar separation cannot be carried out. The distinction between these classes will be greatly facilitated by the availability of more precise parallaxes, as expected from the next Gaia data releases. Finally, the classification types considered in this work are as follows: DCEP_F, DCEP_1O, DCEP_2O, DCEP_MULTI6, ACEP_F, ACEP_1O, BLHER, WVIR, RVTAU, CEP, RRAB, RRC, OTHER, where CEP means that the object is a cepheid candidate but we could not determine the type.
Before proceeding with the analysis (i.e. the construction of PW/P−ABL diagrams), we checked the goodness of the Gaia astrometric solution for the 2116 MW DR2 Cepheids. According to Lindegren et al. (2018) a parameter measuring the goodness of the fit is the astrometric_excess_noise (ϵi), measuring the excess of noise of the source. If ϵi > 0, the residuals are statistically larger than expected. The additional parameter astrometric_excess_noise_sig (D) measures the significance of ϵi. If D ≤ 2 then ϵi is probably not significant and the source could have a good astrometric solution even if ϵi is large. More recently, Lindegren (2018) devised a new parameter called the renormalised unit weight error (RUWE) that is not part of the official Gaia DR2; this parameter consists in a renormalisation of the astrometric χ2. According to Lindegren (2018) values of RUWE ≤1.4 should indicate good astrometry. We cross-matched the two indicators and decided to take as objects with good astrometry those with RUWE ≤1.4, ϵi ≤ 1, D ≤ 2, resulting in 151 out of 2116 stars with astrometry that is not reliable. The position of these stars in the PW/P−ABL relations was not taken into account for the classification, which then was based only on the shape of the LCs and on Fourier parameters.
Having set out all the tools, we proceeded with the reclassification by looking first at the position of the star in the PW/P−ABL relations. Because of the large relative error on parallax, the position of the targets in these diagrams is often ambiguous, i.e. compatible with different cepheid types. This occurs in particular for periods shorter than three days, i.e. characteristics of DCEPs, ACEPs and BLHERs. Moreover, DCEPs and WVIRs candidate positions largely overlap when the relative error on the parallax is larger than ∼30%. We then passed to a visual inspection of the LCs and of the period-Fourier parameters diagrams. Particularly useful were the P-R21 and the P-ϕ21 diagrams to separate DCEP_F from DCEP_1O and low-period DCEP_F from ACEP_F and BLHER, respectively. Despite all these efforts, in some cases the classification of Cepheids with sawtooth LC shape and periods ∼1−2 days was difficult, as the shape of the LCs of DCEP_F, ACEP_F, and BLHER are very similar in this period range and the differences can only be revealed in very well sampled and precise LCs; this condition is not always fulfilled in our case. Also the position of these objects in the P-ϕ21 diagram was sometimes not conclusive. In some ambiguous cases we assigned to the ACEP class objects with high Galactic latitude, as we do not expect DCEPs in the MW halo. A similar distinction cannot be carried out between BLHER and ACEPs, as these classes share the same locations in the MW. In any case, the classification of these objects might be subject to a revision when more accurate Gaia parallaxes and metallicity estimates are available, given that both ACEPs and BLHERs are expected to be more metal poor with respect to DCEPs; this classification will allow us to disentangle clearly the PL/PW relations for the different cepheid types as occurs in the LMC/SMC. For 13 objects with clear cepheid-like LC and correct position in the P-Fourier parameters diagrams we were not able to assign a more precise type, and we indicated these sources with CEP. Their detailed subclassification will be determined using future Gaia releases.
The result of the procedure described above is shown in Table 5, in which we report for each of the 2116 MW Cepheids the new classification and all the data from Gaia DR2 used in the reclassification process. These include the parameters to estimate the goodness of the astrometry and the parameter E(BP/RP), indicating the excess of flux in the GBP, GRP bands with respect to the G band. Values larger than 2 usually indicate problems with colours. This parameter is reported for completeness but it affects very few objects. A detailed description of the different columns can be found in the table caption. In the notes (last column) we report special cases, for example when the literature period was used or the astrometry was not usable. An inspection of the table reveals that no classification was possible for 128 objects for various reasons specified in the notes, of which the most common are the lack of precise parallaxes or LCs that are scanty or incomplete. A total of 1257 stars have been classified as Cepheids of any type: 84 objects as RR Lyrae and 647 as variables of other type (in addition to the 128 stars with no classification).
Table with the new classification.
An overall comparison of the new classification for the 1257 Cepheids with the literature is shown in Table 6. An inspection of the table shows that we changed the literature classification for 270 objects, whereas 274 are new Cepheids completely unknown in the literature or indicated as variable.
Comparison of the reclassified object with the literature.
To visualise the results, we show in Fig. 3 (top panels) the PW relations for the stars classified as Cepheids except those with negative parallaxes (203 objects). Error bars are not shown for clarity reasons. The different types of variables are identified in the figure with different colours (see caption of the figure). An inspection of the figure reveals that because of the large errors in parallaxes, objects belonging to different cepheid types are mixed and it is not easy to define tight PW relations as those for the LMC/SMC. The situation is improved if we restrict to objects with relative error on parallaxes lower than 20%. This is shown in the bottom panels of Fig. 3.
 |
Fig. 3. Results for the reclassified MW sample: PW relations. The colour code is as in Fig. 1. Top and bottom panels: complete sample and that with relative error on parallax better than 20%, respectively. The solid lines represent the least-squares fit to the data obtained with the ABL method (see text). The PW relations are of the form WA = α + β log P. Left panels: PW relations obtained with β coefficient treated as unknown parameter in Eq. (7). Right panels: β coefficient fixed and equal to that obtained from the LMC. |
We can compare these results with those reported in Fig. 7 of Clementini et al. (2019). A large part of the objects below the dashed line in that figure, more than 700 objects that were expected to be contaminating stars, now disappear and are classified as “OTHER” or not classified; about 150 of these were known in the literature as non-pulsating variables (see Table 2). However not all the objects in the lower part of the diagram disappeared, as several objects that are clearly cepheid variables can be found several magnitudes below (some also above) the relevant PW sequence. This is not surprising since, among the other issues: First, the astrometric solution for DR2 did not take into account duplicity and therefore the presence of companions can not only affect the photometry, but also the parallax. Second, the chromatic correction for the astrometric solution is based on the mean magnitude and not on the epoch colour (see Lindegren et al. 2018).
The P-R21/ϕ21 and P-R31/ϕ31 diagrams for the reclassified Cepheids are shown in Fig. 4. A comparison with the similar Figs. 37 and 38 of Clementini et al. (2019) shows that the sequences of the different types of Cepheids are now better defined and more congruent with those in the MCs.
Similarly, the location on the sky in Galactic coordinates for the reclassified Cepheids is shown in Fig. 5. Left and right panels of the figure display the location of DCEPs and ACEPs/T2CEPs, respectively. The DCEPs are now located preferentially along the MW disc, as expected for this population I stars, whereas ACEP/DCEP are distributed more homogeneously across the MW including the centre and the halo, as expected (compare with Fig. 39 in Clementini et al. 2019).
 |
Fig. 5. Aitoff projection in Galactic coordinates of the objects reclassified in this work. Left panel: DCEPs (pulsating in any mode: red filled circles). Right panel: T2CEPs (of any type: blue filled circles) and ACEPs (pulsating in any mode: magenta filled circles). |
3.2.1. Cepheid stars hosted by stellar clusters or dwarf galaxies orbiting the MW
Having completed the reclassification, we checked whether some of the objects comprised in the MW sample are actually hosted by a stellar systems such as Galactic open or globular clusters (OC; GC) or by dwarf galaxies orbiting the MW. To reach our goal, we first inspected the literature and then tested new possible associations. As for the literature, we relied on the work by Anderson et al. (2013) and by Clement et al. (2001) for the association between DCEPs and open clusters and between RRLs/ACEPs/T2CEPs, and GCs. Different sources were adopted for the association with dwarf galaxies in the local group. The result of this work is reported in Table 7. An inspection of the table shows that 53 and 66 Cepheids of different types were already known from the OGLE survey to be hosted by LMC and SMC, respectively.
Association of pulsator in the all sky sample with open/globular clusters and with dwarf galaxies satellites of the MW.
We also searched additional associations between Cepheids in the MW sample and the above quoted stellar systems. However, we did not investigate new associations between DCEPs and OCs, as this complex work would deserve an entire new paper. We searched new MCs objects by simply overlapping the Cepheids in the surroundings of these galaxies (i.e. from −56° ≤Dec ≤ −80°, 0h ≤ Ra ≤ 4h and 4h ≤ Ra ≤ 8h for the SMC and LMC, respectively) with the precise PL/PW relations holding for these systems. In case an object with a certain cepheid type falls within 3σ of the relative PL/PW sequences (Table 1), we considered a positive match and assigned the object to the LMC or SMC. In this way we assigned 8 and 7 new Cepheids of different types to the LMC and SMC, respectively (see Table 7 for details). Thus we have a total of 61 and 73 Cepheids hosted by the LMC and SMC, respectively. These objects were then used to derive the PL/PW relations for the MCs calculated in Sect. 2 and listed in Table 1. The effect of the few tens DCEPs added to the LMC/SMC samples is insignificant, whereas the addition of the ACEPs increased the sample significantly.
As for the possible association with GCs or other dwarf galaxies in the local group, we cross-matched the position of the Cepheids in the MW sample with the positions of these objects, looking for objects within the tidal radii of GCs or within twice the semimajor axes of the dwarf galaxies; we adopted Harris (1996) or McConnachie (2012) for the positions and tidal radii or semimajor axes values for clusters or dwarf galaxies, respectively. We then used Gaia DR2 photometry and proper motions (PMs) to check if the target has a position in the colour-magnitude diagram (CMD) and PMs compatible with the rest of the stars of the investigated system. As a result of this exercise, we were able to associate 1 ACEP_F variable with the URSA MINOR dwarf spheroidal galaxy, 1 WVIR pulsator with the GC NGC 6254, and a variable of unknown type to NGC 6266 (see Table 7).
3.2.2. Distribution of the MW DCEPs on the Galactic plane
To further show the properties of the clean DCEPs sample, it is interesting to investigate the distribution of these pulsators on the Galactic plane. To this aim, we first calculate the Galactocentric Cartesian distances by subtracting the heliocentric space vector of the Galactic centre, D0 from the heliocentric space vector of our targets D⊙ as follows:
or
where D0 is the distance of the Sun from the Galactic centre and l, b, and d the Galactic longitude, Galactic latitude, and heliocentric distance, respectively, of each DCEP. The heliocentric distances d in kpc were obtained from the PW obtained for the MW DCEP_F sample (first line of Table 3, see next section) using the simple equation
where W and WA are the apparent and absolute Wesenheit magnitudes, respectively. We also used the same procedure for DCEP_1O (because their PW relation is much more uncertain), by fundamentalising their periods using the equation PF = P1O/(0.716−0.027 log P1O), where PF and P1O are the periods of DCEP_F and DCEP_1O, respectively (Feast & Catchpole 1997). Finally, the distance of the targets from the Galactic centre is given as
The distribution of DCEPs on the Galactic plane is shown in the top panel of Fig. 6, where known and newly discovered DCEPs are depicted with blue and red symbols, respectively. The figure shows that, as expected, most of the known pulsators are placed within few kiloparsec from the Sun, whereas the majority of the new sources are further away. We also note that the DCEPs investigated in this work trace the Local Arm and the Perseus Arm. It is also interesting to look at the distribution of the pulsators around the Galactic plane. This is shown in the bottom panel of Fig. 6, where we plot the height (Z) of each object as a function of the Galactocentric distance RGC for selected intervals of the Galactocentric angular coordinate Φ that is 0 in the direction of the Sun and increases counterclockwise. The figure clearly shows the presence of the well-known disc warp, especially for 0° < Φ < 120°. These results are in agreement with the works by Chen et al. (2019) and Skowron et al. (2018), who used different DCEP samples to study the warp of the MW disc. A detailed discussion of the warp as traced by DCEPs is beyond the scope of present paper and the works cited provide in-depth discussions on the arguments.
 |
Fig. 6. Top panel: polar map of the Galactic plane depicted by known (blue filled circles) and newly discovered (red filled circles) DCEPs (pulsating in any mode). The Galactic centre is in the middle; the circles have radii of 10, 20, and 30 kpc, respectively. A yellow disc represents the position of the Sun. We note that the Galactocentric polar coordinate Φ is 0° in the direction of the Sun. Bottom panel: distribution of the distances from the Galactic plane (Z) as a function of the Galactocentric distance (RGC) for different intervals of Φ. The warping of the disc is clearly visible. |
4. PW relations for MW Cepheids
The new dataset of reclassified Cepheids allows us to derive the PW relation directly from the data for MW DCEPs and T2CEPs. We preferred not to try with ACEPs because of the paucity of the sample and the considerable dispersion in the PW plane, resulting from the large parallax errors; ACEPs are generally significantly fainter than DCEPs. We note that the 107 DCEPs belonging to LMC/SMC (see Sect. 7) were excluded from the MW DCEP sample adopted for the following analysis to avoid contamination by much less metallic objects with respect to the MW sources. We decided not to exclude T2CEPs from both MCs and other GC/dwarf galaxies satellites of the MW because the properties of these objects are expected to be more homogeneous in different environments.
To use all the Cepheids in our sample we are forced to adopt only the Wesenheit magnitude, as we do not know individual reddenings for each cepheid, making impossible for the moment to derive meaningful PL relations. Similarly, we did not attempt to add a metallicity term in Eq. (7) (see below), as this information is lacking for a consistent part of our sample.
To derive the PW relations we decided to use the ABL defined below. We underline that the adoption of this quantity has the decisive advantage to use the parallax in a linear fashion, avoiding almost any kind of bias, as no selection is done on the cepheid sample. Indeed, the employment of the ABL allows us to include in the analysis objects with negative parallaxes. A detailed discussion of the advantages of the ABL method is provided in other papers (see e.g. Arenou & Luri 1999; Gaia Collaboration 2017).
The ABL for the absolute Wesenheit magnitude WA is defined as follows:
where we used the definition of PW relation: WA = α + β log P; WA and W are the absolute and relative Wesenheit magnitudes, respectively. The observed quantities are W, P, and ϖ. The unknown α and β values can be obtained using a least-squares fit procedure.
We applied this technique to estimate the PW relations for DCEP_F, DCEP_1O, and T2CEP, where this last sample includes only BLHER and WVIR as above for the LMC and SMC. In more detail, the fitting procedure has been carried out using the nonlinear least-squares (nls) routine included in the R package7. We adopted a weighted fitting conjugated with the bootstrap method to measure robust errors on the parameters of the fit. In practice, the procedure is repeated 1000 times and for each bootstrap we obtained a value of α and β; we increased the number of bootstraps until the results did not depend on this number. The average values for these parameters and their standard deviations are obtained from the resulting distributions. An example of the results is shown in Fig. 7, where the distributions of α and β are reported, as well as that of the residuals around the ABL function. The results of the fitting procedure for the different cases are shown in the first three rows of Table 3.
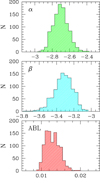 |
Fig. 7. Example of the results of the bootstrap procedure described in the text in the case of the PW in the form WA = α + β log P applied to DCEP_F. From top to bottom, the different panels show the distribution of the parameters α, β and of the residuals of data around the ABL function, respectively. |
A comparison of the PW slopes between LMC and MW in Tables 1 and 3 reveals that the slopes of the PW relations for the DCEP_F and T2CEPs are completely consistent with each other within the errors, whereas for DCEP_1O the discrepancy is of the order of 2σ level, where the slope of the MW sample is steeper than that of LMC. However the large error on the slope of the MW sample makes this comparison not very stringent.
We note that the low dependence on metallicity of the slope for DCEP_Fs is in agreement with previous works (both in theoretical and observational) as it is generally found that the slope of the PW for many different band combinations has a very small dependence on the metallicity (see e.g. Fiorentino et al. 2007, 2013; Ngeow et al. 2012; Di Criscienzo et al. 2013; Gieren et al. 2018, and references therein). We return to this argument in the next section. Similarly, for T2CEPs we do not find a significant dependence of the slope of the PW on the average metallicity of the parent population, again in agreement with literature (see e.g. Matsunaga et al. 2009, 2011; Ripepi et al. 2015).
To the aim of comparing the zero points of the PW relations holding for MW and LMC, we imposed the proper values of β for the LMC in Eq. (7) and rerun the fitting procedure with the same modality as before. The result of this operation is reported in the second series of three rows in Table 1 and graphically in the right panels of Fig. 3. As expected the zero points of the relations for DCEP_Fs and T2CEPs are not significantly different than in the previous case, whereas the contrary is true for DCEP_1Os. We use these results in Sect. 4.2.
As a final note, we underline that because of the lack of thorough information in the literature, in this work we do not consider the source of uncertainty represented by the duplicity among DCEPs whose incidence is highly uncertain, but estimated to be as large as 35–50% or even more (see Anderson & Riess 2018, and references therein). The presence of companions for DCEPs affects not only the parallaxes measured by Gaia (duplicity is not taken into account in DR2), but also their photometry, thus possibly representing a potential significant source of uncertainty. The future Gaia data releases will allow us to also face this important issue.
4.1. PL relations in G, GBP, and GRP bands for MW DCEPs
To the aim of providing PL relations in the Gaia G, GBP, and GRP bands for the MW Cepheids, we need an estimate of the reddening. As the Gaia DR2 does not include reliable interstellar extinctions yet, we have to use literature data. Thus, we found that reliable E(B − V) values are available for a subsample of 301 objects classified as DCEPs in Table 5. The main source for the reddening was Fernie (1990), whereas additional values were taken from Majaess et al. (2008), Ngeow (2012), and Kashuba et al. (2016). Only a few objects possess reliable reddening estimates among MW T2CEPs, therefore we did not try to calculate PLs for these objects. As for the metallicity, we used the results by Genovali et al. (2013, 2014, 2015).
The reddening values found in the literature are listed in Table 8 together with the mode of pulsation (268 and 33 DCEP_Fs and DCEP_1Os, respectively), metallicity estimate, and sources for reddening and metallicity, respectively (last two columns).
Reddening and metallicity for the 301 known MW Cepheids having Gaia DR2 intensity averaged magnitudes in the G, GBP, and GRP bands coming from the Cepheids&RRLyrae SOS pipeline.
Before proceeding, we first have to estimate the absorption in the Gaia bands in terms of E(B − V). To this aim we used again the Jordi et al. (2010) tables, and adopting the same procedure outlined in Sect. 2, we obtained starting values of 2.90, 3.60, and 2.15 for the ratios A(G)/E(B − V), A(GBP)/E(B − V), and A(GRP)/E(B − V), respectively.
We used again the ABL formulation of Eq. (7) and the bootstrap technique to derive the relevant PL/PW relations. Now the observed magnitudes in the exponent of the right term can be the apparent Wesenheit W or the observed de-reddened magnitudes G0, 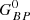 , and
, and 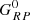 . With this formulation and the same procedure of Sect. 4 we calculated the PL relations in the Gaia G, GBP, and GRP band for the MW DCEPs subsample described above. Analysing the dispersion of the residuals, we checked the above defined total-to-selective extinction ratios, by varying their values and re-estimating the dispersion of the residuals (of the ABL) at any step. We retained the ratio values that returned the smallest dispersions. These values are shown in Eqs. (8)–(10), where the uncertainties were estimated by looking at the values of total-to-selective extinction ratios that produced an increase in the dispersion. We remark that, owing to the large G, GBP and GRP bandwidths, these total-to-selective ratios are only valid in the interval of colours spanned by Cepheids. These relations are written as
. With this formulation and the same procedure of Sect. 4 we calculated the PL relations in the Gaia G, GBP, and GRP band for the MW DCEPs subsample described above. Analysing the dispersion of the residuals, we checked the above defined total-to-selective extinction ratios, by varying their values and re-estimating the dispersion of the residuals (of the ABL) at any step. We retained the ratio values that returned the smallest dispersions. These values are shown in Eqs. (8)–(10), where the uncertainties were estimated by looking at the values of total-to-selective extinction ratios that produced an increase in the dispersion. We remark that, owing to the large G, GBP and GRP bandwidths, these total-to-selective ratios are only valid in the interval of colours spanned by Cepheids. These relations are written as
Finally, adopting the relations of Eqs. (8)–(10) we calculated the PL relations in the Gaia G, GBP, and GRP band for the MW DCEPs subsample. The results are shown in the second part of Table 3 and Fig. 8. We note that we also recalculated the PW using the subsample adopted here. An inspection of Table 3 shows agreement within 1σ between the PWs derived using the full sample and subsample of DCEP_Fs. The same comparison is less meaningful for DCEP_1Os because of the huge errors caused by the intrinsic large dispersion of the full sample and by the small statistic in the case of the subsample.
 |
Fig. 8. Resulting PL/PW relations for the MW selected sample of DCEPs having reddening estimate and intensity averaged magnitudes in G, GBP and GRP bands coming from the Cepheids&RRLyrae SOS pipeline. Orange and light blue symbols represent DCEP_F and DCEP_1O, respectively. The solid lines are the least-squares fits to the data obtained using the ABL formulation (see text). As in Fig. 3, left and right panels show the relations obtained leaving all the parameters free to vary and fixing the value of β in Eq. (7), respectively. The coefficient of the regression lines are shown in Table 3. An underscript “A” means absolute magnitudes whereas a superscript 0 characterises de-reddened quantities. |
As for the subsample discussed in this section we also have the information about metallicity available (see Table 8); we tried to derive PW relations using the following ABL definition including an additional term to take into account the dependence of the zero point on the metallicity [Fe/H] as follows:
where WA and W are the absolute and relative Wesenheit magnitudes, respectively. In principle, the β term also depends on metallicity, but a comparison of the slopes for DCEP_Fs in the LMC (Table 1) and MW (first line of Table 3), shows that the dependence of β on metallicity can be expected reasonably low to be ignored. As this is not true for the PLs, in the following we use only the Wesenheit magnitudes.
Adopting the usual bootstrap technique applied to the ABL formulation of Eq. (11), we obtain the result reported in the penultimate line of Table 3 and Fig. 9. The derived metallicity term γ = −0.237 ± 0.199 dex mag−1, even if only barely significant (1σ), means that at fixed period and colour, metal poor stars are fainter. These results are in good agreement with Groenewegen (2018) who derived PL/PW relations in the optical and near-infrared bands adopting a subsample of DCEPs with Gaia DR2 parallaxes and literature photometry/spectroscopy and also with theoretical predictions for the dependence of DCEP optical PW functions on metallicity (see Fig. 9 in Caputo et al. 2000). Again, to compare the results for the MW and LMC, we recalculated the ABL of Eq. (11) but imposed the LMC value for the term β. The outcome of this exercise is shown in the last line of Table 3 and Fig. 9. Not surprisingly, the metallicity term becomes much less significant, as part of the metallicity dependence has been absorbed by the variation of the slope.
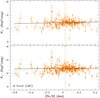 |
Fig. 9. Dependence of the PW relation from [Fe/H]. Orange symbols represent DCEP_F pulsators, whereas the solid lines are the results of the fitting procedure for the ABL formulation of Eq. (11) in two cases: (i) all parameters free to vary (top panel); (ii) β parameter fixed to the value of LMC (bottom panel). The coefficient of the regression lines are shown in the last two lines of Table 3. |
To obtain more stringent constraint on the dependence of DCEP PW and PL relations on metallicity we require the more precise parallaxes expected in the next Gaia releases; we also need to increase the sample of DCEPs possessing accurate and homogeneous measurements of metallicity by means of high resolution spectroscopy, possibly extending the metallicity range spanned by the MW DCEPs analysed in this work. In fact, only a few objects reach a metallicity value as low as that of the LMC ([Fe/H] ∼ −0.4 dex); the large majority of the pulsators cluster around [Fe/H] ∼ +0.05 ± 0.13 dex (see Table 8).
4.2. Distance of the LMC and zero points of the Gaia DR2 parallaxes for Cepheids
In the previous sections we estimated the PW relations in the Gaia bands for both the LMC and the MW using the slopes of the LMC. This operation makes it straightforward to estimate the distance of the LMC, that is an important anchor for the extragalactic distance scale, by comparing the zero points of the relative and absolute PWs in the LMC and MW, respectively. We performed this exercise for DCEP_Fs and T2CEPs as the PW for DCEP_1Os is too uncertain. For DCEP_Fs we used both the PW without and with the metallicity term. In this last case we adopted [Fe/H] = −0.43 dex for the LMC (Mucciarelli et al. 2011), whereas for the MW we took the average of the distribution of metallicities listed in Table 8, i.e. [Fe/H] = +0.05 ± 0.13 dex. The results are reported in the second column of Table 9, where the errors on the distance moduli (DMs) have been calculated summing in quadrature the uncertainties on the zero points (α terms) and the metallicity (γ) when needed (see Tables 1 and 3). As a result, the DMLMC obtained are always significantly longer than the commonly accepted value of ∼18.50 mag (see e.g. Pietrzyński et al. 2013; de Grijs et al. 2014; Riess et al. 2018b), even if the parallax zero point correction of +0.046 mas by Riess et al. (2018b) has already been applied.
Results for the distance of LMC (see text).
Conversely, if we use this value for the LMC distance as reference, we can recalculate the zero point offset of the Gaia DR2 parallaxes, discovering that the parallaxes zero point offset needed to obtain a DMLMC ∼ 18.50 mag is of the order of +0.1 and +0.07 mas for the DCEP_F and T2CEPs, respectively. These results are agree well with a similar analysis carried out by Groenewegen (2018), which provides a more detailed discussion.
5. Summary
In this paper we have re-analysed the sample of Cepheids published in the context of Gaia DR2 by Clementini et al. (2019). The main achievements of this work are the following:
-
We calculated the PL/PW relations in the Gaia bands G, GBP and GRP for all the cepheid types (DCEP, ACEP, T2CEP) both in the LMC and SMC. These relations will be incorporated in the next versions of the Gaia Cepheids&RRLyrae SOS pipeline adopted to classify the Cepheids in the Gaia DR3 (see Clementini et al. 2019).
-
We carried out a careful re-analysis of the classification of the 2116 Cepheids of all types reported by Clementini et al. (2019) as belonging to the MW. We first conducted a literature search for alternative classification and period determination for these objects. Afterwards we reclassified each object by visually inspecting its LC and position in the PW and period-Fourier parameters. As a result, a total of 1257 stars were classified as cepheid of any type, 84 objects as RR Lyrae, and 647 as variables of other type (in addition to the 128 stars with no classification). Among these 1257 Cepheids, 713 were Cepheids already known in the literature, 274 are new Cepheids completely unknown in the literature or indicated generically as variable, and 270 objects were known in the literature with a different classification. In total we classified 800 DCEPs, 108 ACEPs, and 336 T2CEPs, plus 13 Cepheids for which we were not able to find an appropriate subclassification in type. Among the MW sample we individuated a total of 61 and 73 Cepheids of different types hosted by the LMC and SMC, of which 8 and 7 of these samples were not known in the literature as LMC/SMC objects. In addition, we were able to associate an ACEP_F variable with the URSA MINOR dwarf spheroidal galaxy, a WVIR pulsator with the GC NGC 6254, and a variable of unknown type to NGC 6266.
-
Using the reclassified cepheid sample, we used the ABL formulation to derive PW relations in the Gaia bands for the MW DCEP_F, DCEP_1O and T2CEP (BLHER and WVIR). The use of the ABL formulation allows us to derive slopes and zero points for the PW that are almost unbiased, as we did not carry out any kind of selection on the sample. The adoption of a subsample (301 objects) of well-characterised MW DCEPs possessing reliable reddening and metallicity estimates, also allowed us to calculate the PL relations for the G, GBP, and GRP bands for DCEP_F and DCEP_1O. In addition, using the quoted subsample, we were able to investigate for the first time the dependence on metallicity of the PW relation for DCEP_Fs in the Gaia bands. As a result, we derived a modestly significant (1σ) dependence (γ = −0.237 ± 0.199 dex mag−1), in the sense that at fixed period and colour metal poor stars are fainter. More precise parallaxes and spectroscopic measures will be needed to address firmly this point.
-
We also calculated the PW relations for the MW by imposing the slope of the PW relations in the LMC and redetermining the zero points. By comparing the relative zero points between the MW and the LMC PW for DCEP_F and T2CEP, we obtained two different estimates of the LMC distance. These values are larger than the usually accepted value for the LMC DM ∼18.50 mag. To reconcile the results found in this work with the latter, we need to increase the zero points of the Gaia DR2 parallax by at least 0.07 mas, in agreement with recent literature results.
The Gaia DR2 photometry and parallax for Cepheids in the MW allowed a significant step forward in the classification of the different type of Cepheids. Indeed, the excellent photometric quality, even conjugated the relatively low-accurate parallaxes for the sample of objects discussed in this paper, allowed us to revise the literature classification for more than 200 objects.
In conclusion, without entering in details beyond the scope of present paper, the results presented in this work seem to confirm the Groenewegen (2018) suggestion that the parallaxes for MW Cepheids in the Gaia DR2, appear still too uncertain to allow a significative decrease of the error on the value of H0. To this we have to add the uncertainties on the extinction law, the impact of metallicity, and binarity, affecting both astrometry and photometry of Cepheids.
Great improvements are awaited from the future Gaia DR3 and DR4 for all these issues. Indeed, these releases are expected to present extremely accurate photometry and astrometry corrected for the effect of multiplicity, as well as individual information on reddening, metallicity, and duplicity for a large portion of the sky. Therefore, DR3 and DR4 will certainly allow us to make consistent steps forward in the accuracy of the extragalactic distance scale, helping to reduce the uncertainty on the value of H0 to less than 1%.
DCEP_MULTI class is in turn subdivided into subclasses according to the period ratios of the modes pulsating simultaneously, for example fundamental/first overtone (F/1O). In this paper when we classify an object as DCEP_MULTI, we are assuming that the period ratios found in the Gaia DR2 are correct.
Acknowledgments
We thanks our anonymous referee whose comments helped to improve the paper. We gratefully thank G. Clementini for stimulating discussions on the subject of this paper. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. In particular, the Italian participation in DPAC has been supported by Istituto Nazionale di Astrofisica (INAF) and the Agenzia Spaziale Italiana (ASI) through grants I/037/08/0, I/058/10/0, 2014-025-R.0, and 2014-025-R.1.2015 to INAF (PI M.G. Lattanzi). This research has made use of the International Variable Star Index (VSX) database, operated at AAVSO, Cambridge, Massachusetts, USA. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France
References
- Alfonso-Garzón, J., Domingo, A., Mas-Hesse, J. M., & Giménez, A. 2012, A&A, 548, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, R. I., & Riess, A. G. 2018, ApJ, 861, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, R. I., Eyer, L., & Mowlavi, N. 2013, MNRAS, 434, 2238 [NASA ADS] [CrossRef] [Google Scholar]
- Andrae, R., Fouesneau, M., Creevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arenou, F., & Luri, X. 1999, Harmonizing Cosmic Distance Scales in a Post-HIPPARCOS Era, 167, 13 [Google Scholar]
- Berdnikov, L. N., Kniazev, A. Y., Sefako, R., et al. 2015, Astron. Lett., 41, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Bersier, D., & Wood, P. R. 2002, AJ, 123, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Caputo, F., Marconi, M., & Musella, I. 2000, A&A, 354, 610 [NASA ADS] [Google Scholar]
- Catelan, M., & Smith, H. A. 2015, Pulsating Stars (Wiley-VCH) [CrossRef] [Google Scholar]
- Chen, X., Wang, S., & Deng, L. 2019, Nat. Astron., 202, 33 [Google Scholar]
- Clement, C. M., Muzzin, A., Dufton, Q., et al. 2001, AJ, 122, 2587 [NASA ADS] [CrossRef] [Google Scholar]
- Clementini, G., Ripepi, V., Leccia, S., et al. 2016, A&A, 595, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clementini, G., Ripepi, V., Molinaro, R., et al. 2019, A&A, 622, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coppola, G., Marconi, M., Stetson, P. B., et al. 2015, ApJ, 814, 71 [NASA ADS] [CrossRef] [Google Scholar]
- de Grijs, R., Wicker, J. E., & Bono, G. 2014, AJ, 147, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Di Criscienzo, M., Marconi, M., Musella, I., Cignoni, M., & Ripepi, V. 2013, MNRAS, 428, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, A. J., Graham, M. J., Djorgovski, S. G., et al. 2014, ApJS, 213, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, A. J., Djorgovski, S. G., Catelan, M., et al. 2017, MNRAS, 469, 3688 [NASA ADS] [CrossRef] [Google Scholar]
- Debosscher, J., Blomme, J., Aerts, C., & De Ridder, J. 2011, A&A, 529, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubath, P., Rimoldini, L., Süveges, M., et al. 2011, MNRAS, 414, 2602 [NASA ADS] [CrossRef] [Google Scholar]
- Feast, M. W., & Catchpole, R. M. 1997, MNRAS, 286, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Fernie, J. D. 1990, ApJS, 72, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Fiorentino, G., Marconi, M., Musella, I., & Caputo, F. 2007, A&A, 476, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiorentino, G., Musella, I., & Marconi, M. 2013, MNRAS, 434, 2866 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Clementini, G., et al.) 2017, A&A, 605, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genovali, K., Lemasle, B., Bono, G., et al. 2013, A&A, 554, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genovali, K., Lemasle, B., Bono, G., et al. 2014, A&A, 566, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genovali, K., Lemasle, B., da Silva, R., et al. 2015, A&A, 580, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieren, W., Storm, J., Konorski, P., et al. 2018, A&A, 620, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2018, A&A, 619, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, D. I., Harrison, T. E., & McNamara, B. J. 2009, AJ, 138, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Holl, B., Audard, M., Nienartowicz, K., et al. 2018, A&A, 618, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivezić, Ž., Smith, J. A., Miknaitis, G., et al. 2007, AJ, 134, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Jayasinghe, T., Kochanek, C. S., Stanek, K. Z., et al. 2018, MNRAS, 477, 3145 [NASA ADS] [CrossRef] [Google Scholar]
- Jordi, C., Gebran, M., Carrasco, J. M., et al. 2010, A&A, 523, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kashuba, S. V., Andrievsky, S. M., Chekhonadskikh, F. A., et al. 2016, MNRAS, 461, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D.-W., Protopapas, P., Bailer-Jones, C. A. L., et al. 2014, A&A, 566, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kinemuchi, K., Harris, H. C., Smith, H. A., et al. 2008, AJ, 136, 1921 [NASA ADS] [CrossRef] [Google Scholar]
- Leavitt, H. S., & Pickering, E. C. 1912, Harvard College Observatory Circular, 173, 1 [Google Scholar]
- Lemasle, B., Hajdu, G., Kovtyukh, V., et al. 2018, A&A, 618, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L. 2018, “Re-normalising the astrometric chi-square in Gaia DR2”, Gaia Technical Note: GAIA-C3-TN-LU-LL-124-01 [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madore, B. F. 1982, ApJ, 253, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Majaess, D. J., Turner, D. G., & Lane, D. J. 2008, MNRAS, 390, 1539 [NASA ADS] [Google Scholar]
- Martínez-Vázquez, C. E., Stetson, P. B., Monelli, M., et al. 2016, MNRAS, 462, 4349 [NASA ADS] [CrossRef] [Google Scholar]
- Matsunaga, N., Feast, M. W., & Menzies, J. W. 2009, MNRAS, 397, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Matsunaga, N., Feast, M. W., & Soszyński, I. 2011, MNRAS, 413, 223 [NASA ADS] [CrossRef] [Google Scholar]
- McConnachie, A. W. 2012, AJ, 144, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Mucciarelli, A., Cristallo, S., Brocato, E., et al. 2011, MNRAS, 413, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Ngeow, C.-C. 2012, ApJ, 747, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Ngeow, C.-C., Kanbur, S. M., Bellinger, E. P., et al. 2012, Ap&SS, 341, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Palaversa, L., Ivezić, Ž., Eyer, L., et al. 2013, AJ, 146, 101 [CrossRef] [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gieren, W., et al. 2013, Nature, 495, 76 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Planck Collaboration Int. XLVI. 2016, A&A, 596, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pojmanski, G. 1997, Acta Astron., 47, 467 [NASA ADS] [Google Scholar]
- Pojmanski, G. 2002, Acta Astron., 52, 397 [NASA ADS] [Google Scholar]
- Richards, J. W., Starr, D. L., Miller, A. A., et al. 2012, ApJS, 203, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Ripepi, V., Moretti, M. I., Marconi, M., et al. 2012, MNRAS, 424, 1807 [NASA ADS] [CrossRef] [Google Scholar]
- Ripepi, V., Moretti, M. I., Marconi, M., et al. 2015, MNRAS, 446, 3034 [NASA ADS] [CrossRef] [Google Scholar]
- Ripepi, V., Marconi, M., Moretti, M. I., et al. 2016, ApJS, 224, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Ripepi, V., Cioni, M.-R. L., Moretti, M. I., et al. 2017, MNRAS, 472, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018a, ApJ, 855, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018b, ApJ, 861, 126 [Google Scholar]
- Samus’, N. N., Kazarovets, E. V., Durlevich, O. V., Kireeva, N. N., & Pastukhova, E. N. 2017, Astron. Rep., 61, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., McMillan, P., & Eyer, L. 2019, ArXiv e-prints [arXiv:1902.02355] [Google Scholar]
- Sesar, B., Hernitschek, N., Mitrović, S., et al. 2017, AJ, 153, 204 [Google Scholar]
- Skowron, D. M., Skowron, J., Mróz, P., et al. 2018, ArXiv e-prints [arXiv:1806.10653] [Google Scholar]
- Soszyński, I., Udalski, A., Szymański, M. K., et al. 2008, Acta Astron., 58, 293 [NASA ADS] [Google Scholar]
- Soszyński, I., Udalski, A., Szymański, M. K., et al. 2015a, Acta Astron., 65, 233 [NASA ADS] [Google Scholar]
- Soszyński, I., Udalski, A., Szymański, M. K., et al. 2015b, Acta Astron., 65, 329 [NASA ADS] [Google Scholar]
- Soszyński, I., Udalski, A., Szymański, M. K., et al. 2016, Acta Astron., 66, 131 [NASA ADS] [Google Scholar]
- Soszyński, I., Udalski, A., Szymański, M. K., et al. 2017a, Acta Astron., 67, 103 [NASA ADS] [Google Scholar]
- Soszyński, I., Udalski, A., Szymański, M. K., et al. 2017b, Acta Astron., 67, 297 [NASA ADS] [Google Scholar]
- Soszyński, I., Udalski, A., Szymański, M. K., et al. 2018, Acta Astron., 68, 89 [NASA ADS] [Google Scholar]
- Subramanian, S., & Subramaniam, A. 2015, A&A, 573, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, C. L., Henden, A. A., & Price, A. 2006, Soc. Astron. Sci. Annu. Symp., 25, 47 [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woźniak, P. R., Vestrand, W. T., Akerlof, C. W., et al. 2004, AJ, 127, 2436 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Acronyms for the literature variability types
In Table A.1 we expand the variability types adopted for Table 2.
Acronyms adopted in Table 2 to indicate the different variability types.
All Tables
Table with the literature classification for 1416 objects among the 2116 candidate Cepheids in the MW by Clementini et al. (2019).
Average peak-to-peak amplitude ratio Amp(GBP)/Amp(GRP) for the different types of Cepheids considered in this work.
Association of pulsator in the all sky sample with open/globular clusters and with dwarf galaxies satellites of the MW.
Reddening and metallicity for the 301 known MW Cepheids having Gaia DR2 intensity averaged magnitudes in the G, GBP, and GRP bands coming from the Cepheids&RRLyrae SOS pipeline.
All Figures
 |
Fig. 1. For the LMC, PL/PW relations in the form mag = α + β log P. From top to bottom panels, mag is represented by the apparent W, G, GBP, and GRP magnitudes, respectively. Orange filled circles: DCEP_F; cyan filled circles: DECP_1O; magenta four-starred symbols: ACEP_F; dark green four-starred symbols: ACEP_1O; green open triangles: BLHER; violet open triangles: WVIR; and magenta open triangles: RVTAU. |
| In the text | |
 |
Fig. 2. As in Fig. 1 but for the SMC. |
| In the text | |
 |
Fig. 3. Results for the reclassified MW sample: PW relations. The colour code is as in Fig. 1. Top and bottom panels: complete sample and that with relative error on parallax better than 20%, respectively. The solid lines represent the least-squares fit to the data obtained with the ABL method (see text). The PW relations are of the form WA = α + β log P. Left panels: PW relations obtained with β coefficient treated as unknown parameter in Eq. (7). Right panels: β coefficient fixed and equal to that obtained from the LMC. |
| In the text | |
 |
Fig. 4. Fourier parameters for the reclassified objects. The colour code is as in Fig. 1. |
| In the text | |
 |
Fig. 5. Aitoff projection in Galactic coordinates of the objects reclassified in this work. Left panel: DCEPs (pulsating in any mode: red filled circles). Right panel: T2CEPs (of any type: blue filled circles) and ACEPs (pulsating in any mode: magenta filled circles). |
| In the text | |
 |
Fig. 6. Top panel: polar map of the Galactic plane depicted by known (blue filled circles) and newly discovered (red filled circles) DCEPs (pulsating in any mode). The Galactic centre is in the middle; the circles have radii of 10, 20, and 30 kpc, respectively. A yellow disc represents the position of the Sun. We note that the Galactocentric polar coordinate Φ is 0° in the direction of the Sun. Bottom panel: distribution of the distances from the Galactic plane (Z) as a function of the Galactocentric distance (RGC) for different intervals of Φ. The warping of the disc is clearly visible. |
| In the text | |
 |
Fig. 7. Example of the results of the bootstrap procedure described in the text in the case of the PW in the form WA = α + β log P applied to DCEP_F. From top to bottom, the different panels show the distribution of the parameters α, β and of the residuals of data around the ABL function, respectively. |
| In the text | |
 |
Fig. 8. Resulting PL/PW relations for the MW selected sample of DCEPs having reddening estimate and intensity averaged magnitudes in G, GBP and GRP bands coming from the Cepheids&RRLyrae SOS pipeline. Orange and light blue symbols represent DCEP_F and DCEP_1O, respectively. The solid lines are the least-squares fits to the data obtained using the ABL formulation (see text). As in Fig. 3, left and right panels show the relations obtained leaving all the parameters free to vary and fixing the value of β in Eq. (7), respectively. The coefficient of the regression lines are shown in Table 3. An underscript “A” means absolute magnitudes whereas a superscript 0 characterises de-reddened quantities. |
| In the text | |
 |
Fig. 9. Dependence of the PW relation from [Fe/H]. Orange symbols represent DCEP_F pulsators, whereas the solid lines are the results of the fitting procedure for the ABL formulation of Eq. (11) in two cases: (i) all parameters free to vary (top panel); (ii) β parameter fixed to the value of LMC (bottom panel). The coefficient of the regression lines are shown in the last two lines of Table 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



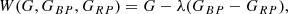
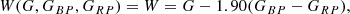
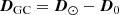
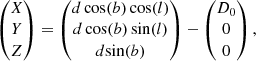
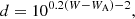
![$$ \begin{aligned} {R}_{\mathrm{GC}}=\sqrt{[d \cos (b) \cos (l) - D_0]^2+d^2 \cos (b)^2 \sin (l)^2+d^2 \sin (b)^2}. \end{aligned} $$](/articles/aa/full_html/2019/05/aa34506-18/aa34506-18-eq18.gif)
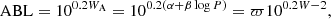
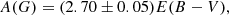
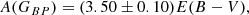
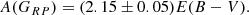
![$$ \begin{aligned} \mathrm{ABL}=10^{0.2 W_{\rm A}}=10^{0.2(\alpha +\beta \log P +\gamma [\mathrm{Fe/H}])}=\varpi 10^{0.2W-2} ,\end{aligned} $$](/articles/aa/full_html/2019/05/aa34506-18/aa34506-18-eq25.gif)