| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | L4 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201935401 | |
| Published online | 05 April 2019 | |
Letter to the Editor
Fast magnetoacoustic wave trains with time-dependent drivers
1
Centre for Fusion, Space and Astrophysics, Department of Physics, University of Warwick, Coventry CV4 7AL, UK
e-mail: christopher.goddard@warwick.ac.uk
2
School of Space Research, Kyung Hee University, 446-701 Yongin, Gyeonggi, Korea
3
Centre for Mathematical Plasma Astrophysics, Mathematics Department, KU Leuven, Celestijnenlaan 200B bus 2400, 3001 Leuven, Belgium
Received:
5
March
2019
Accepted:
18
March
2019
Context. Frequent observations of quasi-periodic rapidly-propagating wave trains in coronal structures have been made in the last decade. The dispersive evolution of fast magnetohydrodynamic waves propagating in coronal waveguides can provide a physical interpretation for many of these observations.
Aims. Previous studies have considered the generation of fast wave trains by impulsive drivers which deposit energy instantaneously. The signatures of dispersively formed wave trains must depend on the temporal nature of the driver. We investigate the effect of varying the temporal width of the driving perturbation.
Methods. 2D magnetohydrodynamic numerical simulations of impulsively generated wave trains in a guiding field-aligned density enhancement were performed with the novel addition of a time-dependant driver.
Results. The final spatial and spectral signatures of the guided wave trains are found to depend strongly on the temporal duration of the initial perturbation. In particular, the wavelength (or frequency) of highest spectral amplitude is found to increase (decrease) with increasing temporal duration, whereas the spectral width decreases. Additionally, the efficiency of generation of fast wave trains is found to decrease strongly with increasing temporal width of the driver, with a cut-off at twice the internal Alfvén crossing time.
Key words: magnetohydrodynamics / methods: numerical / Sun: corona / Sun: oscillations
© ESO 2019
1. Introduction
Active regions in the solar corona are comprised of highly inhomogeneous plasma, containing a range of structures with enhanced (or reduced) density compared to the surrounding plasma. Impulsive energy releases can excite different magnetohydrodynamic (MHD) wave modes within these structures. One such example are rapidly-propagating quasi-periodic wave trains, first detected during eclipses using white-light coronographs (Williams et al. 2001, 2002; Katsiyannis et al. 2003), qualitatively similar time series from radio band data were shown in Roberts et al. (1983).
The spatial and temporal resolution provided by the Solar Dynamics Observatory (SDO) Atmospheric Imaging Assembly (AIA) allows the detection of these propagating quasi-periodic waves in extreme ultraviolet (EUV) images (e.g., Liu et al. 2011; Nisticò et al. 2014), with several recent studies focussing on the apparent initiation mechanism (e.g., Li et al. 2018a; Shen et al. 2018).
These disturbances are interpreted as a series of fast magnetoacoustic waves of the m = 0 azimuthal symmetry (i.e. sausage waves) (e.g., Cooper et al. 2003; Ofman et al. 2011). These are known to be highly dispersive in coronal waveguides if their wavelength is comparable to the waveguide width. Therefore an impulsive broadband driver can result in a quasi-periodic series of fast waves (simply “wave train”, hereafter) if measured a sufficient distance from the perturbation, due to different spectral harmonics propagating at different speeds (Roberts et al. 1983, 1984).
The dispersive formation of these wave trains has been the subject of numerous MHD numerical simulations, the first being Murawski & Roberts (1994). Nakariakov et al. (2004) demonstrated the similarity of the obtained wave signatures to observations, and used wavelet transforms to analyse their time-dependent power spectrum, resulting in a characteristic “crazy tadpole” signature, i.e. a broadband “head” and narrowband “tail”. Since then wavelet analysis has been frequently used to visualise the obtained wave train signatures in both observational and numerical studies. Further theoretical studies have focused on different perpendicular density profiles of the waveguide (e.g., Yu et al. 2017; Li et al. 2018b), wave train formation in current sheets (e.g., Jelínek & Karlický 2012; Mészárosová et al. 2014), accounting for 2D and cylindrical effects (Pascoe et al. 2013; Shestov et al. 2015), amplitudes entering the non-linear regime (Pascoe et al. 2017), and analytical estimations (e.g., Oliver et al. 2015).
Fast magnetoacoustic wave trains in coronal structures are well resolved, temporally and spatially, in modern observations. However, exact details of their excitation, evolution and damping remain unknown, as such their seismological potential has yet to be exploited. Further motivation for the study such wave trains comes from recent advances in the use of radio-band data for their study (Goddard et al. 2016; Kumar et al. 2017; Kolotkov et al. 2018; Kaneda et al. 2018), and their potential role in the modulation of flaring emission for solar and stellar flares (e.g., Van Doorsselaere et al. 2016).
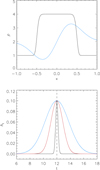 |
Fig. 1. Top panel: transverse density profile of the waveguide. Overplotted in blue is the spatial profile of the vx velocity pulse in arbitrary units. Bottom panel: temporal profile of the driver amplitude for three different driver durations, [0.29, 1.47, 2.94] τAi. The centre of the driving pulse, t0, is indicated by the vertical dashed line. |
These observed wave trains may be excited in coronal structures by some kind of impulsive driver. Candidates include energy deposition during flares and reconnection and mechanical displacement via plasma motions such as jets and coronal mass ejections. These processes all have some characteristic time scale over which they should operate, however to date almost all studies of dispersively formed fast magnetoacoustic wave trains use an instantaneous driver. A harmonic driver was used in Ofman & Liu (2018), however the effect of this on the final wave train signature was not explored. The effect of time-dependent drivers on MHD waves and oscillations have been studied in various other contexts for closed systems; for example driven kink oscillations of coronal loops (e.g., Pascoe et al. 2015; Guo et al. 2019) and the driving of MHD waves in the magnetosphere (e.g., Elsden & Wright 2018).
The aim of this Letter is to study the effect of varying the temporal duration of the driver on the resulting dispersively formed fast wave train, which has yet to be investigated in any capacity. The numerical model is described in Sect. 2 and the results are presented in Sect. 3. Conclusions and discussion of the implications of the results are presented in Sect. 4.
2. Model
The numerical setup is similar to previous studies which have used the 2D slab geometry (e.g., Nakariakov et al. 2004; Pascoe et al. 2017). The magnetic field is straight and uniform in the z-direction, with strength B0. An MHD waveguide is modelled with a field-aligned plasma density enhancement. The density structure transverse to the field (x-direction) is modelled as the generalised symmetric Epstein profile
where ρi is the density at the waveguide centre, ρe is the density outside the waveguide, p determines the density profile steepness, and w is the waveguide half-width. The parameters chosen for this study are ρi/ρe = 4, p = 8 and w = 0.5 (in normalised units). The effect of varying these parameters has been the subject of previous studies, and so they remain constant here.
The plasma is set in equilibrium by defining the internal energy density ϵ as
to counter act the density enhancement, where pgas is the (constant) gas pressure and γ = 5/3. The gas pressure is set to give a plasma beta of β = pgas/pmag = 0.01, where 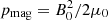 , which is a typical value assumed for solar coronal structures.
, which is a typical value assumed for solar coronal structures.
The time-dependent driver is a localised compressive velocity perturbation of the sausage symmetry applied at the boundary (z = 0), about the centre of the density enhancement (x = 0 = x0). It takes the form
where δx defines the spatial width of the driver, taken to be equal to the waveguide half-width to efficiently excite the fundamental mode of the waveguide. At defines the temporal evolution of the applied perturbation, and takes the form
where A0 is the maximum applied amplitude, taken to be 0.1 for all simulations and σt controls the temporal duration of the perturbation, which is centred on t0. Additionally, we define δt as the full-width at half-maximum (FWHM) of the temporal profile. Examples of the transverse density profile and the spatial and temporal profiles of the driver are shown in Fig. 1.
The MHD code LARE2D (Arber et al. 2001) is used to perform the simulations in the ideal MHD regime. The 2.5D approximation in this code gives ∂/∂y = 0, however due to the equilibrium and driver used vy and By remain zero and the model is essentially 2D.
The resolution used in all simulations was 1200 × 7500 (x, z) grid points, and convergence tests at a resolution of 2400 × 15000 (x, z) grid points show no notable differences. In normalised units the domain size is 110, or 220 w, in the z direction. In normalised “unstretched” units the domain size is 4 in x direction. Open boundary conditions are used for all boundaries except the driven lower z boundary, which has zero-gradient and zero-velocity conditions for all parameters except vx, which is prescribed by the driving Eq. (3). Due to imperfect open boundaries reflected waves occur at the upper and lower x boundaries. To ensure they do not interact with the waveguide the grid spacing in the x direction is severely stretched beyond −1 < x < 1, any deviation in this region is not important as only the guided waves, measured at x = 0, are considered in this study. The simulation domain can be seen in the top panel of Fig. 2.
 |
Fig. 2. Top panel: perturbation to the equilibrium density at t = 110 from a driver with δt = 0.58 τAi. The slow wave can be seen at z ∼ 10 and the fast wave train between z ∼ 40 and z ∼ 100, both propagating to the right. The waveguide width is indicated by 2w, and the magnetic field direction by B. Bottom panel: pertubation to the equilibrium density measured along the centre of the waveguide (x = 0) from the above simulation output. The region between the dashed vertical lines denotes the section of the signal used for analysis of the fast wave train. |
The length scales (X, Z), time scales (T), and speeds (V) in physical units are related to the dimensionless variables via X = x (2w), T = t t0, and V = v v0, where w, t0, and v0 are the chosen normalisation constants and v0 = 2w/t0. The choice of normalisation should naturally be consistent with the MHD approximations. For further details see Arber et al. (2001).
3. Results
Numerical simulations are performed for several values of driver duration in the range 0.29 > δt > 2.94 τAi, relative to the internal Alfvén transit time, τAi = (2w)/CAi (here CAi = 0.5 due to the normalisation). All other parameters remain as defined in Sect. 2. The simulations are run until t = 110, allowing the fast wave train to undergo sufficient dispersive evolution. The density perturbation, ρ − ρi, at t = 110 is then extracted along the z axis at x = 0, as opposed to recording the time evolution at a fixed point in space. An example wave train signature is shown in Fig. 2, showing the fast wave train as well as the broadband slow magnetoacoustic wave which is also excited, from a driver with δt = 0.58 τAi. The vertical dashed lines in the bottom panel denote the section of the signal used for further analysis.
In Fig. 3 the density perturbations from the wave trains are shown for three different driver durations, δt = [0.29, 1.12, 1.77]τAi, top to bottom. On the right are the corresponding wavelet spectra (Torrence & Compo 1998), plotted as the spectral amplitude. Each also includes a plot of the global wavelet spectrum (GWS) of the spectral amplitude. A clear difference between the wave train signatures can be seen, as the longer wavelengths (lower frequencies) become more dominant for longer driver durations. The wave train amplitude can also be seen to decrease, despite the total energy of the driver increasing for higher values of δt.
 |
Fig. 3. Left panel: pertubation to the equilibrium density measured along the centre of the waveguide (x = 0) at t = 110. Three different driver durations were used, δt = [0.29, 1.12, 1.77]τAi, top to bottom. Right panel: corresponding wavelet spectra plotted as the spectral amplitude and the global wavelet spectrum (GWS) of the normalised spectral amplitude. |
We can define a maximum threshold of δt above which the fast wave train is no longer efficiently excited. To do this we form the ratio of maximum density perturbation of the fast wave train and slow wave, Awt/AS. Since the peak amplitude of the driver remains constant the total energy applied by the driver is increased with higher values of δt, hence this ratio of wave mode amplitudes is used rather than just the amplitude of the wave train. Awt/AS is plotted against δt, in units of τAi, in the first panel of Fig. 4. A strong negative relationship between the two is observed. We define the cut-off to occur at δt = 2 τAi. At this point the wave train amplitude is 3 orders of magnitude lower than the slow wave amplitude, and so would be practically impossible to detect observationally.
 |
Fig. 4. Left panel: amplitude ratio of the fast wave train and slow wave measured at t = 110 plotted against the driver duration in units of the Alfvén transit time across the waveguide. The cutoff above which the fast wave train is no longer considered to be efficiently excited is shown by the vertical dashed line. Middle panel: wavelength of peak spectral amplitude (in units of the waveguide width) of the fast wave train plotted against the driver duration. Right panel: spectral width of the fast wave train signal plotted against the driver duration. |
To quantify the effect of driver duration, for δt < 2 τAi, we plot the wavelength of peak spectral amplitude (λp, in units of the waveguide width), and the FWHM of the spectral amplitude distribution against the driver duration. These are shown in middle and right panels of Fig. 4. The spectral properties are obtained by fitting a Gaussian to the GWS. As noted above, a shift to longer wavelengths can clearly be seen with increasing δt, and conversely the width of the spectral distribution decreases. For data taken in the time domain the period and spectral width would also vary in the same way, however a direct conversion cannot be made due to the presence of dispersion. This result is similar to the effect of increasing the spatial width of the driver (making it spectrally narrower), which results in a more monochromatic wave train (see Nakariakov et al. 2005). Here, a driver of greater temporal width is also spectrally narrower, resulting in a more monochromatic wave train signature. Over the range of driver durations considered in Fig. 4 the peak wavelength and spectral width vary by 20% and 45% respectively, compared to their minimum values.
It is not currently possible to make analytical approximations for comparison to these numerical simulations, however the results can be understood by considering how the spectral profile of the driver is changing. The spectral amplitude increases with δt, whereas the spectral width decreases, i.e. there are more monotonic and lower frequencies within the driver spectrum for larger δt. Increasing δt therefore deposits more energy into the waveguide, but less into higher frequencies. Above a certain value the driver spectrum is such that the natural frequencies of the fast waves in the waveguide are no longer efficiently excited, whereas the amplitude of the slow waves is still increasing with the spectral amplitude. For very large values of δt the slow wave amplitude would also begin to decrease.
4. Conclusions
The effect of a time-dependant driver on dispersively formed fast magnetoacoustic wave trains in coronal waveguides has been investigated. A strong dependence of the wave train characteristics on the driver duration was found. Additionally it has been shown that a fast wave train is no longer excited for driver durations δt ≳ 2τAi.
This dependence on the driver duration is extremely important in attempts to unlock the seismological potential of these waves. Varying other parameters such as the spatial scale of the driver, and the transverse density profile of the waveguide can have similar effects on the final wave train signature (e.g., Nakariakov et al. 2005; Pascoe et al. 2013, 2017; Yu et al. 2017). Therefore an effort to clearly distinguish these factors in both theoretical and observational studies should be made. Furthermore, future numerical or analytical studies of fast wave trains in the corona should consider the effect of a time dependent driver.
More realistic temporal driver profiles could be considered in future work. For example, an observationaly justified flare profile could be used (Gryciuk et al. 2017), assuming the energy deposition could follow the same temporal behaviour. However, without clear evidence of the exact nature of the driving mechanism in several observations this is not yet required. In principle, the weakly-evolving slow wave pulse could bring us information about the temporal or spatial shape of the driver. However, such a study is not possible until more routine detections of the slow pulse in observations (see Zhang et al. 2015).
The findings of this work add further intricacy to the already highly complicated prospect of using these wave train signatures to perform seismology. We have shown that, other parameters remaining constant, the variation of the driver duration produces detectable differences in the spectral properties of the wave trains. Over the range of driver durations considered the peak wavelength and spectral width vary by 20% and 45% respectively, compared to their minimum values.
Acknowledgments
This work was supported by the British Council via the Institutional Links Programme (Project 277352569 – Seismology of Solar Coronal Active Regions) (CRG, VMN) and the BK21 plus program through the National Research Foundation funded by the Ministry of Education of Korea (VMN). DJP was supported by the GOA-2015-014 (KU Leuven) and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 724326). Software: Lare2d (Arber et al. 2001), Wavelet Analysis (Torrence & Compo 1998). The authors thank D. Marsden and I. Larsson for their contributions.
References
- Arber, T., Longbottom, A., Gerrard, C., & Milne, A. 2001, J. Comput. Phys., 171, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, F. C., Nakariakov, V. M., & Williams, D. R. 2003, A&A, 409, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elsden, T., & Wright, A. N. 2018, J. Geophys. Res. (Space Phys.), 123, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Goddard, C. R., Nisticò, G., Nakariakov, V. M., Zimovets, I. V., & White, S. M. 2016, A&A, 594, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gryciuk, M., Siarkowski, M., Sylwester, J., et al. 2017, Sol. Phys., 292, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, M., Van Doorsselaere, T., Karampelas, K., et al. 2019, ApJ, 870, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Jelínek, P., & Karlický, M. 2012, A&A, 537, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaneda, K., Misawa, H., Iwai, K., et al. 2018, ApJ, 855, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Katsiyannis, A. C., Williams, D. R., McAteer, R. T. J., et al. 2003, A&A, 406, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolotkov, D. Y., Nakariakov, V. M., & Kontar, E. P. 2018, ApJ, 861, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., Nakariakov, V. M., & Cho, K.-S. 2017, ApJ, 844, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L., Zhang, J., Peter, H., et al. 2018a, ApJ, 868, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Li, B., Guo, M.-Z., Yu, H., & Chen, S.-X. 2018b, ApJ, 855, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Title, A. M., Zhao, J., et al. 2011, ApJ, 736, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Mészárosová, H., Karlický, M., Jelínek, P., & Rybák, J. 2014, ApJ, 788, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Murawski, K., & Roberts, B. 1994, Sol. Phys., 151, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Arber, T. D., Ault, C. E., et al. 2004, MNRAS, 349, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Pascoe, D. J., & Arber, T. D. 2005, Space Sci. Rev., 121, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Nisticò, G., Pascoe, D. J., & Nakariakov, V. M. 2014, A&A, 569, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L., & Liu, W. 2018, ApJ, 860, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., Liu, W., Title, A., & Aschwanden, M. 2011, ApJ, 740, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R., Ruderman, M. S., & Terradas, J. 2015, ApJ, 806, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., & Kupriyanova, E. G. 2013, A&A, 560, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Wright, A. N., De Moortel, I., & Hood, A. W. 2015, A&A, 578, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Goddard, C. R., & Nakariakov, V. M. 2017, ApJ, 847, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1983, Nature, 305, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Tang, Z., Li, H., & Liu, Y. 2018, MNRAS, 480, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Shestov, S., Nakariakov, V. M., & Kuzin, S. 2015, ApJ, 814, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Torrence, C., & Compo, G. P. 1998, Bull. Am. Meteorol. Soc., 79, 61 [Google Scholar]
- Van Doorsselaere, T., Kupriyanova, E. G., & Yuan, D. 2016, Sol. Phys., 291, 3143 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, D. R., Phillips, K. J. H., Rudawy, P., et al. 2001, MNRAS, 326, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, D. R., Mathioudakis, M., Gallagher, P. T., et al. 2002, MNRAS, 336, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, H., Li, B., Chen, S.-X., Xiong, M., & Guo, M.-Z. 2017, ApJ, 836, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Zhang, J., Wang, J., & Nakariakov, V. M. 2015, A&A, 581, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1. Top panel: transverse density profile of the waveguide. Overplotted in blue is the spatial profile of the vx velocity pulse in arbitrary units. Bottom panel: temporal profile of the driver amplitude for three different driver durations, [0.29, 1.47, 2.94] τAi. The centre of the driving pulse, t0, is indicated by the vertical dashed line. |
| In the text | |
 |
Fig. 2. Top panel: perturbation to the equilibrium density at t = 110 from a driver with δt = 0.58 τAi. The slow wave can be seen at z ∼ 10 and the fast wave train between z ∼ 40 and z ∼ 100, both propagating to the right. The waveguide width is indicated by 2w, and the magnetic field direction by B. Bottom panel: pertubation to the equilibrium density measured along the centre of the waveguide (x = 0) from the above simulation output. The region between the dashed vertical lines denotes the section of the signal used for analysis of the fast wave train. |
| In the text | |
 |
Fig. 3. Left panel: pertubation to the equilibrium density measured along the centre of the waveguide (x = 0) at t = 110. Three different driver durations were used, δt = [0.29, 1.12, 1.77]τAi, top to bottom. Right panel: corresponding wavelet spectra plotted as the spectral amplitude and the global wavelet spectrum (GWS) of the normalised spectral amplitude. |
| In the text | |
 |
Fig. 4. Left panel: amplitude ratio of the fast wave train and slow wave measured at t = 110 plotted against the driver duration in units of the Alfvén transit time across the waveguide. The cutoff above which the fast wave train is no longer considered to be efficiently excited is shown by the vertical dashed line. Middle panel: wavelength of peak spectral amplitude (in units of the waveguide width) of the fast wave train plotted against the driver duration. Right panel: spectral width of the fast wave train signal plotted against the driver duration. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




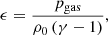
![$$ \begin{aligned} { v}_x = x A_{t} \exp \left[ - \left(\frac{x - x_\mathrm{0} }{\delta x}\right)^2\right], \end{aligned} $$](/articles/aa/full_html/2019/04/aa35401-19/aa35401-19-eq4.gif)
![$$ \begin{aligned} A_{\rm t} = A_{0} \exp \left[ - \left(\frac{t - t_\mathrm{0} }{\sigma _{\rm t}}\right)^2\right], \end{aligned} $$](/articles/aa/full_html/2019/04/aa35401-19/aa35401-19-eq5.gif)