EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 624 (April 2019) A&A, 624 (2019) A111 Full HTML
Open Access
Issue
A&A
Volume 624, April 2019
Article Number A111
Number of page(s) 14
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201833603
Published online 19 April 2019

© A. M. Amarsi et al. 2019

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Open Access funding provided by Max Planck Society.

1 Introduction

As the second most abundant metal at the present epoch, carbon is interesting in a variety of astrophysical contexts. Via the C/O ratio, carbon has an oversized influence on the structure of the atmospheres (e.g. Madhusudhan 2012) and interiors (e.g. Kuchner & Seager 2005) of exoplanets. Carbon is similarly influential on the structure of the atmospheres (e.g. Gallagher et al. 2017) and interiors (e.g. Basu & Antia 2008) of stars, and helps shape the properties of early stars (e.g. Bromm & Loeb 2003). Carbon is produced from a number of different sites including core collapse supernova (e.g. Woosley et al. 2002), AGB stars (e.g. Karakas 2014), and Wolf-Rayet stars (e.g. Limongi & Chieffi 2018); as such the Galactic Chemical Evolution of carbon is likely to be metallicity dependent and is still rather uncertain (e.g. Kobayashi et al. 2011).

Thus, accurate carbon abundances measured across the Galaxy are of great interest to the community. In late-type stars, C I lines are among the most commonly used carbon abundance diagnostics (e.g. Takeda et al. 2013; Nissen et al. 2014; Zhao et al. 2016), and can be measured down to [Fe/H]1 ≈ − 3.0 (e.g. Fabbian et al. 2009). However, in late-type stellar atmospheres, C I is sensitive to departures from local thermodynamic equilibrium (LTE; e.g. Vernazza et al. 1981; Stürenburg & Holweger 1990; Takeda 1992; Asplund et al. 2005; Takeda & Honda 2005; Fabbian et al. 2006; Alexeeva & Mashonkina 2015). For reliable results based on C I lines, non-LTE effects need to be taken into account.

A question to ask of non-LTE studies in general, is how realistic are the model atoms being used. For C I, the main uncertainties have hitherto been related to the completeness of the model atom (e.g. Stürenburg & Holweger 1990), and to the treatment of neutral hydrogen impact excitation (e.g. Fabbian et al. 2006; Caffau et al. 2010; Alexeeva & Mashonkina 2015). This latter point has lately been given considerable attention in the context of other elements. Lacking collisional cross-sections based on expensive quantum chemistry calculations of the molecular structure (e.g. Belyaev & Barklem 2003; Belyaev et al. 2010, 2012), works have until recently typically either neglected neutral hydrogen impact excitation, or included them using the Drawin recipe (Drawin 1968, 1969; Steenbock & Holweger 1984; Lambert 1993). This recipe however is not well-founded from a physical point of view, and is typically in error by orders of magnitude, with the errors going in different directions for different transitions (e.g. Barklem 2016a, and references therein).

Recently, new recipes for neutral hydrogen impact excitation have become available that are both physically motivated and are relatively inexpensive to compute. In our study of neutral oxygen (Amarsi et al. 2018a), we suggested employing the asymptotic two electron model of Barklem (2016b), combined with the free electron model of Kaulakys (1991). These two models account for different physical mechanisms, with the asymptotic model particularly suitable for low level transitions while the free electron model should perform well for lines from intermediate- and high-excitation levels. Since the permitted optical and infrared C I lines are all in this regime, we expect that the mechanism represented by the free electron model is important here.

One way to validate model atoms is to use them in analyses of the solar spectrum. Trends in abundances inferred from spectral lines of different parameters (e.g. wavelength, line strength, excitation potential) have traditionally been used to probe errors in themodelling. More recently, centre-to-limb variations of spectral lines have been used to probe different recipes of neutral hydrogen impact excitation (Allende Prieto et al. 2004; Asplund 2005; Pereira et al. 2009; Steffen et al. 2015; Lind et al. 2017; Amarsi et al. 2018a). This is because (a) spectral lines observed at the limb form higher up than lines observed at disk-centre, (b) free electrons are the main thermalising agents in the deep solar photosphere, and (c) the relative importance of neutral hydrogen to free electrons as thermalising agents follows the ratio 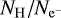NH/Ne−​$N_{\mathrm{H}}/N_{\mathrm{e}^{-}}\!$, which increases with height.

In orderto use the Sun to validate atomic data in this way, one requires a reliable method for spectral line synthesis. The current state-of-the-art employs three-dimensional (3D) radiative-hydrodynamic model solar atmospheres, and 3D non-LTE post-processing radiative transfer (e.g. Amarsi et al. 2018a). To our knowledge, consistent 3D non-LTE calculations for C I in the solar photosphere that are based on a model atom that is sufficiently large for reliable abundance determinations have not been presented in the literature until now.

Here, we present a new model atom for C I line formation (Sect. 2), that uses a physically motivated recipe for the rates of neutral hydrogen impact excitation. We carry out detailed 3D non-LTE calculations for C I lines in the solar photosphere, looking at disk-centre abundance trends as well as centre-to-limb variations of various clean C I lines in order to validate the model atom (Sect. 3). We discuss the implications on the solar carbon abundance and comment on the non-LTE effects on C I lines (Sect. 4). We close with a short summary (Sect. 5).

2 Method

2.1 Line-list

In Table 1 we list the 35 C I lines and single [C I] line for which 3D non-LTE line formation for the Sun were calculated and discussed in detailed (Sect. 3.2). This list was initially constructed by combining the set of lines given in Table 2 of Asplund et al. (2005), with the set of lines assigned a rank of 1 in Table 1 of Caffau et al. (2010). The C I 801.9 nm line was removed from this list on account of being very weak. The C I 1750.6 nm line was also removed, for having a very high excitation potential: the upper level of this transition was collapsed into a super level in the model atom, (Sect. 2.4.5), making the non-LTE effects predicted for this line less reliable. The C I 906.2, 908.9, 909.5, 940.6, and 962.1 nm were added to this list because they are useful diagnostics in the metal-poor regime (Fabbian et al. 2009; Amarsi et al. 2019). We adopted different line parameters to those listed in Asplund et al. (2005) and Caffau et al. (2010) – in particular, using the oscillator strengths listed in the NIST Atomic Spectra Database (Sect. 2.4); the differences in the oscillator strengths are at most around 0.02 dex.

For studying disk-centre abundance trends (Sect. 3.3), it is necessary to avoid lines that may be affected by solar and telluric blends in order to avoid biasing the results. Therefore, a subset of the lines in Table 1 was used. This subset is composed of14 of the 16 C I lines as well as the single [C I] line presented in Table 2 of Asplund et al. (2005); we opted to remove the C I 960.3 nm line because it is too strong to be a reliable abundance indicator, and the C I 2290.6 nm line because of difficulties in measuring its equivalent width. The adopted equivalent widths are those used in Asplund et al. (2009, updated from Asplund et al. 2005), except for two lines: the C I 711.1 and 711.3 nm lines. These two lines areblended with faint CN lines; the new equivalent widths (Sect. 3.3) have taken these blends into account (0.08 and 0.20 pm respectively; J. Melendez, priv. comm.).

For studying centre-to-limb variations (Sect. 3.4), another subset of the lines in Table 1 was used, due to the availability of high quality observational data. This subset is composed of the C I 505.2, 538.0, 658.8, 711.1, 711.3, 833.5, 960.3, and 965.8 nm lines. Most of the infrared lines from Table 1 were not included because the analysis was based on the “SS3” atlas of Stenflo (2015) that only extends to 1000 nm. The other C I lines missing from this selection are, toward the limb, too contaminated by blends or are too difficult to continuum-normalise because of surrounding blends, to be useful here.

To aid intuition, in Fig. 1 we show the contribution functions of the intensity depression of the C I 505.2 nm (χexc. = 7.7 eV) and 960.3 nm (χexc. = 7.5 eV) lines, and the [C I] 872.7 nm (χexc. = 1.3 eV) line, at the two different μ values (μ = 1.0 and μ = 0.145) considered in the centre-to-limb variation analysis (Sect. 3.4). These were computed in the same way as in Sect. 2.1.3 of Amarsi et al. (2018a); namely, by computing the full 3D contribution function (Amarsi 2015, integrand of Eq. (12)), after averaging over surfaces of equal optical depth and over time, and integrating over wavelength.

thumbnail Fig. 1

Contribution functions to the intensity depression for the C I 505.2 and 960.3 nm lines, and the [C I] 872.7 nm line, integrated over wavelength, at two different viewing angles. The contribution functions have been normalised such that under each, the area is equal to unity.

2.2 Radiative transfer code

The 3D non-LTE radiative transfer code BALDER (Amarsi et al. 2018b) was used. The code originated from MULTI3D (Botnen & Carlsson 1999; Leenaarts & Carlsson 2009), but has been developed and modified, utilising a new opacity package and other improvements for stellar abundance analyses. In this work, the underlying algorithm that solves the statistical equilibrum was replaced, from that presented in Sect. 2.3 of Rybicki & Hummer (1992), to that presented in Sect. 2.4 of that same paper. This was motivated by numerical issues in certain cases, namely of overlapping radiative transitions combined with relatively inefficient collisional coupling. The calculations on 1D model atmospheres were performed in the same way as the calculations on 3D model atmospheres, the only difference being the inclusion of microturbulent broadening in the 1D case (e.g. Gray 2008, Chapter 17).

Table 1

Parameters of the full set of lines for which 3D non-LTE effects are discussed.

2.3 Model atmospheres

The 3D non-LTE radiative transfer calculations were performed in post-processing across eight snapshots, equally spaced in 21 h of solar time, of the same 3D radiative-hydrodynamic model solar atmosphere that was used in Amarsi et al. (2018a), calculated using the STAGGER code (Nordlund & Galsgaard 1995; Stein & Nordlund 1998; Collet et al. 2011). The mean effective temperature of the whole 21 h sequence 5773 K, with a standard deviation of 16 K; the mean effective temperature of the eight snapshots is also 5773 K. For comparison the reference solar effective temperature is 5772 K (Prša et al. 2016).

The calculations were performed for various carbon abundances in steps of 0.2 dex, around a central value of log ɛC = 8.43 (Asplund et al. 2009). Repeating the abundance analysis using steps of 0.4 dex instead, resulted in inferred abundances that changed by at most 0.01 dex (for the [C I] 872.7 nm line).

For testing purposes, post-processing radiative transfer calculations were performed on the horizontally- and temporally-averaged 3D model solar atmosphere (hereafter ⟨3D⟩). The averaging was performed over the full 21 h sequence. This is the same ⟨3D⟩ model solar atmosphere that was used in Amarsi et al. (2018a). For interpreting the 3D effects, radiative transfer calculations were also performed on a 1D hydrostatic model solar atmosphere, which was calculated using the ATMO code (Magic et al. 2013, Appendix A). The ATMO model was constructed assuming a microturbulence of ξ = 1.0 km s−1, and using the same equation of state and opacity binning scheme as used for the STAGGER model solar atmosphere, permitting a fair comparison.

For both the 1D and the ⟨3D⟩ model solar atmospheres, the post-processing radiative transfer calculations were performed for the same carbon abundances as were used on the 3D model solar atmosphere (i.e. in steps of 0.2 dex, around a central value of log ɛC = 8.43). These calculations were performed for a single, depth-independent microturbulence of ξ = 1.0 km s−1.

thumbnail Fig. 2

Grotrian diagrams for C I and C II in the comprehensive model atom. Levels that do not resolve fine structure are shown as red lines.

2.4 Model atom

2.4.1 Overview

In this section we focus on the construction and reduction of the model atom for C I. The procedure is similar to that presented in Amarsi et al. (2018a) for O I. The model atom was constructed in two steps. In the first step, a comprehensive model atom was constructed, which we illustrate in Fig. 2. In the second step, the comprehensive model was reduced in complexity (Sect. 2.4.5), to generate what we refer to as the standard model atom, which we illustrate in Fig. 3. Reducing the size of the model atom is necessary to make the calculations presented here feasible; nevertheless the reduced model atom still encapsulates the relevant physics. In addition to the standard model atom, further models were used to test the sensitivity of the results to different ingredients and assumptions (Sect. 2.4.6).

In all cases, after the non-LTE iterations were completed on a reduced model atom, the final emergent intensities were calculated by applying the departure coefficients to the comprehensive model atom, taking care to preserve the total population number. In this way the final emergent intensities were based on accurate partition functions and the correct fine structure splitting, forhigher accuracy.

2.4.2 Energy levels

We illustrate the structure of the comprehensive model atom in Fig. 2. Experimental fine structure energies were taken from the compilation of Moore (1993) via the NIST Atomic Spectra Database (Kramida et al. 2015), and, to make the model more complete, theoretical energies calculated under the assumption of pure LS coupling, from Luo & Pradhan (1989) for C I and Berrington & Seaton (1985) for C II via the Opacity Project online database (TOPbase; Cunto et al. 1993), were also used. Care was taken not to duplicate levels in the model, by using the NIST set only for lower lying levels (up to 10.43 eV above the ground state for C I, and 18.05 eV above the ground state for C II) and the TOPbase set for the remainder. The TOPbase energies were not extracted directly: instead, they were calculated from the stipulated effective principal quantum numbers, combined with the experimental ionisation limits from NIST. The C III ground state was also included in the comprehensive model atom.

2.4.3 Radiative transitions

Fine structure oscillator strengths were taken from Hibbert et al. (1993), Tachiev & Froese Fischer (2001), and Froese Fischer (2006) for C I, and Tachiev & Froese Fischer (2000) and Nussbaumer & Storey (1981) for C II, via NIST. For completeness this set was merged with theoretical oscillator strengths calculated under the assumption of pure LS coupling, from Luo & Pradhan (1989) for C I and Yan et al. (1987) for C II, via TOPbase. Photoionisation cross-sections were also taken from TOPbase, and smoothed over using a Gaussian filter (e.g. Bard & Carlsson 2008). For all bound–bound transitions, natural broadening coefficients were calculated from the lifetimes stipulated in TOPbase. Where possible, collision broadening due to neutral hydrogen was calculated after the theory of Anstee, Barklem, and O’Mara (ABO), by interpolating the tables presented in Anstee & O’Mara (1995), Barklem & O’Mara (1997), and Barklem et al. (1998).

Where possible, the TOPbase radiative transitions that connect fine structure level(s) were split, using the relative strengths tabulated in Sect. 27 of Allen (1973). These tables are valid in the LS coupling regime, which is expected to be a good approximation for C I.

thumbnail Fig. 3

Grotrian diagram for C I in the standard model atom, after reducing the comprehensive model by removing C III and all excited levels of C II, and by constructing super levels. Levels that do not resolve fine structure are shown as red lines, and super levels are shown as long horizontal lines. Some of the C I lines explicitly considered in this work have been highlighted; “~ 711 nm” refers to the C I 711.1 and 711.3 nm lines, and “~ 960 nm” refers to the C I 960.3 and 965.8 nm lines.

2.4.4 Collisional transitions

For electron impact excitation of C I, the rate coefficients presented by Wang et al. (2013) calculated under the B-spline R-matrix formalism (BSR e.g. Zatsarinny 2006) were adopted where possible. The data set is complete up to 2s2 2p 3d 3Po (9.83 eV above the ground state). The BSR data of Wang et al. (2013) were also used for electron impact ionisation of C I. Comparisons of BSR with independent methods for other species signal the reliability of this approach (e.g. Barklem et al. 2017). Where the BSR data set is incomplete, the semi-empirical recipe of van Regemorter (1962) was used for excitation (imposing a minimum oscillator strength of 0.05), while the empirical formula presented in Allen (1973) was used for ionisation.

For electron impact excitation of C II, included in the comprehensive model atom, the cross-sections presented by Wilson et al. (2005), calculated under the close-coupling R-matrix formalism (e.g. Burke & Robb 1976), were adopted where possible. As for C I, this data set was completed using the semi-empirical recipe of van Regemorter (1962), while the empirical formula presented in Allen (1973) was used for electron impact ionisation of C II.

As we mentioned in Sect. 2.4.1, we adopt a new approach for neutral hydrogen impact excitation of C I. Following the approach of Amarsi et al. (2018a) for O I, the rate coefficients predicted by the asymptotic two-electron model, based on linear combinations of atomic orbitals (“LCAO”), of Barklem (2016b) were added to the rate coefficients predicted by the free electron model (“Free”), of Kaulakys (1991). We refer to this combined approach as “LCAO+Free”. The Barklem (2017) code was used to determine the rate coefficients in the lattercase; these were redistributed among spin states following Eqs. (8) and (9) of Barklem (2016a). The asymptotic two electron model was also used to calculate charge transfer between C I and neutral hydrogen (C+H ↔C+ + H−). Neutral hydrogen impact ionisation (C+H ↔C+ + e− + H) was also included, through Eq. (8) of Kaulakys (1985), but was found to be of much lower importance.

Neutral hydrogen impact excitation of C II was neglected in the model. Neglecting these processes may in principle lead to overestimating the departures from LTE, and increase the influence of the statistical equilibrium of C II, on the C I line strengths. Ultimately however, we found that the overall influence of C II on C I lines is anyway small, (Sect. 2.4.5), so the exact treatment of these processes is unimportant here.

2.4.5 Standard model atom

The comprehensive model atom in Fig. 2 is too large to use in full 3D non-LTE radiative transfer calculations. It was therefore reduced, following a similar procedure to that described in Amarsi et al. (2018a) for our O I model atom. The reduction was performed in several steps as we outline below.

First, all of the excited C II levels as well as the C III level were removed. Tests revealed that these levels have only a very small impact on the C I line strengths: for the lines listed in Table 1, the differences in the equivalent widths in the emergent flux are negligible in the ⟨3D⟩ model solar atmosphere (much less than 0.0001 dex). Previous studies have included several of the lower-lying C II levels (e.g. Fabbian et al. 2006 and Alexeeva & Mashonkina 2015 include the nine lowest C II levels, up to around 18 eV above the C II ground state), which is more accurate but apparently not essential. The relative insensitivity of C II on the statistical equilibrium of C I can be understood from the high ionisation energy of C I (11.26 eV), which ensures that C I is the majority species in the solar photosphere; also, the first excited state of C II has a large separation from the ground state (5.33 eV), so that only the ground state of C II needs to be considered here.

Second, high-excitation C I levels (10.5 eV above the ground state) that are closely separated in energy (within 0.5 eV of each other) and that are within the same spin system, were collapsed into super levels. This is valid under the assumption that the composite levels are collisionally-coupled and therefore have identical departure coefficients. Within a super level, energies were weighted using their Boltzmann factors, adopting a temperature of 5000 K that is characteristic of the line formation region. Transitions connected to super levels were collapsed into super transitions, in the way described in Amarsi & Asplund (2017). In the ⟨3D⟩ model solar atmosphere this reduction has an impact of around 0.003 dex on the equivalent width in the flux in the worst case, the C I 3406.5 nm line of high excitation potential; for the other lines the impact is less than 0.001 dex.

The resulting, reduced model atom is the standard atom used in this work. Abundance results and centre-to-limb variations are based on this model atom, unless otherwise indicated. We illustrate the model atom in Fig. 3.

2.4.6 Test atoms

For testing purposes, a further reduction was made to the standard model atom described in Sect. 2.4.5: namely, fine structure was collapsed following the method described in, for example, Amarsi & Asplund (2017). We refer to this as the “No FS” model. In the ⟨3D⟩ model solar atmosphere the equivalent widths in the fluxes of the lines were affected by up to 0.008 dex. The error is lowest in the vertical intensity and grows for more inclined rays as the line formation moves outwards. For example, for the C I 960.3 nm line that forms over a region extending high up in the atmosphere (Fig. 1), the error for μ = 1.0 is 0.006 dex, while the error at μ = 0.145 is almost 0.03 dex. In general, for abundance determinations from disk-integrated observations of late-type stars, errors of this magnitude are not significant; (for this reason, the “No FS” atom was used in our recent study of halo stars; Amarsi et al. 2019). However, for studying solar centre-to-limb variations, it is important to retain fine structure in the model atom.

To quantify the influence of neutral hydrogen impact excitation, a further model atom was constructed, wherein all neutral hydrogen impact excitation rate coefficients were set to zero. Given that fine structure has only a small impact on the statistical equilibrium, to reduce the computational cost fine structure was also collapsed in this test atom. We refer to this as the “No FS / C+H exc.” model.

thumbnail Fig. 4

Departure coefficients across the ⟨3D⟩ model atmosphere, for the lowest 42 terms of C 1 (up to 2s2 2p 4d 3Po) as well as the ground state of C II. A solar carbon abundance of log ɛC = 8.43 was assumed. The low-excitation levels indicated in the plot span the ground state up to 2s.2p 3 5 So (4.18 eV), while the high-excitation levels indicated in the plot span 2s2.2p.3p 1P (8.54 eV) up to the ionisation limit (11.26 eV). The intermediate-excitation levels are those levels between them: 2s2.2p.3s 3Po (7.49 eV), 2s2.2p.3s 1Po (7.68 eV), and 2s.2p3 3Do (7.95 eV). Departure coefficients are shown for the standard model atom (Fig. 3). The impact of collapsing fine structure, and of removing neutral hydrogen impact excitation, are also shown.

3 Results

3.1 Departure coefficients

In Fig. 4 we illustrate departure coefficients across the ⟨3D⟩ model atmosphere, as predicted by the standard (reduced) model atom used throughout this study. There are broadly three groups of departure coefficients, corresponding to levels of low, intermediate, and high excitation potential; C II belonging to the last group. At solar metallicity, the departures from LTE are driven by photon losses in the many strong C I lines (e.g. Stürenburg & Holweger 1990). There is a population cascade, that starts in the levels of high excitation potential and propagates down to the levels of intermediate excitation potential (2s 2.2p.3s 3Po, 2s 2.2p.3s 1Po, and 2s.2p3 3Do), with levels of higher excitation potential underpopulating more. The low-excitation levels are all highly populated, and thus their populations are only marginally perturbed by this cascade (i.e. their departure coefficients stay close to unity).

We illustrate in Fig. 4 what happens when fine structure is collapsed in the model atom (“No FS”). As discussed in Sect. 2.4.5, fine structure has a small impact on the statistical equilibrium. It can be seen that in the regions − 2≲ log τR ≲ 0, the departure coefficients are closer to unity in this case than in the standard case. This is because collapsing fine structure leads to stronger lines, that consequently form higher up in the solar atmosphere; therefore, the departures from LTE start to occur higher up in the solar atmosphere. However, it can also be seen that even higher up, log τR ≲−2, the departure coefficients are further from unity in this case than in the standard case. This is because, when fine structure is collapsed, the stronger lines have larger photon losses and thus drive larger departure from LTE.

We also illustrate in Fig. 4 what happens when neutral hydrogen impact excitation is neglected in the model atom (“No FS / C+H exc.”). Of all the collisional processes included in the model atom, these have the largest impact on the statistical equilibrium, generally acting to balance photon losses in the C I lines. When neutral hydrogen impact excitation is neglected, the departures from LTE set in much deeper in the atmosphere, with significant departures already at log τR ≈−0.5. It can also be seen that neutral hydrogen impact excitation is responsible for strong coupling within the different groups of levels (of low, intermediate, and high excitation potential).

3.2 3D/non-LTE abundance differences

To quantify the 3D non-LTE effects in the solar photosphere, equivalent widths were calculated for all of the lines listed in Table 1, using different modelling approaches (e.g. 3D non-LTE, 1D LTE). From these equivalent widths, abundance differences with respect to 3D non-LTE were calculated, by finding the abundance in, for example, the 1D LTE approach, that is needed to match the 1D LTE equivalent width to the 3D non-LTE equivalent width, for a fixed 3D non-LTE carbon abundance. We hereafter refer to these abundance differences as “abundance errors”, in contrast to the commonly used term “abundance corrections” that is understood to represent abundance differences with respect to 1D LTE. In Fig. 5 we illustrate these abundance errors that are based on equivalent widths, in the solar atmosphere, for the disk-centre intensity as well as for the disk-integrated flux.

In accordance with previous 1D non-LTE studies (Fabbian et al. 2006; Alexeeva & Mashonkina 2015), the 3D LTE versus 3D non-LTE abundance errors, that quantify the non-LTE effects, are generally positive in both the disk-centre intensity and disk-integrated flux, reaching up to around 0.1 dex in the latter. In other words, the non-LTE abundance corrections tend to be negative. There are trends in the middle and lower panels that indicate the departures from LTE are more severe for stronger C I lines (larger log W∕λ), and for C I lines of intermediate excitation potential (Elow ≈ 7.5–8.0 eV).

The reason why the abundance corrections are usually negative can be understood by looking again at the departure coefficients in Fig. 4. Levels of intermediate excitation potential do not depart severely from their LTE populations, whereas levels of high excitation potential are severely underpopulated with respect to LTE. Consequently, C I lines of intermediate excitation potential are subject to a source function effect (the ratio of the line source function to the Planck function follows βupper∕βlower; Rutten 2003). The line source function drops below the LTE expectation, and thus strengthens the C I lines with respect to LTE. Stronger lines are more susceptible to this effect, as their formation extends higher up into the atmosphere where the departures from LTE are greater.

Similarly, C I lines of high excitation potential are also susceptible to the source function effect. This is because higher levels show a larger underpopulation with respect to LTE (so βupper∕βlower still deviates from unity). For such lines, however, there is also a competing opacity effect (βlower drops below unity) that acts to weaken the C I lines with respect to LTE (the line strength follows the line opacity).

The [C I] 872.7 nm line does not depart from LTE. This is expected because the lower and upper levels of the transition are both of low-excitation and are thus both highly populated (since C I is the majority species in the solar photosphere). They are therefore relatively insensitive to changes in the populations in the intermediate- and high-excitation C I levels.

We illustrate in Fig. 5 the sensitivity of the results to the treatment of fine structure, by presenting errors associated with collapsing all fine structure in the model atom (“No FS”). As anticipated (Sect. 2.4.6), the abundance errors are close to zero. They grow for stronger lines, which have significant line formation higher up in the photospherewhere fine structure has a larger impact on the statistical equilibrium (as seen in Fig. 4).

We alsoillustrate in Fig. 5 the sensitivity of the results to neutral hydrogen impact excitation, by presenting errors associated with neglecting these processes (“No FS / C+H exc.”). These processes have only a small influence on the line strengths of the optical lines considered here: less than around 0.05 dex on the fluxes interms of abundances, at least in the Sun. Their influence is much larger on the near infrared lines (between 800 and 1100 nm) of intermediate excitation potential, where including them tends to weaken the lines considerably. For these lines the effects can reach up to around 0.3 dex on the fluxes interms of abundances, at least in the Sun. Neutral hydrogen impact excitation leads to closer coupling between the lower and upper levels of the near infrared lines (Sect. 3.1), and acts to reduce the source function effect described above.

Figure 5 illustrates that the 1D non-LTE versus 3D non-LTE abundance errors, that quantify the 3D effects, are typicallyslightly smaller in magnitude than the non-LTE effects. However, these 3D effects go in the opposite direction to the non-LTE effects: they are mainly negative (corresponding to positive 3D abundance corrections, such that the 1D non-LTE C I lines aretoo strong, relative to 3D non-LTE). For the lines emergent at disk-centre, the differences are typically around 0.05 dex, but can reach almost 0.1 dex; for the disk-integrated flux, the differences are less severe (less than 0.05 dex). Figure 5 shows that, at disk-centre, the 3D effects are correlated with the line strengths (log W∕λ) of the C I lines. Reducing the microturbulence only slightly alleviates the 3D effects on the lines. Rather, the 1D non-LTE versus 3D non-LTE abundance differences are caused by differences in the atmospheric stratification in 1D and in 3D; in support of this, we found that ⟨3D⟩ non-LTE versus 3D non-LTE abundance corrections are much less severe (less than 0.03 dex at disk-centre).

Since the vast majority of spectroscopic stellar analyses today are based on 1D LTE, we also illustrate 1D LTE versus 3D non-LTE abundance errors in Fig. 5. As discussed above, the 3D effects and the non-LTE effects tend to go in opposite directions, at least for the C I lines considered in this work. Consequently, the 1D LTE versus 3D non-LTE abundance errors are intermediate between the negative 1D non-LTE ones (3D effects) and the positive 3D LTE ones (non-LTE effects). For the disk-centre intensity, they are always negative, which indicates that 3D effects are more important than non-LTE effects. On the other hand, for the disk-integrated flux, they tend to be positive, which indicates that non-LTE effects are more important than 3D effects. The middle row, second column of Fig. 5 reveals that the differences are typically of the order 0.05 dex in the disk-integrated flux.

3.3 Abundance trends

In Table 2 we show our measured equivalent widths for the [C I] line and C I lines measured inthe disk-centre intensity spectrum, together with the solar carbon abundances inferred from different modelling approaches. Uncertainties in the equivalent widths were assumed to be 5%, after consideration of other published equivalent widths (Grevesse et al. 1991; Biemont et al. 1993; Asplund et al. 2005; Caffau et al. 2010). Uncertainties in the oscillator strengths (Table 1) were also folded into the error budget, simply assuming a one-to-one mapping of the error in log gf to the error in log ɛC, adopting the errors stipulated in NIST.

The mean abundances presented in the final row were then calculated after weighting individual lines i in the usual way: 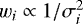wi∝1/σi2$w_{i}\propto1/\sigma_{i}^{2}$. Under the assumption that all of the uncertainties are uncorrelated, the standard error in the weighted means presented in the final row is 0.02 dex. The forbidden [C I] 872.2 nm line was also included in this weighted mean (i.e. it was treated equally to the permitted C I lines). We discuss the mean abundance and its error further, in Sect. 4.2.

The 3D non-LTE versus 3D LTE abundance differences in Table 2 are not very severe: typically around 0.01 dex. This can becontrasted with the values plotted in Fig. 5, which can be in excess of 0.10 dex. This is because the lines selected for determining the solar carbon abundance are relatively insensitive to departures from LTE. Using the disk-centre intensity, rather than the disk-integrated flux, further reduces the impact of non-LTE effects. This means that the inferred solar carbonabundance should be less sensitive to any residual modelling errors arising from the non-LTE model atom and radiative transfer.

In Fig. 6 we illustrate the inferred solar carbon abundances as functions of different line parameters. These plots are a useful check of possible systematic errors in the models. However, they have less diagnostic power on different non-LTE models, owing to the large scatter in the inferred line-by-line abundances. For clarity, we only display the abundances inferred from the 3Dnon-LTE, 3D LTE, and 1D LTE models in these plots.

Using the 3D non-LTE model, consistent abundances are obtained from the different C I lines, within a standard deviation of 0.06 dex. This large dispersion may indicate systematic errors in the models, rather than uncertainties in the equivalent width measurements. It is similar to the typical uncertainties in the individual oscillator strengths (Table 1), and could therefore be in part explained by errors in the oscillator strengths.

There is a slight trend in the inferred abundance with wavelength, and a more noticeable trend with line strength (log W∕λ) that is significant at the 2σ level. Larger abundances tend to be inferred from the stronger C I lines than from the weaker ones. The trend is mainly driven by the very low abundances inferred from the two weak C I 658.8 and 711.1 nm lines, as observed previously by Asplund et al. (2005). To bring these two lines into agreement with the other lines, their log gf values would need to be decreased by about 0.1 dex, or around 2σ if the errors in Table 1 are to be believed. Improved C I oscillator strengths would be highly desirable to help resolve this issue.

thumbnail Fig. 5

Abundance errors (i.e. abundance differences with respect to 3D non-LTE) for the lines listed in Table 1, when observed as disk-centre intensity (left column) or as disk-integrated flux (right column). The [C I] 872.7 nm line is not shown in these plots. Positive abundance errors imply negative abundance corrections. A fixed 3D non-LTE solar carbon abundance of 8.43 dex was assumed.
Table 2

Equivalent widths in the disk-centre solar intensity and inferred solar carbon abundances from the different models.

3.4 Centre-to-limb variations

The centre-to-limb variations of a selection of C I lines (Sect. 2.1) were studied using the high-resolution, high signal-to-noise “SS3” atlas of Stenflo (2015) of the limb to disk-centre ratio atlas 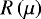R(μ)$R\left(\mu\right)$: r(μ)≡I(μ)/Icont.(μ),R(μ)≡r(μ)/r(1.0). \begin{eqnarray*} r\left(\mu\right)&\equiv& I\left(\mu\right)/I^{\text{cont.}}\left(\mu\right),\\ R\left(\mu\right)&\equiv&r\left(\mu\right)/r\left(1.0\right). \vspace*{-1pt}\end{eqnarray*}

Stenflo (2015) provide data continuously from roughly 400 to 1000 nm, for μ = 0.145, and state that the uncertainty in the viewing angle is at least σμ ≈ 0.01.

The limb to disk-centre ratios predicted by (a) the 3D non-LTE model, (b) the 3D non-LTE model but collapsing all fine structure in the model atom (“No FS”), (c) the 3D non-LTE model but neglecting collapsing all fine structure in the model atom and neglecting neutral hydrogen impact excitation (“No FS / C+H exc.”), and (d) the 3D LTE model, were fit to the observations. The 1D models were not considered here for two reasons. First, we are mainly interested in comparing different non-LTE modelling approaches; this is best done using the 3D models. Second, the 1D models are complicated by the requirements of extra broadening, usually in the form of microturbulence and macroturbulence fudge parameters.

Prior to performing the fits, the atlas was renormalised using clean regions close to each C I line. When fitting each C I line, the absolute wavelength calibration of the atlas was treated as a free parameter. The viewing angle was permitted to vary freely within the assumed uncertainty of σμ = 0.01. For each line and each model, the solar carbon abundance was set to the values inferred from analysing the disk-centre equivalent widths, and was permitted to vary freely within an assumed uncertainty of 0.05 dex. For most of the lines, the adopted disk-centre abundances can be found in Table 2. The C I 833.5, 960.3, and 965.8 nm lines are missing from that table, as they are not ideal solar carbon abundance indicators (Sect. 2.1). Therefore, for these lines the abundance analysis presented in Sect. 3.3 was repeated, this time adopting disk-centre intensity equivalent widths from Asplund et al. (2005) for the C I 960.3 nm line, and from Biemont et al. (1993) for the other two lines.

We illustrate the comparison of the model predictions to the observations for the different C I lines in Figs. 7 and 8. Not all of the lines studied have diagnostic power: the four different models predicted almost identical limb to disk-centre ratios for the C I 658.8 and 711.1 nm lines in the bottom row of Fig. 7, and for these two lines all four models are able to satisfactorily reproduce the observations.

As we mentioned in Sect. 2.1, the C I 711.3 nm is blended with a CN line, that amount for around 7% of the total disk-centre intensity equivalent width. The centre-to-limb variation of the molecular blend is different to that of the C I line, and this is reflected in the results for the C I 711.3 nm in Fig. 8: the limb to disk-centre ratios of the different models are very similar, nevertheless, the ratio is slightly too strong compared to the observations (the discrepancy is more noticeable, when this plot is contrasted against the plot of the C I 711.1 nm line in Fig. 7). We stress again that our equivalent width and inferred abundances in Table 2 have taken this blend into account.

The results for the C I 833.5, 960.3, and 965.8 nm lines in Fig. 8 clearly favour the 3D non-LTE model over the 3D LTE model. This is evidence for the need to take departures from LTE into account, and for the accuracy of our model atom. The quality of the fits is not perfect, but this is understandable since the C I 960.3 nm line is blended with a CN line in the far red wing, while the C I 833.5 and C I 965.8 nm lines clearly suffer from several small blends (including a Ti I line in the blue wing of the C I 833.5 nm line), which is why they are not considered reliable abundance diagnostics.

The C I 833.5, 960.3, and 965.8 nm lines in Fig. 8 show that the standard model atom, in which fine structure is retained, is able to fit the observations slightly better than the model atom in which fine structure is collapsed. This is as expected from the discussion in Sect. 2.4.6, with fine structure having a larger impact on the statistical equilibrium higher up in the atmosphere.Nevertheless, the difference between the two model predictions for the limb to disk-centre ratios is not very large.

Finally, it can be seen that neutral hydrogen impact excitation is indeed important in the solar photosphere. This is clearly demonstrated by the results for the C I 833.5, 960.3, and 965.8 nm lines in Fig. 8, and also by the results for the C I 505.2 and 538.0 nm lines in Fig. 7. This result is interesting, given that the model adopts a new prescription for neutral hydrogen impact excitation (“LCAO+Free”), as described in Sect. 2.4.4.

thumbnail Fig. 6

Inferred solar carbon abundances for different lines and models, based on disk-centre intensities. The [C I] 872.7 nm line is not shown in these plots. Error bars are only shown for the 3D non-LTE model. Weighted linear fits are overdrawn.

4 Discussion

4.1 Comparison with previous studies

In Sect. 3.2, we found that the non-LTE abundance corrections for C I lines tend to be negative in the solar photosphere. This result can be compared with other 1D non-LTE analyses (e.g. Stürenburg & Holweger 1990; Asplund et al. 2005; Fabbian et al. 2006; Caffau et al. 2010; Alexeeva & Mashonkina 2015): these all predict negative non-LTE abundance corrections, in agreement with our result.

The most recent and comprehensive 1D non-LTE study is that of Alexeeva & Mashonkina (2015). They constructed a large model C I atom that included fine structure. In their later study (Alexeeva et al. 2016), they updated their model atom to include the more reliable BSR electron impact excitation and ionisation data (Zatsarinny 2006), that was also adopted here, this had only a small impact on their results (Alexeeva, priv. comm.). The main difference between their model and that adopted here is the prescriptionfor neutral hydrogen impact excitation: they adopted the Drawin recipe (Drawin 1968, 1969; Steenbock & Holweger 1984; Lambert 1993), whereas the model used here adopted the “LCAO+Free” approach described in Sect. 2.4.4.

Comparing Fig. 2 of Alexeeva & Mashonkina (2015) with Fig. 4 here, the departure coefficients between the two studies are in good qualitative agreement. The low-excitation levels stay close to unity, the intermediate-excitation levels are slightly overpopulated with respect to LTE, and the high-exctation levels underpopulate with respect to LTE. As illustrated in Fig. 4 here, the extent of the departures from LTE are very sensitive to neutral hydrogen impact excitation, and this can explain for example the larger overpopulation of the intermediate-excitation levels compared to ours.

thumbnail Fig. 7

Comparison of the observed limb (μ ≈ 0.145) to disk-centre (μ = 1.0) normalised intensity ratios with different model predictions, for different lines. The solar carbon abundances were set independently for each line and model using disk-centre intensity equivalent widths. The solar carbon abundances and limb viewing angle were allowed to vary within their respective uncertainties, as described in Sect. 3.4. See also Fig. 8.

4.2 Solar carbon abundance

In Sect. 3.3 the solar carbon abundance was inferred from different C I lines as a diagnostic for the 3D non-LTE line formation models. We can also use this analysis to comment on the solar carbon abundance; a fully consistent 3D non-LTE determination has not been presented in the literature before.

Our derived abundance is log ɛC = 8.44 ± 0.02. The value isthe weighted mean from the fully consistent 3D non-LTE analysis presented in Table 2. The uncertainty was calculated in a way similar to the way explained in Sect. 4.1 of Scott et al. (2015): the systematic error arising from the non-LTE modelling was estimated by taking half the difference between the 3D LTE and 3D non-LTE results (0.004 dex), and the systematic error arising from the 3D modelling was estimated by taking half the difference between the 1D non-LTE and 3D non-LTE results (0.013 dex). These were combined in quadrature (0.014 dex). This systematic error was combined in quadrature with the standard error in the weighted mean (0.016 dex), to get the final uncertainty (0.02 dex).

Our derived value is consistent with the current standard value of log ɛC = 8.43 ± 0.05 (Asplund et al. 2009). In fact, it is in good agreement with the abundances inferred from each of the five different diagnostics employed in that work: the [C I] 872.7 nm line (8.41 dex), 16 C I lines (8.42 dex), CH Δv = 1 lines (8.44 dex), CH A - X lines (8.43 dex), and C2 Swan lines (8.46 dex).

The [C I] line is insensitive to departures from LTE in the solar photosphere, and is relatively insensitive to the model atmosphere (see Asplund et al. 2009, Table 2). Most of the differences between the result of Asplund et al. (2009), of 8.41 dex, and our result of 8.45 dex, can be attributed to their larger oscillator strength: log gf = −8.136, compared toour log gf = − 8.165, which leads to a 0.03 dex difference in inferred abundance.

Our derived carbon abundance is significantly lower than the value of Caffau et al. (2010, 2011), who inferred log ɛC = 8.50 ± 0.06. Their abundances were based on a 3D LTE analysis of the [C I] 872.7 nm line and 44 C I lines; as with Asplund et al. (2009), they applied negative 1D non-LTE versus 1D LTE abundance corrections for the C I lines.

The main reason for the discrepancy between our result and that of Caffau et al. (2010, 2011) can be traced to differences in the equivalent widths. Their equivalent widths tend to be systematically larger than those adopted here. Adopting their equivalent widths, and lines for that they assigned a rank of 1, we obtain a solar carbon abundance that is around 0.07 dex larger than our derived value: that is, log ɛC ≈ 8.51, in good agreement with their result. Looking carefully at the line shapes as well as databases of known lines in the solar spectrum, one can see that around two thirds of the C I lines used by Caffau et al. (2010, 2011) are blended, and are therefore not suitable abundance indicators, tending to bias the inferred carbon abundance upwards. Including blended lines also results in a significantly larger scatter in the results, with a standard deviation in the line-by-line carbon abundances of 0.11 dex: compare Fig. 3 of Asplund et al. 2005 with Fig. 3 of Caffau et al. 2010, noting the difference in scales.

thumbnail Fig. 8

Comparison of the observed limb (μ ≈ 0.145) to disk-centre (μ = 1.0) normalised intensity ratios with different model predictions, for different lines. The solar carbon abundances were set independently for each line and model using disk-centre intensity equivalent widths. The solar carbon abundances and limb viewing angle were allowed to vary within their respective uncertainties, as described in Sect. 3.4. See also Fig. 7.

4.3 Solar C/O ratio

We briefly comment on the solar C/O ratio, having also recently presented a similar 3D non-LTE analysis of the O I 777 nm triplet (Amarsi et al. 2018a). In that work, we obtained log ɛO = 8.69 ± 0.03, in agreement with the current standard value (Asplund et al. 2009). Combining this with our value of log ɛC = 8.44 ± 0.02, and assuming that these two uncertainties are uncorrelated, a solar C/O ratio of 0.56± 0.05 is inferred. This is consistent with the C/O ratios of Asplund et al. (2009), and also of Caffau et al. (2011), namely 0.55± 0.09 and 0.55± 0.12 respectively.

There remains a discrepancy with recent in situ measurements of the fast solar wind from polar coronal holes: 0.67± 0.06 (von Steiger & Zurbuchen 2016). We caution however that the C/O ratio in the solar wind may not be reflective of that in the solar photosphere owing to the First Ionisation Potential (FIP) effect and related fractionation effects (e.g. Serenelli et al. 2016). Nevertheless, current models suggest that such effects have only a small impact on the C/O ratio (e.g. Laming 2015, Table 4), reflecting the similar ionisation potentials of neutral carbon and neutral oxygen.

On the other hand, this C/O ratio is larger than that measured in solar neighbourhood B-type stars. Nieva & Przybilla (2012) infer a larger oxygen abundance and a smaller carbon abundance from B-type stars, and infer a C/O ratio of 0.37± 0.05, significantly lower than our solar estimate. The C/O ratio at the solar surface should roughly reflect that of the present-day local cosmos, andconsequently that in short-lived B-type stars, because to first order carbon and oxygen are expected to be similarly affected by thermal diffusion, gravitational settling, and radiative acceleration, and should have had similar Galactic chemical enrichment histories (e.g. Asplund et al. 2009, and references therein). As discussed in Sect. 7.5 of Nieva & Przybilla (2012), a higher C/O ratio in the Sun compared to in nearby B-type stars is probably a sign that the Sun wasborn at a location closer to the centre of the Galaxy and later migrated outwards to its present location.

5 Conclusion

We have presented a new model atom for non-LTE analyses of C I line formation in late-type stars. We used the model atom together with detailed 3D non-LTE radiative transfer calculations across a 3D hydrodynamic model solar atmosphere, and analysed the solar spectrum. The model atom successfully reproduced the observed limb to disk-centre ratios of various C I lines, and conclusively ruled out 3D LTE as a viable model. We also presented the first consistent 3D non-LTE solar carbon abundance determination. Our derived value is log ɛC = 8.44 ± 0.02. The new solar carbon abundance is consistent with the current standard value of log ɛC = 8.43 ± 0.05 presented in Asplund et al. (2009). Combined with an earlier 3D non-LTE solar oxygen abundance of log ɛO = 8.69 ± 0.03, a solar C/O ratio of 0.56 ± 0.05 was inferred, again consistent with the current standard value of 0.55 ± 0.09.

The true nature of inelastic collisions with neutral hydrogen, and their role on non-LTE stellar spectroscopy, is a decades-old problem. The main improvement in our model atom compared with previous studies is the more realistic, “LCAO+Free” description of neutral hydrogen impact excitation. This approach was first motivated in our earlier study of the solar centre-to-limb variation of the high excitation potential O I 777 nm triplet (Amarsi et al. 2018a). As in that work, the 3D non-LTE line formation model in this work successfully reproduced the limb to disk-centre ratios of various C I lines, only when neutral hydrogen impact excitation was included. This suggests that the “LCAO+Free” recipe is a suitable approach for non-LTE modelling of neutral lines in late-type stars, although we cannot rule out some unknown, compensating systematic errors in our models. Since neglecting neutral hydrogen impact excitation can impart abundance errors of up to 0.3 dex on disk-integrated fluxes, at least for C I lines in the Sun, it is important to take these collisional processes into account.

Acknowledgements

We thank the referee, Lyudmila Mashonkina, for carefully reading and providing helpful suggestions on the manuscript, and in particular for insight and comments which helped identify a numerical issue with the code and thus greatly improved the paper. We also thank Sofya Alexeeva for answering in detail our various questions about her analysis, and Karin Lind and Amanda Karakas for comments on the manuscript. A.M.A. acknowledges funds from the Alexander von Humboldt Foundation in the framework of the Sofja Kovalevskaja Award endowed by the Federal Ministry of Education and Research. P.S.B. acknowledges support from the Swedish Research Council and the project grant “The New Milky Way” from the Knut and Alice Wallenberg Foundation. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (grant DNRF106). M.A. gratefully acknowledges funding from the Australian Research Council (grants DP150100250 and FL110100012). Some of the computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the Multidisciplinary Center for Advanced Computational Science (UPPMAX) and at the High Performance Computing Center North (HPC2N) under project SNIC2018-3-465. This work was supported by computational resources provided by the Australian Government through the National Computational Infrastructure (NCI) under the National Computational Merit Allocation Scheme.

References

  1. Alexeeva, S. A., & Mashonkina, L. I. 2015, MNRAS, 453, 1619 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alexeeva, S. A., Ryabchikova, T. A., & Mashonkina, L. I. 2016, MNRAS, 462, 1123 [NASA ADS] [CrossRef] [Google Scholar]
  3. Allen, C. W. 1973, Astrophysical Quantities (London: Athlone Press) [Google Scholar]
  4. Allende Prieto, C., Asplund, M., & Fabiani Bendicho, P. 2004, A&A, 423, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Amarsi, A. M. 2015, MNRAS, 452, 1612 [NASA ADS] [CrossRef] [Google Scholar]
  6. Amarsi, A. M., & Asplund, M. 2017, MNRAS, 464, 264 [NASA ADS] [CrossRef] [Google Scholar]
  7. Amarsi, A. M., Barklem, P. S., Asplund, M., Collet, R., & Zatsarinny, O. 2018a, A&A, 616, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Amarsi, A. M., Nordlander, T., Barklem, P. S., et al. 2018b, A&A, 615, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Amarsi, A. M., Nissen, P. E., Asplund, M., Lind, K., & Barklem, P. S. 2019, A&A, 622, L4 [Google Scholar]
  10. Anstee, S. D., & O’Mara, B. J. 1995, MNRAS, 276, 859 [NASA ADS] [CrossRef] [Google Scholar]
  11. Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
  12. Asplund, M., Grevesse, N., Sauval, A. J., Allende Prieto, C., & Blomme, R. 2005, A&A, 431, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bard, S., & Carlsson, M. 2008, ApJ, 682, 1376 [NASA ADS] [CrossRef] [Google Scholar]
  15. Barklem, P. S. 2016a, A&ARv, 24, 9 [NASA ADS] [CrossRef] [Google Scholar]
  16. Barklem, P. S. 2016b, Phys. Rev. A, 93, 042705 [NASA ADS] [CrossRef] [Google Scholar]
  17. Barklem, P. S. 2017, Astrophysics Source Code Library [record ascl:1701.005] [Google Scholar]
  18. Barklem, P. S., & O’Mara, B. J. 1997, MNRAS, 290, 102 [Google Scholar]
  19. Barklem, P. S., O’Mara, B. J., & Ross, J. E. 1998, MNRAS, 296, 1057 [Google Scholar]
  20. Barklem, P. S., Osorio, Y., Fursa, D. V., et al. 2017, A&A, 606, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Basu, S., & Antia, H. M. 2008, Phys. Rep., 457, 217 [NASA ADS] [CrossRef] [Google Scholar]
  22. Belyaev, A. K., & Barklem, P. S. 2003, Phys. Rev. A, 68, 062703 [NASA ADS] [CrossRef] [Google Scholar]
  23. Belyaev, A. K., Barklem, P. S., Dickinson, A. S., & Gadéa, F. X. 2010, Phys. Rev. A, 81, 032706 [NASA ADS] [CrossRef] [Google Scholar]
  24. Belyaev, A. K., Barklem, P. S., Spielfiedel, A., et al. 2012, Phys. Rev. A, 85, 032704 [NASA ADS] [CrossRef] [Google Scholar]
  25. Berrington, K. A., & Seaton, M. J. 1985, J. Phys. B At. Mol. Phys., 18, 2587 [NASA ADS] [CrossRef] [Google Scholar]
  26. Biemont, E., Hibbert, A., Godefroid, M., & Vaeck, N. 1993, ApJ, 412, 431 [NASA ADS] [CrossRef] [Google Scholar]
  27. Botnen, A., & Carlsson, M. 1999, Astrophys. Space Sci. Lib., 240, 379 [NASA ADS] [CrossRef] [Google Scholar]
  28. Bromm, V., & Loeb, A. 2003, Nature, 425, 812 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
  29. Burke, P. G., & Robb, W. D. 1976, Advances in Atomic and Molecular Physics, (Netherlands: Elsevier), 11, 143 [NASA ADS] [CrossRef] [Google Scholar]
  30. Caffau, E., Ludwig, H.-G., Bonifacio, P., et al. 2010, A&A, 514, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
  32. Collet, R., Magic, Z., & Asplund, M. 2011, J. Phys. Conf. Ser., 328, 012003 [NASA ADS] [CrossRef] [Google Scholar]
  33. Cunto, W., Mendoza, C., Ochsenbein, F., & Zeippen, C. J. 1993, A&A, 275 L5 [NASA ADS] [Google Scholar]
  34. Drawin, H. W. 1968, Z. Phys., 211, 404 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Drawin, H. W. 1969, Z. Phys., 225, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Fabbian, D., Asplund, M., Carlsson, M., & Kiselman, D. 2006, A&A, 458, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Fabbian, D., Nissen, P. E., Asplund, M., Pettini, M., & Akerman, C. 2009, A&A, 500, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Froese Fischer, C. 2006, J. Phys. B At. Mol. Phys., 39, 2159 [NASA ADS] [CrossRef] [Google Scholar]
  39. Gallagher, A. J., Caffau, E., Bonifacio, P., et al. 2017, A&A, 598, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres (Cambridge: Cambridge University Press) [Google Scholar]
  41. Grevesse, N., Lambert, D. L., Sauval, A. J., et al. 1991, A&A, 242, 488 [NASA ADS] [Google Scholar]
  42. Hibbert, A., Biemont, E., Godefroid, M., & Vaeck, N. 1993, A&AS, 99, 179 [NASA ADS] [Google Scholar]
  43. Karakas, A. I. 2014, MNRAS, 445, 347 [NASA ADS] [CrossRef] [Google Scholar]
  44. Kaulakys, B. P. 1985, J. Phys. B At. Mol. Phys., 18, L167 [NASA ADS] [CrossRef] [Google Scholar]
  45. Kaulakys, B. P. 1991, J. Phys. B At. Mol. Phys., 24, L127 [Google Scholar]
  46. Kobayashi, C., Karakas, A. I., & Umeda, H. 2011, MNRAS, 414, 3231 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kramida, A., Ralchenko, Y., Reader, J., & NIST ASD Team 2015, NIST Atomic Spectra Database (ver. 5.3), Available: http://physics.nist.gov/asd (2015, November 2) [Google Scholar]
  48. Kuchner, M. J., & Seager, S. 2005, ArXiv e-prints [arXiv:astro-ph/0504214] [Google Scholar]
  49. Lambert, D. L. 1993, Phys. Scr., T47, 186 [CrossRef] [Google Scholar]
  50. Laming, J. M. 2015, Liv. Rev. Sol. Phys., 12, 2 [Google Scholar]
  51. Leenaarts, J., & Carlsson, M. 2009, in The Second Hinode Science Meeting: Beyond Discovery-Toward Understanding, eds. B. Lites, M. Cheung, T. Magara, J. Mariska, & K. Reeves, ASP Conf. Ser., 415, 87 [NASA ADS] [Google Scholar]
  52. Limongi, M., & Chieffi, A. 2018, ApJS, 237, 13 [NASA ADS] [CrossRef] [Google Scholar]
  53. Lind, K., Amarsi, A. M., Asplund, M., et al. 2017, MNRAS, 468, 4311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Luo, D., & Pradhan, A. K. 1989, J. Phys. B At. Mol. Phys., 22, 3377 [NASA ADS] [CrossRef] [Google Scholar]
  55. Madhusudhan, N. 2012, ApJ, 758, 36 [NASA ADS] [CrossRef] [Google Scholar]
  56. Magic, Z., Collet, R., Asplund, M., et al. 2013, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Moore, C. E. 1993, in Tables of Spectra of Hydrogen, Carbon, Nitrogen, and Oxygen Atoms and Ions, ed. J. Gallagher (Boca Raton: CRC press), 352 [Google Scholar]
  58. Nieva, M.-F., & Przybilla, N. 2012, A&A, 539, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Nissen, P. E., Chen, Y. Q., Carigi, L., Schuster, W. J., & Zhao, G. 2014, A&A, 568, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Nordlund, Å., & Galsgaard, K. 1995, A 3D MHD code for Parallel Computers, Tech. rep., Niels Bohr Institute, University of Copenhagen [Google Scholar]
  61. Nussbaumer, H., & Storey, P. J. 1981, A&A, 96, 91 [NASA ADS] [Google Scholar]
  62. Pereira, T. M. D., Asplund, M., & Kiselman, D. 2009, A&A, 508, 1403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Prša, A., Harmanec, P., Torres, G., et al. 2016, AJ, 152, 41 [NASA ADS] [CrossRef] [Google Scholar]
  64. Rutten, R. J. 2003, Radiative Transfer in Stellar Atmospheres (The Netherlands: Utrecht University) [Google Scholar]
  65. Rybicki, G. B., & Hummer, D. G. 1992, A&A, 262, 209 [NASA ADS] [Google Scholar]
  66. Scott, P., Grevesse, N., Asplund, M., et al. 2015, A&A, 573, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Serenelli, A., Scott, P., Villante, F. L., et al. 2016, MNRAS, 463, 2 [NASA ADS] [CrossRef] [Google Scholar]
  68. Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 [NASA ADS] [Google Scholar]
  69. Steffen, M., Prakapavičius, D., Caffau, E., et al. 2015, A&A, 583, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [Google Scholar]
  71. Stenflo, J. O. 2015, A&A, 573, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Stürenburg, S., & Holweger, H. 1990, A&A, 237, 125 [NASA ADS] [Google Scholar]
  73. Tachiev, G., & Froese Fischer, C. 2000, J. Phys. B At. Mol. Phys., 33, 2419 [NASA ADS] [CrossRef] [Google Scholar]
  74. Tachiev, G., & Froese Fischer, C. 2001, Can. J. Phys., 79, 955 [NASA ADS] [CrossRef] [Google Scholar]
  75. Takeda, Y. 1992, PASJ, 44, 649 [Google Scholar]
  76. Takeda, Y., & Honda, S. 2005, PASJ, 57, 65 [NASA ADS] [Google Scholar]
  77. Takeda, Y., Honda, S., Ohnishi, T., et al. 2013, PASJ, 65, 53 [Google Scholar]
  78. van Regemorter, H. 1962, ApJ, 136, 906 [NASA ADS] [CrossRef] [Google Scholar]
  79. Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
  80. von Steiger, R., & Zurbuchen, T. H. 2016, ApJ, 816, 13 [NASA ADS] [CrossRef] [Google Scholar]
  81. Wang, Y., Zatsarinny, O., & Bartschat, K. 2013, Phys. Rev. A, 87, 012704 [NASA ADS] [CrossRef] [Google Scholar]
  82. Wilson, N. J., Bell, K. L., & Hudson, C. E. 2005, A&A, 432, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
  84. Yan, Y., Taylor, K. T., & Seaton, M. J. 1987, J. Phys. B At. Mol. Phys., 20, 6399 [NASA ADS] [CrossRef] [Google Scholar]
  85. Zatsarinny, O. 2006, Comput. Phys. Commun., 174, 273 [NASA ADS] [CrossRef] [Google Scholar]
  86. Zhao, G., Mashonkina, L., Yan, H. L., et al. 2016, ApJ, 833, 225 [NASA ADS] [CrossRef] [Google Scholar]
1

[A/B] = (logNA/logNB)*−(logNA/logNB)⊙${\mathrm{\left[A/B\right]}}\,{=}\, \left(\log{N_{\mathrm{A}}}/\log{N_{\mathrm{B}}}\right)_{*}- \left(\log{N_{\mathrm{A}}}/ \log{N_{\mathrm{B}}}\right)_{\odot}$.

All Tables

Table 1

Parameters of the full set of lines for which 3D non-LTE effects are discussed.

In the text
Table 2

Equivalent widths in the disk-centre solar intensity and inferred solar carbon abundances from the different models.

In the text

All Figures

thumbnail Fig. 1

Contribution functions to the intensity depression for the C I 505.2 and 960.3 nm lines, and the [C I] 872.7 nm line, integrated over wavelength, at two different viewing angles. The contribution functions have been normalised such that under each, the area is equal to unity.
In the text
thumbnail Fig. 2

Grotrian diagrams for C I and C II in the comprehensive model atom. Levels that do not resolve fine structure are shown as red lines.
In the text
thumbnail Fig. 3

Grotrian diagram for C I in the standard model atom, after reducing the comprehensive model by removing C III and all excited levels of C II, and by constructing super levels. Levels that do not resolve fine structure are shown as red lines, and super levels are shown as long horizontal lines. Some of the C I lines explicitly considered in this work have been highlighted; “~ 711 nm” refers to the C I 711.1 and 711.3 nm lines, and “~ 960 nm” refers to the C I 960.3 and 965.8 nm lines.
In the text
thumbnail Fig. 4

Departure coefficients across the ⟨3D⟩ model atmosphere, for the lowest 42 terms of C 1 (up to 2s2 2p 4d 3Po) as well as the ground state of C II. A solar carbon abundance of log ɛC = 8.43 was assumed. The low-excitation levels indicated in the plot span the ground state up to 2s.2p 3 5 So (4.18 eV), while the high-excitation levels indicated in the plot span 2s2.2p.3p 1P (8.54 eV) up to the ionisation limit (11.26 eV). The intermediate-excitation levels are those levels between them: 2s2.2p.3s 3Po (7.49 eV), 2s2.2p.3s 1Po (7.68 eV), and 2s.2p3 3Do (7.95 eV). Departure coefficients are shown for the standard model atom (Fig. 3). The impact of collapsing fine structure, and of removing neutral hydrogen impact excitation, are also shown.
In the text
thumbnail Fig. 5

Abundance errors (i.e. abundance differences with respect to 3D non-LTE) for the lines listed in Table 1, when observed as disk-centre intensity (left column) or as disk-integrated flux (right column). The [C I] 872.7 nm line is not shown in these plots. Positive abundance errors imply negative abundance corrections. A fixed 3D non-LTE solar carbon abundance of 8.43 dex was assumed.
In the text
thumbnail Fig. 6

Inferred solar carbon abundances for different lines and models, based on disk-centre intensities. The [C I] 872.7 nm line is not shown in these plots. Error bars are only shown for the 3D non-LTE model. Weighted linear fits are overdrawn.
In the text
thumbnail Fig. 7

Comparison of the observed limb (μ ≈ 0.145) to disk-centre (μ = 1.0) normalised intensity ratios with different model predictions, for different lines. The solar carbon abundances were set independently for each line and model using disk-centre intensity equivalent widths. The solar carbon abundances and limb viewing angle were allowed to vary within their respective uncertainties, as described in Sect. 3.4. See also Fig. 8.
In the text
thumbnail Fig. 8

Comparison of the observed limb (μ ≈ 0.145) to disk-centre (μ = 1.0) normalised intensity ratios with different model predictions, for different lines. The solar carbon abundances were set independently for each line and model using disk-centre intensity equivalent widths. The solar carbon abundances and limb viewing angle were allowed to vary within their respective uncertainties, as described in Sect. 3.4. See also Fig. 7.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.