| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | L2 | |
| Number of page(s) | 7 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201834900 | |
| Published online | 28 February 2019 | |
Letter to the Editor
Alpha particle thermodynamics in the inner heliosphere fast solar wind
1
Department of Physics, Imperial College London, London SW7 2AZ, UK
e-mail: david.stansby14@imperial.ac.uk
2
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Univ. Paris Diderot, Sorbonne Paris Cité, 5 place Jules Janssen, 92195 Meudon, France
3
Space Sciences Laboratory, University of California, Berkeley, CA 94720, USA
Received:
17
December
2018
Accepted:
19
February
2019
Context. Plasma processes occurring in the corona and solar wind can be probed by studying the thermodynamic properties of different ion species. However, most in situ observations of positive ions in the solar wind are taken at 1 AU, where information on their solar source properties may have been irreversibly erased.
Aims. In this study we aim to use the properties of alpha particles at heliocentric distances between 0.3 AU and 1 AU to study plasma processes occurring at the points of observation, and to infer processes occurring inside 0.3 AU by comparing our results to previous remote sensing observations of the plasma closer to the Sun.
Methods. We reprocessed the original Helios positive ion distribution functions, isolated the alpha particle population, and computed the alpha particle number density, velocity, and magnetic field perpendicular and parallel temperatures. We then investigated the radial variation of alpha particle temperatures in fast solar wind observed between 0.3 AU and 1 AU.
Results. Between 0.3 AU and 1 AU alpha particles are heated in the magnetic field perpendicular direction and cooled in the magnetic field parallel direction. Alpha particle evolution is bounded by the alpha firehose instability threshold, which provides one possible mechanism to explain the observed parallel cooling and perpendicular heating. Closer to the Sun our observations suggest that the alpha particles undergo heating in the perpendicular direction, whilst the large magnetic field parallel temperatures observed at 0.3 AU may be due to the combined effect of double adiabatic expansion and alpha particle deceleration inside 0.3 AU.
Key words: solar wind / Sun: heliosphere
© ESO 2019
1. Introduction
The solar wind is a tenuous magnetised plasma flowing from the surface of the Sun to the edge of the heliosphere. Although protons form the bulk of the positive ions in the fast solar wind by number density (∼95%), alpha particles (doubly ionised helium) comprise ∼5% by ion number density, and therefore ∼10% by ion charge density, and ∼20% by mass density (Robbins et al. 1970; Kasper et al. 2007). In the weakly collisional fast solar wind at 1 AU the alphas are hotter than protons by a factor of around 5 (Tracy et al. 2015; Kasper et al. 2017). This is often assumed to be a remnant of a process in the corona that heats heavy ions to higher temperatures than protons, for which several proposed mechanisms exist (e.g. see the review of Cranmer & Winebarger 2019). Remote sensing observations of multiple heavy ions close to the Sun support this hypothesis (Landi & Cranmer 2009; Hahn & Savin 2013).
In addition to preferential heavy ion heating, the mechanism that heats protons in coronal holes deposits energy preferentially in the direction perpendicular to the magnetic field. This is inferred from both in situ observations in the inner heliosphere down to 0.3 AU (Marsch et al. 1982a; Matteini et al. 2007) and remote sensing observations of neutral hydrogen (which reflect the ionised hydrogen distribution function due to frequent collisionless charge exchange) closer to the Sun (Kohl et al. 1998; Dolei et al. 2016). However, measurements of the preferential perpendicular heating of other ion species are sparse. From remote sensing, the only other observations are of oxygen ions, which are also observed to undergo preferential perpendicular heating (Kohl et al. 1998; Cranmer et al. 2008).
From in situ measurements, 3D velocity distribution functions (VDF), which are unambiguously needed to determine both parallel and perpendicular temperatures, are typically only measured for protons and alpha particles. At 1 AU alpha particles are close to isotropy in all speed ranges (Marsch et al. 1982b; Maruca et al. 2012), which leaves open the possibility that collisional processes and wave-particle interactions have irreversibly erased information on source properties such as the presence or absence of temperature anisotropies closer to the Sun. This means observations are needed closer to the Sun to distinguish between properties set by processes occurring in the corona and properties resulting from evolution as the solar wind propagates radially away from the Sun.
The Helios mission, comprising two spacecraft in orbit around the Sun from 0.29–1 AU, measured 3D alpha particle distribution functions, but studies using this data closer to the Sun than 0.5 AU have been limited to a handful of papers (Marsch et al. 1982b, 1983; Schwartz & Marsch 1983; Thieme et al. 1989; Geranios 1989). In this work the 3D alpha distribution functions measured by Helios in the fast solar wind at 0.29–0.8 AU are used to present, for the first time, a detailed study of the thermodynamics of alpha particles in the fast solar wind inside 1 AU.
2. Data processing
In order to extract parameters of the alpha particle population we used the positive ion VDFs measured on board Helios by the E1 electrostatic analyser experiment (Rosenbauer et al. 1981).
Because alpha particles have a mass to charge ratio twice that of protons, at the same velocity they have a higher energy per charge, and therefore it is possible to separate the distribution using an energy per charge threshold, above which measurements are dominated by protons and below which they are dominated by alpha particles (Marsch et al. 1982a,b). However, there are still a significant number of alpha particles present just below this threshold. This means taking moments of the truncated alpha particle distribution significantly underestimates the true number density and temperatures, but as long as enough of the distribution function is present, fitting avoids this problem. This is nicely illustrated by Fig. 16 of Marsch et al. (1982a) in which core parallel temperatures (calculated through fitting) are systematically higher than total parallel temperatures (calculated from moments). We therefore chose to fit analytic bi-Maxwellian distribution functions to the separated alpha distribution function. We note that as a result of this choice caution should be applied when comparing our results to other alpha particle results using Helios data (including Marsch et al. 1982b; Schwartz & Marsch 1983), which for the most part used numerical moments of the truncated distribution function.
We stress that, although a secondary alpha beam is sometimes observed in the solar wind (Feldman et al. 1973, 1993), the limited energy resolution of the Helios ion instrument means we do not think the fitting process was capable of distinguishing between an “alpha core” and “alpha beam” population. A subset of the fits from each individual interval were inspected by eye and found accurately to characterise the width of the distribution (and therefore also the thermal energy) in both perpendicular and parallel to the magnetic field.
For specific details of the alpha fitting process and figures comparing the fits to the measured distribution functions, see Appendix A. The fitting process returned the alpha number density (nα), velocity (vα) and temperatures parallel (Tα∥) and perpendicular (Tα⊥) to the local magnetic field (B) for each distribution function. The original distribution functions that were fit are openly available, and the code used to fit the distributions is also available and documented, making the resulting fits reproducible. The outputted fit parameters have also been made freely available for use in further research. For more details and links to both the code and data, see Appendix A.
The observation dates of the 11 high speed streams used in this study are available online1. To check the validity of our fitted parameters we performed the following checks against previously published observations of alpha particles in the inner heliosphere:
-
Thermal speeds are the same order of magnitude as those measured by the MESSENGER mission in fast solar wind (Gershman et al. 2012), providing validation from independent instrumentation and processing.
-
Temperature anisotropies are the same sense and order of magnitude as the fits presented in Fig. 16 of Marsch et al. (1982a), providing validation from an independent processing of the Helios data.
-
The alpha particle abundance (ratio of alpha number density to proton core number density) has a median of 4.3%, which agrees well with alpha abundances measured in fast solar wind at 1 AU (Kasper et al. 2007) and beyond (Liu et al. 1995).
In the rest of this paper alpha particle properties are compared to concurrent proton properties taken from the dataset of Stansby et al. (2018a). We note that these parameters are specific to the proton core and not the entire proton population, which means that Tp⊥ values are systematically higher and Tp∥ values systematically lower than previous estimates from Helios data (for more details see Stansby et al. 2018a, Sect. 4.3). Proton parameters are denoted with a p subscript and alpha parameters with an α subscript. For each species i = p, α, the parallel beta was calculated as βi∥ = nikBTi∥/(|B|2/2μ0).
3. Results
3.1. Radial trends
Figure 1 shows the evolution of Tα⊥ and Tα∥ in the selected fast solar wind streams from 0.29–0.8 AU. At 0.3 AU the alpha particles are hotter than protons in both the perpendicular direction (Tα⊥ ≈ 3Tp⊥) and the parallel direction (Tα∥ ≈ 18Tp∥). In the absence of any collisions or wave-particle interactions the plasma temperatures are expected to follow a double adiabatic profile as the plasma propagates away from the Sun (Chew et al. 1956; Matteini et al. 2011). Figure 1 shows this prediction modelled forwards from the observed temperatures at 0.3 AU. For comparison, proton temperatures with corresponding adiabatic predictions are also shown in blue, along with the range of data recorded in fast solar wind (vr > 500 km s−1) at 1 AU by WIND.
 |
Fig. 1. Radial evolution of alpha (green) and proton (blue) temperatures in fast solar wind. Each cross is measured in a single continuous high speed stream. The width of crosses gives the range of radial distances sampled in each stream. The centre of the cross is at the median value, and the lower and upper bounds are the first and third quartiles of the data. Bars at 1 AU are taken from the WIND swe_h1 dataset. Shaded areas are a double adiabatic prediction (Chew et al. 1956) based on an ideal Parker spiral magnetic field (Parker 1958), for constant solar wind speeds in the range 600–800 km s−1. |
In the perpendicular direction (Fig. 1, top panel), both the alphas and protons cool more slowly than the double adiabatic prediction, but evolve with distance in a similar manner such that Tα⊥/Tp⊥ = const ≈ 3. The slower decrease of the proton perpendicular temperature in fast wind with respect to the double adiabatic prediction is well known (Marsch et al. 1982a; Hellinger et al. 2011), and our results indicate that the alpha perpendicular temperature undergoes a similarly slow decrease.
In the parallel direction (Fig. 1, middle panel) Tα∥ decreases faster than the double adiabatic prediction, meaning there must be at least one mechanism that is cooling the alpha particles in the parallel direction between 0.3 AU and 1 AU. This parallel cooling drives a decrease from Tα∥/Tp∥ ≈ 18 at 0.3 AU to Tα∥/Tp∥ ≈ 14 at 0.8 AU. In combination the fast decrease of Tα∥ and slow decrease of Tα⊥ means that the alpha temperature anisotropy increases with radial distance, strongly deviating from the double adiabatic prediction (Fig. 1, bottom panel).
3.2. Instability bounded evolution
While the protons at 0.3 AU have Tp⊥/Tp∥ > 1 (Marsch et al. 1982a, 2004), the alphas have Tα⊥/Tα∥ < 1. This has previously been mentioned by Marsch et al. (1982b), but Fig. 1 shows that this feature persists across the two observed fast solar wind streams at 0.3 AU. To make the difference between proton and alpha anisotropies clearer, the top panel of Fig. 2 shows the joint distribution of T⊥/T∥ and β∥ for both protons and alpha particles in data taken at distances 0.3 AU < r < 0.4 AU. The alphas have similar parallel beta values to the protons (βα∥ ≈ βp∥ ≈ 0.1), but much lower temperature anisotropies.
 |
Fig. 2. Joint probability distribution of parallel beta and temperature anisotropy for protons (blue) and alphas (green) at radial distances 0.3–0.4 AU (top panel) and 0.6–0.7 AU (bottom panel) in fast solar wind. The contours are logarithmically spaced from the maximum bin count to 0.1 times the maximum bin count. The dashed lines show the alpha firehose instability threshold for normalised growth rates of γ/Ωα = 10−3 (left-hand curve) and 10−2 (right-hand curve). See Appendix B for details of the instability curve calculation. The large spread in alpha particle values is likely partly due to experimental uncertainties in fitting alpha number densities and parallel temperatures. |
Double adiabatic expansion of the solar wind acts to reduce T⊥/T∥ and increase β∥ with radial distance (Chew et al. 1956; Matteini et al. 2011). As radial distance increases, this has the effect of moving the plasma closer to instability boundaries in the T⊥/T∥ – β∥ parameter space. At 0.6–0.7 AU (Fig. 2, bottom panel) the protons have moved to higher β∥ and lower anisotropies, but they only start to encounter the instability boundaries at r ≈ 1 AU (Matteini et al. 2007, 2013). The alphas reach an instability threshold at smaller heliocentric distances than this for two reasons: they already have low temperature anisotropies at 0.3 AU, bringing them closer to the T⊥ < T∥ instability boundaries than protons, and the instability boundaries for alphas are located at lower beta relative to the proton instability boundaries (Matteini et al. 2015). To confirm this, Fig. 2 shows the numerical instability threshold for the alpha firehose instability (see Appendix B for details of the threshold calculation).
The distribution of data relative to the instability thresholds at the two distances is consistent with the alpha particles being restricted from moving to lower Tα⊥/Tα∥ and higher βα∥ because these properties are limited by the alpha firehose instability. This agrees with similar observations of alpha particles at 1 AU, which show a wide spread of alpha parameters bounded by theoretical instability curves (Maruca et al. 2012). In addition, at 0.3 AU the well-known anti-correlation of T⊥/T∥ and β∥ present for the protons (Marsch et al. 2004) is also present in the alpha particles, but by 0.6 AU the anti-correlation for the alpha particles has been removed.
3.3. Heating rates
The amount of heating or cooling relative to simple double adiabatic expansion can be roughly estimated from these observations. In order to minimise the effect of varying temperatures due to different solar wind source properties, the heating rate was evaluated using two streams observed at 0.3 AU and 0.65 AU identified by Perrone et al. (2018) as originating from the same coronal hole (their streams A7 and A8).
The expected temperatures only due to adiabatic evolution depend on the ratios of number densities and magnetic field strengths at the two points of interest (Chew et al. 1956) as follows:
where the left-hand side are predicted temperatures and the right-hand side contains quantities measured at 0.3 AU (subscript “1”) and at 0.65 AU (subscript “2”).
The total energy density at any given distance is partitioned into the perpendicular and parallel directions: ϵ⊥ = nkBT⊥, 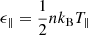 . These values can be evaluated at 0.65 AU using the observed number density and either the observed temperatures, or the predicted temperatures. The difference between the estimated energy density and observed energy density then gives a measure of the total energy added or removed from the plasma during transit, Δϵ⊥, ∥. To obtain a rough estimate for the heating rates (Q⊥, ∥), Δϵ⊥, ∥ was divided by the transit time Δt = Δr/vαr, where Δr = 0.35 AU is the radial distance between the two observations and vαr = 725 km s−1 is the average alpha particle radial velocity.
. These values can be evaluated at 0.65 AU using the observed number density and either the observed temperatures, or the predicted temperatures. The difference between the estimated energy density and observed energy density then gives a measure of the total energy added or removed from the plasma during transit, Δϵ⊥, ∥. To obtain a rough estimate for the heating rates (Q⊥, ∥), Δϵ⊥, ∥ was divided by the transit time Δt = Δr/vαr, where Δr = 0.35 AU is the radial distance between the two observations and vαr = 725 km s−1 is the average alpha particle radial velocity.
Estimates of the heating rates were calculated using the median observed values of nα and |B| in each stream, and therefore do not assume a speed profile or any specific magnetic field geometry in between the two points. Upper and lower limits were calculated using first and third quartile temperature values in each stream. Performing the calculations gives2
Although the range of values in each case spans about a decade, the alphas are clearly heated in the perpendicular direction and cooled in the parallel direction.
4. Discussion
The radial evolution of alpha particle temperatures (Fig. 1) is inconsistent with a simple double-adiabatic prediction: Tα∥ decreases faster than predicted with radial distance and Tα⊥ decreases more slowly. In addition the alpha particles lie near the thresholds for anisotropy instabilities at 0.3 AU (Fig. 2). The continual driving of temperature anisotropy instabilities is therefore one probable cause of the non-adiabatic evolution. These instabilities act locally to increase Tα⊥ and decrease Tα∥ according to both theory (e.g. Verscharen et al. 2013; Matteini et al. 2015; Seough & Nariyuki 2016) and expanding box simulations of an electron-proton-alpha solar wind (Hellinger et al. 2003; Hellinger & Trávníček 2013).
In addition to temperature anisotropy instabilities there are many other proposed mechanisms that could influence the observed non-adiabatic behaviour: i.e. alpha streaming instabilities (e.g. Gary et al. 2000; Verscharen et al. 2013, 2015; Markovskii et al. 2019), parametric decay instabilities (e.g. He et al. 2016), stochastic heating (e.g. Chandran 2010; Wang et al. 2011), ion cyclotron heating (e.g. Xie et al. 2004), or dissipation of turbulence (e.g. Perrone et al. 2014a,b; Maneva et al. 2015). Recently it has become clear that judging the stability of a plasma based solely on the distribution of data in a single anisotropy-beta parameter space is overly simplistic (Klein et al. 2017). In the future our new alpha dataset can be used with other methods to evaluate instabilities to which the alpha particles contribute (e.g. Bourouaine et al. 2013; Chen et al. 2016; Klein et al. 2018).
Previous estimates of proton heating rates in the fast solar wind from 0.3–0.65 AU show evidence of heating in the perpendicular direction and cooling in the parallel direction (Hellinger et al. 2011), with
These proton heating/cooling estimates are an order of magnitude larger than our estimates for the alpha heating rates, however converting the heating rates to a heating rate per particle using the observed median number density ratio of nα/np = 0.043 reveals that the heating rate per particle is likely higher for alpha particles than protons. This is in agreement with solar wind simulations that show alpha particles undergoing more heating than protons (Hellinger & Trávníček 2013; Perrone et al. 2014a; Valentini et al. 2016).
Our results also provide clues about plasma conditions closer to the Sun than 0.3 AU. Figure 3 shows an overview of ion temperatures in the solar wind inside 1 AU from both in situ and remote sensing measurements. In this work we provided the radial variation of alpha particles from 0.3 AU to 1 AU, which is shown alongside remote sensing measurements of hydrogen and oxygen close to the Sun, and in situ measurements of protons from 0.3 AU to 1 AU and oxygen at 1 AU.
 |
Fig. 3. Measurements of fast solar wind ion temperatures inside 1 AU. Top panel: perpendicular (triangles) and parallel (circles) temperatures for protons (blue), alpha particles (green), and oxygen ions (orange). New results from this work are alpha particles at large distances. The TH0⊥ values close to the Sun are from the polar measurements in Fig. 2 of Dolei et al. (2016). The TO5+⊥ values are from Fig. 5 of Cranmer et al. (2017), originally reported by Cranmer et al. (2008). |
Measurements at 1 AU of weakly collisional fast solar wind indicate that heavy ion temperatures are proportional to ion mass (Tracy et al. 2016). If we assume that this holds close to the Sun, and the alpha perpendicular temperature is less than the observed oxygen perpendicular temperature, there is an upper limit on the average rate at which Tα⊥ can decrease inside 0.3 AU. This upper limit is Tα⊥ ∼ r−1, which means inside 0.3 AU the alpha particles must be heated above the double adiabatic prediction (assuming a radial magnetic field) of ∼r−2.
Making a prediction in the parallel direction is more complicated because the double adiabatic prediction for T∥ depends on evolution of both the magnetic field strength and number density (Eq. (2)). In fast solar wind alpha particles stream faster than the protons at a large fraction of the local Alfvén speed. Because the Alfvén speed decreases with distance, the alpha particles decelerate as they travel away from the Sun (Marsch et al. 1982b). Because the radial particle flux must be conserved, nαr2 must increase with distance. If the alpha particles also stream at a significant fraction of the local Alfvén speed inside 0.3 AU, they also undergo deceleration between the Sun and 0.3 AU. This means that nα would decrease slower than a 1/r2 constant-speed spherical expansion, and as a consequence Tα∥ would increase with distance. A double adiabatic evolution alongside alpha particles continuously decelerating would manifest itself as a significant increase in Tα∥, providing a mechanism to generate the high values of Tα∥ and low values of Tα⊥/Tα∥ we observed at 0.3 AU without the need to invoke additional heating or cooling mechanisms inside 0.3 AU.
Finally, although our conclusions on the evolution of alpha particle properties inside 0.3 AU are somewhat inconclusive, they provide context for measurements taken SWEAP instrument suite on Parker Solar Probe (Kasper et al. 2016; Fox et al. 2016), which will measure the properties of alpha particles inside 0.25 AU, filling in a large part of the unexplored region in Fig. 3.
Acknowledgments
The authors thank Petr Hellinger for helpful discussions, and thank the anonymous referee for comments that improved discussion of the results. D. Stansby is supported by STFC studentship ST/N504336/1. D. Perrone and T. S. Horbury are supported by STFC grant ST/N000692/1. L. Matteini is supported by the Programme National PNST of CNRS/INSU co-funded by CNES. Work at UC Berkeley was supported by NASA grants NNX14AQ89G and 80NSSC18K0370.
References
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bourouaine, S., Verscharen, D., Chandran, B. D. G., Maruca, B. A., & Kasper, J. C. 2013, ApJ, 777, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Caswell, T. A., Droettboom, M., Hunter, J., et al. 2018, matplotlib/matplotlib v3.0.2, DOI: 10.5281/zenodo.1482099 [Google Scholar]
- Chandran, B. D. G. 2010, ApJ, 720, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C. H. K., Matteini, L., Schekochihin, A. A., et al. 2016, ApJ, 825, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Chew, G. F., Goldberger, M. L., & Low, F. E. 1956, Proc. Roy. Soc. A Math. Phys. Eng. Sci., 236, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., & Winebarger, A. R. 2019, ARA&A, in press [arXiv:1811.00461] [Google Scholar]
- Cranmer, S., Panasyuk, A., & Kohl, J. 2008, ApJ, 678, 1480 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., Gibson, S. E., & Riley, P. 2017, Space Sci. Rev., 212, 1345 [Google Scholar]
- Dolei, S., Spadaro, D., & Ventura, R. 2016, A&A, 592, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldman, W. C., Asbridge, J. R., Bame, S. J., & Montgomery, M. D. 1973, J. Geophys. Res., 78, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, W. C., Gosling, J. T., McComas, D. J., & Phillips, J. L. 1993, J. Geophys. Res. Space Phys., 98, 5593 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Gary, S. P., Yin, L., Winske, D., & Reisenfeld, D. B. 2000, Geophys. Res. Lett., 27, 1355 [NASA ADS] [CrossRef] [Google Scholar]
- Geranios, A. 1989, Il Nuovo Cimento C, 12, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Gershman, D. J., Zurbuchen, T. H., Fisk, L. A., et al. 2012, J. Geophys. Res. Space Phys., 117 [Google Scholar]
- Hahn, M., & Savin, D. W. 2013, ApJ, 763, 106 [NASA ADS] [CrossRef] [Google Scholar]
- He, P., Gao, X., Lu, Q., & Wang, S. 2016, ApJ, 827, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Hellinger, P., & Trávníček, P. M. 2013, J. Geophys. Res. Space Phys., 118, 5421 [Google Scholar]
- Hellinger, P., Trávníček, P., Mangeney, A., & Grappin, R. 2003, Geophys. Res. Lett., 30 [CrossRef] [Google Scholar]
- Hellinger, P., Trávníček, P., Kasper, J. C., & Lazarus, A. J. 2006, Geophys. Res. Lett., 33, L09101 [NASA ADS] [CrossRef] [Google Scholar]
- Hellinger, P., Matteini, L., Štverák, Š., Trávníček, P. M., & Marsch, E. 2011, J. Geophys. Res. Space Phys., 116 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kasper, J. C., Stevens, M. L., Lazarus, A. J., Steinberg, J. T., & Ogilvie, K. W. 2007, ApJ, 660, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Kasper, J. C., Abiad, R., Austin, G., et al. 2016, Space Sci. Rev., 204, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Kasper, J. C., Klein, K. G., Weber, T., et al. 2017, ApJ, 849, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, K. G., Kasper, J. C., Korreck, K. E., & Stevens, M. L. 2017, J. Geophys. Res. Space Phys., 122, 9815 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, K., Alterman, B., Stevens, M., Vech, D., & Kasper, J. 2018, Phys. Rev. Lett., 120, 205102 [NASA ADS] [CrossRef] [Google Scholar]
- Kohl, J. L., Noci, G., Antonucci, E., et al. 1998, ApJ, 501, L127 [Google Scholar]
- Landi, E., & Cranmer, S. R. 2009, ApJ, 691, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, S., Marsch, E., Livi, S., et al. 1995, Geophys. Res. Lett., 22, 2445 [NASA ADS] [CrossRef] [Google Scholar]
- Maneva, Y. G., Ofman, L., & Viñas, A. 2015, A&A, 578, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markovskii, S. A., Chandran, B. D. G., & Vasquez, B. J. 2019, ApJ, 870, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Mühlhäuser, K.-H., Schwenn, R., et al. 1982a, J. Geophys. Res., 87, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Mühlhäuser, K.-H., Rosenbauer, H., Schwenn, R., & Neubauer, F. M. 1982b, J. Geophys. Res., 87, 35 [Google Scholar]
- Marsch, E., Mühlhäuser, K. H., Rosenbauer, H., & Schwenn, R. 1983, J. Geophys. Res., 88, 2982 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Ao, X.-Z., & Tu, C.-Y. 2004, J. Geophys. Res., 109, A04102 [NASA ADS] [CrossRef] [Google Scholar]
- Maruca, B. A., Kasper, J. C., & Gary, S. P. 2012, ApJ, 748, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Matteini, L., Landi, S., Hellinger, P., et al. 2007, Geophys. Res. Lett., 34, L20105 [NASA ADS] [CrossRef] [Google Scholar]
- Matteini, L., Hellinger, P., Landi, S., Trávníček, P. M., & Velli, M. 2011, Space Sci. Rev., 172, 373 [Google Scholar]
- Matteini, L., Hellinger, P., Goldstein, B. E., et al. 2013, J. Geophys. Res. Space Phys., 118, 2771 [Google Scholar]
- Matteini, L., Hellinger, P., Schwartz, S. J., & Landi, S. 2015, ApJ, 812, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Perrone, D., Bourouaine, S., Valentini, F., Marsch, E., & Veltri, P. 2014a, J. Geophys. Res. Space Phys., 119, 2400 [NASA ADS] [CrossRef] [Google Scholar]
- Perrone, D., Valentini, F., Servidio, S., Dalena, S., & Veltri, P. 2014b, Eur. Phys. J. D, 68, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perrone, D., Stansby, D., Horbury, T., & Matteini, L. 2018, MNRAS, 483, 3730 [Google Scholar]
- Robbins, D. E., Hundhausen, A. J., & Bame, S. J. 1970, J. Geophys. Res., 75, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenbauer, H., Schwenn, R., Miggenrieder, H., et al. 1981, Helios E1 (plasma) Instrument Technical Document, DOI: 10.5281/zenodo.1240455 [Google Scholar]
- Schwartz, S. J., & Marsch, E. 1983, J. Geophys. Res., 88, 9919 [NASA ADS] [CrossRef] [Google Scholar]
- Seough, J., & Nariyuki, Y. 2016, Phys. Plasmas, 23, 082113 [NASA ADS] [CrossRef] [Google Scholar]
- Stansby, D., Salem, C., Matteini, L., & Horbury, T. 2018a, Sol. Phys., 293, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Stansby, D., Rai, Y., Broll, J., & Shaw, S. 2018b, heliopython/heliopy: HelioPy 0.6.3, DOI: 10.5281/zenodo.1697088 [Google Scholar]
- Thieme, K. M., Marsch, E., & Rosenbauer, H. 1989, J. Geophys. Res., 94, 2673 [NASA ADS] [CrossRef] [Google Scholar]
- Tracy, P. J., Kasper, J. C., Zurbuchen, T. H., et al. 2015, ApJ, 812, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Tracy, P. J., Kasper, J. C., Raines, J. M., et al. 2016, Phys. Rev. Lett., 116, 255101 [NASA ADS] [CrossRef] [Google Scholar]
- Valentini, F., Perrone, D., Stabile, S., et al. 2016, New J. Phys., 18, 125001 [Google Scholar]
- Verscharen, D., & Chandran, B. D. G. 2018, Res. Notes AAS, 2, 13 [CrossRef] [Google Scholar]
- Verscharen, D., Bourouaine, S., & Chandran, B. D. G. 2013, ApJ, 773, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Verscharen, D., Chandran, B. D. G., Bourouaine, S., & Hollweg, J. V. 2015, ApJ, 806, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Wang, C. B., Yoon, P. H., & Wu, C. S. 2011, Geophys. Res. Lett., 38 [Google Scholar]
- Xie, H., Ofman, L., & Viñas, A. 2004, J. Geophys. Res., 109, A08103 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Alpha particle velocity distribution function fitting
 |
Fig. A.1. Example solid angle integrated distribution function (blue line with crosses), along with the previously fitted proton distribution function (orange), and fitted alpha particle distribution function (green). The vertical dashed black line shows the threshold above which the distribution function was dominated by alpha particles. The x-axis units are chosen to be linearly proportional to particle velocity for a given particle mass and charge, and the y-axis is normalised to the peak value. |
To separate the alpha particle VDF from the proton VDF, the difference in the ratio of the on board electrostatic analyser and current analyser was used (see Fig. 1, Marsch et al. 1982b). In this way the ratio of particle flux to charge flux was evaluated; this is twice as high for the alphas than the primary proton peak. The first energy per charge bin in the energy spectra above the proton peak where the particle to charge flux dropped below 0.8 was taken as the dividing point between the proton and alpha VDFs. If any of the angular bins at this energy were too close to the fitted proton core, the threshold was moved outward until it was at least 2 proton core thermal widths away from the proton core peak. All points with energies above (and not including) this energy per charge were assumed to be part of the alpha distribution. Figure A.1 shows an example energy spectrum along with the location of the threshold.
Once the alpha part of the VDF was separated, we followed a similar process to Stansby et al. (2018a) who fitted the proton core population in the same measured VDFs. The distribution was rotated into a field aligned frame, and a bi-Maxwellian distribution function fitted (see Eq. (1) of Stansby et al. 2018a for its functional form). The fitting process returned six fit parameters, from which the alpha number density (nα), velocity (vα) and temperatures parallel (Tα∥) and perpendicular (Tα⊥) to the magnetic field were calculated.
Figure A.1 shows a comparison of the solid angle integrated distribution function, along with the corresponding fitted distribution. Figure A.2 shows two cuts of the experimentally measured distribution function in the planes perpendicular (LH panel) and parallel (RH panel) to the local magnetic field, along with a comparison between an isocontour of the data and the fitted distribution function.
 |
Fig. A.2. Cuts of a 3D alpha VDF in the plane perpendicular to the magnetic field (LH panel) and a plane that contains the magnetic field (RH panel), centred on the fitted bulk speed. The sharp cut-offs in both plots are artificial and due to removal of the proton-dominated areas of the distribution function. The contours are logarithmically spaced. The dashed black lines show the contour at 1/e times the maximum value, which is one thermal width away from the bulk speed, and the red ellipses show the corresponding contour for the fitted bi-Maxwellian. |
The resulting values of T∥α and T⊥α are significantly higher than values reported previously (Marsch et al. 1982b). This is because previous values were calculated from numerical integration of the truncated distribution function (i.e. only points to the right of the dashed black line in Fig. A.1). This method explicitly assumes that no alpha particles are present below the threshold, underestimating the width, and therefore the temperature, of the true alpha particle distribution.
The original distribution functions are available at the Helios data archive3. The code used to fit the alpha particle VDFs4 and the fitted alpha particle parameters5 are also available on the Helios data archive. Researchers interested in using alpha particle parameters from intervals of Helios data not analysed in this Letter are encouraged to contact the first author.
Appendix B: Instability curve calculation
To generate the instability curves shown in Fig. 2 the New Hampshire Dispersion Solver (NHDS; Verscharen & Chandran 2018) was used. The three-fluid proton-alpha-electron dispersion relation was numerically solved for a range of wavevectors, and the highest growth rate, γ, determined as a function of the input plasma parameters. The input parameters are listed in Table B.1, and were chosen based on average values observed in the proton and alpha data. Variations in the observed proton parameters between 0.3 AU and 0.65 AU result in very small changes to the instability threshold, so for simplicity only one threshold was calculated for both distances based on average values observed at 0.3 AU. The electron drift speed and number density were set to enforce charge neutrality and zero net current. Only instabilities with propagation parallel to the magnetic field were investigated, as for Tα⊥/Tα∥ < 1 they have higher growth rates than the obliquely propagating modes (Maruca et al. 2012).
The alpha temperature anisotropy and parallel beta were varied to calculate ![$ \left [ \Omega_{c\alpha}^{-1} \gamma \right ] \left ( T_{\alpha\perp} / T_{\alpha\parallel}, \beta_{\alpha\parallel} \right ) $](/articles/aa/full_html/2019/03/aa34900-18/aa34900-18-eq9.gif) on a fixed grid (e.g. as in, Hellinger et al. 2006), where Ωcα is the alpha particle gyrofrequency given by Ωcα = qα|B|/mα. The γ = 10−3Ωcα and γ = 10−2Ωcα contours were then interpolated from this grid, and are shown in Fig. 2.
on a fixed grid (e.g. as in, Hellinger et al. 2006), where Ωcα is the alpha particle gyrofrequency given by Ωcα = qα|B|/mα. The γ = 10−3Ωcα and γ = 10−2Ωcα contours were then interpolated from this grid, and are shown in Fig. 2.
Plasma parameters used to derive the instability curves shown in Fig. 2.
Appendix C: Data and software
The WIND particle data used in this study are available at ftp://spdf.gsfc.nasa.gov/pub/data/wind/swe/swe_h1/. The Helios distribution function data are available on the Helios data archive (http://helios-data.ssl.berkeley.edu/), along with the corresponding fitted proton parameters (also available at https://zenodo.org/record/1009506). For details and links to alpha particle code and data, see Appendix A.
Data were retrieved using HelioPy v0.6.3 (Stansby et al. 2018b) and processed using astropy v3.1 (Astropy Collaboration 2018). Figures were produced using Matplotlib v3.0.2 (Hunter 2007; Caswell et al. 2018). Code to reproduce Figs. 1–3 can be found at https://github.com/dstansby/publication-code.
All Tables
All Figures
 |
Fig. 1. Radial evolution of alpha (green) and proton (blue) temperatures in fast solar wind. Each cross is measured in a single continuous high speed stream. The width of crosses gives the range of radial distances sampled in each stream. The centre of the cross is at the median value, and the lower and upper bounds are the first and third quartiles of the data. Bars at 1 AU are taken from the WIND swe_h1 dataset. Shaded areas are a double adiabatic prediction (Chew et al. 1956) based on an ideal Parker spiral magnetic field (Parker 1958), for constant solar wind speeds in the range 600–800 km s−1. |
| In the text | |
 |
Fig. 2. Joint probability distribution of parallel beta and temperature anisotropy for protons (blue) and alphas (green) at radial distances 0.3–0.4 AU (top panel) and 0.6–0.7 AU (bottom panel) in fast solar wind. The contours are logarithmically spaced from the maximum bin count to 0.1 times the maximum bin count. The dashed lines show the alpha firehose instability threshold for normalised growth rates of γ/Ωα = 10−3 (left-hand curve) and 10−2 (right-hand curve). See Appendix B for details of the instability curve calculation. The large spread in alpha particle values is likely partly due to experimental uncertainties in fitting alpha number densities and parallel temperatures. |
| In the text | |
 |
Fig. 3. Measurements of fast solar wind ion temperatures inside 1 AU. Top panel: perpendicular (triangles) and parallel (circles) temperatures for protons (blue), alpha particles (green), and oxygen ions (orange). New results from this work are alpha particles at large distances. The TH0⊥ values close to the Sun are from the polar measurements in Fig. 2 of Dolei et al. (2016). The TO5+⊥ values are from Fig. 5 of Cranmer et al. (2017), originally reported by Cranmer et al. (2008). |
| In the text | |
 |
Fig. A.1. Example solid angle integrated distribution function (blue line with crosses), along with the previously fitted proton distribution function (orange), and fitted alpha particle distribution function (green). The vertical dashed black line shows the threshold above which the distribution function was dominated by alpha particles. The x-axis units are chosen to be linearly proportional to particle velocity for a given particle mass and charge, and the y-axis is normalised to the peak value. |
| In the text | |
 |
Fig. A.2. Cuts of a 3D alpha VDF in the plane perpendicular to the magnetic field (LH panel) and a plane that contains the magnetic field (RH panel), centred on the fitted bulk speed. The sharp cut-offs in both plots are artificial and due to removal of the proton-dominated areas of the distribution function. The contours are logarithmically spaced. The dashed black lines show the contour at 1/e times the maximum value, which is one thermal width away from the bulk speed, and the red ellipses show the corresponding contour for the fitted bi-Maxwellian. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



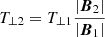
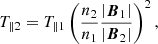
![$$ {Q_{ \bot \alpha }}{\rm{ }} = + \left[ {4.11_{0.4}^{10}} \right] \times {10^{ - 17}} {\rm{W}}{{\rm{m}}^{ - 3}} $$](/articles/aa/full_html/2019/03/aa34900-18/aa34900-18-eq4.gif)
![$$ {Q_{\parallel \alpha }} = - \left[ {13.7_{5.7}^{22}} \right] \times {10^{ - 17}} {\rm{W}}{{\rm{m}}^{ - 3}}. $$](/articles/aa/full_html/2019/03/aa34900-18/aa34900-18-eq5.gif)
![$$ {Q_{ \bot p}} \approx + \left[ {{{10}^{ - 16}} - {{10}^{ - 15}}} \right] {\rm{W}}{{\rm{m}}^{ - 3}} $$](/articles/aa/full_html/2019/03/aa34900-18/aa34900-18-eq6.gif)
![$$ {Q_{\parallel p}} \approx - \left[ {{{10}^{ - 16}} - {{10}^{ - 15}}} \right] {\rm{W}}{{\rm{m}}^{ - 3}}. $$](/articles/aa/full_html/2019/03/aa34900-18/aa34900-18-eq7.gif)