EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 676 (August 2023) A&A, 676 (2023) A137 Full HTML
Open Access
Issue
A&A
Volume 676, August 2023
Article Number A137
Number of page(s) 6
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202346815
Published online 23 August 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Solar wind observations show that the alpha particles often exhibit anisotropic velocity distribution functions (Marsch et al. 1982; Marsch 2012), that is, the parallel temperature component Tα∥ relative to the ambient magnetic field B0 differs from the perpendicular component Tα⊥. Alpha temperature anisotropy is widely detected in various space plasmas from near the solar surface by Parker Solar Probe (Phan et al. 2022) to 0.3–1 AU by Helios (Stansby et al. 2019), near 1 AU by Wind (Gary et al. 2016; Jian et al. 2016), and 1–5 AU by Ulysses (Gary et al. 2002). The observed anisotropic alpha particles are distributed in the regions of 0.1 < Tα⊥/Tα∥ < 10 and 10−3 < βα∥ < 1, and the distribution in the Tα⊥/Tα∥–βα∥ space exhibits a distorted rhomboid-like pattern (Maruca et al. 2012), where βα∥ represents the ratio of the alpha parallel thermal pressure to the magnetic pressure. Several physical processes have been proposed to explain the constraint of alpha temperature anisotropy, including the adiabatic expansion (Chew et al. 1956), Coulomb collisions (Kasper et al. 2008; Vafin et al. 2019), and wave-particle interactions (Gary et al. 2005a; Perrone et al. 2014; Li et al. 2020; Bourouaine et al. 2011a,b). Understanding the mechanism that constrains the anisotropic alpha is critical to understanding solar wind dynamics.

Alpha temperature anisotropy constitutes a possible source of free energy that can drive plasma instabilities (Gary 1993; Verscharen et al. 2013). In the case of Tα⊥ > Tα∥, the anisotropic alpha tends to generate the Alfvén/ion cyclotron (A/IC) wave at the quasi-parallel propagation and the mirror wave at the oblique propagation (Gary et al. 1993), while in the opposite case of Tα⊥ < Tα∥, the parallel firehose (PF) and oblique firehose (OF) instabilities can be induced (Seough & Nariyuki 2016), which correspond to the parallel magnetosonic or “whistler” wave and the oblique Alfvén wave, respectively. Hybrid simulations further demonstrate that these excited waves can exchange the energy from particles to waves through wave–particle interactions, which cause the temperature distribution of anisotropic alpha to approach the quasi-isotopic state (Gary & Winske 1993; Lu & Wang 2006; Lu et al. 2009; Matteini et al. 2015; Markovskii & Vasquez 2022). Therefore, the alpha temperature anisotropy instability might provide constraints on the anisotropic alpha distribution in the solar wind.

Observational and theoretical techniques have been combined by several authors in order to extensively analyze the alpha temperature anisotropy in the solar wind (Chen et al. 2016; DeWeese et al. 2022). Maruca et al. (2012) proposed that the kinetic instabilities induced by both the anisotropic proton and anisotropic alpha are more consistent with the observations of anisotropic alpha particles. Bourouaine et al. (2013) suggested that both the temperature anisotropy and drift velocity of alpha particles are of importance in regulating the velocity distribution and preferential heating of alpha particles. Although various plasma instabilities have been proposed for the constraint of anisotropic alpha, few investigations have considered plasma instabilities in different types of the solar wind. Moreover, plasma parameters have different properties between the slow and fast solar wind. Hellinger et al. (2006) investigated the comparison between Wind observations and Vlasov theory in the slow and fast solar wind, but their analyses were limited to the proton temperature anisotropy.

In the present work, we investigate the distribution of alpha temperature anisotropy in the slow and fast solar wind and also compare the Wind observations with Vlasov theory. Our results greatly explain the limits on the distribution of alpha temperature anisotropy in the slow and fast solar wind. The following sections are presented in this paper. First, we present the Wind observations in Sect. 1. Then, we present our analysis of comparisons between observations and instability thresholds in Sect. 3. Finally, we provide our conclusions in Sect. 4.

2. Observations and results

The ion parameter data used in this study are derived from the Faraday Cup instruments in the Solar Wind Experiment (SWE) on the Wind spacecraft. Here, we adopt the data period of 2005–2015. Figure 1 depicts the distribution of data points for the alpha temperature anisotropy in the plane of Tα⊥/Tα∥ and vsw (the flow velocity of the solar wind) for (a) both the slow and fast solar wind, where the dashed line represents the flow velocity of the solar wind vsw = 500 km s−1, (b) the slow solar wind with vsw < 500 km s−1, and (c) the fast solar wind with vsw > 500 km s−1. In our work, there are 3 126 909 sample numbers of data points selected in Fig. 1a, and the sample numbers are 2 509 180 and 617 729 in Figs. 1b and c, respectively. In Figs. 1a–c, the space plane is separated into 14 400 (120 × 120) bins, and the color shading represents the numbers of data points per bin. In Fig. 1, many of the data points are distributed in the region of 300 km s−1 < vsw < 500 km s−1, and a minority of data points are located in the region of 500 km s−1 < vsw < 600 km s−1. The findings suggest that the alpha temperature anisotropy events appear more frequently in the slow solar wind than in the fast solar wind.

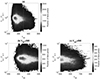thumbnail Fig. 1.

Distribution of data points for the alpha temperature anisotropy in the Tα⊥/Tα∥ − vsw plane for (a) both the slow and fast solar wind, where the dashed line represents the flow velocity of the solar wind vsw = 500 km s−1, (b) the slow solar wind with vsw < 500 km s−1, and (c) the fast solar wind with vsw > 500 km s−1.

Figure 2 depicts the distribution of data points for the alpha temperature anisotropy in the plane of Tα⊥/Tα∥ and Tp⊥/Tp∥ (where Tp⊥ and Tp∥ represent the perpendicular proton temperature and parallel proton temperature, respectively) for (a) the slow solar wind with vsw < 500 km s−1, where the dashed line represents the strong correlation Tα⊥/Tα∥ = Tp⊥/Tp∥; and (b) the fast solar wind with vsw > 500 km s−1. As depicted in Fig. 2, in the fast solar wind, there is no obvious correlation between Tα⊥/Tα∥ and Tp⊥/Tp∥. In the slow solar wind, a tight correlation is found between Tα⊥/Tα∥ and Tp⊥/Tp∥, and this correlation can be expressed such that Tα⊥/Tα∥ = (Tp⊥/Tp∥)k, where the correlation index k = 1, indicating a greater value compared with the previously reported k = 0.5 (Maruca et al. 2012). This is due to the fact that the correlation index k = 1 is derived from only the condition of the slow solar wind, ignoring the data points in the fast solar wind.

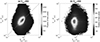thumbnail Fig. 2.

Distribution of data points for the alpha temperature anisotropy in the Tα⊥/Tα∥ − Tp⊥/Tp∥ plane for (a) the slow solar wind with vsw < 500 km s−1, where the dashed line represents the strong correlation Tα⊥/Tα∥ = Tp⊥/Tp∥, and (b) the fast solar wind with vsw > 500 km s−1.

Figure 3 shows the distribution of data points for the alpha temperature anisotropy in the plane of Tα⊥/Tα∥ and Tα∥/Tp∥ (where Tα∥/Tp∥ represents the ratio of the alpha parallel temperature to proton parallel temperature) for (a) the slow solar wind with vsw < 500 km s−1, and (b) the fast solar wind with vsw > 500 km s−1. Figure 3 demonstrates that, in the slow solar wind, many of the data points for the anisotropic alpha are located in the condition of the temperature ratio Tα∥/Tp∥ ∼ 1, with a few data points appearing in the condition of Tα∥/Tp∥ ∼ 4. In the fast solar wind, most of the data points are located in the region of 3 < Tα∥/Tp∥ < 6. These results imply that in the slow solar wind, the alpha and the proton have close parallel temperatures, that is, Tα∥ ∼ Tp∥, whereas in the fast solar wind, the alpha has a greater parallel temperature than the proton by a factor of about four, that is Tα∥ ∼ 4Tp∥.

thumbnail Fig. 3.

Distribution of data points for the alpha temperature anisotropy in the Tα⊥/Tα∥ − Tα∥/Tp∥ plane for (a) the slow solar wind with vsw < 500 km s−1, and (b) the fast solar wind with vsw > 500 km s−1.

Figure 4 depicts the distribution of data points for the alpha temperature anisotropy in the plane of Tα⊥/Tα∥ and vα/vA (where vα and vA represent the drift velocity of the alpha relative to the proton and the local Afvén velocity, respectively) for (a) the slow solar wind with vsw < 500 km s−1, and (b) the fast solar wind with vsw > 500 km s−1. As shown in Fig. 4, in the slow solar wind the normalized drift velocity of the alpha to proton vα/vA is close to zero, that is, vα/vA ∼ 0, while in the fast solar wind, the alpha particles move faster than the protons with the normalized drift velocity 0.4 < vα/vA < 0.6.

thumbnail Fig. 4.

Distribution of data points for the alpha temperature anisotropy in the Tα⊥/Tα∥ − vα/vA plane for (a) the slow solar wind with vsw < 500 km s−1, and (b) the fast solar wind with vsw > 500 km s−1.

Both theoretical and observational results have shown that the alpha particles with different drift velocity can play important roles in the plasma heating in the solar wind (Gary et al. 2005b; Kasper et al. 2008; Bourouaine et al. 2011a,b). In the region of lower drift velocity vα/vA ≤ 0.5, the alpha cyclotron damping dominates, and the alpha particles are scattered in the directions perpendicular to B0, which results in an increase in Tα⊥ and a decrease in Tα∥. As a result, the parallel temperature of alpha particles is close to that of protons (Tα∥/Tp∥ ∼ 1), which is consistent with Fig. 3a. In the region of larger drift velocity vα/vA ≥ 0.5, only the proton cyclotron damping occurs, and the protons are preferentially scattered in the perpendicular directions of B0, which lead to the increase in Tp⊥ and the decrease in Tp∥. Consequently, the parallel temperature of alpha particles is larger than that of protons (Tα∥/Tp∥ ∼ 4), which is agreement with Fig. 3b.

According to the previous works of Kasper et al. (2008) and Bourouaine et al. (2011b), there is a clear dependency between the collision age and the solar wind velocity. In particular, the data distribution with a larger collision age corresponds to slow solar wind, and that with a lower collision age corresponds to fast solar wind (Kasper et al. 2008; Bourouaine et al. 2011b). For the case of lower collision age, most data points are distributed in the conditions with larger solar wind velocity vsw > 500 km s−1, isotropic proton Tp⊥/Tp∥ ∼ 1, larger temperature ratio Tα∥/Tp∥ ∼ 4, and larger drift velocity vα/vA ∼ 0.6. For the case of larger collision age, most data points are located in the conditions with lower solar wind velocity vsw < 500 km s−1, stronger anisotropy correlation Tα⊥/Tα∥ = Tp⊥/Tp∥, lower temperature ratio Tα∥/Tp∥ ∼ 1, and lower drift velocity vα/vA ∼ 0. Therefore, Coulomb collision could play an important role in the distribution of plasma parameters, especially in the slow solar wind.

3. Comparison between Wind observations and Vlasov theory

To determine the role of the above free energy in the constraint of alpha temperature anisotropy in the slow and fast solar wind, we compared the Wind observations for the alpha temperature anisotropy with linear Vlasov theory. In the linear Vlasov analysis, we adopt the PDRK/B0 solver (Xie & Xiao 2016; Xie 2019) to numerically solve the Vlasov equation, which can yield the dispersion relation for all plasma waves. 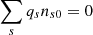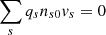In the theoretical model, we consider a three-component plasma: the background proton (p), the alpha (α), and the background electron (e), and the plasma system has neutral-charge and no current conditions, that is, ∑ s q s n s 0 = 0 $ \sum\limits_s {q_s n_{s0} = 0} $ and ∑ s q s n s 0 v s = 0 $ \sum\limits_s {q_s n_{s0} \mathit{v}_s = 0} $, where ns0 and vs represent the density and the drift velocity of species s, respectively. Some plasma parameters are used such as the electron density ne = 5 × 106 m−3, the background magnetic field B0 = 5 × 10−9 T, and the ratio of alpha density to electron density nα/ne = 0.05. Other plasma parameters applied in theoretical computations are shown in Table 1, which are derived from solar wind observation data as presented in Figs. 2–4. In the numerical calculation, the instability threshold is characterized by the growth rate γ/ωcp = 10−2 (Maruca et al. 2012; Bourouaine et al. 2013), and the area with the growth rate γ/ωcp > 10−2 is considered the unstable region.

Table 1.

Plasma parameters adopted in theoretical calculations.

Figure 5 depicts the distribution of data points for the alpha temperature anisotropy in the Tα⊥/Tα∥ − βα∥ plane for (a) the slow solar wind with vsw < 500 km s−1, and (b) the fast solar wind with vsw > 500 km s−1. In Fig. 5, the Wind observation data and theoretical instability thresholds are compared, where the solid lines correspond to the A/IC and PF instabilities, and the dashed lines correspond to the mirror and OF instabilities. The lines with different colors in Figs. 5a and b correspond to different background plasma parameters as given in Table 1. According to a previous work by Maruca et al. (2012), the A/IC, mirror, PF, and OF instabilities are distributed in the propagation regions of θ ∼ 0, 40° < θ < 50°, θ ∼ 0, and 55° < θ < 65°, respectively. In our work, we consider the A/IC instability at θ = 0, mirror instability at θ = 60°, PF instability at θ = 0, and OF instability at θ = 45°, respectively. As shown in Fig. 5a, the alpha temperature anisotropy is mainly distributed in the regions of 0.1 < Tα⊥/Tα∥ < 10 and 0.001 < βα∥ < 0.8, and its maximum occurrence rate corresponds to βα∥ ∼ 0.07. As shown in Fig. 5b, the anisotropic alpha is mainly located in the regions of 0.1 < Tα⊥/Tα∥ < 9 and 0.001 < βα∥ < 1, and its maximum occurrence rate corresponds to βα∥ ∼ 0.15. Compared with Figs. 5a and b, there is a difference in the distribution of the anisotropic alpha with both Tα⊥/Tα∥ and βα∥ for the slow and fast solar wind. Moreover, the alpha parallel beta βα∥ is larger in the fast solar wind compared with the slow solar wind.

thumbnail Fig. 5.

Distribution of data points for the alpha temperature anisotropy in the Tα⊥/Tα∥ − βα∥ plane for (a) the slow solar wind with vsw < 500 km s−1, and (b) the fast solar wind with vsw > 500 km s−1. The observational data are compared with the instability thresholds, with the solid lines representing the A/IC and PF instabilities, and the dashed lines representing the mirror and OF instabilities. The lines with different colors in panels (a) and (b) correspond to different background plasma parameters as given in Table 1.

From Fig. 5a, it is obvious that the distribution of the alpha temperature anisotropy is constrained by the instability thresholds of PF, OF, A/IC, and mirror instabilities in the condition of Tα⊥/Tα∥ = Tp⊥/Tp∥ and Tα∥/Tp∥ = 4. In the condition of Tα⊥/Tα∥ = Tp⊥/Tp∥ and Tα∥/Tp∥ = 1, the instability thresholds of PF and OF instabilities are shifted to lower βα∥, and those of A/IC and mirror instabilities are shifted to lower Tα⊥/Tα∥. From Fig. 5b, we see that the apparent constraint of the alpha temperature anisotropy shows close compatibility with the instability thresholds of PF and A/IC instabilities in the condition of vα/vA = 0. In the condition of vα/vA = 0.6, the instability threshold of the PF instability extends to lower βα∥, and that of the A/IC instability is shifted to lower Tα⊥/Tα∥.

Our results indicate that the proton temperature anisotropy and the parallel temperature ratio of alpha to proton can play an important role in regulating the distribution of alpha temperature anisotropy in the slow solar wind. In the slow solar wind, the PF, OF, A/IC, and mirror instabilities accompanied with Tα⊥/Tα∥ = Tp⊥/Tp∥ and Tα∥/Tp∥ = 4 can provide apparent boundaries on the distribution of anisotropic alpha. Moreover, the PF and OF instabilities associated with Tα⊥/Tα∥ = Tp⊥/Tp∥ and Tα∥/Tp∥ =  1 can further limit many of the data points toward the quasi-isotropic condition. On the other hand, our results suggest that the drift velocity between alpha and proton can play a critical role in limiting the distribution of alpha temperature anisotropy in the fast solar wind. In the fast solar wind, the PF and A/IC instabilities can put apparent boundaries on the distribution of anisotropic alpha. Moreover, the PF instability associated with vα/vA ∼ 0.6 can further constrain many of data points close to the quasi-isotropic condition.

It should be noted that the instability-driven ion temperature anisotropy can contribute to not only the constraint on ion temperature anisotropy, but also the preferential parallel heating of alpha with respect to protons, especially in the fast solar wind. Previous works by Kasper et al. (2008) and Bourouaine et al. (2011a,b) demonstrated that when the normalized drift velocity of alpha to proton satisfies vα/vA > 0.5, the A/IC waves are invalid for alpha particle heating because of the weak ion-cyclotron resonance. However, the Landau damping may be significant, which results in the preferential parallel heating of alpha particles. Therefore, in the fast solar wind, the parallel temperature of alpha particles is higher than that of protons due to the heating mechanism of the Landau damping.

4. Conclusions

Solar wind observations frequently reveal that the alpha temperature anisotropy is ubiquitous in the solar wind (Marsch et al. 1982; Gary et al. 2002; Marsch 2012). The distribution of anisotropic alpha is widely considered to be regulated by various instabilities via wave–particle interactions (Maruca et al. 2012; Bourouaine et al. 2013; Chen et al. 2016; DeWeese et al. 2022). However, the detailed constraint mechanism remains undefined, especially for different types of solar wind. In this work, we investigate the distribution of alpha temperature anisotropy and the correlation with background plasma parameters in the slow and fast solar wind. We also present a comparison between observations of the alpha temperature anisotropy and the predictions of Vlasov theory.

It is found that the distribution of the alpha temperature anisotropy is sensitive to the flow velocity of the solar wind vsw, the proton temperature anisotropy Tp⊥/Tp∥, the parallel temperature ratio of alpha to proton Tα∥/Tp∥, and the drift velocity of alpha to proton vα/vA. In the slow solar wind with vsw < 500 km s−1, the alpha temperature anisotropy takes place preferentially in conditions where there is a stronger anisotropy correlation Tα⊥/Tα∥ = Tp⊥/Tp∥, a lower temperature ratio Tα∥/Tp∥ ∼  1, and a lower drift velocity vα/vA ∼ 0, but a few anisotropic alpha appears in the condition where there is a larger temperature ratio Tα∥/Tp∥ ∼ 4. In the fast solar wind with vsw > 500 km s−1, the preferential plasma conditions for the occurrence of the alpha temperature anisotropy are isotropic proton Tp⊥/Tp∥ ∼ 1, larger temperature ratio Tα∥/Tp∥ ∼ 4, and larger drift velocity vα/vA ∼ 0.6.

In summary, the current study provides a reasonable physical model for regulating the distribution of alpha temperature anisotropy in the slow and fast solar wind. In the slow solar wind, the PF, OF, A/IC, and mirror instabilities associated with Tα⊥/Tα∥ = Tp⊥/Tp∥ and Tα∥/Tp∥ = 4 can provide apparent boundaries on the distribution of anisotropic alpha, and the PF and OF instabilities associated with Tα⊥/Tα∥ = Tp⊥/Tp∥ and Tα∥/Tp∥ = 1 can further limit many of the data points toward the quasi-isotropic condition. In the fast solar wind, the PF and A/IC instabilities can put apparent boundaries on the distribution of anisotropic alpha, and the PF instability associated with vα/vA ∼ 0.6 can further constrain many of the data points close to the quasi-isotropic condition. Alpha temperature anisotropy instabilities together with different types of free energy are able to explain the observed alpha temperature anisotropy in the slow and fast solar wind.

Acknowledgments

The current study was funded by the NSFC under grants Nos. 12103018, 41974197, 42174202 and 42174195, and partly by the Excellent Young Scientists Fund in Henan Province under grant Nos. 232300421072 and 222300420061. We also acknowledge the Wind team for providing the data (https://spdf.gsfc.nasa.gov/pub/data/wind/). We would like to thank the anonymous referee for the valuable suggestions and comments, which were helpful in improving the quality of this paper.

References

  1. Bourouaine, S., Marsch, E., & Neubauer, F. M. 2011a, ApJ, 728, L3 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bourouaine, S., Marsch, E., & Neubauer, F. M. 2011b, A&A, 536, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bourouaine, S., Verscharen, D., Chandran, B. D. G., et al. 2013, ApJ, 777, L3 [CrossRef] [Google Scholar]
  4. Chen, C. H. K., Matteini, L., Schekochihin, A. A., et al. 2016, ApJ, 825, L26 [NASA ADS] [CrossRef] [Google Scholar]
  5. Chew, G. F., Goldberger, M. L., & Low, F. E. 1956, Proc. R. Soc. London Ser. A., 236, 112 [NASA ADS] [CrossRef] [Google Scholar]
  6. DeWeese, H., Maruca, B. A., Qudsi, R. A., et al. 2022, ApJ, 941, 12 [CrossRef] [Google Scholar]
  7. Gary, S. P. 1993, Theory of Space Plasma Microinstabilities (Cambridge: Cambridge University Press) [Google Scholar]
  8. Gary, S. P., & Winske, D. 1993, J. Geophys. Res., 98, 9171 [NASA ADS] [CrossRef] [Google Scholar]
  9. Gary, S. P., Fuselier, S. A., & Anderson, B. J. 1993, J. Geophys. Res., 98, 1481 [NASA ADS] [CrossRef] [Google Scholar]
  10. Gary, S. P., Goldstein, B. E., & Neugebauer, M. 2002, J. Geophys. Res. (Space Phys.), 107, 1169 [Google Scholar]
  11. Gary, S. P., Lavraud, B., Thomsen, M. F., et al. 2005a, Geophys. Rev. Lett., 32, L13109 [NASA ADS] [CrossRef] [Google Scholar]
  12. Gary, S. P., Smith, C. W., & Skoug, R. M. 2005b, J. Geophys. Res. (Space Phys.), 110, A07108 [NASA ADS] [CrossRef] [Google Scholar]
  13. Gary, S. P., Jian, L. K., Broiles, T. W., et al. 2016, J. Geophys. Res. (Space Phys.), 121, 30 [NASA ADS] [CrossRef] [Google Scholar]
  14. Hellinger, P., Trávníček, P., Kasper, J. C., et al. 2006, Geophys. Rev. Lett., 33, L09101 [NASA ADS] [CrossRef] [Google Scholar]
  15. Li, Q. H., Yang, L., Xiang, L., et al. 2020, ApJ, 892, 98 [NASA ADS] [CrossRef] [Google Scholar]
  16. Lu, Q. M., & Wang, S. 2006, J. Geophys. Res. (Space Phys.), 111, A05204 [NASA ADS] [Google Scholar]
  17. Lu, Q., Du, A., & Li, X. 2009, Phys. Plasmas, 16, 042901 [NASA ADS] [CrossRef] [Google Scholar]
  18. Markovskii, S. A., & Vasquez, B. J. 2022, ApJ, 930, 120 [NASA ADS] [CrossRef] [Google Scholar]
  19. Jian, L. K., Moya, P. S., Viñas, A. F., & Stevens, M. 2016, AIP Conf. Proc., 1720, 040007 [CrossRef] [Google Scholar]
  20. Kasper, J. C., Lazarus, A. J., & Gary, S. P. 2008, Phys. Rev. Lett, 101, 26110 [CrossRef] [Google Scholar]
  21. Marsch, E. 2012, Space Sci. Rev., 172, 23 [Google Scholar]
  22. Maruca, B. A., Kasper, J. C., & Gary, S. P. 2012, ApJ, 748, 137 [NASA ADS] [CrossRef] [Google Scholar]
  23. Marsch, E., Rosenbauer, H., Schwenn, R., et al. 1982, J. Geophys. Res., 87, 35 [NASA ADS] [CrossRef] [Google Scholar]
  24. Matteini, L., Hellinger, P., Schwartz, S. J., et al. 2015, ApJ, 812, 13 [CrossRef] [Google Scholar]
  25. Perrone, D., Bourouaine, S., Valentini, F., et al. 2014, J. Geophys. Res. (Space Phys.), 119, 2400 [NASA ADS] [CrossRef] [Google Scholar]
  26. Phan, T. D., Verniero, J. L., Larson, D., et al. 2022, Geophys. Rev. Lett., 49, e96986 [NASA ADS] [CrossRef] [Google Scholar]
  27. Seough, J., & Nariyuki, Y. 2016, Phys. Plasmas, 23, 082113P [NASA ADS] [CrossRef] [Google Scholar]
  28. Stansby, D., Perrone, D., Matteini, L., et al. 2019, A&A, 623, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Vafin, S., Riazantseva, M., & Pohl, M. 2019, ApJ, 871, L11 [NASA ADS] [CrossRef] [Google Scholar]
  30. Verscharen, D., Bourouaine, S., & Chandran, B. D. G. 2013, ApJ, 773, 163 [NASA ADS] [CrossRef] [Google Scholar]
  31. Xie, H., & Xiao, Y. 2016, Plasma Sci. Technol., 18, 97 [NASA ADS] [CrossRef] [Google Scholar]
  32. Xie, H. S. 2019, Comput. Phys. Commun., 244, 343 [CrossRef] [Google Scholar]

All Tables

Table 1.

Plasma parameters adopted in theoretical calculations.

In the text

All Figures

thumbnail Fig. 1.

Distribution of data points for the alpha temperature anisotropy in the Tα⊥/Tα∥ − vsw plane for (a) both the slow and fast solar wind, where the dashed line represents the flow velocity of the solar wind vsw = 500 km s−1, (b) the slow solar wind with vsw < 500 km s−1, and (c) the fast solar wind with vsw > 500 km s−1.
In the text
thumbnail Fig. 2.

Distribution of data points for the alpha temperature anisotropy in the Tα⊥/Tα∥ − Tp⊥/Tp∥ plane for (a) the slow solar wind with vsw < 500 km s−1, where the dashed line represents the strong correlation Tα⊥/Tα∥ = Tp⊥/Tp∥, and (b) the fast solar wind with vsw > 500 km s−1.
In the text
thumbnail Fig. 3.

Distribution of data points for the alpha temperature anisotropy in the Tα⊥/Tα∥ − Tα∥/Tp∥ plane for (a) the slow solar wind with vsw < 500 km s−1, and (b) the fast solar wind with vsw > 500 km s−1.
In the text
thumbnail Fig. 4.

Distribution of data points for the alpha temperature anisotropy in the Tα⊥/Tα∥ − vα/vA plane for (a) the slow solar wind with vsw < 500 km s−1, and (b) the fast solar wind with vsw > 500 km s−1.
In the text
thumbnail Fig. 5.

Distribution of data points for the alpha temperature anisotropy in the Tα⊥/Tα∥ − βα∥ plane for (a) the slow solar wind with vsw < 500 km s−1, and (b) the fast solar wind with vsw > 500 km s−1. The observational data are compared with the instability thresholds, with the solid lines representing the A/IC and PF instabilities, and the dashed lines representing the mirror and OF instabilities. The lines with different colors in panels (a) and (b) correspond to different background plasma parameters as given in Table 1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.