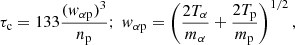EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 682 (February 2024) A&A, 682 (2024) A152 Full HTML
Open Access
Issue
A&A
Volume 682, February 2024
Article Number A152
Number of page(s) 5
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202347134
Published online 15 February 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The two main ion components of the solar wind are protons (H+; the predominant component of the solar wind) and alpha particles (He2+). Beyond the number density (Bame et al. 1977), these two solar wind ion species have other different characteristics (e.g., velocities, temperatures, temperature anisotropy, etc.; see reviews by Marsch 2012; Verscharen et al. 2019). In particular, previous observations (e.g., Helios, Ulysses, Wind) have revealed alpha particles’ preferential heating and acceleration compared to protons (Ryan & Axford 1975; Marsch et al. 1982; Yermolaev & Stupin 1990; von Steiger et al. 1995; Ďurovcová et al. 2019; Mostafavi et al. 2022). Different mechanisms have been suggested to be responsible for the preferential heating and acceleration of alpha particles, including the resonant absorption of ion cyclotron waves (Isenberg & Vasquez 2009; Jian et al. 2010; Kasper et al. 2013; Navarro et al. 2020), low-frequency Alfvén wave turbulence (Chandran 2010), drift instabilities (Verscharen et al. 2013), stochastic heating (Chandran 2010; Chandran et al. 2013), and reconnection (Drake et al. 2009; Artemyev et al. 2014; Duan et al. 2022).

The solar wind in the inner heliosphere is frequently described as a collisionless plasma. However, there is observational evidence for the role collisions play in the solar wind in the inner heliosphere. Coulomb collisions can lead plasma towards thermal equilibrium and regulate the non-thermal effects of protons and alpha particles (Feldman et al. 1974; Neugebauer 1976; Livi et al. 1986; Marsch & Goldstein 1983; Hernandez & Marsch 1985; Klein et al. 1985; Kasper et al. 2008; Tracy et al. 2015; Alterman et al. 2018; Ďurovcova et al. 2021). The parameters commonly used in studying the collisionality are the “collisional age” (Ac; Kasper et al. 2008) and “Coulomb number” (Nc; Kasper et al. 2017). We note that Ac and Nc are the number of collisions experienced during solar wind expansion and the number of collisions at the spacecraft’s position without accounting for propagation effects, respectively. Therefore, the Coulomb number only depends on the properties of the solar wind at the location of the measurements and does not account for its history. Kasper et al. (2008) analyzed Wind spacecraft data at 1 au and studied the dependency of non-thermal features of the solar wind on collisionality. They showed that solar wind properties at 1 au are strongly organized by the Nc of the solar wind plasma. When Nc ≪ 1, the plasma is collisionless and interactions between ion species are rare. Therefore, non-thermal features are present, and alphas and protons are not in equilibrium. However, when Nc ≥ 1 the plasma is “collisionally old”, Coulomb collisions can ultimately reduce or negate the non-thermal signatures (i.e., Tα ≈ Tp and Vα ≈ Vp; where Tα/p and Vα/p are the alpha and proton temperature and velocity, respectively.

Wind observations at 1 au showed that the alpha-to-proton temperature ratio (Tα/Tp) and differential velocity (Vα − Vp) correlate positively with the solar wind speed (Kasper et al. 2008, 2017; Maruca et al. 2013). While slow solar wind has relatively large collisional age, which leads alphas and protons toward equilibrium, the fast wind is not as thermally equilibrated and has a larger temperature ratio and differential velocity. Maruca et al. (2013) showed that Tα/Tp has a complex and bimodal distribution at 1 au (i.e., the mean value of Tα/Tp for the slow and fast wind is about 1 and 4, respectively). They applied a radial evolution model to 1 au observations and predicted what could be observed at 0.1 au, considering the effect of Coulomb collisions. Their Tα/Tp results at 0.1 au showed only one peak for all solar wind speeds and, thus, these authors suggested that similar mechanisms may lead to preferential heating of alpha particles in both slow and fast wind. This hypothesis could only be confirmed with in situ observations close to the Sun.

NASA’s Parker Solar Probe (PSP; Fox et al. 2016) is now venturing closer to the Sun than ever before (down to 13.28 R⊙ to date), thus enabling insights into the properties of the newly heated solar wind. The present paper focuses on the non-thermal features of the young solar wind within 0.3 au for the first time. In Sect. 2, we show the selection of the PSP data. We analyze PSP observations during close approaches to the Sun to study the alpha-to-proton temperature ratio and differential velocity (Sect. 3). We investigate the collisionality of the young solar wind and examine how the collisional effect organizes the non-thermal features. Moreover, we compare our results from PSP observations with the previously obtained results at 1 au made by Wind (Kasper et al. 2008; Maruca et al. 2013). These results expand our knowledge about the solar wind’s origin and evolution from the Sun to larger distances. In Sect. 4, we summarize and conclude the paper.

2. Data sources and selection

The PSP mission is poised to unravel the mysteries of the Sun by becoming the first-ever spacecraft to take in situ measurements of the Sun’s corona (Fox et al. 2016; Raouafi et al. 2023). The science payload includes complementary instrument suites to characterize the emerging young solar wind well inside the orbit of Mercury. The payload includes an ion sensor to directly measure velocity distributions of protons and alpha particles. In this work, we use the Solar Wind Electrons Alphas and Protons (SWEAP) instrument on board PSP to study the solar wind ions properties (Kasper et al. 2016). The SWEAP instrument uses two sensors for measuring ions, the Solar Probe Analyzer for Ions (SPAN-I; Livi et al. 2022) and the Solar Probe Cup (SPC; Kasper et al. 2016; Case et al. 2020), to measure of the bulk thermal solar wind. Here, we focus on both protons and alpha particles and, thus, we use SPAN-I, which consists of both an electrostatic analyzer and time-of-flight section for mass-per-charge determination (Livi et al. 2022). Thus, SPAN-I can separately resolve the distribution functions of protons and alpha particles, enabling us to reliably distinguish these two ion components. This study makes use of the cleaned alpha product, which removes the effects of proton contamination (see, Livi et al. 2022, for more information). SPAN-I is situated on the ram side of the PSP spacecraft and is optimized for ion observations near the closest approach, when the solar wind aberration due to the spacecraft motion (i.e., the high tangential speed of the spacecraft) is sufficiently high to bring it into the SPAN-I’s field of view (FOV). In order to have reliable plasma moments, we limit our analyses to times when the core of both alpha and proton distributions are within the FOV of SPAN-I (see Mostafavi et al. 2022, for more details). To better facilitate this requirement, we developed a code to search for times that the peaks of the distributions are located at or below a threshold azimuthal angle (ϕth = 163°). Thus, the SPAN-I moments used in this study produce reliable results due to carefully selecting PSP intervals. It’s worth noting that we did not exclude the proton beam whenever it was present in this current analysis.

In a study by Verscharen & Marsch (2011), it was demonstrated that the presence of waves can result in the dispersion of the VDF, potentially leading to “apparent” heating effects when dealing with low-resolution data. For instance, they showed that data collected by the Helios, which records solar wind properties at 40.5-s intervals, is characterized by a lower resolution, resulting in data averaging over long time periods. However, the SPAN-I dataset offers significantly higher resolutions, bringing observations closer to their respective local distribution functions. While it is acknowledged that wave effects on VDF may manifest as minor “apparent” heating in certain cases, it is important to note that the calibration of data based on these effects is beyond the scope of the current study.

We calculate the alpha-proton differential velocity using Vαp = sign(|Vα|−|Vp|)|Vα − Vp| (Steinberg et al. 1996; Ďurovcová et al. 2017; Mostafavi et al. 2022). This equation considers the directions of both vectors and identifies the data intervals when alpha particles are faster than protons and vice versa.

To calculate the Coulomb number at the position of the spacecraft, we used Nc = R/(Vpτc) (Hernández et al. 1987; Salem et al. 2003; Kasper et al. 2008, 2017), where R is the distance from the Sun to PSP, Vp is the solar wind proton speed, and τc is the time-scale for α − p energy exchange due to small-angle Coulomb scattering. Then, τc can be calculated by (details in Kasper et al. 2008):

τ c = 133 ( w α p ) 3 n p ; w α p = ( 2 T α m α + 2 T p m p ) 1 / 2 , $$ \begin{aligned} \tau _{\rm c} = 133 \frac{(w_{\alpha \mathrm{p}})^3}{n_{\rm p}}; \ w_{\alpha \mathrm{p}} = \left(\frac{2 T_\alpha }{m_\alpha } + \frac{2 T_{\rm p}}{m_{\rm p}}\right)^{1/2}, \end{aligned} $$(1)

where mα/p is alpha and proton mass and np is the proton density. The Coulomb number, Nc, used in this paper indicates an approximation of collisions at the spacecraft’s position based on local plasma properties with no accounting for propagation effects of the solar wind.

To assess the uncertainties associated with SPAN-I measuring partial moments, we compared the density obtained from partial moments to the total plasma densities obtained from the analysis of the plasma quasi-thermal noise (QTN) spectrum measured by the PSP/FIELDS Radio Frequency Spectromete1 (Moncuquet et al. 2020; Pulupa et al. 2017). Thanks to the careful selection of our data sets, these number densities are comparable, thereby demonstrating the reliability of our data (Mostafavi et al. 2022). We used magnetic field data from the FIELDS instrument (Bale et al. 2016) to compute the Alfvén speed as V A = B / μ 0 ( n p m p + n α m α ) $ V_{\mathrm{A}} = B/\sqrt{\mu_0 (n_{\mathrm{p}} m_{\mathrm{p}}+ n_\alpha m_\alpha)} $, where B is the magnetic field magnitude and μ0 is the permeability of vacuum.

We have removed data instances corresponding to the presence of coronal mass ejections (CMEs) from our dataset. This exclusion is essential to ensure that our results are directly associated with the unperturbed solar wind, unaffected by the influence of these transient events.

3. Data analysis and discussion

To examine how the young solar wind’s non-thermal properties are organized by collisionality, we analyzed PSP observations during encounter 10, when it was located at about 0.06 au. Figure 1 shows the alpha-to-proton temperature ratio (Tα/Tp; panel a) and differential velocity over Alfvén speed (|Vαp|/VA; panel b) as a function of the Coulomb number (Nc). The white horizontal line in Fig. 1a denotes thermal equilibrium (Tα = Tp). Both the alpha-to-proton temperature ratio and normalized differential flow decrease as the Coulomb number increases. These trends are similar to 1 au observations as reported by Kasper et al. (2008, 2017), showing that non-thermal features are correlated with the Coloumb number or collisionality. It is important to emphasize that a direct comparison of nonthermal features observed by the PSP and Wind spacecraft, with respect to the same Coulomb number value, is not practical. As mentioned previously, the Coulomb number relies on factors such as the distance from the Sun, solar wind speed, and density at the measurement location and does not account for its history. However, it is possible to compare temperature ratio values solely at different distances. PSP observations show that young solar wind close to the Sun has extensive non-thermal features (i.e., Tα/Tp even goes up to about 16) compared to solar wind at 1 au (i.e., Tα/Tp maximum goes to 6–7; Kasper et al. 2017). This suggests that alpha particles in the nascent solar wind originate with relatively high temperatures compared to protons at the source (Cranmer & Winebarger 2019), whereby processes regulating thermal equilibrium occur during propagation to 1 au and/or other local effects (e.g., such as wave activity) are more pronounced at this small distance and are heating and accelerating alphas more efficiently than protons. Turbulence and wave-particle interactions can influence the solar wind on much smaller timescales than collisions and thus regularly cause deviations from local thermal equilibrium (Marsch 2006; Verscharen et al. 2019). For example, previous studies have shown that ion cyclotron waves could be essential for the local acceleration of the ions, particularly alphas (Chandran 2010; Isenberg & Vasquez 2009; Bourouaine et al. 2011; Perrone et al. 2014; Bowen et al. 2022). Jian et al. (2010) compared ion cyclotron waves observed at 0.3 au with 1 au observations and showed that the occurrence rate and wave power of these waves decrease significantly with heliocentric distance. Another possible mechanism responsible for the local heating of solar wind ions is stochastic heating which is a nonlinear heating mechanism that is enhanced close to the Sun (Bourouaine & Chandran 2013; Martinović et al. 2020). These local heating mechanisms may then also be responsible for the extensive heating of alpha particles close to the Sun, as observed by PSP.

thumbnail Fig. 1.

Probability of non-thermal properties of alpha particles with respect to protons as a function of Coulomb number, Nc, during encounter 10. Panels a and b show the alpha-to-proton temperature ratio, Tα/Tp, and the magnitude of differential speed over local Alfvén speed, |Vαp|/VA, are ordered by collisionality. The white horizontal line in panel a represents the thermal equilibrium when Tα = Tp. The white dashed vertical lines in panels a and b show Nc = 0.02 and be used in Fig. 2.

Wind data at 1 au showed that the Tα/Tp positively correlates with solar wind speed (Kasper et al. 2008; Maruca et al. 2013). Slow solar wind (Vp < 400 km s−1) is collisionally old at 1 au and, thus, alphas and protons are at the local thermal equilibrium (Tα = Tp). However, the fast wind is not thermally equilibrated and has larger Tα/Tp (between 4 and 6). Maruca et al. (2013) considered Coulomb collisions as an explanation for this difference and applied a model to predict the Tα/Tp at 0.1 au based on the inputs from Wind data at 1 au. Their analytical model showed an entirely different profile of temperature ratios compared to 1 au observations. Unlike the 1 au observations, in which Tα/Tp is characterized by a bimodal distribution with two distinct peaks for the slow and fast wind, the prediction of 0.1 au showed one peak with no dependence on solar wind speed. This raised the question of whether both fast wind and slow wind have similar heating mechanisms driving the preferential heating of alpha particles and whether the observed distribution at 1 au was primarily a consequence of differing collisional age. At present, PSP now enables insights into the properties of the newly heated solar wind near the source. We used PSP data to study the non-thermal features of fast and slow wind close to the Sun and compare them with what Maruca et al. (2013) predicted. PSP has not yet observed a large number of high-speed solar wind during the intervals when the core of the solar wind was within the FOV of SPAN-I. The only time that SPAN-I observed considerable fast wind with speeds greater than 400 km s−1 was near the perihelion of encounter 10, located at about 0.06 au from the Sun. Thus, encounter 10 provided a unique dataset that includes both slow and fast wind to analyze their non-thermal properties (i.e., Tα/Tp and |Vαp|/VA). Figure 2a shows the probability distribution of the proton speed during encounter 10, showing that our dataset during this encounter included a significant sampling of both fast and slow wind with an almost similar number of points. The distribution of Tα/Tp observed by PSP in encounter 10 comprises two peaks (yellow region in Fig. 2b). The left hump with a smaller temperature ratio is mainly associated with slow wind (Vp < 400 km s−1; the pink region in Fig. 2b), whereas the right hump with a larger temperature ratio is associated with fast wind (Vp > 400 km s−1; the orange region in Fig. 2b). While the observed temperature ratio shows that the preferential ion heating is not restricted to only fast solar wind and that all the solar wind (slow to fast) experience preferential heating, alpha particles in fast wind are heated more significantly (see Fig. 2b). The observed difference in temperature ratios between slow and fast solar wind so close to the Sun suggests slow and fast solar wind may have different mechanisms for heating alphas and/or are from different sources. However, the bimodal distribution observed by PSP at 0.06 au is not as well separated and distinct as Wind observed at 1 au (see Fig. 1 in Maruca et al. 2013). Since solar wind at 1 au has gone through more Coulomb collisions and, thus, fast wind and slow wind have had more time to thermalize differently (Marsch 2012; Kasper et al. 2017). The predicted value of Tα/Tp at 0.1 au by Maruca et al. (2013) only considered collisions between 0.1 and 1 au without considering local effects and has a peak around 5.4. However, PSP observations show that Tα/Tp has larger values than predicted. This could suggest the existence of local effects acting to heat alpha particles preferentially. The distribution of differential velocity over Alfvén speed, |Vαp|/VA, is also plotted for different solar wind speeds in Fig. 2c, showing the same feature described in Fig. 2b.

thumbnail Fig. 2.

Distribution of the temperature ratio and the differential velocity as a function of solar wind speed and collisional age. (a): Probability distribution of the proton velocity shows that our dataset during encounter 10 includes a similar amount of fast and slow solar wind with velocities greater and smaller than 400 km s−1, respectively. (b): Distribution of Tα/Tp for different solar wind speeds. Yellow, pink, and orange shaded regions show the Tα/Tp of the combined, slow and fast solar wind, respectively. (d): Distribution of Tα/Tp for all, small, and large Coulomb numbers are shown in yellow, red, and green shaded regions, respectively. The distribution of differential velocity over Alfvén speed is plotted based on different solar wind speeds and Coulomb numbers in panels c and e. Error bars are shown in all panels.

Kasper et al. (2008, 2017) and Maruca et al. (2013) previously reported that Coulomb collisions organize the non-thermal features better than other solar wind properties (e.g., solar wind speed) at 1 au. To explore this at PSP, Figures 2d and 2e show the distribution of Tα/Tp and |Vαp|/VA for different Coulomb numbers. Even though PSP is very close to the Sun (∼0.062 au) and the solar wind has experienced fewer collisions than by the time it reaches 1 au, non-thermal properties are still correlated more strongly with the number of Coulomb collisions (Figs. 2d and e) than with the solar wind speed (Figs. 2b and c).

Kasper et al. (2017) proposed that preferential heating of the alpha particles is predominately active within a boundary near the Sun that may correlate with the Alfvénic critical surface (Kasper & Klein 2019). Our dataset of encounter 10 (‘2021-11-21/05:00’ – ‘2021-11-21/15:00’) was almost during an interval when PSP was measuring super-Alfvénic wind but was very close to the Alfvénic surface (Badman et al. 2023). This may explain the observation of very intense preferential heating of alpha particles by being close to the source. In future studies (when more statistics of sub-Alfvénic wind are available), we plan to study PSP measurements within the Alfvénic surface to finally understand the mystery behind the non-thermal heating of solar wind minor ions and its source.

4. Summary

In this letter, we use PSP data to investigate the effect of collisions on the thermalization of solar wind ions very close to the Sun (i.e., around 0.07 au). In particular, we examine the non-thermal features of solar wind protons and alphas distribution functions, such as their temperature ratio and differential velocity. PSP observations have shown that the non-thermal features of plasma are inversely proportional with collisionality and Coulomb number, similar to 1 au observations. The alpha-to-proton temperature ratio and the differential velocity decrease as the plasma becomes more collisional. This confirms that Coulomb collisions could reduce the non-thermal properties even close to the source of the solar wind and might lead to thermal equilibrium at larger distances when the plasma has undergone more collisions.

Alpha particles observed by PSP are intensively preferentially heated close to the Sun. The large alpha-to-proton temperature ratio may suggest that the observation point is close to the source of the heating mechanisms. This may be amplified by some local effects close to the Sun, such as wave-particle interactions, turbulence fluctuations, reconnection, and stochastic heating. For example, ion cyclotron waves that are pronounced close to the Sun resonate more efficiently with alpha particles and thus produce extra heating. The effect of wave-particle interactions on preferential heating on alpha particles is beyond the scope of the present work and will be investigated in the future.

Wind observations at 1 au have shown that the alpha-to-proton temperature ratio has a bimodal distribution. In which slow solar wind is almost thermally equilibrated (Tα = Tp), whereas fast wind still has some non-thermal features and a mean value of Tα/Tp ∼ 4. As observed by PSP, the preferential heating of alpha particles is not restricted to the fast solar wind. In fact, all solar wind (both fast and slow) experiences the preferential heating of alphas close to the Sun and develops a large temperature ratio. However, two distinct peaks in the temperature ratio distribution (bimodal distribution) show that fast solar wind has a larger temperature ratio value and may suggest a different heating mechanism or source than the slow solar wind. The different heating mechanisms for slow and fast wind can be studied more carefully in the future with a larger, statistically significant dataset, as more PSP observations of both fast and slow wind are recorded from inside and outside of the Alfvénic surface. Moreover, PSP observations showed that the non-thermal features are better organized by Coulomb numbers than the solar wind speed, as has been reported in 1 au observations too.

It has been predicted that the region of preferential heating of minor ions terminates at or near the Alfvén surface (Kasper et al. 2017; Kasper & Klein 2019). The intense temperature ratio observed by PSP at its perihelia close to the Sun may suggest that it is proximal to the heating source. PSP crossed the Alfvénic surface for the first time during its eighth encounter near 16Rs (Kasper et al. 2021). Since then, PSP has been in the sub-Alfvénic patches or blobs (Chhiber et al. 2022) for a short period during each encounter (Bandyopadhyay et al. 2022; Raouafi et al. 2023). The question of whether the preferential heating stops or keeps increasing close to the Sun will be determined by current and future PSP measurements of the Sub-Alfvénic plasma, when the data are statistically more significant. This issue is beyond the scope of this work and will be addressed in a future work.

Acknowledgments

Parker Solar Probe was designed, built, and is now operated by the Johns Hopkins Applied Physics Laboratory as part of NASA’s Living with a Star (LWS) program (contract NNN06AA01C). Support from the LWS management and technical team has played a critical role in the success of the Parker Solar Probe mission. We acknowledge the support from NASA HGIO grant 80NSSC23K0419. PM acknowledges the support by the International Space Science Institute (ISSI) in Bern, through ISSI International Team project 563 (Ion Kinetic Instabilities in the Solar Wind in Light of Parker Solar Probe and Solar Orbiter Observations). The authors acknowledge CNES (Centre National de Etudes Spatiales), CNRS (Centre National de la Recherche Scientifique), the Observatoire de PARIS, NASA and the FIELDS/RFS team for their support to the PSP/SQTN data production, and the CDPP (Centre de Donnees de la Physique des Plasmas) for their archiving and provision. The FIELDS experiment on the PSP spacecraft was designed and developed under NASA contract NNN06AA01C. RCA acknowledges support from NASA grants 80NSSC22K0993 and 80NSSC21K0733. JLV acknowledges support from NASA PSP-GI 80NSSC23K0208.

References

  1. Alterman, B. L., Kasper, J. C., Stevens, M. L., & Koval, A. 2018, ApJ, 864, 112 [Google Scholar]
  2. Artemyev, A. V., Zimbardo, G., Ukhorskiy, A. Y., & Fujimoto, M. 2014, A&A, 562, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Badman, S. T., Riley, P., Jones, S. I., et al. 2023, J. Geophys. Res., submitted [Google Scholar]
  4. Bale, S. D., Goetz, K., Harvey, P. R., et al. 2016, Space Sci. Rev., 204, 49 [Google Scholar]
  5. Bame, S. J., Asbridge, J. R., Feldman, W. C., & Gosling, J. T. 1977, J. Geophys. Res., 82, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bandyopadhyay, R., Matthaeus, W. H., McComas, D. J., et al. 2022, ApJ, 926, L1 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bourouaine, S., & Chandran, B. D. G. 2013, ApJ, 774, 96 [Google Scholar]
  8. Bourouaine, S., Marsch, E., & Neubauer, F. M. 2011, ApJ, 728, L3 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bowen, T. A., Chandran, B. D., Squire, J., et al. 2022, Phys. Rev. Lett., 129 [Google Scholar]
  10. Case, A. W., Kasper, J. C., Stevens, M. L., et al. 2020, ApJS, 246, 43 [Google Scholar]
  11. Chandran, B. D. G. 2010, ApJ, 720, 548 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chandran, B. D. G., Verscharen, D., Quataert, E., et al. 2013, ApJ, 776, 45 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chhiber, R., Matthaeus, W. H., Usmanov, A. V., Bandyopadhyay, R., & Goldstein, M. L. 2022, MNRAS, 513, 159 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cranmer, S. R., & Winebarger, A. R. 2019, ARA&A, 57, 157 [Google Scholar]
  15. Drake, J. F., Cassak, P. A., Shay, M. A., Swisdak, M., & Quataert, E. 2009, ApJ, 700, L16 [Google Scholar]
  16. Duan, D., He, J., Zhu, X., et al. 2022, EGU General Assembly 2022, Vienna, Austria, EGU22-11028, https://doi.org/10.5194/egusphere-egu22-11028 [Google Scholar]
  17. Ďurovcová, T., Šafránková, J., Němeček, Z., & Richardson, J. D. 2017, ApJ, 850, 164 [Google Scholar]
  18. Ďurovcová, T., Šafránková, J., & Němeček, Z. 2019, Sol. Phys., 294, 97 [CrossRef] [Google Scholar]
  19. Ďurovcova, T., Šafránková, J., & Němeček, Z. 2021, ApJ, 923, 170 [CrossRef] [Google Scholar]
  20. Feldman, W. C., Asbridge, J. R., & Bame, S. J. 1974, J. Geophys. Res., 79, 2319 [NASA ADS] [CrossRef] [Google Scholar]
  21. Fox, N. J., Velli, M. C., Bale, S. D., et al. 2016, Space Sci. Rev., 204, 7 [Google Scholar]
  22. Hernandez, R., & Marsch, E. 1985, J. Geophys. Res., 90, 11062 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hernández, R., Livi, S., & Marsch, E. 1987, J. Geophys. Res., 92, 7723 [CrossRef] [Google Scholar]
  24. Isenberg, P. A., & Vasquez, B. J. 2009, ApJ, 696, 591 [NASA ADS] [CrossRef] [Google Scholar]
  25. Jian, L. K., Russell, C. T., Luhmann, J. G., et al. 2010, J. Geophys. Res., 115 [Google Scholar]
  26. Kasper, J. C., & Klein, K. G. 2019, ApJ, 877, L35 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kasper, J. C., Lazarus, A. J., & Gary, S. P. 2008, Phys. Rev. Lett., 101 [Google Scholar]
  28. Kasper, J. C., Maruca, B. A., Stevens, M. L., & Zaslavsky, A. 2013, Phys. Rev. Lett., 110, 091102 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kasper, J. C., Abiad, R., Austin, G., et al. 2016, Space Sci. Rev., 204, 131 [Google Scholar]
  30. Kasper, J. C., Klein, K. G., Weber, T., et al. 2017, ApJ, 849, 126 [NASA ADS] [CrossRef] [Google Scholar]
  31. Kasper, J., Klein, K., Lichko, E., et al. 2021, Phys. Rev. Lett., 127 [Google Scholar]
  32. Klein, L. W., Ogilvie, K. W., & Burlaga, L. F. 1985, J. Geophys. Res.: Space Phys., 90, 7389 [NASA ADS] [CrossRef] [Google Scholar]
  33. Livi, S., Marsch, E., & Rosenbauer, H. 1986, J. Geophys. Res., 91, 8045 [NASA ADS] [CrossRef] [Google Scholar]
  34. Livi, R., Larson, D. E., Kasper, J. C., et al. 2022, ApJ, 938, 138 [NASA ADS] [CrossRef] [Google Scholar]
  35. Marsch, E. 2006, Liv. Rev. Sol. Phys., 3 [Google Scholar]
  36. Marsch, E. 2012, Space Sci. Rev., 172, 23 [Google Scholar]
  37. Marsch, E., & Goldstein, H. 1983, J. Geophys. Res., 88, 9933 [NASA ADS] [CrossRef] [Google Scholar]
  38. Marsch, E., Mühlhäuser, K.-H., Rosenbauer, H., Schwenn, R., & Neubauer, F. M. 1982, J. Geophys. Res., 87, 35 [NASA ADS] [CrossRef] [Google Scholar]
  39. Martinović, M. M., Klein, K. G., Kasper, J. C., et al. 2020, ApJS, 246, 30 [Google Scholar]
  40. Maruca, B. A., Bale, S. D., Sorriso-Valvo, L., Kasper, J. C., & Stevens, M. L. 2013, Phys. Rev. Lett., 111, 241101 [CrossRef] [Google Scholar]
  41. Moncuquet, M., Meyer-Vernet, N., Issautier, K., et al. 2020, ApJS, 246, 44 [Google Scholar]
  42. Mostafavi, P., Allen, R. C., McManus, M. D., et al. 2022, ApJ, 926, L38 [NASA ADS] [CrossRef] [Google Scholar]
  43. Navarro, R. E., Muñoz, V., Valdivia, J. A., & Moya, P. S. 2020, ApJ, 898, L9 [NASA ADS] [CrossRef] [Google Scholar]
  44. Neugebauer, M. 1976, J. Geophys. Res., 81, 78 [NASA ADS] [CrossRef] [Google Scholar]
  45. Perrone, D., Bourouaine, S., Valentini, F., Marsch, E., & Veltri, P. 2014, J. Geophys. Res.: Space Phys., 119, 2400 [NASA ADS] [CrossRef] [Google Scholar]
  46. Pulupa, M., Bale, S. D., Bonnell, J. W., et al. 2017, J. Geophys. Res.: Space Phys., 122, 2836 [NASA ADS] [CrossRef] [Google Scholar]
  47. Raouafi, N. E., Matteini, L., Squire, J., et al. 2023, Space Sci. Rev., 219 [CrossRef] [Google Scholar]
  48. Ryan, J. M., & Axford, W. I. 1975, Z. Geophys., 41, 21 [Google Scholar]
  49. Salem, C., Hubert, D., Lacombe, C., et al. 2003, ApJ, 585, 1147 [Google Scholar]
  50. Steinberg, J. T., Lazarus, A. J., Ogilvie, K. W., Lepping, R., & Byrnes, J. 1996, Geophys. Res. Lett., 23, 1183 [Google Scholar]
  51. Tracy, P. J., Kasper, J. C., Zurbuchen, T. H., et al. 2015, ApJ, 812, 170 [NASA ADS] [CrossRef] [Google Scholar]
  52. Verscharen, D., & Marsch, E. 2011, Ann. Geophys., 29, 909 [Google Scholar]
  53. Verscharen, D., Bourouaine, S., Chandran, B. D. G., & Maruca, B. A. 2013, ApJ, 773, 8 [NASA ADS] [CrossRef] [Google Scholar]
  54. Verscharen, D., Klein, K. G., & Maruca, B. A. 2019, Liv. Rev. Sol. Phys., 16 [Google Scholar]
  55. von Steiger, R., Geiss, J., Gloeckler, G., & Galvin, A. B. 1995, Space Sci. Rev., 72, 71 [NASA ADS] [CrossRef] [Google Scholar]
  56. Yermolaev, Y., & Stupin, V. 1990, Planet. Space Sci., 38, 1305 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Probability of non-thermal properties of alpha particles with respect to protons as a function of Coulomb number, Nc, during encounter 10. Panels a and b show the alpha-to-proton temperature ratio, Tα/Tp, and the magnitude of differential speed over local Alfvén speed, |Vαp|/VA, are ordered by collisionality. The white horizontal line in panel a represents the thermal equilibrium when Tα = Tp. The white dashed vertical lines in panels a and b show Nc = 0.02 and be used in Fig. 2.
In the text
thumbnail Fig. 2.

Distribution of the temperature ratio and the differential velocity as a function of solar wind speed and collisional age. (a): Probability distribution of the proton velocity shows that our dataset during encounter 10 includes a similar amount of fast and slow solar wind with velocities greater and smaller than 400 km s−1, respectively. (b): Distribution of Tα/Tp for different solar wind speeds. Yellow, pink, and orange shaded regions show the Tα/Tp of the combined, slow and fast solar wind, respectively. (d): Distribution of Tα/Tp for all, small, and large Coulomb numbers are shown in yellow, red, and green shaded regions, respectively. The distribution of differential velocity over Alfvén speed is plotted based on different solar wind speeds and Coulomb numbers in panels c and e. Error bars are shown in all panels.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.