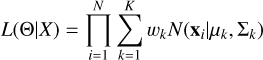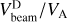| Issue |
A&A
Volume 669, January 2023
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 12 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202243719 | |
| Published online | 20 January 2023 | |
Innovative technique for separating proton core, proton beam, and alpha particles in solar wind 3D velocity distribution functions
1
INAF − Istituto di Astrofisica e Planetologia Spaziali,
Via Fosso del Cavaliere 100,
00133
Roma, Italy
e-mail: rossana.demarco@inaf.it
2
Johns Hopkins University Applied Physics Laboratory,
Laurel, MD
20723, USA
3
Planetek Italia S.R.L.,
Via Massaua, 12,
70132
Bari, BA, Italy
4
ASI − Italian Space Agency,
via del Politecnico snc,
00133
Rome, Italy
5
INAF − Osservatorio Astronomico di Torino,
Via Osservatorio 20,
10025
Pino Torinese (TO), Italy
6
Mullard Space Science Laboratory, University College London,
Holmbury St. Mary, Dorking,
Surrey
RH5 6NT, UK
7
Institut de Recherche en Astrophysique et Planétologie,
9 avenue du Colonel Roche,
BP 4346,
31028
Toulouse Cedex 4, France
8
Southwest Research Institute,
6220 Culebra Road,
San Antonio, TX
78238, USA
9
Imperial College London,
South Kensington Campus,
London
SW7 2AZ, UK
Received:
5
April
2022
Accepted:
15
November
2022
Context. The identification of proton core, proton beam, and alpha particles in solar wind ion measurements is usually performed by applying specific fitting procedures to the particle energy spectra. In many cases, this turns out to be a challenging task due to the overlapping of the curves.
Aims. We propose an alternative approach based on the statistical technique of clustering, a standard tool in many data-driven and machine learning applications.
Methods. We developed a procedure that adapts clustering to the analysis of solar wind distribution functions. We first tested the method on a synthetic data set and then applied it to a time series of solar wind data.
Results. The moments obtained for the different particle populations are in good agreement with the official data set and with the statistical studies available in the literature.
Conclusions. Our method is shown to be a very promising technique that can be combined with the traditional fitting algorithms in working out difficult cases that involve the identification of particle species in solar wind measurements.
Key words: solar wind / plasmas / methods: statistical / instabilities / methods: data analysis
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
One of the primary goals of space physics missions is the determination of the particle velocity distribution function, f(v, t) (VDF, hereafter). This represents the particle number density in the 3D velocity space at a time, t. The moments of the VDF define the macroscopic quantities characterizing the plasma, such as density, velocity, and temperature. The form of the VDF provides essential information about the kinetic processes taking place in the plasma. Turbulent heating, dissipative processes, wave-particle interactions, leave their signature on the VDF, which departs from the equilibrium Maxwellian shape, as seen in many experimental (Marsch 2006; Tu & Marsch 2002) and numerical works (Hellinger & Trávníček 2011; Valentini et al. 2014, 2016). In order to determine the VDF, plasma particles must be sampled and classified according to their velocity and direction of arrival. This can be done through specific detectors, such as electrostatic analyzers (Carlson & McFadden 1998) and Faraday cups (Ogilvie et al. 1995), which are fundamental components of the payload of many space missions. These sensors, however, can only measure the particle flux as a function of the energy per charge ratio of the particles. This means that an ambiguity is present when different ion species are involved, as in the case of the solar wind, composed for the ~95% of protons and for ~4%, of alpha particles, plus minor ions. Alpha particle velocity is similar to proton velocity, but their mass-per-charge ratio is twice that of protons. Consequently, when a 3D VDF is integrated over the angles and represented as a function of the velocity, at least two peaks can usually be observed in the 1D spectrum: a first peak which corresponds to protons and a second peak at about 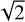 the protons’ bulk velocity, which is related to the alpha particles. This is due to the fact that, when lacking more specific information, we must plot the VDF as if the particles are all protons and the mass-per-charge factor of the alpha particles is included in the alpha velocity. The displacement between the two peaks ranges from ~100 km s−1 to ~300 km s−1, depending on the velocity of the wind. If the thermal speed of the two species is so low that no significant overlapping between the curves is present, the two distributions can be separated without any crucial assumptions. More often, there is a variable superposition of the spectra and a fitting procedure is needed to extrapolate the VDFs, as discussed, for instance, in Marsch et al. (1982b) and Robbins et al. (1970). Furthermore, in many solar wind spectra, a secondary proton population, namely, the proton beam, is observed. Several authors have extensively studied the properties of beams in the solar wind in the inner heliosphere (Feldman et al. 1973; Marsch et al. 1982b; Livi & Marsch 1987; Steinberg et al. 1996; Tu et al. 2004; Kasper et al. 2006; Klein et al. 2018; Alterman et al. 2018; Durovcová et al. 2019a,b) and in the outer heliosphere (Goldstein et al. 2010; Neugebauer et al. 1996; Neugebauer & Goldstein 2013). The beam drifts with respect to the proton core along the magnetic field direction, at a velocity of the order of the local Alfvén speed (Tu et al. 2004; Alterman et al. 2018). Due to this small separation from the core, the identification of the beam is usually a difficult task. Basically, it is identified by searching for secondary peak in the 1D cuts of the VDF along the magnetic field and then the parameters of the distribution are obtained applying a Maxwellian fit. Often, constraints are set in order to find a stable solution (Tu et al. 2004; Alterman et al. 2018; Wilson et al. 2018). In cases of strong overlapping between core, beam, and alpha particles, the fitting procedure is not possible and approximate estimates must be obtained, at least for protons and alphas, usually by splitting the VDF at som energy value. More recently, machine learning techniques are becoming more and more popular in space physics, and neural networks trained on 2D images of VDFs integrated over the solid angles have been applied to the problem of particle separation with good results (Vech et al. 2021). Here, we present a possible alternative method directly applied to the 3D VDFs measured by an electrostatic analyzer, which could be used to separate a proton core, proton beam, and alpha particles in solar wind measurements. This innovative method is based on the statistical technique of clustering. We introduce the method in Sect. 2. In Sect. 3, we illustrate its application to a simulated measurement of solar wind ions. In Sect. 4, we discuss the performance of the algorithm. Finally, in Sect. 5, we present the results of the application of our method to real data.
the protons’ bulk velocity, which is related to the alpha particles. This is due to the fact that, when lacking more specific information, we must plot the VDF as if the particles are all protons and the mass-per-charge factor of the alpha particles is included in the alpha velocity. The displacement between the two peaks ranges from ~100 km s−1 to ~300 km s−1, depending on the velocity of the wind. If the thermal speed of the two species is so low that no significant overlapping between the curves is present, the two distributions can be separated without any crucial assumptions. More often, there is a variable superposition of the spectra and a fitting procedure is needed to extrapolate the VDFs, as discussed, for instance, in Marsch et al. (1982b) and Robbins et al. (1970). Furthermore, in many solar wind spectra, a secondary proton population, namely, the proton beam, is observed. Several authors have extensively studied the properties of beams in the solar wind in the inner heliosphere (Feldman et al. 1973; Marsch et al. 1982b; Livi & Marsch 1987; Steinberg et al. 1996; Tu et al. 2004; Kasper et al. 2006; Klein et al. 2018; Alterman et al. 2018; Durovcová et al. 2019a,b) and in the outer heliosphere (Goldstein et al. 2010; Neugebauer et al. 1996; Neugebauer & Goldstein 2013). The beam drifts with respect to the proton core along the magnetic field direction, at a velocity of the order of the local Alfvén speed (Tu et al. 2004; Alterman et al. 2018). Due to this small separation from the core, the identification of the beam is usually a difficult task. Basically, it is identified by searching for secondary peak in the 1D cuts of the VDF along the magnetic field and then the parameters of the distribution are obtained applying a Maxwellian fit. Often, constraints are set in order to find a stable solution (Tu et al. 2004; Alterman et al. 2018; Wilson et al. 2018). In cases of strong overlapping between core, beam, and alpha particles, the fitting procedure is not possible and approximate estimates must be obtained, at least for protons and alphas, usually by splitting the VDF at som energy value. More recently, machine learning techniques are becoming more and more popular in space physics, and neural networks trained on 2D images of VDFs integrated over the solid angles have been applied to the problem of particle separation with good results (Vech et al. 2021). Here, we present a possible alternative method directly applied to the 3D VDFs measured by an electrostatic analyzer, which could be used to separate a proton core, proton beam, and alpha particles in solar wind measurements. This innovative method is based on the statistical technique of clustering. We introduce the method in Sect. 2. In Sect. 3, we illustrate its application to a simulated measurement of solar wind ions. In Sect. 4, we discuss the performance of the algorithm. Finally, in Sect. 5, we present the results of the application of our method to real data.
2 Methods: Cluster analysis and Gaussian mixture models
Cluster analysis, or clustering (Aggarwal & Reddy 2014; Barber 2012), is a task that involves grouping together observations that share some property. Data in the same cluster are more similar to each other than they are to data belonging to another cluster. Clustering is a central technique in unsupervised learning and big data, and it is widely used in many fields such as pattern recognition, data summarization, information retrieval, and image processing. It differs from classification, where observations are assigned to a group through an algorithm trained on predefined categories (supervised learning). There are plenty of clustering algorithms conceived for various situations and data types and, in general, it is optimal to choose the most appropriate for the particular application at hand, since different clustering algorithms are likely to provide different results based on the same data. In our case, the most convenient algorithm falls under the category of model-based clustering, where it is assumed that the data are described by a mixture of probability distributions. Each cluster can be represented mathematically by a parametric probability distribution and the clustering problem then boils down to a parameter estimation problem. Among model-based clustering methods, the Gaussian mixture model (GMM) is perhaps the most commonly used. In a GMM, given a set of N observations, X = {x1,…,xN}, where xi is a vector in a d-dimensional space, the probability of an observation, xi, is assumed to be the outcome of a linear combination of K Gaussian probability distributions, namely:
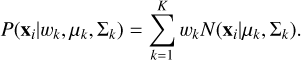 (1)
(1)
In this equation, K represents the number of distributions involved, wk is the mixing proportion of the kth distribution, with 0 < wk < 1 and 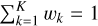 , and N(xi|μk, Σk) is the multivariate Gaussian distribution, namely:
, and N(xi|μk, Σk) is the multivariate Gaussian distribution, namely:
![$ N\left( {\left. {{{\bf{x}}_i}} \right|{\mu _k},{\sum _k}} \right) = {1 \over {\sqrt {{{\left( {2\pi } \right)}^d}\left| {{\sum _k}} \right|} }}\exp \,\left[ { - {1 \over 2}{{\left( {{{\bf{x}}_i} - {\mu _k}} \right)}^T}\sum _k^{ - 1}\left( {{{\bf{x}}_i} - {\mu _k}} \right)} \right], $](/articles/aa/full_html/2023/01/aa43719-22/aa43719-22-eq4.png) (2)
(2)
where μk is the mean vector, Σk the covariance matrix, and k = (1, …, K). In the following, we use the following short notations: θk = (wk, μk, ∑k) to indicate the parameters of the kth Gaussian and Θ = {θ1, …, θK} to refer to all the parameters of the model. In order to learn a GMM clustering model, given the dataset X = {xi} drawn from a mixture of K distributions, we have to estimate the parameters Θ that define the clusters. This is done by maximizing the log-likelihood function of the model. If the N observations are generated independently, the probability of observing the entire set X is just the product of the single probabilities, and the equation to be solved is:
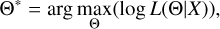 (3)
(3)
is the likelihood of the model explaining the observed data. Equation (3) can be solved analytically for a single Gaussian but not for a mixture. In this case, in fact, we do not know which distribution generated the various points, and, consequently, the probabilities of the data points cannot be computed. In this sense, the likelihood L(Θ|X) is said to be incomplete. The missing data (or latent variables) are variables that clarify whether a given point comes from the kth Gaussian or not. The problem of maximizing the likelihood function in case of missing data is usually addressed by the expectation maximization (EM for short) algorithm (Dempster et al. 1977), which is essentially an optimization procedure that iteratively maximizes the likelihood function, starting from an initial guess of the parameters, Θ. In a nutshell, the model is trained by repeating two steps until some convergence criterion is met: the expectation step, in which a membership in each distribution is assigned to the data starting from the current estimate of the parameters; and the maximization step, where the likelihood function is maximized with respect to the parameters, Θ. The EM algorithm and its implications are discussed in many specialized books and papers (see e.g. McLachlan & Peel 2000; McLachlan & Krishnan 2008). Therefore, we do not describe the algorithm in this work, limiting the details to a consideration of the EM results. Besides the parameters Θ that identify the clusters, results of the EM are also the so-called “responsibilities” of the data points. The responsibilities, γi,k, denote the membership value of a point, xi, in the specific cluster k. They range from 0 to 1 and for each observation xi, ∑k γi,k = 1. In this way, a “soft clustering” is allowed, where each data point has a certain probability of belonging to each cluster. The input data to the GMM model are simply the observed 3D velocities, and the EM algorithm explores the domain to make sense of the arrangement of the data points. There is no need to specify the magnetic field orientation or the expected location for beam and alphas to find the families. The results of the algorithm are the parameters Θ of the model, but most importantly, for each data point, we obtain the membership in each group. By multiplying these probabilities for the value of the distribution function in that velocity bin, we have three separate 3D distribution functions for the proton core, proton beam, and alpha particles.
3 Application of the GMM method to solar wind ion measurements: Testing on synthetic data
We designed an automated procedure where the distribution functions are fetched, for each family the procedure isolates the VDF and derives the moments: the zeroth order moment, namely, the density, the first-order moment, the velocity vector, and the second-order moment, namely the pressure tensor. For the clustering step, we used the Python package sklearn.mixture included in the scikit-learn library (Pedregosa et al. 2011), version 1.0.2. In order to evaluate the performance of our algorithm we carried out several tests on synthetic data. The results depend on a number of physical and instrumental parameters, such as the range of velocities and densities involved and thermal velocities of the families, as well as the energy and angular resolution of the sensor. All these factors determine the fine resolution of the VDF and the overlapping of the curves, affecting the capability of separating the families. Here, we present a test where we refer to an hypothetical instrument inspired by the sensor PAS on board Solar Orbiter (Müller et al. 2013). The Proton-Alpha Sensor, one of the three sensors of the solar wind analyzer SWA (Owen et al. 2020), collects the solar wind ions with an energy per charge ratio between 200 eV and 20 keV divided in 92 channels that are exponentially distributed. The angular resolution is 5° achieved by nine channels in elevation and 11 channels in azimuth and the time cadence, in normal mode, is 4 s, although each VDF is acquired in about 1 s. With the help of a simulated PAS detector (De Marco et al. 2016, 2020) given the values of density, bulk velocity vector, parallel, and perpendicular temperatures for core, beam, and alpha particles, we generated 2000 VDFs composed of the three families, with noise added. Our algorithm was then applied to each VDF, the moments were computed and compared to those in input. The initial moments of each populations were selected randomly in the ranges indicated in Table 1. Velocities are expressed in the spacecraft reference frame. The randomly generated sets of moments, while they do not cover all the possible solar wind conditions, represent a sufficient number of cases to investigate the behaviour of the algorithm and evidence some characteristics of its performance.
Figure 1 displays the errors in the density estimation for core and beam (top panel) and alphas (bottom panel). Errors are considered as a signed quantity in order to highlight overestimation and underestimation. The top panel shows the errors for core and beam densities as a function of the input velocity separation between the two families, which is representative of the overlapping. Clearly, the error is larger in case of smaller separations and the errors in core and beam are anti-correlated. This is not surprising, given that core and beam share many velocity bins, therefore data points that are erroneously attributed to the core are taken from the beam and vice versa. Moreover the core is always overestimated and the beam is always underestimated. In contrast to what happens for protons, the error in the alpha density, reported in the bottom part of Fig. 1 as a function of the input velocity distance between proton beam and alphas, does not vary with the separation, since there is a minor superposition of the species. The few large errors here are due to unresolved beams, whose data points are assigned to alphas. If we consider the velocity separation between the alphas and beam as it seen by the sensor and ingested to the algorithm, namely, with alpha velocities including the factor 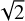 , these errors are found at small separations between the alphas and beam (not shown here). This effect is due to the non-linearity of the transformation of the velocity separation. We return on the issue of the missed beams in the following section. An insight in the errors in core and beam densities is given in Fig. 2, which displays the distribution of the relative errors. We can see that in roughly 12% of cases, the relative error in core density is greater than 20%, while relative errors in beams show a slower decreasing trend. Figure 3 illustrates the error on the estimate of the bulk velocity, V, for core and beam (top panel) and for alphas (bottom panel). While alpha particles velocity is almost equally overestimated and underestimated, the speeds of the core and beam are slightly overestimated, most of the time. There are a few large errors in beam velocity in cases of small core-beam separation. These are due to a misclassification of the beams. In fact, if we plot the error in V for the beam as a function of the output density ratio, Nbeam/Ncore (Fig. 4), we can see that the large errors refer to really tiny beams, with a density lower than 3% of the core, while the minimum input ratio, Nbeam/Ncore, is 0.2. This means that sometimes beams with small separation from the core are not identified and a beam is instead located in the region of velocities (and densities) proper of the alpha particles. Finally, Fig. 5 displays the difference in the temperature anisotropy, T⊥/Т‖, between the output and input. For the core and beam, the anisotropy is recovered to a very good degree, while the alphas are slightly more anisotropic. In both cases, larger errors are concentrated in VDFs with a small displacement between particle families or they are due to a misclassification of beams, which is reflected in the poor definition of alpha particles.
, these errors are found at small separations between the alphas and beam (not shown here). This effect is due to the non-linearity of the transformation of the velocity separation. We return on the issue of the missed beams in the following section. An insight in the errors in core and beam densities is given in Fig. 2, which displays the distribution of the relative errors. We can see that in roughly 12% of cases, the relative error in core density is greater than 20%, while relative errors in beams show a slower decreasing trend. Figure 3 illustrates the error on the estimate of the bulk velocity, V, for core and beam (top panel) and for alphas (bottom panel). While alpha particles velocity is almost equally overestimated and underestimated, the speeds of the core and beam are slightly overestimated, most of the time. There are a few large errors in beam velocity in cases of small core-beam separation. These are due to a misclassification of the beams. In fact, if we plot the error in V for the beam as a function of the output density ratio, Nbeam/Ncore (Fig. 4), we can see that the large errors refer to really tiny beams, with a density lower than 3% of the core, while the minimum input ratio, Nbeam/Ncore, is 0.2. This means that sometimes beams with small separation from the core are not identified and a beam is instead located in the region of velocities (and densities) proper of the alpha particles. Finally, Fig. 5 displays the difference in the temperature anisotropy, T⊥/Т‖, between the output and input. For the core and beam, the anisotropy is recovered to a very good degree, while the alphas are slightly more anisotropic. In both cases, larger errors are concentrated in VDFs with a small displacement between particle families or they are due to a misclassification of beams, which is reflected in the poor definition of alpha particles.
Values of density, velocity, parallel and perpendicular temperature used in the simulations.
 |
Fig. 1 Difference between densities computed after the separation and ground truth for core and beam for 2000 synthetic VDFs as a function of the absolute value of input separation between core and beam (top). Error in density for alpha particles as a function of the absolute value of the velocity separation between proton beam and alpha particles (bottom). |
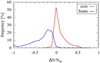 |
Fig. 2 Distribution of the relative density error in core and beam for 2000 synthetic VDFs. |
 |
Fig. 3 Error in the bulk velocity of core and beam for 2000 synthetic VDFs as a function of the separation between core and beam (top). Error in the bulk velocity of alpha particles as a function of the velocity separation between proton beam and alphas (bottom). |
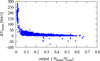 |
Fig. 4 Error in the bulk velocity for the beam as a function of the output ratio between beam and core density. |
 |
Fig. 5 Error in temperature anisotropy for core and beam for 2000 synthetic VDFs as a function of the separation between core and beam (top). Error in temperature anisotropy for alpha particles as a function of the velocity separation between proton beam and alphas (bottom). |
4 Measuring the algorithm performance
In order to trust the clustering results, we need a method for assessing the performance of the algorithm. A closely related problem involves deciding on the “true” number of clusters in a data set. In GMM, as in other clustering algorithms, the number of clusters to be found is an input parameter. Setting aside the possibility to visually inspect the outcome in each step of a pipeline, we need an automated method that can assure us we have identified meaningful subgroups. The selection of the optimal number of clusters and the evaluation of the clustering results are widely investigated topics (see e.g., Halkidi et al. 2004, and reference therein). The usual approach is to try different cluster numbers and select the solution which optimizes specific validity scores. However, as pointed out in many papers (Smyth 1996; Vargha 2016; Wang & Xu 2019, among others), the choice of a suitable score is not obvious. In the absence of a ground truth, validity scores are often based on concepts such as compactness and separation between clusters, or they favour schemes where the data points exhibit a high degree of membership in one cluster. Both these objectives are not necessarily the best options for our purposes. Moreover, scores are often computationally expensive, which means their adoption is not recommended for a pipeline where we need to evaluate thousands of VDFs. Indeed, we calculated a number of common indexes, in particular the Akaike Information Criterion (Akaike 1974), the Bayesian Information Criterion (Wit et al. 2012), the silhouette score (Rousseeuw 1987), the Calinski-Harabasz index (Calinski & Harabasz 1974), Xie-Beni index (Xie & Beni 1991), the Fukuyama-Sugeno index (Fukuyama & Sugeno 1989), and the partition coefficient (Bezdek 1973), on a set of simulated VDFs made of different number of particle families. They can be helpful in identifying definitely wrong solutions, but none of these indicators guarantee the identification of the correct number of clusters. Therefore, in order to check that we are obtaining plausible results, we follow another path, taking advantage of what we already know about the physical situation from previous studies. Our strategy is to set the number of clusters to be identified equal to three. This means that the algorithm will almost certainly find three groups, but some of the solutions can be discarded if we rely on physical considerations. Primarily, we set a minimum distance between the clusters in order to accept them as a good solution. In Alfvénic wind, the particular type of wind considered in this paper, we can choose the Alfvén speed. Another suitable limit can be imposed on the distance between core and alpha particles. Other anomalies may occur, such as clusters with an irrelevant number of data points or clusters with marginal membership. These solutions suggest that, while the algorithm did cluster the data, there is no clear indication of three “robust” clusters. If one or more of these situations occur, an error code is issued clarifying the situation, the solutions is rejected and the test is repeated with two clusters and so on. The requirement of having up to three clusters could be limiting in some cases. However, it does catch on to the common scenario in solar wind and, along with our procedure for discarding poor solutions, it can be easily handled in a data processing pipeline. We performed a test on synthetic VDFs to see whether the VDFs are correctly classified according to the right number of sub-populations. We simulated 8000 test VDFs, as outlined in Sect. 3 according to the parameters contained in Table 1. Overall, 2000 are composed of proton core, proton beam, and alpha particles, 2000 are composed of core and alphas, 2000 are composed of proton core and proton beam, and 2000 are just one-family VDFs. Table 2 shows the so called confusion matrix obtained in the test. The confusion matrix summarizes the errors of the model in predicting classes. The entries are the number of VDFs made up of the number of particle families reported in the corresponding column, which are recognized as being composed of the families reported in the corresponding row. On the principal diagonal, we can read the number of VDFs that are correctly classified in the three cases. A perfect classifier would result in a confusion matrix where all the values off the diagonal are zero. With our procedure applied to the data set described above, the VDFs with three particle populations are correctly inferred in 92.25% of cases, while in 7.75% of them, there are missed beams, namely VDFs with three families which are recognized as composed of two families, protons (unseparated), and alphas. To figure out the reason for these unsolved beams we look to Fig. 6, where we report the frequency counts of the missed beams normalized to the number of beams in the interval, as a function of the distance between core and beam. We can see that most of the missed beams are less than ~50 km s−1 away from the core (we required a minimum distance of 30 km s−1 between core and beam to accept the solution). The separation between core and beam seems to be the pivotal quantity when searching for the beams; in fact, the distribution of unsolved beams as a function of other quantities, as for example, the density or temperature, does not show any particular tendency. With regard to VDFs with two particle populations, there is a slight difference according to whether we consider the two families as proton core and beam or proton core and alphas. The VDFs composed of proton core and alphas are correctly inferred in 90.5% of cases, while in the remaining 9.5%, a third population is identified. It seems that these fake beams have a slightly greater probability to be found in case of cores characterized by higher velocities and small temperatures and alpha particle with small densities, which implies more noise. The VDFs composed of proton core and proton beam are correctly separated in 96.85% of cases. In two cases, three families were erroneously found, and in 61 cases, 3.05% of the total, they are not separated at all. Finally, at least in the case under study, one-particle population VDFs are always correctly inferred. Another known issue of the EM algorithm is that it is guaranteed to converge to a local maximum of the likelihood function in Eq. (4), with a strong dependence on initial conditions (see e.g., McLachlan & Krishnan 2008). The mitigation strategy here can only consist of running multiple instances of the clustering with different initial conditions and choosing the solution with the highest final likelihood. Finally, noisy or corrupt data may confuse the algorithm, leading to formally correct, but generally unsuitable solutions. The problem of the data cleaning, as is well known, is vital in every machine learning project. Incorrect or irrelevant data should be fixed in a pre-processing stage. Real VDFs used in this paper have been cleaned using the local outlier factor (LOF) algorithm (Breunig & Sander 2000) in order to exclude stray points. This algorithm compares the local density of each data point to the local density of its k-nearest neighbors, assigning a score to each point. Outliers tend to have a higher LOF score. Points with LOF score above the 95th percentile were excluded from the analysis.
Confusion matrix showing the classification of 8000 test VDFs.
 |
Fig. 6 Distribution of the VDFs with unresolved proton beams as a function of the input distance between core and beam. |
 |
Fig. 7 Contour lines of the ion VDF observed by PAS, in a quasi-perpendicular magnetic configuration, in the plane identified by the radial direction R and the magnetic field vector (left). Contours have been computed after integration of the VDF along the direction perpendicular to this plane. The arrow indicates the direction of the local magnetic field vector. Right panel shows the same VDF integrated in polar and azimuth angles with the three ion families highlighted in different colors. |
5 Application to solar wind data
In this section, we show the result of the application of our numerical technique to solar wind data collected by the plasma suite SWA (Solar Wind Analyser) (Owen et al. 2020) on board the Solar Orbiter mission (Müller et al. 2020). Launched in February 2020, Solar Orbiter is a one-of-a-kind mission that takes advantage of a unique combination of both in-situ measurements and remote sensing observations (García Marirrodriga et al. 2021), for the first time, on board a single spacecraft in the inner heliosphere. The main goal of this mission is to perform unprecedented magnetic connectivity analysis between the solar atmosphere and the inner heliosphere (Zouganelis et al. 2020). In particular, we use data produced by the Proton and Alpha Sensor (PAS), introduced in Sect. 3. The 4s time resolution proton moments, relative VDFs, and magnetic field parameters from the MAG instrument (Horbury et al. 2020) can be downloaded from ESA Solar Orbiter Archive1 (SOAR). We focus on a sub-interval of the first stream observed by Solar Orbiter after launch. This particular time interval ranges from July 14 at 09:11 to July 16 at 18:30 of the year 2020 and corresponds to the most Alfvénic part of a slow Alfvénic stream recently analyzed by several authors (D’Amicis et al. 2021b; Louarn et al. 2021; Lavraud et al. 2021, among others). Since the main goal of this paper is to show that our numerical tool is able to separate the three main components of the ion VDF, namely, core, beam, and alphas, while detector resolution is a non-trivial concern in this regard, we concentrate our attention on an Alfvénic time interval where the chances of having a proton beam resolved by currently available plasma detectors are much higher compared to non-Alfvénic wind (see e.g., Marsch et al. 1982b). Alfvénic slow wind has already been observed in the inner heliosphere at different heliocentric distances and for different phase of the solar cycle (Bale et al. 2019; Kasper et al. 2019; Perrone et al. 2020; Stansby et al. 2020; Parashar et al. 2020; D’Amicis et al. 2021a). It is a particular solar wind regime identified for the first time as a single case study by Marsch et al. (1981) and then statistically by D’Amicis et al. (2011). Further studies by D’Amicis & Bruno (2015) and D’Amicis et al. (2019) characterized this solar wind regime based on a dedicated focus on the similarities with typical fast and Alfvénic wind streams and on their importance in the context of the general problem of solar wind acceleration (D’Amicis et al. 2021c). The selected time interval contains 49484 VDFs taken at 4s. Before proceeding to validate our analysis, we show, along with an example, the capabilities of this innovative numerical technique. Figure 7 refers to the VDF of 14 July 2020 at 11:58:55.467982. For this VDF, the magnetic field is quasi-perpendicular to the bulk velocity. The left panel shows the VDF isocontours in the V − B plane after integration in the direction perpendicular to it (only the proton part of the VDF is reported here). The V − B plane contains the local magnetic field vector, B, and the radial component, VR, of the velocity vector (Marsch et al. 1982b). This particular reference frame is chosen to better highlight the presence of the proton beam, which propagates along the local magnetic field; its presence in Fig. 7 is suggested by the bulge centered around the black solid line, indicating the magnetic field direction. Proton beam drifts along this direction at a speed of the order of or higher than the local Alfvén speed (Marsch et al. 1982b). In this particular case, the effect of the spacecraft velocity has not yet been removed and the VDF is represented as it appears in the velocity space of PAS. This is particularly instructive for those who are not familiar with this type of measurement. Obviously, the velocity aberration due to the spacecraft velocity has always been removed from the final moments in our analysis. On the right-hand side of Fig. 7, we show the 1D VDF after integration on polar and azimuthal angles. The three populations, as identified by our algorithm, are highlighted in different colors: red for the proton core, blue for the proton beam, and green for the alphas. The three panels (a, b, and c) of Fig. 8 show the VDF for the proton core, proton beam and alphas, respectively, for the same distribution of Fig. 7. Similarly to the VDF representation adopted in Fig. 7, the contour plane is identified by the radial direction, R, and the local magnetic field vector. As for panel a of Fig. 7, the effect of the spacecraft velocity has not yet been removed. Contours have been computed after integrating the VDF in the direction perpendicular to the plane. The local magnetic field direction is also shown by the solid line in each panel. The core and beam show some temperature anisotropy with respect to the magnetic field direction and the beam drifts along this direction at a speed around 1.55 times the local Alfvén speed of 52 km s−1. A quite interesting feature is the alpha particle distribution in panel c. This distribution, as expected, is peaked at a speed around 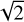 the speed of the proton core. In addition, the contours are nicely elongated in the direction of the magnetic field, suggesting the presence of a beam of alpha particles similarly to early observations by Helios s/c (Marsch et al. 1982a). Finally, it is important to point out that our technique was able to separate the three populations for 45 218 VDFs from the original 49484, which comprises more than 91% of the total number of VDFs. However, we cannot exclude the possibility that other minor ions such as O6+, which is the dominating minor species (Bochsler 2007), might contribute (albeit minimally) to the contours. For example, O6+ ions would be found moving at a speed of about 1.6 times the speed of the proton core.
the speed of the proton core. In addition, the contours are nicely elongated in the direction of the magnetic field, suggesting the presence of a beam of alpha particles similarly to early observations by Helios s/c (Marsch et al. 1982a). Finally, it is important to point out that our technique was able to separate the three populations for 45 218 VDFs from the original 49484, which comprises more than 91% of the total number of VDFs. However, we cannot exclude the possibility that other minor ions such as O6+, which is the dominating minor species (Bochsler 2007), might contribute (albeit minimally) to the contours. For example, O6+ ions would be found moving at a speed of about 1.6 times the speed of the proton core.
The only touchstone we have available to test our results is represented by the moments of level 2 (L2) of PAS provided by the SOAR. Our comparison, however, can only be qualitative, since the L2 data do not separate the proton beam from the core of the distribution and alpha population is separated by searching the minimum in the energy spectra between the proton energy peak and the alpha energy peak. If no minimum can be found, the alpha particles are not separated. As a consequence, moments relative to the proton core will be qualitatively compared to moments on the SOAR while proton beam and alpha particles will be compared on statistical basis to the results available from the literature. We chose this particular time interval to select a solar wind status relatively homogeneous in order to avoid (as much as possible) mixing together Alfvénic and non-Alfvénic winds. Figure 9 shows the solar wind stream selected for this analysis. This plasma sample corresponds to the most Alfvénic part of the slow wind stream observed in the middle of July 2020 (see also D’Amicis et al. 2021b). The panels refer to the time series of the main moments for core, beam, and alphas, derived by integrating over each velocity distribution function separated by the clustering procedure, respectively. The three top panels (a, b, and c) show a rather good agreement with some larger discrepancies for the number density and total temperature. In particular, the L2 time series show a higher number density and a higher total temperature. The reason for this is that moments derived without separating the proton beam from the core of the VDF retain the contribution from the beam, which in our case is much less relevant to the moments of the core. The presence of a proton beam along the local magnetic field direction, if not separated from the core, not only contributes to increase the core number density estimation but also to increase the parallel temperature and, as a consequence, the total temperature. The beam density time profile (panel d) runs generally around 2.5 cm−3, roughly 1/4 of the core number density. The beam temperature (panel f) is remarkably similar to the core temperature with a Pearson correlation coefficient CP = 0.86. The alpha particle number density is generally below 1 cm−3, which means a few percent of the core number density, as expected. The alpha speed (panel h) resembles the speed profile of the beam although with slightly lower values (CP = 0.85). Also, the alpha temperature profile (panel i) closely resembles the temperature profile of core (CP = 0.76) and beam (CP = 0.80) although at much higher level as expected. At this point, to further test the validity of the moments relative to the proton beam and the alpha population identified by our clustering technique, we built histograms of a few relevant parameters to be compared (as closely as possible) to similar studies available in the literature. The distributions of these parameters are shown in the three panels of Fig. 10. From top to bottom, panel a shows the ratio between proton beam and proton core number density (solid line) and the ratio between alpha particles and proton core number density (dashed line); panel b shows the ratio between beam total temperature and core total temperature (solid line) and the equivalent parameter for the alpha particles (dashed line); the solid line in panel c shows the distribution of the beam velocity drift normalized to the local Alfvén speed and projected onto the local magnetic field direction by means of cos θD, where θD is the angle between the velocity drift vector and the local magnetic field vector. The equivalent parameter for the alpha particles is indicated by the dashed line. The disrtribution of the relative density for the proton beam is slightly asymmetric with a longer tail at higher values with respect to the peak. The average value is a bit larger than 0.2 and quite close to the peak value. This value is in remarkable agreement with the value based on Helios data reported in Fig. 14 of Marsch et al. (1982b) at approximately the same distance from the sun and for similar wind speed interval, namely, between 400 and 500 km s−1. The distribution relative to the alpha particles is quite symmetric with respect to the average (~0.044) which is in good agreement with previous estimates, such as in Robbins et al. (1970), Kasper et al. (2007), Aellig et al. (2001), among others. In particular, there is a remarkable agreement also with the estimate reported by Stansby et al. (2019), based on Helios observations, who found that the average value for this parameter was 0.043. However, although these authors only analyzed fast wind, the agreement we found should not come as a surprise since it has been shown that fast wind, which is generally Alfvénic, shares many similar properties with the slow Alfvénic wind, such as the one that stands as the object of this study (D’Amicis et al. 2019). With regard to the beam’s normalized total temperature (reported in panel b) we do not have statistical determinations available in the literature to make comparisons. In any case, our analysis shows that the proton beam is slightly hotter than the core by about 18%. The ratio between alphas and core total temperature is much larger, indicating an average value of 5.18. In this case, we have a rather good agreement with previous estimates (Tracy et al. 2015; Kasper et al. 2017). These authors found that within fast solar wind, the alphas are hotter than the protons by a factor of about 5. The drift velocity distribution shown in panel c by the solid line indicates that, on average, the beam drifts at a speed around 1.76 × VAlfvén along the magnetic field direction. In this case, our results indicate an average drift speed a bit higher than the average value reported on the histogram shown in the middle panel of Fig. 13 by Marsch et al. (1982b) relative to wind speed between 400 and 600 km s−1 at a similar heliocentric distance. In their study, these authors found that the distribution is characterized by an average value of 1.50. The dashed line shows the distribution of the alpha velocity drift projected onto the local magnetic field. The average value of this distribution is 1.01. This value is in good agreement with estimates by Marsch et al. (1982a) obtained for Alfvénic fast wind. However, there are other estimates of this parameter in the solar wind that have reported that the typical value is less than 0.7 (Kasper et al. 2008, 2017). More recently, Alterman et al. (2018) found that the expected value for this parameter should be around 0.67. The same authors found that, on average, the proton beam should drift at a speed 1.7 times larger than the alpha drift. This means that in our case, the beam drift speed should be around 1.7 × 1.01 = 1.72 the Alfvén speed, which agrees remarkably well with our findings. We note that differing values of the average normalized drift velocity reported by other authors (see papers cited above) might be due to the different heliocentric distance or to the selected type of wind – which in our case is limited to the Alfvénic one. In addition, we should also expect that beam and alpha drift-velocity would be field-aligned, as has already been shown by several authors (Marsch 2006). Figure 11 shows the histograms of the angle between beam drift-velocity and local magnetic field and the angle between alphas drift-velocity and the same magnetic field vector. As expected, proton beam and alphas drift quasi-parallel to the local field direction, however, the beam drift-velocity histogram is much more peaked than the one for the alphas. At the moment, we do not know whether this effect is due to a larger uncertainty in determining the bulk velocity vector for the alphas given the presence of unresolved alpha particle beams or, instead, due to some other physical phenomenon. In particular, the drift-angle distribution for the beam has an average value of 5.95°, with a peak value around 2.5°, compared to an average value of 11.71° and a peak value around 8.5° for the alphas.
Following Tu et al. (2004), we tested the empirical relation that links together the beam velocity drift normalized to the local Alfvén speed, 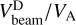 , and the plasma beta of the proton core, β‖c. The relation
, and the plasma beta of the proton core, β‖c. The relation 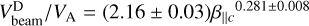 was found by Tu et al. (2004) in the framework of a study about beam generation mechanisms in the solar wind possibly related to ion-beam instabilities. These authors analyzed Helios 2 data recorded during the 90 days of the primary mission from 1.0 AU to 0.3 AU, considering only those proton velocity distribution functions with a wind speed higher than 600 km s−1; this was done with the intent of selecting mainly Alfvénic time intervals. They picked out about 600 VDFs. In our case, the analysis is limited just to a time interval slightly shorter than 2.5 days, but we can rely over a much larger number of VDFs. In Fig. 12, we show the distribution we obtained from our data reduction and the related power law fit, which results in a good agreement with that shown by Tu et al. (2004); however, we do obtain a lower correlation coefficient (−0.63) compared to their ~0.82, which is probably partly due to the stringent requirements they applied to their data selection.
was found by Tu et al. (2004) in the framework of a study about beam generation mechanisms in the solar wind possibly related to ion-beam instabilities. These authors analyzed Helios 2 data recorded during the 90 days of the primary mission from 1.0 AU to 0.3 AU, considering only those proton velocity distribution functions with a wind speed higher than 600 km s−1; this was done with the intent of selecting mainly Alfvénic time intervals. They picked out about 600 VDFs. In our case, the analysis is limited just to a time interval slightly shorter than 2.5 days, but we can rely over a much larger number of VDFs. In Fig. 12, we show the distribution we obtained from our data reduction and the related power law fit, which results in a good agreement with that shown by Tu et al. (2004); however, we do obtain a lower correlation coefficient (−0.63) compared to their ~0.82, which is probably partly due to the stringent requirements they applied to their data selection.
The left-hand panel of Fig. 13 shows normalized histograms of proton core, proton beam, and alpha temperature anisotropy. The histogram for the beam is slightly shifted at a higher anisotropy with respect to the core, especially the tail at higher values. However, the average values of the anisotropy for the core (1.26) and the beam (1.31) lie together within the same associated error interval. As expected (Marsch et al. 1982a) the situation is different for the alphas, whose histogram is shifted to the left with an average value quite smaller than 1. On the right-hand panel, we show the plot for the instability plane for core, beam and alpha populations. The instability plane is built by reporting temperature anisotropy values versus plasma beta β‖, first introduced by Gary et al. (2001), Kasper et al. (2002), Hellinger & Trávníček (2006). As indicated in the plot, the different solid lines indicate different plasma instabilities adopted from Hellinger & Trávníček (2006) for a maximum growth rate γ − 10−3 Ωc, where Ωc is the local ion-cyclotron frequency. However, these instability contours have been derived for a single bi-Maxwellian proton population and, as such, they would not be directly applicable to our case; thus, we display them mainly for reference. Besides the instability lines for the protons, we also show the parallel firehose instability threshold for the alphas for a normalized growth rate γ = 10−3 Ωα, as shown in Fig. 2 of Stansby et al. (2019). The core and beam anisotropy have been plotted versus their respective values of β‖, as well as the alpha anisotropy. As already shown in several previous studies (Hellinger & Trávníček 2006; Matteini et al. 2007; Bale et al. 2009; Telloni & Bruno 2016) the core population is stable within the instability lines corresponding to the mirror instability for T⊥/T‖ > 1 and the oblique firehose instability for T⊥/T‖ < 1. On the other hand, the beam is characterized by roughly the same degree of anisotropy as the core population, but smaller β‖, such that the stability of this population seems to be regulated by the proton cyclotron instability. Matteini et al. (2013) also showed the proton beam population in the instability plane. The data they used refer to about two years’ worth of data during 1995 and 1996, encompassing Ulysses’s first north pole passing. During this time interval, Ulysses covered a radial distance from 1.3 to about 5 AU and a large latitudinal excursion, from −30° to +80°. Comparing our results with the results shown in their Fig. 6, it appears that the core population in both cases is characterized by an anisotropy >1 and a plasma beta β‖ < 1; however, in Matteini et al. (2013), the anisotropy seems to be quite higher than what we observe. On the other hand, the anisotropy of their beam population is clearly < 1, while our analysis attributes to the beam an anisotropy > 1 and slightly larger than that of the core. It is difficult to understand the reason for this discrepancy but we have to consider that the physical environment at Ulysses and at Solar Orbiter is quite different and we plan to focus on this in the near future. Partially overlapped to the beam distribution, we find the alpha distribution, which is characterized by both temperature anisotropy and plasma beta generally less than 1. The spread of these values, although limited, is in quite good agreement with that shown by Maruca et al. (2012), who analyzed a much larger database, spanning about 16 yr of Wind observations. Indeed, we recorded a much narrower spread of our values of β‖, in comparison with the bottom panel of Fig. 2 by Stansby et al. (2019), which is relative to reanalyzed Helios data between 0.6 and 0.7 AU. In any case, the alpha distribution we show in Fig. 13 appears to be well limited by the parallel firehose instability. Among other authors who have previously discussed the VDF instability, we would like to mention Klein et al. (2018). While their analysis cannot be directly compared to ours or that of Matteini, it is relevant to improve the general understanding of the origin of instability phenomena. These authors discussed the instability of VDFs (using the anisotropy and beta referring to the core only), finding that VDFs with a resolved proton beam and/or with a relatively high alpha drift speed are more unstable.
 |
Fig. 8 Ion families identified in the distribution function represented in Fig. 7. Panel a: contour lines for the core distribution in the plane identified by the radial direction, R, and the magnetic field vector. Contours have been computed after integration of the VDF along the direction perpendicular to this plane. Panels b and c refer to the proton beam and alpha populations, respectively. Solid straight line in each panel show the direction of the local magnetic field vector. The contribution from the s/c velocity has not been removed. |
 |
Fig. 9 Overview of the solar wind sample detected by the PAS sensor on board Solar Orbiter from July 14:09:11 to July 16:18:42 (DoY 196-198) 2020. Panels from top to bottom refer to the time series of: (a) proton core number density, Ncore; (b) core speed, Vcore; (c) core total temperature, Tcore; (d) beam number density, Nbeam; (e) beam speed Vbeam; (f) beam total temperature, Tbeam; (g) alpha particle number density, Nalpha; (h) alpha particle speed Valpha; (i) alpha particle total temperature, Talpha. The units are: cm−3 for density, km s−1 for velocity and eV for temperature. In panels a, b, and c, the red solid lines refer to the proton time series of N, V and T from the SOAR. See text for details. |
 |
Fig. 10 Histograms of the relevant parameters of proton beam and alpha particles. The three panels from top to bottom show: (a) the distributions of proton beam and alphas number density normalized to the proton core number density Ncore; (b) the distributions of proton beam and alphas total temperature normalized to the proton core total temperature Tcore; (c) the distributions of proton beam and alphas velocity drift along the local magnetic field direction normalized to the local Alfvén speed (VD cos θD)/VA. Beam distributions are indicated by a solid line, alpha distributions by a dashed line. |
 |
Fig. 11 Histograms of the angle between beam drift-velocity and local magnetic field (solid line) and the angle between alphas drift-velocity and the same magnetic field vector (dashed line). Mean and standard deviation values are indicated for each histogram. |
 |
Fig. 12 Beam velocity drift, normalized to the local Alfvén speed |
 |
Fig. 13 Histograms of the temperature anisostropies and instability plane. Left panel: normalized histograms of temperature anisotropy, defined as T⊥/T‖, for proton core (red line), proton beam (blue line), and alphas (green line). Right panel: temperature anisotropy vs. β‖, commonly known as instability plane for core (red), beam (blue), and alphas (green). Different solid lines indicate plasma instabilities: proton cyclotron and mirror for T⊥/T‖ > 1 and oblique firehose and parallel firehose for T⊥/T‖ < 1. |
6 Conclusions
Clustering is a form of unsupervised learning, meaning that no labels are available for training. The membership of data is deduced solely from the arrangement of the points in the input space. In the Gaussian mixture model, the EM algorithm iteratively assigns the observed data to a component of a mixture of several components, associating to each data point a membership in the distribution. We applied the clustering techniques to the 3D VDFs of solar wind data, in order to separate proton core, proton beam, and alpha particles, which are usually separated by means of fitting procedures in a reduced 2D space. Since our method consists of a data-driven approach, it makes no assumptions on the underlying physical situation. Even though we elaborated on a set of rules to exclude clear non-physical solutions, the results of our procedure are not without ambiguities, due to the well-known critical points of clustering, such as the identification of the best number of clusters and the convergence to a sub-optimal solution. Moreover, we may obtain “wrong” solutions due to noisy or corrupt data. For these reasons, human oversight is still needed in a final stage for science-level data. Nevertheless, we have shown that our method can be a powerful tool which can complement and strengthen the traditional techniques. This is confirmed by the good agreement between the values we estimated for some representative plasma parameters and corresponding values reported in literature. In addition, our clustering technique gives us the capability to separate proton core and beam for quite a large fraction of the entire data set we analyzed (about 91 % of the total number of VDFs), which makes this new numerical technique a valid tool for advancing our understanding of solar wind turbulence and kinetic processes.
References
- Aellig, M. R., Lazarus, A. J., & Steinberg, J. T. 2001, Geophys. Res. Lett., 28, 2767 [NASA ADS] [CrossRef] [Google Scholar]
- Aggarwal, C. C., & Reddy, C. K., 2014, Data Clustering: Algorithms and Applications (CRC Press) [CrossRef] [Google Scholar]
- Akaike, H. 1974, IEEE Trans. Automatic Control, 19, 716 [CrossRef] [Google Scholar]
- Alterman, B. L., Kasper, J. C., Stevens, M. L., & Koval, A. 2018, ApJ, 864, 112 [Google Scholar]
- Bale, S. D., Kasper, J. C., Howes, G. G., et al. 2009, Phys. Rev. Lett., 103, 211101 [NASA ADS] [CrossRef] [Google Scholar]
- Bale, S. D., Badman, S. T., Bonnell, J. W., et al. 2019, Nature, 576, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Barber, D. 2012, Bayesian Reasoning and Machine Learning (USA: Cambridge University Press) [Google Scholar]
- Bezdek, J. 1973, J. Cybernet., 3 [Google Scholar]
- Bochsler, P. 2007, A&ARv, 14, 1 [Google Scholar]
- Breunig, M. M., Kriegel, H.-P. N. R. T., & Sander, J. 2000, in ACM, 93 [Google Scholar]
- Calinski, T., & Harabasz, J. 1974, Commun. Stat., 3, 1 [Google Scholar]
- Carlson, C. W., & McFadden, J. P. 1998, Design and Application of Imaging Plasma Instruments (American Geophysical Union (AGU)), 125 [Google Scholar]
- D’Amicis, R., & Bruno, R. 2015, ApJ, 805, 84 [Google Scholar]
- D’Amicis, R., Bruno, R., & Bavassano, B. 2011, J. Atmos. Solar-Terrestrial Phys., 73, 653 [CrossRef] [Google Scholar]
- D’Amicis, R., Matteini, L., & Bruno, R. 2019, MNRAS, 483, 4665 [NASA ADS] [Google Scholar]
- D’Amicis, R., Alielden, K., Perrone, D., et al. 2021a, A&A, 654, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Amicis, R., Bruno, R., Panasenco, O., et al. 2021b, A&A, 656, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Amicis, R., Perrone, D., Bruno, R., & Velli, M. 2021c, J. Geophys. Res., 126, e28996 [Google Scholar]
- De Marco, R., Marcucci, M., Bruno, R., et al. 2016, J. Instrum., 11, C08010 [NASA ADS] [CrossRef] [Google Scholar]
- De Marco, R., Bruno, R., D’Amicis, R., Telloni, D., & Perrone, D. 2020, A&A, 639, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dempster, A. P., Laird, N. M., & Rubin, D. B. 1977, J. Roy. Stat. Soc. B (Methodological), 39, 1 [Google Scholar]
- Durovcová, T., Nemecek, Z., & Šafránková, J. 2019a, ApJ, 873, 24 [CrossRef] [Google Scholar]
- Durovcová, T., Šafránková, J., & Nemecek, Z. 2019b, Sol. Phys., 294, 97 [CrossRef] [Google Scholar]
- Feldman, W. C., Asbridge, J. R., Bame, S. J., & Montgomery, M. D. 1973, J. Geophys. Res., 78, 6451 [NASA ADS] [CrossRef] [Google Scholar]
- Fukuyama, Y., & Sugeno, M. 1989, in Proc. 5th Fuzzy Syst. Symp, 247 [Google Scholar]
- García Marirrodriga, C., Pacros, A., Strandmoe, S., et al. 2021, A&A, 646, A121 [CrossRef] [EDP Sciences] [Google Scholar]
- Gary, S. P., Skoug, R. M., Steinberg, J. T., & Smith, C. W. 2001, Geophys. Res. Lett., 28, 2759 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, B. E., Neugebauer, M., & Zhou, X. Y. 2010, in American Institute of Physics Conference Series, 1216, Twelfth International Solar Wind Conference, eds. M. Maksimovic, K. Issautier, N. Meyer-Vernet, M. Moncuquet, & F. Pantellini, 261 [Google Scholar]
- Halkidi, M., Batistakis, Y., & Vazirgiannis, M. 2004, J. Intell. Inform. Syst., 17, 107 [Google Scholar]
- Hellinger, P., & Trávnícek, P. M. 2011, J. Geophys. Res., 116 [Google Scholar]
- Hellinger, P. & Trávnícek, P. 2006, J. Geophys. Res., 111, A01107 [NASA ADS] [Google Scholar]
- Horbury, T., Obrien, H., Carrasco, B. I., et al. 2020, A&A, 642, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasper, J. C., Lazarus, A. J., & Gary, S. P. 2002, Geophys. Res. Lett., 29, 1839 [Google Scholar]
- Kasper, J. C., Lazarus, A. J., Stevens, M., & Steinberg, J. T. 2006, in 36th COSPAR Scientific Assembly, 36, 3485 [NASA ADS] [Google Scholar]
- Kasper, J. C., Stevens, M. L., Lazarus, A. J., Steinberg, J. T., & Ogilvie, K. W. 2007, ApJ, 660, 901 [Google Scholar]
- Kasper, J. C., Lazarus, A. J., & Gary, S. P. 2008, Phys. Rev. Lett., 101, 261103 [Google Scholar]
- Kasper, J. C., Klein, K. G., Weber, T., et al. 2017, ApJ, 849, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Kasper, J. C., Bale, S. D., Belcher, J. W., et al. 2019, Nature, 576, 228 [Google Scholar]
- Klein, K. G., Alterman, B. L., Stevens, M. L., Vech, D., & Kasper, J. C. 2018, in Solar Heliospheric and Interplanetary Environment (SHINE 2018), 6 [Google Scholar]
- Klein, K. G., Alterman, B. L., Stevens, M. L., Vech, D., & Kasper, J. C. 2018, Phys. Rev. Lett., 120, 205102 [NASA ADS] [CrossRef] [Google Scholar]
- Lavraud, B., Kieokaew, R., Fargette, N., et al. 2021, A&A, 656, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Livi, S., & Marsch, E. 1987, J. Geophys. Res., 92, 7255 [NASA ADS] [CrossRef] [Google Scholar]
- Louarn, P., Fedorov, A., Prech, L., et al. 2021, A&A, 656, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsch, E. 2006, Living Rev. Solar Phys., 3, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Rosenbauer, H., Schwenn, R., Muehlhaeuser, K. H., & Denskat, K. U. 1981, J. Geophys. Res., 86, 9199 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Mühlhäuser, K.-H., Rosenbauer, H., Schwenn, R., & Neubauer, F. M. 1982a, J. Geophys. Res., 87, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Mülhäuser, K.-H., Schwenn, R., et al. 1982b, J. Geophys. Res., 87, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Maruca, B. A., Kasper, J. C., & Gary, S. P. 2012, ApJ, 748, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Matteini, L., Landi, S., Hellinger, P., et al. 2007, Geophys. Res. Lett., 34, L20105 [Google Scholar]
- Matteini, L., Hellinger, P., Goldstein, B. E., et al. 2013, J. Geophys. Res. (Space Phys.), 118, 2771 [NASA ADS] [CrossRef] [Google Scholar]
- McLachlan, G. J., & Peel, D. 2000, Finite Mixture Models (New York: Wiley Series in Probability and Statistics) [CrossRef] [Google Scholar]
- McLachlan, G., & Krishnan, T. 2008, The EM Algorithm and Extensions, 2nd edn., Wiley Series in Probability and Statistics (Hoboken, NJ: Wiley) [CrossRef] [Google Scholar]
- Müller, D., Marsden, R. G., St Cyr, O. C., & Gilbert, H. R. 2013, Sol. Phys., 285, 25 [CrossRef] [Google Scholar]
- Müller, D., St Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Neugebauer, M., Goldstein, B. E., Smith, E. J., & Feldman, W. C. 1996, J. Geophys. Res., 101, 17047 [NASA ADS] [CrossRef] [Google Scholar]
- Neugebauer, M., & Goldstein, B. E. 2013, in American Institute of Physics Conference Series, 1539, Solar Wind 13, eds. G. P. Zank, J. Borovsky, R. Bruno, et al., 46 [Google Scholar]
- Ogilvie, K. W., Chornay, D. J., Fritzenreiter, R. J., et al. 1995, Space Sci. Rev., 71, 55 [Google Scholar]
- Owen, C. J., Bruno, R., Livi, S., et al. 2020, A&A, 642, A16 [EDP Sciences] [Google Scholar]
- Parashar, T. N., Goldstein, M. L., Maruca, B. A., et al. 2020, ApJS, 246, 58 [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Perrone, D., D’Amicis, R., De Marco, R., et al. 2020, A&A, 633, A166 [EDP Sciences] [Google Scholar]
- Robbins, D. E., Hundhausen, A. J., & Bame, S. J. 1970, J. Geophys. Res., 75, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Rousseeuw, P. J. 1987, J. Comput. Appl. Math., 20, 53 [Google Scholar]
- Smyth, P. 1996, in Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, KDD’96 (AAAI Press), 126 [Google Scholar]
- Stansby, D., Perrone, D., Matteini, L., Horbury, T. S., & Salem, C. S. 2019, A&A, 623, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stansby, D., Matteini, L., Horbury, T. S., et al. 2020, MNRAS, 492, 39 [Google Scholar]
- Steinberg, J. T., Lazarus, A. J., Ogilvie, K. W., Lepping, R., & Byrnes, J. 1996, Geophys. Res. Lett., 23, 1183 [Google Scholar]
- Telloni, D., & Bruno, R. 2016, MNRAS, 463, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Tracy, P. J., Kasper, J. C., Zurbuchen, T. H., et al. 2015, ApJ, 812, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Tu, C. Y., & Marsch, E. 2002, J. Geophys. Res., 107, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Tu, C. Y., Marsch, E., & Qin, Z. R. 2004, J. Geophys. Res., 109, A05101 [NASA ADS] [Google Scholar]
- Valentini, F., Servidio, S., Perrone, D., et al. 2014, Phys. Plasmas, 21, 082307 [NASA ADS] [CrossRef] [Google Scholar]
- Valentini, F., Perrone, D., Stabile, S., et al. 2016, New J. Phys., 18, 125001 [NASA ADS] [CrossRef] [Google Scholar]
- Vargha, A., B. L. R.-T. 2016, J. Person-Oriented Res., 2, 78 [CrossRef] [Google Scholar]
- Vech, D., Stevens, M. L., Paulson, K. W., et al. 2021, A&A, 650, A198 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, X., & Xu, Y. 2019, IOP Conf. Ser. Mater. Sci. Eng., 569, 052024 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, Lynn B. I., Stevens, M. L., Kasper, J. C., et al. 2018, ApJS, 236, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Wit, E., Van den Heuvel, E., & Romeijn, J.-W. 2012, Am. J. Bot., 66 [Google Scholar]
- Xie, X. L., & Beni, G. 1991, IEEE Trans. Pattern Anal. Mach. Intell., 13, 841 [CrossRef] [Google Scholar]
- Zouganelis, I., De Groof, A., Walsh, A. P., et al. 2020, A&A, 642, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Values of density, velocity, parallel and perpendicular temperature used in the simulations.
All Figures
 |
Fig. 1 Difference between densities computed after the separation and ground truth for core and beam for 2000 synthetic VDFs as a function of the absolute value of input separation between core and beam (top). Error in density for alpha particles as a function of the absolute value of the velocity separation between proton beam and alpha particles (bottom). |
| In the text | |
 |
Fig. 2 Distribution of the relative density error in core and beam for 2000 synthetic VDFs. |
| In the text | |
 |
Fig. 3 Error in the bulk velocity of core and beam for 2000 synthetic VDFs as a function of the separation between core and beam (top). Error in the bulk velocity of alpha particles as a function of the velocity separation between proton beam and alphas (bottom). |
| In the text | |
 |
Fig. 4 Error in the bulk velocity for the beam as a function of the output ratio between beam and core density. |
| In the text | |
 |
Fig. 5 Error in temperature anisotropy for core and beam for 2000 synthetic VDFs as a function of the separation between core and beam (top). Error in temperature anisotropy for alpha particles as a function of the velocity separation between proton beam and alphas (bottom). |
| In the text | |
 |
Fig. 6 Distribution of the VDFs with unresolved proton beams as a function of the input distance between core and beam. |
| In the text | |
 |
Fig. 7 Contour lines of the ion VDF observed by PAS, in a quasi-perpendicular magnetic configuration, in the plane identified by the radial direction R and the magnetic field vector (left). Contours have been computed after integration of the VDF along the direction perpendicular to this plane. The arrow indicates the direction of the local magnetic field vector. Right panel shows the same VDF integrated in polar and azimuth angles with the three ion families highlighted in different colors. |
| In the text | |
 |
Fig. 8 Ion families identified in the distribution function represented in Fig. 7. Panel a: contour lines for the core distribution in the plane identified by the radial direction, R, and the magnetic field vector. Contours have been computed after integration of the VDF along the direction perpendicular to this plane. Panels b and c refer to the proton beam and alpha populations, respectively. Solid straight line in each panel show the direction of the local magnetic field vector. The contribution from the s/c velocity has not been removed. |
| In the text | |
 |
Fig. 9 Overview of the solar wind sample detected by the PAS sensor on board Solar Orbiter from July 14:09:11 to July 16:18:42 (DoY 196-198) 2020. Panels from top to bottom refer to the time series of: (a) proton core number density, Ncore; (b) core speed, Vcore; (c) core total temperature, Tcore; (d) beam number density, Nbeam; (e) beam speed Vbeam; (f) beam total temperature, Tbeam; (g) alpha particle number density, Nalpha; (h) alpha particle speed Valpha; (i) alpha particle total temperature, Talpha. The units are: cm−3 for density, km s−1 for velocity and eV for temperature. In panels a, b, and c, the red solid lines refer to the proton time series of N, V and T from the SOAR. See text for details. |
| In the text | |
 |
Fig. 10 Histograms of the relevant parameters of proton beam and alpha particles. The three panels from top to bottom show: (a) the distributions of proton beam and alphas number density normalized to the proton core number density Ncore; (b) the distributions of proton beam and alphas total temperature normalized to the proton core total temperature Tcore; (c) the distributions of proton beam and alphas velocity drift along the local magnetic field direction normalized to the local Alfvén speed (VD cos θD)/VA. Beam distributions are indicated by a solid line, alpha distributions by a dashed line. |
| In the text | |
 |
Fig. 11 Histograms of the angle between beam drift-velocity and local magnetic field (solid line) and the angle between alphas drift-velocity and the same magnetic field vector (dashed line). Mean and standard deviation values are indicated for each histogram. |
| In the text | |
 |
Fig. 12 Beam velocity drift, normalized to the local Alfvén speed |
| In the text | |
 |
Fig. 13 Histograms of the temperature anisostropies and instability plane. Left panel: normalized histograms of temperature anisotropy, defined as T⊥/T‖, for proton core (red line), proton beam (blue line), and alphas (green line). Right panel: temperature anisotropy vs. β‖, commonly known as instability plane for core (red), beam (blue), and alphas (green). Different solid lines indicate plasma instabilities: proton cyclotron and mirror for T⊥/T‖ > 1 and oblique firehose and parallel firehose for T⊥/T‖ < 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.