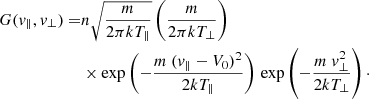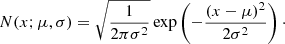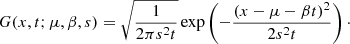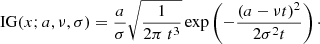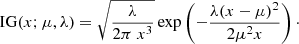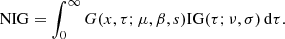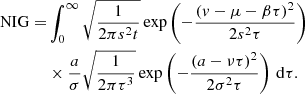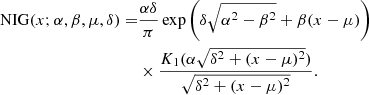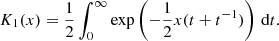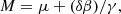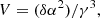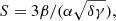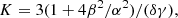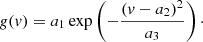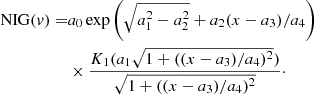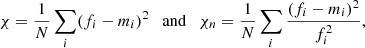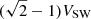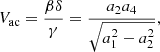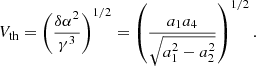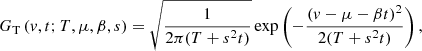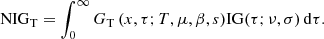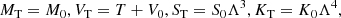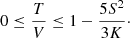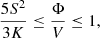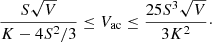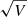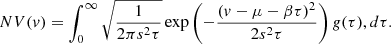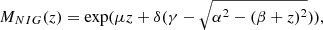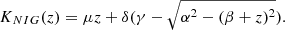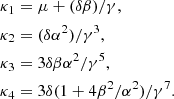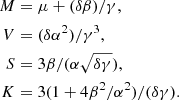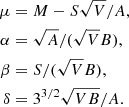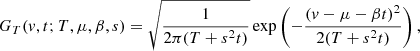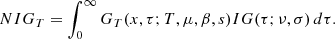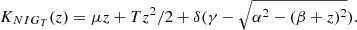| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 14 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202347874 | |
| Published online | 31 January 2024 | |
Skewness and kurtosis of solar wind proton distribution functions: The normal inverse-Gaussian model and its implications
1
Institut de Recherche en Astrophysique et Planétologie, CNRS, Université de Toulouse, CNES, Toulouse, France
e-mail: philippe.louarn@irap.omp.eu
2
Department of Surface and Plasma Science, Faculty of Mathematics and Physics, Charles University, 18000 Prague 8, Czech Republic
3
Mullard Space Science Laboratory, University College London, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
4
INAF – Istituto di Astrofisica e Planetologia Spaziali, Via Fosso del Cavaliere 100, 00133 Roma, Italy
5
Southwest Research Institute, 6220 Culebra Road, San Antonio, TX 78238, USA
6
AKA-Toulouse, Toulouse, France
7
Laboratoire de Physique des Plasmas, École Polytechnique, Palaiseau, France
8
Department of Climate and Space Sciences and Engineering, The University of Michigan, Ann Harbour, MI, USA
9
Leonardo S.p.A, Viale del lavoro 101, 74123 Taranto, Italy
10
Space and Atmospheric Physics, The Blackett Laboratory, Imperial College London, London SW7 2AZ, UK
11
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, 5 Place Jules Janssen, 92195 Meudon, France
12
Space Sciences Laboratory, University of California, Berkeley, CA 94720, USA
13
Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS, Pessac, France
14
Space Science Center, University of New Hampshire, 8 College Road, Durham, NH 03824, USA
Received:
4
September
2023
Accepted:
2
November
2023
Context. In the solar wind (SW), the particle distribution functions are generally not Gaussian. They present nonthermal features that are related to underlying acceleration and heating processes. These processes are critical in the overall dynamics of this expanding astrophysical fluid.
Aims. The Proton Alpha Sensor (PAS) on board Solar Orbiter commonly observes skewed proton distributions, with a more populated high-energy side in the magnetic field direction than the Gaussian distribution. Our objectives are: (1) to identify a theoretical statistical function that adequately models the observed distributions and (2) to use its statistical interpretation to constrain the acceleration and heating processes.
Methods. We analyzed the 3D velocity distribution functions (VDFs) measured by PAS and compared them to model statistical functions.
Results. We show that the normal inverse Gaussian (NIG), a type of hyperbolic statistical distribution, provides excellent fits of skewed and leptokurtic proton distributions. NIG can model both the core distribution and the beam, if present. We propose an interpretation that is inspired by the mathematical formulation of the NIG. It assumes that the acceleration or heating mechanism can be modeled as a drifting diffusion process in velocity space, controlled (or subordinated) by the time of interaction of the particles with “accelerating structures”. The probability function of the interaction time is an inverse Gaussian (IG), obtained by considering a random drift across structures of a given size. The control of the diffusion by interaction times that follow an IG probability function formally defines the NIG distribution. Following this model, we show that skewness and kurtosis can be used to estimate the kinetic and thermal energy gains provided by the interaction with structures. For example, in the case studies presented here, the analyzed populations would have gained kinetic energy representing approximately two to four times their thermal energy, with an increase in velocity – due to acceleration – of from one-tenth to one-third of the observed flow velocity. We also show that the model constrains the initial temperature of the populations.
Conclusions. Overall, the NIG model offers excellent fits of the observed proton distributions. Combining the skewness and the kurtosis, it also leads to constraints in the part of acceleration and heating due to the interactions with structures in the formation of the proton populations. We suggest that these effects add to the classical thermal evolution of the bulk velocity and temperature resulting from SW expansion.
Key words: plasmas / solar wind
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The solar wind is an almost collisionless plasma in which the velocity distribution functions (VDFs) of the different species can differ significantly from the thermodynamic equilibrium functions. Thanks to direct in situ measurements, in particular those of the Helios probes, the deviations from isotropic Maxwellian distributions are well documented (see Marsch 2006, for a review). In particular, concerning the protons, the distributions generally show a temperature anisotropy, with T⊥ > T∥, where the subscripts refer to the magnetic field direction. The distributions are also frequently the juxtaposition of a core and a beam population, with relative drifts along the magnetic field (B) at about the Alfvénic velocity (VA; Marsch et al. 1981, 1982).
Observations of these nonthermal features have inspired numerous theoretical and numerical works designed to improve our understanding of the associated kinetic processes and instabilities, as well as their role in the heating and acceleration of particles, their links with turbulence, and their effects on the general dynamics of the solar wind (see Tu & Marsch 1995; Marsch 2006; Bruno & Carbone 2013; Viall & Borovsky 2020; Verscharen et al. 2019; Matteini et al. 2012).
To a certain extent, Gaussian functions are sufficient to fit some of the observed nonthermal features in the proton (and more heavy ions) populations. When the fits are applied separately in the parallel and perpendicular directions, this leads to the classical bi-Maxwellian description. The anisotropy is then described by the T⊥/T∥ ratio. Similarly, the beam – if present – can be simply described by the juxtaposition of a second bi-Maxwellian population. Useful determinations of the fluid parameters (density, velocity and temperature) of the different proton populations can then be derived, which allow relatively straightforward comparisons with well-established instability theories. Classic examples concern beam-plasma instabilities and the perpendicular heating at the cyclotron resonance (Marsch et al. 2004; Hollweg & Isenberg 2002; Cranmer 2000) as well as the comparison between the histograms of the observed proton distribution anisotropy and the parametric thresholds of the firehose, mirror, and cyclotron instabilities (Gary et al. 1997; Kasper et al. 2002; Hellinger et al. 2006). Recently, De Marco et al. (2023) proposed an alternative approach based on the statistical technique of clustering, which is a standard tool in many data-driven and machine learning applications. This innovative technique is directly applied to the 3D VDF – which is considered as a linear combination of Gaussian distributions – in order to localize the different populations, such as core and beam for both protons and alphas.
Nonetheless, despite the efficiency of Gaussian fits in the analysis of many kinetic processes, it is clear that important nonthermal features cannot be investigated using bi-Maxwellian descriptions. A well-known example concerns the supra-thermal tails. These are best modeled by a Kappa distribution (Vasyliunas 1968), a form of generalized Lorentzian characterized by a quasi-Gaussian core and a power-law tail (Livadiotis & McComas 2009; Whang 1971; Cuperman et al. 1983; Demars & Schunk 1990; Maksimovic et al. 1997; Pierrard & Lazar 2010).
As developed in the present paper, the observations performed by the Proton Alpha Sensor (PAS) on board Solar Orbiter highlight another form of deformation that cannot be described by a Gaussian (or Kappa) function: an asymmetry or skewness in the “thermal” domain. We use the term thermal to designate a domain extending over a few times the thermal velocity below and above the mean velocity of the considered population (the core or the beam). Examples are given in Louarn et al. (2021). Systematically, it is observed that the profiles of the beam along the parallel to B direction have a much steeper “low energy” side than “high energy” side. The more populated energetic side is also a sign of positive excess kurtosis (leptokurtic distributions). As developed here, these first observations can be confirmed by PAS measurements made in various solar wind situations. The skewness is therefore more of the norm than the exception; it is almost systematic for the beam, and is also observed for the core but often to a lesser degree.
In Louarn et al. (2021), the asymmetry and the “heavy tail” are described by fitting with (half) a Gaussian and (half) a Kappa to the low and high energy part of the distribution, respectively. Our goal is to go beyond this ad hoc method and to investigate whether classical statistical functions can be used to describe skewed and leptokurtic proton populations. We also aim to obtain new insights into the underlying acceleration and heating processes. In particular, we show that the normal inverse Gaussian (NIG) functions offer (1) remarkable models of the observed distributions and (2) an interesting “toy” model of acceleration or heating processes.
In Sect. 2, we provide a simple explanation of how the NIG is constructed using the concept of statistical mixture and why this may lead to an interesting new tool to model the SW proton distributions. Section 3 describes the data and methods. Section 4 details examples of skewed functions and their fits in different types of solar wind. In Sect. 5, we discuss possible implications and applications of the modeling of heating and acceleration processes, before providing our conclusions in Sect. 6.
2. The normal-inverse Gaussian
For completeness, we first reiterate the formula of the classical bi-Maxwellian distributions (written in the convection frame, such as V⊥0 = 0):
On this basis, our reference statistical model is therefore the Gaussian (or normal) distribution:
Below, we use this to establish “reference” fits of the f(v∥) profiles, with the core and the beam fitted separately if necessary. The performances of the reference fits are then compared with those relying on more specific skewed distributions.
Among the various possibilities of skewed distributions, we choose the NIG distribution (Barndorff-Nielsen 1997) which is now widely applied in various fields, such as financial modeling, turbulence, biology, medical, and technical applications. It shows interesting mathematical properties for statistical applications (Barndorff-Nielsen & Shepard 2001) and is also well adapted to modeling semi-heavy distributions. In the following, we propose a step-by-step derivation of the NIG that highlights why it may have interesting applications in space plasma physics.
As formalized by Barndorff-Nielsen (1997), the NIG distribution is defined as a variance-mean mixture of a normal distribution with the inverse Gaussian as the mixing distribution. This process can be described as the subordination of a Brownian motion by an inverse Gaussian process. Let us explicitly apply this definition to construct a NIG distribution. A more technical approach is proposed in Appendix A, where some properties of the variance–mean mixtures and the NIG function are given.
The first step is to consider a Brownian drifting process. Let us assume that it is defined with drift β, initial position μ, and diffusion coefficient s. Initially (t = 0), the distribution is a Dirac located at μ. At time t, the distribution is then the drifting normal distribution:
Applied in the velocity domain, this drifting diffusion can be considered as a particularly simple model of combined acceleration and heating. For example, it may describe how a Gaussian distribution evolves through energy exchanges between particles and a turbulent field. The term βt is related to a time variation of the mean velocity and therefore to an acceleration, when s2t describes an increase in temperature with time. In the following, we designate the distribution corresponding to t = 0 as the “initial distribution”.
To build the NIG, one has to take into account a second (and independent) drifting Brownian process (drift ν, initial position 0, and variance σ2) and consider the distribution of the time a particle takes to reach a fixed position a. This is the classical “first passage time” problem for drifting Brownian motions and defines the inverse Gaussian (IG) distribution (or Wald distribution). The first passage time distribution is given by:
Its mathematical normalized form is
A review of the mathematical properties and applications of the IG can be found in Folks & Chhikara (1978). Inverse Gaussian is a skewed distribution defined for x > 0; it has a semi-heavy asymptotic tail that behaves as ∼t−3/2exp(−αx).
For the present application, the IG can model the distribution of the “interaction” times between a particle and a “structure” of a given size, in a situation of drifting Brownian relative motion. Indeed, consider a particle that enters a structure of size a. If their relative motion is modeled as a drifting Brownian process (with ν as the drift and σ the diffusion coefficient), the distribution of first passage time at a (and therefore the distribution of interaction times) is precisely described by Eq. (4). Here, we use the term “structure” to refer to a defined region of space in which the particles exchange energy with electromagnetic fields, either in an organized way (acceleration) or randomly (heating).
The final step of the NIG construction is to mix the Gaussian and the IG processes. The mixture is defined as:
It is also said that the first drifting Brownian process has been “subordinated” by the IG process. This can be interpreted as a form of averaging of the acceleration or heating mechanism by the probability of the interaction time between the particles and the “accelerating or heating” structure (or, in other words, the probability of residence time in the region where fields and particles exchange energy and momentum). In the following, this model is referred as the “NIG process”.
Considering the velocity (v) as the variable, the formula used to calculate the NIG is
This integral can be expressed in a closed form, which leads to the formula of the NIG. Its normalized expression is (Barndorff-Nielsen 1997)
To obtain this formula, we take advantage of the fact that the modified Bessel function of the third kind and index 1 (K1) verifies
The correspondence between (7) and (8) is obtained by substituting (x, α, β, μ, δ) in (8) with  or, for a physical non-normalized form, with
or, for a physical non-normalized form, with  . It is important to note that the diffusion coefficients (s and σ) are normalization factors of the other parameters; they are introduced for the physical coherency of the model but one can put s = 1 and σ = 1 without changing the mean, variance, skewness, or kurtosis.
. It is important to note that the diffusion coefficients (s and σ) are normalization factors of the other parameters; they are introduced for the physical coherency of the model but one can put s = 1 and σ = 1 without changing the mean, variance, skewness, or kurtosis.
The NIG presents similarities to the IG. In particular, it has asymptotically semi-heavy tails that behave as ∼|x|−3/2exp(βx − α|x|), and are therefore lighter than power laws and Kappa distributions but heavier than Gaussians. These asymmetric asymptotes, linear in logarithm scale, characterize the so-called “hyperbolic” statistical distributions. Contrary to IG, they are defined for positive and negative x. Elsewhere, for α → ∞ and β → 0, the NIG tends to the normal distribution. The four parameters are interpreted in the following way. Here, α controls the steepness of the distribution; larger values of α imply lighter tails. β is the skewness parameter; in particular, for β = 0, the distribution is symmetric. μ is the position parameters, and is also the mean of the initial distribution. δ is the scale parameter.
As detailed in Appendix A, the mean, variance, skewness, and excess kurtosis of the NIG are respectively
with 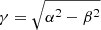 .
.
Inversely, the parameters (α, β, μ, δ) are uniquely determined from the mean, variance, skewness, and kurtosis provided that the condition K − (5/3)S2 ≥ 0 is fulfilled. This condition comes from the fact that the quantity 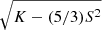 is required in the derivation of α, β, and δ (see Appendix A for details). As discussed below, this condition is important for estimation of the acceleration and heating.
is required in the derivation of α, β, and δ (see Appendix A for details). As discussed below, this condition is important for estimation of the acceleration and heating.
Figure 1 displays different model distributions, both in linear and logarithm scales. In the leftmost panel, the Gaussian (red) and Kappa (orange) are compared to NIG (black) functions. To ease the visual comparison, we use parameters that lead to relatively close maxima and dispersion of the different distributions. The key features are clearly the symmetry of the Gaussian and Kappa, the skewness of the NIG, and the differences in the asymptotic behaviors of the different families. We note, in particular, the linear asymptotic variation of log(NIG), which is a property of hyperbolic distributions. The NIG functions (as the IG, not shown here) are semi-heavy distributions in between the light-tailed Gaussian and the heavy-tailed Kappa. We also illustrate how the parameters influence the shape of the NIG. Relatively modest (less than 20%) variations of α imply significant changes (> 2) in the slope of the asymptotic tails. We also note the key role of β in the control of the skewness. In practice, the fit of the observed distributions gives values of α between 2 and 12 and slightly (10%) smaller β. The observed skewness varies from less that 0.1 (symmetric) to 1.5 (strongly skewed population).
 |
Fig. 1. Examples of model distributions. Upper panels: Linear scale. Lower panels: Logarithmic scale. From left to right columns: (1) Gaussian (red), Kappa (orange), and NIG (black) distributions. (2) NIG: Variations of α (tail heaviness) with (β, δ) = (2., 1.). (3) NIG: Variations of β (skewness) with (α, δ) = (2.5, 1.). (4) NIG: Variation of δ (dispersion) with (α, β) = (2.5, 2.). The black, blue, and red curves correspond to increasing values of the parameter. |
A fundamental point of the NIG model is to relate the skewness (linked to β) to a drift in velocity space and therefore, physically, to an acceleration. Without acceleration (β = 0), the distribution remains symmetric. The observation of skewed distributions therefore indicates than an acceleration process operates somewhere between the low corona and the point of observation. The formation of skewed distributions can also be interpreted as an increase in the heat density flux. Simultaneously, the NIG process heats the population and increases the density in its high-energy side, which leads to an increase in both the variance and kurtosis.
3. Data and fitting method
General presentations of the Solar Orbiter mission and its Solar Wind Analyzer (SWA) can be found in Müller et al. (2020) and Owen et al. (2020). We use the 3D VDF measured by the Proton Alfa Sensor (PAS) and, for the projections, the magnetic field measured by MAG (Horbury et al. 2020).
The 2D slice – f(v∥, v⊥) – and the 1D profiles – f(v∥) – are obtained by projecting the original 3D VDF (L2 product of PAS/SWA, given in RTN frame, available at ESA Solar Orbiter archive or at CDPP/CNES/IRAP) onto the magnetic frame (V∥, V⊥, 1, V⊥, 2). This frame is defined with the axes centered on the solar wind velocity (VSW), V⊥, 1 in the (B, VSW) plane and V⊥, 2 perpendicular to it. We use the vector B measured at the central time of the VDF sampling. f(v∥, v⊥) is the average of the VDF over a slice of ±30 km s−1 in thickness from the (V∥, V1⊥) plane. Similarly, f(v∥) is the average of this 2D slice over ±30 km s−1 from the v∥ axis. The f(v∥) profile is thus the average of the 3D VDF over [−30 km s−1, +30 km s−1]2 from the v∥ axis. We do not discuss the f(v⊥) profiles here, which are assumed to be Gaussian or at least symmetric.
PAS measures 3D VDF with an energy resolution of δE/E ∼ 8 − 10% and a 6° ×6° angular resolution. The size of the pixels in the velocity phase space therefore changes with the measured energy. For solar wind speed (VSW)∼400 − 500 km s−1 – which is the case for most of the examples considered here – PAS samples the interesting part of the phase space, where most of the protons are, with pixel sizes of ∼12, 50, and 50 km s−1 in the R, T, and N directions, respectively (Solar Orbiter points to the Sun, meaning that the x axis of PAS is along the R direction). The best resolution of f(v∥) is obtained in situations of quasi-radial magnetic field (resolution of ∼12 km s−1). As f(v∥) typically spans over 150−200 km s−1, the profile is then determined at approximately 20 successive velocity steps. Moreover, as the thickness of the slice is wider than PAS pixels (in azimuth and elevation), f(v∥) is constructed at each velocity by at least two measurements made at adjacent angles. Thus, on a velocity domain of 150−200 km s−1, f(v∥) is constructed from at least 30 to 40 independent measurements. We use a procedure that linearly interpolates the measurements on a thinner velocity grid (1.3 km s−1 resolution). This does not change the moment of the distribution, in particular the variance, skewness, and kurtosis.
It is also important to note that the time resolution of PAS offers unprecedented capabilities to study detailed structures in the VDF. Indeed, the core of the distribution is typically measured in 0.25 s (PAS samples 1 energy in 1 ms). PAS then gets “instantaneous” pictures of the VDF that are immune to possible smearing effects due to fluctuations (at least up to frequencies of ∼4 Hz). This may be the reason why PAS so often measured non-Gaussian distributions compared to past instruments.
The maximum value of the VDF presented in this article corresponds to ∼2−300 counts/pixel and the whole VDF is determined with typically 2000−3000 counts. The total dynamics between Max(f(v∥)) and the one count level is therefore of a few hundred counts. This is sufficient to analyze the general structure of the central part of the distribution – that is, up to 3−4σ from the maximum – and to study the variance, skewness, and kurtosis of the thermal part of the proton populations. The “far” high-energy tail behavior of the distribution is not the focus of the present article. As shown below, the statistics can also be increased by summing several successive samplings.
The Gaussian fit involves three parameters:
The NIG fit involves five parameters:
The NIG parameters (α, β, μ, δ) are then given by (a1/a4, a2/a4, a3, a4).
To perform the fits, we exclude the domain of velocity where the alphas significantly contribute to the counts. As PAS measures the alphas at about twice the energy of the SW protons, this is simply done by considering the part of the distribution where 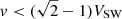 (in SW frame). Different domains of fit are also defined depending on the studied population. The core distribution is fitted in a limited domain centered on the peak of the distribution (generally a domain of 60−100 km s−1). The secondary population – a beam or a shoulder if present – is then defined by the difference between the measured distribution and the core fit.
(in SW frame). Different domains of fit are also defined depending on the studied population. The core distribution is fitted in a limited domain centered on the peak of the distribution (generally a domain of 60−100 km s−1). The secondary population – a beam or a shoulder if present – is then defined by the difference between the measured distribution and the core fit.
The fits are perform using gradient-expansion algorithms, such as those proposed by classical software widely used in the community. Formula (8) might appear a little complex, but in practice the NIG is easy to insert into the algorithms. We verified that the results do not change with (moderate) modifications to the initialization values. The quality of the fits is evaluated from the variance between the distribution and the fit (the classical χ goodness-of-fit between the distribution f and the model m). We also considered the variance of the normalized difference between the distribution and the fit (χn):
where the sum is performed over a specified domain of N points. χ is dominated by the large values of the function when χn gives an equal weight to all points. χn is therefore more adapted to controlling the quality of the fit in the tails of the distribution. To obtain a more intuitive interpretation of the fit quality, we also computed the average value of the normalized difference (Δ = ⟨|f − m|/f⟩).
The mean, variance, skewness, and (excess) kurtosis of the distributions were computed using the classical formula: if E is the expectation operator, M = E[v], V = E[(v − M)2], S = E[(v − M)3]/V3/2, K = E[(v − M)4]/V2. The link between this and the classical plasma parameters is straightforward: M is the flow velocity and V is related to the pressure by P = nmpV, where n and mp are respectively the density and the proton mass, meaning that the kinetic temperature is T = mpV/kB, where kB is the Boltzmann constant. Finally, the skewness is related to the heat flux density: Q = (1/2)mpnSV3/2. Let us emphasize that the f(v∥) profile is considered here so that these quantities are projected along the B direction.
4. Application to PAS observations
4.1. Skewed distributions in a quiet solar wind
We first consider an example of relatively quiet solar wind, with a quasi-perfect radial magnetic field for several hours. Observations were performed on March 19, 2022 when Solar Orbiter was at 0.37 au from the Sun (Fig. 2). VSW is almost constant for the whole time period: ∼420 km s−1. From 10:00 to 14:00, the density (N) increases from ∼20 to 28 cm−3. The temperature shows a relatively sharp increase around 11:00, from T ∼ 15 to 30 eV. B remains almost radial for the whole time period (BR ∼ 30 nT). The level of fluctuation is low, with V, B, and N fluctuating by less than 5% from 10:00 to 14:00. Interestingly, this low level of activity is not reflected in the energy spectrogram, which shows significant variation. From 8:00 to 10:30, the core population is observed from 0.7 to 1.1 keV and the pressure is isotropic. Later, from 10:30 to 11:30, the population spreads in energy, up to 2 keV, which also corresponds to the temperature increase. Simultaneously, P∥ increases by a factor 2 when P⊥ remains constant. This anisotropic but quiet solar wind is observed until 14:00, when a more turbulent time period starts, with B perturbations reaching 50% of the total field. Louarn et al. (2021) show that P∥/P⊥ > 1 could indicate that a beam and a core population are superposed. As detailed below, this can also be the result of the formation of skewed distributions.
 |
Fig. 2. PAS and MAG observations (19/03/2022). From top to bottom: (a) Time/energy ion spectrogram (500 eV–4 keV, unit: s−1 cm−2 sr−1 keV−1). (b) and (c): Proton density and temperature. (d): Pressure – parallel in red, perpendicular in blue and green. (e)–(g): Magnetic and velocity field components in RTN frame. The vertical lines show the selected times. |
Figure 3 shows f(v∥) profiles measured at 12:30, 13:00, and 13:10. In each case, ten successive VDFs (thus covering 40 s) are superposed (top panels) and the averages over these ten distributions are presented below. At a given velocity, fluctuations are observed from one VDF to the next, but they remain limited in amplitude (less than 10%). Over a few tens of seconds, their shapes then remain stable, with an almost constant thermal dispersion and similar asymmetries. A secondary structure is often present – as a “shoulder” at 50−80 km s−1 from the main peak – and is also relatively stable in position. As seen in the middle and lower panels, these features are reflected in the average distributions: (1) the skewness, visible even in the immediate vicinity of the main peak, (2) the shoulder (or beam), with a drift significantly smaller than VA from the core (VA is indicated by blue vertical lines), and (3) a slight accumulation of particles where the alphas are expected to be measured, typically above 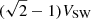 (indicated by red vertical lines) from the main peak. These features evolve from one set to the other. The core is particularly sharp at 12:30, corresponding to T∥ ∼ 6 eV; it then widens to T∥ > 10 eV, at 13:00.00 and 13:00:10, and becomes more asymmetric. Simultaneously, the beam decreases in energy and seems to merge with the core. The alphas are difficult to identify except as a small bump on the profile seen at 13:00. The skewness varies with the part of the distribution that is considered. For the peak (defined by f(v∥) > Fm/2, where Fm is the maximum of f(v∥)), the measured skewness (S) is 0.09, 0.15, and 0.14 (at 12:30, 13:00, and 13:10, respectively). For the global proton distribution (we consider f(v∥)> Fm/10), the skewness is 0.68, 0.59, and 0.82 at the same time stamps. These distributions are visually similar to the NIG presented in Fig. 1. In particular, they exhibit the typical hyperbolic shape of the NIG with an apparent triangular profile in logarithmic plots (compared with the blue and red curves in the rightmost panel; Fig. 1).
(indicated by red vertical lines) from the main peak. These features evolve from one set to the other. The core is particularly sharp at 12:30, corresponding to T∥ ∼ 6 eV; it then widens to T∥ > 10 eV, at 13:00.00 and 13:00:10, and becomes more asymmetric. Simultaneously, the beam decreases in energy and seems to merge with the core. The alphas are difficult to identify except as a small bump on the profile seen at 13:00. The skewness varies with the part of the distribution that is considered. For the peak (defined by f(v∥) > Fm/2, where Fm is the maximum of f(v∥)), the measured skewness (S) is 0.09, 0.15, and 0.14 (at 12:30, 13:00, and 13:10, respectively). For the global proton distribution (we consider f(v∥)> Fm/10), the skewness is 0.68, 0.59, and 0.82 at the same time stamps. These distributions are visually similar to the NIG presented in Fig. 1. In particular, they exhibit the typical hyperbolic shape of the NIG with an apparent triangular profile in logarithmic plots (compared with the blue and red curves in the rightmost panel; Fig. 1).
 |
Fig. 3. Skewed distributions observed at 12:30, 13:00, and 13:10 (19/03/2022) in SW frame. The top panels show the superposition of ten successive f(v∥) profiles (in s3/km6). The averages are shown below in linear and logarithmic scales. The blue lines indicate VA and the red ones |
4.2. Examples of fits
As a first example (Fig. 4), we consider the average distribution measured at 12:30 (the one in the left column, Fig. 3). f(v∥) shows a relatively sharp maximum, and therefore to describe the core, we chose a domain of fit of ±50 km s−1 centered on the peak. Both Gaussian and NIG (not shown in the figure) fits were performed, resulting in similar χ. The core can indeed be considered as symmetric (S < 0.1) and we therefore adopt the Gaussian fit (Mc, blue in the plot) because it requires fewer parameters. This Gaussian core is unable to capture the shoulder of the distribution and cannot describe the skewness. The remaining part of the distribution (the beam), which is defined as f(v∥)−Mc(v∥) and shown in orange in the plot, is therefore considered; it corresponds to ∼40% of the core. This population shows a strong asymmetry, with S ∼ 1, and is better fitted with a NIG (NigB, also in blue) than a Gaussian. The sum Mc + NigB is presented in green. This sum clearly provides an excellent model: it is generally so close to the measured distributions that it is almost merged with the measurements and is difficult to distinguish except in between the two bumps. We also performed a NIG fit of the whole distribution (NigT in red). When estimated on the “proton” domain, the ratio χ(Mc + NigB)/χ(NigT) is 0.36. The mixed (Mc + NigB) fit is therefore better than NigT and two separate populations need to be considered here.
 |
Fig. 4. Average distribution at 12:30 (same as in Fig. 3). The Gaussian fit of the core (Mc) and the NIG fit of the beam (NigB) are shown in blue. Mc + NigB, almost undiscernible from the measured distribution, is shown in green. The NIG fit of the whole distribution (NigT) is shown in red. |
An interesting point concerns the alphas. As seen in the figure, a tiny population adds to NigB in the domain where alphas should be detected, typically 80 km s−1 < v < 200 km s−1. Directly from f(v∥), this population is barely visible, but it becomes clear from the comparison with NigB. Quantitatively, this tiny population that adds to NigB corresponds to ∼5% of the total distribution (assuming the same perpendicular temperature), which is about the nominal proportion.
Other examples are presented in Figs. 5 and 6. In each case, the Gaussian and NIG are systematically applied on the different populations (core, beam, and global distribution). The quality of the fits is then estimated using χ and χn.
 |
Fig. 5. Examples of fits (19/03/2022): Gaussian (blue) and NIG (orange) fits of the core (Mc and NigC). For 13:00:04 and 08, Gaussian fit of the beam (Mb, in blue) and sum (Mc + Mb) in green, visible between the two bumps. NIG fit of the whole distribution (NigT, in red). The unit is s3/km6. |
 |
Fig. 6. Examples of fits (19/03/2022): Gaussian fit of the core (Mc) and NIG fit of beam (NigB) in blue, complete fit (Mc+ NigB) in green, NIG fit of the whole distribution (NigT) in red. |
Figure 5 shows the distributions observed around 13:00, and their fits. Compared to the previous example, they show less clear signatures of beam and present a wider core. The Gaussian fit of the core (Mc) is shown in blue. It is calculated in a domain of 100 km s−1 centered on the peak of the distribution. This Gaussian core is clearly unable to describe the skewness. As above, the remaining part of the distribution (f − Mc) is therefore considered and its Gaussian fit is performed (Mb, in blue). Their sum Mc + Mb (in green, shown for 13:00:04 and 08) joins the bumps corresponding to Mc and Mb, and models the shoulder. The beam represents about 35% of the core. For the average distribution (rightmost panel), the beam is too small for a reliable fit and Mb is not shown.
We also performed two NIG fits for each distribution. The first (NigC, in orange) is calculated on the same domain as Mc and is used to evaluate the skewness of the core. The second (NigT, in red) is performed for the whole proton domain (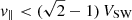 ). Not surprisingly, given the observed skewness, the NIG fits are generally better. For the core (Mc and NigC), χ and χn are estimated on the domain of the fits (100 km s−1 width, centered on the peak). For the three successive examples, the ratios of χ obtained from the Gaussian and the NIG fit (χ(Mc)/χ(NigC)) are = 3.6, 1.3, and 2.8 (in the entire article, the series of values are given in the order of the examples shown in the figure). On the same domain, the average normalized difference Δ between the distribution and NigC is: 6.5%, 7.4%, and 4.5%, which can be considered as excellent. The skewness evaluated from the fit (NigC) is also close to that measured from the distributions: respectively 0.24 and 0.19 at 13:00:04.
). Not surprisingly, given the observed skewness, the NIG fits are generally better. For the core (Mc and NigC), χ and χn are estimated on the domain of the fits (100 km s−1 width, centered on the peak). For the three successive examples, the ratios of χ obtained from the Gaussian and the NIG fit (χ(Mc)/χ(NigC)) are = 3.6, 1.3, and 2.8 (in the entire article, the series of values are given in the order of the examples shown in the figure). On the same domain, the average normalized difference Δ between the distribution and NigC is: 6.5%, 7.4%, and 4.5%, which can be considered as excellent. The skewness evaluated from the fit (NigC) is also close to that measured from the distributions: respectively 0.24 and 0.19 at 13:00:04.
The global NIG fit (NigT) is better overall, even if the sum Mc + Mb better approximates the shoulder. When estimated over the proton domain, the ratio χ(Mc + Mb)/χ(NigT) for the three successive examples is 2.3, 1.5, and 2.3. If one considers χn to better take into account the tails, the quality of the fits is even more in the favor of the NIG, with ratios χn(Mc + Mb)/χn(NigT) of 27, 6.2, and 4.7. The fit and the distribution present similar skewness, respectively, 0.59 and 0.67 (for f > Fm/10).
Again, here, the alphas appear as a tiny population above NigT in the domain 80 km s−1 < v < 200 km s−1. They correspond to 3.5% to 3.9% of the total population (assuming the same perpendicular temperature). For comparison, the fraction of alphas is ∼10% when Mc + Mb is considered, which is certainly a large overestimation. The NIG fit therefore allows us to better estimate the alphas in these particular cases. Moreover, let us note that the hyperbolic tail of (NigT) impressively joins f(v∥) beside the alpha population, at about the one count level.
This analysis shows that the global NIG fit (NigT) may better fit the whole distribution, even if Gaussian combinations (here, Mc + Mb) are able to describe specific nonthermal features, such as the shoulder. The distributions observed at 10:30, 11:25, and 14:45 show other examples of core and beam superposition (Fig. 6). In each case, ten successive VDFs are considered. The fits are performed on the average distribution, which allows us to increase the statistics. At 10:30, the core is almost symmetric (S ∼ 0.05) and is fitted with a Gaussian (Mc). The beam represents 20% of the core. Its best fit is a NIG (NigB) with a relatively strong skewness (S ∼ 0.5). The global NIG fit (NigT) appears to give a good fit but one that is less precise than Mc + NigB. The ratio χ(Mc + NigB)/χ(NigT) is 0.35 and the sum Mc + NigB is indeed an excellent fit, with K < 5%. The remaining alpha population is also visible and here represents ∼6% of the total population. The distribution at 11:25 is also best fitted by a Gaussian core and a NIG beam. The beam is just more dense in proportion (40% of the core). By contrast, the distribution at 14:45 is an example of a “pure” NIG distribution. NigT indeed gives a very good fit, with Δ ∼ 7%. S ∼ 0.26 and one can consider that there is no need to add a secondary population. One point to notice is the relatively large proportion of alphas (8%).
Overall, these various examples explain the advantage of using the NIG to describe the observed skewed populations. When present, the beam is systematically asymmetric and the superposition of a Gaussian core and a NIG beam offers the best fit. This also allows us to better identify the alpha population and estimate its proportion.
It is also interesting to note that, from 10:00 to 14:45, one observes an almost continuous transition from a dominant Gaussian core (at 10:30 and before), with T ∼ 15 eV, to a progressive apparition of a beam (11:25 and 12:30) that finally represents ∼40% of the core, which also corresponds to the increase in temperature (up to 30 eV). For all these distributions, the Mc + NigB fit is the best. Then, at 13:00 and later, the beam progressively merges with the core, which is also hotter. The beam remains visible as a shoulder in the distribution and the simple NigT offers the best fit of the global distribution. At the end of the sequence (14:45, when a more turbulent solar wind starts to be observed), the distribution is a simple skewed function excellently described by a NIG.
4.3. Case of an Alfvénic wind
We complement the analysis with examples of distributions observed in a turbulent solar wind. We consider the Alfvénic wind observed on July 14–15, 2020 and already described in Louarn et al. (2021) and D’Amicis et al. (2021). The average values of B, N, V, and temperature (T) are, respectively: B ∼ 12 nT, N ∼ 14 cm−3, V ∼ 430 km s−1, and T ∼ 22 eV. This wind is characterized by a large level of fluctuation on timescales of shorter than a minute, with excellent B, V correlations. These fluctuations typically reach 10%−20% of the mean value of N and T (∼2 cm3 ∼3 eV), and 30%−50% of B (∼5 nT).
Distributions observed in this slow Alfvénic wind are presented and discussed in Louarn et al. (2021). They almost systematically consist in the juxtaposition of a core and a beam. The core presents the classical T∥ < T⊥ anisotropy, and the beam drifts at ∼1.2 VA relative to the core. Its f(v∥) profile is asymmetric, with a high-energy tail that has been modeled by a Kappa function. We investigate how the modeling could be revisited using the NIG function.
Three examples are shown in Fig. 7. B is inclined with respect to the radial direction (by 10−20°) and the alphas only marginally contribute to the f(v∥) profile. The same fitting procedure as above is applied. Although the core is rather symmetric (S < 0.1 for f > Fm/2), it appears that the best fits are obtained with NigC for 10:48 and 19:09. As seen in the figure, the differences between NigC and Mc may appear subtle; they are nonetheless important regarding the asymptotic contribution of the core. The beam f-NigC is quite asymmetric (S > 0.3) and well fitted with a NIG. In particular, we obtain a remarkable model of the tail of the distribution, very close to a linear curve in logarithm scales. At 20:30, Mc and NigC lead to very close χ and we therefore keep the Gaussian fit. In general, these fits are excellent, with Δ smaller than 5% and even 4% at 20:30.
 |
Fig. 7. Examples of distributions and fits in an alfvénic wind (14/07/2020): The Gaussian fit of the core (Mc) is shown in light blue, the NIG fits of the core (NigC) and beam (NigB) are in blue and their sum in green. |
This analysis shows that there are situations for which the core is better fitted by a NIG, suggesting that both the core and the beam populations have been accelerated or heated by a NIG process. The general conclusion of this observational study is the excellent quality of the fits provided by the NIG model, with an average normalized difference between the fit and the measurements of less than 5%.
5. Towards constraints on acceleration and heating processes
5.1. Application of the nominal NIG model
Given the good quality of the fits provided by the NIG model, it is tempting to examine how it can be used to quantitatively estimate the acceleration and heating processes resulting from particle interactions with electromagnetic structures, in general. These effects would have to be added to the thermally driven evolution of the speed and the temperature linked to the expansion of the solar wind itself.
Both can be estimated from the NIG model in a straightforward manner. The mean of the NIG is μ + (δβ)/γ. As the Gaussian is initially located at μ, Vac = (δβ)/γ is therefore the increase in flow velocity. This quantifies the effect of the acceleration. Likewise, as the NIG model assumes that the initial population is a Dirac peak, the variance gives the gain in thermal velocity: 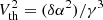 .
.
Using the coefficient of the NIG fits, one can estimate Vac and Vth, as
These estimates are given in Table 1 for the various populations analyzed in Sect. 4. The model predicts that, almost systematically, Vac is significantly larger than Vth, with Vac/Vth often above 2, meaning a ratio 4 between the kinetic and thermal energy gains. Only three cases of dominant thermal energy increases are found, corresponding to the distributions with the lowest skewness (S < 0.5). The SW speed is about 400 km s−1 for the events discussed here, which suggests that from one-tenth to one-third of the final SW speed is related to interactions that may be described according to the NIG model.
Coefficients of the fits, predicted gains in flow, and thermal velocities (Vac, Vth in km s−1).
The hypothesis of an initial null temperature is an ideal case. In the following section, we therefore examine how these predictions are changed if one considers a NIG process starting with an initial Gaussian of finite temperature.
5.2. NIG with initial finite temperature
We analyze here the case of a Gaussian of finite initial temperature T that evolves according to the same diffusive process as in Formula (3) and construct the mixture with an IG. The diffusion in velocity space is then given by:
and the mixture to calculate (NIGT) is
The moments of NIGT are obtained from the cumulant generating function (see Appendix A); they are closely related to those of the “associated” NIG (the NIG having the same α, β... as NIGT). Subscripting the moments of NIGT and those of the associated NIG as T and 0, respectively, one can indeed show that
with 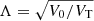 .
.
It is worth noting that the increases in the various moments resulting from the NIG process are independent of the initial temperature T. In particular, one still gets Vac = (δβ)/γ and Vth = (δα2/γ3)1/2, showing that the acceleration and heating are independent of T. We note that this is also the case for the heat flux density, which is proportional to SV3/2, according to Formula (21). To quantify the acceleration and the heating, it is therefore sufficient to estimate the parameters (α, β...) from the moments M, V, S, and K of the observed distribution.
The problem is that an additional parameter (T) has been introduced, meaning that the system is now undetermined. Nevertheless, a parametric study is possible: one can determine α, β... for a given T and examine how Vac and Vth vary with T. In practice, let us consider an observed distribution with moments M, V, S, and K. For a given T, the moments of the associated NIG are then obtained by inverting Formula (21) so that α, β... can be deduced from the formula given in Appendix A.
Interestingly, this gives a condition for T. Indeed, α, β... are defined provided that 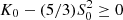 . Making the substitution with K and S, this inequality constrains the maximal value of T. It is indeed equivalent to
. Making the substitution with K and S, this inequality constrains the maximal value of T. It is indeed equivalent to
In other words, this allows us to determine whether a distribution with moments M, V, S, and K may result from a NIG process (the condition is 5K/(3S2)≤1), and if this is the case, it gives the maximal temperature of the initial Gaussian.
This condition constrains the heating (noted Φ) that may be provided by the NIG process:
and, furthermore, one can show that the gain in velocity (Vac) is such that
Using these formulae, the minimal and maximal values of Vac and Vth are given in Table 2 as the minimal gain in thermal energy (Φmin).
Gains in kinetic and thermal velocity predicted by the NIG process (Vac and Vth and minimal heating (Φmin).
It is found that Φ is generally larger than 0.8 and can reach 0.95. The model therefore predicts that the initial Gaussians have, almost systematically, a low temperature, often less than 20% of the final (and actually measured) one. The measured temperature can therefore be predominantly described as resulting from a NIG process. Let us note that the predicted gain in velocity (Vac) may vary by a factor 2, depending on the initial temperature.
The estimates and measurements are put in a more general context in Fig. 8, where Φmin and the gain in velocity are presented as a function of the kurtosis and the skewness. This plot can be interpreted in the following way: (1) For low skewness and large kurtosis (S < 0.5, K > 2), Φmin can be as low as 0.2, which means that it is possible to construct the observed distribution starting from an initial hot Gaussian, with a temperature of up to 80% of the measured one. The predicted gain in velocity (Formula (20)) is a small fraction of the thermal velocity (typically less than 50%). The observed distribution can therefore be reproduced by a NIG process that adds a modest fraction of acceleration and heating (a few tens of percent of the thermal dispersion). (2) Conversely, for large skewness and large kurtosis (S > 1, K > 2), Φmin is close to 1 and the temperature of the initial Gaussian cannot exceed a small fraction of the final one (typically less than 30%). A strong acceleration is also predicted (Formula (20)), representing several times the thermal velocity. It is interesting to note that most of the studied distributions belong to this second category; these are indicated by the red stars in Fig. 8.
 |
Fig. 8. Minimal gain in thermal energy (Φmin) normalized to the variance V, and minimal velocity gain normalized to the thermal velocity |
This analysis therefore shows that the strongly skewed distribution (S > 1) discussed in our case studies is excellently reproduced by the NIG model, but this requires consideration of initial distributions which have much lower temperatures (less than 20%) and smaller bulk velocities (by 20%−40%) than the final (and observed) values. In other words, a dominant part of the thermal energy (more than 80%) as well as of the velocity (typically, 80−200 km s−1) can be interpreted as resulting from a NIG process. This does not provide information on the precise nature of the underlying wave–particle interaction but simply tells us that it can be described as a diffusion in velocity space controlled by an interaction time that follows an IG probability distribution.
The case of the beams is interesting. The model predicts that the beams are formed from distributions with an extremely low initial temperature (VDF 3, 4, 5... with Φ > 0.95). In practice, this means that the particles that are accelerated and heated to form the beam initially occupy a very tiny fraction of the velocity space (mathematically, a Dirac peak). This is coherent with the principle of a wave–particle resonant process: only particles with specific velocities would be concerned by the acceleration or heating process.
6. Discussion and conclusion
The primary aim of this study is to better describe the skewed SW proton populations observed by PAS. We show that excellent fits of the projection of the distribution along the magnetic field (f(v∥) profiles) can be obtained using the normal-inverse Gaussian (NIG) distribution. This family of statistical functions indeed offers a versatile model for skewed distributions with a positive excess kurtosis (leptokurtic distributions). A key point is also the description of the tails of the distributions: the NIGs are hyperbolic distributions with tails that are linear in logarithm scales (semi-heavy tails). This is observed on the measured distributions and constitutes a distinct point compared to the “light tailed” Gaussian distributions or, inversely, the “heavy tailed” Kappa distributions.
The NIG fit can be applied to the whole distribution or to the core and beam parts separately. The average normalized difference between the fit and the measured profile can be less than 5%, which, in practice, leads to visually excellent fits. It can also be verified that the moments obtained from the measurements themselves and those resulting from the fits are relatively close (∼15% difference for the skewness). The beams generally present a strong skewness (S > 1) when the cores are more Gaussian.
In the second part of the present study, we applied the above theory to estimate the parts of heating and acceleration that have to be provided to obtain the observed distributions and explain their skewness and kurtosis. We first used the nominal NIG model, with an initial Dirac peak. However, to better constrain the kinetic and thermal energy gains, we developed an improved NIG model to take into account initial distributions with a finite temperature. From the observed variance, skewness, and kurtosis, we conclude that the NIG process has accelerated the population by ∼40 to 200 km s−1, which is typically between one-tenth and one-third of the observed SW velocity. The model also predicts that the strongly skewed populations that are discussed in this article, with S > 1, obtained most of their thermal energy (more than 80%) from the NIG process, starting from initially low temperature distributions.
When applied to beam populations, we suggest that the prediction of initial distributions of low temperature is coherent with wave–particle resonant processes. The initial distribution then occupies a tiny fraction of the velocity phase space, which can be modeled as a Dirac. In this case, the NIG process may provide interesting constraints on the acceleration and heating. For core or global populations, we also show that excellent NIG fits are obtained. However, the prediction of an initial low temperature is more difficult to interpret. We indeed expect that the NIG process starts from a hot Gaussian, especially if the process occurs close to the Sun. There are several possible explanations. One is that there is, in reality, no NIG process operating on global distributions: the process is systematically a wave-resonant interaction and the globally skewed distributions are formed simply as a result of the subsequent merging of the beam with the core population. The second possibility is that the NIG process may actually act on the global distribution in a high-temperature plasma close to the Sun with, therefore, low S and K produced. In this case, during the SW expansion, if S and K were to evolve so that the ratio S2/K increases, one would erroneously interpret the measured ratio. Also in this case, without knowing this evolution, ones cannot infer the initial temperature.
In a general way, the NIG model offers a generic description of combined acceleration and heating processes. It is perhaps even the simplest model that can be constructed from diffusion and random drifts, which are, physically, extremely well established and general processes. The NIG model therefore provides a simple interpretation of higher moments of the distributions than the mean and the variance, and the possibility to estimate the combined effect of acceleration and heating in the evolution of the particle populations. There are several possible developments of the present analysis. On the observational side, a statistical study is needed to confirm the generality of the NIG process in various SW conditions. It would also be interesting to analyze how S and K vary with distance to the Sun, and what can be inferred about acceleration and heating. On the modeling side, it would be useful to implement the NIG process in models of SW expansion, considering the additional heating and acceleration, as well as the production of heat density flux. Finally, the model could be applied to other environments and processes, such as auroral particle acceleration in planetary magnetospheres.
Acknowledgments
The French part of this work is supported by CNES and CNRS. IRAP acknowledges also supports from University of Toulouse/UPS. Solar Orbiter SWA work at UCL/MSSL is currently funded under STFC grants ST/X/002152/1 and ST/W001004/1. The work of L.P. is supported by the Czech Science Foundation. Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA.
References
- Barndorff-Nielsen, A. E. 1978, Scand. J. Stat., 5, 151 [Google Scholar]
- Barndorff-Nielsen, A. E. 1997, Scand. J. Stat., 24, 1 [CrossRef] [Google Scholar]
- Barndorff-Nielsen, A. E., & Shepard, N. 2001, J. R. Stat. Soc.: Ser. B, 63, 167 [CrossRef] [Google Scholar]
- Bruno, R., & Carbone, V. 2013, Liv. Rev. Sol. Phys., 10, 2 [Google Scholar]
- Cranmer, S. R. 2000, ApJ, 532, 1197 [NASA ADS] [CrossRef] [Google Scholar]
- Cuperman, S., Weiss, I., & Dryer, M. 1983, ApJ, 273, 363 [NASA ADS] [CrossRef] [Google Scholar]
- D’Amicis, R., Bruno, R., Panasenco, et al. 2021, A&A, 656, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Marco, R., Bruno, R., Jagarlamudi, V. K., et al. 2023, A&A, 669, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Demars, H. G., & Schunk, R. W. 1990, Planet. Space Sci., 38, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Folks, J. L., & Chhikara, R. S. 1978, J. R. Stat. Soc.: Ser. B, 40, 263 [Google Scholar]
- Gary, S. P., Wang, J., Winske, D., & Fuselier, S. A. 1997, J. Geophys. Res., 102, 27159 [NASA ADS] [CrossRef] [Google Scholar]
- Hellinger, P., Trávníček, P., Kasper, J. C., & Lazarus, A. J. 2006, Geophys. Res. Lett., 33, L09101 [NASA ADS] [CrossRef] [Google Scholar]
- Hollweg, J. V., & Isenberg, P. A. 2002, J. Geophys. Res.: Space Phys., 107, 1147 [NASA ADS] [Google Scholar]
- Horbury, T. S., O’Brien, H., Carrasco Blazquez, I., et al. 2020, A&A, 642, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasper, J. C., Lazarus, A. J., & Gary, S. P. 2002, Geophys. Res. Lett., 29, 1839 [Google Scholar]
- Livadiotis, G., & McComas, D. J. 2009, J. Geophys. Res.: Space Phys., 114, A11105 [NASA ADS] [CrossRef] [Google Scholar]
- Louarn, P., Fedorov, A., Prech, L., et al. 2021, A&A, 656, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maksimovic, M., Pierrard, V., & Riley, P. 1997, Geophys. Res. Lett., 24, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E. 2006, Liv. Rev. Sol. Phys., 3, 1 [Google Scholar]
- Marsch, E., Rosenbauer, H., Schwenn, R., Muehlhaeuser, K. H., & Denskat, K. U. 1981, J. Geophys. Res., 86, 9199 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Schwenn, R., Rosenbauer, H., et al. 1982, J. Geophys. Res., 87, 52 [Google Scholar]
- Marsch, E., Ao, X. Z., & Tu, C. Y. 2004, J. Geophys. Res.: Space Phys., 109, A04102 [NASA ADS] [CrossRef] [Google Scholar]
- Matteini, L., Hellinger, P., Landi, S., Travineck, P. M., & Velli, M. 2012, Space Sci. Rev., 172, 373 [CrossRef] [Google Scholar]
- Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Owen, C. J., Bruno, R., Livi, S., et al. 2020, A&A, 642, A16 [EDP Sciences] [Google Scholar]
- Pierrard, V., & Lazar, M. 2010, Sol. Phys., 267, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Rydberg, T. H. 1997, Commun. Stat. Stoch. Models, 13, 887 [CrossRef] [Google Scholar]
- Tu, C. Y., & Marsch, E. 1995, Space Sci. Rev., 73, 1 [Google Scholar]
- Vasyliunas, V. M. 1968, J. Geophys. Res., 73, 7519 [NASA ADS] [CrossRef] [Google Scholar]
- Verscharen, D., Klein, K. G., & Maruca, B. A. 2019, Liv. Rev. Sol. Phys., 16, 5 [Google Scholar]
- Viall, N. M., & Borovsky, J. E. 2020, J. Geophys. Res.: Space Phys., 125, e26005 [NASA ADS] [CrossRef] [Google Scholar]
- Whang, Y. C. 1971, J. Geophys. Res., 76, 7503 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Variance–mean mixture and normal-inverse Gaussian
This section summarizes some elementary properties of normal mean–variance mixtures and the NIG distribution. More detailed analyses can be found in Barndorff-Nielsen (1978), Barndorff-Nielsen (1997), and Rydberg (1997). The probability density function of a normal variance–mean mixture with g as the mixing probability density is given by
The associated moment-generating function can easily be obtained, for example, by the direct calculation of ∫exp(zv)NV(v)dv. It writes:
where Mg is the moment-generating function of g.
The NIG is obtained by considering that g is an inverse Gaussian. Then, by straightforward means (see Rydberg 1997), it can be shown that the moment generating function is:
with 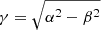 . Here, we use the definition of the NIG given by formula (8). The cumulant generating function of the NIG is therefore
. Here, we use the definition of the NIG given by formula (8). The cumulant generating function of the NIG is therefore
The successive cumulants given by 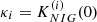 are then used to obtain the mean (M), variance (V), skewness (S), and (excess) kurtosis (K). One gets:
are then used to obtain the mean (M), variance (V), skewness (S), and (excess) kurtosis (K). One gets:
As M = κ1, V = κ2, 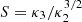 , and
, and 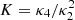 :
:
We consider the normalized (or excess) kurtosis, here.
In reverse, the parameters of the NIG can be obtained from the moments. Noting A = 3K − 4S2 and B = K − (5/3)S2, one can verify that
We note that this imposes the condition: B = K − (5/3)S2 ≥ 0.
 |
Fig. A.1. Examples of NIGT for s = 1, σ = 1, β = 1, ν = 1, a = 2, and T/V0 = 0, 0.5, 1, 1.5, 2, and 2.5 (Formula 16 and 17). Lower panel: Mean, variance, skewness, and kurtosis. |
The NIG process assumes that the Gaussian is initially a Dirac peak and therefore has a null initial temperature. It is interesting to construct a mixture from a “realistic” initial Gaussian (i.e., a Gaussian of finite temperature) that evolves according to the same diffusive process as in formula (3):
and the mixture to calculate (NIGT) is then
Examples of NIGT obtained by numerical integrations are shown in Figure 8. We use the following parameters: μ = 0, β = 2., s = 1.8, ν = 0.5, a = 0.5, and σ = 0.5. The mean, variance, skewness, and kurtosis of the associated ’ideal’ NIG (for T = 0) are respectively: 8., 29., 1.1, and 2.4. The plots correspond to NIGT obtained with increasing values of initial temperature (from blue to red: T/V = 0, 0.33, 0.66, 1, 2 and 4, where V is the variance of the ideal NIG). This shows that NIGT(v; T, α, β, μ, δ) is very similar to NIG(v; α, β, μ, δ), with the same kind of semi-heavy tails. However, we note that both the skewness and the kurtosis sharply decrease as T increases.
As for NIG, it is straightforward to get the cumulant generating function of NIGT:
Then, it can be shown that the expressions of the cumulants of NIGT are identical to those of NIG, except that κ2 now writes: κ2 = T + (δα2)/γ3. Subscripting the mean, variance, skewness, and kurtosis of NIGT and NIG with T and 0 and noting 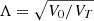 , we then obtain: MT = M0, VT = T + V0, ST = S0.Λ3, and KT = K0.Λ4. These formula are used in section 5 to estimate the gain in kinetic and thermal energy resulting from the NIG process.
, we then obtain: MT = M0, VT = T + V0, ST = S0.Λ3, and KT = K0.Λ4. These formula are used in section 5 to estimate the gain in kinetic and thermal energy resulting from the NIG process.
All Tables
Coefficients of the fits, predicted gains in flow, and thermal velocities (Vac, Vth in km s−1).
Gains in kinetic and thermal velocity predicted by the NIG process (Vac and Vth and minimal heating (Φmin).
All Figures
 |
Fig. 1. Examples of model distributions. Upper panels: Linear scale. Lower panels: Logarithmic scale. From left to right columns: (1) Gaussian (red), Kappa (orange), and NIG (black) distributions. (2) NIG: Variations of α (tail heaviness) with (β, δ) = (2., 1.). (3) NIG: Variations of β (skewness) with (α, δ) = (2.5, 1.). (4) NIG: Variation of δ (dispersion) with (α, β) = (2.5, 2.). The black, blue, and red curves correspond to increasing values of the parameter. |
| In the text | |
 |
Fig. 2. PAS and MAG observations (19/03/2022). From top to bottom: (a) Time/energy ion spectrogram (500 eV–4 keV, unit: s−1 cm−2 sr−1 keV−1). (b) and (c): Proton density and temperature. (d): Pressure – parallel in red, perpendicular in blue and green. (e)–(g): Magnetic and velocity field components in RTN frame. The vertical lines show the selected times. |
| In the text | |
 |
Fig. 3. Skewed distributions observed at 12:30, 13:00, and 13:10 (19/03/2022) in SW frame. The top panels show the superposition of ten successive f(v∥) profiles (in s3/km6). The averages are shown below in linear and logarithmic scales. The blue lines indicate VA and the red ones |
| In the text | |
 |
Fig. 4. Average distribution at 12:30 (same as in Fig. 3). The Gaussian fit of the core (Mc) and the NIG fit of the beam (NigB) are shown in blue. Mc + NigB, almost undiscernible from the measured distribution, is shown in green. The NIG fit of the whole distribution (NigT) is shown in red. |
| In the text | |
 |
Fig. 5. Examples of fits (19/03/2022): Gaussian (blue) and NIG (orange) fits of the core (Mc and NigC). For 13:00:04 and 08, Gaussian fit of the beam (Mb, in blue) and sum (Mc + Mb) in green, visible between the two bumps. NIG fit of the whole distribution (NigT, in red). The unit is s3/km6. |
| In the text | |
 |
Fig. 6. Examples of fits (19/03/2022): Gaussian fit of the core (Mc) and NIG fit of beam (NigB) in blue, complete fit (Mc+ NigB) in green, NIG fit of the whole distribution (NigT) in red. |
| In the text | |
 |
Fig. 7. Examples of distributions and fits in an alfvénic wind (14/07/2020): The Gaussian fit of the core (Mc) is shown in light blue, the NIG fits of the core (NigC) and beam (NigB) are in blue and their sum in green. |
| In the text | |
 |
Fig. 8. Minimal gain in thermal energy (Φmin) normalized to the variance V, and minimal velocity gain normalized to the thermal velocity |
| In the text | |
 |
Fig. A.1. Examples of NIGT for s = 1, σ = 1, β = 1, ν = 1, a = 2, and T/V0 = 0, 0.5, 1, 1.5, 2, and 2.5 (Formula 16 and 17). Lower panel: Mean, variance, skewness, and kurtosis. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.