| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202346202 | |
| Published online | 27 April 2023 | |
Letter to the Editor
Direct observation of solar wind proton heating from in situ plasma measurements
1
Space Sciences Laboratory, University of California, Berkeley, CA, USA
e-mail: forrest.mozer@gmail.com
2
University of Michigan, Ann Arbor, MI 48103, USA
Received:
21
February
2023
Accepted:
9
April
2023
Aims. We determine the perpendicular and parallel proton heating rate in the solar wind, which is one of the primary goals of the Parker Solar Probe mission.
Methods. To estimate the perpendicular and parallel proton heating rates from direct particle measurements by the SPAN electrostatic analyzers, the strong correlation between the proton temperature and the solar wind speed must be removed. This speed dependence is removed by normalization factors that convert the instantaneous temperature to the value it would have if the solar wind speed were 400 km s−1. One-hour and five-hour averages of the normalized perpendicular and parallel temperatures, measured on orbits 6–9, between 20 and 160 solar radii, are compared to the radial dependence they would have if there were no heating.
Results. For the first time, perpendicular proton heating has been measured between 20 and 160 solar radii while there is neither heating nor cooling of the parallel protons below 70 solar radii. The extrapolated proton perpendicular temperature at one AU in a 400 km s−1 solar wind is 25 eV, which compares well with several earlier measurements. This result attests to the quality of the temperature measurements made by the particle detectors on the Parker Solar Probe. The heating rates, in ergs cm−3 s−1, that produced the observed perpendicular temperature are 6e−12 at 20 solar radii, 1e−13 at 50 solar radii, and 5e−14 at 160 solar radii.
Key words: Sun: fundamental parameters / Sun: heliosphere / solar wind
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
NASA1 stated that “the primary science goals for the Parker Solar Probe mission are to trace how energy and heat move through the solar corona...” A first step toward this understanding is determining the proton heating rate as a function of solar distance. In this Letter, we present the first direct observation of this heating rate near the Sun from measurements of proton distributions on the Parker Solar Probe.
Estimates of this heating rate, based on models of the heating mechanism, have been developed (Bandyopadhyay et al. 2020; Chandran et al. 2009; Cranmer 2020; Hellinger et al. 2013; Hewish & Wyndham 1963; Ingale et al. 2015; Janardhan et al. 2011; Manoharan et al. 2000; Sasikumar Raja et al. 2016, 2019; Vech et al. 2017; Raja et al. 2017). These estimates vary over a huge range (see Table 1 of Raja et al. 2021).
Direct measurements of the proton heating rate using Helios data and modeled parameters (Hellinger et al. 2011, 2013) produced a proton parallel cooling close to the Sun that progressively changed into heating farther away from it. Marsch et al. (1983), using a similar data set, observed the proton evolution to be essentially adiabatic in the parallel direction. Zaslavsky (2023), using the same Helios data set, concluded that there is no parallel heating or cooling between about 65 solar radii and 1 AU. Using an analysis technique similar to that of Zaslavsky, the Parker Solar Probe proton measurements on orbits 6, 7, 8, and 9 are used to determine the parallel and perpendicular proton heating from 20 to 150 solar radii.
Plasma measurements on the Parker Solar Probe are impacted by the necessity for keeping the instruments cool near the Sun. The electrostatic analyzers of the SPAN instrument (Livi et al. 2022) are behind a heat shield that sometimes blocks part of the instrument field of view, so they sometimes produce only part of the full distribution function. Through observation of the temperature measurements described in this Letter, it is found that there is little or no suggestion of temperature measurement problems in this data.
2. Normalization factor
An issue with determining the proton heating arises from the strong correlation between the proton temperature and the solar wind speed (Burlaga & Ogilvie 1970; Hundhausen et al. 1970; Elliott et al. 2012; Case & Kasper 2014; Perrone et al. 2019a,b; Shi et al. 2020), which dominates the heating and must be removed before the in situ heating can be estimated (Mozer et al. 2022). The reason for this wind speed-temperature correlation is not understood and it is not the subject of this Letter. Instead, this Letter describes a method for removing the wind speed effect from the proton temperature measurement to thereby obtain information on the proton heating rate.
This issue is discussed in Fig. 1, which illustrates data from the Parker Solar Probe orbit 10 perihelion pass. Panels c and d give the measured perpendicular and parallel proton temperatures, which strongly correlate with the solar wind speed of panel b. This correlation is so strong that there is a major difference between the temperatures measured during the incoming and outgoing legs of the orbit, which completely shields the expected decrease with the radius on each leg.
 |
Fig. 1. Perpendicular (panel c) and parallel (panel d) proton temperatures measured from 15 to 100 solar radii (panel a) during Parker Solar Probe orbit 10. The solar wind speed (panel b) strongly correlates with the temperatures to the extent that the temperatures are asymmetric about perihelion. In panels e and f, a normalization factor has been applied to the temperatures to convert them from those measured at the local speed to those that would have been measured if the wind speed had been 400 km s−1. This normalization makes the resulting temperatures maximum near perihelion and they decrease with radial distance in a manner consistent with adiabatic cooling. |
A method has been developed to normalize the temperature measurement made at wind speed, Vsw, to the temperature that would exist if the wind speed had been 400 km s−1. This normalization factor has been applied to the temperatures of panels c and d of Fig. 1 to obtain the 400 km s−1 equivalent temperatures illustrated in panels e and f. The dependence on the solar wind speed is eliminated in these 400 km s−1 temperatures, they are reasonably symmetric about perihelion, and they decrease with radial distance. These results validate the use of the normalization factor in estimating the proton heating.
The normalization factors are derived in section II, after which they are applied to the temperatures measured on orbits 6, 7, 8, and 9 to determine the average 400 km s−1 equivalent temperature versus radius. This result, combined with the temperatures expected in the absence of heating, allows a quantitative estimate of the average proton perpendicular and parallel heating versus solar radius between 20 and 150 solar radii. The data for these analyses come from the SPAN instrument (Livi et al. 2022) of the SWEAP instrument package (Kasper et al. 2016) on the Parker Solar Probe. The perpendicular and parallel temperatures were obtained from the trace of the temperature matrix (Paschmann et al. 2000), which was combined with the magnetic field measured in the same detector frame of reference to produce the desired data.
During the perihelion passes of orbits 6–9, the spacecraft crossed any given solar radius many times. The proton temperature and solar wind speed at 20, 30, 50, and 80 solar radii during these many times are plotted in Fig. 2; the top panel gives the perpendicular temperatures and the bottom panel gives the parallel temperatures. Each panel contains the data averaged over one-hour and five-hour intervals. The one-hour least-squares fits are steeper than the five-hour fits in both cases, as expected because the more data that is averaged, the smaller the variation should be. The linear least-squares fit to each of these data sets (the dashed lines) describe the zeroth order dependence of the proton temperature on the solar wind speed. To estimate the uncertainty of the resultant temperature measurements, there are two such least-squares fits for each temperature that are carried through the full analysis and compared. As an example, the least-squares equation for the one-hour-averaged perpendicular temperature (top panel of Fig. 2) is
 |
Fig. 2. Perpendicular (upper panel) and parallel (lower panel) one-hour-averaged (black dots) and five-hour-averaged (red dots) measurements of the temperatures vs. solar wind speed at 20, 30, 50, and 80 solar radii on Parker Solar Probe orbits 6, 7, 8, and 9. Linear least-squares fits to these data are illustrated as the black and red dashed curves whose equations are also given in the figure. |
where T⊥1 is the one-hour-averaged proton temperature in eV and Vsw is the solar wind speed in km s−1.
From Eq. (1) the one-hour-averaged perpendicular temperature at any speed, Vsw, may be converted to the temperature at a speed of 400 km s−1 by multiplying the measured temperature by the normalization factor
Similar normalizations for the one-hour-averaged T∥ and the five-hour-averaged T⊥ and T∥ have also been obtained from the least-squares equations given in Fig. 2. These temperature normalizations from velocity, Vsw, to 400 km s−1 are shown to work well, in part because the observed velocities are confined to the narrow range of 200–550 km s−1. Similar temperature dependences on the solar wind speed have been reported by Elliott et al. (2012) and Perrone et al. (2019a,b) but a direct comparison of the current results with these earlier determinations is not possible because the earlier results pertained only to fast streams, the core temperature, or events in a coronal hole plasma.
3. Theory of perpendicular and parallel proton heating
Zaslavsky (2023) described the magnetohydrodynamic (MHD) heating theory in which
where Q is the heating rate, T⊥ and T∥ are the proton perpendicular and parallel temperatures, n is the plasma density, r is the distance from the Sun, C⊥ = T⊥/B, C∥ = (T∥ ⋅ n2/B2), and B is the magnetic field.
These equations are considered in the limit that the heat flux is negligible, as assumed by Zaslavsky (2023). To estimate the temperature variation with distance in the absence of heating, Q⊥ and Q∥ are set to zero. This may be done by setting C⊥ and C∥ to constant values, which is equivalent to conserving the first adiabatic invariant.
4. Perpendicular proton heating
A normalization factor like that of Eq. (2) was applied to the ∼10 000 one-hour averages of the perpendicular and the parallel proton temperatures measured on the four passes between 20 and 150 solar radii. Each temperature was estimated twice, once for the one-hour-averaged data and again for the five-hour-averaged data, with the comparison between the two averaged plots providing information on the uncertainty in the temperature resulting from the application of the normalization factors. Figure 3 presents the resulting 400 km s−1 perpendicular temperature versus solar radius and the temperature expected if Q⊥ = 0, called T⊥(Q = 0), using the measured magnetic field (not a model). The T⊥(Q = 0) plot is normalized by equating it to the temperature at 20 solar radii. This temperature curve is also proportional to the magnetic field strength because, in the absence of heating, the first adiabatic invariant, T⊥/B, is conserved. Also included is the curve of R−4/3 which is the temperature variation expected for adiabatic expansion of an isotropic, unheated gas (Mozer et al. 2022).
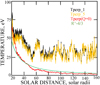 |
Fig. 3. 400 km s−1 normalized perpendicular proton temperatures vs. solar radius, as obtained from one-hour-averaged (black curve) and five-hour averaged (yellow curve) raw temperature measurements after multiplication by normalization factors given in Fig. 2. The temperatures were obtained from ∼10 000 h of data collected on four orbits. Comparison of these normalized perpendicular temperatures with the temperature expected in the absence of heating (red curve) shows that the perpendicular protons were heated in situ between 20 and 160 solar radii. The R−4/3 green curve is the temperature expected for no heating of an isotropic plasma. |
Both measured T⊥ curves in Fig. 3 exhibit large, short-term variations and a long-term trend that shows heating occurred because the measured T⊥ values are greater than that obtained for Q = 0. The short-term variations result from the data not having been scrubbed to remove, for example, the effects of switchbacks, heliospheric current sheet crossings, and space and time variability of the coronal boundary conditions. For example, the variations in T⊥ near 60 solar radii in Fig. 3 result from heliospheric current sheet crossings in this region by three of the studied orbits. The standard deviations of the individual measurements in Fig. 3 vary from about 10–20 eV. All the measured temperatures have similar short-term variations that should be ignored in favor of viewing the average trend of any parameter with radial distance. Because the one-hour-averaged T⊥ and the five-hour averaged T⊥ are in good agreement, the temperature normalization routine does not introduce important uncertainties in the result. The data quality in Fig. 3 offers strong evidence for the reliability of temperature measurements made on the Parker Solar Probe.
The heating can be shown from plots of the 400 km s−1 perpendicular temperature divided by T⊥(Q = 0), where T⊥(Q = 0) is also the first adiabatic invariant. Figure 4 shows that the first adiabatic invariant was not conserved and that heating occurred throughout the radial range.
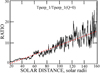 |
Fig. 4. 400 km s−1 normalized perpendicular temperature divided by the temperature that would have existed in the absence of heating. This ratio is the first adiabatic invariant, which is not conserved because the protons were heated from 20 to 160 solar radii. |
The heating can be estimated by calculating the Q given in Eq. (3), (while neglecting the heat flux terms), by using the one-hour-averaged perpendicular temperature of Fig. 3, and by assuming a steady state such that d/dt is equal to Vd/dr. Figure 5 plot of this heating rate shows that, in erg cm−3 s, the heating rate at 15 solar radii was 6e−12, at 50 solar radii it was 1e−13, and at 170 solar radii it was 5e−14. Also shown in Fig. 5 is the curve of R−10/3, which is the heating rate of a uniformly heated, ideal, isotropic, MHD system. That this curve and the measured rate are very similar speaks well for the quality of the measured protons on the Parker Solar Probe.
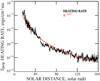 |
Fig. 5. Heating rate as a function of solar radius required for the perpendicular protons to have the temperatures given in Fig. 3. The red curve is the heating expected for an isotropic plasma. |
The heating rate of Fig. 5 was produced from the assumption that the solar wind speed was 400 km s−1 at all distances. If the average solar wind speed increased from 350 to 450 km s−1 as a function of radial distance, as suggested by McGregor et al. (2011), the temperature near the Sun, estimated from Eq. (2), would be 13% lower than that given in Fig. 3, while the temperature farther from the Sun would be greater by the same factor. The net effect is that the heating in Fig. 5 would increase by about 25%. Additionally, these data are averages over four orbits, and the data from the different pairs of orbits typically varied by factors less than about 2. For these reasons, the heating rate in a specific orbit may differ from the curve of Fig. 5 by a factor of 2 or less.
Earlier measurements, using plasma data from Helios and Ulysses, have estimated perpendicular proton heating in the solar wind (Marsch et al. 1983; Hellinger et al. 2011; Cranmer et al. 2009; Zaslavsky 2023; and references therein). It is useful to compare these earlier estimates with the current data. The earlier estimates from in situ data covered the range of about 65 solar radii to 1 AU while the current data covers the range down to 15 solar radii. The earlier estimates ignored the effect of the temperature dependence on the solar wind speed by considering only measurements in the high-speed or slow-speed solar wind while the current data includes all solar wind speeds. The earlier perpendicular heating rates are in the same general ballpark as the current data, but detailed comparisons cannot be made because of the different measurement conditions.
5. Parallel proton heating
Figure 6 presents the measured parallel temperatures and that which would have existed if there were no heating (in red). That three curves overlap on average shows that there is no parallel heating or cooling of parallel protons between 20 and 70 solar radii. The red curve of temperature with no heating is not extended beyond about 70 solar radii because reliable plasma density data was not available to compute its value, (n/B)2, with sufficient accuracy. However, we might assume that (n/B)2 is approximately constant beyond 70 solar radii because both the numerator and the denominator vary with distance as R−4 farther from the Sun. In this case T∥ would be constant beyond 70 solar radii, as has been found experimentally. In addition, Zaslavsky (2023) showed, with Helios data, that there was no parallel heating or cooling of the high-speed solar wind from 65 solar radii to 1 AU. Thus, in spite of earlier measurements that suggested otherwise (Hellinger et al. 2011, 2013), we conclude that the first adiabatic invariant is conserved for parallel protons from near the Sun to 1 AU and that there is no heating or cooling required to maintain the observed temperature.
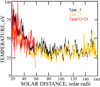 |
Fig. 6. Parallel proton temperatures between 20 and 160 solar radii, measured for two averaging times. The red curve of (n/B)2 is proportional to the parallel temperature expected in the absence of heating or cooling. It extends to only about 70 solar radii because there were no sufficiently reliable plasma density measurements beyond that point. The agreement between the three curves shows that there was neither heating nor cooling of the parallel electrons below 70 solar radii. |
6. Conclusions
In this Letter it is shown, for the first time, that the proton perpendicular temperature increases with solar radius relative to that in the absence of heating and that the perpendicular protons are heated throughout their trajectories from 20 to 160 solar radii. A quantitative estimate of this heating is provided. Meanwhile, the parallel protons are shown to be neither heated nor cooled between 20 and 70 solar radii, and they are most likely not heated or cooled beyond that distance.
Acknowledgments
This work was supported by NASA contract NNN06AA01C. The author acknowledges the extraordinary contributions of the Parker Solar Probe spacecraft engineering team at the Applied Physics Laboratory at Johns Hopkins University. D. Larson is acknowledged for providing the plasma data. The work of I.V. was supported by NASA Heliophysics Guest Investigator grant 80NSSC21K0581. O.V.A. was supported by NASA grants 80NSSC22K0433, 80NSSC21K1770, and 80NSSC20K0697.
References
- Bandyopadhyay, R., Goldstein, M. L., Maruca, B. A., et al. 2020, ApJS, 246, 48 [Google Scholar]
- Burlaga, L. F., & Ogilvie, K. W. 1970, Sol. Phys., 15, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Case, A. W., & Kasper, J. C. 2014, AGU Fall Meeting 2014 SH31A [Google Scholar]
- Chandran, B. D. G., Quataert, E., Howes, G. G., Xia, Q., & Pongkitiwanichakul, P. 2009, ApJ, 707, 1668 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R. 2020, ApJ, 900, 105 [Google Scholar]
- Cranmer, S. R., Matthaeus, W. H., Breech, B. A., & Kasper, J. C. 2009, ApJ, 702, 1604 [Google Scholar]
- Elliott, H. A., Henney, C. J., McComas, D. J., Smith, C. W., & Vasquez, B. J. 2012, J. Geophys. Res. Space Phys., 117 [Google Scholar]
- Hellinger, P., Travnichek, P. M., Štverák, Š., Matteini, L., & Velli, M. 2013, J. Geophys. Res. Space Phys., 118, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Hellinger, P., Matteini, L., Štverák, Š., Travnichek, P. M., & Marsch, E. 2011, J. Geophys. Res. Space Phys., 116, A09105 [NASA ADS] [Google Scholar]
- Hewish, A., & Wyndham, J. D. 1963, MNRAS, 126, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Hundhausen, A. J., Bame, S. J., Asbridge, J. R., & Sydoriak, S. J. 1970, J. Geophys. Res., 75, 4643 [NASA ADS] [CrossRef] [Google Scholar]
- Ingale, M., Subramanian, P., & Cairns, I. 2015, MNRAS, 447, 3486 [NASA ADS] [CrossRef] [Google Scholar]
- Janardhan, P., Bisoi, S. K., Ananthakrishnan, S., Tokumaru, M., & Fujiki, K. 2011, Geophys. Res. Lett., 38 [Google Scholar]
- Kasper, J. C., Abiad, R., Austin, G., et al. 2016, Space Sci. Rev., 204, 131 [Google Scholar]
- Livi, R., Larson, D. E., Kasper, J. C., et al. 2022, ApJ, 938, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Manoharan, P. K., Kojima, M., Gopalswamy, N., Kondo, T., & Smith, Z. 2000, ApJ, 530, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E., Muhlhauser, K. H., Rosenbauer, H., & Schwenn, R. 1983, J. Geophys. Res. Space Phys., 88, 2982 [NASA ADS] [CrossRef] [Google Scholar]
- McGregor, S. L., Hughes, W. J., Arge, C. N., Owens, M. J., & Odstrcil, D. 2011, J. Geophys. Res. Space Phys., 116 [Google Scholar]
- Mozer, F. S., Bale, S. D., Cattell, C. A., et al. 2022, ApJ, 927, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Paschmann, G., Fazakerley, A. N., & Schwartz, S. J. 2000, in Analysis Methods for Multi-Spacecraft Data, eds. G. Paschmann, & P. Daly, ISSI Scientific Reports Series, 1, 125 [Google Scholar]
- Perrone, D., Stansby, D., Horbury, T. S., & Matteini, L. 2019a, MNRAS, 483, 3730 [Google Scholar]
- Perrone, D., Stansby, D., Horbury, T. S., & Matteini, L. 2019b, MNRAS, 488, 2380 [Google Scholar]
- Raja, K. S., Subramanian, P., Ramesh, R., Vourlidas, A., & Ingale, M. 2017, ApJ, 850, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Raja, K. S., Subramanian, P., Ingale, M., Ramesh, R., & Maksimovic, M. 2021, ApJ, 914, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Sasikumar Raja, K., Ingale, M., Ramesh, R., et al. 2016, J. Geophys. Res. Space Phys., 121, 605 [Google Scholar]
- Sasikumar Raja, K., Janardhan, P., Bisoi, S. K., et al. 2019, Sol. Phys., 294, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, C., Velli, M. C. M., Panasenco, O., et al. 2020, SH033, conference Name: AGU Fall Meeting Abstracts [Google Scholar]
- Vech, D., Klein, K. G., & Kasper, J. C. 2017, ApJ, 850, L11 [Google Scholar]
- Zaslavsky, A. 2023, Geophys. Res. Lett., 50, e2022GL101548 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Perpendicular (panel c) and parallel (panel d) proton temperatures measured from 15 to 100 solar radii (panel a) during Parker Solar Probe orbit 10. The solar wind speed (panel b) strongly correlates with the temperatures to the extent that the temperatures are asymmetric about perihelion. In panels e and f, a normalization factor has been applied to the temperatures to convert them from those measured at the local speed to those that would have been measured if the wind speed had been 400 km s−1. This normalization makes the resulting temperatures maximum near perihelion and they decrease with radial distance in a manner consistent with adiabatic cooling. |
| In the text | |
 |
Fig. 2. Perpendicular (upper panel) and parallel (lower panel) one-hour-averaged (black dots) and five-hour-averaged (red dots) measurements of the temperatures vs. solar wind speed at 20, 30, 50, and 80 solar radii on Parker Solar Probe orbits 6, 7, 8, and 9. Linear least-squares fits to these data are illustrated as the black and red dashed curves whose equations are also given in the figure. |
| In the text | |
 |
Fig. 3. 400 km s−1 normalized perpendicular proton temperatures vs. solar radius, as obtained from one-hour-averaged (black curve) and five-hour averaged (yellow curve) raw temperature measurements after multiplication by normalization factors given in Fig. 2. The temperatures were obtained from ∼10 000 h of data collected on four orbits. Comparison of these normalized perpendicular temperatures with the temperature expected in the absence of heating (red curve) shows that the perpendicular protons were heated in situ between 20 and 160 solar radii. The R−4/3 green curve is the temperature expected for no heating of an isotropic plasma. |
| In the text | |
 |
Fig. 4. 400 km s−1 normalized perpendicular temperature divided by the temperature that would have existed in the absence of heating. This ratio is the first adiabatic invariant, which is not conserved because the protons were heated from 20 to 160 solar radii. |
| In the text | |
 |
Fig. 5. Heating rate as a function of solar radius required for the perpendicular protons to have the temperatures given in Fig. 3. The red curve is the heating expected for an isotropic plasma. |
| In the text | |
 |
Fig. 6. Parallel proton temperatures between 20 and 160 solar radii, measured for two averaging times. The red curve of (n/B)2 is proportional to the parallel temperature expected in the absence of heating or cooling. It extends to only about 70 solar radii because there were no sufficiently reliable plasma density measurements beyond that point. The agreement between the three curves shows that there was neither heating nor cooling of the parallel electrons below 70 solar radii. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



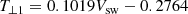
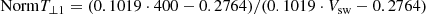
![$$ \begin{aligned}&Q_{\perp } = n\cdot T_{\perp } [\mathrm{d}(\log C_{\perp })/\mathrm{d}t] + \text{ heat} \text{ flux} \text{ terms} \end{aligned} $$](/articles/aa/full_html/2023/05/aa46202-23/aa46202-23-eq3.gif)
![$$ \begin{aligned}&Q_{\parallel } = n\cdot T_{\parallel } [\mathrm{d}(\log C_{\parallel })/\mathrm{d}t] + \text{ heat} \text{ flux} \text{ terms} \end{aligned} $$](/articles/aa/full_html/2023/05/aa46202-23/aa46202-23-eq4.gif)