| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 8 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201834551 | |
| Published online | 01 March 2019 | |
Letter to the Editor
Protostellar Outflows at the EarliesT Stages (POETS)
II. A possible radio synchrotron jet associated with the EGO G035.02+0.35
1
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: asanna@mpifr-bonn.mpg.de
2
INAF, Osservatorio Astronomico di Cagliari, via della Scienza 5, 09047 Selargius, CA, Italy
3
INAF, Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
4
Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
5
NRAO, 520 Edgemont Road, Charlottesville, VA 22903, USA
6
Dublin Institute for Advanced Studies, Astronomy & Astrophysics Section, 31 Fitzwilliam Place, Dublin 2, Ireland
7
Instituto de Radioastronomía y Astrofísica UNAM, Apartado Postal 3-72 (Xangari), 58089 Morelia, Michoacán, México
Received:
31
October
2018
Accepted:
23
January
2019
Centimeter continuum observations of protostellar jets have revealed knots of shocked gas where the flux density decreases with frequency. This spectrum is characteristic of nonthermal synchrotron radiation and implies both magnetic fields and relativistic electrons in protostellar jets. Here, we report on one of the few detections of a nonthermal jet driven by a young massive star in the star-forming region G035.02+0.35. We made use of the NSF’s Karl G. Jansky Very Large Array (VLA) to observe this region at C, Ku, and K bands with the A- and B-array configurations, and obtained sensitive radio continuum maps down to an rms of 10 μJy beam−1. These observations allow for a detailed spectral index analysis of the radio continuum emission in the region, which we interpret as a protostellar jet with a number of knots aligned with extended 4.5 μm emission. Two knots clearly emit nonthermal radiation and are found at similar distances, of approximately 10 000 au, at each side of the central young star, from which they expand at velocities of several hundred km s−1. We estimate both the mechanical force and the magnetic field associated with the radio jet, and infer a lower limit of 0.4 × 10−4 M⊙ yr−1 km s−1 and values in the range 0.7–1.3 mG.
Key words: stars: formation / radio continuum: ISM / H II regions / ISM: jets and outflows / techniques: high angular resolution / stars: individual: G035.02+0.35
© A. Sanna et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
The centimeter continuum emission of ionized protostellar jets is a preferred tracer to image the outflow geometry, and, knowing the ionization fraction of local hydrogen gas, to quantify the mass-loss rate at scales from a few 10s to 1000s au of the central young star (e.g., Reynolds 1986; Tanaka et al. 2016). Radio jet properties have recently been reviewed by Anglada et al. (2018). The flux density (Sν) of radio jets typically increases with frequency (ν) within a few 1000s au of the central star (Sν ∝ να), showing a partially opaque spectral index (0 < α < 2). These spectra are interpreted as thermal free-free emission from ionized particles that are accelerated within their own electric field. Notably, along the axis of a few radio jets, the spectrum is occasionally inverted at the loci of bright knots of ionized gas (e.g., Rodríguez et al. 2005; Carrasco-González et al. 2010; Moscadelli et al. 2013; Rodríguez-Kamenetzky et al. 2016; Osorio et al. 2017), showing spectral index values much lower than the optically thin limit (−0.1). These spectra are interpreted as evidence for (nonthermal) synchrotron emission from strong jet shocks against the ambient medium, where ionized particles would be sped up to relativistic velocities via diffusive shock acceleration (e.g., Padovani et al. 2015, 2016).
For the prototypical synchrotron jet HH 80–81, Carrasco-González et al. (2010) detected linear polarization of the centimeter continuum emission for the first time, proving that the negative slope of the radio spectrum is due to synchrotron radiation. Polarized maser emission associated with protostellar outflows provides further evidence for the presence of magnetic fields, and observations of maser cloudlets at milliarcsecond resolution show a strong correlation between the local orientation of proper motion and magnetic field vectors (e.g., Surcis et al. 2013; Sanna et al. 2015; Goddi et al. 2017; Hunter et al. 2018). In this Letter, we report on one of the very few detections of a nonthermal jet emitted by a young massive star, which was discovered in the star-forming region G035.02+0.35 as part of the Protostellar Outflow at the EarliesT Stage (POETS) survey (Moscadelli et al. 2016; Sanna et al. 2018, hereafter Paper I).
The star-forming region G035.02+0.35 hosts diverse stages of stellar evolution, including a hot molecular core (HMC) near to a hyper-compact (HC) H II region (e.g., Brogan et al. 2011; Beltrán et al. 2014). At a parallax distance of 2.33 kpc from the Sun (Wu et al. 2014), the entire region emits a bolometric luminosity of 1−3 × 104 L⊙ (Beltrán et al. 2014; Towner et al., in prep.). G035.02+0.35 was surveyed with the IRAC instrument on board Spitzer and classified as an extended green object (EGO) associated with bright 4.5 μm emission, which is a tracer of ambient gas shocked by early outflow activity (Cyganowski et al. 2008, 2009; Lee et al. 2013). Cyganowski et al. (2011) made a census of the 8 GHz continuum sources at the center of the IR nebula with the B-configuration of the Very Large Array (VLA). They identified five compact radio sources above a threshold of 100 μJy beam−1. Here, we make use of the longest VLA baselines at 6, 15, and 22 GHz (the C, Ku, and K bands, respectively) to image the continuum emission at a sensitivity of 10 μJy beam−1. Observation information was presented in Paper I and is summarized in Table B.1. We have performed a detailed spectral index analysis for each radio continuum component, and we identified an extended radio jet with nonthermal knots. This radio jet is driven by the HMC source at the base of the IR nebula.
2. Results
In Fig. 1 we present a radio continuum map at C band of G035.02+0.35, obtained at a resolution of 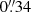 . For a direct comparison with previous observations, we adopt the same labeling of radio continuum components introduced by Cyganowski et al. (2011, from CM1 to CM5), and extend the source numbering to the new radio components detected in this paper (CM6, CM7, and CM8). We detect eight distinct radio continuum sources at multiple frequencies above a threshold of 27 μJy beam−1 (3σ); six of them are distributed within a radius of 0.1 pc from CM2. CM2 coincides in position with the brightest millimeter peak in the region, which is also the richest site of molecular line emission, named core A in Beltrán et al. (2014, their Figs. 2 and 4). The spectral energy distribution of CM2 has a constant spectral index of 0.69 between 1 and 7 cm, which is consistent with thermal jet emission from a young star. Its radio luminosity, of approximately 5 mJy kpc2 at 8 GHz, is indicative of an early B-type young star, according to the correlation between radio jet and bolometric luminosities (e.g., Fig. 6 of Paper I). The radio continuum emission from CM2 was previously presented in Paper I (see also Fig. 3 of Cyganowski et al. 2011). In the following, we comment on the radio continuum components detected near to CM2.
. For a direct comparison with previous observations, we adopt the same labeling of radio continuum components introduced by Cyganowski et al. (2011, from CM1 to CM5), and extend the source numbering to the new radio components detected in this paper (CM6, CM7, and CM8). We detect eight distinct radio continuum sources at multiple frequencies above a threshold of 27 μJy beam−1 (3σ); six of them are distributed within a radius of 0.1 pc from CM2. CM2 coincides in position with the brightest millimeter peak in the region, which is also the richest site of molecular line emission, named core A in Beltrán et al. (2014, their Figs. 2 and 4). The spectral energy distribution of CM2 has a constant spectral index of 0.69 between 1 and 7 cm, which is consistent with thermal jet emission from a young star. Its radio luminosity, of approximately 5 mJy kpc2 at 8 GHz, is indicative of an early B-type young star, according to the correlation between radio jet and bolometric luminosities (e.g., Fig. 6 of Paper I). The radio continuum emission from CM2 was previously presented in Paper I (see also Fig. 3 of Cyganowski et al. 2011). In the following, we comment on the radio continuum components detected near to CM2.
 |
Fig. 1. Extended radio jet emission driven by source CM2 in G035.02+0.35. Middle panel: continuum map obtained with the A-configuration of the VLA at C band (without constraints on uv-coverage). Contour levels, at multiples of the 1σ rms, are indicated at the top; levels higher than 10σ are drawn in gray shades. The beam size is shown in the bottom left corner. A scale bar in units of au is drawn near the bottom axis. The field of view covers the radio continuum sources detected within 0.1 pc from CM2 (CM8 in Fig. B.1), whose centimeter spectral index (α) traces radio thermal jet emission (from Paper I). Labels are indicated in red near each source. Components CM3, CM4, and CM6 are aligned along a position angle of 25.5° ± 0.6° with respect to CM2 (dotted line), tracing the location of four jet knots. Ticks are marked along the jet direction in steps of 6000 au from CM2. Side panels: centimeter spectral energy distribution of radio components surrounding CM2. Each plot shows the logarithm of the integrated flux (in mJy) as a function of the logarithm of the observed frequency (in Hz) for four data points. Details for CM2 were presented in Paper I. Different frequency bands are labeled near the bottom axis together with the reference wavelength; gray shades mark the boundary of each band. The spectral index values (α) and their uncertainties, derived from a linear fit of the four data points, are specified in the upper left corner of each panel. Assuming an electron temperature of 104 K, the spectral energy distribution of source CM1 is well reproduced by a model of homogeneous H II region with a Strömgren radius (RS) of 630 au, number of Lyman photons (NLy) of 1045.85 s−1, electron density (ne) of 8.8 × 104 cm−3, and emission measure of 4.8 × 107 pc cm−6. |
In Table B.2 we list the integrated fluxes at C, Ku, and K bands for each radio continuum component. These fluxes were computed within a common uv-distance range of 40–800 kλ, as described in Paper I, and the C-band data were split into two sub-bands of 2 GHz each. In the side panels of Fig. 1, we analyze the spectral energy distribution of each radio component.
CM1 is the brightest radio continuum source in the region, and it is located west-southwest of CM2, at a projected distance of 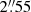 (or 5944 au). Its spectral energy distribution is characteristic of a photoionized H II region that is hyper compact, with an angular size (best fit) of
(or 5944 au). Its spectral energy distribution is characteristic of a photoionized H II region that is hyper compact, with an angular size (best fit) of 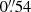 , corresponding to a Strömgren radius (RS) of 630 au. This size is consistent with the (deconvolved) size obtained directly by fitting the observed image. The four data points are consistent with a homogeneous H II region model with constant electron density and temperature, fixed to 104 K (see Fig. 1). This model implies a number of Lyman photons (NLy) of 1045.85 s−1, and an electron density (ne) and emission measure (EM) of 8.8 × 104 cm−3 and 4.8 × 107 pc cm−6, respectively. The number of Lyman photons corresponds to that emitted by a zero-age main-sequence (ZAMS) star of spectral type between B1–B0.5 and bolometric luminosity of 8−9 × 103 L⊙ (e.g., Thompson 1984). These values are consistent with those reported by Cyganowski et al. (2011) after scaling their distance (3.43 kpc) to the current value (2.33 kpc).
, corresponding to a Strömgren radius (RS) of 630 au. This size is consistent with the (deconvolved) size obtained directly by fitting the observed image. The four data points are consistent with a homogeneous H II region model with constant electron density and temperature, fixed to 104 K (see Fig. 1). This model implies a number of Lyman photons (NLy) of 1045.85 s−1, and an electron density (ne) and emission measure (EM) of 8.8 × 104 cm−3 and 4.8 × 107 pc cm−6, respectively. The number of Lyman photons corresponds to that emitted by a zero-age main-sequence (ZAMS) star of spectral type between B1–B0.5 and bolometric luminosity of 8−9 × 103 L⊙ (e.g., Thompson 1984). These values are consistent with those reported by Cyganowski et al. (2011) after scaling their distance (3.43 kpc) to the current value (2.33 kpc).
The spectral index of components CM3 to CM7 was computed with the linear regression fit drawn in each panel of Fig. 1, where we also report the spectral index values with 1σ uncertainty. Notably, CM3 and CM4 have negative spectral slopes steeper than the optically thin limit. Their spectra are consistent with nonthermal radiation within a confidence level of 3σ. Instead, the spectral indices of CM5, CM6, and CM7 are consistent with optically thin free-free radiation within 1σ.
In particular, the peak positions of radio components CM2, CM3, CM4, and CM6 are well-aligned on the plane of the sky. The four points fit a straight line that is oriented at a position angle of 25.5° with a small uncertainty of 0.6° (dotted line in Fig. 1). CM3 and CM4 are located at either side of CM2 at a similar distance of 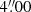 (9320 au) and
(9320 au) and 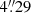 (9996 au), respectively; CM6 is located closer to CM2 at a distance of
(9996 au), respectively; CM6 is located closer to CM2 at a distance of 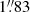 (4252 au). Unlike CM2, the radio continuum emission from CM3, CM4, and CM6 does not coincide with compact dust emission (e.g., Fig. 2 of Beltrán et al. 2014). The linear distribution and the spectral index analysis support the following interpretation: CM2, CM3, CM4, and CM6 trace the same ionized jet, with CM2 pinpointing the origin where the central powering source is surrounded by partially opaque plasma, while CM3 and CM4 arise from two shocks that emit synchrotron radiation located symmetrically with respect to CM2, and CM6 marks a shock emitting optically thin free-free radiation located closer to CM2.
(4252 au). Unlike CM2, the radio continuum emission from CM3, CM4, and CM6 does not coincide with compact dust emission (e.g., Fig. 2 of Beltrán et al. 2014). The linear distribution and the spectral index analysis support the following interpretation: CM2, CM3, CM4, and CM6 trace the same ionized jet, with CM2 pinpointing the origin where the central powering source is surrounded by partially opaque plasma, while CM3 and CM4 arise from two shocks that emit synchrotron radiation located symmetrically with respect to CM2, and CM6 marks a shock emitting optically thin free-free radiation located closer to CM2.
In Fig. 2 we provide further evidence supporting the interpretation of a single radio jet, by comparing the spatial distribution of the radio continuum emission with the morphology of the 4.5 μm emission (another typical outflow tracer). The 4.5 μm map has previously been presented in Beltrán et al. (2014, their Fig. 2), who processed the Spitzer/IRAC data making use of the high-resolution deconvolution algorithm by Velusamy et al. (2008). The EGO has a bipolar structure centered on CM2 and oriented in the direction of the radio continuum sources CM3, CM4, and CM6, which in turn appear to bisect the EGO. Additional arguments in favor of the jet interpretation are discussed in Appendix A, based on the proper motions of CM3 and CM4 with respect to CM2, and on the elongated morphology of the continuum emission. In the following, we refer to the position angle of 25.5° as the jet axis.
 |
Fig. 2. Comparison between the radio jet emission driven by source CM2 (yellow contours) and the 4.5 μm nebula imaged by Spitzer in the region (green scale). The radio continuum map is the same as in Fig. 1, together with the jet direction and ticks (dotted white line). Contour levels are indicated at the bottom. The logarithmic (green) scale of the 4.5 μm emission is drawn in the top wedge. The enhanced resolution (HPBW) of the Spitzer map is shown in the bottom left corner (see Sect. 2 for details). |
We also detect two additional radio continuum sources farther from CM2 (in projection) along the axis of the jet, CM7 (Fig. 1) and CM8 (Fig. B.1). CM7 is 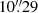 (0.116 pc) away from CM2 and only slightly offset at a position angle of 35°. CM8 is
(0.116 pc) away from CM2 and only slightly offset at a position angle of 35°. CM8 is 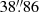 (0.439 pc) away from CM2 to the northeast and elongated in the direction of the jet axis. They could mark farther knots of (optically thin) ionized gas caused by the jet passage.
(0.439 pc) away from CM2 to the northeast and elongated in the direction of the jet axis. They could mark farther knots of (optically thin) ionized gas caused by the jet passage.
The position of CM5, well away from the jet axis, argues that it traces a separate object. Its radio continuum flux, which is approximately constant between 1 and 7 cm, is consistent with a small, optically thin H II region (RS ≲ 100 au). The ionized flux can be reproduced with a number of Lyman photons of about 1043.45 s−1 (e.g., Eq. (1) of Cyganowski et al. 2011), coming from a young star with a spectral type later than B2.5 and a bolometric luminosity of approximately 1 × 103 L⊙.
3. Discussion
In the following, we quantify the mass loss (Ṁjet) and momentum (ṗjet) rates of the radio jet. We also estimate the magnetic field strength (Bmin) at the position of the synchrotron knots.
First, we applied Eq. (1) of Sanna et al. (2016) to estimate the mass ejected per unit time at the position of CM2 as a function of the flux density (Sν), frequency (ν), and spectral index of the continuum emission (α), the turn-over frequency of the radio jet spectrum (νm), the semi-opening angle of the radio jet (ψ), its inclination with respect to the line of sight (i), and the expanding velocity of the ionized gas (Vjet). We assumed that the radio jet can be approximated by a conical flow, where gas is isothermal at a constant temperature of 104 K, and it is uniformly and fully ionized (x0 = 1). In Table 1 we list the values used in the calculation.
Properties of the thermal radio jet at the position of CM2.
Values of spectral index and integrated flux density for CM2 at 8.0 GHz were obtained from Table 3 of Paper I. The spectral index was approximated to 0.6 within the uncertainty of its measurement, and it is consistent with the assumption of conical flow (e.g., Eq. (5) of Anglada et al. 2018). A lower limit to the turn-over frequency is set by the higher frequency of the K-band observations (26 GHz), although the mass-loss rate does not depend on the turn-over frequency for α = 0.6. We estimated the jet opening angle (2 × ψ) by drawing the tangents to the 3σ contours of CM3 from the peak position of CM2. These tangents are approximately symmetric with respect to the jet axis and define an aperture of 12°. The extended bipolar geometries of the radio continuum emission and IR nebula suggest that the jet axis is nearly perpendicular to the line of sight, although a direct measurement is not available. We assumed an inclination (i) in the range 60°–90°, which changes the mass-loss rate by less than a few percent. We further considered a lower limit to the jet velocity of 200 km s−1 based on the proper motion analysis in Appendix A, which provides an estimate of the shock velocities.
These values imply a jet mechanical force (ṗjet) at its origin of 0.4 × 10−4 M⊙ yr−1 km s−1. However, in the calculation we followed a conservative approach, assuming that the jet is entirely ionized; this assumption implies a lower limit of the mass-loss (and momentum) rate that is inversely proportional to the ionization fraction. In contrast, previous statistical studies of radio jets assumed a low-ionization fraction in the range 10–20% (e.g., Purser et al. 2016; Anglada et al. 2018), which is supported by near-IR (NIR) observations (e.g., Fedriani et al. 2018). Moreover, in the case of a massive young star undergoing an accretion burst (S255 NIRS3), Cesaroni et al. (2018) showed that the radio thermal jet emission is produced by a low-ionization degree (∼10%). For this reason, in Table 1 we also estimate the radio jet properties assuming that its gas is mostly neutral and is moving at high velocities of 600 km s−1. Rodríguez-Kamenetzky et al. (2016) showed that jet velocities of about 500–600 km s−1 might be needed to efficiently promote particle acceleration (and synchrotron emission) in the shocks against the ambient medium. Under these conditions, we estimate an upper limit to the jet mechanical force of 3.2 × 10−3 M⊙ yr−1 km s−1. This value is consistent with the relationship between mechanical force and radio luminosity of jets reported in Fig. 9 of Anglada et al. (2018), where a low-ionization fraction was assumed.
Second, we estimated the minimum-energy magnetic field strength, Bmin, which minimizes together the kinetic energy of the relativistic particles and the energy stored in the magnetic field. For a direct comparison of Bmin in another radio synchrotron jet, we followed the same calculations as Carrasco-González et al. (2010). We used the classical minimum-energy formula, which is valid in Gaussian CGS units: Bmin = [4.5c12 (1 + k)LR]2/7(R3ϕ)−2/7, where LR is the synchrotron luminosity measured in a spherical source of radius R. The filling factor, ϕ, accounts for a smaller region of synchrotron radiation with respect to the source size. The two coefficients, c12 and k, depend on the integrated radio spectrum and on the energy ratio among relativistic particles in the region, respectively (e.g., Govoni & Feretti 2004; Beck & Krause 2005).
In Table 2 we list the values used to calculate Bmin. We estimated the magnetic field strength for sources CM3 and CM4 separately and obtained values of 1.3 mG and 0.7 mG, respectively. On the one hand, these values are a factor 6–3 times higher than the magnetic field strength (0.2 mG) estimated by Carrasco-González et al. (2010) in the radio jet HH 80–81. These differences might be consistent with the uncertainty of the prior assumptions, such as ϕ and k. On the other hand, because the synchrotron knots in HH 80–81 are located ten times farther away from their exciting protostar than CM3 and CM4 are from CM2, the magnetic field strength might reasonably be lower for this case (e.g., Seifried et al. 2012). Interestingly, in the synchrotron component of the jet driven by NGC6334I–MM1B, OH maser emission provides an independent Zeeman measurement of the magnetic field strength locally (0.5–3.7 mG), which is consistent with the values estimated above (Brogan et al. 2016, 2018; Hunter et al. 2018). We further note that the 6.7 GHz CH3OH masers detected at the position of CM2 show linearly polarized emission, and this emission supports a magnetic field orientation aligned with the direction of the jet axis (Surcis et al. 2015, their Fig. 5).
Minimum-energy magnetic field strength in the radio jet.
Although more data are required to fully confirm the proposed interpretation in terms of a single jet with synchrotron knots, these findings overall suggest that G035.02+0.35 can provide a preferred laboratory for studying the role of magnetic fields in the acceleration and collimation of protostellar jets (e.g., Kölligan & Kuiper 2018).
Acknowledgments
We gratefully acknowledge the thoughtful comments from an anonymous referee who helped improve the paper. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. M.P. acknowledges funding from the European Unions Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 664931. A.C.G. received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 743029)
References
- Anglada, G., Rodríguez, L. F., & Carrasco-González, C. 2018, A&ARv, 26, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., & Krause, M. 2005, Astron. Nachr., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Beltrán, M. T., Sánchez-Monge, Á., Cesaroni, R., et al. 2014, A&A, 571, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brogan, C. L., Hunter, T. R., Cyganowski, C. J., et al. 2011, ApJ, 739, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Brogan, C. L., Hunter, T. R., Cyganowski, C. J., et al. 2016, ApJ, 832, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Brogan, C. L., Hunter, T. R., Cyganowski, C. J., et al. 2018, ApJ, 866, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco-González, C., Rodríguez, L. F., Anglada, G., et al. 2010, Science, 330, 1209 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cesaroni, R., Moscadelli, L., Neri, R., et al. 2018, A&A, 612, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cyganowski, C. J., Whitney, B. A., Holden, E., et al. 2008, AJ, 136, 2391 [NASA ADS] [CrossRef] [Google Scholar]
- Cyganowski, C. J., Brogan, C. L., Hunter, T. R., & Churchwell, E. 2009, ApJ, 702, 1615 [NASA ADS] [CrossRef] [Google Scholar]
- Cyganowski, C. J., Brogan, C. L., Hunter, T. R., & Churchwell, E. 2011, ApJ, 743, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Fedriani, R., Caratti o Garatti, A., & Coffey, D. 2018, A&A, 616, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goddi, C., Surcis, G., Moscadelli, L., et al. 2017, A&A, 597, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Govoni, F., & Feretti, L. 2004, Int. J. Mod. Phys. D, 13, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, T. R., Brogan, C. L., MacLeod, G. C., et al. 2018, ApJ, 854, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Kölligan, A., & Kuiper, R. 2018, A&A, 620, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, H.-T., Liao, W.-T., Froebrich, D., et al. 2013, ApJS, 208, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Moscadelli, L., Cesaroni, R., Sánchez-Monge, Á., et al. 2013, A&A, 558, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moscadelli, L., Sánchez-Monge, Á., Goddi, C., et al. 2016, A&A, 585, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osorio, M., Díaz-Rodríguez, A. K., Anglada, G., et al. 2017, ApJ, 840, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, M., Hennebelle, P., Marcowith, A., & Ferrière, K. 2015, A&A, 582, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., Marcowith, A., Hennebelle, P., & Ferrière, K. 2016, A&A, 590, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Purser, S. J. D., Lumsden, S. L., Hoare, M. G., et al. 2016, MNRAS, 460, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Schneps, M. H., Moran, J. M., et al. 1988, ApJ, 330, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, S. P. 1986, ApJ, 304, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez, L. F., Garay, G., Brooks, K. J., & Mardones, D. 2005, ApJ, 626, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Kamenetzky, A., Carrasco-González, C., Araudo, A., et al. 2016, ApJ, 818, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Sanna, A., Surcis, G., Moscadelli, L., et al. 2015, A&A, 583, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanna, A., Moscadelli, L., Cesaroni, R., et al. 2016, A&A, 596, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanna, A., Moscadelli, L., Goddi, C., Krishnan, V., & Massi, F. 2018, A&A, 619, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seifried, D., Pudritz, R. E., Banerjee, R., Duffin, D., & Klessen, R. S. 2012, MNRAS, 422, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Surcis, G., Vlemmings, W. H. T., van Langevelde, H. J., Hutawarakorn Kramer, B., & Quiroga-Nuñez, L. H. 2013, A&A, 556, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Surcis, G., Vlemmings, W. H. T., van Langevelde, H. J., et al. 2015, A&A, 578, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tanaka, K. E. I., Tan, J. C., & Zhang, Y. 2016, ApJ, 818, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, R. I. 1984, ApJ, 283, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Velusamy, T., Marsh, K. A., Beichman, C. A., Backus, C. R., & Thompson, T. J. 2008, AJ, 136, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y. W., Sato, M., Reid, M. J., et al. 2014, A&A, 566, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Proper motions and elongation of the radio jet
In this section, we compare our C-band observations with the X-band observations reported by Cyganowski et al. (2011). The aim is to reveal the proper motion of the radio jet and provide further proof that CM2, CM3, CM4, and CM6 belong to the same radio jet.
Cyganowski et al. (2011) observed G035.02+0.35 with the B configuration of the VLA at X-band (3.6 cm) on 2009 May 7–14, five years before our C-band observations. In their Table 2, they reported the centroid positions of CM1, CM2, CM3, and CM4 at that epoch, obtained from a two-dimensional Gaussian fit (CM5 was not fitted because it is only marginally detected). The X-band map had a beam size of 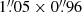 , oriented at position angle of 8.9°, and an rms of 0.03 mJy beam−1.
, oriented at position angle of 8.9°, and an rms of 0.03 mJy beam−1.
To directly compare the C- and X-band observations, we used the task clean of CASA and imaged the C-band dataset excluding uv-distances greater than 300 kλ to approximate the uv-coverage of the X-band dataset. We also applied a natural weighting and set a restoring beam size equal to that of the X-band map. The resulting C-band map (Fig. A.1) well resembles that at X-band presented in Fig. 1 of Cyganowski et al. (2011), where the continuum component CM6 is blended with CM1 and CM2. Notably, with respect to Fig. 1, the continuum emission in Fig. A.1 shows a higher degree of elongation in the direction of the jet axis, meaning that we retrieved extended jet emission that is resolved out with the longest baselines (i.e., greater uv-distances). In particular, the deconvolved (Gaussian) size of sources CM2 (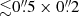 at a position angle of 17° ± 10°) and CM3 (
at a position angle of 17° ± 10°) and CM3 (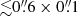 at a position angle of 21° ± 5°) proves a strong elongation of the radio continuum emission (a factor ≥2.5) and that this elongation is consistent with the estimated direction of the jet, within the uncertainties.
at a position angle of 21° ± 5°) proves a strong elongation of the radio continuum emission (a factor ≥2.5) and that this elongation is consistent with the estimated direction of the jet, within the uncertainties.
 |
Fig. A.1. Proper motion analysis of the radio continuum sources in G035.02+0.35. Left panel: 2014 C-band map (contours) processed under similar conditions of uv-coverage and restoring beam size as the 2009 X-band map of Cyganowski et al. (2011), for comparison. Contour levels are indicated to the bottom at multiples of the 1σ rms; the beam size is shown in the bottom left corner. Radio continuum labels, jet axis, and ticks are the same as in the Fig. 1. Red and blue crosses mark the centroid positions of CM1, CM2, CM3, and CM4 in May 2014 and 2009, respectively, as obtained from a two-dimensional Gaussian fit of the C- and X-band maps (X-band positions from Table 2 of Cyganowski et al. 2011). Individual centroids have been registered by aligning the positions of CM2 in 2014 and 2009. Right panels: zoom-in near to the centroids of CM3 (top), CM1 (middle), and CM4 (bottom). The extent of each map is the same; angular offsets (in arcsec) are referred to the phase center. The size of each cross quantifies the uncertainty in the centroid position (see Sect. A). For CM1, CM3, and CM4, we indicate the magnitude of the proper motions (and uncertainty) inferred from the displacement of their centroids between the two epochs. The dotted line and the gray shadow mark the jet axis and its 3σ uncertainty (±1.8°), respectively. |
In Fig. A.1 we compare the position of the continuum sources in May 2014 (red crosses) and May 2009 (blue crosses). Similar to Cyganowski et al. (2011), we fit sources CM1, CM2, CM3, and CM4 with a two-dimensional Gaussian distribution in order to determine their centroid positions (Table A.1). We then compared the relative position of these centroids between the two epochs by aligning the positions of CM2, which corresponds to the origin of the radio jet.
Proper motion study of CM1, CM3, and CM4 with respect to CM2.
In the right panels of Fig. A.1, we enlarge the regions around CM1, CM3, and CM4 for a detailed analysis of the centroid positions. The size of the red and blue crosses quantifies the positional uncertainty of the Gaussian fits; this uncertainty is calculated from the following formula: (FWHM/2) × (σ/I), where I and σ are the peak intensity and the rms noise, respectively (e.g., Reid et al. 1988). The FWHM is conservatively taken equal to the common beam size of the C- and X-band maps. These plots show that CM3 and CM4 are moving away from the position of CM2 and are consistent with the jet axis (dotted line) within a confidence level of about 2σ. The gray shadow marks the 3σ uncertainty of the jet axis. This result gains more strength when compared to the position of CM1, which has not significantly changed in time, and it further supports the interpretation that CM3 and CM4 belong to the same radio jet that originates at the position of CM2.
In the right panels of Fig. A.1, we also report the magnitude of the proper motions for CM1, CM3 and CM4 with respect to CM2, estimated from the displacement of their centroids (Col. 9 of Table A.1). For CM3, we calculate a velocity of 120 km s−1 with an uncertainty of 90 km s−1. For CM4, we calculate a velocity of 220 km s−1 with an uncertainty of 200 km s−1. These values are consistent with the proper motions of nonthermal knots measured in other sources (e.g., Rodríguez-Kamenetzky et al. 2016), providing an estimate of the shock velocities and a lower limit on the underlying jet velocity.
Appendix B: Additional material
Summary of VLA observations toward G035.02+0.35 (code 14A-133).
Continumm fluxes of centimeter sources in G035.02+0.35.
 |
Fig. B.1. Radio continuum map (left) and spectral index analysis (right) of component CM8, which is located to the NE of CM2, at a projected distance of |
All Tables
All Figures
 |
Fig. 1. Extended radio jet emission driven by source CM2 in G035.02+0.35. Middle panel: continuum map obtained with the A-configuration of the VLA at C band (without constraints on uv-coverage). Contour levels, at multiples of the 1σ rms, are indicated at the top; levels higher than 10σ are drawn in gray shades. The beam size is shown in the bottom left corner. A scale bar in units of au is drawn near the bottom axis. The field of view covers the radio continuum sources detected within 0.1 pc from CM2 (CM8 in Fig. B.1), whose centimeter spectral index (α) traces radio thermal jet emission (from Paper I). Labels are indicated in red near each source. Components CM3, CM4, and CM6 are aligned along a position angle of 25.5° ± 0.6° with respect to CM2 (dotted line), tracing the location of four jet knots. Ticks are marked along the jet direction in steps of 6000 au from CM2. Side panels: centimeter spectral energy distribution of radio components surrounding CM2. Each plot shows the logarithm of the integrated flux (in mJy) as a function of the logarithm of the observed frequency (in Hz) for four data points. Details for CM2 were presented in Paper I. Different frequency bands are labeled near the bottom axis together with the reference wavelength; gray shades mark the boundary of each band. The spectral index values (α) and their uncertainties, derived from a linear fit of the four data points, are specified in the upper left corner of each panel. Assuming an electron temperature of 104 K, the spectral energy distribution of source CM1 is well reproduced by a model of homogeneous H II region with a Strömgren radius (RS) of 630 au, number of Lyman photons (NLy) of 1045.85 s−1, electron density (ne) of 8.8 × 104 cm−3, and emission measure of 4.8 × 107 pc cm−6. |
| In the text | |
 |
Fig. 2. Comparison between the radio jet emission driven by source CM2 (yellow contours) and the 4.5 μm nebula imaged by Spitzer in the region (green scale). The radio continuum map is the same as in Fig. 1, together with the jet direction and ticks (dotted white line). Contour levels are indicated at the bottom. The logarithmic (green) scale of the 4.5 μm emission is drawn in the top wedge. The enhanced resolution (HPBW) of the Spitzer map is shown in the bottom left corner (see Sect. 2 for details). |
| In the text | |
 |
Fig. A.1. Proper motion analysis of the radio continuum sources in G035.02+0.35. Left panel: 2014 C-band map (contours) processed under similar conditions of uv-coverage and restoring beam size as the 2009 X-band map of Cyganowski et al. (2011), for comparison. Contour levels are indicated to the bottom at multiples of the 1σ rms; the beam size is shown in the bottom left corner. Radio continuum labels, jet axis, and ticks are the same as in the Fig. 1. Red and blue crosses mark the centroid positions of CM1, CM2, CM3, and CM4 in May 2014 and 2009, respectively, as obtained from a two-dimensional Gaussian fit of the C- and X-band maps (X-band positions from Table 2 of Cyganowski et al. 2011). Individual centroids have been registered by aligning the positions of CM2 in 2014 and 2009. Right panels: zoom-in near to the centroids of CM3 (top), CM1 (middle), and CM4 (bottom). The extent of each map is the same; angular offsets (in arcsec) are referred to the phase center. The size of each cross quantifies the uncertainty in the centroid position (see Sect. A). For CM1, CM3, and CM4, we indicate the magnitude of the proper motions (and uncertainty) inferred from the displacement of their centroids between the two epochs. The dotted line and the gray shadow mark the jet axis and its 3σ uncertainty (±1.8°), respectively. |
| In the text | |
 |
Fig. B.1. Radio continuum map (left) and spectral index analysis (right) of component CM8, which is located to the NE of CM2, at a projected distance of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



