| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 7 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201833836 | |
| Published online | 26 February 2019 | |
Astronomical bounds on the modified Chaplygin gas as a unified dark fluid model
1
College of Medical Laboratory, Dalian Medical University, Dalian 116044, PR China
e-mail: lh@dmu.edu.cn
2
Department of Physics, Liaoning Normal University, Dalian 116029, PR China
Received:
12
July
2018
Accepted:
13
January
2019
The modified Chaplygin gas could be considered to abide by the unified dark fluid model because the model might describe the past decelerating matter dominated era and at present time it provides an accelerating expansion of the Universe. In this paper, we have employed the Planck 2015 cosmic microwave background anisotropy, type-Ia supernovae, observed Hubble parameter data sets to measure the full parameter space of the modified Chaplygin gas as a unified dark matter and dark energy model. The model parameters Bs, α, and B determine the evolutional history of this unified dark fluid model by influencing the energy density ρMCG = ρMCG0[Bs + (1 − Bs)a−3(1 + B)(1 + α)]1/(1 + α). We assumed the pure adiabatic perturbation of unified modified Chaplygin gas in the linear perturbation theory. In the light of Markov chain Monte Carlo method, we find that Bs = 0.727+0.040+0.075−0.039−0.079, α = −0.0156+0.0982+0.2346−0.1380−0.2180, B = 0.0009+0.0018+0.0030−0.0017−0.0030 at 2σ level. The model parameters α and B are very close to zero and the nature of unified dark energy and dark matter model is very similar to cosmological standard model ΛCDM.
Key words: dark energy / cosmological parameters
© ESO 2019
1. Introduction
In modern cosmology, many theoretical models have been used to explain the current accelerating expansion Amendola & Tsujikawa (2010). Accelerating expansion of the Universe has been shown from the type Ia supernova (SNIa) observations Riess et al. (1998), Perlmutter et al. (1999) in 1998. Other more recent and updated observational results, including current cosmic microwave background (CMB) anisotropy measurement from Planck 2015 Planck Collaboration I (2016), Planck Collaboration XI (2016), Planck Collaboration XIII (2016), and the updated SNIa data sets from the Joint Light-curve Analysis (JLA) sample SDSS Collaboration (2014), also strongly support the present acceleration of the Universe. The latest release of Planck 2015 full-sky maps about the CMB anisotropies Planck Collaboration XIII (2016) indicates that baryon matter component occupies about 4% for total energy density, and about 96% energy density in the Universe is invisible which includes dark energy and dark matter. Dark energy (DE) as an exotic component with negative pressure drives the accelerated expansion of the Universe. And it is shown that DE takes up about two-thirds of the total energy density from cosmic observations. The remaining one third is dark matter (DM). In this way several theoretical DE models have already been constructed, for the reviews and papers, see Amendola & Tsujikawa (2010), Weinberg (1989), Sahni & Starobinsky (2000), Carroll (2001), Peebles & Ratra (2003), Padmanabhan (2003), Copeland et al. (2006). However there exists another possibility that the invisible energy component is a unified dark fluid, in other words, a mixture of dark matter and dark energy.
If one treats the dark energy and dark matter as a unified dark fluid, the corresponding models have been put forward and studied in Kunz (2009), Capozziello et al. (2006), Hipolito-Ricaldi et al. (2010), Ananda & Bruni (2006), Balbi et al. (2006), Xu et al. (2011, 2012a,b), Kamenshchik et al. (2001), Barrow (1988), Bento et al. (2002, 2004), Barreiro et al. (2008), Li et al. (2009), Wu & Yu (2007), Park et al. (2010), Liang et al. (2011), Xu (2013a,b), Li & Xu (2014a,b), Lu et al. (2008), Xu & Lu (2010), Aviles & Cervantes-Cota (2011), Luongo & Quevedo (2012), Camera et al. (2009, 2011), Bertacca et al. (2008), Yang & Xu (2013), Bruni et al. (2013), Piattella et al. (2010), Benaoum (2002), Ferreira & Avelino (2015), Bilic et al. (2004), Beca & Avelino (2007), Avelino et al. (2004, 2008, 2014), Beca et al. (2003), Avelino & Ferreira (2015).
In these unified dark fluid models, the Chaplygin gas (CG) and its generalized models have been widely studied in order to explain the accelerating universe in Kamenshchik et al. (2001), Barrow (1988), Bento et al. (2002, 2004), Barreiro et al. (2008), Li et al. (2009), Wu & Yu (2007), Park et al. (2010), Xu et al. (2011, 2012b), Liang et al. (2011), Xu (2013a,b), Li & Xu (2014a,b), Lu et al. (2008), Xu & Lu (2010) Benaoum (2002), Ferreira & Avelino (2015), Bilic et al. (2004), Avelino et al. (2004, 2008, 2014), Beca & Avelino (2007), Beca et al. (2003), Avelino & Ferreira (2015). The most interesting property for this kind of scenarios is that two unknown dark sections-dark energy and dark matter can be unified by using an exotic equation of state. The original Chaplygin gas model can be obtained from the string Nambu-Goto action in the light cone coordinate Pedram & Jalalzadeh (2008). In modern cosmology, the Chalygin gas could be considered as an dark fluid which might describe the past decelerating matter dominated era and at present time it provides an accelerating expansion of the Universe. For the generalized Chaplygin gas (GCG) model Bento et al. (2002), the equation of state 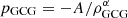 is characterized by two model parameters A and α. Ferreira & Avelino (2015) considered an extended family of GCG models parameterized by three positive real parameters A, α, and β, which, for two specific choices of β [β = 1 and β = (1 + α)/(2α)], is described by two different Lagrangians previously identified in the literature with GCG. Besides, a modified Chaplygin gas (MCG) model Benaoum (2002), which is a unified dark matter and dark energy model, is also an example of a dark fluid model. MCG model could be considered as the further generalization of GCG, whose equation of state is
is characterized by two model parameters A and α. Ferreira & Avelino (2015) considered an extended family of GCG models parameterized by three positive real parameters A, α, and β, which, for two specific choices of β [β = 1 and β = (1 + α)/(2α)], is described by two different Lagrangians previously identified in the literature with GCG. Besides, a modified Chaplygin gas (MCG) model Benaoum (2002), which is a unified dark matter and dark energy model, is also an example of a dark fluid model. MCG model could be considered as the further generalization of GCG, whose equation of state is 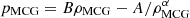 , with three degrees of freedom. This unified dark fluid model could also be adopted to explain the accelerating expansion of the Universe.
, with three degrees of freedom. This unified dark fluid model could also be adopted to explain the accelerating expansion of the Universe.
For the perturbation analysis of the CG and its generalized models, one might usually draw a different conclusion from the non-linear clustering effect or linear perturbation level. When one considers the non-linear clustering of the unified dark fluid, which may result in significant changes to the background evolution of the universe in unified dark energy models, see Bilic et al. (2004), Avelino et al. (2004, 2008, 2014), Beca & Avelino (2007), Beca et al. (2003), and has recently been shown, the GCG may be consistent with current observational constraints over a wide region of parameter space, assuming that there is a sufficiently high level of non-linear clustering on small scales Avelino et al. (2014). In addition, when one focusses only on the cosmological effect in the linear perturbation theory, one could also use the recent observations to test the model parameter space of the CG and its generalized models, such as Xu et al. (2011, 2012b).
In order to constrain the model parameter space of MCG model in the linear perturbation theory, Xu et al. (2011) treated the dark energy and dark matter as a whole energy component, performed a global fitting on MCG model by the Markov chain Monte Carlo (MCMC) method by the observational data sets: CMB from WMAP-7 WMAP Collaboration (2011), BAO Percival et al. (2010), SNIa from Union2 SCP Collaboration (2010) data. The tight constraint had been obtained: 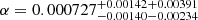 ,
, 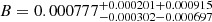 , and
, and 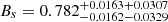 at 2σ level. For the very small values of MCG parameters α and B, it was concluded that MCG is very close to Λ cold dark matter (ΛCDM) model. Moreover, Avelino & Ferreira (2015) presents the much stronger constraints imposed in MCG model by the observed rotation curves of spiral galaxies, the results show that B < 10−8 if the MCG is to be regarded as a unified dark fluid.
at 2σ level. For the very small values of MCG parameters α and B, it was concluded that MCG is very close to Λ cold dark matter (ΛCDM) model. Moreover, Avelino & Ferreira (2015) presents the much stronger constraints imposed in MCG model by the observed rotation curves of spiral galaxies, the results show that B < 10−8 if the MCG is to be regarded as a unified dark fluid.
In the light of Xu et al. (2011), we test the parameter space of MCG model in the linear perturbation theory with the recently released data sets, CMB from Planck 2015 Planck Collaboration I (2016), Planck Collaboration XI (2016), Planck Collaboration XIII (2016), SNIa from JLA sample SDSS Collaboration (2014), and the observed Hubble parameter data Moresco et al. (2016), it is worth anticipating that a different observational constraint could be obtained.
This paper is organized as follows. In Sect. 2, we show the background and perturbation equations of MCG model when the pure adiabatic contribution has been considered. In Sect. 3, based on the MCMC method, the global fitting results of MCG model parameters are obtained by the joint observational data sets. Then, analyze the measurement results. Conclusion are drawn in the last section.
2. The background and perturbation equations of modified Chaplygin gas model
The MCG fluid is treated as a unified component in the Universe, its equation of state is
where B, A and α are model parameters. It is obvious that the GCG model is recovered when the value of B is zero.
By adopting the continuity equation, one could calculate the energy density of MCG fluid as
for B ≠ −1, where 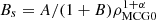 . We take Bs, B and α as MCG model parameters, and they would be constrained by the observational data sets. From Eq. (2), one can find that 0 ≤ Bs ≤ 1 is demanded to keep the positivity of energy density. If α = 0 and B = 0 in Eq. (2), the standard ΛCDM model is recovered. Taking MCG as a unified dark fluid, the equation of state of MCG is
. We take Bs, B and α as MCG model parameters, and they would be constrained by the observational data sets. From Eq. (2), one can find that 0 ≤ Bs ≤ 1 is demanded to keep the positivity of energy density. If α = 0 and B = 0 in Eq. (2), the standard ΛCDM model is recovered. Taking MCG as a unified dark fluid, the equation of state of MCG is
In the flat Universe, one has the Friedmann equation
where ΩMCG = 1 − Ωb − Ωr, H and H0 are the Hubble parameter and its present value, Ωb and Ωr are dimensionless energy density parameters of baryon and radiation.
Here, we consider the perturbation evolution of MCG fluid in order to explore the effects on the CMB anisotropic power spectrum. Under the assumption of pure adiabatic contribution to the perturbations Xu et al. (2012b), the sound speed of MCG is
According to the conservation of energy–momentum tensor 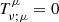 , ignoring the shear perturbation, one could the deduce the perturbation equations of density contrast and velocity divergence for MCG in the linear perturbation theory Xu et al. (2012b)
, ignoring the shear perturbation, one could the deduce the perturbation equations of density contrast and velocity divergence for MCG in the linear perturbation theory Xu et al. (2012b)
where the dot denotes the derivative of conformal time, the notations follow Ma and Bertschinger Ma & Berschinger (1995). In our calculation, the shear perturbation σMCG = 0 is assumed and the adiabatic initial conditions are used.
3. Observational data sets and methodology
In this section we first describe the astronomical data with the statistical technique to constrain the MCG scenarios and the results of the analyses. We include the following sets of astronomical data.
-
CMB: We used CMB data from the Planck 2015 measurements Planck Collaboration I (2016) and Planck Collaboration XI (2016), where we combined the full likelihoods
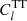 ,
, 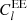 ,
, 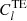 in addition with low-l polarization
in addition with low-l polarization 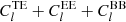 , which notationally is same with “PlanckTT, TE, EE + lowP” of Planck Collaboration XI (2016).
, which notationally is same with “PlanckTT, TE, EE + lowP” of Planck Collaboration XI (2016). -
JLA: This is the supernovae Type Ia sample that contains 740 data points spread in the redshift interval z ∈ [0.01, 1.30] SDSS Collaboration (2014). This low-redshift sample is the first indication for an accelerating universe.
-
Cosmic chronometers (CC): The Hubble parameter measurements from most old and passively evolving galaxies, known as cosmic chronometers have been considered to be potential candidates to probe the nature of dark energy due to their model-independent measurements. For a detailed description on howthe Hubble parameter values can be measured at different redshifts through this CC approach, and its usefulness, we refer to Moresco et al. (2016). Here, we have used 30 measurements of the Hubble parameter at different redshifts within the range 0 < z < 2.
So the total likelihood χ2 can be constructed as
In order to extract the observational constraints of the MCG scenarios, we use the publicly available MCMC package COSMOMC Lewis & Bridle (2002) equipped with a convergence diagnostic followed by the Gelman and Rubin statistics, which includes the CAMB code to calculate the CMB power spectrum. We modified this code for the MCG model with the perturbation of unified dark fluid. We have used the following eight-dimensional parameter space
where Ωbh2 stands for the density of the baryons and dark matter, 100θMC refers to the ratio of sound horizon and angular diameter distance, τ indicates the optical depth, Bs, α, and B are three added parameters of MCG model, ns is the scalar spectral index, and As represents the amplitude of the initial power spectrum. The pivot scale of the initial scalar power spectrum ks0 = 0.05 Mpc−1 is used. In the MCMC analysis, we took the following priors to model parameters: Ωbh2 ∈ [0.005, 0.1], ΘS ∈ [0.5, 10], τ ∈ [0.01, 0.8], Bs ∈ [0, 1], α ∈ [ − 1, 1], B ∈ [ − 1, 1], ns ∈ [0.5, 1.5] and log[1010As]∈[2.7, 4].
4. Analysis the fit results
In this section we summarize the main observational results extracted from the MCG unified model by using the three different combined observational data, CMB+JLA, CMB+CC, CMB+JLA+CC, described in Sect. 3 above. In Table 1 we summarize the main results of global fitting results, at the first sight, the combination CMB+CC provide a slightly different constraint results of the model parameters, comparing with CMB+JLA and CMB+JLA+CC. One could see that for the combination CMB+CC, both the mean value and best-fit value of the parameter Bs and H0 are lower, meanwhile the other two combination CMB+JLA and CMB+JLA+CC show the higher the mean value of best-fit value Bs and H0. Testing the result of the parameter α, the observational data sets favor a negative value, except for the mean value from CMB+JLA. Testing the result of the parameter B, the observational data sets support a very small and positive value, its order is 10−3 or 10−4. All the results of three different observational combination support that the parameters α and B are very close to zero, it means that the nature of MCG model is very similar to cosmological standard model ΛCDM. In order to clearly and visually show the difference between different combination, we have also plotted the one-dimensional marginalized posterior distribution on individual parameters in Fig. 1 which are fully corresponding to the Table 1. It is easy to see that for the parameters Ωbh2, τ, log[1010As], ns are almost the same for the three different combination of data sets, however one would see the obvious difference in the mean values with error bars for the parameters 100θMC, Bs, α, B, H0 (H0 is a derived parameter). Besides, the combination CMB+JLA and CMB+JLA+CC provide the nearly identical results, and these two cases’ global fittings show us their somewhat tighter constraint than that of CMB+CC. For the MCG model, the CC data set could not improve the constraint results.
 |
Fig. 1. One-dimensional marginalized distribution on individual parameters, whose results are obtained by the different combination of observational data sets CMB+CC (gray line), CMB+JLA (red line), and CMB+JLA+CC (green line). |
Then, we also show the one-dimensional marginalized posterior distribution and two-dimensional marginalized posterior distribution contours which include the MCG model parameters Bs, α, B are shown in Fig. 2, one could see that the parameter Ωbh2 owns the vague correlation with the other parameters, the MCG model parameters Bs and α show the obvious positive correlation, meanwhile, the parameters Bs and B, α and B show the negative correlation, both Bs and B show the distinct positive correlation with the derived parameter H0, but the correlation between α and H0 is not clear. Here we also extract the two-dimensional contours for several parameter pairs Bs − α, B − α, H0 − α, Bs − B, α − B, and H0 − B in Fig. 3, and the three-dimensional figures with colors between the parameter pairs Bs − α, Bs − B, and α − B and the present Hubble parameter H0 in Fig. 4. From the one-dimensional, two-dimensional, three-dimensional figures and the Table 1, one could see that the combinations CMB+JLA and CMB+JLA+CC show better constraint results than CMB+CC. The recent observational data sets, especially the combination CMB+JLA and CMB+JLA+CC, support both the negative and positive values of the parameters α and B which is close to zero, and testing the results of the combination CMB+JLA+CC, the mean value and best-fit value of α is negative, ones of B positive. The mean value of parameter Bs would be larger than 0.7 from both the combination CMB+JLA and CMB+JLA+CC, the mean value of parameter H0 would be larger than 68 km s−1 Mpc−1 from both the combination CMB+JLA and CMB+JLA+CC.
 |
Fig. 2. One-dimensional marginalized distribution on individual parameters and two-dimensional contours of MCG model at 1σ and 2σ regions, whose results are obtained by the different combination of observational data sets CMB+JLA (gray line or contour), CMB+CC (red line or contour), and CMB+JLA+CC (green line or contour). |
 |
Fig. 3. Two-dimensional contours of MCG model at 1σ and 2σ regions for the parameters pair, the dashed vertical line is corresponding to the parameter α = 0 or B = 0, whose results are obtained by the different combination of observational data sets CMB+CC (gray contour), CMB+JLA (red contour), and CMB+JLA+CC (green contour). |
 |
Fig. 4. Three-dimensional figures with colors of MCG model between the parameters pair Bs, α, B and derived parameter H0 for three different observational combination, the dashed vertical line is corresponding to the parameter α = 0 or B = 0, whose results, from left to right, are obtained by the different combination of observational data sets CMB+CC (left panel), CMB+JLA (middle panel), and CMB+JLA+CC (right panel). |
In order to well understand the effects of model parameters on the CMB temperature anisotropic power spectra, we plot the temperature power spectra of CMB, where one of three model parameters Bs, α, B varies, where the other relevant parameters are fixed to their mean values as listed in Table 1. The panels of Fig. 5 show, respectively, the effects of parameters Bs, α, and B on CMB power spectra. The model parameter α modifies the power law of the energy density of MCG, then it makes the gravity potential evolution at late epoch of the universe. As results, one can see the integrated Sachs–Wolfe (ISW) effect on the large scale as shown in the left panel of Fig. 5. In the early epoch, MCG behaves like cold dark matter with almost zero equation of state and speed of sound 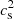 , therefore the variation of the values of α will change the ratio of energy densities of the effective cold dark matter and baryons. One can read the corresponding effects from the variation of the first and the second peaks of CMB power spectra. For various values of the model parameter Bs, decreasing the values of Bs, which is equivalent to increase the value of effective dimensionless energy density of cold dark matter, causes matter and radiation to become equal earlier, therefore decreasing the sound horizon. As a result, the first peak is depressed. Changing the value of the model parameter B, changes both the peak height and peak location. Decreasing the values of B decreases the peak height, and the peak location moves to the high-l region, because changing B causes the proportional relation of dark matter and baryons to change. Figure 6 shows CMB power spectra and its corresponding raito with mean values listed in Table 1 for MCG model and ΛCDM model. The black dashed line represents the ΛCDM model with mean values taken from Planck 2015 Planck Collaboration XIII (2016) constraint results. One can see that the MCG model matches both observational data points and the ΛCDM model well.
, therefore the variation of the values of α will change the ratio of energy densities of the effective cold dark matter and baryons. One can read the corresponding effects from the variation of the first and the second peaks of CMB power spectra. For various values of the model parameter Bs, decreasing the values of Bs, which is equivalent to increase the value of effective dimensionless energy density of cold dark matter, causes matter and radiation to become equal earlier, therefore decreasing the sound horizon. As a result, the first peak is depressed. Changing the value of the model parameter B, changes both the peak height and peak location. Decreasing the values of B decreases the peak height, and the peak location moves to the high-l region, because changing B causes the proportional relation of dark matter and baryons to change. Figure 6 shows CMB power spectra and its corresponding raito with mean values listed in Table 1 for MCG model and ΛCDM model. The black dashed line represents the ΛCDM model with mean values taken from Planck 2015 Planck Collaboration XIII (2016) constraint results. One can see that the MCG model matches both observational data points and the ΛCDM model well.
 |
Fig. 5. Effects on CMB temperature power spectra for the different values of the model parameter α and Bs. In the left figure, the blue dashed, red solid, and green dotted-dashed lines are for Bs = 0.827, 0.727, 0.627, respectively; in the middle figure, the blue dashed, red solid, and green dotted-dashed lines are for α = 0.5, −0.0156, −0.5, respectively; in the right figure, the blue dashed, red solid, and green dotted-dashed lines are for B = 0.05, −0.0009, −0.05, respectively; the other relevant parameters are fixed with the mean values of CMB+JLA+CC as shown in Table 1. |
Mean values of model parameters with 1σ and 2σ errors and best-fit values from the joint constraint, whose results are obtained by the different combination of observational data sets CMB+CC (second column), CMB+JLA (third column), and CMB+JLA+CC (fourth column).
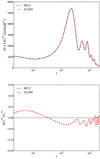 |
Fig. 6. CMB temperature power spectrum vs. multiple moment l, the red solid line is for the unified dark fluid model with mean values of CMB+JLA+CC as shown in Table 1, the black dashed line is for the ΛCDM model with the same observational combination. |
5. Summary
In this paper, we have employed the Planck 2015 cosmic microwave background anisotropy, type-Ia supernovae, and observed Hubble parameter data sets to measure the full parameter space of the modified Chaplygin gas as a unified dark matter and dark energy model. The parameters Bs, α, and B determine the evolutionary history of this unified dark fluid model by influencing the energy density ρMCG = ρMCG0[Bs + (1 − Bs)a−3(1 + B)(1 + α)]1/(1 + α). We assumed the pure adiabatic perturbation of unified modified Chaplygin gas. In the light of the MCMC method, we find that at 2σ level, 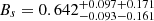 ,
, 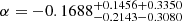 ,
, 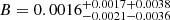 from CMB+CC,
from CMB+CC, 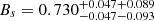 ,
, 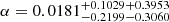 ,
, 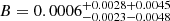 from CMB+JLA,
from CMB+JLA, 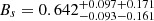 ,
, 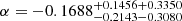 , and
, and 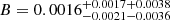 from CMB+JLA+CC. A tight constraint is obtained as shown in Table 1 and Fig. 2. The results of all three different observational combinations support the idea that the parameters α and B are very close to zero, the order of α is 10−2, the order of B is 10−4. This means that the nature of the MCG model is very similar to the cosmological standard model ΛCDM. The MCG model can well match both observational data points and the ΛCDM model. Currently available data sets of CMB, JLA, and CC could not distinguish MCG model from ΛCDM model.
from CMB+JLA+CC. A tight constraint is obtained as shown in Table 1 and Fig. 2. The results of all three different observational combinations support the idea that the parameters α and B are very close to zero, the order of α is 10−2, the order of B is 10−4. This means that the nature of the MCG model is very similar to the cosmological standard model ΛCDM. The MCG model can well match both observational data points and the ΛCDM model. Currently available data sets of CMB, JLA, and CC could not distinguish MCG model from ΛCDM model.
Here we have not used the baryon acoustic oscillation (BAO) data to test the MCG model parameter space, because if one wants to use the BAO data to test a unified dark fluid model, one needs to know the sound horizon at the redshift of drag epoch zd. Usually, zd is obtained by using the accurate fitting formula Eisenstein & Hu (1998) which is valid if the matter scalings ρb ∝ a−3 and ρc ∝ a−3 are respected. Obviously, this is not true for the unified dark fluid model. One might reconsider the fiducial cosmology according to the analysis of Percival et al. (2010), Hamann et al. (2010), and Xu et al. (2012b), this will be an important research field in our future work.
Acknowledgments
H. Li’s work is supported by the National Natural Science Foundation of China under Grant No. 81601855. W. Yang’s work is supported by the National Natural Science Foundation of China under Grants No. 11705079 and 11647153.
References
- Amendola, L., & Tsujikawa, S. 2010, Dark Energy: Theory and Observations (New York: Cambridge University Press) [Google Scholar]
- Ananda, K. N., & Bruni, M. 2006, Phys. Rev. D, 74, 023523 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Aviles, A., & Cervantes-Cota, J. L. 2011, Phys. Rev. D, 84, 083515 [NASA ADS] [CrossRef] [Google Scholar]
- Avelino, P. P., & Ferreira, V. M. C. 2015, Phys. Rev. D, 91, 083508 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Avelino, P. P., Beca, L. M. G., de Carvalho, J. P. M., Martins, C. J. A. P., & Copeland, E. J. 2004, Phys. Rev. D, 69, 041301 [NASA ADS] [CrossRef] [Google Scholar]
- Avelino, P. P., Beca, L. M. G., & Martins, C. J. A. P. 2008, Phys. Rev. D, 77, 063515 [NASA ADS] [CrossRef] [Google Scholar]
- Avelino, P. P., Bolejko, K., & Lewis, G. F. 2014, Phys. Rev. D, 89, 103004 [NASA ADS] [CrossRef] [Google Scholar]
- Balbi, A., Bruni, M., & Quercellini, C. 2006, Phys. Rev. D, 76, 103519 [NASA ADS] [CrossRef] [Google Scholar]
- Barrow, J. D. 1988, Nucl. Phys. B, 310, 743 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Barreiro, T., Bertolami, O., & Torres, P. 2008, Phys. Rev. D, 78, 043530 [NASA ADS] [CrossRef] [Google Scholar]
- Beca, L. M. G., & Avelino, P. P. 2007, MNRAS, 376, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Bento, M. C., Bertolami, O., & Sen, A. A. 2002, Phys. Rev. D, 66, 043507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bento, M. C., Bertolami, O., & Sen, A. A. 2004, Phys. Rev. D, 70, 083519 [NASA ADS] [CrossRef] [Google Scholar]
- Benaoum, H. B., ArXiv e-prints [arXiv:hep-th/0205140] [Google Scholar]
- Bertacca, D., Bartolo, N., Diaferio, A., & Matarrese, S. 2008, JCAP, 10, 023 [NASA ADS] [CrossRef] [Google Scholar]
- Beca, L. M. G., Avelino, P. P., De Carvalho, J. P. M., & Martins, C. J. A. P. 2003, Phys. Rev. D, 67, 101301 [NASA ADS] [CrossRef] [Google Scholar]
- Bilic, N., Lindebaum, R. J., Tupper, G. B., & Violier, R. D. 2004, JCAP, 11, 008 [NASA ADS] [CrossRef] [Google Scholar]
- Bruni, M., Lazkoz, R., & Rozas-Fernandez, A. 2013, MNRAS, 431, 2907 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, S. M. 2001, Liv. Rev. Relat., 4, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Camera, S., Bertacca, D., Diaferio, A., et al. 2009, MNRAS, 399, 1995 [NASA ADS] [CrossRef] [Google Scholar]
- Camera, S., Kitching, T. D., Heavens, A. F., et al. 2011, MNRAS, 415, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Capozziello, S., Nojiri, S., & Odintsov, S. D. 2006, Phys. Lett. B, 632, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Copeland, E. J., Sami, M., & Tsujikawa, S. 2006, Int. J. Mod. Phys. D, 15, 1753 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1998, ApJ, 496, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, V. M. C., & Avelino, P. P. 2015, Phys. Rev. D, 98, 043515 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, J., Hannestad, S., Raffelt, G. G., & Wong, Y. Y. Y. 2010, JCAP, 07, 022 [NASA ADS] [CrossRef] [Google Scholar]
- Hipolito-Ricaldi, W. S., Velten, H. E. S., & Zimdahl, Z. 2010, Phys. Rev. D, 82, 063507 [NASA ADS] [CrossRef] [Google Scholar]
- Kamenshchik, A. Y., Moschella, U., & Pasquier, V. 2001, Phys. Lett. B, 511, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Kunz, M. 2009, Phys. Rev. D, 80, 123001 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., & Xu, L. 2014a, Eur. Phys. J. C, 74, 2765 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, W., & Xu, L. 2014b, Eur. Phys. J. C, 74, 2870 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, Z., Wu, P., & Yu, H. 2009, JCAP, 09, 017 [NASA ADS] [Google Scholar]
- Liang, N., Xu, L., & Zhu, Z. 2011, A&A, 527, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lu, J., Xu, L., Chang, B., Gui, Y., & Liu, H. 2008, Phys. Lett. B, 662, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Luongo, O., & Quevedo, H. 2012, Astrophys. Space Sci., 338, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C. P., & Berschinger, E. 1995, ApJ, 455, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Moresco, M., Pozzetti, L., Cimatti, A., et al. 2016, JCAP, 05, 014 [NASA ADS] [CrossRef] [Google Scholar]
- Padmanabhan, T. 2003, Phys. Rep., 380, 235 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Park, C. G., Hwang, J. C., Park, J., & Noh, H. 2010, Phys. Rev. D, 81, 063532 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E., & Ratra, B. 2003, Rev. Mod. Phys., 75, 559 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pedram, P., & Jalalzadeh, S. 2008, Phys. Lett. B, 659, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Piattella, O. F., Bertacca, D., Bruni, M., & Pietrobon, D. 2010, JCAP, 01, 014 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2016, A&A, 594, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Sahni, V., & Starobinsky, A. A. 2000, Int. J. Mod. Phys. D, 9, 373 [NASA ADS] [Google Scholar]
- SCP Collaboration (Amanullah, R., et al.) 2010, ApJ, 716, 712 [NASA ADS] [CrossRef] [Google Scholar]
- SDSS Collaboration (Betoule, M., et al.) 2014, A&A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weinberg, S. 1989, Rev. Mod. Phys., 61, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- WMAP Collaboration (Komatsu, E., et al.) 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, P., & Yu, H. 2007, Phys. Lett. B, 644, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L. 2013a, Phys. Rev. D, 87, 043503 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L. 2013b, Eur. Phys. J. C, 73, 2344 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, L., & Lu, J. 2010, JCAP, 03, 025 [NASA ADS] [Google Scholar]
- Xu, L., Wang, Y., & Noh, H. 2011, Eur. Phys. J. C, 72, 1931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, L., Wang, Y., & Noh, H. 2012a, Phys. Rev. D, 85, 043003 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L., Lu, J., & Wang, Y. 2012b, Eur. Phys. J. C, 72, 1883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, W., & Xu, L. 2013, Phys. Rev. D, 88, 023505 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mean values of model parameters with 1σ and 2σ errors and best-fit values from the joint constraint, whose results are obtained by the different combination of observational data sets CMB+CC (second column), CMB+JLA (third column), and CMB+JLA+CC (fourth column).
All Figures
 |
Fig. 1. One-dimensional marginalized distribution on individual parameters, whose results are obtained by the different combination of observational data sets CMB+CC (gray line), CMB+JLA (red line), and CMB+JLA+CC (green line). |
| In the text | |
 |
Fig. 2. One-dimensional marginalized distribution on individual parameters and two-dimensional contours of MCG model at 1σ and 2σ regions, whose results are obtained by the different combination of observational data sets CMB+JLA (gray line or contour), CMB+CC (red line or contour), and CMB+JLA+CC (green line or contour). |
| In the text | |
 |
Fig. 3. Two-dimensional contours of MCG model at 1σ and 2σ regions for the parameters pair, the dashed vertical line is corresponding to the parameter α = 0 or B = 0, whose results are obtained by the different combination of observational data sets CMB+CC (gray contour), CMB+JLA (red contour), and CMB+JLA+CC (green contour). |
| In the text | |
 |
Fig. 4. Three-dimensional figures with colors of MCG model between the parameters pair Bs, α, B and derived parameter H0 for three different observational combination, the dashed vertical line is corresponding to the parameter α = 0 or B = 0, whose results, from left to right, are obtained by the different combination of observational data sets CMB+CC (left panel), CMB+JLA (middle panel), and CMB+JLA+CC (right panel). |
| In the text | |
 |
Fig. 5. Effects on CMB temperature power spectra for the different values of the model parameter α and Bs. In the left figure, the blue dashed, red solid, and green dotted-dashed lines are for Bs = 0.827, 0.727, 0.627, respectively; in the middle figure, the blue dashed, red solid, and green dotted-dashed lines are for α = 0.5, −0.0156, −0.5, respectively; in the right figure, the blue dashed, red solid, and green dotted-dashed lines are for B = 0.05, −0.0009, −0.05, respectively; the other relevant parameters are fixed with the mean values of CMB+JLA+CC as shown in Table 1. |
| In the text | |
 |
Fig. 6. CMB temperature power spectrum vs. multiple moment l, the red solid line is for the unified dark fluid model with mean values of CMB+JLA+CC as shown in Table 1, the black dashed line is for the ΛCDM model with the same observational combination. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



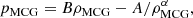
![$$ \begin{aligned} \rho _{\rm MCG}=\rho _{\rm MCG0}\left[B_{s}+(1-B_{s})a^{-3(1+B)(1+\alpha )}\right]^{\frac{1}{1+\alpha }}, \end{aligned} $$](/articles/aa/full_html/2019/03/aa33836-18/aa33836-18-eq10.gif)
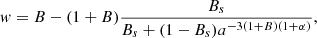
![$$ \begin{aligned} \frac{H^{2}}{H^{2}_{0}}=\Omega _{\rm b}a^{-3}+\Omega _{r}a^{-4}+\Omega _{\rm MCG} \left[B_{s}+(1-B_{s})a^{-3(1+B)(1+\alpha )}\right]^{\frac{1}{1+\alpha }}, \end{aligned} $$](/articles/aa/full_html/2019/03/aa33836-18/aa33836-18-eq13.gif)
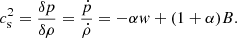
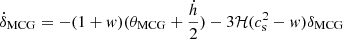
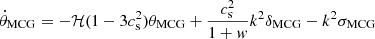
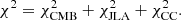
![$$ \begin{aligned} P\equiv \{\omega _{\rm b},100\theta _{\rm MC},\tau , B_{s}, \alpha , B, n_{\rm s}, \log [10^{10}A_{\rm s}]\} \end{aligned} $$](/articles/aa/full_html/2019/03/aa33836-18/aa33836-18-eq23.gif)