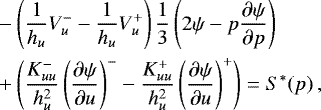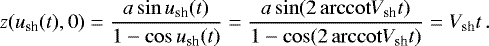| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A203 | |
| Number of page(s) | 13 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201833999 | |
| Published online | 21 February 2019 | |
Fermi bubbles from stochastic acceleration of electrons in a Galactic outflow
1
Institute for Theoretical Physics and Cosmology (TTK), RWTH Aachen University,
Sommerfeldstr. 16,
52074
Aachen,
Germany
e-mail: pmertsch@physik.rwth-aachen.de
2
Niels Bohr International Academy, Niels Bohr Institute,
Blegdamsvej 17,
2100
Copenhagen,
Denmark
3
Kavli Institute for Particle Astrophysics & Cosmology,
2575 Sand Hill Road, M/S 29,
Menlo Park,
CA
94025,
USA
4
Department of Physics and Applied Physics, Stanford University,
Stanford,
CA
94305,
USA
Received:
1
August
2018
Accepted:
7
December
2018
The discovery of the Fermi bubbles – a huge bilobular structure seen in GeV gamma-rays above and below the Galactic centre – implies the presence of a large reservoir of high energy particles at ~10 kpc from the disk. The absence of evidence for a strong shock coinciding with the edge of the bubbles, and constraints from multi-wavelength observations point towards stochastic acceleration by turbulence as a likely mechanism of acceleration. We have investigated the time-dependent acceleration of electrons in a large-scale outflow from the Galactic centre. For the first time, we present a detailed numerical solution of the particle kinetic equation that includes the acceleration, transport and relevant energy loss processes. We also take into account the addition of shock acceleration of electrons at the bubble’s blast wave. Fitting to the observed spectrum and surface brightness distribution of the bubbles allows determining the transport coefficients, thereby shedding light on the origin of the Fermi bubbles.
Key words: acceleration of particles / shock waves / turbulence / cosmic rays / ISM: jets and outflows / gamma rays: ISM
© ESO 2019
1 Introduction
The detection of the Fermi bubbles – a huge bi-lobular structure seen in GeV gamma-rays – is certainly one of the great discoveries made with the Fermi/LAT instrument. Due to their position on the sky (see below), they are likely emanating from the Galactic centre and the most speculated about sources are the supermassive black hole at the Galactic centre and star formation or star burst in the Galactic centre region. These processes shape Galactic structure on the largest scales and as such the Fermi bubbles allow us to study Galactic feedback in our own backyard. Furthermore, given their prominence in gamma-rays, they are an important arena for studies of sources of diffuse GeV emissions, like searches for signals from self-annihilation or decay of dark matter. Finally, the production of the gamma-rays and the acceleration of the underlying particles are of astrophysical interest in itself.
Originally, the Fermi bubbles were observed in a search (Dobler et al. 2010) for the gamma-ray counterpart of a microwave excess seen from the inner Galaxy (Finkbeiner 2004; Dobler & Finkbeiner 2008; Ade et al. 2013). A more detailed analysis (Su et al. 2010) unveiled some surprising properties that were later largely confirmed by Ackermann et al. (2014). In the following we summarise the most important observational properties of the Fermi bubbles in gamma-rays.
Geometry
The Fermi bubbles are approximately centred at zero Galactic longitude, symmetric about the Galactic plane, 50° wide in longitude with each bubble extending up to 50° in latitude, see, for example, Fig. 22 of Ackermann et al. (2014). On these scales, they constitute the first evidence for an outflow from the Milky Way. (On smaller scales, there had previously been evidence in X-rays in an x-shaped feature around the Galactic centre.) The bubbles’ symmetry about the Galactic plane and their being centred around zero longitude imply an origin at Galactic centre (distance dGC ≃ 8.5 kpc). A wind with a constant speed of 1000 km s−1 would need about 9.9 Myr to expand into a bubble of size ~dGC tan50° ≃ 10.1 kpc, modulus projection effects: at a latitude of 50°, we might be seeing the limb-brightened edge of a bubble of radius dGC sin50° ≃ 6.5 kpc, thus reducing the time-scale to 6.4 Myr. We note that because the eastern edge of the northern bubble is very close to the position of the North Polar Spur, which is part of the radio Loop I. Initially, this led to claims of the bubbles being associated with the Loop I structure (Casandjian & Grenier 2009).
Spectrum
The gamma-ray flux shows a hard spectrum, mostly ∝ E−2 and extending from a few hundred MeV up to a few hundred GeV, see, for example, Fig. 18 of Ackermann et al. (2014). At lower energies, the spectrum is significantly harder, and at high energies there is evidence for a spectral softening or an exponential cut-off. This spectral shape immediately invites speculation about its physical origin, that is whether the gamma-rays are of leptonic (from inverse-Compton scattering) or hadronic (π0 decay) origin. Given the estimates of the physical conditions, inside the bubbles, see below, bremsstrahlung is most likely negligible.
While the spectral shoulder around a few hundred MeV determined in the earlier analysis (Su et al. 2010) seemed to be well fit by the kinematic feature fromπ0 decay, the new best-fit spectrum appears to be extending to lower energies. Likely, a hadronic model needs to have a spectral break (a steeper spectrum of the underlying protons at lower energies). This is in addition to the required spectral break or cut-off at high energies. The physical origin of these breaks is a priori unclear.
In leptonic models these breaks are easily explained. The inverse-Compton spectrum is naturally rather hard: in the Thomson regime, a gamma-ray spectrum ∝ ɛ−s with (s ~ 2) with a cutoff at ɛcut of a few hundred GeV can be produced byan electron spectrum ∝ E−Γe−E∕Ecut with Γ = 2s − 1 ~ 3 and 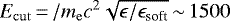 GeV for soft photon energies of ɛ ~ 1 eV. These estimates are strictly only valid in the Thomson regime. In the numerical computations, however, we have used the full Klein–Nishina cross-section and taken into account the relativistic corrections.
GeV for soft photon energies of ɛ ~ 1 eV. These estimates are strictly only valid in the Thomson regime. In the numerical computations, however, we have used the full Klein–Nishina cross-section and taken into account the relativistic corrections.
Surface brightness
The surface brightness shows little variation over the bubbles, but has sharp edges as can already be seen in the residual map, cf. for example Fig. 29 of Ackermann et al. (2014). More quantitatively, this is evidenced by profiles of the gamma-ray flux across the bubble edge, shown for instance in Fig. 22 of Ackermann et al. (2014). There is clearly a jump in intensity from a value close to zero (after template subtraction) outside to a relatively constant value inside the bubbles. In fact, the only substructure seen is a rather large enhancement of emissivity in the east of the southern bubble, called the “cocoon”, the origin of which is yet unknown. There have also been claims of evidence for a narrow and extended, jet-like feature (Su & Finkbeiner 2012), however, the analysis by the Fermi Collaboration (Ackermann et al. 2014) has found this feature not to be significant.
The flat surface brightness and sharp edges are one of the most puzzling features of the bubbles. The sharp edges require an efficient confinement of the gamma-ray producing particles and the flat surface brightness requires a peculiar distribution of volume emissivity. Idealising each bubble as a spherically symmetric volume with outer radius R, only an emissivity that varies with radius r as 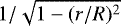 will give a flat surface brightness and sharp edges.
will give a flat surface brightness and sharp edges.
Spectral uniformity
The bubbles show similar morphologies in different energy bins ranging from 1 to 500 GeV (see e.g. Fig. 22 of Ackermann et al. 2014) or equivalently the spectrum is uniform in different parts of the bubbles. Specifically, the gamma-ray spectrum has been analysed in different latitude bands and the spectrum in the bubble edge region and the interior have been compared: for the latitude bands, no variation has been found above and below ± 10°. Between − 10° and + 10° there is an excess at the Galactic Centre (Hooper & Slatyer 2013), likely with a spherical symmetry, and its connection to the Fermi bubbles is unclear at this point (Ackermann et al. 2017). Furthermore, no variation between the edge region and the interior was found (Su et al. 2010; but see also Keshet & Gurwich 2017).
The spectral uniformity is also very surprising for such an extended structure. Leptonic models in particular would be expected to lead to some variation, depending on the region of energising of the high-energy electrons. This is due to cooling losses by synchrotron radiation and inverse-Compton emission. A conservative estimate of the cooling time is 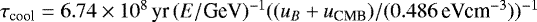 , for magnetic fields and radiation fields of energy densities
, for magnetic fields and radiation fields of energy densities 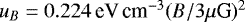 and uCMB = 0.262 eV cm−3, respectively, that is of the same order as the bubble age for 100 GeV electrons. Therefore, electrons energised in the Galactic plane will be subject to considerable cooling while travelling out into the bubble volume. This results in softer spectra at larger distances from the Galactic centre and thus a softer gamma-ray spectrum at higher latitudes. In addition, the energy densities in the radiation backgrounds that the electron inverse-Compton scatter on should be varying with distance from the disk: while the CMB is of course spatially uniform, the energy densities in both the optical/UV and the infrared backgrounds should become smaller further away from the disk. The fact that this is not observed implies that the variation in the radiation backgrounds must be counter-balanced by a variation in the electron spectrum to some degree.
and uCMB = 0.262 eV cm−3, respectively, that is of the same order as the bubble age for 100 GeV electrons. Therefore, electrons energised in the Galactic plane will be subject to considerable cooling while travelling out into the bubble volume. This results in softer spectra at larger distances from the Galactic centre and thus a softer gamma-ray spectrum at higher latitudes. In addition, the energy densities in the radiation backgrounds that the electron inverse-Compton scatter on should be varying with distance from the disk: while the CMB is of course spatially uniform, the energy densities in both the optical/UV and the infrared backgrounds should become smaller further away from the disk. The fact that this is not observed implies that the variation in the radiation backgrounds must be counter-balanced by a variation in the electron spectrum to some degree.
While the discovery of the Fermi bubbles was certainly a surprise, it was not the first hint at the presence of Galaxy-scale outflows. Kiloparsec-scale outflows have been observed for starburst galaxies, for example in ionised gas. Even in our own Milky Way, there had been hints at the presence of a Galaxy-scale outflow, possibly connected with high-energy cosmic rays: observationsin soft X-rays, most notably from ROSAT, showed signs of an x-shaped feature, interpreted as evidence of a biconical outflow in analogy with structures seen in other galaxies.
The presence of a population of high-energy cosmic ray electrons was already hinted at by the microwave haze, an excess of microwaves from the Galactic centre, pointing at a similarly hard electron spectrum (Finkbeiner 2004; Dobler & Finkbeiner 2008; Ade et al. 2013). Note, however, the possible influence of systematic effects due to template subtraction; Mertsch & Sarkar 2010. The search for a counterpart of the microwave haze in gamma-rays was in fact what motivated the first study that lead to the discovery of the Fermi bubbles (Dobler et al. 2010).
X-rays
A number of studies have investigated the properties of the thermal gas in the Fermi bubbles and in the Galactic halo from X-ray observations. The parameters can be either inferred from the thermal, soft X-ray spectrum (Kataoka et al. 2013, 2015) or from individual Oxygen lines (Miller & Bregman 2016). The gas densities inferred are of the order ngas ~ 10−3 cm−3 and the temperatures of the gas just outside the bubbles vary between kT ≃ 0.3 keV and 0.5 keV. This is higher than the canonical temperatureof the Galactic halo of kT ≃ 0.2 keV and requires a heating agent, perhaps a weak shock with a low Mach number; 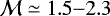 . Finally, with the typical sound speed in the Galactic halo of cs ≃ 200 km s−1, one infers shock speeds of vsh ≃ 300–500 km s−1.
. Finally, with the typical sound speed in the Galactic halo of cs ≃ 200 km s−1, one infers shock speeds of vsh ≃ 300–500 km s−1.
The absence of evidence for a strong shock coinciding with the bubble edge implies that diffusive shock acceleration at the bubble edge cannot be the primary mechanism of acceleration. If electrons get accelerated in the Galactic plane or even in a hypothetical large-scale jet along the Galactic minor axis, they need to travel over distances of several kpc without much energy loss to fill the bubble volume. As a result they will suffer severe cooling losses and a gradual softening of their spectrum, or even quench the electron density completely. Note further that the low shock speeds found by the X-ray modelling lead to even larger dynamical times than with the 1000 km s−1 assumed above, making the energy losses even more important.
Quasar absorption
The observation of absorption by the gas associated with the bubbles from a background quasar can also be used to set bounds on the outflow speed. In the UV absorption lines from PDS 456 two (asymmetric) components with velocities of v ≃ − 235 and + 250 km s−1 with respect to the local standard of rest could be identified (Miller & Bregman 2016). For the conical outflow assumed in that study, this implies an upper limit on the outflow speed of ≳ 900 km s−1. This seems to be in conflict with the shock speed inferred from the X-ray modelling described above. Note, however, that the outflow speed inferred from the absorption lines of one quasar is very dependent on the assumed geometry of the flow. Future observations of additional sight lines towards other quasars can help mapping out the flow structure, thus possibly also constraining it geometry, and might bring the results into agreement with the values inferred from X-rays.
The Fermi bubbles have also generated a great deal of interest on the modelling side (Crocker & Aharonian 2011; Cheng et al. 2011, 2012, 2014, 2015a,b; Zubovas et al. 2011; Mertsch & Sarkar 2011; Zubovas & Nayakshin 2012; Guo & Mathews 2012; Yang et al. 2012, 2013; Lacki 2014; Crocker et al. 2014, 2015; Fujita et al. 2013, 2014; Thoudam 2013; Mou et al. 2014, 2015; Sarkar et al. 2015; Sasaki et al. 2015; Yang & Ruszkowski 2017). The variety of models is most conveniently classified by:
-
the source of energy: super massive black hole or stellar winds/supernovae;
-
the acceleration region: jet or sources in the disk or in situ (by shocks or turbulence);
-
the nature of the high-energy particles: hadrons or leptons.
Of course, the individual options are not mutually exclusive. For instance, in hadronic models, the bulk of the high-energy gamma-rays comes from decay of neutral pions. Charged pions, however, get produced at similar rates and, given the radiation fields, their e± byproducts can inverse-Compton scatter soft photons into low energy gamma-rays. However, in this particular scenario the synchrotron spectrum would be too soft (Ackermann et al. 2014)
As a full discussion of all proposed models is beyond the scope of this paper, only two particular classes of models will be presented, and a few concrete examples will be shown.
Jet models
Astrophysical jets are thought to be powered by accretion onto a spinning, compact object, like neutron stars or black holes. Given the position and symmetry of the Fermi bubbles, the supermassive black hole at the Galactic centre is a prime candidate. Although conspicuously quiet (its X-ray luminosity is currently more than 11 orders below the Eddington luminosity), there is indirect evidence for earlier epochs of active accretion, for example from X-ray reflections.
Jets are usually associated with high speeds ≳1000 km s−1. This allows for the electrons to be less impacted by energy losses than in starburst/star formation models and therefore the source of energisation of the high-energy electrons can be in the Galactic disk or inside the jet. (Note, however, that the jet speed is not necessarily directly implying the dynamical age as the bubbles can be formed by a fountain-like back flow due to the termination of the jet by the ram pressure of gas in the Galactic halo.)
One of the earliest studies of a leptonic jet model employing a hydrodynamical simulation (Guo & Mathews 2012) found that the lateral extent of the Fermi bubbles could be explained if the jet was underdense but slightly overpressured. If active at 10% of the Eddington luminosity for 1–2 Myr until about a Myr ago, the morphology would match the observations. A subsequent MHD simulation of the Fermi bubbles blown up by a jet (Yang et al. 2012) showed further that the shock compression at the bubble edges would compress the magnetic field such that it gets aligned with the bubble edge. We will return to this point in Sect. 2.3.
Star formation/star burst models
The Galactic winds that get collectively powered by an ensemble of stellar winds or supernova activity are usually operating at smaller speeds, ≲500 km s−1. This implies a larger dynamic time-scales than for the jet model, leading to a preference in the literature for hadronic models, as leptons would cool too fast. In hadronic models, on the other hand, cosmic rays need to be accumulated over much longer time scales, given the low gas densities on the order of 10−3 cm−3 (see Sect. 1), to produce the observed gamma-ray fluxes. In turn, this and the observed hard E−2 spectrum require an effective confinement of the high-energy cosmic rays to the bubbles and a suppression of (energy-dependent) escape (see, however, Keshet & Gurwich 2017). The sources of high energy particles are nevertheless oftentimes assumed to be in the Galactic disk.
The most detailed numerical star formation/star burst model for the Fermi bubbles as of yet (Sarkar et al. 2015) employs a hydrodynamical code to investigate the interaction of a Galactic wind with the circumgalactic medium. It is found that a luminosity of 5 × 1040 erg s−1 and a density in the halo of 10−3 cm−3 can reproduce the morphology observed in gamma-rays and is also in agreement with X-ray observations. Interestingly, this luminosity is close to the one inferred from the current star formation rate, SFR ≃ 0.007–0.1 M⊙ yr−1, when assuming an efficiency of 30% for conversion into mechanical power, 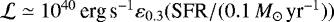 .
.
The outflow from the inner Galaxy leads to a shock structure known from the heliosphere or supernova remnants, with a radial forward shock at ~ 11 kpc, a more tangled contact discontinuity extending to ~8 kpc above the Galactic centre and a very much tangled reverse shock a few kiloparsecs inside of the contact discontinuity. Thus, in this model, the edge of the gamma-ray bubble does not coincide with the projection of the forward shock, but rather the contact discontinuity. Whether this is due to the diffusion prescription of Sarkar et al. (2015) changing across the contact discontinuity would need to be explored further.
The observation of γ-rays from the bubbles implies a huge reservoir of high-energy particles in the Galactic halo, but the source and the mechanism of acceleration of these particles has not been established thus far. Other sources of non-thermal particles, like supernova remnants, pulsar wind nebulae, jets in active galaxies or winds in starburst galaxies, show evidence of shocks through X-rays or ionization lines. The Fermi bubbles, however, show no such evidence of a (strong) shock, raising the question of the possible mechanism of acceleration. Acceleration by plasma turbulence (or “stochastic acceleration”, SA), however, can fill the bubbles with high-energy electrons (see, Petrosian 2012 for a recent review of SA).
A first SA model for the Fermi bubbles (Mertsch & Sarkar 2011) was presented quickly after their discovery. This model was employing the solution of a simplified version of the transport equation. Specifically, diffusion was ignored as a spatial transport process and advection was the only transport process. In this framework, cosmic ray electrons are just passively advected with the downstream flow while being stochastically accelerated. The time scale hierarchy tdyn ≫ tcool ≫ tacc of dynamical, cooling and acceleration times, allows a steady-state solution of the variation of electron spectrum with radius for a given spatial variation of these time scales and the escape time, tesc. While successful in explaining the overall spectrum of the bubbles as well as the sharp edges, the lack of diffusive transport was an important shortcoming. In addition, the interstellar radiation fields on which the cosmic ray electrons scatter was assumed homogeneous which must be an oversimplification. What is needed is a detailed numerical model, taking into account all the spatial transport processes (diffusion, advection), energy losses (ionisation, bremsstrahlung, synchrotron, inverse Compton scattering) and energy gains (shock and SA).
In the remainder of this paper, we will present our computation of the SA of high-energy electrons in the Fermi bubbles. Section 2 introduces our method for solving the transport equation on a grid that is suited for the geometry of the bubbles. We will define three setups and specify the parameter values considered. We will show our result for those three setups in Sect. 3 and comment on compatibility with observational data. Section 4 contains a discussion of the energetics of our models. In Sect. 5 we summarise and conclude.
2 Method
2.1 Transport equation
We start by considering the following transport equation for the (isotropic) phase space density f(r, p, t), for example (Blandford & Eichler 1987),
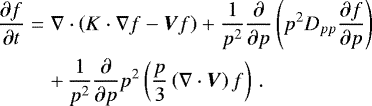 (1)
(1)
Here, spatial transport is governed by the diffusion tensor K and the advection velocity V, the latter also leading to adiabatic gains/losses through the divergence term. Momentum space diffusion depends on the diffusion coefficient Dpp.
For numerical convenience, we reformulate Eq. (1) in terms of ψ = 4πp2 × f, the differential (in momentum) particle density which is related to the total particle density n = ∫ dp ψ. We also add momentum and catastrophic losses − ∂(ṗψ)∕∂p and − ψ∕τ and a source term S,
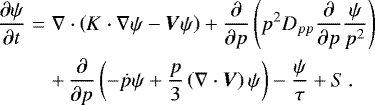 (2)
(2)
2.2 Shock equation
At the shock, we need to carefully evaluate the transport Eq. (2) because of the discontinuity in V (and in other transport parameters). We denote quantities upstream (downstream) of the shock by a minus (plus) sign. We demand ψ to be continuous across the shock,
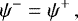
and allow for the presence of sources at the shock, S*δ(r −rsh), so that by continuity
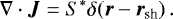
With Gauss’ theorem, we can write this as
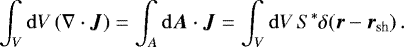 (3)
(3)
The particle density flux J is here
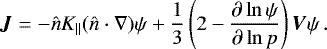 (4)
(4)
where 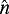 is a unit vector normal to the shock.
is a unit vector normal to the shock.
For numerical solution of the transport and shock equations, we need to specify a coordinate system.
 |
Fig. 1 Toroidal coordinates. Surfaces of constant v are tori of varying radii surrounding the foci ring of radius a and are shown in red. Surfaces of constant u are spheres of varying radii that all intersect the foci ring and are shown in blue. |
2.3 Coordinates
A convenient choice of coordinates should help simplify the computation, for example in that it eases or altogether eliminates the transformation from the simulation coordinates to the frame in which the diffusion tensor is diagonal. The method for treating the discontinuity of the shock requires for the shock normal to be aligned with one coordinate direction.
Given the bi-lobular shape of the bubbles as observed in gamma-rays (Su et al. 2010; Ackermann et al. 2014) and used in the (M)HD simulations (Guo & Mathews 2012; Yang et al. 2012), leads us to employ toroidal coordinates (u, v, ϕ) which map to cartesian coordinates (x, y, z) through
![\begin{align}x &= \frac{a \sinh{v} \cos{\phi}}{\cosh{v} - \cos{u}} \, ,\\[1.5pt] y &= \frac{a \sinh{v} \sin{\phi}}{\cosh{v} - \cos{u}} \, ,\\[1.5pt] z &= \frac{a \sin{u}}{\cosh{v} - \cos{u}} \, .\end{align}](/articles/aa/full_html/2019/02/aa33999-18/aa33999-18-eq14.png)
In Fig. 1, we show a plot of surfaces of constant u and v. Surfaces of constant u are spheres of varying radii that all intersect a foci ring of radius a. Surfaces of constant v are tori of varying radii surrounding the foci ring. We set a = 1 kpc throughout unless otherwise noted.
From the transformation between cartesian and toroidal coordinates, Eqs. (5)–(7), we can compute the scale factors
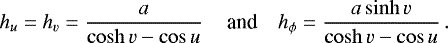 (8)
(8)
Here and in the following, we assume azimuthal (ϕ) symmetry and also define the cylindrical radial coordinate 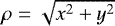 .
.
2.3.1 Transport equation in toroidal coordinates
We can write the transport Eq. (2) in toroidal coordinates,
![\begin{align*} \frac{\partial \psi}{\partial t} &= \left[ \frac{(\cosh v - \cos u)^2}{a^2} K_{uu} \right] \frac{\partial^2 \psi}{\partial u^2} \nonumber \\ & + \left[ - \frac{(\cosh v - \cos u) \sin u}{a^2} K_{uu} + \frac{(\cosh v - \cos u)^2}{a^2} \dfrac{\partial K_{uu}}{\partial u} \right] \frac{\partial \psi}{\partial u} \nonumber \\ & + \left[ - \frac{\cosh v - \cos u}{a} V_u \right] \frac{\partial \psi}{\partial u} \nonumber \\ & + \left[ \frac{(\cosh v - \cos u)^2}{a^2} K_{vv} \right] \frac{\partial^2 \psi}{\partial v^2} \nonumber \\ & + \left[ \frac{(\cosh v - \cos u)(1 - \cosh v \cos u)}{a^2 \sinh v} K_{vv} \right. \nonumber \\ & \left. + \frac{(\cosh v - \cos u)^2}{a^2} \dfrac{\partial K_{vv}}{\partial v} \right] \frac{\partial \psi}{\partial v} \nonumber \\ & + D_{pp} \dfrac{\partial^2 \psi}{\partial p^2} + \left[ \dfrac{\partial D_{pp}}{\partial p} - \frac{2}{p} D_{pp} \right] \dfrac{\partial \psi}{\partial p} \nonumber \\ & + \left[ -\dot{p} + \frac{p}{3} (\nabla \cdot \vec{V} ) \right] \dfrac{\partial \psi}{\partial p} \nonumber \\ & + \left[ \frac{2}{p^2} D_{pp} - \frac{2}{p} \dfrac{\partial D_{pp}}{\partial p} - \dfrac{\partial \dot{p}}{\partial p} - \frac{2}{3} (\nabla \cdot \vec{V}) - \frac{1}{\tau} \right] \psi + S \, .\end{align*}](/articles/aa/full_html/2019/02/aa33999-18/aa33999-18-eq17.png) (9)
(9)
A comment about the velocity divergence,
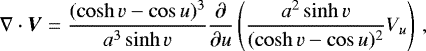
is in order. For an incompressible flow, 0 ≡∇⋅V, but if we want fronts to follow lines of constant u, then we require the v-dependence (see discussion in Sect. 2.6.1 below)
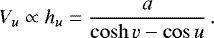
We note that in Eq. (9)
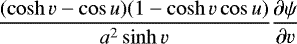 (10)
(10)
is indeterminate for v → 0 as sinhv → 0 and ∂ψ∕∂v → 0 (due to symmetry). Employing l’Hôpital’s rule, we can replace this by
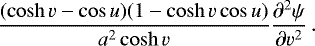 (11)
(11)
2.3.2 Shock equation in toroidal coordinates
If the shock is in the u-plane and the flux is perpendicular to the shock, J = Juû, Eq. (3) reads
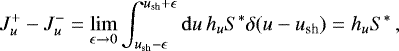 (12)
(12)
where (cf. Eq. (4))
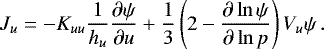 (13)
(13)
2.4 Finite-difference method
Parabolic partial differential equations like the transport equation (Eq. (2)) are oftentimes solved numerically by finite-difference methods. Here, we numerically solve the transport equation in toroidal coordinates (cf. Eq. (9)) in the widely used Crank–Nicolson scheme (Crank et al. 1947). This is a semi-implicit method which results in a tridiagonal system that can be efficiently solved by the Thomas algorithm. The difficulty in the case at hand is the presence of the shock which breaks the tridiagonality of the involved matrix. In particular at the shock position, we solve the shock equation (Eq. (14)) instead of the transport equation (Eq. (9)). Here we follow a method outlined by Langner (2004) which treats transport in the heliosphere in the presence of the helioshperic termination shock.
2.5 Computational grid
The computational grid is three dimensional: two spatial, toroidal coordinates (u and v) and one momentum coordinate (p). Choosing the spatial grids to be linear renders the coefficients for the finite difference scheme particularly simple and offers the added advantage of fine resolution close the Galactic centre and at the bases of the bubbles. For the momentum grid we chose logarithmic spacing in order to evenly sample the spectra which will be close to power law:
![\begin{align}&u_i = u_{\mathrm{min}} + i \Delta r = u_{\mathrm{min}} + \frac{i}{n} (u_{\mathrm{max}} - u_{\mathrm{min}}) \, , \quad \hspace*{-0.5pt}\,i = 0, \mathellipsis n, \\[4pt] &v_j = v_{\mathrm{min}} + j \Delta \theta = v_{\mathrm{min}} + \frac{j}{m} (v_{\mathrm{max}} - v_{\mathrm{min}}) \, , \quad j = 0, \mathellipsis m, \\[4pt] &p_k = p_{\mathrm{min}} \mathrm{e}^{k \Delta \ln p} = p_{\mathrm{min}} \mathrm{e}^{k \left[ \ln \left( p_{\mathrm{max}} / p_{\mathrm{min}} \right) \right] / q} \, , \quad \ \;k = 0, \mathellipsis q. \end{align}](/articles/aa/full_html/2019/02/aa33999-18/aa33999-18-eq25.png)
For the minimum and maximum coordinate values and number of grid points, we need to balance accuracy and computational speed under the constraint of suppressing numerical artefacts, for example oscillations. Here, we have chosen the following grid parameters:
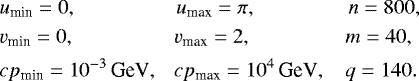
For umax = π and vmax →∞, the computational domain is covering the whole ρ–z plane. To limit the size of the grid while assuming linear spacing, we limit vmax to finite values. This will affect the transport and acceleration of particles close to ρ = 1 kpc; however, due to the presence of strong diffuse, conventional emission, the Galactic disk is usually excluded from diffuse studies, cf., for example, Su et al. (2010); Ackermann et al. (2014).
The spatial part of the computational grid is shown in Fig. 2.
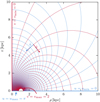 |
Fig. 2 Spatial part of the computational grid. For clarity, we only show n = 100 spacings in the u-direction here, whereas in the numerical simulations, we have chosen n = 800 throughout. Note also that the use of vmax = 2 instead of ∞ ignores a small region of space. |
2.6 Parameters
Diffusion is only really isotropic in the limit of a small regular magnetic field B0 , that is when the fractional turbulence level 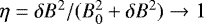 . In the general case, the symmetric part of the diffusion tensor K can be written as K = diag(K⊥, K⊥, K∥), in cartesiancoordinates where without loss of generality we have assumed that B0 ∥ẑ. In quasi-linear theory, K∥ and K⊥ scale differently with the turbulence level η); K∥ ∝ η−1 while K⊥ ∝ η. In our case, we assume
. In the general case, the symmetric part of the diffusion tensor K can be written as K = diag(K⊥, K⊥, K∥), in cartesiancoordinates where without loss of generality we have assumed that B0 ∥ẑ. In quasi-linear theory, K∥ and K⊥ scale differently with the turbulence level η); K∥ ∝ η−1 while K⊥ ∝ η. In our case, we assume 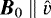 and so K⊥ = Kuu ∝ η and K∥ = Kvv ∝ η−1, and adopt amomentum dependence consistent with resonant interactions with Kolmogorov turbulence,
and so K⊥ = Kuu ∝ η and K∥ = Kvv ∝ η−1, and adopt amomentum dependence consistent with resonant interactions with Kolmogorov turbulence,

For the momentum diffusion coefficient, we are employing a relation from quasi-linear theory,
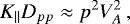 (21)
(21)
where VA is the Alfvén speed. This fixes the momentum dependence of Dpp,
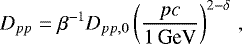 (22)
(22)
and parametrises its normalisation relative to K∥ through the Alfvén speed 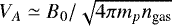 ,
,

We assume the shock to follow an isocontour in u and in order for advection fronts to follow lines of constant u, we choose the advection velocity V = Vuû and its absolute value proportional to the scale factor hu = a∕(coshv − cosu). We introduce an additional u-dependence, (1 − cosu), and define the compression ratio r of the shock, that is the ratio of upstream to downstream speed in the shock frame, such that
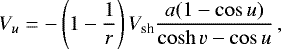 (26)
(26)
This results in the shock travelling with constant speed Vsh along the z-axis:
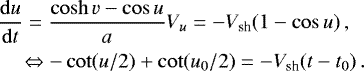
With t0 = 0 and u0 = u(t0) = π,
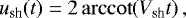
With the Vsh = 3 × 10−7 kpc yr ≃ 300 km s−1 that we adopt, the shock reaches a height of z = 6 kpc in t = 20 Myr. And with the u-dependence in Eq. (26) we get
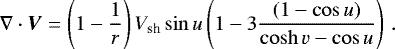
Here, weset the compression ratio to 4, but it is strictly only so along the z-axis.
One can estimate the timescales for shock acceleration and stochastic acceleration as 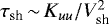 and τSA ~ p2∕Dpp ~
and τSA ~ p2∕Dpp ~ 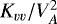 with the ratio
with the ratio 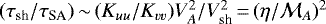 , where
, where 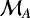 is the Alfv́en Mach number (see, Petrosian 2012). In the following, we adopt VA = 300 km s−1 everywhere. The shock velocity, however, is not constant along the shock as the bubble expands more slowly laterally than vertically. At the top, vsh = 300 km s−1 which coincides with the Alfvén speed and thus the rates for shock acceleration and stochastic acceleration will be equal for isotropic diffusion (Kuu = Kvv). For anisotropic diffusion (Kuu < Kvv), shock acceleration even operates faster than stochastic acceleration. In contrast, at the foot of the bubble, the shock velocity is much lower than the Alfvén speed, rendering shock acceleration inefficient. In either case, the effectivevolume where shock acceleration operates is rather small because of the small diffusion length Kuu ∕Vu.
is the Alfv́en Mach number (see, Petrosian 2012). In the following, we adopt VA = 300 km s−1 everywhere. The shock velocity, however, is not constant along the shock as the bubble expands more slowly laterally than vertically. At the top, vsh = 300 km s−1 which coincides with the Alfvén speed and thus the rates for shock acceleration and stochastic acceleration will be equal for isotropic diffusion (Kuu = Kvv). For anisotropic diffusion (Kuu < Kvv), shock acceleration even operates faster than stochastic acceleration. In contrast, at the foot of the bubble, the shock velocity is much lower than the Alfvén speed, rendering shock acceleration inefficient. In either case, the effectivevolume where shock acceleration operates is rather small because of the small diffusion length Kuu ∕Vu.
We idealise the shock as a surface of constant pseudo-radius u. Furthermore, we assume that the (large-scale) B-field (which defines the coordinate system in which the diffusion tensor is diagonal) is aligned with these surface of constant u, that is 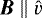 where
where  is the unit vector of the pseudo-polar coordinate, v.
is the unit vector of the pseudo-polar coordinate, v.
The interstellar radiation fields (ISRFs) affect both the momentum losses of the electrons and the generation of gamma-rays through inverse-Compton scattering (Blumenthal & Gould 1970). Here we adopt a model1 (Porter & Strong 2005) from version 50 of the GALPROP code (Moskalenko & Strong 1998; Orlando & Strong 2013). This contains the energy density of the ISRF on a grid in cylindrical coordinates. We bilinearly interpolate from the cylindrical grid to our toroidal grid. As the cylindrical grid only extends to z = ±5 kpc, we linearly extrapolate for |z| > 5 kpc, but set the ISRF to zero if it were otherwise negative. The left three panels of Fig. 3 show the energy densities in the CMB, IR and UV/optical ranges as a function of ρ and z.
The coherent magnetic field is assumed to follow lines of constant u (see above), that is 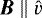 , but we only use this to define the coordinates in which the diffusion tensor is diagonal. For synchrotron losses and the computation of radio/microwave fluxes we ignore the regular field for the time being. Instead, we only consider a turbulent component with rms value
, but we only use this to define the coordinates in which the diffusion tensor is diagonal. For synchrotron losses and the computation of radio/microwave fluxes we ignore the regular field for the time being. Instead, we only consider a turbulent component with rms value
![\begin{equation*} B_{\text{rms}}(\rho, z) = B_0 \exp \left[ -\frac{\rho}{\rho_0} - \frac{z}{z_0} \right] \, . \end{equation*}](/articles/aa/full_html/2019/02/aa33999-18/aa33999-18-eq46.png) (27)
(27)
Here and in the following, we choose the set of parameters B0 = 3 μG, ρ0 = 5 kpc and z0 = 1 kpc as a fiducial model. The energy density of this turbulent magnetic field is shown in the rightmost panel of Fig. 3.
For the source term Q, we simply adopt a Dirac delta function, both in position and in momentum,
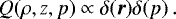 (28)
(28)
The normalisation is determined by fitting to the gamma-ray data from Fermi/LAT (Ackermann et al. 2014). Specifically, we require the maximum gamma-ray flux in our map at 10 GeV to be E2J = 8 × 10−7GeV cm−2 s−1 sr−1.
In principle we would have liked to also investigate the possibility of accelerating electrons from the thermal background. However, for an ambient temperature T this would have required extending the momentum grid down to thermal momenta of the order pc ≃ kBT ≃ 8.6 keV (T∕(108 K)), that is by an additional three orders of magnitude. Apart from increasing the size of the momentum grid by more than 40%, the short acceleration time tsa = p2∕Dpp ∝ pδ at low momenta would have required much finer time-stepping (by a factor ~ 10), significantly increasing the computational cost further.
In the following we present three exemplary setups for the bubbles, showing a conceptual evolution from the simplest possible model that however fails, to a more complicated model that can reproduce the data sufficiently well. For each setup, we detail and justify our parameter choices before comparing our results to the available gamma–ray and microwave data. See Fig. 4 for a schematic overview of the three setups, but refer to the text below for explanations.
 |
Fig. 3 Energy densities ε of the CMB, IR and optical/UV parts of the ISRF as well as the energy density of the B-field in the ρ–z plane. We define the energy ranges as 4.3 × 10−5–1.4 × 10−2 eV for the CMB, 1.4 × 10−2–0.22 eV for the IR and 0.22–14 eV for the optical/UV. |
2.6.1 Model 1: isotropic diffusion
In the first setup, we consider diffusion inside the bubbles to be isotropic,
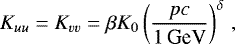 (29)
(29)
where β = vparticle∕c, K0,uu = K0,vv = 10−7 kpc2 yr−1 ≈ 3 × 1028 cm2 s−1 and δ = 1∕3. This is closeto the diffusion coefficient inferred from the boron-to-carbon ratio measured at the solar position, Kiso(1 GeV) ≃ 4.1 × 1028 cm2 s−1 (Trotta et al. 2011). Outside the bubbles, in the Galactic halo, we adopt K0,uu = 10−8 kpc2 yr−1 ≈ 3 × 1027 cm2 s−1 and K0,vv = 10−6 kpc2 yr−1 ≈ 3 × 1029 cm2 s−1, that is diffusion is markedly anisotropic (η = 10), with particles diffusing faster along the v-direction than along the u-direction.
As a fiducial value for the momentum diffusion coefficient, we here adopt 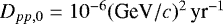 inside the bubbles, so an acceleration time
inside the bubbles, so an acceleration time
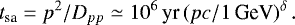 (30)
(30)
The Alfvén speed VA ≃ 300 km s−1 can be accommodated by, for example B0 ≃ 6 μG and ngas ≃ 2 × 10−3 cm−3. Outside the bubbles, we set 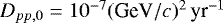 , in line with the usual scaling.
, in line with the usual scaling.
2.6.2 Model 2: anisotropic diffusion
For the second setup, we consider the possibility that also diffusion inside the bubbles is anisotropic. Specifically, we adopt Kuu,0 = K⊥,0 = 10−7 kpc2 yr−1 and Kvv,0 = K∥,0 = 10−6 kpc2 yr−1 inside and Kuu,0 = K⊥,0 = 10−8 kpc2 yr−1 and Kvv,0 = K∥,0 = 10−5 kpc2 yr−1 outside the bubbles. We keep δ at 1∕3.
We set 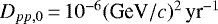 inside the bubbles and
inside the bubbles and 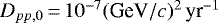 outside the bubbles. All the other parameters plus the ISRFs and the B-field are as in the first model, cf. Sect. 2.6.1.
outside the bubbles. All the other parameters plus the ISRFs and the B-field are as in the first model, cf. Sect. 2.6.1.
 |
Fig. 4 Schematic overview of the three models. (See text for explanations.) |
Summary of parameter choices in models 1, 2 and 3.
2.6.3 Model 3: anisotropic diffusion and turbulent shell
In the presence of a source of turbulence, the assumption of (almost) isotropic diffusion of the first (second) setup can be justified. In the following we assume that the shock itself is generating such turbulence through hydrodynamic (e.g. Raleigh–Taylor or Kelvin–Helmholtz) instabilities. To take into account that this turbulence could be dissipated at large, kiloparsec distances from the shock, we constrain this region to a shell behind the shock and assume strongly anisotropic diffusion in the rest of the bubble volume (cf. the right panel of Fig. 4). In particular, we choose

This setup has the added benefit that according to quasi–linear theory, the stochastic acceleration rate Dpp ∕p2 is also enhanced in a thin shell,

To match the synchrotron emission, we changed B0 to 10 μG and z0 to 2 kpc, keeping ρ0 = 5 kpc.
In Table 1, we have summarised the most important parameters for the three setups.
3 Results
3.1 Model 1: isotropic diffusion
In the upper panel of Fig. 5, we show gamma-ray sky maps of model 1 at E = 1, 10, 102 and 103 GeV produced byInverse Compton emission of the CR electrons. The lower left panel shows the spectra for different directions in the bubbles, each line corresponding to a direction marked by crosses in the sky maps (upper panel) using the same colour coding.
The spatial variation of the spectra is rather limited and on average the spectra nicely reproduce the measurements of the overall bubble spectrum by Fermi/LAT (Ackermann et al. 2014). In particular, there is a clear spectral cut-off at a few hundred GeV that is due to the competition between acceleration and energy losses. The simulated spectra also nicely reproduce the curvature below a GeV due to very hard electron spectra.
In the bottom right panel of Fig. 5, we also show the flux profiles along the gradient directions indicated in the sky maps (upper panels). It can be seen that even in this simple setup, the flux is increasing mostly within ~ 10° of the bubble edge, but visually it appears in the sky maps that the bubbles’ edges are still too soft.
3.2 Model 2: anisotropic diffusion
A first attempt at fixing the soft edges consist of adopting moderately anisotropic diffusion inside the bubbles (model 2); this should prevent the electrons accelerated further out in the bubble from returning to the centre and create a less centre-brightened profile. In Fig. 6, we present the gamma-ray maps, spectra and profiles in much the same way as in Fig. 5. Comparing both figures, it appears that the edges have not become much sharper. If anything, the bubbles are now slightly more bottom-heavy.
3.3 Model 3: anisotropic diffusion and turbulent shell
In Fig. 7 we show gamma-ray maps, spectra and angular profiles for model 3, in much the same way as in Figs. 5 and 6. Comparing with these, we note that the angular profile is indeed sharpened. In particular at the top of the bubble, the intensity increases within less than 10° from the bubble edge. Comparing the sky maps at 1 and 10 GeV, it is apparent that the morphology is still spectrally rather uniform, as is in fact observed (Su et al. 2010; Hooper & Slatyer 2013; Ackermann et al. 2014). This is even more obvious from the bottom left panel of Fig. 7.
In orderto investigate the origin of the sharper edges, we show the distribution of CR electrons and their spectra in Fig. 8. More precisely, in the top panels of Fig. 8, we show the distribution of electron energy p4 f ~ p2ψ ~ E2n as a function of position at energies pc = 1, 10, 102 and 103 GeV and at time t = 2.4 × 107 yr. While electrons of energies below ~1 GeV are very much confined to the surroundings of the Galactic centre, at 100 GeV and 1 TeV the distribution extends up to and beyond the shock. This is due to the fact that high energy electrons have a larger diffusion coefficient and have thus travelled further from the source at the Galactic centre while being further accelerated. At 1 TeV, one can also make out the effect of shock acceleration which is strongest at the top of the bubble where the advection speed is highest, cf. Eq. (26). This is leading to a higher electron energy closer to the shock which helps with producing the flat intensity profile in gamma-rays.
The bottom panel of Fig. 8 shows the electron spectra p4 f for six positions in the bubbles, marked by the crosses in the top panels. It can be seen that for z ≳ 3 kpc, the electron spectrum is very steep, f ~ p−1. The spectral index lies between those predicted for a steady-state situation without (f ~ p0) and with (f ~ p−3) efficient particle escape (cf., e.g. Stawarz & Petrosian 2008). The electron energy p4 f is peaked at a few hundred GeV. This energy scale is set by competition between stochastic acceleration and radiative energy losses, tsa (pmax) = tcool(pmax). This leads to a pile-up of high-energy electrons just below the maximum energy.
Figure 8 shows a marked difference with respect to the other setups: the energy range around 1 and 10 GeV is almost devoid of electrons. At lower energies, the spectrum is very soft and peaked.
This spectrum is essentially due to the shell geometry assumed in model 3: we recall that due to the scaling of the momentum diffusion coefficient with turbulence, stochastic acceleration is most efficient in the shell. In addition, perpendicular diffusion is very much suppressed inside the bubbles and in the halo. Therefore, only electrons which were advected into the shell at early times are being stochastically accelerated. Those that did not reach the shell at early times will not be able to catch up with the shell through advection or through diffusion. This constitutes essentially a selection mechanism that limits the number of electron injected into stochastic acceleration. The edges of the bubbles in gamma-rays are now sharper than before, a consequence of high-energy electrons only being present in the shell.
Having successfully reproduced the gamma-ray emission, we now ask whether the electrons could also explain the Galactic microwave haze (Dobler & Finkbeiner 2008; Ade et al. 2013). In Fig. 9, we show the synchrotron sky maps at ν = {0.1, 1, 10, 102} GHz and the synchrotron spectra at various positions in the sky. One can see that the general morphological characteristics of the microwave haze can be reproduced. The enhanced emission around the direction (ℓ, b) = (±15, ±10) would likelybe obscured by conventional diffuse synchrotron emission from the Galaxy. The synchrotron emission shows a relatively sharp edge in longitude, but decreases rather smoothly beyond b = ±20° as observed (Ade et al. 2013). The computed spectra nicely match the spectral index of − 0.5 observed at a few tens of GHz, with a hardening below a few GHz; this can explain why no radio counterpart of the microwave haze has been observed (see, however Carretti et al. 2013). We note that the data points in Fig. 9 are the average spectrum of the haze and should thus be compared to the average of the model lines.
 |
Fig. 5 Top panels: gamma-ray sky maps at E = 1, 10, 102 and 103 GeV for model 1 (homogeneous bubble, isotropic diffusion) at time t = 2.4 × 107 yr. The coloured crosses show the directions for which the gamma-ray spectra are shown in the bottom left panel of this figure. The three dots mark the directions where the gradient angular directions are computed and the lines show these directions. The gamma-ray profile along these is shown in the bottom right panel of this figure. Bottom left panel: gamma-ray spectra in the directions marked by the crosses in the top panel of this figure. The data points are from Ackermann et al. (2014), showing the statistical errors only, the shaded band is reflecting the systematic uncertainty. Bottom right panel: angular profiles along the directions shown in the top panel of this figure for gamma-rays in the energy range 10− 500 GeV. The data points are again from Ackermann et al. (2014). |
 |
Fig. 6 Sameas Fig. 5, but for model 2 (homogeneous bubble, anisotropic diffusion) and at time t = 2.4 × 107 yr. |
 |
Fig. 7 Sameas Fig. 5, but for model 3 (bubble with shell, anisotropic diffusion) and at time t = 2.4 × 107 yr. |
 |
Fig. 8 Top panels: distribution of electron energy p4f ~ p2ψ ~ E2n at momenta pc = 1, 10, 102, 103 GeV for model 3 at time t = 2.4 × 107 yr. The black star marks the position of the source where electrons get steadily injected with a momentum pc = 10−2 GeV and the dashed circle is the shock position at t = 2.4 × 107 yr. The coloured crosses mark the positions for which the electron spectra are shown in the bottom panel of this figure. Bottom panel: spectra p4f at time t = 2.4 × 107 yr for the six positions marked by the crosses in the top panel of this figure. |
4 Discussion
Given the simulated spatial and spectral distributions of non-thermal CR electrons, it is straight-forward to check the energetics of our models. We start by assuming a star formation rate of 0.1 M⊙ yr−1 in the inner few hundred parsecs of the Galaxy. This implies (cf., e.g. Thompson et al. 2006) a supernova rate of ~ 4 × 10−4 yr−1 in the same region. With the canonical kinetic energy of 1051 erg per supernova, the mechanical power of the inner Galaxy available for maintaining a large-scale outflow is thus 1040 erg s−1 (in line with, e.g. Sarkar et al. 2015; Crocker & Aharonian 2011). We note that launching a 300 km s−1 wind of protons with density10−2 cm−3 from a circular disk of 300 pc radius requires only ~1039 erg s−1, that is 10% of the kinetic power available. Over the dynamical time of ~2 × 107 yr this would supply the total kinetic energy of Wtotal ~ 6 × 1054 erg.
Yang et al. (2012) have estimated the time scales for growth of turbulence on large scales by the Rayleigh–Taylor (RT) and Kelvin–Helmholtz (KH) instabilities as

Here, η denotes the density contrast between the two media, g is the acceleration, λ the wavelength of the turbulent mode and Δv is the shear. Typically, η ~ 0.25, such that both τRT and τKH are smaller thanthe dynamical time scale and both instabilities can in principle lead to growth of turbulence. The mean turbulent energy density for δvturb = 10 km s−1 is Uturb ≃ 5 × 10−3 eV cm−3 and the total turbulent kinetic energy for one bubble of 4 kpc radius is Wδv ≃ 7 × 1052 erg, about a percent of the total kinetic energy provided by the inner Galaxy.
This number is to be compared with the energy in turbulent magnetic fields that is required to explain the size of the diffusion coefficients (see Sects. 2.6.1 and 2.6.2). The parallel diffusion coefficient due to pitch-angle scattering in quasi-linear theory (Schlickeiser 2002) is related to plasma and turbulence characteristics as
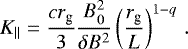 (39)
(39)
Adopting a gyroradius of rg = 3 × 1012 cm for GeV electrons in μG magnetic fields, L = 6 kpc, and 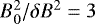 or 30, we find K∥ = 10−6 or 10−5 kpc2 yr−1 (cf. Table 1). The perpendicular diffusion coefficients scales like
or 30, we find K∥ = 10−6 or 10−5 kpc2 yr−1 (cf. Table 1). The perpendicular diffusion coefficients scales like 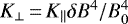 and thus we produce the required K⊥ = 10−7 and 10−8 kpc2 yr−1.
and thus we produce the required K⊥ = 10−7 and 10−8 kpc2 yr−1.
We can now check the total energy WδB in turbulent magnetic fields from the simulation. Integrating over the volume of one bubble, we find WδB ≃ 1, 0.4 and 2 × 1053 erg for models 1, 2 and 3. This is roughly in equipartition with the turbulent kinetic energy computed above.
Lastly, we have also integrated the non-thermal (>100 MeV) electron energy density over the bubbles volume. (We have excluded the region within 1 kpc from the Galactic centre since in model 3 the distinction between the thermal and non-thermal parts of the spectrum is not quite clear there.) We find total energies WCR of 1, 2 and 2 × 1050 erg, again for models 1, 2 and 3.
We conclude that of the total kinetic energy Wtotal ~ 6 × 1054 erg only a few percent need to be transferred into the energy of turbulent magnetic fields, WδB ≃ 1053 erg, and that an even smaller fraction of WCR ~ 1050 erg is residing in accelerated CR electrons.
 |
Fig. 9 Top panels: sky maps of the synchrotron intensity at 0.1, 1, 10 and 100 GHz for model 3 (anisotropic diffusion and turbulent shell) at time t = 2.4 × 107 yr, produced by the same electrons shown in Fig. 7. Bottom panel: synchrotron spectra for the different directions indicated in the legend and marked by the crosses in the lower panel of Fig. 7. The data points are from Ade et al. (2013) and the bow-tie is from Dobler & Finkbeiner (2008). |
5 Summary and conclusion
We have reviewed the observations of the Fermi bubbles in gamma-rays relevant for the modelling of the emission, transport and acceleration processes with particular focus on their puzzling morphological and spectral properties; namely the constancy of their surface brightness with abrupt edges and relatively uniform hard spectra. We discussed X-ray emission and UV absorption line observations which give (somewhat conflicting) bounds on the outflow velocities in the bubbles and include in our discussion the observations of so-called microwave haze. We reviewed briefly some of the models proposed for production of the bubbles including MHD simulation, jet and Galactic wind models.
Our main focus, however, is the acceleration of particles, their transport and emission characteristics with the primary goal of explaining the puzzling morphological and spectral characteristics. We present arguments in favor of leptonic rather than hadronic models and develop kinetic equations to described the acceleration and transport of electrons throughout the bubbles. We include effects of the stochastic acceleration by turbulence and those of a low Mach number shock with special attention to the momentum and spatial diffusion coefficients in the magnetised medium of the bubble. We also include the effects of energy loss due to inverse Compton and synchrotron processes in inhomogeneous magnetic and soft photon (CMB, infrared and optical/UV) fields.
We present results from three different models with similar characteristics of the (better understood) loss mechanisms but with different assumptionsabout more uncertain acceleration and other transport characteristics. The first model has isotropic spatial diffusion in the bubble (η = 1) and anisotropic (Kuu ≪ Kvv; η = 10) in the halo and higher acceleration rate inside the bubble. This model results in surface brightness distribution not as uniform as observed and can be ruled out. The second model has anisotropic diffusion both inside (η = 3.16) and (even stronger) outside (η = 31.6) in the halo. This model results in a uniform surface brightness but the bubble edge is not as sharp as observed. The third model consists of arelatively thick finite size shell expanding into the halo with mildly anisotropic diffusion in the shell (η = 3.16) but with a much stronger anisotropy inside and outside in the halo (η = 31.6). Accelerationrate is ten times higher in the shell than outside. This model produces a sharper edge and agrees with the observed spectral distribution in gamma-rays and microwave ranges.
We conclude that the gamma-ray as well as microwave spectral and morphological features of the Fermi bubbles can be reproduced by the inverse-Compton and synchrotron emission from electrons accelerated by turbulence generated in a mildly supersonic outward flowing shell. This finding is strengthening the scenario where the bubbles are inflated by a wind powered by star formation or star burst activity. Another possibility for inflating the bubbles is a jet from past AGN activity at the centre of the galaxy. Whether an in situ acceleration of particles in the jet environment can lead to explanation of observed characteristics of the bubbles as done by our model would require a separate study. If such a future study were to conclude that jet models could not produce the observed properties, it would strengthen the above conclusions based on our current study.
Acknowledgements
The authors are grateful to Anna Franckowiak and Dmitry Malyshev for continued discussion. This work was supported by Danmarks Grundforskningsfond under grant no. 1041811001. P.M. was further supported by DoE contract DE-AC02-76SF00515 and a KIPAC Kavli Fellowship. This research was funded in part by NASA through Fermi Guest Investigator grant NNH13ZDA001N.
References
- Ackermann, M., Albert, A., Atwood, W. B., et al. 2014, ApJ, 793, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2017, ApJ, 840, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Ade, P. A. R., Aghanim, N., Arnaud, M., et al. 2013, A&A, 554, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R., & Eichler, D. 1987, Phys. Rep., 154, 1 [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Carretti, E., Crocker, R. M., Staveley-Smith, L., et al. 2013, Nature, 493, 66 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Casandjian, J.-M., & Grenier, I. 2009, ArXiv e-prints [arXiv:0912.3478] [Google Scholar]
- Cheng, K. S., Chernyshov, D. O., Dogiel, V. A., Ko, C. M., & Ip, W. H. 2011, ApJ, 731, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Chernyshov, D. O., Dogiel, V. A., et al. 2012, ApJ, 746, 116 [Google Scholar]
- Cheng, K. S., Chernyshov, D. O., Dogiel, V. A., & Ko, C. M. 2014, ApJ, 790, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Chernyshov, D. O., Dogiel, V. A., & Ko, C. M. 2015a, ApJ, 799, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Chernyshov, D. O., Dogiel, V. A., & Ko, C. M. 2015b, ApJ, 804, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Crank, J., Nicolson, P., & Hartree, D. R. 1947, Proc. Camb. Philos. Soc., 43, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Crocker, R. M., & Aharonian, F. 2011, Phys. Rev. Lett., 106, 101102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Crocker, R. M., Bicknell, G. V., Carretti, E., Hill, A. S., & Sutherland, R. S. 2014, ApJ, 791, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Crocker, R. M., Bicknell, G. V., Taylor, A. M., & Carretti, E. 2015, ApJ, 808, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., & Finkbeiner, D. P. 2008, ApJ, 680, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Dobler, G., Finkbeiner, D. P., Cholis, I., Slatyer, T. R., & Weiner, N. 2010, ApJ, 717, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2004, ApJ, 614, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y., Ohira, Y., & Yamazaki, R. 2013, ApJ, 775, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y., Ohira, Y., & Yamazaki, R. 2014, ApJ, 789, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, F., & Mathews, W. G. 2012, ApJ, 756, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Hooper, D., & Slatyer, T. R. 2013, Phys. Dark Univ., 2, 118 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kataoka, J., Tahara, M., Totani, T., et al. 2013, ApJ, 779, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, J., Tahara, M., Totani, T., et al. 2015, ApJ, 807, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Keshet, U., & Gurwich, I. 2017, ApJ, 840, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Lacki, B. C. 2014, MNRAS, 444, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Langner, U. W. 2004, PhD Thesis, Potchefstroom University, South Africa [Google Scholar]
- Mertsch, P., & Sarkar, S. 2010, JCAP, 1010, 019 [NASA ADS] [CrossRef] [Google Scholar]
- Mertsch, P., & Sarkar, S. 2011, Phys. Rev. Lett., 107, 091101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Miller, M. J., & Bregman, J. N. 2016, ApJ, 829, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Moskalenko, I. V., & Strong, A. W. 1998, ApJ, 493, 694 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mou, G., Yuan, F., Bu, D., Sun, M., & Su, M. 2014, ApJ, 790, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Mou, G., Yuan, F., Gan, Z., & Sun, M. 2015, ApJ, 811, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Orlando, E., & Strong, A. 2013, MNRAS, 436, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Petrosian, V. 2012, Space Sci. Rev., 173, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, T. A., & Strong, A. W. 2005, Proceedings of the 29th International Cosmic Ray Conference (ICRC 2005): Pune, India, August 3–11, 2005, 4, 77 [Google Scholar]
- Sarkar, K. C., Nath, B. B., & Sharma, P. 2015, MNRAS, 453, 3827 [NASA ADS] [CrossRef] [Google Scholar]
- Sasaki, K., Asano, K., & Terasawa, T. 2015, ApJ, 814, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Berlin, Germany: Springer) [CrossRef] [Google Scholar]
- Stawarz, L., & Petrosian, V. 2008, ApJ, 681, 1725 [NASA ADS] [CrossRef] [Google Scholar]
- Su, M., & Finkbeiner, D. P. 2012, ApJ, 753, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Su, M., Slatyer, T. R., & Finkbeiner, D. P. 2010, ApJ, 724, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, T. A., Quataert, E., & Waxman, E. 2006, ApJ, 654, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Thoudam, S. 2013, ApJ, 778, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Trotta, R., Johannesson, G., Moskalenko, I. V., et al. 2011, ApJ, 729, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H. Y. K., & Ruszkowski, M. 2017, ApJ, 850, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H. Y. K., Ruszkowski, M., Ricker, P. M., Zweibel, E., & Lee, D. 2012, ApJ, 761, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H. Y. K., Ruszkowski, M., & Zweibel, E. 2013, MNRAS, 436, 2734 [NASA ADS] [CrossRef] [Google Scholar]
- Zubovas, K., & Nayakshin, S. 2012, MNRAS, 424, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Zubovas, K., King, A. R., & Nayakshin, S. 2011, MNRAS, 415, 21 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Toroidal coordinates. Surfaces of constant v are tori of varying radii surrounding the foci ring of radius a and are shown in red. Surfaces of constant u are spheres of varying radii that all intersect the foci ring and are shown in blue. |
| In the text | |
 |
Fig. 2 Spatial part of the computational grid. For clarity, we only show n = 100 spacings in the u-direction here, whereas in the numerical simulations, we have chosen n = 800 throughout. Note also that the use of vmax = 2 instead of ∞ ignores a small region of space. |
| In the text | |
 |
Fig. 3 Energy densities ε of the CMB, IR and optical/UV parts of the ISRF as well as the energy density of the B-field in the ρ–z plane. We define the energy ranges as 4.3 × 10−5–1.4 × 10−2 eV for the CMB, 1.4 × 10−2–0.22 eV for the IR and 0.22–14 eV for the optical/UV. |
| In the text | |
 |
Fig. 4 Schematic overview of the three models. (See text for explanations.) |
| In the text | |
 |
Fig. 5 Top panels: gamma-ray sky maps at E = 1, 10, 102 and 103 GeV for model 1 (homogeneous bubble, isotropic diffusion) at time t = 2.4 × 107 yr. The coloured crosses show the directions for which the gamma-ray spectra are shown in the bottom left panel of this figure. The three dots mark the directions where the gradient angular directions are computed and the lines show these directions. The gamma-ray profile along these is shown in the bottom right panel of this figure. Bottom left panel: gamma-ray spectra in the directions marked by the crosses in the top panel of this figure. The data points are from Ackermann et al. (2014), showing the statistical errors only, the shaded band is reflecting the systematic uncertainty. Bottom right panel: angular profiles along the directions shown in the top panel of this figure for gamma-rays in the energy range 10− 500 GeV. The data points are again from Ackermann et al. (2014). |
| In the text | |
 |
Fig. 6 Sameas Fig. 5, but for model 2 (homogeneous bubble, anisotropic diffusion) and at time t = 2.4 × 107 yr. |
| In the text | |
 |
Fig. 7 Sameas Fig. 5, but for model 3 (bubble with shell, anisotropic diffusion) and at time t = 2.4 × 107 yr. |
| In the text | |
 |
Fig. 8 Top panels: distribution of electron energy p4f ~ p2ψ ~ E2n at momenta pc = 1, 10, 102, 103 GeV for model 3 at time t = 2.4 × 107 yr. The black star marks the position of the source where electrons get steadily injected with a momentum pc = 10−2 GeV and the dashed circle is the shock position at t = 2.4 × 107 yr. The coloured crosses mark the positions for which the electron spectra are shown in the bottom panel of this figure. Bottom panel: spectra p4f at time t = 2.4 × 107 yr for the six positions marked by the crosses in the top panel of this figure. |
| In the text | |
 |
Fig. 9 Top panels: sky maps of the synchrotron intensity at 0.1, 1, 10 and 100 GHz for model 3 (anisotropic diffusion and turbulent shell) at time t = 2.4 × 107 yr, produced by the same electrons shown in Fig. 7. Bottom panel: synchrotron spectra for the different directions indicated in the legend and marked by the crosses in the lower panel of Fig. 7. The data points are from Ade et al. (2013) and the bow-tie is from Dobler & Finkbeiner (2008). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.