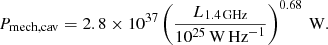| Issue |
A&A
Volume 622, February 2019
LOFAR Surveys: a new window on the Universe
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833883 | |
| Published online | 19 February 2019 | |
The LoTSS view of radio AGN in the local Universe
The most massive galaxies are always switched on
1
SUPA, Institute for Astronomy, Royal Observatory, Blackford Hill, Edinburgh, EH9 3HJ UK
e-mail: jsm@roe.ac.uk
2
Centre for Astrophysics Research, School of Physics, Astronomy and Mathematics, University of Hertfordshire, College Lane, Hatfield, AL10 9AB UK
3
ASTRON, The Netherlands Institute for Radio Astronomy, Postbus 2, 7990 AA Dwingeloo, The Netherlands
4
GEPI, Observatoire de Paris, CNRS, Universite Paris Diderot, 5 place Jules Janssen, 92190 Meudon, France
5
Department of Physics & Electronics, Rhodes University, PO Box 94 Grahamstown, 6140 South Africa
6
University of Hamburg, Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
7
School of Physical Sciences, The Open University, Walton Hall, Milton Keynes, MK7 6AA UK
8
Leiden Observatory, Leiden University, PO Box 9513 2300 RA Leiden, The Netherlands
9
CSIRO Astronomy and Space Science, PO Box 1130 Bentley, WA, 6102 Australia
10
Astrophysics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford, OX1 3RH UK
11
INAF – Istituto di Radioastronomia, Via Gobetti 101, 40129 Bologna, Italy
12
School of Physics, University College Dublin, Belfield, Dublin 4, Republic of Ireland
Received:
16
July
2018
Accepted:
28
October
2018
This paper presents a study of the local radio source population, by cross-comparing the data from the first data release (DR1) of the LOFAR Two-Metre Sky Survey (LoTSS) with the Sloan Digital Sky Survey (SDSS) DR7 main galaxy spectroscopic sample. The LoTSS DR1 provides deep data (median rms noise of 71 μJy at 150 MHz) over 424 square degrees of sky, which is sufficient to detect 10 615 (32 per cent) of the SDSS galaxies over this sky area. An improved method to separate active galactic nuclei (AGN) accurately from sources with radio emission powered by star formation (SF) is developed and applied, leading to a sample of 2121 local (z < 0.3) radio AGN. The local 150 MHz luminosity function is derived for radio AGN and SF galaxies separately, and the good agreement with previous studies at 1.4 GHz suggests that the separation method presented is robust. The prevalence of radio AGN activity is confirmed to show a strong dependence on both stellar and black hole masses, remarkably reaching a fraction of 100 per cent of the most massive galaxies (> 1011 M⊙) displaying radio-AGN activity with L150 MHz ≥ 1021 W Hz−1; thus, the most massive galaxies are always switched on at some level. The results allow the full Eddington-scaled accretion rate distribution (a proxy for the duty cycle) to be probed for massive galaxies, and this accretion rate is found to peak at Lmech/LEdd ≈ 10−5. More than 50 per cent of the energy is released during the ≤2 per cent of the time spent at the highest accretion rates, Lmech/LEdd > 10−2.5. Stellar mass is shown to be a more important driver of radio-AGN activity than black hole mass, suggesting a possible connection between the fuelling gas and the surrounding halo. This result is in line with models in which these radio AGN are essential for maintaining the quenched state of galaxies at the centres of hot gas haloes.
Key words: surveys / galaxies: evolution / galaxies: active / radio continuum: galaxies
© ESO 2019
1. Introduction
The large-scale structure of the Universe is driven by the gravitational collapse of dark matter haloes and the subsequent merging of these into progressively larger structures (filaments, sheets, groups, and clusters) building the “cosmic web”. Galaxies then form within dark matter haloes by radiative cooling of baryons (White & Rees 1978). The efficiency by which baryons are converted into stars is highly dependent on the mass of the dark matter halo: the stellar-mass to halo-mass relation peaks at Mhalo ≈ 1012 M⊙, at which mass around 20 per cent of baryons are converted into stars (e.g. Behroozi et al. 2010; Moster et al. 2010; Wechsler & Tinker 2018).
At halo masses below this peak, the heating of gas by ultraviolet radiation from both the host galaxy and cosmic background, and the ejection of gas by supernova-driven winds (e.g. Benson et al. 2003; Baugh 2006), combine to lower the SF efficiency in galaxies. At halo masses above 1012 M⊙, the overall SF efficiency of haloes is reduced from SF being terminated, or quenched, in a subset of the galaxy population. Peng et al. (2010) studied the fraction of passive, red galaxies in the local Universe as a function of both mass and environment and argued that there were two distinct mechanisms for this quenching of SF, which operates independently: “environment quenching”, which applies mainly to satellite galaxies, and “mass quenching” of the most massive galaxies. Subsequent work has broadly confirmed these trends (Peng et al. 2012; Gabor & Davé 2015; Zu & Mandelbaum 2016; Cochrane & Best 2018). Nevertheless, the physical drivers of these quenching mechanisms remain widely debated, in particular the extent to which mass quenching is driven by internal galactic processes such as active galactic nuclei (AGN) as compared to the role of the dark matter halo.
Mass quenching has frequently been attributed to the effects of AGN because AGN activity is observed to occur in the high-mass galaxies in which SF needs to be quenched (e.g. Heckman & Best 2014) and because it is well established (e.g. Silk & Rees 1998; Fabian 1999; King 2003; Fabian 2012) that winds and outflows driven by quasar activity can terminate SF in a manner that also gives rise to the observed correlation between the mass (or velocity dispersion) of a galaxy bulge and the mass of the central black hole (e.g. Magorrian et al. 1998; Gebhardt et al. 2000; see review by Kormendy & Ho 2013). However, mass quenching could also be closely linked to halo properties owing to the strong correlation between stellar mass and halo mass. As noted by Bower et al. (2006), when gas falls into a dark matter halo of mass below a few ×1011 M⊙, the timescale for it to cool is shorter than its infall time, and so it arrives at the central galaxy cold and is able to be efficiently converted into stars. At higher halo masses, however, the infalling gas suffers a virial shock and its cooling time exceeds the dynamical time, leading to a hydrostatic halo of hot (X-ray emitting) gas that is built up (e.g. Birnboim & Dekel 2003; Kereš et al. 2005). This transition in the nature of accreted gas leads to a natural explanation for the decrease in SF efficiency in high-mass haloes.
Regardless of the initial quenching mechanism, the hot gas in massive haloes radiates and cools and, especially in rich, undisturbed environments, might be expected to form a cooling flow (see Fabian 1994), which would result in high levels of gas deposition and star formation (SF) in the central galaxy. A source of heating is required to offset the cooling and prevent this. It is now widely accepted that radio AGN are responsible for this: radio-AGN activity (either current or recently terminated) is seen in essentially all of the central galaxies of cool-core clusters (Burns 1990; Dunn & Fabian 2006; Best et al. 2007) and these AGN are able to deposit the jet energy directly and efficiently into the intracluster medium by inflating bubbles/cavities (see reviews by McNamara & Nulsen 2007; Fabian 2012). Estimates of the radio-AGN heating rate in these clusters (as determined from the cavity enthalpy coupled with a buoyancy timescale; e.g. Bîrzan et al. 2004; Cavagnolo et al. 2010) show that these are well matched to the radiative cooling rates of the hot gas (e.g. McNamara & Nulsen 2007). This forms a natural feedback cycle, whereby the hot gas offers both a source of fuel for the radio AGN through cold chaotic accretion (e.g. Gaspari et al. 2013) and a confining medium for the radio source to expand against and deposit its energy into (see review by Heckman & Best 2014).
Radio AGN feedback is likely to be important on galactic scales as well and massive galaxies are also located in hot hydrostatic envelopes (e.g. Croston et al. 2007; Mingo et al. 2011, 2012). It was the inclusion of this “jet-mode” (or “maintenance-mode”) feedback from radio AGN into semi-analytic models of galaxy formation that allowed Croton et al. (2006) and Bower et al. (2006) to naturally explain the shape of the galaxy luminosity function and the bimodal nature of the galaxy population. Modern hydrodynamical simulations, including a feedback term (associated with radio AGN) that suppresses gas cooling in hot haloes, are also successful at reproducing the local observed trends in galaxy properties (e.g. Gabor & Davé 2015). These results provide support for so-called halo-quenching models for the switch off of SF in massive galaxies.
Observationally, considerable advances in our understanding of the importance of radio AGN have been made over the last one to two decades; a major driver of this has been the availability of uniform, wide-area spectroscopic surveys such as the Two-degree Field Galaxy Redshift Survey (2dFGRS; Colless et al. 2001) and the Sloan Digital Sky Survey (SDSS; York et al. 2000; Stoughton et al. 2002), coupled with wide-area radio surveys, especially the National Radio Astronomy Observatory (NRAO) Very Large Array (VLA) Sky Survey (NVSS; Condon et al. 1998) and the Faint Images of the Radio Sky at Twenty centimetres survey (FIRST; Becker et al. 1995). Cross-matching of radio and optical surveys (e.g. Sadler et al. 2002; Best et al. 2005b; Mauch & Sadler 2007; Best & Heckman 2012) has allowed detailed statistical studies of the prevalence and properties of radio-AGN activity.
Best et al. (2005a) showed that the fraction of massive galaxies that host radio-AGN activity is a very strong function of stellar mass (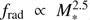 ) or black hole mass (
) or black hole mass (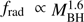 ), reaching as high as ≈30 per cent at the highest stellar masses, to the radio luminosity limit of their analysis (L1.4 GHz ≈ 1023 W Hz−1); see also Brown et al. (2011) for a deeper study of a much smaller sample. Best et al. (2006) and Best et al. (2007) built upon this to estimate the time-averaged heating rate associated with this radio-AGN activity, assuming that all massive galaxies go through recurrent radio-AGN outbursts and that the observed radio-AGN prevalence could be used as a measure of the duty cycle of the AGN activity. They found that this heating rate exceeded the heating rate that is necessary to counterbalance the typical radiative cooling losses of the hot gas, and that radio-AGN heating is therefore able to explain the old, red, and dead nature of massive galaxies in hot haloes.
), reaching as high as ≈30 per cent at the highest stellar masses, to the radio luminosity limit of their analysis (L1.4 GHz ≈ 1023 W Hz−1); see also Brown et al. (2011) for a deeper study of a much smaller sample. Best et al. (2006) and Best et al. (2007) built upon this to estimate the time-averaged heating rate associated with this radio-AGN activity, assuming that all massive galaxies go through recurrent radio-AGN outbursts and that the observed radio-AGN prevalence could be used as a measure of the duty cycle of the AGN activity. They found that this heating rate exceeded the heating rate that is necessary to counterbalance the typical radiative cooling losses of the hot gas, and that radio-AGN heating is therefore able to explain the old, red, and dead nature of massive galaxies in hot haloes.
Although this broad understanding is in place, several open questions remain about the detailed process of radio-AGN feedback. One such question concerns the duty cycle of radio-AGN activity. Kauffmann & Heckman (2009) and Best & Heckman (2012) studied the distribution of Eddington-scaled accretion ratios at low Eddington ratios and found that, down to their limit of around L/LEdd = 10−3, these follow roughly a power law with increasing numbers of low Eddington ratio sources (see also Heckman & Best 2014). Deeper radio data are needed to probe lower radio luminosities, and hence track the full distribution of accretion rates, over wide enough sky areas to build significant samples. Such data would also allow a much larger fraction of lower stellar mass sources to be detected, enabling investigation of the relationships between duty cycle, radio luminosity distribution, and stellar mass.
The LOFAR Two-Metre Sky Survey (LoTSS; Shimwell et al. 2017) offers a new opportunity to advance these studies and address some of these questions. This large-area 150 MHz survey with the LOw Frequency ARray (LOFAR; van Haarlem et al. 2013) reaches more than an order of magnitude deeper than the FIRST survey for sources of typical spectral index, and is even more advantageous for steep spectrum sources (older electron populations). Furthermore, it also has high sensitivity to extended radio structure, thus avoiding the need for the complicated combination of FIRST and NVSS that Best et al. (2005b) needed to adopt. This paper cross-matches data from the first data release (DR1; Shimwell et al. 2019) of LoTSS with the main galaxy sample of the SDSS to provide new insights into the prevalence, duty cycle, and impact of radio-AGN activity in the local Universe.
The layout of the paper is as follows. Section 2 describes the sample of galaxies to be studied and the cross-matching between the radio and optical catalogues. Section 3 then outlines the procedure to filter the radio-AGN subset of these sources from the bulk population of star-forming galaxies (SFGs). The radio spectral index properties of these sources, and the resultant local radio luminosity function at 150 MHz are discussed in Sects. 4 and 5, respectively. Section 6 then considers the prevalence of radio AGN as a function of both stellar mass and black hole mass, comparing the results to previous studies, and using the large sample to break the degeneracy between these two parameters. Section 7 examines the distribution of Eddington-scaled accretion rates of the most massive galaxies. Finally, the results of the paper are summarised in Sect. 8, and their implications are discussed. Throughout the study, a cosmology with ΩΛ0 = 0.7, Ωm0 = 0.3, and H0 = 70 km s−1 Mpc−1 is assumed.
2. The sample and data
The LoTSS (Shimwell et al. 2017) is a high-resolution survey that will cover the full northern hemisphere at frequencies ranging from 120 to 168 MHz1. The LoTSS DR1 (Shimwell et al. 2019) covers 424 square degrees centred in the Hobby-Eberly Telescope Dark Energy Experiment (HETDEX; Hill et al. 2008) Spring Field region (right ascension 10h45m00s to 15h30m00s and declination 45 ° 00′00″ to 57 ° 00′00″) and contains over 300 000 sources with a signal of at least five times the noise level. It is composed of 58 overlapping pointings with 8 hours of observation in each one. The median rms noise is ≈71 μJy beam−1 and 95 per cent of the area in the release has an rms noise level below 150 μJy beam−1. The angular resolution is 6 arcsec and the positional accuracy is better than 0.2 arcsec for high signal-to-noise sources; the positional accuracy increases to ≈0.5 arcsec for the faintest sources with a flux density of less than 0.6 mJy. Detailed information about the LoTSS DR1 is presented in Shimwell et al. (2019). The radio sources were associated with their optical and mid-infrared counterparts in the Panoramic Survey Response and Rapid Response System (Pan-STARRS; Kaiser et al. 2002, 2010) and the Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010) surveys (with a completeness and reliability at the ≈99 per cent level) using a combination of statistical likelihood ratio techniques and visual classification methods (Williams 2019). Finally, photometric redshifts were derived and rest-frame magnitudes were obtained for the sources (Duncan et al. 2019, although those data are not used in the current paper).
The galaxy sample selected for this study is based on the spectroscopic data from the seventh data release of the SDSS (SDSS DR7; Abazajian et al. 2009). There are 34 709 galaxies from the SDSS Main Galaxy Sample (broadly complete between magnitudes 14.5 and 17.77 in r band; Strauss et al. 2002) that overlap with the region covered by the LoTSS DR1. An upper redshift limit of z = 0.3 is applied, which reflects the approximate limit of main galaxy sample spectroscopy (nz > 0.3 = 47). A lower redshift limit of z = 0.01 is also applied, as below this the SDSS fibres probe such a small region of the galaxy that derived galaxy parameters become unreliable (nz < 0.01 = 413). Galaxies with a non-zero z warning flag were discarded as their redshifts could be unreliable (nz warning = 34). The catalogue contains duplicated observations for some of the objects and a single observation of each object was selected to avoid multiple counting on the statistics (nduplicates = 711). With all of these constraints, a sample of 33 504 galaxies was obtained in the LoTSS DR1 area.
All the SDSS sources are bright in the optical band and have clear corresponding PanSTARRS detections. Therefore, the radio counterparts of SDSS galaxies were found by cross-matching the positions of SDSS galaxies with the PanSTARRS counterparts of the LoTSS sources. LoTSS sources present accurate PanSTARRS-LoTSS cross identifications even for extended sources due to the efforts shown in Williams (2019). The positions of the SDSS sources were cross-matched with the optical (PanSTARRS) positions using a search radius of 2 arcsec. This radius is sufficiently large to obtain essentially all the genuine counterparts with no significant contamination by random matches. In any case, the results are largely insensitive to this choice of cross-match radius if it is within the range of 1–2 arcsec since the PanSTARRS to SDSS astrometric agreement is typically accurate to fractions of an arcsecond. A LoTSS counterpart was found for 10 615 of the SDSS sample (32 per cent). The LoTSS data release provides mosaics with the rms noise level for each position, which also allows the flux density limit at 150 MHz to be determined for the SDSS galaxies without a LoTSS cross-match. This limit was set at five times the rms noise level, which corresponds to the approximate catalogue limit for LoTSS (Shimwell et al. 2019). There are 43 sources for which the measured LoTSS total flux density is slightly below five times the rms noise. For completeness these sources were removed from the catalogue and considered as non-detections.
The MPA-JHU2 value-added catalogue (Brinchmann et al. 2004) offers improved and additional information to the SDSS data. In particular, the nebular emission lines were measured after the subtraction of the contribution of the stellar populations (Tremonti et al. 2004) and are used for the selection of AGN in the next section. We also use the stellar mass of the galaxies presented in the catalogue, as derived by Kauffmann et al. (2003b). Additional parameters used in this paper are the 4000Å break strength (D4000), and the velocity dispersion (σ). The latter can be used to estimate the mass of the central black hole: the relation adopted in this paper is that of McConnell & Ma (2013), i.e. log10(MBH/M⊙)=8.32 + 5.64log10[σ/(200 km s−1)]. Best & Heckman (2012) cross-matched the SDSS DR7 spectroscopic catalogue against the NVSS and FIRST radio surveys to derive the 1.4 GHz properties of these sources; data from their catalogues are also used in the analysis.
3. Selection of radio AGN
A significant challenge in deep radio surveys such as LoTSS is to separate radio AGN from SFGs, for which the radio emission is associated with the SF in the galaxy, but there may or may not also be a radio-quiet AGN present; radio AGN are defined in this work as galaxies for which their radio emission is dominated by a jet originating from the central supermassive black hole. Star-forming galaxies emit at radio wavelengths primarily due to synchrotron emission from shocks associated with supernovae, and hence their radio luminosity correlates broadly with the star formation rate (SFR; e.g. Condon 1992), although there are indications that the relationship can also depend on other parameters such as galaxy mass (e.g. Gürkan et al. 2018; Read 2018). Star-forming galaxies dominate the radio source counts at flux densities S150 MHz ≤ 1 mJy (Wilman et al. 2008; de Zotti et al. 2010; Williams et al. 2016; Calistro Rivera et al. 2017) and cannot be ignored at higher flux densities.
A common method of separating SFGs from AGN is through their optical emission-line properties, in particular using emission line diagnostic diagrams (Baldwin et al. 1981; Kauffmann et al. 2003a; Kewley et al. 2006). One shortcoming of this method is that it cannot be used for objects without clear emission line detections. Although for radio-selected samples, these sources are mostly weak-lined radio AGN (e.g. Sadler et al. 2002). An additional complication is the radio-quiet AGN. The origin of the radio emission in these sources remains widely debated, with both SF and weak radio jets contributing, and the dominant mechanism varying between sources (e.g. White et al. 2017, and references therein). In the local Universe, regardless of the presence or not of weak jets, radio-quiet AGN are frequently associated with SFGs (e.g. Kauffmann et al. 2003a; see also discussion in Heckman & Best 2014) and, at the depth of surveys like LoTSS, such SF may lead to the galaxy being detected in the radio. The emission line fluxes of such sources can be driven by the hard ionising spectrum of the AGN, leading to an AGN classification by optical line diagnostics, but such SF-dominated sources should not be included in samples of radio AGN.
An alternative approach to identify radio AGN is to compare the radio and far-infrared luminosities of sources (e.g. Machalski & Condon 1999; Sabater et al. 2012; Mingo et al. 2016). This technique makes use of the relatively tight far-infrared radio correlation (FIRC) of SFGs (e.g. Yun et al. 2001; Smith et al. 2014): objects with a radio excess above that predicted from the FIRC can be identified as radio AGN. This is a powerful method (albeit still limited by the intrinsic scatter in the FIRC), but is generally not applicable because of the absence of sufficiently deep far-IR data.
Best et al. (2005a) proposed an alternative method for identification of radio AGN, using the “D4000 vs. Lrad/M*” plane. The parameter D4000 is the strength of the 4000 Å break in the galaxy spectrum, and Lrad/M* is the ratio of radio luminosity to stellar mass. Best et al. (2005a) showed that for a wide range of different SF histories, SFGs occupy largely the same region of this plane, since both D4000 and Lrad/M* depend broadly on the specific SFR of the galaxy. Best et al. (2005a) used these theoretical tracks to propose a diagnostic division line between radio AGN and SFGs whereby the radio-quiet AGN were classified together with the SFGs.
Kauffmann et al. (2008) considered an alternative diagnostic, making use of the ratio of radio luminosity to Hα luminosity. In this work, the latter is used as a proxy for SFR, following the same principles as the separation via the FIRC. Using this separation they also proposed a modification to the division line on the D4000 vs. Lrad/M* diagnostic of Best et al. (2005a). Best & Heckman (2012) then further built upon this work by devising a scheme to separate radio AGN from SFGs using a combination of the revised D4000 vs. Lrad/M* diagnostic, the emission line diagnostic diagram, and the radio luminosity to Hα luminosity relation.
In this paper, the identification of the radio-AGN subsample builds upon the work of Best & Heckman (2012), but with some significant modifications. First, the division lines are recast into 150 MHz luminosities (as detailed in the next subsection) owing to the observing frequency of LoTSS. Second, a fourth diagnostic test is also included in the analysis, made feasible by the availability of WISE data. Star-forming galaxies separate from the typical hosts of radio AGN in their WISE colours, particularly in W2–W3 (4.6–12 micron colour; Yan et al. 2013): Herpich et al. (1826) use a cut at W2–W3 = 2.5 (in Vega magnitudes; W2–W3 ≈0.7 in AB magnitudes) to separate galaxies with and without SF, although it is also clear from their plots that this separation is far from clean. Third, we make use of the analysis by Gürkan et al. (2018) of the LOFAR data in the Herschel-ATLAS North Galactic Plane (hereafter H-ATLAS) field (Hardcastle et al. 2016). These LOFAR data are similar to those of LoTSS and have the same SDSS and WISE properties available. But Gürkan et al. (2018) have done detailed spectral energy distribution fitting, incorporating the available Herschel data in a self-consistent manner using MAGPHYS (da Cunha et al. 2008; see also Smith et al. 2012) to derive accurate SFRs and allow more precise separation of SFGs from radio AGN based on the radio luminosity to SFR relation. This complementary sample therefore provides an opportunity to test and optimise the calibration of the diagnostic division lines, and the resultant combined classification scheme, as outlined below.
3.1. Adopted individual diagnostics for population separation
Figure 1 shows the four classification methods along with the classification lines adopted. Sources are colour-coded by their final adopted classification (see Sect. 3.2). The details of the classification in each of the four diagnostics is now discussed in turn.
 |
Fig. 1. Location of the LoTSS sources on the four diagnostic plots used to separate the radio AGN from those galaxies where the radio emission is powered by SF. Upper left panel: “D4000 vs. L150 MHz/M*” method, developed by Best et al. (2005b). Upper right panel: [OIII]/Hβ vs. [NII]/Hα emission line ratio diagnostic diagram of Baldwin et al. (1981). Lower left panel: LHα vs. L150 MHz relation. Lower right panel: this WISE W1–W2 vs. W2–W3 colour–colour diagnostic. In all plots, the dotted lines indicate the division(s) used for that classification method (see Sect. 3.1 for further details); in the cases of the upper left and lower left plots, there are two division lines; sources between the two lines are deemed to be “intermediate” by that classification method. The different symbols reflect the final combined classification of each source: radio AGN are plotted as red diamonds and SFGs as black crosses. In the lower left plot, arrows indicate upper limits to the Hα luminosity. |
The upper left panel of Fig. 1 shows D4000 vs. L150 MHz/M*, based on that of Best et al. (2005a). The upper dotted line shows the revised division proposed by Kauffmann et al. (2008) and adopted by Best & Heckman (2012); the radio luminosity is converted to 150 MHz from 1.4 GHz by assuming a spectral index of α = 0.7 (for Sν ∝ ν−α; this spectral index is the canonical value from (Condon et al. 2002), with a similar typical value found for LOFAR sources by Calistro Rivera et al. 2017). However, applying these classifications to the H-ATLAS data indicated that this conservative cut left many genuine radio AGN within the star-forming region and led to significant numbers of misclassifications in the final combined classifications. In contrast, (as noted by Kauffmann et al. 2008) the original cut of Best et al. (2005a) led to some SFGs being misclassified as radio AGN and, especially at the lower radio luminosities probed by LoTSS, also led to misclassification of some radio AGN with large values of D4000 as SFGs. Therefore, a second diagnostic line was introduced that tracked the original Best et al. (2005a) line until D4000 = 1.7 and then continued horizontally (lower dotted line on the upper left panel of Fig. 1); this form was chosen to maximise agreement with the more sophisticated Gürkan et al. (2018) classifications of the (much smaller) H-ATLAS sample. Galaxies above the upper dotted line were classified as radio AGN via this diagnostic, galaxies below the lower dotted line were classified as SFGs, and galaxies between the two lines were deemed intermediate. Only a handful of galaxies could not be classified on this diagnostic because of an absence of a reliable mass measurement. Table 1 shows the number of objects classified into each category by each diagnostic. It also shows the resultant overall classification statistics of these galaxies (see Sect. 3.2) and can thus be used to judge the importance of each diagnostic in the overall classification.
Numbers of sources classified in each category by each different classification method.
The upper right panel of Fig. 1 shows the [O III]/Hβ vs. [NII]/Hα line diagnostic diagram that is widely used to separate AGN and SFGs owing to the relative strength of the four emission lines involved and the broad independence of the line ratios on dust extinction. The division proposed by Kauffmann et al. (2003a) is adopted: AGN and SFGs are divided at log([OIII]/Hβ) = 1.3 + 0.61/(log([N II]/Hα) − 0.05). Seventy-four per cent of the radio source sample are classifiable by this method, while the rest lack detections for at least one of the lines. This is a significantly higher fraction of classifiable objects than the ∼30 per cent found by Best & Heckman (2012), largely because the deeper radio survey contains a far higher fraction of (stronger lined) SFGs. As discussed above (and evident on Fig. 1) objects selected as AGN by this diagnostic may be significantly contaminated by radio-quiet AGN, and so for these objects this diagnostic diagram is not given much weight in the final classification (cf. Tables 1 and 2). However, the absence of AGN signatures provides a more useful diagnostic: essentially all ∼5000 sources (47 per cent of the sample) that fall in the SFG region of this diagnostic plot have an overall classification of SFG (see Table 1).
Number of sources and overall classification for different combinations of the four classification methods (with at least five sources).
The LHα vs. L150 MHz diagnostic is shown in the lower left panel of Fig. 1. Best & Heckman (2012) used just a single conservative cut on this diagnostic. However, as with the D4000 vs. L150 MHz/M* diagnostic, comparison with the H-ATLAS data indicates that any single separation line leads to significant numbers of misclassifications. Therefore, again, two separation lines are adopted: log(LHα/L⊙) = log(L150 MHz/W Hz−1) − 16.9 and log(LHα/L⊙) = log(L150 MHz/W Hz−1)− 16.1. Galaxies with measured Hα luminosity, or an upper limit on this, below the lower line are classified as radio AGN on this diagnostic. Those which have measured Hα luminosities, or upper limits, between the two lines are deemed intermediate, and those with a measured Hα luminosity above the upper line are classified as SFGs. We found 1.7 per cent of sources have upper limits on LHα above the upper line and are left unclassified.
Finally, the lower right panel of Fig. 1 shows a plot of W1–W2 vs. W2–W3 mid-infrared WISE colours. The sources are classified on this plot according to a simple division at W2–W3 = 0.8 (AB). This value was again optimised based on comparison with the H-ATLAS sample and is very similar to the division adopted by Herpich et al. (1826). We found 7 per cent of sources did not possess a W2–W3 colour and so were unclassified. This diagnostic is somewhat crude, and was largely only used where the other diagnostics produced intermediate or contradictory classifications.
3.2. Combination of diagnostics and final classification
For each individual classification method, sources may be classified as a radio AGN, classified as having their radio emission associated with SF, or be unclassified. For two of the four diagnostics, an intermediate classification is also possible. This leads to 144 different possible combinations of classifications, where in some cases the classifications may disagree. Best & Heckman (2012) discussed how to combine these individual classifications in order to obtain a single overall classification. Their classifications are broadly adopted here, but need to be expanded to incorporate the new intermediate classes and the WISE diagnostics. In this work, the approach taken was to apply these diagnostics to the equivalent data for the H-ATLAS sample from Gürkan et al. (2018), and compare against the more sophisticated classifications available for that sample. Specifically, for each possible combination of the four diagnostics, the H-ATLAS sources with that combination were identified, and the majority classification of that sample (SF or radio AGN) was adopted as the overall classification for that combination. In most cases this outcome was very clear with the H-ATLAS sources having (almost) uniformly the same classification; only for a few of the (less common) combinations, where the different diagnostic methods suggest different classifications, was the H-ATLAS sample also more heterogeneous in its classifications, suggesting (as expected) more uncertainty in the overall classification. Based on this comparison with H-ATLAS, the overall potential contamination from misclassification is estimated to be ≲3 per cent.
Table 2 shows the final classifications adopted and the number of sources in each category; to save space, classifications with fewer than five sources are not listed separately, but the overall contribution of these is indicated at the bottom of the table. In total, 2121 sources are classified as radio AGN, and 8494 sources are classified as having their radio emission associated with SF3.
4. Spectral indices of local radio AGN
It is well established that the low-luminosity radio AGN have typically much smaller physical sizes that their more luminous counterparts. Best et al. (2005b) found that the vast majority of radio sources in their SDSS-NVSS-FIRST cross-match are unresolved at the ≈5″ resolution of the FIRST survey (see also Baldi & Capetti 2010). Higher resolution radio studies have confirmed these sources to be AGN, but have shown that they either remain unresolved down to sub-arcsecond (sub-kpc) resolution or present weak jets on scales of at most a few kiloparsec (Baldi et al. 2015). The core radio morphologies of these sources and their host galaxy properties largely resemble those of the more powerful extended radio sources, but they lack the extended emission; the explanation for this is still a matter of debate (e.g. Baldi et al. 2018; and references therein). For our radio-AGN sample, 28 per cent of the sources show multiple components and 15 per cent can be modelled by a single Gaussian but are resolved according to the criteria shown by Shimwell et al. (2019). The remaining 57 per cent of the sources are unresolved single components, although this figure raises quickly with decreasing flux density.
A characteristic property of these radio AGN that can offer clues as to their nature is the radio spectral index: compact radio cores and hotspots display much flatter spectra than extended radio components. de Gasperin et al. (2018) have measured the spectral index properties of radio sources from wide-area sky surveys and have found evidence that these flattened towards lower radio flux densities; similar flattening at lower flux densities has been seen in deeper studies of small sky areas (e.g. Prandoni et al. 2006) and is often ascribed to lower luminosity AGN. However, the spectral indices of these local very low-luminosity AGN have only been investigated for small samples (de Gasperin et al. 2011), indicating a mix of flat and steep spectrum sources.
Of the 2121 LoTSS-selected radio AGN, 496 of these sources are in common with the NVSS-FIRST sample of Best & Heckman (2012), and therefore have available 1.4 GHz flux densities. The cross-matching process of Best & Heckman (2012, see also Best et al. 2005b) uses an approach that combines NVSS and FIRST data, such that the matched sources benefit from the angular resolution of FIRST (which is similar to that of LoTSS) but also the sensitivity to extended structure offered by NVSS (which LoTSS also possesses due to the dense LOFAR core). This combination thus minimises any possible biases in spectral indices originating from a mismatch in resolution/sensitivity of different surveys. The relation between LoTSS luminosity and stellar mass, including which galaxies are also detected in NVSS/FIRST, is shown in Fig. 2. In this figure it is clear how LoTSS probes a population of galaxies that remained undetected in NVSS/FIRST.
 |
Fig. 2. Distribution of LoTSS luminosities with respect to the stellar masses. The SF galaxies detected only in LoTSS are plotted with different symbols (circles) than those that are also detected in NVSS/FIRST (stars). Radio AGN are indicated with three-spoked asterisks in red for galaxies detected only in LoTSS and in olive for galaxies detected in both LoTSS and NVSS/FIRST. |
The distribution of 150 MHz–1.4 GHz spectral indices for these radio AGN is shown in Fig. 3, as a function of 1.4 GHz flux density; the LoTSS data are sufficiently deeper than the NVSS/FIRST data that the LoTSS limit provides essentially no constraint on this plot. At high flux densities (S1.4 GHz > 20 mJy) the median spectral index is 0.63, which is very much in line with the canonical value of 0.7 (Condon et al. 2002). The scatter of the spectral indices at the lower flux densities are mainly caused by the uncertainty in the measurements but a possible general trend towards flat or even inverted spectrum sources was also explored.
 |
Fig. 3. Spectral index distribution of the radio-AGN galaxies with both LoTSS and 1.4 GHz measurements, as a function of 1.4 GHz flux density. Individual sources are shown as blue dots and the medians of different bins in 1.4 GHz flux density are shown as orange crosses. The vertical lines correspond to the standard deviation on each bin. The median spectral index at flux densities S1.4 GHz > 20 mJy is 0.63. The weak decrease in median spectral index at lower flux densities may be driven by selection biases in the 1.4 GHz sample, as indicated by the black dashed line that simulates the effect of this (see text for details). |
The median spectral index decreases towards 0.4 at the lowest flux densities, and the faintest radio sources display a wide range of spectral indices, including some flat spectrum sources. If correct this would be consistent with the suggestion of Whittam et al. (2017), using higher frequency source counts, of an increasing core fraction towards lower flux densities. However, it must be noted that at the lowest flux densities the distribution may be skewed by selection biases in the FIRST-NVSS sample as the 3 mJy flux density limit of that sample (set by the NVSS limits) is approached, boosting the number of apparently flatter spectrum sources. These selection biases were investigated using a Monte Carlo simulation. The distribution of spectral indices for sources with S1.4 GHz > 20 mJy was fitted using a Gaussian. Then, for each source with a flux density measured at 150 MHz, 10 000 random spectral indices were drawn from the Gaussian and the corresponding S1.4 GHz was calculated. If this was below the NVSS detection limit (3 mJy) then that iteration of that source was discarded (as it would not have been within the subsample of sources with measured spectral indices); otherwise it was retained. The retained values were then used to compute the mean spectral index as a function of 1.4 GHz flux density. The results of the simulation are plotted in Fig. 3. It is clear that the trend of the spectral index to decrease at the lower flux densities is consistent with being driven entirely by the biases arising from the combination of statistical flux errors and selection limits. That would indicate that the bulk of the compact radio AGN are not simply flat spectrum radio cores with an absence of extended emission, but rather that they are broadly scaled-down versions of the more luminous extended sources (see also discussion in Baldi et al. 2018). This conclusion fits in with the view of the recurrent nature of radio-AGN activity, discussed in Sect. 7.
The typical spectral index found in Fig. 3 is also needed to provide a reliable conversion factor for comparison of the LoTSS results with previous measurements at higher frequencies. For the remainder of the paper (and for consistency with the value adopted for the AGN/SF separation) the canonical spectral index for radio AGN of 0.7 is adopted, which is close to the observed median. This spectral index corresponds to the following conversion in luminosities: log10(L1.4 GHz)≈log10(L150 MHz)−0.68.
5. Local 150 MHz luminosity function
The local 150 MHz radio luminosity functions for both SFGs and radio AGN were determined using the standard technique, ρ = ∑i1/Vi (Schmidt 1968; Condon 1989), where Vi is the volume within which source i could be detected. The calculation of Vi for each source requires careful consideration of both the radio and optical redshift limits, in particular taking into account the variable flux limit of the LoTSS survey as a function of sky location (Shimwell et al. 2019).
For each source, Vi was calculated as follows. First, the redshift range z < 0.3 was divided into narrow redshift slices (in practice, 3000 slices of width Δz = 0.0001 were used). The radio luminosity of the source in question was then used to calculate the flux density that the source would have at the mid-point of each redshift slice, assuming a spectral index of 0.7. The LoTSS rms maps were used to calculate the sky area over which a source of that flux density could be detected above the 5σ limit (see Shimwell et al. 2019), and hence the volume available to that source within the redshift slice. Finally, the optical magnitude limits of the SDSS main galaxy selection (14.5 < r < 17.77) were used to determine upper and lower redshift limits at which the source could be included in the SDSS sample (if these magnitude limits lay outside the sample selection limits of zmin = 0.01 and zmax = 0.3 then the latter were used instead). The available volume in all redshift slices between those two limits was then summed. The radio luminosity functions were then derived by summing 1/Vi across all sources, and Poisson statistics were used to estimate the uncertainties. It should be emphasised that at some luminosities the formal statistical uncertainties are small and are likely to be underestimates, and systematic errors such as AGN/SF classification dominated the error budget. No correction is made for incompleteness in the LoTSS survey, but as shown by Shimwell et al. (2019) this is small above the 5σ threshold (at least for point sources, which the low-luminosity radio AGN are likely to be). It may possibly contribute to the slight downturn in the faintest luminosity bin.
The derived radio luminosity functions of AGN and SF galaxies are provided separately in Table 3 and shown in Fig. 4. For comparison, the local 1.4 GHz luminosity functions of radio AGN and SF galaxies are overlaid, converted to 150 MHz by adjusting the break luminosity using the spectral index of 0.7. The plotted line for the radio AGN is the parameterisation of Heckman & Best (2014), which averages over a wide selection of previous 1.4 GHz radio luminosity function determinations (Machalski & Godlowski 2000; Sadler et al. 2002; Best et al. 2005b; Mauch & Sadler 2007; Best & Heckman 2012), while that of SF galaxies uses the parameterisation of Mauch & Sadler (2007). As can be seen, the agreement between the 1.4 GHz and 150 MHz radio luminosity functions is good (as is that with earlier 150 MHz luminosity functions in the H-ATLAS field by Hardcastle et al. 2016). The slight offset in the SF galaxies can either be explained by the use of a different spectral index (the agreement above the break is almost perfect if α = 0.6 is used instead), or be caused by slightly different redshift distributions of the two samples, given the strong cosmological evolution of this population. These results give confidence in the robustness of the separation of SF galaxies from AGN, which is important for the analysis in the subsequent sections of the paper.
Local 150 MHz luminosity functions of AGN and SF galaxies separately.
 |
Fig. 4. Local 150 MHz luminosity functions of AGN (red circles) and SF galaxies (blue diamonds) separately. Also shown for comparison (black dashed lines) are the local 1.4 GHz luminosity function for radio AGN (using the parameterisation of Heckman & Best 2014) and SF galaxies (using the parameterisation of Mauch & Sadler 2007), converted to 150 MHz by scaling the break frequency with a spectral index of 0.7. |
The luminosity function of radio AGN continues to increase with the same power-law slope down to the lowest flux densities probed by LoTSS. As argued by Mauch & Sadler (2007), this cannot continue indefinitely without the integrated space density of radio AGN exceeding the space density of massive galaxies which are believed to host these objects. Mauch & Sadler (2007) calculated a limit of L1.4 GHz ≈ 1019.5 W Hz−1 below which the radio luminosity function must turn down if their hosts are all brighter than L* ellipticals, where L* is the break of the optical luminosity function, and Cattaneo & Best (2009) derived a similar value assuming that the host galaxies require a black hole more massive than 106 M⊙. This limit corresponds to around 1020.2 W Hz−1 at 150 MHz, less than an order of magnitude below the faintest luminosities probed by LoTSS. This issue is investigated in more detail in the following sections, by breaking down the radio-AGN prevalence by both (stellar or black hole) mass and radio luminosity separately.
6. Fraction of radio AGN
It is well-established that there is a strong increase in the prevalence of radio-AGN activity with the mass of the galaxy (e.g. Best et al. 2005a; Mauch & Sadler 2007; Sabater et al. 2013). The left panel of Fig. 5 shows the fraction of the SDSS galaxies that host a radio AGN above a given luminosity limit, as a function of the stellar mass of the galaxy; this is shown for different cut-offs on the radio luminosity, from L150 MHz ≥ 1021 W Hz−1 to L150 MHz ≥ 1025 W Hz−1 in increments of 0.5 dex. For each limit, the fraction is computed by considering only the galaxies that could be detected above the given luminosity limit, with a flux density of five times the rms noise level. The error bars were computed using the Agresti-Coull binomial proportion confidence interval (Agresti & Coull 1998) with the confidence interval covering 68 per cent of the probability (roughly equivalent to 1 sigma in a normal distribution). The results show the expected increase in the prevalence of radio AGN with stellar mass, as seen in previous studies at high luminosities, but are able to extend this down to lower radio luminosities. Remarkably, for limits of L150 MHz ≥ 1021 W Hz−1, the fraction of galaxies hosting radio AGN reaches 100 per cent for stellar masses above 1011 M⊙. At limits below or equal to L150 MHz ≥ 1022 W Hz−1, the 100 per cent fraction is reached for masses above 1012 M⊙. This is consistent with the results of Brown et al. (2011), who studied a much smaller sample of nearby very massive galaxies and also found near ubiquity of radio emission from either AGN or SF activity.
 |
Fig. 5. Left panel: fraction of galaxies that host a radio AGN above a given luminosity limit, as a function of stellar mass, for multiple radio luminosity limits (shown in different colours). Right panel: fraction of galaxies hosting radio AGN brighter than a given radio luminosity, separated by their stellar mass. The various stellar mass ranges are shown in different colours. The solid lines represent the results of this (150 MHz) study and dotted lines show the results from Best et al. (2005a) at 1.4 GHz (converted assuming a spectral index of 0.7). The error bars correspond to a confidence interval equivalent to one sigma. The fractions of radio AGN are shown only up to L150 MHz ≈ 1025 W Hz−1 because the number of galaxies above this limit is relatively low and render very large error bars. The highest mass bin would reach a value compatible with 100 per cent within the error at L150 MHz ≤ 1021.7 W Hz−1 but those points are not shown owing to the large error bars. |
The right panel of Fig. 5 shows the same results in an alternative way. The fraction of galaxies hosting radio AGN is presented with respect to the luminosity limit for multiple strata of stellar mass. For comparison, this figure also shows the results of Best et al. (2005a) at higher luminosities at 1.4 GHz, converted using a spectral index of 0.7. The results agree in the overlapping luminosities, but the current analysis extends almost two orders of magnitude lower in terms of radio luminosity. The new data discard the flattening towards lower luminosity limits that was hinted at in Best et al. (2005a) and Mauch & Sadler (2007), instead indicating that the prevalence reaches 100 per cent by the lowest luminosities, at least for the higher mass ranges.
Figure 6 considers the prevalence of radio-AGN activity in relation to the mass of the black hole; it is similar to Fig. 5 but for black hole masses instead of stellar masses. In the left panel of Fig. 6 an increase in the fraction of radio AGN is seen with respect to the black hole mass. As with previous 1.4 GHz studies, this has a shallower slope than found for stellar mass. Furthermore, in this case the slope appears to flatten at the highest black hole masses for each luminosity bin and the maximum fraction reaches at most 30–50 per cent. The right panel of Fig. 6 compares the results against the 1.4 GHz data. For this comparison, the data of Best et al. (2005a) were re-analysed using new black hole masses derived using the velocity dispersion to black hole mass relation adopted in this paper (see Sect. 2; this is different from the relation that Best et al. 2005a originally used). Once again, the agreement is excellent, and in this case the flattening persists and the fraction never reaches 100 per cent even for the highest black hole masses.
 |
Fig. 6. Left panel: fraction of galaxies that host a radio AGN above a given radio luminosity, as a function of the black hole mass, for various radio luminosity limits (shown in different colours). Right panel: fraction of galaxies hosting radio AGN brighter than a given radio luminosity, separated by their black hole mass. Colours, lines, and errors bars as in Fig. 5. In the left panel, the line corresponding to L150 MHz ≤ 1021 W Hz−1 is omitted from the plot owing to its large error bars. |
The stronger dependence of the radio-AGN fraction on stellar mass than on black hole mass found in Figs. 5 and 6 suggests that stellar mass is a more important factor in triggering radio-AGN activity. However, there is a strong correlation between black hole mass and stellar mass (e.g. Reines & Volonteri 2015) that must be considered before reaching this conclusion. There is also a consideration that the black hole masses have larger uncertainties on their measurements because of the underlying scatter in the relationship between black hole mass and velocity dispersion from which they are estimated. In order to disentangle the effect of black hole mass and stellar mass, the fraction of radio AGN with respect to the black hole mass was computed in bins of different stellar masses (left panel of Fig. 7) and the fraction with respect to the stellar mass was computed in bins of different black hole masses (right panel of Fig. 7) for galaxies with L150 MHz ≥ 1022.5 W Hz−1. This threshold in flux density maximises the number of galaxies available for the stratified study, which minimises the size of the error bars and scatter of the radio-AGN fractions, but consistent results are found for other radio luminosity limits. The error bars and fractions are computed as in Figs. 5 and 6. From Fig. 7 it is clear that the fraction of radio AGN is mainly driven by the stellar mass. The black hole mass also has some residual effect but minimal in comparison with the effect of the stellar mass; indeed it is plausible that the remaining trend with black hole mass is simply a result of a residual correlation between black hole and stellar mass within the narrow stellar mass bin. The dominance of the stellar mass dependence points at an external trigger, rather than the properties of the black hole itself being the key driver. It is consistent with the properties of the gas that fuels the AGN being closely linked to the stellar mass of the galaxy (e.g. Sabater et al. 2013), perhaps through the strong relationship between stellar mass and halo mass.
 |
Fig. 7. Left panel: fraction of galaxies that host a radio AGN with L150 MHz ≥ 1022.5 W Hz−1, as a function of the black hole mass, for multiple stellar mass bins (shown in different colours). Right panel: fraction of galaxies hosting radio-AGN with L150 MHz ≥ 1022.5 W Hz−1, as a function of the stellar mass, separated by their black hole mass (shown in different colours). |
It is apparent in the left hand panels of both Figs. 5 and 6 that there is a visible reduction in the slope of the frad vs. M* relation from higher to lower luminosity limits. Janssen et al. (2012) split the radio-AGN population into high- and low-excitation sources, which correspond broadly to those fuelled at high Eddington rates by the accretion of cold gas in SFGs, and those fuelled at low rates by the accretion of gas from cooling hot haloes (e.g. Hardcastle et al. 2007; see discussion in Heckman & Best 2014). Janssen et al. (2012) showed that the high-excitation population of radio AGN presents a more moderate dependency with the mass than low-excitation radio-AGN, and are more dominant at lower masses. The flattening in Fig. 5 may well be related to this, as the lower radio luminosities typically probe lower stellar masses.
7. Distribution of Eddington-scaled accretion rates
The distribution of Eddington-scaled accretion rates of AGN has been previously studied by Kauffmann & Heckman (2009) and Best & Heckman (2012). Kauffmann & Heckman (2009) examined the accretion rates of emission-line selected AGN, deriving radiative AGN luminosities by scaling from the [OIII] 5007 emission line. They found that red (quenched) galaxies followed a power-law distribution of Eddington-scaled accretion rates, rising towards lower accretion rates down to their lower observable limit of L/LEdd ∼ 10−3. Best & Heckman (2012) studied radio-selected AGN and derived Eddington-scaled luminosities by summing the radiative luminosity (scaled from [OIII] 5007) and the jet mechanical luminosity (from the radio luminosity; see below). They also found that the distribution rose strongly down to L/LEdd ∼ 10−3 for the bulk of the radio population and that this was dominated by the jet mechanical luminosity except for the small population of strong emission line radio sources, which mostly occurred at high Eddington ratios (see also discussion in Heckman & Best 2014).
With the deeper LoTSS DR1 data it is possible to reach much lower limits in the Eddington ratio distribution. In this paper, this is only considered for the high stellar mass population (masses higher than 1011 M⊙). Consideration of just this population has two advantages: First, at these masses it was shown in Sect. 6 that essentially all galaxies host a radio AGN, so the full Eddington rate distribution should be recoverable; second, at these masses the sample is expected to be dominated by the jet-mode AGN (e.g. Janssen et al. 2012), meaning that a homogeneous population of sources is probed and that the Eddington ratio can be estimated using just the jet mechanical power.
The mechanical power of the radio jets in a given radio source would ideally be inferred directly from the properties of the radio source, by comparison with radio source evolution models (see, for example, Hardcastle et al. 2019). However, such inference requires knowledge of the environments of the radio sources, which is not available for the current sample. Furthermore, radio source evolution models are generally most accurate for Fanaroff & Riley (1974) Class II (FRII) sources, whereas at the low radio luminosities probed in this work most of the sources are either of FRI class or are compact. A common alternative approach for estimating the jet mechanical energy is therefore to scale directly from the radio luminosity. Such a conversion does not capture the intrinsic physical variations for individual sources; the radio luminosity of a radio source evolves throughout its lifetime even if the jet power remains constant (e.g. Kaiser et al. 1997). But for population-based analyses, such as that in this paper, the use of an average conversion factor can provide a suitably accurate approximation.
The jet mechanical power to radio luminosity conversion is commonly estimated from the cavities inflated by radio sources in the surrounding intergalactic or intracluster medium, as observed in X-rays. The total mechanical energy supplied by the radio jets is typically assumed to be 4pV, where p is the pressure of the surrounding medium, V the volume of the cavity, and the factor 4 comes from summing the work performed to inflate the cavities (pV) and the enthalpy of the relativistic plasma in the radio lobes (3pV). When combined with an estimate of the source age, for which the buoyancy timescale of the cavities is typically used (e.g. Churazov et al. 2001), this allows the mechanical power of the jet to be estimated. This is found to correlate with the observed radio luminosity (Bîrzan et al. 2004; Rafferty et al. 2006; Bîrzan et al. 2008; Cavagnolo et al. 2010), although with significant scatter, as expected from the discussion above.
An alternative jet mechanical power to radio luminosity conversion was presented by Willott et al. (1999) based on the synchrotron properties of the radio source. For this, assumptions need to be made about the composition of the radio jet plasma (see also Croston et al. 2018), and the cut-offs of the electron energy distribution. These are similar to the assumptions required for direct jet power inference for individual sources.
Heckman & Best (2014) showed that the scaling relations determined from cavity-based methods and those of Willott et al. (1999) provide broadly consistent estimates of the jet mechanical powers, at least at the moderate-to-high radio luminosities that dominate the energetic output of the AGN; this gives confidence that the assumptions made in each method are understood and broadly justified. They proposed the following population-averaged conversion between radio luminosity and jet mechanical power:
This expression is adopted in this work, modified to 150 MHz assuming a spectral index of 0.7.
Using this, the distribution of Eddington-scaled accretion ratios for galaxies with masses between 1011 M⊙ and 1012 M⊙ is shown in Fig. 8. For each bin in Lmech/LEdd, this is calculated by considering the number of galaxies with detections in this range of accretion rates as compared to all the galaxies that could be detectable to that Eddington limit (with a detection above five times the rms noise level). The errors correspond to the 95 per cent confidence interval using the Agresti-Coull binomial proportion confidence intervals. The accretion rate distribution increases from higher to lower accretion rates as previously determined, with this continuing down to Lmech/LEdd ≈ 10−5 when the distribution flattens. A remaining small proportion of the galaxies have Lmech/LEdd below 10−5.75, indicated by the orange point on Fig. 8 (which distributes these over the next four bins), indicating that the distribution must fall below Lmech/LEdd ∼ 10−6.
 |
Fig. 8. Distribution of Eddington-scaled accretion rate for radio AGN (solid blue line). The error bars correspond to the 95 per cent confidence interval. The cumulative distribution obtained from the Kaplan-Meier estimator (solid green line) running from higher towards lower accretion rates is shown. The orange cross represents the remaining fraction of galaxies spread over the following 4 bins. The distribution flattens and peaks at Lmech/LEdd ≈ 10−5. A Kaplan-Meier estimator fit finds the median of the distribution at Lmech/LEdd = 10−4.98. We note that the conversion between radio luminosities and mechanical power is uncertain at low luminosities (e.g. Hardcastle et al. 2019). |
The distribution of Eddington-scaled accretion rates was also checked using survival analysis. The Kaplan-Meier estimator (Kaplan & Meier 1958) was computed using the Lifelines package (Davidson-Pilon et al. 2018) in Python. Left-censoring was used, with detections marked as events and non-detections as limits using the Lmech/LEdd corresponding to five times the rms noise limit at the position. The results fully agree with the binned method shown before. The median of the distribution is found at Lmech/LEdd = 10−4.98; the mean of the distribution is at Lmech/LEdd = 10−3.53.
If all the galaxies belong to the same population the relative fractions can be directly linked to the time spent by the AGN at each accretion rate (duty cycle). It is interesting to note, therefore, that although the distribution peaks (i.e. galaxies spend most of their time) at relatively low accretion rates, the bulk of the time-averaged energy output for these galaxies is produced during the relatively short times corresponding to the higher Eddington-scaled accretion rates. The Kaplan-Meier distribution can be weighted by the energy output corresponding to each Lmech/LEdd and, integrating along this distribution, it is possible to find the average energy output corresponding to a given Lmech/LEdd. In this way, it is found that 50 per cent of the energy output is emitted when Lmech/LEdd ≥ −2.5 ; the other 50 per cent is emitted at accretion rates below this value. Using the original distribution, the average time spent by a radio AGN at Lmech/LEdd ≥ −2.5 is only ≈1.7 per cent of the total. Hence, 50 per cent of the energy is released during the ≤2 per cent of the time spent at the highest accretion rates.
Considering that the distribution covers the full range of accretion rates, the total time-averaged mechanical energy output for high-mass radio AGN can be estimated. To do that, the mean accretion rate was computed from the mean Eddington-scaled value using the typical mass for the black holes in the selected stellar mass range: the median black hole mass of 108.3 M⊙ corresponds to LEdd = 1039.5 W, and this Lmech is expected to have an average value of ≈1036 W (1043 erg s−1) through the lifetime and population of radio AGN. This result is broadly in line with the findings of Best et al. (2006)
It is interesting to compare this average AGN heating rate against the cooling radiation losses of the X-ray haloes surrounding these galaxies. Kim & Fabbiano (2015), and references therein, consider scaling relations between X-ray luminosity and K-band luminosity. Considering the median stellar mass of the galaxies in the mass range selected above (1011.21 M⊙) and assuming that for these old ellipticals the K-band luminosity can be used as a proxy of the stellar mass (with a mass-to-light ratio of order unity), this AGN heating rate is significantly above the X-ray luminosity expected for individual ellipticals. Instead, it is more similar to the values found by Kim & Fabbiano (2015) for the central galaxies of groups and clusters, and of the same order of magnitude of that associated with the inflation of bubbles/cavities in clusters (e.g. McNamara & Nulsen 2007; Diehl et al. 2008). This is consistent with recurrent radio-AGN activity in these high-mass galaxies providing sufficient energy to control cooling in their surrounding groups and clusters and providing the feedback that maintains the host galaxies as quenched, as expected (see also Hardcastle et al. 2019).
8. Summary and conclusions
The LoTSS DR1 and the SDSS main spectral galaxy sample have been combined to study the prevalence of radio AGN in the local Universe (0.01 ≤ z ≤ 0.3). There are 33 504 SDSS galaxies in the LoTSS area and 32 per cent of these are detected by LoTSS. The main results of this study are as follows:
-
The method to classify and separate radio AGN from SFGs has been adapted to the 150 MHz frequency of LoTSS and improved by both the inclusion of WISE colours and the calibration of diagnostic lines against the well-studied sample of Gürkan et al. (2018). A total of 2121 radio AGN were identified.
-
The distribution of 150 MHz–1.4 GHz spectral indices was obtained. A median spectral index of 0.63, in line with the canonical value of 0.7, is found at high flux densities (S1.4 GHz > 20 mJy). The median spectral index decreases at lower flux densities, but simulations indicate that this may be entirely driven by selection effects whereby steeper spectrum sources are missed in the shallower high-frequency data sets.
-
The local radio luminosity function at 150 MHz has been derived for radio AGN and SFGs separately down to lower luminosities than has previously been possible. The radio-AGN luminosity function agrees well with previous determinations of the luminosity function at 1.4 GHz, which gives confidence in the robustness of the AGN/SF separation method.
-
The prevalence of radio AGN, as selected at 150 MHz, has been studied as a function of the stellar and black hole masses. As previously seen at high luminosity at higher frequencies, the fraction of galaxies hosting radio AGN rises strongly with mass. This relation is seen to be flatter at lower luminosities and lower stellar masses.
-
Stellar mass is a stronger driver of the fraction of AGN than the black hole mass. Indeed, once the correlation between black hole and stellar mass is accounted for, the radio-AGN fraction still rises strongly with stellar mass (at fixed black hole mass) but shows little or no dependence on black hole mass (at fixed stellar mass). This is indicative of the stellar mass being better linked to the properties of the gas that fuels the AGN and drives the activity.
-
Remarkably, 100 per cent of galaxies with masses higher than 1011 M⊙ host radio AGN when limits below or equal to L150 MHz ≥ 1021 W Hz−1 are considered. This suggests that the most massive galaxies are always switched on, even if it is at relatively low radio powers.
-
The full distribution of Eddington-scaled accretion rates was derived for the most massive galaxies (stellar masses between 1011 M⊙ and 1012 M⊙). This is shown to rise with decreasing Eddington fraction down to Lmech/LEdd ∼ 10−5 and to drop sharply below Lmech/LEdd ∼ 10−6. However, the bulk of the energy output is produced during the relatively short times that AGN are powering jets close to their maximum powers.
The use of LoTSS has permitted the exploration of a wider parameter space than previous studies. The results are very much in line with previous work, but the extension to lower luminosities has greatly extended the scope of that work. The discovery that the most massive galaxies are always on as a radio source at the luminosity levels that LoTSS reaches and that stellar mass appears to be a more important driver of activity than black hole mass, both indicate that the radio-AGN activity is controlled by the fuel supply to the radio AGN, which connects more closely to the stellar mass. This fits the popular picture whereby this fuel is connected to cooling of hot gas within the dark matter halo, and the radio-AGN activity is instrumental in maintaining the host galaxies as old, red, and dead.
Considering that the DR1 of LoTSS covers only 2 per cent of the final LoTSS area, an improvement of at least one order of magnitude in the volume of LoTSS data can be expected in the near future (next two to three years). These larger samples will allow a more detailed exploration of additional aspects of the triggering of radio AGN. In particular, it will be very interesting to directly test the picture above by separating the radio-AGN luminosity distribution by additional parameters such as environment (see Sabater et al. 2013, 2015) and mass to separate the roles of these two critical parameters. Furthermore, the forthcoming availability of extensive spectroscopic data for LoTSS sources out to higher redshifts, through the WEAVE-LOFAR survey (Smith et al. 2016), will allow cosmic evolution to be examined. These topics will constitute the focus of future detailed studies.
Although the central frequency of the LoTSS band is 144 MHz, the bandwidth is large and the sensitivity-weighted mean frequency depends on position within the mosaic owing to the frequency-dependent primary beam size. To avoid an impression of undue precision, we use 150 MHz throughout the paper to refer to the LoTSS frequency.
These AGN/SF classifications are used in Hardcastle et al. (2019) to help to establish criteria to define larger AGN and SF galaxy samples from the wider LoTSS sample without SDSS spectroscopy.
Acknowledgments
We would like to thank the anonymous referee for useful comments that improved this paper. This paper is based (in part) on data obtained with the International LOFAR Telescope (ILT) under project codes LC2_038 and LC3_008. LOFAR (van Haarlem et al. 2013) is the LOw Frequency ARray designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, which are owned by various parties (each with their own funding sources) and are collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefited from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Université d’Orléans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, The Netherlands; The Science and Technology Facilities Council, UK. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. This work was carried out in part on the Dutch national e-infrastructure with the support of SURF Cooperative through e-infra grants 160022 & 160152. PNB, JS, and RKC are grateful for support from the UK Science and Technology Facilities Council (STFC) via grant ST/M001229/1 and ST/R000972/1. KJD and AS acknowledge support from the European Research Council under the European Unions Seventh Framework Programme (FP/2007-2013)/ERC Advanced Grant NEWCLUSTERS-321271 MJH and WLW acknowledge support from the UK Science and Technology Facilities Council ST/M001008/1. JHC acknowledges support from the STFC under grants ST/R00109X/1 and ST/R000794/1. APM would like to acknowledge the support from the NWO/DOME/IBM programme “Big Bang Big Data: Innovating ICT as a Driver For Astronomy”, project #628.002.001. GG acknowledges the CSIRO OCE Postdoctoral Fellowship. F.d.G. is supported by the VENI research programme with project number 1808, which is financed by the Netherlands Organisation for Scientific Research (NWO). LKM acknowledges the support of the Oxford Hintze Centre for Astrophysical Surveys, which is funded through generous support from the Hintze Family Charitable Foundation. This publication arises from research partly funded by the John Fell Oxford University Press (OUP) Research Fund. IP acknowledges support from INAF under PRIN SKA/CTA ’FORECaST’ SM acknowledges funding through the Irish Research Council New Foundations scheme and the Irish Research Council Postgraduate Scholarship scheme. This research made use of ASTROPY, a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018); IPYTHON (Pérez & Granger 2007); MATPLOTLIB (Hunter 2007); NUMPY (Walt et al. 2011); PANDAS (McKinney 2010); SCIPY (Jones et al. 2001), TOPCAT (Taylor 2005), and KERN suite (Molenaar & Smirnov 2018).
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Agresti, A., & Coull, B. A. 1998, Am. Stat., 52, 119 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Baldi, R. D., & Capetti, A. 2010, A&A, 519, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldi, R. D., Capetti, A., & Giovannini, G. 2015, A&A, 576, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldi, R. D., Capetti, A., & Massaro, F. 2018, A&A, 609, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baugh, C. M. 2006, Rep. Prog. Phys., 69, 3101 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Conroy, C., & Wechsler, R. H. 2010, ApJ, 717, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, A. J., Bower, R. G., Frenk, C. S., et al. 2003, ApJ, 599, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., & Heckman, T. M. 2012, MNRAS, 421, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., Kaiser, C. R., Heckman, T. M., & Kauffmann, G. 2006, MNRAS, 368, L67 [NASA ADS] [Google Scholar]
- Best, P. N., Kauffmann, G., Heckman, T. M., et al. 2005a, MNRAS, 362, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., Kauffmann, G., Heckman, T. M., & Ivezić, V. 2005b, MNRAS, 362, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., von der Linden, A., Kauffmann, G., Heckman, T. M., & Kaiser, C. R. 2007, MNRAS, 379, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Birnboim, Y., & Dekel, A. 2003, MNRAS, 345, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Bîrzan, L., Rafferty, D. A., McNamara, B. R., Wise, M. W., & Nulsen, P. E. J. 2004, ApJ, 607, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Bîrzan, L., McNamara, B. R., Nulsen, P. E. J., Carilli, C. L., & Wise, M. W. 2008, ApJ, 686, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., Heckman, T. M., et al. 2004, ArXiv e-prints [arXiv:astro-ph/0406220] [Google Scholar]
- Brown, M. J. I., Jannuzi, B. T., Floyd, D. J. E., & Mould, J. R. 2011, ApJ, 731, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. O. 1990, AJ, 99, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Calistro Rivera, G., Williams, W. L., Hardcastle, M. J., et al. 2017, MNRAS, 469, 3468 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., & Best, P. N. 2009, MNRAS, 395, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Cavagnolo, K. W., McNamara, B. R., Nulsen, P. E. J., et al. 2010, ApJ, 720, 1066 [NASA ADS] [CrossRef] [Google Scholar]
- Churazov, E., Brüggen, M., Kaiser, C. R., Böhringer, H., & Forman, W. 2001, ApJ, 554, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Cochrane, R. K., & Best, P. N. 2018, MNRAS, 480, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., Dalton, G., Maddox, S., et al. 2001, MNRAS, 328, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1989, ApJ, 338, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., & Broderick, J. J. 2002, AJ, 124, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Croston, J. H., Kraft, R. P., & Hardcastle, M. J. 2007, ApJ, 660, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Croston, J. H., Ineson, J., & Hardcastle, M. J. 2018, MNRAS, 476, 1614 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson-Pilon, C., Kalderstam, J., Kuhn, B., et al. 2018, CamDavidsonPilon/lifelines: v0.14.3 [Google Scholar]
- de Gasperin, F., Merloni, A., Sell, P., et al. 2011, MNRAS, 415, 2910 [NASA ADS] [CrossRef] [Google Scholar]
- de Gasperin, F., Intema, H. T., & Frail, D. A. 2018, MNRAS, 474, 5008 [NASA ADS] [CrossRef] [Google Scholar]
- de Zotti, G., Massardi, M., Negrello, M., & Wall, J. 2010, A&ARv, 18, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Diehl, S., Li, H., Fryer, C. L., & Rafferty, D. 2008, ApJ, 687, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, K., Sabater, J., Rottgering, H., et al. 2019, A&A, 622, A3 (LOFAR SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunn, R. J. H., & Fabian, A. C. 2006, MNRAS, 373, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 1994, ARA&A, 32, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 1999, MNRAS, 308, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
- Gabor, J. M., & Davé, R. 2015, MNRAS, 447, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Ruszkowski, M., & Oh, S. P. 2013, MNRAS, 432, 3401 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Gürkan, G., Hardcastle, M. J., Smith, D. J. B., et al. 2018, MNRAS, 475, 3010 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2007, MNRAS, 376, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Gürkan, G., van Weeren, R. J., et al. 2016, MNRAS, 462, 1910 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Williams, W. L., Best, P. N., et al. 2019, A&A, 622, A12 (LOFAR SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heckman, T. M., & Best, P. N. 2014, ARA&A, 52, 589 [Google Scholar]
- Herpich, F., Mateus, A., & Stasińska, G. 1826, MNRAS, 462 [Google Scholar]
- Hill, G. J., Gebhardt, K., Komatsu, E., et al. 2008, in Panoramic Views of Galaxy Formation and Evolution, eds. T. Kodama, T. Yamada, & K. Aoki, ASP Conf. Ser., 399, 115 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Janssen, R. M. J., Röttgering, H. J. A., Best, P. N., & Brinchmann, J. 2012, A&A, 541, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open Source Scientific Tools for Python [Google Scholar]
- Kaiser, C. R., Dennett-Thorpe, J., & Alexander, P. 1997, MNRAS, 292, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., Aussel, H., Burke, B. E., et al. 2002, Survey and Other Telescope Technologies and Discoveries, 4836, 154 [Google Scholar]
- Kaiser, N., Burgett, W., Chambers, K., et al. 2010, Ground-based and Airborne Telescopes III, 7733, 77330E [Google Scholar]
- Kaplan, E. L., & Meier, P. 1958, J. Am. Stat. Assoc., 53, 457 [Google Scholar]
- Kauffmann, G., & Heckman, T. M. 2009, MNRAS, 397, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003a, MNRAS, 346, 1055 [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003b, MNRAS, 341, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., & Best, P. N. 2008, MNRAS, 384, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Kereš, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D.-W., & Fabbiano, G. 2015, ApJ, 812, 127 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. 2003, ApJ, 596, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
- Machalski, J., & Condon, J. J. 1999, ApJS, 123, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Machalski, J., & Godlowski, W. 2000, A&A, 360, 463 [NASA ADS] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Mauch, T., & Sadler, E. M. 2007, MNRAS, 375, 931 [NASA ADS] [CrossRef] [Google Scholar]
- McConnell, N. J., & Ma, C.-P. 2013, ApJ, 764, 184 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, W. 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 51 [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mingo, B., Hardcastle, M. J., Croston, J. H., et al. 2011, ApJ, 731, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Mingo, B., Hardcastle, M. J., Croston, J. H., et al. 2012, ApJ, 758, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Mingo, B., Watson, M. G., Rosen, S. R., et al. 2016, MNRAS, 462, 2631 [NASA ADS] [CrossRef] [Google Scholar]
- Molenaar, G., & Smirnov, O. 2018, Astron. Comput., 24, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Somerville, R. S., Maulbetsch, C., et al. 2010, ApJ, 710, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Renzini, A., & Carollo, M. 2012, ApJ, 757, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Prandoni, I., Parma, P., Wieringa, M. H., et al. 2006, A&A, 457, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rafferty, D. A., McNamara, B. R., Nulsen, P. E. J., & Wise, M. W. 2006, ApJ, 652, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Read, S., Smith, D. J. B., Gurkan, G., et al. 2018, MNRAS, submitted [Google Scholar]
- Reines, A. E., & Volonteri, M. 2015, ApJ, 813, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Sabater, J., Verdes-Montenegro, L., Leon, S., Best, P., & Sulentic, J. 2012, A&A, 545, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sabater, J., Best, P. N., & Argudo-Fernández, M. 2013, MNRAS, 430, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Sabater, J., Best, P. N., & Heckman, T. M. 2015, MNRAS, 447, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Sadler, E. M., Jackson, C. A., Cannon, R. D., et al. 2002, MNRAS, 329, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Shimwell, T. W., Röttgering, H. J. A., Best, P. N., et al. 2017, A&A, 598, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimwell, T. W., Tasse, C., Hardcastle, M. J., et al. 2019, A&A, 622, A1 (LOFAR SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silk, J., & Rees, M. J. 1998, A&A, 331, L1 [NASA ADS] [Google Scholar]
- Smith, D. J. B., Dunne, L., da Cunha, E., et al. 2012, MNRAS, 427, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. J. B., Jarvis, M. J., Hardcastle, M. J., et al. 2014, MNRAS, 445, 2232 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. J. B., Best, P. N., Duncan, K. J., et al. 2016, in SF2A-2016: Proceedings of the Annual Meeting of the French Society of Astronomy and Astrophysics, eds. C. Reylé, J. Richard, L. Cambrésy, et al., 271 [Google Scholar]
- Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Strauss, M. A., Weinberg, D. H., Lupton, R. H., et al. 2002, AJ, 124, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walt, S. V. D., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Wechsler, R. H., & Tinker, J. L. 2018, ARA&A, 56, 435 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. V., Jarvis, M. J., Kalfountzou, E., et al. 2017, MNRAS, 468, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Whittam, I. H., Jarvis, M. J., Green, D. A., Heywood, I., & Riley, J. M. 2017, MNRAS, 471, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, W. L., van Weeren, R. J., Röttgering, H. J. A., et al. 2016, MNRAS, 460, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, W. L., Hardcastle, M. J., & Best, P. N., et al. 2019, A&A, 622, A2 (LOFAR SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willott, C. J., Rawlings, S., Blundell, K. M., Lacy, M., et al. 1999, MNRAS, 309, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Wilman, R. J., Miller, L., Jarvis, M. J., et al. 2008, MNRAS, 388, 1335 [NASA ADS] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, L., Donoso, E., Tsai, C.-W., et al. 2013, AJ, 145, 55 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Zu, Y., & Mandelbaum, R. 2016, MNRAS, 457, 4360 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Numbers of sources classified in each category by each different classification method.
Number of sources and overall classification for different combinations of the four classification methods (with at least five sources).
All Figures
 |
Fig. 1. Location of the LoTSS sources on the four diagnostic plots used to separate the radio AGN from those galaxies where the radio emission is powered by SF. Upper left panel: “D4000 vs. L150 MHz/M*” method, developed by Best et al. (2005b). Upper right panel: [OIII]/Hβ vs. [NII]/Hα emission line ratio diagnostic diagram of Baldwin et al. (1981). Lower left panel: LHα vs. L150 MHz relation. Lower right panel: this WISE W1–W2 vs. W2–W3 colour–colour diagnostic. In all plots, the dotted lines indicate the division(s) used for that classification method (see Sect. 3.1 for further details); in the cases of the upper left and lower left plots, there are two division lines; sources between the two lines are deemed to be “intermediate” by that classification method. The different symbols reflect the final combined classification of each source: radio AGN are plotted as red diamonds and SFGs as black crosses. In the lower left plot, arrows indicate upper limits to the Hα luminosity. |
| In the text | |
 |
Fig. 2. Distribution of LoTSS luminosities with respect to the stellar masses. The SF galaxies detected only in LoTSS are plotted with different symbols (circles) than those that are also detected in NVSS/FIRST (stars). Radio AGN are indicated with three-spoked asterisks in red for galaxies detected only in LoTSS and in olive for galaxies detected in both LoTSS and NVSS/FIRST. |
| In the text | |
 |
Fig. 3. Spectral index distribution of the radio-AGN galaxies with both LoTSS and 1.4 GHz measurements, as a function of 1.4 GHz flux density. Individual sources are shown as blue dots and the medians of different bins in 1.4 GHz flux density are shown as orange crosses. The vertical lines correspond to the standard deviation on each bin. The median spectral index at flux densities S1.4 GHz > 20 mJy is 0.63. The weak decrease in median spectral index at lower flux densities may be driven by selection biases in the 1.4 GHz sample, as indicated by the black dashed line that simulates the effect of this (see text for details). |
| In the text | |
 |
Fig. 4. Local 150 MHz luminosity functions of AGN (red circles) and SF galaxies (blue diamonds) separately. Also shown for comparison (black dashed lines) are the local 1.4 GHz luminosity function for radio AGN (using the parameterisation of Heckman & Best 2014) and SF galaxies (using the parameterisation of Mauch & Sadler 2007), converted to 150 MHz by scaling the break frequency with a spectral index of 0.7. |
| In the text | |
 |
Fig. 5. Left panel: fraction of galaxies that host a radio AGN above a given luminosity limit, as a function of stellar mass, for multiple radio luminosity limits (shown in different colours). Right panel: fraction of galaxies hosting radio AGN brighter than a given radio luminosity, separated by their stellar mass. The various stellar mass ranges are shown in different colours. The solid lines represent the results of this (150 MHz) study and dotted lines show the results from Best et al. (2005a) at 1.4 GHz (converted assuming a spectral index of 0.7). The error bars correspond to a confidence interval equivalent to one sigma. The fractions of radio AGN are shown only up to L150 MHz ≈ 1025 W Hz−1 because the number of galaxies above this limit is relatively low and render very large error bars. The highest mass bin would reach a value compatible with 100 per cent within the error at L150 MHz ≤ 1021.7 W Hz−1 but those points are not shown owing to the large error bars. |
| In the text | |
 |
Fig. 6. Left panel: fraction of galaxies that host a radio AGN above a given radio luminosity, as a function of the black hole mass, for various radio luminosity limits (shown in different colours). Right panel: fraction of galaxies hosting radio AGN brighter than a given radio luminosity, separated by their black hole mass. Colours, lines, and errors bars as in Fig. 5. In the left panel, the line corresponding to L150 MHz ≤ 1021 W Hz−1 is omitted from the plot owing to its large error bars. |
| In the text | |
 |
Fig. 7. Left panel: fraction of galaxies that host a radio AGN with L150 MHz ≥ 1022.5 W Hz−1, as a function of the black hole mass, for multiple stellar mass bins (shown in different colours). Right panel: fraction of galaxies hosting radio-AGN with L150 MHz ≥ 1022.5 W Hz−1, as a function of the stellar mass, separated by their black hole mass (shown in different colours). |
| In the text | |
 |
Fig. 8. Distribution of Eddington-scaled accretion rate for radio AGN (solid blue line). The error bars correspond to the 95 per cent confidence interval. The cumulative distribution obtained from the Kaplan-Meier estimator (solid green line) running from higher towards lower accretion rates is shown. The orange cross represents the remaining fraction of galaxies spread over the following 4 bins. The distribution flattens and peaks at Lmech/LEdd ≈ 10−5. A Kaplan-Meier estimator fit finds the median of the distribution at Lmech/LEdd = 10−4.98. We note that the conversion between radio luminosities and mechanical power is uncertain at low luminosities (e.g. Hardcastle et al. 2019). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.