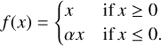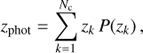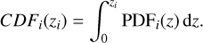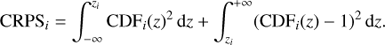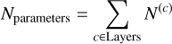| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 15 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201833617 | |
| Published online | 21 December 2018 | |
Photometric redshifts from SDSS images using a convolutional neural network
1 Aix-Marseille Univ., CNRS/IN2P3, CPPM, Marseille, France
e-mail: pasquet@cppm.in2p3.fr
2 Sorbonne Université, CNRS, UMR 7095, Institut d’ Astrophysique de Paris, 98 bis bd Arago, 75014
Paris, France
3 Aix-Marseille Univ., CNRS, CNES, LAM, Marseille, France
Received:
11
June
2018
Accepted:
24
October
2018
We developed a deep convolutional neural network (CNN), used as a classifier, to estimate photometric redshifts and associated probability distribution functions (PDF) for galaxies in the Main Galaxy Sample of the Sloan Digital Sky Survey at z < 0.4. Our method exploits all the information present in the images without any feature extraction. The input data consist of 64 × 64 pixel ugriz images centered on the spectroscopic targets, plus the galactic reddening value on the line-of-sight. For training sets of 100k objects or more (≥20% of the database), we reach a dispersion σMAD < 0.01, significantly lower than the current best one obtained from another machine learning technique on the same sample. The bias is lower than 10−4, independent of photometric redshift. The PDFs are shown to have very good predictive power. We also find that the CNN redshifts are unbiased with respect to galaxy inclination, and that σMAD decreases with the signal-to-noise ratio (S/N), achieving values below 0.007 for S/N > 100, as in the deep stacked region of Stripe 82. We argue that for most galaxies the precision is limited by the S/N of SDSS images rather than by the method. The success of this experiment at low redshift opens promising perspectives for upcoming surveys.
Key words: galaxies: distances and redshifts / surveys / methods: data analysis / techniques: image processing
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Panoramic imaging surveys for cosmology are underway or in preparation phase (HSC, LSST, Euclid, WFIRST). They will deliver multiband photometry for billions of galaxies for which reliable redshifts are necessary to study the large scale structure of the universe and to constrain the dark energy equation-of-state using weak gravitational lensing. However, spectroscopic redshifts are extremely time-intensive and it has become necessary to use photometric redshifts. The projections for cosmic shear measurements estimate that the true mean redshift of objects in each photometric redshift bin must be known to be better than ∼0.002(1 + z) (Knox et al. 2006) with stringent requirements on the fraction of unconstrained catastrophic outliers (Hearin et al. 2010). Another challenge is the derivation of robust redshift probability distribution functions (PDFs, Mandelbaum et al. 2008) for a complete understanding of the uncertainties attached to any measurements in cosmology (e.g., galaxy clustering, weak lensing tomography, baryon acoustic oscillations) or galaxy evolution (e.g., luminosity and stellar mass functions, galaxy density field reconstruction, cluster finders).
Two main techniques are traditionally used to perform this task: template fitting and machine learning algorithms. The template fitting codes (e.g., Arnouts et al. 1999; Benítez 2000; Brammer et al. 2008) match the broadband photometry of a galaxy to the synthetic magnitudes of a suite of templates across a large redshift interval1. This technique does not require a large spectroscopic sample for training: when a representative set of galaxy template has been found it can be applied to different surveys and redshift range. However, they are often computationally intensive due to the brute-force approach to explore the pre-generated grid of model photometry. Moreover poorly known parameters such as dust attenuation, can lead to degeneracies in color − redshift space. On the other hand, the machine learning methods, such as artificial neural network (Collister & Lahav 2004), k-nearest neighbors (KNN; Csabai et al. 2007) or random forest techniques (Carliles et al. 2010) were shown to have similar or better performances when a large spectroscopic training set is available. However, they are only reliable within the limits of the training set and the current lack of spectroscopic coverage in some color space regions and at high redshift remains a major issue for this approach. For these reasons, template-fitting methods are still considered and new approaches have emerged which combine several techniques to maximize the photometric redshift PDF estimations (e.g., Carrasco Kind & Brunner 2014; Cavuoti et al. 2017).
One limiting factor for all the above methods is the input information. The accuracy of the output photometric redshifts is limited by that of the photometric measurements (Hildebrandt et al. 2012). Magnitudes or colors are affected by the choice of aperture size, point spread function (PSF) variations, overlapping sources, and even modeled magnitudes (accounting for PSF and galaxy luminosity profiles) capture only a fraction of the information present in the images.
Over the past few years, deep learning techniques have revolutionized the field of image recognition. By bypassing the condensed information of manual feature extraction required by previous methods they can offer unprecedented image classification performance in a number of astronomical problems, including galaxy morphological classification (e.g., Dieleman et al. 2015; Huertas-Company et al. 2015), lensed images (Lanusse et al. 2018), classification of light curves (Charnock & Moss 2017; Pasquet-Itam & Pasquet 2018). Thanks to the speed boost from graphic processing units (GPU) technology and large galaxy spectroscopic sample such as the SDSS survey, Hoyle (2016); D’Isanto & Polsterer (2018) show that deep convolutional neural networks (CNNs) were able to provide accurate photometric redshifts from multichannel images, instead of extracted features, taking advantage of all the information contained in the pixels, such as galaxy surface brightness and size, disk inclination, or the presence of color gradients and neighbors. To do so, Hoyle (2016) use a deep CNN-inspired by the architecture of Krizhevsky et al. (2012a), on 60 × 60 RGBA images, encoding colors (i − z, r − i, g − r) in RGB layers and r band magnitudes in the alpha layer. The use of only four bands (griz) allowed them to mimic the DES experiment. They divide the spectroscopic redshift distribution into bins and extracted the redshift bin that the galaxy was most likely to be in. To obtain a PDF, they then randomly extract 100 60 × 60 stamps from an original 72 × 72 image stamp, and rerun the CNN algorithm. D’Isanto & Polsterer (2018) use a deep CNN model, based on a LeNet-5 architecture (LeCun et al. 1998), using 28 × 28 pixel images in the five SDSS bands (ugriz) as well as all the color combinations as input. They modify the fully connected part of the CNN to include a mixture density network (with one hidden layer) to describe the output PDF as a Gaussian mixture model. These two first-of-their-kind analyses based on existing architectures, achieved competitive photometric redshift accuracies compared to other machine learning techniques based on boosted decision tree or random forest.
In this paper, we present a deep learning model for the estimation of photometric redshifts and their associated PDF using the TensorFlow framework (v1.4.1). In contrast to previous studies, our input consists of ugriz images only (no color images are produced), from the flux-limited spectroscopic Main Galaxy Sample (MGS) of the SDSS. The paper is organized as follows. In Sect. 2, we describe the data used in this study. In Sect. 3, we introduce the CNN concepts and the particular CNN architecture we are proposing. In Sect. 4, we present our results for the estimation of photometric redshifts and associated PDFs. In Sect. 5, we investigate the impact of reducing the size of the training set. In Sect. 6, we analyze the behavior of the CNN with respect to a number of galaxy properties and observing conditions. Our results are summarized in Sect. 7.
2. Data
The SDSS is a multiband imaging and spectroscopic redshift survey using a dedicated 2.5-m telescope at Apache Point Observatory in New Mexico. It provides deep photometry (r < 22.5) in ugriz passbands. Our input data are selected from the data release 12 (DR12; Alam et al. 2015) by using the SDSS CasJob website (the MySQL query is given in Appendix A). From the SDSS database, we retrieved 516 525 sources classified as galaxy, with dereddened petrosian magnitudes r ≤ 17.8 and spectroscopic redshifts z ≤ 0.4. For all we queried the equatorial coordinates (RA, Dec), dereddened Petrosian magnitudes, ellipticities (b/a), galactic extinction (Schlegel et al. 1998), PSF full-widths-at-half-maximum (FWHMs) and sky background values in all bands. The spatial distribution of the final sample and its redshift distribution are shown in Fig. 1. The color code indicates the mean galactic reddening excess in each cell, which increases sharply in the vicinity of the galactic plane.
 |
Fig. 1. Spatial distribution of the final sample of SDSS galaxies, with its spectroscopic redshift distribution (top-right inset). The color code indicates the average galactic extinction per pixel. The gray line shows the galactic plane. |
We also retrieved the photometric redshifts of Beck et al. (2016; hereafter B16) , which are the only such redshifts available for comparison in DR12. They were computed with a k-NN method (Csabai et al. 2007, local linear regression) that included five dimensions (r magnitude and u − g, g − r, r − i, i − z colors) and trained with deep and high redshift spectroscopic surveys in addition to the SDSS. These photometric redshifts have similar or better accuracies than those inferred from random forests or prediction trees on the MGS sample (Carrasco Kind & Brunner 2013; Carliles et al. 2010), and may thus serve as reference for machine learning photometric redshifts based on photometric measurements.
We downloaded all the “corrected frames” image data of the SDSS data release 8 from the SDSS Science Archive Server, including the 118 runs on Stripe 82 that are part of the release (Aihara et al. 2011a). The image headers include the astrometric fix applied to the SDSS data release 9 (Aihara et al. 2011b). The frames come background-subtracted and photometrically calibrated with an identical magnitude zero-point (Padmanabhan et al. 2008; Blanton et al. 2011). All 4 689 180 frames and their celestial coordinates are indexed in a table for query with a homemade query tool2 (v0.4). The purpose of this tool is to provide the list of all images likely to overlap a given sky area.
For every entry in the galaxy sample we queried the list of overlapping frames for each of the 5 SDSS filters and ran the SWARP tool3 (v1.38, Bertin et al. 2002) to resample to a common pixel grid and stack all the available image data. We relied on the WCS parameters in the input image headers (Calabretta & Greisen 2002) for the astrometry. Because of limitations with WCS parametrization, positions are good to about 1 pixel. Differences in position between channels are expected to be less, because the different channels follow roughly the same path along the scanning direction. However systematic or random misalignments across or between channels should not impact measurably the classifier’s performance as long as they remain statistically identical for both the training and test datasets.
The result is a 64 × 64 × 5 pixel datacube in a gnomonic projection centered on the galaxy coordinates, and aligned with the local celestial coordinate system. The output pixel scale is identical to that of the input images (0.396 arcsec). We chose a Lánczos-3 resampling kernel (Duchon 1979) as a compromise between preserving image quality and minimizing the spread of possible image artifacts. Other SWARP settings are also set to default, except for background subtraction, which is turned off.
The number of overlapping frames contributing to a given output pixel in a given filter ranges from one or two for “regular” SDSS images, to 64 for some of the galaxies in Stripe 82. No attempt is made to remove singular images, to mask out neighbors or to subtract light contamination from close bright sources, hence all galaxy images are included in the final dataset unmodified.
Machine learning algorithms dealing with pixel data are generally trained with gamma-compressed images (e.g., in JPEG or PNG format). Yet our tests did not show any improvement of the classifier performance after applying dynamic range compression. We therefore decided to leave the dynamic range of the images intact. Figure 2 shows five image cutouts from the dataset.
 |
Fig. 2. Random examples from the image dataset. Images in the 5 SDSS channels were linearly remapped to red, green, blue, with saturation α = 2.0 and display γ = 2.2 applied following the prescriptions from Bertin (2012). |
3. The convolutional neural network
3.1. Neural networks
Artificial neural networks (NNs) are made of interconnected, elementary computing units called neurons. As in biology where a natural neuron is an electrically excitable cell that processes and transmits information via synapses connected to other cells, an artificial neuron receives a vector of inputs, each with a different weight, and computes a scalar value sent to other neurons. Once the type of neuron and the network topology have been defined, the network behavior relies solely on the strength of the connections (synaptic weights) between neurons. The purpose of learning (or training) is to iteratively adjust the synaptic weights until the system behaves as intended.
Multilayered neural network models are currently the basis of the most powerful machine learning algorithms. In this type of NN, neurons are organized in layers. Neurons from a layer are connected to all or some of the neurons from the previous layer.
Convolutional neural networks (CNNs) are a special type of multilayered NNs. CNN classifiers are typically composed of a number of convolutional and pooling layers followed by fully connected layers.
3.2. Convolutional layers
A convolutional layer operates on a data cube, and computes one or several feature maps, also stored as a datacube. The feature maps inside a convolutional layer are generally computed independently of one another. The purpose of a feature map is to emphasize regions of the input datacube that correlate with a specific pattern, represented by a set of adjustable kernels (one per input data plane in our case). In practice, the correlation process is achieved by convolving the outputs from the previous layer with the kernels. During training, the kernels, which had been initially populated with random values, are updated to become progressively relevant to the classification (or regression; see Fig. 3). The convolved arrays plus an adjustable offset are then summed and an activation function applied element-wise to form the feature map.
 |
Fig. 3. Representation of the first convolution layer with two kernels of convolution to simplify the schema. The multispectral image of a galaxy in the five SDSS filters is fed to the network. Each kernel is convolved with the multichannel images. The convolved images are summed, an additive bias is added and a non-linear function is applied, to produce one feature map. |
For the first convolution layer the input datacube is typically a multispectral image (64 × 64 × 5 pixels in the case of our images taken through the ugriz SDSS filters). Subsequent layers operate on feature maps from the previous layers.
Non-linear activation functions introduce non-linearity into the network. The most commonly used activation function is the ReLU (Rectified Linear Unit, Nair & Hinton 2010) defined by f(x)=max(x, 0). More recently, He et al. (2015) introduced a Parametric ReLU (PReLU) with parameter α adjusted through basic gradient descent:
3.3. Pooling layers
Pooling layers reduce the size of input feature maps through down-sampling along the spatial dimensions (2 × 2 elements in our case). The down-sampling operation typically consists in taking the mean or the max of the elements. Pooling allows feature maps to be computed on multiple scales at a reduced computational cost while providing some degree of shift invariance. Invariance toward transformations of the input image can further be reinforced by data augmentation (Goodfellow et al. 2009; Zhu et al. 2015).
3.4. Fully connected layers
Contrary to their convolution layer equivalents, the neurons of a fully connected layer are connected to every neuron of the previous layer, and do not share synaptic weights. In conventional CNNs, the fully connected layers are in charge of further processing the features extracted by the convolutional layers upstream, for classification or regression.
3.5. Output layer
We chose to handle the estimation of photometric redshifts as a classification problem, as opposed to using (non-linear) regression. Previous studies (e.g., Pasquet-Itam & Pasquet 2018) demonstrate the benefits of this approach. Each class corresponds to a narrow redshift bin δz. The galaxy at the center of the input multispectral image belongs to a single class (i.e., is at a single redshift).
The classes being mutually exclusive, we imposed that the sum of the outputs be 1 by applying the softmax activation function (Bridle 1990) to the output layer. The network was trained with the cross-entropy loss function (Baum & Wilczek 1987; Solla et al. 1988). The output of this type of classifier was shown, both theoretically and experimentally, to provide good estimates of the posterior probability of classes in the input space (Richard & Lippmann 1991; Rojas 1996). This of course requires the neural network to be properly trained and to have enough complexity.
3.6. Our CNN architecture
The overall architecture4 is represented in Fig. 4. The network takes as input a batch of images of size 64 × 64, centered on the galaxy coordinates, in five channels corresponding to the five bands (u, g, r, i, z). The first layer performs a convolution with a large kernel of size 5 × 5. The pooling layer that follows reduces the size of the image by a factor of two. All the poolings in the network are computed by selecting the mean value in the sliding window. Although many studies use max pooling for classification problems, our experience with SDSS images is that average pooling performs better. The fact that most image pixels are dominated by background noise may explain why max pooling is not so reliable.
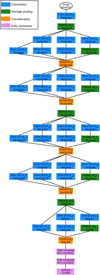 |
Fig. 4. Classifier architecture (see Sect. 3.6 for a detailed description). The neural network is composed of a first convolution layer, a pooling layer and five inception blocks followed by two fully connected layers and a softmax layer. The size and the number of feature maps are indicated for each layer. Further details can be found in Table A.1. |
We also found the PReLU activation function to perform better than the traditional ReLU in convolutional layers. One possible explanation may be that the negative part of the PReLU does not saturate, allowing faint signals below the threshold (e.g., those dominated by background noise) to propagate throughout the layer.
The remaining convolution part of the network is organized in multiscale blocks called inception modules (Szegedy et al. 2015). Each inception module is organized in two stages. In the first stage, the feature maps are convolved by three “1 × 1” convolution layers. These layers are used to combine input feature maps and reduce their number before the more computationally expensive convolutions of the second stage. In this second stage, feature maps are processed in parallel in a pooling layer and a pair of larger convolution layers with size 3 × 3 and 5 × 5 helps identify larger patterns. Then, resulting feature maps are concatenated along the depth dimension before going to the next layer. We note that the final inception module does not include the 5 × 5 convolution layer as the last feature maps (8 × 8) have become too small to generate a useful output.
All the feature maps coming out from the last multiscale block are concatenated and sent to a fully connected layer of 1096 neurons. One extra input containing the Galactic reddening value for the current galaxy is also added at this stage (Sect. 6.1).
After a second fully connected layer of 1096 neurons comes the output softmax layer. We set the number of classes to Nc = 180 redshift bins over the range 0–0.4, with constant width δz = 2.2 × 10−3. We believe that this sampling offers a reasonable compromise between the number of galaxies in each bin and redshift quantization noise. Such a large number of classes is not uncommon in modern classification challenges (e.g., Russakovsky et al. 2015). As we shall see, the resulting distribution (a vector of 180 posterior probabilities) provides a reliable estimate of the photometric redshift PDF.
The number and sizes of the feature maps are provided in Table A.1. In Appendix B we also describe the computational time needed for the various training steps.
In total the number of adjustable parameters is 27 391 464 (see Eq. (B.1)). A common concern with large neural networks is overfitting, which happens whenever a model with too many free parameters learns irrelevant and noisy details of the training data to the extent that it negatively impacts its performance. To make sure that our classifier was not overfitting, we monitored the loss on both the training and validation sets during the training stage. The PIT distribution (Sect. 4.3) also proved a valuable monitoring tool. Other methods we tested for addressing overfitting are batch normalization (Ioffe & Szegedy 2015) and dropouts (Srivastava et al. 2014). However they did not improve the performance of our classifier.
3.7. Photometric redshift estimation
Although photometric redshift PDFs may be directly incorporated into larger Bayesian schemes for inferring model parameters (e.g., cosmological parameters), they may also be used to compute point estimates of the individual redshifts. We estimate the photometric redshift of a given galaxy by computing its expected value from its PDF P(zk ):
where zk is the midpoint value of the kth redshift bin. Assuming that P(zk ) is reliable over the whole redshift range (see Sect. 4.3), Eq. (2) provides a minimum mean square error estimation of the photometric redshift given the data.
Alternatively, we tested non-linear regression models with a multilayered neural network to estimate photometric redshifts directly from the softmax layer PDF output, using both a quadratic and median absolute deviation (MAD) cost functions (see Sect. 4.1). After training with the spectroscopic redshifts, both models performed almost identically and did not provide any significant improvement in accuracy over Eq. (2).
3.8. Experimental protocol
We divided the database into a training sample containing 80% of the images and a testing sample composed of the remaining 20%. To ensure that the CNN is not affected by galaxy orientation, we augmented the training set with randomly flipped and rotated (with 90deg steps) images. We also selected 20 000 images in the training database to create a validation sample that allows us to control the performance of the model.
To increase the performance, we trained an ensemble of classifiers as it was shown to be more accurate than individual classifiers (e.g., Krizhevsky et al. 2012b). Moreover the generalization ability of an ensemble is usually stronger than that of base learners. This step involves training N times one model with the same training database but a different initialization of the weights. As a compromise between computation time and accuracy, we chose N = 6. The individual decisions were then averaged out to obtain the final values of the photometric redshifts. We also averaged the PDFs, although we are aware that the result is a pessimistic estimate of the true PDF. Other combination methods will be investigated in a future analysis. In the following sections, the terms photometric redshift and PDF refer to averages over the six trainings. We also processed five cross-validations of the database to evaluate the stability of the network. This involves performing five learning phases, each with its own training sample (80% of the initial database) and testing sample (the remaining 20%), so as to test each galaxy once.
Table 1 shows the performance of each cross-validation, using the metrics (bias, σMAD and η) defined in Sect. 4.1. The bias varies slightly but the standard deviation and the fraction of outliers do not change significantly. Therefore we find the network to be statistically robust. In the following, the quoted values for the bias, standard deviation and fraction of outliers are the average values over 5 cross-validations, unless otherwise stated. Figure 5 summarises the protocol of the training process.
Stability of the CNN over five cross-validations.
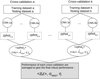 |
Fig. 5. Schema of the experimental protocol. For each training and testing datasets, six models are trained and averaged to get the final photometric redshift values. Moreover five cross-validations are performed. Their respective performances are averaged to provide the final scores (bias, σMAD and η). |
4. Results
In this section, we present the overall performance of our method for the estimation of photometric redshifts, and describe our tests of the statistical reliability of the PDFs.
4.1. Metrics
To assess the quality of the photometric redshifts, we adopted the following commonly used statistics:
-
the residuals, Δz = (zphot − zspec)/(1 + zspec), following the definition of Cohen et al. (2000);
-
the prediction bias, < Δz> , defined as the mean of the residuals;
-
the MAD deviationσMAD = 1.4826 × MAD, where MAD (Median Absolute Deviation) is the median of |Δz − Median(Δz)|5;
-
the fraction η of outliers with |Δz|> 0.05, chosen to be ∼5 times the σMAD achieved by the CNN.
The statistics for the network described in the previous section are reported in Table 1, as well as in the first row of Table 2 (mean values over the five cross-validations). The normalized distribution of Δz is shown in Fig. 6. The green line shows a Gaussian distribution with the inferred sigma and bias. The hatched zones define the catastrophic outliers.
Statistics for various CNN trials, with the B16 results in parenthesis where the comparison is relevant.
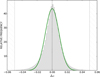 |
Fig. 6. Normalized Δz distribution. The green line is a Gaussian distribution with the sigma and bias defined in Sect. 4.1 and reported in Table 2. The hatched parts define the catastrophic outliers. |
4.2. Photometric redshifts
The distribution of the photometric vs. spectroscopic redshifts obtained from the CNN (Fig. 7, left panel) shows a striking decrease of the dispersion around the truth value compared to B16 (right panel), the latest and only comparable study. This is reflected in the scores for the three statistics: a factor of 1.5, 6 and 4 improvement for the σMAD, bias and outlier rate respectively (the B16 values are listed in parenthesis in Table 2). However we observe a plateau near z ∼ 0.3 for the CNN, where high redshift objects are significantly under-represented (galaxies with z ∼ 0.3 represent 0.1% of the training database)6. This trend is not observed in B16 as they use a larger training set that extend to much higher redshift.
 |
Fig. 7. Comparison between the photometric redshifts predicted by the CNN (left panel) and by B16 (right panel) against the spectroscopic redshifts. The galaxy density and the statistics are averaged over the five cross-validation samples. |
Figure 8 shows the bias as a function of both spectroscopic redshift and photometric redshift, with the corresponding redshift distributions and the B16 results for comparison. The photometric redshifts predicted by the CNN tend to be slightly over(under)-estimated below(above) the median redshift of the training sample, meaning they are biased toward the most highly populated redshift bins. However the bias remains small and never exceeds 1σ. It is also significantly smaller than the bias induced by the B16 method. Most importantly, none is found as a function of photometric redshifts. This is particularly noteworthy for future large missions. The photometric redshift requirement for Euclid is Δz ≤ 0.002 in photometric redfshift bins (yellow shaded zone), well achieved by the present method.
 |
Fig. 8. Mean residuals as a function of spectroscopic redshifts (gray) and CNN redshifts (red). The dashed lines show the corresponding results for B16. The histograms are the respective redshift distributions. The CNN redshifts tend to be slightly over(under)-estimated below(above) the most populated redshift bins of the training sample, that is, they are biased toward the region of highest training. The effect is larger for B16, however no bias is found as a function of photometric redshift in either case. |
To understand the origin of the spectroscopic redshift dependent bias, one must realize that neural networks are naturally sensitive to priors in the training sample. Indeed, if the input redshift distribution was flat, the model would have the same number of examples at each redshift value and so redshift predictions would be equiprobable. However for real galaxy samples the distribution of redshifts is not flat, it peaks at a particular redshift. So the model will be more constrained by galaxies around this peak value than by galaxies in the wings of the distribution. This prior distribution causes a bias in predictions as all the predictions are not equiprobable and so the model tends to predict the most probable value. This behavior is expected from all machine learning methods. In the case of our classifier, the PDF should be a good estimation of the redshift posterior probability density, given an input datacube.
4.3. Probability distribution functions
The PDFs of a subset of randomly selected galaxies from the test set are shown in Fig. 9, together with the galaxy RGB images. As proposed by Polsterer et al. (2016), we use two statistics to assess the overall prediction quality of our PDFs: the probability integral transform (PIT) and the continuous ranked probability score (CRPS).
 |
Fig. 9. Random examples of PDFs obtained from the CNN. The red dotted lines indicate the values of the spectroscopic redshifts and the blue ones the photometric redshifts estimated by the CNN and computed as the softmax weighted sum of the redshift values in each bin of the PDF. |
The PIT statistic (Dawid 1984) is based on the histogram of the cumulative probabilities (CDF) at the true value, in other words, the spectroscopic redshift. For galaxy i at spectroscopic redshift zi, with redshift probability distribution function PDFi, the PIT value is
A flat PIT distribution indicates that the PDFs are not biased with respect to the spectroscopic redshifts and are neither too narrow nor too wide, whereas convex or concave distributions point to under or over-dispersed PDFs, respectively (Polsterer et al. 2016). Excessively narrow PDFs will often miss the target, overproducing PIT values close to zero or one, whereas PDFs that are too wide will encompass the true redshifts more often than not and therefore favor intermediate PIT values. The PIT distribution for each of the six models in our ensemble of classifiers, and for the final PDFs (see Sect. 3.8) are shown in Fig. 10. Each individual model exhibits a nearly flat PIT distribution, indicating well behaved PDFs. The PIT distribution of the final (averaged) PDFs is slightly over dispersed, as expected from our pessimistic choice of combination.
 |
Fig. 10. Distribution of the Probability Integral Transforms (PIT) for each of the six models, and for the final PDFs. Each model exhibits a nearly flat PIT distribution, which assesses the very good quality of the PDFs. The PIT distribution of the final (averaged) PDFs (see Sect. 3.8) is slightly over dispersed, as expected from our pessimistic choice of combination. The dashed green and red lines result from expanding and shrinking, respectively, the Δz of a flat model by 20%. |
The CRPS is a performance score (well known in meteorological predictions, Hersbach 2000) that quantifies how well the predicted PDF represents the true spectroscopic redshift. For galaxy i, it is defined as:
The mean CRPS (∼0.007) is reported in the last column of Table 2. This value is significantly lower than the CRPS quoted by D’Isanto & Polsterer (2018) or Tanaka et al. (2018; ∼0.1 and 0.02 respectively), although a fair comparison is difficult as these studies encompass larger redshift domains. However, the small mean CRPS and the nearly flat PIT distribution reflect the high reliability of our PDFs.
To further assess the quality of the PDFs, we measured their “widths”, defined as the redshift interval resulting from chopping off their left and right wings in equal measure, so as to keep 68% of the probability distribution7. Removing the widest 10% (20%) of the PDFs (width > 0.0383 (0.0335)) significantly improve σMAD and η, as reported in Table 2. These improvements reinforce our confidence that our PDFs properly reflect the photometric redshift uncertainties.
5. Size of the training database
As acquiring large spectroscopic samples for training is very observing time intensive, it is crucially important to assess the performance of our CNN as a function of training size. Our baseline network made use of 400 000 galaxies (80% of the database). We trained the same model on 250 000 and 100 000 galaxies (50% and 20% of the database respectively), and also adapted the network by reducing its depth and width for a 10 000 galaxy training sample (2% of the database).
The statistics of these three trials are reported in Table 2. We find practically no fall in performance between the training on 400 000 objects and that on 100 000, which is a particularly encouraging result. Although the global statistics deteriorate significantly with 10 000 training sources, they remain comparable to the results of B16, which is also remarkable. Moreover, for all three trials including the 10 000 sources training sample, all the trends, or lack thereof, plotted in the next section remain nearly indistinguishable from our baseline 400 000 sources training case.
6. Further behavioral analysis of the CNN
In this section, we describe our study of how the performance of the CNN varies with a number of characteristics of the input images relating to galaxy properties or observing conditions.
6.1. Galactic reddening
As illustrated in Fig. 1, the SDSS spans a large range in Galactic extinction. The effect of E(B − V) on the observed colors of a galaxy can mimic that of a redshift increase. The impact of including the reddening information into the training, or not, is illustrated on Fig. 11 (left panel). Without this information provided to the classifier, a strong reddening-dependent bias is observed (orange line). A weaker trend is observed for B16, who use SDSS de-reddened magnitudes. The small size of the sample at high galactic extinction most likely prevents the CNN from properly accounting for this degeneracy, hence our choice to include the reddening information into our model, which successfully removes the trend (red line).
 |
Fig. 11. Left panel: bias as a function of Galactic extinction for the classifier with and without integrating E(B − V) into the training (red and orange lines respectively) and for B16 (green). The CNN tends to overestimate redshifts in obscured regions (confusing galactic dust attenuation with redshift dimming), unless E(B − V) is used for training. Right panel: bias as a function of disk inclination for galaxies classified as star-forming or starburst. The CNN is virtually unbiased wrt ellipticity, unlike B16. |
6.2. Galaxy inclination
As Galactic reddening, the inclination of a galaxy reddens its color but also affects the shape of the attenuation curve in a complex way (Chevallard et al. 2013). It has been a major issue for the estimation of photometric redshifts, especially with SED fitting codes (Arnouts et al. 2013). Figure 11 (right panel) shows that the CNN is very robust to galaxy inclination, unlike the B16 method, which is strongly biased, especially at high inclination. The network is able to account for this effect thanks to the large training sample, helped by the data augmentation process that further expanded it by rotating and flipping the images. While B16 only uses the photometric information, Yip et al. (2011) show that machine learning methods can better handle this bias if the inclination information is included into their training.
6.3. Neighboring galaxies
We investigated the impact of neighboring sources on the performance of the CNN using the SDSS DR12 neighbors table, which contains all photometric pairs within 0.5 arcmin. We selected the spectroscopic galaxies with at least one photometric neighbor with r ≤ 21 within a distance of 2–17 arcsec (therefore within the image cut-outs used by the CNN). With this definition, 48% of our spectroscopic targets have neighbors.
Only 5% of the galaxies in the dataset have a neighbor brighter than themselves (a few examples can be seen in Fig. 9), which appears to have no impact on the accuracy of their CNN redshift estimation compared to lone galaxies with matching r-band magnitude distributions (not matching these distributions induces different σMAD simply because that of galaxies with neighbors brighter than themselves has a significantly steeper slope, that is, a higher fraction of faint galaxies, than those without). However the MAD deviation is significantly improved for galaxies with fainter neighbors (43%) compared to those without: σMAD = 0.00887 and 0.00937 respectively. In this case, the r-band magnitude and signal-to-noise distributions of the two samples are similar, thus matching is not necessary. The σMAD discrepancy is not due to differences in these qualities of the central targets. On the other hand, the redshift distributions are different and the MAD deviation of galaxies with neighbors becomes noticeably smaller than that of galaxies without neighbors only past the mean redshift of the overall sample, as shown in Fig. 12. Not only has the CNN “seen” more examples with neighbors than without at higher redshift, it can also be argued that it has actually learned how to use neighboring sources to improve the accuracy of the redshift estimation. This can occur, first, by using the redshift correlation of real close pairs, especially when they share very similar colors and surface brightnesses (e.g., early types in cluster cores), and second, by obtaining further information on image quality from any type of sources in the vicinity.
 |
Fig. 12. σMAD as a function of redshift for galaxies with and without neighbors (red and green lines respectively), as defined in Sect. 6.3. The respective redshift distributions are shown at the bottom. |
6.4. Variations throughout the surveyed area
Figure 13 shows the spatial variations of the bias and of the PDF widths on the celestial sphere (the color code refers to the mean quantities per cell). Overall, both quantities, which we find to be uncorrelated, show little variation throughout the surveyed area. However we identify a small region of the SDSS (∼2.4%) where both are puzzlingly below average in quality (red patch toward the pole).
 |
Fig. 13. Spatial distribution of the mean bias (left panel) and of the mean PDF width (right panel). The locations of the SZ and of the Stripe 82 region (see Sect. 6.4) are indicated. |
This SZ appears to coincide with Stripe 38 and 39, but with no evidence of sky background, PSF or photometric calibration issues. Although it is in a region of high Galactic extinction, excess reddening doesn’t seem to cause the problem as it is not detected in the other regions of equally high galactic extinction (Fig. 1). Inadequate reddening does not explain it either as the region also stands out when E(B − V) is not included into the training.
The bias on this patch alone is ∼30 times larger than on the full test sample (+0.0033 vs. +0.0001), and also ∼10 times larger for B16. Removing the region from the test sample reduces the bias by a factor of 2.5, while σMAD is unaffected (see Table 2).
We also note the Stripe 82 region, which exhibits narrower than average PDFs (dark blue stripe in the right panel of Fig. 13). This point is addressed in the next section. Figure 14 shows the mean PDF in these two atypical regions compared to that of the full sample.
 |
Fig. 14. Mean PDF in the SDSS patch showing defective photometric redshift and PDF quality (SZ) and in the Stripe 82 region, compared to the mean PDF of the full sample. The PDFs have been translated so that 0 corresponds to the spectroscopic redshifts. |
6.5. Effect of noise
The Stripe 82 region, which combines repeated observations of the same part of the sky, gives us the opportunity to look into the impact of signal-to-noise ratio (S/N) on our photometric redshift estimations. The statistics for this region alone are reported in Table 2. The resulting σMAD outperforms that of the other tests (and can be further reduced by removing the widest PDFs). Thus increasing the S/N improves the performance of the classifier, even though the training was predominantly done using images with lower S/Ns.
We further tested the impact of S/N by training the same model (Fig. 4) on two different datasets: one with Stripe 82 images only, one without Stripe 82. The statistics are reported in Table 2. Removing Stripe 82 from the training set has no impact on the performance of the network outside of Stripe 82, unsurprisingly given the small perturbation it induces, and only slightly degrades σMAD on Stripe 82. This confirms that a CNN network mostly trained on low S/N images performs better on higher S/N images.
Evaluating whether training on high S/N images improves the performance on low and/or high S/N images is more difficult. Training the network on Stripe 82 images reduces the training set to only ∼16 000 galaxies, a very small sample for deep learning. The testing on Stripe 82 shows that σMAD is slightly higher and the bias lower, compared to training with the full dataset: a better match between the training and test sets may be compensating for the reduced training size. The performance outside of Stripe 82 is degraded; this may be due to mismatched datasets (Stripe 82 images are too deep for the CNN to be able to classify shallow images well enough) and/or to the small size of the training sample. We can only conclude that small training sets with higher S/N images do not help the performance on low S/N images.
A more detailed analysis of this effect is presented in Fig. C.1, which shows the behavior of the redshift bias and σMAD as a function of S/N in all five bands. The S/Ns were derived simply from the Petrosian magnitude errors quoted in the SDSS catalog. Stripe 82 galaxies were removed from this analysis, as the SDSS DR12 catalog does not provide photometric errors for the stacked images used in this work (see Sect. 2). As may be expected from the results on Stripe 82, σMAD gradually improves toward the highest S/N in all bands, with values lower than ∼0.006 for S/N ≥ 200 (∼17 000 sources).
σMAD seems to plateau at the low-end of S/Ns, an effect that is not seen with B16. This is perhaps surprising but good news for the faintest sources, although it must be taken with a grain of salt as our S/N derived from Petrosian magnitude errors may be unreliable for faint objects. The redshift bias shows no clear trend within the uncertainties at low S/N but increases at high S/N. As high S/N objects are preferentially at low redshift (z ≤ 0.1), it probably simply reflects the bias discussed in Sect. 4.2, where galaxies with spectroscopic redshifts below the peak of the training set distribution have their photometric redshifts slightly overestimated.
6.6. Influence of the PSF
As Fig. C.1 shows, σMAD appears to be relatively immune to PSF variations, with only a slight increase for the worst observing conditions in individual bands (middle panel) or in case of large PSF variations between two bands (right panel). On the other hand, the redshift bias shows a small trend with seeing (middle and right panels), similar to that seen in B16, but with opposite signs. Larger PSFs generate an apparent decrease of the apparent surface brightness of galaxies that are not well resolved. We note that SDSS observations are carried out through the different filters within a few minutes of interval, and therefore under very similar atmospheric conditions. This situation is likely to be worse for imaging surveys where the different channels are acquired during separate nights or even runs. Such datasets may require PSF information to be explicitly provided as input to the classifier in addition to the pixel and extinction data.
7. Summary and discussion
In this paper we have presented a deep CNN used as a classifier, that we trained and tested on the Main Galaxy Sample of the SDSS at z ≤ 0.4, to estimate photometric redshifts and their associated PDFs. Our challenge was to exploit all the information present in the images without relying on pre-extracted image or spectral features. The input data consisted of 64 × 64 pixel ugriz images centered on the spectroscopic target coordinates, and the value of galactic reddening on the line-of-sight. We tested 4 sizes of training set: 400k, 250k, 100k, and 10k galaxies (80%, 50%, 20% and 2% of the full database, respectively).
In all but the final case we obtain a MAD dispersion σMAD = 0.0091. This value is significantly lower than the best one published so far, obtained from another machine learning technique (KNN) applied to photometric measurements by Beck et al. (2016) for the same galaxies (σMAD = 0.0135). Restricting the training set to only 10 000 sources (although the CNN was not optimized for such a small number) increases dispersion by 60%, but is still competitive with the current methods.
The bias shows a quasi-monotonic trend with spectroscopic redshift, largely due to the prior imposed by the training set redshift distribution, as expected from PDFs behaving as posterior probabilities. However, the bias is independent of photometric redshift and lower than 10−4 at z ≤ 0.25, far below the 0.002 value required for the scientific goals of the future Euclid mission.
We also find that: firstly, our photometric redshifts are essentially unbiased with respect to galactic extinction and galaxy inclination; secondly, the PDFs have very good predictive power, with a nearly flat distribution of the PIT. Removing the widest PDFs improves the already small σMAD and fraction of outliers; thirdly σMAD decreases with the S/N, achieving values below 0.007 for S/N > 100, as in the deep stacked region of Stripe 82; finally, variations of the PSF FWHM induce a small but measurable amount of systematics on the estimated redshifts, which prompts for the inclusion of PSF information into future versions of the classifier.
We conclude that, with a moderate training sample size (≤100 000), the CNN method is able to extract the relevant information present in the images to derive photometric redshifts and associated redshift PDFs whose accuracy surpasses the current methods. The dependency of σMAD with S/N suggests that we have reached a point where the precision of individual photometric redshifts in the SDSS is essentially limited by image depth, not by the method.
This work opens very promising perspectives for the exploitation of large and deep photometric surveys, which encompass a larger redshift range and where spectroscopic follow-up is necessarily limited. New issues will arise regarding the representativity of the galaxy population in the spectroscopic samples across the whole redshift range, that will require dedicated investigations (e.g., Beck et al. 2017) in anticipation of the LSST and Euclid surveys.
Baum (1962) first developed this method by observing the spectral energy distribution of six elliptic galaxies in the Virgo cluster in nine bands from 3730 Å to 9875 Å.
The neural network model and examples are available at: https://github.com/jpasquet/photoz
Our definition of σMAD differs from the modified version adopted by Ilbert et al. (2006), in which the median residual is not subtracted.
A preliminary test showed that the size of the training batches of images, progressively fed to the CNN, may be at least partly responsible for this plateau: doubling the size improved the prediction at the highest redshifts and moved the plateau upward. Better balancing the redshifts inside each batch may be necessary. This point will be addressed in a future analysis.
Acknowledgments
This work has been carried out thanks to the support of the OCEVU Labex (ANR-11-LABX-0060), the Spin(e) project (ANR-13-BS05-0005, http://cosmicorigin.org), the “Programme National Cosmologie et Galaxies” (PNCG) and the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the “Investissements d’Avenir” French government program managed by the ANR. This publication makes use of Sloan Digital Sky Survey (SDSS) data. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.
References
- Aihara, H., Allende Prieto, C., An, D., et al. 2011a, ApJS, 193, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Aihara, H., Allende Prieto, C., An, D., et al. 2011b, ApJS, 195, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Le Floc’h, E., Chevallard, J., et al. 2013, A&A, 558, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baum, E. B., & Wilczek, F. 1987, Proceedings of the 1987 International Conference on Neural Information Processing Systems, NIPS’87 (Cambridge, MA, USA: MIT Press), 52 [Google Scholar]
- Baum, W. A. 1962, in Problems of Extra-Galactic Research, ed. G. C. Mc Vittie, IAU Symp, 15, 390 [NASA ADS] [Google Scholar]
- Beck, R., Dobos, L., Budavári, T., Szalay, A. S., & Csabai, I. 2016, MNRAS, 460, 1371 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Lin, C.-A., Ishida, E. E. O., et al. 2017, MNRAS, 468, 4323 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez, N. 2000, ApJ, 536, 571 [Google Scholar]
- Bertin, E. 2012, in Astronomical Data Analysis Software and Systems XXI, eds. P. Ballester, D. Egret, & N. P. F. Lorente, ASP Conf. Ser., 461, 263 [Google Scholar]
- Bertin, E., Mellier, Y., Radovich, M., et al. 2002, in Astronomical Data Analysis Software and Systems XI, eds. D. A. Bohlender,D. Durand, & T. H. Handley, ASP Conf. Ser., 281, 228 [Google Scholar]
- Blanton, M. R., Kazin, E., Muna, D., Weaver, B. A., & Price-Whelan, A. 2011, AJ, 142, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Bridle, J. S. 1990, in Neurocomputing, eds. F. F. Soulié, & J. Hérault (Berlin, Heidelberg: Springer), 227 [Google Scholar]
- Calabretta, M. R., & Greisen, E. W. 2002, A&A, 395, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carliles, S., Budavári, T., Heinis, S., Priebe, C., & Szalay, A. S. 2010, ApJ, 712, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco Kind, M., & Brunner, R. J. 2013, MNRAS, 432, 1483 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco Kind, M., & Brunner, R. J. 2014, MNRAS, 442, 3380 [NASA ADS] [CrossRef] [Google Scholar]
- Cavuoti, S., Tortora, C., Brescia, M., et al. 2017, MNRAS, 466, 2039 [NASA ADS] [CrossRef] [Google Scholar]
- Charnock, T., & Moss, A. 2017, ApJ, 837, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Chevallard, J., Charlot, S., Wandelt, B., & Wild, V. 2013, MNRAS, 432, 2061 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Hogg, D. W., Blandford, R., et al. 2000, ApJ, 538, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Collister, A. A., & Lahav, O. 2004, PASP, 116, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Csabai, I., Dobos, L., Trencséni, M., et al. 2007, Astron. Nachr., 328, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Dawid, A. P. 1984, J. R. Stat. Soc. Ser. A (Gen.), 147, 278 [CrossRef] [Google Scholar]
- Dieleman, S., Willett, K. W., & Dambre, J. 2015, MNRAS, 450, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- D’Isanto, A., & Polsterer, K. L. 2018, A&A, 609, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duchon, C. E. 1979, J. Appl. Meteorol., 18, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Goodfellow, I., Lee, H., Le, Q. V., Saxe, A., & Ng, A. Y. 2009, in Advances in Neural Information Processing Systems 22, eds. Y. Bengio, D. Schuurmans, J. D. Lafferty, C. K. I. Williams, & A. Culotta (New York: Curran Associates, Inc.), 646 [Google Scholar]
- He, K., Zhang, X., Ren, S., & Sun, J. 2015, Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), ICCV’15 (Washington, DC, USA: IEEE Computer Society), 1026 [CrossRef] [Google Scholar]
- Hearin, A. P., Zentner, A. R., Ma, Z., & Huterer, D. 2010, ApJ, 720, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Hersbach, H. 2000, Weather Forecast., 15, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrandt, H., Erben, T., Kuijken, K., et al. 2012, MNRAS, 421, 2355 [Google Scholar]
- Hoyle, B. 2016, Astron. Comput., 16, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Huertas-Company, M., Gravet, R., Cabrera-Vives, G., et al. 2015, ApJS, 221, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ioffe, S., & Szegedy, C. 2015, in ICML, eds. F. R. Bach, & D. M. Blei, JMLR Workshop and Conference Proceedings, 37, 448 (JMLR.org) [Google Scholar]
- Knox, L., Song, Y.-S., & Zhan, H. 2006, ApJ, 652, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Krizhevsky, A., Sutskever, I., & Hinton, G. E. 2012a, Advances in Neural Information Processing Systems 25: 26th Annual Conference on Neural Information Processing Systems, 2012, Proceedings of a Meeting Held December 3–6, 2012 (Nevada, United States: Lake Tahoe), 1106 [Google Scholar]
- Krizhevsky, A., Sutskever, I., & Hinton, G. E. 2012b, in Advances in Neural Information Processing Systems 25, eds. F. Pereira, C. J. C. Burges, L. Bottou, & K. Q. Weinberger (New York: Curran Associates, Inc.), 1097 [Google Scholar]
- Lanusse, F., Ma, Q., Li, N., et al. 2018, MNRAS, 473, 3895 [NASA ADS] [CrossRef] [Google Scholar]
- LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. 1998, Proc. IEEE, 86, 2278 [Google Scholar]
- Mandelbaum, R., Seljak, U., Hirata, C. M., et al. 2008, MNRAS, 386, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Nair, V., & Hinton, G. E. 2010, in Proceedings of the 27th International Conferenceon Machine Learning (ICML-10), eds. J. Fürnkranz, & T. Joachims (Athens, Greece: Omni Press), 807 [Google Scholar]
- Padmanabhan, N., Schlegel, D. J., Finkbeiner, D. P., et al. 2008, ApJ, 674, 1217 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pasquet-Itam, J., & Pasquet, J. 2018, A&A, 611, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polsterer, K. L., D’Isanto, A., & Gieseke, F. 2016, ArXiv e-prints [arXiv:1608.08016] [Google Scholar]
- Richard, M., & Lippmann, R. 1991, Neural Comput., 3, 461 [CrossRef] [Google Scholar]
- Rojas, R. 1996, Neural Comput., 8, 41 [CrossRef] [Google Scholar]
- Russakovsky, O., Deng, J., Su, H., et al. 2015, Int. J. Comput. Vision, 115, 211 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Solla, S., Levin, E., & Fleisher, M. 1988, Complex Syst., 2, 625 [Google Scholar]
- Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R. 2014, J. Mach. Learn. Res., 15, 1929 [Google Scholar]
- Szegedy, C., Wei, L., Yangqing, J., et al. 2015, 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 1 [Google Scholar]
- Tanaka, M., Coupon, J., Hsieh, B.-C., et al. 2018, PASJ, 70, S9 [Google Scholar]
- Yip, C.-W., Szalay, A. S., Carliles, S., & Budavári, T. 2011, ApJ, 730, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, H., Chen, X., Dai, W., et al. 2015, 2015 IEEE International Conference on Image Processing (ICIP), 3735 [CrossRef] [Google Scholar]
Appendix A: SQL query
Characteristics of each layer of the CNN architecture.
We selected galaxies with spectroscopic redshifts from the Main Galaxy Sample of the DR12 by running the following SQL query on the CasJob website:
SELECT
za.specObjID,za.bestObjID,za.class,za.subClass,za.z,za.zErr,
po.objID,po.type,po.flags, po.ra,po.dec,
...
(po.petroMag_r - po.extinction_r) as dered_petro_r,
...
zp.z as zphot, zp.zErr as dzphot,
zi.e_bv_sfd,zi.primtarget,zi.sectarget,zi.targettype,
zi.spectrotype, zi.subclass,
...
INTO mydb.SDSS_DR12
FROM SpecObjAll za
JOIN PhotoObjAll po ON (po.objID = za.bestObjID)
JOIN Photoz zp ON (zp.objID = za.bestObjID)
JOIN galSpecInfo zi ON (zi.SpecObjID = za.specObjID)
WHERE
za.z > 0 and za.zWarning = 0
and za.targetType = “SCIENCE” and za.survey = “sdss”
and za.class = “GALAXY” and zi.primtarget ≥ 64
and po.clean = 1 and po.insideMask = 0
and dered_petro_r ≤ 17.8
This results in a final sample of 516 546 galaxies.
Appendix B: Detailed CNN architecture
In this section we provide more detail on our architecture. The total number of parameters can be computed from Table A.1 with the formulae below.
blue
with c a specific layer and c − 1 the previous layer, k (c) the spatial size of kernels on the convolution layer c, n (c) the number of neurons on the layer c.
We explain the computational time needed for the training steps, with one GTX Titan X card. The time needed to pass forward and backward a batch composed of 128 galaxies through the network takes 0.21 s. So an epoch, which is the time needed to pass the entire dataset, takes about 14 min. We let the network converge in 120 000 iterations at most, which corresponds to 30 epochs. Therefore the training phase takes approximatively seven hours.
Appendix C: Impact of image quality on the CNN performance
 |
Fig. C.1. σMAD and bias as a function of signal-to-noise ratio (S/N = 1.086/petroMagErr) and PSF FWHM in the five bands, and of PSF FWHM offset between two bands (recentered at the mean value). The CNN results are shown in red, the B16 results in green. |
All Tables
Statistics for various CNN trials, with the B16 results in parenthesis where the comparison is relevant.
All Figures
 |
Fig. 1. Spatial distribution of the final sample of SDSS galaxies, with its spectroscopic redshift distribution (top-right inset). The color code indicates the average galactic extinction per pixel. The gray line shows the galactic plane. |
| In the text | |
 |
Fig. 2. Random examples from the image dataset. Images in the 5 SDSS channels were linearly remapped to red, green, blue, with saturation α = 2.0 and display γ = 2.2 applied following the prescriptions from Bertin (2012). |
| In the text | |
 |
Fig. 3. Representation of the first convolution layer with two kernels of convolution to simplify the schema. The multispectral image of a galaxy in the five SDSS filters is fed to the network. Each kernel is convolved with the multichannel images. The convolved images are summed, an additive bias is added and a non-linear function is applied, to produce one feature map. |
| In the text | |
 |
Fig. 4. Classifier architecture (see Sect. 3.6 for a detailed description). The neural network is composed of a first convolution layer, a pooling layer and five inception blocks followed by two fully connected layers and a softmax layer. The size and the number of feature maps are indicated for each layer. Further details can be found in Table A.1. |
| In the text | |
 |
Fig. 5. Schema of the experimental protocol. For each training and testing datasets, six models are trained and averaged to get the final photometric redshift values. Moreover five cross-validations are performed. Their respective performances are averaged to provide the final scores (bias, σMAD and η). |
| In the text | |
 |
Fig. 6. Normalized Δz distribution. The green line is a Gaussian distribution with the sigma and bias defined in Sect. 4.1 and reported in Table 2. The hatched parts define the catastrophic outliers. |
| In the text | |
 |
Fig. 7. Comparison between the photometric redshifts predicted by the CNN (left panel) and by B16 (right panel) against the spectroscopic redshifts. The galaxy density and the statistics are averaged over the five cross-validation samples. |
| In the text | |
 |
Fig. 8. Mean residuals as a function of spectroscopic redshifts (gray) and CNN redshifts (red). The dashed lines show the corresponding results for B16. The histograms are the respective redshift distributions. The CNN redshifts tend to be slightly over(under)-estimated below(above) the most populated redshift bins of the training sample, that is, they are biased toward the region of highest training. The effect is larger for B16, however no bias is found as a function of photometric redshift in either case. |
| In the text | |
 |
Fig. 9. Random examples of PDFs obtained from the CNN. The red dotted lines indicate the values of the spectroscopic redshifts and the blue ones the photometric redshifts estimated by the CNN and computed as the softmax weighted sum of the redshift values in each bin of the PDF. |
| In the text | |
 |
Fig. 10. Distribution of the Probability Integral Transforms (PIT) for each of the six models, and for the final PDFs. Each model exhibits a nearly flat PIT distribution, which assesses the very good quality of the PDFs. The PIT distribution of the final (averaged) PDFs (see Sect. 3.8) is slightly over dispersed, as expected from our pessimistic choice of combination. The dashed green and red lines result from expanding and shrinking, respectively, the Δz of a flat model by 20%. |
| In the text | |
 |
Fig. 11. Left panel: bias as a function of Galactic extinction for the classifier with and without integrating E(B − V) into the training (red and orange lines respectively) and for B16 (green). The CNN tends to overestimate redshifts in obscured regions (confusing galactic dust attenuation with redshift dimming), unless E(B − V) is used for training. Right panel: bias as a function of disk inclination for galaxies classified as star-forming or starburst. The CNN is virtually unbiased wrt ellipticity, unlike B16. |
| In the text | |
 |
Fig. 12. σMAD as a function of redshift for galaxies with and without neighbors (red and green lines respectively), as defined in Sect. 6.3. The respective redshift distributions are shown at the bottom. |
| In the text | |
 |
Fig. 13. Spatial distribution of the mean bias (left panel) and of the mean PDF width (right panel). The locations of the SZ and of the Stripe 82 region (see Sect. 6.4) are indicated. |
| In the text | |
 |
Fig. 14. Mean PDF in the SDSS patch showing defective photometric redshift and PDF quality (SZ) and in the Stripe 82 region, compared to the mean PDF of the full sample. The PDFs have been translated so that 0 corresponds to the spectroscopic redshifts. |
| In the text | |
 |
Fig. C.1. σMAD and bias as a function of signal-to-noise ratio (S/N = 1.086/petroMagErr) and PSF FWHM in the five bands, and of PSF FWHM offset between two bands (recentered at the mean value). The CNN results are shown in red, the B16 results in green. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.