| Issue |
A&A
Volume 662, June 2022
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 28 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202142751 | |
| Published online | 14 June 2022 | |
Photometric redshift estimation with convolutional neural networks and galaxy images: Case study of resolving biases in data-driven methods
1
Aix-Marseille Univ., CNRS/IN2P3, CPPM, Marseille, France
e-mail: lin@cppm.in2p3.fr
2
UMR TETIS, Univ. Montpellier, France
3
AgroParisTech, Cirad, CNRS, Irstea, Montpellier, France
4
Aix Marseille Univ., CNRS, CNES, LAM, Marseille, France
Received:
25
November
2021
Accepted:
11
February
2022
Deep-learning models have been increasingly exploited in astrophysical studies, but these data-driven algorithms are prone to producing biased outputs that are detrimental for subsequent analyses. In this work, we investigate two main forms of biases: class-dependent residuals, and mode collapse. We do this in a case study, in which we estimate photometric redshift as a classification problem using convolutional neural networks (CNNs) trained with galaxy images and associated spectroscopic redshifts. We focus on point estimates and propose a set of consecutive steps for resolving the two biases based on CNN models, involving representation learning with multichannel outputs, balancing the training data, and leveraging soft labels. The residuals can be viewed as a function of spectroscopic redshift or photometric redshift, and the biases with respect to these two definitions are incompatible and should be treated individually. We suggest that a prerequisite for resolving biases in photometric space is resolving biases in spectroscopic space. Experiments show that our methods can better control biases than benchmark methods, and they are robust in various implementing and training conditions with high-quality data. Our methods hold promises for future cosmological surveys that require a good constraint of biases, and they may be applied to regression problems and other studies that make use of data-driven models. Nonetheless, the bias-variance tradeoff and the requirement of sufficient statistics suggest that we need better methods and optimized data usage strategies.
Key words: galaxies: distances and redshifts / surveys / methods: data analysis / techniques: image processing
© Q. Lin et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Estimating galaxy redshifts is crucial for studies of galaxy evolution and cosmology. While redshifts obtained by spectroscopic measurements (spec-z) typically have high accuracy, they are highly time intensive and not ideal for the extremely large data sizes from ongoing or future imaging surveys (e.g., the Dark Energy Survey, the Euclid survey, the Hyper Suprime Cam Subaru Strategic Program, the Nancy Grace Roman Space Telescope, the Vera C. Rubin Observatory Legacy Survey of Space and Time, etc.). Therefore, photometric redshifts (photo-z) have become an alternative for galaxies that lack spectroscopically confirmed redshifts.
There are two broad categories of methods for estimating photometric redshifts for individual galaxies: template-fitting methods, and data-driven methods (see Salvato et al. 2019 for a review). Template-fitting methods model the galaxy spectral energy distribution (SED) and infer redshifts by fitting the galaxy photometry based on the SED templates (e.g., Arnouts et al. 1999; Feldmann et al. 2006; Ilbert et al. 2006; Greisel et al. 2015; Leistedt et al. 2019).
Data-driven or empirical methods predict redshifts by establishing a function or a density estimator that maps the input photometry or images to redshift estimates. These include self-organizing maps (SOMs; e.g., Way & Klose 2012; Carrasco Kind & Brunner 2014; Speagle & Eisenstein 2017; Buchs et al. 2019; Wilson et al. 2020), artificial neural networks (ANNs; e.g., Collister & Lahav 2004; Bonnett 2015; Hoyle 2016; D’Isanto & Polsterer 2018; Pasquet et al. 2019; Mu et al. 2020; Ansari et al. 2021; Schuldt et al. 2021), and other machine learning algorithms (e.g., Gerdes et al. 2010; Carrasco Kind & Brunner 2013; Rau et al. 2015; Beck et al. 2016; Jones & Singal 2017; Hatfield et al. 2020). In particular, studies such as Pasquet et al. (2019) developed models to predict redshift probability densities for individual galaxies. These models are trained with stamp images of galaxies as input and categorical labels converted from spectroscopic redshift, that is, they turn the problem of redshift estimation into a classification problem. Spectroscopic redshifts are not true redshifts, but they are used as training labels and the reference for testing as they are generally measured with good accuracy. Images of galaxies may be superior to other forms of input such as galaxy photometry because the model may further incorporate the spatial flux information of galaxies and avoid biases inherited from photometry extraction. Unlike template-fitting methods, data-driven methods do not depend on any theoretical modeling as all information is learned from data.
In addition to individual estimates, calibrating redshift sample distributions is important for applications such as weak-lensing analyses (e.g., Mandelbaum et al. 2008; Hemmati et al. 2019; Euclid Collaboration 2021). Other than assembling individual estimates, the redshift distribution for a photometric sample can be calibrated by conducting a spatial cross correlation with a reference sample that has accurate spectroscopic redshift information (e.g., Newman 2008; Davis et al. 2017; Morrison et al. 2017; Kovetz et al. 2017; Gatti et al. 2022).
In general, these methods show systematic effects from different sources. For example, template-fitting methods are problematic when the SED templates do not match the physical properties of the galaxy sample that is to be fit, while data-driven methods fail outside the photometric parameter space that is covered by the training sample. The hybridization of empirical and template methods or cross-correlation and template methods has the potential to improve the estimation accuracy (e.g., Cavuoti et al. 2016; Sánchez & Bernstein 2018; Alarcon et al. 2020; Soo et al. 2021), and it is promising to develop composite likelihood inference frameworks for photometric redshift estimation (e.g., Rau et al. 2022).
Data-driven methods such as deep-learning neural networks have been increasingly used in many astrophysical applications mainly in the manner of supervised learning. In addition to the photometric redshift estimation discussed above, data-driven methods have outperformed benchmark techniques in a few other cases, such as estimating the mass of the Local Group (McLeod et al. 2017), measuring galaxy cluster masses (Armitage et al. 2019; Ntampaka et al. 2015, 2019; Yan et al. 2020), measuring galaxy properties (Domínguez Sánchez et al. 2018; Bonjean et al. 2019; Wu & Boada 2019), estimating cosmological parameters (Ravanbakhsh et al. 2016; Gupta et al. 2018; Ribli et al. 2019), and analyzing forming planets (Alibert & Venturini 2019). Nonetheless, purely data-driven methods may not be able to perfectly capture salient information for a certain task, and the output estimates would easily be biased in various ways. This issue has been noted in a few studies (e.g., Voigt et al. 2014; Zhang et al. 2018a; Hosenie et al. 2020; Burhanudin et al. 2021; Cranmer et al. 2021), but the possibilities of resolving the biases in data-driven models have not been extensively explored in the field of astrophysics.
Using photometric redshift estimation as an example, we examine and resolve the following forms of biases in our work:
(a) Class-dependent residuals
This is known as the long-tail recognition problem in the domain of computer science, in which the training data follows an imbalanced distribution with low number density in the tail classes. A network trained with imbalanced data tends to give predictions that are skewed toward overpopulated classes, resulting in class-dependent uals. This bias is presented as a nonzero dependence of the mean residuals as a function of redshift in our work, where we considered each spectroscopic redshift bin [zspec, zspec + δzspec] as a class. Several techniques for resolving this bias outside astrophysics are known, including data-level resampling (e.g., Chawla et al. 2002; Han et al. 2005; García et al. 2012; Buda et al. 2018), algorithm-level exploitation of class-dependent losses or techniques (e.g., Huang et al. 2016, 2020; Khan et al. 2018, 2019; Cao et al. 2019; Cui et al. 2019; Hayat et al. 2019; Duarte et al. 2021; Wu et al. 2021), and feature transfer or augmentation (e.g., Liu et al. 2019; Tong et al. 2019; Yin et al. 2019; Okerinde et al. 2021). We note that it might be nontrivial to apply a correction with a tenable statistical basis or determine representative features for astronomical data, and it is more difficult to use these techniques for the redshift estimation problem than for a classic classification problem because there are nonuniform correlations between redshift bins. With these considerations, we adopt and extend the technique presented by Kang et al. (2020) at the data level without introducing complex algorithms or loss functions. This also serves as a framework for resolving mode collapse (discussed below).
Furthermore, although data can be undersampled to suppress overpopulated classes, for some underpopulated classes, the number density might be too low or even zero, precluding the reconstruction of a flat distribution via resampling. In particular, there are virtually zero-populated classes beyond the boundaries set by the finite coverage of data. Depending on the amplitude of estimation errors, skewness close to the boundaries of the output might be significant. This effect exists even when the training data follow a perfectly uniform distribution inside the coverage of data.
In our work on photometric redshift estimation, mean residuals can be computed with two different views. One view is defined in spectroscopic space, and the other is defined in photometric space: (i) mean residuals as a function of spectro-scopic redshift, that is, defined in each spectroscopic redshift bin [zspec, zspec + δzspec], quantifying the deviations relative to ground-truth values. (ii) Mean residuals as a function of photometric redshift, that is, defined in each photometric redshift bin [zphoto, zphoto + δzphoto], quantifying the deviations relative to measured or expected values. The correction of these residuals is essential for applications such as weak-lensing analyses when a sample is divided into tomographic redshift bins (e.g., Mandelbaum et al. 2008; Hemmati et al. 2019; Euclid Collaboration 2021). We note that the biases given by these two definitions are intercorrelated and cannot be eliminated simultaneously in the presence of inhomogeneous estimation errors that have different projections in spectroscopic space and in photometric space. In other words, correcting biases defined with one view will cause biases with the other if the measurements are imperfect. Therefore, the biases with these two views have to be considered separately according to the specific requirement of the study. While Pasquet et al. (2019) did not find strong zphoto-dependent residuals in simple cases where training data and test data were randomly sampled from the same parent distribution, we are interested in controlling biases in more general scenarios. In the methods presented in this paper, we must first resolve biases in spectroscopic space to produce a least-biased reference sample for calibrating measurements in photometric space.
(b) Mode collapse
This typically refers to the phenomenon that the output sample distribution has collapsed modes that are not representative of the full diversity of the actual distribution. The problem of mode collapse is widely discussed in the context of generative adversarial networks (GANs; e.g., Arjovsky & Bottou 2017; Kodali et al. 2017; Srivastava et al. 2017; Zhang et al. 2018b; Jia & Zhao 2019; Bhagyashree et al. 2020; Thanh-Tung & Tran 2020; Li et al. 2021), but it also exists in other situations (e.g., Nguyen et al. 2018; Ruff et al. 2018; Chong et al. 2020). A conceptually similar problem that limits the performance of a model is boundary distortion (Santurkar et al. 2018). This refers to the phenomenon that a classifier trained with GAN-generated data instances has a skewed decision boundary compared with a classifier that is trained with real data, because GAN-generated data lack diversity. In our work, we use the term “mode collapse” to indicate the inability of the classifier to reproduce the diversity of the target output domain.
Collapsed modes can be understood as local regions with overconfidence or degeneracies, meaning that estimated values are not smoothly distributed, but are concentrated at discrete positions, resulting in a series of spikes that cause the estimated sample distribution to deviate from the actual distribution. Mode collapse may be caused by noise and contamination from nearby sources in images that pollute the information necessary for determining correct output estimates. Furthermore, adjacent redshift bins are usually correlated, which may hinder a clear distinction of similar redshift values and lead to fuzzy decision boundaries between bins. In addition, the network may be under-trained or lack complexity, so that it is unable to fully capture salient information in the data. Mode collapse implies an imbalance between the locally collapsed output due to an imperfect mapping from the input and the perfect target output imposed by hard (one-hot) labels. We therefore solve for mode collapse by leveraging soft labels.
The goal of this work is not to achieve a better global accuracy or a lower catastrophic rate compared to the best current results; rather, we attempt to develop methods for examining and resolving biases. These methods are critical to photometric redshift estimation for cosmological applications (e.g., Laureijs et al. 2011), and they are also expected to be applicable to a wider variety of cases involving data-driven models. Because the prior in density estimates produced by neural networks is unresolved, we only focus on point estimates in our work. We note that the biases discussed in this work would exist for both the training set and the test set regardless of whether they follow the same distribution in parameter space. Other than these biases, another commonly known bias is the mismatch or covariate shift between the training set and the test set, which means that the two sets differ in the input domain. This would be a particularly challenging problem if the training set does not completely cover the parameter space represented by the test set, typically, faint objects without spectroscopic follow-up. We expect that our methods are robust to some degree of mismatch in number density between the two sets as long as there is no coverage mismatch. A full discussion of coverage mismatch is beyond the scope of this work.
The outline of this paper is as follows. In Sect. 2 we describe the data, including galaxy images and spectroscopic redshift labels. The images were collected from two surveys, from the Sloan Digital Sky Survey (SDSS), and from the Canada-France-Hawaii Telescope Legacy Survey (CFHTLS). In Sect. 3 we introduce our methods for resolving class-dependent residuals and mode collapse with respect to both spectroscopic and photometric redshifts. Section 4 presents our main experiments for bias correction for photometric redshift estimation and links this to cosmological applications. In Sect. 5 we focus on the behaviors of the biases by investigating how the biases would evolve with varying implementing and training details. We also test the validity of our methods. Detailed discussions are presented in Appendix D. In Sect. 6 we compare our estimated photometric redshifts with those obtained by other studies. Finally, we conclude in Sect. 7 and discuss the prospects for future research.
2 Data
2.1 Sloan Digital Sky Survey
The Sloan Digital Sky Survey (SDSS) is a wide-field imaging and spectroscopic survey that covers roughly one-third of the celestial sphere. The first dataset in our work consists of stamp images of 496 524 galaxies and associated spectroscopi-cally determined redshifts selected by Pasquet et al. (2019) from SDSS Data Release 12 (Alam et al. 2015). Each stamp image covers one of the five photometric passbands (ugriz) and has 64 × 64 pixels in spatial dimensions, corresponding to a pixel scale of 0.396 arcsec. A galaxy is aligned to the center of each image using its angular coordinates. The pair of five images in the five passbands and the associated spectroscopic redshift forms a data instance. The dataset covers z < 0.4 in spectroscopic redshift and r < 17.8 in dereddened r-band petrosian magnitude. Due to the good data quality and the relatively restricted parameter space (i.e., low redshifts and high brightnesses), the SDSS dataset was the main source of data for developing and evaluating our bias correction methods. Similar to Pasquet et al. (2019), we randomly selected 393219 instances as a training sample and 103305 instances as a test sample. More detailed descriptions can be found in Pasquet et al. (2019) and Alam et al. (2015).
2.2 Canada-France-Hawaii Telescope Legacy Survey
In order to apply our methods in a larger parameter space (i.e., high redshifts and faint magnitudes), we also exploited multiband (ugriz) galaxy images acquired from the two components of the Canada-France-Hawaii Telescope Legacy Survey (CFHTLS; see Hudelot et al. 2012 for the latest data release). One component is the Deep Survey that covers 4 deg2 in four disconnected fields and reaches a depth of r = 25.6, which is defined as the 80% completeness limit for stellar sources. The other component is the Wide Survey, which covers four fields over a total area of 155 deg2 with a depth of r = 25.0.
The spectroscopic redshifts for the CFHTLS images are a compilation of data from released wide and/or deep spec-troscopic surveys. These include the COSMOS Lyman-Alpha Mapping And Mapping Observations survey (CLAMATO; Data Release 1; Lee et al. 2018), the DEEP2 Galaxy Redshift Survey (Data Release 4; Newman et al. 2013), the Galaxy And Mass Assembly survey (GAMA; Data Release 3; Baldry et al. 2018), the SDSS survey (Data Release 12), the UKIDSS Ultra-Deep Survey (UDS; McLure et al. 2013; Bradshaw et al. 2013), the VANDELS ESO public spectroscopic survey (Data Release 4; Garilli et al. 2021), the VIMOS Public Extragalactic Redshift Survey (VIPERS; Data Release 2; Scodeggio et al. 2018), the VIMOS Ultra-Deep Survey (VUDS; Le Fèvre et al. 2015), the VIMOS VLT Deep Survey (VVDS; Le Fèvre et al. 2013), the WiggleZ Dark Energy Survey (Final Release; Drinkwater et al. 2018) and the zCOSMOS survey (Lilly et al. 2007). From these redshift surveys, we only took the most secure spectro-scopic redshifts that are identified with high signal-to-noise ratios (S/Ns) or were measured with multiple spectral features (equivalent to the VIPERS or VVDS redshift flags, i.e., 3 ≤ zFlag ≥ 4). We refer to them as high-quality (HQ) redshifts.
We also included the most secure low-resolution prism red-shift measurements for bright sources (zFlag = 4,I ≤ 22.5) from the PRIsm MUlti-object Survey (PRIMUS; Data Release 1; Coil et al. 2011; Cool et al. 2013), and the secure grism redshift measurements from the 3D-HST survey (Data Release v4.1.5; Skelton et al. 2014; Momcheva et al. 2016). They are referred to as low-resolution (LR) spectroscopic redshifts.
We selected 26249 HQ and 6007 LR galaxies from the CFHTLS Deep fields and 108 510 HQ and 17 427 LR galaxies from the Wide fields as two separate datasets (denoted "CFHTLS-DEEP" and "CFHTLS-WIDE", respectively) with spectroscopic redshifts ranging up to z ~ 4.0 and dereddened r-band magnitudes in a range of 12.3 < r < 27.2. Like the SDSS dataset, the extracted stamp images are in the format of 64 × 64 × 5 pixels, corresponding to a pixel scale of 0.187 arcsec (described in detail in Treyer et al., in prep.). We randomly selected 10000 instances from the Deep fields and 10000 instances from the Wide fields with high-quality spectroscopic redshifts as separate test samples. They were not mixed because the Deep and Wide fields have potential systematics. The remaining 22 256 instances from the Deep fields and 115 937 instances from the Wide fields were regarded as training samples. They were used separately in training when bias correction was applied.
2.3 Data processing
We reduced the pixel intensity of the CFHTLS images by a factor of 1000 so that the majority of pixel values lie below one. The pixel intensity of all images was then rescaled with the following equation:
 (1)
(1)
where I and I0 stand for the rescaled intensity and the original intensity, respectively. This rescaling operation reduces the disparity between the galaxy peak flux and the remaining flux so that the network can have comparable responses to more pixels.
3 Methods
3.1 Artificial neural networks
As Pasquet et al. (2019) and Treyer et al. (in prep.), we used artificial neural networks (ANNs) to estimate photometric red-shifts in the manner of supervised learning. An ANN can be viewed as a multivariable function or a conditional probability density estimator that maps the input to the target output, which consists of a sequence of layers inspired by biological neural networks. In vanilla ANNs, the layers are fully connected (tailored for one-dimensional input) and composed of neurons that usually contain free parameters (or weights) and nonlinear activation functions (Sigmoid, ReLU, PReLU, etc.). In particular, for classification tasks, a Softmax function is usually applied to the output layer, producing a vector normalized to unity and thus mimicking a probability density distribution. The network is usually trained iteratively with mini-batches of training data. With a loss function defined for a given task, gradients with respect to the weights of each neuron throughout the network are calculated via backpropagation. The weights are updated via gradient descent in order to minimize the loss. Once the loss converges or does not vary rapidly, a parameterization of the network is established that encodes the relation between the input and the target output, which is collectively determined by the training data and the model implementation strategies, including the network architecture, the loss function, and the training procedure. For purely data-driven methods such as ANNs, the training data and the model are the main sources of prior information that affect the prediction for the test data.
Convolutional neural networks (CNNs) form a special category of ANNs. Unlike vanilla ANNs, the input of CNNs can be high-dimensional, for instance, multiband images. CNNs possess convolutional layers with kernels (or filters) composed of only a few neurons that are designed for scanning over the whole input image and extracting local information, outputting image-like feature maps. The extracted features become more abstract from layer to layer and gradually evolve from the pixel level to the object level. Pasquet et al. (2019) used CNNs with galaxy images instead of photometric information in order to incorporate the spatial flux distribution and avoid biases from photometry extraction. This produced results with a better accuracy than benchmark methods (e.g., Beck et al. 2016), even though using images instead of photometry as input increases the dimensionality of the input and introduces the risk of fitting irrelevant spatial information. This therefore requires more training data.
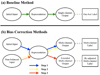 |
Fig. 1 Paradigms of the baseline method and our methods for correcting zspec-dependent residuals and mode collapse. The baseline method does not explicitly specify a representation and produces single-channel output estimates that only require one-hot labels for training. In contrast, our methods split representation learning and classification into three consecutive steps and produces multichannel output estimates. The labels for training the model match the dimensions of the output estimates, and they are softened and readjusted in step 3 according to the biases. The dashed arrows indicate that the part of the model prior to the representation is fixed in steps 2 and 3. |
3.2 Bias correction
In this subsection, we present our proposed procedure for correcting the two biases (summarized in algorithm Sect. 1). As mentioned in Sect. 1, residuals can be defined as a function of either spectroscopic or photometric redshift. These two cases have to be treated separately. Specifically, in our bias correction methods, steps 1-3 are applied to correct zspec-dependent residuals and mode collapse (Fig. 1). These steps are built on CNN models with a statistical basis (Appendix A) leveraging preestimated redshifts for analyzing and resolving biases, which should be applied in advance of step 4. Step 4 is a direct calibration applied to correct zphoto-dependent residuals, which relies on actual requirements of bias correction and may not be necessary. These four steps are compared with a baseline method that is not corrected for biases. Although we discuss this procedure only in the setting of photometric redshift estimation, we note that it is potentially applicable to any study that involves data-driven models.
As we discuss in Sect. 3.2.2, correcting zspec-dependent residuals requires a selection of data from the original training dataset. It is impractical to train a deep network using only a selected small subset of data. However, as illustrated by Kang et al. (2020), the learning procedure of a model can be split into representation learning and classification. In this idea, the whole network is first trained with all training data to obtain a representation at a chosen hidden layer, which is usually a low-dimensional embedding of information from input data (see, e.g., Bengio et al. (2013) for a review of representation learning); then the classification output can be fine-tuned or retrained with the representation fixed. Decoupling representation learning and classification enables us to apply the bias correction techniques solely in the phase of classification even in the presence of a biased representation, as long as full representativeness is essentially maintained in the representation. Fixing the representation also enables us to apply bias correction using a small subset of data without strong overfitting.
For steps 1-3 in our main experiments, we adopted the network architecture from Pasquet et al. (2019) (denoted Net_P; illustrated in Fig. 2). This architecture uses the multiscale inception modules (e.g., Szegedy et al. 2015) to extract features at different resolution scales. The feature maps produced by a set of convolutional and pooling layers and inception modules, expected to encapsulate the extracted salient information, are flattened, concatenated with an additional input of galactic reddening E(B – V), and fed into fully connected layers for the final prediction. The network from Treyer et al. (in prep.) (denoted Net_T) has fewer trainable parameters, but a deeper architecture. We note that overfitting is likely to occur for both networks as a result of the limited training data. To apply our bias correction methods, the penultimate fully connected layer of the network, which has 1,024 nodes, was used to obtain a representation, and the last fully connected layer was replaced by a multichannel output unit (discussed in Sect. 3.2.1).
In addition, we only focus on classification problems. It is simpler to apply our bias correction methods to classification problems than regression problems, as the probability density predicted by classification is easier to modify than a single collapsed point estimate predicted by regression. Extensions to regression problems may be explored in future work. Furthermore, the output of a classification model is a density estimate subject to the prior imposed by the model implementation and the training data. A full posterior distribution should be a marginalization over all such prior and possible parameteriza-tions, which is not tractable. Therefore, we only focused on point estimates in our analysis. While Pasquet et al. (2019) and Treyer et al. (in prep.) took zmean (i.e., the probability-weighted mean redshift) and zmedian (i.e., the median redshift drawn from the probability distribution) as point estimates, respectively, we considered zmode (i.e., the redshift corresponding to the maximum probability density) as point estimates for both our methods and the baseline method, as it is least biased by the prior (discussed in Appendix B). We elaborate on the details of each step below.
 |
Fig. 2 Graphic illustration of the CNN models for the baseline method and our methods for correcting zspec-dependent residuals and mode collapse. We use the network architecture adopted by Pasquet et al. (2019), in which multiscale inception modules (Szegedy et al. 2015) are used and the galactic reddening of galaxies is input in addition to images. The representation is obtained at the penultimate fully connected layer. The classification module is elaborated in the red rectangle: while the baseline method takes a final fully connected layer as a single-channel output for redshift prediction, our methods take parallel fully connected layers as multiple output channels to predict redshifts that also incorporate the magnitude information (discussed in Sect. 3.2.1). The labels n and m indicate the dimensions of the output layers, whose values are given in Table 1 for the SDSS data and the CFHTLS data. ≥ n means that additional bins are appended to the redshift outputs in step 3. |
Bias correction steps
3.2.1 Step 1: Replacing the last fully connected layer by a multichannel unit and learning a representation
Because the data with which a model is trained span a multidimensional spectroscopic and photometric parameter space, imbalances in any influencing dimension would bias the redshift prediction. For instance, a model with the standard singlechannel output (i.e., the baseline method) tends to assign higher redshifts to infrequent low-redshift faint galaxies if the galaxy brightness in each redshift bin is poorly balanced in the training data, even though the brightness is not explicitly predicted.
Therefore, it is important to explicitly specify and balance these influencing dimensions. For simplicity, we used two dominant variables, spectroscopic redshift and dereddened r-band magnitude, to approximate the multidimensional parameter space. We adopted a multichannel output unit in our methods that consists of one magnitude output with m bins and m associated redshift outputs (Fig. 3), where the magnitude information can be explicitly predicted. Before they are extended in step 3 (discussed in Sect. 3.2.3), the redshift outputs preserve the same binning and coverage as the single-channel output (with n bins), each corresponding to a bin in the magnitude output. All the red-shift outputs and the magnitude output are implemented as single fully connected layers with the Softmax activation and connected to a common layer, which is taken as the representation in our analysis (Fig. 2). In other words, the outputs are conditionally independent given the representation. The final redshift output prediction incorporates all the outputs and marginalizes over the magnitude, that is,
where  and p
and p denote the density distributions predicted by the magnitude output and the redshift outputs, respectively.
denote the density distributions predicted by the magnitude output and the redshift outputs, respectively.  denotes the jth bin in the r-band magnitude output, and the index runs over m bins. This multichannel unit is essentially a classification module that can be fine-tuned or retrained for bias correction after the representation is obtained. It builds a basis for the successive bias correction steps and can also be regarded as a way of regularizing the model and preventing overfitting.
denotes the jth bin in the r-band magnitude output, and the index runs over m bins. This multichannel unit is essentially a classification module that can be fine-tuned or retrained for bias correction after the representation is obtained. It builds a basis for the successive bias correction steps and can also be regarded as a way of regularizing the model and preventing overfitting.
As shown in Fig. 3, the input space is divided into a grid of zspec-magnitude cells, with 2m − 1 rows in magnitude and n bins in redshift. The non-negligible r-band magnitude measurement errors might lead data instances to incorrect magnitude rows in the input space. Directly using incorrect magnitudes as labels for the magnitude output would confuse the model. Therefore, we adopted a magnitude output with bins that have interlacing coverages over the input space. Specifically, each magnitude row in the input space is accounted for by one or two adjacent bins in the magnitude output in an alternating manner; each magnitude bin is responsible for three adjacent magnitude rows (or two rows at the borders). The rows that contribute to two bins alleviate the potential confusion at the boundary between the bins. In practice, the n redshift bins cover the whole spectroscopic red-shift distribution of the data, whereas the 2m − 1 magnitude rows only cover the dominant portion of the r-band magnitude distribution. The data instances that lie above or below the grid are reassigned to the uppermost or lowermost magnitude rows.
While only high-quality data should be used for the subsequent steps, it is possible to use data with various systematics and S/Ns for representation learning because the focus at this stage is to build an informative representation rather than control the biases. We trained our model with all data from scratch as the baseline method, but the last fully connected layer that gives a single-channel classification output was replaced by the multichannel output unit. We used the cross-entropy loss function for each output, that is,
 (3)
(3)
where p stands for the probability density predicted by the Soft-max activation for each of the redshift outputs or the magnitude output, and y is the corresponding one-channel label, one component of the integrated multichannel label. The index j runs over all bins in each redshift output or the magnitude output. By convention, both p and y were normalized to unity. The labels for the magnitude output obeys the one-hot or two-hot encoding, depending on whether the magnitude value lies in a row that contributes to one or two magnitude bins in the target output due to the interlacing correspondence. The labels for the redshift out-put(s) associated with the activated magnitude bin(s) are one-hot (but they are softened in step 3; this is discussed in Sect. 3.2.3), whereas flat labels are used for the remaining redshift outputs (i.e., yj = 1/n for all bins where n is the number of bins) in order to impose confusion on the nonactivated magnitude bins. The final output combines the density distributions predicted by all the redshift outputs weighted by the corresponding probabilities given by the magnitude output (i.e., Eq. (2)).
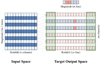 |
Fig. 3 Correspondence of the input parameter space and the target output space represented by the multichannel output unit. The input space is divided into a grid with 2m − 1 rows covering different magnitudes and n columns covering different redshifts. The output unit is comprised of one magnitude output with m bins and m corresponding redshift outputs. Each redshift output has n bins corresponding to the input space before being extended in step 3. The values of n and m for the SDSS data and the CFHTLS data are given in Table 1. The shaded green boxes indicate the extended redshift intervals. Each of the rows in the input space is connected to one or two redshift outputs alternately. Equivalently, each redshift output responds to three adjacent input rows (or two rows at the edges). As an example, in response to a data instance drawn from the input space indicated by the red star, two bins are activated in the target magnitude output (shown in dark red) while the other bins remain null (shown in light blue). One bin is activated in each of the two corresponding redshift outputs (before using readjusted soft labels in step 3), while the remaining redshift outputs have a flat response over all bins (shown in light red). |
3.2.2 Step 2: To correct for zspec-dependent residuals induced by overpopulated classes
The zspec-dependent residuals are strongly affected by over-populated classes. We note that simply increasing the rate of occurrences of the instances from other classes in training cannot effectively damp the dominance of overpopulated classes, presumably because this does not balance the information content in different classes. Therefore, we attempted to correct the influence of overpopulated classes by constructing a nearly balanced training subset via undersampling. Specifically, in each zspec-magnitude cell (zspec, ri) in the division of the input space, a number of instances from the training dataset are randomly selected no more than a predefined balancing threshold th; all the cells with number densities above the threshold are thus considered overpopulated and trimmed. In this manner, the balancing is carried out over both the redshift dimension and the magnitude dimension (Fig. 4). Then, the resampled subset is exploited to fine-tune the multichannel output unit pretrained in step 1 with a fixed representation.
In other words, we attempted to create a nearly flat prior over all bins so that the trained model did not favor overpopulated bins, even though they may originally hold more information content that is useful for the model prediction. Nonetheless, resampling in a two-dimensional subspace inevitably overlooks high-order information in the intrinsic heterogeneous multidimensional parameter space, but incorporating more dimensions in the output unit further complicates the model and aggravates the sparsity of data. We therefore only focused on the first-order correction in the two-dimensional subspace and left the higherorder correction for future work. It should also be noted that the overall estimation accuracy would be slightly traded off by a smaller size of the training sample.
 |
Fig. 4 Two-dimensional distributions (zspec, r-band magnitude) for the SDSS dataset before and after balancing the number density. The color indicates the relative number density in logarithmic scale. As shown, the data cannot be perfectly balanced due to the existence of underpopulated classes. |
3.2.3 Step 3: To correct for mode collapse and zspec-dependent residuals induced by underpopulated classes
The use of a nearly balanced training subset in step 2 is unlikely to completely eliminate the zspec-dependent residuals due to unaddressed underpopulated classes. In principle, overpopulated and underpopulated classes may relatively be defined with the balancing threshold th, but not all classes can be reconciled with a low threshold because of limited statistics and/or zero-populated classes, especially the hypothetical zero-populated classes outside the finite parameter space covered by the data. Furthermore, collapsed modes exist regardless of the balancing of training data.
Using the same nearly balanced training subset and the fixed representation from step 2, we considered treating mode collapse and underpopulation-induced zspec-dependent residuals jointly by replacing the one-hot redshift components of the multichannel labels with soft Gaussian labels for the activated redshift outputs. In particular, the dispersions of the soft Gaussian labels were introduced to suppress mode collapse, and the means were readjusted to address underpopulation-induced zspec-dependent residuals. They were determined according to the preestimated redshifts from step 2.
As a prerequisite, we first extended the range of the redshift output with more bins to allow for the softening and readjustment of labels especially for data instances close to the boundaries. We note that density or point estimates that exceed the initial boundaries were permitted, in particular negative estimates if the lower boundary was shifted below zero.
(a) Determining the dispersions
We applied a uniform dispersion to soften all the hard labels for a given redshift output corresponding to a given bin in the magnitude output. The dispersion is denoted with σ1(ro), which is a function of the given magnitude bin ro. It was fit by minimizing the Kullback-Leibler divergence between the zspec subsample distribution at the given magnitude bin ro from step 2 and the corresponding predicted zphoto subsample distribution convolved with a Gaussian function whose dispersion is σ1(ro), that is,
![$\arg \,\mathop {\min}\limits_{{\sigma _1}\left({{r_o}} \right)} \,{D_{{\rm{KL}}}}\left[ {p\left({\left. {{z_{{\rm{spec}}}}} \right|{r_o}} \right)\left\| {\left({p*{N_{\sigma _0^2\left({{r_o}} \right)}}} \right)\left({\left. {{z_{{\rm{photo}}}}} \right|{r_o}} \right)} \right.} \right],$](/articles/aa/full_html/2022/06/aa42751-21/aa42751-21-eq7.png) (4)
(4)
where p(zSpec|r0) and p(zphoto|r0) denote the zspec and zphoto sub-sample distributions given the magnitude bin ro, respectively;  denotes the Gaussian function with a dispersion of σ1(ro). In other words, the fitted dispersions are thought to offer the minimum amount of softening for smoothing out the spikes in the zphoto subsample distribution so as to approximate the zspec subsample distribution. The soft Gaussian labels with these dispersions can be leveraged to train the multichannel output unit and correct for mode collapse.
denotes the Gaussian function with a dispersion of σ1(ro). In other words, the fitted dispersions are thought to offer the minimum amount of softening for smoothing out the spikes in the zphoto subsample distribution so as to approximate the zspec subsample distribution. The soft Gaussian labels with these dispersions can be leveraged to train the multichannel output unit and correct for mode collapse.
In order to avoid introducing imbalance along the red-shift dimension, we did not use redshift-dependent dispersions. Nonetheless, the fitted dispersions are different for different magnitude bins, which is a sign of varying photometric properties, data quality, and statistics. Dividing the input data into the two-dimensional space is thus required to apply separate fits for the dispersions. Additionally, for data instances from a magnitude row in the input space that is linked to two bins in the magnitude output, two different dispersions were fit and applied separately to two redshift outputs.
In contrast to hard labels that assign no weight to any non-activated redshift bins, soft labels would naturally account for the correlations between bins because the dispersions implicitly indicate the influential scales around the central values. These soft labels are also different from the "smoothing labels" proposed by Müller et al. (2019), that is, uniform smoothing over all nonactivated bins. However, we are cautious about a tradeoff between the use of soft labels and the constraint of estimation errors. The dispersions would be dramatically overestimated if the preestimated photometric redshifts were at a low accuracy, and applying soft labels with overestimated dispersions would further boost errors, making the estimation unreliable. In this sense, the proper fit of dispersions (and more generally, the whole procedure of bias correction) relies on a good control of estimation errors.
(b) Determining the means
The use of original spectroscopic redshifts as hard labels in step 2 yields a scattering profile for each redshift estimate, which models the probability distribution of being randomly scattered to different values under the influence of the subsample corresponding to a given bin in the magnitude output. For a flat zspec subsample distribution, the scattering profile for each instance was assumed to be a Gaussian function (different from the soft Gaussian labels), whose mean or center of mass is aligned with its spectroscopic redshift. In contrast, an imbalanced zspec subsample distribution due to underpopulated bins would imprint nonzero skewness on the scattering profile and alter its mean. Therefore, we attempted to compensate for this skewness by relocating the soft labels (illustrated in Fig. 5).
We assumed that the skewed scattering profile is simply a bin-wise product of the initial Gaussian profile and the shape of the subsample distribution. The validity of this assumption is tested in Appendix C.
The dispersion of the initial Gaussian scattering profile was estimated as the local error at a given spectroscopic redshift and a given bin in the magnitude output. Assuming a uniform error distribution along the redshift as σ1(ro) may be oversimplified. Therefore, we attempted to model the underlying evolving variance by determining a redshift-dependent quadratic error curve for each magnitude bin (denoted with 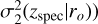 . We first estimated the squared distances d2 between zphoto and zspec in each cell (zspec, ro) and averaged their mean and median, which gives the average squared distances
. We first estimated the squared distances d2 between zphoto and zspec in each cell (zspec, ro) and averaged their mean and median, which gives the average squared distances  that is,
that is,
![$\matrix{{\overline {{d^2}} \left({\left. {{z_{{\rm{spec}}}}} \right|{r_o}} \right) = {1 \over 2}\left[ {{\rm{Mean}}\left({{d^2}\left({{z_{{\rm{spec}}}},{r_o}} \right)} \right) + {\rm{Median}}\left({{d^2}\left({{z_{{\rm{spec}}}},{r_o}} \right)} \right)} \right]} \hfill \cr {{\rm{where}}\,\,\,{d^2}\left({{z_{{\rm{spec}}}},{r_o}} \right) = {{\left({{z_{{\rm{photo}}}} - {z_{{\rm{spec}}}}} \right)}^2}\,\,\,{\rm{with}}\,{\rm{given}}\,\,\,\left({{z_{{\rm{spec}}}},{r_o}} \right).} \hfill \cr} $](/articles/aa/full_html/2022/06/aa42751-21/aa42751-21-eq10.png) (5)
(5)
where  =
=  with given
with given 
The reason for averaging the mean and the median is that the former may be driven by outliers, while the latter is typically lower than the underlying variance. We also note that if an instance is from a magnitude row in the input space connected to two bins in the magnitude output, it contributes to two redshift outputs separately for estimating the squared distances.
The average squared distances  can be seen as the raw estimates of variances for the scattering profiles. However, these raw estimates contain random fluctuations, and the correlations between redshift bins are not taken into account. Knowing that
can be seen as the raw estimates of variances for the scattering profiles. However, these raw estimates contain random fluctuations, and the correlations between redshift bins are not taken into account. Knowing that  fit with Eq. (4) characterizes the influential scale around each bin, we obtained the quadratic error curve
fit with Eq. (4) characterizes the influential scale around each bin, we obtained the quadratic error curve  by further convolving
by further convolving  with a Gaussian function with a dispersion of
with a Gaussian function with a dispersion of 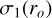 that is,
that is,
 (6)
(6)
In addition, because we make use of the labels softened by  on top of the already existing estimation errors, the final estimates of variances for the scattering profiles should be the quadratic error curves
on top of the already existing estimation errors, the final estimates of variances for the scattering profiles should be the quadratic error curves  expanded by
expanded by  in quadrature, that is,
in quadrature, that is,
 (7)
(7)
With a scattering profile estimated for each instance, the underpopulation-induced imbalance (characterized by the shift of the mean of the skewed profile relative to its spectroscopic redshift) can be offset by readjusting the mean of the Gaussian label, that is,
 (8)
(8)
z* stands for the new mean of the Gaussian label, z0 stands for the spectroscopic redshift, and z stands for the mean of the skewed scattering profile, which is the product of p and
and  , the zspec subsample distribution at the given magnitude bin r0 and the initial Gaussian scattering profile with a mean of zQ and a variance of Var
, the zspec subsample distribution at the given magnitude bin r0 and the initial Gaussian scattering profile with a mean of zQ and a variance of Var In particular, the imbalances at the boundaries of the finite coverage of data can be corrected for in the same manner by assigning zero number density to the hypothetically zero-populated classes exceeding the boundaries.
In particular, the imbalances at the boundaries of the finite coverage of data can be corrected for in the same manner by assigning zero number density to the hypothetically zero-populated classes exceeding the boundaries.
To summarize, using the predetermined redshift point estimates for the nearly balanced training subset from step 2, we estimated the dispersions and the means of the soft Gaussian labels according to Eqs. (4) and (8), respectively. The new labels were exploited to retrain the multichannel output unit with an extended redshift range, using the same training subset and keeping the learned representation fixed. With this step, both mode collapse and zspec-dependent residuals induced by underpopulated classes are expected to be corrected.
 |
Fig. 5 Determining the means of soft labels. zQ, z, and z* stand for the spectroscopic redshift of a given galaxy, the mean of its skewed scattering profile, and the determined mean of its soft label, respectively, also indicated by the vertical dotted blue, green, and red lines. The skewed scattering profile is assumed to be a bin-wise product of the initial Gaussian profile and the shape of the subsample distribution in the given magnitude bin. Ideally, if the subsample distribution is perfectly balanced (top row), the product profile remains a Gaussian function such that the mean Z of the profile and the mean z* of the soft label align with the spectroscopic redshift value z0. On the other hand, if the subsam-ple distribution has underpopulated regions (bottom row), the product profile is affected by nonflatness and deviates from a Gaussian function (i.e., it is skewed; shown as the green curve), which produces a shifted mean Z. The mean z* of the soft label in this case should be determined according to Eq. (8). |
3.2.4 Step 4: To correct for zphoto-dependent residuals
This step is not necessary for studies that require bias correction with respect to zspec. However, cosmological applications such as weak-lensing analyses require a calibration of the mean photometric redshift in each tomographic bin, which necessitates the correction of zphoto-dependent residuals. Although the knowledge of zphoto-dependent residuals is not accessible from the test sample, we may obtain this knowledge from the training sample as long as the same sampling process applies to each zspec-magnitude cell  in both samples. We note that ri in this case stands for a magnitude row in the input space rather than a bin in the magnitude output. In principle, for a test sample with any expected two-dimensional zspec-magnitude distribution, we can construct a sample with the same distribution by resampling from the training data. Then in each zphoto-magnitude cell
in both samples. We note that ri in this case stands for a magnitude row in the input space rather than a bin in the magnitude output. In principle, for a test sample with any expected two-dimensional zspec-magnitude distribution, we can construct a sample with the same distribution by resampling from the training data. Then in each zphoto-magnitude cell  , the bias (i.e., the deviation between the mean zphoto and the mean zspec) estimated with the resampled training data can be subtracted from the zphoto estimated with the test data. We emphasize that we attempted to match the zspec-magnitude distributions rather than the zphoto-magnitude distributions because the latter cannot guarantee the same zphoto – zspec deviations for both samples. Furthermore, this step only requires the reference training data to have the same sampling as the test data, thus it is not limited to CNN models.
, the bias (i.e., the deviation between the mean zphoto and the mean zspec) estimated with the resampled training data can be subtracted from the zphoto estimated with the test data. We emphasize that we attempted to match the zspec-magnitude distributions rather than the zphoto-magnitude distributions because the latter cannot guarantee the same zphoto – zspec deviations for both samples. Furthermore, this step only requires the reference training data to have the same sampling as the test data, thus it is not limited to CNN models.
Correctly estimating the zspec-magnitude distribution of the test sample is important in this procedure because it enables the resampled training sample and the test sample to have the same bias distribution over all zphoto-magnitude cells. For simplicity, the estimated zphoto-magnitude distribution of the test sample corrected for zspec-dependent residuals and mode collapse was regarded as its expected zspec-magnitude distribution. We note that it is necessary to first apply steps 1-3 to correct for zspec-dependent biases because these biases (e.g., spikes due to mode collapse) may modify the zphoto-magnitude distribution. However, the estimated zphoto-magnitude distribution is still not identical to the zspec-magnitude distribution due to the existence of estimation errors. Nonetheless, given the similarity between the zphoto and zspec distributions, we did not attempt to correct estimation errors in order to avoid other biases.
4 Main experiments and results
4.4 Training protocol
Throughout this work, we train CNN models and apply our bias correction methods for each dataset (SDSS, CFHTLS-WIDE, and CFHTLS-DEEP) using the training data. Unless otherwise noted, we show results only with the test data, assuming that the training and test samples both follow the same sampling process in each redshift-magnitude cell (zspec, ri) in the input space. We only allow this assumption to be violated in the stage of representation learning where the goal is to expand the information volume learned by the model despite the presence of distinct systematics or sub-structures in the training data. However, the existence of such systematics would jeopardize the balancing of the data distribution, thus the training data must be purified for the later stage of bias correction. For example, the CFHTLS-DEEP data generally have better S/Ns than the CFHTLS-WIDE data because their exposure time is longer. Because the model may not be well generalizable over different noise properties, we considered separating these two CFHTLS datasets for bias correction. In our work, the training sample used for bias correction and the test sample were randomly selected from the same parent distribution for each given dataset, although their overall distributions were allowed to be different if they followed the same sampling in each redshift-magnitude cell.
The data coverage and the hyperparameters used in training for each dataset are detailed in Tables 1 and 2. To train our models, we adopted the mini-batch gradient descent technique with the default Adam optimizer (Kingma & Ba 2015). In each training iteration, a mini-batch of training instances was randomly selected from the training sample, consisting of image-label pairs. The images were randomly flipped and rotated with 90 deg steps under the assumption of spatial invariance. For the SDSS dataset, the baseline method and step 1 were conducted using the whole training sample of 393 219 instances. In steps 2 and 3, the constructed nearly balanced training subset was down-sampled to 60 000 instances to fit the soft Gaussian labels (Eqs. (4) and (8)). Since we only need to train the output unit of a network with fewer training instances after step 1, the number of iterations and the mini-batch size were reduced.
For the CFHTLS datasets, the CFHTLS-DEEP training sample of 22 256 instances and the CFHTLS-WIDE training sample of 115937 instances were mixed for the baseline method and step 1 with both high-quality and low-resolution spectroscopic redshifts. For steps 2 and 3, the CFHTLS-DEEP sample and the CFHTLS-WIDE sample had to be considered separately, however, due to potential systematics, producing two separate models for the two datasets. In addition, only the instances with high-quality spectroscopic redshift in the training samples were used for bias correction, similar to those in the test samples. There are 11 220 high-quality instances in the nearly balanced training subset for the CFHTLS-DEEP sample and down-sampled 60000 instances for the CFHTLS-WIDE sample.
Finally, we leveraged the strategy of averaging an ensemble of models to improve the performance. For the baseline method, we trained the network five times. The training was conducted in the same way each time, but with a different initialization of weights and different selections of mini-batches. The output redshift density estimates from the five individual models were averaged and a point estimate was obtained from each average density estimate. For our methods, we similarly trained five individual models, each with steps 1-3 applied consecutively. Each time step 1 started with a different initialization; then without averaging, the pretrained model was passed to steps 2 and 3 with a different but randomly selected nearly balanced training subset. For efficiency, the averaging was only applied to the final output estimates in step 3.
Data coverage in spectroscopic redshift and r-band magnitude.
Hyperparameters in training.
4.2 Correction for zspec-dependent residuals and mode collapse
The results of correcting zspec-dependent residuals and mode collapse are illustrated in Figs. 6 and 7 with the SDSS and the CFHTLS-WIDE test data, respectively. To exclusively demonstrate the outcome of bias correction, we do not show the result for the CFHTLS-DEEP dataset due to limited statistics, but we evaluate the quality of zphoto estimation for this dataset in Appendix E. The redshift residual of each data instance indicates the difference between the estimated photometric and spectroscopic redshift, whose error bar was estimated via the quadratic error curves  given by Eq. (6) (rather than Eq. (7)) with
given by Eq. (6) (rather than Eq. (7)) with  fit on the nearly balanced training subset and
fit on the nearly balanced training subset and  estimated on the test data. If a data instance contributes to two redshift outputs, the two estimated quadratic errors were averaged. The mean residual is defined as the weighted mean in each spectroscopic redshift bin
estimated on the test data. If a data instance contributes to two redshift outputs, the two estimated quadratic errors were averaged. The mean residual is defined as the weighted mean in each spectroscopic redshift bin ![$\left[ {{z_{{\rm{spec}}}},{z_{{\rm{spec}}}} + \delta {z_{{\rm{spec}}}}} \right]$](/articles/aa/full_html/2022/06/aa42751-21/aa42751-21-eq34.png)
For the baseline method with either the SDSS data or the CFHTLS-WIDE data, the mean residual generally follows a decreasing trend as a function of spectroscopic redshift, predominantly resulting from the imbalanced distribution of the training data. To better demonstrate the divergent bias levels in low- and high-redshift regions for each step, we applied the following piecewise linear fit:
 (9)
(9)
<> denotes the weighted mean. A, B, C, and D are the parameters to be fit. The boundary zb defines two redshift intervals (zb = 0.15 and 0.6 for the SDSS data and the CFHTLS-WIDE data, respectively). As the second interval roughly covers the high-redshift tail of a sample for which the prediction would be easily affected by the low-redshift region, it is more sensitive to the correction of redshift dependence. The slopes of the fitted lines approach zero with our correction methods, implying that the dependence on spectroscopic redshift can essentially be lifted. The change between step 1 and step 2 (step 2 and step 3) indicates the removal of the influence from the overpop-ulated (underpopulated) bins. Additionally, there is no large gap between the baseline and step 1, meaning that the biases cannot be resolved in step 1, but this step is a prerequisite for the successive bias correction steps.
The consequence of mode collapse can be seen as strong spikes in the sample distribution of estimated photometric red-shifts for the baseline method in contrast to the sample distribution of spectroscopic redshifts. We note that this is not due to the effect of discretized binning because the typical separation between two spikes is wider than the bin size. Similarly, as presented in Fig. 8, the data points are distributed along parallel lines as local concentrations, centered at discrete photometric redshift values. In particular, the last mode is located at a red-shift lower than the maximum redshift, which may be the reason for the plateau at z ~ 0.3 observed by Pasquet et al. (2019) (see Fig. 7 therein) where the instances with the highest spectroscopic redshifts are assigned with relatively lower photometric red-shifts. However, with step 3, the spikes and the concentrated lines can be substantially removed.
The intensity of mode collapse can be quantified by the total variation distance
 (10)
(10)
where pphoto (z) and Pspec (z) are the normalized zphoto and zspec sample distributions, respectively. This metric is sensitive to the vertical separation between the two distributions, especially conspicuous features such as spikes. We also constructed zphoto sample distributions for which collapsed modes were smoothed out by randomly drawing the same number of instances as the zspec sample based on the < Δz > − zspec curves. These simulated distributions set the lower limits of the total variation distances, which are shown as the shaded areas in Figs. 6 and 7.
By plotting the total variation distance against the slope of the linear fit in the second redshift interval for different cases, we demonstrate that our methods up to step 3 achieve considerable reduction of both zspec-dependent residuals and mode collapse. As step 3 treats mode collapse and underpopulation-induced zspec-dependent residuals simultaneously, we further illustrate the correction of each of the two biases with two variant cases of step 3: step 3a (which leverages hard labels with adjusted means), and step 3b (which leverages soft labels with unadjusted means). For the SDSS data, step 3a flattens the slope, but fails to reduce the total variation distance, whereas step 3b produces the opposite result, suggesting that softening the labels and readjusting the means are both necessary, and they account for the correction of the two biases, respectively. For the CFHTLS-WIDE data, step 3a fails to compensate for the negative slope, probably due to the influence of amplified mode collapse.
In addition, we examined another variant case step 3\2, in which step 3 was applied directly after step 1 without trimming overpopulated bins by step 2. For the CFHTLS-WIDE data, the maximum number density (i.e., 268) is comparable with the chosen balancing threshold (i.e., 100), thus the results from step 3 and step 3\2 are similar. However, for the SDSS data, the maximum number density (i.e., 2626) is much higher than the chosen threshold (i.e., 200). It seems that the untrimmed high peak number density is detrimental to the validity of labeling readjustment and thus excessively lifts up the high-redshift tail, as indicated by the unrealistic positive slope, which suggests that step 2 is required (more is discussed in Appendix D.1).
We quantified the accuracy of the photometric redshift estimation using the estimate of standard deviation based on the median absolute deviation (MAD),
 (11)
(11)
In all the cases, σMAD gradually degrades as the magnitude increases, indicating large estimation errors for faint galaxies. Furthermore, we observe that the biases are tightly connected to estimation errors. Stronger biases are usually associated with larger errors, and the correction for stronger biases would further introduce more errors. We note that the multichannel output unit, the restricted subset of training data, and the soft labels would all contribute additional errors compared to the baseline method. While not strong for the SDSS data, this compromise is more significant for the CFHTLS data because the redshift range is wider and there are fewer training data.
 |
Fig. 6 Main results of correcting zspec-dependent residuals and mode collapse with the SDSS data and the network Net_P. Upper panel: mean residuals as a function of spectroscopic redshift for the baseline method and steps 1-3 of our methods with the SDSS data and the network Net_P. The corresponding < Δz > − zspec piecewise linear fits (Eq. (9)) are shown as dashed lines with the same colors. Zero residual is indicated by the horizontal dashed black line. Middle panel: sample distributions of the estimated photometric and spectroscopic redshift in different cases. Lower left panel: σMAD (Eq. (11)) as a function of r-band magnitude. Lower right panel: total variation distance between the zphoto and zspec sample distributions (Eq. (10)) as a function of the slope of the < Δz > − zspec piecewise linear fit (Eq. (9)) in the high-redshift interval. The shaded area shows the total variation distance with the 1 a uncertainty for the simulated zphoto sample distribution for the baseline method that is expected to have no mode collapse. Step 3\2 denotes a case in which step 3 is applied without step 2. Step 3a denotes a variant case of step 3 in which hard labels are used instead of soft labels, but the means are adjusted. Step 3b denotes a case in which soft labels are used but the means are not adjusted. |
 |
Fig. 8 Predicted photometric redshifts as a function of spectroscopic redshift, color-coded with number density. The baseline method and steps 1-3 of our methods are compared using the SDSS data and the network Net_P. The dashed red lines indicate the boundaries (zphoto − zspec)/(1 + zspec) = ±0.05 for outliers defined for the SDSS data as in Pasquet et al. (2019) and Treyer et al. (in prep.). |
 |
Fig. 9 Main results of correcting zphoto-dependent residuals with the SDSS data and the network Net_P. Upper panels: spectroscopic redshift and r-band magnitude distributions for the SDSS training data and the test data. In addition to the original test sample, two other test samples are constructed that are biased toward medium redshifts (zspec ~ 0.12) or high magnitudes (r ~ 17.5). Middle panels: mean residuals as a function of spectroscopic redshift for the baseline method and step 3 with the three test samples and the network Net_P. The results from step 4 are also plotted in light purple for comparison. Steps 1-3 are applied in advance of the calibration by step 4. Lower panels: mean residuals as a function of photometric redshift for the baseline method and step 4 with the three test samples and the network Net_P. The results from step 3 are also plotted in light red for comparison. |
4.3 Correction for zphoto-dependent residuals
Figures 9 and 10 show the outcomes of correcting zphoto-dependent residuals and the comparison with those of correcting for zspec-dependent residuals using the SDSS test data. While Pasquet et al. (2019) exploited training data and test data whose distributions were identical, we applied our methods in scenarios in which their distributions are mismatched. We constructed three test samples with different distributions in order to mimic mismatches due to selection effects, which are unmodified or biased toward medium redshifts (zspec ~ 0.12) or high magnitudes (r ~ 17.5). The model was trained with the original training sample or with a sample in which 90% of the medium-redshift instances (0.08 < zspec < 0.12) were artificially discarded, mimicking an artifact due to combining samples from different sources, for instance. In each of the six cases, we performed step 4 five times; the residuals were corrected each time with a different set of resampled training data that had the same sample size as the test sample. The final output estimates for step 4 are given by averaging the five folds of corrected zphoto estimates. Furthermore, we note that the error bar of the mean residual as a function of zphoto should not be estimated using the quadratic error curves  given by Eq. (6) because the independent variable is zphoto rather than zspec; thus we took the root mean square error (RMSE) of residuals in each photometric redshift bin [zphoto, zphoto + δ zphoto] as the error bar.
given by Eq. (6) because the independent variable is zphoto rather than zspec; thus we took the root mean square error (RMSE) of residuals in each photometric redshift bin [zphoto, zphoto + δ zphoto] as the error bar.
As already illustrated in Fig. 6, we detected a negative slope for the baseline method in all the cases for the mean residual as a function of zspec. This negative slope can be corrected for by step 3, while the correction leads to a positive slope for the mean residual as a function of zphoto. The positive slope can then be corrected for by step 4, but this in turn reproduces a negative slope as a function of zspec because the dependences on zspec and zphoto cannot be reconciled (as mentioned in Sect. 1). Whether step 4 is applied or not relies on the definition of the mean residual required for the actual analysis.
Regarding the zphoto-dependent residuals, although Pasquet et al. (2019) claimed that zero dependence on zphoto can be achieved without the need for bias correction (in a restricted range zphoto < 0.25; see Fig. 8 therein), we are cautious that this is not always guaranteed. Nonzero dependence would most probably exist if the distributions for the training data and the test data were not identical. For instance, the test samples with the modified distributions produce slopes that are steeper than those with the original distribution. The artifact in the training sample creates a tilde on top of the mean residual evolving trend, which may only be handled via balancing the training data. Additionally, as discussed in Appendix D.3, the dependence of the mean residuals on zphoto may be evolving depending on how well the model fits the data, even when there is no mismatch between the training data and the test data. In contrast, steps 3 and 4 of our methods reliably remove the dependence on zspec or zphoto in all the cases.
 |
Fig. 10 Same as Fig. 9, but that the number density within 0.08 < zspec < 0.12 for the training sample is reduced by 90%. |
4.4 Mean redshift measurement for tomographic analysis
The mean photometric redshift in each tomographic bin is an important quantity to analyze cosmic shear tomography because the cosmic shear signal is primarily dependent on the mean distance of sources. For the Euclid mission, the accuracy of mean redshift measurement is required to be \Δz\ < 0.002 (Laureijs et al. 2011), which sets a stringent demand on the performance of photometric redshift estimation approaches. Therefore, we evaluated our methods in this regard.
The residual of the mean redshift in a tomographic bin is defined as
 (12)
(12)
This is different from the definition of the mean residual in Eq. (9). We examined the evolution of Δ<z> with regard to photometric redshifts and r-band magnitudes. Although Δ<z> is already a characterization of the deviation between the zphoto and zspec sample distributions, we also used the 1-Wasserstein distance to quantify their difference. The 1-Wasserstein distance between the normalized zphoto and zspec probability density distributions Pphoto and Pspec can be formulated as
 (13)
(13)
where Fphoto(z) and Fspec(z) are the corresponding cumulative density distributions. This metric is a measure of the horizontal distance and can be interpreted as an effective redshift separation between the two distributions. Unlike the total variation distance (Eq. (10)), this metric mainly captures the broad-scale discrepancy and is insensitive to small fluctuations induced by mode collapse.
Figure 11 shows the mean redshift calibrations for the SDSS data, the CFHTLS-DEEP data, and the CFHTLS-WIDE data. We used a restricted CFHTLS-DEEP sample with a magnitude cut r < 24, which alleviates the impact of faint galaxies. The mean redshift measurement for the SDSS data is highly accurate. The effective redshift separations indicated by the Wasserstein distances remain small over all magnitudes. The correction conducted by step 4 lowers the residuals as a function of zphoto and meets the |Δz| < 0.002 requirement. For the CFHTLS datasets, however, this requirement is only fulfilled in the low-magnitude and low-redshift intervals. Large errors are associated with high redshifts or high magnitudes, which is implied by the growth of the Wasserstein distances. Noticeably, the bias correction contributes to a boost of the Wasserstein distances as a result of the compromise between biases and errors. These observations indicate the difficulty of estimating reliable photometric redshifts for the high-redshift regime with data-driven methods mainly due to limited and nonrepresentative spectroscopic data. This difficulty places a demand on optimizing the exploitation of data, updating the existing algorithms, and exploring composite methods.
 |
Fig. 11 Mean redshift calibrations with the network Net_P. Upper panels: residuals of mean redshifts (different from mean residuals) in each zphoto tomographic bin for the baseline method and step 4 of our methods using the network Net_P with the SDSS data, the CFHTLS-DEEP data, and the CFHTLS-WIDE data. A magnitude cut r < 24 is applied to the CFHTLS-DEEP data to create a restricted sample. The shaded areas indicate the requirement for the accuracy of photometric redshift estimation (i.e., |Δz| < 0.002). Steps 1-3 are applied in advance of the calibration by step 4. Middle panels: same as the upper panels, but residuals of mean redshifts are estimated in r-band magnitude bins. Lower panels: 1-Wasserstein distance between the zphoto and zspec sample distributions (Eq. (13)) as a function of r-band magnitude. |
5 Discussion of the bias behaviors
Following our discussions of correcting for zspec-dependent biases, we investigated the behaviors of biases and the performance of our methods by controlling the CNN models with varying implementing and training conditions. We summarize the main results in this section, and more details are provided in Appendix D.
Appendix D.1 discusses the impact of the balancing threshold that determines the size and flatness of the nearly balanced training subset in steps 2 and 3. As the threshold varies, we find a tradeoff between zspec-dependent residuals and the estimation accuracy for step 2 due to overfitting, while the correction by step 3 remains robust.
Appendix D.2 discusses the impact of the bin size of redshift outputs. Although a large bin size tends to introduce a non-negligible quantization error, the sparsity of data would be enhanced as the bin size shrinks, leading to a compromised accuracy and a tendency for mode collapse.
Appendix D.3 discusses the impact of the number of training iterations. It indicates how well a model fits data, which is an influencing factor for underfitting or overfitting. In general, there is a transition from underfitting to overfitting as the training proceeds. For the baseline method, underfitting and overriding would increase estimation errors and zspec-dependent residuals for test data and change the behavior of zphoto-dependent residuals. Underfitting would yield strong mode collapse, whereas overfitting would smooth out collapsed modes by random errors. Our methods are still valid given an underfitted or overfitted representation.
Appendix D.4 discusses the impact of the training sample size. It characterizes the total volume of information provided by the training data, which is another influencing factor for overfitting. The consequence of reducing the sample size is similar to that of having more training iterations. If the original training sample was provided to construct the nearly balanced subset, our methods would still be robust over different degrees of overfitting.
Appendix D.5 discusses the impact of random Gaussian errors added to labels, which determines the fuzziness of the input-output mapping. The labeling errors would boost estimation errors, but suppress mode collapse. Our methods would remain robust if errorless high-quality data were used for bias correction.
Appendix D.6 discusses the impact of the model complexity using a set of networks with different architectures. It characterizes the capacity of a model to acquire information from data. We find that a model with a higher complexity would produce a better estimation accuracy and smaller biases, and sufficient model complexity is necessary for obtaining an informative representation for bias correction. This also implies that the existence of class-dependent residuals may be inherently governed by the data distribution rather than the model, although their amplitudes are strongly affected by the model complexity.
6 Comparison with current results
Finally, we validated our results with reference to current results from Pasquet et al. (2019) and Treyer et al. (in prep.) using CNN models, as well as those from Beck et al. (2016) using k-nearest neighbors (KNNs) applied on galaxy photometry and those obtained by SED fitting using the Le Phare code (Arnouts et al. 1999; Ilbert et al. 2006). These results were compared in terms of zspec and zphoto-dependent residuals. In order to be consistent with our test samples, 103305 instances in the SDSS sample within 0 < zspec < 0.4 from Beck et al. (2016) or Pasquet et al. (2019) and 10,000 instances in the CFHTLS-WIDE sample within 0 < zspec < 4.0 from Treyer et al. (in prep.) or the Sed fitting method were selected. Furthermore, we note that Pasquet et al. (2019) and Treyer et al. (in prep.) used zmean and zmedian as the point estimates of photometric redshifts, respectively, whereas we used zmode in this work. We directly compare results from these different studies despite the disagreement in the choice of point estimates.
Figure 12 shows that the mean residuals as a function of zspec for the reference results from Beck et al. (2016), Pasquet et al. (2019), Treyer et al. (in prep.), and the SED fitting method all significantly deviate from zero close to the borders of the redshift range, but step 3 of our methods is able to reduce these deviations. In particular, the KNN approach applied by Beck et al. (2016) produces a similar but worse trend for the SDSS data than the CNN approach by Pasquet et al. (2019), probably because the estimation errors are larger. The SED fitting method may suffer from degeneracies in galaxy photometry or a lack of representative templates in addition to limited accuracy, which may be the reason for the bump around zspec ~ 0.4 on top of the nonflat tails for the CFHTLS-WIDE data. The methods we propose in this work for data-driven models may complement SED fitting approaches to deal with such effects.
For the zphoto-dependent residuals, our results from step 4 and the reference results from the data-driven approaches are similar. The drop at zphoto ~ 0.25 for the SDSS data from Pasquet et al. (2019) is eliminated by our methods, and the plateau at z ~ 0.3 observed by Pasquet et al. (2019) is removed as a result of correcting for mode collapse. Although our methods do not result in biases as strong as produced by the SED fitting method for the CFHTLS-WIDE data, there are non-negligible errors at high redshifts that confine the robustness of our methods, suggesting that a good control of estimation errors is a precondition for bias correction.
7 Conclusion
We analyzed two biases that are generally present in data-driven methods, namely class-dependent residuals and mode collapse, which are two effects imposed by the prior of training data and the model implementation. Using photometric redshift estimation as a case study, we discussed the statistical basis of bias correction (Appendix A) and proposed a multistep procedure to correct for the biases based on CNNs trained with spectro-scopic samples of galaxy images. The first three steps are CNN based, while the last step is a direct calibration. In particular, we suggested that the residuals can be defined as a function of spec-troscopic redshift (zspec) or photometric redshift (zphoto), which have to be separately taken into consideration according to the actual analysis. The correction of biases in spectroscopic space by the first three steps have to be performed as a prerequisite before the calibration in photometric space by the last step is applied. The highlights of our methods are summarized below.
A multichannel unit was used as the output in place of the conventional single-channel fully connected layer with the Softmax activation, so that r-band magnitudes of galaxies could be explicitly predicted.
The learning procedure of a model was split into representation learning and classification. Bias correction was performed solely in the phase of classification with a fixed representation.
A nearly balanced subset of training data was constructed via resampling in order to resolve overpopulation-induced zspec-dependent residuals.
Underpopulation-induced zspec-dependent residuals and mode collapse were resolved by exploiting soft Gaussian labels, whose dispersions and means were determined using the preestimated redshifts from the preceding step.
zphoto-dependent residuals were resolved by reconstructing the distribution of the test sample with the training data and subtracting the mean zphoto − zspec deviation in each cell of the zphoto-magnitude grid, which is a direct calibration independent of CNN models.
We applied our methods to the SDSS data that cover 0 < zspec < 0.4, as well as to the CFHTLS data in a wider range of 0 < zspec < 4.0 from the Deep and Wide fields. In terms of bias control, our methods achieve better performance than the baseline method, the KNN method from Beck et al. (2016), the SED fitting method using the Le Phare code (Arnouts et al. 1999; Ilbert et al. 2006), and the CNN models from Pasquet et al. (2019) and Treyer et al. (in prep.). We also examined a few implementing details and assumptions behind our methods, and analyzed their effects on the behaviors of the biases. The results indicate that our methods are generally robust under varying conditions as long as high-quality data are provided for bias correction. We reiterate that representation learning may be less concerned with system-atics or low S/Ns, whereas bias correction requires higher data quality. Therefore, it is important to identify and understand the internal structures and systematics within data, so that a good control of biases can be ensured.
Despite the merits, we caution that the main difficulty of our methods is the tradeoff between resolving biases and reducing estimation errors. The use of zmode as point estimates yields the least biases compared to zmean and zmedian (Appendix B), but the accuracy and the catastrophic rate may be compromised (Appendix E). Additional errors may be introduced through the use of the multichannel output unit and the training with a restricted subset of data and soft labels, but these are all necessary for bias correction. In addition, biases scale with estimation errors in such a way that correcting large biases caused by large errors would yield even larger errors. It is thus important to have a good constraint of estimation errors before the bias correction. In spite of increasing errors, we prioritized bias correction in this work because it is critical to cosmological analysis.
The calibration of residuals with the CFHTLS data in high-redshift intervals is unable to meet the accuracy requirement of |Δz| < 0.002 for a Euclid-like survey. This partial failure for the CFHTLS data points to the difficulty of applying data-driven methods to the high-redshift regime provided with a shortage of spectroscopic training data with good S/Ns. Given limited spectroscopic follow-ups for the upcoming imaging surveys, there is an increasing need for optimizing the exploitation of training data, either at the data level (data augmentation, resampling, etc.) or at the algorithm level (feature extraction, domain adaptation, etc.). In the stage of representation learning in particular, the model may incorporate various supervised and unsupervised-learning techniques to maximize the usage of data in divergent forms. It is also worth investigating hybrid methods that take advantage of complementary information from individual approaches. For instance, multiple methods may be explored and integrated for a composite likelihood analysis (e.g., Shuntov et al. 2020; Rau et al. 2022). Domain knowledge may also be injected to fill in the gap for under-represented or missing data, which would be essential to alleviate the difficulty in the high-redshift regime.
Although we only discussed our bias correction methods in the context of a supervised-learning classification problem, we note that our work puts forward a framework that can be generalized to regression problems combined with unsupervised-learning components. For this, we have shown that the existence of class-dependent residuals may be inherently determined by the unbalanced data distribution rather than the model (Sect. 4.3 and Appendix D.6). Our methods are not limited to the photometric redshift estimation problem either. It is promising to apply our methods to similar studies that involve data-driven models. Furthermore, we studied point estimates rather than density estimates produced by neural networks due to unresolved prior. The justification for the use of density estimates and the correction of associated biases will be explored in future work.
 |
Fig. 12 Mean residuals as a function of spectroscopic or photometric redshift with the SDSS data and the CFHTLS-WIDE data. The results from steps 3 and 4 of our methods with the network Net_P are compared with those produced by data-driven methods from Pasquet et al. (2019), Beck et al. (2016), Treyer et al. (in prep.), and SED fitting using the Le Phare code (Arnouts et al. 1999; Ilbert et al. 2006). The results from step 3 (step 4) are plotted in light red (purple) for comparison in the lower (upper) panels. Steps 1-3 are applied in advance of the calibration by step 4. For consistency with our test samples, 103 305 SdSs galaxies and 10000 CFHTLS-WIDE galaxies in the given redshift ranges are selected from these studies for the plot. We note that we take zmode (i.e., the redshift at the peak probability) as the point estimates of photometric redshifts, whereas Pasquet et al. (2019) took zmean (i.e., the probability-weighted mean redshift) and Treyer et al. (in prep.) took zmed¡an (i.e., the median redshift drawn from the probability distribution). |
Acknowledgements
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No713750. Also, it has been carried out with the financial support of the Regional Council of Provence-Alpes-Côte d'Azur and with the financial support of the A*MIDEX (n° ANR-11-IDEX-0001-02), funded by the Investissements d'Avenir project funded by the French Government, managed by the French National Research Agency (ANR). This work has been carried out thanks to the support of the DEEPDIP ANR project (ANR-19-CE31-0023) and the Programme National Cosmologie et Galaxies (PNCG) of CNRS/INSU with INP and IN2P3, co-funded by CEA and CNES. This work makes use of Sloan Digital Sky Survey (SDSS) data. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the U.S. Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University. This work is based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l'Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at Terapix and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.
Appendix A Formalism to estimate photometric redshift
This appendix presents a statistical basis for the bias correction methods discussed in our work. Photometric redshift estimation with neural networks can be viewed as a probability density estimation problem. In general, the density of zSPec given the data D is mapped to the density of zPhoto via the following formula:
 (A.1.)
(A.1.)
where encodes the potential prior information imposed by the data D and the model implementation Φ (see also Malz & Hogg 2020; Malz 2021). Ideally, we expect
encodes the potential prior information imposed by the data D and the model implementation Φ (see also Malz & Hogg 2020; Malz 2021). Ideally, we expect  to be close to
to be close to  . However, Eq. A.1 is not an identity mapping between the two densities since
. However, Eq. A.1 is not an identity mapping between the two densities since  is different from δ(zphoto-zSPec); P'(zphoto|D, Φ) will suffer from biases induced by q(zphto|zSPeC, D, Φ).
is different from δ(zphoto-zSPec); P'(zphoto|D, Φ) will suffer from biases induced by q(zphto|zSPeC, D, Φ).
As it is nontrivial to marginalize over the prior from the data D and the model implementation O, we introduce an auxiliary term zphto|, D, Φ) to reestimate the density of zPhto that is supposed to neutralize the influence from q(zPhoto|zSPec, D, Φ),
 (A.2.)
(A.2.)
The reestimated density P"(zphotoD, Φ) is expected to resemble the actual density P(zSPec|D). In other words, the exploitation of bias correction techniques can be represented by the introduction of the term §(zphoto|zPhto, D, Φ). Following this idea, we exploit a multistep procedure in our work in which bias correction methods are applied based on a preestimation of the zPh0t0 density, that is, P'(zPhoto|D, Φ) (or multiple preestimations if necessary).
Appendix B Comparison of point estimates
In our work, probability density distributions of photometric red-shifts are predicted by the classification model. These density estimates are not full posterior distributions because the prior imposed by the training data and the model implementation has not been marginalized over. To alleviate the influence from the prior, we use the point estimates derived from the density estimates in our analysis.
We consider three choices of point estimates: (a) zmode, which is the redshift at the bin with the maximum probability. (b) zmean, which is the probability-weighted mean redshift over all bins. (c) zmed;an, which is the median redshift drawn from the probability distribution over all bins. Different choices of point estimates would result in dissimilar biases. Fig. B.1 shows that zmean − zspec (or zmedian − zspec) evolves with zspec The measures are overestimated for the low-z instances on average, but underestimated for the high-z instances. In particular,zmedian and Z median is corrected with Z mean_ zmode (or zmedian − zmode) for the instances with the lowest redshifts, which is due to the window function imposed by the finite red-shift range of the density estimates set by the model because it causes zmean and zmed;an to be more concentrated on the central value of the redshift range. This correlation is more pronounced for our methods as the predicted density estimates are widened compared to the baseline method. We note that step 3 (and subsequently, step 4) is performed based on preestimated zmode, but the overall behaviors would be similar for zmean based or zmed!an based bias correction. Similar trends can also be found with the CFHTLS datasets. Therefore, we suggest that zmean and zmed!an are not statistically sound choices of point estimates. In comparison, the influence of this window function is weaker for zmode (although it has stronger mode collapse) because zmode is determined by the bin with the peak probability rather than the global density distribution. We thus take zmode as the point estimates for our methods and the baseline method throughout this work.
 |
Fig. B.1 Comparison of three choices of point estimates (zmode, zmean, and zmedian) for the baseline method and steps 1 – 4 of our methods using the SDSS data and the network Net_P. All data points are color-coded with zspec • As the three point estimates for each data instance are shifted by the same amount in step 4, the differences between any two point estimates remain unchanged as in step 3. |
Appendix C Modeling the impact of underpopulated classes
The outcome from step 2 of our methods has zspec-dependent residuals caused by under-populated bins. As discussed in Section 3.2.3, the effect of underpopulated bins can be characterized by a separation between the actual spectroscopic redshift and the mean of the skewed scattering profile for each instance, which is mutually determined by a initial Gaussian scattering profile and the zspec number density of the subsample under a linearity assumption. We attempt to test this assumption by comparing the actual < Δz > − zspec curves using the subsets of training data from step 2 against the expected residual curves derived based on skewed scattering profiles. The expected mean residual in each zspec bin is determined as
 (C.1.)
(C.1.)
where z0 is the initial zspec value; z is the mean of the skewed scattering profile as in Eq. 8, regarded as the expected zphoto value. We follow the same procedure as explained in Section 3.2.3 to estimate the quadratic error curves  and the scattering profiles, but the variances are replaced with
and the scattering profiles, but the variances are replaced with  . We also rescale
. We also rescale  by a set of factors k in order to vary the shapes of the skewed scattering profiles and evaluate the effect on the expected residual curves.
by a set of factors k in order to vary the shapes of the skewed scattering profiles and evaluate the effect on the expected residual curves.
Fig. C.1 shows the results with the SDSS data and the CFHTLS-WIDE data. With varying rescaling factors, the amplitudes of the simulated residuals stretch over a wide range, especially for highly underpopulated regions that are typically subject to large errors and significant imbalances. This indicates that a proper modeling of skewed scattering profiles is mostly required for bias correction over these regions. The overall rough agreement between the expected curves without rescaling (i.e., k = 1) and the actual curves strengthens the validity of the assumption of scattering profiles and the procedure for determining the means of the soft labels in step 3. The assumption may not hold if predominant peaks exist in number density (Appendix D.1), but this violation is circumvented in our case as the overpopulated bins have been trimmed in step 2.
 |
Fig. C.1 Comparison between the actual and the expected < Δz > − zspec curves for the SDSS data and the CFHTLS-WIDE data, respectively. The actual curves are derived with the subsets of training data from step 2 (represented by the yellow lines). The expected curves are determined by the means of the scattering profiles as in Eq. 8, but the variances are replaced with the estimated quadratic error curves and rescaled by a set of different factors k (represented by the dotted lines). |
Appendix D Detailed discussion of bias behaviors
In this appendix, we present the details of our investigation into bias behaviors discussed in Section 5. Without losing generality, we conduct experiments only on the SDSS data and the network Net_P unless otherwise noted. The results are shown with the test data.
D.1 Impact of the balancing threshold
The balancing threshold determines the flatness of the nearly balanced training subset used to suppress the impact of overpop-ulated bins in steps 2 and 3 and is one of the key parameters in our methods. A low threshold may lead to insufficient statistics and cause strong overfitting, whereas a high threshold may be ineffective for correcting zspec-dependent residuals induced by overpopulated classes. In Figs. D.1 and D.2, we examine the performance of our methods with a set of different thresholds for the SDSS data and the CFHTLS-WIDE data using the network Net_P. We show the results from steps 2 and 3, as well as those from step 1 and step 3\2 (with step 2 skipped), which are expected to be the limits of steps 2 and 3, respectively, as the threshold approaches the maximum number density. The estimation accuracy is indicated by σMAD (Eq. 11). The dependence of mean residuals on zspec is indicated by the slopes in the two redshift intervals from the piecewise linear fit (Eq. 9). The intensity of mode collapse is quantified by the total variation distance (Eq. 10). The dotted curves show the total variation distances for the simulated zphoto sample distributions, which are expected to be free from mode collapse. Ideally, after bias correction, the slopes are expected to be zero, and the total variation distances are expected to be close to the simulated values.
As the threshold evolves, there is a major tradeoff between aMAD and the slope in the high-redshift interval for step 2. Since the construction of the training subset reduces statistics and causes an increase in estimation errors, this issue would be circumvented by simply increasing the balancing threshold and regarding all bins except the one with the peak density as underpopulated bins. As discussed in Section 3.2.3, the influence from underpopulated bins can be modeled by assuming a Gaussian scattering profile linearly modified by the local number density. This assumption might be violated if the peak number density is significantly high, as suggested by the growth of a mad and the overly corrected slopes with the SDSS data for step 3 when the threshold is above 200. Therefore, it is necessary to trim the peak densities before modeling the scattering profiles. Based on our observations from the figures, we take 200 and 100 as the thresholds in the main experiments for the SDSS data and the CFHTLS-WIDE data, respectively. Each of them is a tradeoff between suppressing the overpopulated bins and avoiding overfitting.
D.2 Impact of the bin size
A redshift bin defines a small interval within which continuous redshifts are collapsed to a single value. As the predicted redshift point estimates are defined in bins, they can only take discrete values, which would introduce a quantization error. In Fig. D.3 we present the result of our experiment on implementing different bin sizes using the SDSS data and the network Net_P. The bin size is controlled by the number of bins in a redshift output (before being extended in step 3). For example, a discretization of 20 bins yields a bin size of 0.4/20 = 0.02. In step 3, n/2 additional bins are appended to each side of the initial redshift output (where n is the initial number of bins), except that 20 bins are appended to each side in the case of 20 initial bins.
The case with the smallest number of bins (i.e., 20) has the highest σMAD, suggesting a large quantization error. The correction of biases for this case also seems problematic. For the baseline method, σMAD appears to increase as the number of bins grows, probably due to a tendency for overfitting. A large number of bins would also make the data sparse, resulting in small-scale spikes in the zphoto sample distribution and enlarging the total variation distance. In addition, the slopes of the < Δz > − zspec curves are not strongly affected by the bin size. Same as the choice by Pasquet et al. (2019), we take 180 bins in the main experiments for the SDSS sample, as this intermediate number is a compromise between avoiding the sparsity of data and limiting the quantization error.
 |
Fig. D.1 σMAD (Eq. 11), the slopes of the < Δz > − zSPec piecewise linear fit (Eq. 9) and the total variation distance between the zPh0t0 and zSPec sample distributions (Eq. 10) as a function of the balancing threshold that defines the nearly balanced training subset for steps 2 and 3 of our methods. As the threshold approaches the maximum number density (2,626 in this case), the results from step 2 are expected to converge to those from step 1, and those from step 3 are expected to converge to those from step 3\2 in which step 2 is skipped. The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. We compare the methods using the SDSS data and the network Net_P. |
D.3 Impact of the number of iterations
The performance of a model is influenced by the number of iterations conducted in training, as it (together with the mini-batch size) determines the average number of times each instance is fed into the model and how well the model fits the training sample. In general, a model trained from scratch would gradually depart from a state of underfitting as the number of training iterations increases, and there might be a trend of overfitting if the volume of information in the training sample does not match the complexity of the model. Using the SDSS data and the network Net_P, we explore this evolution trend by continuously training the network and saving the trained parameters at a set of different iterations for the baseline method and step 1. We do not change the numbers of iterations for steps 2 and 3, however.
As shown in Fig. D.4, the estimation accuracy (indicated by σMAD) for the baseline method improves first but declines after a turning point around 60,000 iterations, implying a shift from underfitting to overfitting. The turning point suggests the number of iterations with which the model reaches a proper fit. The decrease in the estimation accuracy is less significant for step 1, probably due to the regularizing effect imposed by the multichannel output unit.
Interestingly, the total variation distance between the zphoto and zspec sample distributions decreases monotonically as the training proceeds, suggesting that mode collapse is heavily associated with underfitting, while overfitting has a positive effect on reducing mode collapse. This trend can also be seen in Fig. D.5 for the baseline method. With a low number of iterations (e.g., 20,000), only a coarse input-output mapping can be established due to underfitting, thus the data points are grouped into large clusters shown as the conspicuous concentrated lines. As the training continues, the grouping of points becomes finer and the plateau on the top gradually shifts upward. Eventually, with an excessively large number of iterations (e.g., 240,000), the redshift estimates predicted by the overfitted model tend to have large random scatters, which smears out the local concentrations caused by mode collapse.
We also examine the influence on mean residuals estimated in spectroscopic redshift bins or photometric redshift bins for the baseline method. As presented in Fig. D.6, the < Δz > – zSPec curve tends to be steeper with stronger underfitting, which results from the presence of overpopulated classes and the hard red-shift boundaries set by the model that cause the zphoto estimates from each zspec bin to become skewed toward the location of the peak number density. For the same reason, the mean residuals for the high-zphoto bins are below zero, meaning that each zphoto bin is contributed by inward skewness more significantly than outward scattering. However, outward scattering dominates inward skewness for the low-zphoto bins, thus the mean residuals below zPh0t0 ~ 0.1 are also negative.
When the training passes the point of proper fit and starts to overfit, the slope of the < Δz > – zSPec curve would become more negative again as a result of increasing estimation errors. The high-zPh0t0 tail of the < Δz > - zPh0t0 curve shifts from negative to positive, implying that outward scattering is becoming more predominant due to larger random errors. Based on these observations, we suggest that the zero dependence on zphoto (but with a drop at the high-z tail) achieved by Pasquet et al. (2019) would not be ensured unless a precise control of training is carried out.
Additionally, in spite of the suboptimal (mainly underfitted) representations established with different numbers of iterations, the validity of our bias correction methods is verified in all these cases. We use a number of 60,000 iterations for representation learning in the main experiments, but mild underfitting or overfitting would not produce any major impact. We continue discussing the effect of overfitting in Appendix D.4.
 |
Fig. D.3 σMAD (Eq. 11), the slopes of the < Δz > - zspec piecewise linear fit (Eq. 9) and the total variation distance between the zphoto and zspec sample distributions (Eq. 10) as a function of the number of bins in the output redshift density estimate (before being extended in step 3). The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. The baseline method and steps 1 - 3 of our methods are compared using the SDSS data and the network Net_P. |
D.4 Impact of the sample size
The size of the training sample is one of the most important factors influencing the performance of a model. Predominantly, a complex model would easily overfit on a small training sample. As a complement to the experiment of varying the number of training iterations (discussed in Appendix D.3), we investigate the effect of overfitting by controlling the size of the training sample for the baseline method and the representation learning in step 1 using the SDSS data and the network Net_P. However, we use the original training sample to construct a nearly balanced subset for steps 2 and 3.
As illustrated in Fig. D.7, the estimation accuracy (indicated by σMAD) gradually drops as a result of increased overfitting when the sample size decreases, in general leading to higher residuals suggested by the steeper < Δz > - zspec curves, but weaker mode collapse suggested by the lower total variation dis tances between the zphoto and zspec sample distributions, which is similar to the consequence of conducting more training iterations. On the other hand, the performance of bias correction appears robust for different degrees of overfitting. Presumably, the training subset contains previously unseen instances that help reidentify salient information from the biased representation and reduce overfitting in the classification phase. We therefore claim that an overfitted representation may still be applicable for bias correction as long as this overfitting can be neutralized with the classification module.
 |
Fig. D.4 σMAD (Eq. 11), the slopes of the < Az > - zspec piecewise linear fit (Eq. 9) and the total variation distance between the zphoto and zspec sample distributions (Eq. 10) as a function of the number of training iterations conducted for the baseline method and step 1 of our methods. The number of iterations for steps 2 and 3 remains the same as in the main experiments. The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. We compare the methods using the SDSS data and the network Net_P. |
D.5 Impact of labeling errors
In our main experiments, the labels used in training are assumed to contain no errors for the SDSS data and the high-quality CFHTLS data. Using the SDSS data and the network Net_P, we examine whether Gaussian labeling errors would have an effect on the behavior of the biases and the performance of our methods. We randomly draw Gaussian errors with a series of given dispersions (azs) and add them to the initial spectroscopic red-shifts for the training data (but not the test data). The erroneous spectroscopic redshifts are fixed and those within the redshift range [0, 0.4] are converted into labels used for the baseline method and the representation learning in step 1. As shown in Fig. D.8, introducing labeling errors leads to an increase in estimation errors indicated by σMAD and may have an impact on the slopes of the < Az > - zspec curves. Similar to the effect of over-fitting, the increasing labeling errors would yield more random incorrect redshift estimates, which helps suppress mode collapse and results in decreased total variation distances between the zphoto and zspec sample distributions.
 |
Fig. D.5 Predicted photometric redshifts as a function of spectroscopic redshift color-coded with number density for the baseline method. We compare cases with different numbers of iterations in training using the SDSS data and and the network Net_P. The dashed red lines indicate the boundaries (zphoto - zspec+ zspec) = ±0.05 for outliers defined for the SDSS data as in Pasquet et al. (2019) and Treyer et al. (in prep.). |
Since high-quality spectroscopic redshifts are required for bias correction, we then use the initial errorless labels for training in steps 2 and 3. The outcomes of bias correction remain similar in all the cases even for the one with a substantially large dispersion az = 0.2, given that high-quality labels are provided for bias correction. We thus claim that our methods are valid for a representation established with labels that have Gaussian errors, as long as the salient information of the mapping from the input to the correct target output is preserved. While labeling errors should be avoided for bias correction, the requirement on the data quality may be less demanding for representation learning, and the data with a variety of systematics may be used simultaneously. Despite this claim, we caution that the labeling errors drawn from a Gaussian distribution may not be representative of the actual distribution of catastrophic failures caused by misidentification of spectral lines, for example. Further investigation with realistic labeling errors is required in future work.
D.6 Impact of the model complexity
The complexity of a model determines the volume of information that can be learned from data and thus affects the performance of the model. A more complex model would generally have lower errors and biases in its prediction if not overfitted. We investigate whether our methods are robust with models that have different complexities using the SDSS data. In addition to the networks from Pasquet et al. (2019) and Treyer et al. (in prep.) (denoted with “Net_P” and “Net_T”, respectively), we experiment on other three simple networks that differ in the number of layers (summarized below). Likewise, the penultimate fully connected layer of each network is used to obtain a representation.
 |
Fig. D.6 Mean residuals estimated in coarse bins as a function of spec-troscopic or estimated photometric redshift for the baseline method. We compare cases with different numbers of iterations in training using the SDSS data and and the network Net_P. The horizontal dashed black lines indicate zero residual. |
Net_S1
3 X 3 convolution with 64 kernels, stride 1, zero padding and the ReLU activation
Global average pooling
Concatenation with E(B - V)
Fully connected layer with 256 neurons and the ReLU activation
Fully connected layer with 256 neurons and the ReLU activation
Fully connected layer with 180 neurons or multichannel output unit
Net_S2
3 X 3 convolution with 64 kernels, stride 1, zero padding and the ReLU activation
2 X 2 average pooling with stride 2
3 X 3 convolution with 64 kernels, stride 1, zero padding and the ReLU activation
Global average pooling
Concatenation with E(B - V)
Fully connected layer with 256 neurons and the ReLU activation
Fully connected layer with 256 neurons and the ReLU activation
Fully connected layer with 180 neurons or multichannel output unit
Net_S3
3 X 3 convolution with 64 kernels, stride 1, zero padding and the ReLU activation
2 X 2 average pooling with stride 2
3 X 3 convolution with 64 kernels, stride 1, zero padding and the ReLU activation
2 X 2 average pooling with stride 2
3 X 3 convolution with 64 kernels, stride 1, zero padding and the ReLU activation
Global average pooling
Concatenation with E(B - V)
Fully connected layer with 256 neurons and the ReLU activation
Fully connected layer with 256 neurons and the ReLU activation
Fully connected layer with 180 neurons or multichannel output unit
 |
Fig. D.7 σMAD (Eq. 11), the slopes of the < Az > – zSPec piecewise linear fit (Eq. 9) and the total variation distance between the zPh0t0 and zSPec sample distributions (Eq. 10) as a function of the total number of instances in the training sample for the baseline method and step 1 of our methods. The nearly balanced training subset in steps 2 and 3 is constructed using the original training set without reducing the sample size. The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. We compare the methods using the SDSS data and the network Net_P. |
 |
Fig. D.8 σMAD (Eq. 11), the slopes of the < Δz > – zspec piecewise linear fit (Eq. 9) and the total variation distance between the zphoto and zspec sample distributions (Eq. 10) as a function of the dispersion of Gaussian errors az introduced to the redshift labels for the training data used for the baseline method and step 1 of our methods. The Gaussian errors are not applied to the training data in steps 2 and 3, or the test data. The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. We compare the methods using the SDSS data and the network Net_P. |
As shown in Fig. D.9, σMAD, the slopes of the < Δz > – zspec curves and the total variation distance between the zphoto and zspec sample distributions all evolve almost monotonically as the model complexity increases for the baseline method and step 1, implying that a model with a higher complexity would be more capable of reducing underfitting and producing a better estimation accuracy and smaller biases. The outcomes of bias correction degrade for the three simple networks, probably because the representations in these cases do not contain as much salient information for determining the output as in more complex models. This suggests that a sufficient model complexity is required in order to obtain a good representation and effectively apply bias correction. In addition, all these cases show similar < Δz > – zspec curves in spite of different slopes, suggesting that the uneven data distribution inherently determines the existence of class-dependent residuals.
 |
Fig. D.9 σMAD (Eq. 11), the slopes of the < Δz > – zspec piecewise linear fit (Eq. 9) and the total variation distance between the zphoto and zspec sample distributions (Eq. 10) as a function of different network architectures with increasing complexity (defined in the text). The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. The baseline method and steps 1 - 3 of our methods are compared using the SDSS data. |
Appendix E Evaluation of the estimation quality
Despite a prioritized focus on bias correction in this work, we present a broader evaluation on the quality of estimated photometric redshifts. For each dataset (i.e., SDSS, CFHTLS-DEEP and CFHTLS-WIDE), we leverage three evaluation metrics used by Pasquet et al. (2019) and Treyer et al. (in prep.): the global mean residual < Δz >, σMAD (Eq. 11), and the outlier fraction η>a with |Δz| > α. We adopt a = 0.05 for the SDSS dataset and a = 0.15 for the CFHTLS datasets. These metrics are applied to the three point estimates (zmode, zmean, and zmedian) obtained with the network Net_P.
The results are listed in Tabs. E.1, E.2, and E.3. Because the data are limited, the zphoto estimation for the CFHTLS-DEEP dataset has the worst accuracy, which makes our bias correction methods unreliable. As demonstrated in our work, the accuracy may be compromised by bias correction. In particular, there is a dramatic boost of errors for zmean with step 3 especially for the CFHTLS datasets. We note that this only indicates the consequence of zmode based bias correction, but similar trends would be found for zmean based or zmedian based correction. Although σMAD and η>a for zmode may be worse than those for zmean or zmedian, we adopt zmode to achieve a better control of biases (Appendix B).
Evaluation of the photometric redshift estimation for the SDSS dataset.
Evaluation of the photometric redshift estimation for the CFHTLS-DEEP dataset.
Evaluation of the photometric redshift estimation for the CFHTLS-WIDE dataset.
Finally, we caution that it might not be statistically meaningful to evaluate global properties for heterogeneous samples with these metrics. With sufficient statistics, it would be preferable to evaluate the behavior of subsamples in which data instances are homogeneously sampled.
References
- Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [Google Scholar]
- Alarcon, A., Sánchez, C., Bernstein, G. M., & Gaztañaga, E. 2020, MNRAS, 498, 2614 [NASA ADS] [CrossRef] [Google Scholar]
- Alibert, Y., & Venturini, J. 2019, A&A, 626, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ansari, Z., Agnello, A., & Gall, C. 2021, A&A, 650, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arjovsky, M., & Bottou, L. 2017, ArXiv e-prints [arXiv:1701.04862] [Google Scholar]
- Armitage, T.J., Kay, S.T., & Barnes, D.J. 2019, MNRAS, 484, 1526 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [Google Scholar]
- Baldry, I. K., Liske, J., Brown, M. J. I., et al. 2018, MNRAS, 474, 3875 [Google Scholar]
- Beck, R., Dobos, L., Budavári, T., Szalay, A. S., & Csabai, I. 2016, MNRAS, 460, 1371 [Google Scholar]
- Bengio, Y., Courville, A. C., & Vincent, P. 2013, IEEE Trans. Pattern Analy. Mach. Intell., 35, 1798 [CrossRef] [Google Scholar]
- Bhagyashree, Kushwaha, V., & Nandi, G.C. 2020, in 2020 IEEE 4th Conference on Information Communication Technology (CICT), 1–6 [Google Scholar]
- Bonjean, V., Aghanim, N., Salomé, P., et al. 2019, A&A, 622, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnett, C. 2015, MNRAS, 449, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Bradshaw, E. J., Almaini, O., Hartley, W. G., et al. 2013, MNRAS, 433, 194 Article number, page 18 of 28 [NASA ADS] [CrossRef] [Google Scholar]
- Buchs, R., Davis, C., Gruen, D., et al. 2019, MNRAS, 489, 820 [Google Scholar]
- Buda, M., Maki, A., & Mazurowski, M. A. 2018, Neural Netw., 106, 249 [CrossRef] [Google Scholar]
- Burhanudin, U. F., Maund, J. R., Killestein, T., et al. 2021, MNRAS, 505, 4345 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, K., Wei, C., Gaidon, A., Arechiga, N., & Ma, T. 2019, in Advances in Neural Information Processing Systems, eds. H. Wallach, H. Larochelle, A. Beygelzimer, et al. (USA: Curran Associates, Inc.), 32 [Google Scholar]
- Carrasco Kind, M., & Brunner, R. J. 2013, MNRAS, 432, 1483 [Google Scholar]
- Carrasco Kind, M., & Brunner, R. J. 2014, MNRAS, 438, 3409 [NASA ADS] [CrossRef] [Google Scholar]
- Cavuoti, S., Tortora, C., Brescia, M., et al. 2016, MNRAS, 466, 2039 [Google Scholar]
- Chawla, N. V., Bowyer, K. W., Hall, L. O., & Kegelmeyer, W. P. 2002, J. Artif. Intell. Res., 16, 321 [CrossRef] [Google Scholar]
- Chong, P., Ruff, L., Kloft, M., & Binder, A. 2020, in 2020 International Joint Conference on Neural Networks (IJCNN), IEEE, 1–9 [Google Scholar]
- Coil, A. L., Blanton, M. R., Burles, S. M., et al. 2011, ApJ, 741, 8 [Google Scholar]
- Collister, A. A., & Lahav, O. 2004, PASP, 116, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Cool, R. J., Moustakas, J., Blanton, M. R., et al. 2013, ApJ, 767, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, M., Tamayo, D., Rein, H., et al. 2021, Proc. Natl. Acad. Sci., 118, 2026053118 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, Y., Jia, M., Lin, T.-Y., Song, Y., & Belongie, S. 2019, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) [Google Scholar]
- Davis, C., Gatti, M., Vielzeuf, P., et al. 2017, ArXiv e-prints [arXiv:1710.02517] [Google Scholar]
- D’Isanto, A., & Polsterer, K. L. 2018, A&A, 609, A111 [Google Scholar]
- Domínguez Sánchez, H., Huertas-Company, M., Bernardi, M., Tuccillo, D., & Fischer, J. L. 2018, MNRAS, 476, 3661 [Google Scholar]
- Drinkwater, M. J., Byrne, Z. J., Blake, C., et al. 2018, MNRAS, 474, 4151 [Google Scholar]
- Duarte, K., Rawat, Y., & Shah, M. 2021, in 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), 2733 [CrossRef] [Google Scholar]
- Euclid Collaboration ( Ilbert, O., et al.) 2021, A&A, 647, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldmann, R., Carollo, C. M., Porciani, C., et al. 2006, MNRAS, 372, 565 [NASA ADS] [CrossRef] [Google Scholar]
- García, V., Sánchez, J., & Mollineda, R. 2012, Knowledge-Based Syst., 25, 13 [CrossRef] [Google Scholar]
- Garilli, B., McLure, R., Pentericci, L., et al. 2021, A&A, 647, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gatti, M., Giannini, G., Bernstein, G. M., et al. 2022, MNRAS, 510, 1223 [Google Scholar]
- Gerdes, D. W., Sypniewski, A. J., McKay, T. A., et al. 2010, ApJ, 715, 823 [Google Scholar]
- Greisel, N., Seitz, S., Drory, N., et al. 2015, MNRAS, 451, 1848 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A., Zorrilla Matilla, J. M., Hsu, D., & Haiman, Z. 2018, Phys. Rev. D, 97, 103515 [NASA ADS] [CrossRef] [Google Scholar]
- Han, H., Wang, W.-Y., & Mao, B.-H. 2005, in Advances in Intelligent Computing, eds. D.-S. Huang, X.-P. Zhang, & G.-B. Huang (Berlin, Heidelberg: Springer), 878 [CrossRef] [Google Scholar]
- Hatfield, P. W., Almosallam, I. A., Jarvis, M. J., et al. 2020, MNRAS, 498, 5498 [NASA ADS] [CrossRef] [Google Scholar]
- Hayat, M., Khan, S., Zamir, W., Shen, J., & Shao, L. 2019, Max-margin Class Imbalanced Learning with Gaussian Affinity [Google Scholar]
- Hemmati, S., Capak, P., Masters, D., et al. 2019, ApJ, 877, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Hosenie, Z., Lyon, R., Stappers, B., Mootoovaloo, A., & McBride, V. 2020, MNRAS, 493, 6050 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, B. 2016, Astron. Comput., 16, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, C., Li, Y., Loy, C. C., & Tang, X. 2016, in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 5375 [CrossRef] [Google Scholar]
- Huang, C., Li, Y., Loy, C. C., & Tang, X. 2020, IEEE Trans. Pattern Anal. Mach. Intell., 42, 2781 [CrossRef] [Google Scholar]
- Hudelot, P., Cuillandre, J. C., Withington, K., et al. 2012, VizieR Online Data Catalog: II/317 [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jia, J., & Zhao, Q. 2019, in 2019 12th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), 1 [Google Scholar]
- Jones, E., & Singal, J. 2017, A&A, 600, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kang, B., Xie, S., Rohrbach, M., et al. 2020, in International Conference on Learning Representations [Google Scholar]
- Khan, S. H., Hayat, M., Bennamoun, M., Sohel, F. A., & Togneri, R. 2018, IEEE Trans. Neural Netw. Learn. Syst., 29, 3573 [CrossRef] [Google Scholar]
- Khan, S., Hayat, M., Zamir, S. W., Shen, J., & Shao, L. 2019, in 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 103 [CrossRef] [Google Scholar]
- Kingma, D. P., & Ba, J. 2015, in 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings, ed. Y. Bengio, & Y. LeCun [Google Scholar]
- Kodali, N., Abernethy, J., Hays, J., & Kira, Z. 2017, ArXiv e-prints [arXiv:1705.07215] [Google Scholar]
- Kovetz, E. D., Raccanelli, A., & Rahman, M. 2017, MNRAS, 468, 3650 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013, A&A, 559, A14 [Google Scholar]
- Le Fèvre, O., Tasca, L. A. M., Cassata, P., et al. 2015, A&A, 576, A79 [Google Scholar]
- Lee, K.-G., Krolewski, A., White, M., et al. 2018, ApJS, 237, 31 [Google Scholar]
- Leistedt, B., Hogg, D. W., Wechsler, R. H., & DeRose, J. 2019, ApJ, 881, 80 [Google Scholar]
- Li, Y., Wang, Q., Zhang, J., Hu, L., & Ouyang, W. 2021, Neurocomputing, 435, 26 [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [Google Scholar]
- Liu, Z., Miao, Z., Zhan, X., et al. 2019, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2537 [Google Scholar]
- Malz, A. I. 2021, Phys. Rev. D, 103, 083502 [NASA ADS] [CrossRef] [Google Scholar]
- Malz, A. I., & Hogg, D. W. 2020, ApJ, submitted, [arXiv:2007.12178] [Google Scholar]
- Mandelbaum, R., Seljak, U., Hirata, C. M., et al. 2008, MNRAS, 386, 781 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, M., Libeskind, N., Lahav, O., & Hoffman, Y. 2017, J. Cosmol. Astropart. Phys., 2017, 034 [CrossRef] [Google Scholar]
- McLure, R. J., Pearce, H. J., Dunlop, J. S., et al. 2013, MNRAS, 428, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Momcheva, I. G., Brammer, G. B., van Dokkum, P. G., et al. 2016, ApJS, 225, 27 [Google Scholar]
- Morrison, C. B., Hildebrandt, H., Schmidt, S. J., et al. 2017, MNRAS, 467, 3576 [Google Scholar]
- Mu, Y.-H., Qiu, B., Zhang, J.-N., Ma, J.-C., & Fan, X.-D. 2020, Res. Astron. Astrophys., 20, 089 [Google Scholar]
- Müller, R., Kornblith, S., & Hinton, G. E. 2019, in Advances in Neural Information Processing Systems, ed. H. Wallach, H. Larochelle, A. Beygelzimer, et al. (USA: Curran Associates, Inc.), 32 [Google Scholar]
- Newman, J. A. 2008, ApJ, 684, 88 [Google Scholar]
- Newman, J. A., Cooper, M. C., Davis, M., et al. 2013, ApJS, 208, 5 [Google Scholar]
- Nguyen, Q., Mukkamala, M. C., & Hein, M. 2018, in Proceedings of Machine Learning Research, Vol. 80, Proceedings of the 35th International Conference on Machine Learning, eds. J. Dy, & A. Krause (PMLR), 3740 [Google Scholar]
- Ntampaka, M., Trac, H., Sutherland, D. J., et al. 2015, ApJ, 803, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Ntampaka, M., ZuHone, J., Eisenstein, D., et al. 2019, ApJ, 876, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Okerinde, A., Hsu, W., Theis, T., Nafi, N., & Shamir, L. 2021, in Computer Analysis of Images and Patterns, eds. N. Tsapatsoulis, A. Panayides, T. Theocharides, et al. (Cham: Springer International Publishing), 322 [CrossRef] [Google Scholar]
- Pasquet, J., Bertin, E., Treyer, M., Arnouts, S., & Fouchez, D. 2019, A&A, 621, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rau, M. M., Seitz, S., Brimioulle, F., et al. 2015, MNRAS, 452, 3710 [NASA ADS] [CrossRef] [Google Scholar]
- Rau, M. M., Morrison, C. B., Schmidt, S. J., et al. 2022, MNRAS, 509, 4886 [Google Scholar]
- Ravanbakhsh, S., Oliva, J., Fromenteau, S., et al. 2016, in Proceedings of the 33rd International Conference on International Conference on Machine Learning - 48, ICML’16 (JMLR.org), 2407 [Google Scholar]
- Ribli, D., Pataki, B. A., & Csabai, I. 2019, Nat. Astron., 3, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Ruff, L., Vandermeulen, R., Goernitz, N., et al. 2018, in Proceedings of Machine Learning Research, Vol. 80, Proceedings of the 35th International Conference on Machine Learning, eds. J. Dy, & A. Krause (PMLR), 4393 [Google Scholar]
- Salvato, M., Ilbert, O., & Hoyle, B. 2019, Nat. Astron., 3, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchez, C., & Bernstein, G. M. 2018, MNRAS, 483, 2801 [Google Scholar]
- Santurkar, S., Schmidt, L., & Madry, A. 2018, in International Conference on Machine Learning, PMLR, 4480 [Google Scholar]
- Schuldt, S., Suyu, S. H., Cañameras, R., et al. 2021, A&A, 651, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scodeggio, M., Guzzo, L., Garilli, B., et al. 2018, A&A, 609, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shuntov, M., Pasquet, J., Arnouts, S., et al. 2020, A&A, 636, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skelton, R. E., Whitaker, K. E., Momcheva, I. G., et al. 2014, ApJS, 214, 24 [Google Scholar]
- Soo, J. Y. H., Joachimi, B., Eriksen, M., et al. 2021, MNRAS, 503, 4118 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., & Eisenstein, D. J. 2017, MNRAS, 469, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Srivastava, A., Valkov, L., Russell, C., Gutmann, M. U., & Sutton, C. 2017, in Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17 (Red Hook, NY, USA: Curran Associates Inc.), 3310–3320 [Google Scholar]
- Szegedy, C., Liu, W., Jia, Y., et al. 2015, in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) [Google Scholar]
- Thanh-Tung, H., & Tran, T. 2020, in 2020 International Joint Conference on Neural Networks (IJCNN), IEEE, 1–10 [Google Scholar]
- Tong, H., Liu, B., Wang, S., & Li, Q. 2019, ArXiv e-prints [arXiv:1901.08429] [Google Scholar]
- Voigt, T., Fried, R., Backes, M., & Rhode, W. 2014, Adv. Data Anal. Classification, 8, 195 [CrossRef] [Google Scholar]
- Way, M. J., & Klose, C. D. 2012, PASP, 124, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, D., Nayyeri, H., Cooray, A., & Häußler, B. 2020, ApJ, 888, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J. F., & Boada, S. 2019, MNRAS, 484, 4683 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, T., Liu, Z., Huang, Q., Wang, Y., & Lin, D. 2021, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 8659 [Google Scholar]
- Yan, Z., Mead, A. J., Van Waerbeke, L., Hinshaw, G., & McCarthy, I. G. 2020, MNRAS, 499, 3445 [NASA ADS] [CrossRef] [Google Scholar]
- Yin, X., Yu, X., Sohn, K., Liu, X., & Chandraker, M. 2019, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) [Google Scholar]
- Zhang, J., Zhang, Y., & Zhao, Y. 2018a, AJ, 155, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Z., Li, M., & Yu, J. 2018b, in SIGGRAPH Asia 2018 Technical Briefs, SA ’18 (New York, NY, USA: Association for Computing Machinery) [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Paradigms of the baseline method and our methods for correcting zspec-dependent residuals and mode collapse. The baseline method does not explicitly specify a representation and produces single-channel output estimates that only require one-hot labels for training. In contrast, our methods split representation learning and classification into three consecutive steps and produces multichannel output estimates. The labels for training the model match the dimensions of the output estimates, and they are softened and readjusted in step 3 according to the biases. The dashed arrows indicate that the part of the model prior to the representation is fixed in steps 2 and 3. |
| In the text | |
 |
Fig. 2 Graphic illustration of the CNN models for the baseline method and our methods for correcting zspec-dependent residuals and mode collapse. We use the network architecture adopted by Pasquet et al. (2019), in which multiscale inception modules (Szegedy et al. 2015) are used and the galactic reddening of galaxies is input in addition to images. The representation is obtained at the penultimate fully connected layer. The classification module is elaborated in the red rectangle: while the baseline method takes a final fully connected layer as a single-channel output for redshift prediction, our methods take parallel fully connected layers as multiple output channels to predict redshifts that also incorporate the magnitude information (discussed in Sect. 3.2.1). The labels n and m indicate the dimensions of the output layers, whose values are given in Table 1 for the SDSS data and the CFHTLS data. ≥ n means that additional bins are appended to the redshift outputs in step 3. |
| In the text | |
 |
Fig. 3 Correspondence of the input parameter space and the target output space represented by the multichannel output unit. The input space is divided into a grid with 2m − 1 rows covering different magnitudes and n columns covering different redshifts. The output unit is comprised of one magnitude output with m bins and m corresponding redshift outputs. Each redshift output has n bins corresponding to the input space before being extended in step 3. The values of n and m for the SDSS data and the CFHTLS data are given in Table 1. The shaded green boxes indicate the extended redshift intervals. Each of the rows in the input space is connected to one or two redshift outputs alternately. Equivalently, each redshift output responds to three adjacent input rows (or two rows at the edges). As an example, in response to a data instance drawn from the input space indicated by the red star, two bins are activated in the target magnitude output (shown in dark red) while the other bins remain null (shown in light blue). One bin is activated in each of the two corresponding redshift outputs (before using readjusted soft labels in step 3), while the remaining redshift outputs have a flat response over all bins (shown in light red). |
| In the text | |
 |
Fig. 4 Two-dimensional distributions (zspec, r-band magnitude) for the SDSS dataset before and after balancing the number density. The color indicates the relative number density in logarithmic scale. As shown, the data cannot be perfectly balanced due to the existence of underpopulated classes. |
| In the text | |
 |
Fig. 5 Determining the means of soft labels. zQ, z, and z* stand for the spectroscopic redshift of a given galaxy, the mean of its skewed scattering profile, and the determined mean of its soft label, respectively, also indicated by the vertical dotted blue, green, and red lines. The skewed scattering profile is assumed to be a bin-wise product of the initial Gaussian profile and the shape of the subsample distribution in the given magnitude bin. Ideally, if the subsample distribution is perfectly balanced (top row), the product profile remains a Gaussian function such that the mean Z of the profile and the mean z* of the soft label align with the spectroscopic redshift value z0. On the other hand, if the subsam-ple distribution has underpopulated regions (bottom row), the product profile is affected by nonflatness and deviates from a Gaussian function (i.e., it is skewed; shown as the green curve), which produces a shifted mean Z. The mean z* of the soft label in this case should be determined according to Eq. (8). |
| In the text | |
 |
Fig. 6 Main results of correcting zspec-dependent residuals and mode collapse with the SDSS data and the network Net_P. Upper panel: mean residuals as a function of spectroscopic redshift for the baseline method and steps 1-3 of our methods with the SDSS data and the network Net_P. The corresponding < Δz > − zspec piecewise linear fits (Eq. (9)) are shown as dashed lines with the same colors. Zero residual is indicated by the horizontal dashed black line. Middle panel: sample distributions of the estimated photometric and spectroscopic redshift in different cases. Lower left panel: σMAD (Eq. (11)) as a function of r-band magnitude. Lower right panel: total variation distance between the zphoto and zspec sample distributions (Eq. (10)) as a function of the slope of the < Δz > − zspec piecewise linear fit (Eq. (9)) in the high-redshift interval. The shaded area shows the total variation distance with the 1 a uncertainty for the simulated zphoto sample distribution for the baseline method that is expected to have no mode collapse. Step 3\2 denotes a case in which step 3 is applied without step 2. Step 3a denotes a variant case of step 3 in which hard labels are used instead of soft labels, but the means are adjusted. Step 3b denotes a case in which soft labels are used but the means are not adjusted. |
| In the text | |
 |
Fig. 7 Same as Fig. 6, but with the CFHTLS-WIDE data. |
| In the text | |
 |
Fig. 8 Predicted photometric redshifts as a function of spectroscopic redshift, color-coded with number density. The baseline method and steps 1-3 of our methods are compared using the SDSS data and the network Net_P. The dashed red lines indicate the boundaries (zphoto − zspec)/(1 + zspec) = ±0.05 for outliers defined for the SDSS data as in Pasquet et al. (2019) and Treyer et al. (in prep.). |
| In the text | |
 |
Fig. 9 Main results of correcting zphoto-dependent residuals with the SDSS data and the network Net_P. Upper panels: spectroscopic redshift and r-band magnitude distributions for the SDSS training data and the test data. In addition to the original test sample, two other test samples are constructed that are biased toward medium redshifts (zspec ~ 0.12) or high magnitudes (r ~ 17.5). Middle panels: mean residuals as a function of spectroscopic redshift for the baseline method and step 3 with the three test samples and the network Net_P. The results from step 4 are also plotted in light purple for comparison. Steps 1-3 are applied in advance of the calibration by step 4. Lower panels: mean residuals as a function of photometric redshift for the baseline method and step 4 with the three test samples and the network Net_P. The results from step 3 are also plotted in light red for comparison. |
| In the text | |
 |
Fig. 10 Same as Fig. 9, but that the number density within 0.08 < zspec < 0.12 for the training sample is reduced by 90%. |
| In the text | |
 |
Fig. 11 Mean redshift calibrations with the network Net_P. Upper panels: residuals of mean redshifts (different from mean residuals) in each zphoto tomographic bin for the baseline method and step 4 of our methods using the network Net_P with the SDSS data, the CFHTLS-DEEP data, and the CFHTLS-WIDE data. A magnitude cut r < 24 is applied to the CFHTLS-DEEP data to create a restricted sample. The shaded areas indicate the requirement for the accuracy of photometric redshift estimation (i.e., |Δz| < 0.002). Steps 1-3 are applied in advance of the calibration by step 4. Middle panels: same as the upper panels, but residuals of mean redshifts are estimated in r-band magnitude bins. Lower panels: 1-Wasserstein distance between the zphoto and zspec sample distributions (Eq. (13)) as a function of r-band magnitude. |
| In the text | |
 |
Fig. 12 Mean residuals as a function of spectroscopic or photometric redshift with the SDSS data and the CFHTLS-WIDE data. The results from steps 3 and 4 of our methods with the network Net_P are compared with those produced by data-driven methods from Pasquet et al. (2019), Beck et al. (2016), Treyer et al. (in prep.), and SED fitting using the Le Phare code (Arnouts et al. 1999; Ilbert et al. 2006). The results from step 3 (step 4) are plotted in light red (purple) for comparison in the lower (upper) panels. Steps 1-3 are applied in advance of the calibration by step 4. For consistency with our test samples, 103 305 SdSs galaxies and 10000 CFHTLS-WIDE galaxies in the given redshift ranges are selected from these studies for the plot. We note that we take zmode (i.e., the redshift at the peak probability) as the point estimates of photometric redshifts, whereas Pasquet et al. (2019) took zmean (i.e., the probability-weighted mean redshift) and Treyer et al. (in prep.) took zmed¡an (i.e., the median redshift drawn from the probability distribution). |
| In the text | |
 |
Fig. B.1 Comparison of three choices of point estimates (zmode, zmean, and zmedian) for the baseline method and steps 1 – 4 of our methods using the SDSS data and the network Net_P. All data points are color-coded with zspec • As the three point estimates for each data instance are shifted by the same amount in step 4, the differences between any two point estimates remain unchanged as in step 3. |
| In the text | |
 |
Fig. C.1 Comparison between the actual and the expected < Δz > − zspec curves for the SDSS data and the CFHTLS-WIDE data, respectively. The actual curves are derived with the subsets of training data from step 2 (represented by the yellow lines). The expected curves are determined by the means of the scattering profiles as in Eq. 8, but the variances are replaced with the estimated quadratic error curves and rescaled by a set of different factors k (represented by the dotted lines). |
| In the text | |
 |
Fig. D.1 σMAD (Eq. 11), the slopes of the < Δz > − zSPec piecewise linear fit (Eq. 9) and the total variation distance between the zPh0t0 and zSPec sample distributions (Eq. 10) as a function of the balancing threshold that defines the nearly balanced training subset for steps 2 and 3 of our methods. As the threshold approaches the maximum number density (2,626 in this case), the results from step 2 are expected to converge to those from step 1, and those from step 3 are expected to converge to those from step 3\2 in which step 2 is skipped. The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. We compare the methods using the SDSS data and the network Net_P. |
| In the text | |
 |
Fig. D.2 Same as Fig. D.1, but with the CFHTLS-WIDE data. |
| In the text | |
 |
Fig. D.3 σMAD (Eq. 11), the slopes of the < Δz > - zspec piecewise linear fit (Eq. 9) and the total variation distance between the zphoto and zspec sample distributions (Eq. 10) as a function of the number of bins in the output redshift density estimate (before being extended in step 3). The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. The baseline method and steps 1 - 3 of our methods are compared using the SDSS data and the network Net_P. |
| In the text | |
 |
Fig. D.4 σMAD (Eq. 11), the slopes of the < Az > - zspec piecewise linear fit (Eq. 9) and the total variation distance between the zphoto and zspec sample distributions (Eq. 10) as a function of the number of training iterations conducted for the baseline method and step 1 of our methods. The number of iterations for steps 2 and 3 remains the same as in the main experiments. The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. We compare the methods using the SDSS data and the network Net_P. |
| In the text | |
 |
Fig. D.5 Predicted photometric redshifts as a function of spectroscopic redshift color-coded with number density for the baseline method. We compare cases with different numbers of iterations in training using the SDSS data and and the network Net_P. The dashed red lines indicate the boundaries (zphoto - zspec+ zspec) = ±0.05 for outliers defined for the SDSS data as in Pasquet et al. (2019) and Treyer et al. (in prep.). |
| In the text | |
 |
Fig. D.6 Mean residuals estimated in coarse bins as a function of spec-troscopic or estimated photometric redshift for the baseline method. We compare cases with different numbers of iterations in training using the SDSS data and and the network Net_P. The horizontal dashed black lines indicate zero residual. |
| In the text | |
 |
Fig. D.7 σMAD (Eq. 11), the slopes of the < Az > – zSPec piecewise linear fit (Eq. 9) and the total variation distance between the zPh0t0 and zSPec sample distributions (Eq. 10) as a function of the total number of instances in the training sample for the baseline method and step 1 of our methods. The nearly balanced training subset in steps 2 and 3 is constructed using the original training set without reducing the sample size. The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. We compare the methods using the SDSS data and the network Net_P. |
| In the text | |
 |
Fig. D.8 σMAD (Eq. 11), the slopes of the < Δz > – zspec piecewise linear fit (Eq. 9) and the total variation distance between the zphoto and zspec sample distributions (Eq. 10) as a function of the dispersion of Gaussian errors az introduced to the redshift labels for the training data used for the baseline method and step 1 of our methods. The Gaussian errors are not applied to the training data in steps 2 and 3, or the test data. The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. We compare the methods using the SDSS data and the network Net_P. |
| In the text | |
 |
Fig. D.9 σMAD (Eq. 11), the slopes of the < Δz > – zspec piecewise linear fit (Eq. 9) and the total variation distance between the zphoto and zspec sample distributions (Eq. 10) as a function of different network architectures with increasing complexity (defined in the text). The dotted curves show the total variation distances for the simulated zphoto sample distributions that are expected to have no mode collapse. The baseline method and steps 1 - 3 of our methods are compared using the SDSS data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



