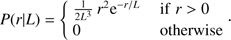| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201833824 | |
| Published online | 30 October 2018 | |
Chemical analysis of very metal-poor turn-off stars from SDSS-DR12⋆
1
GEPI, Observatoire de Paris, PSL Research University, CNRS, 61 Avenue de l’Observatoire, 75014 Paris, France
e-mail patrick.francois@obspm.fr
2
UPJV, Université de Picardie Jules Verne, 33 rue St Leu, 80080 Amiens, France
3
GEPI, Observatoire de Paris, PSL Research University, CNRS, Place Jules Janssen, 92190 Meudon, France
4
Department of Engineering and Applied Sciences, Sophia University, Chiyoda-ku, Tokyo 102-8554, Japan
5
iTHEMS Research Group, RIKEN, Wako, Saitama 351-0198, Japan
6
Instituto de Astrofìsica de Canarias, Vía Láctea, 38205 La Laguna, Tenerife, Spain
7
Universidad de La Laguna, Departamento de Astrofísica, 38206 La Laguna, Tenerife, Spain
8
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei Muenchen, Germany
9
National Observatory of Japan, Mitaka, Tokyo, Japan
10
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
11
Dipartimento di Fisica e Astronomia, Universitá di Firenze, Via G. Sansone 1, Sesto Fiorentino, Italy
12
INAF/Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, Firenze, Italy
Received:
11
July
2018
Accepted:
13
August
2018
Context. The most metal-poor stars are the relics of the early chemical evolution of the Galaxy. Their chemical composition is an important tool to constrain the nucleosynthesis in the first generation of stars. The aim is to observe a sample of extremely metal-poor star (EMP stars) candidates selected from the Sloan Digital Sky Survey Data Release 12 (SDSS DR12) and determine their chemical composition.
Aims. We obtain medium resolution spectra of a sample of six stars using the X-shooter spectrograph at the Very Large Telescope (VLT) and we used ATLAS models to compute the abundances.
Methods. Five stars of the sample have a metallicity [Fe/H] between −2.5 dex and −3.2 dex. We confirm the recent discovery of SDSS J002314.00+030758.0 as a star with an extremely low [Fe/H] ratio. Assuming the α-enhancement [Ca/Fe] = +0.4 dex, we obtain [Fe/H] = −6.1 dex.
Results. We could also determine its magnesium abundance and found that this star exhibits a very high ratio [Mg/Fe]≤ +3.60 dex assuming [Fe/H] = −6.13 dex. We determined the carbon abundance and found A(C) = 6.4 dex. From this carbon abundance, this stars belongs to the lower band of the A(C)–[Fe/H] diagram.
Key words: stars: Population II / Galaxy: abundances / Galaxy: halo
© ESO 2018
1. Introduction
The lambda cold dark matter (Λ-CDM) cosmological model has received an impressive confirmation from the Wilkinson Microwave Anisotropy Probe (WMAP) and Planck satellites (Planck Collaboration Int. XLVII 2016; and references therein) over in recent years. The average redshift at which reionization occurs is found to lie between z = 7.8 and 8.8, depending on the model of reionization adopted. It may be that all the first stars were massive or exceedingly massive, with a very short lifetime (Bromm et al. 2009), although other more recent numerical simulations suggest that the distribution of possible masses of the first stars may be much broader than previously believed (Hirano et al. 2015), and may even extend down to solar mass or below (Greif et al. 2011) leading to stars which are still alive and observable today. Until recently, the deepest survey searching for metal-poor stars was the Hamburg-ESO survey (HES), which reached V = 16 (Christlieb et al. 2008), although the first aim of this survey was the search for distant quasars. Thanks to the Hamburg-ESO survey, several stars of extremely low iron content have been discovered. However, these stars are extremely rich in C and O, so that their overall metal content is in fact comparable to the metal content of globular cluster stars, with [M/H] ≃ −2.3 dex.
Major progress with respect to HES can be found in an exploration of the data of the Sloan Digital Sky Survey (SDSS). Ludwig et al. (2008) have developed an analysis tool that allows us to estimate the metallicity of turn-off (TO) stars from the low resolution SDSS spectra. This tool can be used to derive the metallicity and to select extremely metalpoor candidates using the strongest lines (calcium H&K) in the spectrum used as a proxy for the metallicity. It is, however, not yet possible to firmly evaluate the metallicity precisely below [Fe/H] = −3.0 dex, because at very low metallicity the metallic lines become almost impossible to detect at the resolution of the SDSS spectra (Aoki et al. 2013). The only solution to alleviate this degeneracy is to observe these candidates at a higher resolution to confirm their metallicities. The SDSS-based metallicities found by the method of Ludwig et al. (2008) are essentially confirmed by the analysis at higher resolution. This method has been very successful and has led to a series of papers that have already been published (Caffau et al. 2011a,b, 2014, 2016; Caffau & Bonifacio 2012; Bonifacio et al. 2015, 2018). The most metal-poor stars are formed out of gas that has been very likely enriched by the ejecta of a single or a few supernovae. From the determination of the chemical composition of these stars, we can derive important constraints on the nucleosynthesis in the first generation of stars who enrich the primordial gas and on the chemical inhomogeneites during the early evolution of our Galaxy. These abundance determinations can also be used to constrain the scenario of formation of the first low mass stars (Caffau et al. 2011a).
From the recent analysis of SDSS DR12 data, we have detected new extremely metal-poor candidates that have never been observed at high resolution. In this article, we report the detailed analysis of six new extremely metal-poor candidates observed with the X-shooter spectrograph installed on Kueyen at the ESO Very Large Telescope (VLT) on Cerro Paranal in Chile. Similar observations have been conducted for a different set of stars from the northern hemisphere at the Subaru telescope using the High Dispersion Spectrograph (HDS) in the framework of a French-Japanese collaboration.
2. Observations
The observations were performed in service mode with Kueyen (VLT Unit 2) and the high-efficiency spectrograph X-shooter (D’Odorico et al. 2006; Vernet et al. 2011). The log book of the observations is reported in Table 1. The X-shooter spectra range from 300 nm to 2400 nm and are registered by three detectors. The observations have been performed in staring mode with 1×1 binning and a slit width of 0.8″ for the ultra-violet (UVB) arm and and 0.9″ for the visible (VIS) arm. This corresponds to a resolving power of R = 6190 in the UVB arm and R = 7410 in the VIS arm. The stellar light is divided between the three arms by X-shooter. We analysed here only the UVB and VIS spectra. The stars we observed are faint and have most of their flux in the blue part of the spectrum, so that the signal-to-noise ratio (S/N) of the infra-red spectra is too low to allow the analysis. The spectra were reduced using the X-shooter pipeline (Goldoni et al. 2006), which performs the bias and background subtraction, cosmic ray-hit removal (Van Dokkum 2001), sky subtraction (Kelson 2003), flat-fielding, order extraction, and merging.
Observation log.
Figure 1 shows the spectra of some stars of the sample centred on the magnesium triplet. The spectra shown on this figure correspond to the stars for which magnesium abundances have been determined.
 |
Fig. 1. X-shooter spectra of the stars centred on the magnesium triplet. The continuum of the three spectra located in the lower part of the plot has been shifted downward for clarity. The vertical lines indicate the location of the magnesium absorption lines. |
3. Stellar parameters
The stellar parameters have been derived taking into account the SDSS photometry. The effective temperatures in Table 2 have been computed by Caffau & Bonifacio (2013a). The effective temperature has been derived from the photometry, using the (g − z)0 colour and the calibration described in Ludwig et al. (2008) taking into account the reddening according to the Schlegel et al. (1998) extinction maps and corrected as in Bonifacio et al. (2000). We also determine the spectroscopic temperatures by fitting the H line. For the first four stars of Table 2, we found slightly lower temperatures (≃200 K) than the photometric temperatures. For the two remaining stars, SDSS J003730.31+245750.6 and SDSS J162049.87+322323.2, it was difficult to obtain a reliable estimate of the temperature due to the low S/N of the spectra.
Adopted stellar parameters for the list of targets.
The Gaia parallaxes (Gaia Collaboration 2018; Arenou et al. 2018) for our stars are very imprecise; one star has a negative parallax and the others all have a relative error Ȉ50% or larger (up to 2100%). In order to get some insight into the luminosities of our stars, we used the distance estimates of Bailer-Jones et al. (2018).
Bailer-Jones et al. (2018) use a probabilistic approach to distance estimation. The first hypothesis is that the Gaia parallaxes have a Gaussian likelihood, and for each star the mean value of the distribution and its standard deviation are given in the Gaia catalogue in the columns parallax and parallax_error, respectively. To this they add a prior of an exponentially decreasing space density1, where L > 0 is a length scale (see also Bailer-Jones 2015; Astraatmadja & Bailer-Jones 2016). In the model of Bailer-Jones et al. (2018), L varies with Galactic longitude and latitude, (l, b). This amounts to making an assumption on the spatial structure of the Galaxy. In this sense these distances are biased and should not be over-interpreted. We nevertheless proceed with caution to use these distance estimates to see if they can help us discriminate between dwarfs and sub-giants. Combining the Gaussian likelihood and the prior Bailer-Jones et al. (2018) obtain a posterior probability distribution for the distance to each star. They use the mode of this distribution as their distance estimate and they define two distances, rlo and rhi, such that the probability that the true distance r lies in the interval [rlo, rhi] is 0.6827. In this sense this interval is akin to a ±1σ interval of a Gaussian distribution. However, since the posterior probability defined by Bailer-Jones et al. (2018) is asymmetric, the estimated distance is not at the centre of this interval. We use the estimated distance to compute the absolute magnitude for each star and rlo and rhi as estimates of the error on the distance and translate these to errors in estimated absolute magnitudes.
In Fig. 2, we plotted BP−RP versus the absolute G magnitude with two different hypotheses for the reddening (BP and RP are the magnitudes measured respectively by the two low resolution spectrographs, the Blue Photometer (BP) and the Red Photometer (RP) on-board the Gaia satellite). The red dots represent the stars assuming E(BP−RP) = 0 whereas the green dots represent our stars’ photometry with an extinction correction E(BP − RP) using the E(B − V) correction of the The Panoramic Survey Telescope and Rapid Response System (PanSTARRS; Chambers et al. 2016) and the conversion relations E(BP−RP) = E(B − V) + 0.07 and AG = AV = 3.1 × E(B − V) (where AG and AV are the extinction in the G and the V band) from Andrae et al. (2018). We could then compare the location of our stars with the isochrones computed by Chieffi (priv. comm.). The age has been set at t = 14 Gyr and the two metallicities are z = 2 × 10−5 and z = 2 × 10−6.
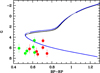 |
Fig. 2. Comparison of the location of the stars and isochrones on a G magnitude versus (BP−RP) magnitude diagram. The two isochrones on the plot have been computed for an age of 14 Gyr (black line: z = 2 × 10−5 and blue line: z = 2 × 10−6). BP−RP (BP and RP are the magnitudes measured respectively by the two low resolution spectrographs, the Blue Photometer (BP) and the Red Photometer (RP) onboard the Gaia satellite) versus the absolute G magnitude, with two different hypotheses for the reddening. The red dots represent the stars assuming E(BP − RP) = 0 whereas the green dots represent our stars’ photometry with an extinction correction E(BP−RP) using the E(B−V) correction of PanSTARRS (Chambers et al. 2016) and the conversion relations E(BP − RP) = E(B − V) + 0.07 and AG = AV = 3.1 × E(B − V) (where AG and AV are the extinction in the G and the V band) from Andrae et al. (2018). |
It is clear from Fig. 2 that all our stars are warmer than even the lowest luminosity giant stars, whatever the assumption on the reddening. We can thus safely exclude the possibility that any of them is an evolved giant. An ambiguity exists, however, between stars that are on the main sequence (MS) and sub-giant stars. Considering the isochrones shown in Fig. 2, over the colour range spanned by our stars, the mean log g of MS stars is 4.5 and that of sub-giant stars 3.7 (for Z = 10−6) or 3.8 (for Z = 10−5). The turn-off corresponds to log = 4.1. Noting that, with the distance estimates of Bailer-Jones et al. (2018) none of the stars is luminous enough to be considered a sub-giant, we make the simplifying assumption that they are all MS and assume log g = 4.5. This assumption has no impact on the derived abundances of the neutral species, it affects only the singly ionized species.
We attribute the fact that the stars do not fall neatly on any of the isochrones to the limitation of the distance estimates of Bailer-Jones et al. (2018). We consider it likely that all the stars are MS, but we cannot robustly exclude the possibility that any of them is a TO or an early sub-giant. To understand what would be the implication of this, we derived abundances also assuming a lower gravity of log g = 4.0. Taken at face value, the luminosities derived from the distance estimates of Bailer-Jones et al. (2018) would imply higher surface gravities such as log g = 5.0 or even 5.5. However, since no isochrone predicts such high gravities for warm stars, like those in the present sample, we discard this possibility.
4. Analysis
The determination of the abundances has been done line by line using a grid of synthetic spectra, computed with the local thermodynamical equilibrium (LTE) spectral synthesis code turbospectrum (Alvarez & Plez 1998; Plez 2012) and based on ATLAS models. From a set of well-selected absorption lines, the code computes the abundance using fitting techniques. The best-fit profile is obtained by interpolating in a series of pre-calculated spectra. The synthetic spectra have been computed with ATLAS9 models. However, for SDSS J0023+0307, which has a very peculiar chemical composition, we relied on ATLAS12 models that allow us to compute models with a nonstandard chemical composition mix. The procedure to derive the chemical composition is described by Caffau et al. (2013b) and has been used in several other papers on the determination of the chemical composition of extremely metal-poor stars (Bonifacio et al. 2015; Caffau et al. 2016). We adopted the solar abundances of Caffau et al. (2011b) for C and Fe and the abundances of Lodders et al. (2009) for the other elements.
5. Errors
Table 3 lists the computed errors in the elemental abundances ratios due to typical uncertainties in the stellar parameters. The errors were estimated varying Teff by ±100 K, log g by ±0.5 dex, and vt by ±0.5 dex in the model atmosphere of SDSS J232854.99+023924.5; other stars give similar results. In this star, we could measure the Mg, Si, Ca, Ba, and Sr abundances. The main uncertainty comes from the error in the placement of the continuum when the synthetic line profiles are matched to the observed spectra. This error is of the order of 0.2–0.5 depending on the species under consideration, the largest value being for the neutron capture elements. When several lines are available, the typical line to line scatter for a given elements is 0.1–0.2 dex. We can also see from Table 3 that assuming a lower gravity for the stars (i.e. log g = 4.0 instead of log g = 4.5 dex) shifts the abundances by at most 0.2 dex.
Estimated errors in the element abundance ratios [X/Fe] for the star SDSS J232854.99+023924.5.
6. Results and discussion
The abundance results for the five less metal-poor stars have been gathered in Tables 4 and 5, and the results for SDSS J002314.00+030758.0 are reported in the next section.
Fe abundances.
Abundances of and neutron-capture elements.
In Fig. 3, we plotted the abundance ratios [Mg/Fe] and [Ca/Fe] as a function of [Fe/H] for our sample of stars using the solar abundances from Lodders et al. (2009).
 |
Fig. 3. [Mg/Fe] and [Ca/Fe] vs. [Fe/H]. Red circles: this paper; Blue circle: BPS CS 22949−037Depagne et al. (2002), green circle: SMSS J031300−670839.3 (Keller et al. 2014); blue diamond: SDSS J1313−0019 (Frebel et al. 2015); blue square: HE 1327−2329 (Aoki et al. 2006); blue triangle: HE 0107−5240 (Christlieb et al. 2004); small grey circle: evolved stars from Roederer et al. (2014); small orange circles: main sequence stars from Roederer et al. (2014); black triangles: data from Yong et al. (2013). |
It is interesting to note that three stars of the sample are calcium poor. As their [Mg/Fe] abundance ratios appear also rather low, it is very likely that the origin of the low [Ca/Fe] comes from the [Fe/H] abundance determination, which is difficult on these medium resolution and rather low S/N spectra.
We adopted the [Fe/H] from Aguado et al. (2018) for SDSS J002314.00+030758.0. As their measurements are based on spectra with much higher S/N (≥170 per pixel at 450 nm) than our spectra, although of lower resolution, the upper limit [Fe/H]≤−4.0 dex we obtained is likely to be much higher than the true [Fe/H] that this star may have. Assuming an [α/Fe] overabundance of 0.4 dex, a value generally found in halo stars, we derive an iron abundance of [Fe/H] = −6.13 dex. We will consider during the discussion the possibility that this star may have a much higher iron abundance, with [Fe/H] = −5 dex, a factor of 40 larger than the upper limit derived by Aguado et al. (2018). We have added in this plot the results for evolved and unevolved stars from Roederer et al. (2014) and the results from Yong et al. (2013). We also include the stars CS 22949−037 (Depagne et al. 2002), HE 0107−5240 (Christlieb et al. 2004), HE 1327−2329 (Aoki et al. 2006), SDSS J1313−0019 (Frebel et al. 2015), and SMSS J031300−670839.3 (Keller et al. 2014). We could measure the magnesium abundance in four stars of our sample. The calcium was detected and measured in five stars. We can see that the star SDSS J002314.00+030758.0 stands out, revealing very high overabundances of Mg and Ca sharing this peculiarity with Keller’s star (SMSS J031300−670839.3) and to a lesser extent Depagne’s star (CS 22949−037). We could also measure the abundance of Si in SDSS J002314.00+030758.0 and found A(Si) = 4.2 dex, leading to [Si/Fe] = 3.25 dex for an iron abundance [Fe/H] = −6.6 dex and [Si/Fe] = 2.75 dex for an iron abundance [Fe/H] = −6.1 dex. In their star, Keller et al. (2014) derived an upper limit of A(Si)≤4.3 dex. The other stars of our sample have a moderate to solar [Mg/Fe] ratio. In SDSS J232854.99+023924.5, we could measure the barium abundance. With [Ba/Fe] = 1.58 dex, this star could be classified as a CEMP-s star. Unfortunately, strontium could not be measured. We could only derive an upper limit of [Sr/Fe]≤0.86 dex.
7. SDSS J002314.00+030758.0
The abundance results for the star SDSS J002314.00+030758.0 are listed in Table 6. The assumed gravity is in agreement with the one adopted by Aguado et al. (2018).
Abundances measured in SDSS J002314.00+030758.0
In Fig. 4, we plotted the computed spectrum in the region of the G-band carbon molecular band with different assumptions on the carbon abundance for the star. The best fit is found for A(C) = 6.4 dex. This result is in good agreement with the upper limit A(C) = 6.3 dex found by Aguado et al. (2018). In Fig. 5, we show our stars in the A(C)–[Fe/H] diagram (Spite et al. 2013), together with data from the literature. When we apply the three-dimensional (3D) correction from Gallagher et al. (2016) to this value, we find that it is further reduced by −0.45 dex so that A(C) = 6.05 dex. It is interesting to note the star SDSS J002314.00+030758.0 is located in a region with CEMP stars that have a rather low carbon abundance of about A(C) = 6.5 dex. The bimodal distribution of CEMP stars was first suggested by Spite et al. (2013) and later supported by the extended study of Bonifacio et al. (2015) who interpreted the low-carbon band stars as being the genuine fossil records of a gas cloud that has been enriched by a faint supernova providing carbon and the lighter elements. Alternatively, Yoon et al. (2016) proposed a separation among the CEMP stars along three regions instead of the two bands system from Spite et al. (2013).
 |
Fig. 4. Synthetic spectra of SDSS J002314.00+030758.0 in the region of the CH G-band (continuous lines) superimposed on the observed spectrum (small crosses). The theoretical spectra are represented as blue lines correspond to carbon abundances A(C) = 6.0, 6.6 and 6.9 dex. The red line represent the best fit to the observed spectrum and corresponds to a carbon abundance A(C) = 6.4 dex. |
 |
Fig. 5. Carbon abundances A(C) of CEMP stars as a function of [Fe/H]. Large open black squares represent our results. The other symbols are literature data. Details can be found in Bonifacio et al. (2015). |
The difference between these two classifications comes from the definition of the C-rich stars: [C/Fe] = +0.7 in Yoon et al. (2016) compared to [C/Fe] = +1.0 in the present paper. Our choice of the definition of the C-rich stars is based on the fact that, in the group of normal (not C-rich) stars, [C/Fe] = +0.45 ± 0.15 dex (Bonifacio et al. 2009). The normal metal-poor stars are already C-rich as they are generally alpha-rich. We thus suspect that the group II of Yoon et al. (2016) is only the tail of the distribution of the normal metal-poor stars. In this classification system, SDSS J002314.00+030758.0 would belong to their group III of CEMP stars.
SDSS J002314.00+030758.0 also shares the same abundance anomalies as the more metal-rich star CS 22949−037 (Depagne et al. 2002). This star is a CEMP-no star with [Fe/H] ≃ −4.00 dex, [Mg/Fe] = +1.58 dex, and [Ca/Fe] = +0.35 dex, leading to [Mg/Ca] = 1.23 dex, a remarkable overabundance shared with SDSS J002314.00+030758.0 and SMSS J031300−670839.3, in which we found a large [Mg/Ca] ratio close to +3.2 dex. Adopting [Fe/H] = −6.6 dex, we found [Mg/Fe] = 4.16 dex and [Ca/Fe] = 0.87 dex. With [Fe/H] = −5.0 dex, we obtain [Mg/Fe] = 2.56 dex and [Ca/Fe] = −0.73 dex. Such a low [Ca/Fe] has never been found in a star with [Fe/H]≤−4.0 dex. If this star has indeed [Fe/H]≥−5.0 dex, its chemical composition would be unique. On the other hand, if we assume a [Ca/Fe] representative of the halo population ([Ca/Fe] = +0.4 dex), we find [Mg/Fe] = +3.69 dex close to the value found by Keller et al. (2014) for SMSS J031300−670839.3. New high quality spectra will be necessary to better constrain the [Fe/H] and refine the value found by Aguado et al. (2018).
A similar high [Mg/Fe] ratio is also found by Keller et al. (2014) who measured a [Mg/Ca] ratio of +2.9 dex in SMSS J031300−670839.3, and by Aoki et al. (2006) who measured a [Mg/Ca] ratio of +0.90 dex in HE 1327−2326. These high [Mg/Ca] ratio stars are very peculiar and rare and so far limited to the most metal-poor stars, although this behaviour is not shared by all the stars with extremely low metallicity. Indeed, HE 0107−5240 and SDSS J1313−0019 have [Fe/H] below −5.0 dex and a [Mg/Ca] ratio corresponding closely to a solar ratio as measured in the vast majority of the stars in the metallicity range ≃−2.0 to ≃−4.0 dex.
We gather in Table 7 the abundance ratios found for our sample. For SDSS J002314.00+030758.0, we computed the abundance ratios with two assumptions for the iron abundance, the first with [Fe/H] = −6.6 dex assuming the upper limit from Aguado et al. (2018) and the second with [Fe/H] = −6.13 with [Fe/H] deduced from the calcium abundance and assuming [Ca/Fe] = +0.4 dex.
[X/Fe] abundance ratios for and neutron-capture elements.
In order to explain the chemical composition anomalies found in these CEMP-no metal-poor stars with a high enrichment in -elements, several astrophysical processes have been invoked. Faint supernovae models have been developed (Umeda & Nomoto 2003, 2005) more recently by Nomoto et al. (2013) and Tominaga et al. (2014) to explain how a supernova, without sufficient explosion energy to create the heavy elements, releases ejecta enriched only in C, N, O, and light metals like Na, Al, Mg, and Ca. Alternatively, Hirschi (2007) and Meynet et al. (2010) suggested that rapidly rotating stars, known as spinstars, could produce abundance distributions similar to those found in the CEMP-no stars with a high level of enrichment in light metals. The wide range in [Mg/Ca] ratio found in the most metalpoor stars favours the existence of a diversity of nucleosynthesis conditions where magnesium can be produced in much larger quantities than calcium. In conclusion, this is consistent with an environment of formation for CEMP-no stars polluted only by zero-metallicity stars (e.g. de Bennassuti et al. 2017; Bonifacio et al. 2015), which most likely had different masses and possibly different explosion energies that could produce various amount of Mg.
8. Conclusions
In this article, we reported the chemical analysis of six new extremely metal-poor candidates observed with the X-shooter spectrograph. We determined the abundances of some elements (C, Mg, Ca, Si, Sr, and Ba) in the majority of these stars. Five stars of the sample show abundance ratios that are typical of metal-poor stars in the metallicity range −3.5 dex≤[Fe/H]≤−2.0 dex. The dwarf star SDSS J002314.00+030758.0 appears to be extremely iron-poor. We found an upper limit of [Fe/H] < −4.00 dex, a value which is in agreement with the even stronger upper limit computed by Aguado et al. (2018) with [Fe/H] < −6.60 dex. Our low S/N does not allow us to give a more constraining [Fe/H] determination. Assuming a [Ca/Fe] representative of the halo population ([Ca/Fe] = +0.4 dex), we obtain [Fe/H] = −6.1 dex. We could determine the carbon abundance using the G band. We obtained A(C) = 6.4 dex (6.05 in 3D), which places this star in the lower band of the A(C)–[Fe/H] diagram (Spite et al. 2013; Bonifacio et al. 2015) confirming the existence of the lower carbon band in the most metal-poor stars. Assuming the lower limit [Fe/H] = −6.6 dex from Aguado et al. (2018) as a conservative estimate of its iron content, the [C/Fe] ratio would give ≃+4.6 dex. Assuming [Fe/H] = −5 dex, the [C/Fe] remains extremely high with a value of [C/Fe] = +3.0 dex. Given the large amount of carbon present in this star, its total metallicity lies in the range of the metallicities found in Galactic globular clusters.
Adopting the same lower limit [Fe/H] = −6.6 dex from Aguado et al. (2018), we found that SDSS J0023+0307 has remarkably high magnesium and calcium abundances, sharing this peculiarity with CS 22949−037 (Depagne et al. 2002), SMSS J031300−670839.3 (Keller et al. 2014), and HE 1327−2326 (Aoki et al. 2006). These four stars have also a high [Mg/Ca] ratio (>0.90 dex) in contrast with the other extremely iron-poor stars HE 0107−5240 (Christlieb et al. 2004) and SDSS J1313−0019 (Frebel et al. 2015), suggesting different channels for the enrichment of the gas that formed most metal-poor stars we observe today.
Acknowledgments
This work was supported by JSPS and CNRS under the Japan-France Research Cooperative Program (CNRS PRC No 1363), the JSPS Grants-in-Aid for Scientific Research (26400232, 26400237), and the RIKEN iTHEMS Project. P. F. acknowledges support by the Conseil Scientifique de l’Observatoire de Paris. S. S. acknowledges support by the Italian Ministry of Education, University, and Research (MIUR) through a Rita Levi Montalcini Fellowship. AJG acknowledges the Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject A5) of the German Research Foundation (DFG). In memoriam to our dear colleague Yuhri Ishimaru (1967–2017), who was member of this collaboration.
References
- Aguado, D., Allende Prieto, C., Gonzales Hernandez, J., & Rebolo, R. 2018, ApJ, 854, 34 [Google Scholar]
- Astraatmadja, T. L., & Bailer-Jones, C. A. L. 2016, ApJ, 832, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Alvarez, R., & Plez, B. 1998, A&A, 330, 1109 [NASA ADS] [Google Scholar]
- Andrae, R., Fouesneau, M., Creeevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aoki, W., Christlieb, N., Norris, J. E., et al. 2006, ApJ, 639, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Beers, T. C., Lee, Y. S., et al. 2013, AJ, 145, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Arenou, F., Luri, X., & Babusiaux, C., et al. 2018, A&A, 616, A17 [Google Scholar]
- Bailer-Jones, C. A. L. 2015, PASP, 127, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifacio, P., Monai, S., & Beers, T. C. 2000, AJ, 120, 2065 [NASA ADS] [CrossRef] [Google Scholar]
- Bonifacio, P., Spite, M., & Cayrel, R. 2009, A&A, 501, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonifacio, P., Sbordone, L., Caffau, E., et al. 2012, A&A, 542, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonifacio, P., Caffau, E., Spite, M., et al. 2015, A&A, 579, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonifacio, P., Caffau, E., Spite, M., et al. 2018, A&A, 612, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bromm, V., Yoshida, N., Hernquist, L., & McKee, C. F. 2009, Nature, 459, 49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Caffau, E., Bonifacio, P., François, P., et al. 2011a, Nature, 477, 67 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., Freytag, B., & Bonifacio, P. 2011b, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Bonifacio, P., François, P., et al. 2012, A&A, 542, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Bonifacio, P., François, P., et al. 2013a, A&A, 560, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Bonifacio, P., Sbordone, L., et al. 2013b, A&A, 560, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Sbordone, L., Bonifacio, P., et al. 2014, Mem. Soc. Astron. It., 85, 222 [NASA ADS] [Google Scholar]
- Caffau, E., Bonifacio, P., Spite, M., et al. 2016, A&A, 595, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, K. C., Magnier, E. A., & Metcalfe, N. 2016, ArXiv e-prints [arXiv:1612.05560] [Google Scholar]
- Christlieb, N., Gustaffson, B., Barklem, P., et al. 2004, ApJ, 603, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Christlieb, N., Schorck, T., Frebel, A., et al. 2008, A&A, 484, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Bennassuti, M., Salvadori, S., Schneider, R., Valiante, R., & Omukai, K. 2017, MNRAS, 465, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Depagne, E., Hill, V., Spite, M., et al. 2002, A&A, 390, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Odorico, S., Dekker, H., Mazzoleni, R., et al. 2006, SPIE, 6269, 33 [NASA ADS] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Frebel, A., Chiti, A., Ji, A., Jacobson, H., & Placco, V. 2015, A&A, 810, L27 [Google Scholar]
- Gallagher, A. J., Caffau, E., Bonifacio, P., et al. 2016, A&A, 593, 48 [Google Scholar]
- Goldoni, P., Royer, F., François, P., et al. 2006, SPIE, 6269, 2 [Google Scholar]
- Greif, T. H., Springel, V., White, S. D. M., et al. 2011, ApJ, 737, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Hirano, S., Hosokawa, T., Yoshida, N., Omukai, K., & Yorke, H. W. 2015, MNRAS, 448, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschi, R. 2007, A&A, 461, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keller, S. C., Bessel, M., Frebel, A., et al. 2014, Nature, 506, 403 [Google Scholar]
- Kelson, D. 2003, PASP, 115, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., Plame, H., & Gail, H. P. 2009, in Solar System, ed. J. E. Trümper, Landolt-Börnstein – Group VI Astronomy and Astrophysics Numerical Data and Functional Relationships in Science and Technology, 4B, 4.4, 44 [Google Scholar]
- Ludwig, H., Bonifacio, P., Caffau, E., et al. 2008, Phys. Scr., 133 [Google Scholar]
- Meynet, G., Hirschi, R., Ekstrom, S., et al. 2010, A&A, 521, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA&A, 51, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVII. 2016, A&A, 596, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plez, B. 2012, Astrophysics Source Code Library [record ascl:1205.004] [Google Scholar]
- Plez, B., Brett, J. M., & Nordlund, A. 1992, A&A, 256, 551 [NASA ADS] [Google Scholar]
- Roederer, I. U., Preston, G. W., Thompson, I. B., et al. 2014, AJ, 147, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Spite, M., Caffau, E., Bonifacio, P., et al. 2013, A&A, 552, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tominaga, N., Iwamoto, N., & Nomoto, K. 2014, ApJ, 785, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2003, Nature, 422, 871 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Umeda, H., & Nomoto, K. 2005, ApJ, 619, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Van Dokkum, P. 2001, PASP, 562, 35 [Google Scholar]
- Vernet, J., Dekker, H., & D’Odorico, S. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yong, D., Norris, J., Bessel, M., et al. 2013, ApJ, 762, 27 [CrossRef] [Google Scholar]
- Yoon, J., Beers, T. C., Placco, V., et al. 2016, ApJ, 833, 20 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Estimated errors in the element abundance ratios [X/Fe] for the star SDSS J232854.99+023924.5.
All Figures
 |
Fig. 1. X-shooter spectra of the stars centred on the magnesium triplet. The continuum of the three spectra located in the lower part of the plot has been shifted downward for clarity. The vertical lines indicate the location of the magnesium absorption lines. |
| In the text | |
 |
Fig. 2. Comparison of the location of the stars and isochrones on a G magnitude versus (BP−RP) magnitude diagram. The two isochrones on the plot have been computed for an age of 14 Gyr (black line: z = 2 × 10−5 and blue line: z = 2 × 10−6). BP−RP (BP and RP are the magnitudes measured respectively by the two low resolution spectrographs, the Blue Photometer (BP) and the Red Photometer (RP) onboard the Gaia satellite) versus the absolute G magnitude, with two different hypotheses for the reddening. The red dots represent the stars assuming E(BP − RP) = 0 whereas the green dots represent our stars’ photometry with an extinction correction E(BP−RP) using the E(B−V) correction of PanSTARRS (Chambers et al. 2016) and the conversion relations E(BP − RP) = E(B − V) + 0.07 and AG = AV = 3.1 × E(B − V) (where AG and AV are the extinction in the G and the V band) from Andrae et al. (2018). |
| In the text | |
 |
Fig. 3. [Mg/Fe] and [Ca/Fe] vs. [Fe/H]. Red circles: this paper; Blue circle: BPS CS 22949−037Depagne et al. (2002), green circle: SMSS J031300−670839.3 (Keller et al. 2014); blue diamond: SDSS J1313−0019 (Frebel et al. 2015); blue square: HE 1327−2329 (Aoki et al. 2006); blue triangle: HE 0107−5240 (Christlieb et al. 2004); small grey circle: evolved stars from Roederer et al. (2014); small orange circles: main sequence stars from Roederer et al. (2014); black triangles: data from Yong et al. (2013). |
| In the text | |
 |
Fig. 4. Synthetic spectra of SDSS J002314.00+030758.0 in the region of the CH G-band (continuous lines) superimposed on the observed spectrum (small crosses). The theoretical spectra are represented as blue lines correspond to carbon abundances A(C) = 6.0, 6.6 and 6.9 dex. The red line represent the best fit to the observed spectrum and corresponds to a carbon abundance A(C) = 6.4 dex. |
| In the text | |
 |
Fig. 5. Carbon abundances A(C) of CEMP stars as a function of [Fe/H]. Large open black squares represent our results. The other symbols are literature data. Details can be found in Bonifacio et al. (2015). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.