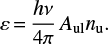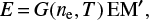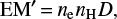| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 13 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201833466 | |
| Published online | 16 October 2018 | |
Statistical analysis of UV spectra of a quiescent prominence observed by IRIS⋆
1
Astronomical Institute, The Czech Academy of Sciences, 25165 Ondřejov, Czech Republic
e-mail: e-mail: sonja.jejcic@guest.arnes.si
2
Faculty of Mathematics and Physics, University of Ljubljana, 1000 Ljubljana, Slovenia
3
Astronomical Institute of Slovak Academy of Sciences, 05960 Tatranská Lomnica, Slovak Republic
Received:
21
May
2018
Accepted:
27
June
2018
Context. The paper analyzes the structure and dynamics of a quiescent prominence that occurred on October 22, 2013 and was observed by several instruments including the Interface Region Imaging Spectrograph (IRIS).
Aims. We aim to determine the physical characteristics of the observed prominence using Mg II k and h (2796 and 2803 Å), C II (1334 and 1336 Å), and Si IV (1394 Å) lines observed by IRIS. In addition we study the dynamical behavior of the prominence.
Methods. We employed the one-dimensional non-LTE (departures from the local thermodynamic equilibrium – LTE) modeling of Mg II lines assuming static isothermal-isobaric slabs. We selected a large grid of models with realistic input parameters expected for quiescent prominences (temperature, gas pressure, effective thickness, microturbulent velocity, height above the solar surface) and computed synthetic Mg II lines. The method of Scargle periodograms was used to detect possible prominence oscillations.
Results. We analyzed 2160 points of the observed prominence in five different sections along the slit averaged over ten pixels due to low signal to noise ratio in the C II and Si IV lines. We computed the integrated intensity for all studied lines, while the central intensity and reversal ratio was determined only for both Mg II and C II 1334 lines. We plotted several correlations: time evolution of the integrated intensities and central intensities, scatter plots between all combinations of line integrated intensities, and reversal ratio as a function of integrated intensity. We also compared Mg II observations with the models. Results show that more than two-thirds of Mg II profiles and about one-half of C II 1334 profiles are reversed. Profiles of Si IV are generally unreversed. The Mg II and C II lines are optically thick, while the Si IV line is optically thin.
Conclusions. The studied prominence shows no global oscillations in the Mg II and C II lines. Therefore, the observed time variations are caused by random motions of fine structures with velocities up to 10 km s−1. The observed average ratio of Mg II k to Mg II h line intensities can be used to determine the prominence’s characteristic temperature. Certain disagreements between observed and synthetic line intensities of Mg II lines point to the necessity of using more complex two-dimensional multi-thread modeling in the future.
Key words: Sun: filaments, prominences / radiative transfer / line: profiles / methods: statistical / Sun: oscillations
The movies associated to Figs. 1 and 7 are available at https://www.aanda.org
© ESO 2018
1. Introduction
Prominences are relatively dense and cool plasma structures embedded in the low-density, hot corona. Prominence plasma is supported against gravity by the coronal magnetic fields. Prominences can be seen in emission as bright prominences above the limb or as dark filaments visible in absorption against the solar disk. Depending on their location, nature, and lifetime we classify them as quiescent or active region prominences. Quiescent prominences are long-lasting structures with lifetimes of several days or weeks. On the other hand, active region prominences are short-lived structures lasting for several hours or days. However, quiescent prominences may also sometimes become unstable and suddenly erupt. Reviews of the physics of solar prominences can be found in Labrosse et al. (2010), Mackay et al. (2010), Vial & Engvold (2015) and Schmieder et al. (2014a). Observations of quiescent prominences were reviewed by Heinzel (2007), their observational characteristics by Parenti (2014), and the modeling of prominences and their fine structures was reviewed by Gunár (2014). A distinct class of eruptive prominences was found to be embedded in the core of the coronal mass ejections (CMEs). These prominences have relatively hot temperatures (around 105 K), low electron density and low gas pressure (see e.g., Heinzel et al. 2016; Jejčič et al. 2017).
Observations made by space-borne and ground-based instruments show that even the quiescent prominences, which have relatively stable large-scale structures, show highly dynamical small-scale structures with plasma flows, small amplitude periodic oscillations, and apparent lifetimes as short as several minutes. Typical prominence fine structures consist of a large number of horizontal and quasi-vertical threads and knots of cool plasma, with typical widths of several hundred kilometers (or even less, see, e.g., Lin et al. 2005). Low amplitude oscillations with periods of several tenths of minutes are observed in line intensities, line widths, and line-of-sight (LOS) velocities, while theoretical models show temporal variations of temperature, electron density, and velocity (see, e.g., Oliver & Ballester 2002; Arregui et al. 2012; Heinzel et al. 2014b). These periodic oscillations are most likely related to standing or propagating magnetohydrodynamic (MHD) waves and are under investigation.
The Interface Region Imaging Spectrograph (IRIS, De Pontieu et al. 2014) is capable of taking high resolution spectra and slit-jaw images (SJIs) in the far ultraviolet (FUV) and near ultraviolet (NUV) regions. Several ultraviolet (UV) spectral lines observed by IRIS can be used to study individual prominence fine structures in great detail. This allows us to gain a better understanding of their nature, evolution, and behavior. With a combination of spectroscopic observations and non-LTE (departures from the local thermodynamic equilibrium – LTE) radiative transfer prominence models we can derive several key parameters of prominence plasma, such as the temperature, electron density (which is proportional to the gas pressure), LOS velocity, integrated line intensity, and optical thickness of the prominence plasma in the used spectral line.
The spectroscopic analysis of the IRIS profiles of Mg II k and h lines made by Schmieder et al. (2014b) and Levens et al. (2016, 2017) in combination with the results of the one-dimensional (1D) non-LTE modeling of Schmieder et al. (2014b) and Levens et al. (2016, 2017) show that these two lines are relatively strong, optically thick (up to 103 or 104), and sensitive to Doppler brightening or dimming effects for velocities larger than 20 km s−1. Observations show that Mg II profiles can be unreversed (single), reversed, or composite profiles formed by the superposition of several individual Doppler-shifted single profiles emitted along a single LOS. Models show that unreversed profiles occur at lower values of gas pressure, while at higher pressure values the reversal becomes more pronounced with the temperature. The non-LTE models that included the prominence-corona transition region (PCTR) can explain the shape of some reversed profiles (Heinzel et al. 2015). In addition, C II and Si IV IRIS spectra were studied by Levens et al. (2016). These authors found that Si IV lines are very faint and have a low signal-to-noise ratio (S/N).
In the present paper we analyze IRIS observations of a quiescent prominence and study the correlations between the intensities of Mg II, C II, and Si IV lines, together with the correlations between different plasma parameters derived by modeling. We also study the dynamics of this prominence and investigate the presence of possible oscillations.
The paper is organized in the following way. In Sect. 2 we present the used UV observations of Mg II, C II, and Si IV lines obtained by IRIS. Section 3 deals with the analysis of observed IRIS UV spectra. Section 4 describes the dynamics of the observed prominence structures: time evolution of the LOS velocities, integrated intensities, and the central intensity of selected UV lines together with the potential prominence oscillations. In Sect. 5 we show the results of our statistical analysis, which demonstrate correlations between Mg II, C II, and Si IV lines together with 1D non-LTE modeling of Mg II lines and CHIANTI (an atomic database for spectroscopic diagnostics of astrophysical plasmas) computations of Si IV line. Discussion and conclusions are presented in Sect. 6.
2. IRIS observations
On October 22 and 23, 2013 a coordinated observing campaign was carried out with two space-borne spectrographs: SUMER (Solar Ultraviolet Measurements of Emitted Radiation; Wilhelm et al. 1995) on board the Solar and Heliospheric Observatory (SoHO) and IRIS (Interface Region Imaging Spectrograph; De Pontieu et al. 2014). Several ground-based instruments were also involved, among them the Multichannel Flare Spectrograph (MFS1) and the Horizontal Sonnen Forschung Anlage 2 (HSFA2; Kotrč 2009) at the Astronomical Institute of the Czech Academy of Sciences, Ondřejov, and the COronal Multichannel Polarimeter for Slovakia (COMP-S; Kučera et al. 2010) at the Astronomical Institute of the Slovak Academy of Sciences. A quiescent, although rather dynamic, prominence was observed at the NW solar limb on October 22, 2013 by IRIS in both the FUV and NUV parts of the spectra between 8:41 and 10:49 UT and by SUMER in the hydrogen Lyman lines between 07:00 and 08:33 UT. The spectrographs at the Astronomical Institute of the Czech Academy of Sciences observed in the Hα, Hβ, D3, and Ca II H (3968 Å) lines between 10:38 and 11:39 UT.
 |
Fig. 1. SJI in Mg II 2796 Å channel obtained at 09:12:53 UT corresponding to eighth slit position of eighth raster of prominence observation. An area around the slit position is zoomed for better visibility. Five sections selected for analysis are marked by color bars in the right panel. The movie corresponding to this figure is available online where the white box indicates the range of data we used for analysis. |
 |
Fig. 2. Example of Mg II k and h spectra at 2796 and 2803 Å (left panel), C II spectra at 1334 and 1336 Å (middle panel), and Si IV spectrum at 1394 Å (right panel) at 9:12:53 UT as indicated in Fig. 1. |
 |
Fig. 3. Example of Mg II k and h profiles at 2796 and 2803 Å (left panel), C II profiles at 1334 and 1336 Å (middle panel), and Si IV profile at 1394 Å (right panel) for the middle section along the slit at 9:12:53 UT (see Fig. 1). |
IRIS observed spectra in three different wavelength bands: two in FUV with wavelength ranges 1332 Å–1358 Å and 1389 Å–1407 Å and one in NUV within the range 2783 Å–2835 Å. These observations include lines of C II 1334 Å and 1336 Å, Fe XII 1349 Å, O I 1356 Å, Si IV 1394 Å and 1403 Å, and Mg II k and h (2796 and 2803 Å), together with SJIs in Si IV 1403 Å and Mg II 2796 Å channels. The field of view (FOV) was 5 arcsec × 174 arcsec for each spectrum and 167 arcsec × 174 arcsec for each SJI. The IRIS observations consist of 30 repetitions (rasters) each with 16 different slit positions within one raster, with steps of 0.35 arcsec, exposure time 15 s, and step cadence 16.6 s, which gives in total 480 spectra. Exposure time of all SJIs was 33 s, which gives in total 240 images. The spectral resolution of the C II spectra was 51.9 mÅ, while for Mg II and Si IV it was 50.9 mÅ. Spatial resolution along the slit was 0.332 arcsec. The line intensities of level-2 data expressed in counts per second, which have been already corrected for dark current, flat-field, and geometrical distortion, were calibrated into absolute radiometric units using the procedure published, for example, by Kleint et al. (2016). An example of one SJI obtained in the Mg II 2796 Å channel at 09:12:53 UT is shown in Fig. 1. The corresponding slit position is marked by a vertical full white line while two white vertical dashed lines show boundaries of rastering.
3. Characteristics and analysis of IRIS UV spectra
Here we focus on the analysis of both FUV and NUV spectra observed by the IRIS spectrograph. Two FUV spectral bands of IRIS contain two weak C II lines at 1334 Å and 1336 Å as well as one even weaker Si IV line at 1394 Å. The C II line at 1336 Å actually consists of two components that are mutually blended. In the NUV region we analyze the two strong Mg II k and h lines at 2796 Å and 2803 Å, respectively. Hereafter we will skip the wavelength units in the names of all selected lines.
Examples of Mg II, C II, and Si IV spectra observed at 9:12:53 UT are shown in Fig. 2 for the slit position indicated in Fig. 1. In the lower part of all spectra a bright solar limb is visible together with dynamical spicules while the middle part corresponds to the prominence location. These prominence spectra are typical for a quiescent prominence because there are no significant Doppler motions. We chose five sections along the prominence slit to have information about the structure and dynamics of different parts of the prominence (see Fig. 1). Because the prominence is rather weak with low S/N ratios in C II and in Si IV line intensities, we averaged the signal over ten pixels along the slit for all five selected sections. Due to this averaging we reduced the spatial resolution along the slit. The right panel of Fig. 1 shows the zoomed region around the given slit position with the five sections marked by different colors. All the analysis is made for these five averaged sections and all plots will be presented using this color coding.
Examples of the Mg II, C II, and Si IV line profiles for observations obtained at 9:12:53 UT from the middle section (see Fig. 1) are shown in Fig. 3. In this example the Mg II and C II line profiles are reversed, while the faint Si IV line exhibits only one emission peak without any central reversal. Both Mg II lines show a similar shape of the asymmetrical and reversed profiles where the blue peak is lower than the red one. Although profiles of the C II 1334 and 1336 lines are also reversed and asymmetrical, they differ in shape from each other because the profile of the latter is a composition of two blended components. However, the asymmetry of the C II 1334 line is qualitatively the same as that of the Mg II lines. Asymmetrical reversed profiles generally give us information about the dynamics along the LOS of the prominence. A comparison between all profiles shows that noise is negligible only for the Mg II lines where S/N ≥ 500. The level of S/N ∼ 15 in spectral intensities of the two C II lines is still acceptable, while for the Si IV line the ratio S/N ∼ 4 is rather low for any detailed profile analysis. All other lines observed by IRIS at the prominence are even fainter and noisier and therefore they are not used in our analysis.
 |
Fig. 4. Examples of temporal evolution of integrated intensity of Mg II, C II, and Si IV lines for fourth slit position and five selected sections (left panel) and corresponding Scargle periodograms (right panel). Color coding is the same as in Fig. 1. Dashed lines show 1% and 5% FAP levels. |
For a comparison of the observed Mg II spectral line profiles with the synthetic ones obtained by a non-LTE model, in many cases it is more useful to compare characteristics of the profiles – such as integrated intensity E, asymmetry, central reversal, width – instead of a direct comparison of the profiles. For spectral lines with large optical thickness in their cores, one of the most important profile characteristics is the depth of the central reversal. Moreover, there is also a good connection between this characteristics and the physical parameters of the prominence plasma, such as temperature, density, and ionization degree. In the works of Gunár et al. (2010), Berlicki et al. (2011), and Schwartz et al. (2015) where prominence observations in the hydrogen Lyman series were statistically compared with the two-dimensional (2D) non-LTE models of the prominence fine structures, the depth of the central reversal together with the statistical population of reversed profiles showed a clear connection with the prominence plasma density. The depth of the central reversal was defined in those works as a ratio of minimal intensity at the reversal to the average of the maximal intensities at two peaks (by definition reversed profiles have this ratio lower than one). Here we follow the paper of Heinzel et al. (2014a) and compute the reversal ratio as the ratio of the averaged line-peak to line-center intensity, thus reversed profiles have a reversal ratio larger than one. Integrated intensities of the Mg II, C II, and Si IV lines are computed in absolute radiometric units for five selected sections along the slit after subtracting the continuous background. Central intensities ICenter and reversal ratios are computed only for the Mg II and C II 1334 lines because the C II 1336 line is blended and the Si IV 1394 line is unreversed and noisy. Doppler velocities of the Mg II and C II lines are computed as well but without the Si IV 1394 line because it is too faint and noisy.
4. Dynamics of the observed prominence
The width of one raster scan in a horizontal direction is about 5.6 arcsec, which gives a roughly 4000 km-wide strip (see the width between two white dashed vertical lines in Fig. 1). Five selected sections along the slit (marked with different colors in Fig. 1) cover only parts of the prominence structure where some dynamics are expected. For each selected section we get 27 points (rasters) marked with different colors. We excluded three rasters due to high contamination. Time variations of integrated intensities of the Mg II, C II, and Si IV lines for the fourth slit position and five selected sections along the slit are shown in the left panel of Fig. 4. We clearly see that the C II and Si IV lines have a few orders of magnitude lower integrated intensities than Mg II lines, because C II and Si IV lines are generally weak and noisy lines. The blended C II 1336 line is brighter than the single C II 1334 line, the Si IV 1394 line is the weakest, and the Mg II k line is brighter than the Mg II h line as reported, for example, by Heinzel et al. (2014a), Schmieder et al. (2014b), Levens et al. (2016) and Liu et al. (2015).
To check whether these time variations of integrated intensities are real or caused by noise, one has to compute correlation coefficients between the integrated intensities of all line combinations for five selected sections, which gives in total 432 points at a given section. The results are presented in Table 1. Correlation coefficients between both Mg II lines in selected sections are close to 1 and for both C II lines are around 0.8. These values indicate that time variations of integrated intensities in the Mg II and C II lines are real and not caused by the noise. Our impression is that these time variations of integrated intensities in the C II and Mg II lines could be consistent with long period linear oscillations as reported by Heinzel et al. (2014b) and Zapiór et al. (2016). A detailed analysis of the linear oscillations of the studied prominence is described in Sect. 4.1.
Correlation coefficients for a given section between both integrated intensities of Mg II lines and both C II lines together with combinations of Mg II, C II, and Si IV lines.
 |
Fig. 5. Temporal evolution of central intensity of Mg II k (left panel), Mg II h (middle panel), and C II ,1334 (right panel) lines for fourth slit position and five selected sections. |
Correlation coefficients between the Mg II and C II lines are up to 0.7, between Si IV and Mg II lines up to 0.4, and between Si IV and C II lines up to 0.5. These values show that there is a weak correlation between different combinations of all these lines. These differences seem to be related to the fact that these lines are formed at different depths along the LOS in the prominence and that the Si IV line exhibits low S/N. The Mg II and C II lines are formed in cool parts at a formation temperature of around 10 000–20 000 K. The Si IV 1394 line is formed in PCTR around 80 000 K.
Figure 5 shows the time variations of the central intensities for both Mg II lines and the C II 1334 line for the fourth slit position and five selected sections. A detailed analysis for all 432 points at a given section shows no correlation between integrated intensities and central intensities for a given line as presented in Table 2. These correlation coefficients with values between 0.3 and 0.6 indicate that the C II and Mg II lines are optically thick. Therefore the central line intensity is not proportional to integrated intensity.
We have computed also Doppler velocities of the Mg II and C II lines for all profiles (we omitted the Si IV line because it is too faint and noisy). Single unreversed profiles were fitted with a Gaussian while the reversed ones were fitted with the Gaussian using only their wings. The left panel of Fig. 6 shows time variations of the LOS velocities of the Mg II and C II lines with values up to 10 km s−1.
Correlation coefficients for a given section between integrated intensities and central intensities for Mg II k line, Mg II h line, and C II 1334 line.
 |
Fig. 6. Examples of Doppler velocity of Mg II and C II lines for fourth slit position and selected sections (left panel) and corresponding Scargle periodograms (right panel). Dashed lines show 1% and 5% FAP levels. |
 |
Fig. 7. Dopplergrams for Mg II and C II lines (left panel) together with 2D maps of integrated intensity (right panel). The movie corresponding to this figure is available online. |
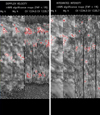 |
Fig. 8. Spectral power of the Doppler signal (left panel) and maximum intensity signal (right panel). Each rectangle corresponds to the spectral line indicated above. Red curves limit areas with FAP < 1%. |
4.1. Prominence oscillations
From the spectra collected in the raster mode, we calculated the Doppler line shift for all slit positions averaged over ten pixels (see Sect. 3) for both Mg II and C II lines. We skip the weak and noisy Si IV line. The collected data series in raster mode allowed us to construct 2D Dopplergrams for the Mg II and C II lines as well as 2D maps of the integrated intensity (see Fig. 7). They covered an area of 5.6 × 83 arcsec, which corresponds to 30 × 430 pixels (see in Fig. 1 the box defined by two short, white, solid horizontal lines and two white, vertical, dashed lines). From a series of individual snapshots we created an online movie corresponding to Fig. 7. With a time evolution of Doppler velocity and integrated intensity we performed a Scargle periodogram analysis (Scargle 1982) for each pixel independently. We used the Scargle periodogram because it allows us to analyze a dataset with gaps, which was our case. An example of the time evolution of Doppler velocity and integrated intensity together with a Scargle periodogram for selected pixels are presented in the Figs. 4 and 6.
For each pixel we took the value of the maximum peak in the periodogram and we constructed 2D maps of spectral power for the Mg II and C II lines (see Fig. 8). In the map we selected areas where the false alarm probability (FAP) level is lower than 1%. A FAP equal to 1% may be interpreted as a 1% probability that a periodogram peak at this level is caused by noise. This value may be interpreted also as a 99% confidence level.
Looking at plots in Figs. 4 and 6 one can have an impression of the existence of oscillations in the dataset, but a periodogram analysis reveals no oscillations. Areas with a FAP < 1% are very small. A FAP level below 1% located in isolated pixels is not sufficient to expect any oscillations in the dataset (Zapiór et al. 2015). Looking at the online movie corresponding to Fig. 1, we detected plasma elements with different Doppler velocity and intensity crossing the FOV where the FAP < 1%. This causes a change of the observed spectral parameter, which mimics one period of oscillations (see for example the plot in Fig. 6 for Sect. 5 of the Mg II k line) and gives a moderate rise of spectral power.
A passage of plasma elements across the observed FOV and its influence on the dataset needs to be noted. One can claim that using our technique it is impossible to detect any periodic signal in a prominence that is dynamic with plasma elements in constant motions. For example, if a thread oscillates in the plane of sky (POS), then when analyzing a fixed pixel in the FOV we take the signal from different plasma elements. However, even for this situation the periodic signal will be present at least in the intensity domain as an effect of the consecutive presence and absence of a particular thread in the analyzed pixel. For a very dense field, any detection of a periodic signal in individual threads may be of course impossible, but the global oscillatory mode in the Doppler domain may be still detected as a coherent signal present in the whole FOV. We follow the methodology described in Terradas et al. (2002). Performing an independent periodogram analysis for each pixel for as long as possible favors the detection of oscillations. Terradas et al. (2002) noted that if the detected oscillatory area is large (more than several pixels) this is a hint of the solar origin of the oscillations. If the observed prominence were a subject of global oscillations, we would detect an oscillatory pattern over the whole prominence body. Taking this into account we conclude that we did not detect any global oscillations in the observed prominence either in the Doppler shift or in the integrated intensity. We did not detect any oscillations of a local character either. However, having in mind previous considerations, we cannot exclude the presence of undetectable local oscillations.
5. Statistical analysis of IRIS UV line intensities
Here we present the behavior of observed integrated intensities of the Mg II, C II, and Si IV lines for five sections, 16 slit positions, and 27 rasters, which give in total 2160 points. A scatter plot between both integrated intensities of the Mg II lines in the upper panel of Fig. 9 shows that observed points practically lie on a straight line. This result is sufficiently robust due to high S/N. Integrated intensities of the Mg II k line vary between 8000 and 32 500 erg s−1 cm −2 sr−1, while in the Mg II h line they vary between 5500 and 23 500 erg s−1 cm −2 sr−1. The lower panel in Fig. 9 shows the ratio between the Mg II k and h integrated intensities as a function of the integrated intensity of the Mg II k line. All observed points show a uniform distribution with the average value of 1.365. This value is consistent with the theoretical values presented in Heinzel et al. (2014a). Figure 10 shows the scatter plot between integrated intensities of the C II 1336 line and C II 1334 line. The scattering of the values in this plot is mainly due to the noise because C II lines are weak. Integrated intensities of the C II 1334 line vary between 150 and 700 erg s−1 cm −2 sr−1, while blended C II 1336 line vary between 250 and 950 erg s−1 cm −2 sr−1. Figure 11 shows scatter plots between the Mg II k and C II 1334 line, the Mg II k and Si IV line, as well as the C II 1334 and Si IV line. In the left panel the scattering is less pronounced than in the middle and right panels indicating that the Si IV line is formed under different conditions; we will discuss this in Sect. 5.2. Integrated intensities of the Si IV line vary between 10 and 180 erg s−1 cm −2 sr−1. Scatter plots between the reversal ratio and integrated intensity of both Mg II lines and the C II 1334 line are presented in Fig. 12. By our definition, the reversal ratio is equal to one for single-peak and flat-core profiles, while the reversed profiles have a reversal ratio higher than one. Statistics show that about 80% of Mg II k profiles, 65% of Mg II h profiles, and 40% of C II 1334 profiles are reversed. The rest show single-peak or flat characteristics. Here we clearly see that the scatter points form a cloud above that of the limit one. We believe that this cloud is formed due to different plasma conditions in optically thick structures along the LOS, such as the temperature, velocity, and gas pressure. In the following subsection we compare synthetic profiles obtained from 1D non-LTE isothermal-isobaric models with the observations of Mg II lines to assess our assumption. Figure 13 shows the histograms of the ratio of blue to red peak intensities of all reversed profiles for both Mg II lines and the C II 1334 line. The red peak is slightly dominant for all lines but the histograms look quite symmetrical. This might confirm our conclusions from the previous section that the observed prominence does not exhibit any large-scale systematic motions like oscillations or waves, which could produce significant line asymmetry. However, random fine-structure motions could be responsible for the shape of these histograms as we discuss later. In Fig. 14 we present the correlation between LOS velocities of both the Mg II lines and Mg II k and C II 1334 lines. The plots are similar to those in the upper panel of Fig. 9 and the left panel of Fig. 11, again showing that correlation between Mg II lines is better than between Mg II and C II lines because Mg II lines are less noisy than C II lines. However, the relatively larger scatter between Mg II and C II lines could be due to the fact that the wings of both lines are not formed at the same depth. Finally, Fig. 15 shows the scatter plot between the peaks separation of the Mg II k or h line, against those for the C II 1334 line. This was aimed as a test of the idea that the two peaks might be due to Doppler shifts of the single-peaked profiles. In that case, the peaks separation would correlate in the Mg II and C II 1334 lines and the correlation coefficient (dashed line) would be equal to a ratio of 2.1 of Mg II and C II 1334 line wavelengths. However, we clearly see that this is not the case and thus we believe that the majority of double-peak profiles are due to true reversal caused by the opacity effects, which do not obey the above correlation rule.
 |
Fig. 9. Comparison between integrated intensity emitted in the Mg II h line~and integrated intensity emitted in the Mg II k line for five selected sections (upper panel) and ratio of integrated intensities between Mg II k and Mg II h lines as function of integrated intensity emitted in Mg II k line (lower panel). |
 |
Fig. 10. Comparison between integrated intensity emitted in C II 1336 line and integrated intensity emitted in C II 1334 line for five selected sections. |
5.1. One-dimensional non-LTE isothermal-isobaric models
Heinzel et al. (2014a) considered 27 isothermal-isobaric models and synthesized the Mg II lines using the non-LTE code for 1D vertical slabs illuminated by the solar disk radiation. Here we compute a larger grid of such models in order to compare the models with the observations. The input parameters of each model are the temperature T, gas pressure p, effective thickness of the slab D, microturbulent velocity ξ, and height above the solar surface H. We neglect the radial flow velocity vrad because we assume static models of a quiescent prominence. The synthetic Mg II profiles are convolved with the IRIS instrumental profile having the Gaussian full width at half maximum (FWHM) equal to 52 mÅ (Heinzel et al. 2015). The microturbulence is treated here in a standard way, representing the velocity distribution of uresolved plasma elements. Additional line broadening can be introduced by randomly distributed LOS velocities of fine structures integrated along a given by LOS. The effects of such random LOS velocities were considered in the frame of 2D prominence models by Gunár et al. (2008). These authors showed, for example, that the LOS motions of fine structures can produce line asymmetries that are qualitatively comparable with observations.
 |
Fig. 11. Comparison between integrated intensities of Mg II k and C II 1334 lines (left panel), Mg II k line and Si IV line (middle panel), and C II 1334 line and Si IV line (right panel) for five selected sections. |
 |
Fig. 12. Comparison between reversal ratio and integrated intensity of Mg II k line (left panel), Mg II h line (middle panel), and C II 1334 line (right panel) for five selected sections. |
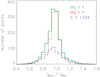 |
Fig. 13. Blue to red peak intensity distribution of reversed profiles for Mg II and C II 1334 lines. |
 |
Fig. 14. Comparison between Doppler velocities of Mg II lines (left panel) and Mg II k and C II 1334 lines (right panel) for five selected sections. |
 |
Fig. 15. Peaks separation of Mg II k line versus C II 1334 line (left panel) and Mg II h line versus C II 1334 line (right panel). The dashed straight line shows the theoretical relation between the lines. |
Large grid of input parameters used for 1D-slab isothermal-isobaric models.
We fixed the height of the prominence slab to 10 000 km to be consistent with Heinzel et al. (2014a). The set of input parameters of the grid of models includes seven characteristic values of temperatures, gas pressures, and effective thicknesses, which gives altogether 343 models for a given microturbulent velocity as is shown in Table 3. From the 1D non-LTE model we obtain the electron density ne, the integrated intensity, reversal ratio, and optical thickness at the center τ of each Mg II line. All model plots are made in the range of observed integrated intensities of the Mg II lines up to 5 × 104 erg s−1 cm −2 sr−1 with 201 models for a given microturbulent velocity, for seven different temperatures marked with different colors. In the following plots, the left panels show the Mg II k line at microturbulent velocities 0, 5, and 8 km s−1 and the right panels show the Mg II h line at the same microturbulent velocities.
 |
Fig. 16. Integrated intensity of Mg II lines as a function of optical thickness for different temperatures at three representative microturbulent velocities. |
 |
Fig. 17. Reversal ratio of Mg II lines as a function of optical thickness for different temperatures at three representative microturbulent velocities. |
 |
Fig. 18. Integrated intensity emitted in Mg II h line versus Mg II k line for all 343 model points at different temperatures (left panels). Right panels: ratio of integrated intensity of the Mg II k line to the Mg II h line versus the integrated intensity of the Mg II k line for different temperatures at three representative microturbulent velocities. |
Figure 16 presents the relationship between the integrated intensities of the Mg II lines and the optical thicknesses at the line centers. Plots clearly show that for our range of observed integrated intensities (roughly between 5000 and 50 000 erg s−1 cm −2 sr−1), the observed prominence is optically thick with optical thicknesses up to 104. Points are more scattered in the case of the Mg II k line (see the left panels) than the Mg II h line because of a higher Mg II k intensity. At lower temperatures the optical thickness reaches higher values in all plots. On the contrary, at higher temperatures, optical thickness becomes lower. At higher temperatures more Mg II ions are ionized, which decreases the opacity and thus the optical thickness. However, at the same time, at higher temperatures we have more collisional excitations (which also increase with higher pressure) and for a given optical thickness we get higher emission in the Mg II lines. As a result we see scatter in the plot because at a given temperature we have seven different pressures. The integrated intensity of both Mg II lines at higher microturbulence for a given optical thickness reaches higher values due to turbulent Doppler brightening (Heinzel et al. 2014a).
Figure 17 shows a comparison between the reversal ratio and optical thickness at the line center for both Mg II lines. The reversal ratio gradually increases with optical thickness at a given temperature. Profiles with optical thickness between 1 and 10 are not yet reversed but become flat. All flat and unreversed profiles (single) have a reversal ratio equal to one according to our definition. Points are more probably scattered due to the effect of pressure and thickness because the reversal ratio depends on optical thickness and optical thickness depends on the density of the lower atomic state, which is proportional to gas pressure at a given temperature. At higher microturbulence the reversal ratio and optical thickness are lower and points are less scattered. The Mg II k line generally reaches higher values of reversal ratio than the Mg II h line.
The left panel of Fig. 18 shows a comparison between the computed integrated intensities in the Mg II h and Mg II k lines for all 343 models at a given microturbulent velocity to show the trend. The correlation between both lines is quite good, points practically lie on a straight line. Slight deviations are related to different temperatures. The plot is consistent with observations (see upper panel of Fig. 9). The right panels of Fig. 18 show the ratio of energy emitted in both Mg II lines as a function of energy emitted in the Mg II k line. The ratio is initially high, around 2.5, and then it decreases with increasing integrated intensity of the Mg II k line to reach a practically constant value for a given temperature. Higher microturbulent velocity gives a lower line ratio. This plot is also consistent with observations (see lower panel of Fig. 9) where the average value is 1.365 and scatter is mainly due to different temperatures of observed prominence structures.
Figure 19 presents the ratio of energy emitted in the Mg II k line to Mg II h line at a given temperature for three representative microturbulent velocities (here we do not consider the additional effect of random motion of unresolved fine structures). From this plot we can conclude that the ratio betwen the lines (see the dashed horizontal line that shows the averaged observed value) can provide a useful diagnostic for the determination of a characteristic temperature of the studied prominence. The best fit is obtained for low temperatures reaching 5000 K and for a microturbulent velocity of 5 km s−1.
Reversal ratio as a function of integrated intensity for both Mg II lines is presented in Fig. 20. The reversal ratio is equal to one for integrated intensities up to about 104−2 × 104 erg s−1 cm −2 sr−1. At higher intensities, the reversal ratio increases gradually for a given temperature. The reversal ratio is higher at a lower microturbulent velocity because the microturbulence smears the line profiles. Scatter mainly depends on temperature and microturbulence. There is no similarity between the models and observations (see the left and middle panels in Fig. 12), which poses a problem for the modeling; we discuss this issue later.
All plots in Fig. 21 show that integrated intensity increases with the emission measure 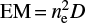 at a given temperature (here we use the standard definition of emission measure). For a given emission measure the integrated intensity is higher at higher microturbulence. Plots show that Mg II becomes fully ionized around 20 000 K.
at a given temperature (here we use the standard definition of emission measure). For a given emission measure the integrated intensity is higher at higher microturbulence. Plots show that Mg II becomes fully ionized around 20 000 K.
5.2. Analysis of Si IV spectra using CHIANTI
Besides the chromospheric UV lines of Mg II and C II, the IRIS spectrograph observed also hotter transition region (TR) spectral lines among which the Si IV line is the most visible at the prominence location. Although the S/N of the spectral intensities of this line is much lower than that of the Mg II and C II lines, the integrated intensity of the Si IV line averaged from all five sections along the slit and from all 16 slit positions within 27 selected rasters can be used to analyze this line emission. The idea is to estimate the geometrical extension of hotter PCTR regions where the Si IV line is formed. Assuming that the Si IV line is optically thin and that it is formed under the coronal approximation, we can use the CHIANTI atomic database (Dere et al. 1997) to calculate theoretical values of the integrated intensity. For the calculations in this paper we used version 8 of CHIANTI (Del Zanna et al. 2015). Total emissivity of the spectral line into unit solid angle is defined as a product of the spontaneous transition rate Aulnu (Einstein coefficient times the population density of the upper atomic level) and the photon energy
The line intensity is then obtained by integration of the emissivity along the LOS through the whole optically-thin PCTR, which basically reduces to a simple multiplication by the effective geometrical thickness D. The number density of ions in the upper level of transition is calculated using the statistical equilibrium. In CHIANTI the ionization and excitation equilibria are solved independently and the relative population of a specific ion is the function of temperature only while the relative population of ions in the upper level depends both on the temperature and electron density. Using the contribution function G(ne, T), the line integrated intensity is
where EM′ is the emission meassure defined in CHIANTI as
with nH being the total hydrogen density (neutrals and protons). Adopting a common solar value of 0.83 for the ratio nH/ne, the emission measure is then calculated as 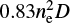 . We have calculated the contribution function for Si IV line at its formation temperature 80 000 K for three representative values of the gas pressure, 0.01, 0.05, and 0.1 dyn cm−2. For hydrogen and helium mixture at high temperatures, gas pressure is related to electron density through the equation of state p = 1.91nekBT, where kB is the Boltzmann constant. Finally, the geometrical thickness is derived using the observed averaged integrated intensity of the Si IV line. Resulting values of the LOS PCTR thicknesses are shown in Table 4. From Fig. 21 we can roughly estimate the prominence gas pressure as 0.1 dyn cm−2 in central cool parts where the Mg II lines are formed. Assuming an isobaric prominence equilibrium, we get rather thin PCTR of the order of tens of kilometers. However, if the PCTR gas pressure is smaller, for example, like in the hydrostatic equilibrium of prominence magnetic dips, the PCTR would be more extended. An extended PCTR is expected in the dipped structures along the magnetic field lines (see, e.g., Gunár et al. 2010).
. We have calculated the contribution function for Si IV line at its formation temperature 80 000 K for three representative values of the gas pressure, 0.01, 0.05, and 0.1 dyn cm−2. For hydrogen and helium mixture at high temperatures, gas pressure is related to electron density through the equation of state p = 1.91nekBT, where kB is the Boltzmann constant. Finally, the geometrical thickness is derived using the observed averaged integrated intensity of the Si IV line. Resulting values of the LOS PCTR thicknesses are shown in Table 4. From Fig. 21 we can roughly estimate the prominence gas pressure as 0.1 dyn cm−2 in central cool parts where the Mg II lines are formed. Assuming an isobaric prominence equilibrium, we get rather thin PCTR of the order of tens of kilometers. However, if the PCTR gas pressure is smaller, for example, like in the hydrostatic equilibrium of prominence magnetic dips, the PCTR would be more extended. An extended PCTR is expected in the dipped structures along the magnetic field lines (see, e.g., Gunár et al. 2010).
 |
Fig. 19. Ratio of Mg II k to Mg II h integrated intensities as function of temperature at zero microturbulence (left panel), 5 km s−1 (middle panel), and 8 km s−1 (right panel). The black asterisk symbols show the average ratio at a given temperature. The horizontal black dashed line marks the observed average value of 1.365. |
 |
Fig. 20. Reversal ratio versus integrated intensity of Mg II lines for different temperatures at three representative microturbulent velocities. |
 |
Fig. 21. Integrated intensity emitted in Mg II line as function of emission measure for different temperatures at three representative microturbulent velocities. |
6. Discussion and conclusions
In this study we have analyzed one of the first IRIS observations of a quiescent prominence. The prominence was observed on October 22, 2013 in NUV wavelengths at two strong Mg II k and h lines at 2796 and 2803 Å, as well as at FUV wavelengths where rather weak C II lines at 1334 and 1336 Å and a faint and noisy Si IV line at 1394 Å were detected. Level 2 data were calibrated to absolute radiometric units. Altogether we got 2160 observational points in five selected sections along the slit with y binning equal to ten pixels due to low S/N in C II, and Si IV lines, and for 16-slit raster with 27 repetitions. In this paper we address several key questions related to prominence structure and dynamics: What is the characteristic temperature and microturbulent velocity, what is the role of PCTR, what are the dynamics of this prominence (i.e. fine-structure dynamics versus global oscillations), and how are the structure and dynamics reflected in the IRIS line profiles and intensities? Having a large number of the observed points, we focused in this study on statistical correlations between various spectral line parameters, rather than on detailed analysis of individual line profiles. In order to understand the physical behavior of such correlations, we also computed a large grid of 1D isothermal-isobaric models using the Mg II code described in Heinzel et al. (2014a). A comparison between observed and computed characteristics of Mg II lines points to limitations of these models. For example, the line-core intensity of the Mg II and C II line will certainly be influenced by the presence of a PCTR around cool fine structures as indicated by our analysis of the Si IV line.
Analysis shows that more than two-thirds of Mg II, and almost one-half of C II 1334 profiles are reversed, which indicates that the prominence structure is mostly optically thick, while Si IV profiles have a single peak indicating small optical thickness of the line. Correlations between integrated intensities of both Mg II lines and both C II lines show that time variations in line intensities are real and not caused by the noise. Detailed analysis shows that there are no global oscillations in the Mg II, and C II lines. From that we conclude that time variations in integrated intensities are caused by fine-structure random motion with LOS velocities up to 10 km s−1. Correlation between LOS velocities of Mg II lines is better than between Mg II and C II lines because Mg II lines are supposed to be formed in a similar region and are less noisy than C II lines. Correlations between integrated intensities and central intensities of Mg II and C II lines (the C II 1336 line, which is a blended line, and the Si IV line, which is weak and noisy, are not considered) show that LOS variations of plasma parameters are reflected only in integrated intensities but not in the line center intensities that seem to form in the foremost fine structures.
Values of typical gas pressures for quiescent prominences, electron densities, contribution functions, and geometrical thicknesses of hotter envelope of the prominence at approximate Si IV line formation temperature 80 000 K.
The ratio of Mg II k to Mg II h line intensity is rather uniform, an average value is equal to 1.365 and is consistent with the values reported by Heinzel et al. (2014a). Compared to the present grid of 1D models this indicates that (i) the Mg II lines are optically thick, (ii) the kinetic temperature can be as low as 5000 K (Fig. 19), and (iii) the microturbulent velocity is around 5 km s−1 or lower rather than the highest one. Such a low temperature would be consistent with extended higher-pressure structures and would correspond to radiative equilibrium models as presented in Heinzel et al. (2014a). In the follow-up study we will also include a PCTR in the modeling to check the robustness of this result, although PCTR will affect only the inner line cores.
Scatter plots for the integrated line intensities of different combinations of elements show weak or no correlations indicating that the lines are not formed in the same plasma volume. There is certain correlation between Mg II k and C II 1334 line intensity (Fig. 11) and this is consistent with the situation in the quiet chromosphere where both lines are formed under similar conditions (Rathore et al. 2015). In contrast, the Si IV line is formed at much higher temperature and thus does not correlate with the Mg II and C II 1334 lines (Fig. 11). Scatter plots between the reversal ratio and integrated intensity of the Mg II and C II 1334 lines give clouds of points above unity because, by our definition, single and flat profiles have values of one and reversed profiles have values higher than one. Plots show that with increasing energy emitted in a given line the reversal ratio first increases and then gradually decreases. The observed reversal ratio is definitely larger than the computed one. For the Mg II k line with energy between 1 and 2 × 104 erg s−1 cm −2 sr−1 many observed points show reversal between 1 and 1.5, while 1D models predict no reversal in this range of intensities for ξ = 5 or 8 km s−1 and a small reversal for zero microturbulence. If we added a PCTR to the 1D models (see, e.g., Heinzel et al. 2015), the theoretical reversal ratio would even decrease. Here we thus face a principal problem of why 1D models cannot reproduce the statistics of reversals in Mg II lines. The situation is improved if we consider 1D models with zero microturbulent velocity (see Fig. 20). One thing is that the microturbulence generally smears the line peaks so that for its lower values the peaks should be higher. However, we also found another reason for strengthening the peaks, which is the effect of partial redistribution (PRD) on peak intensity at low values of microturbulent velocity. As mentioned in Heinzel et al. (2014a), the Mg II line peaks are formed roughly under complete-redistribution (CRD) conditions for models with ξ = 5 km s−1. However, if ξ is small, reaching zero, the peaks are formed already in the PRD regime and thus they reflect the quasi-coherent scattering of the incident peaked radiation, similar to the case of hydrogen Lα. A comparison between PRD and CRD clearly shows this additional effect of the peak enhancement. Our conclusion regarding the Mg II line reversals is that the profiles synthesized from 1D isothermal-isobaric models have smaller reversals than the observed profiles, even when the microturbulent velocity is zero at the extreme. We note that synthetic profiles are sharply peaked in many cases, but these peaks are smeared by the convolution with the IRIS instrumental profile, which is necessary to compare with observations. As a next step, we therefore need to perform simulations of heterogeneous prominence structures with random velocities (Gunár et al. 2008) to see whether they can give results more consistent with current observations.
We have analyzed statistically the peak asymmetry for Mg II and C II 1334 reversed profiles. The histograms show that the red-peak asymmetry slightly dominates, but for the Mg II h line the histogram is rather symmetrical. These results indicate that the peak asymmetry might be due to the random motions of prominence fine structures rather than due to some systematic flows (oscillations or propagating waves). A similar kind of asymmetry was already detected in prominences for hydrogen Lyman lines, where the asymmetry varied from pixel to pixel. This was successfully modeled by Gunár et al. (2010) and Schwartz et al. (2015) in terms of 2D multi-thread structures with prescribed LOS random velocities up to 10 km s−1. In a following paper we will use such 2D models to predict the Mg II line profiles. We note that 10 km s−1 corresponds to a Doppler shift of 0.1 Å for Mg II lines, which is comparable to peak separation from the line center. We therefore expect an important effect of such fine-structure motions on both the line reversal as well as on the peak asymmetry and this cannot be achieved using simple 1D static slab models.
Finally, our analysis of Si IV line intensities using CHIANTI near the line formation temperature, for characteristic gas pressures in a quiescent prominence, gives the LOS effective thicknesses of the PCTR. We plan to extend this kind of analysis also to our 2D fine-structure models with PCTR depending on the orientation of the prominence magnetic field (see, e.g., Gunár et al. 2010, 2014; Gunár & Mackay 2015). A possible role of radiative excitation in the Si IV line is also a subject to be investigated (see, e.g., Gontikakis & Vial 2016).
In a following study we will also use the same grid of 1D models to synthesize C II lines (work in progress) and to compare the results with current observations. However, our ultimate goal is to perform 2D multi-thread radiative transfer simulations for prescribed distribution of the LOS velocities and shapes of the PCTR and to synthesize all IRIS lines analyzed in this paper. Similar simulations have been done already for hydrogen Lyman lines (Gunár et al. 2010, 2012; Berlicki et al. 2011; Schwartz et al. 2015). To compare with observations, we will use SOHO/SUMER Lyman spectra and our ground-based observations in the various lines that are available for this prominence.
Movies
Movie of Fig. 1 Access here
Movie of Fig. 7 Access here
Acknowledgments
SJ, PH, and SG acknowledge support from the Czech Science Foundation (GAČR) through the grant No. 16-18495S. SJ acknowledges financial support from the Slovenian Research Agency No. P1-0188. PS acknowledges support from the project VEGA 2/0004/16 of the Science Agency. PS and SG acknowledge support from the Joint Mobility Project of Academy of Sciences of the Czech Republic and Slovak Academy of Sciences No. SAV-AVČR-18-03. PH and SG acknowledge support from grant 16-17586S of the Czech Science Foundation (GAČR). SJ, PH, MZ, and SG acknowledge support from project RVO:67985815 of the Astronomical Institute of the Czech Academy of Sciences. CHIANTI is a collaborative project involving George Mason University (USA), the University of Michigan (USA) and the University of Cambridge (UK). We thank the anonymous referee for useful comments.
References
- Arregui, I., Oliver, R., & Ballester, J. L. 2012, Liv. Rev. Sol. Phys., 9, 2 [Google Scholar]
- Berlicki, A., Gunár, S., Heinzel, P., Schmieder, B., & Schwartz, P. 2011, A&A, 530, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014, Sol. Phys., 289, 2733 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, G., Dere, K. P., Young, P. R., Landi, E., & Mason, H. E. 2015, A&A, 582, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gontikakis, C., & Vial, J.-C. 2016, A&A, 590, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S. 2014, IAU Symp., 300, 59 [Google Scholar]
- Gunár, S., & Mackay, D. H. 2015, ApJ, 803, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Gunár, S., Heinzel, P., Anzer, U., & Schmieder, B. 2008, A&A, 490, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Schwartz, P., Schmieder, B., Heinzel, P., & Anzer, U. 2010, A&A, 514, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Mein, P., Schmieder, B., Heinzel, P., & Mein, N. 2012, A&A, 543, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gunár, S., Schwartz, P., Dudík, J., et al. 2014, A&A, 567, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P. 2007, ASP Conf. Ser., 368, 271 [NASA ADS] [Google Scholar]
- Heinzel, P., Vial, J.-C., & Anzer, U. 2014a, A&A, 564, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., Zapiór, M., Oliver, R., & Ballester, J. L. 2014b, A&A, 562, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinzel, P., Schmieder, B., Mein, N., & Gunár, S. 2015, ApJ, 800, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Heinzel, P., Susino, R., Jejčič, S., Bemporad, A., & Anzer, U. 2016, A&A, 589, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jejčič, S., Susino, R., Heinzel, P., et al. 2017, A&A, 607, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kleint, L., Heinzel, P., Judge, P., & Krucker, S. 2016, ApJ, 816, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Kotrč, P. 2009, Cent. Eur. Astrophys. Bull., 33, 327 [NASA ADS] [Google Scholar]
- Kučera, A., Ambróz, J., Gömöry, P., Kozák, M., & Rybák, J. 2010, Contrib. Astron. Obs. Skalnate Pleso, 40, 135 [Google Scholar]
- Labrosse, N., Heinzel, P., Vial, J.-C., et al. 2010, Space Sci. Rev., 151, 243 [Google Scholar]
- Levens, P. J., Schmieder, B., Labrosse, N., & López Ariste, A. 2016, ApJ, 818, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Levens, P. J., Labrosse, N., Schmieder, B., López Ariste, A., & Fletcher, L. 2017, A&A, 607, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, Y., Engvold, O., Rouppe van der Voort, L.,Wiik, J. E., & Berger, T. E. 2005, Sol. Phys., 226, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., De Pontieu, B., Vial, J.-C., et al. 2015, ApJ, 803, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D., Karpen, J., Ballester, J., Schmieder, B., & Aulanier, G. 2010, Space Sci. Rev., 151, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R., & Ballester, J. L. 2002, Sol. Phys., 206, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Parenti, S. 2014, Liv. Rev. Sol. Phys., 11, 1 [Google Scholar]
- Rathore, B., Carlsson, M., Leenaarts, J., & De Pontieu, B. 2015, ApJ, 811, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Malherbe, J.-M., & Wu, S. T., 2014a, Nature of Prominences and their Role in Space Weather, IAU Symp., 300 [Google Scholar]
- Schmieder, B., Tian, H., Kucera, T., et al. 2014b, A&A, 569, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwartz, P., Gunár, S., & Curdt, W. 2015, A&A, 577, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terradas, J., Molowny-Horas, R., Wiehr, E., et al. 2002, A&A, 393, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vial, J.-C., & Engvold, O., 2015, Solar Prominences, ASSL, 415 [Google Scholar]
- Wilhelm, K., Curdt, W., Marsch, E., et al. 1995, Sol. Phys., 162, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Zapiór, M., Kotrč, P., Rudawy, P., & Oliver, R. 2015, Sol. Phys., 290, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Zapiór, M., Oliver, R., Ballester, J. L., & Heinzel, P. 2016, ApJ, 827, 131 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Correlation coefficients for a given section between both integrated intensities of Mg II lines and both C II lines together with combinations of Mg II, C II, and Si IV lines.
Correlation coefficients for a given section between integrated intensities and central intensities for Mg II k line, Mg II h line, and C II 1334 line.
Values of typical gas pressures for quiescent prominences, electron densities, contribution functions, and geometrical thicknesses of hotter envelope of the prominence at approximate Si IV line formation temperature 80 000 K.
All Figures
 |
Fig. 1. SJI in Mg II 2796 Å channel obtained at 09:12:53 UT corresponding to eighth slit position of eighth raster of prominence observation. An area around the slit position is zoomed for better visibility. Five sections selected for analysis are marked by color bars in the right panel. The movie corresponding to this figure is available online where the white box indicates the range of data we used for analysis. |
| In the text | |
 |
Fig. 2. Example of Mg II k and h spectra at 2796 and 2803 Å (left panel), C II spectra at 1334 and 1336 Å (middle panel), and Si IV spectrum at 1394 Å (right panel) at 9:12:53 UT as indicated in Fig. 1. |
| In the text | |
 |
Fig. 3. Example of Mg II k and h profiles at 2796 and 2803 Å (left panel), C II profiles at 1334 and 1336 Å (middle panel), and Si IV profile at 1394 Å (right panel) for the middle section along the slit at 9:12:53 UT (see Fig. 1). |
| In the text | |
 |
Fig. 4. Examples of temporal evolution of integrated intensity of Mg II, C II, and Si IV lines for fourth slit position and five selected sections (left panel) and corresponding Scargle periodograms (right panel). Color coding is the same as in Fig. 1. Dashed lines show 1% and 5% FAP levels. |
| In the text | |
 |
Fig. 5. Temporal evolution of central intensity of Mg II k (left panel), Mg II h (middle panel), and C II ,1334 (right panel) lines for fourth slit position and five selected sections. |
| In the text | |
 |
Fig. 6. Examples of Doppler velocity of Mg II and C II lines for fourth slit position and selected sections (left panel) and corresponding Scargle periodograms (right panel). Dashed lines show 1% and 5% FAP levels. |
| In the text | |
 |
Fig. 7. Dopplergrams for Mg II and C II lines (left panel) together with 2D maps of integrated intensity (right panel). The movie corresponding to this figure is available online. |
| In the text | |
 |
Fig. 8. Spectral power of the Doppler signal (left panel) and maximum intensity signal (right panel). Each rectangle corresponds to the spectral line indicated above. Red curves limit areas with FAP < 1%. |
| In the text | |
 |
Fig. 9. Comparison between integrated intensity emitted in the Mg II h line~and integrated intensity emitted in the Mg II k line for five selected sections (upper panel) and ratio of integrated intensities between Mg II k and Mg II h lines as function of integrated intensity emitted in Mg II k line (lower panel). |
| In the text | |
 |
Fig. 10. Comparison between integrated intensity emitted in C II 1336 line and integrated intensity emitted in C II 1334 line for five selected sections. |
| In the text | |
 |
Fig. 11. Comparison between integrated intensities of Mg II k and C II 1334 lines (left panel), Mg II k line and Si IV line (middle panel), and C II 1334 line and Si IV line (right panel) for five selected sections. |
| In the text | |
 |
Fig. 12. Comparison between reversal ratio and integrated intensity of Mg II k line (left panel), Mg II h line (middle panel), and C II 1334 line (right panel) for five selected sections. |
| In the text | |
 |
Fig. 13. Blue to red peak intensity distribution of reversed profiles for Mg II and C II 1334 lines. |
| In the text | |
 |
Fig. 14. Comparison between Doppler velocities of Mg II lines (left panel) and Mg II k and C II 1334 lines (right panel) for five selected sections. |
| In the text | |
 |
Fig. 15. Peaks separation of Mg II k line versus C II 1334 line (left panel) and Mg II h line versus C II 1334 line (right panel). The dashed straight line shows the theoretical relation between the lines. |
| In the text | |
 |
Fig. 16. Integrated intensity of Mg II lines as a function of optical thickness for different temperatures at three representative microturbulent velocities. |
| In the text | |
 |
Fig. 17. Reversal ratio of Mg II lines as a function of optical thickness for different temperatures at three representative microturbulent velocities. |
| In the text | |
 |
Fig. 18. Integrated intensity emitted in Mg II h line versus Mg II k line for all 343 model points at different temperatures (left panels). Right panels: ratio of integrated intensity of the Mg II k line to the Mg II h line versus the integrated intensity of the Mg II k line for different temperatures at three representative microturbulent velocities. |
| In the text | |
 |
Fig. 19. Ratio of Mg II k to Mg II h integrated intensities as function of temperature at zero microturbulence (left panel), 5 km s−1 (middle panel), and 8 km s−1 (right panel). The black asterisk symbols show the average ratio at a given temperature. The horizontal black dashed line marks the observed average value of 1.365. |
| In the text | |
 |
Fig. 20. Reversal ratio versus integrated intensity of Mg II lines for different temperatures at three representative microturbulent velocities. |
| In the text | |
 |
Fig. 21. Integrated intensity emitted in Mg II line as function of emission measure for different temperatures at three representative microturbulent velocities. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.