| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201832992 | |
| Published online | 24 October 2018 | |
Stellar masses, metallicity gradients, and suppressed star formation revealed in a new sample of absorption selected galaxies
1
Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
e-mail: henrikrhodin@dark-cosmology.dk
2
European Southern Observatory, Karl-Schwarzchildstrasse 2, 85748 Garching bei München, Germany
3
Australian Astronomical Observatory, PO Box 915, North Ryde, NSW 1670, Australia
4
The Cosmic Dawn Center, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen Ø, Denmark
Received:
9
March
2018
Accepted:
2
July
2018
Context. Absorbing galaxies are selected via the detection of characteristic absorption lines which their gas-rich media imprint in the spectra of distant light-beacons. The proximity of the typically faint foreground absorbing galaxies to bright background sources makes it challenging to robustly identify these in emission, and hence to characterise their relation to the general galaxy population.
Aims. We search for emission to confirm and characterise ten galaxies hosting damped, metal-rich quasar absorbers at redshift z < 1.
Methods. We identified the absorbing galaxies by matching spectroscopic absorption -and emission redshifts and from projected separations. Combining emission-line diagnostics with existing absorption spectroscopy and photometry of quasar-fields hosting metal-rich, damped absorbers, we compare our new detections with reference samples and place them on scaling relations.
Results. We spectroscopically confirm seven galaxies harbouring damped absorbers (a 70% success-rate). Our results conform to the emerging picture that neutral gas on scales of tens of kpc in galaxies is what causes the characteristic H I absorption. Our key results are: (I) Absorbing galaxies with log10[M⋆,(M⊙)] ≳ 10 have star formation rates that are lower than predicted for the main sequence of star formation. (II) The distribution of impact parameter with H I column density and with absorption-metallicity for absorbing galaxies at z ∼ 2–3 extends to z ∼ 0.7 and to lower H I column densities. (III) A robust mean metallicity gradient of ⟨Γ⟩ = −0.022 ± 0.001 dex kpc−1. (IV) By correcting absorption metallicities for ⟨Γ⟩ and imposing a truncation-radius at 12 kpc, absorbing galaxies fall on top of predicted mass-metallicity relations, with a statistically significant decrease in scatter.
Key words: Galaxy: halo / galaxies: evolution / galaxies: distances and redshifts / galaxies: stellar content / galaxies: star formation
© ESO 2018
1. Introduction
Scaling relations between galaxy observables (direct measurements and derived quantities) allow us to probe what drives galaxy evolution, and act as standard tests for simulations. Historically, scaling relations have been derived for luminosity-selected samples. In particular, such selection criteria have revealed a redshift-dependent relation between the galaxy stellar mass (M⋆) and the gas-phase metallicity (Zgas) in the redshift range z ∼ 0.1–3.5 (Tremonti et al. 2004; Savaglio et al. 2005; Erb et al. 2006; Maiolino et al. 2008); and a relation between M⋆ and star formation rate (SFR; Noeske et al. 2007). These relations were combined as projections of a fundamental redshift-invariant relation tying M⋆, Zgas, and SFR together (Mannucci et al. 2010).
Complementing these luminosity selections, galaxies can be selected via their absorption cross-section in neutral gas when there is a chance alignment of the target with a background quasar along the line of sight. Such configurations imprint strong characteristic absorption lines in the quasar spectrum, caused by the high column density H I gas in either discs, circum-galactic material (CGM) or galaxy haloes. The strongest classes of absorbers are the damped Lyman-α systems (DLAs) with neutral hydrogen column densities log10[NHI (cm−2)] ≥ 20.3 (Wolfe et al. 1986), and the sub-DLAs with column densities of 19.0 ≤ log10 [NHI (cm−2)] < 20.3 (Péroux et al. 2003; Zafar et al. 2013b). Both classes have characteristic Lorentzian damping wings associated with their Lyman-α profiles. Unless otherwise specified, we refer to sub-DLAs and DLAs uniformly as damped absorbers.
With a detectability that is independent of the host galaxy’s brightness, damped absorbers are believed to sample the general galaxy population in a more representative manner, probing a larger dynamic range in stellar mass, gas-phase metallicity, star formation rate and morphology at any redshift. Indeed, this assertion was confirmed by comparing how absorption- and luminosity-selections sample the underlying luminosity function (Berry et al. 2016; Krogager et al. 2017).
This implies that a pure H I selection based on damped absorbers, on average samples lower-mass systems, often below the detection-limit in emission (Fynbo et al. 1999, 2008, 2010; Møller et al. 2002; Pontzen et al. 2008; Krogager et al. 2012; Rahmati & Schaye 2014; Fumagalli et al. 2015). In combination with a small projected separation to the absorption, which causes the quasar to dominate the light-throughout in a blended point spread function (PSF), this has led to a low average detection rate (∼10%) of confirmed counterparts (Møller & Warren 1998; Christensen et al. 2007; Monier et al. 2009; Fynbo et al. 2010, 2011, 2013a; Meiring et al. 2011; Krogager et al. 2012, 2013; Noterdaeme et al. 2012a; Péroux et al. 2012; Rahmani et al. 2016). This has prevented us from characterising the connection the majority of absorbers hold to their galaxy hosts. But presumably, sub-DLAs and DLAs on average sample different environments.
The DLA population contains the bulk of neutral gas throughout cosmic time (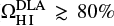 ; Prochaska et al. 2005; Noterdaeme et al. 2009, 2012b), and displays a weak redshift-evolution by a factor of ∼3 from redshift z ∼ 5 to the local universe (Neeleman et al. 2016a). Sub-DLAs account for the bulk of the remaining fraction in the redshift range 1.5 < z < 5.0 (
; Prochaska et al. 2005; Noterdaeme et al. 2009, 2012b), and displays a weak redshift-evolution by a factor of ∼3 from redshift z ∼ 5 to the local universe (Neeleman et al. 2016a). Sub-DLAs account for the bulk of the remaining fraction in the redshift range 1.5 < z < 5.0 (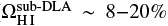 ; Zafar et al. 2013a), the Lyman limit systems (LLS, 17 ≤ log10[NH I (cm−2)] < 19.0) and Lyα forest (log10[NH I (cm−2)] < 17.0) only contributing minor fractions to the total neutral gas content (Songaila & Cowie 2010).
; Zafar et al. 2013a), the Lyman limit systems (LLS, 17 ≤ log10[NH I (cm−2)] < 19.0) and Lyα forest (log10[NH I (cm−2)] < 17.0) only contributing minor fractions to the total neutral gas content (Songaila & Cowie 2010).
The chemical enrichment of the DLA population evolves from ∼1% solar metallicity at z = 5 to ∼10% solar metallicity in the local universe, with a ∼2 dex metallicity-spread at all redshifts (Pettini et al. 1994; Ledoux et al. 2002; Prochaska et al. 2003; Rafelski et al. 2014). This evolution and its scatter is sensitive to the underlying selection function, and can be understood as an interplay between (i) drawing from the full galaxy population at every redshift; (ii) the existence of a mass-metallicity relation at every redshift (Ledoux et al. 2005; Møller et al. 2013; Christensen et al. 2014); and (iii) a metallicity gradient within each galaxy reflecting the gradual build-up of metals in the interstellar medium (ISM) and CGM by stellar feedback and supernovae explosions. Although metallicity measurements in sub-DLAs rely on ionisation corrections (see e.g., Zafar et al. 2017), these systems are believed to be more chemically enriched than DLAs on average – in particular at low redshifts (Péroux et al. 2006; Kulkarni et al. 2007; Meiring et al. 2009; Som et al. 2013, 2015), and there are indications that sub-DLAs arise in more massive galaxies (Kulkarni et al. 2010), which may be caused by selection biases (Dessauges-Zavadsky et al. 2009).
The existence of a statistically significant anti-correlation between log10[NH I (cm−2)] and projected separation based on photometric redshift identifications of hosts was demonstrated by Rao et al. (2011). This is consistent with spectroscopically confirmed systems which indicate that absorbers are distributed over different impact parameters; sub-DLAs showing larger and more scattered impact parameters than DLAs (Møller & Warren 1998; Christensen et al. 2007; Monier et al. 2009; Fynbo et al. 2010, 2011, 2013a; Meiring et al. 2011; Krogager et al. 2012, 2013; Noterdaeme et al. 2012a; Péroux et al. 2012; Rahmani et al. 2016). This distribution is observed in z ≳ 2 simulations, and is attributed to the complex distribution- and flow of H I-gas (Pontzen et al. 2008; Rahmati & Schaye 2014). In addition, the distribution of impact parameters correlates with absorption metallicity ([M/H]abs), suggesting that DLAs probe the size of gaseous discs. This is supported by modelling DLAs as sight-lines through randomly inclined discs in high-z Lyman break galaxies (LBG), which shows that the two are drawn from the same underlying distribution above z ∼ 2 (Møller et al. 2004; Fynbo et al. 2008; Krogager et al. 2017).
Recent developments found a scaling relation that tie velocity-widths of metal lines in absorption to the absorber metallicity (the ΔV90 − [M/H]abs relation). This relation is redshift-dependent (Ledoux et al. 2006; Møller et al. 2013; Neeleman et al. 2013), column-density-dependent (Som et al. 2015), and is interpreted as the absorber equivalent of the MZ-relation. Recognising that the relation can be used to target the most metal-rich absorbers has significantly increased the detection rate of absorbing galaxies in emission to ∼60–70 %, because these are associated with more massive and therefore more luminous galaxies (Fynbo et al. 2010, 2011, 2013a; Krogager et al. 2012, 2013; Noterdaeme et al. 2012a; Péroux et al. 2012; Bouché et al. 2013; Rahmani et al. 2016). Connecting the ΔV90 − [M/H]abs relation to the MZ-relation, Møller et al. (2013) predicted stellar masses in functional form f([M/H]abs, zabs), including a free parameter C[M/H] to reconcile the difference between absorption- and emission-line metallicities. The relation was verified directly by comparing the stellar masses from the functional form to those derived from spectral energy distribution (SED)-fits, spanning three orders of magnitude in stellar mass (Christensen et al. 2014).
To characterise absorption selected galaxies and how they relate to the general galaxy population hinges on the low number of spectroscopically confirmed systems with complementary data in absorption and emission. Here, we attempt to rectify this issue by reporting our results from a long-slit spectroscopic follow-up of candidate hosts at redshifts z < 1.
The paper is organised as follows: Sect. 2 describes the sample selection, observations and archival data; Sect. 3 presents our spectroscopic measurements, extracted physical parameters and stellar masses of the absorbing galaxies. In Sect. 4 we combine with literature samples to investigate distributions and scaling relations. In Sect. 5 we summarise our conclusions. Throughout this paper we assume a flat Λ cold dark matter (ΛCDM) cosmology, with H0 = 70.4 kms−1 Mpc−1 and ΩΛ = 0.727 (Komatsu et al. 2011).
2. Observations and data-reduction
2.1. Sample selection
The sample represents the observed subset of targets as part of a programme to provide spectroscopic redshift-confirmation of damped absorber (log10[NH I (cm−2)] > 19.5) counterparts at low (zabs < 1) redshifts (programme ID 095.A-0890(A); PI: L. Christensen). We proposed ten quasar fields including 12 absorbers for long-slit spectroscopic observations with the ESO/VLT FOcal Reducer and low dispersion Spectrograph 2 (FORS2; Appenzeller et al. 1998). See Sect. 2.2 for more details. However, only eight quasar fields containing ten absorbers were observed. Of these eight quasar fields, Q 1436–0051 and Q 1209+107 both contain two absorbers each. The spatial positions of the candidate-hosts of both absorbers towards Q 1436–0051 allowed them to be observed with a single slit placement, whilst the candidate-hosts in the Q 1209+107 quasar field required two different slit-alignments (PA1 and PA2). In sum, we therefore report the results for nine slit alignments targeting ten absorbers.
Absorber characteristics and photometry of the candidate host galaxies explored with our FORS2 campaign.
Observation log for the VLT/FORS2 long-slit spectroscopic observations of damped absorbing galaxies.
We selected targets with metallicities [M/H]abs ≳ −1 as inferred from relative element ratios measured in high resolution spectra (Table 1 and references therein), and that have a tentative galaxy counterpart based on projected separation and photometric redshift solutions consistent with zabs (Rao et al. 2011). Zinc is minimally depleted onto dust which allowed us to use it as a direct tracer-element for the absorption-metallicity (but see De Cia et al. 2018 for evidence of marginal depletion of zinc onto dust grains, in which case zinc represents a lower limit). For objects where we only had access to iron and chromium measurements, we inferred the absorption metallicity by applying a constant correction factor of 0.3 dex to account for depletion and α–enhancement (Rafelski et al. 2012, our Sect. 3.9). The physical properties of the targets are summarised in Table 1.
At z < 1.65, Lyα falls in the UV. This restricts H I column-density measurements to the systems observed with expensive and competitive space-based observatories. However, damped H I absorbers are accompanied by low-ionisation metal absorption lines, including singly ionised magnesium which is a tracer of DLAs (Rao et al. 2006). For z > 0.11, the Mg II λλ 2796, 2803 Å doublet falls in the optical spectral region, where it is an efficient proxy for damped absorbers (e.g., Ellison 2006; Berg et al. 2017). Our sample was therefore selected from a set of sub-DLA and DLAs with reliable HST H I column-density measurements, initially identified as strong Mg II absorbers.
A large fraction of our targeted absorbers are located at redshifts z ∼ 0.7, originating from the redshift distribution of the imaging campaigns from which they were drawn1. The distribution peaking at this value reflects the tradeoff between a lower number density of LLS, sub-DLAs, and DLAs towards low redshift (Rao et al. 2006; Zafar et al. 2013a) and an increased limiting luminosity towards higher redshifts which prevents the identification of candidate absorbing galaxies from photometric redshift methods (Rao et al. 2011). We targeted standard diagnostic nebulae lines in emission to characterise the galaxies. This allowed us to directly observe how absorbing galaxies fall relative to scaling relations derived from deep imaging surveys of luminosity-selected samples at similar redshifts (Savaglio et al. 2005; Maiolino et al. 2008; Karim et al. 2011; Stott et al. 2014; Whitaker et al. 2014).
2.2. VLT FORS2 data
Long-slit spectra were taken in nine slit-alignments2. The log of observations for the different fields, including slit configuration and average seeing-conditions measured in the reduced spectra are listed in Table 2. The observations were taken with a 1.31 arcsec slit-width, and the slit was aligned to cover both the quasar and the candidate host with relative coordinates based on archival imaging. The observations were carried out with the 600RI and the 600z grisms, covering wavelength-ranges of λλ5120 − 8450 Å and λλ7370 − 10 700 Å at a nominal spectral resolution ℛ600RI = 1000 and ℛ600z = 1390 assuming 1.0 arcsec slit-widths, respectively (Boffin et al. 2015). For all the observations, we used a 2 × 2 binning configuration along spatial and spectral directions.
Line-flux measurements.
We performed a cosmic-ray removal on the raw data frames with P3D (Sandin et al. 2010), an adaptation of the L.A.Cosmic algorithm (van Dokkum 2001). Each frame was subsequently reduced in a standard manner by passing it through the ESO/Reflex pipeline version 5.1.4 (Freudling et al. 2013). Individual exposures were combined into 2D spectra for each object using the average pixel value and a sigma-clipping rejection. In three cases (Q 0153+0009, Q 1209+107 PA1, and Q 1436–0051), the pipeline did an unsatisfactory sky-subtraction, and we post-processed the intermediate Reflex products of those observations with standard IRAF tasks.
For each science-frame, the host-galaxy was flux-calibrated by extracting 1D-spectra of the quasar and target, scaling the quasar spectrum to its Sloan Digital Sky Survey data release 10 (SDSS DR10, Ahn et al. 2014) counterpart, and applying this scaling-solution to the target spectrum. For point-sources, this prevented temporally varying seeing and slit-losses from propagating into systematic errors which would have been introduced in calibrating against spectrophotometric standard stars. However, it did not account for any flux variation caused by intrinsic quasar variability. Based on the the same FORS2 data for Q 1323–0021, Møller et al. (2018) quantified the effect of quasar variability on the flux-calibration. In their work, they found that flux-measurements were correct to within a factor of two, with quasar variability responsible for ∼10%, and slit-losses for the remaining fraction.
The SDSS catalogue does not cover HE 1122–1649. In this field, we assumed that the transmission was the same as for the other fields observed with the same instrument settings. This allowed us to calculate an average sensitivity function which we used to flux-calibrate the target spectrum in the HE 1122–1649 field. Based on five sensitivity functions, we calculated an RMS of 0.5–0.8 × 10−17 ergs s−1 cm−2 in the wavelength region λλ6000-8000 Å. This RMS value is of the same order as integrated line-flux uncertainties (see Table 3), and accounts for weather conditions, slit-losses and quasar variability effects. We therefore confirm that the flux-calibration is robust, and verify that quasar variability, on average, is a minor effect.
To test if a systematic offset in the wavelength-solution exists and to determine velocity-dispersions, we measured central wavelengths and the full-width-half-maximum (FWHM) of skylines proximate to object emission lines in the 2D spectra. Gaussian- and Voigt profile-fitting ensured accurate central wavelengths, but systematically underestimated the FWHM measurements. The central wavelengths were measured against the Ultra-Violet and Echelle Spectrograph (UVES) telluric line catalogue (Hanuschik 2003), yielding an effective offset in the wavelength-solution reported in Table 2. With non-parametric FWHM measurements, we confirm the nominal instrumental resolutions3 renormalised to a 1.31 arcsec slit-width which gives effective resolutions ℛ600RI = 763 (∼393 km s−1) and ℛ600z = 1061 (∼283 km s−1).
2.3. Archival data
In addition to the FORS2 observations described in Sect. 2.2, we compiled the archival data that we required in each of the targeted fields. This included the Galactic extinction towards the lines of sight, the absorber characteristics (zabs, log10[NH I (cm−2)], [M/H]abs) and the candidate host characteristics (zphot and photometry).
The photometry was predominantly taken from Rao et al. (2011), with optical images obtained at the Kitt Peak National Observatory (KPNO) with standard SDSS u′, g′, r′, i′ filters, and near-IR (NIR) images obtained at the Mauna Kea Observatory with the NASA Infrared Telescope’s NSFCAM J, H, K filter set. Exceptions to this included the HE 1122–1649 field, for which all photometry was taken with the du Pont Telescope at the Las Campanas Observatory (Chen & Lanzetta 2003) and the Q 1323–0021 m11200 Å and m13500 Å, for which magnitudes were measured in the collapsed 1D-spectrum (Møller et al. 2018). Where required, we applied Galactic extinction corrections to the photometric magnitudes. Here we note that the magnitudes in the HE 1122-1649 field reported in Chen & Lanzetta (2003) were corrected for Schlegel & Finkbeiner Davis (1998) extinctions. We therefore calculated conversion factors to the re-calibrated Schlafly & Finkbeiner (2011) maps and report these instead. All values and references to each entry are summarised in Table 1.
2.4. NIR photometry for Q 1436–0051
The vicinity of Q 1436–0051 has been studied extensively because it is a crowded field, hosting two absorbers in the quasar spectrum (a sub-DLA at zabs = 0.7377 and a LLS at zabs = 0.9281) and eight objects within a 30×30 arcsec perimeter centred on the quasar (Rao et al. 2011). Of special interest is an object at an impact parameter of 6.4 arcsec, where SDSS reports two source detections, classifying the combined object as a blend of an extended object with zphot = 0.622 ± 0.139 and a star. Rao et al. (2011) considered the same system to be a single object (their object 3), and therefore reported a combined magnitude. With optical photometry, Meiring et al. (2011) resolved the object into two extended objects (their objects 6 and 7) consistent with the redshift of the sub-DLA, likely forming an interacting pair of galaxies (Meiring et al. 2011; Straka et al. 2016).
The slit in our FORS2 observations of Q 1436–0051 was aligned to cover this galaxy configuration. To solve for the stellar mass of each component (see Sect. 3.6), we acquired the calibrated J, H, and K band images used in Rao et al. (2011) from private communication with Sandhya M. Rao, and performed aperture photometry with SExtractor (Bertin & Arnouts 1996) version 2.19.5. We obtained isophotal flux measurements for which we required a 2σ detection threshold above the RMS noise level in the image and that a source encompassed a minimum of five pixels in the detection isophote. With these criteria in place, we resolved the two objects in the K-band image and ensured that we measured a representative flux-ratio of the interacting galaxies by accounting for flux in the extended wings of their flux profiles. We constructed a K-band catalogue for object identification, and used it to extract the flux for each of the two galaxies in the J and H bands. The measured flux-ratios of the components in each band were combined with the total magnitudes (Rao et al. 2011) to assign individual magnitudes to each of the interacting components. The resulting magnitudes are reported in Table 1, and complement the optical photometry in the SED-fitting procedure (see Sect. 3.6).
3. Results
3.1. Spectral point spread function subtraction
To scan the quasar PSF for hidden objects and recover their spectral signatures in search for the absorbing galaxies, we subtracted the quasar continua in a process known as spectral PSF (SPSF) subtraction (Møller 2000; Møller et al. 2000). Conceptually, a model of the quasar trace in the 2D-spectrum was constructed. The model was then subtracted out to isolate line-emission from objects at small projected separations to the quasar. Variations of SPSF subtraction procedures have been used in prior studies, specifically constructed to find metal emission lines in high-redshift DLA galaxies (Møller et al. 2002, 2018; Fynbo et al. 2010, 2013a; Zafar et al. 2011; Krogager et al. 2013).
Here, we built a non-parametric, empirical model of the quasar PSF by averaging the observed spatial profile in two spectral windows immediately bluewards and redwards of each predicted emission-line feature for each science frame. We confirmed that the quasar trace has no gradient along the dispersion direction to within sub-pixel precision. We then assumed that the PSF profile did not vary with wavelength and that the quasar continuum emission could be modelled as a pure power-law across the covered wavelength range. With these assumptions in place, we scaled the strength of the modelled quasar PSF at each wavelength, and the resulting SPSF model was subtracted from the 2D-spectrum.
 |
Fig. 1. Negative colour-mapped two-dimensional VLT/FORS2 SPSF-subtracted spectra (top panels), and the extracted one-dimensional spectra (black; lower panels), centred on the [O II] λ λ 3727,3729 Å doublet. Left panel: Q 1323–0021 field shows excess emission from the DLA counterpart extending above the quasar-trace. Right panel: Q 2328+0022 reveals the presence of the DLA counterpart offset from the trace. In both panels, the fitted doublet-components are overplotted in orange, with the resulting emission profiles in purple. |
Resulting parameters for our sample of absorbing galaxies.
In eight out of ten targeted systems we identified the absorbing galaxy from emission lines at the expected wavelengths (see Table 3). In six of these systems emission lines were detected directly in the science frames, without performing SPSF subtractions. This allowed us to measure line-fluxes without the addition of noise. In passing, we note that the SPSF-subtracted spectrum of Q 1209+107 PA2 did not reveal hidden emission lines from an object at small impact parameter. Instead, we confirm the detection of emission lines at z = 0.3922 in the object first reported by Cristiani (1987) which then remains the best candidate host in that field. Two additional objects were identified as the absorbing galaxies after performing SPSF subtractions (Q 1323–0021 and Q 2328+0022, see Fig. 1). For these two systems, we varied the size and limits of the wavelength windows to see if the residual flux was real, or an artefact of the subtraction. In all realisations of the SPSF-subtraction residual flux was detected at the same locations in the 2D spectra, which confirmed that the signals were real (see Fig. 1). 1D-spectra covering the recovered spectral features of the absorbing galaxies were then extracted with a simple extraction using standard IRAF tasks. By applying a simple extraction, we avoided biasing the flux-measurement by the signal gradient across the quasar PSF (Møller 2000); an effect which would result from the standard optimal extraction weighting scheme (Horne 1986). We defined the extraction apertures relative to the quasar trace, with aperture limits [+0.38″: +1.26″] and [+0.38″: + 1.64″] for Q 1323–0021 and Q 2328+0022, respectively.
In the case of Q 1323–0021, the spatial structure observed in the emission line feature is indicative of a velocity gradient, which makes the redshift determination sensitive to the adopted aperture limits. We note that the extension of the signal below the quasar trace as observed in the 2D-spectrum appears to be real. However, the image statistics suggest that this extension is driven by noise. We therefore set a lower aperture limit ensuring that we only captured the real signal of the absorbing galaxy. Similarly, Møller et al. (2018) used the aperture limits [+0.25″: + 2.5″] above the quasar trace, attributing apparent flux beyond the aperture limits to quasar noise residuals from an imperfect SPSF-subtraction. We determined the redshift to be z[O II] = 0.71717 (see Tables 3 and 4) which is consistent with the Møller et al. (2018) measurement of zref = 0.7170 ± 0.0006.
3.2. Emission line measurements
The FORS2 wavelength coverage allows us to make line detections in [O II] λλ 3727,3729 Å, Hβ λ4861 Å and [O III] λλ4959,5007 Å. From here on, we use the abbreviations [O II], Hβ and [O III] to refer to these ion lines, respectively. We are able to confirm the counterparts to seven out of ten absorbers in eight quasar fields, that is, a conservative detection rate of 70% (see Sect. 3.4 for a discussion on an unlikely host, and Sect. 3.5 for a discussion on the two non-detections).
We extracted line-fluxes by fitting Gaussian profiles to each line, with continuum placement based on a linear fit to regions bluewards and redwards of the transition, free of telluric absorption and skylines. We allowed the slope and normalisation of the continuum and the centroid, linewidth, and amplitude of the line profile to vary in order to retrieve the optimal fit to all lines except for the [O II] line doublet. At the effective resolution of the FORS2 instrument and for the target redshifts, we could not resolve its individual components. We therefore fitted two Gaussian components simultaneously, fixing the linewidths to the same value, tying the centroid-separation to the redshift, and verifying that the best fit parameters yielded a line-ratio consistent with standard low-density nebulae conditions (Osterbrock & Ferland 2006).
Line-centres were converted to velocity space, helio-centric rest-frame corrections were applied, and each velocity solution was converted to a spectroscopic redshift (see Tables 3 and 4). We applied Galactic extinction corrections to the line-fluxes based on the EB−V values provided by the Schlafly & Finkbeiner (2011) extinction maps. Uncertainties in the line-fluxes reflect the propagated statistical errors in the profile fit.
To convert the fitted line-widths to velocity dispersions, σ, we subtracted the instrumental broadening ℛ (km s−1) (see Sect. 2.2) renormalised to the effective seeing, quadratically from the FWHM as
To determine the value of each σ and its errors, we assumed that the FWHM measurements had Gaussian-distributed errors. We then perturbed the FWHM measurements using the measurement uncertainty in the FWHM (see Table 3) to characterise the width of the distribution, centred on the measurement. Having simulated the data, we determined dispersions and errors as the median, 16th- and 84th percentile in the cumulative distribution function (CDF) of the real values below the square-root in Eq. (1).
3.3. Galaxy associations in the Q 1436–0051 field
Past observations indicate that absorbing galaxies can be related to galaxy associations in dense environments (Kacprzak et al. 2010; Rao et al. 2011; Christensen et al. 2014; Péroux et al. 2017). We found a remarkable example of such associations in the field Q 1436–0051, which was observed to host multiple galaxies that coincide with the redshifts of two damped absorbers (![$ \log _{10}[N_\mathrm{{H}\,{I}}\,(\mathrm{cm}^{-2})] = 20.08^{+0.10}_{-0.12} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq43.gif) at zabs = 0.737, and log10[NH I (cm−2)] = 18.40 ± 0.98, consistent with the lower limit of the definition for a sub-DLA, at zabs = 0.928). We confirm the presence of three galaxies at the zabs = 0.737 absorber redshift and two galaxies at the zabs = 0.928 absorber redshift, all remarkably lying within a single slit-position. We show the spatial configuration of these systems in the 2D FORS2 spectrum in Fig. A.1. Based on impact-parameter and redshift [b, zem] of the objects in the slit (see Table A.1), we found the most likely counterparts to be located at [45.5, 0.73749] and [34.9, 0.92886], which is consistent with Object 6 and Object 5, respectively, assuming the nomenclature of Meiring et al. (2011) and Straka et al. (2016). We also note that the host of the zabs = 0.737 absorber is likely part of an interacting system. This issue is discussed further in Sects. 3.6 and 3.8.
at zabs = 0.737, and log10[NH I (cm−2)] = 18.40 ± 0.98, consistent with the lower limit of the definition for a sub-DLA, at zabs = 0.928). We confirm the presence of three galaxies at the zabs = 0.737 absorber redshift and two galaxies at the zabs = 0.928 absorber redshift, all remarkably lying within a single slit-position. We show the spatial configuration of these systems in the 2D FORS2 spectrum in Fig. A.1. Based on impact-parameter and redshift [b, zem] of the objects in the slit (see Table A.1), we found the most likely counterparts to be located at [45.5, 0.73749] and [34.9, 0.92886], which is consistent with Object 6 and Object 5, respectively, assuming the nomenclature of Meiring et al. (2011) and Straka et al. (2016). We also note that the host of the zabs = 0.737 absorber is likely part of an interacting system. This issue is discussed further in Sects. 3.6 and 3.8.
3.4. Unlikely host in the Q 1209+107 PA2 field
The subsequent analysis of our entire sample (see Sect. 4) in relation to known scaling relations and luminosity-selected samples reveals that the candidate absorbing galaxy in the Q 1209+107 PA2 field occupies a unique place in the MZ (Sect. 4.3); on the star-forming main-sequence (Sect. 4.4); and in the metallicity-gradient (Sect. 4.5) parameter spaces. In particular, it is worrying that a low-mass (log10[M⋆ (M⊙)] ∼ 8.2) star-burst galaxy has a super-solar metallicity at a distance of 38 kpc from its luminosity-centre, when the emission-line diagnostics yield a low central oxygen abundance of [O/H] ∼ 8.05.
Guided by these results and discussions, we flag the absorbing galaxy as an unlikely host. Rather, its redshift, mass, metallicity and SFR are suggestive of a smaller member in a group environment around the real host. More likely, the real host is a more massive galaxy which is hiding below the quasar PSF. We note that the SPSF-subtraction did not reveal any hidden line-flux below the quasar trace. We therefore report upper limits on the line-flux from an object under the quasar trace as the 3σ residuals in a ±5 Å spectral window centred on the predicted emission lines in the SPSF-subtracted 1D-spectrum. We found consistent upper limits at a ∼2 × 10−17 ergs s−1 cm−2 flux-level at the predicted position of [O II] and Hβ alike. In the following analysis we treated this candidate as the host, but flagged it where possible, and excluded it in calculations of the statistical properties of the sample as it most likely is not the real host of the absorber. For more details, see the relevant sections.
3.5. Non-detections in the Q 2353–0028 and Q 1209+107 PA1 fields
In this section we discuss the two fields Q 2353–0028 and Q 1209+107 PA1. In these fields, our analyses was unable to identify the absorbing galaxies.
For Q 2353–0028 we observed a single prominent spectral feature associated with the candidate object at λobs = 6565.2 Å. However, this does not coincide with any of the emission lines for the assumed absorber redshift. At the absorber redshift (zabs = 0.6044), this corresponds to redshift differences of |Δz[O II]| = 0.16, |ΔzHβ| = 0.25, and |Δz[O III]| = 0.29, or equivalently to velocity offsets of |Δv[O II]| = 293378 km s−1, |ΔvHβ ∼ 47427 km s−1, and |Δv[O III]| ∼ 54778 km s−1. This leads us to refute the object as the host galaxy. We note that the emission feature is ∼2 Å redwards of the Hα λ6563 Å rest-wavelength, which would place the galaxy at a redshift zgal ∼ 0.0003. However, with no additional emission lines to corroborate with, we consider the low redshift solution unlikely. We note that the quasar itself is located at redshift 0.765 (Rao et al. 2006), and displays a strong [O II] λλ 3727,3729 Å narrow-line doublet at the expected wavelength λ[O II], QSO = 6578 Å. Interpreting the galaxy feature as [O II] emission at the quasar redshift gives a velocity blue-shift Δv[O II] (zQSO) ∼ 592 km s−1 between the quasar and object, which suggests that the observed emission originates from a galaxy in a group at the quasar redshift4. This is also consistent with the uncertain redshift solution based on broad-band photometry, zphot = 0.844 ± 0.300 (Rao et al. 2006).
In the case of PA1 of the Q 1209+107 field we did not find any spectral features of a host at the absorber redshift (zabs = 0.6295) in the SPSF-subtracted frame, nor a stellar continuum at the position of the candidate host. The stellar-continuum of the candidate host is too faint and too proximate (∼1.67 arcsec) to be spatially resolved from the quasar PSF. This prevents us from detecting the object, also from an expected Balmer discontinuity around λ 5940 Å.
3.6. Modelling the spectral energy distribution
We inferred stellar masses of the absorbing galaxies from modelling the spectral energy distribution (SED) with the LePhare code (Arnouts et al. 1999; Ilbert et al. 2006), fitted to broad-band photometric magnitudes corrected for Galactic extinction (Table 1) using the spectroscopically determined emission-line redshifts (Table 4). For matching the photometry, we used Bruzual & Charlot (2003; BC03) simple stellar population (SSP) spectral templates based on Padova 1994 stellar evolutionary tracks and a Chabrier (2003) IMF. The SSPs have exponentially declining star-formation rates, parametrised with fiducial stellar population ages and e-folding time-scales in the ranges [0.01:13.5] Gyrs and [0.1:30] Gyrs, respectively. To model the flux in each photometric band, the filter transmission curves for each instrument used to measure the original magnitudes were retrieved.
The best-fit SED minimises the χ2-statistic across a user-defined grid of free parameters. Our grid encompassed (i) an LMC attenuation-curve (Fitzpatrick & Massa 2007); (ii) a large range of intrinsic reddenings with EB−V ∈ [0.00:1.00] in incremental steps of 0.05 to ensure the preferred EB−V is associated with a χ2-minimum rather than a grid-boundary; (iii) the option to evaluate fits including- and excluding flux contribution from nebular emission.
The resulting SEDs of the absorbing galaxies are shown in Fig. 2, and stellar masses together with the EB−V values are reported in Table 4. Stellar masses and their uncertainties were determined as the median value and from the 16th- and 84th percentiles of a maximum likelihood analysis of the SED-fits χ2-distributions, respectively. We note that for the Q 1323–0021 field, we have priors on the nebular emission and on the EB−V based on detected emission lines and the dust-obscured star formation (Møller et al. 2018). For this object, we therefore prefer a model excluding the nebulae emission lines, and restrict the range of reddening to EB−V ∈ [0.00:0.30].
For Q 1323–0021, the i-band magnitude was removed from the SED-fit, motivated by strong residuals from the QSO PSF-subtraction (Rao et al. 2011). In the Q 1436–0051 field, we solved for M⋆ for both of the interacting components (see Sects. 2.4 and 3.3). In agreement with Rao et al. (2011), we found that the K-band photometry was unreliable. We therefore excluded it from the SED-fitting analysis. This resulted in stellar masses of log10[M⋆ (M⊙)] = 10.41 ± 0.10 and log10[M⋆ (M⊙)] = 9.79 ± 0.07, placing the absorbing galaxy in the category of a minor-merger.
3.7. Intrinsic extinction correction
For three galaxies in the fields of Q 0153+0009, Q 1209+107 PA2, and Q 1436–0051 we detected higher order Balmer-lines (see Table 3 for individual measurements). This allowed us to correct line-fluxes for intrinsic dust extinction based on the Balmer decrement (Eq. (2)). The broad-band colour excess is tied to the deviation in observed-to-intrinsic line-ratios as
where κ is the value of the attenuation curve at the rest-wavelength of the labelled line-transition and (Hβ/H5)obs is the observed flux ratio based on the entries in Table 3. (Hβ/H5)0 is the intrinsic flux ratio with an adopted value of 2.137 assuming case B recombination at T = 104 K and ne ∼ 102–104 cm−3 (Osterbrock & Ferland 2006). We adopted the Fitzpatrick & Massa (2007) LMC attenuation-curve with RV = AV / EB−V = 3.1, but note that extinction corrections based on Balmer lines are relatively insensitive to the choice of attenuation-curve as these behave similar redwards of the 2175 Å extinction bump.
 |
Fig. 2. Spectral energy distribution fits minimising the χ2-statistic for each of the spectroscopically identified host-galaxies. In each panel, we plot the solutions including and excluding nebular emission lines to show its impact on the derived stellar masses. Blue (red) data points refer to included (excluded) magnitudes, with vertical and horizontal error-bars indicating the uncertainty in the photometry and the FWHM of each filter, respectively. Grey squares refer to the transmission-weighted flux in each filter, calculated based on the best-fit SED solution. Upper limits are denoted by triangles. Each panel text displays the LEPHARE best fit reddening before we apply the stellar-to-nebular conversion (Eq. (4)), and the resulting stellar mass. |
We also attempted to use H6, H7 and H8 measurements (see Table 3) to constrain the intrinsic extinction where these lines were observed. However, the flux in the higher order lines decreased rapidly, which introduced large errors. We also attempted to model the observed line-ratios simultaneously, with extinction as a free parameter. However, the large measurement errors in the higher order lines prevented us from better constraining the fit. We therefore took a conservative approach, and used the values based on the strongest Balmer decrement (Hβ/H5) in all cases. We intentionally avoided combining our FORS2 Hβ measurements with literature Hα measurements (see for example Møller et al. 2018 for a Q 1323–0021 Hα measurement based on Sinfoni IFU data), since such a combination would introduce systematic effects.
Under the assumption that the Hα and [O II] star formation rate indicators (Sect. 3.8, Eqs. (5) and (6)) trace similar timescales, any discrepancy between the two can be attributed to abundance effects and dust reddening (Kewley & Geller 2004). Requiring that the two star formation rate indicators be equal, the extinction can be solved for as
where we infer SFRHα from the measured Hβ flux (see Sect. 3.8). Where no direct spectroscopic measurements can be used to quantify the reddening, the EB−V can instead be inferred from the spectral energy distribution fits (see Sect. 3.6). The colour excess of the stellar continuum was empirically tied to the colour excess derived from the nebular emission lines (Calzetti 1997; Calzetti et al. 2000), such that
The resulting EB−V values are reported in Table 4. For completeness, we report all EB−V estimates. Hereafter, we distinguish them using the abbreviations BDEC (Balmer decrement), SFR (star formation rate), and SED (spectral energy distribution) to reflect the method with which the measurements were inferred. We did not detect all emission lines required to determine the EB−V based on both BDEC and SFR for any object. Without having to select between the two methods, we therefore proceeded to apply intrinsic EB−V corrections evaluated from the line measurements when computing the SFRs and [O/H]s reported in Table 4. SED-based EB−V are provided to display our best-fit SED results and for comparing measurements of EB−V with different techniques, but we did not correct any flux measurements with these values. The SED-based EB−V were poorly constrained by the lack of UV-photometry, and were only used to define a grid on which to optimise the SED fits to obtain stellar masses (see Sect. 3.6).
3.8. Star formation
We measured the unobscured star formation rates of the host galaxies with nebulae emission-line diagnostics assuming the standard Hα λ6563 Å Kennicutt (1998) – and the re-calibrated [O II] λλ 3727,3729 Å Kewley & Geller (2004) relations:
Li refers to the dust-corrected intrinsic luminosity in SFR calibrator i. It was determined using the flux fi and the luminosity-distance dL using the python astropy.cosmology tool (Astropy Collaboration 2013) for the assumed cosmology, evaluated for the absorbing galaxy emission-line redshift zem (see Sect. 3.2 and Table 4), as 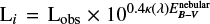 . Here,
. Here, 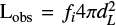 . We note that in the absence of a dust-correction from reliable spectroscopic EB−V measurements (see Sect. 3.7), the SFR can be assumed as a lower limit. The Hα luminosity was inferred from a conversion of the Hβ luminosity, assuming the intrinsic line ratio Hα / Hβ = 2.86 for standard case B recombination (Osterbrock & Ferland 2006).
. We note that in the absence of a dust-correction from reliable spectroscopic EB−V measurements (see Sect. 3.7), the SFR can be assumed as a lower limit. The Hα luminosity was inferred from a conversion of the Hβ luminosity, assuming the intrinsic line ratio Hα / Hβ = 2.86 for standard case B recombination (Osterbrock & Ferland 2006).
The calibration of these relations assumes solar abundances and a Salpeter initial mass function (IMF; Salpeter 1955) with lower- and upper stellar mass cutoffs at 0.1 and 100 M⊙ respectively. As a Hydrogen recombination line, the Hα flux is sensitive to the incident radiation bluewards of the 912 Lyman limit. This makes recombination lines direct probes of young (≤10 Myr) massive (>10 M⊙) stars which dominate the ionising photon budget, and therefore tracers of the near-instantaneous SFR on time-scales of ∼10 Myr. The SFR[O II] relation is based on the [O II] λλ3727,3729 Å collisionally excited forbidden-line doublet, empirically calibrated against Hα to give a quantitative SFR tracer on a similar time-scale (Gallagher et al. 1989; Kennicutt 1992; Kewley & Geller 2004) For internal consistency, we shifted the values to a Chabrier IMF (Chabrier 2003) by applying a downward correction factor of 1.8. For objects where both SFR measurements are possible, we assigned preference to SFRHβ as this is the most direct probe of star formation, and since SFR[O II] is calibrated to this recombination line (see Sect. 4.4 for more information). The resulting SFRs based on both diagnostics and their associated measurement errors are summarised in Table 4.
Emission from the [O II] doublet was used by (Straka et al. 2016; hereafter S16) to measure the SFR of the interacting system in the Q 1436–0051 field (their object 6 and 7, see Sect. 2.4 for more information). They could not resolve the flux from the interacting components. Using a Salpeter IMF, they therefore reported a combined SFR, which they split according to photometric flux-ratios, giving ![$ \mathrm{SFR}_{\mathrm{[{O} {II}]}}^{\mathrm{S16}}(\mathrm{obj}~6)=26 M_\odot \mathrm{yr}^{-1} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq51.gif) and
and ![$ \mathrm{SFR}_{\mathrm{[{O} {II}]}}^{\mathrm{S16}}(\mathrm{obj}~7)=22 M_\odot \mathrm{yr}^{-1} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq52.gif) . Our FORS2 spectrum is able to resolve the individual components of the interacting system (see Appendix A), giving a SFRHβ = 0.48 ± 0.10 M⊙ yr−1 of the confirmed host (see Table 4). The strong contrast between the
. Our FORS2 spectrum is able to resolve the individual components of the interacting system (see Appendix A), giving a SFRHβ = 0.48 ± 0.10 M⊙ yr−1 of the confirmed host (see Table 4). The strong contrast between the ![$ \mathrm{SFR}_{\mathrm{[\textsc{O II}]}}^{\mathrm{S16}} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq53.gif) and our SFRHβ diagnostic makes this field a unique case, granting additional analysis. Our FORS2 spectrum does not cover the [O II] doublet. We therefore matched the continuum light in the calibrated Magellan II spectrum used for the S16 analysis (Straka et al. 2016, and priv. comm. with Lorrie Straka) to the combined i-band magnitude reported in Rao et al. (2011). Under the assumption that the reported S16 flux-level of ×10−17 ergs s−1 cm−2 is in fact ×10−18 ergs s−1 cm−2, the continuum fluxes are consistent. With this rescaling of the flux level, and converting to a Chabrier IMF, we recovered a
and our SFRHβ diagnostic makes this field a unique case, granting additional analysis. Our FORS2 spectrum does not cover the [O II] doublet. We therefore matched the continuum light in the calibrated Magellan II spectrum used for the S16 analysis (Straka et al. 2016, and priv. comm. with Lorrie Straka) to the combined i-band magnitude reported in Rao et al. (2011). Under the assumption that the reported S16 flux-level of ×10−17 ergs s−1 cm−2 is in fact ×10−18 ergs s−1 cm−2, the continuum fluxes are consistent. With this rescaling of the flux level, and converting to a Chabrier IMF, we recovered a ![$ \mathrm{SFR}_{\mathrm{[{O} {II}]}}^{\mathrm{This work}} = 1.02 \pm 0.07 $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq54.gif) M⊙ yr−1, which we also report in Table 4. To within a factor of two, this value is consistent with our FORS2 SFRHβ measurement.
M⊙ yr−1, which we also report in Table 4. To within a factor of two, this value is consistent with our FORS2 SFRHβ measurement.
3.9. Metallicity
We inferred the metallicity of the absorbing galaxy in two independent ways based on (i) strong-line diagnostics with dereddened line-fluxes according to Sect. 3.7 where possible; and (ii) applying a metallicity gradient correction to the known absorption metallicity. Despite being interchangeable, we distinguish between absorption and emission based measurements by referring to the metallicity ([M/H]) and Oxygen abundance 12 + log(O/H), respectively.
Emission-line fluxes in [O II], Hβ and [O III] enabled us to calculate specific line-ratios which correlate with metallicity (Pagel et al. 1979; Maiolino et al. 2008). In the following, we report the results based on the R23, O32, O2 and O3 line-ratios, defined as
respectively. These line-ratios are sensitive to the nebular conditions that govern the individual line-strengths, and observed line-ratios are often compatible with multiple abundances (Osterbrock & Ferland 2006). We therefore assumed the standard R23 diagnostic, invoking the O32 ratio to account for ionisation corrections and break the degenerate solutions in abundance from a characteristic double-branched diagnostic. For systems with limited line-coverage, we report solutions based on the O2 and O3 line-ratios. Where these line-ratios give double-valued abundance-solutions, we report the abundance which closest matches the value inferred from a z = 0.7 mass-metallicity relation (Maiolino et al. 2008, hereafter M08). For internal consistency, these diagnostic line-ratios were converted to oxygen abundances assuming the M 08 calibration (see Table 4). The reported uncertainties reflect the uncertainties in derived line-ratios, excluding the internal scatter present in the M 08 relations. For notes on individual objects, see Appendix B.
The use of different strong-line diagnostics, each displaying its own internal scatter, makes it difficult to analyse the sample in a homogenous way. By combining SED stellar masses with absorption-and emission line metallicities, Christensen et al. (2014) reinterpreted C[M/H] (see Sect. 1) as an average metallicity gradient Γ acting over the impact parameter b connecting the absorption- and emission measurements, C[M/H] = Γb. They retrieved a mean linear metallicity gradient ⟨Γ⟩ = −0.022 ± 0.004 dex kpc−1. In Sect. 4.5 we re-examine their analysis including the results from our work, which gives a revised value of ⟨Γ⟩ = −0.022 ± 0.001 dex kpc−1. Applying this updated correction factor and a 12 kpc truncation radius (see Sect. 4.5) to the absorption-metallicities allowed us to infer a standardised metallicity measurement in emission for each absorbing galaxy as
The calibration of Eq. (8) is tied to the M 08 MZ-relation, which in turn uses the Kewley & Dopita (2002) functional form of the R23 and the O23 diagnostics to convert between observed line-ratios and metallicity. We used zinc as a tracer element of the absorption-metallicity where possible, since it is minimally depleted. Where only iron or chromium measurements exist, we included a standard depletion and α-enhancement correction to the absorption metallicity, [M/H]abs = [Fe/H] + 0.3 dex (Rafelski et al. 2012). We note, however, that such a constant correction does not account for metallicity-dependent depletion, and De Cia et al. (2018) suggest that even zinc can be subject to marginal dust depletion, albeit to a lesser extent than for iron. For this reason, the reported zinc-measurements represent lower limits on the metallicity measurements.
 |
Fig. 3. Left panel: distribution of impact parameter plotted as a function of the column density log10[NHI (cm−2)], colour-coded by stellar mass. Circles refer to data from literature. Our new identifications are plotted as squares. Grey data points represent spectroscopically confirmed absorbing galaxies without stellar mass estimates. The black line represents the median- and the grey lines represent the 1σ scatter in simulated distributions (Rahmati & Schaye 2014) at z = 2. Colour-coded lines represent the median impact parameters for those stellar mass bins, from the same simulations. Right panel: distribution of impact parameters as a function of the absorber metallicity [M/H]abs, colour-coded by column density. The black line marks the median- and the grey lines mark the 1σ, 2σ and 3σ contours based on the model-predictions from Krogager et al. (2017). The grey dotted line marks the distribution envelope. |
4. Discussion
In the following, our sample is discussed in relation to other luminosity- and absorption selected samples. Luminosity-selected data is not illustrated for individual galaxies. We strictly adhere to plotting the scaling relations derived from such samples. The luminosity-selected MZ-relations are taken from M 08, whereas the luminosity-selected star-forming main sequences are taken from Whitaker et al. (2014). We refer to each relation’s reference with the abbreviation M 08 and W14, respectively. Likewise, we refer to Møller et al. (2013) as M 13–in particular when referring to the predicted M 13 MZ-relation. Where relevant parameters are known, individual galaxies in the absorption-selected reference sample are plotted5. This reference sample constitutes the spectroscopically confirmed systems presented in Krogager et al. (2012) and Christensen et al. (2014), referred to as K12 and C14, respectively. In Sect. 4.4 we extend the comparison sample to include the objects in Kanekar et al. (2018).
4.1. Impact parameter as probe of average size
The impact parameter, b, measures the projected distance between the luminosity-centre and a random quasar sightline piercing the gaseous component of a galaxy. Therefore, the distribution of impact parameters conveys information on the average spatial scales and sizes of the gaseous H I regions probed, having folded in detection- and strategy-biases. In Fig. 3, we therefore plot the distribution of b as a function of log10[NH I (cm−2)] (left) and as a function of [M/H]abs (right). The data refer to damped absorbers with spectroscopically confirmed hosts in the reference sample (circles) with the added objects from this work (squares). Our sample effectively extends the observed distributions of Fig. 3 towards (i) lower redshifts; (ii) lower H I column-densities; and (iii) higher absorption-line metallicities.
Building on the results of previous studies (see Sect. 1), the left panel of Fig. 3 conforms to the idea that sub-DLAs and DLAs trace different relations to their hosts; the former having higher scatter- and higher mean impact parameters than the latter, on average. Similar conclusions were reached by Rahmani et al. (2016) who found a transition region at ∼20 kpc, above which no log10[NH I (cm−2)] > 21.0 absorbing galaxy was detected. We find a similar value, which for the combined sample becomes b ∼ 25 kpc. Rao et al. (2011) found that DLAs are statistically closer to the candidate host sightline than sub-DLAs by a factor of two, with ⟨b⟩R11, DLA = 17.4 kpc and ⟨b⟩R11, sub-DLA = 33.3 kpc, respectively. This is remarkably consistent with our findings, which give median impact parameters of ⟨b⟩DLA = 11.1 kpc and ⟨b⟩sub-DLA = 35.8 kpc. These results suggest a characteristic scale-length associated with the column-density distribution of gas in absorption-selected galaxies, and may be connected to the fall-off in gas density with radius.
We overplot the median (black) and 1σ (grey) lines of the impact parameter distribution from the Rahmati & Schaye (2014) simulations. We colour-code the data to the SED log10[M⋆ (M⊙)] (the point is flagged grey if no stellar mass value exists) and overplot the median curves for log10[M⋆ (M⊙)] bins of 7.0–8.5; 8.5–10.0; and 10.0–11.5 (Rahmati & Schaye 2014), in representative colours. This allows us verify whether the observed distribution in the data is captured by the simulations, and to assess whether the retrieved column-density scale-length is mass-dependent. With the current small sample, we find no such dependence.
Overall, the observed scatter is larger, and the median impact parameter increases sharper with decreasing H I column density, relative to the simulations. One suggestion is that this difference is driven by false-positive host galaxy identifications (Rahmati & Schaye 2014). However, such a false-positive identification rate would have to be sensitive to the column-density of the absorber -acting stronger on lower column density absorbers in order to reconcile the observations with simulations. That sub-DLAs are located at large impact parameters does not make them less likely to be the host, an issue discussed in Meiring et al. (2011). In addition, the imposed cut in metallicity limits this bias if absorbing galaxies follow a mass-metallicity relation (M 13).
Instead, the interpretation is complicated by sample pre-selection; detection-bias; strategy-bias, and there may be a size-evolution with redshift. Fundamentally, an absorption-selection introduces a bias towards gaseous systems with large neutral gas cross-sections. In combination with a lower cut on absorption metallicity, this pre-selects towards large, massive, bright galaxies independent of the absorber H I column density, biasing the observations towards large impact parameters. This selection is enhanced by the brightness of the background quasar, which prevents the detection of low luminosity systems -especially at low impact parameters if the region below the quasar trace is not scanned with an SPSF analysis (see Sect. 3.1). In addition, our z < 1 data is a long-slit follow-up of systems with photometric candidate hosts, whereas the z ≥ 2 galaxies are identified from Lyα emission in the Lyα trough or from strong optical emission lines found along any of the three slit position angles configured to cover as much of the region around the quasar as possible, without any pre-selection on candidate host (Fynbo et al. 2010; Krogager et al. 2017). Intuitively the latter observing strategy leads to a higher effective exposure time in the slit-coverage overlap, and therefore to a preferential identification of hosts at low impact parameters.
This strategy-bias is quantified in the right panel of Fig. 3, which shows how the impact parameters (circles and squares) are distributed relative to the modelled expectation (grey contours; Krogager et al. 2017) as a function of absorption metallicity. The data is now colour-coded to the H I column density, with an expected correlation assuming the existence of a luminosity-metallicity relation for damped absorbers (M 13), and that luminosity correlates with size of the absorbing galaxy (K12). In their paper, Krogager et al. (2017) show a remarkable statistical agreement; the 1σ model contours encompassing 69% of their data. This implies that the strategy bias is effectively negligible in their DLA sample, relative to the pre-selection towards large systems.
It is remarkable that the model, developed for z ∼ 2–3 DLAs, has an envelope that encompasses 96% of the spectroscopically confirmed systems (i.e. 27/28 systems, with one outlier) extending towards sub-DLAs and to z ∼ 0.7. To investigate this statistically, we computed the fraction of systems locked into the 1σ-, 2σ-, 3σ-model contours, for which we find 46%; 82%; and 89% of the combined data, respectively. This factor two increase between the 1- and 2σ contours indicates that the model does not statistically match a combined sample of sub-DLAs and DLAs. This is supported by the H I column-densities, which show that the factor of two increase is attributed to the more metal-enriched ([M/H]abs ≥ −0.5) sub-DLAs.
4.2. Drivers of the apparent M⋆ − NHI correlation
It has been suggested that sub-DLAs and DLAs arise in galaxies of different masses (Kulkarni et al. 2010; Meiring et al. 2011) – a suggestion which may alleviate the statistical tension between sub-DLAs and DLAs in the b–[M/H]abs model expectation (see Sect. 4.1 and Fig. 3). To address this question, in Fig. 4 we plot the stellar mass of spectroscopically identified hosts as a function of the H I column density of the associated quasar absorber, colour-coded to the absorption-metallicity, [M/H]abs.
 |
Fig. 4. Stellar masses of spectroscopically confirmed absorbing galaxies as a function of the absorber neutral hydrogen column density, colour-coded by the absorption metallicity. The dotted line marks the traditional distinction between sub-DLAs and DLAs at log10[NH I (cm−2)] = 20.3. The object encircled in red represents the outlier from Q 1209+107 PA2. |
The data suggest an anti-correlation, with higher-mass systems observed to host progressively lower column-density absorbers; and a secondary correlation between the absorption-metallicity and stellar mass, reminiscent of a mass-metallicity relation. But the observed anti-correlation could be a manifestation of multiple effects acting simultaneously; (i) a selection-bias against dusty – and therefore massive, metal-rich systems; and (ii) the cross-section selection biasing the sample number-count to large, massive galaxies with relatively larger projected areas of lower-density gas; the combination of the two making the sampling of the underlying distribution mimic a correlation.
We know that visual attenuation, AV, which is used to parametrise the dust content and the overall reddening of a source is related to the total column of metals. The metal column is itself the product of the neutral hydrogen gas column density and the metallicity. Recent studies have shown that the metal column correlates with the visual attenuation, such that log10(AV/mag) ∝ log10NH I + [M/H] (see Zafar & Watson 2013; Zafar & Møller 2018). Such a preferential dust-bias against high column-density absorbers is therefore consistent with the observed column-density dependent cutoff in stellar mass that we observe in the data, and can -at least in part, be explained by a dust bias against red quasars.
Recent work from the High AV Quasar survey (HAQ; Fynbo et al. 2013b; Krogager et al. 2015; Zafar et al. 2015)– and the extended HAQ (eHAQ; Krogager et al. 2016; Fynbo et al. 2017) survey suggest that a traditional quasar selection is indeed biased against reddened quasars. This is consistent with Noterdaeme et al. (2015) who found that the high column-density (log10 NH I ∼ 22), high metallicity (≳1/10 solar) DLAs induce a colour-change in the background quasar caused by both dust- and hydrogen absorption. This propagates into a dust-bias which preferentially acts on high NH I, massive, metal-rich, dusty galaxies selected against quasar sight-lines.
4.3. The mass-metallicity relation
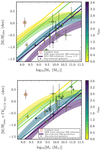 |
Fig. 5. Metallicity as a function of stellar mass for spectroscopically confirmed absorbing galaxies, colour-coded by redshift. Squares indicate the results of this work, whereas circles refer to the absorption-selected reference sample. The M 08 mass-metallicity relations based on luminosity-selected samples, and the M 13 predicted mass-metallicity relations for absorption-selected samples are overplotted at four representative redshifts. Top panel: results assuming the metallicity measured in absorption. Bottom panel: results with an impact-parameter dependent correction factor and a gradient cut-off at a truncation radius of 12 kpc. The object encircled in red represents the outlier from Q 1209+107 PA2. |
We investigated how the absorption-selected galaxy population is distributed relative to known mass-metallicity (MZ) relations of luminosity-selected galaxies. In Fig. 5, we plot two metallicity measurements as a function of the stellar mass. The data represent spectroscopically confirmed absorbing galaxies, with squares denoting the measurements in this work, and circles representing the compiled reference sample. We colour-code the data according to the redshift of each system, and overplot the M 08 MZ relations at redshifts z = 0.07, z = 0.7, z = 2.2, and z = 3.5, matched in colour. Here, we also add a 0.15 dex conservative estimate of the intrinsic scatter in each relation as the shaded regions (Kewley & Ellison 2008, M08).
In Fig. 5 top panel, we use the absorption metallicity as an indicator of the integrated emission metallicity. In addition, we convert the M 13 functional form for M⋆ into a mass-metallicity relation (M 13 MZ-relation) for absorption-selected galaxies, setting C[M/H] = 0. These are plotted for the same four redshifts as the M 08 relations to give a fair comparison. Two observations can be made. Firstly, with the exception of z = 3.5, the M 08- and M 13 MZ relations tangentially match in the near linear low-mass regime, but diverge towards larger masses. Secondly, the data fall systematically below both the M 08 and the M 13 MZ-relations at their respective redshifts. To quantify how well the models describe the data, we calculated the reduced chi-square statistic, 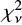 . For M 08, we interpolated the functional forms to the redshifts of the data. Including the 0.15 dex intrinsic scatter in the relation, we found a value
. For M 08, we interpolated the functional forms to the redshifts of the data. Including the 0.15 dex intrinsic scatter in the relation, we found a value 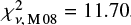 . This can be compared to the corresponding M 13 MZ-relation which, by including their intrinsic scatter of 0.38 dex yields a value
. This can be compared to the corresponding M 13 MZ-relation which, by including their intrinsic scatter of 0.38 dex yields a value  . We here note that whilst the M 13 model is statistically a better fit to the data, this result is driven by a large internal scatter, and does not mitigate the systematically lower metallicities for a given stellar mass and redshift.
. We here note that whilst the M 13 model is statistically a better fit to the data, this result is driven by a large internal scatter, and does not mitigate the systematically lower metallicities for a given stellar mass and redshift.
Following the prescription outlined in Sect. 3.9, in the bottom panel of Fig. 5, we corrected the absorption metallicity for the average metallicity gradient solved in Sect. 4.5. Local galaxies are found to have effective radii ∼6 kpc, with oxygen abundance gradients extending to around ∼2 disc effective radii followed by flat gradients (the CALIFA survey, Sánchez et al. 2014). Motivated by these results, in combination with the metallicity gradient we also applied a truncation-radius at 12 kpc to the data. This effectively converts the absorption measurement into an indirect emission measurement of the metallicity at the galaxy luminosity centre.
It is worth noting that the M 08 MZ-relations were calibrated to metallicity measurements averaged over the emission line regions of star forming galaxies. We can therefore ask whether applying a correction factor to the absorption metallicity will overestimate the luminosity-selected measurement, rendering the comparison meaningless. The individual surveys used to calibrate the M 08 MZ relations at different redshifts have apertures of 0.75–1.3 arcsec (Savaglio et al. 2005, z ∼ 0.76 arcsec (Erb et al. 2006, z ∼ 2.2) and 0.75 arcsec (Maiolino et al. 2008, z ∼ 3.5). A source centred on -and filling the aperture therefore have physical radii of the order 2.8–4.7 kpc; 3.6 kpc and 3.0 kpc for those representative redshifts, respectively. This gives a conservative estimate of the overshooting in the range raperture × ⟨Γ⟩ ∼ 0.06–0.10 dex. Recognising that this range is significantly below individual absorption metallicity uncertainties, and that the exact overshooting is sensitive to the light-distribution across the aperture, we conclude that its net systematic effect on our conclusions are negligible.
In the lower panel, we also overplot the same M 08 relations, and include C[M/H] to the M 13 predicted MZ-relation. To be consistent with the original functional form based on a pure DLA-sample, we reformulated the constant as C[M/H] = ⟨Γ⟩ × ⟨b⟩DLA, for ⟨Γ⟩ = −0.022 dex kpc−1 (see Sect. 4.5), and ⟨b⟩DLA = 11.1 kpc (see Sect. 4.1). Having applied the corrections to the data and to the relations, we now make two new observations. Firstly, rather than overlapping with the M 08 relations at low stellar masses, including C[M/H] renormalises the M 13 MZ-relation and generates convergence at larger stellar masses, on average. Secondly, the systematic bias in the data towards lower metallicity for a given stellar mass and redshift bin is reduced. These conclusions are supported by recalculating the reduced chi-square statistics, which give values of 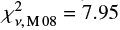 and
and 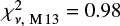 by replacing the intrinsic scatter from M 13 with the updated value of 0.32 (see Sect. 4.5).
by replacing the intrinsic scatter from M 13 with the updated value of 0.32 (see Sect. 4.5).
We therefore conclude that the absorber based MZ-relation provides a better fit to the data. We recognise that this fit is dominated by a large intrinsic scatter that prevents us from discerning any clear redshift evolution. Despite this, the inclusion of a mean metallicity gradient and a truncation radius is physically motivated and has a significant effect on the 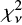 -statistic, reducing it by a factor ∼3. This suggests that we can statistically predict global properties from local measurements.
-statistic, reducing it by a factor ∼3. This suggests that we can statistically predict global properties from local measurements.
4.4. Absorbing galaxies probing sub-main-sequence star-formation
Møller et al. (2018) and Kanekar et al. (2018), based on a recent ALMA survey of molecular gas (Neeleman et al. 2016b; Møller et al. 2018), tried to characterise the relation between the neutral- and molecular gas content and the SFR in absorption-selected galaxies. Based on a sample of two, the former suggested that absorption-selected galaxies sample a missing phase in galaxy evolution; a “post-starburst” phase, characterised by low star-formation and large gas- and molecular fractions (Møller et al. 2018). This is driven by the preceding onset of a starburst phase that drives molecular- and neutral gas to large distances, making such systems susceptible to the H I cross-section selection. In the latter, Kanekar et al. (2018) from a sample of seven, argued that absorption-selected galaxies are consistent with the star-forming main-sequence. However, they retain large molecular masses at all redshifts. The insensitivity of the SFR on molecular gas mass is therefore interpreted as evidence for low molecular gas-densities which inhibit the molecular-gas from converting into stars.
Here, we do not consider CO-detections. This allows us to look at a larger data-set to quantify the absorbing galaxy population relative to the star-formation main sequence as a whole. In Fig. 6, we show how the sample of absorbing galaxies fall relative to the main sequence of star-formation. Square symbols represent the results of this work (SED-based M⋆ and extinction-corrected SFRs, as reported in Table 4); circles refer to literature samples. For completeness, we add to our sample the two systems (B 1629+120g and J 0058+0155g) from Kanekar et al. (2018), not covered by the C14 sample or this study. These two systems are represented by triangles. For galaxies with multiple SFR-tracers ([O II] and Hβ), we assign preference to the Hβ measurement, since this is a direct measure of the SFR based on recombination theory. We note however that in general, the [O II] SFRs show good agreement with the Hβ based measurements. In addition to the measurement errors reported in Table 4, we include a 30% uncertainty to each SFR to account for scatter between the Hβ and the [O II] diagnostic calibrations (Kennicutt 1998; Kewley & Geller 2004). We then colour-code the absorbing galaxies by redshift. For reference, we overplot the star-forming main-sequences at redshift ranges 0.5 < z < 1.0 and 2.0 < z < 2.5 for a Chabrier IMF (Whitaker et al. 2014). We have matched the colours for each relation to representative redshifts of z = 0.75 and z = 2.25, respectively. In addition, we include the 1σ- and 3σ dispersions as the dark- and light shaded regions around each of the relations. These are estimated based on a reported scatter of 0.14 dex for z ∼ 2 and 0.30 dex for z < 1 (Whitaker et al. 2015).
 |
Fig. 6. Star-formation rate as a function of stellar mass for spectroscopically confirmed absorbing galaxies, colour-coded by redshift. Squares indicate the results of this work; circles refer to work by others. Triangles represent CO detected galaxies. For reference, we plot the Whitaker et al. (2014) redshift-dependent star-forming main sequence for two representative redshift ranges together with their 1σ- and 3σ scatter, represented by the dark- and light- shaded regions centred on each relation, respectively. See text in Sect. 4.4 for more details. The object encircled in red represents the outlier from Q 1209+107 PA2. |
The high-redshift (z ∼ 2) absorbing galaxies are consistent with the 3σ scatter of the star-forming main sequence at that redshift, whereas a significant fraction of systems at low (z ≲ 1) redshifts suggest sub-main-sequence star-formation. Despite individual systems showing large scatter, we note that this bias appears significant and real, since the data are not stochastically distributed around the main sequence. With the current sample, we therefore ask whether this suppression, if real, is evolutionary or inherent to the nature of absorption-selected galaxies.
Despite the temptation to see the results as indicative of an evolutionary transition, with galaxies “breaking off” the star-forming main sequence to become quenched at some characteristic redshift z ∼ 0.7 in line with the CO detected DLA galaxies in Kanekar et al. (2018), this is not supported by our data. A majority of the systems with suppressed SFRs lie at the high-mass end of the distribution, whereas the majority of systems at lower stellar masses are consistent with the 3σ scatter. Empirically, this suggests that suppressed SFRs are inherent to absorption-selected galaxies above stellar mass log10 M⋆ (M⊙) ≳ 10, indicated by the grey dotted line in Fig. 6. 88% (7/8 systems) with log10 M⋆ (M⊙) ≳ 10 fall below their respective redshift-relation. Out of these, 63% (5/8 systems) are inconsistent with the 3σ scatter. Despite the low number of systems at high-z, this interpretation is consistent with the Q 0918+1636 system (zabs = 2.583, log10 M⋆ (M⊙) ∼ 10.3), with a single outlier in Q 0738+313 (zabs = 0.221, log10 M⋆ (M⊙) ∼ 9.3) displaying suppressed SFR at lower mass.
The natural question to ask is whether this suppression can be explained by selection effects or a dust bias. Indeed, pre-selecting against HAQ galaxies (Fynbo et al. 2013b; Krogager et al. 2015; Zafar et al. 2015), large fractions of obscured star formation and lack of applying extinction corrections to the SFR will systematically deplete the high mass, high star formation domain of Fig. 6. Ma et al. (2015) showed that massive (10.3 ≤ log10[M⋆ (M⊙)] ≤ 11.5) , dusty galaxies are usually highly star forming, with values of 510–4800 M⊙ yr−1. The extinction corrected SFRs for our galaxies (see Table 4) are low, which suggests that the detected galaxies on average are not very dusty. Based on the high fraction of identified hosts, a dust bias therefore does not appear to affect this study. Albeit difficult to motivate why, we therefore suggest that the suppression of star formation in absorption-selected galaxies is mass-dependent, and not evolutionary.
4.5. The existence of an average metallicity gradient
Cosmological hydrodynamic simulations such as the Galaxies-Intergalactic Medium Calculation (GIMIC, Crain et al. 2009) predict systematic flattening of metallicity-gradients in star-forming disc-galaxies with redshift, from z = 2 to z = 0. In such simulations, this flattening is caused by declining inflows of pristine gas; enrichment by in situ star-formation; and the redistribution of metal-enriched gas from the inner to outer disc, leading to progressive outer disc enrichment. Observations of spatially resolved star-forming galaxies are comparable to these results (Swinbank et al. 2012). Likewise, Stott et al. (2014) suggested that the specific SFR (sSFR), which parametrises how intensely a galaxy is forming stars, drives the observed differences in metallicity gradients. In their framework, observations of high-sSFR systems associated with metal-poor centres and flat- and inverted metallicity-gradients are a consequence of mergers (Rupke et al. 2010) and cold flows (Dekel et al. 2009; Cresci et al. 2010). Similar results were also reported by Queyrel et al. (2012), who found examples of positive gradients in z = 1.2 star-forming galaxies. These mechanisms will channel pristine gas into the galaxy central regions, providing fuel and triggering intense star-formation that increases the sSFR whilst diluting the metallicity in the galactic cores. This leads us to expect a synergy between the metallicity-gradient’s observed dependence on sSFR and redshift, consistent with the fundamental metallicity relation for which galaxies at fixed stellar mass are progressively metal poor for increased SFR (Mannucci et al. 2010).
To see whether we can resolve such evolutionary diagnostics, we first determined individual metallicity-gradients Γi [dex kpc−1]. We recognise, however, that there are important differences between gradients measured in emission on spatially resolved systems to those measured by combining emission with absorption measurements. Despite internal consistency in the derived oxygen abundances reported in Table 4 using the M 08 calibrations, the individual measurements as well as those from literature use different emission-line diagnostics, and therefore represent a heterogenous sample. Additionally, absorption metallicities sample pencil-beams and therefore trace the local metallicity, typically offset from the galaxy centre. In slit spectra however, a spectroscopic emission-line metallicity represents the mean metallicity across the slit-width. For a galaxy at z = 0.7, a representative redshift of our sample, a slit-width of θ = 1.31 arcsec yields a metallicity-estimate averaged over spatial scales of ∼9.5 kpc. We therefore caution against a direct combination of absorption and emission metallicities, since they likely probe different enrichment histories and sample local and global enrichment time-scales, respectively.
To determine Γi homogeneously, we instead used the relation Γi = C[M/H],i/bi (C14). C[M/H],i refers to the predicted metallicity parameter (M 13, their Eq. (6)), evaluated for a system i assuming its SED stellar mass as
and bi refers to the measured impact parameter. We then determined an empirical expectation value of the average metallicity gradient, ⟨Γ⟩, adopting the  -minimisation method used in M 13 and C14. Recognising that Eq. (9) has a natural intrinsic scatter, σnat, we desire the combination [σnat, ⟨Γ⟩] which minimises σnat and for which the
-minimisation method used in M 13 and C14. Recognising that Eq. (9) has a natural intrinsic scatter, σnat, we desire the combination [σnat, ⟨Γ⟩] which minimises σnat and for which the  -statistic is unity. In effect, we seek the solution to
-statistic is unity. In effect, we seek the solution to
where the degrees of freedom (d.o.f.) is N − 1 and not N − 2, since by construction we fix σnat to its minimum value. σC[M/H],i is the propagated uncertainty from the absorption metallicity and from the stellar mass measurements.
For our total FORS2 sample, we found a solution [0.66 ± 0.05, 0.015 ± 0.001]. Combining the new sample with C14, we found [0.44 ± 0.01, 0.018 ± 0.001]. These gradients are shallower than the findings of C14, who found ⟨Γ⟩C14 = −0.022 ± 0.004 dex kpc−1, and only marginally consistent to within the reported errors in our respective studies. We note, however, that we reformulated a method that searched a pre-defined parameter-grid for the minimum σnat into a method seeking the roots of Eq. (10). Having confirmed that the two methods yield consistent values on the same data, we excluded the probable misidentification in Q 1209+107 PA2 (see Sect. 3.4). With this exclusion we retrieved an intrinsic dispersion σnat = 0.32 ± 0.01 and an average gradient of ⟨Γ⟩new = −0.022 ± 0.001 dex kpc−1. This value is in perfect agreement with ⟨Γ⟩C14, and lends further support to the galaxy in Q 1209+107 PA2 being an unlikely host.
In the same work, C14 solved for gradients measured from the direct comparison of metallicity measurements in emission- and absorption line measurements, ([M/H]em − [M/H]abs)/bi, for which they found a mean value of −0.023 ± 0.015 dex kpc−1. Similar work comparing direct measurements yield a median value of −0.022 dex kpc−1 (Péroux et al. 2016), and performing a weighted mean on the three direct measurements reported in Rahmani et al. (2016) gives a metallicity gradient of −0.04 ± 0.01 dex kpc−1. We note however, that Rahmani et al. (2016) reported a best-fit gradient to a compilation of all known measurements, excluding limits and non-detections of −0.002 ± 0.007 dex kpc−1. This would indicate an insignificant metallicity gradient – in contrast with our results, and may reflect the combination of heterogenous diagnostics and local- and global scale metallicity-measurements. Stott et al. (2014) retrieved an average gradient of ΔZ/dr = −0.002 ± 0.007 dex kpc−1 based on 20 disc galaxies at z = 1. Swinbank et al. (2012) recovered metallicity gradients in discs (≲10 kpc) that are negative or flat for seven spatially resolved galaxies at z = 0.84 − 2.23, with an average gradient of Δ log10 (O/H)/ΔR = −0.027 ± 0.005 dex kpc−1.
Having robustly identified the existence of an average metallicity gradient in absorption-selected galaxies with a grid-based and a solver-based model alike, we now consider whether ⟨Γ⟩ correlates with galaxy evolution parameters. In particular, we desire to see whether ⟨Γ⟩ is sensitive to the inclusion of sub-DLAs; whether it shows a redshift-evolution; and whether it correlates with galaxy evolution parameters such as M⋆ or sSFR. Such correlations were found in luminosity-selected star-forming disc-galaxies at z = 1 (Stott et al. 2014). Since the scatter in the sample is larger than the individual measurement errors, we proceeded with the methodology developed, but replaced ⟨Γ⟩ by a linear function of the form ⟨Γ⟩ = θ1x + θ2 in Eq. (10). Here, θ represents the new parameters we seek to optimise, and x is the independent variable.
Retrieved metallicity-gradient correlations.
The resulting correlations are summarised in Table 5. We find a ∼5σ correlation with the H I column density, and a formal 3σ correlation with SFR. A correlation with H I column density may be related to the ionisation-corrections applied to the absorption metallicity, which itself correlates inversely with H I column density. Whether such ionisation corrections explain the observed correlation is beyond the scope of this paper.
If real, the correlation with SFR may suggest that absorption-selected galaxies have sSFRs which are driven by a different mechanism relative to luminosity-selected systems. Such systems show a correlation with sSFR, with slopes of 0.023 ± 0.004, driven by a correlation with M⋆ of the order −0.022 ± 0.009 (Stott et al. 2014). We note however, that with errors of 0.01 and 0.02 on the correlations with M⋆ and sSFR, respectively, the data are consistent with the disc-galaxy correlations, but we lack the number statistics to test the Stott et al. (2014) result.
5. Conclusions
In this paper we spectroscopically confirm seven galaxies harbouring damped absorption systems at redshift z < 1. In addition, we detected a low-mass, star-bursting galaxy at low impact-parameter in the Q 1209+107 quasar field. Further analysis suggests that this is an unlikely host. This has two implications. Firstly, the galaxy hosts for the two damped absorbers in Q 1209+107 are still unidentified. Secondly, the proximity of the unlikely host to the quasar line of sight suggests that the low-redshift zabs = 0.3930 absorber is hosted by a galaxy that belongs to a larger galaxy-group. We also report one non-detection in the Q 1209+107 PA1 field and on a galaxy at the wrong redshift to be related to the absorbing system in the Q 2353–0028 field. With a conservative estimate, our FORS2 campaign therefore had a success-rate of 70%. Combining spectroscopic data in emission with the known properties in absorption and deep multi-band photometry in the quasar fields, we conducted an extensive analysis to characterise the absorbing galaxies. In the following paragraphs we summarise the results.
Despite statistical differences, the observed distribution of impact parameters with H I column-density and with absorption metallicity can be extended from DLAs to sub-DLAs; from high (z ∼ 2 − 3) redshifts to low (z ∼ 0.7) redshifts; and to higher absorption metallicities. Our observations can be used to constrain the models further.
We find no solid evidence for the claim that sub-DLAs and DLAs arise in galaxies of different masses. We argue that the apparent correlation is driven by selection effects, including a dust-bias against massive metal-rich systems and the fact that projected cross-section of low-column-density sub-DLA gas is geometrically larger. This favours the detection of sub-DLAs in large galaxies.
We find a significant mean metallicity gradient of ⟨Γ⟩ = −0.022 ± 0.001 dex kpc−1 based on the absorber properties and known SED stellar masses. This value is consistent with literature values, but has a significantly reduced uncertainty achieved by avoiding the combination of different strong-line diagnostics in emission and by not directly combining metallicity measurements on local (absorption) and global (emission) spatial scales.
Correcting the absorption-metallicities for our mean metallicity-gradient and assuming a physically motivated truncation-radius of 12 kpc, absorption-selected galaxies fall on top of predicted MZ-relations. Applying these corrections significantly reduces the scatter around the relations, and suggests that global properties can indeed be predicted from local absorption measurements.
Based on the current sample, absorption-selected galaxies with stellar masses above log10 [M⋆ (M⊙)] ∼ 10 show sub-main-sequence star formation. Whereas this has been interpreted as an effect of probing a particular evolutionary phase or as a transition from the nature of absorbing galaxies between high- and low redshifts, the fact that such a suppression is not seen at lower masses is indicative of a mass-dependence.
Acknowledgments
This work was supported by grant ID DFF-4090-00079. We would also like to extend our gratitude to Sandhya Rao and Lorrie Straka for sharing data; and to Jens-Kristian Krogager and Alireza Rahmati for sharing their model- and simulation predictions. This research made use of Astropy, a community-developed core Python package for Astronomy. In addition, it has made use of SDSS DR10. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.
See for example Rao et al. (2011) where ∼63% of the systems were identified at the 3σ level in the redshift range 0.5 < z < 0.8.
see Sect. 2.1 for a detailed account of the number of fields, absorbers, and slits used.
We note that two new stellar masses of absorbing galaxies were recently published in Augustin et al. (2018). The paper appeared too late for us to include those objects in our reference sample, but a quick comparison confirms that the new objects fall on the relations presented in this paper.
References
- Ahn, C. P., Alexandroff, R., Allende Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Appenzeller, I., Fricke, K., Furtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Augustin, R., Péroux, C., Møller, P., et al. 2018, MNRAS, 478, 3120 [NASA ADS] [CrossRef] [Google Scholar]
- Berg, T. A. M., Ellison, S. L., Prochaska, J. X., et al. 2017, MNRAS, 464, L56 [NASA ADS] [CrossRef] [Google Scholar]
- Berry, M., Somerville, R. S., Gawiser, E., et al. 2016, MNRAS, 458, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boffin, H. M. J., Dumas, C., & Kaufer, A. 2015, VLT-MAN-ESO-13100-1543 [Google Scholar]
- Boissé, P., Le Brun, V., Bergeron, J., & Deharveng, J.-M. 1998, A&A, 333, 841 [NASA ADS] [Google Scholar]
- Bouché, N., Murphy, M. T., Kacprzak, G. G., et al. 2013, Science, 341, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 1997, AIPC Conf. Proc., 408, 403 [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-W., & Lanzetta, K. M. 2003, ApJ, 597, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, L., Wisotzki, L., Roth, M. M., et al. 2007, A&A, 468, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christensen, L., Møller, P., Fynbo, J. P. U., & Zafar, T. 2014, MNRAS, 445, 225 (C14) [NASA ADS] [CrossRef] [Google Scholar]
- Crain, R. A., Theuns, T., Vecchia, C. D., et al. 2009, MNRAS, 399, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Cresci, G., Mannucci, F., Maiolino, R., et al. 2010, Nature, 467, 811 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cristiani, S. 1987, A&A, 175, L1 [NASA ADS] [Google Scholar]
- De Cia, A., Ledoux, C., Petitjean, P., & Savaglio, S. 2018, A&A, 611, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dekel, A., Sari, R., & Ceverino, D. 2009, ApJ, 703, 785 [Google Scholar]
- de la Varga, A., Reimers, D., Tytler, D., Barlow, T., & Burles, S. 2000, A&A, 363, 69 [NASA ADS] [Google Scholar]
- Dessauges-Zavadsky, M., Ellison, S. L., & Murphy, M. T. 2009, MNRAS, 396, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L. 2006, MNRAS, 368, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freudling, W., Romaniello, M., Bramich, D. M., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fumagalli, M., O’Meara, J. M., Xavier Prochaska, J., Rafelski, M., & Kanekar, N. 2015, MNRAS, 446, 3178 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. U., Moller, P., & Warren, S. J. 1999, MNRAS, 305, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Prochaska, J. X., Sommer-Larsen, J., Dessauges-Zavadsky, M., & Møller, P. 2008, ApJ, 683, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Laursen, P., Ledoux, C., et al. 2010, MNRAS, 408, 2128 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Ledoux, C., Noterdaeme, P., et al. 2011, MNRAS, 413, 2481 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Geier, S. J., Christensen, L., et al. 2013a, MNRAS, 436, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Krogager, J.-K., Venemans, B., et al. 2013b, ApJS, 204, 14 [Google Scholar]
- Fynbo, J. P. U., Krogager, J.-K., Heintz, K. E., et al. 2017, A&A, 606, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallagher, J. S., Bushouse, H., & Hunter, D. A. 1989, ApJ, 97, 700 [Google Scholar]
- Hanuschik, R. W. 2003, A&A, 407, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hewett, P. C., & Wild, V. 2007, MNRAS, 379, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Arnouts, S., Mccracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kacprzak, G. G., Murphy, M. T., & Churchill, C. W. 2010, MNRAS, 406, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Kanekar, N., Prochaska, J. X., Christensen, L., et al. 2018, ApJ, 856, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Karim, A., Schinnerer, E., Martínez-Sansigre, A., et al. 2011, ApJ, 730, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. J. 1992, ApJ, 388, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Geller, M. J. 2004, ApJ, 127, 2002 [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Krogager, J.-K., Fynbo, J. P. U., Møller, P., et al. 2012, MNRAS, 424, 1 (K12) [Google Scholar]
- Krogager, J.-K., Fynbo, J. P. U., Ledoux, C., et al. 2013, MNRAS, 433, 3091 [NASA ADS] [CrossRef] [Google Scholar]
- Krogager, J.-K., Geier, S., Fynbo, J. P. U., et al. 2015, ApJS, 217, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Krogager, J.-K., Fynbo, J. P. U., Heintz, K. E., et al. 2016, ApJ, 832, 21 [Google Scholar]
- Krogager, J.-K., Møller, P., Fynbo, J. P. U., & Noterdaeme, P. 2017, MNRAS, 469, 2959 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, V. P., Khare, P., Péroux, C., et al. 2007, ApJ, 661, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, V. P., Khare, P., Som, D., et al. 2010, New Astron., 15, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Le Brun, V., Bergeron, J., Boissé, P., & Deharveng, J. M. 1997, A&A, 321, 733 [NASA ADS] [Google Scholar]
- Ledoux, C., Bergeron, J., & Petitjean, P. 2002, A&A, 385, 802 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ledoux, C., Petitjean, P., Møller, P., Fynbo, J., & Srianand, R. 2005, Proc. IAU, 199, 433 [CrossRef] [Google Scholar]
- Ledoux, C., Petitjean, P., Fynbo, J. P. U., Møller, P., & Srianand, R. 2006, A&A, 457, 71 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Ma, J., Gonzalez, A. H., Spilker, J. S., et al. 2015, ApJ, 812, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 (M08) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Meiring, J. D., Kulkarni, V. P., Lauroesch, J. T., et al. 2008, MNRAS, 384, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Meiring, J. D., Lauroesch, J. T., Kulkarni, V. P., et al. 2009, MNRAS, 397, 2037 [NASA ADS] [CrossRef] [Google Scholar]
- Meiring, J. D., Lauroesch, J. T., Haberzettl, L., et al. 2011, MNRAS, 410, 2516 [NASA ADS] [CrossRef] [Google Scholar]
- Møller, P. 2000, The Messenger, 99, 31 [NASA ADS] [Google Scholar]
- Møller, P., & Warren, S. J. 1998, MNRAS, 299, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Møller, P., Warren, S. J., Fall, S. M., Jakobsen, P., & Fynbo, J. U. 2000, The Messenger, 99, 33 [NASA ADS] [Google Scholar]
- Møller, P., Warren, S. J., Fall, S. M., Fynbo, J. U., & Jakobsen, P. 2002, ApJ, 574, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Møller, P., Fynbo, J. P. U., & Fall, S. M. 2004, A&A, 422, 33 [Google Scholar]
- Møller, P., Fynbo, J. P. U., Ledoux, C., & Nilsson, K. K. 2013, MNRAS, 430, 2680 (M13) [NASA ADS] [CrossRef] [Google Scholar]
- Møller, P., Christensen, L., Zwaan, M. A., et al. 2018, MNRAS, 474, 4039 [NASA ADS] [CrossRef] [Google Scholar]
- Monier, E. M., Turnshek, D. A., & Rao, S. 2009, MNRAS, 397, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Neeleman, M., Wolfe, A. M., Prochaska, J. X., & Rafelski, M. 2013, ApJ, 769, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Neeleman, M., Prochaska, J. X., Ribaudo, J., et al. 2016a, ApJ, 818, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Neeleman, M., Prochaska, J. X., Zwaan, M. A., et al. 2016b, ApJ, 820, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Nestor, D. B., Pettini, M., Hewett, P. C., Rao, S., & Wild, V. 2008, MNRAS, 390, 1670 [NASA ADS] [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, 43 [Google Scholar]
- Noterdaeme, P., Petitjean, P., Ledoux, C., & Srianand, R. 2009, A&A, 505, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Laursen, P., Petitjean, P., et al. 2012a, A&A, 540, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Petitjean, P., Carithers, W. C., et al. 2012b, A&A, 547, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noterdaeme, P., Petitjean, P., & Srianand, R. 2015, A&A, 578, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, in Astrophysics of gaseous nebulae and active galactic nuclei, 2nd, eds. D. E. Osterbrock, & G. J. Ferland (Sausalito, CA: University Science Books) [Google Scholar]
- Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Péroux, C., Dessauges-Zavadsky, M., D’Odorico, S., Kim, T.-S., & McMahon, R. G. 2003, MNRAS, 345, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Péroux, C., Meiring, J. D., Kulkarni, V. P., et al. 2006, MNRAS, 372, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Péroux, C., Meiring, J. D., Kulkarni, V. P., et al. 2008, MNRAS, 386, 2209 [NASA ADS] [CrossRef] [Google Scholar]
- Péroux, C., Bouché, N., Kulkarni, V. P., York, D. G., & Vladilo, G. 2011, MNRAS, 410, 2237 [NASA ADS] [CrossRef] [Google Scholar]
- Péroux, C., Bouché, N., Kulkarni, V. P., York, D. G., & Vladilo, G. 2012, MNRAS, 419, 3060 [NASA ADS] [CrossRef] [Google Scholar]
- Péroux, C., Quiret, S., Rahmani, H., et al. 2016, MNRAS, 457, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Péroux, C., Rahmani, H., Quiret, S., et al. 2017, MNRAS, 464, 2053 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., Smith, L. J., Hunstead, R. W., & King, D. L. 1994, ApJ, 426, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Pontzen, A., Governato, F., Pettini, M., et al. 2008, MNRAS, 390, 1349 [NASA ADS] [Google Scholar]
- Prochaska, J. X., Gawiser, E., Wolfe, A. M., Castro, S., & Djorgovski, S. G. 2003, ApJ, 595, 9 [Google Scholar]
- Prochaska, J. X., Herbert-Fort, S., & Wolfe, A. M. 2005, ApJ, 635, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Queyrel, J., Contini, T., Kissler-Patig, M., et al. 2012, A&A, 539, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rafelski, M., Wolfe, A. M., Prochaska, J. X., Neeleman, M., & Mendez, A. J. 2012, ApJ, 755, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Rafelski, M., Neeleman, M., Fumagalli, M., Wolfe, A. M., & Prochaska, J. X. 2014, ApJ, 782, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Rahmani, H., Péroux, C., Turnshek, D. A., et al. 2016, MNRAS, 463, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Rahmati, A., & Schaye, J. 2014, MNRAS, 438, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Rao, S. M., Turnshek, D. A., & Nestor, D. B. 2006, ApJ, 636, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Rao, S. M., Ele Belfort-Mihalyi, M., Turnshek, D. A., et al. 2011, MNRAS, 416, 1215 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S. N., Kewley, L. J., & Barnes, J. E. 2010, ApJ, 710, L156 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Iglesias-Páramo, J., et al. 2014, A&A, 563, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandin, C., Becker, T., Roth, M. M., et al. 2010, A&A, 515, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savaglio, S., Glazebrook, K., Le Borgne, D., et al. 2005, ApJ, 635, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., & Finkbeiner Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Som, D., Kulkarni, V. P., Meiring, J., et al. 2013, MNRAS, 435, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Som, D., Kulkarni, V. P., Meiring, J., et al. 2015, ApJ, 806, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A., & Cowie, L. L. 2010, ApJ, 721, 1448 [NASA ADS] [CrossRef] [Google Scholar]
- Stott, J. P., Sobral, D., Swinbank, A. M., et al. 2014, MNRAS, 443, 2695 [NASA ADS] [CrossRef] [Google Scholar]
- Straka, L. A., Johnson, S., York, D. G., et al. 2016, MNRAS, 458, 3760 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Sobral, D., Smail, I., et al. 2012, MNRAS, 426, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., Franx, M., Leja, J., et al. 2014, ApJ, 795, 104, (W14) [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Whitaker, K. E., Franx, M., Bezanson, R., et al. 2015, ApJ, 811, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfe, A. M., Turnshek, D. A., Smith, H. E., & Cohen, R. D. 1986, ApJS, 61, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Zafar, T., & Møller, P. 2018, MNRAS, submitted [Google Scholar]
- Zafar, T., & Watson, D. 2013, A&A, 560, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zafar, T., Møller, P., Ledoux, C., et al. 2011, A&A, 532, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zafar, T., Péroux, C., Popping, A., et al. 2013a, A&A, 556, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zafar, T., Popping, A., & Péroux, C. 2013b, A&A, 556, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zafar, T., Møller, P., Watson, D., et al. 2015, A&A, 584, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zafar, T., Møller, P., Péroux, C., et al. 2017, MNRAS, 465, 1613 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Group analysis in Q1436–0051
 |
Fig. A.1. Negative colour-mapped FORS2 spectral segments of the Q 1436–0051 field, observed during our campaign. Boxes highlight the identified emission lines, colour-coded to emphasize systems at similar redshifts. |
Galaxies at relatively small projected distances from the quasar Q1436–0051.
Appendix B: Notes in individual abundance measurements
Here, we present the abundance measurements based on flux-ratios for individual objects. We evaluated the flux-ratios as the median-value with lower and upper uncertainties based on the 16th- and 84th percentile of the CDF. The CDF was generated from 1E6 realisations of the flux-ratios assuming normal-distributed fluxes centred on the measurement, with a width characterised by the flux uncertainty. In order to differentiate between abundances measured with different diagnostics, we use the following notation: [O/H]diagnostic where the subscript refers to the diagnostic line-ratio as defined in Eq. (7) used. If the line-ratio is consistent with two abundances, we refer to these with “l” or “u” superscripts to denote the lower branch and upper branch value, respectively. When a comparison to the mass-metallicity relation is made, we refer to this value as [O/H]MZ,M 08. In this comparison, we do not consider internal scatter present in the M 08 MZ-relation. HE 1122–1649. The O2 line-ratio gives an oxygen abundance ![$ [\mathrm{O/H}]_{\mathrm{O}_2} = 8.70^{+0.17}_{-0.20} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq68.gif) . This is consistent with the value inferred from the mass-metallicity relation, [O/H]MZ,M 08 = 8.57.
. This is consistent with the value inferred from the mass-metallicity relation, [O/H]MZ,M 08 = 8.57.
Q 0153+0009. The O3 line-ratio gives a double-valued abundance, with a lower- and upper abundance branch value of ![$ [\mathrm{O/H}]_{\mathrm{O}_3}^l = 7.02^{+0.03}_{-0.03} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq69.gif) and
and ![$ [\mathrm{O/H}]_{\mathrm{O}_3}^u = 8.75^{+0.03}_{-0.03} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq70.gif) , respectively. The upper-branch abundance is consistent with the value inferred from the mass-metallicity relation, [O/H]MZ,M 08 = 8.81. We note that the reported uncertainties are underestimated. This is in part because we have not accounted for internal scatter in the M 08 calibration, and in part because the abundance calibration is insensitive to variations in the flux-ratio around the measured value.
, respectively. The upper-branch abundance is consistent with the value inferred from the mass-metallicity relation, [O/H]MZ,M 08 = 8.81. We note that the reported uncertainties are underestimated. This is in part because we have not accounted for internal scatter in the M 08 calibration, and in part because the abundance calibration is insensitive to variations in the flux-ratio around the measured value.
Q 1209+107 PA2. The R23 line-ratio, to within the 1σ uncertainty, does not constrain the abundance. Interpreting the large line-ratio as indicative of a unique abundance at the maximum line-ratio gives [O/H]R23 = 8.05. The O2 line-ratio gives a double-valued abundance, with a lower- and upper branch value of ![$ [\mathrm{O/H}]_{\mathrm{O}_2}^l {=} 8.55^{+0.05}_{-0.04} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq71.gif) and
and ![$ [\mathrm{O/H}]_{\mathrm{O}_2}^u {=} 8.83^{+0.03}_{-0.04} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq72.gif) , respectively. Likewise, the O3 line-ratio also gives a double-valued abundance, with a lower- and upper branch value of
, respectively. Likewise, the O3 line-ratio also gives a double-valued abundance, with a lower- and upper branch value of ![$ [\mathrm{O/H}]_{\mathrm{O}_3}^l = 7.62^{+0.05}_{-0.04} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq73.gif) and
and ![$ [\mathrm{O/H}]_{\mathrm{O}_3}^u = 8.16^{+0.04}_{-0.05} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq74.gif) , respectively, and the O32 line-ratio gives an abundance
, respectively, and the O32 line-ratio gives an abundance ![$ \mathrm{[O/H]}_{\mathrm{O}_{32}} = 8.35^{+0.02}_{-0.02} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq75.gif) . The inferred abundance from the mass-metallicity relation gives [O/H]MZ,M 08 = 8.02. This is consistent with our interpretation of the R23. We therefore report the R23 value.
. The inferred abundance from the mass-metallicity relation gives [O/H]MZ,M 08 = 8.02. This is consistent with our interpretation of the R23. We therefore report the R23 value.
Q 1436–0051. We infer f[O III]λ4959 assuming the standard line-strength conversion f[O III]λ4959 = 0.34f[O III]λ5007. Combining our FORS2 measurements with our re-measured f[O II]3727,3729 line-flux in the Magellan II spectrum (Straka et al. 2016, see Sect. 3.8), we find an R23 line-ratio consistent with a double-valued abundance. The lower- and upper branch values are ![$ \mathrm{[O/H]}_{\mathrm{R}_{23}}^l = 7.93^{+0.12}_{-0.33} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq76.gif) and
and ![$ \mathrm{[O/H]}_{\mathrm{R}_{23}}^u = 8.16^{+0.35}_{-0.11} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq77.gif) , respectively. The O2 line-ratio is outside the range to constrain the abundance. The O3 line-ratio gives an upper branch abundance
, respectively. The O2 line-ratio is outside the range to constrain the abundance. The O3 line-ratio gives an upper branch abundance ![$ \mathrm{[O/H]}_{\mathrm{O}_3}^u = 8.82^{+0.08}_{-0.08} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq78.gif) , but we note that the flux-ratio is marginally consistent with a lower-branch abundance
, but we note that the flux-ratio is marginally consistent with a lower-branch abundance ![$ \mathrm{[O/H]}_{\mathrm{O}_3}^l \sim 7.02 $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq79.gif) . The O32 line-ratio gives an abundance
. The O32 line-ratio gives an abundance ![$ \mathrm{[O/H]}_{\mathrm{O}_{32}} = 9.11^{+0.07}_{-0.06} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq80.gif) . We believe that the large scatter in abundances as determined with the different diagnostics is driven by the combination of spectroscopic data from different telescopes, at different slit-placements, and taken in different conditions. To avoid introducing such systematic differences in the abundance measurements, and noting the consistency with the value inferred from the mass-metallicity relation [O/H]MZ,M 08 = 8.92, we assumed the [O/H]O3 upper branch abundance.
. We believe that the large scatter in abundances as determined with the different diagnostics is driven by the combination of spectroscopic data from different telescopes, at different slit-placements, and taken in different conditions. To avoid introducing such systematic differences in the abundance measurements, and noting the consistency with the value inferred from the mass-metallicity relation [O/H]MZ,M 08 = 8.92, we assumed the [O/H]O3 upper branch abundance.
Q 2335+1501. The O2 line-ratio gives a double-valued abundance, with a lower- and upper branch value of ![$ [\mathrm{O/H}]_{\mathrm{O}_2}^l = 8.34^{+0.36}_{-0.19} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq81.gif) and
and ![$ [\mathrm{O/H}]_{\mathrm{O}_2}^u = 8.96^{+0.09}_{-0.26} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq82.gif) , respectively. We note that the upper branch abundance is consistent with the value inferred from the mass-metallicity relation, [O/H]MZ,M 08 = 8.82.
, respectively. We note that the upper branch abundance is consistent with the value inferred from the mass-metallicity relation, [O/H]MZ,M 08 = 8.82.
All Tables
Absorber characteristics and photometry of the candidate host galaxies explored with our FORS2 campaign.
Observation log for the VLT/FORS2 long-slit spectroscopic observations of damped absorbing galaxies.
All Figures
 |
Fig. 1. Negative colour-mapped two-dimensional VLT/FORS2 SPSF-subtracted spectra (top panels), and the extracted one-dimensional spectra (black; lower panels), centred on the [O II] λ λ 3727,3729 Å doublet. Left panel: Q 1323–0021 field shows excess emission from the DLA counterpart extending above the quasar-trace. Right panel: Q 2328+0022 reveals the presence of the DLA counterpart offset from the trace. In both panels, the fitted doublet-components are overplotted in orange, with the resulting emission profiles in purple. |
| In the text | |
 |
Fig. 2. Spectral energy distribution fits minimising the χ2-statistic for each of the spectroscopically identified host-galaxies. In each panel, we plot the solutions including and excluding nebular emission lines to show its impact on the derived stellar masses. Blue (red) data points refer to included (excluded) magnitudes, with vertical and horizontal error-bars indicating the uncertainty in the photometry and the FWHM of each filter, respectively. Grey squares refer to the transmission-weighted flux in each filter, calculated based on the best-fit SED solution. Upper limits are denoted by triangles. Each panel text displays the LEPHARE best fit reddening before we apply the stellar-to-nebular conversion (Eq. (4)), and the resulting stellar mass. |
| In the text | |
 |
Fig. 3. Left panel: distribution of impact parameter plotted as a function of the column density log10[NHI (cm−2)], colour-coded by stellar mass. Circles refer to data from literature. Our new identifications are plotted as squares. Grey data points represent spectroscopically confirmed absorbing galaxies without stellar mass estimates. The black line represents the median- and the grey lines represent the 1σ scatter in simulated distributions (Rahmati & Schaye 2014) at z = 2. Colour-coded lines represent the median impact parameters for those stellar mass bins, from the same simulations. Right panel: distribution of impact parameters as a function of the absorber metallicity [M/H]abs, colour-coded by column density. The black line marks the median- and the grey lines mark the 1σ, 2σ and 3σ contours based on the model-predictions from Krogager et al. (2017). The grey dotted line marks the distribution envelope. |
| In the text | |
 |
Fig. 4. Stellar masses of spectroscopically confirmed absorbing galaxies as a function of the absorber neutral hydrogen column density, colour-coded by the absorption metallicity. The dotted line marks the traditional distinction between sub-DLAs and DLAs at log10[NH I (cm−2)] = 20.3. The object encircled in red represents the outlier from Q 1209+107 PA2. |
| In the text | |
 |
Fig. 5. Metallicity as a function of stellar mass for spectroscopically confirmed absorbing galaxies, colour-coded by redshift. Squares indicate the results of this work, whereas circles refer to the absorption-selected reference sample. The M 08 mass-metallicity relations based on luminosity-selected samples, and the M 13 predicted mass-metallicity relations for absorption-selected samples are overplotted at four representative redshifts. Top panel: results assuming the metallicity measured in absorption. Bottom panel: results with an impact-parameter dependent correction factor and a gradient cut-off at a truncation radius of 12 kpc. The object encircled in red represents the outlier from Q 1209+107 PA2. |
| In the text | |
 |
Fig. 6. Star-formation rate as a function of stellar mass for spectroscopically confirmed absorbing galaxies, colour-coded by redshift. Squares indicate the results of this work; circles refer to work by others. Triangles represent CO detected galaxies. For reference, we plot the Whitaker et al. (2014) redshift-dependent star-forming main sequence for two representative redshift ranges together with their 1σ- and 3σ scatter, represented by the dark- and light- shaded regions centred on each relation, respectively. See text in Sect. 4.4 for more details. The object encircled in red represents the outlier from Q 1209+107 PA2. |
| In the text | |
 |
Fig. A.1. Negative colour-mapped FORS2 spectral segments of the Q 1436–0051 field, observed during our campaign. Boxes highlight the identified emission lines, colour-coded to emphasize systems at similar redshifts. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




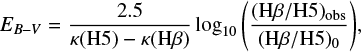
![$\begin{equation}E_{B-V} = \frac{2.5}{\kappa_{\mathrm{[\textsc{O II}]}} - \kappa_{\mathrm{H}\alpha}} \log _{10} \Bigg(\frac{\mathrm{SFR}_{\mathrm{H\alpha}}}{\mathrm{SFR}_{\mathrm{[\textsc{O II}]}}} \Bigg)~, \end{equation}$](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq45.gif)
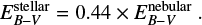
![$\begin{equation} \begin{split} \mathrm{SFR}_{\mathrm{H}\alpha \mathrm{,10\,Myr}}[M_\odot\,\mathrm{yr}^{-1}] & = 7.9 \times 10^{-42} {L}_{\mathrm{H}\alpha}\,[\mathrm{ergs\,s}^{-1}] \\ & = 2.3 \times 10^{-41} {L}_{\mathrm{H}\beta}\,[\mathrm{ergs\,s}^{-1}]~, \end{split} \end{equation} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq47.gif)
![$\begin{equation} \mathrm{SFR}_{\mathrm{[{O} {II}]}\mathrm{,10 Myr}}[M_\odot \mathrm{yr}^{-1}] = 6.58 \times 10^{-42} {L}_{\mathrm{[{O} {II}]}} [\mathrm{ergs s}^{-1}]~.\end{equation} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq48.gif)
![$$\begin{equation} \begin{aligned} &\mathrm{R}_{23} = (f_{\mathrm{[\textsc{O II}]} \lambda \lambda 3727,3729} + f_{\mathrm{[\textsc{O III}]} \lambda \lambda 4959,5007}) / f_{\mathrm{H}\beta} \\ &\mathrm{O}_{32} = f_{\mathrm{[\textsc{O III}]} \lambda \lambda 4959,5007} / f_{\mathrm{[\textsc{O II}]} \lambda \lambda 3727,3729} \\ &\mathrm{O}_2 = f_{[\mathrm{\textsc{O II}}]\lambda \lambda 3727,3729} / f_{\mathrm{H \beta}} \\ &\mathrm{O}_3 = f_{[\mathrm{\textsc{O III}}]\lambda 5007} / f_{\mathrm{H \beta}}, \end{aligned}\end{equation} $$](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq55.gif)
![$\begin{equation} {[\mathrm{M/H}]}_{\mathrm{em}} = {[\mathrm{M/H}]}_{\mathrm{abs}} + \langle {\Gamma} \rangle b~ \vert _{b \leq 12 \mathrm{kpc}}. \end{equation} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq56.gif)
![$\begin{equation} C_{{\mathrm{[M/H]}},i} = \frac{\log _{10} [M_{\star,i}^{\mathrm{SED}} (M_\odot)]}{1.76} - \mathrm{[M/H]}_{\mathrm{abs},i} - 0.35z_{\mathrm{abs},i} - 5.04~, \end{equation} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq63.gif)
![$\begin{equation} 0 = \Bigg( \frac{1}{\mathrm{d.o.f.}} \sum_{i=1}^{N} \frac{\big(C_{\mathrm{[M/H]},i} - \langle {\Gamma} \rangle b_i\big)^2}{\sigma ^2_{\mathrm{nat}} + \sigma^2_{C_{\mathrm{[M/H]},i}}} \Bigg) - C^2_{\mathrm{d.o.f.}}~, \end{equation} $](/articles/aa/full_html/2018/10/aa32992-18/aa32992-18-eq66.gif)