| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 22 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201732538 | |
| Published online | 16 October 2018 | |
Influence of stellar structure, evolution, and rotation on the tidal damping of exoplanetary spin-orbit angles
1
Université Paris-Sud, CNRS, Institut d’Astrophysique Spatiale, UMR8617,
91405
Orsay Cedex,
France
2
Max Planck Institute for Solar System Research,
Justus-von-Liebig-Weg 3,
37077
Göttingen,
Germany
e-mail: damiani@mps.mpg.de
3
IRFU, CEA, Université Paris-Saclay,
91191
Gif-sur-Yvette,
France
4
Université Paris Diderot, AIM, Sorbonne Paris Cité, CEA, CNRS,
91191
Gif-sur-Yvette,
France
Received:
22
December
2017
Accepted:
24
March
2018
Context. It is debated whether close-in giant planets can form in-situ and if not, which mechanisms are responsible for their migration. One of the observable tests for migration theories is the current value of the obliquity, that is, the angle between the stellar equatorial plane and the orbital plane. However, after the main migration mechanism has ended, the obliquity and the semi-major axis keep on evolving due to the combined effects of tides and magnetic braking. The observed correlation between effective temperature and measured projected obliquity in well-characterised systems has been taken as evidence of such mechanisms being at play.
Aims. Our aim is to produce an improved model for the tidal evolution of the obliquity, including all the components of the dynamical tide for circular misaligned systems. This model is developed to take into account the strong variations in structure and rotation of stars during their evolution, and their consequences for the efficiency of tidal dissipation.
Methods. Our model uses an analytical formulation for the frequency-averaged dissipation in convective layers for each mode, depending only on global stellar parameters and rotation. It also includes the effect of magnetic braking in the framework of a double zone stellar model.
Results. For the orbital configurations of typical hot Jupiters, the obliquity is generally damped on a much shorter timescale than the semi-major axis. The final outcome of tidal evolution is also very sensitive to the initial conditions, with Jupiter-mass planets being either quickly destroyed or put on more distant orbits, depending on the initial ratio of planetary orbital momentum to stellar spin momentum. However, we find that everything else being the same, the evolution of the obliquity around low-mass stars with a thin convective zone is not slower than around those with a thicker convective zone. On the contrary, we find that more massive stars, which remain faster rotators throughout their main-sequence, produce more efficient dissipation.
Key words: stars: evolution / stars: rotation / planet-star interactions
© ESO 2018
1 Introduction
Over the last twenty years, tremendous observational efforts have resulted in the complete characterisation and determination of the orbital properties of several hundreds of exoplanetary systems (Winn & Fabrycky 2015). For about a hundred of them, this includes measurements of the Rossiter–MacLaughlin effect (Rossiter 1924; McLaughlin 1924), a signature in radial velocities produced during a transit that contains information about the obliquity Θ of the system, that is, the angle between the stellar spin axis and the orbital normal. Most of the time, what is observed is the projection on the sky of this angle, usually called λ. The constraint obtained on Θ through the observation of λ has a complex nature, but when λ is observed to be large, then it is more likely that Θ is also large. Moreover, when the orbit is seen edge-on, the value of λ can distinguish whether the orbit is prograde or retrograde (Fabrycky & Winn 2009). Those measurements are especially valuable because the obliquity of exoplanetary systems is one of the main observables allowing us to put constraints on their formation and evolution.
In the case of close-in planets, however, which constitute the vast majority of systems with known obliquities, the orbital elements keep evolving after the end of the main migration mechanism under the influence of tides. According to Winn et al. (2010) and Albrecht et al. (2012), observations seem to show that hot stars with hot Jupiters have high obliquities. They interpret this as evidence of tidal evolution, acting upon a population of initially randomly distributed obliquities. Indeed, tidal dissipation is expected to be more efficient in stars that have important convective envelopes because of the turbulent friction acting on the tidal flows (Zahn 1966; Goldreich & Keeley 1977; Ogilvie & Lesur 2012; Mathis et al. 2016). Thus a cooler star’s spin would realign with the orbit more rapidly. Because the mass of the outer convection zone on the main sequence decreases rapidly with increasing stellar mass after 1.2 M⊙, which corresponds to an effective temperature of Teff ≈ 6250 K, this would naturally explain the sharp increase in λ that occurs around this effective temperature. This interpretation would favour a single migration mechanism, capable of producing randomly distributed obliquities.
There is a major flaw in this reasoning: if tides are efficient at damping the obliquity of hot Jupiters, they would also lead to significant orbital decay, and the planet would be destroyed before re-alignment. This result is obtained with the classical theory of the hydrostatic equilibrium tides (see e.g. Zahn 1966; Remus et al. 2012; Ogilvie 2013), an approximation that seems to be incompatible with other orbital properties of hot Jupiters (Ogilvie & Lin 2007). Corrections to the equilibrium tide are provided by the dynamical tide, that is, the response of a rotating fluid to the harmonic forcing of a time-varying perturbing potential. This includes excitation and damping of inertial waves due to the Coriolis acceleration in convective regions, and the excitation and damping of gravity waves due to buoyancy modified by rotation (then called gravito-inertial waves) in radiative regions (Ogilvie & Lin 2004, 2007).
In the framework of the dynamical tide, Lai (2012) suggested that tidal dissipation efficiency may not be the same for different processes such as spin-orbit alignment and orbital decay. Barker & Ogilvie (2009, Appendix A) pointed out that in the case of a misaligned system, the tidal potential has a finite number of components, corresponding to all combinations of the order m and degree l (− l ≤ m ≤ l) of the spherical harmonics decomposition, and that in general each of the distinct components will generate a tidal perturbation with its owndissipation efficiency. The efficiency of tidal dissipation is usually parameterised by a dimensionless quality factor Q proportional to the ratio of the total kinetic energy of the tidal distortion to the energy dissipated in one tidal period (e.g. Zahn 2008). In the theory, for the quadrupolar term, Q always appears in the combination Q′≡ (3∕2)(Q∕k2), where k2 is the staticLove number of the star that measures its density stratification. Therefore, Q′ is the most widely used parameter to estimate tidal dissipation efficiency. The lower the value of Q′ the stronger the tidal dissipation. In general, Q′ depends on l, m, the tidal frequency (a linear combination of stellar rotation frequency and orbital frequency), and the structure of the body under consideration. Thus a rigorous treatment of the tidal dissipation should consider thesum of the effects associated with the different tidal components each having its specific Q′ (Ogilvie 2014).
Using the tidal prescription proposed by Lai (2012), Valsecchi & Rasio (2014) have computed the coupled evolution of the orbital elements and stellar spin of five representative systems, taking into account the combined effects of tides, stellar wind, mass loss, magnetic braking, and stellar evolution. Their results show that, accounting for all the relevant physical mechanisms, the current properties of the systems they consider can indeed be naturally explained. However, an important limitation of this study is the absence of a reliable estimation for the tidal quality factor 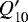 (in the notations introduced by Lai 2012) of the obliquity tide (corresponding to the component associated with a torque but with no dissipated power). In their study,
(in the notations introduced by Lai 2012) of the obliquity tide (corresponding to the component associated with a torque but with no dissipated power). In their study, 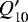 is a free parameter that is allowed to vary within a broad range of values, instead of being imposed by stellar properties, in order to reproduce the observations. While this approach validates Lai (2012) basic idea, it is not enough to accurately constrain the initial distribution of the obliquity of the population of known hot Jupiters.
is a free parameter that is allowed to vary within a broad range of values, instead of being imposed by stellar properties, in order to reproduce the observations. While this approach validates Lai (2012) basic idea, it is not enough to accurately constrain the initial distribution of the obliquity of the population of known hot Jupiters.
Another fundamental limitation of their approach, inherited from Lai (2012) formulation, is that they only consider one of the components of the dynamical tide to have a possibly different tidal quality factor from the others. Indeed, this parametrisation may be reasonable for the current observed orbital state of known hot Jupiters, for which the orbital frequency is usually much greater than the stellar rotation frequency. Then in this case, there is only one mode that is capable of exciting inertial waves in the star. However, when the orbital frequency is shorter than the rotation frequency, which can in general be the case in early stages, other components of the tide may fall into the frequency range of inertial waves, and the resulting dissipation can also contribute to the evolution of the semi-major axis. As already shown by other studies, this clearly stresses the need to take into account the rotational history of the star to compute the tidal evolution of the system (Bolmont et al. 2012; Damiani & Lanza 2015).
In this paper, we propose a tidal evolution model that follows Lai’s theory and we take into account the dynamical tide. We expand on this and the work of Valsecchi & Rasio (2014) by including all the seven components of the quadrupolar term of the tidal potential in the orbital evolution. Moreover, in a similar approach to Mathis (2015b), we also include an analytical formulation of the tidal dissipation efficiency associated with each mode, as a function of stellar structure and rotation, by using the frequency-averaged formulation for dissipation in convective zones derived by Ogilvie (2013). In a series of papers (Mathis 2015b; Lanza & Mathis 2016; Bolmont & Mathis 2016; Gallet et al. 2017; Bolmont et al. 2017), this approach has already shown the importance of the evolution of stellar structure and rotation for the frequency-averaged dissipation efficiency. This requires the use of a double-zone model, one zone representing the radiative core and the other the convective envelope, accounting for the evolution of stellar structure in time. We also use a double-zone semi-empirical model for magnetic braking (Gallet & Bouvier 2013; Penev et al. 2014) to account for the evolution of stellar rotation and the internal redistribution of angular momentum within the star.
The paper is organised as follows. In Sect. 2, we formulate the double-zone tidal model for the evolution of the obliquity in exoplanetary systems. We also describe and give the motivations for our approximations. In Sect. 3, we compute thefrequency-averaged dissipation for different modes involved in the evolution of the semi-major axis and obliquity, and we discuss its dependence with mass and rotation. In Sect. 4, we compute the coupled evolution of semi-major axis, stellar rotation, and obliquity for a sample of initially misaligned systems and discuss the different characteristic timescales. In Sect. 5, we discuss the main results and perspectives of this work.
2 The double-zone weak friction model for tidal interaction
We consider a star of mass M⋆ orbited by a planet of mass Mp. The star is modelled as a deformable core of homogeneous density ρc and mean radius Rc in uniform rotation, surrounded by an envelope of homogeneous lesser density ρe and mean radius R⋆ also rotating uniformly at the angular frequency Ωe, but not necessarily the same frequency as that of the core Ωc. We only consider the tides raised by the planet on the star. As shown by other authors (e.g. Leconte et al. 2010), for typical hot Jupiters, tides raised on the planet result in the evolution of the planetary spin magnitude and direction towards their equilibrium value within a timescale of about 105 yr. This time is sufficiently short compared to the typical stellar evolution timescales to safely neglect the effects of tidal dissipation in the planet on the overall evolution in the case of a circular orbit. We also neglect the mutual interaction of the tidal bulges and consider that the tide-generating potential of the planet is that of a mass point. This hypothesis should be relaxed only if the semi-major axis is a < 5R⋆ and if the gravitational quadrupolar moment is J2 > 10−2 for the planet (Mathis & Le Poncin-Lafitte 2009). The planet generates a time-varying tidal potential Ψ that changes the shape and as a result, the exterior potential Φ of the star. In polar coordinates, the time-varying tidal potential produced by the point-like planet can be expanded in terms of spherical harmonics 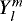 of degree l and order m. For an eccentric orbit, Ψ must be expanded for an infinite number of terms. However, for a circular orbit, not necessarily in the equatorial plane of the reference frame, there is a finite number of tidal components for any given value of l. Here we are interested in the evolution of the obliquity of the orbit resulting from the dissipation of the tides in the star, so we limit our study to the case of circular orbits, and produce a tidal evolution model that is valid for arbitrary values of the obliquity.
of degree l and order m. For an eccentric orbit, Ψ must be expanded for an infinite number of terms. However, for a circular orbit, not necessarily in the equatorial plane of the reference frame, there is a finite number of tidal components for any given value of l. Here we are interested in the evolution of the obliquity of the orbit resulting from the dissipation of the tides in the star, so we limit our study to the case of circular orbits, and produce a tidal evolution model that is valid for arbitrary values of the obliquity.
2.1 Dynamical tidal potential and response in the circular case
We use spherical polar coordinates (r, θ, ϕ), where r is the radial distance from the centre of the star, θ is the colatitude, and ϕ is the azimuthal angle. We adopt an inertial coordinate system with polar axis aligned with the star’s angular momentum L⋆. We note Θ, the angle between the orbital angular momentum Lo and L⋆, a, the semi-major axis of the relative orbit of the planet, and Ω0, its mean orbital angular velocity. We chose the y-axis in the direction L⋆ ×Lo. Neglecting precession, the tide-raising potential of the planet can be written as
![\begin{eqnarray*}{\mathrm{\Psi}}(r, \theta,\phi, t) &=&\textrm{Re} \left[\sum_{l = 2}^{\infty} \sum_{m=-l}^{l} \sum_{p=0}^{l} \frac{G M_{\textrm{p}} R_{\star}^l}{a^{l+1}} \right.\nonumber\\ &&\times\left. W_l^{l-2p} d^{(l)}_{m, l-2p}({\mathrm{\Theta}}) e^{-i(l-2p) {\mathrm{\Omega}}_0 t} \left(\frac{r}{R_{\star}}\right)^l {Y}{_{l}^{m}}(\theta, \phi) \right], \end{eqnarray*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq4.png) (1)
(1)
where G is the gravitational constant, 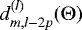 are the Wigner d-matrix elements that only depend on Θ, and
are the Wigner d-matrix elements that only depend on Θ, and
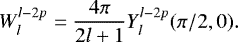 (2)
(2)
Each tidal component rotates with the angular velocity ω given by
 (3)
(3)
where p is an integer with 0 ≤ p ≤ l that arises from the inclination of the orbital plane. This defines the tidal frequency in the inertial frame. In a frame that rotates with the spin angular velocity Ωe, the tidal frequency must be Doppler shifted and we thus define 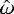 , the tidal frequency in the fluid frame
, the tidal frequency in the fluid frame
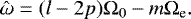 (4)
(4)
While the tidal frequency can be positive or negative, the physical forcing frequency is positive and is thus simply defined as 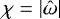 . Since we have
. Since we have 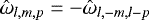 , the (m, p) component is physically identical to the (−m, l − p) component.
, the (m, p) component is physically identical to the (−m, l − p) component.
When the amplitude of the tidal disturbance is small, as is generally the case for close-in exoplanetary systems and for axisymmetric bodies, the tidal response of the perturbed body can be determined by treating each component of the tidal potential independently, and considering that the total response is simply the sum of each component. Taking the Fourier transform of the equations ofmotion, mass conservation, and gravitational potential leads to a purely spatial problem in which the frequency ω appears as a parameter.
Considering a tidal potential of the form 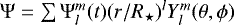 , we write the perturbed stellar gravitational potential in the form
, we write the perturbed stellar gravitational potential in the form 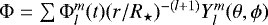 . We denote the temporal Fourier transforms with a tilde and we associate to each component of the perturbed gravitational potential an array of potential Love numbers
. We denote the temporal Fourier transforms with a tilde and we associate to each component of the perturbed gravitational potential an array of potential Love numbers 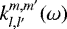 , which quantify the frequency-dependent response of the star to tidal forcing:
, which quantify the frequency-dependent response of the star to tidal forcing:
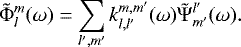 (5)
(5)
For an axisymmetric body, 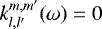 unless m′ = m. The part of the response that has the same form as the applied potential is thus quantified by the potential Love numbers
unless m′ = m. The part of the response that has the same form as the applied potential is thus quantified by the potential Love numbers 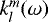 :
:
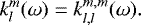 (6)
(6)
2.2 Tidal dissipation
Stars are fluid bodies that cannot be considered as purely frictionless. Dissipation of mechanical energy occurs even in adiabatically stratified fluid layers through turbulent friction or partial wave reflection at the interface with stably stratified zones for example. The fluid dynamics of tidally forced bodies is a very active field of research (see e.g. Ogilvie 2014), but whatever the mechanism actually responsible for dissipation, it suffices to say here that the response of a fluid body to tidal excitation is not frictionless and some energy is transferred to the perturbed body. In the presence of dissipation, the perturbed external gravitational potential of the star involves complex Love numbers and the imaginary part of the Love numbers ![$\textrm{Im}[k_l^m(\omega)]$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq19.png) quantifies the component of the response that is out of phase with the tidal forcing, and is associated with transfers of energy and angular momentum.
quantifies the component of the response that is out of phase with the tidal forcing, and is associated with transfers of energy and angular momentum.
The rates of transfer of energy and of the axial component of angular momentum from the orbit to the body, measured in an inertial frame, define the tidal power P and the tidal torque T, respectively.So for each component of the tidal potential of the form of Eq. (1), averaged over azimuth in the case m = 0, it can be shown (Ogilvie 2013) that 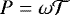 and
and 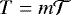 , where
, where 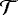 depends on the amplitude of the tidal component and on
depends on the amplitude of the tidal component and on ![$\textrm{Im}[k_l^m(\omega)]$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq23.png) . To compute the evolution of orbital elements associated with these transfers of energy and angular momentum, we use an approximation similar to the one made in the equilibrium theory of tides. We consider that the tidal response resembles the hydrostatic one in the absence of dissipation, and that dissipation introduces a small frequency-dependent phase lag in the response of the body. However, contrary to the usual equilibrium theory of tides, we do not impose that all components have the same phase-lag. So for each component of the tidal potential, we assume that dissipation introduces separate frequency-dependent phase lags
. To compute the evolution of orbital elements associated with these transfers of energy and angular momentum, we use an approximation similar to the one made in the equilibrium theory of tides. We consider that the tidal response resembles the hydrostatic one in the absence of dissipation, and that dissipation introduces a small frequency-dependent phase lag in the response of the body. However, contrary to the usual equilibrium theory of tides, we do not impose that all components have the same phase-lag. So for each component of the tidal potential, we assume that dissipation introduces separate frequency-dependent phase lags 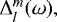 which can be related to the imaginary part of the Love numbers (Efroimsky & Makarov 2013; Ogilvie 2013) with
which can be related to the imaginary part of the Love numbers (Efroimsky & Makarov 2013; Ogilvie 2013) with
![\begin{equation*} \textrm{Im}[k_l^m(\omega)] = \vertk_l^m(\omega)\vert \sin {\mathrm{\Delta}}_l^m(\omega), \end{equation*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq25.png) (7)
(7)
where ![$\textrm{Im}[k_l^m(\omega)]$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq26.png) has the same sign as
has the same sign as 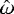 . As detailed in Ogilvie (2014), typically
. As detailed in Ogilvie (2014), typically ![$\textrm{Re}[k_l^m(\omega)]$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq28.png) is a quantity of order unity, only weakly dependent on m and ω, and can be well approximated by its hydrostatic value. The hydrostatic Love number kl is a real quantity and does not depend on m. Its evaluation for a fluid body is a classical problem involving the Clairaut’s equation (see Appendix. B). In the weak friction approximation (Alexander 1973), we thus consider that
is a quantity of order unity, only weakly dependent on m and ω, and can be well approximated by its hydrostatic value. The hydrostatic Love number kl is a real quantity and does not depend on m. Its evaluation for a fluid body is a classical problem involving the Clairaut’s equation (see Appendix. B). In the weak friction approximation (Alexander 1973), we thus consider that 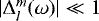 so that
so that
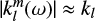 (8)
(8)
In general, the tidal response involves resonances with stellar oscillations when the tidal frequency matches that of an appropriate mode. In convection zones, for solar-like slow rotating stars, the frequencies of tidal oscillations typically lie in the range of inertial modes, for which the Coriolis acceleration provides the restoring force. The eigenfrequencies of inertial modes in the frame that rotates with angular velocity Ωe are dense in the interval [−2Ωe, 2Ωe], but do not exist outside of this range. The spatial structure of the inertial modes implies that any spherical harmonic potential resonates with only a finite number of inertial modes. As shown, for example, by Ogilvie & Lin (2004, 2007), enhanced tidal dissipation rates are expected when the tidal potential can resonantly excite those inertial modes. Dissipation has then a complex dependence on the tidal frequency, and thus on both the rotational and orbital period. As dissipation depends on the internal structure of the body and on its rotation, the computation of ![$\textrm{Im}[k_l^m(\omega)]$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq32.png) becomes very heavy when one is interested in the secular effects of the tidal torque in the evolution of the orbital element as the star itself is evolving (Mathis et al. 2016).
becomes very heavy when one is interested in the secular effects of the tidal torque in the evolution of the orbital element as the star itself is evolving (Mathis et al. 2016).
Here, we use a simplified model for tidal dissipation, which does not involve the complicated details of the frequency-dependence of the responsefunctions, and we neglect the enhancement of dissipation due to resonances. Indeed, as shown by Ogilvie (2013), the typical level of dissipation can be approximated using a simple analytical formulation of the frequency-averaged dissipation ![$\int^{\infty}_{-\infty} \textrm{Im}[k_l^m(\omega)] \textrm{d}\omega/\omega$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq33.png) , obtained by means of an impulse calculation. Their solution depends on the internal structure of the body, either homogeneous or double-layered, but makes no assumption on the details of dissipation mechanisms, so it is smooth and free of surface effects (like wave reflection at the interface between convective and radiative zones). Their derivations are done for arbitrary degree and order of the tidal components. Taking up their work, we use here
, obtained by means of an impulse calculation. Their solution depends on the internal structure of the body, either homogeneous or double-layered, but makes no assumption on the details of dissipation mechanisms, so it is smooth and free of surface effects (like wave reflection at the interface between convective and radiative zones). Their derivations are done for arbitrary degree and order of the tidal components. Taking up their work, we use here ![$\int^{\infty}_{-\infty} \textrm{Im}[k_l^m(\omega)] \textrm{d}\omega/\omega$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq34.png) as a measure of the tidal response in the low-frequency part of the spectrum where inertial waves are found, when the details of the frequency-dependent response curve are filtered out. Thus, we define an average phase-shift
as a measure of the tidal response in the low-frequency part of the spectrum where inertial waves are found, when the details of the frequency-dependent response curve are filtered out. Thus, we define an average phase-shift 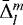 for the tidal component of degree l and order m obtained using the frequency-averaged formulation of Ogilvie (2013)1:
for the tidal component of degree l and order m obtained using the frequency-averaged formulation of Ogilvie (2013)1:
![\begin{equation*}\int^{\infty}_{-\infty} \textrm{Im}[k_l^m(\omega)] \frac{\textrm{d} \omega}{\omega} \approx k_l \int^{\infty}_{-\infty}{\mathrm{\Delta}}_l^m(\omega)\frac{\textrm{d} \omega}{\omega} \equiv k_l \bar{{\mathrm{\Delta}}}_{l}^{m}. \end{equation*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq36.png) (10)
(10)
This averaged phase-shift 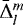 can be related to an average positive-definite time-lag
can be related to an average positive-definite time-lag 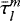 . They are obtained by assuming that, in the fluid frame, components of different p but same l and m have the same time-lags, which is equivalent to assuming that the relevant tidal frequency is
. They are obtained by assuming that, in the fluid frame, components of different p but same l and m have the same time-lags, which is equivalent to assuming that the relevant tidal frequency is 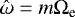 . Since the tidal dissipation rate is a positive-definite quantity, by construction
. Since the tidal dissipation rate is a positive-definite quantity, by construction 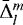 is also positive-definite. Because
is also positive-definite. Because 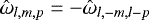 , we must have
, we must have 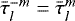 , and thus
, and thus
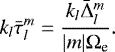 (11)
(11)
Subsequently, we compute the tidal power and torque associated with every component of the tidal potential, but instead of using a frequency-dependent time-lag associated to ![${\textrm{Im}[k_l^m(\omega)] = k_l \tau_{l, m, p} {\hat{\omega}}}$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq44.png) , we approximate it to
, we approximate it to ![${\textrm{Im}[k_l^m(\omega)] \approx k_l \bar{\tau}_{l}^{m} {\hat{\omega}}}$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq45.png) . For the axisymmetric m = 0 component, the axial component of the tidal torque vanishes, but not the tidal power averaged over azimuths, because tidal deformation modulates the moment of inertia of the star. Hence, we compute the average time-lag for m = 0 considering that the relevant frequency is the orbital frequency:
. For the axisymmetric m = 0 component, the axial component of the tidal torque vanishes, but not the tidal power averaged over azimuths, because tidal deformation modulates the moment of inertia of the star. Hence, we compute the average time-lag for m = 0 considering that the relevant frequency is the orbital frequency:
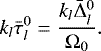 (12)
(12)
The frequency-averaged formulation derived from Ogilvie’s work corresponds to the dissipation of tidally excited inertial waves. Yet those waves exist only when 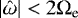 . Outside of this range, the dissipation efficiency corresponds to that of the equilibrium tide. Hence, we introduce a frequency dependence for the value of
. Outside of this range, the dissipation efficiency corresponds to that of the equilibrium tide. Hence, we introduce a frequency dependence for the value of  by considering
by considering
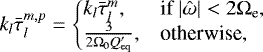 (13)
(13)
where the value of 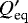 remains uncertain and we perform calculations considering a range of values to study the sensitivity of the model (see Sect. 4).
remains uncertain and we perform calculations considering a range of values to study the sensitivity of the model (see Sect. 4).
Following Ogilvie (2013), we thus write the average energy transfer ⟨Ė ⟩ associated with the component of degree l as
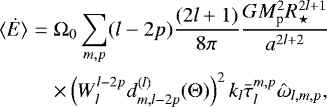 (14)
(14)
and the corresponding axial component of the tidal torque Tz:
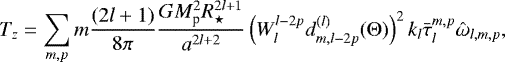 (15)
(15)
where we calculate the value of 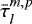 using Eqs. (10)–(13).
using Eqs. (10)–(13).
Up to this point, all our derivations are valid for arbitrary values of l and m and, in principle, they allow the computation of the tidal response for any spherical harmonic of the multipole expansion of the tidal potential. As can be seen in Eq. (1), the contribution of the spherical harmonic of degree l is proportional to rl, so usually only the quadrupolar terms are retained in the formulation of the temporal evolution of orbital elements. Explicitly then, for the quadrupolar components, Eq. (14) yields
![\begin{eqnarray*}{\langle \dot{E}\rangle} &=& \frac{3}{64} \frac{G M_{\textrm{p}}^2 R_{\star}^5}{a^6} {\mathrm{\Omega}}_0 \left[ 6 \sin^4 {\mathrm{\Theta}} (2 {\mathrm{\Omega}}_0) k_2 \bar{\tau}_{2}^{0,2} \right.\nonumber\\ &&+\,4 \sin^2 {\mathrm{\Theta}} \left(1+\cos {\mathrm{\Theta}} \right)^2 (2{\mathrm{\Omega}}_0-{\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{1,0} \nonumber\\ &&-\, 4 \sin^2 {\mathrm{\Theta}} \left(1-\cos {\mathrm{\Theta}} \right)^2 (-2{\mathrm{\Omega}}_0-{\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{1,2} \nonumber\\ &&+\, \left(1+\cos {\mathrm{\Theta}} \right)^4 (2{\mathrm{\Omega}}_0-2{\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{2,0} \nonumber\\ &&\left. - \left(1 - \cos {\mathrm{\Theta}}\right)^4 (-2{\mathrm{\Omega}}_0-2{\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{2,2} \right], \end{eqnarray*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq54.png) (16)
(16)
and for Eq. (15) we have
![\begin{eqnarray*}T_{z} &=& \frac{3}{64} \frac{G M_{\textrm{p}}^2 R_{\star}^5}{a^6} \left[ 2 \sin^2 {\mathrm{\Theta}} (1+\cos {\mathrm{\Theta}})^2 (2{\mathrm{\Omega}}_0 - {\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{1,0} \right. \nonumber\\ &&+\, 8 \sin^2 {\mathrm{\Theta}} \cos^2 {\mathrm{\Theta}} (-{\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{1,1}\nonumber\\ &&+\, 2 \sin^2 {\mathrm{\Theta}} (1-\cos {\mathrm{\Theta}})^2(-2{\mathrm{\Omega}}_0 - {\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{1,2} \nonumber\\ &&+\, \left(1+\cos {\mathrm{\Theta}}\right)^4 (2{\mathrm{\Omega}}_0 - 2{\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{2,0} + 4 \sin^4 {\mathrm{\Theta}} k_2 \bar{\tau}_{2}^{2,1} (- 2{\mathrm{\Omega}}_{\textrm{e}}) \nonumber\\ &&\left.+\, \left(1-\cos {\mathrm{\Theta}} \right)^4 k_2 \bar{\tau}_{2}^{2,2} (-2{\mathrm{\Omega}}_0 - 2{\mathrm{\Omega}}_{\textrm{e}}) \right]. \end{eqnarray*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq55.png) (17)
(17)
The y-component only contributes to precession, which we are neglecting here. The perpendicular component of the torque is computed following the formulation of Lai (2012)2:
![\begin{eqnarray*}T_x &=& \frac{3}{64}\frac{G M_{\textrm{p}}^2 R_{\star}^5}{a^6} \sin {\mathrm{\Theta}} \Big[ 6 \sin^2 {\mathrm{\Theta}} (2{\mathrm{\Omega}}_0) k_2 \bar{\tau}_{2}^{0,2} \nonumber\\ &&+\, 2 (1+\cos {\mathrm{\Theta}})^2 (2-\cos {\mathrm{\Theta}}) (2{\mathrm{\Omega}}_0 - {\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{1,0} \nonumber\\ &&-\, 8 \cos^3 {\mathrm{\Theta}} (-{\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{1,1} \nonumber\\ &&-\, 2 (1-\cos {\mathrm{\Theta}})^2 (2+\cos {\mathrm{\Theta}}) (- 2{\mathrm{\Omega}}_0 - {\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{1,2}\nonumber\\ &&+\, (1+\cos {\mathrm{\Theta}})^3 (2{\mathrm{\Omega}}_0 - 2{\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{2,0} \nonumber\\ &&-\, 4 \sin^2 {\mathrm{\Theta}} \cos {\mathrm{\Theta}} (- 2{\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{2,1}\nonumber\\ &&\left. -\, ( 1-\cos {\mathrm{\Theta}})^3 (-2{\mathrm{\Omega}}_0 - 2 {\mathrm{\Omega}}_{\textrm{e}}) k_2 \bar{\tau}_{2}^{2,2}\right]. \end{eqnarray*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq56.png) (18)
(18)
2.3 Stellar angular momentum modelling
The angular momentum of the star 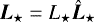 is modelled with core-envelope decoupling under the assumptions of the double-zone model introduced by MacGregor & Brenner (1991):
is modelled with core-envelope decoupling under the assumptions of the double-zone model introduced by MacGregor & Brenner (1991):
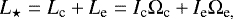 (19)
(19)
where Ic and Ie are the moment of inertia for the core and the envelope respectively. The core and the envelope are assumed to rotate as solid bodies with different angular velocities. As noted in Ogilvie (2013), in a differentially rotating body there is no simple global relation between the tidal dissipation rate and the rates of energy and angular momentum transfer as computed from Eqs. (14), (15), and (18). However, those quantities depend on stellar parameters only through the mean stellar radius at the surface, the static Love number, and the average time-lag. The static (real) Love numbers link the interior structure of the star to its external potential through the surface value of the logarithmic derivative of the deformation (Kopal 1959). Here we neglect the effect of the centrifugal force on the shape of the star, so the internal discontinuity in rotation speed is irrelevant. The impulsing forcing approach used to estimate the average time-lag also neglects the effect the Coriolis acceleration on the non-wavelike part of the displacement, so the boundary condition specifying the solution remains the same even if we consider that the core rotates at a different angular velocity to the envelope. Moreover, as is clearly apparent in Eqs. (96)–(98) of Ogilvie (2013), only the convective envelope of the star is involved in the tidal energy transfer, since we are only considering the dissipation of tidally excited inertial wave. Here we suppose that the envelope rotates rigidly and as such our assumptions are fully compatible with the derivations of Ogilvie (2013), setting the angular velocity to that of the envelope. Furthermore, we consider that the tidal torque is applied on the envelope of the star, but we allow angular momentum exchanges between the two zones. As a matter of fact, in the piece-wise homogeneous rigidly rotating model considered in Ogilvie (2013), the non-barotropic nature of the density jump results in a singularity of vorticity at the interface. In the double-zone model considered here, considering our simplifying assumptions regarding rotation and other overlooked mechanisms that may beinvolved, we simply parametrise the transfer of angular momentum between the zones by a quantity Δ L defined as
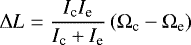 (20)
(20)
at a rate determined by a coupling timescale τc. For the dependence of τc on stellar rotation, we follow Spada et al. (2011) and consider a two-valued function with
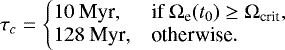 (21)
(21)
We follow the evolution of the star from its formation until the end of its main sequence, that is, before the core starts contracting during the sub-giant phase. Initially the star is fully convective and is assumed to rotate rigidly. We consider a phase of disc locking, where the net effect of interactions with the disc is that of keeping the surface angular velocity of the star constant for the disc lifetime,
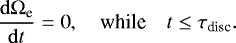 (22)
(22)
The disc lifetime τdisc may vary, but it is in general shorter than the PMS (Pre-Main-Sequence), as observations show that most primordial discs have disappeared by the first 10 Myr (Ribas et al. 2014). As the radiative core develops, a quantity of material contained in a thin shell at the base of the convective zone, with a velocity of Ωe, becomes radiative, producing an angular momentum transfer towards the core:
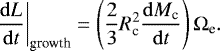 (23)
(23)
From the moment the disc disappears, the star experiences angular momentum loss through its magnetised wind. We assume that because of wind braking, the envelope loses angular momentum at a rate given by the parametric formula (Kawaler 1988):
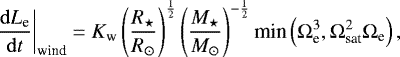 (24)
(24)
where Kw determines the braking intensity and Ωsat is the angular frequency threshold defining a saturated (when Ωe ≥Ωsat) regime of angular momentum loss.
In conclusion, the evolution of the stellar angular momentum is modelled with the differential equations:
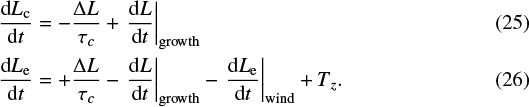
2.4 Tidal evolution of orbital elements
The transferof energy from the orbit to the rotation of the star due to tides results in the variation of the semi-major axis through the relationship
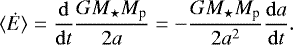 (27)
(27)
For hot Jupiters, the quadrupolar components of the tidal potential is strongly dominant due to the small ratio between stellar radius and semi-major axis, even during the PMS. The evolution of the semi-major axis is straightforwardly obtained using Eq. (16). As can be seen in Eq. (14), tidal components with p = 1 do not contribute to the transfer of energy. Moreover, for m = 0, the components with p = 0 and p = 2 are physically identical. Sothere are only five components that contribute to the evolution of the semi-major axis. The importance of each of them depends on their respective tidal frequency, the average time-lag, and a weighting factor that is a function of the instantaneous value of Θ. This quantity is shown in Fig. 1 (top panel). For Θ = 0, only the l = 2, m = 2, p = 0 component contributes to the evolution of the semi-major axis.
The magnitude of the orbital angular momentum Lo = ||Lo|| is
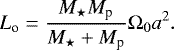 (28)
(28)
Because we consider here that only the envelope is involved in tidal energy transfer, we will consider the evolution of the orientation of the direction of the spin of the envelope, so
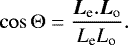 (29)
(29)
By definition, 0 ≤Θ ≤ π, the orbit is polar when Θ = π∕2 and retrograde when Θ > π∕2. Supposing that in the absence of magnetic braking, the total angular momentum is conserved, we get
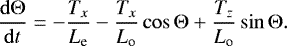 (30)
(30)
The differential equation governing the evolution of the obliquity can thus be obtained using Eqs. (17) and (18). Here, all the seven physical components of the tidal forcing will contribute to the evolution of the obliquity. Their relative importance is a function of the instantaneous value of Θ and of Lo ∕Le. It is shown in Fig. 1 (bottom panel) for Lo∕Le = 0.5.
 |
Fig. 1 Relative geometrical contribution of each tidal component of degree l = 2 in the evolution of the semi-major axis (Eq. (27); top panel) and the obliquity (Eq. (30)) as a function of the instantaneous value of the obliquity for m = 0 (red), m = 1 (green), and m = 2 (blue); p = 0 (solid), p = 1 (dot-dashed), and p = 2 (dashed). For the obliquity (bottom panel), the relative contribution of each component depends on the orbital-to-spin angular momentum magnitude ratio, here taken for illustration purposes at 0.5. Those factors do not include the factor |
3 Evolution of tidal dissipation as a function of stellar mass and evolutionary stage
As can be seen from Eqs. (16)–(18), (26), (27), and (30), the coupled evolution of the orbital elements depends on the dissipation efficiency of the tides raised by the three components of the quadrupole moment l = 2 of the tidal potential: the m = 0 zonal harmonic, the m = 1 tesseral harmonic, and the m = 2 sectoral harmonic. The so-called obliquity tide (l = 2, m = 1, p = 1), which has the frequency 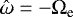 regardless of the orbital frequency, contributes to the tidal torque but has no associated variation of mechanical energy. However, it is important to note that other terms associated with the zonal or tesseral harmonics participate in both angular momentum and energy transfer, but their contribution to the evolution of the semi-major axis is non-null only when sin Θ≠0, that is, when the system is not aligned or anti-aligned.
regardless of the orbital frequency, contributes to the tidal torque but has no associated variation of mechanical energy. However, it is important to note that other terms associated with the zonal or tesseral harmonics participate in both angular momentum and energy transfer, but their contribution to the evolution of the semi-major axis is non-null only when sin Θ≠0, that is, when the system is not aligned or anti-aligned.
The effect of stellar structure and evolution on the frequency-averaged dissipation of the sectoral (l = m = 2) harmonic have already been computed in other studies (Mathis 2015b; Lanza & Mathis 2016; Bolmont & Mathis 2016; Gallet et al. 2017; Bolmont et al. 2017). In the impulsive forcing problem, the value of m affects the energy dissipated by inertial waves through the coupling of the spheroidal and toroidal wavelike velocity components due to the Coriolis force. The only difference between the energy transfer from the sectoral harmonic and the zonal and tesseral ones stems from the contribution of the toroidal part, related to the coupling coefficient 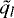 ,
,
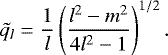 (31)
(31)
To compare the evolution of ![$\int^{\infty}_{-\infty} \textrm{Im}[k_l^m(\omega)] \textrm{d}\omega/\omega$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq72.png) for the sectoral and tesseral harmonics, we computed it for models of a 1 M⊙ and a 1.2 M⊙ and two values of initial stellar rotation frequency 3Ω⊙ and 25 Ω⊙. Those values correspond to rotation periods of ~ 8.5 and 1 days, respectively, and are representative of the range of surface rotation periods measured in clusters younger than ~2 Myr for stars in this mass range (e.g. Gallet & Bouvier 2015). The stellar structure quantities and their time derivatives are taken from evolutionary models by Baraffe et al. (1998). To obtain the variables of our piecewise-homogeneous fluid model, we compute the mean density in each layer simply using the mass and thickness of the corresponding zone. We plot in Fig. 2 the temporal evolution of α, the core to envelope radius ratio (top panel), and f, the envelopeto core density ratio (bottom panel; see also Appendix A), which we get from the stellar models for the two masses considered here.
for the sectoral and tesseral harmonics, we computed it for models of a 1 M⊙ and a 1.2 M⊙ and two values of initial stellar rotation frequency 3Ω⊙ and 25 Ω⊙. Those values correspond to rotation periods of ~ 8.5 and 1 days, respectively, and are representative of the range of surface rotation periods measured in clusters younger than ~2 Myr for stars in this mass range (e.g. Gallet & Bouvier 2015). The stellar structure quantities and their time derivatives are taken from evolutionary models by Baraffe et al. (1998). To obtain the variables of our piecewise-homogeneous fluid model, we compute the mean density in each layer simply using the mass and thickness of the corresponding zone. We plot in Fig. 2 the temporal evolution of α, the core to envelope radius ratio (top panel), and f, the envelopeto core density ratio (bottom panel; see also Appendix A), which we get from the stellar models for the two masses considered here.
Our evolution begins at t0 ~ 1.5 Myr, when stars are almost fully convective, justifying our assumption of solid-body rotation as our initial condition. After the disc-locking phase, the angular momentum of the star evolves as a consequence of both structural evolution and magnetic braking (see Sect. 2.3). Here the parameters are taken from Spada et al. (2011) and summarised in Table 1. There is a lack of reliable calibration of the magnetic braking laws in the framework of the double-zone model for stars with M⋆ > 1.1 M⊙. Here, we simply assume the same values apply also to our 1.2 M⊙ model for all parameters, except for Kw, that we divide by a factor ten as in Barker & Ogilvie (2009).
To allow easy comparison with the values found in the literature for the equilibrium tide, we also give the conversion of our estimation of the dissipation rate as the traditional equivalent modified tidal quality factor Q′, using the relationship
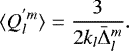 (32)
(32)
Here we get a value of Q′ that is not exactly frequency-averaged, but rather corresponds to a frequency average of the phase lag (see Mathis 2015a, for a discussion on this point). The results are shown in Fig. 3.
We see that the m = 0 and m =1 components are almost identical due to similar contributions of the toroidal part to the impulse energy, and they are more than one order of magnitude greater thanthe m = 2 component during the main-sequence. This clearly shows that assuming that different components have the same time-lag, as is done in the equilibrium tide theory, severely underestimates the participation of the tesseral harmonics of the tide, when the tidal frequency is within the range allowing the existence of inertial waves. Overall, we find that the value of 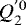 and
and 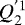 assumes a value between 1 and 106 throughout stellar evolution across slow and fast rotators. For 1.2 M⊙ mass stars, fast rotators can have
assumes a value between 1 and 106 throughout stellar evolution across slow and fast rotators. For 1.2 M⊙ mass stars, fast rotators can have 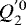 and
and 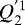 smaller than 100 throughout their evolution. This is extremely efficient for fluid dissipation, and is comparable to the value of Q′ estimated for the rocky bodies of the solar system, estimated in the framework of the equilibrium tide (Lainey 2016).
smaller than 100 throughout their evolution. This is extremely efficient for fluid dissipation, and is comparable to the value of Q′ estimated for the rocky bodies of the solar system, estimated in the framework of the equilibrium tide (Lainey 2016).
We must stress that we are using here a simplified model, which considers that the densities in the radiative core and the convective envelope are both homogeneous. For the sectoral harmonic l = m = 2, Ogilvie (2013) has shown, using polytropes of different indexes and in the presence of a solid core, that using various density profiles can change the frequency-averaged dissipation rate by orders of magnitude depending on the core to envelope radius ratio α (see Fig. 10 in Ogilvie 2013). The general trend, for α ≳ 0.3, is that the dissipation becomes less efficient as the star gets more centrally condensed. In addition, Lin & Ogilvie (2017) have shown numerically that the dissipation rate of the obliquity tide, for a fluid body containing a solid core, is enhanced by one to two orders of magnitude in the homogeneous case compared to the more realistic case of a polytropic density of index 1 (we refer the reader to Figs. 4 and 7 in their article). Here, we use a piecewise-homogeneous fluid model. Therefore, we cannot exclude the possibility that modelling the convective envelope as homogeneous may artificially enhance the dissipation and this could potentially significantly modify our results regarding the timescales of tidal evolution. In addition, we know from previous works (e.g. Ogilvie & Lin 2004, 2007; Barker & Ogilvie 2009) that the dissipation of tidal inertial waves can vary over several orders of magnitude as a function of the tidal frequency. At a given frequency, it may thus differ from its frequency-averaged value. However, we expect this latter to provide us with a reasonable order of magnitude of the dissipation value that we can use in planetary systems’ secular evolution models.
Dissipation is strongly affected by stellar rotation. In the magnetic braking model considered here, initially fast and slow rotators converge to a common rotation rate after the first Gyr of evolution, but they have very different behaviours during the first hundreds of Myr. During this phase, the angular momentum evolution is driven by the evolution of the structure of the star, dominated by its global contraction. Thus, the value of Q′ during this phase is very similar for the two stellar masses considered here, with 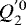 and
and  –103 and
–103 and  –105 depending on the value of the initial rotation. Those values are maintained during the first 20–30 Myr of evolution. This implies that any hot Jupiter that would reach a three-day period orbit in the first tens of Myr would spiral into the star and be destroyed by tides within a few 105 years, if the tidal frequency falls within the range of inertial waves and if the rotation period of the star is greater than three days, regardless of the mass of the host. Yet, one should keep in mind that the values obtained here may be considered as upper bounds on the dissipation because of the hypothesis of homogeneous density in the convective envelope.
–105 depending on the value of the initial rotation. Those values are maintained during the first 20–30 Myr of evolution. This implies that any hot Jupiter that would reach a three-day period orbit in the first tens of Myr would spiral into the star and be destroyed by tides within a few 105 years, if the tidal frequency falls within the range of inertial waves and if the rotation period of the star is greater than three days, regardless of the mass of the host. Yet, one should keep in mind that the values obtained here may be considered as upper bounds on the dissipation because of the hypothesis of homogeneous density in the convective envelope.
On the main sequence, the stellar structure stops evolving and the evolution of the dissipation is mainly controlled by the rotation frequency of the envelope. For the 1 M⊙ mass star, we see a steady decrease in dissipation efficiency, with 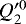 and
and  –105 and
–105 and  –109. For the 1.2 M⊙ mass star, dissipation efficiency appears to plateau around
–109. For the 1.2 M⊙ mass star, dissipation efficiency appears to plateau around 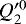 and
and 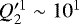 –103 and
–103 and 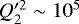 –107, because angular momentum loss is reduced and the star spins down less efficiently. After about 4 Gyrs, the mass of the convective envelope becomes negligible and our computation of Q′ suffers from numerical instabilities inherent to the stellar evolutionary track we are using. These orders of magnitude are in agreement with those obtained by Gallet et al. (2017), who also computed the impact of the simultaneous structural and rotational evolution of low-mass stars on the dissipation of tidal inertial waves in their convective envelope (we refer the reader to their Figs. 4 and 5 – top left panel) for the l = m = 2 components.
–107, because angular momentum loss is reduced and the star spins down less efficiently. After about 4 Gyrs, the mass of the convective envelope becomes negligible and our computation of Q′ suffers from numerical instabilities inherent to the stellar evolutionary track we are using. These orders of magnitude are in agreement with those obtained by Gallet et al. (2017), who also computed the impact of the simultaneous structural and rotational evolution of low-mass stars on the dissipation of tidal inertial waves in their convective envelope (we refer the reader to their Figs. 4 and 5 – top left panel) for the l = m = 2 components.
Interestingly here, unlike what is found in Gallet et al. (2017), we see that despite the less important convective zone of the 1.2 M⊙ mass star, the energy dissipated by the inertial waves for this stellar mass is about the same order of magnitude, if not greater, than for the 1 M⊙ mass star, for a given set of l, m, and initial rotation frequency. This may seem to be also in contradiction with previous numerical simulations that showed that this dissipation rate should scale with the extent of the convection zone (Ogilvie & Lin 2007; Barker & Ogilvie 2009). However, one must remember that those simulations were computed at a fixed rotation rate while here we compute the evolution of the rotation of the star as its internal structure evolves. To better compare our results with these numerical simulations, we show in Fig. 4 the frequency-averaged dissipation obtained with our model along the evolution of the stellar structure, but fixing the rotation frequency of the star at 8.5 Ω⊙, which corresponds to the rotation period of three days, a value chosen arbitrarily by Ogilvie & Lin (2007) and Barker & Ogilvie (2009) to illustrate their results.
Firstly let us consider the case of the l = m = 2 component. For this component, the frequency dependent dissipation rate of inertial waves for a solar mass star rotating with the three-day period has been computed in Ogilvie & Lin (2007). Besides the complex dependance upon tidal frequency, their equivalent Q′ ranges between 106 and 108. Using the same numerical set up, Barker & Ogilvie (2009) obtained, for a 1.2 M⊙ mass star rotating at the same angular velocity, a significantly lower Q′, ranging between 108 and 1010 for the same tidal component. Here, on the main sequence, we obtain Q′~ 106 and Q′~ 107 for the respective masses. Considering again that our model assumes piecewise-homogeneous density, which leads to upper bounds on the dissipation, our results are thus in reasonable agreement with the trends of these more realistic numerical simulations, albeit the difference in dissipation as a function of mass is less contrasted. Again, this is in broad agreement with Gallet et al. (2017; compare their Fig. 4 top left and bottom left panels) where the difference in dissipation between a 1 M⊙ and a 1.2 M⊙ mass star is found to be greater when considering only the effect of structure, compared to the case when the evolution of both the structure and rotation is taken into account. Comparing Figs. 3 and 4 (and also top left and bottom left panels of Fig. 4 in Gallet et al. 2017, although in their case the 1.2 M⊙ mass star always dissipates less), it is clear that the main factor affecting the difference in dissipation on the main sequence between the two stellar models considered here is thus the evolution of stellar rotation: the 1.2 M⊙ mass star spins down less rapidly and thus maintains a dissipation rate throughout its main sequence similar to those of the 1 M⊙ mass star independently from the thickness of their respective convective envelope.
Nevertheless, for a given initial rotation rate, as previously noted, the dissipation of the m = 0 and m = 1 components is always orders of magnitude greater than for the m = 2 component. This seems to disagree with previous results from numerical simulations computed in Barker &Ogilvie (2009), who showed that the dissipation evaluated for different values of m is similar in magnitude. Such a discrepancy is also observed between the frequency-averaged estimation and numerical results obtained by Lin & Ogilvie (2017) for the dissipation rate of the obliquity tide in the case of an homogeneous fluid containing a solid core. Indeed, they show in their Fig. 4 the dimensionless dissipation rate 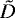 of the obliquity tide as defined in their Eq. (69) for a homogeneous fluid. It ranges between 10−5 and 1 depending on the value of the fractional core radius. However, Fig. 6 of Ogilvie (2013; second red line from the top, also partly reproduced in Fig. 5) shows that the frequency-averaged, dimensionless, rotation normalised, equivalent dissipation for the same homogeneous fluid is greater than 10 and diverges as α → 1. The dissipation rate computed in Lin & Ogilvie (2017) is not exactly equivalent to the quantity obtained in the impulsive response formulation in Ogilvie (2013). However, the forcing frequency is independent of the orbital frequency of the planet for the obliquity tide, and both quantities, if we relate them through an equivalent quality factor Q′, should agreeto a factor of the order of unity. This does not seem to be the case and may be related to the effect of precessional forces.
of the obliquity tide as defined in their Eq. (69) for a homogeneous fluid. It ranges between 10−5 and 1 depending on the value of the fractional core radius. However, Fig. 6 of Ogilvie (2013; second red line from the top, also partly reproduced in Fig. 5) shows that the frequency-averaged, dimensionless, rotation normalised, equivalent dissipation for the same homogeneous fluid is greater than 10 and diverges as α → 1. The dissipation rate computed in Lin & Ogilvie (2017) is not exactly equivalent to the quantity obtained in the impulsive response formulation in Ogilvie (2013). However, the forcing frequency is independent of the orbital frequency of the planet for the obliquity tide, and both quantities, if we relate them through an equivalent quality factor Q′, should agreeto a factor of the order of unity. This does not seem to be the case and may be related to the effect of precessional forces.
In addition, compared to the fluid case, the boundary conditions imposed by a solid core have large repercussions on the functional dependence of the frequency-averaged tidal dissipation with the core size. This can be appreciated in Fig. 5, where we plot the result of the frequency-averaged dissipation, divided by 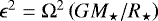 , in the cases of a homogeneous fluid with a solid core and of the piecewise fluid model considered here, for all components of the quadrupolartidal forcing.
, in the cases of a homogeneous fluid with a solid core and of the piecewise fluid model considered here, for all components of the quadrupolartidal forcing.
First, we can clearly see that the piecewise-homogeneous fluid has overall less efficient dissipation for all values of m. This is expected since the core in this model is not perfectly rigid but instead undergoes some tidal deformation. This produces slower horizontal flow than in the solid core case, and through the Coriolis force, a smaller wavelike velocity.
Next, in the range of parameters corresponding to main sequence values (see Fig. 2), the dissipation of the zonal and tesseral components clearly dominates that of the sectoral component in the case of the piecewise fluid model. This quantitative difference exists also in the solid-core case but is mainly important for thick convection zones.
Here in the piecewise-homogeneous fluid model, the integrated response to a tesseral harmonic is always much stronger than the response to the sectoral harmonic. This seems to be a robust result for the dissipation computed for an impulsive forcing. However, the question of the effect of the density profile on the relative dissipations of the different tidal components has not yet been investigated beyond the two simple models discussed here. This requires further theoretical investigations that are beyond the scope of this article. Let us note here that, in the present model, the difference in stellar structure between a 1 M⊙ and a 1.2 M⊙ mass star on the main sequence (mainly stemming from the density of the envelope) has little effect on the tidal dissipation for the m = 0 and m = 1 components, but has a greater impact on the m = 2 component.
Again, the predominant factor here will be the evolution of stellar rotation. Since the 1.2 M⊙ mass star remains a fast rotator throughout its main sequence, it has overall a more efficient dissipation, if we consider that our impulsive response formulation provides a robust measure of the dissipative properties of the star.
This would tend to produce an anti-correlation of obliquity with stellar effective temperature, contrary to what is observed. Nevertheless, this result is very sensitive to the model chosen for angular momentum evolution. For example, Gallet et al. (2017) use a different prescription for the angular momentum evolution of the star. They use stellar evolution models that take into account rotation, with angular momentum transport operated through meridional circulation and diffusion by shear turbulence. This results in a much less efficient coupling between the radiative zone and convective envelope than the model used here (Charbonnel et al. 2013). Moreover, in their model, the magnetic braking law involves a parametrisation based on the Rossby number. Consequently, for the l = m = 2 mode, they find that dissipation scales with the extent of the convective zone for stellar mass between 1 and 1.4 M⊙ on the main sequence, with 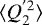 increasing by about an order of magnitude over this mass range. Here our results differ because we allow the coupling of the radiative and convective zones, which affects the rotation rate of the envelope and thus the value of the dissipation. We estimate tidal dissipation efficiency using a simplified model, valid in the convective zone only and which assumes rigid body rotation, but our computations show that even in this framework, the internal angular momentum transport throughout the star may have a strong impact on tidal dissipation efficiency.
increasing by about an order of magnitude over this mass range. Here our results differ because we allow the coupling of the radiative and convective zones, which affects the rotation rate of the envelope and thus the value of the dissipation. We estimate tidal dissipation efficiency using a simplified model, valid in the convective zone only and which assumes rigid body rotation, but our computations show that even in this framework, the internal angular momentum transport throughout the star may have a strong impact on tidal dissipation efficiency.
To conclude, we find different dissipation efficiencies associated to different modes, and this supports the possibility of having different timescales for the tidal evolution of the semi-major axis and the obliquity. But the absolute value of the dissipation is also very sensitive to the evolution of the rotation of the star. With the magnetic braking law used here, this would tend to produce an anti-correlation of obliquity with stellar effective temperature, contrary to what is observed. In any case, the value we find here would implytypical timescales for tidal evolution that could be much shorter than the main-sequence lifetime of the star, depending on the orbital configuration. Thus, the final state of hot Jupiter systems is not easily inferred from the relative values of 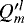 alone, but must also consider the initial rotation period of the star and the coupled evolution of orbital elements.
alone, but must also consider the initial rotation period of the star and the coupled evolution of orbital elements.
 |
Fig. 2 Temporal evolution of the core-to-envelope ratio (top panel) and envelope-to-core density ratio (bottom panel) for our models of a 1 M⊙ star (in red) and a 1.2 M⊙ star (in blue). |
Values of the parameters used to plot Fig. 3 for the 1 M⊙ model (from Spada et al. 2011).
 |
Fig. 3 Temporal evolution of the frequency-averaged imaginary part of the potential Love number corresponding to components of degree l = 2 and m = 0 (red), m = 1 (green) and m = 2 (blue) for models of a 1 M⊙ (left panel) and 1.2 M⊙ (right panel) mass stars. The solid and dashed lines correspond to a star initially rotating with Ω (t0) = 3 Ω⊙, and Ω (t0) = 25 Ω⊙, respectively. A conversion to the modified tidal quality factor Q′ is given on the right y-axis. |
 |
Fig. 4 Temporal evolution of the frequency-averaged imaginary part of the potential Love number corresponding to components of degree l = 2 and m = 0 (red), m = 1 (green), and m = 2 (blue) for models of a 1 M⊙ (left panel) and 1.2 M⊙ (right panel) mass stars. The rotation rate of the star does not evolve in time and is set at all times at Ω = 8.5 Ω⊙ for both models. A conversion to the modified tidal quality factor Q′ is given on the right y-axis. |
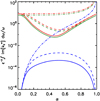 |
Fig. 5 Frequency-integral of the imaginary part of the Love numbers, weighted by 1∕ω and divided by ϵ2, versus fractional core size for the quadrupolar component l = 2. The colour of the lines corresponds to different values of m: m = 0 (red), m = 1 (green), and m = 2 (blue). The dashed-dotted line shows the analytical result of the impulse calculation for a homogeneous fluid body with a solid core. The dashed line shows the same but in the case of the piecewise-homogeneous fluid model with a density ratio of 2 × 10−2, adequatefor a solar mass star on the main sequence. The solid line corresponds again to the piecewise-homogeneous fluid model but with a density ratio of 4 × 10−3, appropriate for a 1.2 M⊙ mass star on the main sequence. |
4 Coupled evolution of semi-major axis and obliquity
Using Eqs. (16)–(18), (26), (27), and (30), we compute the coupled temporal evolution of the orbital elements for different values of initial obliquity, semi-major axis, and stellar rotation. Our evolution begins again at t0 ~ 1.5 Myr, when stars are almost fully convective, and thus rotating as a solid body. It stops at the end of the main-sequence phase (i.e. after 10 Gyr for the 1 M⊙ star and 5 Gyr for the 1.2 M⊙ star) or when the planet reaches the Roche limit (![$a_{\textrm{R}}=2.422 R_{\textrm{p}}\sqrt[3]{M_{\star}/M_{\textrm{p}}}$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq91.png) , with Rp = 1.2RJup for a Jupiter-mass planet), or alternatively when the star is spinning faster than the break-up velocity (
, with Rp = 1.2RJup for a Jupiter-mass planet), or alternatively when the star is spinning faster than the break-up velocity (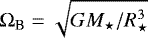 ). During the disc-locking phase, we consider that the planet is maintained on its orbit by its interaction with the disc. Since the rotational evolution of the star is clearly important for tidal evolution, and the distinction between initially slow and fast rotators may be paramount, we opted to relate the disc-lifetime τdisk and the coupling timescale τc to the initialrotation rate of the star following the prescription of Gallet & Bouvier (2015). However, keeping the prescription of Spada et al. (2011) for the other parameters as in the previous section resulted in problematic evolutions in the case of initially fast rotating 1.2 M⊙ mass stars. For most of the initial parameter space explored, tidal evolution would lead either to the star spinning up to the break-up velocity or the planet reaching the Roche limit before the first few Myrs. This suggests that the chosen angular momentum loss model may not apply to this kind of host. Therefore, and in the lack of calibration for angular momentum loss rate in the framework of the double-zone model for 1.2 M⊙ mass stars, we opted for a parametrisation akin to the one proposed by Matt et al. (2015) for the solid rotation case. Namely, we take the same value for the scaling factor Kw for all masses, and we include the mass dependence through the value of the saturation threshold Ωsat. In this prescription, Ωsat is inversely proportional to the convective turnover timescale in the star τcz:
). During the disc-locking phase, we consider that the planet is maintained on its orbit by its interaction with the disc. Since the rotational evolution of the star is clearly important for tidal evolution, and the distinction between initially slow and fast rotators may be paramount, we opted to relate the disc-lifetime τdisk and the coupling timescale τc to the initialrotation rate of the star following the prescription of Gallet & Bouvier (2015). However, keeping the prescription of Spada et al. (2011) for the other parameters as in the previous section resulted in problematic evolutions in the case of initially fast rotating 1.2 M⊙ mass stars. For most of the initial parameter space explored, tidal evolution would lead either to the star spinning up to the break-up velocity or the planet reaching the Roche limit before the first few Myrs. This suggests that the chosen angular momentum loss model may not apply to this kind of host. Therefore, and in the lack of calibration for angular momentum loss rate in the framework of the double-zone model for 1.2 M⊙ mass stars, we opted for a parametrisation akin to the one proposed by Matt et al. (2015) for the solid rotation case. Namely, we take the same value for the scaling factor Kw for all masses, and we include the mass dependence through the value of the saturation threshold Ωsat. In this prescription, Ωsat is inversely proportional to the convective turnover timescale in the star τcz:
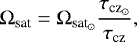 (33)
(33)
where  and
and 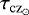 are normalisation values and where τcz is computed from the effective temperature on the ZAMS (Zero Age Main Sequence) according to the prescription of Cranmer & Saar (2011). Tables 2 and 3 list the values of all adopted parameters for stellar angular momentum loss in the present section. This slightly different magnetic braking model produces a qualitatively similar evolution of dissipation to the one presented in Fig. 3, but now, most of the 1.2 M⊙ hosts do not enterthe saturated regime of the magnetic braking law. The peak of their rotation speed is not as high during the initial spin-up phase, so even though they do not enter the saturated regime, their instantaneous rate of angular speed loss is weaker than for the 1 M⊙ stars, during the first Gyr of evolution.
are normalisation values and where τcz is computed from the effective temperature on the ZAMS (Zero Age Main Sequence) according to the prescription of Cranmer & Saar (2011). Tables 2 and 3 list the values of all adopted parameters for stellar angular momentum loss in the present section. This slightly different magnetic braking model produces a qualitatively similar evolution of dissipation to the one presented in Fig. 3, but now, most of the 1.2 M⊙ hosts do not enterthe saturated regime of the magnetic braking law. The peak of their rotation speed is not as high during the initial spin-up phase, so even though they do not enter the saturated regime, their instantaneous rate of angular speed loss is weaker than for the 1 M⊙ stars, during the first Gyr of evolution.
Finally, we performed orbital evolution calculations considering a range of the value of 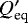 defined in Eq. (13) (corresponding to the frequency range where inertial waves cannot exist). It turns out that in most cases, the results do not change significantly for
defined in Eq. (13) (corresponding to the frequency range where inertial waves cannot exist). It turns out that in most cases, the results do not change significantly for 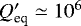 –1010 (see e.g. Hansen 2010, 2012). Thus we present here the results obtained with
–1010 (see e.g. Hansen 2010, 2012). Thus we present here the results obtained with 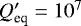 . We integrate the set of equations presented in Sect. 2.4 using a fourth-order Runge–Kutta integrator with an adaptive time-step routine (Press et al. 1992). Examples of evolutions are given in Fig. 6 and for a 1 M⊙ mass star and Fig. 8.
. We integrate the set of equations presented in Sect. 2.4 using a fourth-order Runge–Kutta integrator with an adaptive time-step routine (Press et al. 1992). Examples of evolutions are given in Fig. 6 and for a 1 M⊙ mass star and Fig. 8.
Let us first consider the case of a solar-mass star orbited by a Jupiter-mass planet at 0.1 AU at the start of the evolution (Fig. 6). On the top panel, we see that the evolution of the obliquity depends mainly on the initial rotation frequency of the star, whatever the obliquity’s initial value. This is expected in our model where the efficiency of tidal dissipation is directly related to the rotation frequency of the star, knowing that in this orbital configuration, inertial waves can be excited throughout the first Gyr of evolution, as can be seen in Fig. 7.
For initially slow rotators (solid lines), tidal dissipation is not efficient and this results in very little evolution of both the semi-major axis and the obliquity over the lifetime of the system. For initially moderately rotating stars (dotted-lines), tidal dissipation becomes significant and the value of sin Θ makes an important contribution to the typical timescale of evolution of the semi-major axis. For both quasi-aligned prograde and retrograde systems, sinΘ ≈ 1 and both the obliquity and the semi-major axis do not change significantly in time. But for 80° ≲Θ ≲ 120°, sin Θ < < 1, the semi-major axis decreases very rapidly and the planet reaches the Roche Lobe during the first 10 Myrs of evolution. However, in this case, tidal evolution does not change significantly the value of the obliquity before the final engulfment.
For initially fast rotators (dashed lines) the prograde and retrograde orbits do not behave in a mirrored way. For systems starting almost aligned (Θ < 60°), the typical timescale for evolution of the semi-major axis and the obliquity appear to be similar, and faster than for the initially moderately rotating star. Since at the beginning of the evolution, Ω0 < < cosΘΩe, the tides tend to push the planet on a wider orbit, and the obliquity is damped as the star contracts and Ωe increases. When Ωe reaches its maximum, the star enters its phase of spin down in the saturated regime, and tidal dissipation becomes less efficient. Essentially, both the semi-major axis and the obliquity stop evolving and they keep the value they reached after the first ~ 40 Myrs of evolution. The almost polar orbit starting with Θ = 80° has a somewhat different behaviour starting with a faster evolution of the semi-major axis which, in this case, decreases in time, because cosΘ ≈ 0 and thus Ω0 > > cosΘΩe. When the star starts spinning down, the tidal regime changes and the evolution of the obliquity becomes faster than that of the semi-major axis. This changes again when the frequency ratio between the star and the orbit does not allow the excitation of the dynamical tide any more and tidal evolution resumes, damping the obliquity but with little effect on the semi-major axis. On the other hand, systems with fast rotators starting retrograde with Θ > 100° are much more unstable and the planet is immediately engulfed as negative angular momentum is transferred (from the orbit to the star because |Ω0 | < < |cosΘΩe|) into the axial component of the orbital angular momentum through an increasing value of Θ because the system is retrograde.
The evolution starting with Θ = 160° is a remarkable example. As the obliquity reaches perfect retrograde alignment (Θ = 180°) the m = 0 and m = 1 components of the tides cease to dissipate energy and the rate of evolution of the semi-major axis reduces dramatically. The system is now capable of maintaining a retrograde very close-in orbit for about two Gyrs, the star continuously being spun down to the point of reaching sub-solar rotation by the end of the evolution. Within the space of initial conditions considered here, this is the only track for which tidal evolution affects significantly the spin of the star on secular timescales.
Finally,Fig. 8 shows a similar evolutionary track but this time for a 1.2 M⊙ star. Qualitatively, we find again the same respective differences between the outcome of tidal evolution of initially slow, moderate, and fast rotators. However, the star is now rotating faster throughout its main sequence and consequently maintains a strong dissipation for most of its lifetime. This results in a faster evolution of the obliquity even aroundslowly rotating stars. In this set of simulations, all systems reach values of obliquity inferior to 10° after the first Gyr of evolution, except some initially retrograde systems that settle on well-aligned retrograde orbits.
The same general trends are observed if the planet is starting its evolution on a shorter orbit. Figure 10 shows the same kind of simulations but with now a Jupiter-mass planet starting on a 0.05 AU orbit, close to where hot Jupiters are observed. Now in these orbital configurations inertial waves can be only be excited episodically during the evolution, especially for initially slow rotators, as can be seen in Fig. 11. However, there is little qualitative difference compared to the previous case. Typical timescales of evolution are faster, but the obliquity tends to evolve faster than the semi-major axis, in all cases. However, the 1.2 M⊙ star remainsmore efficient at damping any initial non-null obliquity. This suggests that tidal dissipation in the convective zone alone is not enough to interpret the observed correlation between effective temperature and obliquity. Clearly, others physical mechanisms are at play.
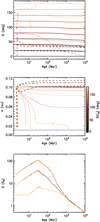 |
Fig. 6 Temporal evolution of the obliquity (top panel), semi-major axis (middle panel), and rotation frequency of the envelope (bottom panel) for a 1MJup planet orbiting a 1 M⊙ star starting at a(t0) = 0.1 AU. The line colours indicate the value of the initial obliquity as indicated on the colour scale in the middle panel. The solid, dotted, and dashed lines correspond to a star initially rotating with Ω (t0) = 3, 8.5, and 25Ω⊙, respectively.The solid blue line in the middle panel indicates the Roche limit, where our evolution is stopped. |
 |
Fig. 7 Temporal evolution of the frequency-averaged imaginary part of the potential Love number corresponding to components of degree l = 2, m = 1 (top panel) and l = m = 2 (bottom panel) along the tidal evolution of the systems shown in Fig. 6 of a 1MJup planet orbiting 1 M⊙ mass star starting at a(t0) = 0.1 AU. The line styles and colours correspond to those of the tracks shown in Fig. 6. The dissipation starts with the value expected from the dissipation of inertial waves and assumes the equilibrium tide constant Q′ value only after the first Gyr for most orbital configurations. |
 |
Fig. 9 Same as Fig. 7 but for a 1.2 M⊙ mass host. The line styles and colours correspond to those of the tracks shown in Fig. 8. The dissipation starts with the value expected from the dissipation of inertial waves and assumes the equilibrium tide constant Q′ value only after the first Gyr for most orbital configurations. |
 |
Fig. 10 Same as Fig. 6 (left panels) for a 1 M⊙ mass host and Fig. 8 (right panels) for a 1.2 M⊙ mass host, but with a planet orbiting at a(t0) = 0.05 AU when the evolution starts. |
 |
Fig. 11 Same as Fig. 7 (left panels) and Fig. 9 (right panels), but for a 1 MJup planet initially starting with a(t0) = 0.05 AU. |
5 Conclusions
We have implemented for the first time a model of tidal evolution for the obliquity in circular exoplanetary systems that uses an ab initio estimation of tidal dissipation based on the physical properties of the host star, and tied to a known mechanism: the excitation and damping of inertial waves in convection zones. Even though we do not apply a full frequency-dependent treatment of the dynamical tide, our formulation retains some dependence on tidal frequency through the use of different tidal dissipation efficiency for different components of the tidal potential. Moreover, we also condition the value of dissipation on the range of tidal frequencies where inertial waves are excited (Ogilvie 2013; Mathis 2015b). We use here a simplified piecewise-homogeneous fluid body model. This may enhance the obtained value of the dissipation compared to a case where the realistic density profile is taken into account (Ogilvie 2013). Moreover, the actual dissipation at a given frequency could differ from the frequency-averaged dissipation by several orders of magnitude (e.g. Ogilvie & Lin 2004, 2007), so that we cannot exclude the possibility that real systemsmay behave differently from this simplified model (e.g. Witte & Savonije 2002; Auclair-Desrotour et al. 2014).
We find that the frequency-averaged tidal dissipation is very sensitive on the angular velocity of the convective envelope, as it scales as 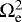 for all modes. We also find that for the quadrupole moment of the tidal potential, the dissipation due to the sectoral harmonic (l = 2, m = 2) is about one to two orders of magnitude less efficient than the dissipation due to both the zonal (l = 2, m = 0) and the tesseral (l = 2, m = 1) harmonic, for both models of 1 M⊙ and 1.2 M⊙ mass stars. We predict that the dissipation in the 1.2 M⊙ mass star is not significantly reduced compared to that of the 1 M⊙ mass star for all modes considered here, despite a smaller convective zone. This is due to the fact that the evolution of tidal dissipation in convective envelopes of low-mass stars is mainly driven by their rotational evolution on the main sequence (Gallet et al. 2017). More massive stars remain fast rotators until the end of the main sequence, as a consequenceof a less efficient magnetic braking. This explains why their dissipation is comparable to that of less massive stars.
for all modes. We also find that for the quadrupole moment of the tidal potential, the dissipation due to the sectoral harmonic (l = 2, m = 2) is about one to two orders of magnitude less efficient than the dissipation due to both the zonal (l = 2, m = 0) and the tesseral (l = 2, m = 1) harmonic, for both models of 1 M⊙ and 1.2 M⊙ mass stars. We predict that the dissipation in the 1.2 M⊙ mass star is not significantly reduced compared to that of the 1 M⊙ mass star for all modes considered here, despite a smaller convective zone. This is due to the fact that the evolution of tidal dissipation in convective envelopes of low-mass stars is mainly driven by their rotational evolution on the main sequence (Gallet et al. 2017). More massive stars remain fast rotators until the end of the main sequence, as a consequenceof a less efficient magnetic braking. This explains why their dissipation is comparable to that of less massive stars.
In this framework, typical timescales of evolution for the orbital elements cannot be simply formulated in terms of global parameters. However, our simulations show that, for typical orbital configurations of hot Jupiters, the damping timescale of the obliquity is generally shorter than that of the semi-major axis, except for the case of rapidly rotating stars with planets on very inclined orbits. This is a formal proof of concept of the conjecture put forward by Lai (2012), where the dynamical tide does indeed lead to different speeds of evolution for the semi-major axis and the obliquity.
Nevertheless, our simulations fail to produce slower tidal evolution for more massive stars, in the range of mass corresponding to low-mass stars developing a radiative core and a convective envelope. The obliquity and/or the semi-major axis are damped before the star reaches the main sequence for both stellar masses considered here, when the initial rotation period is shorter than approximately three days (i.e. Ωe ≳ 8.5Ω⊙) and the initial semi-major axis is smaller than ~ 0.05 AU (i.e. P approximately four days). For planets starting with Θ ≳ 150°, tidal dissipation can bring the planet onto a meta-stable retrograde aligned orbit (Θ = 180°), as found in other studies (Lai 2012; Valsecchi & Rasio 2014). For initially slow rotators, an initial misalignment can be maintained throughout the life of the system, but in this case the obliquity of planets orbiting more massive hosts is consistently damped on shorter timescales.
This would thus fail to explain the observed correlation between effective temperature and obliquity. However, many factors are at play here and our simulations show that the final outcome of tidal evolution is very sensitive to the initial conditions. In addition, the first few Myr of evolution are determinant for the final outcome. This is also where our model is more affected by the parameters of the magnetic braking law, such as the duration of the disc-locking phase, the coupling timescale for exchange of angular momentum between the radiative core and the convective envelope, or the saturation threshold.
One of the most severe limitations of magnetic braking laws using the double-zone model is the paucity of calibration points. To this day, there is only a handful of main sequence Sun-like stars for which constraints on internal differential rotation and age can be obtained using asteroseismology (Benomar et al. 2015; Nielsen et al. 2017). Precise measurements of internal differential rotation are only available for the Sun (Thompson et al. 2003; García et al. 2007; Fossat et al. 2017; Gehan et al. 2018), where it is measured to be weak through most of the interior, except maybe in the innermost region of the core. There is also a general lack of stars of known age, rotation period, and mass for masses smaller than 1 M⊙ and ages greater than 600 Myr (Gallet & Bouvier 2015).
Clearly, those parameters play a role as important as the actual mechanism responsible for tidal dissipation in the global outcome of tidal evolution. A better understanding of the fundamental underlying mechanisms is required to be able to retrace the tidal evolution of hot Jupiters and eventually understand their migration and formation.
However, even with a perfect understanding of magnetic braking and internal angular momentum transport (we refer the reader to e.g. Maeder 2009; Mathis 2013; Réville et al. 2016, for the latest advances), this study would just be a first step in the theoretical effort to produce tidal models accurate enough to constrain migration scenarios. Indeed, in all scenarios of migration that do not involve interactions with the protoplanetary disc, the eccentricity of a proto-hot Jupiter must be excited to high values to allow its subsequent circularisation on a close-in orbit (Dawson & Johnson 2018). Our model here is not suitable for the treatment of eccentricity. In the classical equilibrium tide, it is easy to show that the circularisation of the orbit in a star-planet system is mainly produced by the dissipation of tides raised in the planet. Here we neglect those tides, so that our model would need to include them to also account for the evolution of the eccentricity. Since we are neglecting the interactions of tidal bulges between them, the orbital evolution due to the tides raised and dissipated in the planet can simply be obtained by adding the torque resulting from the response of the planet to the point-mass-like tidal potential exerted by the star. The efficiency of tidal dissipation on the planet could also use the frequency-averaged formulation of Ogilvie (2013), assuming that the planet could be considered as a homogeneous body with a solid core (Guenel et al. 2014). Because this formulation is very sensitive to the core size, this raises the question of the mass of the solid core in gas giants, for which there is still no definite observational evidence, even in the case of our own Jupiter. Finally, in the case of an eccentric orbit, the dynamical tide assumes an infinite number of terms and non-dominant harmonics can be important through resonant contributions. In this case, the frequency-averaged dissipation would be needed for arbitrary values of l and m, and the analytical formulation we have made explicit in Appendix can be used. The introduction of the eccentricity in the model is thus the next step to improve models of tidal evolution and constrain migration scenarios.
To get a complete picture, it would also be necessary to take into account the dissipation of tidal gravity waves (Zahn 1970) (or gravito-inertial waves for those strongly modified by rotation, e.g. Ogilvie & Lin 2007) in the radiative cores of low-mass stars through linear thermal diffusion (Zahn 1975; Goodman & Dickson 1998; Terquem et al. 1998; Ivanov et al. 2013; Chernov et al. 2013) or non-linear breaking mechanisms (Barker & Ogilvie 2010; Barker 2011). This dissipation can be of the same order of magnitude as that of tidal inertial waves in the external convective envelope (we refer the reader for instance to Fig. 15 in Ivanov et al. 2013). Therefore, tidal gravity (gravito-inertial) waves can also play a key role in shaping the orbital dynamics of short-period systems and the rotational evolution of their components (see e.g. the examples studied by Guillot et al. 2014; Chernov et al. 2017; Weinberg et al. 2017). As in the case of tidal inertial waves, the dissipation of tidal gravito-inertial waves in the radiative core of low-mass stars depends on their mass, their age, and their rotation. This dependence, combined with observational constraints on the orbital state of short-period systems, can also allow us to constrain the mass and the evolutionary state of the host star (Chernov et al. 2017; Weinberg et al. 2017). Besides, the effects of differential rotation, both in convective and in radiative zones, should also be taken into account, as it is expected that the range of frequencies at which tidal (gravito-)inertial waves may propagate is broader than in the case of solid-body rotation (Baruteau & Rieutord 2013; Guenel et al. 2016a; Mirouh et al. 2016) while co-rotation resonances may enhance their dissipation (Goldreich & Nicholson 1989; Guenel et al. 2016b). Finally, one should also consider the effects of the elliptic instability (e.g. Cébron et al. 2013; Le Bars et al. 2015; Barker 2016) and of magnetic fields on tidal inertial and gravito-inertial waves (Wei 2016; Lin & Ogilvie 2018; Wei 2018).
Efforts to confront observations of hot Jupiters and migration theories require also better observational constraints. In the very near future, these studies will benefit from the observations of the ground-based near-IR SPIRou instrument (Spectro Polarimétre Infra-Rouge; Moutou et al. 2015) and of the space missions TESS (Transiting Exoplanet Survey Satellite; Ricker et al. 2015) and CHEOPS (CHaracterising ExOPlanets Satellite; Broeg et al. 2013). Currently, one of the most stringent limitations to test migration theories is the poor constraint we have on the age of most known hot-Jupiter systems. Besides, measuring the internal rotation profile of stars, possibly down to the core (García et al. 2007; Beck et al. 2012; Mosser et al. 2012; Deheuvels et al. 2014, 2015; Benomar et al. 2015; Fossat et al. 2017; Gehan et al. 2018), would help us to better understand the mechanisms involved in the evolution of their angular momentum (e.g. Maeder 2009; Mathis 2013, and references therein). In this context, it is clear that a mission like PLATO (PLAnetary Transits and Oscillations of stars; Rauer et al. 2014), which will provide the complete characterisation of host stars using asteroseismology, will enable a breakthrough for dynamical studies, thanks to the precise and accurate determination of stellar radii and masses, differential rotation and, above all, ages.
Acknowledgements
The authors are grateful to the referee, Adrian Barker, for several valuable comments on the first version of the manuscript that helped improved the quality of the work. C.D. wishes to thank J.P. Marques, M. Janvier, T. Appourchaux, R. Cameron, and E. Bolmont for helpful discussions. C.D. acknowledges funding from the ANR (Agence Nationale de la Recherche, France) programme IDEE (ANR-12-BS05-0008) “Interaction Des Étoiles et des Exoplanètes”, and from the German Space Agency (Deutsches Zentrum für Luftind Raumfahrt) under PLATO grant 50OO1501. S.M. acknowledges funding from European Research Council (ERC) under SPIRE grant (647383), and from CNES PLATO grant at CEA Saclay.
Appendix A Analytical integrated response for a piecewise-homogeneous fluid body
In Ogilvie (2013), the computation of the frequency-averaged dissipation ![$\int^{\infty}_{-\infty} \textrm{Im}[k_l^m(\omega)] \textrm{d}\omega/\omega$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq100.png) for inertial waves in a piece-wise homogeneous body is given in Appendix B for the l = m = 2 mode. It is the only mode required to compute the tidal evolution of coplanar circular systems. Here we need to compute this value for other values of m, namely m = 0 and m =1. In this appendix, we recall the main steps leading to the formulation of
for inertial waves in a piece-wise homogeneous body is given in Appendix B for the l = m = 2 mode. It is the only mode required to compute the tidal evolution of coplanar circular systems. Here we need to compute this value for other values of m, namely m = 0 and m =1. In this appendix, we recall the main steps leading to the formulation of ![$\int^{\infty}_{-\infty} \textrm{Im}[k_l^m(\omega)] \textrm{d}\omega/\omega$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq101.png) as derived by Ogilvie (2013). We derive the formulation of
as derived by Ogilvie (2013). We derive the formulation of ![$\int^{\infty}_{-\infty} \textrm{Im}[k_l^m(\omega)] \textrm{d}\omega/\omega$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq102.png) for arbitrary values of l and m, which is not provided explicitly in Ogilvie (2013) but is needed to study the obliquity tides.
for arbitrary values of l and m, which is not provided explicitly in Ogilvie (2013) but is needed to study the obliquity tides.
A.1 Low-frequency tidal forcing of a rotating barotropic fluid
The star is considered as a steady axisymmetric body weakly perturbed by a tidal gravitational potential Ψ (see Eq. (1)). We focus on its convective zone that rotates with uniform angular velocity Ω. It is also considered to be a barotropic ideal fluid of pressure p uniquely related to the density ρ. Finally, we assume isentropy so we can write dp∕ρ = h, h being the specific enthalpy. In the reference frame rotating with the envelope, the linearised equations of motion, mass conservation, and gravitational potential are

where the prime denotes an Eulerian perturbation, the dot denotes ∂∕∂t, and ξ is the displacement. The external tidal potential is Ψ and Φ′ represents the internal self-gravitational potential perturbation. Thus, W is a reduced pressure perturbation. In the low-frequency limit, this quantity can be neglected to leading order and thus the right-hand side of Eq. (A.2) can be set to 0. Even with this simplification, solving the system Eqs. (A.1)–(A.4) is a task that requires further approximations if progress is to be made analytically.
Thus, solutions are sought by decomposition: all quantities are supposed to be the sum of a non-wavelike part and a wavelike part. The non-wavelike part is an instantaneous hydrostatic response to the tidal potential. It is calculated by neglecting the Coriolis force, but involves the correct Eulerian perturbations of internal potential, pression, and density induced by the tidal forcing. The wavelike part is the component of the response that is driven by the Coriolis force and satisfies the anelastic approximation where acoustic waves are filtered out, with rigid boundary conditions on surfaces with both vacuum and the core. The non-wavelike part therefore satisfies the following equations:

together with the wavelike part that verifies

where 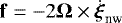 is the Coriolis force per unit mass acting on the non-wavelike part that drives the wavelike-like part of the solution. The boundary conditions are also decomposed as
is the Coriolis force per unit mass acting on the non-wavelike part that drives the wavelike-like part of the solution. The boundary conditions are also decomposed as

where R⋆ is the mean radius of the free surface of the star and α = Rc∕R⋆ with Rc the mean radius of the radiative zone.
The system of ordinary differential equations for the wavelike and non-wavelike parts, together with their respective boundary conditions at interfaces, form our initial-value problem. This can be solved by means of Fourier (or Laplace) transforms methods. Let us consider the case where the tidal force derives from a potential ![${\mathrm{\Psi}} = \textrm{Re}\left[A_l(r/R_{\star})^l Y_l^m(\theta, \phi) e^{-i{\hat{\omega}} t}\right]$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq108.png) , in the fluid frame with coordinates (r, θ, ϕ) defined in Sect. 2.1, and Al an amplitude of appropriate dimensions. Taking the Fourier transform of Eqs. (A.9) and (A.10) is formally equivalent to assuming that the forcing and the response depend harmonically in time through a common factor
, in the fluid frame with coordinates (r, θ, ϕ) defined in Sect. 2.1, and Al an amplitude of appropriate dimensions. Taking the Fourier transform of Eqs. (A.9) and (A.10) is formally equivalent to assuming that the forcing and the response depend harmonically in time through a common factor 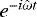 .
.
A.2 Impulsive forcing
It is important to stress that even if the Eqs. (A.5)–(A.8) contain time derivatives, they do in fact imply that the response is instantaneously related to the tidal potential and the corresponding boundary conditions are instantaneous in time. Taking the Fourier transforms of those equations for an impulsive forcing thus brings back the problem to an hydrostatic setting with only spatial dependence. If we consider a tidal potential with the temporal dependence
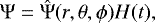 (A.18)
(A.18)
where H(t) is the Heaviside step function, we place ourselves in the special case where the wave-like part of the response experiences an impulsive effective force that derives from this potential. In this case, the spatial structure of the tidal potential
![\begin{equation*}\hat{{\mathrm{\Psi}}} = \textrm{Re} \left[A_l\left(\frac{r}{R_{\star}}\right)^l Y_l^m(\theta, \phi) \right]= \textrm{Re} \left[\hat{{\mathrm{\Psi}}_l}(r) Y_l^m(\theta, \phi) \right], \end{equation*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq111.png) (A.19)
(A.19)
and the associated perturbed internal gravitational potential
![\begin{equation*} \hat{{\mathrm{\Phi}}}'_{\textrm{nw}} = \textrm{Re} \left[\hat{{\mathrm{\Phi}}}'_{\textrm{nw},l}(r) Y_l^m(\theta, \phi) \right], \end{equation*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq112.png) (A.20)
(A.20)
are the only components intervening in the Fourier-transformed problem. The Fourier transforms of Eqs. (A.6) and (A.8) combine to produce the inhomogeneous Helmholtz equation:
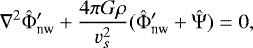 (A.21)
(A.21)
where vs is the sound speed, which projects on the considered spherical harmonics
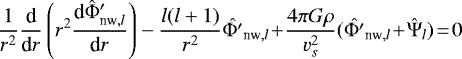 (A.22)
(A.22)
in Rc < r < R⋆. The known tidal potential 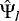 is of the form
is of the form 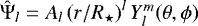 for the impulse problem and
for the impulse problem and 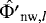 is the internal perturbed gravitational potential to be solved for. For the two-layered model, the solutions to this equation can be written under the form
is the internal perturbed gravitational potential to be solved for. For the two-layered model, the solutions to this equation can be written under the form
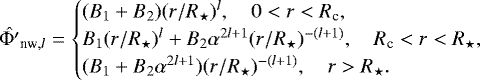 (A.23)
(A.23)
The coefficients must satisfy the matching conditions to ensure that the boundaries are equipotentials

with f = ρe∕ρc and α = Rc∕R⋆, where ρc and ρe denote the density of the core and of the envelope, respectively. We give here the explicit algebraic solutions for B1 and B2 as a function of the stellar parameters, which are not made explicit in Ogilvie (2013):
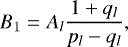 (A.26)
(A.26)
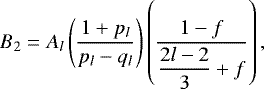 (A.27)
(A.27)
Next, we use Eq. (A.5) to find the non-wavelike tidal displacement by using the change of variable Wnw = Ẍ so that its Fourier transform can be rewritten as
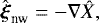 (A.30)
(A.30)
where ![$\hat{X} = \textrm{Re} [\hat{X}_l (r) Y_l^m(\theta, \phi)]$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq124.png) . It projects on the spherical harmonics
. It projects on the spherical harmonics 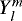 as
as
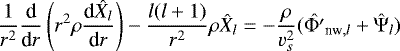 (A.31)
(A.31)
for Rc < r < R⋆. The solution satisfies Poisson’s equation and can be written in the form
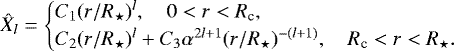 (A.32)
(A.32)
The regularity of 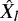 at each interface requires
at each interface requires 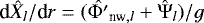 . This implies the following relationships between the coefficients C1, C2, C3, B1, and B2:
. This implies the following relationships between the coefficients C1, C2, C3, B1, and B2:

Again, this can be written in terms of densities and radii for the two-layered model as
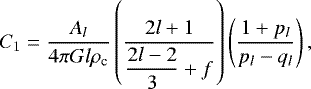 (A.35)
(A.35)
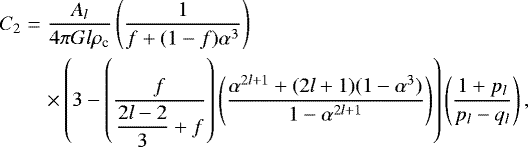 (A.36)
(A.36)
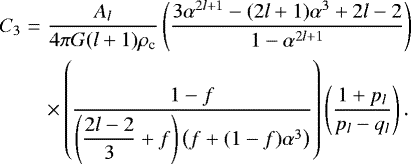 (A.37)
(A.37)
This gives the explicit form for  that determines the non-wavelike displacement
that determines the non-wavelike displacement  . From
. From 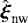 we deduce the impulsive effective force
we deduce the impulsive effective force 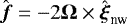 that allows us to solve for the wavelike part of the response.
that allows us to solve for the wavelike part of the response.
Assuming that the fluid is at rest before the impulse, and considering that the Coriolis force does not act on the wavelike velocity during the impulse process (besides providing the effective restoring force from its action on the non-wavelike velocity), the wavelike velocity 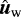 is given by
is given by
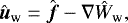 (A.38)
(A.38)
where the pressure perturbation Ŵw satisfies the anelastic approximation
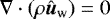 (A.39)
(A.39)
and the boundary conditions ûw,r = 0. The wavelike velocity can be projected on to vector spherical harmonics using standard methods used to describe stellar oscillations. We note âl(r) and 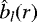 the coefficients representing the spheroidal part and ĉl±1(r) the toroidal part. The wavelike velocity is written as
the coefficients representing the spheroidal part and ĉl±1(r) the toroidal part. The wavelike velocity is written as
![\begin{eqnarray*}{\hat{\boldsymbol{u}}_{\textrm{w}}}& = &\textrm{Re} [\boldsymbol{e}_r \hat{a}_l^m(r) Y_l^m + r^2 \hat{b}_l^m(r) \nabla Y_l^m \nonumber\\ &&-r^2 \hat{c}_{l-1}^m(r)\ \boldsymbol{e}_r \times \nabla Y_{l-1}^m - r^2 \hat{c}_{l+1}^m(r)\boldsymbol{e}_r \times \nabla Y_{l+1}^m ]. \end{eqnarray*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq142.png) (A.40)
(A.40)
These spheroidal and toroidal components satisfy ordinary differential equations according to Eq. (A.38), which involves 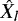 found previously from the non-wavelike part, and Ŵw of the wavelike part. If we write
found previously from the non-wavelike part, and Ŵw of the wavelike part. If we write ![$\hat{W}_{\textrm{w}} = \textrm{Re} [\hat{W}_l^m(r) Y_l^m(\theta, \phi)]$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq144.png) , it can be shown that
, it can be shown that 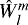 satisfies
satisfies
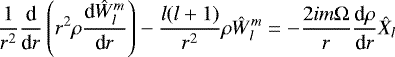 (A.41)
(A.41)
with boundary conditions 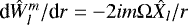 at r= Rc and r = R⋆. Consequently,
at r= Rc and r = R⋆. Consequently,  satisfies Poisson’s equation and the solution is
satisfies Poisson’s equation and the solution is
![\begin{equation*}{\hat{W}_{l}^m} = \begin{cases} -2 i m {\mathrm{\Omega}} \frac{C_1}{l}(r/R_{\star})^l, \quad 0 < r < R_{\textrm{c}}, \\ -2 i m {\mathrm{\Omega}} \left[\frac{C_2}{l} (r/R_{\star})^l - \frac{C_3}{l+1} \alpha^{2l+1} (r/R_{\star})^{-(l+1)}\right], \;\; R_{\textrm{c}} < r< R_{\star}. \end{cases} \end{equation*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq149.png) (A.42)
(A.42)
Using Eqs. (A.32) and (A.42), the spheroidal and toroidal parts of the initial velocity just after the impulse can be made explicit. This yields null values for the spheroidal component for all values of l,  , and a toroidal part given by
, and a toroidal part given by
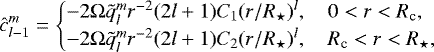 (A.43)
(A.43)
where 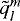 is a coefficient arising from the coupling of spheroidal and toroidal velocity components by the Coriolis force, given in Eq. (31). The energy transfer associated to the impulsive response is given by
is a coefficient arising from the coupling of spheroidal and toroidal velocity components by the Coriolis force, given in Eq. (31). The energy transfer associated to the impulsive response is given by
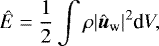 (A.45)
(A.45)
which, thanks to the projection given in Eq. (A.40), is simply found to be
 (A.46)
(A.46)
Thus, inserting Eqs. (A.43) and (A.44) into Eqs. (A.48) and (A.49), we get
![\begin{eqnarray}{\hat{E}}_l^m&=&0,\\ {\hat{E}}_{l-1}^m&=&l (l-1) (2l+1) \left(\tilde{q}_l^m\right)^2 {\mathrm{\Omega}}^2 R_{\star}\nonumber\\ &&[\rho_{\textrm{c}} \alpha^{2l+1} \vert C_1\vert^2 + \rho_{\textrm{e}} (1- \alpha^{2l+1}) \vert C_2\vert^2],\\ {\hat{E}}_{l+1}^m&=& (l+1)(l+2) (2l+1) \left(\tilde{q}_{l+1}^m\right)^2 {\mathrm{\Omega}}^2 R_{\star} \nonumber\\ &&\rho_{\textrm{e}} \alpha^{2l+1} (1-\alpha^{2l+1}) \vert C_3\vert^2 , \end{eqnarray}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq157.png)
which are readily expressed in terms of stellar quantities using Eqs. (A.35)–(A.37):
![\begin{eqnarray*} {\hat{E}}_{l-1}^m&=&l (l-1) (2l+1) \left(\tilde{q}_l^m\right)^2 {\mathrm{\Omega}}^2 R_{\star} \left(\frac{A_l}{4 \pi G l \rho_{\textrm{c}}}\right)^2 \left( \frac{1+p_l}{p_l-q_l}\right)^2 \nonumber\\ &&\times\left[\rho_{\textrm{c}} \alpha^{2l+1} \left(\frac{2l+1}{\displaystyle{\frac{2l-2}{3}}{+}f}\right)^2 {+} \rho_{\textrm{e}} \left(1- \alpha^{2l+1}\right) \left(\frac{1}{f+(1-f)\alpha^3}\right)^2 \right.\nonumber\\ &&\times\left.\left(3 - \left(\frac{f}{\displaystyle{\frac{2l-2}{3}}+f} \right)\left(\frac{\alpha^{2l+1} + (2l+1)(1-\alpha^3)}{1-\alpha^{2l+1}}\right)\right)^2 \right], \end{eqnarray*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq158.png) (A.53)
(A.53)
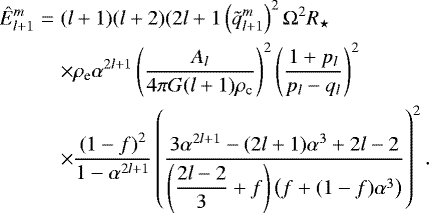 (A.54)
(A.54)
It can be shown that for a tidal potential of the form ![${{\mathrm{\Psi}} = \textrm{Re}[A_l(r/R_{\star})^l Y_l^m (\theta, \phi) e^{-i \omega t}]}$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq160.png) , the rate of energy transfer given by
, the rate of energy transfer given by 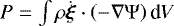 is related to the potential Love numbers through
is related to the potential Love numbers through
![\begin{equation*} P = \frac{(2l+1) R_{\star}}{ 4 \pi G}\frac{1}{2}{\vert A_l\vert^2} \omega {\textrm{Im}}[k_l^m(\omega)]. \end{equation*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq162.png) (A.55)
(A.55)
By analogy, in the Fourier-transformed problem, again assuming that the force derives from a tidal potential of the form ![${{\mathrm{\Psi}} = \textrm{Re}[A_l(r/R_{\star})^l Y_l^m (\theta, \phi) e^{-i \omega t}]}$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq163.png) , we define the complex dimensionless response functions
, we define the complex dimensionless response functions 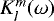 as
as
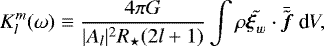 (A.56)
(A.56)
so that the total energy transferred to the wavelike tide is, using the same analogy,
![\begin{equation*} {\hat{E}}= 2 \frac{(2l+1)R_{\star}}{4 \pi G}\int_{-\infty}^{\infty} \omega {\textrm{Im}} \left[K_l^m(\omega)\right] \left\vert \tilde{{\mathrm{\Psi}}}_l^m (\omega)\right\vert^2 \frac{\textrm{d} \omega}{\omega}. \end{equation*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq166.png) (A.57)
(A.57)
In the case of an impulsive tidal potential, the energy transfer is simply
![\begin{equation*} {\hat{E}}= 2 \frac{(2l+1)R_{\star}}{4 \pi G}\frac{A_l^2}{8\pi}\int_{-\infty}^{\infty} \textrm{Im} \left[K_l^m(\omega)\right] \frac{\textrm{d} \omega}{\omega}, \end{equation*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq167.png) (A.58)
(A.58)
and using Eq. (A.46), we finally get
![\begin{equation*} \int_{-\infty}^{\infty} \textrm{Im} \left[K_l^m(\omega)\right] \frac{\textrm{d} \omega}{\omega} = \frac{{\hat{E}}_{l-1}^m+{\hat{E}}_{l+1}^m }{(2l+1) R_{\star} G}\left(\frac{4\pi G}{A_l}\right)^2, \end{equation*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq168.png) (A.59)
(A.59)
where ϵ is a dimensionless parameter measuring stellar rotation normalised to the breakup velocity
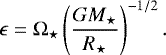 (A.61)
(A.61)
Lastly, to the level of accuracy of our approximations, we have ![$ \textrm{Im} \left[K_l^m(\omega)\right] = \textrm{Im} \left[k_l^m(\omega)\right]$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq171.png) . So in this way we get an expression of
. So in this way we get an expression of ![$\int^{\infty}_{-\infty} \textrm{Im}[k_l^m(\omega)] \textrm{d}\omega/\omega$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq172.png) that depends only on the angular velocity and the masses and radii of the radiative core and the convective envelope, valid for arbitrary values of l and m.
that depends only on the angular velocity and the masses and radii of the radiative core and the convective envelope, valid for arbitrary values of l and m.
Appendix B Static Love numbers
We stress here that the Helmholtz-like Eq. (A.21) for the non-wavelike part in the Fourier-transform problem, neglecting the effect of the Coriolis force, is exactly equivalent to the one that would be obtained by combining Newton’s second law of action and Poisson’s equation, for a non-rotating fluid in hydrostatic equilibrium experiencing the static perturbing gravitational potential from a point-like companion. The general form of the solutions given in Eq. (A.23) also describes the gravitational potential arising from the mass of the tidally distorted star in hydrostatic equilibrium at any point r in space.
Indeed, as is well-known, in a frame of reference centred on the star, the gravitational potential produced by a point-like companion of mass Mp placed at rp = (rp, θ′, ϕ′) with rp > R⋆ can be expanded over the Legendre polynomials. The tidal potential Ψ is simply the potential from which derives the variable part of the perturbing force, so
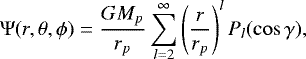 (B.1)
(B.1)
where γ denotes the angular separation between the vectors r and rp (e.g. Murray & Dermott 1999). We have, by the addition theorem for spherical harmonics,
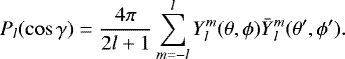 (B.2)
(B.2)
In hydrostatic equilibrium, any surface of a fluid body characterised by equal density and equal pressure corresponds to a surface of equal total potential of forces acting upon the body. Because of the tidal force, the star in hydrostatic equilibrium cannot assume a perfectly spherical shape. Following Kopal (1959), without any loss of generality, we can assume that on such a surface the radial distance r can be written as
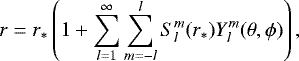 (B.3)
(B.3)
where the 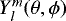 are the normalised spherical harmonics following the Condon–Shortley phase convention, and
are the normalised spherical harmonics following the Condon–Shortley phase convention, and 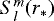 are complex functions of the mean radius r* that must verify
are complex functions of the mean radius r* that must verify
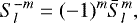 (B.4)
(B.4)
for r to be a real quantity. By virtue of the uniqueness of the potential function, and because the density must remain constant over an equipotential, the density can be regarded as a function of the single variable r*, denoting the mean radius of the corresponding equipotential. Thus, for an arbitrary point (r, θ, ϕ) in the interior of the star, we can write the interior self-potential U of this distorted configuration as
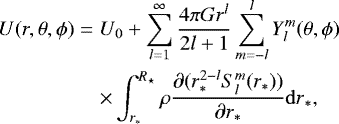 (B.5)
(B.5)
where ρ is the density, R⋆ denotes the mean radius at the surface of the body, and we have introduced
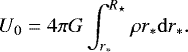 (B.6)
(B.6)
In the same way, the exterior potential V (r, θ, ϕ) can be expressed as
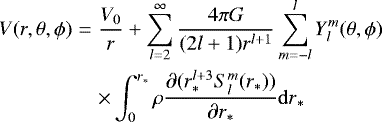 (B.7)
(B.7)
Now let Φ be the total potential of forces acting on any arbitrary point. In hydrostatic equilibrium, the function Φ is to remain constant over any surface of equal pressure of density, over which r verifies Eq. (B.3). By binomial expansion of r, neglecting squares and higher order of 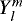 , the shape of an equipotential is described by the spherical harmonic expansion with coefficients
, the shape of an equipotential is described by the spherical harmonic expansion with coefficients 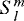 that are solutions of the equation
that are solutions of the equation
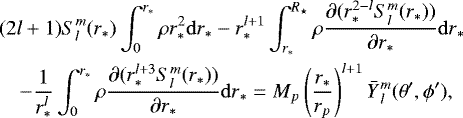 (B.9)
(B.9)
for any l ≥ 1 and − l ≤ m ≤ l. This is the well-known Clairaut’s equation. It implicitly specifies the spherical harmonics describing the form of equipotential level surfaces as distorted by an external force derived from the potential Eq. (B.1). Solving Clairaut’s equation allows us to derive the explicit form of the radial distance rS describing the free surface of the perturbed body of mass M⋆ in terms of the mass Mp of the perturber
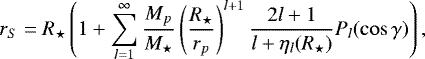 (B.10)
(B.10)
where ηl(R⋆) is the surface value of the logarithmic derivative of the shape coefficients
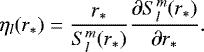 (B.11)
(B.11)
The potential produced by this distorted configuration at any point (r, θ, ϕ), with r > > R⋆ using the centre of mass of the extended body as the origin, is generally written as
![\begin{equation*}{\mathrm{\Phi}}(r,\theta,\phi) = \frac{G M_{\star}}{r} \left[1 + \sum_{l=2}^{\infty} k_l \frac{M_p}{M_{\star}} \left(\frac{R_{\star}}{r_p}\right)^{l+1} \left(\frac{R_{\star}}{r}\right)^{l} P_l(\cos \gamma) \right], \end{equation*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq188.png) (B.12)
(B.12)
where kl are called the static Love numbers (Love 1911). Using Eqs. (B.10) and (B.7), the static Love numbers are found tobe
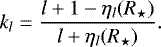 (B.13)
(B.13)
Thus, the Love numbers link the external potential to the internal structure through the surface value of the logarithmic derivative ofthe shape coefficients.
For certain density distributions, Clairaut’s equation admits simple solutions in a closed form and the Love number can take explicit forms. For example, we have the well-known result
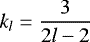 (B.14)
(B.14)
if the density remains uniform throughout the interior of the body, and
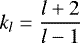 (B.15)
(B.15)
if the whole mass of the configuration were confined to an infinitesimally thin surface shell. If the whole mass of the configuration is condensed at its centre, obviously, kl = 0 for all l, and the exterior potential (B.12) is that of a point mass.
Now in this paper, we consider a two-layer model that simplifies the actual density distribution within the star. To our knowledge, the expression of the Love numbers in this case is not easily available in recent literature so we provide it here for convenience, since it is a direct by-product of our derivations. Since we consider that ρc and ρe are uniform within their respective layers, Clairaut’s equation, taken at the core boundary, simplifies to
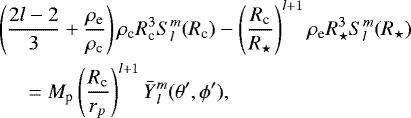 (B.16)
(B.16)
while it gives at the free surface
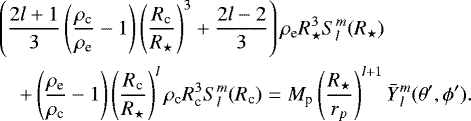 (B.17)
(B.17)
Using those two equations to solve for 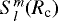 and
and 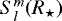 and letting f = ρe∕ρc, we find
and letting f = ρe∕ρc, we find

where pl and ql are defined in Eqs. (A.28) and (A.29), respectively. Those expressions are equivalent to the ones derived by Remus et al. (2015) for a two-layer planet. They considered the case of a purely elastic solid core, which is equivalent to the fluid case when setting the shear modulus to zero. For the two-layer model considered here, the potential at any point (r, θ, ϕ) with r > > R⋆ produced bythe distorted configuration can be then written in the form
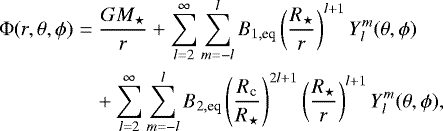 (B.20)
(B.20)
where we have abbreviated
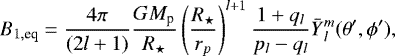 (B.21)
(B.21)
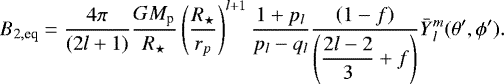 (B.22)
(B.22)
Finally, the potential produced by the distorted star Eq. (B.20) can also be rearranged to take the form of Eq. (B.12) where the static Love number now has the explicit expression:
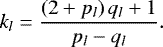 (B.23)
(B.23)
This yields the expected 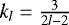 in the limit case of a homogeneous body with ρe = ρc.
in the limit case of a homogeneous body with ρe = ρc.
The correspondence with Eqs. (A.26) and (A.27) is easily made by considering that, in the hydrostatic case, the tidal potential expressed as Eq. (B.1) yields
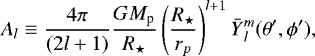 (B.24)
(B.24)
with Al a constant since the perturber is considered here to be static.
In the dynamical case, if one neglects the Coriolis force, the reasoning presented here still holds, but the coordinates of the perturber now must assume a temporal dependence. Therefore, the non-wavelike part of the response (which is equivalent to the instantaneous adjustment of the star when neglecting the Coriolis force) can easily be solved by considering an adequate setting where the temporal dependence of the coordinates of the perturber is removed and Al is indeed a constant. This is done in Ogilvie (2013) by using a frame of reference that rotates with the star, considering a tidal forcing of impulsive nature, and taking the problem into the Fourier domain (see also Remus et al. 2012). For the circular misaligned problem, the same method can be used. In this case, the radial coordinate of the companion is constant over an orbit with rp = a. Its latitudinal coordinate θ′ intervenes only through the spherical harmonics 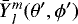 , which can be expressed as a function of the obliquity Θ by a simple rotation of the axis of the reference frame (hence the Wigner-d matrix coefficient in Eq. (1)). Thus, the temporal dependence only persists in the exponential term of
, which can be expressed as a function of the obliquity Θ by a simple rotation of the axis of the reference frame (hence the Wigner-d matrix coefficient in Eq. (1)). Thus, the temporal dependence only persists in the exponential term of 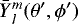 , which contributes to the harmonic forcing and defines the tidal frequency in the rotating frame.
, which contributes to the harmonic forcing and defines the tidal frequency in the rotating frame.
References
- Albrecht, S., Winn, J. N., Butler, R. P., et al. 2012, ApJ, 744, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, M. E. 1973, Ap&SS, 23, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Auclair-Desrotour, P., Le Poncin-Lafitte, C., & Mathis, S. 2014, A&A, 561, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschildt, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Barker, A. J. 2011, MNRAS, 414, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, A. J. 2016, MNRAS, 460, 2339 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, A. J. & Ogilvie, G. I. 2009, MNRAS, 395, 2268 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, A. J. & Ogilvie, G. I. 2010, MNRAS, 404, 1849 [NASA ADS] [Google Scholar]
- Baruteau, C. & Rieutord, M. 2013, J. Fluid Mech., 719, 47 [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Benomar, O., Takata, M., Shibahashi, H., Ceillier, T., & García, R. A. 2015, MNRAS, 452, 2654 [NASA ADS] [CrossRef] [Google Scholar]
- Bolmont, E. & Mathis, S. 2016, Celest. Mech. Dyn. Astron., 126, 275 [Google Scholar]
- Bolmont, E., Raymond, S. N., Leconte, J., & Matt, S. P. 2012, A&A, 544, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolmont, E., Gallet, F., Mathis, S., et al. 2017, A&A, 604, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Broeg, C., Fortier, A., Ehrenreich, D., et al. 2013, Eur. Phys. J. Conf., 47, 03005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cébron, D., Le Bars, M., Le Gal, P., et al. 2013, Icarus, 226, 1642 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonnel, C., Decressin, T., Amard, L., Palacios, A., & Talon, S. 2013, A&A, 554, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chernov, S. V., Papaloizou, J. C. B., & Ivanov, P. B. 2013, MNRAS, 434, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, S. V., Ivanov, P. B., & Papaloizou, J. C. B. 2017, MNRAS, 470, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R. & Saar, S. H. 2011, ApJ, 741, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Damiani, C. & Lanza, A. F. 2015, A&A, 574, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, R. I. & Johnson, J. A. 2018, ARA&A, submitted [arXiv:1801.06117] [Google Scholar]
- Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., Ballot, J., Beck, P. G., et al. 2015, A&A, 580, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Efroimsky, M. & Makarov, V. V. 2013, ApJ, 764, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D. C. & Winn, J. N. 2009, ApJ, 696, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Fossat, E., Boumier, P., Corbard, T., et al. 2017, A&A, 604, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F. & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F. & Bouvier, J. 2015, A&A, 577, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., Bolmont, E., Mathis, S., Charbonnel, C., & Amard, L. 2017, A&A, 604, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García, R. A., Turck-Chièze, S., Jiménez-Reyes, S. J., et al. 2007, Science, 316, 1591 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gehan, C., Mosser, B., Michel, E., Samadi, R., & Kallinger, T. 2018, A&A, 615, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P. & Keeley, D. A. 1977, ApJ, 211, 934 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P. & Nicholson, P. D. 1989, ApJ, 342, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J. & Dickson, E. S. 1998, ApJ, 507, 938 [NASA ADS] [CrossRef] [Google Scholar]
- Guenel, M., Mathis, S., & Remus, F. 2014, A&A, 566, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guenel, M., Baruteau, C., Mathis, S., & Rieutord, M. 2016a, A&A, 589, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guenel, M., Mathis, S., Baruteau, C., & Rieutord, M. 2016b, ArXiv e-prints [arXiv:1612.05071] [Google Scholar]
- Guillot, T., Lin, D. N. C., Morel, P., Havel, M., & Parmentier, V. 2014, EAS Pub. Ser., 65, 327 [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, B. M. S. 2010, ApJ, 723, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S. 2012, ApJ, 757, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanov, P. B., Papaloizou, J. C. B., & Chernov, S. V. 2013, MNRAS, 432, 2339 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D. 1988, ApJ, 333, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Kopal, Z. 1959, Close Binary Systems, International Astrophysics Series (London, UK: Chapman & Hall LTD.), 5 [Google Scholar]
- Lai, D. 2012, MNRAS, 423, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V. 2016, Celest. Mech. Dyn. Astron., 126, 145 [Google Scholar]
- Lanza, A. F. & Mathis, S. 2016, Celest. Mech. Dyn. Astron., 126, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bars, M., Cébron, D., & Le Gal P. 2015, Annu. Rev. Fluid Mech., 47, 163 [Google Scholar]
- Leconte, J., Chabrier, G., Baraffe, I., & Levrard, B. 2010, A&A, 516, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, Y. & Ogilvie, G. I. 2017, MNRAS, 468, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y. & Ogilvie, G. I. 2018, MNRAS, 474, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Love, A. E. H. 1911, Some Problems of Geodynamics (Cambridge, UK: Cambridge University Press) [Google Scholar]
- MacGregor, K. B. & Brenner, M. 1991, ApJ, 376, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars, Astronomy and Astrophysics Library (Berlin: Springer) [Google Scholar]
- Mathis, S. 2013, in Lect. Notes Phys., eds. M. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. J. Green (Berlin: Springer), 865, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, S. 2015a, in SF2A-2015: Proceedings of the Annual Meeting of the French Society of Astronomy and Astrophysics, eds. F. Martins, S. Boissier, V. Buat, L. Cambrésy, & P. Petit, 401 [Google Scholar]
- Mathis, S. 2015b, A&A, 580, L3 [Google Scholar]
- Mathis, S., & Le Poncin-Lafitte C. 2009, A&A, 497, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., Auclair-Desrotour, P., Guenel, M., Gallet, F., & Le Poncin-Lafitte C. 2016, A&A, 592, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matt, S. P., Brun, A. S., Baraffe, I., Bouvier, J., & Chabrier, G. 2015, ApJ, 799, L23 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. B. 1924, ApJ, 60 [Google Scholar]
- Mirouh, G. M., Baruteau, C., Rieutord, M., & Ballot, J. 2016, J. Fluid Mech., 800, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Boisse, I., Hébrard, G., et al. 2015, in SF2A-2015: Proceedings of the Annual Meeting of the French Society of Astronomy and Astrophysics, eds. F. Martins, S. Boissier, V. Buat, L. Cambrésy, & P. Petit, 205 [Google Scholar]
- Murray, C. D. & Dermott, S. F. 1999, Solar System Dynamics (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Nielsen, M. B., Schunker, H., Gizon, L., Schou, J., & Ball, W. H. 2017, A&A, 603, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ogilvie, G. I. 2013, MNRAS, 429, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I. 2014, ARA&A, 52, 171 [Google Scholar]
- Ogilvie, G. I. & Lesur, G. 2012, MNRAS, 422, 1975 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I. & Lin, D. N. C. 2004, ApJ, 610, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I. & Lin, D. N. C. 2007, ApJ, 661, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Penev, K., Zhang, M., & Jackson, B. 2014, PASP, 126, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN. The Art of Scientific Computing, 2nd edn. (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Remus, F., Mathis, S., & Zahn, J.-P. 2012, A&A, 544, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remus, F., Mathis, S., Zahn, J. P., & Lainey, V. 2015, A&A, 573, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Réville, V., Folsom, C. P., Strugarek, A., & Brun, A. S. 2016, ApJ, 832, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, Á., Merín, B., Bouy, H., & Maud, L. T. 2014, A&A, 561, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [NASA ADS] [CrossRef] [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60 [Google Scholar]
- Spada, F., Lanzafame, A. C., Lanza, A. F., Messina, S., & Collier Cameron A. 2011, MNRAS, 416, 447 [NASA ADS] [Google Scholar]
- Terquem, C., Papaloizou, J. C. B., Nelson, R. P., & Lin, D. N. C. 1998, ApJ, 502, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, M. J., Christensen-Dalsgaard, J., Miesch, M. S., & Toomre, J. 2003, ARA&A, 41, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Valsecchi, F. & Rasio, F. A. 2014, ApJ, 786, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Wei, X. 2016, ApJ, 828, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Wei, X. 2018, ApJ, 854, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, N. N., Sun, M., Arras, P., & Essick, R. 2017, ApJ, 849, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N. & Fabrycky, D. C. 2015, ARA&A, 53, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Fabrycky, D., Albrecht, S., & Johnson, J. A. 2010, ApJ, 718, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Witte, M. G. & Savonije, G. J. 2002, A&A, 386, 222 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahn, J. P. 1966, Ann. Astrophys., 29, 313 [NASA ADS] [Google Scholar]
- Zahn, J. P. 1970, A&A, 4, 452 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1975, A&A, 41, 329 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 2008, EAS Pub. Ser., 29, 67 [Google Scholar]
We recall the reasoning behind the formulation of ![$\int^{\infty}_{-\infty} \textrm{Im}[k_l^m(\omega)] \textrm{d}\omega/\omega$](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq206.png) and derive its expression in terms of global stellar parameters for arbitrary values of l and m in Appendix A.
and derive its expression in terms of global stellar parameters for arbitrary values of l and m in Appendix A.
The computations of the tidal power in Lai (2012; Eq. (25)) and Ogilvie (2013; Eq. (41)) are equivalent to a factor (2l + 1)∕8π with the notations we have introduced.
All Tables
Values of the parameters used to plot Fig. 3 for the 1 M⊙ model (from Spada et al. 2011).
All Figures
 |
Fig. 1 Relative geometrical contribution of each tidal component of degree l = 2 in the evolution of the semi-major axis (Eq. (27); top panel) and the obliquity (Eq. (30)) as a function of the instantaneous value of the obliquity for m = 0 (red), m = 1 (green), and m = 2 (blue); p = 0 (solid), p = 1 (dot-dashed), and p = 2 (dashed). For the obliquity (bottom panel), the relative contribution of each component depends on the orbital-to-spin angular momentum magnitude ratio, here taken for illustration purposes at 0.5. Those factors do not include the factor |
| In the text | |
 |
Fig. 2 Temporal evolution of the core-to-envelope ratio (top panel) and envelope-to-core density ratio (bottom panel) for our models of a 1 M⊙ star (in red) and a 1.2 M⊙ star (in blue). |
| In the text | |
 |
Fig. 3 Temporal evolution of the frequency-averaged imaginary part of the potential Love number corresponding to components of degree l = 2 and m = 0 (red), m = 1 (green) and m = 2 (blue) for models of a 1 M⊙ (left panel) and 1.2 M⊙ (right panel) mass stars. The solid and dashed lines correspond to a star initially rotating with Ω (t0) = 3 Ω⊙, and Ω (t0) = 25 Ω⊙, respectively. A conversion to the modified tidal quality factor Q′ is given on the right y-axis. |
| In the text | |
 |
Fig. 4 Temporal evolution of the frequency-averaged imaginary part of the potential Love number corresponding to components of degree l = 2 and m = 0 (red), m = 1 (green), and m = 2 (blue) for models of a 1 M⊙ (left panel) and 1.2 M⊙ (right panel) mass stars. The rotation rate of the star does not evolve in time and is set at all times at Ω = 8.5 Ω⊙ for both models. A conversion to the modified tidal quality factor Q′ is given on the right y-axis. |
| In the text | |
 |
Fig. 5 Frequency-integral of the imaginary part of the Love numbers, weighted by 1∕ω and divided by ϵ2, versus fractional core size for the quadrupolar component l = 2. The colour of the lines corresponds to different values of m: m = 0 (red), m = 1 (green), and m = 2 (blue). The dashed-dotted line shows the analytical result of the impulse calculation for a homogeneous fluid body with a solid core. The dashed line shows the same but in the case of the piecewise-homogeneous fluid model with a density ratio of 2 × 10−2, adequatefor a solar mass star on the main sequence. The solid line corresponds again to the piecewise-homogeneous fluid model but with a density ratio of 4 × 10−3, appropriate for a 1.2 M⊙ mass star on the main sequence. |
| In the text | |
 |
Fig. 6 Temporal evolution of the obliquity (top panel), semi-major axis (middle panel), and rotation frequency of the envelope (bottom panel) for a 1MJup planet orbiting a 1 M⊙ star starting at a(t0) = 0.1 AU. The line colours indicate the value of the initial obliquity as indicated on the colour scale in the middle panel. The solid, dotted, and dashed lines correspond to a star initially rotating with Ω (t0) = 3, 8.5, and 25Ω⊙, respectively.The solid blue line in the middle panel indicates the Roche limit, where our evolution is stopped. |
| In the text | |
 |
Fig. 7 Temporal evolution of the frequency-averaged imaginary part of the potential Love number corresponding to components of degree l = 2, m = 1 (top panel) and l = m = 2 (bottom panel) along the tidal evolution of the systems shown in Fig. 6 of a 1MJup planet orbiting 1 M⊙ mass star starting at a(t0) = 0.1 AU. The line styles and colours correspond to those of the tracks shown in Fig. 6. The dissipation starts with the value expected from the dissipation of inertial waves and assumes the equilibrium tide constant Q′ value only after the first Gyr for most orbital configurations. |
| In the text | |
 |
Fig. 8 Same as Fig. 6 but for a 1.2 M⊙ host. The line colors and styles have the same meaning. |
| In the text | |
 |
Fig. 9 Same as Fig. 7 but for a 1.2 M⊙ mass host. The line styles and colours correspond to those of the tracks shown in Fig. 8. The dissipation starts with the value expected from the dissipation of inertial waves and assumes the equilibrium tide constant Q′ value only after the first Gyr for most orbital configurations. |
| In the text | |
 |
Fig. 10 Same as Fig. 6 (left panels) for a 1 M⊙ mass host and Fig. 8 (right panels) for a 1.2 M⊙ mass host, but with a planet orbiting at a(t0) = 0.05 AU when the evolution starts. |
| In the text | |
 |
Fig. 11 Same as Fig. 7 (left panels) and Fig. 9 (right panels), but for a 1 MJup planet initially starting with a(t0) = 0.05 AU. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{equation*} \textrm{Im}[k_l^m(\omega)] \approx k_l {\mathrm{\Delta}}_l^m(\omega). \end{equation*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq31.png)
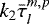
![\begin{align}p_l &=\frac{2l-2}{3}\left(1+\left(\frac{2l+1}{2l-2}\right)\left(\frac{1}{f}-1\right)\alpha^3\right),\\[5pt] q_l &= \frac{1- f }{\displaystyle{\frac{2l-2}{3}} + f } \alpha^{2l+1}.\end{align}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq122.png)
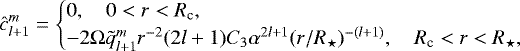
![\begin{eqnarray}{\hat{E}}_l^m&=&0,\\ {\hat{E}}_{l-1}^m&=&\frac{1}{4} \int_{R_{\textrm{c}}}^{R_{\star}} \rho r^2 [l(l-1)r^2 \vert\hat{c}_{l-1}^m\vert^2] {\mathrm{d}r},\\ {\hat{E}}_{l+1}^m&=&\frac{1}{4} \int_{R_{\textrm{c}}}^{R_{\star}} \rho r^2 [(l+1)(l+2)r^2 \vert\hat{c}_{l+1}^m\vert^2] {\mathrm{d}r}.\end{eqnarray}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq156.png)
![\begin{eqnarray*} &&\int_{-\infty}^{\infty} \textrm{Im} \left[K_l^m(\omega)\right] \frac{\textrm{d} \omega}{\omega}= \frac{4}{3}\left(\frac{l-1}{l}\right) \epsilon^2 \left( \frac{1+p_l}{p_l-q_l}\right)^2 \left( \frac{f}{f+(1-f)\alpha^3}\right)\nonumber\\ &&\quad\times\left[\left(\tilde{q}_{l}^m\right)^2 \left(\frac{2l+1}{\displaystyle{\frac{2l-2}{3}}+f}\right)^2 \left(f+(1-f)\alpha^3\right)^2 \left(\frac{ \alpha^{2l+1} }{f} \right) \right.\nonumber\\ &&\quad+ \left(\tilde{q}_{l}^m\right)^2 \left(1- \alpha^{2l+1}\right) \left(3 - \left(\frac{f}{\displaystyle{\frac{2l-2}{3}}+f} \right)\left(\frac{\alpha^{2l+1} + (2l+1)(1-\alpha^3)}{1-\alpha^{2l+1}}\right)\right)^2\nonumber\\ &&\quad+ \left(\tilde{q}_{l+1}^m\right)^2 \left(\frac{l}{l-1}\right)\left(\frac{l+2}{l+1}\right) \left(\frac{1-f} {\displaystyle{\frac{2l-2}{3}}+f}\right)^2 \left(\frac{\alpha^{2l+1}}{1-\alpha^{2l+1}}\right)\nonumber\\ &&\quad\times\Bigg. \left(3\alpha^{2l+1} - (2l+1)\alpha^3 + 2l-2 \right)^2 \Bigg], \end{eqnarray*}](/articles/aa/full_html/2018/10/aa32538-17/aa32538-17-eq169.png)