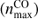| Issue |
A&A
Volume 617, September 2018
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833266 | |
| Published online | 28 September 2018 | |
Probability distribution functions of gas surface density in M 33
1
INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
e-mail: edvige@arcetri.astro.it
2
IBM Research Division, T. J. Watson Research Center, 1101 Kitchawan Road, Yorktown Hts., NY 10598, USA
3
Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N, Allée Geoffroy Saint-Hilaire, 33615 Pessac, France
4
Center for Astrophysical Sciences, The Johns Hopkins University, 3400 N. Charles Street, Baltimore, MD 21218, USA
Received:
19
April
2018
Accepted:
29
June
2018
Aims. We examine the interstellar medium (ISM) of M 33 to unveil fingerprints of self-gravitating gas clouds throughout the star-forming disk.
Methods. The probability distribution functions (PDFs) for atomic, molecular, and total gas surface densities are determined at a resolution of about 50 pc over regions that share coherent morphological properties and considering cloud samples at different evolutionary stages in the star formation cycle.
Results. Most of the total gas PDFs are well fit by log-normal functions whose width decreases radially outward. Because the HI velocity dispersion is approximately constant throughout the disk, the decrease in PDF width is consistent with a lower Mach number for the turbulent ISM at large galactocentric radii where a higher fraction of HI is in the warm phase. The atomic gas is found mostly at face-on column densities below NHlim = 2.5 × 1021 cm−2, with small radial variations of NHlim. The molecular gas PDFs do not show strong deviations from log-normal functions in the central region where molecular fractions are high. Here the high pressure and rate of star formation shapes the PDF as a log-normal function, dispersing self-gravitating complexes with intense feedback at all column densities that are spatially resolved. Power-law PDFs for the molecules are found near and above NHlim, in the southern spiral arm and in a continuous dense filament extending at larger galactocentric radii. In the filament nearly half of the molecular gas departs from a log-normal PDF, and power laws are also observed in pre-star-forming molecular complexes. The slope of the power law is between −1 and −2. This slope, combined with maps showing where the different parts of the power law PDFs come from, suggests a power-law stratification of the density within molecular cloud complexes, in agreement with the dominance of self-gravity.
Key words: ISM: clouds / galaxies: individual: M 33 / galaxies: ISM / ISM: molecules / turbulence
© ESO 2018
1. Introduction
The formation and evolution of self-gravitating structures in the interstellar medium (ISM) is a key ingredient of star formation. Stars form in the dense parts of interstellar clouds where self-gravity overwhelms local gas pressure, causing collapse McKee & Ostriker (2007). The connections between these dense parts and their surrounding gas can reveal the processes involved. If the cloud is part of a shell (Palmeirim, et al. 2017), of a converging flow (Whitworth et al. 2018), or of a spiral arm shock front (Elmegreen et al. 2014), the clouds are likely to have been formed or influenced by the associated pressures, after which gravity could have made the central parts dense enough for star formation. If disk gravitational instabilities generate spiral arms and filaments that fragment into molecular clouds, even the birth of these complexes might be driven by gravity out to the edges of their HI envelopes.
The column density and density where environmental processes lose their influence and self-gravity takes over are indicators of the driving pressures and timescales for cloud evolution. The column density at the threshold for strong gravity in a medium of pressure P is Σthres ~ (2P/πG)0.5, and the dynamical time for evolution is proportional to the idealized free-fall time at density ρ, which is tff = (32Gρ/3π)−0.5. In interacting galaxies, where the pressure is high, the column density and density at the transition should both be high, making star-forming clouds opaque, fully molecular, and quickly evolving. Conversely, in the far-out parts of spiral galaxies and in dwarf irregulars, where the pressure is low, the transition should be at a low density, making the timescales long and possibly placing the first stages of collapse in the atomic medium (e.g., Michalowski et al. 2015; Meidt 2016; Elmegreen 2018).
The best way to determine the transition point from environmental to internal cloud control is by mapping the dynamical state of the cloud and its surroundings (i.e., which region is collapsing, accreting, or in virial equilibrium, and the type of support against gravity). Our galaxy offers the possibility of studying individual star-forming regions, identifying dense clumps, filaments, and shocks, and mapping their column densities and velocity fields. This has been done in several local regions (e.g., Deharveng et al. 2015; Figueira et al. 2017), but it is difficult to do in external galaxies (Hirota et al. 2011; Donovan Meyer et al. 2013; Colombo et al. 2014; Tosaki et al. 2017; Baba et al. 2017; Faesi et al. 2018) because we lack the spatial resolution to identify high column density clumps.
An alternative to cloud-scale mapping is the use of column density probability distribution functions (PDFs) from maps of gas emission or absorption. The PDF for gas in a large-scale map gives the probability distribution of column density averaged over all of the clouds and intercloud regions. This does not allow the history of individual star-forming clouds to be determined, but it can give the average column density above which cloud self-gravity is the main driving force of cloud evolution, and no longer environmental pressure. This is possible because self-gravity gives a cloud an internal density structure that is a power law with radius, such as ρ(r) ∝ r−1.5 or r−2 (e.g., Shu 1977), as observed, for example, by Mueller et al. (2002). Then the PDF has a matching power law at high density even if the cloud has locally a log-normal PDF from compressible turbulence (Elmegreen 2011). Small-scale collapse inside a turbulent cloud also produces a power-law tail that extends to lower densities as time proceeds, while turbulent motions broaden the PDF (Girichidis et al. 2014). Computer simulations showing this power-law extension have been reported by Klessen (2000), Vázquez-Semadeni et al (2008), Kritsuk et al. (2011), Federrath & Klessen (2013), Pan et al. (2016), and elsewhere. Log-normal distributions without self-gravity were first discussed and simulated by Vázquez-Semadeni (1994), Passot & Vázquez-Semadeni (1998) and Padoan et al. (1997). The lower limit to the power-law part of the PDF corresponds approximately to the column density at the edge of the self-gravitating part of the cloud, and therefore gives the pressure at that place (e.g., Kainulainen et al. 2011). Sensitivity limits, however, are important and should be taken into account since, for example, the total PDF may not curve over at low column density if the detection limits for gas are close to the apparent PDF peak (Alves et al. 2017).
PDFs have been extensively studied and observed in the local interstellar medium also using extinction or dust emission. In the Milky Way the resolution is sufficiently high to trace the molecular clumps that form individual stars (Kainulainen et al. 2009, 2011; Froebrich & Rowles 2010; Lombardi et al. 2010; Schneider et al. 2012, 2015b). Lombardi et al. (2010) found a log-normal PDF using extinction maps in a large region around Perseus and Taurus in the solar neighborhood, with a slight excess over the log-normal above AV ~ 2 mag. Power-law PDF extensions were also found in dust emission (Schneider et al. 2013, 2015a,c; Lombardi et al. 2015) and molecular line emission (Schneider et al. 2016) up to AV ~ 100 mag (Schneider et al. 2015b). Schneider et al. (2012) measured the PDFs of dust emission in the Rosette molecular cloud and found that it became a power law above AV = 9 mag in the central regions and above 4 mag in other regions; it was a log-normal far from the Rosette nebula. It is still not clear, however, whether non-star-forming clouds have power-law extensions. Although in most external galaxies we cannot yet resolve the cores of individual star-forming clumps, we may still trace where gravity takes over ISM pressure on a larger scale, and it can be useful to compare the PDFs in various environments, such as galaxy centers, spiral arms, and interarms, and as a function of galactocentric distance and cloud type.
M 33 is a good candidate to examine for these questions because it is the nearest isolated spiral galaxy. Recent surveys of the ISM throughout the whole star-forming disk of M 33 have mapped the atomic and molecular gas phases with high resolution (Gratier et al. 2012; Druard et al. 2014; Corbelli et al. 2014). The Hα and GALEX ultraviolet data complement the Spitzer mid-infrared survey to trace star formation from the embedded to the exposed young stellar clusters (Verley et al. 2009; Sharma et al. 2011). The possible association between 566 giant molecular clouds (GMCs) and 600 young stellar cluster candidates (YSCCs) has helped in defining the duration of the lifecycle of GMCs in M 33 (Corbelli et al. 2017). Still, it is unclear what drives the transition from inactive gas to a star-forming cloud. Moreover, if stellar feedback disrupts these clouds, it is of interest to determine whether this disruption affects only the small-scale structure of the ISM or if it also contributes to the global disk morphology (Wada et al. 2000). The presence of turbulence in the ISM of M 33 has been investigated via power spectra using optical or far-infrared images (Elmegreen et al. 2003; Combes et al. 2012). A recent numerical simulation of the large-scale structure of the M 33 disk (Dobbs et al. 2018) points out the role of both stars and gas in triggering the formation of high-density filaments by gravitational instabilities. At the same time, the presence of very low density cavities in the interarm regions underlines the need for a high level of feedback (e.g., ~10% of the total energy of massive stars) to deposit turbulent energy. The purpose of this paper is to understand the role of turbulence and gravity in triggering the formation of GMCs and star formation throughout the disk of M 33. Because there is the strong evidence of non-negligible turbulent motion in the M 33 disk, we interpret the log-normal PDFs that we detect in the ISM of this galaxy as due to turbulence, although there might be other features associated with clouds that can produce log-normal column density distributions (Tassis et al. 2010).
The analysis of the PDF for the molecular gas in M 33 by Druard et al. (2014) has shown deviations from a log-normal shape for gas column density above ~1.7 × 1021 cm−2. The authors attributed the deviations of a galaxy-wide PDF to self-gravity, but did not draw any definitive conclusion on the cloud scale that is affected by gravitational contraction. The coarse spatial resolution of CO observations in external galaxies in fact does not allow an analysis of the details of individual clouds and hence prevents distinguishing a free-fall contraction of the whole GMC complex from self-gravity of clumps and cores inside them. The publication of a complete GMC catalog in the star-forming disk of M 33 and of a further analysis of the GMC properties (Corbelli et al. 2017), which followed the complete census of molecular gas presented by Druard et al. (2014), opens the possibility of investigating the role of gravity in different types of GMCs that are likely GMCs at different evolutionary stages. Furthermore, making use of high angular resolution HI data products presented by Corbelli et al. (2014), we can examine the PDFs of atomic and total gas. For the molecular component we extend the analysis of Druard et al. (2014) to specific disk areas or cloud types where self-gravity or turbulence plays a major role, and determine if the PDFs depend on star formation rate or galactocentric distance and what this implies on the resolved scale of ~50 pc. This is particularly relevant for M 33 given that disk gravitational instabilities and high levels of stellar feedbacks both play a role in shaping the atomic gas distribution in the disk (Dobbs et al. 2018).
In what follows, the data used and cloud types are outlined in Sect. 2, the PDFs and power-law slopes are presented in Sect. 3. Results are discussed in Sect. 4 and summarized in Sect. 5.
2. Data
In analyzing the data of M 33, we assume a distance of 840 kpc (Freedman et al. 1991; Gieren et al. 2013), which implies a linear scale of 4.1 pc per arcsec and 0.24 kpc per arcmin. As position angle and inclination of the gaseous disk, we use PA = 20° and i = 54° based on the averages for a tilted ring model fitted to the 21 cm velocity field at R < 7 kpc (Corbelli et al. 2014). The PDF is analyzed for face-on values of H-atom column densities.
2.1. Neutral atomic gas traced by HI 21 cm line emission
The neutral atomic gas distribution has been mapped at high-resolution combining Very Large Array (VLA) and Green Bank Telescope (GBT) observations of the 21 cm HI line emission as described by Corbelli et al. (2014). We generally chose an angular resolution that was lower than the limit in the VLA+GBT surveys in order to trace the faint diffuse emission more sensitively, and we chose a spectral resolution of 1.29 km s−1. The moment task in MIRIAD was used to generate the moment maps. The moment-0 map is the integrated intensity map of the 21 cm line, the moment-1 or mean velocity map is the map of the weighted mean velocity along the line of sight, and the moment-2 or velocity dispersion map is the map of the intensity-weighted mean deviation of the velocity along the line of sight. For each pixel i, the values of integrated intensity, Ii, mean velocity, Vi, and velocity dispersion, σ21,i, were computed using Si,j, the 21 cm line intensity in the velocity channel centered on νj, as follows:
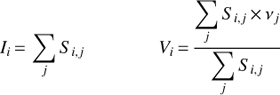 (1)
(1)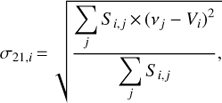 (2)
(2)
where the sum extends over all spectral channels with detectable emission. The images we use in this paper mostly have a 10 arcsec (41 pc) restored beam size and are masked to mitigate contributions from foreground Milky Way emission. The pixel size is 4 arcsec, which is smaller than the beam size. To check the high column density PDF, we also use images at 5 arcsec spatial resolution with a pixel size of 2 arcsec. The radial trend of the HI line width is inferred from the moment-2 map at a spatial resolution of 10 arcsec.
Analysis of the moment-0 map at 10 arcsec resolution indicates a noise standard deviation σHI = 0.0049 Jy beam−1 km s−1 = 5.4 × 1019 H cm−2 on a pixel-by-pixel basis. We considered only pixels with a flux above 3σHI, and traced the statistical analysis down to this limiting flux value, which corresponds to a face-on column density of about 1020 H cm−2.
We assumed that the line-of-sight velocity dispersion σ21, defined above, is isotropic. The map of the velocity dispersion of the M 33 disk at 21 cm can be an indicator of the turbulence and kinetic energy of the HI gas, especially for nearby galaxies, which can be imaged at high resolution to avoid line broadening due to disk dynamics. We show the moment-2 map in the left panel of Fig. 1 using black contours to outline the high density HI filaments or arms, as shown by the 21 cm moment-0 map in the right panel of the same figure. In the dispersion map we masked out all pixels corresponding to the two regions with large infall/outflow of gas: the stream toward the central region just south of the nucleus, and a smaller region above the northern arm. In these areas, the signal is a superposition of emission lines at two velocities, one corresponding to gas in the disk, and the other being due to extraplanar gas.
 |
Fig. 1. Velocity dispersion (moment-2) map of the 21 cm line emission in M 33 at 10 arcsec resolution (left panel). The black contours underline the location of the bright HI filaments or arms, they are drawn at 0.2 Jy beam−1 km s−1 and overlaid also on the moment-0 map in the right panel. The two areas that have been masked out for the likely presence of gas infall/outflow (the stream toward the central region in the southern half and a smaller region above the northern arm) have anomalously large velocity dispersions and have yellow-red colors in the velocity dispersion map. The color legend for the velocity dispersion map (left panel) is in units of km s−1, and for the intensity map (right panel), it is in Jy beam−1 km s−1. Maps are centered on RA = 23.4620417 and Dec = 30.6602222, (M33 coordinates). |
2.2. Molecular gas and the GMCs population
We used molecular data of the deep 12CO(J = 2−1) whole-disk survey carried out with the IRAM-30 m telescope (Druard et al. 2014) at 10.7″ resolution (44 pc). From the spectral cube of this database at a spatial resolution of 12″ and at a spectral resolution of 2.6 km s−1, a catalog of 566 giant molecular clouds (GMCs) has been presented by Corbelli et al. (2017), following a procedure described and used for M 33 by Gratier et al. (2012). The main-beam temperature noise for the dataset at 12″ resolution is 0.033 K in each channel. The moment-0 or brightness map that we used has 3 arcsec pixels and on average σCO = 0.27 K km s−1, considering a typical spectral window of 25 km s−1 per beam. Using a CO-to-H2 conversion factor X = N(H2)/ICO(1−0) = 4 × 1020 cm−2/(K km s−1) (Gratier et al. 2017), twice the galactic value, and an intrinsic line ratio  (Druard et al. 2014), we estimate
(Druard et al. 2014), we estimate 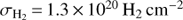 . This is an average estimate of the map noise because there are variations in the main-beam temperature noise and of the signal width throughout the disk. To trace the PDF, we considered only pixels with a flux above 3σCO and traced the statistical analysis down to the corresponding limiting column density, which in terms of total H atoms reads 3σH ≃ 7.8 × 1020 H cm−2 (i.e., 4.6 × 1020 H cm−2 face-on value).
. This is an average estimate of the map noise because there are variations in the main-beam temperature noise and of the signal width throughout the disk. To trace the PDF, we considered only pixels with a flux above 3σCO and traced the statistical analysis down to the corresponding limiting column density, which in terms of total H atoms reads 3σH ≃ 7.8 × 1020 H cm−2 (i.e., 4.6 × 1020 H cm−2 face-on value).
Molecular clouds have been classified by Corbelli et al. (2017) into three broad categories: clouds without obvious star formation (A), clouds with embedded star formation (B), and clouds with exposed star formation (C). An online catalog lists several cloud properties such as cloud radius and luminous mass computed by converting the total CO line luminosity of a cloud into mass as given by Eq. (1) of Corbelli et al. (2017). Clouds of type A, B, and C have average luminous masses of 1.3, 2.6, and 3.1 × 105 M⊙ respectively. As noted by Corbelli et al. (2017) and by Braine et al. (2018), the average cloud mass grows from non-star-forming to exposed star-forming clouds. The total H2 mass in clouds of A, B, and C type is 0.16, 0.14, and 0.79 × 108 M⊙, respectively. Adding the unclassified D-type clouds, we have a total molecular hydrogen mass of 1.12 × 108 M⊙ in GMCs or a total GMC gas mass (considering He and heavy elements, i.e., taking a hydrogen fraction of 0.73%) of 1.53 × 108 M⊙. This is about half of the total molecular ISM mass. The rest is in lower-mass molecular clouds (below the survey resolution limit), which we call “diffuse molecular gas”, even though some of this gas may be self-gravitating. By selecting 630 mid-infrared (MIR) sources from the list of Sharma et al. (2011) that are YSCCs in the early formation and evolutionary phases, Corbelli et al. (2017) determined that they are strongly correlated with the GMCs (the correlation length is on the order of 17 pc, which is smaller than the typical GMC radius). Since age estimates of the YSCCs are between 3.5 and 8 Myr, given the fractions of GMCs in each class (i.e., presumably in each evolutionary phase), the GMC lifetime was estimated to be 14.2 Myr, with the longest phase being the C-type phase, when the YSCCs break out of their clouds before total gas dispersal.
To sample the surface density distribution for each cloud, we can either use the corresponding pixels identified by the cloud extraction algorithm, or use the cloud radius rc to find the associated pixels. Although most of GMCs are rather spherical, a few of them have an elongated shape and look filamentary. We have carried out the analysis using both selection criteria at first but found no meaningful differences in the resulting PDFs. We therefore decided to use the cloud radii listed by Corbelli et al. (2017) to select pixels corresponding to each GMC. This simplifies the procedure to find the atomic gas at and around cloud positions. The average GMC radius decreases from 26 to 22 to 18 pc from A- to B- to C-type clouds, even though the mass increases in this sequence. This seem to suggest that GMCs are more compact as they evolve, likely collapsing and shrinking as they collect more material and begin to form stars. It is not clear, however, if GMCs of type C are more bound and dominated by gravity since the presence of young stars in these molecular complexes might increase the local turbulence. It is therefore of interest to investigate the PDFs of GMC at each evolutionary stage.
2.3. Selected regions and total gas maps
Using the cold gas images, we selected four regions that might be of interest for cloud formation and destruction and that have enough pixels with CO emission above the thresholds to ensure a statistically significant analysis. These are the central region (CR) and three other regions that have prominent HI overdensities and non-negligible H2 fractions, namely the northern arm (NA), the southern arm (SA), and the eastern filaments (EF). The latter feature is the HI overdensity that starts at NGC 604 (the brightest HII region in M 33 located at 9.1 arcmin to the north and 7.5 arcmin to the east in Fig. 1) and extend radially outward (as an extension of the northern arm toward the south). Figure 2 shows these regions on the 21 cm emission map of M 33. We mark all pixels with CO J = 2−1 integrated emission above 3σCO using one color for each selected region and using green for the interarm regions (IA). We refer to the interarm region when we analyze everything that is not in one of the selected areas, although there are filament segments that are included in it. We do not have the sensitivity to select only the truly interarm ISM.
By analyzing individual regions or radial bins separately, we minimize mixing data relative to gas with different scale heights and disk gravity. The southern arm looks less disturbed than the northern arm, and it is the only arm that fits density wave models well, as underlined by Humphreys & Sandage (1980). This justifies a separate analysis of the PDFs relative to each arm. Results for the eastern filament were checked by also considering the same region without the area in and around NGC 604. This was done in order to ensure that the large star-forming region alone does not drive the detected properties.
A GMC belongs to a selected region when its center is within the boundaries of the region (not necessarely the whole GMC or its HI envelope). To collect pixels with CO or HI emission above the threshold associated with the n-cloud, we required that the distance 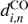 and
and 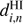 between the i-pixel center and the n-cloud center satisfies
between the i-pixel center and the n-cloud center satisfies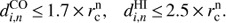 (3)
(3)
For a Gaussian-shaped radial distribution of the cloud brightness, we recover 90% of the total cloud molecular mass with this selection. For the HI envelope, the factor 2.5 encompasses pixels next to the GMC without appreciable CO emission.
The total hydrogen gas map is the sum of the molecular and atomic gas surface densities pixel by pixel. The CO J = 2−1 map was aligned with the HI 21 cm map and the HI and CO line brightnesses converted into H atom column densities. Before adding the molecular gas surface density to the atomic one, we masked out all 4 arcsec wide pixels with H2 column density below 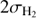 (we masked out pixels below 2 and not
(we masked out pixels below 2 and not 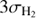 because the aligned CO map with 4 arcsec pixels has a lower noise than the original
because the aligned CO map with 4 arcsec pixels has a lower noise than the original 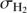 value). Given the subsolar metallicities of M 33, it is likely that there is not much molecular gas at lower surface densities because of radiative dissociation. Because the HI image has a better sensitivity than the CO image in tracing the hydrogen column density, the lower limit for sampling the total gas column density is the same as that of the HI gas.
value). Given the subsolar metallicities of M 33, it is likely that there is not much molecular gas at lower surface densities because of radiative dissociation. Because the HI image has a better sensitivity than the CO image in tracing the hydrogen column density, the lower limit for sampling the total gas column density is the same as that of the HI gas.
 |
Fig. 2. Map of regions selected for this study. The gray background image is the 21 cm map of M 33, and the six yellow ellipses indicate the boundary of the radial bins: 1, 2, 3, 4, 5, and 7 kpc. The colored dots indicate all pixels where the CO J = 2−1 integrated emission is above 3σCO, and they are color-coded according to the different selected regions described in the text: cyan for the central region (CR), blue for the northern arm (NA), magenta for the southern arm (SA), red for the eastern filament (EF), and green for the interarm (IA). |
3. Global and local gas PDFs throughout the M 33 disk
The PDFs of inclination-corrected gas surface densities were made by summing pixels in logarithmic bins for HI, H2, or total gas using units of H atoms cm−2. One set of PDFs was made for different radial intervals, and another set of PDFs was made by summing pixels in four selected regions. In this last case, the PDFs corresponding to three types of GMCs and the diffuse CO are also shown (diffuse CO is where CO emission is associated with unresolved low-mass clouds or is truly diffuse). The three GMC types are GMC-A (containing no trace of star formation), GMC-B (with only embedded star formation), and GMC-C (with exposed HII regions).
In order to localize deviations of the PDF from a log-normal distribution, we investigated the local slopes defined as the derivative of the PDF in every column density bin (logarithmically spaced). Local slopes were computed by fitting a line segment through two adjacent bins on each side. A log-normal PDF will have a linearly decreasing slope, while a power-law PDF will have a constant slope. Log-normal PDFs fit to the data are also shown later in this Section. As described in Sect. 1 and discussed in the next section, compressible turbulence shapes the gas surface density PDF as a log-normal, while self-gravity gives a cloud an internal density structure and a power-law PDF.
3.1. PDF across arms, filaments, clouds, and the galaxy center
Figure 3 shows the molecular gas PDFs: in the bottom panels for gas in the different GMC types and diffuse (color-coded using different colors), and with thick lines for the total molecular gas (regardless of GMC type or diffuse). The columns correspond to six different regions in the galaxy, as indicated at the top. The full disk is on the left and includes all pixels with CO brightness above 3σCO, followed by the central region, the northern and southern spiral arms, and the eastern filament. The combination of molecular gas that is not in CR, NA, SA, or EF is labeled “interarm” (IA) and is shown on the right. In the top five panels, Fig. 3 shows the local slopes of these PDFs: SCO (black dots) are the PDF slopes for total molecular emission, SGMC−A, SGMC−B, SGMC−C, and Sdiff are the PDF slopes for molecular gas in GMC-type A, B, C, and diffuse. The log-normal parts of the PDFs in the bottom panels have linearly decreasing slopes, while the power-law parts of the PDFs have constant slopes, and in this case, the point distributions in the slope panels flatten. The panels show linearly decreasing trends in the center and in the northern arm, while the eastern filament has constant slopest. For the total CO, the PDFs have power-law parts in the southern arm, eastern filament and interarm regions. The southern arm and filament also show power-law parts for individual GMC types. Elsewhere, the PDFs are approximately log-normal, or too irregular to detect a deviation from log-normal.
For the total molecular gas in the whole disk (black, left panel), the power-law part of the PDF starts at a column density of ~1021.1 cm−2, which corresponds to about 0.7 magnitudes of visual extinction; AV = 0.7 mag is obtained using the conversion factor in Bohlin et al. (1978), but it can have slightly lower values given the metallicities of M 33 (Magrini et al. 2010). We would like to remark that the whole-disk PDF shown in Fig. 3 is the same as that presented by Druard et al. (2014), being drawn from the same data. However, we used the slope to infer the column density interval in which the PDF deviates from a log-normal distribution instead of fitting a log-normal function because of the limited range of column density sampled. The ascending side of the PDF, at low column densities, is not traced because of the sensitivity limits of the survey and of molecular gas dissociation thresholds. This leaves large uncertainties in the parameters of the best-fit log-normal functions, which in the next subsection are only shown for a qualitative comparison with the data. The analysis of the slopes shows a power-law behavior that starts at slightly lower column densities than those found by Druard et al. (2014; 1.3 × 1021 H atoms cm−2 versus 3.4 × 1021 H atoms cm−2). The spatial resolution of the survey limits the analysis to NH < 1022 H atoms cm−2 since these high column density regions tend to be small in physical size and cover only a small portion of the beam. This explains the sharp drop in the molecular gas PDF at high column density.
In Fig. 4 we show the atomic gas PDF obtained from HI in the proximity of GMCs, that is, 21 cm column densities at a distance smaller than 2.5 cloud radii with respect to the cloud centers. It is evident that the PDF drops at high column density, above 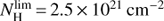 . In the central region, the drop of the HI PDF in cloud envelopes occurs at slightly lower column densities. To interpret
. In the central region, the drop of the HI PDF in cloud envelopes occurs at slightly lower column densities. To interpret 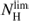 , we recall that the molecular fraction as a function of the total gas column density has been investigated in several galaxies and also in M 33 (Fig. 13 of Gardan et al. 2007). The gas mass fraction in molecular form increases as the gas surface density increases, with lower fractions found for gas at large galactocentric distances. However, the trend of molecular gas mass fractions with atomic gas surface densities has not been explicitly investigated in M 33. With the sensitivity and resolution of the current surveys, we find average molecular mass fractions on the order of 0.5 as the HI column density approaches
, we recall that the molecular fraction as a function of the total gas column density has been investigated in several galaxies and also in M 33 (Fig. 13 of Gardan et al. 2007). The gas mass fraction in molecular form increases as the gas surface density increases, with lower fractions found for gas at large galactocentric distances. However, the trend of molecular gas mass fractions with atomic gas surface densities has not been explicitly investigated in M 33. With the sensitivity and resolution of the current surveys, we find average molecular mass fractions on the order of 0.5 as the HI column density approaches 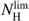 at galactocentric distances smaller than 4 kpc; lower average fractions, on the order of 0.3, are found in the outermost regions. Hence
at galactocentric distances smaller than 4 kpc; lower average fractions, on the order of 0.3, are found in the outermost regions. Hence 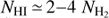 when the HI column density is on the order of
when the HI column density is on the order of 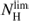 , and we interpret
, and we interpret 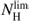 as the maximum sustainable atomic column density in the M 33 disk. Molecules can form where the atomic gas column density is lower than
as the maximum sustainable atomic column density in the M 33 disk. Molecules can form where the atomic gas column density is lower than 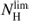 , especially in the inner disk, where gas volume densities and dust abundances are high. However, molecules always form where NHI is close to
, especially in the inner disk, where gas volume densities and dust abundances are high. However, molecules always form where NHI is close to 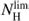 or the total gas column density is higher than
or the total gas column density is higher than 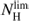 throughout the whole star-forming disk of M 33 (or AV > 2.4 if we consider metallicities lower than about 0.4 dex than solar in M 33).
throughout the whole star-forming disk of M 33 (or AV > 2.4 if we consider metallicities lower than about 0.4 dex than solar in M 33).
The HI PDF is approximately a power law at low column density. This is particularly evident in the interarm PDF and in the total HI PDF (labeled All in Fig. 4), which both extend toward lower column densities. Figure 4 clearly shows deviations from a log-normal distribution in the HI PDF of All, EF, and IA PDFs. Slopes are constant for NH < 5 × 1020 cm−2. What causes the deviation from a log-normal distribution at low column density? Numerical simulations of density fluctuations in compressible polytropic turbulence by Passot & Vázquez-Semadeni (1998) suggest that at low density, the PDF can approach a power law if the polytropic index γ > 1. Values of γ > 1 imply an equation of state where the Mach number increases with decreasing density. Then the PDF becomes broader than the isothermal case at low density, producing a power law instead of a log-normal. This scenario may apply to the interarm and other low-density regions if the voids produced by feedback or divergent flows in a spiral arm have higher Mach numbers than the clouds. We can exclude that the power-law PDF observed for the HI at low column density is due to noise or incomplete sampling in interferometric observations. Ossenkopf-Okada et al. (2016) have in fact shown that the impact of the observational noise needs to be at least 10% of the PDF peak column density to affect the shape of the PDF at column densities 5–10 times lower than the peak. The noise level in the HI map is about 5% of the PDF peak column density, however, and deviations from a log-normal are detected starting from column densities that are only 2–3 times lower than the peak. Moreover, our use of single-disk data to complement VLA interferometric observations and achieve a complete uv-plane coverage should avoid possible PDF distortions. Before drawing any definite conclusion on what drives the low column density PDF, possible resolution limits need to be considered if the low-density gas were made of unresolved low-mass clouds.
Figure 5 plots the PDFs for HI (blue), H2 (red), and total H (black) in the left two columns, and the slopes with the corresponding colors in the right two columns. The six rows are different bins of galactocentric distance, which are, from bottom to top, 0–1, 1–2, 2–3, 3–4, 4–5, and 5–7 kpc. The fourth bin from the bottom shows the clearest power-law structure for the molecules, with an index of −2.2, starting at a column density of ~1021 cm−2. In this radial bin the power law is even present for the total gas, starting at ~1021.4 cm−2, and the PDF is highly symmetric between the high- and low-density side. The large stellar cluster NGC 604 and the gas in its proximity lie in this radial interval. Approximate power laws are also present in the two outermost radial bins in the molecular PDFs. Here some caution should be used in interpreting the sharper PDF fall-off of the molecular gas, which can be caused by dark CO, that is, by a population of compact molecular clouds that are undetected by the CO survey, or by radial variations of the CO-to-H2 conversion factor. A higher CO-to-H2 conversion factor at large galactocentric radii would increase the PDF at high column densities and give a more symmetric total gas PDF as well.
The atomic gas PDFs in separate radial bins, as displayed in Fig. 5, show similar drops at high column densities as the PDFs of HI cloud envelopes in Fig. 4. On a linear scale, the HI column density is distributed smoothly around a peak value at about 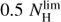 with only a few pixels extending above
with only a few pixels extending above 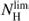 . The galaxy has no HI gas with face-on column densities above 4×1021 cm−2. We have used the 21 cm map at a higher spatial resolution (half of what was normally used in this paper) to check this finding, but no significant variations were detected. We cannot exclude that there are localized opacity corrections to the HI column density above
. The galaxy has no HI gas with face-on column densities above 4×1021 cm−2. We have used the 21 cm map at a higher spatial resolution (half of what was normally used in this paper) to check this finding, but no significant variations were detected. We cannot exclude that there are localized opacity corrections to the HI column density above 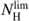 (Braun et al. 2009; Braun 2012). As in Fig. 4, the HI PDFs drop more slowly than a log-normal at low column densities, and they are close to a power law. The power-law slopes are between ~2 and ~4 outward of 2 kpc, increasing toward larger galactocentric radii.
(Braun et al. 2009; Braun 2012). As in Fig. 4, the HI PDFs drop more slowly than a log-normal at low column densities, and they are close to a power law. The power-law slopes are between ~2 and ~4 outward of 2 kpc, increasing toward larger galactocentric radii.
 |
Fig. 3. Bottom panels: PDFs of the molecular gas column density in units of H atoms cm−2 for the total molecular gas in the disk (black heavy curves), and for the gas in three GMC types: A (non-star forming), B (embedded star formation), and C (exposed star formation) in blue, red, and green, respectively. The PDF for diffuse molecular gas (meaning low-mass clouds or truly diffuse) is marked in magenta. All PDFs have been normalized to the number of pixels at the peak of the total molecular gas distribution |
 |
Fig. 4. PDF (left panels) and the local PDF slope (right panels) of the HI column density in and around the population of GMCs in the whole disk of M 33 (labeled All, bottom panel), in the four selected regions (intermediate panels), and in the interarm (top panel), labeled as in Sect. 2.3 and in the caption of Fig. 2. |
 |
Fig. 5. PDFs (left) and PDF slopes (right) of the atomic (blue), molecular (red), and total (black) hydrogen gas in six radial bins increasing from bottom to top and separated by 1 kpc intervals for all but the top row, where the radial interval is 2 kpc. The label in the upper left corner of the leftmost panels indicates the radial boundaries of each bin in kpc. Each PDF has been normalized to its peak value. The fourth bin from the bottom (radius 3–4 kpc) has a clear power-law structure in the molecules and total gas. |
3.2. PDF widths and the 21 cm line velocity dispersions
The widths of total gas PDFs become narrower from 1 kpc to large galactocentric radii. If the possible presence of dark CO means that the widths of the molecular PDFs at large radii are uncertain, this radial trend can be inferred also from the low column density side of the PDF, which is dominated by the atomic gas. However, there is no radial trend for the HI velocity dispersion, as shown by the 21 cm moment-2 map in Fig. 1. In Fig. 6 the filled squares indicate radial averages of the 21 cm velocity dispersion, σ21, with their standard deviations. The flatness of the radial distribution is remarkable, and the resolution of the 21 cm survey for this galaxy is excellent to avoid line broadening due to large-scale motion in the disk, such as a rising rotation curve in the center or spiral arm dynamical perturbations. For several galaxies the observed 21 cm line velocity dispersion decreases toward large galactocentric radii (Tamburro et al. 2009). We would like to point out that when we lower the spatial resolution of the HI survey by a factor 10, we also detect a decrease in velocity dispersion from a central value of 21 km s−1 to about 14 km s−1 at the edge of the star-forming disk. The resolution and sensitivity of the 21 cm dataset used in this paper, together with the regular morphology and low inclination of this nearby spiral galaxy, seems appropriate for using the 21 cm line broadening as tracer of turbulent motion. There are some variations in the HI dispersion throughout the disk as shown by the dispersion map in Fig. 1.
In Fig. 6 we use the open symbols to plot radial averages of the kinetic energy per unit area estimated as 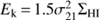 in units of 1045 ergs pc−2. Radial averages of the velocity dispersion and of the HI surface densities are about constant throughout the star forming disk (Corbelli et al. 2014), but since their small variations are correlated in the inner disk, variations in the kinetic energy per unit area are more evident, even though they are lower than a factor 2. The energy density Ek peaks around 2 kpc due to the presence of the southern and northern arms where the kinetic energy density in the atomic gas is about 5 × 1046 ergs pc−2. The energy density decreases beyond 3 kpc and drops at the edge of the star-forming disk at about 7 kpc because of the low gas surface density there. Of the four selected regions, the interarm and the eastern filament regions have the lowest kinetic energy densities for the atomic phase. The eastern filament is an HI over-density, but the HI velocity dispersion is lower by about 2 km s−1 than in the arms.
in units of 1045 ergs pc−2. Radial averages of the velocity dispersion and of the HI surface densities are about constant throughout the star forming disk (Corbelli et al. 2014), but since their small variations are correlated in the inner disk, variations in the kinetic energy per unit area are more evident, even though they are lower than a factor 2. The energy density Ek peaks around 2 kpc due to the presence of the southern and northern arms where the kinetic energy density in the atomic gas is about 5 × 1046 ergs pc−2. The energy density decreases beyond 3 kpc and drops at the edge of the star-forming disk at about 7 kpc because of the low gas surface density there. Of the four selected regions, the interarm and the eastern filament regions have the lowest kinetic energy densities for the atomic phase. The eastern filament is an HI over-density, but the HI velocity dispersion is lower by about 2 km s−1 than in the arms.
The values of the velocity dispersion are well above 6−8 km s−1, which is the expected thermal width for the warm phase of the ISM, hence turbulent velocities dominate throughout the whole disk. The decrease in PDF width for total and atomic hydrogen at large galactocentric radii could then be due to a decrease in Mach number (which is on the order of unity). Because the velocity dispersion is constant, this would imply that the average thermal temperature of the gas increases with radius, possibly as a result of a transition to a higher fraction of HI in the warm phase as the stellar surface density, and hence the disk pressure decreases.
In Fig. 7 we show the best-fit log-normal functions to the molecular gas PDFs in the selected regions. It is clear that log-normal functions fit the data in the center and northern arm region better than in the southern arm and eastern filament region. The peak and the width of log-normal functions were considered free parameters in the intervals [−0.4,0.4] and [0,1], respectively (data uncertainties were estimated using Poisson statistics). Even though the significance of the deviations is larger for the all-disk and interarm distribution, we show the four regions here to underline some differences between their PDFs. For example, in the regions where the PDFs are truly log-normal, namely the center and northern arm, the GMCs of type C clearly show a wider log-normal distribution than GMCs of types A and B, likely because the newly born massive stars in type C GMCs increase the turbulent motion.
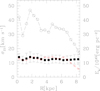 |
Fig. 6. Radial average values of the 21 cm velocity dispersion and their standard deviations are shown with filled squares with error bars. The open circles indicate the average energy per square parsec in the same radial bins; energy values have been normalized to 1045 ergs pc−2. The asterisks connected by a dashed line (red) indicate radial averages of the atomic gas surface density in solar masses per square parsec. |
 |
Fig. 7. Best-fit log-normal functions to the PDF of the total CO, and of the CO in GMCs of type A, B, C, and diffuse in the four selected regions of the M 33 disk. Each PDF is normalized to its maximum value. |
3.3. Interarm and gravity-dominated filaments
In this section we investigate some details of the power-law parts of the molecular gas PDFs as shown in Fig. 3. The all-disk, southern arm, eastern filament, and interarm all show a molecular gas PDF that deviates from a log-normal at NH > 1021 cm−2, and it closely resembles a power law. To prove that the power-law behavior of the molecular gas PDF in the eastern filaments is a property of the gas in the filament and not a result of the gas around the bright stellar cluster NGC 604 located at one extreme, we also carried out the analysis without the pixels around NGC 604, but the same conclusions apply.
The power-law PDF for molecules in the southern arm or in the eastern filament could be the result of self-gravity in GMCs, which gives them a power-law internal density profile (Klessen 2000; Vázquez-Semadeni et al 2008; Kritsuk et al. 2011; Girichidis et al. 2014). A similar interpretation has been suggested by Druard et al. (2014) when they detected an excess in the galaxy-wide PDF at high column densities. To better investigate this possibility, we color in Fig. 8 the different parts of the molecular power law to determine where they arise in the southern arm. We display the HI map of the southern arm in the background and underline in yellow all pixels with molecular densities that have 1021 < NH < 2.5 × 1021 cm−2, in cyan all pixels that have 2.5 × 1021 < NH < 4 × 1021 cm−2, and finally, we show in blue where NH > 4 × 1021 cm−2. The blue regions tend to be in the cores of the yellow and cyan regions, indicating that the power-law PDF results from a power-law internal structure inside GMCs. This is consistent with the model where cloud self-gravity causes the power-law PDF in these regions. Most of the yellow regions with no cyan or blue pixels in the center are type-A GMCs, which are located in the inner part of the arm. These pristine clouds presumably are compressed and accrete mass as they cross the arm, developing a high-density core that fragments and form stars, changing their status to type C. We estimate that about 70% of the molecular gas in the southern arm and eastern filament has column densities above 1021 cm−2 where it deviates from a log-normal distribution. At the resolution of our survey, the slope or power-law index can be as low as −1.2 to −1.5 for CO in the eastern filament or southern arm, while it is −2 for the overall CO PDF and −2.8 for interarms.
Power-law PDFs are also observed for galactic GMCs, and they have similar internal density gradients. For example, Schneider et al. (2015c) determined power-law PDF tails above 4–5 magnitudes of visual extinction for four local molecular clouds using dust emission maps, and showed that the power-law slopes in the PDF corresponded to the slopes of the density distributions inside the clouds, as expected for self-gravitating clouds. Schneider et al. (2015a) measured PDFs for four infrared dark clouds using dust emission and found them to be power law throughout, regardless of their internal star formation rates, with a transition to log-normal in the lower column density regions surrounding the dark clouds. Cloud core infall was also observed in CO, demonstrating that the power-law structure for these clouds is derived from self-gravity. Evidently, power-law PDFs are common, and galactic studies show that the origin of those power laws can often be traced to power-law internal density structures inside individual clouds. Some of the excess dense gas can come from local compression as well, as demonstrated for particular regions near bright nebulae (Schneider et al. 2012).
The power-law index increases when we average data from regions where some gas follows a power law and some gas follows a log-normal distribution. However, we would like to point out that a power-law PDF for a column density might have another explanation that applies to the interarm region. Here the presence of small unresolved cloudlets implies that the gas that is observed in each resolution element can be described as a random collection of individual clouds that follow a power-law mass distribution function, dP/dM ∝ M−κ. For κ ~ 1.5 (e.g., Solomon et al. 1987), the distribution function of column density is a power law with a slope of about −1.5 on a log-log plot if the average gas density is about constant and cloud surface density and size scale as M1/3. Steeper mass function slopes such as κ ~ 1.8 have been observed for molecular clouds in our Galaxy or in external galaxies (Heithausen et al. 1998; Rosolowsky 2005), and these would agree better with the observed slope of −2.8 for the power law of the interarm PDF if clouds are unresolved. Very recently, Braine et al. (2018) have shown that the slope of the cloud mass spectrum in M 33 steepens from κ = 1.4 to κ = 1.9 moving radially outward. The mass distribution of star clusters in interarms also suggests a steeper cloud mass spectrum (κ ~ 2) in these regions (Messa et al. 2018). In the interarm, there appears to be no correspondence between different parts of the PDF power law and different parts of individual clouds, such as a core-envelope structure. Moreover, samples of each cloud type in the interarm seem to have a log-normal PDF, representing turbulent conditions. Still, the PDF for all of the clouds is close to a power law, and this may be a stochastic effect from cloud sampling when the cloud size is smaller than the beam. A comprehensive analysis of theoretical predictions for the observed PDF of HI and H2 clouds below the spatial resolution limits of the surveys needs further investigation and will be addressed in forthcoming paper.
 |
Fig. 8. Image of the southern arm with the HI map in the background and colors underlining the CO core-envelope cloud structure that follow a power-law PDF. For the CO emission we plot in yellow all pixels with molecular surface densities 1021 < NH < 2.5 × 1021 cm−2, in cyan all pixels that have 2.5 × 1021 < NH < 4 × 1021 cm−2, and finally, we show in blue the core of GMCs with NH > 4 × 1021 cm−2. |
4. Discussion
Figures 3 and 5 indicate that the molecular gas with high surface density in M 33 has a PDF that is log-normal in the central regions and northern arm and follows a power law in the southern arm and filaments and in the interarm regions. The molecular gas has a power-law PDF in general at mid-radii, and even the total gas PDF somewhat follows a power law at 3–4 kpc radius. The total gas has more of a log-normal PDF, presumably because it includes both the atomic and molecular phases, with the latter being dominant at high column densities.
The question we set out to address in this paper is where and how the transition from weakly self-gravitating gas to strongly self-gravitating clouds occurs. The most direct interpretation of the data presented in the previous section is that this transition occurs at the same time as the gas is converted from atoms into molecules because the signature of self-gravity, the power-law PDF, is primarily located in the molecules at column densities close to Σlim. However, this is not necessarily the case. Much of the HI might also be part of the power-law cloud structure, perhaps even an extension of the same power law, in a shielding layer around the molecules, and we cannot see this because the turbulent compressions in the HI are much larger than the radial density range.
The power-law PDF is usually interpreted as the result of a turbulent cloud with a radial gradient in the average density (Klessen 2000; Vázquez-Semadeni et al 2008; Kritsuk et al. 2011). The turbulence presumably gives each small region a log-normal PDF in volume density, but the centroid density of that PDF varies with radius in proportion to the average density (for a constant compressive Mach number). The sum of all the local log-normals in a whole cloud becomes a power law, overwhelming the local log-normals, when the total density range from the radial gradient exceeds the fluctuating density range in each local piece of turbulence (Elmegreen 2011). This situation is fairly easy to achieve for the molecular gas because the density range in the radial gradient can be large, a factor of 100 or more, and that range exceeds the local compressions from turbulence at a modest Mach number. For an HI envelope, the radial density range can be much smaller, perhaps only a factor of 10 from the cloud edge where the turbulent pressure equals the ambient pressure to the base of the envelope where molecules appear. If the density variations from turbulent compressions in the HI envelope exceed the average density variation over radius, then the power-law component of the HI PDF may not be visible. The HI PDF at higher than average density mostly shows the sudden drop from the conversion to molecules, so the radial structure of the gas cannot be determined this way.
This model where turbulent fluctuations dominate density gradients in the atomic envelopes of clouds explains why the power-law parts of the PDFs generally disappear in the total hydrogen gas, which approximately follows a log-normal with smaller widths at larger galactocentric radii. The HI and total gas are close to a log-normal form around the peak, even though the molecular parts of the clouds and perhaps each entire cloud has a power-law radial profile in density. The PDF slope levels off to a constant value at the high density, molecule-dominated end, where the internal power-law density structure of the cloud dominates the turbulent density fluctuations in the molecules. For small clouds, the transition from atoms to molecules occurs at scales that are not sampled by the 50 pc resolution of our survey.
Power-law PDFs at high column density can also appear even without self-gravity if the polytropic index, γ, is lower than 1. According to Passot & Vázquez-Semadeni (1998), low γ leads to an increasing Mach number at higher density because the thermal temperature drops, and this causes higher density compressions than in an isothermal gas. The result is a broadening of the PDF at high density and a power-law structure.
However, cloud temperature gradients might reverse when star formation occurs in the cloud core, like for C-type GMCs where we still detect a power-law PDF in some selected regions.
While this γ effect may be present to some extent, numerical simulations of cloud assembly and collapse also show power laws just from self-gravity. GMCs might assemble through thermal and gravity-driven instabilities in the atomic gas, and they start collapsing at about 10 Myr, with self-gravity driving departures of the PDF from a log-normal. This is shown for example by Ballesteros-Paredes et al. (2011) using the results of numerical simulations of cloud formation and evolution by converging flows by Heitsch & Hartmann (2008). The eastern filament indeed lies in an atomic-dominated region, similar to that examined in the numerical simulations, and shares similar inflow Mach number (the eastern filament Mach number is 1.5, resulting from a velocity dispersion of σ21 = 11 km s−1 in warm HI gas). The PDF of the eastern filament (Fig. 3) is in fact very similar to the PDF shown in Fig. 2 of Ballesteros-Paredes et al. (2011; see panels relative to 13–14 Myr) at a similar spatial resolution.
The shape of the column density PDF on large scales may also depend on the relative times spent in the turbulence-dominated phase and in the gravity-dominated phase. If gravitational contraction to a power-law density structure occurs during cloud formation and feedback-driven turbulence occurs during cloud disruption, then regions with a gradual formation and a fast disruption should have a higher fraction of the mass in the pre- and early star formation phases when the power-law PDF is still apparent. Whether these phases show up in molecules or atoms depends also on the ease with which molecules can be formed. In the central regions of galaxies where the pressure is high, a high fraction of the ISM can be molecular, including even some non-gravitating clouds. This distinction may be relevant to our observation that regions close to the galaxy center have a molecular PDF that looks like a log-normal, while filaments farther out have a molecular PDF that looks more like a power law. Near the center, the molecular PDF apparently includes more of the turbulent ISM and in that sense is like the atomic-gas PDF farther out. The high pressure in the central regions increases the column density threshold for strong gravity, making this regime still undetectable at the resolution of the actual surveys. The filaments farther out, on the other hand, tend to form molecules at the same time as the gas becomes self-gravitating, so the molecular PDF shows the power-law density structure in that gas.
For the southern arm, departures from a log-normal shape are present for all three types of GMCs, which share similar widths, for NH ≃ 3 × 1021 cm−2. For the center and northern arm, type-C GMCs have a wider PDF than type-A or B GMCs, with a possible sign of gravity-driven power laws only at very high column densities, on the order of 1022 cm−2. Clearly, in these regions the power-law regime driven by gravity is a short-lived phase prior to the birth of stars that stir the GMCs again, and molecular hydrogen forms rapidly without self-gravity (Dobbs et al. 2008).
The interpretation of the PDF shape for unresolved clouds in the diffuse molecular gas or interarm, which shows deviations from a log-normal distribution, requires some further investigation, which will be presented elsewhere. The slopes are steeper there than in overdensity regions, and the PDFs of individual GMC classes do not show strong deviations from a log-normal distribution. Only a few pixels have a high column density in these regions, so that most for the detected CO does not show the core-halo cloud structure as in the southern arm (Fig. 8). It might be that heating in the interarm regions is more effective in warming-up the outer cloud envelopes, which are also of lower mass, so that we have γ < 1 without strong gravity. Alternatively, for smaller mass clouds, the resolution of the survey might not be good enough to measure surface densities and detect the self-gravitating parts of individual clouds.
5. Summary
We examined in detail the PDFs of the atomic and molecular ISM of M 33 at a resolution of about 50 pc on a cloud-by-cloud basis and in the overall gas distribution in selected disk areas to possibly unveil fingerprints of self-gravitating gas at these spatial scales. In particular, we focused on spatially resolved GMC complexes and on sensitive high-resolution atomic gas imaging to sample different regions across the star-forming disk. As shown by Dobbs et al. (2018), gaseous spiral features, that is, filamentary overdensities in the atomic gas, form as a result of gravitational instabilities in the disk of M 33. At the same time, feedback must take place in order to form large cavities between the filaments, which can break as shock fronts propagate in the ISM. As the galactocentric distance increases, the rate of star formation per unit area decreases, as does the gravity due to the stellar surface density. It is not clear a priori if disk dynamical instabilities trigger gas collapse, H2 formation and new star formation episodes quenched by stellar feedback or if recycled turbulent gas, driven by shocks in the ISM, makes a fast transition to a gravity-driven regime on very small scales. A first analysis of the PDF throughout the M 33 disk, shown in this paper, suggests that both regimes can take place. We have sampled different regions with the aim to trace non-gravitating turbulent complexes as well as gravity bound clouds in a statistical way, using a high-resolution all-disk survey of the ISM in M 33. We summarize the main results below.
The face-on atomic gas column density distribution drops beyond
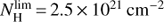 at all galactocentric radii; no HI is detected at
at all galactocentric radii; no HI is detected at 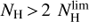 . The peak of the atomic gas PDF is at about 1021 H cm−2 (or about 0.5
. The peak of the atomic gas PDF is at about 1021 H cm−2 (or about 0.5 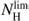 ), with a slight increase of this value if we sample the envelope of molecular complexes. Around the PDF peak, the HI here has a log-normal distribution. The slope of the PDF at low column densities becomes constant with a power-law structure, and this might be connected to the presence of cavities in the interarms where the warm/cold interface is located, particularly if γ > 1.
), with a slight increase of this value if we sample the envelope of molecular complexes. Around the PDF peak, the HI here has a log-normal distribution. The slope of the PDF at low column densities becomes constant with a power-law structure, and this might be connected to the presence of cavities in the interarms where the warm/cold interface is located, particularly if γ > 1.The width of the HI PDF has its maximum value at a distance of about 2–3 kpc from the center, likely due to the presence the two main arms. Here the kinetic energy density in the atomic gas has its maximum value. The dispersion of the HI gas varies by about a factor 2 across the disk, but radial averages show a constant trend with values on the order of 13 km s−1 and a radial decrease of only 1 km s−1 beyond 4 kpc. This constant trend suggest a ubiquitous presence of turbulence. The smaller width of the PDF at large galactocentric radii can be explained as a decrease in Mach number as disk flares and more warm HI fills the ISM.
The PDF of the molecular gas, as traced by CO, follows a log-normal shape in the central region. This also applies to the gas associated with GMCs at various evolutionary stages. The molecular PDF of the northern arm looks very similar to that of the central region. In the well-defined southern arm, a power-law distribution is instead detected around and beyond
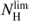 , which is likely due to gravity shaping the structure of GMCs at all evolutionary stages, prior to and during star formation.
, which is likely due to gravity shaping the structure of GMCs at all evolutionary stages, prior to and during star formation.The PDF of molecular hydrogen in the outermost filament that is rich in CO shows a power law with indexes between −1 and −1.5. This is also detected in all the evolutionary phases of the GMCs, which presumably assemble from atomic gas through thermal and gravitationally driven dynamical instabilities, and turbulence is less effective in shaping the cloud structure. In the outer filament and in the southern arm, different parts of the PDF power law correspond to different parts of individual clouds, such as a core-envelope structure.
The analysis presented in this paper suggests that on intermediate scales, self-gravity plays an early role in molecular cloud assembly and dominates the internal cloud structure in regions that are free of excessive feedback.
Acknowledgments
We acknowledge funding from the INAF PRIN-SKA 2017 program 1.05.01.88.04 and the stimulating environment offered by the scientific and organizing committee of the Sexten Center for Astrophysics
References
- Alves, J., Lombardi, M., & Lada, C. J. 2017, A&A, 606, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baba, J., Morokuma-Matsui, K., & Saitoh, T. R. 2017, MNRAS, 464, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Ballesteros-Paredes, J., Vázquez-Semadeni, E., Gazol, A., et al. 2011, MNRAS, 416, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Braine, J., Rosolowsky, E., Gratier, P., Corbelli, E., & Schuster, K.-F. 2018, A&A, 612, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braun, R. 2012, ApJ, 749, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Braun, R., Thilker, D. A., Walterbos, R. A. M., & Corbelli, E. 2009, ApJ, 695, 937 [Google Scholar]
- Colombo, D., Hughes, A., Schinnerer, E. 2014, ApJ, 784, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., Boquien, M., Kramer, C., et al. 2012, A&A, 539, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corbelli, E., Thilker, D., Zibetti, S., Giovanardi, C., & Salucci, P. 2014, A&A, 572, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corbelli, E., Braine, J., Bandiera, R., et al. 2017, A&A, 601, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deharveng, L., Zavagno, A., Samal, M. R., et al. 2015, A&A, 582, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobbs, C. L., Glover, S. C. O., Clark, P. C., & Klessen, R. S. 2008, MNRAS, 389, 1097 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dobbs, C. L., Pettitt, A. R., Corbelli, E., & Pringle, J. E. 2018, MNRAS, 478, 3793 [NASA ADS] [CrossRef] [Google Scholar]
- Donovan Meyer, J., Koda, J., Momose, R., et al. 2013, ApJ, 772, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Druard, C., Braine, J., Schuster, K. F., et al. 2014, A&A, 567, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, B. G. 2011, ApJ, 737, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 2018, ApJ, 854, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Leitner, S. N., Elmegreen, D. M., & Cuillandre, J.-C. 2003, ApJ, 593, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., Elmegreen, B. G., Erroz-Ferrer, S., et al. 2014, ApJ, 780, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Faesi, C. M., Lada, C. J., & Forbrich, J. 2018, ApJ, 857, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath C., & Klessen R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Figueira, M., Zavagno, A., Deharveng, L., et al. 2017, A&A, 600, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Froebrich, D., & Rowles, J. 2010, MNRAS, 406, 1350 [NASA ADS] [Google Scholar]
- Freedman, W. L., Wilson, C. D., & Madore, B. F. 1991, ApJ, 372, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Gardan, E., Braine, J., Schuster, K. F., Brouillet, N., & Sievers, A. 2007, A&A, 473, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gieren, W., Górski, M., Pietrzyński, G., et al. 2013, ApJ, 773, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Girichidis, P., Konstandin, L., Whitworth, A. P., & Klessen, R. S. 2014, ApJ, 781, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Gratier, P., Braine, J., Rodriguez-Fernandez, N. J., et al. 2012, A&A, 542, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratier, P., Braine, J., Schuster, K., et al. 2017, A&A, 600, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heithausen, A., Bensch, F., Stutzki, J., Falgarone, E., & Panis, J. F. 1998, A&A, 331, L65 [NASA ADS] [Google Scholar]
- Heitsch, F., & Hartmann, L. 2008, ApJ, 689, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Hirota, A., Kuno, N., Sato, N., et al. 2011, ApJ, 737, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Humphreys, R. M., & Sandage, A. 1980, ApJS, 44, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Banerjee, R., et al. 2011, A&A, 530, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klessen, R. S. 2000, ApJ, 535, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., & Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Lada, C. J., & Alves, J. 2010, A&A, 512, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2015, A&A, 576, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magrini, L., Stanghellini, L., Corbelli, E., Galli, D., & Villaver, E. 2010, A&A, 512, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Messa, M., Adamo, A., Calzetti, D., et al. 2018, MNRAS, 477, 1683 [NASA ADS] [CrossRef] [Google Scholar]
- Michalowski, M. J., Gentile, G., Hjorth, J., et al. 2015, A&A, 582, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mueller, K. E., Shirley, Y. L., Evans, N. J., II, & Jacobson, H. R. 2002, ApJS, 143, 469 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E. 2016, ApJ, 818, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 2015, ApJ, 806, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf-Okada, V., Csengeri, T., Schneider, N., Federrath, C., & Klessen, R. S. 2016, A&A, 590, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padoan P., Nordlund A., Jones B. J. T. 1997, MNRAS, 288, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeirim, P., Zavagno, A., Elia, D., et al. 2017, A&A, 605, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pan, L., Padoan, P., Haugbølle, T., & Nordlund, Å. 2016, ApJ, 825, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Passot, T., & Vázquez-Semadeni, E. 1998, Phys. Rev. E, 58, 4501 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E. 2005, PASP, 117, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N. Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., André, Ph., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N. Csengeri, T., Klessen, R.S., et al. 2015a, A&A, 578, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S. Girichidis, P., et al. 2015b, MNRAS, 453, L41 [CrossRef] [Google Scholar]
- Schneider, N., Ossenkopf, V., Csengeri, T., et al. 2015c, A&A, 575, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S. Motte, F., et al. 2016, A&A, 587, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sharma, S., Corbelli, E., Giovanardi, C., Hunt, L. K., & Palla, F. 2011, A&A, 534, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Tamburro, D., Rix, H.-W., Leroy, A. K., et al. 2009, AJ, 137, 4424 [NASA ADS] [CrossRef] [Google Scholar]
- Tassis, K., Christie, D. A., Urban, A., et al. 2010, MNRAS, 408, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Tosaki, T., Kohno, K., Harada, N., et al. 2017, PASJ, 69, 18 [NASA ADS] [Google Scholar]
- Vázquez-Semadeni, E. 1994, ApJ, 423, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni E., González, R. F., Ballesteros-Paredes, J., Gazol, A., & Kim, J. 2008, MNRAS, 390, 769 [NASA ADS] [Google Scholar]
- Verley, S., Corbelli, E., Giovanardi, C., & Hunt, L. K. 2009, A&A, 493, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wada, K., Spaans, M., & Kim, S. 2000, ApJ, 540, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Whitworth, A., Lomax, O., Balfour, S., et al. 2018, PASJ, 70, S55 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Velocity dispersion (moment-2) map of the 21 cm line emission in M 33 at 10 arcsec resolution (left panel). The black contours underline the location of the bright HI filaments or arms, they are drawn at 0.2 Jy beam−1 km s−1 and overlaid also on the moment-0 map in the right panel. The two areas that have been masked out for the likely presence of gas infall/outflow (the stream toward the central region in the southern half and a smaller region above the northern arm) have anomalously large velocity dispersions and have yellow-red colors in the velocity dispersion map. The color legend for the velocity dispersion map (left panel) is in units of km s−1, and for the intensity map (right panel), it is in Jy beam−1 km s−1. Maps are centered on RA = 23.4620417 and Dec = 30.6602222, (M33 coordinates). |
| In the text | |
 |
Fig. 2. Map of regions selected for this study. The gray background image is the 21 cm map of M 33, and the six yellow ellipses indicate the boundary of the radial bins: 1, 2, 3, 4, 5, and 7 kpc. The colored dots indicate all pixels where the CO J = 2−1 integrated emission is above 3σCO, and they are color-coded according to the different selected regions described in the text: cyan for the central region (CR), blue for the northern arm (NA), magenta for the southern arm (SA), red for the eastern filament (EF), and green for the interarm (IA). |
| In the text | |
 |
Fig. 3. Bottom panels: PDFs of the molecular gas column density in units of H atoms cm−2 for the total molecular gas in the disk (black heavy curves), and for the gas in three GMC types: A (non-star forming), B (embedded star formation), and C (exposed star formation) in blue, red, and green, respectively. The PDF for diffuse molecular gas (meaning low-mass clouds or truly diffuse) is marked in magenta. All PDFs have been normalized to the number of pixels at the peak of the total molecular gas distribution |
| In the text | |
 |
Fig. 4. PDF (left panels) and the local PDF slope (right panels) of the HI column density in and around the population of GMCs in the whole disk of M 33 (labeled All, bottom panel), in the four selected regions (intermediate panels), and in the interarm (top panel), labeled as in Sect. 2.3 and in the caption of Fig. 2. |
| In the text | |
 |
Fig. 5. PDFs (left) and PDF slopes (right) of the atomic (blue), molecular (red), and total (black) hydrogen gas in six radial bins increasing from bottom to top and separated by 1 kpc intervals for all but the top row, where the radial interval is 2 kpc. The label in the upper left corner of the leftmost panels indicates the radial boundaries of each bin in kpc. Each PDF has been normalized to its peak value. The fourth bin from the bottom (radius 3–4 kpc) has a clear power-law structure in the molecules and total gas. |
| In the text | |
 |
Fig. 6. Radial average values of the 21 cm velocity dispersion and their standard deviations are shown with filled squares with error bars. The open circles indicate the average energy per square parsec in the same radial bins; energy values have been normalized to 1045 ergs pc−2. The asterisks connected by a dashed line (red) indicate radial averages of the atomic gas surface density in solar masses per square parsec. |
| In the text | |
 |
Fig. 7. Best-fit log-normal functions to the PDF of the total CO, and of the CO in GMCs of type A, B, C, and diffuse in the four selected regions of the M 33 disk. Each PDF is normalized to its maximum value. |
| In the text | |
 |
Fig. 8. Image of the southern arm with the HI map in the background and colors underlining the CO core-envelope cloud structure that follow a power-law PDF. For the CO emission we plot in yellow all pixels with molecular surface densities 1021 < NH < 2.5 × 1021 cm−2, in cyan all pixels that have 2.5 × 1021 < NH < 4 × 1021 cm−2, and finally, we show in blue the core of GMCs with NH > 4 × 1021 cm−2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.