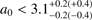| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731475 | |
| Published online | 14 August 2018 | |
The host galaxy of the short GRB 111117A at z = 2.211
Impact on the short GRB redshift distribution and progenitor channels⋆,⋆⋆
1
Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 København Ø, Denmark
e-mail: jselsing@dark-cosmology.dk
2
Max-Planck-Institut für extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
3
INAF – Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate (LC), Italy
4
Instituto de Astrofísica, Facultad de Física, Pontificia Universidad Católica de Chile, Vicuña Mackenna 4860, 7820436 Macul, Santiago, Chile
5
Millennium Institute of Astrophysics, Vicuña Mackenna 4860, 7820436 Macul, Santiago, Chile
6
Department of Particle Physics and Astrophysics, Faculty of Physics, Weizmann Institute of Science, Rehovot 76100, Israel
7
GEPI, Observatoire de Paris, PSL Research University, CNRS, Place Jules Janssen, 92190 Meudon, France
8
Sorbonne Universités, UPMC Univ. Paris 6 et CNRS, UMR 7095, Institut d’Astrophysique de Paris, 98 bis bd Arago, 75014 Paris, France
9
Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
10
Centre for Astrophysics and Cosmology, Science Institute, University of Iceland, Dunhagi 5, 107 Reykjavík, Iceland
11
Instituto de Astrofísica de Andalucía (IAA-CSIC), Glorieta de la Astronomía s/n, 18008 Granada, Spain
12
INAF-Osservatorio Astronomico di Roma, Via Frascati 33, 00040 Monteporzio Catone, Italy
13
ASI-Science Data Centre, Via del Politecnico snc, 00133 Rome, Italy
14
Centre for Astrophysics and Cosmology, University of Nova Gorica, Vipavska 13, 5000 Nova Gorica, Slovenia
15
Department of Physics, University of Warwick, Coventry CV4 7AL, UK
16
Istituto de Astrofisica e Planetologia Spaziali, INAF, Via Fosso del Cavaliere 100, 00133 Roma, Italy
17
Heidelberger Institut für Theoretische Studien, Schloss-Wolfsbrunnenweg 35, 69118
Heidelberg, Germany
18
Department of Physics & Astronomy and Leicester Institute of Space & Earth Observation, University of Leicester, University Road, Leicester LE1 7RH, UK
Received:
27
June
2017
Accepted:
8
February
2018
It is notoriously difficult to localize short γ-ray bursts (sGRBs) and their hosts to measure their redshifts. These measurements, however, are critical for constraining the nature of sGRB progenitors, their redshift distribution, and the r-process element enrichment history of the universe. Here we present spectroscopy of the host galaxy of GRB 111117A and measure its redshift to be z = 2.211. This makes GRB 111117A the most distant high-confidence short duration GRB detected to date. Our spectroscopic redshift supersedes a lower, previously estimated photometric redshift value for this burst. We use the spectroscopic redshift, as well as new imaging data to constrain the nature of the host galaxy and the physical parameters of the GRB. The rest-frame X-ray derived hydrogen column density, for example, is the highest compared to a complete sample of sGRBs and seems to follow the evolution with redshift as traced by the hosts of long GRBs. From the detection of Lyα emission in the spectrum, we are able to constrain the escape fraction of Lyα in the host. The host lies in the brighter end of the expected sGRB host brightness distribution at z = 2.211, and is actively forming stars. Using the observed sGRB host luminosity distribution, we find that between 43% and 71% of all Swift-detected sGRBs have hosts that are too faint at z ~ 2 to allow for a secure redshift determination. This implies that the measured sGRB redshift distribution could be incomplete at high redshift. The high z of GRB 111117A is evidence against a lognormal delay-time model for sGRBs through the predicted redshift distribution of sGRBs, which is very sensitive to high-z sGRBs. From the age of the universe at the time of GRB explosion, an initial neutron star (NS) separation of a0 < 3.1 R⊙ is required in the case where the progenitor system is a circular pair of inspiralling NSs. This constraint excludes some of the longest sGRB formation channels for this burst.
Key words: gamma-ray burst: individual: GRB 111117A / gamma-ray burst: general / galaxies: high-redshift / binaries: general / X-rays: bursts / techniques: imaging spectroscopy
Based on observations collected at ESO/VLT under programme 088.A-0051 and 091.D-0904, at TNG under programme A24TAC_38, at Gemini North under programme GN-2011B-Q-10 and GTC under programme GTC43-11B.
All data, code, and calculations related to the paper along with the paper itself are available at https://github.com/jselsing/GRB111117A
© ESO 2018
1. Introduction
There is mounting evidence that short-duration γ-ray bursts (sGRBs) come from the merger of a neutron star (NS) either with another NS or with a black hole, due to their apparent association with kilonovae (Barnes & Kasen 2013; Tanvir et al. 2013; Berger et al. 2013; Yang et al. 2015; Jin et al. 2016; Rosswog et al. 2017). This association has recently been confirmed by the simultaneous and co-spatial detection of gravitational waves (GWs) from a binary neutron star merger and a sGRB (Abbott et al. 2017a; Goldstein et al. 2017; Savchenko et al. 2017); however, to what degree the sGRB associated with GW170817 is a cosmological sGRB remains an open question (Lyman et al. 2018; Margutti et al. 2018). The absence of associated supernovae in deep searches (e.g., Hjorth et al. 2005a, b; Fox et al. 2005; Kann et al. 2011) supports this idea and distinguishes the physical origin of sGRBs from their long-duration counterparts (but see also Fynbo et al. 2006; Della Valle et al. 2006; Gal-Yam et al. 2006).
The classification of GRBs in two groups initially comes from the bimodal distribution of burst duration and spectral hardness in the BATSE sample (Kouveliotou et al. 1993), where the duration T90 < 2 s has been regarded as the dividing line between long and short GRBs. Additionally, it has been found for long GRBs (lGRBs) that there is a spectral lag in the arrivaltime of photons, with the most energetic ones arriving first. This lag is consistent with zero for sGRBs (Norris & Bonnell 2006). Because both populations have continuous, overlapping distributions in their observables and because telescopes observe in differing bands, it is difficult to impose a single demarcation criterion between the two classes. For this reason, the distinction between long and short GRBs is preferably based on a combination of the high-energy properties (Zhang et al. 2009; Kann et al. 2011; Bromberg et al. 2012, 2013).
The Swift satellite (Gehrels et al. 2004) greatly improved the understanding of sGRB progenitors thanks to its quick localization capability. The bulk of these localizations have associated galaxies at relatively low redshifts with a median redshift of z ~ 0.5 (Berger 2014). Unlike lGRBs, sGRB afterglows are faint, making absorption spectroscopy often ineffective. Therefore, most of these measurements come from the associated hosts and is potentially biased towards lower redshifts. Additionally, because the Swift sensitivity to sGRB decreases sharply with redshift (Behroozi et al. 2014), the intrinsic redshift distribution of sGRBs is largely unknown at higher redshifts.
The host galaxies of sGRBs are diverse. They are more massive and less actively star-forming on average than lGRB hosts (Fong et al. 2013), while in some cases no host galaxy can be identified above the detection threshold of deep followup observations (Berger 2010; Tunnicliffe et al. 2014). Together with their position within their hosts (Fong & Berger 2013), this suggests a progenitor system that can be very long-lived in comparison to lGRBs, with the host stellar mass affecting the sGRB rates more than the star formation rate (SFR; Berger 2014).
The electromagnetic signals from sGRBs are a promising channel to accurately localize NS mergers (Ghirlanda et al. 2016). This epochal breakthrough occurred recently when the first ever NS–NS GW event was detected by LIGO/Virgo (GW 170817) and associated with the weak sGRB 170817A detected by the Fermi and INTEGRAL satellites (Abbott et al. 2017a; Goldstein et al. 2017; Savchenko et al. 2017). The simultaneous detection of a sGRB and a GW provides new promising ways to constrain the binary inclination angle (Arun et al. 2014; Abbott et al. 2017a) and to measure cosmological distances (Nissanke et al. 2010; Abbott et al. 2017b).
The total lifetime of NS binaries depends on their orbit, mass, spin, initial separations, and subsequent inspiral times. The delay time from formation to explosion impacts the timing and distribution of the enrichment of the ISM with heavy r-process elements (van de Voort et al. 2014; Wallner et al. 2015; Ji et al. 2016). Some limits can be calculated using host galaxy star formation history models and spatial distribution of sGRBs within their hosts (Berger 2014). The most distant cosmological bursts, however, offer direct, hard limits on the coalescence timescales.
Here we present a spectrum of the host galaxy of the short GRB 111117A (T90 = 0.46 s) and measure its redshift to be z = 2.211. This value is significantly higher than the previously estimated redshift of z ~ 1.3 based on photometric studies (Margutti et al. 2012; Sakamoto et al. 2013). We present the GRB’s rest frame properties based on this new distance compared to previous analyses and revisit the host properties derived from the new solution to the spectral energy distribution (SED) fit. While no optical afterglow was detected, the excellent localization from a detection of the X-ray afterglow by the Chandra X-ray Observatory allows us to discuss the positioning and environmental properties of this remarkably distant sGRB. We use the ΛCDM cosmology parameters provided by Planck Collaboration XIII (2016) in which the universe is flat with H0 = 67.7 km s−1 Mpc−1 and Ωm = 0.307. All magnitudes are given in the AB system.
2. Observations and results
2.1. Spectroscopic observations and analysis
Spectroscopic observations were carried out using the crossdispersed echelle spectrograph, VLT/X-shooter (Vernet et al. 2011), at four seperate epochs. The burst was observed 38 hours after the Burst Alert Telescope (BAT) trigger under ESO program 088.A-0051 (PI: Fynbo) and again later under ESO program 091.D-0904 (PI: Hjorth). The observations used a simple ABBA nodding pattern, with 5″ nod throws. The X-shooter covers the wavelength range from 3000 Å to 24 800 Å (21 000 Å when the K-band blocking filter is used) across three spectroscopic arms. We carried out the bias-correction, flat-fielding, order tracing, wavelength calibration, rectification, and flux calibration using the VLT/X-shooter pipeline version 2.8.4 (Goldoni et al. 2006; Modigliani et al. 2010) run in physical mode. Because the echelle orders are curved across each detector, a rectification algorithm is employed that introduces correlations between neighboring pixels. We selected a pixel scale of 0.2/0.2/0.6 Å/pix for the UVB/VIS/NIR arm to minimize the degree of correlation while conserving the maximum resolution. The observations were combined and extracted using the scripts described in Selsing et al. (2018) and available online1, where the full spectral point spread function was modeled across each arm and used for the optimal extraction algorithm (Horne 1986). An overview of the spectroscopic observations is given in Table 1, and the slit position is shown in Fig. 1. Each of the epochs was extracted individually and combined in a weighted fashion where the weight at each pixel was chosen as median variance spectrum of the region surrounding that pixel, thus avoiding basing the weight on the pixel variance. Slit-loss correction was applied on the combined spectrum based on the average seeing of the observations. We show the extracted spectrum in Fig. 3.
Overview of the spectroscopic observations.
 |
Fig. 1. FORS2 R-band imaging of the field of GRB 111117A with the X-shooter slit overlaid. The slit position represents four epochs of spectroscopic observations taken at similar position angles. The corresponding photometry is shown in Fig. 3. The blue asterisk indicates the GRB position (RA, Dec) (J2000) = (00h50m46.264s, + 23°00′39″.98) as derived from the Chandra observations in Sakamoto et al. (2013). |
We determine a redshift of z = 2.211 ± 0.001 from the simultaneous detection of emission lines belonging to Lyα, [O II] λ3727, Hβ, [O III]λ4959, [O III]λ5007, and Hα. The [O II]λ3727, Hβ, and [O III]λ4959 lines are detected at low significance (~3-σ). The uncertainty on the redshift is the standard deviation of independent measurements of the redshift based on the individual line centroids (excluding Lyα). We show cutouts of the 2D spectrum at the position of all the detected lines in Fig. 2. The Hα line is only visible in the first epoch due to the K-band blocking filter used for the remaining observations. The nebular lines exhibit a spatial extent of ~1″̣5 and show significant velocity structure along the slit. A drop in the continuum bluewards of the Lyα line further supports the redshift. No spectral evolution is observed across the epochs indicating that there is negligible GRB afterglow contribution to the first epoch spectrum.
 |
Fig. 2. Two-dimensional images of the emission lines corresponding to Lyα, [O II]λ3727, Hβ, [O III]λ4959, [O III]λ5007, and Hα. The location of bright skylines are marked by blue boxes. The locations of the emission lines are indicated with red ellipses. Because the host is observed in nodding mode, negative images of the emission lines appear on both sides in the spatial direction. For the upper left panel containing Lyα, the systemic redshift position of Lyα is marked by a yellow vertical dashed line. The red part of the [O II]λ3727-doublet is affected by atmospheric absorption. |
Using the luminosity of Hα, we can infer the SFR of the host (Kennicutt 1998). At the redshift of the GRB host, Hα is observed at around 21 000 Å where the night sky is very bright. In addition, several bright sky-lines are superposed on the line, making it difficult to obtain an accurate estimate of the Hα flux. Due to their velocity structure, the lines exhibit clear deviations from a Gaussian and given the low signal-to-noise ration (S/N) of the spectra we do not attempt any parametric fits. We instead obtain a limit on the SFR by numerically integrating the part of Hα free of contamination and obtain FH,Xα > 4.1 × 10−17 erg s−1 cm−2. After converting the Kennicutt (1998) relation to a Chabrier (2013) initial mass function using the conversion factor from Madau & Dickinson (2014), we derive a limit of SFR > 7M⊙ yr−1. We additionally obtain the Lyα line flux by numerically integrating the entire Lyα line complex and obtain FLyα = (2.0 ± 0.5) × 10−17 erg s−1 cm−2, where the error on the flux is found by integrating the associated error spectrum over the same spectral region.
From the SED fit (Sect. 2.2) the host is constrained to contain very little or no dust. Consistently, Lyα is detected although its presence does not exclude dust. Therefore, we do not apply a dust-correction to the measured Hα flux here. The [O II] line is close to a region of strong telluric absorption, which is why no SFR is inferred from it.
The total extent of the lines in velocity space is ~450 km s−1. The line profiles shows an asymmetric “double-horned” profile, indicating that we are seeing a galaxy with a large degree of coherent rotational motion relative to the line of sight. If we assume that we are viewing a spiral galaxy edge-on, this is a measure of the rotational velocity of the gas. If we assume that the spectral resolution and the turbulent width of the lines are negligible compared to the rotational velocity, based on the projected size of the source and the width of the lines we can put a constraint on the dynamical mass of the galaxy (de Blok 2014). Based on the physical size along the slit and the velocity width of [O III]λ5007, we infer Mdyn ≳ 1010.8M⊙. Because we are viewing the host inclined at an angle relative to edge-on and because the slit is not aligned along the long axis of the host, this value is a lower limit.
2.2. Imaging observations and SED analysis
In addition to the spectroscopy presented above, we imaged the field of GRB 111117A in multiple broadband filters using the VLT equipped with FORS2 (gRIz filters) and HAWK-I (JHKs filters). These new data are complemented by a re-analysis of some of the imaging used in Margutti et al. (2012) and Sakamoto et al. (2013) that are available to us (GTC gri-band, TNG R-band, and Gemini z-band). A log of the photometric observations and measured brightnesses is given in Table 2. Most of the data were taken long after the GRB had faded when no afterglow contribution was present. Given the faintness of the afterglow (see Sect. 2.3, and Cucchiara et al. 2011; Cenko & Cucchiara 2011), we also expect negligible contribution to the earliest epochs, which is confirmed by the consistency between the two g-band measurements.
Overview of the photometric observations.
All data were reduced, analyzed, and fitted in a similar manner, as described in detail in Krühler et al. (2011) and more recently in Schulze et al. (2018). We use our own Python and IRAF routines to perform a standard reduction that includes bias/flat-field correction, de-fringing (where necessary), skysubtraction, and stacking of individual images. On the final reduced image products, DAOPHOT (Stetson 1987) was used to derive the reported photometry, where the size of the aperture was chosen to be 2″̣0. Because image quality ranges from 0″̣6 – 1″̣7 and the galaxy major axis is ~ 1″, this ensures that, in all cases, the large majority of the flux is collected and low surface brightness light missed in the aperture will not influence the measurement. This method sacrifices some S/N in the best seeing cases for more reliable photometry across differing observing conditions.
Photometric calibration was fixed relative to field stars from the SDSS and 2MASS catalogs in the case of griz and JHKs filters, respectively. For the R- and I-band photometry, we used the color transformations of Lupton2. We convert all magnitudes into the AB system, and correct for a Galactic foreground of EB−V = 0.027 mag (Schlegel et al. 1998, Schlafly & Finkbeiner 2011).
Noteworthy are the discrepancy of our new VLT/FORS2 photometry and of the re-analysis of the Gemini data compared to the z-band measurements of Margutti et al. (2012) and Sakamoto et al. (2013). Both of these authors report z ~ 23, which is brighter than our measurement by ~ 1.0 mag, while data taken in other filters are consistent within the errors. Visual inspection of the Gemini image shows only a marginal detection of the host, which we report here as a ~ 2-σ measurement. More conservatively, the 3-σ upper limit for the Gemini image is z > 24.06. Objects of magnitude z ~ 23 are clearly seen and are significantly brighter than the GRB host galaxy. The consistency between the deeper FORS2 z-band image and the upper limit derived for the Gemini image lends credence to the inferred magnitudes presented here, see Fig. 4.
The multicolor SED is fit using the Bruzual et al. (2003) single stellar population models (SSPs) based on Chabrier (2013) with initial mass function in LePhare (Ilbert et al. 2006), where the redshift is fixed to the spectroscopic value of z = 2.211. For the SED fitting, we create a grid consisting of ~106 different galaxy templates with four metallicities (0.02, 0.2, 0.4, 1.0 Z⊙), different ages, star formation histories, and degrees of extinction. For every model, we calculate the likelihood, and create a probability density function (PDF) for a given parameter by marginalizing over the other parameters. We quote the median of the PDF as the best-fit parameters and the errors are the 16th and 84th percentiles of the PDFs (see, e.g., Schulze et al. 2018 for details on the SED fitting procedure).
The best-fit model is an unreddened galaxy template. The inferred physical parameters are the absolute magnitude (MB = −22.0 ± 0.1 mag), the stellar mass (log(M⋆/M⊙) = 9.9 ± 0.2), the stellar population age (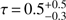 Gyr), and the SFR (SFRSED =
Gyr), and the SFR (SFRSED = 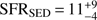 M⊙ yr−1). We show the SED fit in Fig. 3.
M⊙ yr−1). We show the SED fit in Fig. 3.
 |
Fig. 3. Best-fit SED to the derived photometry. The detection of Lyα is predicted from the SED fit and confirmed by the spectroscopic observations. Overplotted in gray is the observed spectrum, binned by 6 Å for presentation purposes. Slit losses have been corrected for based on the average seeing of the observations, as confirmed by the comparison with the photometry. The blue dashed curve is the corresponding error spectrum, smoothed for presentation purposes. The spectral gaps at 5500 Å and 10000 Å are due to the merging of the arms. |
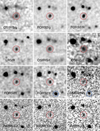 |
Fig. 4. Mosaic showing all used imaging. The host of GRB 111117A is marked by a red circle with a 2″̣0 radius. This is the same size as the aperture used to derive the photometry. Each panel is 20″ in size, north is up, east is left. Worth noting is the relative depth of the GMOS-N and FORS2 z-band images. For reference, the object located to the southeast of the host and marked with a blue dashed circle has an extinction corrected magnitude of 23.11 ± 0.09 (23.10 ± 0.18) in the FORS2 (GMOS-N) z-band. |
Without fixing the redshift to the spectroscopic value, using the revised photometry from Table 2, the photometric redshift of the galaxy is z
phot = 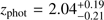 , consistent with the spectroscopic value at the 1-σ confidence level. The large i − z color found in previous works was mistakenly interpreted as the 4000 Å break, driving the galaxy photometric redshift to a lower, erroneous value.
, consistent with the spectroscopic value at the 1-σ confidence level. The large i − z color found in previous works was mistakenly interpreted as the 4000 Å break, driving the galaxy photometric redshift to a lower, erroneous value.
2.3. X-ray temporal and spectral analysis
We retrieved the automated data products provided by the Swift-XRT GRB repository3 (Evans et al. 2009). The X-ray afterglow light curve can be fit with a single power-law decay with an index α = 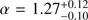 . We performed a time-integrated spectral analysis using data obtained in photon counting (PC) mode in the widest time epoch where the 0.3−1.5 keV to 1.5−10 keV hardness ratio is constant (namely, from t − T0 = 205 s to t − T0 = 203.5 ks, for a total of 29.1 ks of data) to prevent spectral changes that can affect the X-ray column density determination (Kopač et al. 2012). The obtained spectrum is described well by an absorbed power-law model and the best-fit spectral parameters are a photon index of 2.1 ± 0.4 and an intrinsic equivalent hydrogen column density NH,X of
. We performed a time-integrated spectral analysis using data obtained in photon counting (PC) mode in the widest time epoch where the 0.3−1.5 keV to 1.5−10 keV hardness ratio is constant (namely, from t − T0 = 205 s to t − T0 = 203.5 ks, for a total of 29.1 ks of data) to prevent spectral changes that can affect the X-ray column density determination (Kopač et al. 2012). The obtained spectrum is described well by an absorbed power-law model and the best-fit spectral parameters are a photon index of 2.1 ± 0.4 and an intrinsic equivalent hydrogen column density NH,X of 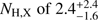 × 1022 cm−2 (z = 2.211), assuming a solar abundance and a Galactic NH,X in the burst direction of 4.1 × 1020 cm−2 (Willingale et al. 2013).
× 1022 cm−2 (z = 2.211), assuming a solar abundance and a Galactic NH,X in the burst direction of 4.1 × 1020 cm−2 (Willingale et al. 2013).
A measure of the optical-to-X-ray flux ratio is parametrized in terms of the darkness-parameter βOX (Jakobsson et al. 2004). Using the optical afterglow limits (r′ > 25.5, 13.5 hr after the burst; Cucchiara et al. 2011; Cenko & Cucchiara 2011), the X-ray light curve can be interpolated and evaluated at the time of the non-detection. We find βOX < 0.79, consistent with the value that was reported in Sakamoto et al. (2013).
3. Reinterpretation of the rest-frame properties
Margutti et al. (2012) find a projected offset between the host nucleus and the GRB site of 1″̣25 ± 0″̣20 arcsec; Sakamoto et al. (2013) find a similar value of 1″̣0 ± 0″̣20 arcsec. These correspond to a projected physical offset at z = 2.221 of 10.6 ± 1.7 kpc and 8.5 ± 1.7 kpc, respectively. Because the angular distance does not change significantly between z = 1.3 and z = 2.211, all conclusions of Margutti et al. (2012) and Sakamoto et al. (2013) relating to host offset are unaffected.
3.1. Classification
Based on the BAT light curve, T90 = 0.46 s, which is shorter than both the prototypical 2 s (Kouveliotou et al. 1993) and the <0.8 s suggested to also exclude the shorter tail of the Swift-observed lGRB population (Bromberg et al. 2012). Additionally, no signs of extended emission was found by Sakamoto et al. (2013). The spectral lag is 0.6 ± 2.4 ms, consistent with zero. As already pointed out by Margutti et al. (2012) and Sakamoto et al. (2013), this is typical of sGRBs (but see also Bernardini et al. 2015). In conjunction with the duration and the spectral hardness (Sakamoto et al. 2011), GRB 111117A is thus securely classified as a sGRB. Because the observed classification indicators, T90 and hardness ratio, do not depend strongly on redshift (Littlejohns et al. 2013), the updated redshift does not change this designation.
The intrinsic luminosity is shown in the X-ray light curve (Fig. 5) and it is subluminous compared to the majority of lGRBs. The inset in Fig. 5 shows the luminosity distribution at 10 ks. The subsamples comprise 402 lGRBs, 31 sGRBs, and GRB 111117A. The sample of lGRBs is from Evans et al. (2007, 2009) and the sample of sGRBs is compiled from Kann et al. (2011), Berger (2014), and D’Avanzo et al. (2014). The mean and the 1-σ dispersions of the samples are log(LlGRB/erg s−1) = 46.59 ± 0.87 and log(LsGRB/erg s−1) = 44.96 ± 0.94 for the lGRB and sGRB samples, respectively. GRB 111117A had log(L/erg s−1) = 44.95 at 10 ks. This is very close to the peak of the sGRB luminosity distribution at 10 ks, but an outlier from the lGRB distribution, further supporting the short classification.
 |
Fig. 5. Rest-frame XRT light curve of GRB 111117A, compared to the general population of XRT light curves of GRBs. The gray shaded region is a compilation of long GRB light curves (Evans et al. 2007, 2009), where the color represents density. The light blue lines are sGRB light curves from bursts with duration of T90 ≲ 2 s and those that were classified as short in Kann et al. (2011), Berger (2014) and D’Avanzo et al. (2014). The thick green line is GRB 111117A. Despite the remarkably high redshift, the luminosity is comparable to the bulk of the short burst population, and subluminous compared to the lGRB population. The inset shows the X-ray luminosity distributions of sGRBs and lGRBs at 10 ks, indicated by the vertical dashed line in the main panel. |
The separation of GRBs in two distinct classes based on their high-energy observables points to an intrinsically different physical origin. Long GRBs are typically interpreted as collapsars (MacFadyen & Woosley 1999) in which a single, massive star undergoes gravitational collapse, where the currently preferred model for sGRBs is the merger of two NSs (Eichler et al. 1989; Nakar 2007). Bromberg et al. (2013) investigated the degree to which high-energy observables of the long and short GRB populations overlap, and quantified the certainty in class membership. According to Bromberg et al. (2013), GRB 111117A has a 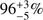 probability of being a sGRB. Compared to two other sGRB candidates at high redshift, GRB 060121 (T
90 = 1.97 ± 0.06 s; de Ugarte Postigo et al. 2006; Levan et al. 2006) at 1.7 ≲ z ≲ 4.5 (
probability of being a sGRB. Compared to two other sGRB candidates at high redshift, GRB 060121 (T
90 = 1.97 ± 0.06 s; de Ugarte Postigo et al. 2006; Levan et al. 2006) at 1.7 ≲ z ≲ 4.5 (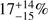 ) and GRB 090426 (T
90 = 1.28 ± 0.09 s; Antonelli et al. 2009; Levesque et al. 2010; Thöne et al. 2011) at z = 2.609 (
) and GRB 090426 (T
90 = 1.28 ± 0.09 s; Antonelli et al. 2009; Levesque et al. 2010; Thöne et al. 2011) at z = 2.609 (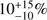 ), the certainty in class membership for GRB 111117A is much higher.
), the certainty in class membership for GRB 111117A is much higher.
Additionally, Horváth et al. (2010) classify both GRB 060121 and GRB 090426 as intermediate-duration bursts because both events have very soft spectra, compared to the hard ones typically seen in sGRBs. Intermediate bursts are very clearly related in their properties to lGRBs (de Ugarte Postigo et al. 2011), so they are unlikely to come from compact object mergers. GRB 111117A is also securely classified as a sGRB according to the Horváth et al. (2010) classification scheme.
A number of other GRBs are thought to be short and at relatively high redshift (z ≳ 0.9). If we consider bursts with a probability of being short fNC > 50%, according to the Bromberg et al. (2013) classification scheme, five sGRB are found: GRB 051210 at z ~ 1.3 (fNC = 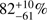 ; Leibler & Berger 2010), GRB 060801 at z = 1.131 (fNC =
; Leibler & Berger 2010), GRB 060801 at z = 1.131 (fNC = 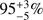 ; Berger et al. 2007), GRB 070714 at z = 0.923 (no fNC due to extended emission; Graham et al. 2009), GRB 090510 at z = 0.903 (fNC =
; Berger et al. 2007), GRB 070714 at z = 0.923 (no fNC due to extended emission; Graham et al. 2009), GRB 090510 at z = 0.903 (fNC = 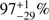 ; McBreen et al. 2010), and GRB 100117 at z = 0.915 (fNC =
; McBreen et al. 2010), and GRB 100117 at z = 0.915 (fNC = 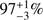 ; Fong et al. 2011). Although in individual cases a secure host association (hence redshift determination) is uncertain, there does seem to be a number of sGRBs at z ~ 1.
; Fong et al. 2011). Although in individual cases a secure host association (hence redshift determination) is uncertain, there does seem to be a number of sGRBs at z ~ 1.
This certainly makes GRB 111117A, by far, the highest redshift sGRB detected to date. The redshift and classification of GRB 111117A imply that it occurred when the universe was younger by ~3 Gyr compared to any other securely classified sGRB ever detected. If the merger of NSs is the primary agent for the r-process element enrichment of the universe (Goriely et al. 2011; Ji et al. 2016; Komiya & Shigeyama 2016; Safarzadeh & Scannapieco 2017), this marks the earliest detection of this process.
3.2. Rest-frame NH,X
We show the recalculated hydrogen equivalent X-ray derived column density, NH,X, in Fig. 6, where we compare it with the distributions of complete samples of both long and short GRBs. The lGRB sample is from Arcodia et al. (2016) and the sGRB sample is from D’Avanzo et al. (2014). From the sGRB sample of D’Avanzo et al. (2014) we have excluded GRB 090426, which likely does not belong in a short sample, as highlighted in Sect. 3.1. Both comparison samples infer NH,X over the largest temporal interval of constant hardness ratio to exclude spectral changes that can affect the X-ray derived column density. The 17 (5) of the 99 (15) long (short) GRBs that do not have measured redshifts have been excluded from our analysis.
 |
Fig. 6. Rest frame, X-ray derived equivalent hydrogen column density of GRB 111117A compared to complete samples of both long and short populations of GRBs. The sample of lGRBs from Arcodia et al. (2016) is shown in red, where detections are also shown with a kernel density estimate of the points, and the limits on NH,X are shown with arrows. The complete sample of sGRB by D’Avanzo et al. (2014) is shown in blue, where again the limits are indicated by arrows. Marginalizations over both axes are shown on the right and at the top of the plot, where the limits are shown as semi-transparent bars and detections as solid ones. The red curves in the marginalization plots are again the kernel density estimates of the Arcodia et al. (2016) sample. |
GRB 111117A occupies a unique position in Fig. 6 with the highest N H,X and highest redshift of all sGRBs. The short sample, excluding GRB 111117A, is located at low redshift (z < 1) and is found to populate a column density environment similar to that of lGRBs at comparable redshifts (D’Avanzo et al. 2014). The inferred hydrogen column density for GRB 111117A seems to follow the trend with increasing NH,X as a function of redshift as found for the lGRB afterglows (Campana et al. 2010; Starling et al. 2013; Arcodia et al. 2016). This is related to what has been found by Kopač et al. (2012) and Margutti et al. (2013) that NH,X seems to be comparable for long and short GRBs when compared at similar redshifts.
The redshift evolution of NH,X in the hosts of lGRBs is not reproduced by Buchner et al. (2017), who use a different NH,X inference methodology. Instead, a correlation between NH,X and host stellar mass is suggested. Assuming that the different NH,X-fitting methodologies yield comparable results, GRB 111117A has a higher NH,X compared to the relation suggested by Buchner et al. (2017) by more than the intrinsic scatter, although some lGRB hosts populate a similar region in the NH,X–M⋆ relation.
The large offset of GRB 111117A relative to the host center derived in Margutti et al. (2012) and Sakamoto et al. (2013) is difficult to reconcile with galaxy-scale gas being the source of the X-ray absorption. Along with the low dust content of the host, the large offset from the host center indicates that the high NH,X arises because the density in the GRB surroundings is high (or possibly because the light from the afterglow transverses localized regions of dense gas; see, e.g., Watson et al. 2013; Krongold & Prochaska 2013). Alternatively, it has been hypothesized that a significant contribution to the observed X-ray NH,X could come from the diffuse intergalactic medium and the intervening systems along the line of sight of the GRB (Campana et al. 2012; Arcodia et al. 2016; but see also Watson et al. 2013; Krongold & Prochaska 2013).
Even assuming a low dust-to-metals ratio, as typically observed in long GRB afterglow sightlines (Galama & Wijers 2001; Schady et al. 2010; Covino et al. 2013), the NH,X value derived from the X-ray spectrum corresponds to significant extinction along the afterglow line of sight (AV ≳ 1 mag), which is contrasted with the absence of dust found from the SED fit and supported by the detection of Lyα. This discrepancy between the extinction derived from the GRB afterglow and that obtained using galaxy-wide measures has also been observed occasionally for lGRBs (Perley et al. 2013). For the one sGRB where both parameters were measured (GRB 130603B; de Ugarte Postigo et al. 2014), they were found to be consistent with AV ~ 1 mag.
The lack of optical detection is also consistent with a high column along the GRB line of sight, as dust extinction could contribute to the optical faintness. On the contrary, its X-ray afterglow flux lies within the expected distribution given its gamma-ray fluence (D’Avanzo et al. 2014). This is not unexpected, as the X-ray flux is independent of the surrounding medium density (Freedman & Waxman 2001; Berger 2003; Nysewander et al. 2009).
3.3. Host galaxy
Because of the secure host association, GRB 111117A does not belong to the hostless class of sGRBs (Berger 2010) and because the host exhibits emission lines, this is indicative of a population of relatively young stars. Like the majority of sGRBs (Fong et al. 2013), the host of GRB 111117A is therefore a late-type galaxy and is entirely consistent in terms of stellar mass and stellar age with the general population of sGRB hosts (〈M*〉 = 1010.1M⊙ and 〈τ*〉 = 0.3 Gyr; Leibler & Berger 2010). Being a late-type host, both the stellar mass and sSFR are entirely within the range expected for the hosts of sGRBs (Behroozi et al. 2014). Our constraint on the dynamical mass is also well accommodated by the expected sGRB host halo mass (Behroozi et al. 2014).
The SFR is ~1 order of magnitude higher than the typical SFR for sGRB host galaxies (Berger 2014) and more similar to the SFR found in the hosts of lGRBs at a corresponding redshift (Krühler et al. 2015). Only two hosts in the sample of short GRBs compiled by Berger (2014) have a more vigorous star formation, placing it at the very upper end of the star formation distribution. The cosmic SFR evolution of the universe likely plays a role due to the proximity of GRB 111117A to the peak of cosmic SFR (Madau & Dickinson 2014). The high SFR is partly a selection effect; a less star-forming galaxy would exhibit weaker emission lines, thus making the redshift harder to determine. Additionally, it is natural to expect some evolution in the hosts of sGRBs with redshift as illustrated for NH,X in Sect. 3.2.
The simultaneous detection of Lyα and Hα allows us to put constraints of the escape fraction of Lyα, fesc(Lyα). Using the intrinsic ratio between Hα and Lyα, assuming case B recombination (Brocklehurst 1971), and the measured fluxes from the spectrum, we find fesc(Lyα) < 0.06. While the fesc(Lyα) scales with the dust column (Hayes et al. 2011), the resonant scattering of Lyα-photons with neutral hydrogen makes the effective path length of Lyα longer than for Hα (Atek et al. 2009). This makes fesc(Lyα) an unreliable proxy for dust column, especially at low dust columns (Atek et al. 2014) where the geometry and dynamics of the H I within the galaxy will affect the Lyα path the most. The fesc(Lyα) inferred for the host is entirely consistent with what is found for field galaxies with similar properties (Oyarzún et al. 2017). The same authors also find that Lyα emitting galaxies mostly have little dust, consistent with what is inferred from the SED fit (see Sect. 2.2). The centroid of the Lyα emission is found to be redshifted by ~240 ± 90 km s−1 with respect to systemic, which is similar to what is found for long GRB hosts (Milvang-Jensen et al. 2012) and Lyman break galaxies (Shapley et al. 2003) where the outflow is attributed to star formation.
4. Implications for the redshift distribution of sGRBs
The redshift distribution of GRBs provides valuable information not only on the conditions that drive the formation of these events, but also on the potential influence these cosmic explosions have on the evolution of the universe. Due to the elevated brightness of lGRBs compared to sGRBs (Berger 2014) and their tendency to be associated with the star-forming and therefore dense regions in their hosts (Fruchter et al. 2006; Lyman et al. 2017), the redshifts of lGRBs are easier to measure than those of their sGRB counterparts, where only a single burst has a redshift measurement from the GRB afterglow (Cucchiara et al. 2013; de Ugarte Postigo et al. 2014). Correspondingly, the redshift distribution of sGRBs is still substantially unconstrained compared to that of lGRBs (see, e.g., Jakobsson et al. 2012; D’Avanzo 2015; Perley et al. 2016).
A single sGRB at high redshift does little in terms of constraining the redshift distribution of sGRBs. In particular, other sGRB host redshifts could have been missed because their hosts are intrinsically fainter and thus the high redshift of GRB 111117A is only measured due to the brightness of its host. Berger (2014) compiled a sample of sGRB host luminosities, normalized by the characteristic galaxy luminosity at their respective redshift, 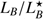 . To convert the SED-inferred MB of GRB 111117A to
. To convert the SED-inferred MB of GRB 111117A to 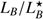 , we use the characteristic absolute B-band magnitude of the Schechter function for blue galaxies (U − V < 0.25) in the redshift window 2.0 ≤ z ≤ 2.5 from Marchesini et al. (2007) and obtain
, we use the characteristic absolute B-band magnitude of the Schechter function for blue galaxies (U − V < 0.25) in the redshift window 2.0 ≤ z ≤ 2.5 from Marchesini et al. (2007) and obtain 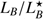 = 1.2.
= 1.2.
Using the complete, flux-limited selection of Swift-detected bursts from D’Avanzo et al. (2014), excluding GRB 111117A and the likely non-sGRB GRB 090426, we have a statistically homogeneous sample from which we can address the implications of the redshift of GRB 111117A. This sample includes sGRBs originating in star-forming galaxies, elliptical galaxies, and apparent hostless sGRBs. Of the 14 hosts in the sample, 10 (71%) have both measured redshifts and 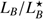 . Compared to the complete sample, the host of GRB 111117A is brighter than 80% of the hosts with measured
. Compared to the complete sample, the host of GRB 111117A is brighter than 80% of the hosts with measured 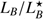 . Even if we conservatively assume that all the hosts missing
. Even if we conservatively assume that all the hosts missing 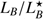 are brighter than the host of GRB 111117A, the host is still brighter than >60% of sGRB hosts. The host of GRB 111117A is brighter than 73% of all 26 hosts with
are brighter than the host of GRB 111117A, the host is still brighter than >60% of sGRB hosts. The host of GRB 111117A is brighter than 73% of all 26 hosts with 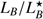 from Berger (2014).
from Berger (2014).
If we assume that we are able to obtain emission-line redshifts from hosts which are at most 0.5 mag fainter (R < 24.5 mag; Krühler et al. 2012), and if they were at the redshift of GRB 11117A, we would miss 60% of the redshifts (6 out of 10 hosts) because the host is too faint. The corresponding number is around 45% (12 out of 26) of the full sample of Berger (2014), reflecting the lower mean 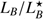 of the complete sample. Because the average SFR of galaxies hosting lGRBs is higher than for galaxies hosting sGRBs, the fraction of missed burst redshifts is likely higher, although the cosmic SFR evolution could play a role in improving redshift determinability at high z.
of the complete sample. Because the average SFR of galaxies hosting lGRBs is higher than for galaxies hosting sGRBs, the fraction of missed burst redshifts is likely higher, although the cosmic SFR evolution could play a role in improving redshift determinability at high z.
A fraction of the bursts missing redshift are host-less, but appear to be spatially correlated with galaxies that are likely at moderate redshifts (Tunnicliffe et al. 2014); should some of the remainder be at high redshift, the missed fraction would increase. If we assume that all the bursts that are missing redshifts are at high z and are missed due to host faintness, 10 out of 14 hosts in the complete sample (71%) would be missed at z = 2.211. This serves as an upper limit on the fraction of missed burst redshifts at high z. Conversely, if all bursts missing redshift were at low redshift and missed for other reasons, 6 out of 14 hosts (43%) would be missed at z = 2.211. The two limits indicate that we would miss between 43% and 71% of Swift-detected sGRB hosts at z ~ 2 due to host faintness.
The theoretical redshift distribution of sGRBs depends on the type of delay-time function used to model the progenitor system. The likelihood preferred lognormal time delay models investigated by Wanderman & Piran (2015) predict a sGRB rate at z = 2.211, around two orders of magnitude lower than the peak rate at z = 0.9. According to Wanderman & Piran (2015), this preference depends critically on the absence of sGRBs at z ≳ 1.2. The higher determined redshift of GRB 111117A, and the likely number of additional high-z sGRB could change the preferred time delay models. The redshift of GRB 111117A, on the other hand, is close to the expected peak in sGRB rate calculated using the power-law delay time models (Behroozi et al. 2014; Wanderman & Piran 2015; Ghirlanda et al. 2016), meaning we would be missing a large fraction of sGRB redshifts.
A critical test to assess whether the power-law delay time models can be accommodated by the current observation is to check if the implied sGRB rate at higher redshift does not exceed the number of observed sGRBs without redshifts. Of the 100 sGRBs observed by Swift, 20 have secure redshifts, and another 7 have a tentative redshift measurement4, meaning that >73% of all sGRBs observed with Swift are missing redshifts. More recently, Fong et al. (2017) and LIGO Scientific Collaboration et al. (2017) compiled a list of 36 (33) sGRBs with redshift measurements and, using this number, the redshift incompleteness of sGRBs decreases to 64%. In addition to the potential number of high-z events already detected but missing redshifts, Behroozi et al. (2014) parametrized the Swift redshift sensitivity and found that the mean detection probability for sGRBs at z ~ 2 was only ~1% of the mean detection probability at z ~ 1, assuming that the unknown beaming angle of sGRBs stays constant with time. What this means is that at present, there is almost no limit on the number of sGRBs that could be at redshifts z > 2.
5. Constraints on progenitor separation
At z = 2.211, the age of the universe is 3 Gyr. If the progenitor systems of sGRBs are the merger of two NSs, this sets a hard upper limit to the coalescence timescale for such a system. In the absence of other mechanisms, the timescale of the orbital decay of the system is set by the energy loss due to GWs, which in turn is set by the mass of the constituent compact objects, the eccentricity of the orbit, and the separation of the two (Postnov & Yungelson 2014). If we assume that the formation timescale of the first galaxies is short compared to the time since the Big Bang (Richard et al. 2011), and that any binary NS formation channel can work sufficiently fast, we can–assuming a mass of each of the NSs in a circular orbit at the time of system formation–place a hard upper limit on the initial separation, a0.
In practice, most NS–NS binaries will be eccentric at formation because of the SN natal kicks. For more eccentric orbits, the coalescence timescale decreases, leading to a larger initial separation constraint. As noted by Postnov & Yungelson (2014), it takes eccentricities >0.6 to significantly shorten the merger time. Due to tidal interactions between the two NSs, the orbits will also tend to circularize with time, lessening the impact of the eccentricity on the constraint.
Additionally, the constraint on initial progenitor separation will change depending on the mass assumed for the constituent NS masses, with higher masses generally resulting in faster inspiral times and weaker constraints of initial separation. We use the NS mass distribution from Kiziltan et al. (2013) to compute a grid of initial progenitor separation constraints, given the range of NS masses allowed. We show the grid in Fig. 7. The double NS binary systems have a constituent mass distribution peaked at 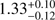 M⊙ (Kiziltan et al. 2013), which corresponds to
M⊙ (Kiziltan et al. 2013), which corresponds to 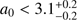 R⊙ where the errors are the 68% posterior predictive intervals.
R⊙ where the errors are the 68% posterior predictive intervals.
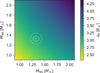 |
Fig. 7. Constraints on the initial progenitor separation, given binary constituent masses. As can be seen, a heavier system will inspiral faster, leading to a weaker constraint on the initial separation of the binary. The most probable value, the 68% and 98% posterior predictive intervals of the NS binary mass distribution from Kiziltan et al. (2013), are shown with the dashed ellipses, which corresponds to a constraint on a maximum initial separation of |
Using the inferred stellar population age from our SED fit, we obtain a less robust limit on the initial separation of 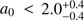 R⊙. However, this does not account for the possibility that there could be an underlying stellar population of older stars from a previous star formation episode. To investigate the possible impact of the presence of an old stellar population, we followed Papovich et al. (2001) and re-fitted the observed SED with the best-fit template to which an additional stellar population of old stars was added. For each template, this old population was set as the SSP with the same parameters as the best-fit SED except the age, which was set to the age of the Universe at the observed redshift. In principle, this can constrain the maximum contribution of old populations within the photometric error bars (for details, see Papovich et al. 2001). We find a negligible contribution to the stellar mass (i.e., variations much smaller than the statistical uncertainty associated with the best-fit template).
R⊙. However, this does not account for the possibility that there could be an underlying stellar population of older stars from a previous star formation episode. To investigate the possible impact of the presence of an old stellar population, we followed Papovich et al. (2001) and re-fitted the observed SED with the best-fit template to which an additional stellar population of old stars was added. For each template, this old population was set as the SSP with the same parameters as the best-fit SED except the age, which was set to the age of the Universe at the observed redshift. In principle, this can constrain the maximum contribution of old populations within the photometric error bars (for details, see Papovich et al. 2001). We find a negligible contribution to the stellar mass (i.e., variations much smaller than the statistical uncertainty associated with the best-fit template).
The delay time between formation and explosion is well accommodated by the models of Belczynski et al. (2006) where a range of binary NS systems and their decays are followed in different host potentials; however, some of the longest delay times are excluded. Given the late-type nature of the host, only a small subset of the longest population synthesis models violates the delay time constraint derived here (O’Shaughnessy et al. 2008). The same holds if NS binaries are primarily formed through dynamical interactions in globular clusters (Lee et al. 2010; Church et al. 2004).
6. Conclusions
We have provided here a revised, spectroscopic redshift measurement for the short GRB 111117A based on host galaxy emission lines, setting it at z = 2.211 ± 0.001. This value supersedes the previous photometric redshift estimates of Margutti et al. (2012) and Sakamoto et al. (2013). The erroneous best-fit SED redshift of previous authors is attributed to a discrepancy in the measured z-band magnitude, and highlights the importance of deep spectroscopic studies of sGRB hosts at medium resolution.
Using the new distance, the X-ray derived NH,X towards GRB 111117A is the highest within a complete sample of sGRBs and is consistent with the NH,X − z evolution traced by the sight lines of lGRBs. The SFR of the host is in the upper end of the sGRB host SFR distribution and no significant amount of dust is present. The high NH,X is at odds with the large projected host offset and the absence of dust. One possible explanation could be that GRB 111117A is formed through a prompt channel of sGRB formation and originates in an unseen star-forming region located in the outskirts of the host, or a localized region of high H I density along the line of sight.
Although a single burst carries little leverage in terms of constraining the redshift distribution of sGRB, the high redshift of GRB 111117A needs to be accommodated in progenitor models. A lognormal delay time model predicts a very low volumetric density of bursts at z ~ 2, whereas a power-law delay time model peaks near the GRB 111117A redshift. If more sGRBs are at similarly high redshifts, but are missed because of the faintness of their hosts and afterglows, a lognormal delay time model will be disfavored. Compared to a complete sample of Swift-detected sGRB, the host of GRB 111117A is more luminous than 80 % of sGRB hosts with measured luminosities. Assuming a host brightness redshift determination threshold for 43–71% of the sample hosts, we would be unable to determine a redshift if they were at a similar redshift to that of GRB 111117A. This could indicate that, potentially, a significant fraction of Swift-detected sGRBs are at high z, but with redshifts unknown due to host faintness.
Using the age of the universe at the time of explosion allows us to set constraints on the maximum separation between the engine constituents at the time of formation. We find that the maximum separation of two NSs at system formation time is a0 < 3.1 R⊙, which excludes some of the formation channels with the longest timescales.
Acknowledgments
We thank the anonymous referee for the constructive report. We thank Jens Hjorth and Lise Christensen for useful discussions regarding the interpretation of this event. We thank Mathieu Puech for testing the possible contribution from an older stellar population in the SED. We thank Peter Laursen for fruitful discussions regarding the Lyα escape fraction. TK acknowledges support through the Sofja Kovalevskaja Award to P. Schady. SDV is supported by the French National Research Agency (ANR) under contract ANR-16-CE31-0003 BEaPro. PDA and SCo acknowledge support from ASI grant I/004/11/3. JJ acknowledges support from NOVA and a NWO-FAPESP grant for advanced instrumentation in astronomy. NRT and KW acknowledge support from STFC Consolidated Grant ST/N000757/1. CT acknowledges support from a Spanish National Research Grant of Excellence under project AYA 2014-58381-P and funding associated with a Ramòn y Cajál fellowship under grant number RyC-2012-09984. AdUP acknowledges support from a Ramón y Cajal fellowship, a BBVA Foundation Grant for Researchers and Cultural Creators, and the Spanish Ministry of Economy and Competitiveness through project AYA2014-58381-P. ZC acknowledges support from the Spanish research project AYA 2014-58381-P and support from Juan de la Cierva Incorporación fellowships IJCI-2014-21669. RSR acknowledges AdUP’s BBVA Foundation Grant for Researchers and Cultural Creators and support from the Italian Space Agency (ASI) through Contract n. 2015-046-R.0 and from the European Union Horizon 2020 Programme under the AHEAD project (grant agreement n. 654215). This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration et al. 2013). The analysis and plotting was achieved using the Python-based packages Matplotlib (Hunter 2007), Numpy, and Scipy (van der Walt et al. 2011), along with other community-developed packages. This work made use of observations obtained with the Italian 3.6 m Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Fundación Galileo Galilei of the INAF (Istituto Nazionale di Astrofisica) at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. Based on data from the GTC Archive at CAB (INTA-CSIC) and on observations obtained at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the National Research Council (Canada), CONICYT (Chile), Ministerio de Ciencia, Tecnología e Innovación Productiva (Argentina), and Ministério da Ciência, Tecnologia e Inovação (Brazil).
This is based on http://www.astro.caltech.edu/grbox/grbox.php, selecting all Swift-detected sGRBs up to GRB 170428A.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017a, Phys. Rev. Lett., 119, 161101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017b, Nature, 551, 85 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Antonelli, L. A., D’Avanzo, P., Perna, R., et al. 2009, A&A, 507, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arcodia, R., Campana, S., & Salvaterra, R. 2016, A&A, 590, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arun, K. G., Tagoshi, H., Pai, A., & Mishra, C. K. 2014, Phys. Rev. D, 90, 024060 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration, Robitaille, T. P., Tollerud, E. J., et al. 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Atek, H., Kunth, D., Schaerer, D., et al. 2009, A&A, 506, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Atek, H., Kunth, D., Schaerer, D., et al. 2014, A&A, 561, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, J., & Kasen, D. 2013, ApJ, 775, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Ramirez-Ruiz, E., & Fryer, C. L. 2014, ApJ, 792, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Perna, R., Bulik, T., et al. 2006, ApJ, 648, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E. 2010, ApJ, 722, 1946 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E. 2014, ARA&A, 52, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Kulkarni, S., & Frail, D. 2003, ApJ, 590, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Fox, D. B., Price, P. A., et al. 2007, ApJ, 664, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E., Fong, W., & Chornock, R. 2013, ApJ, 774, L23 [Google Scholar]
- Bernardini, M. G., Ghirlanda, G., Campana, S., et al. 2015, MNRAS, 446, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Brocklehurst, M. 1971, MNRAS, 153, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Bromberg, O., Nakar, E., Piran, T., & Sari, R. 2012, ApJ, 749, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Bromberg, O., Nakar, E., Piran, T., & Sari, R. 2013, ApJ, 764, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Schulze, S., & Bauer, F. E. 2017, MNRAS, 464, 4545 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Thöne, C. C., de Ugarte Postigo, A., et al. 2010, MNRAS, 402, 2429 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Salvaterra, R., Melandri, A., et al. 2012, MNRAS, 421, 1697 [NASA ADS] [CrossRef] [Google Scholar]
- Cenko, S. B., & Cucchiara, A. 2011, GRB Coord. Network, Circ. Serv, 12577 [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Church, R. P., Levan, A. J., Davies, M. B., & Tanvir, N. 2011, MNRAS, 413, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Covino, S., Melandri, A., Salvaterra, R., et al. 2013, MNRAS, 432, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Cucchiara, A., & Cenko, S. B. 2011, GRB Coord. Network, Circ. Serv, 12567 [Google Scholar]
- Cucchiara, A., Prochaska, J. X., Perley, D., et al. 2013, ApJ, 777, 94 [NASA ADS] [CrossRef] [Google Scholar]
- D’Avanzo, P. 2015, JHEAp, 7, 73 [Google Scholar]
- D’Avanzo, P., Salvaterra, R., Bernardini, M. G., et al. 2014, MNRAS, 442, 2342 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., & Walter, F. 2014, AJ, 147, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Della Valle, M., Chincarini, G., Panagia, N., et al. 2006, Nature, 444, 1050 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- de Ugarte Postigo, A., Castro-Tirado, A. J., Guziy, S., et al. 2006, ApJ, 648, L83 [NASA ADS] [CrossRef] [Google Scholar]
- de Ugarte Postigo, A., Horváth, I., Veres, P., et al. 2011, A&A, 525, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Ugarte Postigo, A., Thöne, C. C., Rowlinson, A., et al. 2014, A&A, 563, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2007, A&A, 469, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, P. A., Beardmore, A. P., Page, K. L., et al. 2009, MNRAS, 397, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, W., & Berger, E. 2013, ApJ, 776, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, W., Berger, E., Chornock, R., et al. 2011, ApJ, 730, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, W., Berger, E., Chornock, R., et al. 2013, ApJ, 769, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Fong, W., Berger, E., Blanchard, P. K., et al. 2017, Astrophys. J. Lett., 848, L23 [Google Scholar]
- Fox, D. B., Frail, D. A., Price, P. A., et al. 2005, Nature, 437, 845 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Freedman, D. L., & Waxman, E. 2001, ApJ, 547, 922 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., Levan, A. J., Strolger, L., et al. 2006, Nature, 441, 463 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fynbo, J. P. U., Watson, D., Thöne, C. C., et al. 2006, Nature, 444, 1047 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Galama, T. J., & Wijers, R. A. M. J. 2001, ApJ, 549, L209 [NASA ADS] [CrossRef] [Google Scholar]
- Gal-Yam, A., Fox, D. B., Price, P. A., et al. 2006, Nature, 444, 1053 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gehrels, N., White, N., Barthelmy, S., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Salafia, O. S., Pescalli, A., et al. 2016, A&A, 594, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldoni, P., Royer, F., François, P., et al. 2006, Proc. SPIE, 6269, 62692K [CrossRef] [Google Scholar]
- Goldstein, A., Veres, P., Burns, E., et al. 2017, Astrophys. J. Lett., 848, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., Bauswein, A., & Janka, H.-T. 2011, ApJ, 738, L32 [Google Scholar]
- Graham, J. F., Fruchter, A. S., Levan, A. J., et al. 2009, ApJ, 698, 1620 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M., Schaerer, D., Östlin, G., et al. 2011, ApJ, 730, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth, J., Sollerman, J., Gorosabel, J., et al. 2005a, ApJ, 630, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Hjorth, J., Watson, D., Fynbo, J. P. U., et al. 2005b, Nature, 437, 859 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horváth, I., Bagoly, Z., Balázs, L. G., et al. 2010, ApJ, 713, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jakobsson, P., Hjorth, J., Fynbo, J. P. U., et al. 2004, ApJ, 617, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Jakobsson, P., Hjorth, J., Malesani, D., et al. 2012, ApJ, 752, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Ji, A. P., Frebel, A., Chiti, A., & Simon, J. D. 2016, Nature, 531, 610 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jin, Z.-P., Hotokezaka, K., Li, X., et al. 2016, Nat. Commun., 7, 12898 [NASA ADS] [CrossRef] [Google Scholar]
- Kann, D. A., Klose, S., Zhang, B., et al. 2011, ApJ, 734, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kiziltan, B., Kottas, A., De Yoreo, M., & Thorsett, S. E. 2013, ApJ, 778, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Komiya, Y., & Shigeyama, T. 2016, ApJ, 830, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Kopač, D., D’Avanzo, P., Melandri, A., et al. 2012, MNRAS, 424, 2392 [NASA ADS] [CrossRef] [Google Scholar]
- Kouveliotou, C., Meegan, C. A., Fishman, G. J., et al. 1993, ApJ, 413, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Krongold, Y., & Prochaska, J. X. 2013, ApJ, 774, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Krühler, T., Schady, P., Greiner, J., et al. 2011, A&A, 526, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krühler, T., Malesani, D., Milvang-Jensen, B., et al. 2012, ApJ, 758, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Krühler, T., Malesani, D., Fynbo, J. P. U., et al. 2015, A&A, 581, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, W. H., Ramirez-Ruiz, E., & van de Ven, G. 2010, ApJ, 720, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Leibler, C. N., & Berger, E. 2010, ApJ, 725, 1202 [NASA ADS] [CrossRef] [Google Scholar]
- Levan, A. J., Tanvir, N. R., Fruchter, A. S., et al. 2006, ApJ, 648, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Levesque, E. M., Bloom, J. S., Butler, N. R., et al. 2010, MNRAS, 401, 963 [NASA ADS] [CrossRef] [Google Scholar]
- LIGO Scientific Collaboration (Virgo Collaboration, Monitor, F. G.-R. B., & INTEGRAL) 2017, ApJ, 848, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Littlejohns, O. M., Tanvir, N. R., Willingale, R., et al. 2013, MNRAS, 436, 3640 [NASA ADS] [CrossRef] [Google Scholar]
- Lyman, J. D., Levan, A. J., Tanvir, N. R., et al. 2017, MNRAS, 467, 1795 [NASA ADS] [Google Scholar]
- Lyman, J. D., Lamb, G. P., Levan, A. J., et al. 2018, Nature, 88 [Google Scholar]
- MacFadyen, A. I., & Woosley, S. E. 1999, ApJ, 524, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Marchesini, D., van Dokkum, P., Quadri, R., et al. 2007, ApJ, 656, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Berger, E., Fong, W., et al. 2012, ApJ, 756, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Zaninoni, E., Bernardini, M. G., et al. 2013, MNRAS, 428, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Alexander, K. D., Xie, X., et al. 2018, ApJ, 856, L18 [NASA ADS] [CrossRef] [Google Scholar]
- McBreen, S., Krühler, T., Rau, A., et al. 2010, A&A, 516, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milvang-Jensen, B., Fynbo, J. P. U., Malesani, D., et al. 2012, ApJ, 756, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Modigliani, A., Goldoni, P., Royer, F., et al. 2010, Proc. SPIE, 7737, 773728 [Google Scholar]
- Nakar, E. 2007, Phys. Rep., 442, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Nissanke, S., Holz, D. E., Hughes, S. A., Dalal, N., & Sievers, J. L. 2010, ApJ, 725, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. P., & Bonnell, J. T. 2006, ApJ, 643, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Nysewander, M., Fruchter, A. S., & Pe’er, A. 2009, ApJ, 701, 824 [NASA ADS] [CrossRef] [Google Scholar]
- O’Shaughnessy, R., Belczynski, K., & Kalogera, V. 2008, ApJ, 675, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Oyarzún, G. A., Blanc, G. A., González, V., Mateo, M., & Bailey, J. I. 2017, ApJ, 843, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Papovich, C., Dickinson, M., & Ferguson, H. C. 2001, ApJ, 559, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Levan, A. J., Tanvir, N. R., et al. 2013, ApJ, 778, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Krühler, T., Schulze, S., et al. 2016, ApJ, 817, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postnov, K. A., & Yungelson, L. R. 2014, LRR, 17, 3 [Google Scholar]
- Richard, J., Kneib, J.-P., Ebeling, H., et al. 2011, MNRAS, 414, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Rosswog, S., Feindt, U., Korobkin, O., et al. 2017, Class. Quantum Gravity, 34, 104001 [Google Scholar]
- Safarzadeh, M., & Scannapieco, E. 2017, MNRAS, 471, 2088 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, T., Barthelmy, S. D., Baumgartner, W. H., et al. 2011, ApJS, 195, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, T., Troja, E., Aoki, K., et al. 2013, ApJ, 766, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Savchenko, V., Ferrigno, C., Kuulkers, E., et al. 2017, Astrophys. J. Lett., 848, L15 [Google Scholar]
- Schady, P., Page, M. J., Oates, S. R., et al. 2010, MNRAS, 401, 2773 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, S., Krühler, T., Leloudas, G., et al. 2018, MNRAS, 473, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- Selsing, J., Malesani, D., Goldoni, P., et al. 2018, A&A, submitted [Google Scholar]
- Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Starling, R. L. C., Willingale, R., Tanvir, N. R., et al. 2013, MNRAS, 431, 3159 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Tanvir, N. R., Levan, A. J., Fruchter, A. S., et al. 2013, Nature, 500, 547 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thöne, C. C., Campana, S., Lazzati, D., et al. 2011, MNRAS, 414, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Tunnicliffe, R. L., Levan, A. J., Tanvir, N. R., et al. 2014, MNRAS, 437, 1495 [NASA ADS] [CrossRef] [Google Scholar]
- van de Voort, F., Quataert, E., Hopkins, P. F., Kere, D., & Faucher-Giguere, C.-A. 2014, MNRAS, 447, 140 [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [CrossRef] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wallner, A., Faestermann, T., Feige, J., et al. 2015, Nat. Commun., 6, 5956 [NASA ADS] [CrossRef] [Google Scholar]
- Wanderman, D., & Piran, T. 2015, MNRAS, 448, 3026 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, D., Zafar, T., Andersen, A. C., et al. 2013, ApJ, 768, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, B., Jin, Z.-P., Li, X., et al. 2015, Nat. Commun., 6, 7323 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zhang, B., Zhang, B.-B., Virgili, F. J., et al. 2009, ApJ, 703, 1696 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. FORS2 R-band imaging of the field of GRB 111117A with the X-shooter slit overlaid. The slit position represents four epochs of spectroscopic observations taken at similar position angles. The corresponding photometry is shown in Fig. 3. The blue asterisk indicates the GRB position (RA, Dec) (J2000) = (00h50m46.264s, + 23°00′39″.98) as derived from the Chandra observations in Sakamoto et al. (2013). |
| In the text | |
 |
Fig. 2. Two-dimensional images of the emission lines corresponding to Lyα, [O II]λ3727, Hβ, [O III]λ4959, [O III]λ5007, and Hα. The location of bright skylines are marked by blue boxes. The locations of the emission lines are indicated with red ellipses. Because the host is observed in nodding mode, negative images of the emission lines appear on both sides in the spatial direction. For the upper left panel containing Lyα, the systemic redshift position of Lyα is marked by a yellow vertical dashed line. The red part of the [O II]λ3727-doublet is affected by atmospheric absorption. |
| In the text | |
 |
Fig. 3. Best-fit SED to the derived photometry. The detection of Lyα is predicted from the SED fit and confirmed by the spectroscopic observations. Overplotted in gray is the observed spectrum, binned by 6 Å for presentation purposes. Slit losses have been corrected for based on the average seeing of the observations, as confirmed by the comparison with the photometry. The blue dashed curve is the corresponding error spectrum, smoothed for presentation purposes. The spectral gaps at 5500 Å and 10000 Å are due to the merging of the arms. |
| In the text | |
 |
Fig. 4. Mosaic showing all used imaging. The host of GRB 111117A is marked by a red circle with a 2″̣0 radius. This is the same size as the aperture used to derive the photometry. Each panel is 20″ in size, north is up, east is left. Worth noting is the relative depth of the GMOS-N and FORS2 z-band images. For reference, the object located to the southeast of the host and marked with a blue dashed circle has an extinction corrected magnitude of 23.11 ± 0.09 (23.10 ± 0.18) in the FORS2 (GMOS-N) z-band. |
| In the text | |
 |
Fig. 5. Rest-frame XRT light curve of GRB 111117A, compared to the general population of XRT light curves of GRBs. The gray shaded region is a compilation of long GRB light curves (Evans et al. 2007, 2009), where the color represents density. The light blue lines are sGRB light curves from bursts with duration of T90 ≲ 2 s and those that were classified as short in Kann et al. (2011), Berger (2014) and D’Avanzo et al. (2014). The thick green line is GRB 111117A. Despite the remarkably high redshift, the luminosity is comparable to the bulk of the short burst population, and subluminous compared to the lGRB population. The inset shows the X-ray luminosity distributions of sGRBs and lGRBs at 10 ks, indicated by the vertical dashed line in the main panel. |
| In the text | |
 |
Fig. 6. Rest frame, X-ray derived equivalent hydrogen column density of GRB 111117A compared to complete samples of both long and short populations of GRBs. The sample of lGRBs from Arcodia et al. (2016) is shown in red, where detections are also shown with a kernel density estimate of the points, and the limits on NH,X are shown with arrows. The complete sample of sGRB by D’Avanzo et al. (2014) is shown in blue, where again the limits are indicated by arrows. Marginalizations over both axes are shown on the right and at the top of the plot, where the limits are shown as semi-transparent bars and detections as solid ones. The red curves in the marginalization plots are again the kernel density estimates of the Arcodia et al. (2016) sample. |
| In the text | |
 |
Fig. 7. Constraints on the initial progenitor separation, given binary constituent masses. As can be seen, a heavier system will inspiral faster, leading to a weaker constraint on the initial separation of the binary. The most probable value, the 68% and 98% posterior predictive intervals of the NS binary mass distribution from Kiziltan et al. (2013), are shown with the dashed ellipses, which corresponds to a constraint on a maximum initial separation of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.