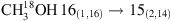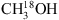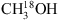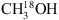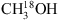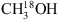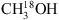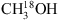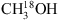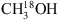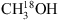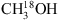| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 33 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201832757 | |
| Published online | 19 July 2018 | |
Low levels of methanol deuteration in the high-mass star-forming region NGC 6334I
1
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: bogelund@strw.leidenuniv.nl
2
National Radio Astronomy Observatory, 520 Edgemont Rd, Charlottesville, VA 22903, USA
3
Sackler Laboratory for Astrophysics, Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
4
INAF, Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
5
Jet Propulsion Laboratory, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
6
Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
7
Max-Planck Institut für Extraterrestrische Physik, Giessenbachstr. 1, 85748 Garching, Germany
Received:
2
February
2018
Accepted:
31
March
2018
Context. The abundance of deuterated molecules in a star-forming region is sensitive to the environment in which they are formed. Deuteration fractions, in other words the ratio of a species containing D to its hydrogenated counterpart, therefore provide a powerful tool for studying the physical and chemical evolution of a star-forming system. While local low-mass star-forming regions show very high deuteration ratios, much lower fractions are observed towards Orion and the Galactic centre. Astration of deuterium has been suggested as a possible cause for low deuteration in the Galactic centre.
Aims. We derive methanol deuteration fractions at a number of locations towards the high-mass star-forming region NGC 6334I, located at a mean distance of 1.3 kpc, and discuss how these can shed light on the conditions prevailing during its formation.
Methods. We use high sensitivity, high spatial and spectral resolution observations obtained with the Atacama Large Millimeter/ submillimeter Array to study transitions of the less abundant, optically thin, methanol-isotopologues: 13CH3OH, CH318OH, CH2DOH and CH3OD, detected towards NGC 6334I. Assuming local thermodynamic equilibrium (LTE) and excitation temperatures of ~120–330 K, we derive column densities for each of the species and use these to infer CH2DOH/CH3OH and CH3OD/CH3OH fractions.
Results. We derive column densities in a range of (0.8–8.3) × 1017 cm−2 for 13CH3OH, (0.13–3.4) × 1017 cm−2 for CH318OH, (0.03–1.63) × 1017 cm−2 for CH2DOH and (0.15–5.5) × 1017 cm−2 for CH3OD in a ~1″ beam. Interestingly, the column densities of CH3OD are consistently higher than those of CH2DOH throughout the region by factors of 2–15. We calculate the CH2DOH to CH3OH and CH3OD to CH3OH ratios for each of the sampled locations in NGC 6334I. These values range from 0.03% to 0.34% for CH2DOH and from 0.27% to 1.07% for CH3OD if we use the 13C isotope of methanol as a standard; using the 18 O-methanol as a standard, decreases the ratios by factors of between two and three.
Conclusions. All regions studied in this work show CH2DOH/CH3OH as well as CH2DOH/CH3OD values that are considerably lower than those derived towards low-mass star-forming regions and slightly lower than those derived for the high-mass star-forming regions in Orion and the Galactic centre. The low ratios indicate a grain surface temperature during formation ~30 K, for which the efficiency of the formation of deuterated species is significantly reduced. Therefore, astration of deuterium in the Galactic centre cannot be the explanation for its low deuteration ratio but rather the high temperatures characterising the region.
Key words: astrochemistry / methods: observational / stars: protostars / ISM: individual objects: NGC 6334I / submillimeter: ISM
© ESO 2018
1. Introduction
The abundance of deuterium (D) formed in the Big Bang sets the primordial D/H in the universe. As stars form and start processing D in their interiors, the deuterium abundance should drop if no other source of D exists. The best estimate of the cosmic D/H is therefore obtained by observing environments with little star formation and chemical processing such as the diffuse interstellar medium (ISM) for which D/H is ~(1.5–2.0) × 10−5 (Linsky 2006; Prodanović et al. 2010). On the other hand, environments with high star-formation rates would be expected to show lower D/H fractionation ratios as a consequence of astration, that is the processing of D in stellar interiors, and a generally higher temperature. This however, contradicts observations of molecules in both high and low-mass star-forming regions that not only show D/H values which are orders of magnitude higher than that of the ISM, but also display multiply deuterated species. An example of a source exhibiting such high deuterium fractionation is the well-studied low-mass protostellar binary IRAS 16293–2422 (hereafter IRAS 16293; van Dishoeck et al. 1995; Ceccarelli et al. 1998). This source is especially interesting because it was the first source towards which both doubly as well as triply-deuterated methanol was detected (Parise et al. 2002, 2004). More recently, IRAS 16293 has been studied by Jørgensen et al. (2017) who have characterised the isotope composition of a number of complex organic molecules. They derived D/H values, that is the column density ratio of isotopologues with respect to their hydrogenated counterparts including the statistical correction for the location of the substituted deuterium, for all detected species in the range 2–8%. Specifically, the D to H ratio of methanol (CH3OH) is found to be ~2%. In addition, the detection of singly and doubly-deuterated formaldehyde (H2CO) and methanol towards seven other low-mass protostars, with deuteration fractions similar to those observed towards IRAS 16293, is reported by Parise et al. (2006). For high-mass star-forming regions the most thorough studies of deuterated species have been carried out towards the hot cores located in the Galactic centre and the Orion Complex. For Sagittarius B2 (Sgr B2), Belloche et al. (2016) report D/H values of 0.38% for acetonitrile (CH3CN) and (0.05–0.12)% for the tentative detections of CH3CH2CN, HC3N and CH3OH. Approximately the same low levels of deuteration were found by Neill et al. (2013), who studied ammonia (NH3), formaldehyde and methanol towards Orion KL and find D/H ~(0.2–0.8)% towards the compact ridge and hot core regions. Similar levels of deuterium in methanol are found by Peng et al. (2012).
While these observations clearly illustrate that deuterated species, including CH3OH, are enhanced in star-forming regions, the explanation of how the various ratios came to be remains incomplete. For the low-mass objects, the high deuteration ratios can, for the most part, be explained by gas-grain astrochemical models where high densities and low dust temperatures allow simple deuterated species to build up rapidly in precursor dark cores (Taquet et al. 2012). In the case of Sgr B2 however, the low deuteration fractions are attributed to the combined effects of astration and a less efficient deuteration process at the high temperatures characterising the Galactic centre. In order to quantify which of these processes influence the deuteration fractionation more, observations of other high-mass star-forming regions, located away from the Galactic centre, are essential.
Deuterium fractionation of simple interstellar molecular species was first studied in detail by Watson (1976) who argued that the large D/H values, especially present in DCN and DCO+, can be understood as a result of ion-molecule exchange reactions in the gas and the difference in zero-point vibrational energies of the hydrogen versus deuterium-containing molecules. The observed deuterated species are then the end product of a chain of reactions starting with the formation of H2D+ from 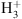 and HD, reacting with neutral molecules to form deuterated ions and subsequently recombining with electrons. This recombination also results in enhanced atomic D/H in the gas at low temperatures, which increases even more when CO, the main destroyer of
and HD, reacting with neutral molecules to form deuterated ions and subsequently recombining with electrons. This recombination also results in enhanced atomic D/H in the gas at low temperatures, which increases even more when CO, the main destroyer of 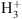 and H2D+, is frozen out on grains (Roberts et al. 2003). As pointed out by Tielens (1983), this enhanced atomic D/H in the gas can be transferred to those molecules that are primarily formed by hydrogenation on grain surfaces. Key examples are H2CO and CH3OH, which both result from the hydrogenation of CO. Thus, the abundances of these deuterated molecules are good tracers of the physical conditions in the gas.
and H2D+, is frozen out on grains (Roberts et al. 2003). As pointed out by Tielens (1983), this enhanced atomic D/H in the gas can be transferred to those molecules that are primarily formed by hydrogenation on grain surfaces. Key examples are H2CO and CH3OH, which both result from the hydrogenation of CO. Thus, the abundances of these deuterated molecules are good tracers of the physical conditions in the gas.
The process of deuteration at low temperatures has also been studied in the laboratory. In particular, Nagaoka et al. (2005) have shown that grain-surface H-D abstraction-addition reactions in solid methanol can account for the methanol D/H values derived from observations. They also note that if the gaseous atomic D/H is higher than 0.1, deuterated methanol may be formed directly through successive hydrogenation or deuteration of CO.
The focus of this work is on methanol, especially its isotopologues 13CH3OH, CH318OH and the two single deuterated species CH2DOH and CH3OD. As described above, methanol is formed primarily on the surface of dust grains (Watanabe & Kouchi 2002; Geppert et al. 2005; Fuchs et al. 2009) and therefore presents a good tracer of the chemistry of interstellar ice. In addition, if formed in environments with high gaseous atomic D/H, methanol will be deuterated. Deuteration levels can therefore be considered a fossil record of the chemical composition not only of the ice, but also of the gas, characterising the region in which it was formed, with the highest ratios associated with the lowest temperatures. However, in order to deduce accurate deuteration ratios, it is critical that the transitions used to derive column densities are optically thin. If this is not the case, deuterium fractions are likely to be overestimated since the lines of the more abundant hydrogenated species are generally optically thick, resulting in underestimated values. To ensure transitions are optically thin, one generally needs to target lines that are weak, that is to say have low Einstein Aij values. Observations of such weak lines have however presented a challenge since line surveys have, for the most part, been conducted using single dish telescopes which are, by and large, less sensitive when compared with interferometric observations. These observations have therefore mostly targeted the brightest lines which may in many cases be optically thick and therefore result in deuteration ratios which are higher than is actually the case. With the unique sensitivity and resolving power offered by the Atacama Large Millimeter/submillimeter Array (ALMA), this is changing. With ALMA it has become possible to probe molecular transitions that are both weaker and are emitted from objects less bright than ever before. Consequently, the field of molecular line surveys and analysis has entered a new epoch where column density determinations no longer, or to a much lesser extent, suffer from misinterpretation due to the increased access to transitions in the optically thin regime.
In this work we focus on NGC 6334I, a region of active high-mass star-formation in the giant molecular cloud complex NGC 6334, also referred to as the Cat’s Paw Nebula. The complex is located in the Scorpius constellation in the southern hemisphere. The region constitutes six main dense cores, identified as discrete continuum sources in the far-infrared, labelled with Roman numerals I–VI (McBreen et al. 1979). Later, an additional, very low temperature source, NGC 6334I(N) was identified ~2′ north of NGC 6334I (Gezari 1982). The distance to the NGC 6334 site has commonly been cited as (1.7 ± 0.3) kpc (Russeil et al. 2012) but recent work on H2O and CH3OH masers associated with the star-forming complex, carried out by Reid et al. (2014) and Chibueze et al. (2014), place the region closer, at distances of 1.34 and 1.26 kpc respectively. Here we will assume a mean distance of 1.3 kpc, corresponding to a galactocentric distance, dGC, of ~7.02 kpc. With a synthesised beam of the observations of 1″.00 × 0″.74, this allows us to probe NGC 6334I at scales of ~1300 AU. NGC 6334I is complex both in structure and composition and very rich in molecular lines (McCutcheon et al. 2000), but has the great advantage of lines with widths of only ~3 km s−1 (as compared to ~20 km s−1 for Sgr B2), reducing the problem of line confusion considerably. The molecular diversity of the region is demonstrated by Zernickel et al. (2012) who use the Herschel Space Observatory and Submillimeter Array (SMA) to investigate ~4300 emission and absorption lines belonging to 46 different molecules and their isotopologues.
NGC 6334I is comprised of multiple hot cores, some of which are themselves multiples. This multiplicity was shown by Brogan et al. (2016) who recently presented an in-depth, high-resolution continuum study of the morphology of the site. In addition to the four previously known millimetre sources associated with the region, labelled MM1-4 and identified by Hunter et al. (2006), Brogan et al. (2016) identify six new sources: five at millimetre wavelengths, MM5-9, and one at centimetre wavelengths, CM2, all within a radius of ~10″ corresponding to 0.06 pc at the distance of the site. Another centimetre source, CM1, is identified 18″ (~0.1 pc) west of the main cluster. In addition to molecular lines and the far-IR and radio continuum sources, indicative of cool, dense and dusty cores, NGC 6334I displays a variety of other star-formation tracers including ultra-compact HII regions and outflows (see e.g. Persi et al. 1996; Leurini et al. 2006; Qiu et al. 2011, and references therein).
The paper is structured in the following way: Sect. 2 introduces the observations, the data reduction process and the analysis method. In Sect. 3 the process of identifying and fitting individual lines and estimating molecular column densities is presented. Section 4 discusses the deuteration levels derived and compare these to those obtained for other objects as well as the predictions from astrochemical models. Finally, Sect. 5 summarises our findings.
2. Observations and analysis method
2.1. Observations
The observations have been described in detail in McGuire et al. (2017), while the analysis and reduction procedures are described in detail in Brogan et al. (2016) and Hunter et al. (2017), and as such only a brief discussion is presented here. Two sets of observations are used. The primary dataset (ALMA Project 2015.1.00150.S) was taken in Cycle 3 at ~1″ resolution (~1300 AU at the distance of NGC 6334I), centred on 302 GHz, and covering ~3 GHz of total bandwidth with an rms noise of ~500 mK. The second dataset (ALMA Project 2015.A.00022.T) was also observed in Cycle 3 but at ~0″.2 (260 AU) resolution, centred around four frequency windows at approximately 281, 293, 338, and 350 GHz each ~3.75 GHz wide, and with an rms noise of ~620 mK and ~900 mK in the lower and higher frequency ranges, respectively. In each case, the most line-free continuum channels were selected and used for both self calibration and continuum subtraction.
2.2. Analysis method
Nine spectra are extracted from the data cube. Each spectrum represents the average of a 1″.00 × 0″.74 region, equivalent to the area of the synthesised beam. The coordinates of the central pixel of each of the regions are summarised in Table 1 and the locations shown in Fig. 1. The positions are chosen so they present a fairly homogeneous sampling of the continuum sources MM1, located in the northern part of NGC 6334I, MM2, located in the western part of the region, and MM3, located in the southern part of the region, as well as their surroundings.
 |
Fig. 1. Velocity integrated intensity map of the 13CH3OH transition at 303.692 GHz with the 1 mm continuum image overlaid in black contours (levels are [10, 20, 40, 80, 160]σ with σ = 0.02 Jy beam−1). The locations at which spectra have been extracted are marked in blue for MM1, green for MM2 and red for MM3. The synthesised beam (~1300 × 962 AU) is shown in the bottom left corner. |
For our line analysis, the software package CASSIS1 is used. CASSIS is a tool for spectral line identification and analysis which reads a list of line data, including rest frequency, ν, upper state energy, Eup, and Einstein Aij coefficients. Once a line has been identified, the line analysis tool is used to produce a synthetic spectrum by providing CASSIS with a number of parameters: excitation temperature, Tex [K], column density of the species, Ns [cm−2], source velocity, υLSR [km s−1], line width, FWHM [km s−1], and angular size of the emitting region (which is assumed to be equal to the area of the synthesised beam), θs [″]. For line input the Jet Propulsion Laboratory (JPL2) and Cologne Database for Molecular Spectroscopy (CDMS3) databases are used.
For the analysis of 13CH3OH and 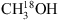 , the CDMS database is used. These entries include the ground and first vibrational states for 13CH3OH and the ground, first and second vibrational states for
, the CDMS database is used. These entries include the ground and first vibrational states for 13CH3OH and the ground, first and second vibrational states for 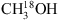 . For the analysis of CH2DOH the JPL datatbase is used. The line intensities in this list are based on the method described by Pearson et al. (2012). The JPL catalogue warns that extreme caution should be taken in determining columns (or concentrations) of CH2DOH directly from b-type and c-type transitions as significant errors can occur, while the a-type transitions are more reliable4. The symmetry of the transitions are defined as follows: ΔKa = even, ΔKc = odd for a-type, ΔKa = odd, ΔKc = odd for b-type and ΔKa = odd, ΔKc = even for c-type (Pearson et al. 2012). We optimise our CH2DOH fit to the 12(2,11)→12(1,12) b-type transition at 301.514 GHz (see Sect. 3.3) and use an updated value for the base 10 logarithm of the integrated line intensity at 300 K for this transition of −3.84 ± 0.2 nm2 MHz (John Pearson, priv. comm.). Also, since the CH2DOH entry only includes the ground vibrational state, a vibrational correction factor of 1.25 has been applied to all listed values (Holger Müller, priv. comm.). To model CH3OD we use the summary of CH3OD frequencies reported by Walsh et al. (2000), the line strengths reported by Anderson et al. (1988, 1933) and the partition function of
. For the analysis of CH2DOH the JPL datatbase is used. The line intensities in this list are based on the method described by Pearson et al. (2012). The JPL catalogue warns that extreme caution should be taken in determining columns (or concentrations) of CH2DOH directly from b-type and c-type transitions as significant errors can occur, while the a-type transitions are more reliable4. The symmetry of the transitions are defined as follows: ΔKa = even, ΔKc = odd for a-type, ΔKa = odd, ΔKc = odd for b-type and ΔKa = odd, ΔKc = even for c-type (Pearson et al. 2012). We optimise our CH2DOH fit to the 12(2,11)→12(1,12) b-type transition at 301.514 GHz (see Sect. 3.3) and use an updated value for the base 10 logarithm of the integrated line intensity at 300 K for this transition of −3.84 ± 0.2 nm2 MHz (John Pearson, priv. comm.). Also, since the CH2DOH entry only includes the ground vibrational state, a vibrational correction factor of 1.25 has been applied to all listed values (Holger Müller, priv. comm.). To model CH3OD we use the summary of CH3OD frequencies reported by Walsh et al. (2000), the line strengths reported by Anderson et al. (1988, 1933) and the partition function of 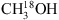 (from the CDMS database) which includes the vibrational levels.
(from the CDMS database) which includes the vibrational levels.
Because CH3OH is a very abundant species in star-forming regions, the lines of the primary 12C-isotope are optically thick and cannot be used to derive column densities and excitation temperatures. Fortunately, many lines of the isotopologues 13CH3OH, 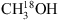 , CH2DOH and CH3OD remain in the optically thin regime, making column density determination of these species possible. We identify a total of 15 transitions belonging to the methanol isotopologues in the covered frequency range: eight of these belong to 13CH3OH, four to
, CH2DOH and CH3OD remain in the optically thin regime, making column density determination of these species possible. We identify a total of 15 transitions belonging to the methanol isotopologues in the covered frequency range: eight of these belong to 13CH3OH, four to 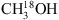 , one to CH2DOH and two to CH3OD. The transitions are summarised in Table 2. Since the frequency range covered is limited to ~3 GHz (301.180–304.165 GHz) only a few transitions of each species are covered. This complicates the definite identification of lines, especially in the case of
, one to CH2DOH and two to CH3OD. The transitions are summarised in Table 2. Since the frequency range covered is limited to ~3 GHz (301.180–304.165 GHz) only a few transitions of each species are covered. This complicates the definite identification of lines, especially in the case of 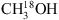 , CH2DOH and CH3OD for which many lines are either very weak or blended to an extent that it is impossible to distinguish the contribution from individual molecular species.
, CH2DOH and CH3OD for which many lines are either very weak or blended to an extent that it is impossible to distinguish the contribution from individual molecular species.
In order to verify the presence of these species in NGC 6334I, a second set of data, covering a larger range of frequencies, is also consulted (see Sect. 2). Based on transitions in these data the presence of the less abundant CH3OH-isotopologues is confirmed. However, since these data are of higher angular resolution (~0″.2) emission is resolved out and we are not able to constrain the column density of either of the deuterated species better than from our primary data set. The upper limits for CH2DOH (which are similar for a- and b-type transitions covered) and CH3OD as well as the column densities for 13CH3OH and 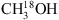 based on these data are consistent with the values derived based on our primary data set. The data are presented in Appendix A but will not be discussed further in the main manuscript.
based on these data are consistent with the values derived based on our primary data set. The data are presented in Appendix A but will not be discussed further in the main manuscript.
For each methanol line candidate we carefully examine transitions belonging to other species (for which the spectroscopy is known and listed in either of the databases mentioned above) at similar frequencies to ensure lines are not incorrectly assigned. In the first step, all species which have not previously been detected in space are excluded. Secondly, species are excluded based on Einstein Aij coefficient and upper state energy. For the remaining blending candidates we investigate if any additional transitions are covered in the data range and if so, whether these can provide additional constraints. If the blending candidates are isotopologues, we search for transitions belonging to the parent species and ensure that column densities are consistent. The process of line assignment and analysis of potential blended transitions will be discussed in detail in Sects. 3.1–3.4.
Assuming LTE and optically thin lines synthetic spectra are created for each methanol isotopologue. Firstly, the excitation temperatures and 13CH3OH column densities for each region are derived by creating a grid of models, with Tex ranging between 50 and 350 K and N ranging between 5 × 1016 and 5 × 1019 cm−2, and selecting the model with the minimal χ2 as the best fit. The 13CH3OH lines are fitted first because these lines are the most numerous and span the largest range of upper state energies. Secondly, the column densities of the remaining methanol isotopologues are optimised keeping the excitation temperature fixed at the value of the best-fit 13C-methanol model. The transitions of each methanol isotopologue, as well as the blending species, are modelled separately, and summed to obtain a full spectrum for each of the nine regions. These spectra are shown in Figs. B.1–B.3.
Finally, to estimate the 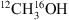 column density used to calculate the deuterium fraction for each spectral region, a 12C/13C value of 62 and a 16O/18O value of 450 is adopted, both derived assuming dGC ~7.02 kpc and the relations for 12C/13C and 16O/18O reported by Milam et al. (2005) and Wilson (1999) respectively.
column density used to calculate the deuterium fraction for each spectral region, a 12C/13C value of 62 and a 16O/18O value of 450 is adopted, both derived assuming dGC ~7.02 kpc and the relations for 12C/13C and 16O/18O reported by Milam et al. (2005) and Wilson (1999) respectively.
Summary of regions and column densities.
Summary of detected lines.
3. Results
3.1. 13CH3OH
Eight transitions of 13CH3OH are detected towards NGC 6334I. For each of these, a synthetic spectrum is created and optimised simultaneously to obtain the best-fit values for Tex and N. However, the same range of frequencies which host the 13C-methanol lines are also known to be occupied by a number of methyl formate (CH3OCHO) transitions. Especially the 13CH3OH transitions at 302.590, 302.882, 303.319 and 303.865 GHz are overlapping with transitions of CH3OCHO. Fortunately, since many transitions of this species are covered in the spectral range, the column density of CH3OCHO can be constrained to a range of (0.6–2.5) × 1017 cm−2 in our beam for all regions. While the contribution from CH3OCHO to the 13CH3OH line fits does not change the value of the best-fit 13CH3OH column density, likely because the upper state energy of these transitions are high, ~700 K, as compared with those of the affected 13CH3OH lines, it is included for completeness. Figure 2 shows the synthetic spectra of the best fit models to 13CH3OH, CH3OCHO and the combination of the two for the transition at 302.590 GHz detected towards each of the regions. Despite this transition having the largest contribution from CH3OCHO, it is evident that at the abundances of CH3OCHO present in NCG 6334I, its effect on the 13CH3OH line is small and it is therefore reasonable to assume that the observed peak in the data at 302.590 GHz is due mainly to 13CH3OH.
 |
Fig. 2. 13CH3OH 10(0,10)→9(1,8) transition at 302.590 GHz (indicated by dash-dotted lines) detected towards each region. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of 13CH3OH without blending, i.e., excluding the contribution from CH3OCHO (including the contribution from CH3OCHO does not change the 13CH3OH column density of the best-fit model). Yellow lines represent the modelled spectra of CH3OCHO and magenta lines represent the sum of the 13CH3OH and CH3OCHO spectra. |
The best-fit column density and excitation temperature for 13CH3OH for each of the regions are listed in Table 1. The values range about an order of magnitude, with the lowest values associated with MM3 I and II, (0.8–0.9) × 1017 cm−2, while the highest, ~8.3 × 1018 cm−2, are found in MM1 I and III. For the remaining regions the values span a range of (1.3–7.4) × 1018 cm−2.
Zoom-ins of the spectra showing the remaining 13CH3OH lines can be found in Appendix C. Generally the single-Tex, single-N models reproduce the data well. It should be noted however, that the transition with the lowest Aij ~10−6 s−1 at 303.865 GHz is consistently under produced by the models as compared with the data by factors of between three and six. The same is true for the line at 302.166 GHz towards the regions around MM1. The reason for this could either be uncertainties in the spectroscopic values for these particular transitions, or that the lines are blended with some unknown species, the spectroscopy of which is not included in either of the JPL or CDMS databases. Alternatively, the explanation could be that some of the transitions which we assume to be optically thin are in fact slightly thick, resulting in underestimated column densities. To test this, we optimise the column density and excitation temperature to the transitions at 302.166 and 303.865 GHz. Doing so, we find that for the modelled spectra to reproduce the data at these frequencies, the column densities need to be higher by factors of between five and ten, as compared to the best-fit column density when fitting to all lines, resulting in the remaining transitions being largely saturated. To improve the fits the individual sources would need to be modelled using an excitation model taking both density and temperature gradients into account. Such a full excitation model would potentially make the saturated lines appear more Gaussian.
3.2.
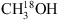
Assuming a 12C/13C value of 62 and a 16O/18O value of 450 implies that the 13CH3OH to 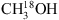 column density ratio is approximately a factor of seven. Adopting this ratio and using the best-fit column density values for 13CH3OH, the majority of the modelled
column density ratio is approximately a factor of seven. Adopting this ratio and using the best-fit column density values for 13CH3OH, the majority of the modelled 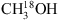 lines appear weaker as compared with the data by about a factor of two. Indeed, when optimising the
lines appear weaker as compared with the data by about a factor of two. Indeed, when optimising the 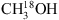 column density, assuming Tex to be the same as for 13CH3OH, the values are only factors of 2–3 lower than those of 13CH3OH. This result suggests that the 13CH3OH lines, which are assumed to be optically thin, are in fact partially optically thick, and therefore the derived column densities may be slightly underestimated, as discussed above.
column density, assuming Tex to be the same as for 13CH3OH, the values are only factors of 2–3 lower than those of 13CH3OH. This result suggests that the 13CH3OH lines, which are assumed to be optically thin, are in fact partially optically thick, and therefore the derived column densities may be slightly underestimated, as discussed above.
As in the case of 13CH3OH, the 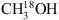 lines are also partly blended. Especially the line at 303.016 GHz overlaps with the transition from another molecular species: O13CS, although the slight shift in frequency of the O13CS line with respect to the line of
lines are also partly blended. Especially the line at 303.016 GHz overlaps with the transition from another molecular species: O13CS, although the slight shift in frequency of the O13CS line with respect to the line of 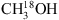 means that the observed peak in the data cannot be due purely to O13CS. Unfortunately no other lines of O13CS are covered in our frequency range and likewise only one line of the parent species, OCS, is in the data range. It is therefore difficult to constrain the contribution of O13CS to the blend from the data itself. Instead the column density for OCS derived by Zernickel et al. (2012) of 1.2 × 1018 cm−2 (assuming a source size of 2.5″) at Tex = 100 K and the 12C/13C value of 62 is used to estimate a column density of O13CS in NGC 6334I of 1.9 × 1016 cm−2. The modelled spectra of this transition as well as the data are shown in Fig. 3. A column density of O13CS of 1.9 × 1016 cm−2 is also consistent with the data in Appendix A; however, while the O13CS lines covered here are not overproduced at this column density, they cannot be better constrained due to blends. To derive the column density of
means that the observed peak in the data cannot be due purely to O13CS. Unfortunately no other lines of O13CS are covered in our frequency range and likewise only one line of the parent species, OCS, is in the data range. It is therefore difficult to constrain the contribution of O13CS to the blend from the data itself. Instead the column density for OCS derived by Zernickel et al. (2012) of 1.2 × 1018 cm−2 (assuming a source size of 2.5″) at Tex = 100 K and the 12C/13C value of 62 is used to estimate a column density of O13CS in NGC 6334I of 1.9 × 1016 cm−2. The modelled spectra of this transition as well as the data are shown in Fig. 3. A column density of O13CS of 1.9 × 1016 cm−2 is also consistent with the data in Appendix A; however, while the O13CS lines covered here are not overproduced at this column density, they cannot be better constrained due to blends. To derive the column density of 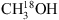 two sets of fits are preformed: the first excludes the O13CS-blended line and optimises the column density to the remaining three transitions (for which no known species listed in the databases contribute significantly to the data peaks), this value is used to set an upper limit for the column density. In the second fit, a contribution from O13CS is included and the
two sets of fits are preformed: the first excludes the O13CS-blended line and optimises the column density to the remaining three transitions (for which no known species listed in the databases contribute significantly to the data peaks), this value is used to set an upper limit for the column density. In the second fit, a contribution from O13CS is included and the 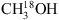 column density is optimised to all lines. The O13CS contribution is kept constant for all regions.
column density is optimised to all lines. The O13CS contribution is kept constant for all regions.
 |
Fig. 3.
|
The column densities derived for 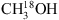 are listed in Table 1. For most regions, the difference between the fit purely considering
are listed in Table 1. For most regions, the difference between the fit purely considering 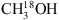 and the fit of
and the fit of 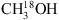 with a contribution from O13CS, is less than a factor of two. For regions MM1 III–V, MM2 II and MM3 however, the O13CS column density derived from Zernickel et al. (2012) results in modelled spectra that overshoot the data at the specific frequency. For these regions only the value for the pure-
with a contribution from O13CS, is less than a factor of two. For regions MM1 III–V, MM2 II and MM3 however, the O13CS column density derived from Zernickel et al. (2012) results in modelled spectra that overshoot the data at the specific frequency. For these regions only the value for the pure-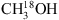 fit is reported. As is the case of 13CH3OH, the derived
fit is reported. As is the case of 13CH3OH, the derived 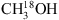 column densities are lowest in regions MM3 I and II, with values between (1.3–1.4) × 1016 cm−2. Slightly higher values, (0.32–1.5) × 1017 cm−2 and (0.41–2.4) × 1017 cm−2, are derived for regions MM2 I and II and MM1 II–V respectively. The highest value is again associated with region MM1 I, (2.0–3.4) × 1017 cm−2. Zoom-ins of all detected
column densities are lowest in regions MM3 I and II, with values between (1.3–1.4) × 1016 cm−2. Slightly higher values, (0.32–1.5) × 1017 cm−2 and (0.41–2.4) × 1017 cm−2, are derived for regions MM2 I and II and MM1 II–V respectively. The highest value is again associated with region MM1 I, (2.0–3.4) × 1017 cm−2. Zoom-ins of all detected 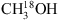 transitions can be seen in Appendix D. Again, the single density and temperature models reproduce the data well, keeping in mind that the main contributor to the peak at 303.016 GHz is O13CS.
transitions can be seen in Appendix D. Again, the single density and temperature models reproduce the data well, keeping in mind that the main contributor to the peak at 303.016 GHz is O13CS.
3.3. CH2DOH
For CH2DOH, the 12(2,11)→12(1,12) transition at 301.514 GHz is detected. Unfortunately, this line too is blended. We constrain the column density of the blending species, CH3NC, based on its characteristic double feature around 301.53 GHz, and derive values in the range (1.1–2.0) × 1014 cm−2 for the regions MM1 I–IV and MM2 I. As in the case of O13CS, these column densities are consistent with the data in Appendix A but cannot be further constrained. For the remaining regions, MM1 V, MM2 II and MM3 I–II, the data do not display any signs of CH3NC. Figure 4 shows the modelled spectra of CH2DOH, both with and without the contribution from the blending species, CH3NC, as well as the sum of the spectra of CH2DOH with blending and CH3NC. For the regions where CH3NC is detected, the difference between the values of the column density of CH2DOH fitted with and without the contribution from CH3NC is approximately a factor of three. No transitions of the more common isomer CH3CN are covered by the data, so the ratio of -CN/-NC cannot be constrained.
 |
Fig. 4. CH2DOH 12(2,11)→12(1,12) transition at 301.514 GHz (indicated by dash-dotted lines) detected towards each region. Frequencies are shifted to the rest frame of the individual regions. Blue and green lines represent the modelled spectra of CH2DOH with and without blending, i.e., including and excluding the contribution from CH3NC, respectively. Yellow lines represent the modelled spectra of CH3NC and magenta lines represent the sum of the spectra of CH2DOH with blending and CH3NC. |
The column densities derived for CH2DOH are listed in Table 1. We note that these include the vibrational correction and uncertainty on the line strength as discussed in Sect. 2.2. As regions MM1 V, MM2 II and MM3 I–II show no clear CH3NC feature, only the value for the pure CH2DOH fit is reported. As in the case of 13CH3OH and 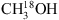 , the lowest CH2DOH column densities are detected towards regions MM3 I and II, both with values in the range of (3.0–6.0) × 1015 cm−2. Region MM2 II also displays low values, (4.0–9.0) × 1015 cm−2, while the values detected towards MM2 I are fairly high, (0.45–1.38) × 1017 cm−2. The highest column density is again detected towards MM1 I, (0.56–1.63) × 1017 cm−2, with the remain regions extracted from the area around MM1 show column densities spanning a range of about an order of magnitude, (0.08–1.10) × 1017 cm−2.
, the lowest CH2DOH column densities are detected towards regions MM3 I and II, both with values in the range of (3.0–6.0) × 1015 cm−2. Region MM2 II also displays low values, (4.0–9.0) × 1015 cm−2, while the values detected towards MM2 I are fairly high, (0.45–1.38) × 1017 cm−2. The highest column density is again detected towards MM1 I, (0.56–1.63) × 1017 cm−2, with the remain regions extracted from the area around MM1 show column densities spanning a range of about an order of magnitude, (0.08–1.10) × 1017 cm−2.
3.4. CH3OD
In addition to the transitions of CH2DOH, we have searched for lines belonging to CH3OD, for which two transitions, one at 303.296 GHz and one at 303.904 GHz (see summary by Walsh et al. 2000), are covered. To derive a column density for this isotopologue, our fits were optimised to the transition at 303.296 GHz. No other transitions in either the JPL nor the CDMS databases are listed at this frequency so the line in the data is considered to be purely due to CH3OD. The modelled spectra and data are shown in Fig. 5 and Appendix E and the derived column densities are listed in Table 1.
 |
Fig. 5. CH3OD 7(2+)→7(1,−) transition at 303.296 GHz (indicated by dash-dotted lines) detected towards each region. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of CH3OD. |
As in the case of CH2DOH, the lowest column densities of CH3OD are detected towards the regions MM3 I and II, with values in the range of (1.5–1.6) × 1016 cm−2. Regions MM2 II and MM1 V have similar column densities of 4.0 and 4.3 × 1016 cm−2 respectively. For the remaining regions, column densities in the range of (1.7–5.5) × 1017 cm−2 are derived. The highest value is again associated with region MM1 I. It is very interesting to note that the column densities derived for CH3OD are consistently higher than those derived for CH2DOH in all regions.
4. Methanol deuteration fractions
In the following sections the CH2DOH/CH3OH and CH2DOH/CH3OD values derived for the nine regions in NGC 6334I, as well as those derived for a number of other sources, will be discussed. These are summarised in Fig. 6 and listed in Table 3.
 |
Fig. 6. Column density ratio of CH2DOH to CH3OH (green) and CH3OD to CH3OH (blue) for NGC 6334I and other objects. For Orion KL the shaded bar indicates the range of ratios derived by Peng et al. (2012). For NGC 6334I shaded and filled bars indicate the ratios derived using the 13C and 18O isotopologues as base respectively. Error bars indicate the range of ratios derived with and without blending. For NGC 6334I MM1 only the region with the lowest (MM1 IV) and highest (MM1 I) ratios are plotted. References. (a)Jørgensen et al. (2017). (b)Bianchi et al. (2017). (c)Neill et al. (2013). (d)Peng et al. (2012). (e)Belloche et al. (2016). |
CH2DOH/CH3OH and CH3OD/CH3OH values derived from 13CH3OH or 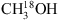 .
.
4.1. NGC 6334I
Using the column densities derived from the 13CH3OH, 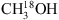 , CH2DOH and CH3OD transitions, we calculate the CH2DOH to CH3OH and CH3OD to CH3OH ratios for each of the spectral regions. These are listed in Table 3. The CH2DOH/CH3OH values range between (0.03–0.34)% and (0.03–0.20)% and the CH3OD/CH3OH values range between (0.27–1.07)% and (0.22–0.61)%, derived from 12C/13C and 16O/18O respectively. In the case of CH2DOH/CH3OH, both the lowest and the highest ratios are associated with region MM2, the lowest detected towards region MM1 II and the highest towards MM2 I. For the CH3OD to CH3OH ratio the lowest values are detected towards MM3 I and MM1 V while the highest is detected towards MM1 I. The mean values over all regions (including the vibrational correction and uncertainty on the line strength of CH2DOH) are 0.13% ± 0.06% and 0.53% ± 0.27% based on the 13C isotopologue and 0.08% ± 0.04% and 0.32% ± 0.09% based on the 18O isotopologue, for CH2DOH/CH3OH and CH3OD/CH3OH respectively. Based on these means the average CH3OD/CH3OH value is twice that of the average CH2DOH/CH3OH value. The CH2DOH to CH3OH and CH3OD to CH3OH ratios derived based on the 13C and 18O isotopologues agree within factors of approximately two for all regions.
, CH2DOH and CH3OD transitions, we calculate the CH2DOH to CH3OH and CH3OD to CH3OH ratios for each of the spectral regions. These are listed in Table 3. The CH2DOH/CH3OH values range between (0.03–0.34)% and (0.03–0.20)% and the CH3OD/CH3OH values range between (0.27–1.07)% and (0.22–0.61)%, derived from 12C/13C and 16O/18O respectively. In the case of CH2DOH/CH3OH, both the lowest and the highest ratios are associated with region MM2, the lowest detected towards region MM1 II and the highest towards MM2 I. For the CH3OD to CH3OH ratio the lowest values are detected towards MM3 I and MM1 V while the highest is detected towards MM1 I. The mean values over all regions (including the vibrational correction and uncertainty on the line strength of CH2DOH) are 0.13% ± 0.06% and 0.53% ± 0.27% based on the 13C isotopologue and 0.08% ± 0.04% and 0.32% ± 0.09% based on the 18O isotopologue, for CH2DOH/CH3OH and CH3OD/CH3OH respectively. Based on these means the average CH3OD/CH3OH value is twice that of the average CH2DOH/CH3OH value. The CH2DOH to CH3OH and CH3OD to CH3OH ratios derived based on the 13C and 18O isotopologues agree within factors of approximately two for all regions.
If the exchange of D into the CH3 and OH functional groups of methanol is equally efficient, the column density ratio of CH2DOH to CH3OD is expected to be equal to three. Interestingly, this is not the case for the regions presented here. Instead, we derive CH2DOH to CH3OD column density ratios of the order ~0.3 (not including the statistical correction factor which would further decrease the ratio by a factor of 3), lower by a factor of six as compared with the lower limit derived by Belloche et al. (2016) for Sgr B2 and factors of four and two as compared with the values derived for Orion KL by Neill et al. (2013) and Peng et al. (2012) respectively. This very low CH2DOH/CH3OD value is just opposite to values found for pre-stellar cores and low-mass protostars, where CH2DOH/CH3OD values up to ten are found (Bizzocchi et al. 2014; Parise et al. 2006), although consistent with the trend of lower ratios inferred for high mass protostars (Ratajczak et al. 2011). The low CH2DOH to CH3OD ratio implies that the deuteration of the OH functional group is more efficient than that of the CH3 group, or that D is more easily abstracted from the CH3 group rather than from the OH group.
Various chemical processes in the gas and ice that can cause the CH2DOH to CH3OD ratio to deviate from the statistical ratio of three are described in Ratajczak et al. (2011) and in Faure et al. (2015). In the gas phase these processes include protonation and dissociative recombination reactions which destroy CH3OD more efficiently than CH2DOH since all recombinations of 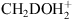 lead to CH2DOH while CH3OHD+ can recombine to either CH3OH or CH3OD with an equal branching ratio (Charnley et al. 1997). However the timescale needed to significantly alter the CH2DOH to CH3OD ratio through these reactions is likely too long, that is more than 105 years, when compared with the typical lifetime of a hot core. In the solid state, experiments carried out by Nagaoka et al. (2005) have shown that H/D substitution in solid CH3OH forms CH2DOH but no CH3OD. Also in the solid state, experiments by Ratajczak et al. (2009) and Faure et al. (2015) have shown that H/D exchanges can occur between water and methanol in warm ices (T ~ 120 K), but only on the OH functional group of methanol and not on the CH3 group. The processes mentioned above favour the formation of CH2DOH over that of CH3OD and consequently lead to an increase in CH2DOH/CH3OD rather than decrease. The low observed ratio therefore remains unexplained.
lead to CH2DOH while CH3OHD+ can recombine to either CH3OH or CH3OD with an equal branching ratio (Charnley et al. 1997). However the timescale needed to significantly alter the CH2DOH to CH3OD ratio through these reactions is likely too long, that is more than 105 years, when compared with the typical lifetime of a hot core. In the solid state, experiments carried out by Nagaoka et al. (2005) have shown that H/D substitution in solid CH3OH forms CH2DOH but no CH3OD. Also in the solid state, experiments by Ratajczak et al. (2009) and Faure et al. (2015) have shown that H/D exchanges can occur between water and methanol in warm ices (T ~ 120 K), but only on the OH functional group of methanol and not on the CH3 group. The processes mentioned above favour the formation of CH2DOH over that of CH3OD and consequently lead to an increase in CH2DOH/CH3OD rather than decrease. The low observed ratio therefore remains unexplained.
It should be noted however, that because the spectroscopy of CH2DOH is not well understood, the CH2DOH/CH3OD value derived may be higher. To better constrain the ratio, future studies are well-advised to target only a-type CH2DOH-transitions rather than b- or c-type transitions, for which the uncertainties on the line strength are not well-constrained, in addition to preferring weak, low Aij transitions, to ensure that lines are optically thin. A refinement of the accuracy of the column density of CH2DOH, will make it possible to investigate the coupling of CH2DOH/CH3OD with environment and chemical evolution. Therefore it may be advantageous to focus future observations on narrow bands with high spectroscopic resolution covering a few well-chosen transitions, rather than broader bands which, albeit potentially covering more lines, might make identification and analysis difficult due to uncertainties in spectroscopic values or blending with features of other species which may not be resolved.
As discussed in Sect. 2.2, the excitation temperature for each region is determined based on a minimal χ2 technique comparing a grid of models with the spectra. The excitation temperatures of the best-fit models range between ~120 and 330 K, the warmest regions associated with the MM1 core and the coldest with the MM3 core. We investigate the effect of varying the excitation temperature on the derived column densities and plot the ratios of CH2DOH to CH3OH and CH3OD to CH3OH as function of Tex in Fig. 7. From this analysis, it is evident that the spread in CH2DOH/CH3OH and CH3OD/CH3OH ascribed to different excitation temperatures (over all regions) is within a factor of two of the value derived for Tex = 200 K. For the individual regions, the variations in CH2DOH/CH3OH and CH3OD/CH3OH over the full range of excitation temperatures are within factors of between two and four. Therefore, it is reasonable to assume that the lines used to optimise our fits are optically thin at excitation temperatures of 100–400 K and consequently that our derived CH2DOH/CH3OH and CH3OD/CH3OH values do not depend critically on an exact determination of Tex. For each value of Tex we also calculate the ratio of the 13C- and 18O-methanol column densities. These ratios differ by less than a factor of two for MM2 and MM3 and a factor of four for MM1, verifying that the transitions are excited under similar conditions. The vibrational correction factor applied to CH2DOH has only little effect on this result.
 |
Fig. 7. Column density ratio as function of excitation temperature. Ratios are normalised to the value derived for Tex = 200 K. Magenta and blue lines represent the CH2DOH to CH3OH and CH3OD to CH3OH column density ratios respectively, while sold and dashed lines indicate the values derived assuming 12C/13C = 62 and 16O/18O = 450 respectively. Different regions are indicated by different markers. |
4.2. Comparison with other sources
Using ALMA, Belloche et al. (2016) investigated the deuterium fractionation of complex organic molecules towards the high mass star-forming region Sgr B2 in the Galactic central region. With the high spatial resolution observations, ~1.4″, they probe scales down to 0.06 pc (~11 620 AU assuming a distance ~8.3 kpc). They report a tentative detection of CH2DOH and derive a deuteration fraction for CH2DOH/CH3OH of 0.12%. Including the statistical weight of the location of the substituted deuterium this value becomes 0.04%. CH3OD is not detected, but an upper limit of 0.07% for CH3OD/CH3OH is reported. This is translated into a lower limit on the CH2DOH to CH3OD ratio of 1.8. Their CH3OH column density is based on LTE modelling of both the 13C and 18O methanol isotopologues. The authors note that the CH2DOH/CH3OH value they derive is lower than what is predicted by the chemical models of Taquet et al. (2014) and Aikawa et al. (2012) but may be explained by the high temperature that characterises the Galactic centre or result from an overall low abundance of deuterium in this region due to the high star formation rates.
For the high-mass star-forming regions in Orion, CH2DOH/CH3OH values are of the same order as for Sgr B2, ranging between (0.08–0.58)%, equivalent to (0.03–0.19)% when the statistical weights are accounted for. These values are derived by Peng et al. (2012), using observations from the IRAM Plateau de Bure Interferometer, and Neill et al. (2013), using data from Herschel/HIFI. In addition, Neill et al. (2013) report a CH3OD/CH3OH value of 0.5 ± 0.1% and a CH2DOH/CH3OD value of 1.2 ± 0.3. A slightly lower CH2DOH/CH3OD value of 0.7 ± 0.3 is reported by Peng et al. (2012). To derive CH3OH column densities Neill et al. (2013) and Peng et al. (2012) use slightly different approaches: Neill et al. (2013) assume a 12C/13C value of 60 and derive the CH3OH density based on transitions of 13CH3OH, while Peng et al. (2012) detect a number of E-type methanol transitions and derive the total CH3OH density assuming an A/E-type abundance of 1.2. Both studies of Orion KL probe scales which are smaller than those studied in Sgr B2: ~10″ and ~2″, corresponding to ~4140 AU and ~830 AU at the distance of Orion KL (~414 pc), for Neill et al. (2013) and Peng et al. (2012) respectively. However, since the beam dilution factor is higher in these studies, meaning that the area over which the emission is averaged is larger, the column density derived, assuming the total emission to be the same, is lower. Also, observations with larger beam sizes, which are more sensitive to large scale structures, generally probe regions of lower temperature, meaning that some molecules may be locked up in icy grain mantles, resulting in lower gas phase abundances. This combination of effects means that the derived column densities, as well as the inferred deuteration ratios, for Orion KL may in fact be higher, if derived from observations with higher angular resolution.
An example of such high-resolution observations are presented by Bianchi et al. (2017) who use 0.15″-resolution ALMA observations to study the Sun-like class 0 protostar HH 212, located in the Orion B cloud, on scales of ~70 AU. From transitions of 13CH3OH and CH2DOH they derive a CH2DOH/CH3OH value of (2.4 ± 0.4)%, equivalent to (0.8 ± 0.1)% after accounting for statistical weights, assuming a 12C/13C value of 70. This deuteration ratio is higher than what has been derived for highmass star-forming regions but lower by an order of magnitude as compared with observations (carried out with single dish telescopes) towards protostars in Perseus. Bianchi et al. (2017) argue that the lower deuteration ratio they find is consistent with the dust temperature of the Orion region being higher than that of the Perseus cloud.
Similarly to HH 212, the low-mass protostellar binary system IRAS 16293, located in the ρ Ophiuchi cloud complex, exhibits a CH2DOH to CH3OH ratio which is much higher than that of the high-mass star-forming regions. With the ALMA-PILS survey (see Jørgensen et al. 2016 for full PILS overview), sampling spatial scales of the order 0.5″, corresponding to 60 AU at the distance of the source (~120 pc), Jørgensen et al. (2017) derive a CH2DOH to CH3OH ratio of 7.1%, equivalent to 2.4% after corrections for statistical weights, assuming a 16O to 18O isotope ratio of 560 to estimate the CH3OH abundance, and a CH3OD to CH3OH ratio of 1.8% resulting in a CH2DOH/CH3OD value of 3.9.
Because of the comparable resolution and methods used, the methanol deuteration ratios derived for IRAS 16293, HH 212 and Sgr B2, may be directly compared to the ratios derived in this study. When doing so, the low levels of deuterium fractionation associated with the regions in NGC 6334I, as compared with the low-mass star-forming regions IRAS 16293 and HH 212, become very apparent (Table 3). It is also interesting to note that while our inferred CH2DOH/CH3OH values for NGC 6334I are similar to what has been derived by Belloche et al. (2016) for Sgr B2, the CH3OD/CH3OH values are higher by up to an order of magnitude as compared with the lower limit reported for Sgr B2.
4.3. Comparison with models
In an effort to better understand the observed variety of deuterated species and their column density ratios, a number of astrochemical models have been put forward, among these the GRAINOBLE model. This code has been described in detail in previous studies (Taquet et al. 2012, 2013, 2014) and here we give only a brief presentation before discussing how the model compares with the levels of deuteration we find in the regions of NGC 6334I.
GRAINOBLE follows the gas-ice interstellar chemistry through a three-phase (gas, ice surface, ice bulk) rate equations approach initially developed by Hasegawa & Herbst (1993). The model takes into account a number of gas-grain processes including the accretion of species onto the grains, desorption back into the gas-phase and reactions between particles at the ice surface and in the ice mantle. The gas-phase chemical network is described in Taquet et al. (2014) and includes the spin states of H2, 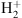 , and
, and 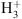 , as well as the deuterated isotopologues of hydrogenated species with four or less atoms and molecules involved in the chemistry of water, methanol, ammonia, and formaldehyde. The ice chemical network follows the formation and the deuteration of the main ice species, following a series of laboratory experiments, and complex organic molecules through radical-radical recombination reactions. Specifically, the pathways for formation and deuteration of methanol include both addition reactions involving atomic D and hydrogenation of solid CO and H2CO at cold (T = 10–15 K) temperatures as well as abstraction reactions, as shown by Hidaka et al. (2009).
, as well as the deuterated isotopologues of hydrogenated species with four or less atoms and molecules involved in the chemistry of water, methanol, ammonia, and formaldehyde. The ice chemical network follows the formation and the deuteration of the main ice species, following a series of laboratory experiments, and complex organic molecules through radical-radical recombination reactions. Specifically, the pathways for formation and deuteration of methanol include both addition reactions involving atomic D and hydrogenation of solid CO and H2CO at cold (T = 10–15 K) temperatures as well as abstraction reactions, as shown by Hidaka et al. (2009).
We investigated the effect of the dust and gas temperatures, T, assumed to be equal, and the total density, nH, on the methanol deuteration. For this purpose, a series of pseudo-time dependent simulations in which the chemistry evolves over time whilst the temperature and density remain constant were run. Figure 8 shows the final ice abundances of CO, H2O, and CH3OH, the deuteration in ices of methanol and the gas phase atomic D to H ratio and the CH2DOH to CH3OD ratio as a function of temperature. Models are shown for three different densities, nH = 104, 105 and 106 cm−3, with respective ages of 2 × 107, 2 × 106, and 2 × 105 years.
 |
Fig. 8. Top panel: final abundances of H2O (red lines), CO (blue lines), and CH3OH (green lines) in ices as a function of temperature. Middle panel: final CH2DOH to CH3OH abundance ratio in ices (green lines) and final atomic D/H in the gas phase (blue lines) as a function of temperature. Bottom panel: final CH2DOH to CH3OD abundance ratio as function of temperature. In all panels three densities are considered: nH = 104 (dashed), 105 (dotted), and 106 (solid) cm−3. |
It is evident that both the ice composition and the methanol deuteration are highly dependent on the considered temperature and total density. The barrierless reactions which form water from atomic oxygen mean that this species is the least dependent on T and nH. Methanol and its deuterated isotopologues are, on the other hand, formed through hydrogenation and/or deuteration of CO and H2CO, which are thought to have high activation barriers. As a consequence, methanol formation can be inhibited at high densities, decreasing the CO hydrogenation, or at high temperatures where CO no longer efficiently freezes-out onto grains. Despite the lower residence time of H and CO on the grains at temperatures above ~20 K, limiting the formation of H2CO and later CH3OH, significant deuteration of methanol occur in the model. This is due to the long timescales considered which enhance the probability that the CO and H or D particles meet on the dust grain and recombine. Also, since it is formed through hydrogenation and/or deuteration processes, the methanol deuteration is governed by the atomic D/H in the gas phase.
Specifically, the strong decrease of the methanol deuteration with temperature, up to three orders of magnitudes with an increase of T from 10 to 40 K, is due to the decreased efficiency of deuterium chemistry in the gas phase with increasing temperature. Atomic D is mostly formed via electronic recombination of 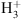 isotopologues, formed through exothermic reactions between
isotopologues, formed through exothermic reactions between 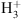 (or with its isotopologues) and HD. Because the efficiency of the backward reactions increase with an increase in temperature, the deuteration of
(or with its isotopologues) and HD. Because the efficiency of the backward reactions increase with an increase in temperature, the deuteration of 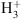 and therefore the production of atomic D is limited at high temperatures. However, the solid CH2DOH to CH3OH ratio does not always scale with the final atomic gas phase D/H. Figure 8 shows how the CH2DOH to CH3OH ratio decreases more efficiently with temperature at high densities but remains fairly constant for nH = 104 cm−3.
and therefore the production of atomic D is limited at high temperatures. However, the solid CH2DOH to CH3OH ratio does not always scale with the final atomic gas phase D/H. Figure 8 shows how the CH2DOH to CH3OH ratio decreases more efficiently with temperature at high densities but remains fairly constant for nH = 104 cm−3.
The model distinguishes the formation of CH2DOH from that of CH3OD. As seen in Fig. 8, the ratio remains close to three throughout the temperature range. This is due to the three reaction channels that form CH2DOH compared with the single channel that forms CH3OD. Also, it is important to note that while the observations trace the methanol deuteration in the gas phase of the hot core surrounding the forming massive protostars, the model describes the predicted deuteration of ices formed during the precursor pre-stellar phase. Therefore, the analysis is implicitly based on the assumption that the gas phase composition around the hot cores reflects the composition of the ices in the pre-stellar phase. As discussed in Sect. 4.1, a number of processes may alter the ice methanol deuteration. Some of these processes are already accounted for in the model, for example the formation of CH2DOH via abstraction reactions, shown experimentally by Nagaoka et al. (2005), is included in the model but contributes little to the overall abundance of CH2DOH. Others, like the H/D exchanges shown to occur between water and methanol in warm ices (Ratajczak et al. 2009; Faure et al. 2015) still need to be implemented and could potentially contribute significantly to the decrease of the CH3OD/CH3OH abundance resulting in a higher CH2DOH to CH3OD ratio in contrast to the low ratios derived for the regions in NGC 6334I.
Based on the model predictions, our inferred deuterium fractionation of methanol in the NGC 6334I regions, indicate a temperature during formation around 30 K. A similar dust temperature of the precursor dense core is reported by Russeil et al. (2013) who use data from Herschel to derive a dust temperature map of the NGC 6334 star-forming region and show that the area is dominated by temperatures ~25–35 K. Such a warm pre-stellar cloud could be the result of heating from a nearby earlier phase of star formation, potentially associated with NGC 6334E a region located between I and I(N) and hosting an O-type star and associated large shell-like HII region (Carral et al. 2002). The small variation in deuterium fractions found towards the individual regions of NGC 6334I may reflect local differences in nH.
5. Summary and conclusion
In this paper we analyse the level of deuterium fractionation in methanol towards the high-mass star-forming region NGC 6334I. We use high spectral resolution observations carried out with ALMA and extract spectra from nine individual locations across the MM1, MM2, and MM3 regions. Based on these, we identify a total of 15 transitions belonging to the isotopologues of methanol. Assuming excitation temperatures of ~120–330 K for the individual regions, we derived column densities for each of the species 13CH3OH, 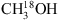 , CH2DOH and CH3OD and calculate CH2DOH/CH3OH and CH3OD/CH3OH. These range from 0.03% to 0.34% and 0.03% to 0.20% for the ratios of CH2DOH to CH3OH and from 0.27% to 1.07% and 0.22% to 0.61% for the ratios of CH3OD to CH3OH, using the 13C and 18O isotopologues to derive the column density of
, CH2DOH and CH3OD and calculate CH2DOH/CH3OH and CH3OD/CH3OH. These range from 0.03% to 0.34% and 0.03% to 0.20% for the ratios of CH2DOH to CH3OH and from 0.27% to 1.07% and 0.22% to 0.61% for the ratios of CH3OD to CH3OH, using the 13C and 18O isotopologues to derive the column density of 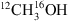 respectively. The highest levels of deuterium fractionation are associated with the regions MM1 I and MM2 I, which are also the brightest regions in the continuum image, while the lowest are detected towards the regions MM2 II and MM3 I both associated with less bright continuum regions. The derived deuterium fractionation ratios only vary by factors of between two and four with excitations temperatures between 100 and 400 K.
respectively. The highest levels of deuterium fractionation are associated with the regions MM1 I and MM2 I, which are also the brightest regions in the continuum image, while the lowest are detected towards the regions MM2 II and MM3 I both associated with less bright continuum regions. The derived deuterium fractionation ratios only vary by factors of between two and four with excitations temperatures between 100 and 400 K.
The derived CH2DOH/CH3OH values are consistently low throughout NGC 6334I with a mean CH2DOH/CH3OH value over all regions of 0.13 ± 0.06% and 0.08 ± 0.04% based on the 13C and 18O isotopologues respectively. This homogeneity of the CH2DOH to CH3OH ratios derived for the different cores indicate that they formed from the same precursor cloud. The levels are also similar to those derived towards Sgr B2 in the Galactic centre (Belloche et al. 2016) as well as those derived for the high-mass star-forming regions in Orion by Peng et al. (2012), but lower by factors of a few when compared with the values derived by Neill et al. (2013) for the same region. Because of the similar values, the low deuterium fractionation found in the Galactic centre is likely not due to astration but rather the high temperatures characterising the region. The methanol deuterium fractionation levels derived for the low-mass systems HH 212 and IRAS 16293 are higher by up to two orders of magnitude when compared with the values inferred for NGC 6334I, clearly illustrating the differences in physical and chemical environment prevailing in high- and low-mass star-forming regions.
Based on the chemical model of Taquet et al. (2014), the CH2DOH to CH3OH ratios detected towards the regions of NGC 6334I indicate a dust temperature at the time of the systems formation ~30 K. This temperature is higher than what is predicted for low-mass star-forming regions where the levels of deuterium in simple molecular species indicate a dust temperature at the time of formation below 20 K.
In addition to CH2DOH, CH3OD is unambiguously detected towards all nine regions of NGC 6334I allowing CH2DOH to CH3OD ratios to be derived. These range from 0.10 to 0.50, the highest value associated with the region MM2 I and the lowest with MM1 II. Our CH2DOH/CH3OD values towards NGC 6334I are lower than what is expected from statistics, assuming the CH3 and OH functional groups of methanol to be equally likely to be deuterated. While CH2DOH to CH3OD ratios of the order of unity have been detected towards high-mass star-forming regions previously, the low levels derived here have not been seen before and may hint at a favoured formation of CH3OD or destruction of CH2DOH in this region which has yet to be explained by models or experiments.
Acknowledgments
A special thanks to Dr. Holger Müller for valuable discussions of the spectroscopy of deuterated methanol. We acknowledge data reduction support from Allegro, the European ALMA Regional Center node in the Netherlands, and Dr. Luke Maud in particular for expert advice. We thank the anonymous referee for constructive comments that improved our manuscript. Support for B.A.M. was provided by NASA through Hubble Fellowship grant #HST-HF2-51396 awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2015.1.00150.S and #2015.A.00022.T. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan) and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This work is based on analysis carried out with the CASSIS software and JPL: http://spec.jpl.nasa.gov/ and CDMS: http://www.ph1.uni-koeln.de/cdms/ spectroscopic databases. CASSIS has been developed by IRAP-UPS/CNRS (http://cassis.irap.omp.eu).
Appendix A: ADS/JAO.ALMA#2015.A.00022.T
This appendix summarises the additional data set introduced in Sect. 2. The data confirm the presence of 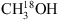 , CH2DOH and CH3OD in NGC 6334I but do not constrain the column densities of O13CS and CH3NC better than the primary data set. This is due to blending with other species and, in the case of O13CS, a limited number of lines covered. The column densities of O13CS and CH3NC derived from the primary data set are consistent with the data in this appendix.
, CH2DOH and CH3OD in NGC 6334I but do not constrain the column densities of O13CS and CH3NC better than the primary data set. This is due to blending with other species and, in the case of O13CS, a limited number of lines covered. The column densities of O13CS and CH3NC derived from the primary data set are consistent with the data in this appendix.
Summary of data set ALMA#2015.A.00022.T.
CH2DOH/CH3OH and CH3OD/CH3OH upper limits from data set ALMA#2015.A.00022.T.
Summary of covered lines with Aij > 10−5 s−1 and Tex < 600 K.
 |
Fig. A.1. 13CH3OH transitions with Tex < 600 K and Aij > 10−5 s−1 detected towards NGC 6334I. Frequencies are shifted to the rest frame of the region. The data and model are shown in black and green respectively. Rest frequencies of individual lines are indicated in red. |
 |
Fig. A.2.
|
 |
Fig. A.3. Selection of CH2DOH transitions with Tex < 400 K and Aij > 10−4 s−1 detected towards NGC 6334I. Frequencies are shifted to the rest frame of the region. The data and model are shown in black and green respectively. Rest frequencies of individual lines are indicated in red. |
 |
Fig. A.4. CH3OD transitions detected towards NGC 6334I. Frequencies are shifted to the rest frame of the region. The data and model are shown in black and green respectively. Rest frequencies of individual lines are indicated in red. |
Appendix B: Full spectra
 |
Fig. B.1. MM1 I–V. Top panels: model components. Bottom panels: data (black) and full model (magenta), i.e., the linear combination of the synthetic spectrum for each species. Frequencies are shifted to the rest frame of the individual regions. |
 |
Fig. B.1. continued. |
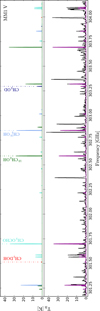 |
Fig. B.1. continued. |
 |
Fig. B.2. MM2 I–II. Top panels: model components. Bottom panels: data (black) and full model (magenta), i.e., the linear combination of the synthetic spectrum for each species. Frequencies are shifted to the rest frame of the individual regions. |
 |
Fig. B.3. MM3 I–II. Top panels: model components. Bottom panels: data (black) and full model (magenta), i.e., the linear combination of the synthetic spectrum for each species. Frequencies are shifted to the rest frame of the individual regions. |
Appendix C: 13CH3OH transitions
 |
Fig. C.1. All 13CH3OH lines detected towards NGC 6334I MM1 I–V. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of 13CH3OH without blending, i.e., excluding the contribution from CH3OCHO (including the contribution from CH3OCHO does not change the 13CH3OH column density of the best-fit model). To enhance the readability of some panels, both data and model have been scaled up by the factor in the top right corner of the respective panel. |
 |
Fig. C.1. continued. |
 |
Fig. C.1. continued. |
 |
Fig. C.2. All 13CH3OH lines detected towards NGC 6334I MM2 I–II. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of 13CH3OH without blending, i.e., excluding the contribution from CH3OCHO (including the contribution from CH3OCHO does not change the 13CH3OH column density of the best-fit model). To enhance the readability of some panels, both data and model have been scaled up by the factor in the top right corner of the respective panel. |
 |
Fig. C.3. All 13CH3OH lines detected towards NGC 6334I MM3 I–II. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of 13CH3OH without blending, i.e., excluding the contribution from CH3OCHO (including the contribution from CH3OCHO does not change the 13CH3OH column density of the best-fit model). To enhance the readability of some panels, both data and model have been scaled up by the factor in the top right corner of the respective panel. |
Appendix D: 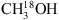 transitions
transitions
 |
Fig. D.1. All |
 |
Fig. D.2. All |
 |
Fig. D.3. All |
Appendix E: CH3OD transitions
 |
Fig. E.1. All CH3OD lines detected towards NGC 6334I MM1 I–V. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of CH3OD in each region. |
 |
Fig. E.2. All CH3OD lines detected towards NGC 6334I MM2 I–II. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of CH3OD in each region. |
 |
Fig. E.3. All CH3OD lines detected towards NGC 6334I MM3 I–II. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of CH3OD in each region. |
References
- Aikawa, Y., Wakelam, V., Hersant, F., Garrod, R. T., & Herbst, E. 2012, ApJ, 760, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, T., Crownover, R. L., Herbst, E., & De Lucia, F. C. 1988, ApJS, 67, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, T., Herbst, E., & Delucia, F. 1993, J. Mol. Spectr., 159, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Müller, H. S. P., Garrod, R. T., & Menten, K. M. 2016, A&A, 587, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, E., Codella, C., Ceccarelli, C., et al. 2017, A&A, 606, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bizzocchi, L., Caselli, P., Spezzano, S., & Leonardo, E. 2014, A&A, 569, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brogan, C. L., Hunter, T. R., Cyganowski, C. J., et al. 2016, ApJ, 832, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Carral, P., Kurtz, S. E., Rodríguez, L. F., et al. 2002, AJ, 123, 2574 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, C., Castets, A., Loinard, L., Caux, E., & Tielens, A. G. G. M. 1998, A&A, 338, L43 [NASA ADS] [Google Scholar]
- Charnley, S. B., Tielens, A. G. G. M., & Rodgers, S. D. 1997, ApJ, 482, L203 [NASA ADS] [CrossRef] [Google Scholar]
- Chibueze, J. O., Omodaka, T., Handa, T., et al. 2014, ApJ, 784, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., Faure, M., Theulé, P., Quirico, E., & Schmitt, B. 2015, A&A, 584, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuchs, G. W., Cuppen, H. M., Ioppolo, S., et al. 2009, A&A, 505, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geppert, W. D., Hellberg, F., Österdahl, F., et al. 2005, IAU Symp., 231, 117 [NASA ADS] [Google Scholar]
- Gezari, D. Y. 1982, ApJ, 259, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 263, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Hidaka, H., Watanabe, M., Kouchi, A., & Watanabe, N. 2009, ApJ, 702, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, T. R., Brogan, C. L., Megeath, S. T., et al. 2006, ApJ, 649, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, T. R., Brogan, C. L., MacLeod, G., et al. 2017, ApJ, 837, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., van der Wiel, M. H. D., Coutens, A., et al. 2016, A&A, 595, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jørgensen, J. K., Müller, H. S. P., Calcutt, H., et al. 2017, A&A, submitted [Google Scholar]
- Leurini, S., Schilke, P., Parise, B., et al. 2006, A&A, 454, L83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linsky, J. L. 2003, Space Sci. Rev., 106, 49 [NASA ADS] [CrossRef] [Google Scholar]
- McBreen, B., Fazio, G. G., Stier, M., & Wright, E. L. 1979, ApJ, 232, L183 [NASA ADS] [CrossRef] [Google Scholar]
- McCutcheon, W. H., Sandell, G., Matthews, H. E., et al. 2000, MNRAS, 316, 152 [NASA ADS] [CrossRef] [Google Scholar]
- McGuire, B. A., Shingledecker, C. N., Willis, E. R., et al. 2017, ApJ, 851, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Nagaoka, A., Watanabe, N., & Kouchi, A. 2005, ApJ, 624, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. L., Crockett, N. R., Bergin, E. A., Pearson, J. C., & Xu, L.-H. 2013, ApJ, 777, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Parise, B., Ceccarelli, C., Tielens, A. G. G. M., et al. 2002, A&A, 393, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Castets, A., Herbst, E., et al. 2004, A&A, 416, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Ceccarelli, C., Tielens, A. G. G. M., et al. 2006, A&A, 453, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearson, J. C., Yu, S., & Drouin, B. J. 2012, J. Mol. Spectr., 280, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, T.-C., Despois, D., Brouillet, N., Parise, B., & Baudry, A. 2012, A&A, 543, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Persi, P., Roth, M., Tapia, M., et al. 1996, A&A, 307, 591 [NASA ADS] [Google Scholar]
- Prodanović, T., Steigman, G., & Fields, B. D. 2010, MNRAS, 406, 1108 [NASA ADS] [Google Scholar]
- Qiu, K., Wyrowski, F., Menten, K. M., et al. 2011, ApJ, 743, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Ratajczak, A., Quirico, E., Faure, A., Schmitt, B., & Ceccarelli, C. 2009, A&A, 496, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ratajczak, A., Taquet, V., Kahane, C., et al. 2011, A&A, 528, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Roberts, H., Herbst, E., & Millar, T. J. 2003, ApJ, 591, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Russeil, D., Zavagno, A., Adami, C., et al. 2012, A&A, 538, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russeil, D., Schneider, N., Anderson, L. D., et al. 2013, A&A, 554, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taquet, V., Ceccarelli, C., & Kahane, C. 2012, ApJ, 748, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Taquet, V., Peters, P. S., Kahane, C., et al. 2013, A&A, 550, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taquet, V., Charnley, S. B., & Sipilä, O. 2014, ApJ, 791, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 1983, A&A, 119, 177 [NASA ADS] [Google Scholar]
- van Dishoeck, E. F., Blake, G. A., Jansen, D. J., & Groesbeck, T. D. 1995, ApJ, 447, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, M., Xu, L.-H., Lees, R., et al. 2000, J. Mol. Spectr., 204, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N., & Kouchi, A. 2002, ApJ, 571, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, W. D. 1976, Rev. Mod. Phys., 48, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L. 1999, Rep. Prog. Phys., 62, 143 [Google Scholar]
- Zernickel, A., Schilke, P., Schmiedeke, A., et al. 2012, A&A, 546, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Velocity integrated intensity map of the 13CH3OH transition at 303.692 GHz with the 1 mm continuum image overlaid in black contours (levels are [10, 20, 40, 80, 160]σ with σ = 0.02 Jy beam−1). The locations at which spectra have been extracted are marked in blue for MM1, green for MM2 and red for MM3. The synthesised beam (~1300 × 962 AU) is shown in the bottom left corner. |
| In the text | |
 |
Fig. 2. 13CH3OH 10(0,10)→9(1,8) transition at 302.590 GHz (indicated by dash-dotted lines) detected towards each region. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of 13CH3OH without blending, i.e., excluding the contribution from CH3OCHO (including the contribution from CH3OCHO does not change the 13CH3OH column density of the best-fit model). Yellow lines represent the modelled spectra of CH3OCHO and magenta lines represent the sum of the 13CH3OH and CH3OCHO spectra. |
| In the text | |
 |
Fig. 3.
|
| In the text | |
 |
Fig. 4. CH2DOH 12(2,11)→12(1,12) transition at 301.514 GHz (indicated by dash-dotted lines) detected towards each region. Frequencies are shifted to the rest frame of the individual regions. Blue and green lines represent the modelled spectra of CH2DOH with and without blending, i.e., including and excluding the contribution from CH3NC, respectively. Yellow lines represent the modelled spectra of CH3NC and magenta lines represent the sum of the spectra of CH2DOH with blending and CH3NC. |
| In the text | |
 |
Fig. 5. CH3OD 7(2+)→7(1,−) transition at 303.296 GHz (indicated by dash-dotted lines) detected towards each region. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of CH3OD. |
| In the text | |
 |
Fig. 6. Column density ratio of CH2DOH to CH3OH (green) and CH3OD to CH3OH (blue) for NGC 6334I and other objects. For Orion KL the shaded bar indicates the range of ratios derived by Peng et al. (2012). For NGC 6334I shaded and filled bars indicate the ratios derived using the 13C and 18O isotopologues as base respectively. Error bars indicate the range of ratios derived with and without blending. For NGC 6334I MM1 only the region with the lowest (MM1 IV) and highest (MM1 I) ratios are plotted. References. (a)Jørgensen et al. (2017). (b)Bianchi et al. (2017). (c)Neill et al. (2013). (d)Peng et al. (2012). (e)Belloche et al. (2016). |
| In the text | |
 |
Fig. 7. Column density ratio as function of excitation temperature. Ratios are normalised to the value derived for Tex = 200 K. Magenta and blue lines represent the CH2DOH to CH3OH and CH3OD to CH3OH column density ratios respectively, while sold and dashed lines indicate the values derived assuming 12C/13C = 62 and 16O/18O = 450 respectively. Different regions are indicated by different markers. |
| In the text | |
 |
Fig. 8. Top panel: final abundances of H2O (red lines), CO (blue lines), and CH3OH (green lines) in ices as a function of temperature. Middle panel: final CH2DOH to CH3OH abundance ratio in ices (green lines) and final atomic D/H in the gas phase (blue lines) as a function of temperature. Bottom panel: final CH2DOH to CH3OD abundance ratio as function of temperature. In all panels three densities are considered: nH = 104 (dashed), 105 (dotted), and 106 (solid) cm−3. |
| In the text | |
 |
Fig. A.1. 13CH3OH transitions with Tex < 600 K and Aij > 10−5 s−1 detected towards NGC 6334I. Frequencies are shifted to the rest frame of the region. The data and model are shown in black and green respectively. Rest frequencies of individual lines are indicated in red. |
| In the text | |
 |
Fig. A.2.
|
| In the text | |
 |
Fig. A.3. Selection of CH2DOH transitions with Tex < 400 K and Aij > 10−4 s−1 detected towards NGC 6334I. Frequencies are shifted to the rest frame of the region. The data and model are shown in black and green respectively. Rest frequencies of individual lines are indicated in red. |
| In the text | |
 |
Fig. A.4. CH3OD transitions detected towards NGC 6334I. Frequencies are shifted to the rest frame of the region. The data and model are shown in black and green respectively. Rest frequencies of individual lines are indicated in red. |
| In the text | |
 |
Fig. B.1. MM1 I–V. Top panels: model components. Bottom panels: data (black) and full model (magenta), i.e., the linear combination of the synthetic spectrum for each species. Frequencies are shifted to the rest frame of the individual regions. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.2. MM2 I–II. Top panels: model components. Bottom panels: data (black) and full model (magenta), i.e., the linear combination of the synthetic spectrum for each species. Frequencies are shifted to the rest frame of the individual regions. |
| In the text | |
 |
Fig. B.3. MM3 I–II. Top panels: model components. Bottom panels: data (black) and full model (magenta), i.e., the linear combination of the synthetic spectrum for each species. Frequencies are shifted to the rest frame of the individual regions. |
| In the text | |
 |
Fig. C.1. All 13CH3OH lines detected towards NGC 6334I MM1 I–V. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of 13CH3OH without blending, i.e., excluding the contribution from CH3OCHO (including the contribution from CH3OCHO does not change the 13CH3OH column density of the best-fit model). To enhance the readability of some panels, both data and model have been scaled up by the factor in the top right corner of the respective panel. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
 |
Fig. C.2. All 13CH3OH lines detected towards NGC 6334I MM2 I–II. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of 13CH3OH without blending, i.e., excluding the contribution from CH3OCHO (including the contribution from CH3OCHO does not change the 13CH3OH column density of the best-fit model). To enhance the readability of some panels, both data and model have been scaled up by the factor in the top right corner of the respective panel. |
| In the text | |
 |
Fig. C.3. All 13CH3OH lines detected towards NGC 6334I MM3 I–II. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of 13CH3OH without blending, i.e., excluding the contribution from CH3OCHO (including the contribution from CH3OCHO does not change the 13CH3OH column density of the best-fit model). To enhance the readability of some panels, both data and model have been scaled up by the factor in the top right corner of the respective panel. |
| In the text | |
 |
Fig. D.1. All |
| In the text | |
 |
Fig. D.2. All |
| In the text | |
 |
Fig. D.3. All |
| In the text | |
 |
Fig. E.1. All CH3OD lines detected towards NGC 6334I MM1 I–V. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of CH3OD in each region. |
| In the text | |
 |
Fig. E.2. All CH3OD lines detected towards NGC 6334I MM2 I–II. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of CH3OD in each region. |
| In the text | |
 |
Fig. E.3. All CH3OD lines detected towards NGC 6334I MM3 I–II. Frequencies are shifted to the rest frame of the individual regions. Green lines represent the modelled spectra of CH3OD in each region. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.