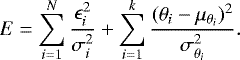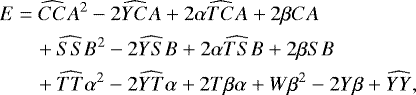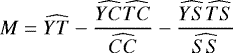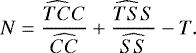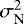| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 12 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201732524 | |
| Published online | 23 July 2018 | |
Estimating activity cycles with probabilistic methods
I. Bayesian generalised Lomb-Scargle periodogram with trend
1
ReSoLVE Centre of Excellence, Aalto University, Department of Computer Science,
PO Box 15400,
00076
Aalto, Finland
e-mail: nigul.olspert@aalto.fi
2
Tartu Observatory,
61602
Tõravere, Estonia
3
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37077
Göttingen, Germany
Received:
21
December
2017
Accepted:
27
March
2018
Context. Period estimation is one of the central topics in astronomical time series analysis, in which data is often unevenly sampled. Studies of stellar magnetic cycles are especially challenging, as the periods expected in those cases are approximately the same length as the datasets themselves. The datasets often contain trends, the origin of which is either a real long-term cycle or an instrumental effect. But these effects cannot be reliably separated, while they can lead to erroneous period determinations if not properly handled.
Aims. In this study we aim at developing a method that can handle the trends properly. By performing an extensive set of testing, we show that this is the optimal procedure when contrasted with methods that do not include the trend directly in the model. The effect of the form of the noise (whether constant or heteroscedastic) on the results is also investigated.
Methods. We introduced a Bayesian generalised Lomb-Scargle periodogram with trend (BGLST), which is a probabilistic linear regression model using Gaussian priors for the coefficients of the fit and a uniform prior for the frequency parameter.
Results. We show, using synthetic data, that when there is no prior information on whether and to what extent the true model of the data contains a linear trend, the introduced BGLST method is preferable to the methods that either detrend the data or opt not to detrend the data before fitting the periodic model. Whether to use noise with other than constant variance in the model depends on the density of the data sampling and on the true noise type of the process.
Key words: methods: statistical / methods: numerical / stars: activity
© ESO 2018
1 Introduction
In the domain of astronomical data analysis the task of period estimation from unevenly spaced time series has been a relevant topic for many decades. Depending on the context, the term period can refer to, for example, rotational period of the star, orbiting period of the star or exoplanet, or the period of the activity cycle of the star. Knowing the precise value of the period is often very important as many other physical quantities are dependent on it. For instance, in the case of active late-type stars with outer convection zones, the ratio of rotational period and cycle period can be interpreted as a measure of the dynamo efficiency. Therefore, measuring this ratio gives us crucial information concerning the generation of magnetic fields in stars with varying activity levels. In practice, both periods are usually estimated through photometry and/or spectrometry of the star.
For the purpose of analysing unevenly spaced time series, many different methods have been developed over the years. Historically one of the most common is the Lomb-Scargle (LS) periodogram (Lomb 1976; Scargle 1982). Statistical properties of the LS and other alternative periodograms have been extensively studied and it has become a well-known fact that the interpretation of the results of any spectral analysis method takes a lot of effort. The sampling patterns in the data together with the finiteness of the time span of observations lead to a multitude of difficulties in the period estimation. One of the most pronounced difficulties is the emergence of aliased peaks (spectral leakage) (Tanner 1948; Deeming 1975; Lomb 1976; Scargle 1982; Horne & Baliunas 1986). In other words one can only see a distorted spectrum as the observations are made at discrete (uneven) time moments and during a finite time. However, algorithms for eliminating spurious peaks from spectra have been developed (Roberts et al. 1987). Clearly, different period estimation methods tend to perform differently depending on the dataset. A comparison of some of the popular methods is provided in Carbonell et al. (1992).
One of the other issues in spectral estimation arises when the true mean of the measured signal is not known. The LS method assumes a zero-mean harmonic model with constant noise variance, so that the data needs to be centred in the observed values before doing the analysis. While every dataset can be turned into a dataset with a zero mean, in some cases owing to pathological sampling (if the empirical mean1 and the true mean differ significantly), this procedure can lead to incorrect period estimates. In the literature this problem has been addressed extensively and several generalisations of the periodogram, which are invariant to the shifts in the observed value, have been proposed. These include the method of Ferraz-Mello (1981), who used Gram-Schmidt orthogonalisation of the constant, cosine, and sine functions in the sample domain. The power spectrum is then defined as the square norm of the data projections to these functions. In Zechmeister & Kürster (2009) the harmonic model of the LS periodogram is directly extended with the addition of a constant term, which has become known as the generalised Lomb-Scargle (GLS) periodogram. Moreover, both of these studies give the formulations allowing nonconstant noise variance. Later, using a Bayesian approach for a model with harmonic plus constant, it has been shown that the posterior probability of the frequency, when using uniform priors, is very similar to the GLS spectrum (Mortier et al. 2015). The benefit of the latter method is that the relative probabilities of any two frequencies can be easily calculated. Usually in the models, likewise in the current study, the noise is assumed to be Gaussianand uncorrelated. Methods involving other than white noise models are discussed in Vio et al. (2010) and Feng et al. (2017). A more thorough overview of important aspects in the spectral analysis is provided in VanderPlas (2017).
The focus of the current paper is on another yet unaddressed issue, namely the effect of a linear trend in the data to period estimation. The motivation to tackle this question arose in the context of analysing the Mount Wilson time series of chromospheric activity (hereafter MW) in a quest to look for long-term activity cycles (Olspert et al. 2018), the length of which is of the same order of magnitude as the dataset length itself. In a previous study by Baliunas et al. (1995) detrending was occasionally, but not systematically, used before the LS periodogram was calculated. The cycle estimates from this study have later been used extensively by many other studies, for example, to show the presence of different branches of stellar activity (e.g. Saar & Brandenburg 1999).
We nowraise the following question – whether it is more optimal to remove the linear trend before the period search or opt not to detrend the data? Like centring, detrending the data before fitting the harmonic model may or may not lead to biased period estimates depending on the structure of the data. The problems arise either due to sampling effects or the presence of very long periods in the data. Based on the empirical arguments given in Sect. 3, we show that it is more preferable to include the trend component directly into the regression model instead of detrending the data a priori or opting not to detrend the data altogether. In the same section we also discuss the effects of noise model of the data to the period estimate. We note that the question that we address in the current study is primarily relevant to the cases for which the number of cycles in the dataset is small. Otherwise, the long coherence time (if the underlying process is truly periodic) allows us to nail down periods, even if there are uneven errors or a small trend. A high number of cycles allows us to get exact periods even, for example, by cycle counting.
The generalised least squares spectrum allowing arbitrary components (including linear trend) was first discussed in Vaníček (1971) and more recently Bayesian approaches including trend component have been introduced in Ford et al. (2011) and Feng et al. (2017).
2 Method
Now we turn to the description of the present method, which is a generalisation of the method proposed in Mortier et al. (2015) and a special case of the method developed in Feng et al. (2017). The model in the latter paper allows noise to be correlated, which we do not consider in the current study. One of the main differences between the models that we discuss and the model in Feng et al. (2017) is that we used Gaussian rather than uniform priors for nuisance parameters (see below). This has important consequences in certain situations as discussed in Sect. 2.2. We introduced a simple Bayesian linear regression model where besides the harmonic component we have a linear trend with slope plus offset2. This is summarised in the following equation:
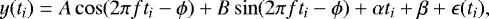 (1)
(1)
where y(ti) and ϵ(ti) are the observation and noise at time ti, f = 1∕P is the frequency of the cycle, and A, B, α, β, and ϕ are free parameters. Specifically, α is the slope and β the offset (γ-intercept). Usually A, B, α, β are called the nuisanceparameters. As noted, we assumed that the noise is Gaussian and independent between any two time moments, but we allow its variance to be time dependent. For parameter inference, we used a Bayesian model, where the posterior probability is given by
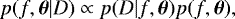 (2)
(2)
where p(D|f, θ) is the likelihood ofthe data, p(f, θ) is the prior probability of the parameters, where for convenience, we grouped the nuisance parameters under the vector ![$\bm{\theta} = \left[A, B, \alpha, \beta\right]\tran$](/articles/aa/full_html/2018/07/aa32524-17/aa32524-17-eq3.png) . Parameter ϕ is not optimised, but set to a frequency-dependent value simplifying the inference such that cross-terms with cosine and sine components vanish (see Sect. 2.1). The likelihood is given by
. Parameter ϕ is not optimised, but set to a frequency-dependent value simplifying the inference such that cross-terms with cosine and sine components vanish (see Sect. 2.1). The likelihood is given by
 (3)
(3)
where ϵi = ϵ(ti) and 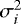 is the noise variance at time moment ti. To make the derivation of the spectrum analytically tractable, we took independent Gaussian priors for A, B, α, β, and a flat prior for the frequency f. This leads to the prior probability given by
is the noise variance at time moment ti. To make the derivation of the spectrum analytically tractable, we took independent Gaussian priors for A, B, α, β, and a flat prior for the frequency f. This leads to the prior probability given by
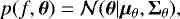 (4)
(4)
where ![$\bm{\mu}_{\theta}=\left[\mu_A, \mu_B, \mu_{\alpha}, \mu_{\beta}\right]\tran$](/articles/aa/full_html/2018/07/aa32524-17/aa32524-17-eq7.png) is the vector of prior means and
is the vector of prior means and 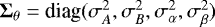 is the diagonal matrix of prior variances.
is the diagonal matrix of prior variances.
The larger the prior variances the less information is assumed to be known about the parameters. Based on what is intuitively meaningful, in all the calculations we used the following values for the prior means and variances:
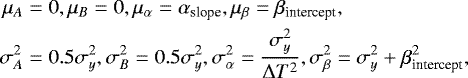 (5)
(5)
where αslope and βintercept are the slope and intercept estimated from linear regression, 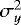 is the sample variance of the data, and ΔT is duration of the data. If one does not have any prior information about the parameters one could set the variances to infinity and drop the corresponding terms from the equations, but in practice to avoid meaningless results with unreasonably large parameter values some regularisation would be required (see Sect. 2.2).
is the sample variance of the data, and ΔT is duration of the data. If one does not have any prior information about the parameters one could set the variances to infinity and drop the corresponding terms from the equations, but in practice to avoid meaningless results with unreasonably large parameter values some regularisation would be required (see Sect. 2.2).
2.1 Derivation of the spectrum
Our derivation of the spectrum closely follows the key points presented in Mortier et al. (2015). Consequently, we use the notion of the variables that is as identical as possible. Using the likelihood and prior defined by Eqs. (3) and (4), the posterior probability of the Bayesian model given by Eq. (2) can be explicitly written as
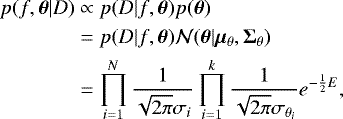 (6)
(6)
Here θi, i = 1,.., k, k = 4, denotes the ith element of θ, i.e. either A, B, α, or β. From Eqs. (1) and (3) we see that the likelihood and therefore posterior probability for every fixed frequency f is multivariate Gaussian w.r.t. the parameters A, B, α, and β. In principle, we are interested in finding the optimum for the full joint posterior probability density p(f, θ|D). But as for every fixed frequency the latter distribution is a multivariate Gaussian, we can first marginalise over all nuisance parameters, find the optimum for the frequency f, for example, by carrying out a grid search, and later analytically find the posterior means and covariances of the other parameters. The marginal posterior distribution for the frequency parameter is expressed as
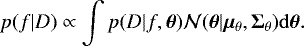 (8)
(8)
The integrals are assumed to be taken over the whole range of parameter values, i.e. from − ∞ to ∞. We introduce the following notations:
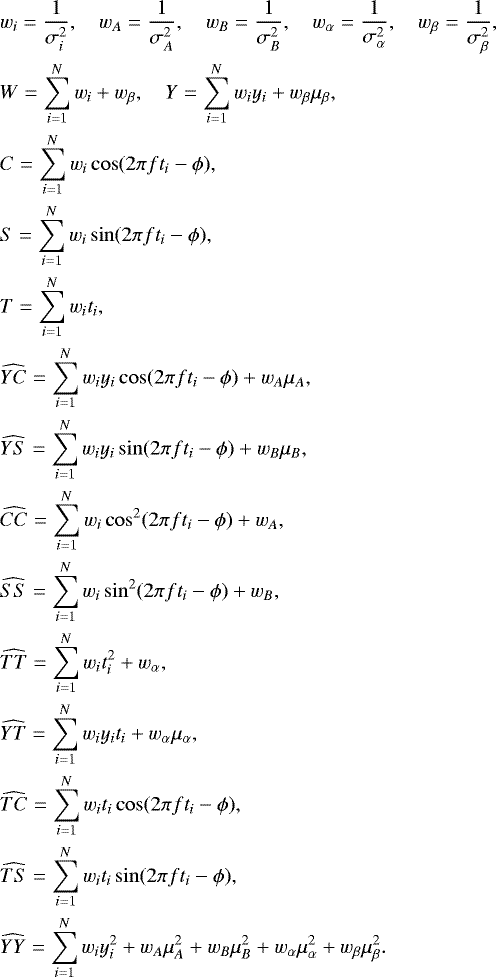 (9)–(22)
(9)–(22)
If the value of ϕ is defined such that the cosine and sine functions are orthogonal (for the proof, see Mortier et al. 2015), namely
![\begin{equation*} \phi=\frac{1}{2}\arctan\left[\frac{\sum_{i=1}^{N}w_i\sin(4\pi f t_i)}{\sum_{i=1}^{N}w_i\cos(4\pi f t_i)}\right], \end{equation*}](/articles/aa/full_html/2018/07/aa32524-17/aa32524-17-eq15.png) (23)
(23)
where we have grouped the terms with A on the first line, terms with B on the second line, and the rest of the terms on the third line.
In the following, we repeatedly use the formula of the following definite integral:
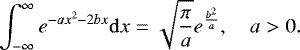 (25)
(25)
To calculate the integral in Eq. (8), we start by integrating first over A and B. Assuming that 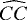 and
and 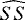 are greater than zero and applying Eq. (25), we get the solution for the integral containing terms with A as follows:
are greater than zero and applying Eq. (25), we get the solution for the integral containing terms with A as follows:
 (26)
(26)
In the last expression, we have grouped onto separate lines the terms with α, terms with β not simultaneously containing α, and constant terms. Similarly, for the integral containing terms with B,
 (27)
(27)
Now we gather the coefficients for all the terms with α2 from the last line of Eq. (24) (keeping in mind the factor –1/2) as well as from Eqs. (26) and (27) into new variableK, i.e.
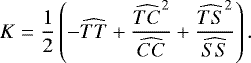 (28)
(28)
We similarly introduce new variable L for the coefficients involving all terms with α from the same equations as follows:
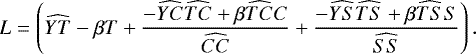 (29)
(29)
After these substitutions, integrating over α can again be accomplished with the help of Eq. (25) and assuming K < 0, i.e.
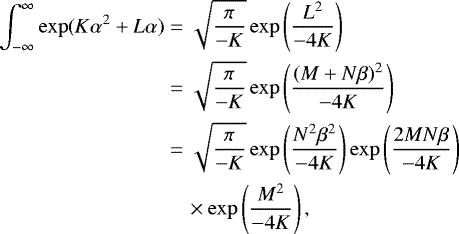 (30)
(30)
At this point what is left to do is the integration over β. To simplify things once more, we gather the coefficients for all the terms with β2 from Eqs. (24), (26), (27), and (30) into new variable P,
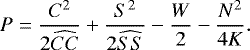 (33)
(33)
We similarlyintroduce new variable Q for the coefficients involving all terms with β from the same equations as follows:
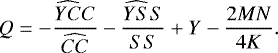 (34)
(34)
With these substitutions we are ready to integrate over β using again Eq. (25) while assuming P < 0, i.e.
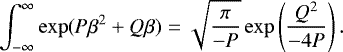 (35)
(35)
After gathering all remaining constant terms from Eqs. (24), (26), (27), and (30), we finally obtain
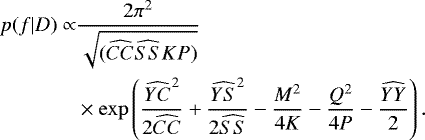 (36)
(36)
For the purpose of fitting the regression curve into the data one would be interested in obtaining the expected values for the nuisance parameters A, B, α, β. This can be easily done after fixing the frequency to its optimal value using Eq. (36) with a grid search, and noticing that p(θ|D, fopt) is a multivariate Gaussian distribution. In the following, we list the corresponding posterior means of the parameters3, i.e.
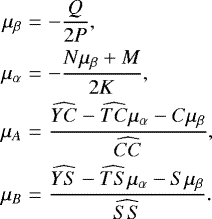 (37)(38)(39)(40)
(37)(38)(39)(40)
Formulas for the full covariance matrix of the parameters and for the posterior predictive distribution, assuming a model with constant noise variance, can be found in Murphy (2012, Chaps. 7.6). The posterior predictive distribution, however, in our case does not include the uncertainty contribution from the frequency parameter.
If we now consider the case when 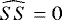 (for more details, see Mortier et al. 2015), we see that also S = 0,
(for more details, see Mortier et al. 2015), we see that also S = 0, 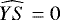 , and
, and 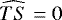 . Consequently the integral for B is proportional to a constant. We can define the analogues of the constants K through Q for this special case as
. Consequently the integral for B is proportional to a constant. We can define the analogues of the constants K through Q for this special case as
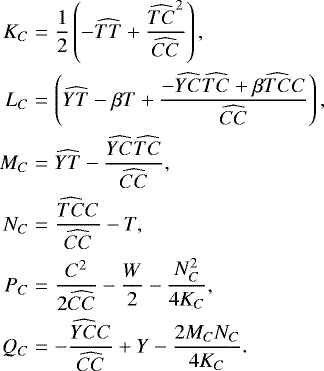 (41)–(46)
(41)–(46)
Finally, we arrive at the expression for the marginal posterior distribution of the frequency:
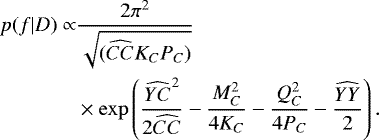 (47)
(47)
Similarly, we can handle the situation when 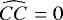 . In the derivation, we also assumed that K < 0 and P < 0. Our experiments with test data showed that the condition for K < 0 was always satisfied, but occasionally P obtained zero values and probably due to numerical rounding errors also very low positive values. These special cases we handled by dropping the corresponding terms from Eqs. (36) and (47). Theoretically, confirming or disproving that the conditions K < 0 and P ≤ 0 always hold is however beyond the scope of current study.
. In the derivation, we also assumed that K < 0 and P < 0. Our experiments with test data showed that the condition for K < 0 was always satisfied, but occasionally P obtained zero values and probably due to numerical rounding errors also very low positive values. These special cases we handled by dropping the corresponding terms from Eqs. (36) and (47). Theoretically, confirming or disproving that the conditions K < 0 and P ≤ 0 always hold is however beyond the scope of current study.
2.2 Importance of priors
In Eq. (4) we defined the priors of the nuisance parameters θ to be Gaussian with reasonable means and variances given in Eq. (5). In this subsection we discuss the significance of this choice to the results. The presence of the linear trend component introduces an additional degree of freedom into the model, which, in the context of low frequencies and short datasets can lead to large and physically meaningless parameter values whenno regularisation is used. This situation is illustrated in Fig. 1, in which we show the difference between the models with Gaussian and uniform priors used for the vector of nuisance parameters θ. The true parameter vector in this example was θ = [0.8212, −0.5707, 0.003258, 0] and the estimated parameter vector for the model with Gaussian priors θ = [0.7431, −0.6624, 0.002112, 0.1353]. However, for the model with uniform priors the estimate θ = [3.016, 98.73, −0.5933, 61.97] strongly deviates from the true vector. As seen from the Fig. 1a, from the point of view of the goodness of fit both of these solutions differ only marginally. From the perspective of parameter estimation (including the period), however, the model with uniform priors leads to substantially biased results. From Fig. 1b it is evident that p(f|D) can become multimodal when uniform priors are used and in the worst-case scenario the global maximum occurs in the low end of the frequency range, instead of the neighbourhood of the true frequency.
 |
Fig. 1 Illustration of importance of priors. Panel a: models fitted to the data with Gaussian priors (red continuous line) and uniform priors (blue dashed curve) for the nuisance parameters. Panel b: the spectra of the corresponding models. The black dotted line shows the position of true frequency. |
2.3 Dealing with multiple harmonics
The formulafor the spectrum is given by Eq. (36), which represents the posterior probability of the frequency f, given data D and our harmonic model, MH, i.e. p(f|D, MH). Although being a probability density, it is still convenient to call this frequency-dependent quantity a spectrum. We point out that if the true model matches the given model, MH, then the interpretation of the spectrum is straightforward, namely being the probability distribution of the frequency. This gives us a direct approach to estimate errors, for example by fitting a Gaussian to the spectral line (Bretthorst 1988, Chap. 2). When the true model has more than one harmonic, the interpretation of the spectrum is no longer direct because of the mixing of the probabilitiesfrom different harmonics. The correct way to address this issue would be to use a more complex model with at least as many harmonics than are expected to be in the underlying process (or even better, to infer the number of components from data). However, as a simpler workaround, the ideas of cleaning the spectrum introduced in Roberts et al. (1987) can be used to iteratively extract significant frequencies from the spectrum calculated using a model with single harmonic.
2.4 Significance estimation
To estimate the significance of the peaks in the spectrum we perform a model comparison between the given model and a model without harmonics, i.e. only with linear trend. One practical way to do this is to calculate
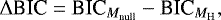 (48)
(48)
where Mnull is the linear model without harmonic, 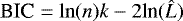 is the Bayesian information criterion (BIC), n is the number of data points, k the number of model parameters, and
is the Bayesian information criterion (BIC), n is the number of data points, k the number of model parameters, and 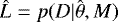 is the likelihood of data for model M using the parameter values that maximise the likelihood. This formula is an approximation to the logarithmic Bayes factor4, more precisely ΔBIC ≈ 2lnK, where K is the Bayes factor. The strength of evidence for models with 2lnK > 10 are considered very strong, models with 6 ≤ 2lnK < 10 strong, and those with 2 ≤ 2lnK < 6 positive. For a harmonic model MH, θ include optimal frequency and coefficients of the harmonic component, slope, and offset for Mnull only the last two coefficients.
is the likelihood of data for model M using the parameter values that maximise the likelihood. This formula is an approximation to the logarithmic Bayes factor4, more precisely ΔBIC ≈ 2lnK, where K is the Bayes factor. The strength of evidence for models with 2lnK > 10 are considered very strong, models with 6 ≤ 2lnK < 10 strong, and those with 2 ≤ 2lnK < 6 positive. For a harmonic model MH, θ include optimal frequency and coefficients of the harmonic component, slope, and offset for Mnull only the last two coefficients.
In the derivation of the spectrum we assume that the noise variance of the data points is known, which is usually not the case. In probabilistic models, this parameter should also be optimised, however in practice often sample variance is taken as the estimate for it. This is also the case with LS periodogram. However, it has been shown that when normalizing the periodogram with the sample variance, the statistical distribution slightly differs from the theoretically expected distribution (Schwarzenberg-Czerny 1998), thus it has an effect on the significance estimation. A more realistic approach, especially in the case when the noise cannot be assumed stationary is to use, for example subsample variances in a small sliding window around the data points.
As a final remark in this section, we want to emphasise that the probabilistic approach does not remove the burden of dealing with spectral aliases due to data sampling. There is always a chance of false detection, thus the interpretation of the spectrum must be carried out with care (for a good example, see Pelt 1997).
3 Experiments
In this section we undertake some experiments to compare the performance of the introduced method with LS and/or GLS periodograms.
3.1 Performance of the method in the absence of a trend
We start with the situation in which no linear trend is present in the actual data, as this kind of a test allowed us to compare the performance of the Bayesian generalised Lomb-Scargle periodogram with trend (BGLST) model, with an additional degree of freedom, to the GLS method. For that purpose we drew n data points randomly from a harmonic process with zero mean and total variance of unity. The time span of the data Δ T was selected to be 30 units. We did two experiments: one with uniform sampling and the other with alternating segments of data and gaps (see below). In the both experiments we varied n in the range from 5 to 100 and noise variance 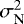 from 0 to 0.5 units. The period of the harmonic was uniformly chosen from the range between 0 and 20 units in the first experiment and from the range between 0 to 6 units in the second experiment. As a performance indicator we used the following statistic, which measures the average relative error of the period estimates:
from 0 to 0.5 units. The period of the harmonic was uniformly chosen from the range between 0 and 20 units in the first experiment and from the range between 0 to 6 units in the second experiment. As a performance indicator we used the following statistic, which measures the average relative error of the period estimates:
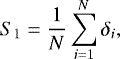 (49)
(49)
where N are the number of experiments with identical set-up, δi = Δi∕ftrue and 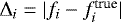 is the absolute error of the period estimate in the ith experiment using the given method (either BGLST or GLS).
is the absolute error of the period estimate in the ith experiment using the given method (either BGLST or GLS).
First we noticed that both methods performed practically identically when the sampling was uniform. This result was only weakly depending on the number of data points n and the value of the noise variance 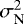 (see Fig. 2a). However, when we intentionally created such segmented sampling patterns that introduced the presence of the empirical trend, GLS started to outperform BGLST more noticeably for low n and/or high
(see Fig. 2a). However, when we intentionally created such segmented sampling patterns that introduced the presence of the empirical trend, GLS started to outperform BGLST more noticeably for low n and/or high 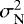 . In the latter experiment we created the datasets with sampling consisting of five data segments separated by longer gaps.In Fig. 2b we show the corresponding results. It is clear that in this special set-up the performance of BGLST gradually gets closer and closer to the performance of GLS when either n increases or
. In the latter experiment we created the datasets with sampling consisting of five data segments separated by longer gaps.In Fig. 2b we show the corresponding results. It is clear that in this special set-up the performance of BGLST gradually gets closer and closer to the performance of GLS when either n increases or 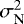 decreases. However, compared to the uniform case, the difference between the methods is bigger for low n and high
decreases. However, compared to the uniform case, the difference between the methods is bigger for low n and high 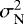 . The existence of the difference in performance is purely due to the extra parameter in BGLST model, and it is a well-known fact that models withhigher number of parameters become more prone to overfitting.
. The existence of the difference in performance is purely due to the extra parameter in BGLST model, and it is a well-known fact that models withhigher number of parameters become more prone to overfitting.
The effect of an offset in the randomly sampled data to the period estimate has been well described in Mortier et al. (2015). Using GLS or BGLS periodograms instead of LS, one can eliminate the potential bias from the period estimates owing to the mismatch between the sample mean and true mean. We conducted another experiment to show the performance comparison of the various methods in this situation. We used otherwise identical set-up as described in the second experiment above, but we fixed n = 25 to more easily control the sample mean and we also set the noise variance to zero. We measured how the performance statistic S1 of the methods changes as function of the sample mean μ (true mean was zero). The results are shown in Fig. 3. We see that the relative mean error of the LS method steeply increases with increasing discrepancy between the true and sample mean, however both the performance of BGLST and GLS stay constant and relatively close to each other. Using non-zero noise variance in the experiment increased S1 of BGLST slightly higher than GLS because of the effects described in the previous experiments, but the results were still independent of μ as expected.
 |
Fig. 2 Performance measure S1 of BGLST (red) and GLS (blue) methods as a function of the number of data points n and noise variance |
 |
Fig. 3 Performance of BGLST, GLS, and LS as function of sample mean μ. Both the true mean and slope are zero. The shaded areas around the curves on this and all subsequent plots show the 95% confidence intervals of the standard error of the statistic. |
3.2 Effect of a linear trend
Let us continue with the question of how much the presence of a linear trend in the data affects the period estimate. To measure the performance of the BGLST method introduced in Sect. 2, we compared plain GLS and GLS with preceding linear detrending (GLS-T). Throughout this section we assumed a constant noise variance. We drew the data with time span Δ T ≈ 30 time units randomly from the harmonic process with a linear trend,
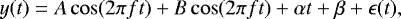 (50)
(50)
where A, B, α, and β are zero mean independent Gaussian random variables with variances 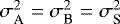 ,
, 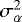 , and
, and 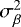 respectively, and ϵ(t) is a zero mean Gaussian white noise process with variance
respectively, and ϵ(t) is a zero mean Gaussian white noise process with variance 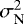 . We varied the trend variance
. We varied the trend variance 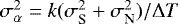 , such that k ∈ [0, 0.1, 0.2, 0.4, 0.8, 1.6]. For each k we generated N = 2000 time series, where each time the signal-to-noise ratio (
, such that k ∈ [0, 0.1, 0.2, 0.4, 0.8, 1.6]. For each k we generated N = 2000 time series, where each time the signal-to-noise ratio (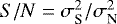 ) was drawn from [0.2, 0.8] and period P = 1∕f from [2, 2∕3ΔT]. In all experiments
) was drawn from [0.2, 0.8] and period P = 1∕f from [2, 2∕3ΔT]. In all experiments 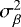 was set equal to
was set equal to 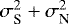 . We repeated the experiments with two forms of sampling: uniform and that one based on the samplings of MW datasets. The prior means and variances for our model were chosen according to Eq. (5).
. We repeated the experiments with two forms of sampling: uniform and that one based on the samplings of MW datasets. The prior means and variances for our model were chosen according to Eq. (5).
In these experiments we compared three different methods: the BGLST, GLS-T, and GLS. We measured the performance of each method using the statistic S1 defined in Eq. (49).
The results for the experiments with the uniform sampling are shown in Fig. 4a and with the sampling taken from the MW dataset in Fig. 4b. On both of the figures we plot the performance measure S1 as function of k. We see that when there is no trend present in the dataset (k = 0), all three methods have approximately the same average relative errors and while for the BGLST method it stays the same or decreases slightly with increasing k, for the other methods the errors start to increase rapidly. We also see that when the true trend increases then GLS-T starts to outperform GLS, however, the performance of both of these methods stays far behind from the BGLST method.
Next we illustrate the benefit of using the BGLST model with two examples in which the differences from the other models are well emphasised. For that purpose, we first generated such a dataset where the empirical slope significantly differs from the true slope. The test contained only one harmonic with a frequency of 0.014038 and a slope 0.01. We again fit three models: BGLST, GLS, and GLS-T. The comparison of the results are shown in Fig. 5. As is evident from Fig. 5a, the empirical trend 0.0053 recovered by the GSL-T method (blue dashed line) differs significantly from the true trend (black dotted line). Both the GSL and GSL-T methods performed very poorly in fitting the data, while only the BGLST model produced a fit that represents the data points adequately. Moreover, BGLST recovers very close to the true trend value 0.009781. From Fig. 5b, it is evident that the BGLST model retrieves a frequency closest to the true value, while the other two methods return values that are too low. The performance of the GLS model is the worst, as expected. The frequency estimates for BGLST, GLS-T, and GLS are correspondingly 0.013969, 0.013573, and 0.01288. This simple example shows that when there is a real trend in the data, detrending can be erroneous owing to the sampling patterns, but it still leads to better results than not detrending at all.
Finally, we would like to show a counterexample where detrending is not the preferred option. This happens when there is a harmonic signal in the data with a very long period, in this test case 0.003596. The exact situation is shown in Fig. 6a, from which it is evident that the GLS-T method can determine the harmonic variation itself as a trend component and lead to a completely erroneous fit. In Fig. 6b, we show the corresponding spectra. As expected, the GLS model, coinciding with the true model, gives the best estimate, while the BGLST model is not far off. The detrending, however, leads to significantly worse estimate. The estimates in the same order are the following: 0.003574, 0.003673, and 0.005653. The value of the trend learned by BGLST method was –0.00041, which is very close to zero.
The lastexample clearly shows that even in the simplest case of pure harmonic, if the dataset does not contain exact number of periods the spurious trend component arises. If pre-detrended, then bias is introduced into the period estimation, however, in the case of the BGLST method the sinusoid can be fitted into the fragment of the harmonic and zero trend can be recovered.
 |
Fig. 4 Results of the experiments with varying linear trend using uniform sampling (panel a) and sampling similar to MW datasets (panel b). |
 |
Fig. 5 Comparison of the results using various models. The true model of the data contains one harmonic, a trend, and additive white Gaussian noise. Panel a: Data (black crosses), BGLST model (red continuous curve), GLS-T model (blue dashed curve), GLS model (green dash-dotted curve), true trend (black dotted line), trend from BGLST model (red continuous line), and empirical trend (blue dashed line) are shown. Panel b: spectra of the corresponding models with vertical lines indicating the locations of maxima. The black dotted line shows the position of the true frequency. |
 |
Fig. 6 Comparison of the results using various models. The true model contains one long harmonic with additive white Gaussian noise. Panel a: Data (black crosses), BGLST model (red continuous curve) and its trend component (red line), GLS-T model with trend added back (blue dashed curve), empirical trend (blue dashed line), and GLS model (green dash-dotted curve) are shown. Panel b: spectra of the corresponding models with vertical lines indicating the locations of maxima. The black dotted line shows the position of the true frequency. |
3.3 Effect of a nonconstant noise variance
We continue with investigating the effect of a nonconstant noise variance to the period estimate. In these experiments the data was generated from a purely harmonic model with no linear trend (both α and β are zero). We compared the results from the BGLST to the LS method. As there is no slope and offset in the model, we set the prior means for these two parameters to zero and variances to very low values. This essentially means that we are approaching the GLS method with a zero mean. In all the experiments the time range of the observations is ti ∈ [0, T], where T = 30 units, the period is drawn from P ~Uniform(5, 15), and the signal variance is 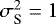 . For each experiment we drew two values for the noise variance
. For each experiment we drew two values for the noise variance 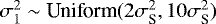 and
and 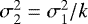 , where, k ∈ [1, 2, 4, 8, 16, 32], which are used in different set-ups as indicated in the second column of Table 1. For each k we repeated the experiments N = 2000 times.
, where, k ∈ [1, 2, 4, 8, 16, 32], which are used in different set-ups as indicated in the second column of Table 1. For each k we repeated the experiments N = 2000 times.
Let 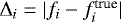 denote the absolute error of the BGLST period estimate in the ith experiment and
denote the absolute error of the BGLST period estimate in the ith experiment and 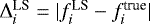 the same for the LS method. Now denoting by δi = Δi∕ftrue and
the same for the LS method. Now denoting by δi = Δi∕ftrue and 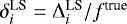 the relative errors of the corresponding period estimates, we measured the following performance statistic, which represents the relative difference in the average relative errors between the methods, i.e.
the relative errors of the corresponding period estimates, we measured the following performance statistic, which represents the relative difference in the average relative errors between the methods, i.e.
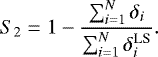 (51)
(51)
The list of experimental set-ups with the descriptions of the models are shown in Table 1. In the first experiment the noise variance linearly increases from 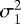 to
to 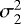 . In practice, this could correspond to decaying measurement accuracy over time. In the second experiment the noise variance abruptly jumps from
. In practice, this could correspond to decaying measurement accuracy over time. In the second experiment the noise variance abruptly jumps from 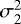 to
to 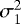 in the middle of the time series. This kind of situation could be interpreted as a change of one instrument to another more accurate instrument. In both of these experiments the sampling is uniform. In the third experiment, we used sampling patterns of randomly chosen stars from the MW dataset and the true noise variance in the generated data is set based on the empirical intra-seasonal variances in the real data. In the first two experiments the number of data points was n = 200 and in the third the number of data points was between 200 and 400, depending on the randomly chosen dataset, which we downsampled.
in the middle of the time series. This kind of situation could be interpreted as a change of one instrument to another more accurate instrument. In both of these experiments the sampling is uniform. In the third experiment, we used sampling patterns of randomly chosen stars from the MW dataset and the true noise variance in the generated data is set based on the empirical intra-seasonal variances in the real data. In the first two experiments the number of data points was n = 200 and in the third the number of data points was between 200 and 400, depending on the randomly chosen dataset, which we downsampled.
In Fig. 7a the results of various experimental set-ups are shown, where the performance statistic S2 is plotted as function of 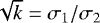 . We see that when the true noise is constant in the data (k = 1), the BGLSTmethod performs identically to the LS method while for greater values of k the difference grows bigger between the methods. For the second experiment, where the noise level abruptly changes, the advantage of using a model with nonconstant noise seems to be the best, while for the other experiments the advantage is slightly smaller, but still substantial for larger k-s.
. We see that when the true noise is constant in the data (k = 1), the BGLSTmethod performs identically to the LS method while for greater values of k the difference grows bigger between the methods. For the second experiment, where the noise level abruptly changes, the advantage of using a model with nonconstant noise seems to be the best, while for the other experiments the advantage is slightly smaller, but still substantial for larger k-s.
In Fig. 8 we show the models with maximally differing period estimates from the second experiment for 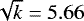 . The left column shows the situation in which the BGLST method outperforms the LS method the most and in the right column vice versa. This plot is a clear illustration of the fact that even though on average the method with nonconstant noise variance is better than LS method, for each particular dataset this might not be the case. Nevertheless it is also apparent from the figure that when the LS method is winning over BGLST method, the gap tends to be slightly smaller than in the opposite situation.
. The left column shows the situation in which the BGLST method outperforms the LS method the most and in the right column vice versa. This plot is a clear illustration of the fact that even though on average the method with nonconstant noise variance is better than LS method, for each particular dataset this might not be the case. Nevertheless it is also apparent from the figure that when the LS method is winning over BGLST method, the gap tends to be slightly smaller than in the opposite situation.
In the previous experiments the true noise variance was known, but this rarely happens in practice. However, when the data sampling is sufficiently dense, we can estimate the noise variance empirically, for example by binning the data using a window with suitable width. We now repeat the experiments using such an approach. In experiment set-ups 1 and 2, we used windows with a length of 1 unit and in the set-up 3 we used intra-seasonal variances. In the first two cases we increased the number of data points to 1000 and in the latter case we used only the real datasets that contained more than 500 points. The performance statistics forthese experiments are shown in Fig. 7b. We see that when the true noise variance is constant (k = 1) then using empirically estimated noise in the model leads to slightly worse results than with constant noise model, however, roughly starting from the value of k = 1.5 in all the experiments the former approach starts to outperform the latter. The location of the break-even point obviously depends on how precisely the true variance can be estimated from the data. This, however depends on the density of the data sampling and the length of the expected period in the data because we want to avoid counting signal variance as a part of the noise variance estimate.
Description of experimental set-ups with nonconstant noise variance.
 |
Fig. 7 Results of the experiments with known nonconstant noise variance. For the definition of S2 see text. Panel a: true noise variance is known. Panel b: noise variance is empirically estimated from the data. The black dotted horizontal lines show the break even point between LS and BGLST. |
 |
Fig. 8 Comparison of the methods for experiment with set-up 2. Panels a and b: data points with black crosses, red continuous curve indicate the BGLST model, and the blue dashed line indicates the LS model fit. Panels c and d: spectra of the models with same colours and line styles. The vertical lines correspond to the optimal frequencies found and the black dotted line shows the true frequency. The plots on two columns correspond to the biggest difference in the period estimates from both methods w.r.t. each other. On the left the BGLST method outperforms the LS method, and on the right vice versa. |
3.4 Real datasets
As the last examples we consider time series of two stars from the MW dataset. In Figs. 9 and 10 we showthe differences between period estimates for the stars HD 37394 and HD 3651 correspondingly. For both stars we see that the linear trends fitted directly to the data (blue dashed lines) significantly differ from the trend component in the harmonic model (red lines) with both types of noise models (compare the left and right columns of the plots), and consequently, also the period estimates in between the methods always tend to vary somewhat.
Especially in the case of HD 37394, the retrieved period estimates differ significantly. Assuming a constant noise variance for this star results in the BGLST and GLS/GLS-T to deviate strongly, the BGLST model producing a significantly larger period estimate. With intra-seasonal noise variance, all three estimates agree more with each other, however, BGLST still gives the longest period estimate. In the previous study by Baliunas et al. (1995), the cycle period for this star has been reported to be 3.6 yrs, which closely matches the period estimate of GLS-T estimate with constant noise variance5. For the GLS method the period estimates using constant and intra-seasonal noise variances were correspondingly 3.71± 0.02 and 5.36± 0.05 yr; for the GLS-T the values were 3.63 ± 0.02 and 5.61 ± 0.05 yr and for the BGLST model 5.84 ± 0.07 and 5.79± 0.05 yr. All the given error estimates correspond to 1σ ranges of the frequency estimates.
In the case of HD 3651, the period estimates of the models are not that sensitive to the chosen noise model, but the dependence on how the trend component is handled is significant. Interestingly, none of these period estimates match the estimate from Baliunas et al. (1995; 13.8 yr). For the GLS method the period estimates using constant and intra-seasonal noise variances were correspondingly 24.44 ± 0.29 and 23.30 ± 0.32 yr; for the GLS-T the values were 20.87 ± 0.29 and 19.65 ± 0.34 yr and for the BGLST model 16.56 ± 0.23 and 16.16 ± 0.14 yr. As can be seen from the model fits in Fig. 10a and b, they significantly deviate from the data, so we must conclude that the true model is not likely to be harmonic. Conceptually the generalisation of the model proposed in the current paper to the nonharmonic case is straightforward, but becomes analytically and numerically less tractable. Fitting periodic and quasi-periodic models to the MW data, which are based on Gaussian processes, are discussed in Olspert et al. (2018).
 |
Fig. 9 Comparison of the results for star HD 37394 using BGLST, GLS-T, and GLS models with constant noise variance in the plots in the left column and intra-seasonal noise variance in the right column. Panels a and b: data (black crosses), BGLST model (red curve), GLST-T model with trend added back (blue dashed curve), GLS model (green dash-dotted curve), the trend component of BGLST model (red line), and the empirical trend (blue dashed line) are shown. Panels c and d: spectra of the models with same colours. The dashed lines indicate the locations of the corresponding maxima. |
 |
Fig. 10 Comparison of the results for star HD 3651 using BGLST, GLS-T, and GLS models. The meaning of the panels and colour coding is identical to those of Fig. 9. |
4 Conclusions
In this paper we introduced a Bayesian regression model that involves, aside from a harmonic component, a linear trend component with slope and offset as well. The main focus of this paper is to address the effect of linear trends in data to the period estimate. We show that when there is no prior information on whether and to what extent the true model of the data contains linear trend, it is more preferable to include the trend component directly to the regression model rather than either detrend the data or opt not to detrend the data before fitting the periodic model.
We note that one can introduce the linear trend part also directly to the GLS model and use the least squares method to solve for the regression coefficients. However, based on the discussion in Sect. 2.2, one should consider adding L2 regularisation to the cost function, i.e. use the ridge regression. This corresponds to the Gaussian priors in the Bayesian approach. While using the least squares approach can be computationally less demanding, the main benefits of the Bayesian approach are the direct interpretability of the spectrum as being proportional to a probability distribution and more straightforward error and significance estimations.
In this work, we used Gaussian independent priors for the nuisance parameters θ and a uniform prior for the frequency parameter f. As mentioned, the usage of priors in our context is solely for the purpose of regularisation. However, if one has actual prior information about the parameters (the shapes of the distributions, possible dependencies between the parameters, the expected locations of higher probability mass, etc.), this could be incorporated into the model using suitable joint distribution. In principle one could also consider different forms of priors than independent Gaussian for θ, but then the problem becomes analytically intractable. In these situations one should use algorithms like Markov chain Monte Carlo (MCMC) to sample the points from the posterior distribution. The selection of uniform prior for f was also made solely to avoid losing the tractability. If one has prior knowledge about f, one could significantly narrow down the grid search interval. This idea was actually used in the current study as we were focussing only on the signals with low frequency periods. However, in the most general intractable case one should still rely on the MCMC methods.
We also showed that if the true noise variance of the data is far from being constant, then by neglecting this knowledge, period estimates start to deteriorate. Unfortunately in practice the true noise variance is almost never known and in many cases impossible to estimate empirically (e.g. sparse sampling rate compared to the true frequency). In this study we, however, focussed only on the long period search task, which made estimating the noise variance on narrow local subsamples possible. Based on the experiments we saw that if the true noise is not constant and the extremes of the S/N differ at least two times, then using a model with empirically estimated noise variance is well justified.
Acknowledgements
This work has been supported by the Academy of Finland Centre of Excellence ReSoLVE (NO, MJK, JP), Finnish Cultural Foundation grant no. 00170789 (NO) and Estonian Research Council (Grant IUT40-1; JP). MJK and JL acknowledge the “SOLSTAR” Independent Max Planck Research Group funding. The HK_Project_v1995_NSO data derive from the Mount Wilson Observatory HK Project, which was supported by both public and private funds through the Carnegie Observatories, the Mount Wilson Institute, and the Harvard-Smithsonian Center for Astrophysics starting in 1966 and continuing for over 36 yr. These data are the result of the dedicated work of O. Wilson, A. Vaughan, G. Preston, D. Duncan, S. Baliunas, and many others.
References
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Bretthorst, L. G. 1988, Bayesian Spectrum Analysis and Parameter Estimation (Berlin: Springer), 48, 209 [Google Scholar]
- Carbonell, M., Oliver, R., & Ballester, J. L. 1992, A&A, 264, 350 [NASA ADS] [Google Scholar]
- Deeming, T. J. 1975, Ap&SS, 36, 137 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Feng, F., Tuomi, M., & Jones, H. R. A. 2017, MNRAS, 470, 4794 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraz-Mello, S. 1981, AJ, 86, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B., Moorhead, A. V., & Veras, D. 2011, ArXiv e-prints [arXiv: 1107.4047] [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Astrophys. Space Sci., 39, 447 [Google Scholar]
- Mortier, A., Faria, J. P., Correia, C. M., Santerne, A., & Santos, N. C. 2015, A&A, 573, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, K. P. 2012, Machine Learning: A Probabilistic Perspective (Cambridge, MA: The MIT Press) [Google Scholar]
- Olspert, N., Lehtinen, J., Käpylä, M. J., Pelt, J., & Grigorievskiy, A. 2018, A&A, in press, DOI: 10.1051/0004-6361/201732525 [Google Scholar]
- Pelt, J. 1997, in Non-parametric Methods for Shift and Periodicity Delection in Irregularly Measured Data, eds. T. Subba Rao, M. B. Priestley, & O. Lessi, 249 [Google Scholar]
- Roberts, D. H., Lehar, J., & Dreher, J. W. 1987, AJ, 93, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Brandenburg, A. 1999, ApJ, 524, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarzenberg-Czerny, A. 1998, MNRAS, 301, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Tanner, R. W. 1948, JRASC, 42, 177 [NASA ADS] [Google Scholar]
- VanderPlas, J. T. 2017, ApJS, 236, 16 [Google Scholar]
- Vaníček P. 1971, Ap&SS, 12, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Vio, R., Andreani, P., & Biggs, A. 2010, A&A, 519, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
The implementation of the method introduced in this paper can be found at https://github.com/olspert/BGLST
Bayes factor is the ratio of the marginal likelihoods of the data under two hypothesis (usually null and an alternative). In frequentist statistics there is no direct analogy to that, but it is common to calculate the p-value of the test statistic (e.g. the χ2 statistic in period analysis). The p-value is defined as the probability of observing the test statistic under the null hypothesis to be larger than that actually observed (Murphy 2012, Chap. 5.3.3).
To be more precise, in their study they used LS with centring plus detrending, but this does not lead to a measurable difference in the period estimate compared to GLST-T for the given datasets. We also note that the datasets used in Baliunas et al. (1995) do not span until 1995, but until 1992 and for the star HD 37394 they have dropped the data prior 1980. However, we do not want to stress the exact comparison between the results, but rather show that when applied to the same dataset, the method used in their study can lead to different results from the method introduced in our study.
All Tables
All Figures
 |
Fig. 1 Illustration of importance of priors. Panel a: models fitted to the data with Gaussian priors (red continuous line) and uniform priors (blue dashed curve) for the nuisance parameters. Panel b: the spectra of the corresponding models. The black dotted line shows the position of true frequency. |
| In the text | |
 |
Fig. 2 Performance measure S1 of BGLST (red) and GLS (blue) methods as a function of the number of data points n and noise variance |
| In the text | |
 |
Fig. 3 Performance of BGLST, GLS, and LS as function of sample mean μ. Both the true mean and slope are zero. The shaded areas around the curves on this and all subsequent plots show the 95% confidence intervals of the standard error of the statistic. |
| In the text | |
 |
Fig. 4 Results of the experiments with varying linear trend using uniform sampling (panel a) and sampling similar to MW datasets (panel b). |
| In the text | |
 |
Fig. 5 Comparison of the results using various models. The true model of the data contains one harmonic, a trend, and additive white Gaussian noise. Panel a: Data (black crosses), BGLST model (red continuous curve), GLS-T model (blue dashed curve), GLS model (green dash-dotted curve), true trend (black dotted line), trend from BGLST model (red continuous line), and empirical trend (blue dashed line) are shown. Panel b: spectra of the corresponding models with vertical lines indicating the locations of maxima. The black dotted line shows the position of the true frequency. |
| In the text | |
 |
Fig. 6 Comparison of the results using various models. The true model contains one long harmonic with additive white Gaussian noise. Panel a: Data (black crosses), BGLST model (red continuous curve) and its trend component (red line), GLS-T model with trend added back (blue dashed curve), empirical trend (blue dashed line), and GLS model (green dash-dotted curve) are shown. Panel b: spectra of the corresponding models with vertical lines indicating the locations of maxima. The black dotted line shows the position of the true frequency. |
| In the text | |
 |
Fig. 7 Results of the experiments with known nonconstant noise variance. For the definition of S2 see text. Panel a: true noise variance is known. Panel b: noise variance is empirically estimated from the data. The black dotted horizontal lines show the break even point between LS and BGLST. |
| In the text | |
 |
Fig. 8 Comparison of the methods for experiment with set-up 2. Panels a and b: data points with black crosses, red continuous curve indicate the BGLST model, and the blue dashed line indicates the LS model fit. Panels c and d: spectra of the models with same colours and line styles. The vertical lines correspond to the optimal frequencies found and the black dotted line shows the true frequency. The plots on two columns correspond to the biggest difference in the period estimates from both methods w.r.t. each other. On the left the BGLST method outperforms the LS method, and on the right vice versa. |
| In the text | |
 |
Fig. 9 Comparison of the results for star HD 37394 using BGLST, GLS-T, and GLS models with constant noise variance in the plots in the left column and intra-seasonal noise variance in the right column. Panels a and b: data (black crosses), BGLST model (red curve), GLST-T model with trend added back (blue dashed curve), GLS model (green dash-dotted curve), the trend component of BGLST model (red line), and the empirical trend (blue dashed line) are shown. Panels c and d: spectra of the models with same colours. The dashed lines indicate the locations of the corresponding maxima. |
| In the text | |
 |
Fig. 10 Comparison of the results for star HD 3651 using BGLST, GLS-T, and GLS models. The meaning of the panels and colour coding is identical to those of Fig. 9. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.