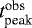| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201732270 | |
| Published online | 17 July 2018 | |
From the earliest pulses to the latest flares in long gamma-ray bursts
1
Università degli Studi dell’Insubria,
via Valleggio 11,
22100
Como, Italy
2
Dipartimento di Fisica G. Occhialini, Università di Milano Bicocca,
Piazza della Scienza 3,
20126
Milano, Italy
e-mail: m.ronchi26@campus.unimib.it
3
INAF – Osservatorio Astronomico di Brera,
via E. Bianchi 46,
23807
Merate, Italy
Received:
9
November
2017
Accepted:
11
March
2018
The prompt emission of gamma-ray bursts extends from the early pulses observed in γ-rays (>15 keV) to very late flares of X-ray photons (0.3–10 keV). The duration of prompt γ-ray pulses is rather constant, while the width of X-ray flares correlates with their peak time, suggesting a possibly different origin. However, pulses and flares have similar spectral properties. Considering internal and external shock scenarios, we derive how the energy and duration of pulses scale with their time of occurrence, and we compare this with observations. The absence of an observed correlation between the prompt emission pulse duration and its time of occurrence favours an “internal” origin and confirms earlier results. We show that the energetic and temporal properties of X-ray flares are also consistent with being produced by internal shocks between slow fireballs with a small contrast between their bulk Lorentz factors. These results relax the requirement of a long-lasting central engine to explain the latest X-ray flares.
Key words: relativistic processes / gamma rays: general / X-rays: bursts
© ESO 2018
1 Introduction
Gamma-ray bursts (GRBs) are very energetic explosions of γ-rays (prompt emission), detected in the keV–MeV energy range, which are characterised by irregular temporal profiles. Light curves show variability timescales as short as few milliseconds (Bhat et al. 1992; Walker et al. 2000; MacLachlan et al. 2013) that appear as a sequence of prompt emission pulses (PP hereafter; Fishman et al. 1993; Bhat et al. 2012). The early follow-up by the X-Ray Telescope (XRT – 0.3–10 keV) on board Swift (Gehrels et al. 2004) showed that large amplitude X-ray flares (XRF, hereafter) are often superimposed on the canonical afterglow emission (Chincarini et al. 2007, 2010; Falcone et al. 2007). Sometimes, XRF can occur even one day after the γ-ray trigger (Bernardini et al. 2011).
According to the fireball model, the prompt emission of GRBs is generated by relativistic internal shocks (IS) produced by shells that are ejected by the inner engine with random velocities (e.g., Rees & Meszaros 1994). In these shocks, a fraction of the total kinetic energy of the fireballs is converted into radiation through synchrotron and inverse Compton emission. This scenario can produce the highly variable light curve of the prompt emission (Kobayashi et al. 1997). Shocks produced by the deceleration of the relativistic outflow by the interstellar medium, external shocks (ES), have been invoked to explain the long-lasting, smoothly decaying, broad band (from the optical to the radio) afterglow emission. However, over-densities of the circum burst medium (CBM) could also produce a variable light curve (e.g., Nakar & Piran 2003).
While IS, being produced by shells with slightly different random velocities, are expected to occur at a constant distance from the central engine, the radius where shocks occur in ES increases as a result of the expanding outflow in the CBM. As a consequence, IS should differ from ES in producing pulses whose duration is not correlated with their time of occurrence. No correlation between the duration and the occurrence time of a pulse of BATSE GRBs was found (Ramirez-Ruiz & Fenimore 2000). This favoured the IS mechanism.
Swift observed X-ray pulses in the 0.3–10 keV energy range (called flares) that show a duration increasing with time (Chincarini et al. 2010; Yi et al. 2016; Kocevski et al. 2007). This property may be consistent with an ES scenario. However, XRFs have spectral properties (e.g., hard to soft evolution and harder spectral shape than the underlying afterglow component) similar to those of PP (Chincarini et al. 2006, 2007, 2010; Falcone et al. 2006; Margutti et al. 2010) and might be due to IS (Chincarini et al. 2007; Curran et al. 2008). The nature of XRFs is challenging for current models: they might demand a long-lived (hours) central engine (e.g., Yu et al. 2015) or they could indicate a short-lived central engine emitting slower shells that dissipate their energy via IS at later times (e.g., Lazzati & Perna 2007). Distinguishing between these two scenarios leads to important implications for the physics of the GRB central engine.
One leading question is whether XRF and PP share the same origin and if they are preferentially produced by IS or ES (the latter due to the interaction with over-densities in the CBM). To answer these questions, we derive under the simplest IS and ES scenarios the expected relation between the pulse duration and its time of occurrence (Sect. 2) and compare with observations (Sect. 3). Discussion and conclusions are presented in Sect. 4. We assume a standard ΛCDM flat cosmology with h = ΩΛ = 0.73.
2 Pulse width in internal/external shocks
Internal shocks are thought to be produced by random collisions between shells with different bulk Lorentz factors Γ. Two shells of equal mass m and comparable thickness δR, moving with Lorentz factors Γ2 > Γ1 ≫ 1, collide at a radius Rc ≃ β2ctc. Here radiation is produced for a timescale comparable to their crossing time. The subscript refers to the spatial ordering of the shells, with the faster (Γ 2) moving behind the slower one (Γ1).
When we assume that the two shells are separated by a distance Δ R, the collision time (as measured by an observer whose viewing angle is 90° with respectto the shells’ motion direction) is (see Lazzati et al. 1999)
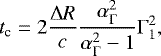 (1)
(1)
where αΓ = Γ2∕Γ1. Following Lazzati et al. (1999), we assume that all the internal (random) energy ϵ of the merged shell is converted into radiation in the collision. This gives an upper limit to the efficiency of conversion of kinetic energy into radiation:
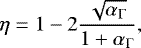 (2)
(2)
which, under the assumption of shells of equal mass, depends only on the relative speed of the colliding shells.
After their collision, the merged shells move with a bulk Lorentz factor  at first-order approximation. We also assume that the width of the merged shell does not increase substantially. An observer located along the direction of the shells’ motion will see a pulse whose duration is given by two contributions (e.g., Sari & Piran 1997; Kocevski et al. 2007): (i) the “curvature” timescale tcurv that is due to the different travel paths of photons emitted simultaneously by the spherical surface (a spherical shell with an angular scale larger than
at first-order approximation. We also assume that the width of the merged shell does not increase substantially. An observer located along the direction of the shells’ motion will see a pulse whose duration is given by two contributions (e.g., Sari & Piran 1997; Kocevski et al. 2007): (i) the “curvature” timescale tcurv that is due to the different travel paths of photons emitted simultaneously by the spherical surface (a spherical shell with an angular scale larger than 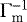 was assumed); and (ii) the “merging” timescale tmerge, that is, the difference of arrival times of photons, emitted along the line of sight, during the time necessary for the two shells to cross one another (also accounting for the relativistic Doppler effect). Therefore, the duration in the rest frame of the source is
was assumed); and (ii) the “merging” timescale tmerge, that is, the difference of arrival times of photons, emitted along the line of sight, during the time necessary for the two shells to cross one another (also accounting for the relativistic Doppler effect). Therefore, the duration in the rest frame of the source is
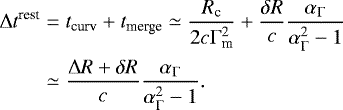 (3)
(3)
According to the standard IS model that is adopted to explain the GRB prompt emission, the relativistic collisions occur between shells that are intermittently ejected from the inner engine, with αΓ ≳2 (e.g., Rees & Meszaros 1994). Assuming that the initial separation ΔR is almost the same, we can see from Eq. (1) that the collision time tc and hence the collision radius Rc are approximately constant (assuming αΓ = 2–5, Γ 1 = 50–200 and Δ R = 109 cm, Rc is 1013−14 cm). Therefore, according to Eq. (3), the duration of pulses produced by IS is constant and should not be correlated with the occurrence time of the peaks in the light curve.
The time when pulses occur in a light curve is related to the trigger time of the detector. Therefore we need to evaluate the delay time between the arrival of the trigger photon (the first produced during the prompt phase) and the photons produced in subsequent relativistic collisions between shells. To better understand this scenario, we assume that the first γ-ray photon is produced at time tc,p at a radius Rc,p = βctc,p. We also assume that the shells producing the following flare/pulse are ejected with a delay time Δ T with respect to the first shells. Their collision occurs at a radius Rc,f and time tc,f. The observer will see the pulse after a time (Rc,p + (ΔT + tc,f − tc,p)c − Rc,f)∕c. The peak time of the pulse tpeak is further increased to Δtrest∕2 (assuming triangular shape). The rest frame peak time is
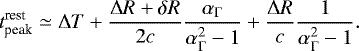 (4)
(4)
In Eq. (4) and onwards, we omit the term Rc,p − ctc,p since its contribution is negligible. If we allow αΓ to assume values lower than 2, 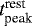 (Eq. (4)) and Δtrest (Eq. (3)) increase as αΓ approaches unity. This means that shells with a small relative speed will collide later, producing a wider pulse, and according to Eq. (2), dissipating less energy in the relativistic shock (see also Barraud et al. 2005).
(Eq. (4)) and Δtrest (Eq. (3)) increase as αΓ approaches unity. This means that shells with a small relative speed will collide later, producing a wider pulse, and according to Eq. (2), dissipating less energy in the relativistic shock (see also Barraud et al. 2005).
In the ES scenario, pulses can be produced by collisions between a relativistic fireball expanding into extended over-density regions (e.g., Dermer & Böttcher 2000, but see Nakar & Granot 2007), at rest with respect to the central engine. We assume that such CBM clumps are distributed at increasing distances from the central engine in shell-like structures. We also require that the thickness Δ L of these shell-like structures is much smaller than their extension. The interaction of the relativistic shell with such clumps could produce pulses of external origin. The main difference with respect to the IS case is that the shell now collideswith targets (the clumps) at rest so that the dissipation is more efficient by far. If the extension of the clumps is always comparable to or grater than the jet aperture, the duration of the pulses are dominated by the curvature term. Thus, the pulse duration scales with the collision radius, which increases linearly with time (R =2Γ2ct) as the shell expands into the CBM.
We consider that as the shell expands into the ISM, it collects mass and progressively slows down. Therefore, the dynamic depends on the density profile of the ISM, and it changes from one collision to another one. We assume that the dissipation radius (at least of the order of the deceleration radius) is larger than Δ L. The leading term in the pulse duration is due to the curvature effect.
The ISM density profile is described as n = n0r−α (α ≥ 0), where n0 represents the particle density at some characteristic radius R0 close to the GRB progenitor (Chevalier & Li 1999; Panaitescu & Kumar 2000). The shell bulk Lorentz factor (Blandford & McKee 1976; Nava et al. 2013) for an adiabatic blast-wave is
![\begin{equation*}\mathrm{\Gamma}(r)=\left[\frac{ E_{\textrm{k}} (17-4 \alpha)}{16 \pi n_0 m_{\textrm{p}} c^2} \right]^{1/2} r^{-(3-\alpha )/2} .\end{equation*}](/articles/aa/full_html/2018/07/aa32270-17/aa32270-17-eq8.png) (5)
(5)
Computing the radius R of fireball at a time t, we obtain the expression of the pulse duration:
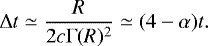 (6)
(6)
Therefore, considering the ES scenario of a shell decelerated by the CBM where pulses are due to over-densities encountered along its path, the pulse width Δ t should increase linearly with time.
In summary, for the prompt phase, IS and ES scenarios predict a pulse duration that should be constant or increasing with time, respectively. So far, observations seem to favour the IS scenario for the prompt phase. The origin of XRF is still controversial. However, as seen above, IS appears to be a viable mechanism to produce their temporal and energetic features (see Sects. 3 and 4).
3 Duration versus peak time
In this section we compare the simple predictions derived in Sect. 2 with available observations. We consider two samples: thePP of Fermi/GBM bursts that were recently published by Bhat et al. (2012), and an ensemble of XRF detected by Swift/XRT (in the [0.3–10] keV energy range) that were published in different papers (Chincarini et al. 2010; Bernardini et al. 2011; Yi et al. 2016). Below we summarize the main features of these samples. Our aim is to study how the temporal properties (duration and peak time) correlate and how the pulse duration and energetic evolves with the pulse time from the earliest PP to the latest XRF.
For the PP we consider the sample of bright GRBs analysed in Bhat et al. (2012, B12 hereafter). They selected 32 bright long GRBs (only 7 with measured redshift), detected by Fermi in its first year of activity, for which the product of their fluence and peak flux is larger than 10−4 erg photons cm−4 s−1. B12 decomposed the observed light curves (considering the data of the NaI [8 keV–1 MeV] and the BGO [200 keV–10 Me V] detectors) as the superposition of log-normal pulses and obtained for each GRB in their sample a set of pulse duration, peak time, and intensity. B12 analysed light curves with a variable time resolution between 25 and 50 ms in order to maximise the number of fitted pulses. Since we are interested in the pulse duration, we considered only the pulses with duration >25 ms, that is, reasonably larger than the time resolution of the light curves analysed by B12. We extracted from their compilation 374 pulses obtained from the analysis of the light curves of the NaI detectors and 228 pulses from the data of the BGO detectors.
For the XRF, different samples are published in the literature: Chincarini et al. (2010, C10), Bernardini et al. (2011, B11), and Yi et al. (2016, Y16). C10 analysed 113 early flares (tpeak < 1000 s) detected by Swift between April 2005 and March 2008. B11, extending their study to flares detected up to December 2009, considered 36 late flares (tpeak > 1000 s). When these two samples are combined, the total number of flares amounts to 149, 59 of which belong to GRBs with measured redshift. Recently, Y16 enlarged the sample of XRFs considering all GRBs up to March 2015. Their catalogue contains 468 bright and significant XRFs, 200 of which have a known redshift. We collected the flares from these three works. The flare durations are estimated differently in these samples: C10 and B11 used the Norris function (Norris et al. 2005) to fit flare light-curves and derived the flare width as the difference between the two characteristic e-folding intensity times along the rising/decaying fitted profile. Therefore, the early and late flares of C10 and B11, sharing the same method, provide a uniform estimate of flare durations. Y16 defined the duration as the difference between the intersection points of the flare-fitted profile and the underlying power-law fitted continuum. Because of these different operative definitions of duration, we verified for the flares in common between C10+B11 and Y16 that the KS probability that they are drawn from the same parent population is >0.1 when the values of Y16 are lowered systematically by a factor 2.5. However, for our analysis, we used the values of Y16 without applying any correction factor. We note that if the durations reported by Y16 were lowered by a factor of 2, they would overlap the C10+B11 points better in Fig. 1, for instance, which would increase the correlation with the peak time.
Figure 1 shows the (observed) duration Δ tobs of pulses as a function of the observed time of the pulse peak 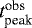 . Prompt emission pulses obtained from B12 are shown by the purple squares and red diamonds (corresponding to BGO and NaI data, respectively), and XRFs are shown by the orange points (Y16), green asterisks (B11), and cyan crosses (C10). Peak times are given with respect to the trigger time of individual GRBs they belong to.
. Prompt emission pulses obtained from B12 are shown by the purple squares and red diamonds (corresponding to BGO and NaI data, respectively), and XRFs are shown by the orange points (Y16), green asterisks (B11), and cyan crosses (C10). Peak times are given with respect to the trigger time of individual GRBs they belong to.
The distribution of PP and XRF in the plane of Fig. 1 seems to describe an overall almost linear continuum extending from short-duration (e.g., 0.01 seconds) early (1 s post trigger) pulses to extremely long and late flares (up to 11 days after the trigger and with comparable duration). We note that a possible selection effect on XRF is due to the time needed for XRT to repoint the GRB. Typically, this time is 1 minute, which is close to the division between PP and XRF in Fig. 1.
We studied the possible correlation between the pulse duration and its peak time in Fig. 1. Considering PP and XRF as two distinct populations, we find a correlation (stronger and more significant for flares) between the pulse duration Δ tobs and the peak time 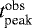 . The Spearman correlation coefficient and its chance probability are r = 0.31 and P ~ 10−15, respectively, for prompt pulses (considering NaI and BGO pulses together, i.e., purple squares and red diamonds in Fig. 1). For XRF, distributed in a larger region of the Δ tobs–
. The Spearman correlation coefficient and its chance probability are r = 0.31 and P ~ 10−15, respectively, for prompt pulses (considering NaI and BGO pulses together, i.e., purple squares and red diamonds in Fig. 1). For XRF, distributed in a larger region of the Δ tobs–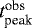 plane with respect to PP, we find r = 0.60 (P ~ 10−61). With the null hypothesis that the two quantities are not correlated and assuming a confidence level of 5%, we have to reject the null hypothesis if the chance probability is lower than P = 0.05. We note that the duration and peak time of late-time flares, that is, flares with duration > 104 s, might suffer from the difficulty of Swift/XRT to continuously follow the flare emission along its orbit. Bernardini et al. (2011) and Yi et al. (2016) considered only flares with a well-covered light curve (i.e., rise, peak, and decay). We verified, however, that the correlation between the flare duration and its peak time holds when we conservatively consider only early- or intermediate-duration flares. We only considered flares with duration <103 s and performed the correlation analysis. We find a correlation coefficient of 0.42 and a chance probability of 10−23.
plane with respect to PP, we find r = 0.60 (P ~ 10−61). With the null hypothesis that the two quantities are not correlated and assuming a confidence level of 5%, we have to reject the null hypothesis if the chance probability is lower than P = 0.05. We note that the duration and peak time of late-time flares, that is, flares with duration > 104 s, might suffer from the difficulty of Swift/XRT to continuously follow the flare emission along its orbit. Bernardini et al. (2011) and Yi et al. (2016) considered only flares with a well-covered light curve (i.e., rise, peak, and decay). We verified, however, that the correlation between the flare duration and its peak time holds when we conservatively consider only early- or intermediate-duration flares. We only considered flares with duration <103 s and performed the correlation analysis. We find a correlation coefficient of 0.42 and a chance probability of 10−23.
Since both Δ tobs–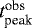 are computed in the observer frame, we verified that the correlations are not induced by the common redshift dependence. Since only a few bursts in B12 sample have measured z, we performed a Monte Carlo simulation by randomly generating redshifts from the GRB formation rate (as reported by Li 2008; Pescalli et al. 2016). We created 104 random samples for which we computed the correlation coefficient. For XRFs, we considered the 259 bursts with measured redshifts. We computed the partial correlation coefficient accounting for the common dependence on z of Δ tobs and
are computed in the observer frame, we verified that the correlations are not induced by the common redshift dependence. Since only a few bursts in B12 sample have measured z, we performed a Monte Carlo simulation by randomly generating redshifts from the GRB formation rate (as reported by Li 2008; Pescalli et al. 2016). We created 104 random samples for which we computed the correlation coefficient. For XRFs, we considered the 259 bursts with measured redshifts. We computed the partial correlation coefficient accounting for the common dependence on z of Δ tobs and 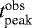 . This test also shows that the correlation found in XRF is solid and not induced by z. For PP, we again find no significant correlation.
. This test also shows that the correlation found in XRF is solid and not induced by z. For PP, we again find no significant correlation.
In order to verify whether there is a correlation within individual bursts, we can compute the correlation coefficient between the pulse duration and its peak time within single events. However, while for XRF there are only a handful of events with more than 4 flares, which prevents assessing the significance of the correlation, it is possible to perform such a test with the PP. We considered within the sample of 32 GRBs of B12 the 16 events with more than 10 pulses. For these we computed individually the correlation coefficient between the duration of the pulses and their time of occurrence. The results are shown in the bottom right inset of Fig. 1. We note that in most cases, no significant correlation is present (i.e., the chance probability is >0.1). These tests suggest that on average, no correlation is present between the pulse width and its time of appearance in PP, as originally found by Ramirez-Ruiz & Fenimore (2000), while a positive correlation exists in XRF (Chincarini et al. 2010; Yi et al. 2016; Kocevski et al. 2007).
Ramirez-Ruiz & Fenimore (2000) considered GRBs detected by BATSE, aligned the light curves to the time of the brightest peak during individual bursts, and normalised the peak-aligned light curves. However, their analysis missed the possible corrections for the redshift on energy and time.
In order to verify that their results include the corrections for z, we selected another sample of Fermi long GRBs (T90 > 2 s) with redshift measurement in the Fermi database (the sample of B12 contains only 7/32 GRBs with z). We find 100 bursts (from GRB 080804 to GRB 160629). We excluded 32 bursts with a signal-to-noise ratio (S/N) lower than 3, GRB 130427, which saturated the Fermi/GBM detectors, and GRB 120624 because the TTE data (necessary to produce high-resolution light curves) were only partially available due to the instrument slewing (Gruber et al. 2012, GCN #13377). The S/N was calculated as 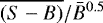 , where S is the signal and B the background. The background was fitted with a polynomial function over two time intervals selected after and before the temporal region containing the event of interest. For the 64 remaining bursts, we extracted the light curves in the common [72, 800] keV rest frame energy range with 256 ms temporal resolution, from the most illuminated NaI detector. In this energy range, NaI detectors have an almost constant response efficiency. The background-subtracted light curves were converted into rest frame times and were resampled on a common time grid. The resolution of the new time grid was chosen in order to faithfully reproduce the original light curves without losing any information on the time structure and variability.
, where S is the signal and B the background. The background was fitted with a polynomial function over two time intervals selected after and before the temporal region containing the event of interest. For the 64 remaining bursts, we extracted the light curves in the common [72, 800] keV rest frame energy range with 256 ms temporal resolution, from the most illuminated NaI detector. In this energy range, NaI detectors have an almost constant response efficiency. The background-subtracted light curves were converted into rest frame times and were resampled on a common time grid. The resolution of the new time grid was chosen in order to faithfully reproduce the original light curves without losing any information on the time structure and variability.
We applied the average peak alignment (APA) method (Mitrofanov et al. 1996) by dividing light curves into three equal parts (according to the rest frame T90 of each bursts). These are the sectors shown in Fig. 2 with different colours. The uncertainty on the pulse-aligned signal (solid line in Fig. 2) is computed as the standard deviation of the signal in each bin. Since secondary peaks are not aligned in time, this results in a large dispersion of the curve in addition to the main (aligned) peak. Following Ramirez-Ruiz & Fenimore (2000), we also separately analysed GRBs with T90 > 20 s and GRBs with T90 < 20 s with the APA method. Even considering these subsamples, we find similar results to those shown in Fig. 2.
By visual inspection of Fig. 2, we confirm that there is no evolution of the pulse width with time during the prompt emission phase of GRBs, even accounting for the energy and time redshift corrections. However, the pulse alignment method has some limitations: it allows us to compare preferentially the main emission episodes of different light curves, and it is rather less sensitive to the whole emission (and weaker pulses) of the GRB. The wings of theprofiles in Fig. 2 show the large uncertainties due to the great diversity of temporal profiles.
In order to further support these results, we also computed the average pulse duration evolution along the GRB. To this aim, we studied the average evolution of the normalised pulse width W∕⟨W⟩ of every single prompt pulse in B12 (purple squares and red diamonds in Fig. 1). We divided each light curve into five sectors, which are fractions of the total GRB duration. For each sector, we renormalised every single pulse to the average duration of all the pulses belonging to the same GRB and thus averaged all the normalised pulses in the same sector. Figure 3 shows the evolution with time of W∕⟨W⟩ for the NaI andBGO pulses. Errors represent the 68% confidence interval of the normalised pulse width.
In the barycentre of the data points, we fitted a linear function W∕⟨W⟩ = mt + q, finding m = 0.1 ± 1.3, q = −0.06 ± 0.34 (χ2 = 0.24) and m = 0.8 ± 1.3, q = −0.04 ± 0.39 (χ2 = 0.15) for NaI and BGO pulses, respectively. The fits and their uncertainty are shown by the orange lines and yellow shaded regions in Fig. 3. These results confirm that the pulse width remains constant with time. The average values of W∕⟨W⟩ of the five sectors and their errors are reported in Table 1.
 |
Fig. 1 Observer frame pulse duration Δtobs vs. the pulse occurrence time (peak time – |
 |
Fig. 2 Peak time aligned signal for the three sectors identified within each GRB. Different combinations of colours and line styles refer to different sectors. |
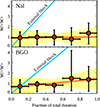 |
Fig. 3 Average evolution of the normalised pulse width with time. The orange solid line represents the linear fit and the yellow shadow the associated uncertainty region. The blue line is the expected behaviour assuming as emission mechanism ES that occur at increasing distance. The top and bottom panels show the results obtained using the pulses of B12 obtained from the NaI and BGO BATSE light curves, respectively. |
Mean values of the normalised width W∕⟨W⟩ in each sector with associated greater and smaller estimated errors and relative number of pulses within the bin.
4 Internal versus external shocks
The blue lines (normalised to the first data point) in Fig. 3 show how the pulse width should increase with time in the ES scenario (Eq. (6)). The absence of a correlation between the pulse width and the peak time (shown by the correlation analysis presented in Sect. 2) and the almost constant average pulse width along the GRB light curves (as found in Fig. 2) favours IS as the leading mechanism for the origin of the dissipation associated with the γ-ray emission of GRBs.
The linear increase of the XRF duration with time (Fig. 1) has been interpreted as a signature of their origin from ES generated by the interaction of the blast wave with shell-like over-dense regions located at increasing distance from the central engine (see also Wang & Loeb 2000; Lazzati et al. 2002; Heyl & Perna 2003). Chincarini et al. (2007) also discussed this mechanism and considered the global fireball deceleration, which could produce the superposition of flares with a monotonically decaying continuum emission (i.e., the standard afterglow).
The distribution of the PP and XRF in Fig. 1 suggests a continuous and monotonic trend. This motivated us to also explore the possibility that XRF can have an internal origin. The IS scenario predicts a constant pulse width and would apparently be disfavoured. However, for the IS case, we assumed that the shock is produced at a constant distance from the central engine. When we relax this assumption, as we showed in Sect. 2, it is possible to also explain XRF through IS produced by shells with slightly different bulk velocities. Additionally, another property of XRF that is expected to be consistent with this interpretation is their energetics. Early flares show a possible decreasing isotropic equivalent energy as a function of their time of occurrence, as pointed out by Margutti et al. (2011). We computed the isotropic equivalent energy of XRFs as 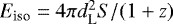 , where S is the fluence in the XRT energy range. Figure 4 shows Eiso for XRFs with measured z as a function of the rest frame peak time
, where S is the fluence in the XRT energy range. Figure 4 shows Eiso for XRFs with measured z as a function of the rest frame peak time 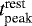 (different symbols refer to different samples, see Sect. 3). Figure 4 shows that there is a trend: flares that occur later are less energetic. We investigated whether this trend might be the result of a decreasing efficiency of IS. We assumed that two shells are created at two different times and have very similar velocities. The smaller the velocity difference, the longer it takes for them to collide, and the lower the produced energy, because their relative kinetic energy is low. In this case, we do expect a trend: the flare Eiso should decrease with
(different symbols refer to different samples, see Sect. 3). Figure 4 shows that there is a trend: flares that occur later are less energetic. We investigated whether this trend might be the result of a decreasing efficiency of IS. We assumed that two shells are created at two different times and have very similar velocities. The smaller the velocity difference, the longer it takes for them to collide, and the lower the produced energy, because their relative kinetic energy is low. In this case, we do expect a trend: the flare Eiso should decrease with 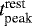 . In order to verify this, we derived how the energy released during the flare scales with the time of occurrence of the flare (Eq. (4)). For the sake of simplicity, we assumed that the shell thickness is equal to their separation (δR ≃ΔR). Equation (4) becomes
. In order to verify this, we derived how the energy released during the flare scales with the time of occurrence of the flare (Eq. (4)). For the sake of simplicity, we assumed that the shell thickness is equal to their separation (δR ≃ΔR). Equation (4) becomes
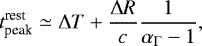 (7)
(7)
where ΔR represents the separation of the shells producing XRF.
To evaluate the time of occurrence of flares 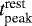 , we allowed ΔT, Δ R, and αΓ to vary in the other two terms.
, we allowed ΔT, Δ R, and αΓ to vary in the other two terms.
An upper limit on the isotropic energy Eiso released in form of radiation during the flare can be derived by applying the efficiency factor η (Eq. (2)) to an initial isotropic equivalent kinetic energy Ekin (fixed at 1054 erg). Thus, knowing how the peak time and the efficiency vary with respect to αΓ (fixing all other parameters), we can determine the change in emitted energy with respect to the time when the pulse occurs. Combining Eqs. (2) and (7), we derived the analytic expression linking Eiso and 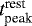 :
:
![\begin{equation*} E_{\textrm{iso}} = E_{\textrm{kin}} \left\lbrace 1- \frac{2\sqrt{c(t_{\textrm{peak}}^{\textrm{rest}}-\mathrm{\Delta} T)\left[ \mathrm{\Delta} R + c(t_{\textrm{peak}}^{\textrm{rest}}-\mathrm{\Delta} T \right]}}{\mathrm{\Delta} R + 2c(t_{\textrm{peak}}^{\textrm{rest}}-\mathrm{\Delta} T)} \right\rbrace .\end{equation*}](/articles/aa/full_html/2018/07/aa32270-17/aa32270-17-eq22.png) (8)
(8)
Figure 4 shows the curves obtained by assuming Δ R = 7 × 1010 (7 × 1012) cm and Δ T = 30 (1000) s as the solid (dashed) red line. Interestingly, independently of the parameter choice, for relatively low values of αΓ (in the limit of shells with slightly different bulk Lorentz factors), the energy released in the flares scales as t−2. These curves show that for some particular combination of parameters, it is possible to produce flares and also to consistently produce an energy of the flares that decreases with the flare occurrence time.
The same scenario allows us to derive the width of the flares as a function of their peak time. Assuming again δR ≃ΔR from Eq. (3), we obtain the rest frame pulse duration:
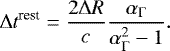 (9)
(9)
Combining this equation with Eq. (7), we obtain the dependence of Δ trest on the peak time:
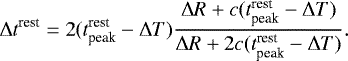 (10)
(10)
This relation is shown by the red curve in Fig. 5: points show the data in the rest frame (for XRF with measured redshifts), and the curve is obtained by assuming Δ R = 7 × 1010 cm and Δ T = 30 s. We are able to explain the increasing duration of the flares with time. The leading dependence of the flare properties (temporal and energetic) is from αΓ. The smaller αΓ (i.e., shells with only slightly different bulk Lorentz factors), the longer the flare duration and its occurrence time and the lower the released energy. With this simple model, we do not aim to derive the parameters of the shells; this is beyond the scope of the present work. Our simple approach considers only two shell encounters. It can explain the overall temporal and energetic tendency of the majority of flares as a succession of IS with decreasing values of αΓ. When we allow for some dispersion of free parameters, it might be possible to account for the dispersion of the XRF in Figs. 4 and 5. Very late flares could still be explained by choosing a particular set of parameters (e.g., extreme values), therefore it seems reasonable to consider the possibility that their origin may be different as well.
 |
Fig. 4 Isotropic energy (computed in the XRT energy range) of XRF versus their rest frame peak time. The right-hand vertical axis shows the values of αΓ (rescaled by 1) corresponding to the values of Eiso through Eq. (2). Different symbols and colours refer to different samples collected from the literature. Orange points, green asterisks, and cyan crosses are associated with XRF (only those with a measured redshift) from Yi et al. (2016), Bernardini et al. (2011), and Chincarini et al. (2010), respectively. The solid (dashed) red line shows the behaviour of the isotropic energy vs. flare peak time predicted considering two shells emitted with a delay Δ T = 30 (1000) s with respect to the start of the prompt emission and with a separation Δ R = 7 × 1010 (7 × 1012) cm. |
5 Discussion and conclusion
We considered the possible dependence of the pulse width on time in GRBs by combining PP with XRF. It is known that PP do not show an increase of the pulse width with time (Ramirez-Ruiz & Fenimore 2000). XRF, instead, show a nearly linear increase of their width with time (Chincarini et al. 2010; Yi et al. 2016; Kocevski et al. 2007). Figure 1 shows PP (from the sample of B12) and XRFs (from the samples of C10, B11, and Y16).
Internal shocks predict that the dissipation of energy between shells coasting with slightly different bulk Lorentz factor should produce random pulses whose duration is uncorrelated with their time of occurrence. On the other hand, the flare width has been observed to increase with time and has so far been considered a signature in favour of an external origin. In this scenario, the production of flares occurs in the interaction of a decelerating blast wave with interstellar medium over-densities located at increasing distance from the central engine. In these two scenarios, the dissipation at increasing radii (as in ES) or at a constant distance (as in IS) determines whether the pulse duration increases with time.
We verified with three different methods (Fig. 1 – bottom right inset, Figs. 2 and 3) and with two independent samples of PP (pulses obtained by the deconvolution of bright Fermi bursts – from B12 – and a sample of 100 GRBs with redshift whose light curves were analysed in this work) that PP show no correlation between their duration and their time of occurrence. Our results fully confirm those obtained with the BATSE data by Ramirez-Ruiz & Fenimore (2000). Although the emission during the prompt phase is highly variable, it can be described as emission due to IS that occur almost at the same distance from the central engine.
XRFs exhibit an (almost linear) increase of their duration with time. Moreover, their peak luminosity Lp anti-correlates with the peak time tpeak: for early flares (tpeak < 1000 s, Chincarini et al. 2010; Margutti et al. 2011), Lp ∝ t−2.7, and becomes shallower, Lp ∝ t−1.7, for late flares (Bernardini et al. 2011). As a consequence (as noted by Margutti et al. 2011), the energy released during the flares should scale as t−1.7 (t−0.7 for late-time flares).
The origin of XRFs is debated in the literature. Temporal and spectral properties of XRFs have led different authors to ascribe them to internal processes, such as dissipation due to the late-time activity of the inner engine (Falcone et al. 2006, 2007; Lazzati & Perna 2007; Maxham & Zhang 2009). Alternatively, XRFs might be produced by ES with over-dense regions of the interstellar medium (e.g., Wang & Loeb 2000; Lazzati et al. 2002; Heyl & Perna 2003; Nakar & Granot 2007) or by the long-lived reverse shock interacting with the tail of the ejecta (Hascoet et al. 2015).
Based on the distribution of PP and XRF in the plane of Fig. 1, we considered the possibility that XRF might also be produced by IS between shells emitted with a certain initial separation and a certain (even small) temporal delay with respect to the prompt shell. If these shells are characterized by low values of αΓ, the time of their encounter is delayed (and therefore the shock development). Later flares last longer and are less efficient in emitting radiation. These results, shown with the red model curves in Figs. 4 and 5, are consistent with the distribution of data in these planes. In this scenario, the leading parameter is the relatively low ratio between the shells’ Lorentz factors, parameterised by αΓ. The asymptotic behaviour, for small αΓ, is approximately t−2, in agreement with the E ∝ LpΔt ∝ t−1.7 also marginally shown by the early flares in Fig. 4. This behaviour also seems to explain the shape of the left boundary of the distribution in the region populated by XRF with low energies and peak time.
We showed that it is possible to explain the energetic and temporal properties of XRF as the result (under appropriate assumptions) of classical IS between a fireball ejected during the prompt emission phase. We do not require that the inner engine is active until late times: late flares, characterised by lower energies, can be produced by relativistic shocks between fireballs with a Lorentz factor ratio αΓ very close to one.
Our results pose the question on the mechanism that is responsible for pairs of shells with largely different bulk Lorentz factors (large Γ -contrasts) early on, producing the prompt emission, and pairs of shells with smaller Γ -contrast later, producing the XRF. While the answer to this question is beyond the scope of the present paper, one possible idea has been suggested (Ghisellini et al. 2007; Ghisellini et al. 2009), suggesting that there can be two phases of accretion onto the black hole.
The first is the accretion of the very dense material left over by the collapse of the stellar core. This dense material can sustain very strong magnetic fields that can extract the spin energy of the black hole. The power thus extracted is very great, allowing the formation of shells of very large Γ -factors. If the accretion is modulated or quasi-intermittent, then it is possible to form shells with very different energetics and bulk Lorentz factors. This phase is followed by the accretion of fallback material, which is less dense. This corresponds to the extraction of lower spin energy from the black hole, and presumably both the maximum and the average values of the bulk Lorentz factors are lower, as is the
Γ -contrast between consecutive shells.
 |
Fig. 5 Rest frame duration vs. occurrence time for XRFs. The right-hand vertical axis shows the values of αΓ (rescaled by 1) corresponding to the values of Δtrest through Eq. (10). Different symbols and colours refer to different sources found in the literature for these parameters. Orange points, green asterisks, and cyan crosses are associated with XRF (only those with a measured redshift) from Yi et al. (2016), Bernardini et al. (2011), and Chincarini et al. (2010), respectively. The red solid line shows the expected relation between the flare width and the time of the flare in the IS shock model (it is obtained by adopting Δ T = 30 s and Δ R = 7 × 1010 cm). |
Acknowledgments
We thank the referee for the valuable comments and suggestions that helped us improve the manuscript. We acknowledge grant 2014 PRIN-INAF for financial support. MR thanks the Brera Observatory for the kind hospitality during his graduatework.
References
- Barraud, C., Daigne, F., Mochkovitch, R., & Atteia, J. L. 2005, A&A, 440, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernardini, M. G., Margutti, R., Chincarini, G., Guidorzi, C., & Mao, J. 2011, A&A, 526, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhat, P. N., Fishman, G. J., Meegan, C. A., et al. 1992, Nature, 359, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Bhat, P. N., Briggs, M. S., Connaughton, V., et al. 2012, ApJ, 744, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & McKee, C. F. 1976, Phys. Fluids, 19, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Li, Z.-Y. 1999, ApJ, 520, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Chincarini, G., Moretti, A., Romano, P., et al. 2006, Nuovo Cimento B Serie, 121, 1307 [NASA ADS] [Google Scholar]
- Chincarini, G., Moretti, A., Romano, P., et al. 2007, ApJ, 671, 1903 [NASA ADS] [CrossRef] [Google Scholar]
- Chincarini, G., Mao, J., Margutti, R., et al. 2010, MNRAS, 406, 2113 [NASA ADS] [CrossRef] [Google Scholar]
- Curran, P. A., Starling, R. L. C., O’Brien, P. T., et al. 2008, A&A, 487, 533 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dermer, C. D., & Böttcher, M. 2000, ApJ, 534, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Falcone, A. D., Burrows, D. N., Lazzati, D., et al. 2006, ApJ, 641, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Falcone, A. D., Morris, D., Racusin, J., et al. 2007, ApJ, 671, 1921 [NASA ADS] [CrossRef] [Google Scholar]
- Fishman, G. J., Meegan, C. A., Wilson, R. B., et al. 1993, A&AS, 97, 17 [NASA ADS] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Ghirlanda, G., Nava, L., & Firmani, C. 2007, ApJ, 658, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Nardini, M., Ghirlanda, G., & Celotti, A. 2009, MNRAS, 393, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Gruber, D., Burgess, J. M., & Connaughton, V. 2012, GRB Coordinates Network, Circular Service, 13377, 1 [Google Scholar]
- Hascoet, R., Beloborodov, A. M., Daigne, F., & Mochkovitch, R. 2015, ArXiv e-prints [arXiv:1503.0833] [Google Scholar]
- Heyl, J. S., & Perna, R. 2003, ApJ, 586, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, S., Piran, T., & Sari, R. 1997, ApJ, 490, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Kocevski, D., Butler, N., & Bloom, J. S. 2007, ApJ, 667, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Lazzati, D., & Perna, R. 2007, MNRAS, 375, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Lazzati, D., Ghisellini, G., & Celotti, A. 1999, MNRAS, 309, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Lazzati, D., Rossi, E., Covino, S., Ghisellini, G., & Malesani, D. 2002, A&A, 396, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, L.-X. 2008, MNRAS, 388, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- MacLachlan, G. A., Shenoy, A., Sonbas, E., et al. 2013, MNRAS, 432, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Guidorzi, C., Chincarini, G., et al. 2010, MNRAS, 406, 2149 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Bernardini, G., Barniol Duran, R., et al. 2011, MNRAS, 410, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Maxham, A., & Zhang, B. 2009, ApJ, 707, 1623 [NASA ADS] [CrossRef] [Google Scholar]
- Mitrofanov, I. G., Chernenko, A. M., Pozanenko, A. S., et al. 1996, ApJ, 459, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E., & Granot, J. 2007, MNRAS, 380, 1744 [NASA ADS] [CrossRef] [Google Scholar]
- Nakar, E., & Piran, T. 2003, ApJ, 598, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Nava, L., Sironi, L., Ghisellini, G., Celotti, A., & Ghirlanda, G. 2013, MNRAS, 433, 2107 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. P., Bonnell, J. T., Kazanas, D., et al. 2005, ApJ, 627, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Kumar, P. 2000, ApJ, 543, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Pescalli, A., Ghirlanda, G., Salvaterra, R., et al. 2016, A&A, 587, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramirez-Ruiz,E., & Fenimore, E. E. 2000, ApJ, 539, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., & Meszaros, P. 1994, ApJ, 430, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., & Piran, T. 1997, ApJ, 485, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, K. C., Schaefer, B. E., & Fenimore, E. E. 2000, ApJ, 537, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X., & Loeb, A. 2000, ApJ, 535, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S.-X., Xi, S.-Q., Yu, H., et al. 2016, ApJS, 224, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Y. B., Wu, X. F., Huang, Y. F., et al. 2015, MNRAS, 446, 3642 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mean values of the normalised width W∕⟨W⟩ in each sector with associated greater and smaller estimated errors and relative number of pulses within the bin.
All Figures
 |
Fig. 1 Observer frame pulse duration Δtobs vs. the pulse occurrence time (peak time – |
| In the text | |
 |
Fig. 2 Peak time aligned signal for the three sectors identified within each GRB. Different combinations of colours and line styles refer to different sectors. |
| In the text | |
 |
Fig. 3 Average evolution of the normalised pulse width with time. The orange solid line represents the linear fit and the yellow shadow the associated uncertainty region. The blue line is the expected behaviour assuming as emission mechanism ES that occur at increasing distance. The top and bottom panels show the results obtained using the pulses of B12 obtained from the NaI and BGO BATSE light curves, respectively. |
| In the text | |
 |
Fig. 4 Isotropic energy (computed in the XRT energy range) of XRF versus their rest frame peak time. The right-hand vertical axis shows the values of αΓ (rescaled by 1) corresponding to the values of Eiso through Eq. (2). Different symbols and colours refer to different samples collected from the literature. Orange points, green asterisks, and cyan crosses are associated with XRF (only those with a measured redshift) from Yi et al. (2016), Bernardini et al. (2011), and Chincarini et al. (2010), respectively. The solid (dashed) red line shows the behaviour of the isotropic energy vs. flare peak time predicted considering two shells emitted with a delay Δ T = 30 (1000) s with respect to the start of the prompt emission and with a separation Δ R = 7 × 1010 (7 × 1012) cm. |
| In the text | |
 |
Fig. 5 Rest frame duration vs. occurrence time for XRFs. The right-hand vertical axis shows the values of αΓ (rescaled by 1) corresponding to the values of Δtrest through Eq. (10). Different symbols and colours refer to different sources found in the literature for these parameters. Orange points, green asterisks, and cyan crosses are associated with XRF (only those with a measured redshift) from Yi et al. (2016), Bernardini et al. (2011), and Chincarini et al. (2010), respectively. The red solid line shows the expected relation between the flare width and the time of the flare in the IS shock model (it is obtained by adopting Δ T = 30 s and Δ R = 7 × 1010 cm). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.