| Issue |
A&A
Volume 611, March 2018
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201732045 | |
| Published online | 04 April 2018 | |
Diffuse γ-ray emission in the vicinity of young star cluster Westerlund 2
1
Max-Planck-Institut für Kernphysik,
PO Box 103980,
69029 Heidelberg,
Germany
e-mail: ryang@mpi-hd.mpg.de
2
Institute for Space Sciences (CSIC–IEEC),
Campus UAB, Carrer de Can Magrans s/n,
08193 Barcelona,
Spain
3
Dublin Institute for Advanced Studies,
31 Fitzwilliam Place,
Dublin 2,
Ireland
Received:
4
October
2017
Accepted:
17
December
2017
We report the results of our analysis of the publicly available data obtained by the Large Area Telescope (LAT) on board the Fermi satellite towards the direction of the young massive star cluster Westerlund 2. We found significant extended γ-ray emission in the vicinity of Westerlund 2 with a hard power-law energy spectrum extending from 1 to 250 GeV with a photon index of 2.0 ± 0.1. We argue that amongst several alternatives, the luminous stars in Westerlund 2 are likely sites of acceleration of particles responsible for the diffuse γ-ray emission of the surrounding interstellar medium. In particular, the young star cluster Westerlund 2 can provide sufficient non-thermal energy to account for the γ-ray emission. In this scenario, since the γ-ray production region is significantly larger than the area occupied by the star cluster, we conclude that the γ-ray production is caused by hadronic interactions of accelerated protons and nuclei with the ambient gas. In that case, the total energy budget in relativistic particles is estimated of the order of 1050 erg.
Key words: gamma rays: ISM / cosmic rays
© ESO 2018
1 Introduction
Westerlund 2 is one of the most massive young star clusters in our Galaxy (see e.g. Portegies Zwart et al. 2010). This star cluster has an age of (2–3) × 106 yr (Piatti et al. 1998) and a total stellar mass of about (1–3) × 104 M⊙ (Ascenso et al. 2007). It hosts at least a dozen O stars and two remarkable Wolf–Rayet (WR) stars, WR 20a and WR 20b, and causes ionisation of the nearby H ii region RCW 49. Radio continuum observations reveal two wind-blown shells in the core of RCW 49 (Whiteoak & Uchida 1997) surrounding the central region of Westerlund 2 and the star WR 20b. Two molecular clouds are also observed in this region, whose velocity dispersion reveals a hint of the cloud collision. The distance to Westerlund 2 is estimated to be 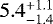 kpc (Furukawa et al. 2009) or 8.0 ± 1.4 kpc (Rauw et al. 2007).
kpc (Furukawa et al. 2009) or 8.0 ± 1.4 kpc (Rauw et al. 2007).
Westerlund 2 has been observed at very high energy (VHE) γ-rays with the H.E.S.S. array of imaging atmospheric Cherenkov telescopes (H.E.S.S. Collaboration et al. 2011; Aharonian et al. 2007). Two extended VHE γ-ray sources, HESS J1023–575 and HESS J1026–582, have been detected in this region, the origins of which are still under debate. These sources may come from the pulsar wind nebulae of the powerful pulsars PSR J1022–5746 and PSR J1028–5819 or from the collective stellar wind interaction in the young clusters. Ackermann et al. (2017) recently reported the detection of two extended sources emitting in the GeV range in the region: FGES J1023.3–5747 is spatially coincident with the TeV source HESS J1023–575; the second source, FGES J1036.4–5834, is a very extended source with a radius of more than 2° and a hard spectrum with a photon index of about 2. The large spatial extension and hard spectrum recall the γ-ray emission from other young star clusters or superbubble systems such as Cygnus cocoon (Ackermann et al. 2011) or NGC 3603 (Yang & Aharonian 2017).
In this paper we investigate this scenario by analysing LAT data obtained towards the direction of Westerlund 2 with a focus on the very extended component of γ-rays, and discuss the possible origin of this radiation.
2 Fermi LAT data analysis
2.1 Spatial analysis
We selected LAT data towards Westerlund 2 for a period of approximately 8 yr (MET 239557417–MET 455067824). For the analysis, we used the standard LAT analysis software package v10r0p51 .
The region of interest (ROI) was selected to be a 15° × 15° square centred on the position of Westerlund 2, i.e. RAJ2000 = 155.992°, Dec J 2000 = −57.764°. Observations with Rock angle larger than 52° are excluded in this analysis. In order to reduce the effect of the Earth albedo background, we excluded the time intervals when the parts of the ROI were observed at zenith angles > 90°. For the spatial analysis, given the crowded nature of the region and to avoid systematic errors due to a poorer angular resolution at low energies, we selected only the photons with energies exceeding 10 GeV. This energy cut reduces the contribution of bright, nearby pulsars, allowing us to describe the emission with an angular resolution of ~ 0.1°. The P8_ R2_v6 version of the post-launch instrument response functions (IRFs) was used and both the front and back converted photons were selected.
The γ-ray count map above 10 GeV in the 8° × 8° region around Westerlund 2 is shown on the left panel of Fig. 1a. We performed a binned likelihood analysis via the tool gtlike. The point sources listed in the 3rd Fermi source catalogue (3FGL; The Fermi-LAT Collaboration 2015) are also shown with a black cross, in case of identified sources and with a blue circle in case of non-associated sources. Those non-associated point-like sources could be part of the extended emission; therefore, in the likelihood fitting, within two degrees from Westerlund 2, we first included all sources from 3FGL catalogue, but we excluded the sources without an association to a known source (Model 1). We also added the background models provided by the Fermi Collaboration (gll_iem_v06.fits and iso_P8R2_SOURCE_V6_v06.txt for the Galactic and the isotropic diffuse components, respectively2 ). In the analysis, the normalisations and spectral indices of sources inside the field of view (FoV) were left free.
After the likelihood fitting (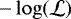 ), we subtracted the best-fit diffuse model and all the identified point sources in the ROI. The resulted residual map is shown in the right panel of Fig. 1b. We found substantial residual emission within a large spatial extension. We modelled those as a uniform disk (Model 2) and then varied the position and the size of the disk to find the best fit parameters. The best-fit result is a uniform disk centred at (
), we subtracted the best-fit diffuse model and all the identified point sources in the ROI. The resulted residual map is shown in the right panel of Fig. 1b. We found substantial residual emission within a large spatial extension. We modelled those as a uniform disk (Model 2) and then varied the position and the size of the disk to find the best fit parameters. The best-fit result is a uniform disk centred at (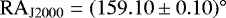 ,
, 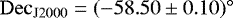 ) with a radius of
) with a radius of 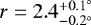 . The TS value is about 500, corresponding to a statistical significance of more than 22σ.
. The TS value is about 500, corresponding to a statistical significance of more than 22σ.
We also tested whether this extended emission is composed by several independent point-like sources. To do this, we included all sources listed in 3FGL catalogue (Model 3). The resulted 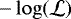 function value is larger than that in the extended template case, even with much more free parameters. To account for the fact that we are selecting only high energy events (10 GeV), we also tested a model including all the sources in 3FHL (Ajello et al. 2017) catalogue instead of 3FGL catalogue (Model 4). No improvement is obtained in the global statistics. Finally, we added FGES J1023–5746 as a disk to Model 2 (Ackermann et al. 2017) with a radius of 0.28° in the model (referred as Model 5 in Table 1) and obtain a TS value for this extended source of 70. Therefore, in the following analysis we included both the 2.4° disk and 0.28° disk as spatial templates. We use the position and extension of FGES J1023–5746 derived by Ackermann et al. (2017). The results described above for the different models are listed in Table 1.
function value is larger than that in the extended template case, even with much more free parameters. To account for the fact that we are selecting only high energy events (10 GeV), we also tested a model including all the sources in 3FHL (Ajello et al. 2017) catalogue instead of 3FGL catalogue (Model 4). No improvement is obtained in the global statistics. Finally, we added FGES J1023–5746 as a disk to Model 2 (Ackermann et al. 2017) with a radius of 0.28° in the model (referred as Model 5 in Table 1) and obtain a TS value for this extended source of 70. Therefore, in the following analysis we included both the 2.4° disk and 0.28° disk as spatial templates. We use the position and extension of FGES J1023–5746 derived by Ackermann et al. (2017). The results described above for the different models are listed in Table 1.
 |
Fig. 1 Left panel: γ-rays count map above 10 GeV in the 8° × 8° region around Westerlund 2. The 3FGL catalogue sources are labelled with a black cross and blue circle for identified and unassociated sources, respectively. The white dashed line shows the extended emission related to FGES J1036.4–5834. Right panel: residual map after subtracting all the identified catalogue source and the diffuse background, centred on the best-fit position of the extended source to the south of Westerlund 2. Also shown are the best-fit 2D disk template (white circle), the position and extension of FGES J1023–5746 (green circle), and the known SNRs and bright pulsars in the field of view. The blue cross labels the position of the star cluster Westerlund 2. The white contours are obtained from the TS-map, for levels 3, 4, and 5. |
Fitting results for various spatial models explained in the text.
2.2 Spectral analysis
For the spectral analysis we applied gtlike in the energy range [0.3, 250] GeV and modelled the spectrum of the 2.4° disk as a power-law function, fixing the position to that found in the spatial analysis. We neglected the emission below 0.3 GeV to avoid systematic errors due to the dominant Galactic diffuse background. The derived photon index is 2.02 ± 0.11(stat) ± 0.1(sys), and the total flux above 1 GeV is 4.2 ± 0.2 × 10−8 cm−2 s−1. The systematic errors come from the uncertainties of the effective area and the point spread function of LAT (Ackermann et al. 2012). The derived spectrum is consistent with the results of FGES J1036.4–5834 in Ackermann et al. (2017), which is 2.08 ± 0.06 ± 0.07.
To obtain the spectral energy distribution (SED) of extended emission to the south of Westerlund 2, we divided the full energy range into 10 logarithmically spaced bands and applied gtlike to each of these bands, in this process the index was fixed to 2. The results of this analysis are shown in Fig. 2. All data points have TS values larger than 4, which corresponds to a significance of larger than ~2σ. The power-law spectrum extends to 250 GeV without any sign of a cut-off or a break. To test the impact of uncertainties characterising the diffuse Galactic background models, in the likelihood fitting we artificially varied the Galactic diffuse background by 6% to estimate the influence on the final flux. While below 1 GeV the uncertainties due to the varied diffuse background can be as large as 30%, they become negligible above 4 GeV. These uncertainties are included in the error bars shown in Fig. 2.
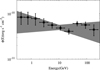 |
Fig. 2 Spectral energy distributions of the extended emission of the 2.4° disk. The grey region represents the statistical error when fitting the global spectrum with a power-law function. |
2.3 Pulsar gating analysis on PSR J1022–5746
The extended emission FGES 1023–5746 spatially coincides with the H.E.S.S. source HESS J1023–575. However, the low energy emission of this region is dominated by the pulsar PSR J1022–5746. To further investigate the emissions from FGES 1023–5746, we performed a pulsar gating analysis on PSR J1022–5746. We produced the phase-folded light curve of PSR J1022–5746 by using ephemeris corresponding to the time period from MJD 54686 to 565833 . To obtain the light curve we adopted a 1° aperture without applying any background subtraction. The resulted light curve is shown in Fig. 3a. We note two peaks located in the phase 0.15 and 0.6, respectively. To reduce a possible bridge emission between the two peaks in the phase interval [0.2, 0.5], we selected a rather narrow band [0.7, 1.0] in the following analysis. We applied the same spectral analysis described above. The derived SEDs are shown in Fig. 3b, both for the emission before and after pulsar gating. We note that the extrapolation of the low energy emission is significantly below the flux of HESS J1023–575. Yet, these two sources can be indirectly connected, namely if the emission in the GeV band is dominated by the pulsar and the VHE emission is linked to the surrounding pulsar wind nebula (PWN), as observed in many pulsar/PWN systems such as the Crab (Abdo et al. 2010b). If we assume the pulsar emission was eliminated in the pulsar gating process, the hardening and extension are difficult to explain in a pulsar/PWN scenario. However we cannot exclude the possibility that magnetospheric emission from the pulsar also exists in the bridge phase interval considered, dominating the GeV emission and preventing us from deriving an accurate of the extended emission coincident with the VHE source.
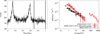 |
Fig. 3 Left panel: phase-folded light curve of pulsar PSR J1022–5746. The two vertical lines indicate the interval in which we selected in the pulsar gating analysis. Right panel: SEDs derived both before (red squares) and after (black squares) pulsar gating. Also shown is the H.E.S.S. data of HESS J1023–575 (red open circles). |
3 Gas around Westerlund 2
The studies of the molecular hydrogen by Dame (2007), Furukawa et al. (2009), and Ohama et al. (2010) show a complex environment around Westerlund 2. Two molecular clouds in the velocity ranges of [−11:9] and [11:21] km s−1 physically coincide with Westerlund 2 and the large H ii region RCW 49. The mass of the molecular gas is estimated to be (1.7 ± 0.8) × 105 M⊙. The γ-ray emission region, however, is much larger than Westerlund 2 and the corresponding molecular clouds. To study the molecular content in this region we used data from the Galactic CO survey of Dame et al. (2001). We used the standard assumption of a linear relationship between the velocity-integrated CO intensity, WCO, and the column density of molecular hydrogen, N(H2). The conversion factor XCO is chosen to be 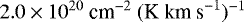 as suggested by Dame et al. (2001) and Bolatto et al. (2013). We integrated the velocity interval between [−11:21] km s−1. The derived molecular gas column density is shown in the top panel of Fig. 4a.
as suggested by Dame et al. (2001) and Bolatto et al. (2013). We integrated the velocity interval between [−11:21] km s−1. The derived molecular gas column density is shown in the top panel of Fig. 4a.
To determine the H ii column density we used the Planck free–free map (Planck Collaboration X 2016). We first converted the emission measure (EM) into free–free intensity using the conversion factor in Table 1 of Finkbeiner (2003). Then we used Eq. (5) of Sodroski et al. (1997) to calculate the H ii column density from the free–free intensity. We note that the H ii column density is inverse proportional to the electron densities ne , which are chosen, following Sodroski et al. (1997), to be 2 and 10 cm−3 as the upper and lower limits, respectively. The derived H ii column density is also shown in Fig. 4b (middle panel). To the southwest of RCW 49 there is another bright H ii region G287.393–00.630 (Anderson et al. 2014). However it has a radial velocity of − 17 km s−1, which is significantly different from that of RCW 49 (~0 km s−1). G287.393–00.630 is likely to be a foreground, although taking into account the uncertainties in the kinematic distance, we cannot exclude the possibility of physical correlation. To account for such uncertainties, we estimated two H ii masses: one derived in the region where RCW 49 is located and another including both RCW 49 and G287.393–00.630. The total gas, adding the contribution traced by the CO and H ii molecules, is shown is Fig. 4c (bottom panel). The masses derived using three different tracers are listed in Table 2. The total mass lies within 2.0 × 106 M⊙ < M < 7.3 × 106 M⊙. Assuming spherical geometry of the γ-ray emission region, its radius is estimated as r = D θ ~ 5.0 kpc × (2.4∕57.29) rad ~ 210 pc. Thus, the averaged over the volume gas number density ngas varies from 7 to 25 cm−3.
 |
Fig. 4 Top panel: gas column densities derived from CO data, integrated in the velocity range of [−11, 21] km s −1. Middle panel: H ii column density derived from the Planck free–free maps. Bottom panel: Total gas column density by summing up the molecular gas and H ii gas. The γ-ray emission is overlaid with white contours together with the positions of the energetic pulsars in the field and the position of Westerlund 2 (green circle). The white disk indicates the γ-ray template, in which the total gas mass is calculated. |
Gas mass derived from various tracers.
4 Origins of the extended γ-ray emissions
Several scenarios can be put forward to explain the large γ-ray emission observed. Under the assumption of γ-ray production in hadronic interactions of cosmic rays (CRs) interacting with interstellar gas, the total γ-ray luminosity of 1036 erg s−1 (for a fiducial distance of 5 kpc) and gas density of 7 cm−3 < ngas < 25 cm−3 result in a total CR energy confined in the γ-ray production area of (4–13) × 1049 erg. This estimate is quite typical for energy release in CRs by a supernova remant (SNR). Thus, at first glance, a single SNR seems an attractive option as the source of production of CRs. However, below we argue that the injection of CRs into the interstellar medium seems to have a continuous character giving a preference to the stellar cluster Westerlund 2 and the colliding wind binary Eta Carina as the suppliers of CRs.
4.1 CRs continuously injected from Westerlund 2
The young star cluster Westerlund 2 contains more than a dozen O stars and two Wolf–Rayet stars. The total mechanical energy in the form of stellar winds in this region is estimated around 1 × 1052 erg (Rauw et al. 2007; Reimer et al. 2008), which could in principle provide a large energy reservoir to power the extensive γ-ray source (Parizot et al. 2004). To account for this large emission, the acceleration of particles, which escape their sources and interact with the surrounding gas, should be accompanied by an efficient diffusion. Because of large number of accelerators within the cluster, one could expect a quasi-continuous injection of CRs into the interstellar medium over the age of the cluster exceeding T0 ≥106 yr. That would translate into a hard spectrum of γ-rays , mimicking the spectrum of accelerated protons, which are continuously accelerated and inflating the extended region. Remarkably, a similar hard γ-ray emission has already been detected from two other young star associations: Cygnus OB2 (Ackermann et al. 2011) and NGC 3603 (Yang & Aharonian 2017) with similar energy budgets in CRs (1.3 × 1049 erg, Ackermann et al. 2011 and (2–10) × 1049 erg, Yang & Aharonian 2017, respectively).
We also note that it is possible that a significant part of CRs has already escaped from the γ-ray emission region. The relation between the total injected CR energy and the CR energy in the γ-ray emission region can be expressed as (Aharonian & Atoyan 1996):
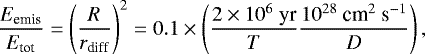 (1)
(1)
where Eemis and Etot are the CR energy budget derived from the γ-ray luminosity and the total injected CR energy, respectively. The parameter R is the size of the γ-ray emission region, rdiff is the total diffusion length of CRs corresponding to the age of the cluster T, and D is the diffusion coefficient. While the age of the cluster is very well known, i.e. T ≈ 2 × 106 yr, the diffusion coefficient is a rather uncertain parameter. In the interstellar medium, it is of order of 1029 cm2 s−1 for 10–100 GeV protons (see e.g. Strong et al. 2007) responsible for 1–10 GeV γ-rays. In this case the total energy in CRs is about 1052 erg, which is two orders of magnitude larger than that derived from γ-ray emissions. This would imply that the majority of accelerated CRs have been already left the region of the observed γ-rays. Such a huge energy in CRs can hardly be provided by a single SNR or the stellar wind. One should note that the diffusion coefficient in this area can be smaller. In particular for the diffusion coefficient 1028 cm2 s−1, the required energy in CRs can be reduced to the level that can be supported by a stellar wind and, for 1027 cm2 s−1, a single SNR is possible. However, the derived radial distribution of the CR density proportional to 1∕r essentially excludes the SNR origin of CRs (see below) unless we assume that CRs are provided by a number of SNRs that have been produced in the cluster over ≈ 106 yr. Given that the CRs are effectively accelerated during the first ≤ 104 yr of SNRs, one would require an unreasonably high (at least 10−4 yr−1) rate of SN explosions in this stellar cluster to support of the CR injection into the interstellar medium in the continuous regime. Therefore, we conclude that, most likely, the young massive stars of the cluster are responsible for these relativistic particles.
4.2 Radial distribution of γ-ray emissivities
The spatial distributions of CRs can provide key information about their injection history. The results obtained in this study do not show a strong correlation between the γ-ray and gas distributions that would be expected in the case of homogeneously distributed CRs. Meanwhile, in the case of continuous injection of CRs by the accelerators located in Westerlund 2 into the surrounding extended regions beyond the cluster, we expected a 1∕R type radial distribution of CRs; this would be the case unless the diffusion coefficient characterising the propagation of CRs suffers dramatic changes over 100–200 pc scales.
To investigate the CR distribution in the context of the hadronic origin of extended γ-ray emissions, we produced the radial profile of the γ-ray emissivity per H atom, which is proportional to the CR density, taking the position of Westerlund 2 as reference. We derived the γ-ray flux above 10 GeV, using the standard likelihood analysis in four regions resulting from splitting the 2.5° disk into subregions. These subregions correspond to regions located to angular distances [0:0.3]°, [0.3:1.0]°, [1.0:3.0]°, and [3.0:4.0]° away from Westerlund 2. The total gas column density is calculated for ne = 10 cm−3, which is the value suggested in Sodroski et al. (1997) for the region inside the solar circle, and excluding the H ii region G287.393–00.630. The resulting radial profile is shown in the right panel of Fig. 5b. We fit the density profile to two hypothesis: a constant value, which represents a homogeneous distribution of CRs formed in an impulsive injection event, and a 1∕r type distribution, which would result from a continuous injection of CRs from Westerlund 2. The latter is favoured with a χ2 /ndf of 1.3 versus a χ2/ndf of 15.6 for the constant case, which strongly support a scenario in which a central source (Westerlund 2) is continuously injecting CRs into the surrounding region. It should be mentioned that the contamination from pulsar J1023–5746 to the first point of Fig. 5b is limited, since we chose the photons above 10 GeV, where the pulsed emission is minimised. Furthermore, even if we neglect this point the other three points also significantly favour a 1∕r type distribution. The χ2/ndf is 1.8 and 6.5 for 1∕r and constant profile, respectively.
We stress that the determination of CRs radial distribution is a powerful tool to site localise the source and derive the injection history of CRs. This approach has been successfully applied earlier to the H.E.S.S observations of the Galactic centre (H.E.S.S. Collaboration et al. 2016). In particular, the 1/r distribution of CRs is a direct proof of the continuous injection of CRs. It can be regarded as a powerful method to identify the continuous CR sources in γ-ray astronomy.
The caveat of the results above is the uncertainty of the gas distribution. We note the velocity integration range [−11, 21] km s−1 derived from the compact clouds near Westerlund 2 could be too high for the whole extended γ-ray emission region. Furukawa et al. (2009) argued that the large velocity dispersion of molecular clouds near Westerlund 2 is caused by both stellar wind acceleration and the collision of clouds. The H ii column density are also uncertain owing to the uncertainties of the free electron density, although the H ii column density has only minor influence on the results in this work. On the other hand, whether the H ii region G287.393–00.630 are associated with the γ-ray emission is not known. A dedicated study on the ISM in this region is required to pin down these uncertainties.
 |
Fig. 5 Upper panel: white circle and black arcs label the regions used to subtract the γ-ray emissivities. The position of Westerlund 2 is shown as a cyan diamond. Lower panel: the profile of γ-ray emissivities per H atom above 1 GeV with respect to the distance to Westerlund 2. For comparison, we show 1∕r (solid curve), and constant (dotted curve) profiles, which are predicted by the continuous injection and the impulsive injection, respectively. |
4.3 Other possible scenarios
In principle, the diffuse γ-ray emissions can be dominated by the leptonic component due to inverse Compton (IC) scattering of electrons. Formally, a γ-ray photon index close to 2 requires relativistic electrons with the differential power-law index of 3. This can be realised, for example, by the radiative cooling of electrons with an initial (acceleration) spectrum of E−2 . The IC component can dominant in the GeV regime due to the presence of enhanced target radiation fields (ISRF) supplied by the young stars of Westerlund 2. The total optical luminosity of all O and WR stars in Westerlund 2 is estimated as about 2 × 1040 erg s−1 (Rauw et al. 2007). For the size of the γ-ray emission region (R ≃200 pc), the contribution of these young stars to the ISRF is only 0.1 eV cm−3, which is significantly lower than the diffuse starlight component in our Galaxy (see e.g. Popescu et al. 2017). More IC contribution is expected if the electrons are accelerated near the stars, since they emit IC γ-rays in a much denser radiation environment. But in this case one would expect a rather compact γ-ray source limited by the angular size of Westerlund 2 cluster contradicting the observations.
The colliding wind binary system Eta Carina is also located inside the γ-ray emission region. The powerful source has also been detected as a compact source in the GeV and TeV regime with the LAT and H.E.S.S. telescopes (Abdo et al. 2010a; Leser et al. 2017). While the high and VHE emission of the compact source may have either a leptonic or hadronic origin, the extended diffuse γ-ray source should be dominated by interactions of CR protons and nuclei with the ambient gas. The injection rate of these particles on timescales of more than 106 yr should be, as in the case of Westerlund 2, as large as 1037 erg s−1 above 10 GeV.
The extended emission could also be superposition of several discrete (unresolved) sources contributing to the total radiation. Indeed, several pulsars and SNRs are located inside the γ-ray emission region. The γ-ray spectra from pulsars typically contain a cut-off at several GeV, thus they can hardly contribute to the ≥ 10 GeV γ-rays detected in the extended structures. At the same time, PWN and SNRs can be considered as natural contributors to hard γ-rays . Two SNRs, SNR G284.3–1.8 and G286.5–1.2, lie within the γ-ray emission region. Both of these have a much smaller radio size compared to the size of the detected extended γ-ray emission. Considering the extension of the remnants, the extended emission can hardly be related to the SNRs themselves. TeV γ-ray emissions has been detected towards the SNR G248.3–1.8, which is believed to be a combined contribution from the binary system 1FGL J1018.6–5856 and the PWN associated with the bright pulsar PSR J1016–5857 (H.E.S.S. Collaboration et al. 2012a). The CRs escaping from those SNRs could also be appealed. In this case, the acceleration time of CRs of energy up to 1 TeV lasts typically no much more than 103 yr. Filling up a 200 pc region requires 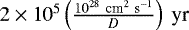 . By then, the high energy CRs should already have escaped the region due to energy-dependent escaping and a soft spectrum would be expected, as observed in ~104 yr mid-age SNRs (see e.g. Yuan et al. 2012), unless the diffusion coefficient in this region is an order of magnitude larger than the average diffusion coefficient in the interstellar medium.
. By then, the high energy CRs should already have escaped the region due to energy-dependent escaping and a soft spectrum would be expected, as observed in ~104 yr mid-age SNRs (see e.g. Yuan et al. 2012), unless the diffusion coefficient in this region is an order of magnitude larger than the average diffusion coefficient in the interstellar medium.
On the other hand, there are more than a dozen pulsars located inside the γ-ray emission region. Four of these have high spin-down luminosities, among which PSR J1023–5746 has a spin down luminosity of more than 1037 erg s−1. Formally, this could be sufficient to explain the detected γ-ray luminosity by high energy photons produced in the surrounding pulsar nebulae. However the huge extension of the detected diffuse radiation (200 pc) significantly exceeds the typical size of PWNe (see e.g. Gaensler & Slane 2006). Thus a single PWN originating the whole diffuse γ-ray emission also seems unlikely. The large emission could still be due to the overlapping emission originated by PWNe associated with those four bright pulsars (their positions indicated in Fig. 1b): PSR J1023–574, PSR J1028–589, PSR J1044–5737, and PSR B1046–58. The first two are middle age and energetic (with spin-down power Ė of 1.1 × 1037 and 8.3 × 1035 erg s−1, respectively;Abdo et al. 2013) pulsars, for which the associated PWN was detected in the TeV regime (H.E.S.S. Collaboration et al. 2011). Despite the compact size of the TeV sources compare to the GeV sources, the bright northernmost GeV spots could be related to a larger PWN emission due to the energy-dependent morphology (Aharonian et al. 2006; H.E.S.S. Collaboration et al. 2012b). The last two pulsars have similar properties with high spin-down luminosities of 8.03 × 1035 and 2.0 × 1035 erg s−1, respectively, and could be powering similar PWNe to explain the extension of the emission into high energies.
Observations with large FoV instruments with good angular resolution are crucial to understand whether the emission is powered by a single source or is a superposition of contributions from several extended sources.
5 Conclusion
The supper bubbles associated with OB associations and star clusters have been proposed as possible production sites of the Galactic CRs (Montmerle 1979; Cesarsky & Montmerle 1983; Bykov 2014). One of the attractive features of this model is the explanation of the observed secondary CR abundances (Binns et al. 2005; Rauch et al. 2009). The recent observations of 60Fe in CRs provide a new support to this hypothesis (Binns et al. 2016). Furthermore, the measurements of γ-ray emissivities reveal a similar radial distribution of CRs with OB stars (Acero et al. 2016; Yang et al. 2016). If CRs are accelerated in such environments, high energy γ-rays are expected from the interactions of the quasi-continuous injected CRs with the ambient gas. Here, we report a statistically significant detection of an extended γ-ray signal from the direction of the young star cluster Westerlund 2. The spectrum of this source is hard and extends up to 250 GeV. This detection, together with the similar reports regarding Cygnus cocoon (Ackermann et al. 2011), 30 Doradus C (H.E.S.S. Collaboration et al. 2015), Westerlund 1 (Abramowski et al. 2012; Ohm et al. 2013) and NGC 3603 (Yang & Aharonian 2017) may contribute to the better understanding of the origin of Galactic CRs in general, and in the high energy phenomena in the super bubbles, in particular.
In the context of the origin of Galactic CRs, the question of whether these objects can also operate as PeVatrons is of particular interest, i.e. whether they can provide the bulk of the locally observed CRs up to the so-called knee around 1 PeV. The most straightforward and unambiguous answer to this question would be the detection of γ-rays extending with a hard energy spectrum to energies well beyond 10 TeV. Apparently, because of the limited detection area, the Fermi LAT observations cannot offer such measurements. In this regard the imaging atmospheric Cherenkov telescopes (IACT) with their huge detection areas and adequate angular and energy resolutions, are powerful tools for the search and study of cosmic PeVatrons. Interestingly, multi TeV-γ-ray emission with a hard spectrum has already been reported from Westerlund 2 by the H.E.S.S. Collaboration (Aharonian et al. 2007; H.E.S.S. Collaboration et al. 2011). But the detected TeV emission from H.E.S.S. has a much smaller extension than that reported here. The limited FoV of the current IACT arrays is not optimal for such extended structures. To deal with the large scale diffuse structures, some other data analysis algorithms such as the likelihood method seem to be more effective tools than the aperture photometry method used today in IACT data analysis. We should note that a very extended TeV emissions has been reported from another similar young stellar cluster, Westerlund 1 (Abramowski et al. 2012; Ohm et al. 2013). This result has been interpreted by Bykov (2014) as an indication of acceleration of protons to PeV energies. However, this tentative result needs further confirmation. A dedicated analysis on Fermi LAT data taking advantage of the updated data calibration and the accumulated exposure also could be helpful.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJ, 723, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 708, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ajello, M., Allafort, A., et al. 2013, ApJS, 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, A&A, 537, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2016, ApJS, 223, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2011, Science, 334, 1103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., et al. (Fermi-LAT Collaboration) 2017, ApJ, submitted [arXiv:1702.00476] [Google Scholar]
- Aharonian, F. A., & Atoyan, A. M. 1996, A&A, 309, 917 [NASA ADS] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 460, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, A&A, 467, 1075 [Google Scholar]
- Ajello, M., Atwood, W. B., Baldini, L., et al. (Fermi-LAT Collaboration) 2017, ApJS, 232, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L. D., Bania, T. M., Balser, D. S., et al. 2014, ApJS, 212, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ascenso, J., Alves, J., Beletsky, Y., & Lago, M. T. V. T. 2007, A&A, 466, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binns, W. R., Wiedenbeck, M. E., Arnould, M., et al. 2005, ApJ, 634, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Binns, W. R., Israel, M. H., Christian, E. R., et al. 2016, Science, 352, 677 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Bykov, A. M. 2014, A&A Rev., 22, 77 [Google Scholar]
- Cesarsky, C. J., & Montmerle, T. 1983, Space Sci. Rev., 36, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M. 2007, ApJ, 665, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Fermi-LAT Collaboration (Ajello M., et al.) 2017, ApJS, 232, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P. 2003, ApJS, 146, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Furukawa, N., Dawson, J. R., Ohama, A., et al. 2009, ApJ, 696, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., & Slane, P. O. 2006, ARA&A, 44, 17 [NASA ADS] [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration, Abramowski, A., Acero, F et al. 2011, A&A, 525, A46 [Google Scholar]
- H.E.S.S. Collaboration, Abramowski, A., Acero, F et al. 2012a, A&A, 541, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration, Abramowski, A., Acero, F et al. 2012b, A&A, 548, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration, Abramowski, A., Aharonian, F et al. 2015, Science, 347, 406 [NASA ADS] [CrossRef] [Google Scholar]
- H.E.S.S. Collaboration, Abramowski, A., Aharonian, F et al. 2016, Nature, 531, 476 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Leser, E., Ohm, S., Füßling, M., et al. 2017, ArXiv e-prints[arXiv:1708.01033] [Google Scholar]
- Montmerle, T. 1979, ApJ, 231, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Ohama, A., Dawson, J. R., Furukawa, N., et al. 2010, ApJ, 709, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Ohm, S., Hinton, J. A., & White, R. 2013, MNRAS, 434, 2289 [Google Scholar]
- Parizot, E., Marcowith, A., van der Swaluw, E., Bykov, A. M., & Tatischeff, V. 2004, A&A, 424, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piatti, A. E., Bica, E., & Claria, J. J. 1998, A&AS, 127, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X 2016, A&A, 594, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, C. C., Yang, R., Tuffs, R. J., et al. 2017, MNRAS, 470, 2539 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Rauch, B. F., Link, J. T., Lodders, K., et al. 2009, ApJ, 697, 2083 [NASA ADS] [CrossRef] [Google Scholar]
- Rauw, G., Manfroid, J., Gosset, E., et al. 2007, A&A, 463, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reimer, O., Aharonian, F., Hinton, J., et al. 2008, in Clumping in Hot-Star Winds, eds. W.-R. Hamann, A. Feldmeier, & L. M. Oskinova, 195 [Google Scholar]
- Sodroski, T. J., Odegard, N., Arendt, R. G., et al. 1997, ApJ, 480, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007, Ann. Rev. Nucl. Part. Sci., 57, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Whiteoak, J. B. Z., & Uchida, K. I. 1997, A&A, 317, 563 [NASA ADS] [Google Scholar]
- Yang, R.-z., & Aharonian, F. 2017, A&A, 600, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, R., Aharonian, F., & Evoli, C. 2016, Phys. Rev. D, 93, 123007 [Google Scholar]
- Yuan, Q., Liu,S., & Bi, X. 2012, ApJ, 761, 133 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left panel: γ-rays count map above 10 GeV in the 8° × 8° region around Westerlund 2. The 3FGL catalogue sources are labelled with a black cross and blue circle for identified and unassociated sources, respectively. The white dashed line shows the extended emission related to FGES J1036.4–5834. Right panel: residual map after subtracting all the identified catalogue source and the diffuse background, centred on the best-fit position of the extended source to the south of Westerlund 2. Also shown are the best-fit 2D disk template (white circle), the position and extension of FGES J1023–5746 (green circle), and the known SNRs and bright pulsars in the field of view. The blue cross labels the position of the star cluster Westerlund 2. The white contours are obtained from the TS-map, for levels 3, 4, and 5. |
| In the text | |
 |
Fig. 2 Spectral energy distributions of the extended emission of the 2.4° disk. The grey region represents the statistical error when fitting the global spectrum with a power-law function. |
| In the text | |
 |
Fig. 3 Left panel: phase-folded light curve of pulsar PSR J1022–5746. The two vertical lines indicate the interval in which we selected in the pulsar gating analysis. Right panel: SEDs derived both before (red squares) and after (black squares) pulsar gating. Also shown is the H.E.S.S. data of HESS J1023–575 (red open circles). |
| In the text | |
 |
Fig. 4 Top panel: gas column densities derived from CO data, integrated in the velocity range of [−11, 21] km s −1. Middle panel: H ii column density derived from the Planck free–free maps. Bottom panel: Total gas column density by summing up the molecular gas and H ii gas. The γ-ray emission is overlaid with white contours together with the positions of the energetic pulsars in the field and the position of Westerlund 2 (green circle). The white disk indicates the γ-ray template, in which the total gas mass is calculated. |
| In the text | |
 |
Fig. 5 Upper panel: white circle and black arcs label the regions used to subtract the γ-ray emissivities. The position of Westerlund 2 is shown as a cyan diamond. Lower panel: the profile of γ-ray emissivities per H atom above 1 GeV with respect to the distance to Westerlund 2. For comparison, we show 1∕r (solid curve), and constant (dotted curve) profiles, which are predicted by the continuous injection and the impulsive injection, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


