| Issue |
A&A
Volume 617, September 2018
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201833356 | |
| Published online | 18 September 2018 | |
Disentangling multiple high-energy emission components in the Vela X pulsar wind nebula with the Fermi Large Area Telescope
1
IRAP, Université de Toulouse, CNRS, UPS, CNES,
31028
Toulouse, France
e-mail: luigi.tibaldo@irap.omp.eu
2
Max-Planck-Institut für Kernphysik,
69029
Heidelberg, Germany
3
Dipartimento di Fisica, Università degli Studi di Torino,
10125
Torino, Italy
4
Laboratoire AIM, CEA-IRFU/CNRS/Université Paris Diderot, Service d’Astrophysique, CEA Saclay,
91191
Gif-sur-Yvette, France
5
Centre d’Études Nucléaires de Bordeaux Gradignan, IN2P3/CNRS,
Université Bordeaux 1, BP120,
33175
Gradignan Cedex, France
Received:
3
May
2018
Accepted:
29
June
2018
Context. Vela X is a pulsar wind nebula in which two relativistic particle populations with distinct spatial and spectral distributions dominate the emission at different wavelengths. An extended 2° × 3° nebula is seen in radio and GeV gamma rays. An elongated cocoon prevails in X-rays and TeV gamma rays.
Aims. We use ~9.5 yr of data from the Fermi Large Area Telescope (LAT) to disentangle gamma-ray emission from the two components in the energy range from 10 GeV to 2 TeV, bridging the gap between previous measurements at GeV and TeV energies.
Methods. We determine the morphology of emission associated to Vela X separately at energies <100 and >100 GeV, and compare it to the morphology seen at other wavelengths. Then, we derive the spectral energy distribution of the two gamma-ray components over the full energy range.
Results. The best overall fit to the LAT data is provided by the combination of the two components derived at energies <100 and >100 GeV. The first component has a soft spectrum, spectral index 2.19 ± 0.16−0.22+0.05, and extends over a region of radius 1.°36±0.°04, consistent with the size of the radio nebula. The second component has a harder spectrum, spectral index 0.9 ± 0.3−0.1+0.3, and is concentrated over an area of radius 0.°63±0.°03, coincident with the X-ray cocoon that had already been established as accounting for the bulk of the emission at TeV energies.
Conclusions. The spectrum measured for the low-energy component corroborates previous evidence for a roll-over of the electron spectrum in the extended radio nebula at energies of a few tens of GeV possibly due to diffusive escape. The high-energy component has a very hard spectrum: if the emission is produced by electrons with a power-law spectrum, the electrons must be uncooled, and there is a hint that their spectrum may be harder than predictions by standard models of Fermi acceleration at relativistic shocks.
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Pulsars generate powerful winds that form nebulae filled by magnetized relativistic plasma, which, in turn, produce nonthermal radiation from radio to gamma rays. Pulsar wind nebulae (PWNe, e.g., Amato 2014) are a prime observational target to understand particle acceleration in relativistic plasmas and are plausibly an important source of high-energy cosmic ray electrons and positrons.
Vela X is the PWN formed by the Vela pulsar PSR J0835−4510. Due to its modest distance from the Sun of only 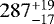 pc (Dodson et al. 2003, from parallax measurement of the pulsar), Vela X is spatially resolved at many wavelengths. Two main components appear to dominate depending on the wavelength (see, e.g., Hinton et al. 2011, and references therein). From radio to microwaves, Vela X appears as an extended 2° × 3° nebula with a butterfly-like morphology, also consistent with GeV gamma-ray observations. The pulsar lies at the position of the butterfly head, and we observe a series of filaments departing from it along the butterfly body, forming an elongated 1° structure dubbed “the cocoon”, which dominates emission in X-rays and TeV gamma rays.
pc (Dodson et al. 2003, from parallax measurement of the pulsar), Vela X is spatially resolved at many wavelengths. Two main components appear to dominate depending on the wavelength (see, e.g., Hinton et al. 2011, and references therein). From radio to microwaves, Vela X appears as an extended 2° × 3° nebula with a butterfly-like morphology, also consistent with GeV gamma-ray observations. The pulsar lies at the position of the butterfly head, and we observe a series of filaments departing from it along the butterfly body, forming an elongated 1° structure dubbed “the cocoon”, which dominates emission in X-rays and TeV gamma rays.
The conventional interpretation originally advocated by de Jager et al. (2008) is that two populations of accelerated electrons with different spectra coexist in Vela X. Hinton et al. (2011) proposed that the extended radio nebula shelters an older electron population accelerated in the first phases of the life of the pulsar and supernova remnant (SNR), and that the highest-energy particles have by now left this region due to diffusive escape. On the other hand, the cocoon could be filled by an electron population accelerated more recently and not yet affected by escape.
This hypothesis is motivated by the prediction of multiple particle populations in middle-aged PWNe evolving in SNRs by Gelfand et al. (2009), and by the hydrodynamical simulations of Blondin et al. (2001), who suggested that the Vela X cocoon is a recent structure formed ~20 kyr after the explosion of the supernova and the birth of the pulsar, due to the SNR reverse shock crushing the PWN. This scenario also justifiesthe morphology of the radio nebula and the off-center position of the pulsar, due to the asymmetric interaction with the SNR. The timescale suggested by the hydrodynamical simulations is in agreement with an age of the pulsar of 20–30 kyr inferred from its spindown history (Lyne et al. 1996).
The gamma-ray spectrum and morphology of Vela X have been studied in detail so far only at energies < 100 GeV using the Large Area Telescope (LAT) aboard the Fermi Gamma-ray Space Telescope (Abdo et al. 2010; Grondin et al. 2013), and at energies > 550 GeV using the High Energy Stereoscopic System (H.E.S.S.; Aharonian et al. 2006; Abramowski et al. 2012). Ackermann et al. (2016) and Ajello et al. (2017) have shown that the most recent Fermi-LAT dataset based on the Pass 8 event-level analysis (Atwood et al. 2013) in fact shows significant emission associated with Vela X at all energies from 10 GeV up to 2 TeV.
In this article, we present a new analysis of Fermi-LAT data > 10 GeV, and use it to disentangle the spectra of the different morphological components in Vela X. Thus, we bridge the gap between previous measurements, and we probe for the first time the spectral distribution of the highest-energy particles in the extended nebula and of the lowest-energy particles in the cocoon.
2 Observations, analysis, and results
2.1 Dataset and analysis generalities
The Fermi-LAT is an imaging pair-tracking telescope that detects gamma rays from 30 MeV to > 1 TeV (Atwood et al. 2009). We use all observations performed using the LAT from MET1 239 610 747 s to 541 486 510 s, that is, over ~9.5 yr of operations. We use all events belonging to the Pass 8 Source class with reconstructed direction within 105° from the local zenith (to eliminate emission from the Earth’s atmosphere) and reconstructed energies > 10 GeV and < 2 TeV. The lower energy limit of 10 GeV minimizes the contamination from the bright Vela pulsar, because the spectrum of the pulsar has a cutoff at 3.0 GeV (Abdo et al. 2013), and also the LAT point spread function2 (PSF) 68% containment radius attains values < 0.°15, much smaller than the size of either component of the PWN. Furthermore, the energy threshold of 10 GeV reduces confusion with the bright interstellar emission from the Milky Way, which has a spectrum softer than Vela X.
We perform a binned maximum likelihood analysis using Poisson statistics. The analysis region is a 5° × 5° square in celestial coordinates (J2000 equinox) with Aitoff projection centered at the position of Vela pulsar. We bin the events over a 0.°1 grid spatially, and using eight bins per decade in energy. For the analysis we employ the Fermi-LAT Science Tools 11-05-03 and the Python package Fermipy (Wood et al. 2017) version 0.15.1. We use the LAT instrument response functions (IRFs) P8R2_SOURCE_V6.
The starting model to be fit to the observations is constructed combining all sources in the most recent LAT high-energy catalogs: the second catalog of Fermi-LAT high-energy sources (2FHL; Ackermann et al. 2016) and the third catalog of Fermi-LAT high-energy sources (3FHL; Ajello et al. 2017). For sources present in both catalogs we take the model from the more recent 3FHL, also consistent with our energy range. We also include a model for interstellar emission produced by cosmic-ray interactions with gas and radiation fields in the Milky Way (Acero et al. 2016) and a spectral model for the isotropic background that accounts for extragalactic diffuse gamma-ray emission and the residual background from cosmic-ray interactions in the LAT misclassified as gamma rays3. We fix the normalization of the isotropic background to one, and leave free the normalization of the interstellar emission model, which has a higher number of predicted event counts for our region.
2.2 Morphological analysis in the low- and high-energy domains
We start by subdividing the whole energy range into a low-energy (LE) range from 10 to 100 GeV, and a high-energy (HE) range from 100 GeV to 2 TeV. We choose 100 GeV based on the extrapolation of the spectra from Abramowski et al. (2012) and Grondin et al. (2013), and the spectral models in Hinton et al. (2011) because we expect the extended nebula (cocoon) to be dominant below (above) this energy. We have verified that the results presented in the article do not depend critically on the exact value of the energy threshold around 100 GeV.
For each energy range we separately derive from the data the morphology of the emission associated with Vela X. First of all, we re-evaluate the significance of all sources in the input catalogs, as quantified through the likelihood ratio test. We compute the test statistic 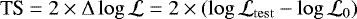 , where
, where 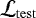 and
and 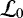 are the maximum likelihood values of the test hypothesis and of the null hypothesis, respectively, that is, for this application, the model including or not including the source. Sources with TS < 2 are removed from the model, and sources with TS < 9 have their spectral parameters fixed to the catalog values. A point source at the position of the Vela pulsar is always left in the model. Following the 3FHL catalog (Ajello et al. 2017), the spectrum of the Vela pulsar is modeled as a log-parabola. The spectral parameters of the Vela pulsar are left free in the LE range, where TS > 9, and fixed to the determination in the catalog in the HE range, where TS < 9. The catalog model of Vela X is removed.
are the maximum likelihood values of the test hypothesis and of the null hypothesis, respectively, that is, for this application, the model including or not including the source. Sources with TS < 2 are removed from the model, and sources with TS < 9 have their spectral parameters fixed to the catalog values. A point source at the position of the Vela pulsar is always left in the model. Following the 3FHL catalog (Ajello et al. 2017), the spectrum of the Vela pulsar is modeled as a log-parabola. The spectral parameters of the Vela pulsar are left free in the LE range, where TS > 9, and fixed to the determination in the catalog in the HE range, where TS < 9. The catalog model of Vela X is removed.
We then apply Fermipy’s iterative point-like source-finding algorithm (Wood et al. 2017, Sect. 4.5) that uses peak finding on a TS map to define new source candidates. Peaks with a minimum TS of nine and minimum separation of 0.°5 from other sources in the model are considered as candidates, and their position is determined by fitting a two-dimensional (2D) parabola to the log-likelihood surface around the peak under the hypothesis of a power-law spectrum. A maximum of ten sources per iteration are added, and the process is iterated until no additional candidates are found or up to a maximum of five iterations. We found a total of 16 source candidates in the LE domain and four source candidates in the HE domain, respectively.
Then, we test the hypothesis that newly found point-like source candidates within Vela X are associated with emission from the extended PWN. They are identified by their positions being in a region with brightness temperature > 2.5 K in the 330 MHz VLA image in Frail et al. (1997). Those sources, 11 in the LE range and 3 in the HE range, are removed from the model, and replaced by an extended disk centered at the TS-weighted barycenter of the point sources’ positions. The extension and center of the disk are then simultaneously fit to the data through a multidimensional likelihood profile scan. This procedure makes it possible to derive the best-fit morphology from the data without being biased by the extended models of Vela X from previous analyses of LAT data. In the LE range the 11 sources are distributed uniformly across the area of the final best-fit disk, while in the HE range the 3 sources are aligned along the direction of the X-ray cocoon. The spectral indices of the point-like sources have very large uncertainties due to the limited statistics, so that their values within each energy range are formally compatible with each other. The remaining source candidates found outside Vela X are listed in Table A.1.
The results from the morphological analyses are reported in Table 1, where the differences in likelihood and number of degrees of freedom are used below. Extended emission spatially associated with Vela X is significantly detected in both energyranges. This is assessed quantitatively using the likelihood ratio test, that is, through the values of 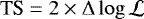 for the disk hypothesis compared to the hypothesis of no emission associated with Vela X, and for the disk hypothesis compared to the point source hypothesis. Although we do not meet all criteria necessary to apply the likelihood ratio test (in both cases the null hypothesis lies on the border of the parameter space of the test hypothesis; see Protassov et al. 2002), based on the Monte Carlo studies in Mattox et al. (1996) and Lande et al. (2012) we assume that in the null hypothesis TS is distributed as
for the disk hypothesis compared to the hypothesis of no emission associated with Vela X, and for the disk hypothesis compared to the point source hypothesis. Although we do not meet all criteria necessary to apply the likelihood ratio test (in both cases the null hypothesis lies on the border of the parameter space of the test hypothesis; see Protassov et al. 2002), based on the Monte Carlo studies in Mattox et al. (1996) and Lande et al. (2012) we assume that in the null hypothesis TS is distributed as 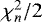 , where the number of degrees of freedom is five (1) for the disk hypothesis compared to the hypothesis of no emission associated with Vela X (for the diskhypothesis compared to the point source hypothesis), that is, the difference in number of degrees of freedom between test and null hypothesis. Following this approach the significance of the detection of the extended disks is estimated as 13σ and 7.3σ in the LE and HE range, respectively. Additionally, the extended disk hypothesis is preferred over the hypothesis of a single point source at 12.5σ and 5.5σ confidence level in the LE and HE range, respectively.
, where the number of degrees of freedom is five (1) for the disk hypothesis compared to the hypothesis of no emission associated with Vela X (for the diskhypothesis compared to the point source hypothesis), that is, the difference in number of degrees of freedom between test and null hypothesis. Following this approach the significance of the detection of the extended disks is estimated as 13σ and 7.3σ in the LE and HE range, respectively. Additionally, the extended disk hypothesis is preferred over the hypothesis of a single point source at 12.5σ and 5.5σ confidence level in the LE and HE range, respectively.
We cannot use the likelihood ratio test to compare the hypothesis of an extended disk to that of multiple point sources, because the two models are not nested (e.g., Protassov et al. 2002). However, we can use the Akaike information criterion (AIC; Akaike 1974). We calculate 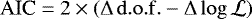 , which results to be − 31.6 (− 13.6) in the LE (HE) domain. The negative values indicate that the disk model is preferred over the model with multiple point sources in both energy ranges. We note that, however, the AIC does not enable us to quantify the significance of the preference of one model over the other.
, which results to be − 31.6 (− 13.6) in the LE (HE) domain. The negative values indicate that the disk model is preferred over the model with multiple point sources in both energy ranges. We note that, however, the AIC does not enable us to quantify the significance of the preference of one model over the other.
The best-fit disk center and extension differ between the LE and HE domains (Table 1). This is also illustrated in Fig. 1. In the figure we show the TS maps in the two energy ranges obtained from the LAT data based on a model that does not include extended emission from Vela X (the disk is removed from the best-fit model). We calculate on the map grid the likelihood of a model with an additional point source with a power-law spectrum with spectral index of two. Then, we overlay onto the TS map the contour of the best-fit disks. We also compare the LAT TS maps and best-fit disks with multiwavelength maps of the region. In the LE range the emission overlaps the whole region of the extended nebula as seen in radio and microwaves, consistent with previous results (Abdo et al. 2010; Grondin et al. 2013). At higher energies the emission becomes more concentrated and is coincident with the X-ray cocoon. The HE emission also overlaps the bulk of the emission seen at higher energies with H.E.S.S. (Aharonian et al. 2006). The extension from our analysis, 68% containment radius of 0.°52±0.°02, is slightly larger than what was measured with H.E.S.S., 0.°43±0.°02. There is also a 0.°6 shift of the emission centroid.
We further assess the correlation with emission at other wavelengths by fitting templates to the LAT data:
-
for the LE component we use the radio map from Frail et al. (1997, Fig. 1), on a 4° × 4° region centered at RA =128.°, Dec = −45.°7; a priori we do not expect an exact proportionality between gamma-ray intensities and radio intensities, because radio emission is produced by synchrotron emission due to magnetic fields, while gamma-ray emission results from inverse-Compton (IC) scattering of low-energy photons;
-
for the HE component we use the gamma-ray map from Abramowski et al. (2012); since the high-energy PSF of the LAT is comparable to that of H.E.S.S., we apply a PSF deconvolution using the Richardson–Lucy algorithm (Lucy 1974) as implemented in the scikit-image Python package (van der Walt et al. 2014); furthermore we use for the template only the region of 0.°8 radius where the significance of the gamma-ray emission detected with H.E.S.S. is the highest (Abramowski et al. 2012).
In the LE domain the likelihoods of the fit with the disk and the radio template are very similar, confirming that there is a very good correlation between gamma-ray and radio emission, with the radio template preferred based on the Akaike information criterion (AIC = −10.2). In the HE domain the disk provides a better fit to the LAT data than the H.E.S.S. template, AIC = −17.4, which is consistent with the shift already noted between emission measured by the LAT and H.E.S.S. In the HE domain, the single disk is preferred even to the combination of radio and H.E.S.S. templates, with AIC = −6. However, counting statistics for the LAT in the HE domain are too low to draw robust conclusions on this point, as well as with respect to the fainter TeV emission beyond the cocoon over an area with radius of 1.°2 detected by H.E.S.S. (Abramowski et al. 2012).
In the LE TS map (Fig. 1), the highest peak corresponds to the object FGES J0830.3−4453 from the LAT catalog of extended Galactic sources detected at energies > 10 GeV (Ackermann et al. 2017). In Ackermann et al. (2017), the bulk of emission from Vela X is accounted for by the source FGES J0832.0−4549, which has an extension radius of 0.°71±0.°05, smaller than the best-fit extension of the disk that we obtained in the LE range, 1.°36±0.°04. Our pointlike source-finding procedure had identified a candidate coincident with FGES J0830.3−4453. This source candidate is one of the 11 that we have removed from the model owing to its overlap with radio emission from Vela X. We have shown that our best-fit disk is preferred to the combination of the 11 point sources based on the AIC.
We further test the significance of an individual source coincident with FGES J0830.3−4453 on top of the radio template, which provides the best representation of the large-scale emission from Vela X in the LE range. Using a multidimensional likelihood profile scan we first localize a point-like source starting from the previously-found seed, and then we simultaneously fit the center and radius of an extended disk source to the data. The TS value for the point-like source hypothesis compared to the hypothesis of no individual source on top of the radio template is 29.4, therefore an individual source is detected with a significance of 4.5σ. The TS value for the hypothesis of a disk source compared to the point-like hypothesis is 7.1, therefore the source is not significantly extended (2.7σ). The point-like source, hereafter referred to as PS J0830.4−4449, is localized at RA =127.°61±0.°03, Dec = −44.°82±0.°04. It will be part of the model for the following steps when using the radio template, and considered as a source of systematic uncertainties in the evaluation of the spectrum of Vela X. Understanding the nature of the excess at the position of PS J0830.4−4449 and its relationship to Vela X is beyond the scope of this paper and left for future work.
Results from morphological analysis of Vela X in low- and high-energy domains.
 |
Fig. 1 Multiwavelength maps of analysis region. The LAT TS maps for energies below and above 100 GeV are derived as described in Sect. 2.2. The VLA map at330 MHz is reproduced from Frail et al. (1997), the H.E.S.S. map for energies > 750 GeV from Abramowski et al. (2012). We also show maps at 44 GHz from the Planck survey (Planck Collaboration I 2016), and at X-rayenergies >0.5 keV from the ROSAT survey (Voges et al. 1999). The blue and red circles show the best-fit disks that account for Vela X in LAT data at energies <100 and > 100 GeV, respectively (Sect. 2.2). The star shows the position of the Vela pulsar. The black circle in the top left plot corresponds to the source FGES J0830.3−4453 (Ackermann et al. 2017), while the white cross shows the position of the source PS J0830.4−4449 found inour analysis. We note that for the LAT maps all sources other than Vela X and FGES J0830.3−4453/PS J0830.4−4449, including the Vela pulsar, were accounted for in the background model. All maps are reprojected onto the same grid as the gamma-ray images. Furthermore, they are smoothed for display to a common resolution of 0.°15. In the top left corner of the LAT maps we show the effective PSF 68% containment circle in the corresponding energy range for a power-law spectral distribution with index 2. |
Results from spectral analysis of Vela X in full energy range >10 GeV: properties of the LE and HE components for different morphological models.
2.3 Full energy range analysis and spectra
We combine the best-fit models from the analyses in the LE and HE ranges and we fit them to the LAT data over the whole energy range from 10 GeV to 2 TeV. For Vela X we include two morphological components: the radio template and the disk fit to the LAT data in the HE range. For both we model the spectrum as a power law. We tested both components for spectral curvature using as model a power law with exponential cutoff, but this resulted in an insignificant likelihood improvement.. Other sources in the region are taken from the LE model, or from the HE model if not present in the LE model. Newly found source candidates are considered to be the same source (thus, taken from the LE model) if their positions are within 0.°2. We eliminate newly found source candidates with TS < 9 over the full energy range. This leaves in the final model only one newly found source candidate, with TS = 9.3 (PS J0842.7−4443, see Table A.1), plus PS J0830.4−4449. The Vela pulsar is included in the model with free spectral parameters. We will refer to this model as model A.
To asses the impact of the assumptions about the morphological representation of Vela X on the spectral properties we consider two alternative models:
-
in model B we replace the radio template and PS J0830.4−4449 with the disk fit to the LAT data in the LE range;
-
in model C we replace the HE disk with the H.E.S.S. template.
From the fit of the three models to the data, we obtain the results shown in Table 2.
Model A is confirmed to be the best representation of the data also over the whole energy range, with AIC − 25.0 and − 26.4 with respect to models B and C, respectively. We can also compare model A with the spatial models of the Vela X region used in the previous catalogs that cover the same energy range, 3FHL (Ajello et al. 2017) and the Fermi Galactic extended source catalog (FGES; Ackermann et al. 2017). In order to do so we replace the radio template, the HE disk, and PS J0830.4−4449 with the extended disks used in the catalogs, that is, 3FHL J0833.1−4511e, and FGES J0830.3−4453 plus FGES J0832.0−4549, respectively. We obtain a decrease of 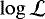 of 91.2 (27.4) for six (one) fewer degrees of freedom for the 3FHL (FGES) model, thus AIC = − 170.4 (–52.8) favors model A from this work as the best representation of the Vela X region. The full energy range fit with model A results in the detection of the soft component with morphology described by the radio template with a significance of 8.4σ, and of the hard component with morphology described by the HE disk (Table 1) with a significance of 5.4σ (see Sect. 2.2 for details about the conversion from TS to significance).
of 91.2 (27.4) for six (one) fewer degrees of freedom for the 3FHL (FGES) model, thus AIC = − 170.4 (–52.8) favors model A from this work as the best representation of the Vela X region. The full energy range fit with model A results in the detection of the soft component with morphology described by the radio template with a significance of 8.4σ, and of the hard component with morphology described by the HE disk (Table 1) with a significance of 5.4σ (see Sect. 2.2 for details about the conversion from TS to significance).
We also evaluate systematic errors in the spectral results due to the LAT effective area uncertainties by applying the “bracketing IRFs” method (Ackermann et al. 2012). For the dataset we use, and neglecting energy dispersion in the analysis, the effective area systematic uncertainties4 are estimated to be 5% for energies between 10 and 100 GeV, and then to increase as a function of energy E as 5% + 10% × [log10(E∕1 MeV) − 5]. The effective area is varied within this uncertainty band according to Eq. (28) in Ackermann et al. (2012). For the flux uncertainties we use B(E) = ±1, while for the uncertainties on the spectral index we adopt the expression in Eq. (29) of Ackermann et al. (2012) with the decorrelation energies E0 = 24 and 640 GeV for the LE and HE components, respectively. Note that there is an additional uncertainty in the absolute energy scale amounting to +4 to –10% (Ackermann et al. 2012) not accounted for in these estimates.
A summary of the spectral parameters including systematic uncertainties is given in Table 3. For the following wewill combine in quadrature systematic uncertainties originating from the morphological representation of Vela X and from the LAT effective area.
Figure 2 shows the spectral energy distribution of the two extended components in Vela X both from the fit over the whole energy range and from a bin-by-bin fit over narrower energy intervals. The spectrum of the HE component is significantly harder than that of the LE component (Table 3, Fig. 2), consistent also with the results obtained in the two separate energy bands in Sect. 2.2. Figure 2 illustrates that the sum of the fluxes from the two components matches well the overall fluxes derived in the 3FHL catalog (Ajello et al. 2017).
Figure 2 shows that the SED of the LE component overlaps with the SED derived from LAT data at energies < 100 GeV by Grondin et al. (2013). The latter study had pointed out a marginal spectral difference between the northern and southern part of the extended nebula in GeV gamma rays. Our statistically limited dataset at energies > 10 GeV does not permit us to address this point. The value of the spectral index of the LE component above 10 GeV, 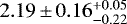 , is fully consistent with the global value in Grondin et al. (2013) obtained using a simple power-law model, 2.24 ± 0.04, but is marginally harder than the high-energy value for a broken power-law model with a break at ~2 GeV, 2.89 ± 0.23 ± 0.05.
, is fully consistent with the global value in Grondin et al. (2013) obtained using a simple power-law model, 2.24 ± 0.04, but is marginally harder than the high-energy value for a broken power-law model with a break at ~2 GeV, 2.89 ± 0.23 ± 0.05.
Figure 2 also shows that the SED of the HE disk connects to the SED measured at energies > 750 GeV with H.E.S.S. (Abramowski et al. 2012). The spectral index of the HE component of 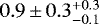 is consistent with that derived from H.E.S.S. data above 750 GeV of 1.32 ± 0.06 ± 0.12 within the uncertainties.
is consistent with that derived from H.E.S.S. data above 750 GeV of 1.32 ± 0.06 ± 0.12 within the uncertainties.
Results from spectral analysis of Vela X in full energy range >10 GeV: summary of the properties of the LE and HE components including systematic uncertainties.
 |
Fig. 2 Spectral energy distribution (SED) of Vela X. We show separately the spectra for the low-energy (LE) and high-energy (HE) components as derived in this work. The lines and shaded bands show the best-fit power laws for each component with their uncertainties, based on the fit using model A. The darker shaded band corresponds to 68% statistical uncertainties only, while the lighter shaded band corresponds to the sum in quadrature of statistical uncertainties and systematic uncertainties from the morphological representation of the sources (models B and C) and the LAT effective area (see Sect. 2.3 for details). The points and 95% confidence level upper limits show the binned SED. For points, capped error bars show the 68% statistical uncertainties only, while the uncapped error bars show the sum in quadrature of statistical uncertainties and systematic uncertainties. Upper limits include systematic uncertainties as well. We also show the overall SEDs of Vela X from H.E.S.S. (Abramowski et al. 2012), from the LAT measurements < 100 GeV (Grondin et al. 2013), and from the 3FHL catalog (Ajello et al. 2017). The dashed lines show the predictions of the radiative model described in Sect. 3. |
3 Discussion and conclusions
The analysis of ~9.5 yr of Fermi-LAT data has enabled us to disentangle the two morphological and spectral components of the Vela X PWN in the 10 GeV–2 TeV energy range, bridging the gap between previous results from the LAT (Grondin et al. 2013) and measurements with H.E.S.S. (Abramowski et al. 2012). At low energies, a soft component (spectral index 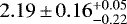 ) extends over a region of radius 1.°36 ± 0.°04, consistent with the extension of the radio nebula. At high energies, a component with a very hard spectrum (spectral index
) extends over a region of radius 1.°36 ± 0.°04, consistent with the extension of the radio nebula. At high energies, a component with a very hard spectrum (spectral index 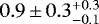 ) is concentrated over an area of radius 0.°63 ± 0.°03, which overlaps the X-ray cocoon, already established as accounting for the bulk of the emission at TeV energies, but with a shift of the emission centroid. Our measurements show that the latter component becomes dominant in the 100–400 GeV energy range.
) is concentrated over an area of radius 0.°63 ± 0.°03, which overlaps the X-ray cocoon, already established as accounting for the bulk of the emission at TeV energies, but with a shift of the emission centroid. Our measurements show that the latter component becomes dominant in the 100–400 GeV energy range.
In Fig. 2, we show for illustration purposes a simple radiative model that approximately reproduces the spectra of the two components. We assume that there are two populations of relativistic electrons, each with a spectrum described by a power law with exponential cutoff
![\begin{equation*} \frac{\mathrm{d}N}{\mathrm{d}E} = N_0 \left(\frac{E}{E_0}\right)^{-p} \exp\left[-\left(\frac{E}{E_{\mathrm{cut}}}\right)^{\alpha}\right]. \end{equation*}](/articles/aa/full_html/2018/09/aa33356-18/aa33356-18-eq15.png) (1)
(1)
The relativistic electrons produce IC emission upscattering photons from the cosmic microwave background (CMB), far infrared emission from dust, and starlight. For the two latter components we assume graybody spectra with temperatures of 30 and 3000 K, respectively, and energy densities of 0.2 and 0.3 eV cm−3, respectively. We use this parametrization to approximate the local interstellar radiation field (e.g., Porter et al. 2008; Popescu et al. 2017). As shown, for example, in Grondin et al. (2013), dust and star emission has a sizable impact on the IC emission from the GeV nebula. Therefore, detailed modeling of the gamma-ray emission from Vela X would require one to take the uncertainties in the radiation fields into account. This is, however, beyond the scope of this paper and left for future work. We calculate IC emission using the formulae by Khangulyan et al. (2014) as implemented in the naima Python package by Zabalza (2015).
For the extended nebula (LE) component we set p = 1.7, as required by radio observations (e.g., Hinton et al. 2011; Grondin et al. 2013). In order to reproduce the LAT spectrum including our new measurements we assume Ecut = 30 GeV and α = 0.6. Our results confirm the roll-over of the electron spectrum at a few tens of GeV found in previous studies. As discussed in Hinton et al. (2011), a steepening of the spectrum at these energies is difficult to explain with energy losses due to synchrotron radiation or IC scattering given the physical conditions in the nebula, and there is no reason to expect it from the particle acceleration mechanism. Additionally, the slower-than-exponential cutoff is not consistent with radiative cooling. Therefore, the roll-over of the spectrum is more likely the result of a different process, such as diffusive escape from the nebula as advocated in Hinton et al. (2011).
For the X-ray cocoon (HE) component we take p = 1.2, Ecut = 30 TeV, and α = 1. These values are consistent with previous results based on X-ray and TeV gamma-ray measurements (e.g., Tibaldo et al. 2017). However, previous measurements were mostly constraining multi-TeV parent electron energies, while here we extend the spectral measurement to lower energies, well below the high-energy spectral cutoff. For a power-law electron spectrum, expected from the most common models of particle acceleration in PWNe (e.g., Sironi & Cerutti 2017), the very hard spectrum of the gamma-ray emission is indicative of electrons that have not yet experienced significant cooling due to radiative losses. This is expected given the age of the cocoon of ~10 kyr (Blondin et al. 2001), since, for the magnetic field strength of 5 μG (de Jager et al. 2008), the cooling time of electrons with energies < 10 TeV is > 30 kyr.
For the same hypothesis of a power-law electron spectrum, in the Thomson regime the IC spectral index Γ is related to the electron spectral index p as Γ =(1 + p)∕2. The electron spectral index p ≃ 2.2−2.4 predicted at late (>10 kyr) times for Fermi acceleration at relativistic shocks (Achterberg et al. 2001; Keshet & Waxman 2005; Sironi & Cerutti 2017) would correspond to an IC spectral index Γ ≃ 1.6−1.7. The value we find of 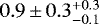 hints that the electron spectrum may be harder in the Vela X cocoon.
hints that the electron spectrum may be harder in the Vela X cocoon.
Several mechanisms discussed in the literature could produce such a harder spectrum. Bykov et al. (2017) predict hard spectra in Vela X for electrons reaccelerated in the converging flow system formed by the plasma outflowing from the wind termination shock and the plasma inflowing from the bowshock caused by the motion of the pulsar within its parent SNR. Another mechanism, often invoked to explain the hard TeV spectra of active galactic nuclei but possibly applicable also to PWNe, is stochastic particle acceleration combined with strong synchrotron and IC energy losses that produce a Maxwellian-like electron spectrum (Schlickeiser 1985; Stawarz & Petrosian 2008). Furthermore, much attention has been given lately to the role played by particle acceleration in magnetic reconnection in PWNe. Magnetic reconnection models generally predict spectra harder than shock acceleration for high wind magnetizations σ ≳ 10 (Sironi & Spitkovsky 2014). This condition may not be realized in Vela X; for example, Bühler & Giomi (2016) estimate σ ≃ 3. However, Guo et al. (2014) argue that hard power-law spectra may also be achieved with σ ~ 1 in sufficiently large reconnection layers. Finally, Horns et al. (2006) proposed a model for TeV emission from Vela X dominated by relativistic ion inelastic collisions. Their model predicts a very hard spectrum at a few hundred GeV. Moreover, the coexistence of ion and IC emission with different spectra may help to explain the shift of the emission centroid found between the LAT and H.E.S.S. measurements.
Spatial and spectral results from this analysis can be incorporated in future multiwavelength studies of Vela X, and compared to comprehensive physical models of the nebula in order to further constrain the mechanisms of particle acceleration and transport. The spatial and spectral properties of Vela X in the energy range above a few tens of GeV are soon expected to be measured in greater detail by the Cherenkov Telescope Array (CTA; Actis et al. 2011).
Acknowledgements
The Fermi-LAT Collaboration acknowledges generous ongoing support from a number of agencies and institutes that have supported both the development and the operation of the LAT as well as scientific data analysis. These include the National Aeronautics and Space Administration and the Department of Energy in the United States, the Commissariat à l’Énergie Atomique and the Centre National de la Recherche Scientifique/Institut National de Physique Nucléaire et de Physique des Particules in France, the Agenzia Spaziale Italiana and the Istituto Nazionale di Fisica Nucleare in Italy, the Ministry of Education, Culture, Sports, Science and Technology (MEXT), High Energy Accelerator Research Organization (KEK) and Japan Aerospace Exploration Agency (JAXA) in Japan, and the K. A. Wallenberg Foundation, the Swedish Research Council and the Swedish National Space Board in Sweden. Additional support for science analysis during the operations phase is gratefully acknowledged from the Istituto Nazionale di Astrofisica in Italy and the Centre National d’Études Spatiales in France. This work performed in part under DOE Contract DE-AC02-76SF00515. G.F. acknowledges the support that made his participation in this project possible: funding from the Erasmus Traineeship program, hospitality by the Max-Planck-Institut für Kernphysik, and mentorship by R. Bonino at the University of Torino. R.Z. acknowledges the Alexander von Humboldt Foundation for financial support, and the Max-Planck-Institut für Kernphysik as hosting institution. This research made use of several community-developed Python packages: Astropy (Astropy Collaboration et al. 2013), Fermipy (Wood et al. 2017), naima (Zabalza 2015), scikit-image (van der Walt et al. 2014), aplpy (Robitaille & Bressert 2012), matplotlib (Hunter 2007). This research also employed the public datasets from the ROSAT All-Sky Survey (http://www.mpe.mpg.de/xray/wave/rosat/) and the Planck mission (http://www.esa.int/Planck). The authors thank N. Bucciantini and B. Cerutti for insightful discussions on the interpretation of the results.
Appendix A Source candidates in the region around Vela X
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 713, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ajello, M., Allafort, A., et al. 2013, ApJS, 208, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowski, A., Acero, F., Aharonian, F., et al. 2012, A&A, 548, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2016, ApJS, 223, 26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Achterberg, A., Gallant, Y. A., Kirk, J. G., & Guthmann, A. W. 2001, MNRAS, 328, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Atwood, W. B., et al. 2016, ApJS, 222, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Baldini, L., et al. 2017, ApJ, 843, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Actis, M., Agnetta, G., Aharonian, F., et al. 2011, Exp. Astron., 32, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 448, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ajello, M., Atwood, W. B., Baldini, L., et al. 2017, ApJS, 232, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Akaike, H. 1974, IEEE Trans. Autom. Control, 19, 716 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Amato, E. 2014, Int. J. Mod. Phys. Conf. Ser., 28, 1460160 [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W., Albert, A., Baldini, L., et al. 2013, 2012 Fermi Symp. proc. - eConf C121028 [arXiv:1303.3514] [Google Scholar]
- Blondin, J. M., Chevalier, R. A., & Frierson, D. M. 2001, ApJ, 563, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Bühler, R., & Giomi, M. 2016, MNRAS, 462, 2762 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M., Amato, E., Petrov, A. E., Krassilchtchikov, A. M., & Levenfish, K. P. 2017, Space Sci. Rev., 207, 235 [NASA ADS] [CrossRef] [Google Scholar]
- de Jager, O. C., Slane, P. O., & LaMassa, S. 2008, ApJ, 689, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Dodson, R., Legge, D., Reynolds, J. E., & McCulloch, P. M. 2003, ApJ, 596, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., Bietenholz, M. F., & Markwardt, C. B. 1997, ApJ, 475, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Gelfand, J. D., Slane, P. O., & Zhang, W. 2009, ApJ, 703, 2051 [NASA ADS] [CrossRef] [Google Scholar]
- Grondin, M.-H., Romani, R. W., Lemoine-Goumard, M., et al. 2013, ApJ, 774, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, F., Li, H., Daughton, W., & Liu, Y.-H. 2014, Phys. Rev. Lett., 113, 155005 [NASA ADS] [CrossRef] [Google Scholar]
- Hinton, J. A., Funk, S., Parsons, R. D., & Ohm, S. 2011, ApJ, 743, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Horns, D., Aharonian, F., Santangelo, A., Hoffmann, A. I. D., & Masterson, C. 2006, A&A, 451, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Keshet, U., & Waxman, E. 2005, Phys. Rev. Lett., 94, 111102 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D., Aharonian, F. A., & Kelner, S. R. 2014, ApJ, 783, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Lande, J., Ackermann, M., Allafort, A., et al. 2012, ApJ, 756, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1974, AJ, 79, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Pritchard, R. S., Graham-Smith, F., & Camilo, F. 1996, Nature, 381, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, C. C., Yang, R., Tuffs, R. J., et al. 2017, MNRAS, 470, 2539 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, T. A., Moskalenko, I. V., Strong, A. W., Orlando, E., & Bouchet, L. 2008, ApJ, 682, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Protassov, R., van Dyk, D. A., Connors, A., Kashyap, V. L., & Siemiginowska, A. 2002, ApJ, 571, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T., & Bressert, E. 2012, Astrophysics Source Code Library [record ascl:1208.017] [Google Scholar]
- Schlickeiser, R. 1985, Particle acceleration in active galactic nuclei-coexistence of mono-energetic, power law and Maxwell-Boltzmann electron energy spectra, eds. T. Neckel, & H. Vehrenberg, 355 [Google Scholar]
- Sironi, L., & Cerutti, B. 2017, Astrophys. Space Sci. Lib., 446, 247 [Google Scholar]
- Sironi, L., & Spitkovsky, A. 2014, ApJ, 783, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Stawarz, Ł., & Petrosian, V. 2008, ApJ, 681, 1725 [NASA ADS] [CrossRef] [Google Scholar]
- Tibaldo, L., Aharonian, F., Bordas, P., et al. 2017, POS(ICRC2017) 719 [arXiv:1708.00388] [Google Scholar]
- van der Walt, S., Schönberger, J. L., Nunez-Iglesias, J., et al. 2014, PeerJ, 2, e453 [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Wood, M., Caputo, R., Charles, E., et al. 2017, PoS(ICRC2017) 824 [arXiv:1707.09551] [Google Scholar]
- Zabalza, V. 2015, International Cosmic Ray Conference, 34, 922 [Google Scholar]
The two models are gll_iem_v06.fits and iso_P8R2_SOURCE_V6_v06.txt, respectively, see https://fermi.gsfc.nasa.gov/ssc/data/access/lat/BackgroundModels.html.
All Tables
Results from spectral analysis of Vela X in full energy range >10 GeV: properties of the LE and HE components for different morphological models.
Results from spectral analysis of Vela X in full energy range >10 GeV: summary of the properties of the LE and HE components including systematic uncertainties.
All Figures
 |
Fig. 1 Multiwavelength maps of analysis region. The LAT TS maps for energies below and above 100 GeV are derived as described in Sect. 2.2. The VLA map at330 MHz is reproduced from Frail et al. (1997), the H.E.S.S. map for energies > 750 GeV from Abramowski et al. (2012). We also show maps at 44 GHz from the Planck survey (Planck Collaboration I 2016), and at X-rayenergies >0.5 keV from the ROSAT survey (Voges et al. 1999). The blue and red circles show the best-fit disks that account for Vela X in LAT data at energies <100 and > 100 GeV, respectively (Sect. 2.2). The star shows the position of the Vela pulsar. The black circle in the top left plot corresponds to the source FGES J0830.3−4453 (Ackermann et al. 2017), while the white cross shows the position of the source PS J0830.4−4449 found inour analysis. We note that for the LAT maps all sources other than Vela X and FGES J0830.3−4453/PS J0830.4−4449, including the Vela pulsar, were accounted for in the background model. All maps are reprojected onto the same grid as the gamma-ray images. Furthermore, they are smoothed for display to a common resolution of 0.°15. In the top left corner of the LAT maps we show the effective PSF 68% containment circle in the corresponding energy range for a power-law spectral distribution with index 2. |
| In the text | |
 |
Fig. 2 Spectral energy distribution (SED) of Vela X. We show separately the spectra for the low-energy (LE) and high-energy (HE) components as derived in this work. The lines and shaded bands show the best-fit power laws for each component with their uncertainties, based on the fit using model A. The darker shaded band corresponds to 68% statistical uncertainties only, while the lighter shaded band corresponds to the sum in quadrature of statistical uncertainties and systematic uncertainties from the morphological representation of the sources (models B and C) and the LAT effective area (see Sect. 2.3 for details). The points and 95% confidence level upper limits show the binned SED. For points, capped error bars show the 68% statistical uncertainties only, while the uncapped error bars show the sum in quadrature of statistical uncertainties and systematic uncertainties. Upper limits include systematic uncertainties as well. We also show the overall SEDs of Vela X from H.E.S.S. (Abramowski et al. 2012), from the LAT measurements < 100 GeV (Grondin et al. 2013), and from the 3FHL catalog (Ajello et al. 2017). The dashed lines show the predictions of the radiative model described in Sect. 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


