| Issue |
A&A
Volume 611, March 2018
|
|
|---|---|---|
| Article Number | A70 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201731698 | |
| Published online | 29 March 2018 | |
Spectral shifting strongly constrains molecular cloud disruption by radiation pressure on dust
1
Universität Heidelberg, Zentrum für Astronomie, Institut für Theoretische Astrophysik,
Albert-Ueberle-Str. 2,
69120
Heidelberg, Germany
e-mail: reissl@uni-heidelberg.de
2
Universität Heidelberg, Interdisziplinäres Zentrum für Wissenschaftliches Rechnen,
Im Neuenheimer Feld 205,
69120
Heidelberg, Germany
3
Department of Astrophysics, American Museum of Natural History,
Central Park West at 79th Street,
New York,
NY
10024-5192, USA
Received:
2
August
2017
Accepted:
1
October
2017
Aim. We aim to test the hypothesis that radiation pressure from young star clusters acting on dust is the dominant feedback agent disrupting the largest star-forming molecular clouds and thus regulating the star-formation process.
Methods. We performed multi-frequency, 3D, radiative transfer calculations including both scattering and absorption and re-emission to longer wavelengths for model clouds with masses of 104–107 M⊙, containing embedded clusters with star formation efficiencies of 0.009–91%, and varying maximum grain sizes up to 200 μm. We calculated the ratio between radiative and gravitational forces to determine whether radiation pressure can disrupt clouds.
Results. We find that radiation pressure acting on dust almost never disrupts star-forming clouds. Ultraviolet and optical photons from young stars to which the cloud is optically thick do not scatter much. Instead, they quickly get absorbed and re-emitted by the dust at thermal wavelengths. As the cloud is typically optically thin to far-infrared radiation, it promptly escapes, depositing little momentum in the cloud. The resulting spectrum is more narrowly peaked than the corresponding Planck function, and exhibits an extended tail at longer wavelengths. As the opacity drops significantly across the sub-mm and mm wavelength regime, the resulting radiative force is even smaller than for the corresponding single-temperature blackbody. We find that the force from radiation pressure falls below the strength of gravitational attraction by an order of magnitude or more for either Milky Way or moderate starbust conditions. Only for unrealistically large maximum grain sizes, and star formation efficiencies far exceeding 50% do we find that the strength of radiation pressure can exceed gravity.
Conclusions. We conclude that radiation pressure acting on dust does not disrupt star-forming molecular clouds in any Local Group galaxies. Radiation pressure thus appears unlikely to regulate the star-formation process on either local or global scales.
Key words: galaxies: star clusters: general / ISM: kinematics and dynamics / ISM: clouds / radiation: dynamics / radiative transfer / scattering
© ESO 2018
1 Introduction
Identifying and characterizing the physical processes that control the formation of stars on local scales within molecular clouds as well as on global scales of galaxies as a whole is one of the key open problems in astronomy and astrophysics (see, e.g., the reviews by Mac Low & Klessen 2004; McKee & Ostriker 2007; Klessen & Glover 2016). A convincing and comprehensive answer is yet to be found. We know that stars form only within the densest and coldest regions of the complex, multi-phase, interstellar medium (ISM). Observations indicate that only a small fraction of the available gas mass actually gets converted into stars: the star formation efficiency per free-fall time in molecular clouds is very low, typically of order of a few percent. A similar conclusion holds for galactic scales, where the overall gas depletion timescale is between 1 and 2 orders of magnitude longer than the dynamical time scale of star-forming clouds, again indicating the processes that convert ISM gas into stars are relatively inefficient. We do not fully understand why this is the case. At first sight, this low efficiency is surprising, because molecular clouds are massive and cold, with masses of 103–106 M⊙ and temperatures in the range 10–30 K (e.g., Blitz et al. 2007). Therefore, when considering only the competition between self-gravity and gas pressure (Jeans 1902), we find that the dense parts of the ISM should be highly unstable against gravitational contraction and should form stars efficiently and on short timescales. These are comparable to the sound crossing or free-fall times of the cloud. This is not observed. Consequently, additional physical agents have been suggested to strongly delay star formation. One of these is the momentum input from stellar radiation (e.g., Tenorio-Tagle & Bodenheimer 1988).
The same problem occurs on galactic scales, where observations indicate gas depletion times, or equivalently the inverse of star formation rate, is rather large ranging, from several hundred million years to several tens of billion of years (see e.g., Bigiel et al. 2008, 2011; Leroy et al. 2008, for a critical discussion, see Shetty et al. 2013, 2014). This is significantly longer than the typical dynamical timescale in a galaxy. Again, we arrive at the conclusion that star formation on galactic scales is inefficient, converting only a few percent of the available gas reservoir into stars in each dynamical timescale, so there must be some physical agents that are causing this behavior, possibly the same ones responsible for inefficient star formation on local cloud scales.
The question remains whether stellar feedback mechanisms can do the job or not. The proposal is that the energy and momentum input from stars into the ISM can regulate stellar birth within an individual star-forming region as well as within a galaxy as a whole, and that this can explain the observed low efficiency. Stars can affect their environment in several ways including supernovae, winds, and radiative pressure (Mac Low & Klessen 2004; McKee & Ostriker 2007; Ballesteros-Paredes et al. 2007; Klessen & Glover 2016; also Hill et al. 2012; Hennebelle & Iffrig 2014, Walch et al. 2015, Girichidis et al. 2016 for high-resolution simulations).
In this paper we focus on radiation pressure on dust grains. The energy in the radiation field produced by a typical stellar population exceeds the mechanical energy input from stellar winds and supernovae by an order of magnitude (Abbott 1982). The key question, however, is whether that radiation can effectively be converted into kinetic energy and counteract gravity to regulate the star formation process.
Ultraviolet and optical photons carry momentum that can effectively be absorbed and scattered by dust grains in the ISM (Tielens 2010; Draine 2011). In the case of young star-forming regions, the deposition of momentum as radiation is absorbed can be shown to produce a response in the ISM pressure consistent with rough hydrostatic equilibrium across expanding structures (e.g., Pellegrini et al. 2007, 2009). One can draw a direct connection between gas densities of H^+/H^0/H_2 interface regions measured with density sensitive nebular line ratios and stellar feedback. Because dust is dynamically coupled to the gas, the momentum transferred from photons to dust grains can drive gas flows, and so can cut off further accretion, as well as contribute to driving ISM turbulence. This momentum transfer can thus help to stabilize molecular clouds on large scales against further collapse, or even drive outflows, while at the same time it might trigger the build-up of new stars incompressed shells of swept up ISM material. It has been proposed that the momentum absorbed by dust can disrupt star-forming molecular clouds in a wide range of different environments, and that this sets the overall star formation efficiency. It has even been suggested that radiation pressure from massive stars and star clusters is the dominant feedback mechanism regulating the global star formation process in galaxies ranging from normal disk galaxies like the Milky Way to starburst systems (Thompson 2008; Krumholz et al. 2009b; Murray et al. 2010; Andrews & Thompson 2011; Krumholz 2012). Radiation pressure has also been invoked to explain the galactic fountains and outflows observed in many galaxies (see, e.g., Thompson et al. 2005, 2015; Murray et al. 2011; Krumholz 2012; Zhang & Thompson 2012; Coker et al. 2013; Rosdahl & Teyssier 2015; Ishibashi & Fabian 2015; Seo & Youdin 2016). We note that the impact of radiation pressure has also been studied for a wide variety of other systems and scales, such as accretion disks around black holes (Begelman 1978; Gu 2012) high-mass stars (Yorke & Sonnhalter 2002; Krumholz et al. 2009a, 2010; Kuiper et al. 2010; Tanaka & Nakamoto 2010; Kuiper & Yorke 2013), low-mass cores, filaments, or shell structures in the ISM (Verdolini et al. 2013; Ochsendorf et al. 2014; Seo & Youdin 2016), and galaxy formation in a cosmological context (Wise et al. 2012; Moody et al. 2014; Sales et al. 2014; Hopkins et al. 2014).
Here, we critically assess the hypothesis that radiation pressure is the main regulatory agent for star formation. Its effectiveness has already been called into question by Krumholz & Thompson (2012), who showed that acceleration of dense gas by radiation pressure produces Rayleigh–Taylor instabilities that allow photon escape. Davis et al. (2014), however, argued that a more accurate treatment of the radiation transfer (RT) showed that outflows could still be driven. We examine the detailed spectral evolution of escaping radiation rather than the dynamics, and conclude that the impact of radiation on molecular cloud evolution and global ISM dynamics may still be dramatically overestimated. We note that similar conclusions have been reached, for example, by Silich & Tenorio-Tagle (2013) and Martínez-González et al. (2014).
In our study we focus on three key points: the efficiency of the coupling between radiation and matter; the fraction of the available radiative energy that can readily be converted into kinetic energy; and taken together, the environmental conditions under which radiation pressure can disrupt star-forming molecular clouds and thus contribute to the self-regulation of stellar birth.
When photons scatter, they just change direction, but keep their original energy. When a photon gets absorbed by a dust grain, on the other hand, reemission occurs at the temperature of the dust grain, in the thermal infrared. Stellar photons in the ultraviolet and optical bands are thus quickly shifted to much longer wavelength. The dust absorption and scattering cross sections for ultraviolet or optical photons are large, so molecular clouds are generally optically thick to them. However, at lower energies and longer wavelength both cross sections drop dramatically, so eventually the cloud becomes transparent to the radiation. The importance of this effect to correctly calculating the effect of radiation pressure on outflows was first appreciated by Habing et al. (1994) in the context of winds from cool giants.
The exact frequency at which this transition occurs depends on the actual absorption and scattering cross sections, which in turn are subject to the chemical composition and size distribution of dust grains, and on the density, velocity and temperature structure of the cloud out of which the star or star cluster has formed. The shift of photons to longer wavelengths as they interact with dust inevitably causes them to reach a wavelength at which the remaining column density out of the cloud is transparent, at which point they escape. The question of how quickly this occurs ultimately determines the answers to the above questions of the impact of radiation pressure on the dynamics of the ISM and the self-regulation of star formation. We have approached this problem by means of three-dimensional (3D), RT simulations. We scan a wide range of cloud and cluster masses, star formation efficiencies, and dust size distributions, with specific focus on the detailed microphysics of the interplay between radiation and matter. Our models are applicable to a variety of star-forming environments, ranging from small groups of stars forming in low-mass clouds similar to those observed in the solar neighborhood up to very massive clusters embedded in high-mass clouds representative of the most extreme star formation conditions seen in the Local Group. In Sect. 2 we introduce our one-dimensional cloud and cluster radial profiles. Then, we describe how we calculated the forces acting on different radial shells in thecloud. As we focus on the detailed interplay between radiation and dust, we provide the details of our dust model and describe our method to self-consistently model absorption and scattering processes using our Monte Carlo radiative transfer code polaris. We consistently account for the shift of the spectral energy distribution toward longer wavelengths as the radiation propagates outwards through the cloud. Our results are presented inSect. 3, where we compute the ratio of radiative to gravitational forces at any given cloud radius, for awide range of model parameters, varying the mass and size of the molecular cloud as well as of the embedded cluster. We considered different grain size distributions and dust temperature calculations. Our set of models covers conditions typical to the solar neighborhood and extends to more extreme starburst systems. In Sect. 4 we discuss observational implications, compare our models with the existing literature, and comment on the limitations of our approach. Finally, we summarize and conclude in Sect. 5.
2 Method
2.1 Initial conditions
2.1.1 Cloud model
We studied spherically symmetric clouds (cloud quantities are subscript MC) with an outer radius of Rout∈ [5, 20, 150] pc. We adopted a Plummer (1911) profile for the density
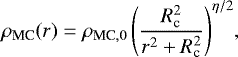 (1)
(1)
where r is the distance from the cloud’s center, Rc fixes the size of the flat inner region,and the exponent η controls the steepness of the power-law fall-off outside. This is a good description for many star-forming regions, which are frequently observed to be centrally condensed (e.g., Lin et al. 2016). We used values of Rc = 0.01Rout and η = 2 typical for star-forming molecular clouds (Motte et al. 1998, 2015; Mueller et al. 2002; Pirogov 2009; Lin et al. 2016) for all models. Since our models have a sharp outer radius Rout, they contain a well defined cloud mass. Integrating Eq. (1), the mass enclosed within a certain radius r is
![$ M_{\textrm{MC}}(r) =4\pi \rho_{\textrm{MC}}R_{\textrm{c}}^2 \left[ r -R_{\textrm{c}} \arctan\left( \frac{r}{R_{\textrm{c}}}\right)\right]\!.$](/articles/aa/full_html/2018/03/aa31698-17/aa31698-17-eq2.png) (2)
(2)
We considered four different values for the central density ρMC ,0 such that the resulting cloud mass MMC ∈ [104, 105, 106, 107] M⊙ (see Table 1). For the dust mass we apply the canonical dust to gas ratio (DGR) of ξ = mdust∕mgas = 0.01 (e.g., Boulanger et al. 2000) in all molecular cloud models.
Physical quantities and notation of the applied models.
2.1.2 Cluster model
In order to model radiation scattering and absorption, we used a realistic incident stellar energy distribution (SED) scaled from a zero age main-sequence, 105 M⊙, solar metallicity cluster (cluster quantities are subscript CL) using starburst99 (Leitherer et al. 1999). The shape of the spectrum therefore remained identical for all cluster models, while the luminosity scales with total cluster mass (see Table 1). We chose a cluster of 105 M⊙ as reference in order to ensure a full sampling of the initial mass function (IMF). This is relatively safe to scale down to the lowest cluster mass of 103 M⊙, where stochasticity becomes important. In lieu of fully exploring stochastic clusters, we note that our approach of scaling from a massive cluster produces a 103 M⊙ luminosity consistent with approximately five O stars, which is five times that of the Orion Trapezium. In a statistical sense, we considered this as an upper limit of the expected feedback from our lowest mass clusters. We considered clusters that are either point-like or have finite radial extent. In the first case, all photons are emitted from a single position, while in the second case, mass and emissivity are spatially distributed following a 3D Gaussian distribution
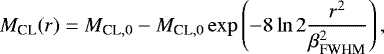 (3)
(3)
where MCL,0 is the total mass of the cluster and βFWHM is the full width at half maximum (FWHM) of the Gaussian mass distribution.
2.2 Forces
2.2.1 Gravity
At each position along the radial distance r from the center of the molecular cloud, the forces of gravity Fgra and radiation Frad act in opposition. The gravitational force experienced by the cloud at every radius includes the contribution from the assumed cluster and that of the gas and dust that compose the cloud. Assuming a perfect dynamical coupling between the two components, we can write
![$ \vec{F}_{\textrm{gra}}(\vec{r}) = -G \frac{m_{\textrm{d}}}{\xi}\frac{{\vec{r}}}{| {\vec{r}}|^3} \left[M_{\textrm{CL}}(|{\vec{r}}|)+M_{\textrm{MC}}(|{\vec{r}}|)\right]\!,$](/articles/aa/full_html/2018/03/aa31698-17/aa31698-17-eq4.png) (4)
(4)
where we have scaled the gravitational force per dust grain by ξ−1 to account for the dust to gas ratio. Only the gravitational force from a point-like cluster decreases with distance r with a simple r−2 law. Gaussian clusters have additional correction terms as defined in Eq. (3), and the same holds for the molecular cloud material where the mass depends on the radius as defined in Eq. (2). For small clusters and massive clouds, this term dominates the gravitational force at large radii. Figure 1 shows in the top panel the contributions of cloud mass and cluster mass to the net gravitational force experienced by the dust grain, assuming a point-like cluster. Here, the central cluster strictly follows a r−2 power law while the chosen mass distribution of the molecular cloud gas leads to a clearly defined maximum in gravitational force from the gas near the edge of the cloud. Consequently, the net gravitational force declines steeply nearthe cloud’s center until the cloud mass becomes dominant toward the edge of the molecular cloud. The bottompanel of Fig. 1 shows the net gravity assuming a cluster with a spatially extended cluster massdistribution in a smaller cloud. The mass distribution of the cluster is Gaussian (Eq. (3)) resulting in an almost constant contribution to net gravity close to the center and a decline steeper than r−1 in the outer parts. The cloud mass produces a small increase in the net gravity in the outer regions.
 |
Fig. 1 Top panel: gravitational force, Fgra, for an M7 molecular cloud model with an outer radius of Rout = 5 pc, the two point-like cluster models C3 and C7 , and their combinations. Bottom panel: same combinations as the top panel for an M6 molecular cloud with an outer radius of Rout = 20 pc and a C6 cluster model with a 3D, Gaussian, spatial extension having FWHM of 1 or 4 pc . |
2.2.2 Radiation
The two ISM components that absorb radiation are gas and dust, and it is important to determine which dominates. For non-ionizing radiation the dominant gas opacity is H2 Lyman–Werner absorption, but these bands cover only a small fraction of the total momentum output of the massive clusters considered here. Thus, for the gas densities considered, dust dominates the absorption of non-ionizingradiation. For ionizing radiation, the dominant gas opacity is photoionization. We were able to estimate the impact of neglecting gas absorption of ionizing radiation (which carries the majority of the momentum)by comparing the relative fraction of radiation absorbed by gas or dust. The change of a photon flux ϕ through a finite path length dr due to absorption is
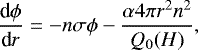 (5)
(5)
where n is the gas density, σ is the dust absorption cross section, α the H recombination rate, r the radius form the source, and Q0(H) is the rate ionizing photons are produced by the cluster. We see that the importance of dust increases as the photoionization rate of the cluster increases, and decreases with increasing gas density because of the quadratic nature of recombination. Taking characteristic values for our clusters, we find that absorption by dust is almost 3 orders of magnitude greater than by gas at a radius corresponding to the Strömgren radius of our low-mass star clusters. For the most massive clusters in the most dense clouds in our suite of models, the ratio of gas to dust absorption increases by 2 orders of magnitude but is still smaller than the contribution from dust. Thus, gas absorption is at most a 10% correction to the models considered here. This is additional justification for our investigation of the impact of radiative pressure acting on dust. For the calculation of the outward radiative force, we recall that at a distance r from a source of radiation with a bolometric luminosity L*, a dust grain with a radius a and an average cross section of ⟨Cpr⟩ will be accelerated by a force (van de Hulst 1981)
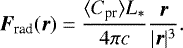 (6)
(6)
The averaged radiative pressure cross section ⟨Cpr⟩ is defined as a flux mean with
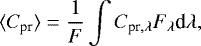 (7)
(7)
where F = ∫ Fλdλ is the overall radiative flux. Applying flux conservation,
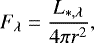 (8)
(8)
where the simplest assumption is that L* = ∫ L*,λdλ represents the integrated spectral luminosity of the cluster. For point-like clusters, the radiative force decreases as r−2 , while for Gaussian clusters the radial dependence is more complicated, as discussed above. Additional complications come from the heating of the dust by cluster radiation. This changes the cross section, as well as the frequency of the thermal radiation re-emitted by the dust grains. Simply assuming a fixed value for the dust temperature independent of radius and the properties of the cluster and cloud introduces errors and biases. Assessing the impact of radiative pressure therefore requires a fully self-consistent model of the local radiation field, where the quantity Lλ (r>) represents the directed local spectrum of radiation after reprocessing by the dust. We combined a physically motivated dust grain model with a state of the art radiative transfer code in order to calculate this reprocessed spectrum, and thus obtain the correct radiative force acting on the dust grain at each radius. By including this process, we go beyond any previous model in this field. Star-forming molecular clouds have widely varying grain size distributions depending on accreted grain properties and local grain growth. This variation strongly influences the coupling of the dust with the radiation field, and thus needs to be modeled consistently to assess the competition between gravitational and radiative forces. In order to account for the wavelength-dependent optical properties of different grain size distributions, we calculated the total radiative force
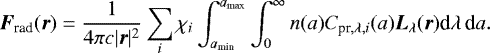 (10)
(10)
Here, χi is the fractional abundance of distinct dust grain materials i, such that ∑ χi = 1, n(a) is the grain size distribution, and the parameters amin and amax, are the smallest and largest grain sizes. The various dust models we consider in this paper are introduced in the next section.
2.3 Dust modeling
The interstellar extinction curve varies only gradually in the ultraviolet and optical wavelength regime, but decreases dramatically from near-infrared to sub-millimeter (sub-mm) and millimeter (mm) wavelengths, with well-defined silicate features occurring at λ = 9.7 μm and λ = 18 μm. The standard Mathis et al. (1977, hereafter MRN) model captures these characteristics. It has a power-law grain size distribution n(a) ∝ a−q, with a lower and upper cut-off radius amin and amax, respectively. The distribution of dust grain sizes arises from the competing processes of dust grain growth by accretion and nucleation and reprocessing toward smaller dust grains by sputtering, and the collision of dust grains with the surrounding gas and each other. The dust is taken to be a mixture with 62.5% astronomical silicate (taken to be olivine) and 37.5% graphite (Draine & Li 2001). The size limits for silicate and graphite in the ISM are [amin, amax] = [10 nm, 100 nm] with a size exponent of q = 3.5 (Weingartner & Draine 2000). For the silicate and graphite components we use sublimation temperatures of 1200 and 3915 K, respectively.We defined the sublimation radius in each molecular cloud model as the distance at which the smallest silicate grains of our dust model start to evaporate. Consequently, the photons of the cluster have no interaction with the dust up to this radius. Later, in Sect. 3.3 we successively increase the maximum grain radius up to amax = 200 μm in our radiative force calculations to determine the influence of dust growth in dense environments such as molecular clouds. For simplicity we assumed the dust grains to be compact spheres. We calculated the required optical dust properties for 250 distinct wavelength bins over an ensemble of 200 dust grain sizes with the miex code (Wolf & Voshchinnikov 2004). This code calculates the cross sections of extinction Cext,λ(a), scattering Csca,λ(a), absorption Cabs,λ(a), and the average scattering angle 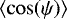 on the basis of Mie scattering theory (Mie 1908) with material specific refractive indices as input. We note that the average scattering angle is also a function of wavelength and dust grain size. For the astronomical silicate and graphite components we used the refractive indices provided by Draine (1994) and Weingartner & Draine (2000) and extrapolated them logarithmically to cover a broader spectral range of λ ∈ [1 nm, 4 mm]. A beam of photons contributes to the radiative force on dust grains by transferring momentum. At each scattering event a part of the incident beam is redirected by an angle ψ and the remaining momentum of the incident beam drops on average by a factor of
on the basis of Mie scattering theory (Mie 1908) with material specific refractive indices as input. We note that the average scattering angle is also a function of wavelength and dust grain size. For the astronomical silicate and graphite components we used the refractive indices provided by Draine (1994) and Weingartner & Draine (2000) and extrapolated them logarithmically to cover a broader spectral range of λ ∈ [1 nm, 4 mm]. A beam of photons contributes to the radiative force on dust grains by transferring momentum. At each scattering event a part of the incident beam is redirected by an angle ψ and the remaining momentum of the incident beam drops on average by a factor of 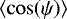 . Therefore, the cross section of radiative pressure required to evaluate Eq. (6) is
. Therefore, the cross section of radiative pressure required to evaluate Eq. (6) is
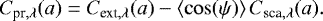 (11)
(11)
In the left column of Fig. 2 we show the resulting size averaged cross sections of extinction, absorption, scattering, and radiative pressure versus wavelength for three of our chosen maximal dust grain radii amax (see also Table 1). At the smallest considered amax = 0.02 μm (model D1 , Fig. 2 top left panel), scattering decreases quickly for λ > 0.1 μm and can be neglected at λ > 1 μm, so extinction as well as the radiative pressure cross section are completely dominated by the absorption behavior of the dust. Since a wavelength of 1 μm corresponds to a temperature of Td ≈ 2900 K and most of the dust embedded in a molecular cloud can be expected to be much cooler, the radiative force quickly becomes irrelevant in an environment with such a narrow dust grain size distribution. Keeping the total dust mass constant while redistributing the grain sizes toward larger dust grains results in an increase of the scattering cross section. For a maximum of amax = 2.0 μm (D3 , Fig. 2 middle left panel) scattering remains relevant up to a wavelength of ≈ 10 μm. The relevance of scattering extends even to the sub-mm and mm wavelength regime for dust grains with sizes up to amax = 200.0 μm (D5 , Fig. 2 bottom left panel). In molecular clouds enriched with large dust grains the radiative force can be enhanced by several orders of magnitude compared to clouds with smaller dust grains. This holds even if the large dust grains are so cold that the spectrum of the cluster is shifted toward mm wavelengths.
The right column of Fig. 2 shows the re-emission probabilities for a dust grain mixture corresponding to the panel on theleft hand side. The color scale gives the probability for a certain wavelength bin to be re-emitted from a size averaged dust grain with a constant temperature from the given size distribution (see Eq. (15)). As the comparison of the left column and the right column of Fig. 2 reveals, the resulting re-emission probabilities match the characteristic bumps of the cross sections of absorption. Furthermore, absorption is directly related to the optical properties of the assumed dust grain materials. Hence, the choice of dust grain materials is also of relevance for the re-emission spectrum of the dust and thus the resulting radiative force acting on the dust grains. The optical depth τλ is related tothe cross section of extinction by integration along a path. Figure 3shows the optical depth as a function of radius and wavelength from the center to the edge of the M4 molecular cloud, applying two different dust grain models. Since all molecular cloud models have the same density distribution scaled by the central density ρMC (see Eq. (1)), the plotted optical depths and density distribution can easily be re-scaled for different molecular cloud masses. As shown in the left panel of Fig. 3, we used the standard MRN dust grain model (D2 , see Table 1) to calculate the optical depth for seven different wavelengths covering the entire spectrum of the pre-calculated dust cross sections. Since the extinction declines toward longer wavelengths, wavelengths exceeding 100 μm do not become optically thick at all for this size distribution. The right panel of Fig. 3 shows the optical depths resulting from the D5 dust model. Since all dust grain models have similar cross sections in the ultraviolet and visible wavelength regime, the optical depth in those regimes is rather similar (see Fig. 3). However, in contrast to the D2 model, in the D5 model, all paths to distances larger than 0.1 pc become optically thick within this relatively modest-sized molecular cloud. This suggests thedust grain size distribution is a central parameter in determining the contribution of radiation to the net balance of forces.
 |
Fig. 2 Left panels: size averaged cross section of extinction Cext, scattering Csca, absorption Cabs, and pressure Cpr over wavelength. Right panels: probability distribution of re-emitted wavelength for different dust temperatures. Different rows are for distinct maximum grain radii corresponding to the dust grain models D1 (top row), D3 (middle row), and D5 (bottom row). |
 |
Fig. 3 Radial optical depth τλ and density ρ distribution for the M4 molecular cloud. The optical depth is calculated for different wavelengths λ applying the dust models D2 (left panel) and D5 (right panel). |
2.4 Radiative transfer
The simulations are performed using polaris, a 3D, Monte Carlo RT code developed for dust temperature and polarization calculations (see Reissl et al. 2016, for detail). We used spherical symmetry, with a grid divided into azimuthal and polar separations of eight distinct octants in the azimuthal and polar directions and 700 radial zones on a logarithmically increasing grid, to assure that the density and temperature differences between adjacent cells remain small. Dealing with single photons would not allow us to correctly treat the conservation of energy when the photon is reprocessed by dust. The code therefore uses distinct monochromatic photon packages to follow their transfer through the grid. For example, when a photon package representing a certain number of ultraviolet photons gets absorbed, it becomes reemitted in the infrared as photon package which carries a larger number of photons but contains the same energy as the absorbed one. As photon packages propagate through the grid they eventually interact with the dust grain mixture in a grid cell. The nature of the interaction is statistically governed by the physical laws. The probability of radiation-dust interaction is determined by the cumulative contributions from each cell the photon package has traveled through. The optical depth a photon package accumulates up to the Nth cell of the grid is
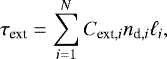 (12)
(12)
with the path length ℓi, the cross section of extinction Cext,i and the number density nd,i of the dust in each cell i. Here, ℓi is defined as the distance between the entrance and exit point of the ray through the boundaries of the cell. The statistical distribution of the optical depth can simply be sampled from τst = −ln(1 − z) (Wolf 2003), where z ∈ [0, 1[ denotes anyrandom number. A photon package interacts with the dust when the condition τext = τst is fulfilled in a particular cell i. In this special case the path length ℓi is defined tobe between the cell wall and the exact point of interaction along the trajectory of the photon package within that cell.
The nature of the interaction itself can be either scattering, or absorption and re-emission. The wavelength-specific dust grain albedo determines the probability of scattering,
![$ \alpha(\lambda) = \frac{C_{{\textrm{sca},\lambda}}}{C_{{\textrm{abs},\lambda}}+C_{{\textrm{sca},\lambda}}} \in [0,1].$](/articles/aa/full_html/2018/03/aa31698-17/aa31698-17-eq15.png) (13)
(13)
If an interaction takes place, we drew a new random number z uniformly in the interval [0, 1[. In the case of z > α the photon package scatters on the dust grain. The scattering event changes the direction of the photon package by an angle of ψ, dependent on the characteristic phase function F(ψ). For spherical dust grains the scattering angle can be sampled from (Henyey & Greenstein 1941; Hong 1985)
![$ F(\psi)=\frac{1-\left\langle \cos\psi \right\rangle^2}{4\pi\left[1+\left\langle \cos\psi \right\rangle^2-2 \cos\psi\right]^{\frac{3}{2}}},$](/articles/aa/full_html/2018/03/aa31698-17/aa31698-17-eq16.png) (14)
(14)
where 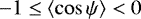 means that back scattering of photons is most likely, while
means that back scattering of photons is most likely, while 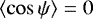 corresponds to isotropic scattering, and
corresponds to isotropic scattering, and 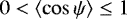 to forward scattering. For z < α the photon package gets absorbed and instantaneously re-emitted by the dust grain in order to sustain local thermodynamic equilibrium. Here, the direction of the thermal radiation is isotropic. In contrast to scattering, the wavelength changes after re-emission. Assuming that the dust grain radiates thermally, the new wavelength has to be randomly sampled from a modified blackbody spectrum that is weighed by the dust absorption coefficient (e.g., Lucy 1999),
to forward scattering. For z < α the photon package gets absorbed and instantaneously re-emitted by the dust grain in order to sustain local thermodynamic equilibrium. Here, the direction of the thermal radiation is isotropic. In contrast to scattering, the wavelength changes after re-emission. Assuming that the dust grain radiates thermally, the new wavelength has to be randomly sampled from a modified blackbody spectrum that is weighed by the dust absorption coefficient (e.g., Lucy 1999),
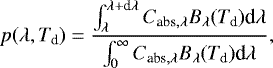 (15)
(15)
where Bλ(T) is the Planck function. Figure 4 shows the resulting spectrum for our fiducial dust temperature of Td = 20 K for different grain size distributions. Because Cabs,λ drops significantly in the thermal regime longwards of λ ≈ 100 μm (see Fig. 2) the modified blackbody is much more narrowly peaked and skewed toward smaller wavelengths than Bλ (T). As we discuss in Sect. 3.2 this has important consequences for the effective optical depth of the cloud and for the spectral energy distribution that is seen by an outside observer.
To compute the radiative forces acting on dust, we extended the polaris code with an additional RT mode implementing the equations introduced in Sect. 2.2. After each 3D simulation we average the results among the eight octants in our grid in order to minimize the noise inherent in Monte Carlo RT simulations.
 |
Fig. 4 Comparison of modified blackbody spectra for the three different dust models displayed in Fig. 2 for a dust temperature of Td = 20 K and upper values of amax of 0.02 μm (D1 ), 2 μm (D3 ), and 200 μm (D5 ), respectively.These spectra are more narrowly peaked and skewed toward smaller wavelengths than the corresponding Planck function Bλ(Td), because the emission is weighted by the absorption cross section, Cabs,λ, which drops significantly at sub-mm and mm wavelengths. |
3 Results
To assess whether a cloud is contracting or expanding in the presence of radiative feedback from a central star cluster, we introduced the parameter
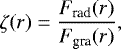 (16)
(16)
which is the ratio of radiative to gravitational forces acting on a fluid element (composed of gas and dust) at any given radius r in the cloud. We calculated ζ for a wide range of model parameters, covering small star-forming clouds in the solar neighborhood as well as conditions expected in starburst systems. More precisely, we varied the mass and size of the molecular cloud, the mass and thus the luminosity of the cluster, as well as the cluster’s spatial extension, and the dust grain size distribution, as summarized in Table 1. We considered the fiducial case of the dust temperature being fixed to a typical value of 20 K, but we also investigate models where it is allowed to vary with distance to the central cluster. We remind the reader that in each model we consistently account for the continuous shift of the spectrum toward longer wavelengths as the radiation propagates outwards to the boundary of the cloud.
3.1 Constant dust temperature
To touch base with the existing literature, we begin our discussion with calculations in which we artificially fix the dust temperature to a constant value of Td = 20 K. We focus on the fiducial model with cloud radius Rout = 5 pc, point cluster geometry, and MRN dust model D2 (see Table 1). Furthermore, we assume a sharp dust sublimation radius Rsub = 1.1 × 10−3 pc (see Sect. 2.3), within which each photon package propagates without interaction. Figure 5 shows the resulting radiative force in comparison to gravity and their ratio ζ for models M4 –M7. For each cloud we study clusters ranging from our minimum cluster mass C3 with 103 M⊙, up to ten times the cloud mass, in steps of 0.5 dex. The exception is the M7 model were the considered cluster mass is only between C3 and C7. This is equivalent to total star formation efficiencies of ϵtot = MCL∕(MCL + MMC) = 9.1–91% in the case of the M4 cloud model and ϵtot = 0.009–50% in the case of the M7 cloud model.
Figure 5 shows that radiation pressure cannot disperse any of these clouds. In every case the outward radiative force is overwhelmed by the inward gravitational force, mostly by factors of ζ ~ 100 or more, only reaching even as high as ζ ~ 0.1 for the 107 M⊙ cloud M7.
Figure 5 also shows that gravitational force scales similarly with cloud and cluster masses. A similar scaling also holds for the radiative force, although there are also marked differences in the overall radial profiles. This results from the strong radial variations in the number of scattering and absorption events for the different cloud and cluster models, as we discuss in more detail below. We find that higher mass clouds have a larger radius within which scattering is still relevant, while the maximum of absorption and re-emission events remains at the same distance. As a consequencethe radiative force declines less steeply with radius. This can lead to a distinct bulge, as in model M5 between 0.02 and 0.1 pc, or even to a complete flattening of the radiative force out to radii of ~ 0.05 pc, as noticeable in models M6 and M7. Here, the dilution of photons with larger distance is fully compensated by an increase in radiation-dust interactions.
3.2 Spectral shift
In order to analyze the radial profile of the radiative force Frad in more detail, we track the position of each scattering and absorption event in the Monte Carlo RT simulations. Figure 6 shows the resulting maps of interactions in our lowest and highest mass clouds for a cluster with 50% star formation efficiency (M4 C4 model in the top row and M7C7 model in the bottom row). We find that scattering is only efficient within R < 3 × 10−3 pc, in fairly distinct wavelength ranges, while absorption and re-emission occur mostly at distances larger than about 3 × 10−2 pc for essentially all wavelengths. However, even further in, absorption and re-emission can not be entirely neglected. Closely related, Fig. 7 illustrates the number of scattering events as well as absorption and re-emission events occurring for the same two models, M4 C4 (top) and M7 C7 (bottom). Cluster radiation longwards of λ ≳ 100 μm barely scatters once, since the low-mass cloud is optically thin at these wavelengths (Fig. 3, left panel). Even for the shortest wavelength emitted by the cluster, the most likely number of scatterings is under five. Since longer wavelengths are unlikely to scatter and shorter wavelengths quickly shift after a few interactions, all photons finally end up at infrared wavelengths. With increasing molecular cloud mass, the optical depth at any given radius increases. As a result the radius within which scattering is relevant gets larger while the maximum of absorption and re-emission events remains at the same distance.
The rapid reprocessing of the light from the central star cluster and the deviation of the resulting radiation field from a single-temperature blackbody has important consequences for the overall optical depth and for the radiative force. As seen in Fig. 8, we examined how this force would change if we adopted the two most extreme assumptions possible. First, we neglected absorption and re-emission at thermal wavelengths (Cabs = 0 cm2) and only rely on scattering of the incident stellar radiation field. The cloud is extremely optically think for radiation in ultraviolet and optical bands, and consequently, the radiative force is boosted by orders of magnitude, easily exceeding gravity. Second, we took the other extreme and neglect scattering (Csca = 0 cm2). That is each stellar photon is immediately absorbed and the corresponding energy is emitted as thermal photons with frequencies sampled from a 20 K modified blackbody (Eq. (15)). We find that the resulting radiative force is very similar to the full model with both scattering as well as absorption and re-emission. This demonstrates again that scattering is rather unimportant for the momentum transfer from the radiation field to dust for the type of clouds considered here and that the spectral shift associated with absorption and re-emission is the key to understanding the impact of radiation pressure.
 |
Fig. 5 Gravity (Fgra, red lines) in comparison to radiative forces (Frad, blue lines) for models M4 (top left), M5 (top right left), M6 (bottom left), and M7 (bottom right). The ratio of forces is defined as ζ = Frad∕Fgra (purple lines). All cases have a constant dust temperature of Td = 20 K, an outer radius of Rout = 5 pc and use dust model D2. We note that ζ < 1 everywhere, implying that radiation pressure does not support the cloud against gravitational contraction. The vertical brown line marks the sublimation radius. |
 |
Fig. 6 Radial and wavelength distribution of the scattering (left) and absorption (right) probability distribution for models M4 C4 D2 (top) and M7C7D2 (bottom). The x-axis gives the radius of interaction while the y-axis is the local wavelength of the photon package at the point of interaction. |
 |
Fig. 7 Number of scattering events (left column) and absorption and re-emission events (right column) experienced by a photon package before escaping the molecular cloud. The same models are shown as in Fig. 6, M4 C4 D2 (top) and M7C7D2 (bottom). The x-axis gives the local wavelength of the photon package at the point of interaction, and the y-axis gives the number of interactions of each type. |
 |
Fig. 8 Radial profile of radiative force (blue lines) for different molecular cloud models M4 (left panel) and M7 (right panel)with an outer radius of Rout = 5 pc and a constant dust temperature of Td = 20 K simulated with cluster models C3 through C7 in half steps.The blue band represents the same simulations with the absorption and reprocessing of radiation switched off (Cabs = 0 cm2), while the green bands result from the same simulations with an instantaneous redistribution of radiation (Csca = 0 cm2). |
 |
Fig. 9 Comparison of radiative and gravitational forces for varying dust size distribution upper cutoffs using dust grain models D1, D2 , D3 , D4 , and D5 with models M4C4 (left panel) and M7C7 (right panel). Notation as in Fig. 5. |
3.3 Varying dust size
To better understand which parameters can increase the ratio ζ of radiative to gravitational force, we now turn our attention to the dust grain model, continuing to hold dust temperature constant at Td = 20 K. We assumeda constant dust mass fraction of 1%, but consider different values for the maximum grain size. This is a key parameter as the size distribution controls the spectral dependence of the scattering and absorption cross sections (see Sect. 2.3).
We used the different dust grain size distributions presented in Table 1 to repeat a subset of the simulations discussed in Sect. 3.1. Since the radiative force scales with the cluster mass, we focus on the extreme models M4 C4 and M7 C7. In Fig. 9 we present the resulting radial distribution of radiative force and gravity. When calculating the radiative force, we consistently took the frequency shift into account as radiation propagates outwards through the cloud, as was done in Fig. 5. For the low-mass cloud M4 C4 (Fig. 9 left panel) the radiative forces resulting from the D1 , D2 , and D3 dust models are quite similar. The radial radiative force profile deviates slightly from a r−2 law and the ratio ζ remains in the gravitationally dominated regime, varying between 10−3 and 10−1. However, with larger dust grains in the system the scattering cross section increases and the cloud becomes optically thick even for longer wavelengths (see also Fig. 3). Here, an effect occurs similar to that in the M7 simulations presented in Sect. 3.1. The radius where scattering events can take place shifts outwards toward the cloud boundary. Therefore, a bulge forms in the radiative force at a distance of about 0.03 pc for the D4 and D5 models. Here, the radiative force and gravity are of the same order of magnitude so the ratio ζ reaches unity for model D5 at a distance of ≈ 0.01–0.1 pc. The same trend occursin the M7C7 model (Fig. 9 right panel). Since this cloud has a higher mass and thus a higher density, it is already optically thick even for the standard MRN (D2) dust model. Hence, the bulge and the slow decrease in radiative force near the center are more pronounced and already become clearly visible for small grain sizes. The radiative force exceeds gravity for dust grain models with an upper cutoff radius of amax ≿ 2 μm. In the most extreme case of the D5 dust model, the number of scattering events increases dramatically even for the longest wavelengths, and the ratio ζ reaches values up to 106. Hence, in the M7C7D3–M7C7D5 models radiation may disrupt the molecular cloud. However, considering the processes of grain growth in the ISM (see, e.g., Zhukovska et al. 2008, 2016) dust with a radius exceeding amax = 200 μm seems improbable.
3.4 Variable dust temperature
Next we explored how the assumption of a constant dust temperature affects our results. In the previous sections the dust temperature was fixed to Td = 20 K as in previous work on this subject. In reality, however, Td varies by over an order of magnitude from the inner to the outer edges of the cloud. Since the dust temperature determines the redistribution of the cluster spectrum toward longer wavelengths, we need to investigate the impact of this assumption and explore how variations in the radial dust temperature change the radiative force. To connect with the discussion in Sect. 3.1, we focused again on the standard MRN dust model (D2 ), and calculate the parameter ζ for the full range of cloud and cluster models listed in Table 1. This time we used the full polaris Monte Carlo RT scheme to self-consistently calculate the dust temperature (see Reissl et al. 2016, for details).
Figure 10 presents the angle-averaged dust temperatures for different molecular cloud models and clusters. The plot demonstrates that the dust temperature can indeed reach several hundred Kelvin near the cloud center. However, it also indicates that Td drops quickly with increasing radius and falls significantly below 20 K at 0.01–0.7 pc, in the outskirts of the cloud. Figure 12 shows the resulting radiative forces and gravity for the molecular cloud models M4 and M7. Similar to the models with large grain sizes presented in Fig. 9, calculations that take radial temperature variation into accountalso show an increase in radiative force compared to simulations with a constant temperature.
However, in the case of variable temperature this is not due to an increase in optical depth (see Fig. 3). A constant temperatureof 20 K leads to an efficient distribution of the initial cluster spectrum toward a wavelength regime where lower extinction allows the photons to escape more easily. With higher temperatures close to the center this shift in wavelength is smaller. Consequently, the photonsremain trapped for longer close to the cloud center. For model M4 (Fig. 12 left panel) this results in an additional bulge in the radial force at a distance of about 0.02 pc similar to that observed in Sect. 3.3. This increased photon trapping is even more effective in the M7 (Fig. 12 right panel). Compared to the calculations assuming a constant dust temperature shown in Fig. 5 (lower right panel) a higher inner temperature leads to a steeper slope. This allows the radiative force to be of the same order as gravity and even to exceed it out to a radius of ~ 0.1 pc. We note, however, that the typical size scale of massive star clusters is about 1 pc (see, e.g., Portegies Zwart et al. 2010, and references therein), considerably larger than the region of radiative acceleration seen here, so values of ζ ≳ 1 are an artifact of our assumption of point-like clusters (model F0 in Table 1).
That is, concentrating the radiation source to a point in the center of the cloud rather than a distributed region increases the radiation pressure in the innermost regions. When we relaxed this assumption in Sect. 3.5, we indeed saw lower values of ζ in the central regions, as expected.
 |
Fig. 10 Grain-size averaged dust temperature distribution for different cluster and molecular cloud models with an outer radius of Rout = 5 pc. The verticaldark brown line marks the sublimation radius. |
 |
Fig. 11 Comparison of radiative and gravitational forces for model M6, except with an outer radius of Rout = 150 pc instead of the 5 pc used in Fig. 5. Again, we considered point-like cluster models C4 to C7 with masses of 104 to 107 M⊙. |
 |
Fig. 12 Comparison of radiative and gravitational forces in models with self-consistent (blue lines) and constant (green lines) dust temperature. Cloud models are M4 (left) and M7 (right), and radiative forces were calculated for cluster models C3, C5 , and C7 and the D2 dust model. The radial dust temperature distributions follow the temperatures shown in Fig. 10. The ratio ζ is shown below (purple) for the variable dust temperature models. |
3.5 Impact of cloud and cluster size
Finally, we investigated the impact of different cloud and cluster sizes, relaxing the simplifying assumption of point-like clusters. We began with cloud size, and repeated our simulations for an M6 model with an outer radius of Rout = 150 pc, rather than 5 pc, with the usual MRN (D2 ) dust model, and with a fixed dust temperatureof Td = 20 K. For the dust sublimation radius we still assumed a value of Rsub = 1.1 × 10−3 pc. As before, we varied the cluster mass from 104 to 107 solar masses, corresponding to star formation efficiencies from 1% to an unrealistically high 91%. This choice of parameters includes a cloud very similar to the model of the Milky Way molecular cloud G298.4-0.3 considered by Murray et al. (2010), who adopted a star formation efficiency of 3%. Figure 11 shows the radiative and gravitational forces and their ratio for this larger cloud. In contrast to the M6 model plotted in Fig. 5 in the top right panel, the larger molecular cloud has a far lower surface density, and subsequently, a slower increase in optical depth. Hence, it is optically thin at much shorter wavelengths, and the probability of interaction between radiation and dust is reduced. However, the radiative force is down by only 2 orders of magnitude in this case because the redistribution in wavelength is also less efficient, so the ratio ζ remains at an almost constant value of ~10−2 in the inner regions of the cloud, rather than dropping below that as in the smaller cloud model. The larger ratio toward the border of the cloud is solely a result of the increasing influence of the cloud mass. Indeed, after its sharp decline near the sublimation radius the radiative force follows an almost exact r−2 power law. The resulting forces of radiation and gravity scale exactly with the considered cluster mass in all of our models. All simulations have also in common that the ratio ζ remains around or below 10−2, making gravity the dominant considered force in these simulations, independent of the combination of cloud modeland cluster mass. We now turn our attention to cluster size. As discussed above, some F0 cluster models show values of ζ ≳ 1 in the innermost 0.1 pc of the cloud, where the intense radiation field can lead to multiple scatterings per photon. This overestimates the strength of radiation pressure for three reasons. First, a point-like cluster maximizes the radiation flux per unit mass in the interior of the cloud, and hence the radiative force. Second, all photons from the cluster are emitted from a common origin. The resulting forces exerted by every photon from absorption and back scattering are therefore purely additive, meaning no component of the radiative force from one star ever cancels another. Third, the dust temperatures near the cluster are maximal for a point-like cluster. A spatially extended cluster produces less radiation energy per dust grain near the center, and so will result in comparatively lower dust temperatures. To investigate these effects we again considered the M6 model, but now with an outer radius of Rout = 20 pc and with a fixed cluster mass of 106 M⊙. The model can be compared to the models of the W49 giant molecular cloud in the Milky Way and the M82 starburst galaxy in Murray et al. (2010), which have cloud masses of 7.5 × 105 and 3 × 106 M⊙ as well as cluster masses of 4.3 × 104 and 7 × 105 M⊙, respectively, with cloud radii of 22 and 30 pc. This corresponds to star formation efficiencies of 6% and 24%, and so our choice of 50% leads to comparatively stronger radiative feedback than Murray et al. (2010). Figure 13 presents our results for clusters with varying sizes. As outlined in Table 1, the stellar distribution is now sampled from a 3D Gaussian distribution with a characteristic full-width half maximum (FWHM) of 0.1, 1, 2, or 4 pc. This changes both the calculation of the gravitational potential and of the radiative output of the cluster (see Sect. 2.1.2). The inward gravitational force no longer follows a r−2 law. It is almost constant within the cluster FWHM with values that are several hundred times smaller than for the point-like cluster. Further out, the forces converge when the potential is dominated by cloud material. The cluster photons are no longer emitted from a single point, but instead the distance is randomly sampled from a 3D Gaussian distribution with the corresponding FWHM. Consequently, the radiative force also changes compared to the previous point-like models. Figure 13 demonstrates that the combined impact of these three effects decreases the effective radiation pressure by a factor of 10–30 as the cluster size increases. As a result, gravity dominates at all radii, by factors of a few in the center and by 3–4 orders of magnitude in the cloud outskirts.
3.6 Results summary
A summary of the full parameter range covered for point-like clusters is presented in Fig. 14. It shows the ratio ζ for all calculations discussed so far, and it demonstrates that for any reasonable permutation of molecular cloud and cluster masses, and for typical Galactic dust grain size distributions the ratio of outward radiative force and inward gravitational force barely reaches unity. Including the effects of extended stellar clusters or larger clouds reduces the ratio further, leaving radiation pressure dominant only in unrealistic cases requiring star formation efficiencies approaching ϵtot~ 100% and maximum dust sizes amax ≿ 2 μm. For typical conditions in the Milky Way or in other Local Group galaxies, radiation pressure on dust grains from young clusters cannot disrupt the parental molecular cloud, and thus this process is not likely to contribute strongly to the (self) regulation of the star formation process.
4 Discussion
To better connect our results to the observational domain, we calculate d the resulting spectral energy distribution that an external observer would see when looking at the cloud. We then compared our models with the existing literature and discuss the limitations of our approach.
4.1 Observational consequences
The rapid absorption of ultraviolet and optical photons by dust grains followed by their re-emission at longer wavelengths (Sect. 3.2), has important observational consequences. The high efficiency of wavelength redistribution by dust is illustrated in Fig. 15, which plots the probability distribution of the final wavelength of photon packages at the edge of the cloud as a function of their initial wavelength of emission from the central cluster. (Photons emitted by the cluster with a wavelength between the far-infrared to mm that escape the cloud without interaction appear as a diagonal line in the upper right corner.) For simplicity we only show results of model M4 C4 with standard grain size distribution D2 and a cloud radius of 5 pc, but we note that a similar result holds for all clouds and clusters considered here. As explained in Sect. 3.2 an outside observer will see emission at sub-mm and mm wavelengths. The figure demonstrates that it is highly unlikely for ultraviolet, visible or near-infrared photons to escape the molecular cloud unaltered even for the lowest mass cloud with the least massive cluster inside. Thus, this finding holds even more strongly for higher mass molecular clouds. Further detail is provided in Figs. 16 and 17, where we plot the frequency-averaged escape probability of photons as a function of cloud radius (left) and the spectrum emerging from the cloud (right). In Fig. 16 we show a range of models. For M4 and M7 cluster models we take the fiducial case with standard MRN dust (D2) and fixed Td = 20 K, and we consider a larger maximum grain size (D4). For M6C6 we adopt the standard radius of 5 pc as well as an inflated one of 150 pc. We see that for models with increasing dust grain sizes and cluster masses, photons escape mostly from the cloud outskirts with only small contributions coming from close to the central star cluster. The exception is the model M6 C6 with Rmax = 150 pc where the cloud mass is distributed over a large volume leading to an decrease in optical depth. We emphasize that all these rather different models result in similar spectra in the case of a constant temperature. They peak at λ ≈ 145 μm, corresponding to a modified blackbody with a temperature of 20 K, and in most cases, they show an extended tail of emission at mm wavelength. The distribution is more narrowly peaked than a single temperaturePlanck function, while it has an extended tail at larger wavelength, in particular for those models with dust where IR radiation can easily escape from the inner cloud layers. Consequently, the observable emission typically falls below the blackbody for wavelengths λ ≲ 1000 μm and lies above it for longer wavelengths. This is well explained by the relative contributions of scattering and absorption events as discussed in Sect. 3.2 and by the corresponding different optical depths at different wavelength. Assuming a constant dust temperature, this behavior is quite insensitive to the adopted cloud mass and size and independent of the star formation efficiency.
In Fig. 17 we show models complementary to the models presented in Fig. 16 with Rmax = 5 pc and D2 dust. By applying a radially dependent dust temperature the observable spectrum is mostly determined by the properties of the (cold) dust in the outer layers of the cloud sufficiently far away from the cluster. Any spectral characteristics of the stars in the center is entirely veiled from an outside observer in our spherical, static approximation. We may only notice that the dust emission appears colder for more massive clouds since almost all of the radiation escapes from the outer layers. Furthermore, we caution that this insensitivity to the parameters of cluster and cloud is in part caused by our assumption of spherical symmetry. In reality, the cluster may be extended and have substructure while the cloud is likely to be clumpy and to exhibit a degree of porosity. This means that certain lines of sight allow for a deeper look into the cloud closer to the emitting stars, so that the resulting spectrum will correspond to a larger range of dust temperatures than the one dimensional model predicts and that it may even contain contributions from the central cluster itself at the late phases of the evolution (see also Sect. 4.3 below).
The extended power-law tail at λ ≳ 1000 μm occurs because, at these wavelengths, all our clouds with standard MRN dust size distribution are essentially transparent (see left side of Fig. 3 for the example of M4 clouds). Therefore, every photon package produced at mm wavelength by thermal dust emission (with probabilities according to Eq. (15)) contributes to the local radiation field inside the cloud and eventually to the spectrum seen by an outside observer. These photons neither get scattered nor absorbed. They are not in local thermodynamic equilibrium with the cloud material and simply add up in number to build up a non-thermal tail in the overall spectrum. This non-thermal tail results in the solid diagonal line seen in the upper right corner of Fig. 15. We note that the right-hand side of Figs. 16 and 17, respectively, show the cluster spectrum in luminosity while Fig. 15 represents the number of photon packages. Hence, the difference of contrast between the figures.
 |
Fig. 13 Top: gravity in comparison to radiative force for varying stellar cluster size in the M6 C6 model with a constant temperature of T = 20 K and an outer radius of Rout = 5 pc. Vertical dotted lines give the FWHM of the Gaussian spatial distribution of the cluster, with values 0.1, 1, 2, and 4 pc . Middle: grain-size averaged dust temperature distribution for the M6C6 model dependent on the different FWHM. Bottom: same as the top panel with the radial dependent dust temperature shown in the middle. |
 |
Fig. 14 Parameter space of the ratio of radiative force to gravity ζ dependent on cluster model C, molecular cloud model M, and the different dust models D1, D2 , D3 , D4 , and D5 . The ratios are calculated for a distance of r = 0.1 pc from the cluster center. The bottom right panel is for the radially dependent temperature distribution shown in the left panel of Fig. 10 while the other panels are for a constant dust temperature of Td = 20 K. We note that this image is smoothed when reading it with MacOS preview. |
 |
Fig. 15 Probability for each permutation of shift between initial wavelength and final wavelength for the M4 C4 model. The abscissa shows the wavelength of the photon packages initially emitted by the cluster while the ordinate shows the final observable wavelength leaving the molecular cloud. |
 |
Fig. 16 Left: escape fraction of photons as a function of cloud radius for various models. All the models are modeled with constant dust temperature Td = 20 K. Right: corresponding spectra visible to an outside observer compared to the normalized stellar input spectrum. All output spectra are very similar and are reasonably well described as a blackbody with a temperature of 20 K. |
 |
Fig. 17 Same as Fig. 16 for selected models with a radially dependent dust temperature Td (r) as shown in the middle panel of Fig. 13. We note the shifted peak wavelengths in the different models. |
4.2 Comparison with existing studies
The calculations presented here strongly suggest that radiation pressure acting on dust cannot be the dominant feedback agent terminating star formation and disrupting the parental cloud around young star clusters. It seems that this process cannot significantly contribute to the self-regulation of stellar birth on either local cloud scales or on global galactic scales except under implausible assumptions about the maximum size of dust grains in molecular clouds. Thisimmediately raises the question of why other studies arrived at the opposite conclusion that radiation pressure on dust is important for regulating the star formation process, and how the models presented here differ from previous calculations in the literature. As outlined in Sect. 1, the effects of radiation pressure have been studied for a wide range of different environments ranging from galaxies as a whole down to scales of planetarysystems. The models most similar to the calculations presented here are those of Murray et al. (2010), as well as Thompson (2008) and Thompson et al. (2015). These authors also studied the impact of star clusters of different masses in the centers of spherical clouds with varying properties. However, unlike us they arrived at the conclusion that radiation pressure on dust is the key to understand cloud disruption. The differences in our studies can be summarized as follows. While we investigate clouds with Plummer-like radial density profiles for the calculation of the ratio between radiative pressure forces and gravitational attraction at any radius, the cited authors assume that jets and winds from the cluster dominate the early evolution of the cloud and create an evacuated bubble with the swept up cloud material accumulated in a dense shell. They then study the impact of radiation illuminating the inner edge of this shell. However, because radiation pressure on dust is mostly a function of the total column density, it is unlikely that the difference in our results comes from deviations in the radial density profiles of the clouds. Sweeping material up into a shell moves the same column density of material to larger radii, reducing its temperature, and thus its opacity. This reduces rather than increases the effectiveness of radiation pressure. Therefore, dynamical effects seem unlikely to assist in driving an outflow. Furthermore, even in models such as shown in Fig. 12 where there is a small range of radii in the inner regions with ζ > 1, the resulting shell will quickly cease to be accelerated as it is moved outwards (see, e.g., Rahner et al. 2017) and its temperature corresponding drops. A similar argument holds for the cloud sizes and masses, as well as for the luminosity of the embedded clusters. As mentioned in Sect. 3.5, our suite of models includes cloud and cluster parameters quite similar to those considered by Murray et al. (2010). As far as we can tell, their assumed dust model resembles our fiducial case with an MRN size distribution (model D2 ). The divergence in results could potentially arise from different assumptions about the dust temperature. For example, the temperature in the shell in the model of Murray et al. (2010) is about 100 K throughout the entire evolution (see their Appendix A.3.2). This is larger than our fiducial choice of 20 K, but comparable to the values we find close to the star cluster in the models discussed in Sect. 3.4. Recall, though, that we find that the dust temperature quickly drops even below 20 K further out in the cloud. Nevertheless, we conclude that the dust temperature is not the primary cause of the difference between our models. Instead, we suspect that the main culprit is the different treatment of radiative transport. We employ the multi-frequency Monte Carlo RT code polaris (see Sect. 2.4) with a detailed treatment of the microphysics of dust scattering and absorption (Sect. 2.3). This allows us to correctly follow the frequency shift as radiation moves outwards through the cloud. That this shift reduces the effective radiation pressure was first noted by Habing et al. (1994) in the context of outflows from cool giant stars, a physically analogous situation. Murray et al. (2010) follow a simpler approach and assume blackbody radiation at each radius of their shell with a typical temperature of order of 100 K for their calculations of the optical depth (see their Appendix A.3.2). We tested the impact of an artificially enhanced dust temperature of 90 K and indeed find a stronger radiative force. However, gravity still dominates. We note in Sects. 3.2and 4.1 that the true spectrum shows noticeable deviations from a single temperature Planck function. It is typically more narrow around the peak and exhibits an extended tail toward longer wavelengths above ~ 1 mm. If one assumes that the local radiation field at each radius is described by a single-temperature blackbody, then one overestimates the optical depth and consequently the resulting radiative pressure force. A further effect that leans in the same direction, but is not accounted for in our models, is that the radiation field effectively acts as a rarefied fluid accelerating a dense fluid when it accelerates the gas. The result is that drives strong Rayleigh–Taylor instabilities that fragment the gas, opening paths for photons to quickly escape the cloud, for example as it was modeled by Krumholz & Thompson (2012). They found that this effect alone might preclude the disruption of clouds by radiation pressure. Although their quantitative result has been called into question based on calculations with an improved RT algorithm Davis et al. (2014) which suggested that cloud disruption might still be able to occur, the qualitative effect remains important, and will combine with the spectral shift we have modeled to further reduce the effectiveness of radiation pressure. We conclude that a realistic assessment of the balance between gravity and radiative forces requires multi-frequency radiative transfer calculations that take the spectral shift toward longer wavelength into account consistently. By doing so, we find boost factors of the momentum transfer from multiple scatterings of order unity rather than several tens to a hundred as has been suggested in the literature.
4.3 Limitations of the model
There are several ways that the 3D radiative transfer model with azimuthally symmetric density distribution presented here could be improved. First, we neglect the momentum input from stellar outflows and winds. In the models of Murray et al. (2010) or Rahner et al. (2017), these dominate over all other feedback mechanisms including radiation pressure, and sweep up the inner parts of cloud into a shell. However, stellar jets and collimated bipolar outflows are likely to pierce through the cloud and deposit their energy and momentum at distances far from the star, so their ability to stop accretion and remove gas from the cluster is subject to debate in the literature (e.g., Banerjee et al. 2007; Matzner & McKee 1999; Offner et al. 2011). Spherical winds from young stars are more efficient in evacuating a bubble and sweeping up cloud material into a dense shell surrounding the central cluster (see, e.g., Rahner et al. 2017). In any case, the total momentum transfer from radiation pressure on dust only depends on the column density through the cloud, and so it is independent of the radial density structure as long as dust and gas are well coupled and as long as the temperature profile remains the same. As noted above, sweeping material farther from the star can even reduce its temperature. Second, we focus on the effects of radiation pressure acting only on dust grains, which has been proposed to be the dominant feedback term (e.g., Murray et al. 2010; Thompson 2008). We do not include the momentum transfer from the interaction of photons with gas (see e.g., Kim et al. 2016), though we argue in Sect. 2.2.2 that this is indeed a good approximation, since it leads to errors of at most ~ 10% for our most massive cloud and cluster models. Therefore we neglect ionization and dissociation as well as other chemicalprocesses, except the destruction of dust grains close to the central star cluster (see Sect. 2.3). The coupling between photons and dust grains only depends on the total column density of dust grains of a given size and the temperature along the line of sight, independent of the details of the radial density profile. We note in this context that the momentum transfer from ionizing radiation would also depend on the local density ρ, because the ionization degree of the material is a function of the recombination rate, which goes as ρ2 (e.g., Tielens 2010; Draine 2011). Third, we neglect the effects of an external radiation field acting on the dust grains. Such a radiation field could alter our results in two ways. On the one hand, the temperature distributions shown in Fig. 10would decrease less steeply in the outer regions of the cloud since the external radiation field would also heat up the dust component. Depending on the mass of the molecular cloud model and the spectral distribution of the external radiation field, one might observe an outer shell with an increased dust temperature. In this case, the peak values of the output spectrum shown in Figs. 16 and 17 would be shifted toward shorter wavelength. Since higher dust temperatures are associated with increased trapping of radiation, this could also result in a small increase in radiative force at the very outer edges of the molecular clouds. On the other hand, the external radiation field would also result in an additional force pushing on the outer shells of the molecular clouds from the outside. This effect would counterbalance the outwards acting radiative force and possibly even reverse the direction of the radiative force. In the most extreme case, it could even lead to a radiation driven implosion (e.g., Klein et al. 1980; Bertoldi 1989). Finally, we also neglect cloud dynamics, including Rayleigh–Taylor instabilities driven by the radiation pressure itself, and any deviations from spherical symmetry, such as filaments or density fluctuations in the cloud material, or substructure in the stellar distribution. However, since the radiative force on dust is a function of column density and temperature only, and since we are interested in a global average, we are confident that our calculations of ζ, the ratio between gravitational attraction and radiation pressure, can answer the question of whether this form of feedback is able to disrupt star-forming clouds with high fidelity.
5 Summary and conclusion
We have employed detailed, multi-frequency, Monte Carlo, RT calculations to study the impact of radiation pressure acting on dust on the evolution of star-forming clouds for a wide range of physical parameters, covering conditions ranging from the solar neighborhood up to massive starburst systems. In order to investigate the competition between outward radiative forces and inward gravitational attraction, we calculated the 3D propagation of radiation emitted from point or extended central clusters embedded in azimuthally symmetric density distributions. Our RT method correctly calculates all the contributions of backscattering radiation to the total net radiative force. This approach includes a detailed treatment of scattering and absorption processes when photons interact with dust grains, so we can follow the radial evolution of the local spectrum as it is absorbed and re-emitted at longer wavelengths. We have further self-consistently computed the temperature profile through our clouds in order to determine its effect on the effective radiation pressure, as well as computing constant temperature models for comparison to previous work. Our model clouds are Plummer spheres with masses of 104 –107 M⊙ harboring central star clusters also having mass 104 –107 M⊙, corresponding to star formation efficiencies from 1% to 91%. We have studied the impact of different dust properties with maximum grain sizes up to 200 μm. We find that radiation pressure acting on dust is almost never able to disrupt star-forming clouds. The overall momentum deposition in the clouds is small. This is because ultraviolet and optical photons from young stars, to which the cloud is optically thick, do not scatter sufficiently often. Instead, they get absorbed and reemitted by the dust at thermal wavelengths. These photons promptly escape, as the cloud is typically optically thin to sub-mm and mm radiation. We conclude that radiation pressure acting on dust cannot disrupt star-forming molecular clouds in galaxies such as we see in the Local Group. This process is therefore unable to regulate the star-formation process on local as well as global scales, contrary to what has been proposed in the literature. We have calculated the resulting spectral energy distribution that an external observer would see when looking at the cloud to better link our models to observations. It is more narrowly peaked than a single-temperature Planck function and exhibits an extended tail of emission at mm wavelengths. More specifically we find
-
In cloudsa MRN grain size distribution extending to maximum grain radius of 2 μm, the strength of gravitational attraction exceeds the force from radiation pressure on dust by 1–2 orders of magnitude. Similar results are found for clouds with properties ranging from the Milky Way to moderate starbursts. The momentum transfer from the stellar radiation field coupling to dust cannot disrupt star-forming clouds in most galaxies.
-
We have varied the cloud size and the cluster size and find that the ratio of radiation pressure to gravity drops as cloud size increases or the cluster becomes more extended. Only for maximum grain sizes exceeding 2–20 μm, in combination with unrealistically high star formation efficiencies, well above 50%, and point-like clustersdo we find that radiative forces can dominate over gravity in clouds with masses exceeding 106 M⊙.
-
We find that the number of scattering events for cluster photons is typically of order unity, so that the absorption-reemission process dominates photon transfer. Only under circumstances where the cloud is optically thin to infrared radiation, and so scattering becomes important at thermal wavelengths, is the momentum transfer from the radiation field onto the cloud material important in the force equation. However, this is only the case for unrealistically large grain sizes in very massive clouds.
-
As the photon packages propagate outwards through the cloud, the original spectrum of the central cluster is quickly absorbed and replaced by thermal emission from dust. In our models with a fixed dust temperature of 20 K, the resulting spectrum peaks at λ ≈ 145 μm. When we allow the dust temperature to consistently adjust to the local radiation field, we find that the peak wavelength of the local spectrum shifts to larger wavelengths as the dust temperature drops toward larger radii. The resulting spectrum is somewhat narrower than a single-temperature blackbody and exhibits a power-law tail at wavelengths λ ≳ 1000 μm.
-
In all cases considered here, the dust in the outer layers of the cloud drops below 20 K, so the approximation of a fixed value of Td = 20 K provides a good estimate of the resulting radiation pressure force.
Although our RT calculations are fully 3D, our model is limited in the sense that it treats the cloud and its embedded cluster in spherical symmetry only. Realistic clouds have filamentary morphology and a high degree of substructure that allows radiation to more easily escape along channels of low density.
In that sense, our calculations constitute an upper limit on the importance of radiation pressure. On the other hand, our models neglect other potentially important feedback processes, such as stellar winds and supernovae. We also ignore ionizing radiation, which can destroy dust grains close to the cluster and form a hot bubble of ionized gas in the center. Taking these processes into account consistently would increase the outward forces acting on the cloud. In the current study, we focused only on one aspect of the overall problem, the importance of radiation pressure acting on dust. A full assessment of the effect of all stellar feedback processes in realistic three-dimensional cloud models remains to be done.
Acknowledgements
We thank Xander Tielens for motivating this paper at the 2015 IMPRS Heidelberg Summer School. Furthermore, we thank Paul Clark, Sam Geen, and Simon Glover for stimulating discussions. S.R., E.P., and R.S.K. acknowledge support from the Deutsche Forschungsgemeinschaft in the Collaborative Research Center (SFB 881) “The Milky Way System” (subprojects B1, B2, and B8) and in the Priority Program SPP 1573 “Physics of the Interstellar Medium” (grant numbers KL 1358/18.1, KL 1358/19.2). R.S.K. further thanks the European Research Council for funding in the ERC Advanced Grant “STARLIGHT” (project number 339177). M.-M.M.L. was partly supported by NSF grant AST11-09395 and by the Alexander-von-Humboldt Stiftung.
References
- Abbott, D. C. 1982, ApJ, 263, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, B. H., & Thompson, T. A. 2011, ApJ, 727, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Ballesteros-Paredes, J., Klessen, R. S., Mac Low, M.-M., & Vazquez-Semadeni, E. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 63 [Google Scholar]
- Banerjee, R., Klessen, R. S., & Fendt, C. 2007, ApJ, 668, 1028 [NASA ADS] [CrossRef] [Google Scholar]
- Bertoldi, F. 1989, ApJ, 346, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A. K., Walter, F., et al. 2011, ApJ, 730, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A. K., Jiménez-Donaire, M. J., et al. 2016, ApJ, 822, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C. 1978, MNRAS, 184, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L., Fukui, Y., Kawamura, A., et al. 2007, Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 81 [Google Scholar]
- Boulanger, F., Cox, P., & Jones, A. P. 2000, in Infrared Space Astronomy, today and tomorrow, eds. F. Casoli, J. Lequeux, & F. David, 70 (Les Houches Summer School), 251 [NASA ADS] [CrossRef] [Google Scholar]
- Coker, C. T., Thompson, T. A., & Martini, P. 2013, ApJ, 778, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Bonnell, I. A., & Whitworth, A. P. 2007, MNRAS, 375, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Ercolano, B., & Bonnell, I. A. 2012, MNRAS, 424, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, S. W., Jiang, Y.-F., Stone, J. M., & Murray, N. 2014, ApJ, 796, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1994, in The First Symposium on the Infrared Cirrus and Diffuse Interstellar Clouds, eds. R. M. Cutri, & W. B. Latter, ASP Conf. Ser., 58, 227 [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton, NJ: Princeton University Press) [Google Scholar]
- Draine, B. T., & Li, A. 2001, ApJ, 551, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Geen, S., Hennebelle, P., Tremblin, P., & Rosdahl, J. 2015a, MNRAS, 454, 4484 [NASA ADS] [CrossRef] [Google Scholar]
- Geen, S., Rosdahl, J., Blaizot, J., Devriendt, J., & Slyz, A. 2015b, MNRAS, 448, 3248 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Tacconi, L. J., Gracia-Carpio, J., et al. 2010, MNRAS, 407, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Girichidis, P., Walch, S., Naab, T., et al. 2016, MNRAS, 456, 3432 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, W.-M. 2012, ApJ, 753, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Habing, H. J., Tignon, J., & Tielens, A. G. G. M. 1994, A&A, 286, 523 [NASA ADS] [Google Scholar]
- Hennebelle, P., & Iffrig, O. 2014, A&A, 570, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henyey, L. G., & Greenstein, J. L. 1941, ApJ, 93, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, A. S., Joung, M. R., Mac Low, M.-M., et al. 2012, ApJ, 750, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, S. S. 1985, A&A, 146, 67 [NASA ADS] [Google Scholar]
- Hopkins, P. F., Quataert, E., & Murray, N. 2011, MNRAS, 417, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Kereš, D., Oñorbe, J., et al. 2014, MNRAS, 445, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Ishibashi, W., & Fabian, A. C. 2015, MNRAS, 451, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Jeans, J. H. 1902, Phil. Trans. R. Soc. London, Ser. A, 199, 1 [Google Scholar]
- Kennicutt, R. C., Jr. 1989, ApJ, 344, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J.-G., Kim, W.-T., & Ostriker, E. C. 2016, ApJ, 819, 137 [NASA ADS] [Google Scholar]
- Klein, R. I., Sandford, M. T., II, & Whitaker, R. W. 1980, Space Sci. Rev., 27, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Glover, S. C. O. 2016, in Star Formation in Galaxy Evolution: Connecting Numerical Models to Reality, Saas-Fee Advanced Course, 43, 85 [Google Scholar]
- Krumholz, M. R. 2012, ApJ, 759, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Thompson, T. A. 2012, ApJ, 760, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Klein, R. I., McKee, C. F., Offner, S. S. R., & Cunningham, A. J. 2009a, Science, 323, 754 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Tumlinson, J. 2009b, ApJ, 699, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Cunningham, A. J., Klein, R. I., & McKee, C. F. 2010, ApJ, 713, 1120 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, R., & Yorke, H. W. 2013, ApJ, 763, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, R., Klahr, H., Beuther, H., & Henning, T. 2010, ApJ, 722, 1556 [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Liu, H. B., Li, D., et al. 2016, ApJ, 828, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1998, A&A, 344, 282L [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-González, S., Silich, S., & Tenorio-Tagle, G. 2014, ApJ, 785, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Matzner, C. D., & McKee, C. F. 1999, ApJ, 526, L109 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F.,& Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Mie, G. 1908, Ann. Phys., 330, 377 [Google Scholar]
- Moody, C. E., Guo, Y., Mandelker, N., et al. 2014, MNRAS, 444, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Motte, F., Louvet, F., & Nguyen Luong, Q. 2015, IAU General Assembly, 22, 2258360 [NASA ADS] [Google Scholar]
- Mueller, K. E., Shirley, Y. L., Evans, N. J., II, & Jacobson, H. R. 2002, ApJS, 143, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., Quataert, E., & Thompson, T. A. 2010, ApJ, 709, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., Ménard, B., & Thompson, T. A. 2011, ApJ, 735, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Ochsendorf, B. B., Verdolini, S., Cox, N. L. J., et al. 2014, A&A, 566, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offner, S. S. R., Lee, E. J., Goodman, A. A., & Arce, H. 2011, ApJ, 743, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, E. W., Baldwin, J. A., Brogan, C. L., et al. 2007, ApJ, 658, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, E. W., Baldwin, J. A., Ferland, G. J., Shaw, G., & Heathcote, S. 2009, ApJ, 693, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Pirogov, L. E. 2009, Astron. Rep., 53, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Rahner, D., Pellegrini, E. W., Glover, S. C. O., & Klessen, R. S. 2017, MNRAS, 470, 4453 [NASA ADS] [CrossRef] [Google Scholar]
- Reissl, S., Wolf, S., & Brauer, R., 2008, A&A, 593, A87 [Google Scholar]
- Rosdahl, J., & Teyssier, R. 2015, MNRAS, 449, 4380 [NASA ADS] [CrossRef] [Google Scholar]
- Sales, L. V., Marinacci, F., Springel, V., & Petkova, M. 2014, MNRAS, 439, 2990 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Seo, Y. M., & Youdin, A. N. 2016, MNRAS, 461, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Kelly, B. C., & Bigiel, F. 2013, MNRAS, 430, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Kelly, B. C., Rahman, N., et al. 2014, MNRAS, 437, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Silich, S., & Tenorio-Tagle, G. 2013, ApJ, 765, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., & Sage, L. J. 1988, ApJ, 334, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, K. E. I., & Nakamoto, T. 2010, ApJ, 714, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Tenorio-Tagle, G., & Bodenheimer, P. 1988, ARA&A, 26, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 1983, ApJ, 271, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2010, The Physics and Chemistry of the Interstellar Medium (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Thompson, T. A. 2008, ApJ, 684, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, T. A., Quataert, E., & Murray, N. 2005, ApJ, 630, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, T. A., Fabian, A. C., Quataert, E., & Murray, N. 2015, MNRAS, 449, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Tsang, B. T.-H., & Milosavljević, M. 2015, MNRAS, 453, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Usero, A., Leroy, A. K., Walter, F., et al. 2015, AJ, 150, 115 [NASA ADS] [CrossRef] [Google Scholar]
- van de Hulst, H. C. 1981, Light Scattering by Small Particles (New York: Dover Publications) [Google Scholar]
- Verdolini, S., Yeh, S. C. C., Krumholz, M. R., Matzner, C. D., & Tielens, A. G. G. M. 2013, ApJ, 769, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Walch, S. K., Whitworth, A. P., Bisbas, T., Wünsch, R., & Hubber, D. 2012, MNRAS, 427, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Walch, S., Girichidis, P., Naab, T., et al. 2015, MNRAS, 454, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2000, BAAS, 32, 1466 [Google Scholar]
- Wise, J. H., Abel, T., Turk, M. J., Norman, M. L., & Smith, B. D. 2012, MNRAS, 427, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S. 2003, Comput. Phys. Commun., 150, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., & Voshchinnikov, N. V. 2004, Comput. Phys. Commun., 162, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Yorke, H. W., & Sonnhalter, C. 2002, ApJ, 569, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, D., & Thompson, T. A. 2012, MNRAS, 424, 1170 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukovska, S., Gail, H.-P., & Trieloff, M. 2008, A&A, 479, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhukovska, S., Dobbs, C., Jenkins, E. B., & Klessen, R. S. 2016, ApJ, 831, 147 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top panel: gravitational force, Fgra, for an M7 molecular cloud model with an outer radius of Rout = 5 pc, the two point-like cluster models C3 and C7 , and their combinations. Bottom panel: same combinations as the top panel for an M6 molecular cloud with an outer radius of Rout = 20 pc and a C6 cluster model with a 3D, Gaussian, spatial extension having FWHM of 1 or 4 pc . |
| In the text | |
 |
Fig. 2 Left panels: size averaged cross section of extinction Cext, scattering Csca, absorption Cabs, and pressure Cpr over wavelength. Right panels: probability distribution of re-emitted wavelength for different dust temperatures. Different rows are for distinct maximum grain radii corresponding to the dust grain models D1 (top row), D3 (middle row), and D5 (bottom row). |
| In the text | |
 |
Fig. 3 Radial optical depth τλ and density ρ distribution for the M4 molecular cloud. The optical depth is calculated for different wavelengths λ applying the dust models D2 (left panel) and D5 (right panel). |
| In the text | |
 |
Fig. 4 Comparison of modified blackbody spectra for the three different dust models displayed in Fig. 2 for a dust temperature of Td = 20 K and upper values of amax of 0.02 μm (D1 ), 2 μm (D3 ), and 200 μm (D5 ), respectively.These spectra are more narrowly peaked and skewed toward smaller wavelengths than the corresponding Planck function Bλ(Td), because the emission is weighted by the absorption cross section, Cabs,λ, which drops significantly at sub-mm and mm wavelengths. |
| In the text | |
 |
Fig. 5 Gravity (Fgra, red lines) in comparison to radiative forces (Frad, blue lines) for models M4 (top left), M5 (top right left), M6 (bottom left), and M7 (bottom right). The ratio of forces is defined as ζ = Frad∕Fgra (purple lines). All cases have a constant dust temperature of Td = 20 K, an outer radius of Rout = 5 pc and use dust model D2. We note that ζ < 1 everywhere, implying that radiation pressure does not support the cloud against gravitational contraction. The vertical brown line marks the sublimation radius. |
| In the text | |
 |
Fig. 6 Radial and wavelength distribution of the scattering (left) and absorption (right) probability distribution for models M4 C4 D2 (top) and M7C7D2 (bottom). The x-axis gives the radius of interaction while the y-axis is the local wavelength of the photon package at the point of interaction. |
| In the text | |
 |
Fig. 7 Number of scattering events (left column) and absorption and re-emission events (right column) experienced by a photon package before escaping the molecular cloud. The same models are shown as in Fig. 6, M4 C4 D2 (top) and M7C7D2 (bottom). The x-axis gives the local wavelength of the photon package at the point of interaction, and the y-axis gives the number of interactions of each type. |
| In the text | |
 |
Fig. 8 Radial profile of radiative force (blue lines) for different molecular cloud models M4 (left panel) and M7 (right panel)with an outer radius of Rout = 5 pc and a constant dust temperature of Td = 20 K simulated with cluster models C3 through C7 in half steps.The blue band represents the same simulations with the absorption and reprocessing of radiation switched off (Cabs = 0 cm2), while the green bands result from the same simulations with an instantaneous redistribution of radiation (Csca = 0 cm2). |
| In the text | |
 |
Fig. 9 Comparison of radiative and gravitational forces for varying dust size distribution upper cutoffs using dust grain models D1, D2 , D3 , D4 , and D5 with models M4C4 (left panel) and M7C7 (right panel). Notation as in Fig. 5. |
| In the text | |
 |
Fig. 10 Grain-size averaged dust temperature distribution for different cluster and molecular cloud models with an outer radius of Rout = 5 pc. The verticaldark brown line marks the sublimation radius. |
| In the text | |
 |
Fig. 11 Comparison of radiative and gravitational forces for model M6, except with an outer radius of Rout = 150 pc instead of the 5 pc used in Fig. 5. Again, we considered point-like cluster models C4 to C7 with masses of 104 to 107 M⊙. |
| In the text | |
 |
Fig. 12 Comparison of radiative and gravitational forces in models with self-consistent (blue lines) and constant (green lines) dust temperature. Cloud models are M4 (left) and M7 (right), and radiative forces were calculated for cluster models C3, C5 , and C7 and the D2 dust model. The radial dust temperature distributions follow the temperatures shown in Fig. 10. The ratio ζ is shown below (purple) for the variable dust temperature models. |
| In the text | |
 |
Fig. 13 Top: gravity in comparison to radiative force for varying stellar cluster size in the M6 C6 model with a constant temperature of T = 20 K and an outer radius of Rout = 5 pc. Vertical dotted lines give the FWHM of the Gaussian spatial distribution of the cluster, with values 0.1, 1, 2, and 4 pc . Middle: grain-size averaged dust temperature distribution for the M6C6 model dependent on the different FWHM. Bottom: same as the top panel with the radial dependent dust temperature shown in the middle. |
| In the text | |
 |
Fig. 14 Parameter space of the ratio of radiative force to gravity ζ dependent on cluster model C, molecular cloud model M, and the different dust models D1, D2 , D3 , D4 , and D5 . The ratios are calculated for a distance of r = 0.1 pc from the cluster center. The bottom right panel is for the radially dependent temperature distribution shown in the left panel of Fig. 10 while the other panels are for a constant dust temperature of Td = 20 K. We note that this image is smoothed when reading it with MacOS preview. |
| In the text | |
 |
Fig. 15 Probability for each permutation of shift between initial wavelength and final wavelength for the M4 C4 model. The abscissa shows the wavelength of the photon packages initially emitted by the cluster while the ordinate shows the final observable wavelength leaving the molecular cloud. |
| In the text | |
 |
Fig. 16 Left: escape fraction of photons as a function of cloud radius for various models. All the models are modeled with constant dust temperature Td = 20 K. Right: corresponding spectra visible to an outside observer compared to the normalized stellar input spectrum. All output spectra are very similar and are reasonably well described as a blackbody with a temperature of 20 K. |
| In the text | |
 |
Fig. 17 Same as Fig. 16 for selected models with a radially dependent dust temperature Td (r) as shown in the middle panel of Fig. 13. We note the shifted peak wavelengths in the different models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.