| Issue |
A&A
Volume 611, March 2018
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 5 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201629904 | |
| Published online | 27 March 2018 | |
Early gray dust formation in the type IIn SN 2005ip
1
Leiden Observatory, Leiden University,
Niels Bohrweg 2,
2333 CA
Leiden, The Netherlands
e-mail: nielsen@strw.leidenuniv.nl
2
Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen,
Juliane Maries Vej 30,
2100
Copenhagen, Ø, Denmark
Received:
14
October
2016
Accepted:
21
December
2017
The physical characteristics of dust formed in supernovae is poorly known. In this paper, we investigate the extinction properties of dust formed in the type IIn SN 2005ip. The observed light curves of SN 2005ip all exhibit a sudden drop around 50 days after discovery. This has been attributed to dust formation in the dense circumstellar medium. We modeled the intrinsic light curves in six optical bands, adopting a theoretical model for the luminosity evolution of supernovae interacting with their circumstellar material. From the difference between the observed and intrinsic light curves, we calculated extinction curves as a function of time. The total-to-selective extinction ratio, RV, was determined from the extinction in the B and V bands. The resulting extinction, AV , increases monotonically up to about 1 mag, 150 days after discovery. The inferred RV value also increases slightly with time, but appears constant in the range 4.5–8, beyond 100 days after discovery. The analysis confirms that dust is likely formed in SN 2005ip, starting about two months after explosion. The high value of RV, that is, gray dust, suggests dust properties different from the Milky Way. While this result hinges on the assumed theoretical intrinsic light curve evolution, it is encouraging that the fitted light curves are as expected for standard ejecta and circumstellar medium density structures.
Key words: dust, extinction / supernovae: individual: SN 2005ip
© ESO 2018
1 Introduction
How do the properties of dust formed in supernovae (SNe) compare to those observed in the interstellar medium (ISM) of galaxies? The total-to-selective extinction ratio, RV , is an empirical indicator of the dependency of the extinction upon wavelength along the line of sight to a reddened object; higher values of RVresult in a more gray (flat) extinction curve. The ratio RVis known to depend on the sizes, shapes, and composition of the dust grains. The average value of RVis around 3 in Local Group galaxies; the Milky Way (MW), and the Large and Small Magellanic Clouds have average RVvalues of 3.1, 3.41, and 2.7, respectively (Gordon et al. 2003). In dense Galactic molecular clouds, higher values of RV~ 4–6 (Cardelli et al. 1989; Tielens 2005) are observed. Recently, RV= 4.5 ± 0.2was measured in 30 Doradus, indicating a gray component in the extinction law, attributed to a larger percentage of large grains (De Marchi et al. 2016).
Core-collapse SNe originate from massive stars with masses more than 8–10 M⊙ (Heger et al. 2003; Colgate & White 1966; Ibeling & Heger 2013), and are divided into various classes, based on their spectral and photometric properties (e.g., Filippenko 1997). Type IIn SNe are characterized by emission lines composed of a narrow velocity component on top of an intermediate or broad velocity width component. The narrow emission originates from the slow moving circumstellar medium (CSM; Schlegel 1990), which is material shed by the progenitor via mass loss in the later stages of the life of a star (e.g., Fox et al. 2010; Gall et al. 2011; Smith 2016). The peak brightnesses of type IIn SNe span a wide range (4–5 mag; Stritzinger et al. 2012). The observed light curves are determined by the morphology of the CSM and by the progenitor star (van Marle et al. 2010). For example, the shape of the light curves of type IIn SNe depend on the initial radius of the star, the ejecta mass and the explosion energy of the SNe, and the density structures of the ejecta and CSM (van Marle et al. 2010; Moriya et al. 2013; Taddia et al. 2015). The range of potential progenitors is large and may include any star with a significant pre-SN eruption, for example, red supergiants or luminous blue variables (LBVs) (Gall et al. 2011; Stritzinger et al. 2012; Van Dyk 2013).
Lucy et al. (1991) noted a shallow optical extinction curve inferred from the light curves of SN 1987A. More recently, Gall et al. (2014) examined the formation of dust in the luminous type IIn SN 2010jl (Newton & Puckett 2010) and found RV≈ 6.4. While this was inferred from significant attenuation of the red wings and corresponding blueshifts of the centroids of the hydrogen emission lines, no broadband color changes were detected in the light curves.
SN 2005ip was discovered on 2005 November 5.2 UT in the Scd galaxy NGC 2906 (Boles et al. 2005; Stritzinger et al. 2012). The measured redshift of the host galaxy is 0.00714, corresponding to a luminosity distance of about 30 Mpc (de Vaucouleurs et al. 1991; Smith et al. 2009). SN 2005ip exhibits clear evidence of narrow line emission arising from the CSM and is thus classified as a type IIn SN (Smith et al. 2009). The exact date of the SN explosion is unknown, but is suggested to be 8–10 days prior to discovery (Smith et al. 2009). The progenitor is believed to be a star with dense CSM. There are two suggestions for a progenitor star of SN 2005ip. One is an extreme red supergiant, as suggested by Smith et al. (2009), because the inferred clumpy medium in the CSM is similar to small scale clumps found in the red hypergiant star VY Canis Majoris. The other suggestion is an LBV star owing to a high mass-loss rate, which is similar to what has been observed in other LBVs (Fox et al. 2010; Katsuda et al. 2014).
There is evidence pointing to dust forming in a cool dense shell (CDS) behind the forward shock passing through the dense CSM as early as 50–100 days past explosion in some SNe, such as SN 1998S, SN 2006jd, or SN 2010jl (Pozzo et al. 2004; Stritzinger et al. 2012; Gall et al. 2014). Indeed, SN 2005ip shows signs of such early dust formation, as inferred from the attenuation of the red wing of the Hα line and the observed drop in the light curves of the optical bands (Stritzinger et al. 2012).
Here wedetermine the extinction properties, notably RV, for the dust formed early in SN 2005ip. We examine its well-sampled light curves (Stritzinger et al. 2012) and model the intrinsic light curves in Sect. 2. From the theoretical and observed light curves we can determine the extinction curve that allows the determination of RV. In Sect. 3 we discuss the possible origins of a shallow extinction curve.
2 Light curves and extinction measurement
2.1 Data
The data we use here consist of optical broadband photometry of SN 2005ip from the Carnegie Supernova Project (Stritzinger et al. 2012; Hamuy et al. 2006). Photometry in the near-infrared bands is not useful for our purposes because it is affected by hot dust emission. As is evident from Fig. 1, a clear drop in the light curves is observed in all six bands at around 50 days past discovery, which is ascribed to dust formation in the SN, for e, by Stritzinger et al. (2012). Throughout this paper the time after the day of discovery is written as t = +x days.
 |
Fig. 1 Optical light curves for the type IIn SN 2005ip. The connected colored filled circles represent the observational data (Stritzinger et al. 2012). The light curves exhibit a marked decrease after about +50 days, which is an indication of early dust formation. The gray curves represent fits of a theoretical model (Eq. (1)) to the light curves between +23 and +47 days. The fitting range is highlighted. The model intrinsic light curves are all clearly brighter than the observed light curves from +50 days and onward. |
2.2 Intrinsic light curves
We fit a theoretical model for the intrinsic light curve to the observed light curves of SN 2005ip between +23 and +47 days, i.e., before dust formation sets in; see Fig. 1. It is then assumed that the model intrinsic light curves are valid beyond +47 days.
The intrinsic light curves are parametrized according to the theoretical model for the light curves of CSM interaction-powered SNe of Moriya et al. (2013). Specifically, for an ejecta density ρejecta ∝ r−n (e.g., Matzner & McKee 1999) and a CSM density ρCSM ∝ r−s, Moriya et al. (2013) found that the bolometric luminosity decays as a power law as a function of time since explosion t′ ,
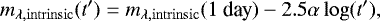 (1)
(1)
where we adopt t′ = t − 9 days (Smith et al. 2009), and
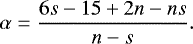 (2)
(2)
For example, for a red supergiant progenitor with n ≈ 12 and a steady wind CSM density structure (s = 2), α = −0.3.
Following Moriya et al. (2013), we leave α as a free parameter, and fit Eq. (1) to the six individual light curves. We choose the temporal fitting range to be +23 to +47 days to be in the range of validity of the model (i.e., well past peak), and to avoid being affected by the effects of dust attenuation. Moriya et al. (2013) considered their model valid up to at least +200 days while Smith et al. (2009) noted a remarkable flattening of the light curvebeyond +160 days. To be conservative, we here assume that the extrapolated model fits are valid up to +150 days. One thousand synthetic datasets were created in a 3σ Gaussian distribution around the original dataset, using a bootstrap Monte Carlo method (Press et al. 2001). The best fits shown in Fig. 1 are seen to overshoot the observed light curves beyond +50 days. We verified that our results do not depend sensitively on the adopted time of explosion or the fitting range.
The fits to the individual light curves yield values of α ranging from −0.77 to −0.41. As shown in Fig. 2 the best-fit values of α are wavelength dependent, where − α increases with wavelength. This suggests some color evolution of the SN light, where the SN becomes slightly bluer with time, before the conspicuous onset of dust formation at around +50 days, consistent with what was found by, for example, Taddia et al. (2013). Within the uncertainties, however, the majority of the light curves are consistent with a value of around α = −0.5 ± 0.1. For example, α = −0.49 would correspond to, for example, (n, s) = (12, 2.3), which is broadly consistent with a red supergiant progenitor.
 |
Fig. 2 Lower panel: inferred values of α as a function of inverse wavelength. The value of α appears to depend slightly on wavelength. An indicative value of α = −0.49 is shown as a red horizontal line. Upper panel: inferred extinction curves at different times. The optical bands used in the study are indicated. The g band is affected by Hβ emission and the r band is affected by Hα emission. The extinction is seen to increase with time and the extinction curves are fairly flat, suggesting gray extinction. |
2.3 Extinction curves
The extinction as a function of time for each photometric band is defined as the difference between the observed light curve and the model intrinsic light curve, as
 (3)
(3)
To minimize the effects of the apparent bumps in the light curves we smoothed the extinction versus time curves by fitting fifth order polynomials.
The resulting extinction curves are shown in Fig. 2 at different epochs. The extinction increases with time, maintaining a fairly constant shape of the extinction curve as a function of inverse wavelength. There are conspicuous dips in the extinction curves in photometric bands containing the strong emission lines Hα (r band) or Hβ (g band).
The total-to-selective extinction is given by the extinction in a specific band and the color excess between two photometric bands (Tielens 2005),
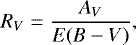 (4)
(4)
where E(B − V ) is the color excess between the B and V bands, AVis the extinction inthe V band, and RVis the total-to-selective extinction ratio with respect to the V band. In order not to bias our results, we decided not to fit parametric extinction curves to the data (upper panel of Fig. 2), but rather calculated RVdirectly from Eq. (4), that is, using the smoothed extinction curves as a function of time in the B and V bands.
Figure 3 shows AVand RVas a function of time. The shaded areas represent the 1σ error range in the values of AVand RV , as obtained from the Monte Carlo resampling of the data. The curves represent the peak values of the distribution. The AVvalue increases monotonically with time up to a level of about 1 mag at +150 days.
The mean value of RVappears to increase with time, although within errors it is consistent with being in the range 4.5–6.5 after +80 days and in the range 4.5–8 beyond +100 days; RV≈ 4.5 represents the maximum lower limit at +120 days while RV≈ 8 represents the minimum upper limit at +150 days. This range is consistent with the value of RV≈ 6.4 found by Gall et al. (2014) for SN 2010jl.
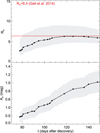 |
Fig. 3 Lowerpanel: AV(connected filled circles) increases monotonically, as expected in the case of dust formation. The shaded area represents the 1σ error region. Upper panel: RVas a function of time. The value of RV= 6.4 found for SN 2010jl (Gall et al. 2014) is indicated as a red horizontal line. |
3 Discussion
The shallow extinction curves obtained here for SN 2005ip are intriguing. The derived RVvalues are higher than the average values for the ISM of the MW, SMC, or LMC, but are consistent with MW RVvalues of some individual sight lines (Cardelli et al. 1989). Furthermore, the derived RVvalues for SN 2005ip are similar to that of SN 2010jl (Gall et al. 2014), which is also a type IIn SN with a dense CSM. Typically, a wavelength dependent extinction curve reflects the dust grain composition and grain size distribution – properties, which can be obtained by fitting detailed dust models to the extinction curve. However, for SN 2005ip, we do not have sufficient information to perform such fits. In what follows, we briefly discuss the possible origin of such a shallow SN extinction curve, that is, a high RV.
In SN 2005ip, the early dust formation is believed to occur in the dense CSM (Smith et al. 2009). The primary formation site is the CDS, which is formed behind the forward shock propagating through the CSM. The CDS environment1 has very different physical and chemical properties than the SN ejecta for which most dust formation models are developed (e.g., Gall et al. 2011; Sarangi & Cherchneff 2015; Mauney et al. 2015; Lazzati & Heger 2016). Such a formation site has been suggested to facilitate the early dust formation in, for example, SN 2006jc (Smith et al. 2008), SN 2010jl (Gall et al. 2014), or SN 2011ja (Andrews et al. 2016). Very high densities can be reached in such a CDS leading to efficient cooling of the material to temperatures ≲2000 K, which are suitable for dust to nucleate and possibly grow to larger sizes through accretion.
Large dust grains: Large μm-sized grains can lead to shallow extinction curves (Maiolino et al. 2001; Nozawa & Fukugita 2013). Large dust grains have been claimed in the remnant of SN 1987A (Wesson et al. 2015; Bevan & Barlow 2016), although these formed later than about three years after the explosion. Larger dust grains, depending on the exposure of the dust grains to sputtering and hard radiation (Slavin et al. 2004), are more likely to survive throughout the SN remnant phase and thus enrich the ISM (Gall et al. 2014; Wesson et al. 2015; Owen & Barlow 2015).
Small, nonstandard dust grains: The wavelength dependence of extinction curves is also determined by the wavelength dependent emissivity of the relevant dust species. Typically, the emissivity of carbonaceous and some silicate dust is highly wavelength dependent for small grains in the optical wavelength regime (Rouleau & Martin 1991; Bladh & Höfner 2012), yielding nearly constant RV≈ 2.4 for graphite, RV≈ 3.8 for carbonaceous dust, and RV≈ 4.5 for silicate dust with grains ≲0.01 μm. For grains of sizes between 0.01 and 0.1 μm, depending on the species, RVcan become as low as ~1.0.
However, SiO2 exhibits very little to no wavelength dependence in the optical wavelength regime for small grains (e.g., Bladh & Höfner 2012, and references therein). This may be an attractive alternative to large carbonaceous grains because small grains are easier to nucleate and grow, provided they are shielded from UV radiation in an optically thick region (Kochanek 2014). However, the absorption efficiency of SiO2 is about 4 orders of magnitude less than that of carbonaceous dust (Bladh & Höfner 2012).
Clumpy medium: An alternative mechanism for producing a shallow extinction curve may involve the semiopaque high-density clumps found in the CSM of SN 2005ip (Smith et al. 2009). If the clumps in the medium were completely opaque, the result would be a wavelength independent extinction curve, which we do not observe. However, if the clumps were not completely opaque they could lead to the shallow extinction curves we see. A similar effect was explored in the case of the clumpy ejecta of SN 1987A (Ercolano et al. 2007).
4 Conclusions
SN 2005ip showed evidence of early dust formation in the densely sampled multicolor optical light curves (Stritzinger et al. 2012). In this paper we have used these data to obtain the total-to-selective extinction ratio, RV , of dust formed in SN 2005ip. In doing so, we used a theoretical model for the light curves of SNe interacting with their circumstellar material (Moriya et al. 2013) to model the intrinsic light curves and fit the early light curves (i.e., prior to the cutoff around +50 days). We obtained the extinction as a function of time in each band as the difference between the observed light curve and the extrapolated model intrinsic light curve up to +150 days. From this we derived the total-to-selective extinction RV .
We find that the obtained extinction curves are shallow; the curves are described by values of 4.5 < RV< 8 from +100 days and onward, which is higher than typically found in the ISM of galaxies such as the MW (RV~ 3.1). The high values of RVare consistent with that derived for SN 2010jl (RV≈ 6.4), where dust model fits to the extinction curves suggested large grain formation (Gall et al. 2014).
The advantage of the large grain scenario is the increased survivability of the grains throughout the SN remnant phase. Unfortunately, it is challenging to form μm-sized carbonaceous grains on such short timescales. It may be easier to form smaller nm-sized grains in high-density regions, although it is unclear if the required species, whose emissivities exhibit littlewavelength dependence in the optical regime, are sufficiently abundant in the CSM. Clumpy material in the CSM may contribute to flattening the extinction curves.
We also demonstrated that taking the extinction of the dust formed into account is essential to derive the intrinsic value of α of the Moriya et al. (2013) model. The value we derive for α appears to be wavelength dependent, but is consistent with α ≈−0.49, as would beexpected for a standard ejecta density ρejecta ∝ r−12 profile (Matzner & McKee 1999) and a steady wind density structure, ρCSM ∝ r−2.3. This is in marked contrast to the values around α ≈−1 found by Moriya et al. (2013), who included the parts of the light curves that are affected by significant dust attenuation.
The method devised here to determine SN dust properties from multicolor light curves may be used to obtain new insight into SN dust formation processes from future high-quality SN light curves,for example, from the Large Synoptic Survey Telescope.
Acknowledgements
A. S. B. N. acknowledges funding from a NWO Vidi fellowship. J. H. was supported by a VILLUM FONDEN Investigator grant (project number 16599). C. G. acknowledges funding from the Carlsberg Foundation. The authors would like to thank A. G. G. M. Tielens and the anonymous referee for helpful comments.
References
- Andrews, J. E., Krafton, K. M., Clayton, G. C., et al. 2016, MNRAS, 457, 3241 [NASA ADS] [CrossRef] [Google Scholar]
- Bevan, A., & Barlow, M. J. 2016, MNRAS, 456, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Bladh, S., & Höfner, S. 2012, A&A, 546, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boles, T., Nakano, S., & Itagaki, K. 2005, Central Bureau Electronic Telegrams, 275, 1 [NASA ADS] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Colgate, S. A., & White, R. H. 1966, ApJ, 143, 626 [NASA ADS] [CrossRef] [Google Scholar]
- De Marchi, G., Panagia, N., Sabbi, E., et al. 2016, MNRAS, 455, 4373 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr. H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies. Vol. I: Explanations and references. Vol. II: Data for galaxies between 0h and 12h . Vol. III: Data for galaxies between 12h and 24h (New York City, USA: Springer) [Google Scholar]
- Ercolano, B., Barlow, M. J., & Sugerman, B. E. K. 2007, MNRAS, 375, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V. 1997, ARA&A, 35, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, O. D., Chevalier, R. A., Dwek, E., et al. 2010, ApJ, 725, 1768 [NASA ADS] [CrossRef] [Google Scholar]
- Gall, C., Hjorth, J., & Andersen, A. C. 2011, A&ARv, 19, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Gall, C., Hjorth, J., Watson, D., et al. 2014, Nature, 511, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamuy, M., Folatelli, G., Morrell, N. I., et al. 2006, PASP, 118, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Ibeling, D., & Heger, A. 2013, ApJ, 765, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Katsuda, S., Maeda, K., Nozawa, T., Pooley, D., & Immler, S. 2014, ApJ, 780, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S. 2014, ArXiv e-prints [arXiv:1407.7856] [Google Scholar]
- Lazzati, D., & Heger, A. 2016, ApJ, 817, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B., Danziger, I. J., Gouiffes, C., & Bouchet, P. 1991, in Supernovae, ed. S. E. Woosley, 82 [CrossRef] [Google Scholar]
- Maiolino, R., Marconi, A., & Oliva, E. 2001, A&A, 365, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matzner, C. D., & McKee, C. F. 1999, ApJ, 510, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Mauney, C., Buongiorno Nardelli, M., & Lazzati, D. 2015, ApJ, 800, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Meikle, W. P. S., Kotak, R., Farrah, D., et al. 2011, ApJ, 732, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Moriya, T. J., Maeda, K., Taddia, F., et al. 2013, MNRAS, 435, 1520 [NASA ADS] [CrossRef] [Google Scholar]
- Newton, J., & Puckett, T. 2010, Central Bureau Electronic Telegrams, 2532 [Google Scholar]
- Nozawa, T., & Fukugita, M. 2013, ApJ, 770, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, P. J., & Barlow, M. J. 2015, ApJ, 801, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzo, M., Meikle, W. P. S., Fassia, A., et al. 2004, MNRAS, 352, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flanney, B. T. 2001, Numerical Recipes in Fortran 77, The art of scientific computing (Cambridge University Press) [Google Scholar]
- Rouleau, F., & Martin, P. G. 1991, ApJ, 377, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Sarangi, A., & Cherchneff, I. 2015, A&A, 575, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, E. M. 1990, MNRAS, 244, 269 [NASA ADS] [Google Scholar]
- Slavin, J. D., Jones, A. P., & Tielens, A. G. G. M. 2004, ApJ, 614, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N. 2016, ArXiv e-prints [arXiv:1612.02006] [Google Scholar]
- Smith, N., Foley, R. J., & Filippenko, A. V. 2008, ApJ, 680, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Silverman, J. M., Chornock, R., et al. 2009, ApJ, 695, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Taddia, F., Fransson, C., et al. 2012, ApJ, 756, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Taddia, F., Stritzinger, M. D., Sollerman, J., et al. 2013, A&A, 555, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taddia, F., Sollerman, J., Fremling, C., et al. 2015, A&A, 580, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M. 2005, The physics and chemistry of the interstellar medium (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Van Dyk, S. D. 2013, AJ, 145, 118 [NASA ADS] [CrossRef] [Google Scholar]
- van Marle, A. J., Smith, N., Owocki, S. P., & van Veelen, B. 2010, MNRAS, 407, 2305 [NASA ADS] [CrossRef] [Google Scholar]
- Wesson, R., Barlow, M. J., Matsuura, M., & Ercolano, B. 2015, MNRAS, 446, 2089 [NASA ADS] [CrossRef] [Google Scholar]
We note that the CDS in other types of SNe, such as SNe IIP may be less massive than for SNe IIn and hence less favorable for dust to efficiently form and grow. For example, Meikle et al. (2011) find that in the IIP SN 2004dj only ~10−6 M⊙ of dust formed, with grain sizes of ~0.2 μm in a CDS with a mass of ~10−4 M⊙.
All Figures
 |
Fig. 1 Optical light curves for the type IIn SN 2005ip. The connected colored filled circles represent the observational data (Stritzinger et al. 2012). The light curves exhibit a marked decrease after about +50 days, which is an indication of early dust formation. The gray curves represent fits of a theoretical model (Eq. (1)) to the light curves between +23 and +47 days. The fitting range is highlighted. The model intrinsic light curves are all clearly brighter than the observed light curves from +50 days and onward. |
| In the text | |
 |
Fig. 2 Lower panel: inferred values of α as a function of inverse wavelength. The value of α appears to depend slightly on wavelength. An indicative value of α = −0.49 is shown as a red horizontal line. Upper panel: inferred extinction curves at different times. The optical bands used in the study are indicated. The g band is affected by Hβ emission and the r band is affected by Hα emission. The extinction is seen to increase with time and the extinction curves are fairly flat, suggesting gray extinction. |
| In the text | |
 |
Fig. 3 Lowerpanel: AV(connected filled circles) increases monotonically, as expected in the case of dust formation. The shaded area represents the 1σ error region. Upper panel: RVas a function of time. The value of RV= 6.4 found for SN 2010jl (Gall et al. 2014) is indicated as a red horizontal line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


