| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731834 | |
| Published online | 11 January 2018 | |
Sloshing in its cD halo: MUSE kinematics of the central galaxy NGC 3311 in the Hydra I cluster⋆
1 Universidade de São Paulo, IAG, Departamento de Astronomia, Rua do Matão 1226, São Paulo - SP, Brazil
e-mail: kadu.barbosa@gmail.com
2 European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching, Germany
3 INAF, Osservatorio Astronomico di Torino, STrada Osservatorio 20, 10025 Pino Torinese, Italy
4 Max-Planck-Institut fur Extraterrestrische Physik, Giessenbachstrasse, 85741 Garching, Germany
5 Departamento de Astronomia, Universidad de Concepción, Concepción, Chile
Received: 25 August 2017
Accepted: 23 October 2017
Context. Early-type galaxies (ETGs) show a strong size evolution with redshift. This evolution is explained by fast “in-situ” star formation at high-z followed by a late mass assembly mostly driven by minor mergers that deposit stars primarily in the outer halo.
Aims. We aim to identify the main structural components of the Hydra I cD galaxy NGC 3311 to investigate the connection between the central galaxy and the surrounding stellar halo.
Methods. We produce maps of the line-of-sight velocity distribution (LOSVD) moments from a mosaic of MUSE pointings covering NGC 3311 out to 25 kpc. Combining deep photometric and spectroscopic data, we model the LOSVD maps using a finite mixture distribution, including four non-concentric components that are nearly isothermal spheroids, with different line-of-sight systemic velocities V, velocity dispersions σ, and small (constant) values of the higher order Gauss-Hermite moments h3 and h4.
Results. The kinemetry analysis indicates that NGC 3311 is classified as a slow rotator, although the galaxy shows a line-of-sight velocity gradient along the photometric major axis. The comparison of the correlations between h3 and h4 with V/σ with simulated galaxies indicates that NGC 3311 assembled mainly through dry mergers. The σ profile rises to ≃ 400 km s-1 at 20 kpc, a significant fraction (0.55) of the Hydra I cluster velocity dispersion, indicating that stars there were stripped from progenitors orbiting in the cluster core. The finite mixture distribution modeling supports three inner components related to the central galaxy and a fourth component with large effective radius (51 kpc) and velocity dispersion (327 km s-1) consistent with a cD envelope. We find that the cD envelope is offset from the center of NGC 3311 both spatially (8.6 kpc) and in velocity (ΔV = 204 km s-1), but coincides with the cluster core X-ray isophotes and the mean velocity of core galaxies. Also, the envelope contributes to the broad wings of the LOSVD measured by large h4 values within 10 kpc.
Conclusions. The cD envelope of NGC 3311 is dynamically associated with the cluster core, which in Hydra I is in addition displaced from the cluster center, presumably due to a recent subcluster merger.
Key words: galaxies: clusters: individual: Hydra I / galaxies: individual: NGC 3311 / galaxies: elliptical and lenticular, cD / galaxies: kinematics and dynamics / galaxies: structure / galaxies: stellar content
The combined datacubes are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/609/A78
© ESO, 2018
1. Introduction
The nearly featureless morphologies of massive early-type galaxies (ETGs) and their radial surface brightness profiles have been a test benchmark for any theories of galaxy formation and evolution since the introduction of the R1/4 law (de Vaucouleurs 1953). This simple analytical formula captures the high degree of central concentration of the light in these objects, but also the large radial extension of their light distribution (Huang et al. 2013). At the brightest end, the most luminous galaxies in the early-type family, the cD galaxies, are embedded in extended envelopes (Schombert 1986), with shallow surface brightness gradient profiles thus fading into the cluster of galaxies that surrounds them.
Recent observations show that massive, passively evolving galaxies are identified already at z ~ 2.5 (Cimatti et al. 2004). In particular, galaxies in the “red nuggets” population are considered to be precursors of the nearby giant ETGs (van Dokkum et al. 2009; Cassata et al. 2010; van Dokkum et al. 2015), although with smaller sizes by a factor of approximately three and higher central stellar velocity dispersions (σ) than the local ETGs with similar stellar masses. Among different proposed formation models, the two-phase formation scenario (De Lucia & Blaizot 2007; Oser et al. 2010, 2012) is able to satisfy these observational constraints. In this model, the central regions of ETGs are formed in a fast dissipative process early in the history of the universe (z ≥ 3), while the evolution at low redshift is dominated by the assembly of a stellar halo, which is stochastically accreted as a consequence of mostly dry mergers (see also Cooper et al. 2013). Such a picture can be probed at low redshift by the observations of cD galaxies, where the processes of late mass accretion are believed to be extreme owing to the large occurrence of galaxy disruption processes that are inherent to the strong gravitational interactions within their massive dark halos.
Currently, several avenues are being pursued to identify the different signatures left by the dissipative (also dubbed in situ) and accretion (also dubbed ex-situ) processes in massive ETGs. For instance, the radial gradients of the stellar populations (metallicity, age, abundance ratios) of ETGs preserve information about accretion history (e.g., Hirschmann et al. 2015; Cook et al. 2016), and some attempts to determine gradients out to large radius were carried out using long-slit (Coccato et al. 2010, 2011), multi-slit (Barbosa et al. 2016), and integral field unit (IFU) (Greene et al. 2013, 2015) spectroscopy. Alternatively, information about the accretion events may be present in the surface brightness profiles. Spavone et al. (2017) give recent results for decompositions that are motivated by the predictions of cosmological simulations, and Huang et al. (2013) and Gonzalez et al. (2005) give results for the identification of galaxy and halo components in extended 2D photometric data.
One open question is whether the 2D surface brightness decomposition in multiple components is supported independently by the maps of the line-of-sight velocity distribution (LOSVD) moments, for example, whether these photometric components can be identified in the kinematic profiles also. Differently from late-type galaxies, where the bulge/disk decomposition of photometric and kinematic profiles is performed routinely (e.g., Cortesi et al. 2011), the identification of the kinematic signatures of the inner and outer stellar components of ETGs are hampered primarily by the low signal-to-noise ratio (S/N) in the spectroscopic absorption line measurements, especially at large galactocentric distances.
Recently, Bender et al. (2015) dealt with the above question in cD galaxies, in the study of NGC 6166. They used a combination of deep long-slit observations with deep photometry and required that the photometric decomposition reproduced the radial gradients of the four LOSVD moments, that is, V, σ, h3, and h4. As a result, the best combined kinematic and photometric model identified two spheroids with low Sérsic indices (n< 4), with very different surface brightnesses and radii, and also different systemic velocities and velocity dispersions. Because of the large value of its effective radius, the outer component was identified with the cD envelope of NGC 6166, and its large velocity dispersion supports the idea that its stars were stripped from galaxies orbiting in Abell 2199. These results highlight the importance of substructures to understand the 2D photometric and kinematic maps of ETGs, but they also raise interesting questions. Are these components useful parameterizations only, or do they comply with the scaling relations for galaxies, like the Faber-Jackson (Faber & Jackson 1976) or the Fundamental plane (Brosche 1973; Djorgovski & Davis 1987; Dressler et al. 1987) relations? Do they qualify as physically distinct components in these galaxies, like bulges and disks in spirals?
In this work, we study the cD galaxy NGC 3311, located at the core of the Hydra I (Abell 1060) cluster, one of the nearest prototypical massive elliptical galaxies. Photometrically, NGC 3311 is the brightest cluster galaxy (BCG) of the cluster, and has an extended and diffuse stellar halo on top of a high surface brightness central component. As shown by Arnaboldi et al. (2012), the surface brightness profile of NGC 3311 requires more than one component to describe its overall asymmetry with respect to the galaxy’s luminous center. Long-slit observations indicate that NGC 3311 has a velocity dispersion profile that rises from a central value of σ0 ≈175 km/s to σ ≈400 km/s at major axis distances of 20 kpc (Ventimiglia et al. 2010; Richtler et al. 2011). Moreover, features in the velocity dispersion profile are correlated with photometric (Hilker et al. 2015, 2017) and stellar population substructures (Coccato et al. 2011; Barbosa et al. 2016). These studies indicate that NGC 3311 may also be described as a central galaxy surrounded by a cD envelope, similarly to NGC 6166.
Our goal is to derive a coherent description of NGC 3311 that can account for both the surface brightness and the LOSVD, to learn about its formation processes. Expanding on the approach used by Bender et al. (2015), we perform a 2D modeling of the data by matching simultaneously 2D surface brightness and LOSVD moments maps. For this purpose, we use recently acquired new deep integral field observations for the central region of the Hydra I cluster with the Multi Unit Spectroscopic Explorer (MUSE) IFU, that allows a detailed study of the kinematics of NGC 3311 with unprecedented spatial resolution, together with deep V-band archival data.
We structure this work as follows. In Sect. 2, we present the analysis of the MUSE data set, including the mosaicing strategy of the observations, data reduction, methodology for LOSVD measurement and validation of the results, and the analysis of the kinematics. In a companion paper (Hilker et al. 2017), we also explore the kinematics of NGC 3311 at larger radii using multiple slit mask spectroscopy with the FOcal Reducer/low dispersion Spectrograph 2 (FORS2) on the Very Large Telescope (VLT). In Sect. 3, we perform a detailed photometric decomposition of NGC 3311 surface brightness with multiple spheroidal components. In Sect. 4, we carry out a unified model of both photometric and kinematic data using the method of finite mixture distribution. In Sect. 5, we discuss the implications of our results for the understanding of cD galaxies, the peculiar velocity of inner galaxy and envelope, the origin of their velocity and radial biases, and the strong radial variation of the LOSVD moments. We summarize and conclude our work in Sect. 6.
Throughout this work, we adopt the distance to the Hydra I cluster of D = 50.7 Mpc, based on the Hubble flow with H0 = 70.5km/s/Mpc (Komatsu et al. 2009) assuming a radial velocity of 3777 km/s (Struble & Rood 1999), which results in 1′′ = 0.262 kpc. We assume an effective radius of Re = 8.4 kpc for NGC 3311 (Arnaboldi et al. 2012).
2. Kinematic analysis of MUSE observations
2.1. Observations and data reduction
We carried out integral field observations of the core of the Hydra I cluster using the MUSE instrument (Henault et al. 2003; Bacon et al. 2004), mounted at the Nasmyth focus of the UT4 8m telescope of the VLT, under ESO programme 094.B-0711A (PI: Arnaboldi). Observations were taken in the wide field mode that covers a 1 × 1 arcmin2 field of view (FOV) with spatial sampling of 0.2 × 0.2 arcsec2. In the case of NGC 3311, it corresponds to a region of 15.7 × 15.7 kpc2. The wavelength coverage is 4650 ≤ λ(Å)≤ 9300 with resolving power varying between 2000 and 4000.
Figure 1 shows the mosaic of pointings adopted in our observations, including four fields, I, II, III, and IV, with exposure times of 730 s, 670 s, 1015 s, and 1370 s respectively. The first three fields are positioned along the major axis of NGC 3311 to probe the center of NGC 3311 and the NE substructure observed in X-ray (Hayakawa et al. 2004) and optical (Arnaboldi et al. 2012) imaging, as well as in the metallicity map (Barbosa et al. 2016). We have an additional pointing, field IV, located next to HCC 007, a spectroscopically confirmed member of the cluster with a systemic velocity of V = 4830 ± 13km/s (Misgeld et al. 2008) that is intended to cover the diffuse stellar tidal tail observed by Arnaboldi et al. (2012). The large companion NGC 3309 is also bound to the Hydra I cluster, with a central systemic velocity of V = 4099 ± 27km/s (Misgeld et al. 2008). However, NGC 3309 does not seem to be interacting with NGC 3311, as indicated by the lack of distortions in the photometric profiles of both galaxies, and contributes to the surface brightness profile of NGC 3311 only at distances larger than 20 kpc (Arnaboldi et al. 2012, see also Sect. 3.2).
 |
Fig. 1 Area coverage of the MUSE observations of NGC 3311, in the core of the Hydra I cluster. The mosaicing consists of four fields; three are aligned with the photometric major axis (I, II, and III) and survey the central region of the galaxy and the NE substructure. The fourth pointing (field IV) is placed on the extended diffuse tail of the lenticular galaxy HCC 007. The V-band image from Arnaboldi et al. (2012) is used in the background, and the black lines show the V-band contours in the range from 21 to 23.5 mag arcsec-2 in intervals of 0.5 mag arcsec-2. |
The data reduction was executed with the MUSE pipeline (Weilbacher et al. 2012), run under the Esoreflex environment (Freudling et al. 2013) that provides a real-time visualization of the data processing. We used the standard recipes for the instrument for the reduction, which includes flat fielding, bias correction, wavelength calibration, sky subtraction, flux calibration, and combination of the cubes. We masked out from the analysis only the saturated star observed in the upper region of field II and its diffraction spikes that are also observed in field III.
In this work, we are interested in the analysis of the LOSVD of the stars in the stellar halo of NGC 3311 only. The large population of low-mass systems in the central region of the Hydra I cluster core, including dwarf galaxies (Misgeld et al. 2008) and ultra-compact dwarfs (Misgeld et al. 2011), will be the subject of a forthcoming paper, and are masked in the current analysis. The masking of these sources is carried out on the white lamp images using the segmentation image produced by Sextractor (Bertin & Arnouts 1996) using a 1.5σ threshold above the local continuum.
2.2. Determination of the stellar line-of-sight velocity distributions
We extracted the kinematics with full spectrum fitting using the penalized pixel-fitting (ppxf) program (Cappellari & Emsellem 2004), which models the observations by a combination of spectral templates convolved with a LOSVD parametrized as a Gauss-Hermite profile (see Gerhard 1993; van der Marel & Franx 1993). A review of ppxf is presented in Cappellari (2017). In the following, we summarize the steps performed in our analysis.
Considering that we are interested in the study of the third (h3) and fourth (h4) moments of the LOSVD, we combined spectra from adjacent unmasked spaxels to increase the S/N of the data with the Voronoi tesselation from Cappellari & Copin (2003). We used the target signal-to-noise of S/N ≈ 70 which, according to simulations from Cappellari & Emsellem (2004), allows the recovery of the LOSVD with a precision better than 5% in the regime of the velocity dispersions found in NGC 3311, that is, σ> 150km/s. However, this large S/N would require the combination of the entire FOV in fields III and IV, which would completely erase any spatial information. Therefore, in addition to the Voronoi binning, we also separated the data into a few radial bins. Figure 2 illustrates the resulting binning scheme and the S/N obtained in this combination process.
 |
Fig. 2 Binning scheme and resulting S/N distribution of the spectra over the stellar halo in NGC 3311 from the MUSE IFU data. Spatial bins are regions of constant S/N and color. Gray regions within the MUSE fields indicate masked spaxels, including low signal to noise (S/N< 10) bins, saturated stars and their diffraction spikes, and all objects detected with sextractor, which may contaminate the measurement of the LOSVDs of the stellar halo. |
We fitted each spectrum with two kinematic components simultaneously, one for the stellar component, that is our main focus in this work, and another component for the gas emission, that is used to improve the fitting. The stellar LOSVDs are calculated using single stellar population templates from Vazdekis et al. (2010), constructed with stellar spectra of the MILES library (Sánchez-Blázquez et al. 2006; Falcón-Barroso et al. 2011a), considering a bimodal initial mass function (see Vazdekis et al. 1996), metallicities in the range −0.66 ≤ [Z/H] ≤ 0.40, ages between 0.1 and 14 Gyr, and two different alpha-element abundances (0 and 0.4). The gas LOSVDs are computed using a set of Gaussian emission line templates including Hβ (λ4861), [O III] (λ4959, λ5007), Hα (λ6565), [N II] (λ6585, λ6550), and [S II] (λ6718, λ6733). Considering that the MUSE spectra has a resolution that varies as a function of the wavelength, we homogenized the spectral resolution of the observations and templates to obtain a full width at half maximum (FWHM) of 2.9 Å.
We used additive polynomials to correct for small variations in the flux calibration between the observations and templates. After the visual inspection of the results, we noticed that our initial constraints for the velocity dispersion in ppxf for the gas component (σ< 1000km/s) resulted in poor fittings because of template mismatch. To avoid such cases, we additionally constrain the fitting by assuming σgas< 80km/s, which is approximately the velocity dispersion of emission lines in the central kiloparsec of NGC 3311, considering that we have not observed any occurrence of strong, broad emission lines.
The wavelength range of the fitting was shown to be of importance in our analysis. The combination of the MUSE observations and the MILES templates ranges allows the determination of the LOSVD using a large wavelength range between 4700 ≲ λ(Å)≲ 7500. We tested the effect of using different wavelength ranges within this dominion, to check for consistency, and we notice that the central velocity dispersion may increase by ~ 30km/s depending on the inclusion wavelengths greater than 6000 Å. This effect is more critical in the center of NGC 3311, where emission lines are stronger, and where interstellar medium (ISM) absorption lines can cause systematic effects in the derived LOSVDs. A more detailed description of the effects of faint emission lines for the determination of the LOSVD is presented in Appendix A. For simplicity and consistency, we restricted our analysis to wavelengths smaller than 5900 Å. Regions with strong residual sky lines, such as those found at λ = 4785 Å, λ = 5577 Å, and λ = 5889 Å are excluded from the fitting process. Figure 3 illustrates the results of our fitting for the central bin of NGC 3311. All velocities were corrected to the heliocentric velocity, calculated with the iraf task rvcorrect.
 |
Fig. 3 Example of the fitting process with ppxf for the MUSE observations of the Hydra I cluster core. The upper panel displays the observed spectrum (black), the best fit for the stellar component (red), and the best fit for the emission lines (blue). The lower panel shows the residuals of the fitting (solid black) and the standard deviation of the noise (dashed green). |
To test our method and have an initial evaluation of the results, we perform a comparison of our results with the literature in Fig. 4, where we show the radial profiles of the four moments of the LOSVDs along the major axis of NGC 3311 at a position angle of 40 ◦. To separate the results from the two sides of the galaxy, we folded the radial axis around the center adopting negative and positive radius for the data towards the northeast and southwest directions respectively. The upper two panels display the velocity and velocity dispersion from Richtler et al. (2011), who observed NGC 3311 using long-slit observations. We also show the results from Hilker et al. (2017), who observed the system using FORS2 “onion-shell”-like multi-slit spectroscopy to study the wide range of velocities in the extended stellar halo. To make the comparison of the long-slit data with 2D observations, we used data points whose luminosity-weighted center falls within pseudo-slits aligned with the long-slit observations using widths of 20′′ (5.24 kpc) and 40′′ (10.48 kpc) for the MUSE and FORS2 data respectively. This comparison indicates that our analysis is in good agreement with previous observations.
 |
Fig. 4 Comparison of the profiles of the four moments of the LOSVDs from this work with literature data. Red circles show the results from long-slit observations of Richtler et al. (2011) at the position angle of 40 ◦ and centered on NGC 3311. Blue (green) circles show the results from this work (Hilker et al. 2017) extracted along the same position angle within a pseudo-slit of 20′′ (40′′) width. The dashed yellow line in the first and second panel indicates the cluster’s velocity and velocity dispersion according to Christlein & Zabludoff (2003). Positive (negative) radius indicate data points towards the southeast (northwest) direction from the center of the galaxy. |
There is considerable scatter in line-of-sight (LOS) velocity and velocity dispersion in Fig. 4 at radii > 10 kpc in both the southeast and northwest directions, and the approach to the cluster values is not smooth. Following previous analyses by Ventimiglia et al. (2011) and Barbosa et al. (2016), our current understanding of the scatter of the first (velocity) and second (velocity dispersion) moment measurements of the LOSVD is related to the presence of substructures, despite the masking of the localized high(-er) surface brightness sources. As shown in Arnaboldi et al. (2012) and Ventimiglia et al. (2011), there is a group of dwarf galaxies with positive LOS velocities (Vsys> 4000km/s) that is seen in projection on top of the offset envelope (see Figs. 14 and 18 in Arnaboldi et al. 2012). In addition to the dwarfs, there is the tidal tail off HCC 026 (Vsys = 4946km/s) that falls within our MUSE B pointing. The residual unmasked light from these satellites contributes to the averaged light of the different Voronoi bins, and increases the scatter in the measurements of the LOSVD moments. For example, contribution from these high velocity dwarfs will shift the measured first moments of the LOSVD to higher values, but their intrinsic velocity dispersion is much smaller than that of the diffuse envelope at the same distance from the center. The results of the spectra decomposition are available for further assessment of this point in Arnaboldi et al. (2012), Fig. 16. As our goal is to characterize the large scale variations of the LOSVD moments in the halo and envelope with radius, we do not wish to model each single velocity measurement, that is, the scatter, but the large scale variations only.
2.3. Systemic velocity
Figure 5 shows the systemic velocity of NGC 3311 obtained with our MUSE observations. We have avoided poor fittings (S/N < 10) and we also do not show the systemic velocity of dwarfs and other compact systems identified in our analysis to highlight only the velocity field of NGC 3311. The typical uncertainty of 6 km/s is calculated as the mean uncertainty considering all the data.
In Fig. 5, the first important result is the difference between the systemic velocity in the galaxy center compared to the velocity in the outer regions. In a previous study of NGC 3311 (Barbosa et al. 2016), we showed that the stellar population properties indicate a separation between the central galaxy and the cD envelope. A division between these two populations is the V-band surface brightness level of μV = 22 mag arcsec-2 or, alternatively, the galactocentric distance of R ≈ Re = 8.4 kpc. We compute the average velocity of the central galaxy within R < Re/ 8 to be 3858 ± 5km/s. The average velocity of the cD envelope from LOS velocity measurements in the region R > Re is VcD = 3894 ± 14km/s. Based on these results, the relative radial velocity of the galaxy in relation to the outer stellar halo is ΔV = 36 ± 15km/s, measured solely by the variation of σ in the integrated stellar light. We return to this point in Sect. 5.1, where we derive the peculiar velocity of NGC 3311 based on our combined modeling of the photometric and kinematic data.
 |
Fig. 5 Map of the LOS velocity (V) for NGC 3311 for all bins with S/N > 10. The typical observational uncertainty for the LOS velocity is 6 km/s. |
Another important result that can be derived from our 2D velocity mapping is the amount of the rotation of the system and its angular momentum, which are connected to the formation and merging history of the galaxy. In our MUSE observations, we are able to study the rotation properties mostly in field I, which contains the central galaxy, but Hilker et al. (2017) give a detailed study of these properties at large radius. We use the program kinemetry (Krajnović et al. 2006) that generalizes the methodology of ellipse fitting with harmonic expansions to obtain surface brightness profiles of galaxies (e.g., Jedrzejewski 1987) to the velocity distribution for a rotating system. Figure 6 summarizes the results, indicating the kinematic semi-major axis (akin) profiles for the rotation velocity (Vrot), the kinematic position angle (PAkin) and minor-to-major axis ratio ((b/a)kin), and the fifth-to-first harmonic ratio (k5/Vrot).
The rotation velocity for the central galaxy increases as a function of the radius, but it is only 30 km/s at its maximum at R ~ Re, which is indeed smaller than the lowest velocity dispersion measured at the galaxy center (σ0 = 175km/s). This result together with the small ellipticity of the system (ε = 0.05, Arnaboldi et al. 2012) indicates an inner galaxy not supported by rotation, according to a simple V/σ versus ε classification (e.g., Emsellem et al. 2007). Moreover, the rotation obtained in this analysis is not even a good representation of the overall velocity map, as indicated by the ratio between the fifth harmonic term and the rotation velocity (k5/Vrot). In kinemetry, k5 represents the first term that is not fitted as part of the cosine expansion of the velocity field, and thus indicates the amount of velocity gradient along the LOS that is not included in a rotation model. As a reference, the atlas3D survey, that investigated a volume-limited sample of 260 early-type galaxies (Krajnović et al. 2011), adopted the threshold of k5/Vrot = 0.04 as the maximum ratio for which a cosine model is a good description of the projected 2D velocity field. However, in the case of NGC 3311, k5/Vrot > 0.04 at all radii in the inner galaxy. Therefore, NGC 3311 is a slow rotator, similarly to other galaxies in the same mass class, in agreement with the recent findings from the MASSIVE survey (Veale et al. 2017).
 |
Fig. 6 Parameters of the rotation model calculated with kinemetry to describe the MUSE velocity field for NGC 3311. From top to bottom, the panels describe the rotation velocity (Vrot), the kinematic position angle (PAkin) and minor-to-major axis ((b/a)kin), and the fifth-to-first harmonic weight of the model(k5/Vrot) as a function of the kinematic semi-major axis akin. The horizontal dashed line in the bottom panel indicates the maximum threshold value of 0.04 for early-type galaxies set by the atlas3D survey. If the cosine function is a good approximation for the 2D velocity field, the k5/Vrot measured values would lie below this line. |
Besides the kinematic classification of NGC 3311, the kinemetry analysis indicates that substructures may have an important role in the description of the velocity field of this galaxy. This is hinted at by the occurrence of the variations in the kinematic position angle and axis ratio of the rotation model, as function of the radial distance. For instance, in the inner region (akin < 2 kpc) there is low support for the rotation model, and the kinematic position angle and axis ratio have strong variations. However, in an intermediate range (2 ≲ akin ≲ 4.5 kpc), the ratio k5/Vrot approaches the value expected for a regular rotator, with a constant axis ratio (b/a)kin ≈ 0.25 and a regular change in the kinematic position angle. Then, in the next following radial range (4.5 ≲ akin ≲ 7 kpc), the rotation velocity becomes larger, but the kinematic position angle and axis ratio are approximately constant. Such variations in the geometric parameters of the radial profiles are typically found in surface brightness profiles of spiral galaxies (e.g., Barbosa et al. 2015), where bulges, disks, and other components overlap in the LOS to produce the surface brightness profiles.
2.4. Velocity dispersion
Figure 7 shows the 2D velocity dispersion (σ) field of NGC 3311. Typical uncertainties in the measurements of the velocity dispersion are of 12 km/s. The most important feature of Fig. 7 is the rising velocity dispersion with radius from the center of the galaxy, which is consistent with long-slit spectroscopy results (Loubser et al. 2008; Ventimiglia et al. 2010; Richtler et al. 2011). In the MUSE data, we measure a central velocity dispersion of ≈ 175 km/s, reaching values of ≈ 750 km/s in the outermost data points (see also Fig. 4).
 |
Fig. 7 Same as Fig. 5 for the LOS velocity dispersion (σ) of NGC 3311. The typical observational uncertainty for the LOS velocity dispersion is 12 km/s. |
Positive gradients for the LOS velocity dispersion profiles were reported in several ETGs (e.g., Loubser et al. 2008; Coccato et al. 2009), including BCGs such as IC 1101 (Dressler 1979), M87 (Murphy et al. 2014) and NGC 6166 (Bender et al. 2015). More recently, Veale et al. (2017, 2018) showed that such velocity dispersion profiles are common among luminous ETGs. However, it is challenging to determine what the maximum velocity dispersion is from these observations and, in particular, whether these velocity dispersions obtained by integrated light reach the cluster’s velocity dispersion values. This is directly observed in NGC 3311, as indicated in Fig. 4, as both the MUSE (this work) and the FORS2 data (Hilker et al. 2017) reach the cluster’s velocity dispersion value of σ = 724km/s (Christlein & Zabludoff 2003).
One interesting property of the 2D velocity dispersion field is the large-scale asymmetry along the photometric major axis. The second panel of Fig. 4 shows that the velocity dispersion profile rises faster and reaches the cluster velocity dispersion towards the northeast direction (negative R). This result indicates the effect of the large northeast structure observed both in X-ray (Hayakawa et al. 2004) and V-band imaging (Arnaboldi et al. 2012). However, considering only the most central region, | R | < 10 kpc, the velocity dispersion profile has a steeper gradient in the opposite direction, that is, towards the southwest direction. When examining the systemic velocity (Fig. 5) and velocity dispersion maps (Fig. 7), close to the isophote contour at μv = 22 mag arcsec-2 in the southeast-most corner of the MUSE pointing I, we identify a subregion where the σ values are in the range 255−300 km/s and the LOS velocities are locally blueshifted with respect to the average values along the same isophote. We consider it as an indication of the presence of kinematic substructure in the LOSVD at that location. In Sect. 3 we will argue that this local variation of the velocity dispersion and LOS velocity is related to a new photometric substructure that is found in our analysis for the first time.
2.5. Skewness h3 and kurtosis h4 2D maps
The higher-order deviations from a Gaussian LOSVD are measured through the third (h3) and fourth (h4) order coefficients of the Gauss-Hermite expansion of the LOSVD (see Gerhard 1993; van der Marel & Franx 1993). Figures 8 and 9 show the 2D maps of h3 and h4 from our MUSE observations, whose typical uncertainties are 0.02 and 0.03 respectively. The parameter h3 is proportional to the skewness and measures the asymmetric (odd) deviations of the LOSVD, that is, whether the distribution has a blueshifted (h3< 0) or redshifted (h3> 0) tail. The parameter h4 is proportional to the kurtosis of the LOSVD and probes the symmetric (even) deviations of the LOSVD, indicating either a more peaked (h4 > 0) or top-hat (h4 < 0) shape in relation with a Gaussian distribution. In steeply falling density regions, such as most of the regions covered in the MUSE observations with the exception of the center, h4 is also related to radial (h4 > 0) or tangential (h4 < 0) anisotropies.
 |
Fig. 8 Same as Fig. 5 for the skewness parameter (h3) of NGC 3311. The typical observational uncertainty for h4 is 0.02. |
 |
Fig. 9 Same as Fig. 5 for the kurtosis parameter (h4) of NGC 3311. The typical observational uncertainty for h3 is 0.03. |
The distribution of the values of the skewness parameter h3 in the area covered by our MUSE pointings has a median value of −0.01 with a standard deviation of 0.04 and there is no (anti)correlation with the velocity gradient of Fig. 5. However, we note the presence of an annulus with slightly positive values of h3 in the surface brightness range 21 ≤ μV ≤ 22 in Fig. 8 that indicates a steeper leading tail of the LOSVD at this location and a variation of h3 with radial distance from the NGC 3311 center. The 2D map of the kurtosis parameter h4 also shows variation with radial distance: the h4 values are near zero in the very central regions, at the northern edge of pointing II, and at the southern edge of pointing I, but are otherwise always positive, in the range 0.03−0.1. The overall distribution of h4 values has a positive median value of 0.05 and a standard deviation of 0.03.
Besides the spatial distribution of h3 and h4, their correlations with V/σ contain information about the merging history of ETGs. For instance, if the galaxy is a regular rotator, the LOSVDs are asymmetric with the prograde tail being steeper than the retrograde ones, that is, the degree of asymmetry measured by h3 correlates with V/σ (Bender et al. 1994). However, such correlations are erased in the occurrence of dry major mergers (Naab et al. 2014).
In Fig. 10 we investigate the correlations of h3,h4 with V/σ, and find little to none. When comparing our results with simulations from Naab et al. (2014), and considering that we have a round and non-rotating galaxy, we conclude that NGC 3311 resembles those galaxies classified as “F” type in Naab et al. (2014), that is, galaxies formed mostly in dry mergers of already passive galaxies. However, the h4 distribution versus V/σ is remarkably offset: the h4 values scatter around a mean value of 0.05, while they are scattered around zero in simulations. The occurrence of positive h4 values is also observed in other massive ETGs (Veale et al. 2017; van de Sande et al. 2017). In Sect. 5, we will discuss this issue further, in the framework of our modeling for the kinematics of NGC 3311.
 |
Fig. 10 Correlation between the Gauss-Hermite high-order moments h3 (left) and h4 (right) with V/σ. |
3. Photometric model for the surface brightness distribution in NGC 3311
So far, we have focused primarily on the analysis of the kinematics of NGC 3311. As a next step, we wish to combine the above results with those from the imaging data to study the late mass assembly of the cD galaxy NGC 3311. For this purpose, we revisit the work of Arnaboldi et al. (2012), who performed a 2D modeling of the surface brightness in the core region of the Hydra I cluster using deep V-band photometry, which led to the identification of a large, diffuse, off-centered envelope around NGC 3311. In this work, we extend the photometric analysis to also include the central region of the galaxy to obtain a more accurate surface brightness profile model for NGC 3311.
3.1. Data and methods
We use Johnson V-band imaging acquired with FORS2 (Appenzeller et al. 1998) at the VLT for the observing program 65.N-0459(A) (PI: Hilker) that we retrieved via the ESO Science Archive Facility. This image covers a field of view of 6.8′ × 6.8′ slightly off-centered from NGC 3311 in order to avoid a bright star towards the northeast direction. We adopted the zero point ZP = 27.43 ± 0.06 from Arnaboldi et al. (2012), and the extinction correction of 0.25 mag derived from Schlegel et al. (1998).
We used the sextractor program (Bertin & Arnouts 1996) to detect sources in the field of view and produce a mask for the photometric fitting. Bright stars and several dwarf galaxies projected onto the main galaxies were masked manually. We also masked the dust lane at the center of NGC 3311. We used bright, not saturated stars in the field of view to estimate the point spread function (PSF), that was calculated using the iraf task psfmeasure (Tody 1986), adopting a Moffat (1969) profile. The resulting PSF has a mean power-law slope of β = 2.956 ± 0.09 and a FWHM of 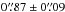 .
.
We used the galfitm software (Vika et al. 2013), an updated version of galfit (Peng et al. 2002), to perform a parametric structural decomposition of the three main galaxies in the core of Hydra I, including the cD galaxy NGC 3311, the large elliptical NGC 3309 situated northwest of NGC 3311 in Fig. 1, and the S0 galaxy HCC 007 to the south of NGC 3311. We provide further details of the fitting method in what follows.
We built the galfitm models from the single Sérsic profiles of the three galaxies, and included additional structural components, described with a Sérsic parametric law, as required from the inspection of the results and the residuals of the model. This iterative method is similar to that applied by Huang et al. (2013), who showed definite improvements in the surface brightness decomposition of ETGs when additional components are added to single Sérsic models. A priori, we had no particular constraints on the number of components, as our intent was to gain a good overall description of the light of NGC 3311, and we adopted the Sérsic law because of its flexibility. We judged the photometric models on the basis of the optimization of the χ2 between models with the goal of achieving the maximum symmetric contribution to the light in NGC 3311 and identifying any non-symmetric features.
Each Sérsic component has seven free parameters, including four to describe the geometry – central coordinates (X and Y), position angle of the semi-major axis (PA), and minor-to-major axis ratio (q = b/a) – which are then used to calculate the isophotal distance R, plus three parameters to describe the light profile given by (Sérsic 1968) ![\begin{equation} I(R)=I_{\rm e}\exp \left \{ -b_n \left [\left ( \frac{R}{R_{\rm e}}\right )^{1/n}-1\right]\right \} \mbox{,} \label{eq:sersic} \end{equation}](/articles/aa/full_html/2018/01/aa31834-17/aa31834-17-eq120.png) (1)where Re is the effective radius, Ie is the intensity at the effective radius, n is the Sérsic index, and bn ≈ 2n−0.32 is a parameter that ensures that Re contains half the light of the galaxy (see Ciotti & Bertin 1999; MacArthur et al. 2003).
(1)where Re is the effective radius, Ie is the intensity at the effective radius, n is the Sérsic index, and bn ≈ 2n−0.32 is a parameter that ensures that Re contains half the light of the galaxy (see Ciotti & Bertin 1999; MacArthur et al. 2003).
 |
Fig. 11 Photometric model of the three main galaxies in the Hydra I cluster core in FORS1 V-band image. Left: observed V-band image calibrated with the zero-point from Arnaboldi et al. (2012). Center: galfitm model including the ten Sérsic components listed in Table 1, obtained with the non-parametric fitting method. Right: residual image (original minus model), normalized by the sigma image that contains the error and noise of the observations. |
Galfit parameters for the photometric model using Sérsic components.
The sky subtraction is an important source of error in the photometric decomposition (see de Jong 1996), and the V-band imaging does not contain any obvious regions where the sky brightness can be measured independently, as most of the field of view contains light from either the cD halo or possible other faint intra cluster light (ICL) structures, such as streams and tidal tails (see Mihos et al. 2005; Iodice et al. 2017). Therefore, we performed the sky subtraction along with the photometric modeling with galfitm by including a constant sky component as a free parameter to the fitting. Simulations by Häussler et al. (2007) showed that the use of a variable sky level does not affect the parameters of the Sérsic profiles strongly.
The main advantage of galfitm is the inclusion of a non-parametric component in the fitting that is suitable to unveil faint and non-axisymmetric structures, such as tidal streams, by finding models for which the residuals are mostly positive. Interestingly, this idea is similar to the maximum symmetric model from Arnaboldi et al. (2012), which enabled the identification of the off-centered envelope around NGC 3311.
3.2. Photometric components for the NGC 3311 extended light distribution
Our final galfitm model for the light in the V-band image of NGC 3311 is shown in Fig. 11. It contains ten Sérsic components, whose parameters are listed in Table 1. HCC 007 and NGC 3309 required three components each, and NGC 3311 required four components. We notice that the residual map has several positive, rather than negative, features, that come as the result of the non-parametric components from galfitm. Considering that we have built a model based solely on the quality of the fitting, the model components are not necessarily associated to distinct physical structures. However, the number of components for each galaxy in our model is in agreement with results from the literature, as discussed below. Moreover, in Sect. 4.3, we will show that the kinematics of these systems support the idea that some of these structures are actually physically motivated.
Three Sérsic components for ETGs − The components that are required to match the 2D light distribution in our model are consistent with those discussed in Huang et al. (2013) for a sample of isolated ETGs. These authors found that ETGs may be decomposed into three, and up to four, structural components when a bi-dimensional parametric fitting is carried out to reproduce the semi-major axis position angle and the ellipticity profiles consistently, in addition to the surface brightness profile. Our model returns values for the effective radii that are in good agreement with those from Huang et al. (2013), whose typical values are Re ≲ 1kpc, Re ≈ 2.5kpc, and Re ≈ 10kpc for decomposition with three components.
Extended envelope around NGC 3311 − the modeling of the light of NGC 3311 clearly requires an additional component, labeled as “D” in Table 1. Component D has a central offset of 8.6 kpc to the northeast direction and has a much larger effective radius of 51 kpc with respect to the other three components. Figure 12 shows the surface brightness profile of NGC 3311 at a fixed position angle of 55 ◦, which is approximately aligned with the semi-major axis from photometric component “A”. This surface brightness profile shows that the off-centered D component is required to explain the excess of light at large galactocentric distances to the northeast of the galaxy center.
This component, the fourth, matches the off-centered envelope found by Arnaboldi et al. (2012) that is also associated with an X-ray’s secondary peak (Hayakawa et al. 2004, 2006) and an excess of metallicity in the stellar populations (Barbosa et al. 2016). Hence on the basis of the photometry, there is a structural component in the light of NGC 3311 that can be identified with a cD halo.
Intracluster light in the Hydra I core and asymmetric substructures in the light of NGC 3311 − a large scale characterization of the ICL in the Hydra I cluster would require a larger field of view than the one available with the FORS1 V-band image. Nonetheless we would like to describe the three most noticeable features in our V-band image that are related to the ICL in the core of the cluster, and may have implications for our kinematic analysis.
Figure 13 shows a subsection of the residuals that highlights the presence of several ICL substructures. The ICL is formed by various mechanisms that unbind stars from their parent halos and may contain from 5% to 50% of all the stars in clusters (see Arnaboldi & Gerhard 2010; Tutukov & Fedorova 2011). Simulations show the variety of shapes of these structures, including tails, plumes, and shells (see Rudick et al. 2006; Murante et al. 2007; Rudick et al. 2009; Cooper et al. 2015) that have been unveiled observationally with deep photometry (e.g., Mihos et al. 2005, 2017; Iodice et al. 2017).
 |
Fig. 12 Surface brightness profile along the photometric major axis at PA = 55 ◦. Top: comparison of the V-band surface brightness (blue dots) with the best fit from galfitm (black solid line). Other solid lines indicate the surface brightness of the subcomponents indicated in Table 1 including A (orange), B (green), C (red), and D (purple). Bottom: residuals between the V-band surface brightness and the model. Positive (negative) radius indicates the distance from the center of NGC 3311 towards the southeast (northwest) direction. |
 |
Fig. 13 ICL substructures observed in the residual map from the modeling of symmetric structures with galfitm. V-band contours are also shown for reference. Black squares represent the MUSE fields, and the colored polygons represent the three most evident substructures in this region. |
A distinct feature is a large tidal tail first discovered by Arnaboldi et al. (2012) that is associated with the galaxy HCC 026, a spectroscopically confirmed member of the Hydra I cluster core (Misgeld et al. 2008). In Fig. 13, HCC 026 is in the upper part of the structure marked by the solid blue line; unfortunately, most of its light falls outside the mosaiced area of our MUSE observations.
The large structure indicated by the dashed green line in Fig. 13 was also identified by Arnaboldi et al. (2012). They suggested that it originates from a broad tidal tail off HCC 007. Our current study indicates that this structure is broader than previously reported, and it is connected to HCC 007 as indicated by the asymmetry of the residuals to the east of the center of HCC 007, after the subtraction of the parametric model.
Finally, the residual map displays a substructure located to the southwest of NGC 3311, marked in Fig. 13 by the red dotted line. This substructure is located at the relative position (− 7,14) kpc from the center of NGC 3311, and it falls partially within the field of view of Field I in our MUSE observations. This structure to the southwest of NGC 3311 may be responsible for the blueshifted LOS velocity and the locally high velocity dispersion observed in the 2D maps in Figs. 5 and 7. In Sect. 4, we provide additional kinematics and photometric evidence for this substructure. The current photometric model does not require a common shared halo including NGC 3311 and NGC 3309. The current galfitm models do not provide evidence for residual light west of NGC 3309. Constraints for additional light at larger radii may come for future wide field photometric data.
We conclude this section by stating that the Sérsic parametric multi-component model produces an overall good match to the surface brightness distribution in the V-band image. The outcome of the current analysis shows the requirement for a fourth component to model the light of NGC 3311. This component has a central offset from the other three, and a very large effective radius (51 kpc), matching the morphological definition of a cD halo for BCGs (Matthews et al. 1964; Morgan & Lesh 1965). However, a point raised by Bender et al. (2015) questions whether one is able to identify physically distinct galaxy components from photometry alone. In the next section, we address this problem in NGC 3311, by coupling the photometry with the 2D kinematics from the new MUSE datacubes.
4. Photometric and kinematic modeling of NGC 3311
The goal of this section is to construct a model that can combine the 2D LOSVDs of NGC 3311 (Sect. 2) on the basis of the photometric components matching the V-band surface brightness (Sect. 3). Our approach is motivated by the work of Bender et al. (2015), which we review in the following, before explaining our generalization.
In their work, Bender et al. (2015) studied NGC 6166, the central galaxy of Abell 2199 and another prototypical cD galaxy. They obtained their kinematics from long-slit observations extending out to 100′′ (~ 60 kpc) from the center of the galaxy using deep observations from the Hobby-Eberly telescope. The velocity dispersion profile of NGC 6166 increases with radius, reaching the cluster velocity dispersion value of 819 km/s, similarly to the velocity dispersion profile of NGC 3311. Besides this, they revisited the photometric data of the system from a variety of sources to produce an accurate surface brightness profile, which they modeled using decompositions into either one or two Sérsic components.
To combine the photometric and kinematic information, Bender et al. (2015) modeled the LOSVD profile as a luminosity-weighted superposition of two Gaussian LOSVDs, each with its own velocity dispersion, whose luminosity follows the surface brightness of the Sérsic components. By fixing the velocity dispersion of the combined model to values of σin = 300km/s and σout = 865km/s for the inner and outer components respectively, they have shown that the best model requires two components with the least overlap in radius. Specifically, the inner component had an effective radius Re,1 = 14.95′′ ≈ 9 kpc and a Sérsic index n1 = 1.52, whereas the outer component had Re, 2 = 181.2′′ ≈ 110 kpc and n2 = 1.83. However, the best combined model is not the best model according to the photometry alone, at least from a χ2 test. Bender et al. (2015) argued that the surface brightness decomposition of the best combined photometric and kinematic model is slightly inconsistent with their photometric data, and thus caution about the use of photometry alone to infer the properties of the stellar halos.
Regarding our case, the photometric parameters of the best combined model from Bender et al. (2015) resemble the parameters of our surface brightness decomposition for NGC 3311 (Table 1), that is, spheroids with low Sérsic indexes (n ≲ 2) and very different radii for the inner and outer components. Moreover, our photometric decomposition naturally indicates that the envelope surface brightness is approximately exponential, in agreement with previous findings (e.g., Seigar et al. 2007; Donzelli et al. 2011). Thus, we now ask the following question: if we suppose that the photometric decomposition of NGC 3311 is identifying structural components, can their kinematics be modeled to reproduce the MUSE LOSVD maps?
To answer this question, we generalize the model used by Bender et al. (2015) in the following ways: 1) we expand the analysis to a 2D approach, which is best suitable to explore the asymmetric surface brightness of NGC 3311, and exploit the capability of the MUSE IFU data; 2) we allow non-Gaussian LOSVDs for the components using a mixture model to predict the higher-order moments h3 and h4 also; and 3) we consider more than two components to account for all the structures observed in the surface brightness distribution. In the next sections, we describe our modeling procedure in detail.
4.1. The finite mixture distribution model
In this section, we briefly review the mathematical background of a finite mixture distribution (FMD), a probabilistic model that represents a probability distribution as a superposition of components, following the description of the model from Frühwirth-Schnatter (2013), and applied to the study of LOSVDs. In this approach, the observed LOSVD ℒ(v) at a given location X = (X,Y) in the plane of the sky is represented as 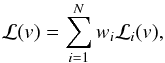 (2)where v is the LOS velocity, ℒi(v) indicate the probability distributions for the i = 1,...,N components, and wi are the weights, which follow the constraints w1 + ... + wn = 1 and wi ≥ 0. In this approach, the quantities that describe ℒ(v) are related to the expected value E [g(v)] of a generic function g(v), defined as
(2)where v is the LOS velocity, ℒi(v) indicate the probability distributions for the i = 1,...,N components, and wi are the weights, which follow the constraints w1 + ... + wn = 1 and wi ≥ 0. In this approach, the quantities that describe ℒ(v) are related to the expected value E [g(v)] of a generic function g(v), defined as ![\begin{equation} E[g(v)]=\int_{-\infty}^{+\infty}g(v)\mathcal{L}(v){\rm d}v. \label{eq:ev} \end{equation}](/articles/aa/full_html/2018/01/aa31834-17/aa31834-17-eq238.png) (3)Given that the components of the mixture distribution are also probability distributions, we can also define the expected values of the components Ei [g(v)] substituting ℒ(v) with ℒi(v) in the equation above. Therefore, from Eqs. (2)and (3), it follows that
(3)Given that the components of the mixture distribution are also probability distributions, we can also define the expected values of the components Ei [g(v)] substituting ℒ(v) with ℒi(v) in the equation above. Therefore, from Eqs. (2)and (3), it follows that ![\begin{equation} {E}[g(v)] = \sum_{i=1}^N w_i E_i[g(v)]\mbox{.} \end{equation}](/articles/aa/full_html/2018/01/aa31834-17/aa31834-17-eq240.png) (4)The mean LOS systemic velocity μ is obtained with g(v) = v, thus
(4)The mean LOS systemic velocity μ is obtained with g(v) = v, thus ![\begin{equation} \mu = E[v] = \sum_{i=1}^N w_i \mu_i\mbox{,} \end{equation}](/articles/aa/full_html/2018/01/aa31834-17/aa31834-17-eq243.png) (5)where μi = Ei [v] are the mean systemic velocities of the components. Similarly, the LOS velocity dispersion σ is obtained with g(v) = (v−μ)2, thus
(5)where μi = Ei [v] are the mean systemic velocities of the components. Similarly, the LOS velocity dispersion σ is obtained with g(v) = (v−μ)2, thus ![\begin{equation} \sigma^2= {\rm Var}[v] = \sum_{i=1}^{N} w_i(\mu_i^2 + \sigma_i^2) - \mu^2\mbox{,} \end{equation}](/articles/aa/full_html/2018/01/aa31834-17/aa31834-17-eq246.png) (6)where σi are the velocity dispersions of the components. In the mixture model, the mth central moment is given by
(6)where σi are the velocity dispersions of the components. In the mixture model, the mth central moment is given by ![\begin{equation} E [(v - \mu)^m] = \sum_{i=1}^{N}\sum_{j=0}^{m}\binom{m}{j}w_i(\mu_i-\mu)^{m-j} E[(v-\mu_i)^j]\mbox{.} \label{eq:centralmoments} \end{equation}](/articles/aa/full_html/2018/01/aa31834-17/aa31834-17-eq249.png) (7)Finally, the skewness γ3 and the kurtosis γ4 are then defined as
(7)Finally, the skewness γ3 and the kurtosis γ4 are then defined as ![\begin{eqnarray} && \gamma_3 =\frac{E[(v-\mu)^3]}{\sigma^3}, \\ && \gamma_4 = \frac{E[(v-\mu)^4]}{\sigma^4} \cdot \end{eqnarray}](/articles/aa/full_html/2018/01/aa31834-17/aa31834-17-eq252.png) The FMD model described so far in this section does not depend on the parametrization of the LOSVD. However, we are interested in using a parametrization that is related to the observation, that is, Gauss-Hermite distributions, where the parameters h3 and h4 are used to describe the skewness and the kurtosis of the LOSVD, instead of γ3 and γ4. The relation between these quantities are then given by (see the documentation of the task xgauprof for the GIPSY package, Vogelaar & Terlouw 2001)
The FMD model described so far in this section does not depend on the parametrization of the LOSVD. However, we are interested in using a parametrization that is related to the observation, that is, Gauss-Hermite distributions, where the parameters h3 and h4 are used to describe the skewness and the kurtosis of the LOSVD, instead of γ3 and γ4. The relation between these quantities are then given by (see the documentation of the task xgauprof for the GIPSY package, Vogelaar & Terlouw 2001) 
4.2. Application of FMD model to the LOSVDs of NGC 3311
To apply the FMD model, we assume that the observed LOSVD at any given position X = (X,Y) is given by the luminosity-weighted mixture of the components in the surface brightness decomposition, each with its own LOSVD. Therefore, the weights are calculated as 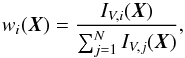 (12)where IV,i(X) is the V-band surface brightness of the component i = 1,...,N at X. Implicitly, this simple modeling considers that the light traces the mass with a mass-to-light ratio that is constant within a given component and that this mass-to-light ratio is the same for all components.
(12)where IV,i(X) is the V-band surface brightness of the component i = 1,...,N at X. Implicitly, this simple modeling considers that the light traces the mass with a mass-to-light ratio that is constant within a given component and that this mass-to-light ratio is the same for all components.
According to the decomposition model described in Sect. 3, the surface brightness within the MUSE observations is dominated by the four components of NGC 3311. This is illustrated in Fig. 14, which shows the weights of the individual components A to D as a function of the radius for a dense grid of points within fields I to IV. We also show the sum of all modeled components E to J, wE−J, which indicates that the sum of the light in other spheroidal components in our observations is not greater than 5%. We also provide the contribution of the sum of components A and B, indicated as wA + B, which are possibly physically associated, as we discuss in the next section. In the actual modeling of NGC 3311, we re-normalize the weights to consider only components A to D.
 |
Fig. 14 Weights for the FMD model of NGC 3311 as a function of the radius within the MUSE fields. The four main components of NGC 3311, A, B, C, and D, are shown individually. The component A + B indicates the sum of the first two components, which are modeled as having the same kinematics. The component E−J indicates the cumulative contribution of all other photometric components that are not included in the kinematic modeling. |
Next we assume that each component has a unique LOSVD characterized by a set of four parameters – μi, σi, h3,i, h4,i, that do not depend on position on the sky. Consequently, the spatial variation of the modeled LOSVD is given only by the linear combination of the weights of the photometric components at the different sky positions. In this way, we are ignoring both ordered motions (rotation) and bulk motions within a given component. This approach resembles the use of isothermal spheres to describe the LOSVDs, where the velocity dispersion does not vary spatially (see Binney & Tremaine 1987), and we allow these spheres to have non-zero skewness and kurtosis values.
4.3. Fitting method
Within the above assumptions, we then calculate μi, σi, h3,i, and h4,i for components i = A,...,D. As indicated in Eq. (7), each central moment depends on the previous moments, so we carry out iterative fittings to calculate each of the sets of parameters sequentially. For example, we compute μi directly from the maps, and then we calculate the velocity dispersions (σi) fixing μi, and, so on up to h4,i. These calculations are performed with the program least_squares from the SciPy package (Oliphant 2007; Perez et al. 2011), using the trust-region reflective gradient method (Branch et al. 1999), which allows a bound-constrained minimization of the parameters, and uncertainties are calculated using bootstrapping simulations.
We initially computed the FMD models using four kinematic components, one for each photometric structure. This approach provided values for μi, σi, and h3,i almost identical to the best model that we discuss in the remaining text, but we encountered problems in obtaining a meaningful value of h4,B. To improve the fitting, we made two modifications to the procedure. Firstly, we used a robust fitting process instead of a simple weighted χ2 minimization, that is, we used an approach that is less sensitive to outliers. This was carried out using the minimization of a loss function ρ(χ2) instead of the simple minimization of the χ2. In particular, we adopted a smooth approximation to absolute value implemented in the program least_squares given by 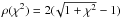 (see Triggs et al. 2000). This alleviated the problem by removing a few outliers from the analysis. However, a better solution for the problem is to assume that components A and B are, from the kinematics point of view, a joint component.
(see Triggs et al. 2000). This alleviated the problem by removing a few outliers from the analysis. However, a better solution for the problem is to assume that components A and B are, from the kinematics point of view, a joint component.
As discussed in the photometric modeling (see Sect. 3.2), we performed a photometric decomposition to obtain the best description of the surface brightness in NGC 3311, but it does not necessarily follow that all these components are physically distinct. A closer inspection of the center of NGC 3311 reveals the presence of a large dust lane, and the use of two compact components (A and B) in the center may not be related to physically independent components, but just as a way to describe the central component better from a mathematical perspective. This is the case of NGC 7507, studied by Huang et al. (2013), where the use of an additional component increases the quality of the photometric decomposition considerably. We believe that the center of NGC 3311 is a similar case; that is, both components A and B are used to describe the surface brightness of the same entity, as was indicated also by very similar kinematics derived for these components when treated disjointly.
4.4. Results
The parameters of our best model are presented in Table 2. As discussed above, components A and B are treated with a unique LOSVD, thus we refer to these components jointly as A + B. The resulting maps of the LOSVDs are displayed in Fig. 15, including the observed LOSVDs (top panels), the best fit model for the FMD model (middle panels), and the residuals between observations and models (bottom panels). To illustrate the radial profiles for the kinematics, Fig. 16 shows the comparison of the observed LOSVDs with the models along a pseudo-slit orientated at a position angle of 40 ◦, similar to the profiles presented in Fig. 4, but now using a logarithmic scale for the radial direction to improve the visualization of the inner data points.
 |
Fig. 15 Comparison of observed kinematics and the finite mixture model in NGC 3311. Top panels: observed four moments of the LOSVD in a Gauss-Hermite expansion, including systemic velocity (V), velocity dispersion (σ), and two high-order moments for the skewness (h3) and kurtosis (h4) of the distribution. Middle panels: best fit for the finite mixture model according to parameters in Table 2 (see text for details). Bottom panels: residuals between the observed fields on top and the best fit models in the middle panels. |
Gauss-Hermite profile parameters for the four photometric components in the finite mixture model.
 |
Fig. 16 Comparison of the radial profiles of the four moments of the LOSVD observed along the semi-major axis at PA =40 ◦ within a pseudo-slit of 3′′ width. Large blue circles indicate the observed values while small orange circles indicate the results for the finite mixture model. Negative (positive) radius indicates data points at the NE (SW) from the center of NGC 3311. |
Evaluation of the model − the major limitation of our modeling are the results at large radii, where the model has a velocity dispersion that is usually smaller than the data. However, there are a number of reasons to explain this results. The first is the presence of substructures at large radii, which increases the scatter of the measured LOSVD. Second, also at large radii, we are dealing with bins with low S/N and larger area in relation to the central bins, which lead to larger uncertainties and, consequently, lower weights in the optimization routine. Finally, there is the issue of the spatial coverage of our observations, which cover only part of the galaxy. Despite these issues, the model is clearly able to recover the large scale properties of the observations, for example, the rising of the LOS velocity and velocity dispersion from the center of NGC 3311, and the large scale northeast and southwest asymmetry, and the residual maps indicate only features on smaller scales that our model was not meant to fit. An interpretation of the scatter to larger velocity dispersions at large radii is given in Hilker et al. (2017).
Component C as a fast rotator − our FMD modeling allows us to revisit the rotation pattern observed in MUSE Field I previously discussed in Sect. 2.3. NGC 3311 is classified as a typical slow rotator, as evidenced by the last panel of Fig. 6 where we showed that the residuals from the kinemetry are always larger than 5% of the rotation velocity. However, at least in the radial range between R ~ 2 and 5 kpc, the ratio k5/Vrot is not much larger than such a threshold. In this radial range, component C dominates the light (see Fig. 14) and may be characterized by a regular rotation pattern.
The maximum rotation in the above radial range is about VC ≈20 km/s, with the value for the velocity dispersion of σC = 188 km/s according to the FMD model. Thus VC/σC ≈ 0.1, and the ellipticity of component C from the photometry is 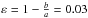 . Given these values, it is possible to classify this component as an oblate isotropic spheroid, similar to the fast rotators in the ATLAS3D survey (Emsellem et al. 2011).
. Given these values, it is possible to classify this component as an oblate isotropic spheroid, similar to the fast rotators in the ATLAS3D survey (Emsellem et al. 2011).
While NGC 3311 as a whole is correctly characterized as slow rotator, we have evidence that an individual structural component, component C, may be regarded as rotating. The implication of the classification of component C as a fast rotator denotes the importance of a detailed analysis of the kinematics in conjunction with photometry, in particular in a complex system such as a cD galaxy, where a large fraction of the light may come from accreted stars.
Kinematical signatures of asymmetric features − our FMD model does not include non-axisymmetric components, such as the elongated features seen in the southwest region of MUSE Field I (see Fig. 13). Yet, this substructure is clearly present, as indicated by the features in the residual map of the velocity dispersion, Fig. 15, where a local enhancement in the velocity dispersion at around ~ 30km/s is observed at the same location. The shape of this substructure is unclear considering the limited area coverage of our MUSE mosaic in that specific region.
The presence of a large number of substructures around BCGs is expected from simulations (e.g., Cooper et al. 2015). Therefore, our model may be used for another application, which is to verify whether streams observed in the photometric decompositions are also imprinting any kinematic signatures. The study of this substructure is beyond the scope of this project, but the confirmation of its existence in the residuals from the model highlights the importance of using a 2D analysis to study massive ETGs.
 |
Fig. 17 Faber-Jackson relation for the subcomponents in NGC 3311 (orange squares) using the V-band photometric model and the velocity dispersion from the finite mixture model. Blue circles indicate the galaxies in the Carnegie-Irvine Galaxy Survey (Ho et al. 2011), while the green lines indicate the results from the SAURON survey (Falcón-Barroso et al. 2011b), including all galaxies (solid line) and slow rotators (dashed line) only. |
4.5. The scaling laws of the components in NGC 3311
The velocity dispersion is considered a proxy for the galaxy mass, and it is among the primary parameters to be used in the scaling relations, such as the Faber-Jackson relation (Faber & Jackson 1976) and the fundamental plane (Brosche 1973; Djorgovski & Davis 1987; Dressler et al. 1987) relations. Here, we investigate whether the properties of the photometric and kinematic components in NGC 3311 comply with scaling relations for isolated ETGs.
Figure 17 shows the Faber-Jackson relation in the V-band, that is, the total integrated magnitude as a function of the velocity dispersion. For comparison, Fig. 17 also shows the Faber-Jackson relation for galaxies in the Carnegie-Irvine Galaxy Survey (Ho et al. 2011) for a sample of 605 bright galaxies in the southern hemisphere. We also indicate the two Faber-Jackson relations obtained by the SAURON survey (Falcón-Barroso et al. 2011b), one including all the galaxies in the survey (solid line) and another including only slow rotators (dashed line). The central component A + B falls below the expected Faber-Jackson relation, but we may attribute that effect to the dust extinction in the central region. The analysis of the emission lines in the central region indicates the extinction is relevant within the inner kiloparsec, having values of E(B−V) ≈ 0.75 in the center. Components C and D do follow the Faber-Jackson relations: component C lies between the relations from the SAURON survey for fast and slow rotators, and component D falls onto that for slow rotators.
In Fig. 18, we show the edge-on projection of the fundamental plane for the three components of NGC 3311. For comparison, we also show the data from Kelson et al. (2000c), who studied a sample of 53 galaxies in the cluster Cl 1358+62 at z = 0.33 to construct the fundamental plane for 30 elliptical and lenticular galaxies. The y-axis shows the fundamental plane projection calculated for the SAURON survey by Falcón-Barroso et al. (2011b) for the V band. To match the data from the SAURON with the data from Kelson et al. (2000c), we offset the fundamental plane by 0.34. Such an offset may be caused by the different methods used for the calculation of parameters: Falcón-Barroso et al. (2011b) use IFU data to calculate luminosity-weighted parameters within one effective radius, while Kelson et al. (2000c) use total magnitudes taken from Hubble Space Telescope (HST) WFPC2 imaging translated to Johnson V magnitudes, whose photometry was obtained by modeling the surface brightnesses with R1/4 profiles and central velocity dispersions (see details in Kelson et al. 2000a,b). We converted their effective radius from arcsec to kpc assuming distances calculated from the redshift of the cluster in the cosmology assumed in this work.
 |
Fig. 18 Edge-on projection of the fundamental plane as a function of the effective radius. We use the fundamental plane equation (solid green lines) from the SAURON survey (Falcón-Barroso et al. 2011b), offset by a factor of 0.34 to match the observations from Kelson et al. ( 2000c, blue circles). The dashed green lines indicate the one standard deviation of the fundamental plane. The components of NGC 3311 identified in our analysis (orange squares) are labeled according to Table 2. |
The tightness of the fundamental plane is regarded as a degree of the virialization of galaxies (Faber et al. 1987). The results of our analysis indicate that the components follow the expected fundamental plane relation for galaxies, including the most luminous components C and D, whose effective radii are larger than those sampled in both SAURON and Kelson et al. (2000c) samples. The values of log Re,V and log σ for component D place it at the high effective radius and sigma end of the fundamental plane for isolated ETGs. This region of the fundamental plane occurs before significant changes in the M/L ratios take place, such as is found in cases with ICL spheroids (Zaritsky et al. 2006).
5. Discussion
The MUSE IFU enables measurements of the spectra from the stellar light in the faint outer regions of ETGs. By coadding field portions it is possible to achieve adequate signal-to-noise ratios and reach out to several effective radii. Such an observing strategy is particularly well suited for BCGs, as it enables measurements of the 2D kinematics maps and metallicities out to very large radii, sampling the extended halos of these objects (Edwards et al. 2016). Our goal for NGC 3311 is to measure the LOS velocity offsets between the galaxy’s bright central regions and the extended halo directly from the Doppler shifts of the absorption lines, and the 2D maps of the four LOSVD moments. The next step will be the analysis of the metallicities (in a forthcoming paper, Barbosa et al., in prep.).
5.1. The peculiar velocity of NGC 3311
We start our discussion with the results for the mean LOS velocities of the different regions of NGC 3311 obtained by our 2D modeling of the velocity field. Our mean LOS velocity for the very center of NGC 3311, vLOS, cen = 3856 ± 10km/s, agrees with the previous measurements of Misgeld et al. (2008), Ventimiglia et al. (2010), and Richtler et al. (2011)1. We can compare this value with that of the mean Hydra I cluster redshift from extended spectroscopic surveys of cluster galaxies (Bird 1994; Christlein & Zabludoff 2003). This gives ⟨ VHydra ⟩ = 3683 ± 46km/s (Christlein & Zabludoff 2003), indicating a relative motion of ΔVLOS = 173km/s for the center of NGC 3311.
Our new MUSE data cubes provide direct evidence for the galaxy’s peculiar velocity from the wavelength shifts of the faint absorption lines on the continuum from the inner bright regions to the faint outer halo. The visual inspection of the mean LOS velocity map showed already that the inner regions of the galaxy, corresponding to photometric and kinematic components A to C, have a different mean velocity from the diffuse outer envelope, the D component. The results of the FMD modeling indicates that the D component is offset by ΔVLOS = 122 ± 13km/s and ΔVLOS = 142 ± 14km/s from components A + B and C, respectively. Assuming a cluster velocity dispersion from satellite members of σHydra = 724 ± 31km/s (Christlein & Zabludoff 2003), our modeling of the MUSE 2D LOS velocity map indicates that component D, that is, the envelope of NGC 3311, has a peculiar LOS velocity of at least 20% of the cluster velocity dispersion with respect to the inner galaxy. These results greatly improve on the early attempts by Bird (1994) to measure the peculiar velocities of this BCG.
5.2. The cD envelope of NGC 3311
In the local universe, peculiar velocities of BCGs with respect to their diffuse envelope or the intracluster light component have been measured for M87 in Virgo (Longobardi et al. 2015), NGC 6166 in Abell 2199 (Bender et al. 2015), and NGC 4874 in the Coma cluster (Gerhard et al. 2007). In NGC 3311, the outer envelope (the D component) dominates over the entire light distribution of NGC 3311, providing 81% of the total light. This outer envelope is not only shifted relative to the central galaxy in the mean velocity, by ΔVLOS = 142 ± 14km/s as discussed in Sect. 5.1, but also in space, by about 33′′ (8.6 kpc, this work) to 50′′ (12.5 kpc; Arnaboldi et al. 2012). Thus also a tangential relative motion must be present, so that we estimate a total relative velocity between central galaxy and cD envelope, of 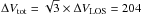 km/s.
km/s.
If we follow the definition of the velocity bias of a BCG given in van den Bosch et al. (2005), and adopt ⟨ σcen ⟩ = ΔVtot and ⟨ σsat ⟩ = σHydra, then the total velocity bias of component D is about bvel = 0.3. We can also compare the spatial offset measured for component D with the estimates from the models of galaxy velocity biases from van den Bosch et al. (2005) and Guo et al. (2015). These works agree on an estimate of the radial bias brad ≃ 1% of the halo virial radius. For halo virial masses ≥ 1014h-1M⊙, Rvir ~ 1 Mpc and the radial bias value is thus ≃ 10 kpc, which is of the same order of magnitude as the spatial offsets measured for component D with respect to the NGC 3311 central regions.
Within the paradigm of galaxy formation in ΛCDM cosmology, BCGs are expected to have non-negligible peculiar velocities in relation to the cluster dark matter halo (van den Bosch et al. 2005; Ye et al. 2017). Because of the large velocity dispersion and spatial extension, the cD envelope lives in a larger volume and its stars move in the potential generated primarily by the closest dark matter distribution, in the cluster core (Dolag et al. 2010). Thus one might expect that the cD envelope is closer in velocity to the cluster core, and that the central galaxy would have been perturbed out of the center of this larger structure, for example, because of close interactions with other satellite galaxies (Murante et al. 2007). This case is dubbed the non-relaxed galaxy (NRG) scenario in the studies of velocity bias by van den Bosch et al. (2005) and Ye et al. (2017). However, the peculiar velocity of a BCG may also arise when the innermost parts of the cluster halo are in motion relative to the cluster dark halo on larger scales. This case is dubbed the non-relaxed halo (NRH) scenario (van den Bosch et al. 2005). NRHs may occur because of subcluster mergers, which could be recognized because they also leave imprints in the X-ray emission and temperature maps (Rowley et al. 2004).
Which of these scenarios applies to NGC 3311? From Hayakawa et al. (2006), Arnaboldi et al. (2012), and our current study, we know that the D component is co-spatial with a high metallicity region in the X-rays ~ 1.5 arcmin northeast of NGC 3311. It also coincides spatially with the X-ray emission from the Hydra I cluster core (see the X-ray image in Fig. 2 of Hayakawa et al. 2004). A faint extended X-ray emission with angular dimension ~ 1′ trailing NGC 3311 to the northeast towards this high metallicity region is also seen. This could be due to ram pressure stripping of the gas (see Chandra observations from Hayakawa et al. 2004), if this feature and the confined (< 2 kpc) strongest X-ray emitting region to the southwest, which is co-spatial with the optical inner region of NGC 3311, are moving with relative velocity ≃ 260km/s during the last 5 × 107 yr (Hayakawa et al. 2004, 2006). This relative velocity is consistent with the velocity of components D relative to A + B and C. If components A + B and C are moving with respect to D, we might then expect the outer envelope to be at rest with respect to the mean cluster redshift, as observed for example for NGC 6166 in the Abell 2199 cluster (Bender et al. 2015).
What is the total relative velocity of component D with respect to the mean cluster redshift of the core region and the cluster on large scales? The mean LOS velocity of the galaxies in the core is 3982 ± 148km/s (Misgeld et al. 2008) and agrees with the mean velocity of the D component, within the error. The difference with the mean cluster redshift ⟨ VHydra ⟩ is ΔVLOS = 295km/s. If we account for the tangential relative motion associated with the spatial offset between the X-ray high metallicity peak and the center of the ICM emission of the Hydra I cluster, which is 28′′ to the southwest of NGC 3311 (Hayakawa et al. 2004), we get 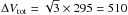 km/s. Hence the inner core halo and the envelope have a velocity bias of at least 40% of the cluster velocity dispersion. The large value of the velocity bias of the cD envelope and the cluster core is similar to what is found for BCGs in Abell clusters (Lauer et al. 2014). The evidence from the X-ray distortions and the large velocity bias of the envelope support the NRH scenario for the peculiar velocities of the different components (A + B, C, and D) in NGC 3311.
km/s. Hence the inner core halo and the envelope have a velocity bias of at least 40% of the cluster velocity dispersion. The large value of the velocity bias of the cD envelope and the cluster core is similar to what is found for BCGs in Abell clusters (Lauer et al. 2014). The evidence from the X-ray distortions and the large velocity bias of the envelope support the NRH scenario for the peculiar velocities of the different components (A + B, C, and D) in NGC 3311.
What is causing the sloshing of the inner core in the Hydra I cluster? Within the inner 100 × 100 kpc2 region centered on NGC 3311, there are 14 galaxies in total with V> 4450km/s that are currently being disrupted and adding debris to the outer envelope (Ventimiglia et al. 2011; Arnaboldi et al. 2012). On a slightly larger scale, that is, 15 arcmin (≃ 236 kpc radius), the mean average redshifts of satellite galaxies is 3982 ± 148km/s (Misgeld et al. 2008) that also is offset to a larger velocity from the value determined by Christlein & Zabludoff over the entire cluster. This is suggestive of an on-going subcluster merging. In such a case, the peculiar velocities of the NGC 3311 components can be understood as the central regions being pulled along by the portion of the inner cluster halo closer to the envelope, because of the on-going subcluster merger. Since the inner high density regions experience stronger deflections (Gerhard et al. 2007; Murante et al. 2007; Ventimiglia et al. 2011), and because of different projections of component velocities relative to the LOS, the LOS velocities with respect to the cluster at larger scales may be different for component D compared to components A + B and C.
5.3. High-order kinematics moments
Ordinary massive ETGs have nearly isothermal mass profiles and nearly Gaussian LOSVDs, with small values of the Hermite higher moments (h3, h4) indicating slow rotation and modest radial anisotropies (e.g., Gerhard et al. 2001; Sonnenfeld et al. 2013; Cappellari et al. 2015). Generally the deviations from Gaussian LOSVDs are small, with the asymmetric deviations signalled by the h3 parameter values being usually larger than the symmetric h4 values (Bender et al. 1994). Our MUSE 2D maps for the moments of the LOSVD in NGC 3311 show relatively large spatial variations for both h3 and h4, with positive values of h4 larger than the h3 values over the entire area. Our model in Sect. 4 indicates that most of the spatial variations of the h3 and h4 maps can be reproduced by the superposition of different components along the LOS whose higher order moments (i.e., the deviations from Gaussian LOSVD) are small. It is the superposition of nearly isothermal spheroids with different light distributions, LOS velocities, and centers that causes the spatial variations in the 2D maps and profiles as seen in Figs. 15 and 16. From the FMD modeling, the inner regions, that is, components A + B and C, are characterized by small negative (−0.056) or null values of the h3 parameter and small negative values (−0.076, −0.010 respectively) for h4, while the outer envelope is associated with a modest negative value (−0.097) for h3 and positive value (0.036) for h4. The superposition of components along the LOS for NGC 3311 reproduces the h3,h4 versus v/σ correlations shown in Fig. 10. These correlations are similar to those computed for simulated galaxies formed from dry mergers or already passive progenitors, according to the “F” type classification in Naab et al. (2014).
Recent studies based on extended IFU, for example, the MASSIVE survey (Veale et al. 2017), and deep long-slit (Bender et al. 2015) observations measured the values of h3, h4 out to two effective radii and showed that the most luminous ETGs (MK< −26.0; Veale et al. 2017) have mean values of ⟨ h4 ⟩ ≃ 0.05 at 2 Re and close to zero in the centers (e.g., van de Sande et al. 2017; Veale et al. 2017). For NGC 3311, the h3,h4 profiles are shown in the two bottom panels of Fig. 16. The skewness h3 is nearly zero out to 2 kpc and then becomes negative at distances larger than 10 kpc, where the LOS velocity increases. The kurtosis h4 is near zero at the center, increase to ≃ 0.1 at 2−4 kpc, and then decrease to smaller positive values at radii > 10 kpc. The h4 positive values measured for NGC 3311 are similar to those measured in other galaxies of the same luminosity class (Veale et al. 2017).
The core-wing structure of the LOSVD that is signalled by positive values of h4 may come about because of radial anisotropy, which causes an overabundance of stars at zero LOS velocity (Gerhard et al. 1998). Radial anisotropy causes the projected LOS dispersion to be underestimated also, and leads to a decreasing σLOS profile with radius (Douglas et al. 2007; de Lorenzi et al. 2009). Positive h4 and increasing σ as observed in NGC 3311 are reminiscent of the properties of simulated massive ETGs in cosmological simulations by Wu et al. (2014). These most massive galaxies have increasing circular velocity curves with radius, radial anisotropy in the 2−5 Re region and a large fraction of accreted stars (Wu et al. 2014).
In Sect. 4, the results from our modeling show that each component has a modest or small anisotropy, with the inner regions, that is, components A + B and C, characterized by negative values for h4 as in the case of tangential anisotropy. The Wu et al. (2014) simulations predict similar values of h4 for components created by dissipative events. Because the outermost component (component D) has a surface brightness profile with the largest effective radius (Re,D = 51 ± 5 kpc) and velocity dispersion σD = 327km/s, it contributes light in the inner 10 kpc from regions with larger circular velocity, giving thus rise to the core-winged structure of the LOSVD, as it is measured.
6. Summary and conclusion
In this work, we presented the detailed analysis of the MUSE mosaiced pointing covering the light of NGC 3311, which allowed the detailed mapping of the LOSVD moments within the central galaxy and part of its extended cD halo. In the first part of the paper, we measured the LOSVD maps from our new MUSE data. Based on the extended maps, we determined the peculiar velocity of the central galaxy in relation to its stellar halo, the rising velocity dispersion profile, and the presence of a cD halo that is kinematically decoupled from the central luminous regions of NGC 3311. The entire galaxy is classified as a slow rotator, with small correlation between the high-order moments h3,h4 with V/σ. The diagnostic diagrams h3, h4 versus V/σ indicate that NGC 3311 is similar to simulated galaxies formed mostly by dry mergers of already passive progenitors.
In the second part of the paper, we revisited the photometry of NGC 3311. Using deep V-band photometry and building upon previous results on the surface brightness decomposition, we carried out a photometric model that includes four Sérsic components. Three out of four components are concentric, while the outer one has a central offset and dominates the light at large radii. This model is able to reproduce the surface brightness distribution in the galaxy and its immediate surroundings in the Hydra I cluster core. The residuals further indicated the presence of asymmetric substructures pointing to recent episodes of minor accretion events.
In the final part of this paper, we developed a simple finite mixture model to describe the LOSVD of the system based on the photometric subcomponents and assuming nearly isothermal spheres with small deviations from Gaussianity. This model describes the large scale properties of the observations very well, including the strong radial variations of the four LOSVD moments and their 2D maps. We conclude that the outer envelope is responsible for the core-winged structure of the LOSVD in the bright central region also, by contributing stars that experience larger circular velocities. The success of this modeling supports the combined approach, surface brightenss profiles, and 2D kinematics modeling, to study massive, non-rotating early-type galaxies and clarify the origin of the radial gradients in the four LOSVD moments in BCGs.
On the basis of these results, we present a strong case for the peculiar velocity of the outer halo of NGC 3311 and measured a velocity bias of 0.3 for this BCG, as a lower limit. The results of the FMD modeling show that the envelope (component D): i) is displaced from the central regions, ii) has a larger effective radius, and iii) has a larger mean velocity and velocity dispersion compared to the central regions. These results, taken together with the morphology of the cospatial X-ray emission, let us conclude that the velocity bias originates from a “non relaxed halo” scenario caused by an on-going subcluster merging in the Hydra I core. We conclude that the cD envelope of NGC 3311 is dynamically associated to the cluster core, which in Hydra I cluster is in addition displaced from the main cluster center, presumably due to a recent subcluster merger.
The result of our analysis depicts NGC 3311 as a massive elliptical whose majority of stars are accreted from merging satellites orbiting in the Hydra I cluster, on preferentially radial orbits. Our next steps will be to constrain the progenitors of the components in NGC 3311, by measuring age and metallicity of their stars.
See extensive discussion in Ventimiglia et al. (2010) on the origin of the systematic offsets with respect to the LOS velocity measurements of Loubser et al. (2008).
Acknowledgments
Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programs 065.N-0459(A), 088.B-0448(B) and 094.B-0711(A). C.E.B. and C.M.d.O. thank the São Paulo Research Foundation (FAPESP) funding (grants 2009/54202-8, 2011/21325-0, 2016/17119-9 and 2016/12331-0). M.A.R. and C.E.B. acknowledge support from the ESO DG discretionary funds. T.R. acknowledges support from the BASAL Center for Astrophysics and Associated Technologies (PFB-06/2007). T.R. also acknowledges an ESO senior visitorship during May-August 2016. The authors wish to acknowledge the anonymous referee for his/her comments.
References
- Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
- Arnaboldi, M., & Gerhard, O. 2010, Highlights of Astronomy, 15, 97 [Google Scholar]
- Arnaboldi, M., Ventimiglia, G., Iodice, E., Gerhard, O., & Coccato, L. 2012, A&A, 545, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacon, R., Bauer, S.-M., Bower, R., et al. 2004, in Ground-based Instrumentation for Astronomy, eds. A. F. M. Moorwood, & M. Iye, Proc. SPIE, 5492, 1145 [Google Scholar]
- Barbosa, C. E., Mendes de Oliveira, C., Amram, P., et al. 2015, MNRAS, 453, 2965 [Google Scholar]
- Barbosa, C. E., Arnaboldi, M., Coccato, L., et al. 2016, A&A, 589, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bender, R., Saglia, R. P., & Gerhard, O. E. 1994, MNRAS, 269, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, R., Kormendy, J., Cornell, M. E., & Fisher, D. B. 2015, ApJ, 807, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic dynamics (Princeton, NJ: Princeton University Press) [Google Scholar]
- Bird, C. M. 1994, AJ, 107, 1637 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, M. A., Coleman, T. F., & Li, Y. 1999, SIAM J. Sci. Comput., 21, 1 [Google Scholar]
- Brosche, P. 1973, A&A, 23, 259 [NASA ADS] [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Copin, Y. 2003, MNRAS, 342, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Romanowsky, A. J., Brodie, J. P., et al. 2015, ApJ, 804, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Cassata, P., Giavalisco, M., Guo, Y., et al. 2010, ApJ, 714, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Christlein, D., & Zabludoff, A. I. 2003, ApJ, 591, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Cimatti, A., Daddi, E., Renzini, A., et al. 2004, Nature, 430, 184 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ciotti, L., & Bertin, G. 1999, A&A, 352, 447 [NASA ADS] [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Coccato, L., Gerhard, O., & Arnaboldi, M. 2010, MNRAS, 407, L26 [NASA ADS] [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., & Ventimiglia, G. 2011, A&A, 533, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cook, B. A., Conroy, C., Pillepich, A., Rodriguez-Gomez, V., & Hernquist, L. 2016, ApJ, 833, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, A. P., D’Souza, R., Kauffmann, G., et al. 2013, MNRAS, 434, 3348 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, A. P., Gao, L., Guo, Q., et al. 2015, MNRAS, 451, 2703 [NASA ADS] [CrossRef] [Google Scholar]
- Cortesi, A., Merrifield, M. R., Arnaboldi, M., et al. 2011, MNRAS, 414, 642 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, R. S. 1996, A&AS, 118, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Lorenzi, F., Gerhard, O., Coccato, L., et al. 2009, MNRAS, 395, 76 [NASA ADS] [CrossRef] [Google Scholar]
- de Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1953, MNRAS, 113, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Djorgovski, S., & Davis, M. 1987, ApJ, 313, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Murante, G., & Borgani, S. 2010, MNRAS, 405, 1544 [NASA ADS] [Google Scholar]
- Donzelli, C. J., Muriel, H., & Madrid, J. P. 2011, ApJS, 195, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, N. G., Napolitano, N. R., Romanowsky, A. J., et al. 2007, ApJ, 664, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1979, ApJ, 231, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Lynden-Bell, D., Burstein, D., et al. 1987, ApJ, 313, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Edwards, L. O. V., Alpert, H. S., Trierweiler, I. L., Abraham, T., & Beizer, V. G. 2016, MNRAS, 461, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2011, MNRAS, 414, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., & Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., Burstein, D., & Dressler, A. 1977, AJ, 82, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., Dressler, A., Davies, R. L., Burstein, D., & Lynden-Bell, D. 1987, in Nearly Normal Galaxies, From the Planck Time to the Present, ed. S. M. Faber, 175 [Google Scholar]
- Falcón-Barroso, J., Sánchez-Blázquez, P., Vazdekis, A., et al. 2011a, A&A, 532, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falcón-Barroso, J., van de Ven, G., Peletier, R. F., et al. 2011b, MNRAS, 417, 1787 [NASA ADS] [CrossRef] [Google Scholar]
- Freudling, W., Romaniello, M., Bramich, D. M., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frühwirth-Schnatter, S. 2013, Finite Mixture and Markov Switching Models, Springer Series in Statistics (Springer) [Google Scholar]
- Gerhard, O. E. 1993, MNRAS, 265, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O., Jeske, G., Saglia, R. P., & Bender, R. 1998, MNRAS, 295, 197 [NASA ADS] [Google Scholar]
- Gerhard, O., Kronawitter, A., Saglia, R. P., & Bender, R. 2001, AJ, 121, 1936 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O., Arnaboldi, M., Freeman, K. C., et al. 2007, A&A, 468, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, A. H., Zabludoff, A. I., & Zaritsky, D. 2005, ApJ, 618, 195 [Google Scholar]
- Greene, J. E., Murphy, J. D., Graves, G. J., et al. 2013, ApJ, 776, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Janish, R., Ma, C.-P., et al. 2015, ApJ, 807, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, H., Zheng, Z., Zehavi, I., et al. 2015, MNRAS, 446, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Häussler, B., McIntosh, D. H., Barden, M., et al. 2007, ApJS, 172, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayakawa, A., Furusho, T., Yamasaki, N. Y., Ishida, M., & Ohashi, T. 2004, PASJ, 56, 743 [NASA ADS] [Google Scholar]
- Hayakawa, A., Hoshino, A., Ishida, M., et al. 2006, PASJ, 58, 695 [NASA ADS] [Google Scholar]
- Henault, F., Bacon, R., Bonneville, C., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, Proc. SPIE, 4841, 1096 [Google Scholar]
- Hilker, M., Barbosa, C. E., Richtler, T., et al. 2015, in Galaxies in 3D across the Universe, eds. B. L. Ziegler, F. Combes, H. Dannerbauer, & M. Verdugo, IAU Symp., 309, 221 [Google Scholar]
- Hilker, M., Richtler, T., Barbosa, C. E., et al. 2017, A&A, submitted [Google Scholar]
- Hirschmann, M., Naab, T., Ostriker, J. P., et al. 2015, MNRAS, 449, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., Li, Z.-Y., Barth, A. J., Seigar, M. S., & Peng, C. Y. 2011, ApJS, 197, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, S., Ho, L. C., Peng, C. Y., Li, Z.-Y., & Barth, A. J. 2013, ApJ, 766, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Iodice, E., Spavone, M., Capaccioli, M., et al. 2017, ApJ, 839, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Jedrzejewski, R. I. 1987, MNRAS, 226, 747 [Google Scholar]
- Kelson, D. D., Illingworth, G. D., van Dokkum, P. G., & Franx, M. 2000a, ApJ, 531, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Kelson, D. D., Illingworth, G. D., van Dokkum, P. G., & Franx, M. 2000b, ApJ, 531, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Kelson, D. D., Illingworth, G. D., van Dokkum, P. G., & Franx, M. 2000c, ApJ, 531, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Cappellari, M., de Zeeuw, P. T., & Copin, Y. 2006, MNRAS, 366, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Emsellem, E., Cappellari, M., et al. 2011, MNRAS, 414, 2923 [NASA ADS] [CrossRef] [Google Scholar]
- Lauer, T. R., Postman, M., Strauss, M. A., Graves, G. J., & Chisari, N. E. 2014, ApJ, 797, 82 [Google Scholar]
- Longobardi, A., Arnaboldi, M., Gerhard, O., & Hanuschik, R. 2015, A&A, 579, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loubser, S. I., Sansom, A. E., Sánchez-Blázquez, P., Soechting, I. K., & Bromage, G. E. 2008, MNRAS, 391, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- MacArthur, L. A., Courteau, S., & Holtzman, J. A. 2003, ApJ, 582, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, T. A., Morgan, W. W., & Schmidt, M. 1964, ApJ, 140, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., Harding, P., Feldmeier, J., & Morrison, H. 2005, ApJ, 631, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., Harding, P., Feldmeier, J. J., et al. 2017, ApJ, 834, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Misgeld, I., Mieske, S., & Hilker, M. 2008, A&A, 486, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misgeld, I., Mieske, S., Hilker, M., et al. 2011, A&A, 531, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
- Morgan, W. W., & Lesh, J. R. 1965, ApJ, 142, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Murante, G., Giovalli, M., Gerhard, O., et al. 2007, MNRAS, 377, 2 [Google Scholar]
- Murphy, J. D., Gebhardt, K., & Cradit, M. 2014, ApJ, 785, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Oser, L., Emsellem, E., et al. 2014, MNRAS, 444, 3357 [NASA ADS] [CrossRef] [Google Scholar]
- Oliphant, T. E. 2007, Comput. Sci. Eng., 9, 10 [CrossRef] [PubMed] [Google Scholar]
- Oser, L., Ostriker, J. P., Naab, T., Johansson, P. H., & Burkert, A. 2010, ApJ, 725, 2312 [NASA ADS] [CrossRef] [Google Scholar]
- Oser, L., Naab, T., Ostriker, J. P., & Johansson, P. H. 2012, ApJ, 744, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Perez, F., Granger, B. E., & Hunter, J. D. 2011, Comput. Sci. Eng., 13, 13 [CrossRef] [Google Scholar]
- Richtler, T., Salinas, R., Misgeld, I., et al. 2011, A&A, 531, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rowley, D. R., Thomas, P. A., & Kay, S. T. 2004, MNRAS, 352, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Rudick, C. S., Mihos, J. C., & McBride, C. 2006, ApJ, 648, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Rudick, C. S., Mihos, J. C., Frey, L. H., & McBride, C. K. 2009, ApJ, 699, 1518 [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J. M. 1986, ApJS, 60, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Seigar, M. S., Graham, A. W., & Jerjen, H. 2007, MNRAS, 378, 1575 [NASA ADS] [CrossRef] [Google Scholar]
- Sérsic, J. L. 1968, Atlas de galaxias australes Cordoba (Argentina: Observatorio Astronomico) [Google Scholar]
- Sonnenfeld, A., Treu, T., Gavazzi, R., et al. 2013, ApJ, 777, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Spavone, M., Capaccioli, M., Napolitano, N. R., et al. 2017, A&A, 603, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Struble, M. F., & Rood, H. J. 1999, ApJS, 125, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Tody, D. 1986, in Instrumentation in astronomy VI, ed. D. L. Crawford, Proc. SPIE, 627, 733 [Google Scholar]
- Triggs, B., McLauchlan, P. F., Hartley, R. I., & Fitzgibbon, A. W. 2000, Bundle Adjustment – A Modern Synthesis, eds. B. Triggs, A. Zisserman, & R. Szeliski (Berlin, Heidelberg: Springer), 298 [Google Scholar]
- Tutukov, A. V., & Fedorova, A. V. 2011, Astron. Rep., 55, 383 [NASA ADS] [CrossRef] [Google Scholar]
- van de Sande, J., Bland-Hawthorn, J., Fogarty, L. M. R., et al. 2017, ApJ, 835, 104 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bosch, F. C., Weinmann, S. M., Yang, X., et al. 2005, MNRAS, 361, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., & Franx, M. 1993, ApJ, 407, 525 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Kriek, M., & Franx, M. 2009, Nature, 460, 717 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Dokkum, P. G., Nelson, E. J., Franx, M., et al. 2015, ApJ, 813, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Casuso, E., Peletier, R. F., & Beckman, J. E. 1996, ApJS, 106, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
- Veale, M., Ma, C.-P., Thomas, J., et al. 2017, MNRAS, 464, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Veale, M., Ma, C.-P., Greene, J. E., et al. 2018, MNRAS, 473, 5446 [NASA ADS] [CrossRef] [Google Scholar]
- Ventimiglia, G., Gerhard, O., Arnaboldi, M., & Coccato, L. 2010, A&A, 520, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventimiglia, G., Arnaboldi, M., & Gerhard, O. 2011, A&A, 528, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vika, M., Bamford, S. P., Häußler, B., et al. 2013, MNRAS, 435, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Vogelaar, M. G. R., & Terlouw, J. P. 2001, in Astronomical Data Analysis Software and Systems X, eds. F. R. Harnden, Jr., F. A. Primini, & H. E. Payne, ASP Conf. Ser., 238, 358 [Google Scholar]
- Weilbacher, P. M., Streicher, O., Urrutia, T., et al. 2012, in Software and Cyberinfrastructure for Astronomy II, Proc. SPIE, 8451, 84510B [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., & Ottaviani, D. L. 1997, ApJS, 111, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X., Gerhard, O., Naab, T., et al. 2014, MNRAS, 438, 2701 [NASA ADS] [CrossRef] [Google Scholar]
- Ye, J.-N., Guo, H., Zheng, Z., & Zehavi, I. 2017, ApJ, 841, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Gonzalez, A. H., & Zabludoff, A. I. 2006, ApJ, 638, 725 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Effect of the interstellar medium absorption lines on the LOSVD
Absorption lines from the ISM, for example, Fraunhofer D-lines (λ5890,5896), may imprint the continuum from the stars and affect the LOSVD measured with ppxf. This effect was shown by Bender et al. (2015) in the cD galaxy NGC 6166, where the velocity dispersion profile remained constant for the sodium line, but was otherwise increasing. However, measuring the properties of these absorption lines is complicated because they are embedded into other absorption lines. While accessing the wavelength range for our analysis, we have tested the profiles for the LOSVD parameters on top of the main optical absorption lines using the bands of the Lick indices (Faber et al. 1977).
The absorption line features of the Lick indices are relatively narrow for the determination of LOSVD with ppxf in our observational setup, so we fitted the LOSVDs of the Lick indices considering also their blue and red sidebands according to the definitions from Worthey & Ottaviani (1997). The determination of the LOSVD in these delimited wavelengths increases the scatter of the profiles considerably, but we noticed that profiles for the LOSVD parameters are compatible for almost all the indices with the exception of Na D and TiO1, which indicate some systematic deviations. Figure A.1 shows the difference in the profiles of these two indices in relation to the mean profiles of the iron indices.
The presence of the ISM absorption D-lines may have caused both the systematically larger velocity dispersion (by about Δσ ≃ 20−80 kms-1) at the outer radius of 8 kpc and also the larger velocity dispersion value (by about Δσ ≃ 20−45 km s-1) at R ≲ 1.5 kpc. The skewness (h3) values for these two absorption features is also systematically lower than the values measured for the other Lick indices. The h4 profiles for the Na D and TiO 1 absorption features show negative values at the center and a steep gradient between 1 and 2 kpc, reaching positive values of h4 ≃ 0.1 at radii larger than 2.5 kpc.
 |
Fig. A.1 Comparison of the LOSVD moments as a function of radius for the wavelength ranges defined according to the Lick indices in the observed field I. Solid lines display the running average of the measured values, and the shaded areas around the lines indicate the typical standard deviation from the mean. |
All Tables
Gauss-Hermite profile parameters for the four photometric components in the finite mixture model.
All Figures
 |
Fig. 1 Area coverage of the MUSE observations of NGC 3311, in the core of the Hydra I cluster. The mosaicing consists of four fields; three are aligned with the photometric major axis (I, II, and III) and survey the central region of the galaxy and the NE substructure. The fourth pointing (field IV) is placed on the extended diffuse tail of the lenticular galaxy HCC 007. The V-band image from Arnaboldi et al. (2012) is used in the background, and the black lines show the V-band contours in the range from 21 to 23.5 mag arcsec-2 in intervals of 0.5 mag arcsec-2. |
| In the text | |
 |
Fig. 2 Binning scheme and resulting S/N distribution of the spectra over the stellar halo in NGC 3311 from the MUSE IFU data. Spatial bins are regions of constant S/N and color. Gray regions within the MUSE fields indicate masked spaxels, including low signal to noise (S/N< 10) bins, saturated stars and their diffraction spikes, and all objects detected with sextractor, which may contaminate the measurement of the LOSVDs of the stellar halo. |
| In the text | |
 |
Fig. 3 Example of the fitting process with ppxf for the MUSE observations of the Hydra I cluster core. The upper panel displays the observed spectrum (black), the best fit for the stellar component (red), and the best fit for the emission lines (blue). The lower panel shows the residuals of the fitting (solid black) and the standard deviation of the noise (dashed green). |
| In the text | |
 |
Fig. 4 Comparison of the profiles of the four moments of the LOSVDs from this work with literature data. Red circles show the results from long-slit observations of Richtler et al. (2011) at the position angle of 40 ◦ and centered on NGC 3311. Blue (green) circles show the results from this work (Hilker et al. 2017) extracted along the same position angle within a pseudo-slit of 20′′ (40′′) width. The dashed yellow line in the first and second panel indicates the cluster’s velocity and velocity dispersion according to Christlein & Zabludoff (2003). Positive (negative) radius indicate data points towards the southeast (northwest) direction from the center of the galaxy. |
| In the text | |
 |
Fig. 5 Map of the LOS velocity (V) for NGC 3311 for all bins with S/N > 10. The typical observational uncertainty for the LOS velocity is 6 km/s. |
| In the text | |
 |
Fig. 6 Parameters of the rotation model calculated with kinemetry to describe the MUSE velocity field for NGC 3311. From top to bottom, the panels describe the rotation velocity (Vrot), the kinematic position angle (PAkin) and minor-to-major axis ((b/a)kin), and the fifth-to-first harmonic weight of the model(k5/Vrot) as a function of the kinematic semi-major axis akin. The horizontal dashed line in the bottom panel indicates the maximum threshold value of 0.04 for early-type galaxies set by the atlas3D survey. If the cosine function is a good approximation for the 2D velocity field, the k5/Vrot measured values would lie below this line. |
| In the text | |
 |
Fig. 7 Same as Fig. 5 for the LOS velocity dispersion (σ) of NGC 3311. The typical observational uncertainty for the LOS velocity dispersion is 12 km/s. |
| In the text | |
 |
Fig. 8 Same as Fig. 5 for the skewness parameter (h3) of NGC 3311. The typical observational uncertainty for h4 is 0.02. |
| In the text | |
 |
Fig. 9 Same as Fig. 5 for the kurtosis parameter (h4) of NGC 3311. The typical observational uncertainty for h3 is 0.03. |
| In the text | |
 |
Fig. 10 Correlation between the Gauss-Hermite high-order moments h3 (left) and h4 (right) with V/σ. |
| In the text | |
 |
Fig. 11 Photometric model of the three main galaxies in the Hydra I cluster core in FORS1 V-band image. Left: observed V-band image calibrated with the zero-point from Arnaboldi et al. (2012). Center: galfitm model including the ten Sérsic components listed in Table 1, obtained with the non-parametric fitting method. Right: residual image (original minus model), normalized by the sigma image that contains the error and noise of the observations. |
| In the text | |
 |
Fig. 12 Surface brightness profile along the photometric major axis at PA = 55 ◦. Top: comparison of the V-band surface brightness (blue dots) with the best fit from galfitm (black solid line). Other solid lines indicate the surface brightness of the subcomponents indicated in Table 1 including A (orange), B (green), C (red), and D (purple). Bottom: residuals between the V-band surface brightness and the model. Positive (negative) radius indicates the distance from the center of NGC 3311 towards the southeast (northwest) direction. |
| In the text | |
 |
Fig. 13 ICL substructures observed in the residual map from the modeling of symmetric structures with galfitm. V-band contours are also shown for reference. Black squares represent the MUSE fields, and the colored polygons represent the three most evident substructures in this region. |
| In the text | |
 |
Fig. 14 Weights for the FMD model of NGC 3311 as a function of the radius within the MUSE fields. The four main components of NGC 3311, A, B, C, and D, are shown individually. The component A + B indicates the sum of the first two components, which are modeled as having the same kinematics. The component E−J indicates the cumulative contribution of all other photometric components that are not included in the kinematic modeling. |
| In the text | |
 |
Fig. 15 Comparison of observed kinematics and the finite mixture model in NGC 3311. Top panels: observed four moments of the LOSVD in a Gauss-Hermite expansion, including systemic velocity (V), velocity dispersion (σ), and two high-order moments for the skewness (h3) and kurtosis (h4) of the distribution. Middle panels: best fit for the finite mixture model according to parameters in Table 2 (see text for details). Bottom panels: residuals between the observed fields on top and the best fit models in the middle panels. |
| In the text | |
 |
Fig. 16 Comparison of the radial profiles of the four moments of the LOSVD observed along the semi-major axis at PA =40 ◦ within a pseudo-slit of 3′′ width. Large blue circles indicate the observed values while small orange circles indicate the results for the finite mixture model. Negative (positive) radius indicates data points at the NE (SW) from the center of NGC 3311. |
| In the text | |
 |
Fig. 17 Faber-Jackson relation for the subcomponents in NGC 3311 (orange squares) using the V-band photometric model and the velocity dispersion from the finite mixture model. Blue circles indicate the galaxies in the Carnegie-Irvine Galaxy Survey (Ho et al. 2011), while the green lines indicate the results from the SAURON survey (Falcón-Barroso et al. 2011b), including all galaxies (solid line) and slow rotators (dashed line) only. |
| In the text | |
 |
Fig. 18 Edge-on projection of the fundamental plane as a function of the effective radius. We use the fundamental plane equation (solid green lines) from the SAURON survey (Falcón-Barroso et al. 2011b), offset by a factor of 0.34 to match the observations from Kelson et al. ( 2000c, blue circles). The dashed green lines indicate the one standard deviation of the fundamental plane. The components of NGC 3311 identified in our analysis (orange squares) are labeled according to Table 2. |
| In the text | |
 |
Fig. A.1 Comparison of the LOSVD moments as a function of radius for the wavelength ranges defined according to the Lick indices in the observed field I. Solid lines display the running average of the measured values, and the shaded areas around the lines indicate the typical standard deviation from the mean. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


