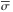| Issue |
A&A
Volume 609, January 2018
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 24 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201731442 | |
| Published online | 02 February 2018 | |
The CARMENES search for exoplanets around M dwarfs
First visual-channel radial-velocity measurements and orbital parameter updates of seven M-dwarf planetary systems⋆,⋆⋆
1 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
e-mail: trifonov@mpia.de
2 Institut für Astrophysik, Georg-August-Universität, Friedrich-Hund-Platz 1, 37077 Göttingen, Germany
3 Centro de Astrobiología (CSIC/INTA), Instituto Nacional de Técnica Aeroespacial, Ctra de Torrejón a Ajalvir, km 4, 28850 Torrejón de Ardoz, Madrid Spain
4 Thüringer Landessternwarte Tautenburg, Sternwarte 5, 07778 Tautenburg, Germany
5 Zentrum für Astronomie der Universtät Heidelberg, Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany
6 Instituto de Astrofísica de Andalucía (IAA-CSIC), Glorieta de la Astronomía s/n, 18008 Granada, Spain
7 Institut de Ciències de l’Espai (CSIC-IEEC), Campus UAB, c/ de Can Magrans s/n, 08193 Bellaterra, Barcelona, Spain
8 Departamento de Astrofísica y Ciencias de la Atmósfera, Facultad de Ciencias Físicas, Universidad Complutense de Madrid, 28040 Madrid, Spain
9 Instituto de Astrofśica de Canarias, Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain,
and Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna ; Spain
10 Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
11 Centro Astronómico Hispano-Alemán (CSIC-MPG), Observatorio Astronómico de Calar Alto, Sierra de los Filabres-04550 Gérgal, Almería, Spain
12 Leiden Observatory, Leiden University, Postbus 9513, 2300 RA, Leiden, The Netherlands
13 Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
14 School of Physics and Astronomy, Queen Mary, University of London, 327 Mile End Road, London E1 4NS, UK
15 Instituto Nacional de Astrofísica, Óptica y Electrónica, Luis Enrique Erro 1, Sta. Ma. Tonantzintla, Puebla, Mexico
16 FRACTAL SLNE. C/ Tulipán 2, P13-1A, 28231 Las Rozas de Madrid, Spain
17 Institut für Theoretische Physik und Astrophysik, Leibnizstraße 15, 24118 Kiel, Germany
18 Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
19 Dipartimento di Fisica, Unversità di Roma, “Tor Vergata”, via della Ricerca Scientifica, 1 – 00133 Roma, Italy
20 Weizmann Institute of Science, 234 Herzl Street, Rehovot 761001, Israel
21 University College Dublin, School of Physics, Belfield, Dublin 4, Ireland
22 European Southern Observatory, Alonso de Córdova 3107, Vitacura, Casilla 19001, Santiago de Chile, Chile
23 The University of Chicago, Edward H. Levi Hall, 5801 South Ellis Avenue, Chicago, Illinois 60637, USA
24 Universidad de Granada, Av. del Hospicio, s/n, 18010 Granada, Spain
25 QUCAM Astronomical Detectors, http://www.qucam.com/
26 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
27 Dpto. de Teoría de la Señal y Comunicaciones, Universidad Carlos III de Madrid, Escuela Politécnica Superior. Avda. de la Universidad, 30. 28911 Leganés, Madrid, Spain
28 Dpto de Física, Ingeniería de Sistemas y Teoría de la Señal, Escuela Politécnica Superior, Universidad de Alicante, Apdo. 99, 03080 Alicante, Spain
Received: 25 June 2017
Accepted: 20 September 2017
Context. The main goal of the CARMENES survey is to find Earth-mass planets around nearby M-dwarf stars. Seven M dwarfs included in the CARMENES sample had been observed before with HIRES and HARPS and either were reported to have one short period planetary companion (GJ 15 A, GJ 176, GJ 436, GJ 536 and GJ 1148) or are multiple planetary systems (GJ 581 and GJ 876).
Aims. We aim to report new precise optical radial velocity measurements for these planet hosts and test the overall capabilities of CARMENES.
Methods. We combined our CARMENES precise Doppler measurements with those available from HIRES and HARPS and derived new orbital parameters for the systems. Bona-fide single planet systems were fitted with a Keplerian model. The multiple planet systems were analyzed using a self-consistent dynamical model and their best fit orbits were tested for long-term stability.
Results. We confirm or provide supportive arguments for planets around all the investigated stars except for GJ 15 A, for which we find that the post-discovery HIRES data and our CARMENES data do not show a signal at 11.4 days. Although we cannot confirm the super-Earth planet GJ 15 Ab, we show evidence for a possible long-period (Pc = 7030-630+970 d) Saturn-mass (mcsini = 51.8-5.8+5.5M⊕) planet around GJ 15 A. In addition, based on our CARMENES and HIRES data we discover a second planet around GJ 1148, for which we estimate a period Pc = 532.6-2.5+4.1 days, eccentricity ec = 0.342-0.062+0.050 and minimum mass mcsini = 68.1-2.2+4.9M⊕.
Conclusions. The CARMENES optical radial velocities have similar precision and overall scatter when compared to the Doppler measurements conducted with HARPS and HIRES. We conclude that CARMENES is an instrument that is up to the challenge of discovering rocky planets around low-mass stars.
Key words: planetary systems / stars: late-type / stars: low-mass / planets and satellites: dynamical evolution and stability
Based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programmes 072.C-0488, 072.C-0513, 074.C-0012, 074.C-0364, 075.D-0614, 076.C-0878, 077.C-0364, 077.C-0530, 078.C-0044, 078.C-0833, 079.C-0681, 183.C-0437, 60.A-9036, 082.C-0718, 183.C-0972, 085.C-0019, 087.C-0831, 191.C-0873.
The appendix tables are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/609/A117
© ESO, 2018
1. Introduction
The quest for extrasolar planets around M dwarfs via precise Doppler measurements is almost two decades old (Marcy et al. 1998; Delfosse et al. 1998; Marcy et al. 2001; Endl et al. 2003; Kürster et al. 2003; Bonfils et al. 2005; Butler et al. 2006; Johnson et al. 2010). To date we are aware of at least 20 planet candidates orbiting nearby M-dwarf stars detected by the radial velocity (RV) method (Bonfils et al. 2013; Hosey et al. 2015), but the real number is likely to be much larger given the fact that the vast majority (70–80%) of the stars in the solar neighborhood are yet poorly explored M dwarfs. Indeed, the recent discoveries of planets in the habitable zone around Proxima Centauri (Anglada-Escudé et al. 2016) and LHS 1140 (Dittmann et al. 2017), and the multiple planet system around the ultra-cool M-dwarf star TRAPPIST-1 (Gillon et al. 2017) provide strong evidence for an enormous population of potentially habitable planets around red dwarfs.
List of CARMENES known exoplanet host stars studied in this paper with their physical characteristics.
M dwarfs are particularly suitable targets to detect temperate low-mass rocky planets primarily for two reasons: (1) the lower masses of M dwarfs compared to those of solar-like stars facilitate the detection of lower mass planets; (2) due to the low flux of M dwarfs, the habitable zone is located closer-in than that of hotter and more massive stars. As a result, planets in the habitable zone of M dwarfs have shorter periods, and thus higher Doppler signals than those orbiting in the habitable zones of more massive stars. However, their active nature can also cause certain observational difficulties. Starspots, plages, or activity cycles can lead to line profile variations, which can be easily mistaken as an RV signal due to an orbiting planet. In addition, non-negligible stochastic stellar jitter can have velocity levels of a few m s-1, making the detection of low-mass planets challenging. Therefore, persistent observations with state-of-the-art RV precision instruments such as HARPS (La Silla Observatory, Chile, Mayor et al. 2003), HARPS-N (Roque de Los Muchachos Observatory, La Palma, Spain, Cosentino et al. 2012), or HIRES (Keck Observatory, Hawaii, USA, Vogt et al. 1994) are needed to disentangle the planet signal from stellar activity. Alternatively, precise RV measurements simultaneously obtained in the optical and in the near-infrared (NIR) domains may provide more evidence in favor or against the planet hypothesis.
These issues and observational philosophy are addressed with the new CARMENES1 instrument and survey (Quirrenbach et al. 2014, 2016; Amado et al. 2013; Alonso-Floriano et al. 2015) using a high-resolution dual-channel (Visual: R = 94 600, NIR: R = 80 400) spectrograph installed at the 3.5 m telescope of the Calar Alto Observatory (Spain). CARMENES is designed to provide precise RV measurements in the optical and NIR wavelength regimes with a precision of 1–2 m s-1. The science program with CARMENES started on Jan 1, 2016 and its main goal is to probe ~300 close M-dwarf stars for the presence of exoplanets, in particular Earth-mass planets in the habitable zone.
In this paper, we present results from observations of single and multiple planetary systems around seven well-known M dwarfs based on precise Doppler measurements taken with the visual channel of CARMENES. While the performance of the NIR channel will be the subject of a future study, the RV precision achievable with the visual channel is compared with those achieved for the same stars with other state-of-the-art planet-hunting spectrographs working in the visible such as HARPS and HIRES. We use the combined RVs to confirm or refute the existence of the announced planets, look for new candidates, and refine the orbital parameters of the planets.
We organize this paper as follows: in Sect. 2, we introduce the seven known M-dwarf planet hosts, for which we obtain Doppler data with CARMENES. In Sect. 3 we discuss the available RV data for these stars and we present our RV analysis strategy. In Sect. 4, we present our results and we discuss each single and multiple planet system individually. In Sect. 5 we provide an overview of the CARMENES performance compared to HARPS and HIRES. Finally, in Sect. 6, we provide a summary of our results and our overall conclusions.
2. The planetary systems
2.1. Target selection
The CARMENES GTO targets were selected from the Carmencita catalog (Caballero et al. 2016a) based on their observability from Calar Alto (δ> −23°), spectral types (M0.0–9.5 V), J magnitude for spectral sub-type (mean magnitude 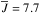 mag), and status as bona-fide single stars with no evidence for a stellar companion within 5′′. Given these selection criteria, several already known M-dwarf planetary systems were naturally included in the CARMENES sample. These systems are the (presumably) single planet systems: GJ 15 A (Howard et al. 2014), GJ 436 (Butler et al. 2004; Maness et al. 2007; Lanotte et al. 2014), GJ 176 (Endl et al. 2008; Forveille et al. 2009), GJ 536 (Suárez Mascareño et al. 2017a) and GJ 1148 (Haghighipour et al. 2010), and the multiple planet systems: GJ 581 (Bonfils et al. 2005; Udry et al. 2007; Mayor et al. 2009; Robertson et al. 2014), and GJ 876 (Marcy et al. 2001; Rivera et al. 2005, 2010).
mag), and status as bona-fide single stars with no evidence for a stellar companion within 5′′. Given these selection criteria, several already known M-dwarf planetary systems were naturally included in the CARMENES sample. These systems are the (presumably) single planet systems: GJ 15 A (Howard et al. 2014), GJ 436 (Butler et al. 2004; Maness et al. 2007; Lanotte et al. 2014), GJ 176 (Endl et al. 2008; Forveille et al. 2009), GJ 536 (Suárez Mascareño et al. 2017a) and GJ 1148 (Haghighipour et al. 2010), and the multiple planet systems: GJ 581 (Bonfils et al. 2005; Udry et al. 2007; Mayor et al. 2009; Robertson et al. 2014), and GJ 876 (Marcy et al. 2001; Rivera et al. 2005, 2010).
 |
Fig. 1 GLS periodograms of the Hα index obtained from CARMENES spectra for the seven known planetary hosts. Horizontal lines show the bootstrapped FAP levels of 10% (dotted line), 1% (dot-dashed line) and 0.1% (dashed line), while red vertical lines indicate the stellar rotational periods listed in Table 1. The Hα index analysis do not yield significant peaks at the known planet periods for these stars. For GJ 15 A we identify several formally significant peaks between 40 and 100 days. For GJ 176 and GJ 536 the Hα index peaks near the rotational periods of these two stars. |
There are actually several more M dwarfs with known planets in our sample, for example, GJ 179 (Howard et al. 2010), GJ 625 (Suárez Mascareño et al. 2017b), GJ 628 (Wright et al. 2016; Astudillo-Defru et al. 2017), GJ 649 (Johnson et al. 2010) and GJ 849 (Butler et al. 2006). However, these stars either have planetary companions with very long orbital periods exceeding the current temporal baseline of the survey, or we have not yet collected a sufficient number of CARMENES data to adequately constrain their planetary architectures. Therefore, we have chosen not to include these stars in this paper.
The seven selected stars are listed in Table 1, sorted by their Carmencita identifier Karmn, followed by their Gliese-Jahreiß (GJ, Gliese & Jahreiß 1991) catalog number, as well as by observational parameters, such as spectral type, distance, Ks magnitude and the estimated rotational period Prot. The M-dwarf mass estimates were derived using a combined polynomial fit of the Ks-band mass–luminosity relationships of Delfosse et al. (2000) and Benedict et al. (2016), and thus represent an update with respect to the literature mass estimates. These seven stars are typical red dwarfs with spectral types M1.0–4.0 V and with masses in the range 0.32–0.53 M⊙. Their relatively long stellar rotation periods, Prot, and their the Hα index activity indicator as defined in Kürster et al. (2003) suggest that these particular stars should not be strongly affected by stellar magnetic activity. In Fig. 1 we show Generalized Lomb-Scargle (GLS; Zechmeister & Kürster 2009) power spectrum2 periodograms of the Hα index activity indicator for the seven stars, obtained from the CARMENES spectra. Our preliminary results of the Hα index measurements show that the periodograms of GJ 176 and GJ 536 have strong peaks near their stellar rotational periods, while for GJ 15 A we find a forest of strong peaks between 40 and 100 days, likely induced by activity. For the remaining four targets, we do not find significant periodic signals at the known stellar rotational periods or the known planetary periods. These stars have been already extensively studied for more activity indicators to ensure robust planet detection (e.g., Queloz et al. 2001; Boisse et al. 2011; Robertson et al. 2014; Suárez Mascareño et al. 2015; Hatzes 2016; Suárez Mascareño et al. 2017c).
Number of literature, archival and CARMENES Doppler measurements for the M-dwarf planet hosts and the number of planets assumed in this paper.
The relative proximity of these M dwarfs ( = 7.9 ± 3.0 pc; Caballero et al. 2016a) results in high proper motions and, hence, in a notable secular acceleration (SA) of the RV (Kürster et al. 2003). The SA is a positive, usually very small, RV drift, but it can accumulate considerably as the baseline of the Doppler observations increases. Therefore, in Table 1 we provide the SA estimates, which were calculated following Zechmeister et al. (2009) from the stars proper motions (μαcosδ, μδ) and parallaxes (π) taken from the Tycho-Gaia Astrometric Solution (TGAS) catalogue of the Gaia DR1 release (Lindegren et al. 2016; Gaia Collaboration 2016a,b).
= 7.9 ± 3.0 pc; Caballero et al. 2016a) results in high proper motions and, hence, in a notable secular acceleration (SA) of the RV (Kürster et al. 2003). The SA is a positive, usually very small, RV drift, but it can accumulate considerably as the baseline of the Doppler observations increases. Therefore, in Table 1 we provide the SA estimates, which were calculated following Zechmeister et al. (2009) from the stars proper motions (μαcosδ, μδ) and parallaxes (π) taken from the Tycho-Gaia Astrometric Solution (TGAS) catalogue of the Gaia DR1 release (Lindegren et al. 2016; Gaia Collaboration 2016a,b).
The results of this work are derived from CARMENES observations of these planetary hosts between January 2016 and April 2017. Most of the planets in these systems were discovered or confirmed as part of high-precision Doppler programs for M-dwarf planets either with HARPS (Bonfils et al. 2005) or with HIRES (Howard et al. 2009). Therefore, these stars have excellent pre-existing RV data, which we use as a benchmark to study the overall precision of our visual CARMENES velocities.
2.2. Literature overview
GJ 15 A:
Using 117 HIRES RVs of GJ 15 A taken between 1997 and 2011, Howard et al. (2014) detected several distinct periodic signals in the Doppler time series. The strongest periodogram peak was reported at 11.44 d followed by a large number of significant peaks in the range of 30 to 120 d, the strongest of which at ~44.0 d. Howard et al. (2014) concluded that the 44.0 day Doppler signal and its neighboring peaks were artifacts of rotating spots induced by stellar activity, since similar periodic variability was also detected in their optical photometry and in the Ca ii H&K lines. The strong ~11.44 day period signal, however, could not be associated with activity and thus suggested a planetary interpretation. The best Keplerian fit with 11.44 day periodicity was found to be consistent with a low-mass planet (msini = 5.35 M⊕) having a nearly circular orbit.
GJ 176:
A Neptune mass (msini = 24.5 M⊕) planet with a period of 10.24 days around GJ 176 was initially proposed by Endl et al. (2008) based on 28 RV measurements taken with the High-Resolution Spectrograph (HRS; Tull 1998) at the Hobby-Eberly Telescope (HET). However, soon after the discovery, the existence of the planet was questioned by Butler et al. (2009), who failed to detect the planet in their 41 HIRES RVs taken between 1998 and 2008. Butler et al. (2009) argued that the higher precision of HIRES when compared to HET-HRS should have been advantageous in recovering the planetary signal, but instead they found an RV scatter of about ~4 m s-1, mostly consistent with the estimated jitter for GJ 176 combined with the instrumental noise. Forveille et al. (2009) presented independent observations with HARPS, which confirmed a planet around GJ 176, but in an 8.8-day orbit and with a lower RV semi-amplitude consistent with a super-Earth planet with a minimum mass of msini = 8.4 M⊕.
GJ 1148:
The moderately eccentric planet GJ 1148 b (eb = 0.31) was discovered based on 37 velocities taken with HIRES (Haghighipour et al. 2010). The RV signal is consistent with a planetary period of ~41.4 days and a semi-amplitude K = 34 m s-1, corresponding to msini = 89 M⊕ (0.28 MJup). The RV data for GJ 1148 are also compatible with a linear trend of ~2.47 m s-1 yr-1, suggesting a possible long-period companion to the system. Additionally, Haghighipour et al. (2010) performed extensive photometric observations of GJ 1148 and found a significant 98.1-day periodicity that most likely arises from spots on the rotating star. Butler et al. (2017) have published an extended HIRES data set for GJ 1148, which seems to show an additional signal in the one-planet fit residuals with a periodicity of ~530 days. Butler et al. (2017) have classified this signal as a planetary candidate, but they neither provide an orbital solution for the possible second planet, nor have they updated the orbital solution for GJ 1148 b.
GJ 436:
This star has a very well studied planet first discovered by Butler et al. (2004) using HIRES data. GJ 436 b has a period of only Pb = 2.64 days, a minimum mass of mbsini = 23 M⊕ and an eccentricity of eb = 0.15. Later, Gillon et al. (2007) found that GJ 436 b is a transiting planet with an estimated radius and mass comparable to that of Neptune and Uranus. It was suggested that GJ 436 has additional planets. A long-period planet was suspected to gravitationally perturb GJ 436 b, thus leading to the planet’s surprising non-zero eccentricity (Maness et al. 2007), or a lower mass Super-Earth planet suspected to be orbiting at a period of 5.2 days in a possible 2:1 Laplace mean-motion resonance (MMR; Ribas et al. 2008), but such claims have not been confirmed. Finally, by studying 171 precise HARPS velocities and Spitzer data, Lanotte et al. (2014) concluded that present data support the presence of only a single planet around the host star.
GJ 536:
Suárez Mascareño et al. (2017a) reported the discovery of a super-Earth like planet orbiting GJ 536 by analyzing 158 HARPS and 12 HARPS-N RV measurements. According to them, GJ 536 b has an orbital period of 8.7076 ± 0.0025 d and a minimum mass of msini = 5.36 ± 0.69 M⊕. In addition to the planetary signal, a strong ~43-d period is evident, but it was attributed to stellar rotation after analyzing the time series of the Ca ii H&K and Hα activity indicators.
GJ 581:
This star has one of the most debated multiple planetary systems when it comes to the number of detected planets. The first planet GJ 581 b, was discovered by Bonfils et al. (2005) followed by Udry et al. (2007), who increased the planet count to three by discovering GJ 581 c and d. The planetary system suggested by Udry et al. (2007) consists of three planets with orbital periods of Pb,c,d ≈ 5.4, 12.9 and 83.6 d and minimum masses of mb,c,dsini ≈ 15.7, 5.0 and 7.7 M⊕, respectively. Later, Mayor et al. (2009) revised the period of GJ 581 d to 66.8 d and discovered an additional 1.7-M⊕ mass planet at 3.15 days named GJ 581 e. A simultaneous analysis of the HIRES and HARPS data for GJ 581 led Vogt et al. (2010) to increase the planet count to six by introducing GJ 581 f and g with Pf,g ≈ 433 and 37 d, suggesting a very compact system where all six planets must have near-circular orbits. Since Vogt et al. (2010), a number of independent studies have disputed some of these discoveries. Forveille et al. (2011) and Tuomi (2011) strongly supported only four planetary companions, arguing against GJ 581 f and g. Baluev (2013) suggested that the impact of red noise on precise Doppler planet searches might lead to false positive detections and, therefore, even GJ 581 d might not be real. Robertson et al. (2014) corrected the available Doppler data for activity and also suggested that the signal of GJ 581 d might be an artifact of stellar activity. Finally, Hatzes (2016) showed an anti-correlation of the 66.8 d period with the Hα equivalent width to confirm that the signal of GJ 581 d is intrinsic to the star. To our knowledge, the currently confirmed planets orbiting the GJ 581 system are three (b, c, e), and in our analysis we will assume this number.
GJ 876:
This star has another well-studied planetary system, currently known to host four planets, three of which are likely in 1:2:4 MMR. The first planet GJ 876 b was independently discovered by Marcy et al. (1998) and Delfosse et al. (1998). The planet was reported to have a period of ~61 days and a minimum mass of msini≈ 860 M⊕, which was the first discovery of a Jovian-mass planet around an M-dwarf star. However, after continued monitoring of this star using HIRES, Marcy et al. (2001) provided strong evidence for a second planet with a minimum mass of msini≈ 250 M⊕ and a period of ~30 days. Marcy et al. (2001) also showed that the planets interact so strongly that a double Keplerian fit is not a valid model. Instead, a three body Newtonian dynamical model is necessary to fit the data, showing that GJ 876 b and GJ 876 c are in a strong 2:1 MMR. After the discovery of GJ 876 c, a super-Earth planet with a short period of only 1.94 d was proposed by Rivera et al. (2005). A dynamical model including a third planet yielded a significant improvement over the two-planet model, suggesting that the innermost planet is real and designated as GJ 876 d. A fourth ~124 day planet named GJ 876 e was proposed by Rivera et al. (2010) because of an additional strong periodicity seen in the three-planet dynamical model. We consider four confirmed planets orbiting GJ 876.
3. Observations and data
3.1. CARMENES data
The two CARMENES spectrographs are grism cross-dispersed, white pupil, échelle spectrograph working in quasi-Littrow mode using a two-beam, two-slice image slicer. The visible spectrograph covers the wavelength range from 0.52 μm to 1.05 μm with 61 orders, a resolving power of R = 94 600, and a mean sampling of 2.8 pixels per resolution element. However, in the standard configuration. Since the dichroic beam splitter in the front end splits the wavelength range around 0.97 μm and because of low sensitivity and flux levels at the blue end of the spectrum effectively only 42 orders from 0.52 μm to 0.97 μm yield useful data in the visible channel. The spectrograph accepts light from two fibers; the first fiber carries the light from the target star, while the second fiber can either be used for simultaneous wavelength calibration or for monitoring the sky. The former configuration was used for all observations presented in this paper. The spectrograph is housed in a vacuum vessel and operated at room temperature. The detector is a back-side illuminated 4112 × 4096 pixel CCD. The CARMENES instrument is described in more detail in Quirrenbach et al. (2016) and in the references therein.
Standard processing of raw CARMENES spectra, such as bias, flat, and cosmic ray correction are automatically performed using the CARACAL (CARMENES Reduction And Calibration, Caballero et al. 2016b) pipeline. The extraction of the spectra is based on flat-relative optimal extraction (FOX; e.g., Zechmeister et al. 2014) and wavelengths are calibrated with algorithms described in Bauer et al. (2015). The precise radial velocities are derived using our custom SERVAL (SpEctrum Radial Velocity AnaLyser, Zechmeister et al. 2018) pipeline, which employs a χ2 fitting algorithm with one of the fit parameters being the RV. The observations are modeled with a template that is established from the observations following a suitable shifting and co-adding approach. Anglada-Escudé & Butler (2012) demonstrated that, in the case of M-dwarf stars, this method can provide higher RV precision than the method of cross-correlation with a weighted binary mask employed in the standard ESO HARPS pipeline.
The data presented in this paper were taken during the early phase of operation of the CARMENES visible-light spectrograph. During this time we identified a number of instrumental effects and calibration issues affecting the data on the m s-1 level. Therefore, taking advantage of the survey-mode observations, we calculated for each GTO night an instrumental nightly zero-point (NZP) of the RVs by using all the stars with small RV variability (RV-quiet stars) observed in that night. The sample of RV-quiet stars was defined as the sub-sample of CARMENES-GTO stars with RV standard deviation < 10 m s-1. We then corrected each RV for its NZP and propagated the NZP error.
After 16 months of observations, the sample of RV-quiet stars includes ~ 200 stars of which 10–20 are observed in a typical night. Prior to the NZP calculation, we corrected each star’s RVs for their own error-weighted average, replaced repeated exposures of a star in a given night by their median, and removed 4σ outliers. The NZP was then taken as the weighted-average RV of the observed RV-quiet stars. The NZP error was derived either from their RV uncertainties or from their RV standard deviation–whichever gave a larger value.
The median NZP uncertainty was found to be ≲ 1 m s-1, while their scatter is ~ 2.5 m s-1. Only a few extreme NZPs were found to be as high as ~ 10 m s-1. For the seven planetary systems investigated here, we found the NZP-corrected RVs to improve the rms velocity dispersion around the best fit models by ~ 25% on average so we used them in our combined modeling with other-instrument’s RVs. We expect that a fuller understanding of the instrument will in the near future enable us to improve the calibration to the point where it is better than the present NZP correction scheme. Examples for the improvement of the rms of the time series of three stars due to the NZP correction are shown in Fig. A.1, while Fig. A.2 provides a comparison of the pre-NZP and post-NZP correction for a larger sample of stars. All CARMENES Doppler measurements and their individual formal uncertainties used for our analysis in this paper are available at the CDS (Tables A.1–A.7).
3.2. Literature and archival data used in this paper
Table 2 provides the total number of available RVs for the seven M-dwarf planet hosts that we use for our analysis. RV data obtained with the HARPS and the HIRES spectrographs that have been in operation for much more than a decade dominate over the RV data taken with the more recent instruments HARPS-N (only for GJ 536) and our ongoing CARMENES survey. GJ 15 A and GJ 1148 have not been observed with HARPS since they are northern targets inaccessible from La Silla. For the rest, we used HARPS spectra from the ESO archive, which we re-processed with our SERVAL pipeline for better precision and consistency. All HIRES data for our selected targets were taken from Butler et al. (2017), who released a large database of RV data collected over the past twenty years with HIRES.
 |
Fig. 2 Panel a: GLS periodogram of the available Doppler data for GJ 176, with horizontal lines showing the bootstrapped FAP levels of 10% (dotted line), 1% (dot-dashed line) and 0.1% (dashed line). Two distinct peaks above the FAP = 0.1% level can be seen at 8.77 d and 39.34 d attributed to a planetary companion and stellar activity, respectively. Panel b: data from CARMENES (red circles), HARPS (blue triangles) and HIRES (green diamonds) phase-folded to our best Keplerian fit consistent with an 8.77 d planet. Panel c: GLS periodogram of the residuals after fitting the 8.77 d signal, revealing a 39.34 d activity peak. |
Both HIRES and HARPS had a major optical upgrade since they were commissioned. HIRES was upgraded with a new CCD in August 2004, while HARPS received new optical fibers in May 2015 (Lo Curto et al. 2015). These upgrades aimed to improve the instrument’s performance, but might also have introduced an RV offset between data taken before and after the upgrades. Further studies did not find a significant RV offset in HIRES (Butler et al. 2017), and in HARPS the offset is also close to zero in the case of M-stars (Lo Curto et al. 2015). Therefore, we did not fit additional RV offsets between the pre- and post-upgrade HIRES and HARPS data in our analysis.
We modeled all available literature and archive RVs together with our CARMENES precise Doppler data. In our analysis we used the individual RV data sets as they were, without removing outliers or binning RVs into one measurement, unless we find obviously wrong RV data (strong outliers over 10σ) or heavy clustering of data with more than 5 RVs taken consecutively. We did not add stellar jitter quadratically to the RV error budget, nor did we model the RV jitter variance of the data simultaneously with our orbital parameter optimization (e.g., Baluev 2009). All data sets were weighted by their nominal formal errors. The main reason for analyzing the RVs in this way is simply because we know little about the stochastic stellar noise and active region evolution in M dwarfs, their true orbital architecture (i.e., additional planets in the system and their mutual inclinations), or any instrumental low-amplitude systematics that might exist in CARMENES, HARPS and HIRES. Thus, any unknown source of noise around our best-fitting model is accounted as a radial-velocity scatter (weighted rms) that we aim to study.
3.3. RV modeling
As a first step in our Doppler time series analysis we employed the GLS periodogram to look for significant periodic signals that might be induced either by known planetary companions, previously undiscovered planetary companions, or stellar activity. The false-alarm probability (FAP) levels of 10%, 1% and 0.1% were calculated by bootstrap randomization creating 1000 randomly reordered copies of the RV data and tested against the GLS algorithm.
To model the orbital parameters, we applied the Levenberg-Marquardt (L-M) based χ2 minimization technique coupled with two models. For bona fide single-planet systems we used a Keplerian model, while the known multiple planet systems were fitted with a self-consistent N-body model based on the Gragg-Bulirsch-Stoer integration method (Press et al. 1992). The N-body modeling scheme was fully described for the HD 82943 2:1 MMR system (Tan et al. 2013) and it was successfully applied to other multiple planet systems such as HD 73526 (Wittenmyer et al. 2014) and η Ceti (Trifonov et al. 2014).
For both models the fitted parameters are the spectroscopic elements: radial velocity semi-amplitude K, orbital period P, eccentricity e, longitude of periastron ϖ, mean anomaly M and the velocity offset γ for each data set included in the analysis; they are valid for the first observational epoch T0. For the N-body model we obtain the parameters in Jacobi coordinates (e.g., Lee & Peale 2003), which is a natural frame for analyzing an RV signal in multiple planet systems. A final output from our models are also the best-fit reduced χ2 (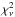 ) and the individual data sets weighted rms statistics, while the best-fit parameter uncertainties are determined by drawing 5000 model-independent synthetic bootstrap samples from the available data (e.g., Press et al. 1992). Each of the combined 5000 bootstrapped data sets is consecutively fitted with the corresponding Keplerian or N-body model, and from the resulting parameter distribution we obtain the 1-σ asymmetric uncertainties.
) and the individual data sets weighted rms statistics, while the best-fit parameter uncertainties are determined by drawing 5000 model-independent synthetic bootstrap samples from the available data (e.g., Press et al. 1992). Each of the combined 5000 bootstrapped data sets is consecutively fitted with the corresponding Keplerian or N-body model, and from the resulting parameter distribution we obtain the 1-σ asymmetric uncertainties.
The best dynamical models are further tested for long-term dynamical stability using the SyMBA symplectic integrator (Duncan et al. 1998), modified to work with Jacobi input elements. We chose a maximum of 10 Myr of integration time, which we believe is adequate to test the long-term stability of our fits. The time step we chose is 1% of the period of the respective innermost planet, thus allowing for precise orbital integrations. We consider a best-fit orbit as unstable if at any given time of the orbital evolution the planetary semi-major axes deviate by more than 10% from their initial values, or if eccentricities reach large values leading to crossing orbits.
 |
Fig. 3 Same as Fig. 2, but for GJ 436. Panels a and b show that the CARMENES, HARPS and HIRES data sets used for the construction of the best fit are fully consistent with a planetary companion with a period of 2.64 d. In panel a: the 1.60 d GLS peak is a 1-day alias of the 2.64 d periodicity induced by the planetary companion. Panel c: shows the GLS periodogram of the best fit residuals, which yields several peaks above the FAP = 0.1%, most likely due to the observational window, stellar activity and their aliases. |
4. Results
4.1. The single planet systems
4.1.1. GJ 176
For GJ 176 we collected 23 precise CARMENES RVs between January 2016 and January 2017. Together with the 111 literature HIRES data and the 71 HARPS RV data points, a total data set of 205 precise RV measurements is obtained that leads to a Keplerian signal with the following orbital parameters: a planetary period Pb = 8.776 d, orbital eccentricity eb = 0.148, and semi-amplitude Kb = 4.49 m s-1, corresponding to a planet with a minimum mass of mbsini ~ 9.1 M⊕ and semi-major axis of ab = 0.066 au. The updated best-fit orbital parameters for GJ 176 b and their bootstrap uncertainties and statistics can be found in Table 3.
Figure 2, panel a shows the GLS power spectrum of the combined data, which reveals the significant planetary signal at 8.77 d. In panel b of Fig. 2, we show the combined data together with the Keplerian model phase-folded with the planetary period, while panel c shows a GLS periodogram of the one-planet model residuals revealing a significant signal at 39.34 d (seen also in panel a). Forveille et al. (2009) attributed the ~40 d RV signal to stellar activity, since it agrees well with the ~40 d periodicity found in their HARPS H+K and Hα activity indices, and the stellar rotation period of GJ 176 (see Table 1 and Kiraga & Stepien 2007; Suárez Mascareño et al. 2017c). The activity nature of the 40 d period was further confirmed by Robertson et al. (2015), who noted that the HIRES and the HARPS data can reveal independently the 8.77 d planetary signal, but the ~ 40 d RV signal is supported only by the HARPS RVs. We confirm these findings. By examining our one-planet fit residuals for each data set, we find that the ~40 d period is seen only in the HARPS RVs, but not in the HIRES nor in the CARMENES data. Robertson et al. (2015) suggested that this peculiar absence of the 40 d period in the HIRES data is likely a result of the higher resolving power of HARPS (and as we think, also due to the bluer spectral region), which makes it more sensitive to line profile variations induced by rotational modulation of stellar spots. Furthermore, complementary to Forveille et al. (2009), our CARMENES Hα-index measurements also suggest a strong peak at a period of 39.70 d (see Fig. 1) leading to the conclusion that the most likely reason for the 39.34 d signal in the HARPS residuals is indeed stellar activity.
From Fig. 2, our CARMENES measurements follow well the best fit model GJ 176 b. Indeed, the CARMENES velocity scatter around the best fit is the lowest among the data sets included to construct the fit with a scatter of rmsCARMENES = 2.95 m s-1, followed by HARPS with rmsHARPS = 4.16 m s-1 and HIRES with rmsHIRES = 4.81 m s-1. The overall weighted rms scatter around the best fit is rms = 4.33 m s-1, which is slightly smaller than the planetary signal. As discussed above, a possible reason for this somewhat large rms seen in GJ 176 is the additional ~40-d periodic stellar activity seen in the HARPS RVs, which we consider as part of the rms scatter.
Although our CARMENES dataset is too small for an independent detection of GJ 176 b, the strongest GLS peak of the CARMENES data exceeds the 10% FAP level at the expected planetary period. A GLS test as a function of the number of data points shows that sequentially adding CARMENES data monotonously decreases the FAP of the planetary signal. This is an indication that CARMENES RVs contain the planetary signal. Additionally, a flat model with variable RV zero offset applied to the CARMENES data has rms = 3.80 m s-1, while a fit to the combined one-planet Keplerian fit leads to rms = 2.95 m s-1, showing an improvement (although insignificant according to an F-test3) when assuming a planet in an 8.77 d orbit. We conclude that the CARMENES data acquired so far support the existence of the 8.77 day planet.
 |
Fig. 4 Same as Figs. 2 and 3, but for GJ 536. Panel a: GLS periodogram of the combined data for GJ 536. The significant periods are at 8.71 d (induced by GJ 536 b) and at 43.78 d, respectively, the latter likely due to the stellar rotational period (Prot≈ 43.3 d). The CARMENES, HARPS, HIRES and HARPS-N (magenta triangles) RV data for GJ 536, and the phase folded best Keplerian fit are shown in panel b. Panel c: GLS periodogram of the best fit residuals, revealing only the 43.75 d activity peak. |
4.1.2. GJ 436
The 113 CARMENES RVs confirm GJ 436 b, showing full consistency with the 356 HIRES RVs from Butler et al. (2017) and the 169 HARPS RV measurements. Our updated Keplerian parameters of GJ 436 b, based on the modeling of all 638 Doppler measurements has 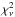 = 3.47, overall rms = 3.27 m s-1, leading to a planet semi-amplitude Kb = 17.38 m s-1, period of Pb = 2.644 days, and eccentricity eb = 0.152. Our orbital period determination for GJ 436 b is consistent with the most precise transit time series photometry values of Pb = 2.64388 ± 0.00006 days performed with the Hubble Space Telescope (Bean et al. 2008). These parameters and the inclination constraints from the transit (ib = 85.80
= 3.47, overall rms = 3.27 m s-1, leading to a planet semi-amplitude Kb = 17.38 m s-1, period of Pb = 2.644 days, and eccentricity eb = 0.152. Our orbital period determination for GJ 436 b is consistent with the most precise transit time series photometry values of Pb = 2.64388 ± 0.00006 days performed with the Hubble Space Telescope (Bean et al. 2008). These parameters and the inclination constraints from the transit (ib = 85.80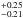 ) yield a planetary dynamical mass of mb = 21.4
) yield a planetary dynamical mass of mb = 21.4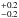 M⊕ and semi-major axis of ab = 0.028
M⊕ and semi-major axis of ab = 0.028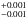 au. Detailed orbital parameters from our fit and their asymmetric bootstrap uncertainties are listed in Table 3.
au. Detailed orbital parameters from our fit and their asymmetric bootstrap uncertainties are listed in Table 3.
In Fig. 3 panel a, we show the GLS periodogram for the merged RV data, which reveals a very strong peak at 2.644 d and its one-day alias at ~1.6 d, while in panel b in Fig. 3 we show our best-fit Keplerian model together with the data phase-folded to the 2.644 day period of the planet. We also inspected the GJ 436 residuals after removing the Doppler contribution from the planet with a GLS periodogram. The right panel of Fig. 3 illustrates many peaks above the 0.1% FAP level, the most significant of them with a period of 23.7 d followed by peaks at 53.2 d, 186.5 d, 11.6 d and others. We find that all three data sets on their own contain many significant GLS peaks in their residuals, which do not mutually agree. For example, all three data sets show a forest of residual periods in the range 42−50 d, but with no clear match between the sets. The 23.7 d peak is seen in CARMENES and HARPS, but not seen in HIRES, which conversely presents the 11.6 d peak. Therefore, we do not associate any of these peaks with the signature of additional companions. They could be due to stellar activity, or potentially be related to the window function of the observations and its aliases.
Our best-fit orbital estimates for GJ 436 are within the uncertainties from the literature, but due to the large number of data from three independent high-precision instruments, they possibly represent the most accurate planetary orbit. We also quantify the CARMENES precision from the scatter around the orbital solution: for GJ 436 our data has a weighted rmsCARMENES = 2.56 m s-1, which is smaller than that of the Butler et al. (2017) data with rmsHIRES = 4.37 m s-1, but slightly higher than the one from HARPS with rmsHARPS = 2.28 m s-1.
Best fit Keplerian parameters for the single planet systems GJ 176, GJ 436 and GJ 536 based on the combined CARMENES and literature RVs.
It is worth noting that three of our CARMENES RVs were obtained during transit (JD = 2 457 490.475, 2 457 511.606 and 2 457 511.617). Similar to the HARPS transit time observations presented in Lanotte et al. (2014), however, we did not detect any excursion potentially related to the Rossiter-McLaughlin effect on GJ 436 due to the expected low amplitude of <1 m s-1.
4.1.3. GJ 536
In our initial CARMENES scheduling program, GJ 536 was assigned moderate priority, and thus visited only nine times between January and June 2016, when the star was observable from Calar Alto. After the planet announcement by Suárez Mascareño et al. (2017a), we secured 19 more Doppler measurements between January and February 2017 in an attempt to cover as much of the planetary orbit as possible. Currently, our 28 CARMENES RVs by themselves do not show any significant GLS peaks, and only sparsely cover one full orbital phase when compared to the HARPS and the literature velocities (Suárez Mascareño et al. 2017a; Butler et al. 2017), which recover well the planetary signal. We aim, however, at studying the individual performance of CARMENES for GJ 536 and check the agreement with the planet signal.
The periodogram power spectrum of the combined HARPS, HARPS-N, HIRES and CARMENES data for GJ 536 in panel a of Fig. 4. A significant peak at P = 8.71 days, is presumably induced by the planet, and another one at 43.78 d, likely by activity, since it is near the stellar rotational period Prot≈ 43.3 d (Suárez Mascareño et al. 2017a). Similar to the case of GJ 176, the ~44 d peak is only seen by HARPS, which seems to be more sensitive to activity induced RV signals than HIRES and CARMENES. Our updated Keplerian orbital parameters for GJ 536 b and statistics are listed in Table 3, while panel b of Fig. 4 illustrates the phase folded best-fit Keplerian model and data. Panel c of Fig. 4 shows that the best-fit residuals yield a significant activity peak at 43.75 d. For GJ 536 b we determine an orbital period of Pb = 8.708 days, an eccentricity of eb = 0.119, and a semi-amplitude of Kb = 3.12 m s-1 implying a super-Earth planet with a minimum mass of mbsini ≈ 6.5 M⊕ and a semi-major axis of ab = 0.067 au. This fit has an overall scatter rms = 2.91 m s-1, which is of the same order as the planetary signal. Our RV data have a scatter around the best fit of rmsCARMENES = 3.08 m s-1, which is lower than the one from HIRES with rmsHIRES = 3.66 m s-1, but higher than HARPS and HARPS-N with rmsHARPS = 2.72 m s-1 and rmsHARPS-N = 2.17 m s-1. The larger rmsHIRES may be the reason why our estimated value of the minimum mass of the planet GJ 536 b is a bit larger than that in Suárez Mascareño et al. (2017a).
We fit a flat model with variable RV zero offset applied only to the CARMENES data alone and we find rmsCARMENES = 3.44 m s-1. An F-test shows that the improvement achieved by the one-planet model for our 28 RVs (rmsCARMENES = 3.08 m s-1) is still insignificant. However, the 8.71-d periodogram peak increases its power and significance when we combine the HIRES and the CARMENES data, meaning that all data sets seem to contain the same signal. Similar to the case of GJ 176, even though we cannot independently confirm the planet around GJ 536, the CARMENES data support the presence of a planetary companion and follow the overall planet signature.
 |
Fig. 5 GJ 1148 Doppler data obtained with HIRES (green diamonds) and CARMENES (red circles) show two distinct periodic signals consistent with two eccentric Saturn mass planets with orbital periods of 41 d and 526 d. Panels a and b show the GLS signal of the dominant planet GJ 1148 b and its single planet Keplerian model phase folded at the best-fit period, respectively. Panels c–e show the GLS analysis of the HIRES, CARMENES and the combined data residuals after subtracting the signal from GJ 1148 b shown in panel b. Both data sets reveal the existence of a second planet candidate with a period near 530 d. Panel f: shows the RV signal of the second planet as determined from the simultaneous two-planet fit, while panels g and h show the individual Doppler signals of GJ 1148 b and GJ 1148 c, respectively, phase folded at their best-fit periods. |
 |
Fig. 6 Panel a: available Doppler measurements for GJ 1148 obtained with HIRES (green diamonds) and CARMENES (red circles) fitted with a two-planet N-body model. Panel b: zoom of the CARMENES time series together with the same model. Panel c: no significant signal is left in the residuals of the two-planet dynamical model. A peak at 62.9 d presents an interesting possibility for a third lower-mass planetary companion that might be locked in a 3:2 MMR with GJ 1148 b, but currently this peak is still below the 1% FAP level. Panel d: results from a stability analysis of the GJ 1148 system composed of planets b and c. This two-planet fit is stable for at least 10 Myr, but for illustrative purposes we plot only a 200 000 yr extent of the orbital evolution of the planetary semi-major axes and eccentricities for the best two-planet dynamical fit. In this configuration the two planets exhibit large secular oscillations of eb and ec with a secular period of ~80 000 years. |
4.2. The multiple planet systems
4.2.1. GJ 1148
In Sect. 2 this target was introduced as a known single-planet host harboring a ~41-d Saturn-mass planet designated as GJ 1148 b (Haghighipour et al. 2010) and a possible second planetary companion with a period of ~530 d (Butler et al. 2017). In this section, we confirm the existence of a second eccentric Saturn-mass planet, hereafter GJ 1148 c, with a period of Pc = 532.6 d, making GJ 1148 a multiple planet system. For the first time, we present its full two-planet orbital configuration. The GJ 1148 c planet discovery is based on the combined 125 literature HIRES RVs presented in Butler et al. (2017) and the additional 52 precise Doppler measurements that we secured with CARMENES. Both data sets independently contain the GJ 1148 b and GJ 1148 c planetary signals, and thus further strengthen the two-planet hypothesis.
We now introduce the RV analysis sequence leading to the detection of GJ 1148 c. In Fig. 5, panel a we show the GLS power spectrum for the available Doppler data, which reveals a strong peak at 41.4 d, attributed to the presence of GJ 1148 b. A single-planet Keplerian model to the combined HIRES and CARMENES data suggests a planetary period of Pb = 41.4 days, a moderately large eccentricity of eb = 0.392, and a semi-amplitude Kb = 37.0 m s-1 from which we derive a minimum mass of mbsini = 92.8 M⊕ and a semi-major axis of ab = 0.166 au. More detailed one planet best-fit parameters and their uncertainties are shown in Table 4, while the phase-folded single-planet fit is shown in Fig. 5, panel b.
Similar to the GJ 1148 best-fit presented in Haghighipour et al. (2010) our one-planet fit has a large overall scatter of rms = 7.05 m s-1, leading to a poor 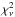 = 11.05. Based on the 37 HIRES discovery RVs, Haghighipour et al. (2010) found that including a linear trend of 2.465 ± 1.205 m s-1 yr-1 led to a better fit, reducing the rms from 9.23 m s-1 to 8.06 m s-1. However, introducing a linear trend in our combined data set of HIRES and CARMENES did not lead to a model improvement, thus we did not fit a linear trend in our analysis. When we analyze the one-planet best-fit residuals, however, we find that both data sets exhibit a significant periodicity around 530 d, which we attribute to the possible second planet GJ 1148 c. The GLS periodograms of the one-planet model residuals for CARMENES, HIRES and the combined data are shown in Fig. 5, panels c−e, respectively. The CARMENES data residuals reveal a significant GLS peak at 538.9 d, while for the HIRES data this peak is even stronger and better resolved (due to the higher number of measurements and longer temporal baseline of the observations) at around 531.5 d. The combined data set residuals reveal two significant peaks at 525.9 d and 1434.3 d. The broad 1434.3 d peak is very likely related to the 1196 d alias of GJ 1148 c and the one sideral year.
= 11.05. Based on the 37 HIRES discovery RVs, Haghighipour et al. (2010) found that including a linear trend of 2.465 ± 1.205 m s-1 yr-1 led to a better fit, reducing the rms from 9.23 m s-1 to 8.06 m s-1. However, introducing a linear trend in our combined data set of HIRES and CARMENES did not lead to a model improvement, thus we did not fit a linear trend in our analysis. When we analyze the one-planet best-fit residuals, however, we find that both data sets exhibit a significant periodicity around 530 d, which we attribute to the possible second planet GJ 1148 c. The GLS periodograms of the one-planet model residuals for CARMENES, HIRES and the combined data are shown in Fig. 5, panels c−e, respectively. The CARMENES data residuals reveal a significant GLS peak at 538.9 d, while for the HIRES data this peak is even stronger and better resolved (due to the higher number of measurements and longer temporal baseline of the observations) at around 531.5 d. The combined data set residuals reveal two significant peaks at 525.9 d and 1434.3 d. The broad 1434.3 d peak is very likely related to the 1196 d alias of GJ 1148 c and the one sideral year.
We investigated the possibility of the 525.9 d signal being caused by stellar activity. A rotational modulation of star spots can be excluded, since the observed 525.9 d RV signal is much longer than the estimated rotational period for GJ 1148 of Prot = 73.5 d sugested by (Hartman et al. 2011) or the somewhat longer period of Prot = 98.1 d given in Haghighipour et al. (2010). However, long-period magnetic cycles in M dwarfs cannot be easily excluded. As we showed in Fig. 1, our CARMENES Hα index measurements for GJ 1148 do not exhibit any significant peaks that could be associated with activity, which supports the GJ 1148 c planet hypothesis. However, even though insignificant, the highest peak in the CARMENES Hα index power spectrum is consistent with signals beyond 500 d, and thus deserves a note of caution. Unfortunately, because of the low significance and low frequency resolution (note the short time baseline in Fig. 6 and the large observational gap between June 2016 and January 2017) the available CARMENES Hα index time series does not allow us to verify whether this activity power is related to the significant ~530 d RV peak.
The HIRES data for GJ 1148 from Butler et al. (2017) contain S- and H-index activity indicator measurements with a much longer temporal baseline than our CARMENES data, and are therefore more suitable to search for long-period activity. The HIRES S-index activity indicator is measured in the Ca ii H&K wavelength region, while the H-index measures the Hα flux variations with respect to the local continuum (for more details see Butler et al. 2017). Figure 7 shows the GLS periodograms of the HIRES activity indicators. The S-index data do not show significant peaks, while the H-index measurements reveal a marginally significant peak at 121.7 d, which cannot be associated with the planetary signals. Therefore, we conclude that the CARMENES and the HIRES activity indicators so far do not show any evidence of a long-period activity cycle, which could mimic a planet. Thus, the most plausible interpretation for the observed ~530 d RV signal is a second eccentric Saturn-mass planet in orbit around GJ 1148.
One-planet Keplerian and a coplanar edge-on two-planet dynamical best-fit parameters for GJ 1148 based on the combined CARMENES and HIRES literature RVs.
A simultaneous double Keplerian model fitting two-planets on initially 41.4 and 527 d-period orbits converged to a best fit with significantly improved 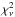 = 2.97 and rms = 3.71 m s-1 when compared to the single-planet fit. Based on our two-planet best fit we derive updated orbital parameters for GJ 1148 b: Kb = 38.37 m s-1, Pb = 41.380 days, eb = 0.379, and for the new planet GJ 1148 c: Kc = 11.34 m s-1, Pc = 532.6 days, ec = 0.341, from which we derive minimum planetary masses of mbsini = 0.304 MJup, mcsini = 0.214 MJup (96.7 and 68.1 M⊕), and semi-major axes ab = 0.166 au, ab = 0.913 au, respectively. The phase-folded Keplerian planetary signals for GJ 1148 b and c are shown in Fig. 5, panels g and h, respectively. No significant GLS peaks are left in the two-planet model residuals, confirming that the 1434.3-day peak is indeed related to the lower frequency alias of the GJ 1148 c planetary signal.
= 2.97 and rms = 3.71 m s-1 when compared to the single-planet fit. Based on our two-planet best fit we derive updated orbital parameters for GJ 1148 b: Kb = 38.37 m s-1, Pb = 41.380 days, eb = 0.379, and for the new planet GJ 1148 c: Kc = 11.34 m s-1, Pc = 532.6 days, ec = 0.341, from which we derive minimum planetary masses of mbsini = 0.304 MJup, mcsini = 0.214 MJup (96.7 and 68.1 M⊕), and semi-major axes ab = 0.166 au, ab = 0.913 au, respectively. The phase-folded Keplerian planetary signals for GJ 1148 b and c are shown in Fig. 5, panels g and h, respectively. No significant GLS peaks are left in the two-planet model residuals, confirming that the 1434.3-day peak is indeed related to the lower frequency alias of the GJ 1148 c planetary signal.
According to an F-test, the double Keplerian best-fit represents a significant improvement over the one-planet model with an extremely convincing false-alarm probability of 2.8 × 10-46. The CARMENES RV scatter for the two-planet model is rmsCARMENES = 2.23 m s-1, which is better than the scatter from HIRES data of rmsHIRES = 4.60 m s-1. From panels f−h in Fig. 5 it can be seen that the scatter around the two-planet fit is significantly reduced when compared to the one-planet best-fit solution shown in panel b. Both the HIRES and the CARMENES data follow very well the two-planet model providing supporting evidence for the multiple planet system architecture of GJ 1148.
As a next step we adopted the two-planet Keplerian best-fit parameters as an initial guess for our more accurate N-body dynamical model. The two-planet dynamical fit parameters and uncertainties are provided in Table 4. The actual fit to the HIRES and the CARMENES data and their residuals are shown in Fig. 6 panel a, while panel b shows a zoom of the fit and the CARMENES time series. In Fig. 6 panel c, the best-fit residuals do not show significant peaks above the 0.1% FAP level. We note, however, an interesting GLS peak at 62.9 d near the 1% FAP level, which could be due to an additional ~7 M⊕ mass planet potentially locked in a 3:2 MMR with GJ 1148 b. However, due to the still insignificant power of this peak and the close proximity to the eccentric GJ 1148 b our confidence in the putative third planet is currently low.
We find that the best-fit parameters from the two-planet N-body fit are practically the same as those from our two-planet Keplerian model. The small difference between our unperturbed Keplerian and our N-body dynamical model is a result of the relatively large separation between the GJ 1148 b and c planets, leading to negligible dynamical interactions during the observational time baseline.
The long-term dynamical interactions for the GJ 1148 system, however, are not negligible. The best dynamical fit is stable for 10 Myr, showing strong long-term secular dynamical interactions due to the large planetary eccentricities. While the planetary semi-major axes are practically constant at ab = 0.166 au and ac = 0.912 au, the orbital eccentricities exhibit large variations in the range of eb = 0.05 to 0.49 and ec = 0.22 to 0.44 with secular time scales of ~80 000 years. This can be seen from the 200 000 year extent of the GJ 1148’s best-fit evolution, which is shown in Fig. 6, panel d. With these large secular eccentricity oscillations, the minimum pericenter distance qmin = a(1−emax) and maximum apocenter distance pmax = a(1 + emax) for the planets are qb≈ 0.08 au, pb≈ 0.25 au and qc≈ 0.50 au, pc ≈ 1.32 au, which makes it unlikely that additional low-mass planets in close proximity to GJ 1148 b and c would be able to survive on stable orbits. Most likely the two Saturn-mass planets are the only companions to GJ 1148 at least up to ~1.4 au.
4.2.2. GJ 581
For GJ 581 we secured 20 precise CARMENES Doppler measurements between January 2016 and February 2017. In addition, we found 251 publicly available ESO HARPS spectra, which we re-processed with SERVAL, and 413 HIRES literature RVs (Butler et al. 2017). The large number of precise HIRES and HARPS data is an excellent opportunity for a comparative analysis with the newly obtained CARMENES data, and a subsequent update of the orbital architecture of the GJ 581 system. GJ 581 is currently known to have three bona-fide planets, which when listed in ascending order by orbital period are designated as GJ 581 e, GJ 581 b and GJ 581 c. Our RV analysis for GJ 581 consisted of several standard consecutive steps of GLS period search and Keplerian fitting. First we identified the strongest GLS peak of the combined data at 5.37 d, corresponding to GJ 581 b. Then using this period as an initial guess we fit a full Keplerian model for GJ 581 b whose residuals revealed a significant GLS peak at 12.9 d, which is due to GJ 581 c. We added an additional Keplerian term and we fit the combined data simultaneously for GJ 581 b and GJ 581 c. The residuals of the two-planet model revealed another strong GLS peak at 66.7 d, which in the past was designated as GJ 581 d (Udry et al. 2007), but is now believed to be due to stellar activity (Baluev 2013; Robertson et al. 2014; Suárez Mascareño et al. 2015; Hatzes 2016; Suárez Mascareño et al. 2017c). We skipped this peak and adopted the next strongest peak at 3.15 d, which is actually induced by GJ 581 e. Finally, we obtained a simultaneous three-planet Keplerian model for GJ 581. We used the Keplerian three-planet best-fit parameters as an initial guess for our more accurate three-planet dynamical model, which takes into account the gravitational interactions between planets GJ 581 e, b, and c, while fitting the RVs.
 |
Fig. 7 GLS periodograms of the S- and H-index measurements from the HIRES data for GJ 1148. Only the H-index periodogram reveals a significant peak at 121,7 d, likely related to activity, but not associated with the stellar rotation for GJ 1148 Prot = 73.5 d (red dashed line), or with either of the planetary periods Pb = 41.4 d and Pc = 532.6 d (blue dashed lines) seen in the HIRES RVs. |
 |
Fig. 8 Panel a: available Doppler measurements for GJ 581 obtained with HIRES (green diamonds), HARPS (blue triangles) and CARMENES (red circles) mutually agree when fitted with a three-planet self-consistent N-body model. Panel b: time series plot for only the CARMENES data show that they are fully consistent with the best-fit three-planet dynamical model yielding an rms = 1.64 m s-1, the lowest among the three data sets. Panel c: GLS power spectrum of the residuals from the three-planet dynamical model for GJ 581. The strong peak at 66.7 d was earlier attributed to a planet designated GJ 581 d, but is now believed to be induced by stellar activity. Several other peaks with periods near 81.8 d, 186.1 d and 371.2 d are significant, but unlikely of planetary nature and most likely also related to activity and the window function. Panel d: dynamical evolution of the best three-planet fit for the GJ 581 planetary system. This fit is stable for at least 10 Myr, but for illustrative purposes we show only a 2000 yr extent of the N-body integration, which clearly shows the perfectly synchronized orbital evolution. In this best-fit configuration the eccentricities of the three planets are oscillating with a period of ~500 yr in addition to the ~50 yr secular perturbations between GJ 581 e and GJ 581 b. |
We converged to a three-planet best-fit solution leading to: Ke = 1.55 m s-1, Pe = 3.153 days, ee = 0.125, Kb = 12.35 m s-1, Pb = 5.368 days, eb = 0.022, and Kc = 3.28 m s-1, Pc = 12.919 days, ec = 0.087. We derived planetary masses and semi-major axes, respectively, as: me,b,c = 1.66, 15.20, 5.65 M⊕ (0.005, 0.050, 0.018 MJup) and ae,b,c = 0.029, 0.041 and 0.074 au. This fit has 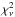 = 5.85 and overall scatter rms = 2.91 m s-1. Detailed orbital parameter estimates and their bootstrap uncertainties are provided in Table 5, while in Fig. 8 panel a, we show the HIRES, HARPS and CARMENES time series data plot fitted with the best three-planet dynamical model. In Fig. 8 panel b we show only the time series from our CARMENES data, which clearly follow the best-fit model that is heavily influenced by the HIRES and HARPS data. The individual data set scatter around the best-fit is lowest for CARMENES with rmsCARMENES = 1.64 m s-1, followed by rmsHARPS = 2.32 m s-1 and rmsHIRES = 3.60 m s-1 showing good consistency between the data sets. The CARMENES data supports the current understanding of the GJ 581 system, while our RV analysis presents an update of its three-planet configuration based on dynamical modeling of all available data.
= 5.85 and overall scatter rms = 2.91 m s-1. Detailed orbital parameter estimates and their bootstrap uncertainties are provided in Table 5, while in Fig. 8 panel a, we show the HIRES, HARPS and CARMENES time series data plot fitted with the best three-planet dynamical model. In Fig. 8 panel b we show only the time series from our CARMENES data, which clearly follow the best-fit model that is heavily influenced by the HIRES and HARPS data. The individual data set scatter around the best-fit is lowest for CARMENES with rmsCARMENES = 1.64 m s-1, followed by rmsHARPS = 2.32 m s-1 and rmsHIRES = 3.60 m s-1 showing good consistency between the data sets. The CARMENES data supports the current understanding of the GJ 581 system, while our RV analysis presents an update of its three-planet configuration based on dynamical modeling of all available data.
Coplanar edge-on best dynamical fit parameters for the multiple planet system GJ 581 based on the combined CARMENES and literature RVs.
A GLS periodogram for the best-fit residuals is shown panel c of Fig. 8. We find several significant residual periodic signals, the strongest of which is at 66.7 d, which was originally believed to be due to an additional planet GJ 581 d, followed by 71.5 d, 81.8 d, 186.1 d, 371.1 d, etc., most of which are likely also due to activity, in particular aliases of the dominant peak and the one year observational window. For example, the second strongest peak at 81.8 d is a 365.25 d alias of 66.7 d. The 371.1 d peak is close to one year period and likely comes from the observational window function, while the 186.1 d is close to half a year which is approximately one observing season, or alternatively this peak might be related to an alias of 371.1 d and 365.25 d.
We find our best fit to be stable for at least 10 Myr, demonstrating that the three-planet system has a perfectly synchronized orbital evolution. In Fig. 8 panel d we show a 2000 yr extent of the orbital evolution. While the planetary semi-major axes are nearly constant, the planetary eccentricities are oscillating with moderate amplitudes and a secular period of ~500 yr in addition to the shorter term ~50-year secular perturbations between planets e and b.
4.2.3. GJ 876
For GJ 876 we obtained 28 precise CARMENES Doppler measurements between June 2016 and December 2016. We find 256 publicly available ESO HARPS spectra, which we re-processed with SERVAL, and 338 HIRES literature RVs (Butler et al. 2017). GJ 876 is known to host four planets, namely GJ 876 d, c, b and e, the last three of which are locked in a strongly interacting 1:2:4 Laplace MMR (Rivera et al. 2010). For our RV analysis we simply combined all available RV data and we applied a four-planet dynamical model starting with coplanar orbital parameters taken from (Rivera et al. 2010). Following their coplanar test we also fixed the line of sight inclination at i = 59°. We did not make further attempts to constrain the coplanar or mutual inclinations for this system, although we are aware that this might lead to an additional model improvement (Nelson et al. 2016).
Our four-planet dynamical fit takes into account 622 precise Doppler measurements taken over twenty years, which is by far the most complete set of high-precision RV data that has been analyzed for this star. Our updated orbital four-planet best-fit configuration suggests: Kd = 6.14 m s-1, Pd = 1.938 days, ed = 0.082, for the inner resonant pair we obtain: Kc = 88.34 m s-1, Pc = 30.126 days, ec = 0.250 and Kb = 212.07 m s-1, Pb = 61.082 days, eb = 0.027, and for the outermost planet e we obtain: Ke = 3.39 m s-1, Pe = 124.4 days, ee = 0.040, valid at the epoch JD = 2 450 602.093, the same as in Rivera et al. (2010). We derive planetary masses and semi-major axes as follows: md,c,b,e = 6.91, 241.5, 760.9, 15.43 M⊕ (0.021, 0.760, 2.394 and 0.049 MJup), and ad,c,b,e = 0.021, 0.134, 0.214 and 0.345 au, respectively. Detailed best-fit orbital parameter estimates and their bootstrap uncertainties are provided in Table 6.
In Fig. 9 panel a we show the HIRES, HARPS and CARMENES data time series fitted with our best four-planet dynamical fit, while panel b shows a zoom only to our CARMENES data. All data sets yield very good agreement with the four-planet best-fit prediction and show similar RV scatter residuals. As in the GJ 581 case, this fit is dominated by the HIRES and the HARPS data, which have much more extensive data sets when compared with the CARMENES RVs. The CARMENES scatter around the best-fit is rmsCARMENES = 2.97 m s-1, close to the one from HARPS with rmsHARPS = 2.95 m s-1, and better than HIRES which has rmsHIRES = 4.35 m s-1.
 |
Fig. 9 Data colors and symbols are the same as in Fig. 8, but for GJ 876. Panel a: the total amount of 622 precise RVs from HARPS, HIRES and CARMENES are fitted with a four-planet Newtonian model. Panel b: zoomed extent of the CARMENES data, which clearly follow the four planet model with a very low rms = 2.97 m s-1, very similar to the HARPS data with rms = 2.95 m s-1, but better than the HIRES data whose rms scatter is 4.35 m s-1. Panel c: GLS power spectrum of the residuals from the four-planet dynamical model for GJ 876 showing several peaks above FAP = 0.1% near 106.0 d, 90.6 d and 441.1 d. However, these are unlikely planetary signals (see text for details). Panel d: our updated four-planet dynamical fit is stable for 10 Myr and is consistent with a chaotic Laplace 1:2:4 MMR orbital evolution between planets b, c and e, already known for this system. Our best fit and orbital evolution of the planetary system, however, suggests smaller (compared to the literature) eccentricity (ed = 0.082) of the innermost planet GJ 876 d. |
Figure 9 panel c shows a GLS periodogram of the best-fit residuals. We find several significant GLS peaks that, when sorted by significance, appear at 106.0 d, 90.6 d, 87.6 d, 441.1 d, 70.5 d, etc. The origin of these periodic signals is likely stellar activity induced by stellar rotation, magnetic cycles, the window function and their aliases. For example Nelson et al. (2016) also found a dominant periodicity around 95 d in their four-planet best-fit residuals for GJ 876 and attributed this signal (and aliases) to stellar activity. They found the same periodicity in the Hα line when analyzing the publicly available HARPS spectra. In the Carmencita catalog (Caballero et al. 2016a) the period for GJ 876 (listed in Table 1) is ~81 d (Díez-Alonso et al., in prep.), which is of the same order of magnitude, but slightly shorter than the 95 d from Nelson et al. (2016) and the ~87 d estimate from Suárez Mascareño et al. (2015). Thus, the true rotation period of GJ 876 likely lies somewhere between these estimates. We do not retrieve a 95 d peak in our combined data residuals, nor we did obtain a significant peak detection in our CARMENES Hα-index measurements. However, the 90 d peak in our four-planet model residuals is close to the current Prot estimates for GJ 876. By fitting a sine model with period of 90.6 d to the residuals we also remove the 70.5 d, 87.6 d and 441.1 d peaks, except the peak at 106.0 d. The 106.0 d period, could be related to differential stellar rotation and spots at two latitudes creating peaks at 90.0 d and 106.0 d. The 106.0 d signal could also be induced by model degeneracy (i.e., imperfect dynamical modeling) since we do not fit for the mutual inclinations of the planets.
Coplanar best dynamical fit parameters for the multiple planet system GJ 876 based on the combined CARMENES and literature RVs.
When compared to the previous four-planet solution of Rivera et al. (2010), our fit is largely consistent, in terms of overall stability, orbital parameters and evolution of planets GJ 876 b, c and e. For clarity, in Fig. 9 panel d we show a 100-yr section of our best fit dynamical evolution of GJ 876, which we find stable for at least 10 Myr. The orbital evolution of our best-fit is consistent with a chaotic 1:2:4 Laplace MMR in agreement with earlier dynamical studies for this system (Rivera et al. 2010; Batygin et al. 2015; Nelson et al. 2016). This is evident from the quasi-periodic pattern of the eccentricity evolution of the outermost planet GJ 876 e (first described by Rivera et al. 2010). It should be noted that the time scale for the eccentricity evolution of planet GJ 876 e is only about 7.5 years and therefore shorter than the observational time baseline of the system. This result, combined with the chaotic nature, imposes an intrinsic limit of the fit quality since small changes well within the uncertainties can change the eccentricity evolution of GJ 876 e significantly. Despite the chaotic behavior, Rivera et al. (2010) found stability for the GJ 876 system over hundreds to thousand Myr.
 |
Fig. 10 Panel a: show GLS periodogram of the combined HIRES (green diamonds) and CARMENES (red circles) data for GJ 15 A, while panels b and c show separate GLS periodograms for the HIRES, and CARMENES data, respectively. Panels d−f show the best-fit models to the combined and the separate data sets. The HIRES data strongly suggest several periodicities, most notable at a period of 11.44 d, which is associated with the putative planet GJ 15 Ab, a period of 45.42 d, attributed to stellar activity, and a few long-period peaks, which disappear when we fit a linear trend to the data. A GLS power spectrum to the 92 CARMENES RVs, however, does not show significant peaks, which is also the case for more recent HIRES RVs (see Fig. 11, bottom panel). No valid Keplerian model with a period of 11.44 d can be fitted to the post-discovery HIRES and CARMENES data, casting doubts on the existence of GJ 15 Ab. The available data for GJ 15 A are dominated by the early HIRES RVs, and thus the putative planetary signal is still detected in the combined data set. |
 |
Fig. 11 The 358 HIRES RVs for GJ 15 A, separated into four subsets of 90, 90, 90, and 88 RVs, respectively, and analyzed individually. The left panels show the GLS periodogram analysis for each of the four subsets, while the right panels show the RV data phase-folded to the best Keplerian fit + a linear trend calculated using the full set of HIRES data (see Fig. 10, panels a and b). The first 90 RVs are taken over a 10 yr period and are consistent with a 11.44 d, a ~40-day and other significant periodic signals. Between Jan. 2010 and Sep. 2011, GJ 15 A likely experienced a period of intensive activity leading to strong periodicity at ~45 d probably causing also the signal around 11.5 d. The same is true for the 90 RVs taken between Aug. 2011 and Dec. 2011, which show periodicities at ~40 d, 20 d, 11 d and 8 d. The last three years of HIRES data, however, are not consistent with signal at 11.44 d. As shown in Fig 10 panels c and d, at later epochs CARMENES is also not showing any periodic signal near 11 d. |
 |
Fig. 12 GLS power and signal semi-amplitude as a function of the number of data for the 11.44 d periodicity, supposed to be induced by a close-in super-Earth planet GJ 15 Ab. The magenta vertical line separates the pre- and post-discovery HIRES data for GJ 15 A, while the red line indicates the beginning of the CARMENES data. Even before the claimed planet discovery, the pre-discovery HIRES data seem to show fading power and semi-amplitude of the signal, and this continues when adding the newly published HIRES data. The descending trend of the power continues when the CARMENES data are added, which by themselves are not consistent with a periodic signal at 11.44 d. |
The new finding in our study is the exceptionally small eccentricity of ed = 0.082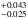 for the innermost planet GJ 876 d. In Rivera et al. (2010) the estimated eccentricity for GJ 876 d was eb = 0.257 ± 0.070, which is more than 2σ away from our estimate. Deviations from the literature values presented in Rivera et al. (2010), however, can be expected as we use more data, larger observational baseline and a slightly larger stellar mass (M = 0.35 M⊙ versus 0.32 M⊙ used in Rivera et al. 2010). We believe that our estimate for ed makes sense because the GJ 876 d’s close orbital separation of only ad = 0.021 au to its host star is expected to cause significant tidal circularization of the orbit. From Fig. 9, panel d planet d exhibits constant, nearly circular orbital evolution and is practically unperturbed by the resonant chain of planets GJ 876 b, c and e. Therefore, if GJ 876 d indeed settled in a nearly circular orbit, it will not have a strong impact on the dynamical best fit solutions obtained in our study and the one by Rivera et al. (2010). Likely the reason for the significant ed deviation from Rivera et al. (2010) is that by using more data and a longer baseline we better constrain the resonant chain and, thus, we obtain more accurately the orbit of GJ 876 d. We do not intend to revisit existing detailed discussions of the resonant architecture of the GJ 876 system, but we note that the small ed is intriguing and may be used as an input to more intensive dynamical and formation studies of this system using all the available data.
for the innermost planet GJ 876 d. In Rivera et al. (2010) the estimated eccentricity for GJ 876 d was eb = 0.257 ± 0.070, which is more than 2σ away from our estimate. Deviations from the literature values presented in Rivera et al. (2010), however, can be expected as we use more data, larger observational baseline and a slightly larger stellar mass (M = 0.35 M⊙ versus 0.32 M⊙ used in Rivera et al. 2010). We believe that our estimate for ed makes sense because the GJ 876 d’s close orbital separation of only ad = 0.021 au to its host star is expected to cause significant tidal circularization of the orbit. From Fig. 9, panel d planet d exhibits constant, nearly circular orbital evolution and is practically unperturbed by the resonant chain of planets GJ 876 b, c and e. Therefore, if GJ 876 d indeed settled in a nearly circular orbit, it will not have a strong impact on the dynamical best fit solutions obtained in our study and the one by Rivera et al. (2010). Likely the reason for the significant ed deviation from Rivera et al. (2010) is that by using more data and a longer baseline we better constrain the resonant chain and, thus, we obtain more accurately the orbit of GJ 876 d. We do not intend to revisit existing detailed discussions of the resonant architecture of the GJ 876 system, but we note that the small ed is intriguing and may be used as an input to more intensive dynamical and formation studies of this system using all the available data.
4.3. The peculiar case of GJ 15 A
4.3.1. The “fading“ GJ 15 Ab
We obtained a total of 174 precise CARMENES RV measurements for GJ 15 A between January 2016 and April 2017, but most of them were taken during technical nights, in which the main goal was to observe intensively several stars and test the nightly stability of the spectrograph. To avoid data clustering from these intensive campaigns, we took three Doppler measurements at random to represent each of the technical nights. Therefore, we present a total of 92 CARMENES RVs that, when combined with the 358 HIRES newly announced literature velocities (Butler et al. 2017) spanning the time from 1997 to 2014, comprise twenty years of precise RV measurements, providing better constraints on the orbital parameters of the proposed planetary companion GJ 15 Ab.
Figure 10 shows results from our RV analysis for GJ 15 A based on the HIRES and CARMENES data separately and when combined. Panel a) shows a GLS periodogram of the combined data, yielding two strong periods at 11.44 d and 45.46 d, similar to those found by Howard et al. (2014), who attributed them to the GJ 15 Ab planetary signal and stellar activity, respectively. We attribute the broad long-period peak consistent with periods exceeding the combined HIRES and CARMENES temporal baseline (7307.525 d) to the negative RV linear trend seen in the GJ 15 A RVs (Howard et al. 2014). Indeed, a linear trend fit to the HIRES data alone, and to the combined data yields an RV trend of −0.39 m s-1 yr-1 (see first column of Table 7), which removes all significant peaks beyond the ~45 d activity period seen in panels a and b. Since, GJ 15 A forms a common-proper motion pair with the M3.5 V star GJ 15 B, Howard et al. (2014) tentatively interpreted the linear trend as a small arc of the long-period binary orbit. We follow a similar reasoning and in our Keplerian modeling of the proposed planet GJ 15 Ab we chose to simultaneously fit an additional linear term to the data.
Figure 10, panel d shows our one-planet best-fit to the combined data, phase-folded to GJ 15 Ab’s best-fit period. This fit is consistent with a planetary semi-amplitude of Kb = 2.13 m s-1, an orbital period Pb = 11.441 days, eccentricity eb = 0.093, and a linear trend of −0.346 m s-1 yr-1, corresponding to a planetary companion with a minimum mass of mbsini = 4.1 M⊕ and a semi-major axis ab = 0.074 au. These orbital estimates and their asymmetric bootstrap uncertainties are listed in the second column of Table 7. Our results yield conclusions similar to those by Howard et al. (2014), showing that the combined data are consistent with the GJ 15 Ab planet and a linear trend. Interestingly, the semi-amplitude of our model is lower than that in Howard et al. (2014), who estimated Kb = 2.93 ± 0.29 m s-1, corresponding to a mbsini = 5.3 M⊕ super-Earth planet.
In Fig. 10, panels b and c we show an independent GLS search of the HIRES and the CARMENES data, respectively, while panels e and f show the best-fit results for the two data sets, phase-folded with GJ 15 Ab’s best-fit period from the combined data. The RV analysis of only the HIRES data reveals that the results from the combined data shown in panels a and d are heavily dominated by HIRES. The 11.44 day planetary signal, the ~45 day activity signal, and the remaining long-period peaks seen in panel a are present in the HIRES RVs. A Keplerian fit to the HIRES data alone also yields results similar to those obtained by the combined data. A GLS periodogram of the CARMENES data alone, however, yields no significant peaks and lacks the 11.44 d signal. In fact, we find that our CARMENES data are more consistent with a flat model (i.e., no planet or activity present). This is a peculiar result for a star with a large number of CARMENES visits. Throughout the paper we have demonstrated that the CARMENES data for our other stars have very good agreement with the HIRES data and even better precision (see Sect. 5). Therefore, there is no reason to assume different circumstances for the particular case of GJ 15A, and we should have been able to detect the 11.44 d signal in our 92 CARMENES RVs.
The question of whether the CARMENES data are consistent or not with HIRES data is addressed in Fig. 11. We split the 358 HIRES RVs into four subsets having approximately the same number of data points as the CARMENES data set: 90, 90, 90 and 88 RVs, respectively. For each of those subsets we searched for significant GLS signals. The left panels in Fig. 11 show the GLS periodograms with horizontal lines showing the bootstrapped FAP levels of 10%, 1% and 0.1%, while the vertical lines show the 11.44 d and 45.46 d peaks seen in the total HIRES data set. In the right panels in Fig. 11, for illustrative purposes, we fold each data sub-set with the best period obtained for the total HIRES data and overplot the best-fitting Keplerian signal, also for the total HIRES data (see Fig. 10, panels a and b). The first data set of 90 RVs was obtained between January 1997 and December 2009 and yields several significant peaks, one at 11.44 d, two near 20 d, and one at 40 d. Between January 2010 and September 2011, we can still see a significant peak near ~11.5 days, but the strongest data peak is now near 50.4 d, followed by 54.3 d and 45.4 d. Likely GJ 15 A experienced an epoch of intense quasi-periodic activity that caused additional peaks near the 50 day peak. The 90 RVs taken between August 2011 and December 2011 show significant GLS peaks at 39.6 d and 19.1 d (probably a harmonic), also likely induced by stellar activity and followed by another peak at 11.6 d, potentially due to the planet candidate, and a 7.4 d peak, which is likely an alias. The last three years of HIRES data (Jan. 2012−Dec. 2014) do not provide any evidence for a planetary signal at 11.44 d, which is consistent with what we find based on the CARMENES follow-up data alone. We note in passing that we inspected the S- and H-indices, which also show periodogram peaks at several of the values found in the RVs, such as 44 d and 11.4 d.
Further, we systematically analyze the GLS power spectrum for the 11.4-day period as a function of the number of observations, the results of which are shown in Fig. 12. We note that instead of the raw Scargle power for this test we adopted the original GLS power formalism, which defines the power as p(ω) = (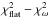 )/
)/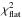 , where
, where 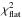 is the χ2 of a flat model applied to the data, while
is the χ2 of a flat model applied to the data, while 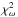 is the χ2 of a sinusoidal model having frequency ω. Here p(ω) is the relative χ2 improvement in a comparison of the two models. It is close to zero when the sinusoidal model does not represent an improvement over the flat model, while is close to unity in the case of a strong improvement (for more details, see Zechmeister & Kürster 2009). Thus, the GLS power is a very informative quantity to study whether a given frequency in the data arises due to a signal rather than from noise. In particular, with our p(ω) vs. Ndata test we probe if by adding more data we increase the evidence for the GJ 15 Ab signal or if we just add noise. We started with the first 90 RVs available for GJ 15 A as after this subset of data (Ndata> 90) the 11.4 d peak was the strongest in the GLS, and we kept adding data and recomputing the power spectrum. Interestingly, the GLS power and semi-amplitude decrease even before the announcement of the planet discovery. The power keeps decreasing when we add the CARMENES RVs.
is the χ2 of a sinusoidal model having frequency ω. Here p(ω) is the relative χ2 improvement in a comparison of the two models. It is close to zero when the sinusoidal model does not represent an improvement over the flat model, while is close to unity in the case of a strong improvement (for more details, see Zechmeister & Kürster 2009). Thus, the GLS power is a very informative quantity to study whether a given frequency in the data arises due to a signal rather than from noise. In particular, with our p(ω) vs. Ndata test we probe if by adding more data we increase the evidence for the GJ 15 Ab signal or if we just add noise. We started with the first 90 RVs available for GJ 15 A as after this subset of data (Ndata> 90) the 11.4 d peak was the strongest in the GLS, and we kept adding data and recomputing the power spectrum. Interestingly, the GLS power and semi-amplitude decrease even before the announcement of the planet discovery. The power keeps decreasing when we add the CARMENES RVs.
At the moment, we are puzzled by the strong periodicity seen in the early HIRES data and the absence of this signal at later HIRES epochs and in our CARMENES data. It seems that we are able to construct a Keplerian fit for GJ 15 A thanks to the contribution of the HIRES data obtained at earlier epochs prior to the planet announcement. More data taken at later epochs are consistent with noise and the semi-amplitude Kb of the planet signal decreases monotonously. Currently, the weighted rmsHIRES scatter of the Keck data for GJ 15 A after removing the planet signal is about 2.61 m s-1. This value is actually larger the rmsCARMENES = 2.40 m s-1 of the CARMENES data without removing any signal.
We conclude that the CARMENES data show no evidence for the planet’s existence, nor do the post-discovery HIRES data. However, the HIRES Doppler data prior to the planet announcement do show a significant 11.44 d periodicity. Incidentally, the 11.44 d signal seen in the HIRES data is almost exactly 1/4 of the second strongest GLS peak at 45.46 days (see Fig. 10). If the latter is due to the stellar rotation period proposed by Howard et al. (2014), then the 11.44 day signal could be an overtone of the activity.
4.3.2. A long-period planet companion?
As we mentioned in Sect. 4.3.1, the long-period orbital motion of the GJ 15 Ab binary is a plausible explanation of the possible linear RV trend seen in the HIRES data for GJ 15 A. We measured a trend of −0.39 ± 0.02 m s-1 yr-1 for GJ 15 A, while given the binary mass ratio μ = 0.391 ± 0.042 (for GJ 15 B we derived a mass of M = 0.162 ± 0.016 M⊙), we would also expect a positive trend of 1.00 ± 0.05 m s-1 yr-1 in the RV data of GJ 15 B. Fortunately, this can be tested as the literature HIRES data for GJ 15 B consist of 30 RVs with a similar temporal base line as for GJ 15 A. In Fig. 13 panel a we show the HIRES RV time series for GJ 15 A and GJ 15 B. With blue continuous lines we plot their best fit linear trend model, while with red dot-dashed lines we plot their predicted trend assuming the respective other binary companion has the correct trend estimate. In the sparse HIRES data of GJ 15 B we indeed measured a marginally significant positive trend of 0.47 ± 0.08 m s-1 yr-1, which is a factor of two smaller than expected, but is ~6σ away from the predicted value. Therefore, given the binary mass ratio of GJ 15 Ab the observed trends are not both compatible with the binary orbit at the same time.
 |
Fig. 13 Panel a: from top to bottom, HIRES RV data for GJ 15 A and GJ 15 B modeled with a linear trend. Blue continuous lines represent the best linear trend model of the GJ 15 A and B datasets, while the red dot-dashed lines show the linear trend expected from the mass ratio of the two stars under the assumption that the other binary companion has the correct trend estimate. Panel b: time series RVs for GJ 15 A obtained with HIRES (green diamonds) and CARMENES (red circles). The fit to the data (black solid line) is a suggestive Keplerian model consistent with a long-period Saturn mass planet on a circular orbit. The dashed blue line represents a third order polynomial approximation to this orbit, which is needed for the statistical analysis (see text). The lower panel shows the residuals to the circular fit. A long-period planet yields a significant improvement over a simpler model fitting only a linear trend. |
To our knowledge, preliminary orbits of the visual binary GJ 15 Ab were calculated only by Lippincott (1972) and Romanenko & Kiselev (2014). Due to the long period these astrometric observations covered only short arcs of the orbit. The binary orbital solution proposed by Lippincott (1972) assumed an eccentricity e = 0 and argument of periastron ω = 0°, and implies a period of P = 2600 yr, inclination i = 61°, ascending node Ω = 45° and time of periastron passage t0 = A.D. 1745. Using these orbital parameters, and considering that the astrometric solutions have 180° ambiguity in Ω we derive a trend of ±0.63 m s-1 yr-1 for the orbital phase where the GJ 15 A HIRES data are obtained. This is in a reasonable agreement with the trend we determine for GJ 15 A, but inconsistent with the trend for GJ 15 B. The more recent binary solution from Romanenko & Kiselev (2014) yields P = 1253 yr, e = 0.59, ω = 331°, i = 46°, Ω = 234° and t0 = A.D. 2327, from which we derived an RV trend for GJ 15 A of about ±0.1 m s-1 for the time of the HIRES observations.
If we assume that Romanenko & Kiselev (2014) provided the more realistic binary orbit and the expected mutual RV acceleration between GJ 15 A and B is small at present epochs, then the HIRES data for GJ 15 A yield the interesting possibility of a long-period orbital motion of a sub-stellar companion. In Fig. 10, panel b we showed that the HIRES RV measurements for GJ 15 A are consistent with a 6997 d significant signal, which can be modeled well with a low-amplitude, long-period sine-like velocity curve (see Fig. 13). We note that in this case no trend is included in the model4.
Best fit Keplerian parameters for GJ 15 A constructed based on the combined CARMENES and HIRES RVs.
To test whether one can indeed make a good case for a long-period planet, we fit the combined data with a long-period circular Keplerian term (i.e., we fixed e = 0, ϖ = 0°, since at this point we cannot provide meaningful constrains for these parameters based on the available data). In Fig. 13, panel b we illustrate the results from this test. The HIRES and the CARMENES RV time series spanning over twenty years are well modeled (black sine curve) with a Saturn-mass planet at a = 5.35 au (P = 7024.8 d). Orbital parameters and uncertainties for this long-period circular planet are shown in the third column in Table 7. This suggestive fit has 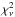 = 6.71 and rms = 2.89 m s-1, while by fitting only a linear trend we obtain
= 6.71 and rms = 2.89 m s-1, while by fitting only a linear trend we obtain 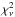 = 7.22 and rms = 2.98 m s-1. Nonetheless, the statistical comparison between a linear trend model and a sine model is complicated by the fact that they are not nested within each other. Therefore, our adopted F-test approach from Bevington & Robinson (2003) is not a appropriate test to validate whether a circular Keplerian indeed leads to a significant improvement (both models have γHIRES, γCARM., but each model is constructed of parameters that the other model does not have, e.g., P, K, M0 vs. a0t). Nested models can be obtained, however, by extending a simple slope model to a third-order polynomial, which like the sine fit has five fitting parameters (γHIRES, γCARM. + a0t + a1t2 + a2t3) and for the temporal extent of the available data is a very good approximation of a circular Keplerian model.
= 7.22 and rms = 2.98 m s-1. Nonetheless, the statistical comparison between a linear trend model and a sine model is complicated by the fact that they are not nested within each other. Therefore, our adopted F-test approach from Bevington & Robinson (2003) is not a appropriate test to validate whether a circular Keplerian indeed leads to a significant improvement (both models have γHIRES, γCARM., but each model is constructed of parameters that the other model does not have, e.g., P, K, M0 vs. a0t). Nested models can be obtained, however, by extending a simple slope model to a third-order polynomial, which like the sine fit has five fitting parameters (γHIRES, γCARM. + a0t + a1t2 + a2t3) and for the temporal extent of the available data is a very good approximation of a circular Keplerian model.
A third order polynomial fit to the combined data has 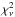 = 6.73 and rms = 2.92 m s-1 and shows a very good agreement with the adopted long-period circular planetary model (see Fig. 13, panel b, blue dashed curve). An F-test yields a FAP = 5.4 × 10-8 that the two additional fitting parameters, which approximate the sine fit significantly improve the linear trend model. Thus we concluded that a circular Keplerian fit is justified, and perhaps indicates the existence of a long-period planet around GJ 15 A.
= 6.73 and rms = 2.92 m s-1 and shows a very good agreement with the adopted long-period circular planetary model (see Fig. 13, panel b, blue dashed curve). An F-test yields a FAP = 5.4 × 10-8 that the two additional fitting parameters, which approximate the sine fit significantly improve the linear trend model. Thus we concluded that a circular Keplerian fit is justified, and perhaps indicates the existence of a long-period planet around GJ 15 A.
Including the 11.44 d signal representing the putative planet GJ 15 Ab leads to similar results. Fitting for the GJ 15 Ab planet simultaneously on the one hand with a linear trend and on the other, with a third order polynomial suggests that the latter is better with a FAP of 1.7 × 10-7. A suggestive two-planet Keplerian fit including the short period planet GJ 15 Ab and the possible long-period circular planet GJ 15 Ac is shown in the last two columns of Table 7. Unfortunately, assuming that a long-period planet is indeed the right model does not improve the detectability of the putative GJ 15 Ab planet. We repeated the same test as in Sect. 4.3.1, but including the determined long-period circular model instead of the linear trend and once again the latest HIRES and new CARMENES data did not strengthen the case for the close-in planet.
For GJ 15 A our CARMENES data cover only about fourteen months, or ~5% of the putative long-period planetary orbit and they currently cannot provide strong evidence for the existence of the outer planet. In addition, as can be seen from Fig. 13, the CARMENES data do not overlap with the HIRES data and, thus, their mutual RV offset parameter is not well constrained. Therefore, the constraints on the long-period fit are poor and currently rely only on the HIRES data. We plan to continue our CARMENES monitoring of GJ 15 A, which will allow us to extend our temporal baseline and see if our CARMENES data are consistent with a positive RV trend as expected from the existence of a long-period planet around GJ 15 A. Until then, the question whether GJ 15 A has two, one, or zero planets remains open.
5. CARMENES vs. HARPS and HIRES
We compare the rms velocity dispersion around the best fit models for the three largest RV data sets used in this paper, namely CARMENES, HARPS and HIRES. Figure 14 compares the external dispersion (weighted rms) and typical internal uncertainties between the three data sets. CARMENES and HIRES data are available for all seven stars, while GJ 15 A and GJ 1148 were not observed with HARPS.
The CARMENES optical velocities have similar RV precision and overall scatter when compared to the RV measurements conducted with HIRES and HARPS. In fact, our RV analysis shows that CARMENES data are more precise and have smaller formal RV errors than the HIRES RVs. The only exception where the HIRES data seem to have smaller RV errors than CARMENES is GJ 15 A. CARMENES however, always shows better weighted rms results to the fits. The formal RV errors of HARPS are usually lower than those from CARMENES, but in terms of RV scatter they seem to be comparable. The two cases where CARMENES shows a larger scatter compared to HARPS are GJ 436 and GJ 536. For GJ 176 and GJ 581 CARMENES is better and for GJ 876 equally good as HARPS.
Nevertheless, we note a few important implications for a fair comparison of the instrument precision. (1) The CARMENES formal RV errors for these stars were boosted from ~1.0 m s-1 to ~1.6 m s-1 by the NZP correction, which added (in quadrature) the NZP uncertainties to the RV uncertainties delivered by SERVAL. (2) Both our CARMENES spectra and the HARPS data were reduced with our SERVAL pipeline. Our HARPS RV measurements resulted in a better RV precision than the one obtained with the official ESO-HARPS pipeline. (3) The HIRES data set from (Butler et al. 2017) includes a considerable number of RVs obtained before the HIRES CCD upgrade in 2004, which then improved the instrument performance. Since in our analysis we do not distinguish between pre- and post-upgrade data, the rmsHIRES is some average taken over the two parts of the dataset. (4) M dwarfs can change their activity level with time. Therefore, the data from the instruments to be compared may have been affected by different stellar jitter levels, which complicates the analysis of the achievable RV precision for a given star.
Overall, our results show that the visual channel of CARMENES is capable of achieving a comparable performance to HARPS and HIRES.
 |
Fig. 14 Weighted mean rms scatter around the best fits (top) and mean formal RV uncertainties (bottom) for HARPS, HIRES and CARMENES. The CARMENES data are more precise and have a lower scatter when compared to HIRES. The internal errors of HARPS are usually smaller than CARMENES, but comparable in terms of RV scatter. The rms scatter for GJ 15 A and GJ 1148 is averaged from the orbital solutions for these two targets given in Tables 7 and 4, respectively. |
6. Summary and conclusions
We present precise optical radial velocity measurements for seven known M-dwarf planet hosts obtained during the first 15 months of CARMENES operations. These planetary systems are the presumably single planet systems: GJ 15 A (Howard et al. 2014), GJ 436 (Lanotte et al. 2014), GJ 176 (Forveille et al. 2009), and GJ 536 (Suárez Mascareño et al. 2017a), and the confirmed multiple planet systems: GJ 1148 (Haghighipour et al. 2010), GJ 581 (Mayor et al. 2009), and GJ 876 (Rivera et al. 2010). These systems were previously intensively observed with high-precision optical spectrographs such as HARPS and HIRES, yielding a large number of high-precision Doppler measurements, which we use as an excellent benchmark for assessing the precision of the new optical CARMENES data. We find that the large number of HIRES and HARPS data together with the new visible-channel CARMENES data yield improved orbital planetary parameters for these systems.
For GJ 176 and GJ 536 we present updated orbital solutions similar to those listed in the literature. We have only ~20–30 new RV CARMENES measurements, that on their own cannot independently confirm the planets around these stars. Our data are, however, consistent with the planetary signals for GJ 176 b and GJ 536 b, showing very small residual values comparable to those from HARPS and HIRES. For these two stars, the CARMENES data strengthen the one-planet orbital solutions.
Our 113 RVs for GJ 436 are sufficient to independently confirm the well-studied short-period Neptune mass (mbsini = 22.2 M⊕) companion around this star. We find full consistency between the CARMENES, HARPS, and HIRES data, leading to a refined orbital elements and physical parameters for GJ 436 b.
In the case of the already intensively studied multiple planet systems GJ 581 and GJ 876, the limited number of additional CARMENES observations are found to be consistent with the HIRES and HARPS data. They follow the best-fit dynamical solutions with very low scatter levels. The best fits for GJ 581 and GJ 876 successfully survived 10 Myr of precise dynamical simulations in agreement with our current understanding for these systems. We find, however, a significantly smaller eccentricity for GJ 876 d than the one often cited in the literature (e.g., Rivera et al. 2010). To our knowledge, our three- and four-planet dynamical models for GJ 581 and GJ 876, respectively, are based on all available high precision RV data and provide a benchmark for more comprehensive dynamical and statistical analyses.
The CARMENES data shed new light on two systems. On the one hand, the planetary nature of the 11.44 d signal reported in GJ 15 A seems controversial since it is absent in the CARMENES data alone, but also in later RVs from HIRES. We speculate that the 11.44 d signal seen in the early HIRES data could be related to stellar activity. On the other hand, our analysis of the GJ 15 A data reveals a possible planet with a period of ~7026 d and a minimum mass of ~52 M⊕.
Based on our CARMENES data we confirm GJ 1148 b and we discover a new outer planet in the GJ 1148 system. We note, however, that Butler et al. (2017) have already mentioned discover the second planetary signal in their more extended HIRES data, but they classified this signal as a “planetary candidate”, and did not provide an orbital solution. Based on the combined HIRES and CARMENES data for GJ 1148 c we derived a period of Pc = 533 d, eccentricity ec = 0.36, and minimum mass mcsini = 68 M⊕. Our two-planet dynamical model is now consistent with two Saturn-mass planets on eccentric orbits with eb = 0.39 and ec = 0.34 and semi-major axes ab = 0.166 au and ac = 0.912 au. We find that this configuration is stable for at least 10 Myr and very likely dynamically stable on the Gyr time scale.
The CARMENES survey is taking radial-velocity time-series measurements of ~300 nearby M-dwarf stars in an attempt to find Earth-mass planets in their habitable zones. In addition, we aim to find additional multiple planetary systems like GJ 581, GJ 876 and GJ 1148 and to place further constraints on planet formation and orbital evolution around low-mass stars. As CARMENES is a new instrument, a critical point was to test the overall capabilities in terms of RV precision and long-term stability of the spectrograph. Based on the results presented in this paper, we conclude that the visible-light spectrograph of the CARMENES instrument has the precision needed to discover exoplanets resembling our Earth, which could provide a habitable environment suitable for sustaining life around nearby M-dwarf stars. An analogous analysis of the performance of the near-infrared spectrograph and pipeline will be presented in a separate paper.
Calar Alto high-Resolution search for M dwarfs with Exo-earths with Near-infrared and optical Echelle Spectrographs, http://carmenes.caha.es
In this work the GLS power spectrum is normalized following the Horne & Baliunas (1986) normalization scheme, while the false-alarm probability (FAP) levels of 10%, 1% and 0.1% were calculated by bootstrap randomization creating 1000 randomly reordered copies of the data time-series (Bieber et al. 1990; Kürster et al. 1997).
We adopted an F-test approach for nested models (see Bevington & Robinson 2003), where the F-ratio is defined as: 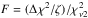 , where Δχ2 =
, where Δχ2 = 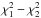 is the difference between two nested models with p1<p2 fitting parameters, ζ = p2−p1 is the number of additional parameters being tested, and
is the difference between two nested models with p1<p2 fitting parameters, ζ = p2−p1 is the number of additional parameters being tested, and 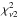 is the reduced
is the reduced 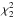 of the model with more parameters.
of the model with more parameters.
However, if the measured marginally significant trend for GJ 15 B is real then a smaller trend is expected for GJ 15 A (see Fig. 13a ), which would lower the amplitude of the long period signal.
Acknowledgments
CARMENES is an instrument for the Centro Astronómico Hispano-Alemán de Calar Alto (CAHA, Almería, Spain). CARMENES is funded by the German Max-Planck-Gesellschaft (MPG), the Spanish Consejo Superior de Investigaciones Científicas (CSIC), the European Union through FEDER/ERF FICTS-2011-02 funds, and the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofísica de Andalucía, Landessternwarte Königstuhl, Institut de Ciències de l’Espai, Insitut für Astrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Landessternwarte Tautenburg, Instituto de Astrofísica de Canarias, Hamburger Sternwarte, Centro de Astrobiología and Centro Astronómico Hispano-Alemán), with additional contributions by the Spanish Ministry of Economy, the German Science Foundation (DFG), the Klaus Tschira Stiftung, the states of Baden-Württemberg and Niedersachsen, the DFG Research Unit FOR2544 “Blue Planets around Red Stars”, and by the Junta de Andalucía. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This work used the Systemic Console package (Meschiari et al. 2009) for cross-checking our Keplerian and Dynamical fits and the python package astroML (VanderPlas et al. 2012) for the calculation of the GLS periodogram. The IEEC-CSIC team acknowledges support by the Spanish Ministry of Economy and Competitiveness (MINECO) and the Fondo Europeo de Desarrollo Regional (FEDER) through grant ESP2016-80435-C2-1-R, as well as the support of the Generalitat de Catalunya/CERCA programme. The IAA-CSIC team acknowledges support by the Spanish Ministry of Economy and Competitiveness (MINECO) through grants AYA2014-54348-C03-01 and AYA2016-79425-C3-3-P as well as FEDER funds. The UCM team acknowledges support by the Spanish Ministry of Economy and Competitiveness (MINECO) from projects AYA2015-68012-C2-2-P and AYA2016-79425- C3-1,2,3-P and the Spanish Ministerio de Educación, Cultura y Deporte, programa de Formación de Profesorado Universitario, under grant FPU15/01476. T.T. and M.K. thank to Jan Rybizki for the very helpful discussion in the early phases of this work. V.J.S.B. is supported by grant AYA2015-69350-C3-2-P from the Spanish Ministry of Economy and Competiveness (MINECO). J.C.S. acknowledges funding support from Spanish public funds for research under project ESP2015-65712-C5-5-R (MINECO/FEDER), and under Research Fellowship program “Ramón y Cajal” with reference RYC2012-09913 (MINECO/FEDER). The contributions of M.A. were supported by DLR (Deutsches Zentrum für Luft- und Raumfahrt) through the grants50OW0204 and 50OO1501. J.L.-S. acknowledges the Office of Naval Research Global (award No. N62909-15- 1-2011) for support. C.d.B. acknowledges that this work has been supported by Mexican CONACyT research grant CB-2012-183007 and the Spanish Ministry of Economy and Competitivity through projects AYA2014-54348-C3-2-R. J.I.G.H., and R.R. acknowledge financial support from the Spanish Ministry project MINECO AYA2014-56359-P. J.I.G.H. also acknowledges financial support from the Spanish MINECO under the 2013 Ramòn y Cajal program MINECO RYC- 2013-14875. V. Wolthoff acknowledges funding from the DFG Research Unit FOR2544 “Blue Planets around Red Stars”, project No. RE 2694/4-1. We thank the anonymous referee for the excellent comments that helped to improve the quality of this paper.
References
- Alonso-Floriano, F. J., Morales, J. C., Caballero, J. A., et al. 2015, A&A, 577, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amado, P. J., Quirrenbach, A., Caballero, J. A., et al. 2013, in Highlights of Spanish Astrophysics VII, eds. J. C. Guirado, L. M. Lara, V. Quilis, & J. Gorgas, 842 [Google Scholar]
- Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Amado, P. J., Barnes, J., et al. 2016, Nature, 536, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Astudillo-Defru, N., Forveille, T., Bonfils, X., et al. 2017, A&A, 602, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baluev, R. V. 2009, MNRAS, 393, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Baluev, R. V. 2013, MNRAS, 429, 2052 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., Deck, K. M., & Holman, M. J. 2015, AJ, 149, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, F. F., Zechmeister, M., & Reiners, A. 2015, A&A, 581, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bean, J. L., Benedict, G. F., Charbonneau, D., et al. 2008, A&A, 486, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benedict, G. F., Henry, T. J., Franz, O. G., et al. 2016, AJ, 152, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Bevington, P. R., & Robinson, D. K. 2003, Data reduction and error analysis for the physical sciences (Boston: Mc Graw-Hill) [Google Scholar]
- Bieber, J. W., Seckel, D., Stanev, T., & Steigman, G. 1990, Nature, 348, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Boisse, I., Bouchy, F., Hébrard, G., et al. 2011, A&A, 528, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Forveille, T., Delfosse, X., et al. 2005, A&A, 443, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butler, R. P., Vogt, S. S., Marcy, G. W., et al. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Johnson, J. A., Marcy, G. W., et al. 2006, PASP, 118, 1685 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Howard, A. W., Vogt, S. S., & Wright, J. T. 2009, ApJ, 691, 1738 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Vogt, S. S., Laughlin, G., et al. 2017, AJ, 153, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, J. A., Cortés-Contreras, M., Alonso-Floriano, F. J., et al. 2016a, in 19th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun (CS19), 148 [Google Scholar]
- Caballero, J. A., Guàrdia, J., López delFresno, M., et al. 2016b, in Observatory Operations: Strategies, Processes, and Systems VI, Proc. SPIE, 9910, 99100E [Google Scholar]
- Cosentino, R., Lovis, C., Pepe, F., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, Proc. SPIE, 8446, 84461V [Google Scholar]
- Delfosse, X., Forveille, T., Mayor, M., et al. 1998, A&A, 338, L67 [Google Scholar]
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
- Dittmann, J. A., Irwin, J. M., Charbonneau, D., et al. 2017, Nature, 544, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, M. J., Levison, H. F., & Lee, M. H. 1998, AJ, 116, 2067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Endl, M., Cochran, W. D., Tull, R. G., & MacQueen, P. J. 2003, AJ, 126, 3099 [NASA ADS] [CrossRef] [Google Scholar]
- Endl, M., Cochran, W. D., Wittenmyer, R. A., & Boss, A. P. 2008, ApJ, 673, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Forveille, T., Bonfils, X., Delfosse, X., et al. 2009, A&A, 493, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forveille, T., Bonfils, X., Delfosse, X., et al. 2011, ArXiv e-prints arXiv:1109.2505] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016a, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016b, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Pont, F., Demory, B.-O., et al. 2007, A&A, 472, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Demory, B.-O., et al. 2017, Nature, 542, 456 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gliese, W., & Jahreiß, H. 1991, Preliminary Version of the Third Catalogue of Nearby Stars, Tech. Rep., NASA/Astronomical Data Center [Google Scholar]
- Haghighipour, N., Vogt, S. S., Butler, R. P., et al. 2010, ApJ, 715, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Noyes, R. W., et al. 2011, AJ, 141, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P. 2016, A&A, 585, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Hosey, A. D., Henry, T. J., Jao, W.-C., et al. 2015, AJ, 150, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, A. W., Johnson, J. A., Marcy, G. W., et al. 2009, ApJ, 696, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, A. W., Johnson, J. A., Marcy, G. W., et al. 2010, ApJ, 721, 1467 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, A. W., Marcy, G. W., Fischer, D. A., et al. 2014, ApJ, 794, 51 [Google Scholar]
- Johnson, J. A., Howard, A. W., Marcy, G. W., et al. 2010, PASP, 122, 149 [NASA ADS] [Google Scholar]
- Kiraga, M., & Stepien, K. 2007, Acta Astron., 57, 149 [NASA ADS] [Google Scholar]
- Kürster, M., Schmitt, J. H. M. M., Cutispoto, G., & Dennerl, K. 1997, A&A, 320, 831 [NASA ADS] [Google Scholar]
- Kürster, M., Endl, M., Rouesnel, F., et al. 2003, A&A, 403, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanotte, A. A., Gillon, M., Demory, B.-O., et al. 2014, A&A, 572, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, M. H., & Peale, S. J. 2003, ApJ, 592, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Lammers, U., Bastian, U., et al. 2016, A&A, 595, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lippincott, S. L. 1972, AJ, 77, 165 [NASA ADS] [CrossRef] [Google Scholar]
- LoCurto, G., Pepe, F., Avila, G., et al. 2015, The Messenger, 162, 9 [NASA ADS] [Google Scholar]
- Maness, H. L., Marcy, G. W., Ford, E. B., et al. 2007, PASP, 119, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Butler, R. P., Vogt, S. S., Fischer, D., & Lissauer, J. J. 1998, ApJ, 505, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Butler, R. P., Fischer, D., et al. 2001, ApJ, 556, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meschiari, S., Wolf, A. S., Rivera, E., et al. 2009, PASP, 121, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, B. E., Robertson, P. M., Payne, M. J., et al. 2016, MNRAS, 455, 2484 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN, The art of scientific computing [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91471F [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2016, in SPIE Conf. Ser. Proc., 9908, 990812 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Font-Ribera, A., & Beaulieu, J.-P. 2008, ApJ, 677, L59 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Rivera, E. J., Lissauer, J. J., Butler, R. P., et al. 2005, ApJ, 634, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Rivera, E. J., Laughlin, G., Butler, R. P., et al. 2010, ApJ, 719, 890 [Google Scholar]
- Robertson, P., Mahadevan, S., Endl, M., & Roy, A. 2014, Science, 345, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, P., Endl, M., Henry, G. W., et al. 2015, ApJ, 801, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Romanenko, L. G., & Kiselev, A. A. 2014, Astron. Rep., 58, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2015, MNRAS, 452, 2745 [NASA ADS] [CrossRef] [Google Scholar]
- Suárez Mascareño, A., González Hernández, J. I., Rebolo, R., et al. 2017a, A&A, 597, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suárez Mascareño, A., González Hernández, J. I., Rebolo, R., et al. 2017b, A&A, 605, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2017c, MNRAS, 468, 4772 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, X., Payne, M. J., Lee, M. H., et al. 2013, ApJ, 777, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Trifonov, T., Reffert, S., Tan, X., Lee, M. H., & Quirrenbach, A. 2014, A&A, 568, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tull, R. G. 1998, in Optical Astronomical Instrumentation, ed. S. D’Odorico, Proc. SPIE, 3355, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Tuomi, M. 2011, A&A, 528, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- VanderPlas, J., Connolly, A. J., Ivezic, Z., & Gray, A. 2012, in Proceedings of Conference on Intelligent Data Understanding (CIDU), 47 [Google Scholar]
- Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, in Instrumentation in Astronomy VIII, eds. D. L. Crawford, & E. R. Craine, Proc. SPIE, 2198, 362 [Google Scholar]
- Vogt, S. S., Butler, R. P., Rivera, E. J., et al. 2010, ApJ, 723, 954 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittenmyer, R. A., Tan, X., Lee, M. H., et al. 2014, ApJ, 780, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, D. J., Wittenmyer, R. A., Tinney, C. G., Bentley, J. S., & Zhao, J. 2016, ApJ, 817, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Kürster, M., & Endl, M. 2009, A&A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Anglada-Escudé, G., & Reiners, A. 2014, A&A, 561, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Azzaro, M., & Bauer, F. 2018, A&A, 609, A12 [CrossRef] [Google Scholar]
Appendix A:
 |
Fig. A.1 Pre- and post- NZP correction RV scatter for three CARMENES targets that we consider as “RV-quiet” stars. The top two panels are for GJ 109, the middle two show GJ 172 and the bottom two GJ 4063. The NZP correction leads to lower rms scatter for almost all RV-quiet stars in the CARMENES sample (see Fig. A2). Note that the mean measurement error |
 |
Fig. A.2 Improvement of the stellar rms due to NZP correction. For this plot we have selected a sample of 126 CARMENES RV-quiet stars, which have at least 10 RV measurements and an overall rms scatter less than 10 m s-1. On average the RV scatter for these stars is reduced when the NZP correction is applied. |
All Tables
List of CARMENES known exoplanet host stars studied in this paper with their physical characteristics.
Number of literature, archival and CARMENES Doppler measurements for the M-dwarf planet hosts and the number of planets assumed in this paper.
Best fit Keplerian parameters for the single planet systems GJ 176, GJ 436 and GJ 536 based on the combined CARMENES and literature RVs.
One-planet Keplerian and a coplanar edge-on two-planet dynamical best-fit parameters for GJ 1148 based on the combined CARMENES and HIRES literature RVs.
Coplanar edge-on best dynamical fit parameters for the multiple planet system GJ 581 based on the combined CARMENES and literature RVs.
Coplanar best dynamical fit parameters for the multiple planet system GJ 876 based on the combined CARMENES and literature RVs.
Best fit Keplerian parameters for GJ 15 A constructed based on the combined CARMENES and HIRES RVs.
All Figures
 |
Fig. 1 GLS periodograms of the Hα index obtained from CARMENES spectra for the seven known planetary hosts. Horizontal lines show the bootstrapped FAP levels of 10% (dotted line), 1% (dot-dashed line) and 0.1% (dashed line), while red vertical lines indicate the stellar rotational periods listed in Table 1. The Hα index analysis do not yield significant peaks at the known planet periods for these stars. For GJ 15 A we identify several formally significant peaks between 40 and 100 days. For GJ 176 and GJ 536 the Hα index peaks near the rotational periods of these two stars. |
| In the text | |
 |
Fig. 2 Panel a: GLS periodogram of the available Doppler data for GJ 176, with horizontal lines showing the bootstrapped FAP levels of 10% (dotted line), 1% (dot-dashed line) and 0.1% (dashed line). Two distinct peaks above the FAP = 0.1% level can be seen at 8.77 d and 39.34 d attributed to a planetary companion and stellar activity, respectively. Panel b: data from CARMENES (red circles), HARPS (blue triangles) and HIRES (green diamonds) phase-folded to our best Keplerian fit consistent with an 8.77 d planet. Panel c: GLS periodogram of the residuals after fitting the 8.77 d signal, revealing a 39.34 d activity peak. |
| In the text | |
 |
Fig. 3 Same as Fig. 2, but for GJ 436. Panels a and b show that the CARMENES, HARPS and HIRES data sets used for the construction of the best fit are fully consistent with a planetary companion with a period of 2.64 d. In panel a: the 1.60 d GLS peak is a 1-day alias of the 2.64 d periodicity induced by the planetary companion. Panel c: shows the GLS periodogram of the best fit residuals, which yields several peaks above the FAP = 0.1%, most likely due to the observational window, stellar activity and their aliases. |
| In the text | |
 |
Fig. 4 Same as Figs. 2 and 3, but for GJ 536. Panel a: GLS periodogram of the combined data for GJ 536. The significant periods are at 8.71 d (induced by GJ 536 b) and at 43.78 d, respectively, the latter likely due to the stellar rotational period (Prot≈ 43.3 d). The CARMENES, HARPS, HIRES and HARPS-N (magenta triangles) RV data for GJ 536, and the phase folded best Keplerian fit are shown in panel b. Panel c: GLS periodogram of the best fit residuals, revealing only the 43.75 d activity peak. |
| In the text | |
 |
Fig. 5 GJ 1148 Doppler data obtained with HIRES (green diamonds) and CARMENES (red circles) show two distinct periodic signals consistent with two eccentric Saturn mass planets with orbital periods of 41 d and 526 d. Panels a and b show the GLS signal of the dominant planet GJ 1148 b and its single planet Keplerian model phase folded at the best-fit period, respectively. Panels c–e show the GLS analysis of the HIRES, CARMENES and the combined data residuals after subtracting the signal from GJ 1148 b shown in panel b. Both data sets reveal the existence of a second planet candidate with a period near 530 d. Panel f: shows the RV signal of the second planet as determined from the simultaneous two-planet fit, while panels g and h show the individual Doppler signals of GJ 1148 b and GJ 1148 c, respectively, phase folded at their best-fit periods. |
| In the text | |
 |
Fig. 6 Panel a: available Doppler measurements for GJ 1148 obtained with HIRES (green diamonds) and CARMENES (red circles) fitted with a two-planet N-body model. Panel b: zoom of the CARMENES time series together with the same model. Panel c: no significant signal is left in the residuals of the two-planet dynamical model. A peak at 62.9 d presents an interesting possibility for a third lower-mass planetary companion that might be locked in a 3:2 MMR with GJ 1148 b, but currently this peak is still below the 1% FAP level. Panel d: results from a stability analysis of the GJ 1148 system composed of planets b and c. This two-planet fit is stable for at least 10 Myr, but for illustrative purposes we plot only a 200 000 yr extent of the orbital evolution of the planetary semi-major axes and eccentricities for the best two-planet dynamical fit. In this configuration the two planets exhibit large secular oscillations of eb and ec with a secular period of ~80 000 years. |
| In the text | |
 |
Fig. 7 GLS periodograms of the S- and H-index measurements from the HIRES data for GJ 1148. Only the H-index periodogram reveals a significant peak at 121,7 d, likely related to activity, but not associated with the stellar rotation for GJ 1148 Prot = 73.5 d (red dashed line), or with either of the planetary periods Pb = 41.4 d and Pc = 532.6 d (blue dashed lines) seen in the HIRES RVs. |
| In the text | |
 |
Fig. 8 Panel a: available Doppler measurements for GJ 581 obtained with HIRES (green diamonds), HARPS (blue triangles) and CARMENES (red circles) mutually agree when fitted with a three-planet self-consistent N-body model. Panel b: time series plot for only the CARMENES data show that they are fully consistent with the best-fit three-planet dynamical model yielding an rms = 1.64 m s-1, the lowest among the three data sets. Panel c: GLS power spectrum of the residuals from the three-planet dynamical model for GJ 581. The strong peak at 66.7 d was earlier attributed to a planet designated GJ 581 d, but is now believed to be induced by stellar activity. Several other peaks with periods near 81.8 d, 186.1 d and 371.2 d are significant, but unlikely of planetary nature and most likely also related to activity and the window function. Panel d: dynamical evolution of the best three-planet fit for the GJ 581 planetary system. This fit is stable for at least 10 Myr, but for illustrative purposes we show only a 2000 yr extent of the N-body integration, which clearly shows the perfectly synchronized orbital evolution. In this best-fit configuration the eccentricities of the three planets are oscillating with a period of ~500 yr in addition to the ~50 yr secular perturbations between GJ 581 e and GJ 581 b. |
| In the text | |
 |
Fig. 9 Data colors and symbols are the same as in Fig. 8, but for GJ 876. Panel a: the total amount of 622 precise RVs from HARPS, HIRES and CARMENES are fitted with a four-planet Newtonian model. Panel b: zoomed extent of the CARMENES data, which clearly follow the four planet model with a very low rms = 2.97 m s-1, very similar to the HARPS data with rms = 2.95 m s-1, but better than the HIRES data whose rms scatter is 4.35 m s-1. Panel c: GLS power spectrum of the residuals from the four-planet dynamical model for GJ 876 showing several peaks above FAP = 0.1% near 106.0 d, 90.6 d and 441.1 d. However, these are unlikely planetary signals (see text for details). Panel d: our updated four-planet dynamical fit is stable for 10 Myr and is consistent with a chaotic Laplace 1:2:4 MMR orbital evolution between planets b, c and e, already known for this system. Our best fit and orbital evolution of the planetary system, however, suggests smaller (compared to the literature) eccentricity (ed = 0.082) of the innermost planet GJ 876 d. |
| In the text | |
 |
Fig. 10 Panel a: show GLS periodogram of the combined HIRES (green diamonds) and CARMENES (red circles) data for GJ 15 A, while panels b and c show separate GLS periodograms for the HIRES, and CARMENES data, respectively. Panels d−f show the best-fit models to the combined and the separate data sets. The HIRES data strongly suggest several periodicities, most notable at a period of 11.44 d, which is associated with the putative planet GJ 15 Ab, a period of 45.42 d, attributed to stellar activity, and a few long-period peaks, which disappear when we fit a linear trend to the data. A GLS power spectrum to the 92 CARMENES RVs, however, does not show significant peaks, which is also the case for more recent HIRES RVs (see Fig. 11, bottom panel). No valid Keplerian model with a period of 11.44 d can be fitted to the post-discovery HIRES and CARMENES data, casting doubts on the existence of GJ 15 Ab. The available data for GJ 15 A are dominated by the early HIRES RVs, and thus the putative planetary signal is still detected in the combined data set. |
| In the text | |
 |
Fig. 11 The 358 HIRES RVs for GJ 15 A, separated into four subsets of 90, 90, 90, and 88 RVs, respectively, and analyzed individually. The left panels show the GLS periodogram analysis for each of the four subsets, while the right panels show the RV data phase-folded to the best Keplerian fit + a linear trend calculated using the full set of HIRES data (see Fig. 10, panels a and b). The first 90 RVs are taken over a 10 yr period and are consistent with a 11.44 d, a ~40-day and other significant periodic signals. Between Jan. 2010 and Sep. 2011, GJ 15 A likely experienced a period of intensive activity leading to strong periodicity at ~45 d probably causing also the signal around 11.5 d. The same is true for the 90 RVs taken between Aug. 2011 and Dec. 2011, which show periodicities at ~40 d, 20 d, 11 d and 8 d. The last three years of HIRES data, however, are not consistent with signal at 11.44 d. As shown in Fig 10 panels c and d, at later epochs CARMENES is also not showing any periodic signal near 11 d. |
| In the text | |
 |
Fig. 12 GLS power and signal semi-amplitude as a function of the number of data for the 11.44 d periodicity, supposed to be induced by a close-in super-Earth planet GJ 15 Ab. The magenta vertical line separates the pre- and post-discovery HIRES data for GJ 15 A, while the red line indicates the beginning of the CARMENES data. Even before the claimed planet discovery, the pre-discovery HIRES data seem to show fading power and semi-amplitude of the signal, and this continues when adding the newly published HIRES data. The descending trend of the power continues when the CARMENES data are added, which by themselves are not consistent with a periodic signal at 11.44 d. |
| In the text | |
 |
Fig. 13 Panel a: from top to bottom, HIRES RV data for GJ 15 A and GJ 15 B modeled with a linear trend. Blue continuous lines represent the best linear trend model of the GJ 15 A and B datasets, while the red dot-dashed lines show the linear trend expected from the mass ratio of the two stars under the assumption that the other binary companion has the correct trend estimate. Panel b: time series RVs for GJ 15 A obtained with HIRES (green diamonds) and CARMENES (red circles). The fit to the data (black solid line) is a suggestive Keplerian model consistent with a long-period Saturn mass planet on a circular orbit. The dashed blue line represents a third order polynomial approximation to this orbit, which is needed for the statistical analysis (see text). The lower panel shows the residuals to the circular fit. A long-period planet yields a significant improvement over a simpler model fitting only a linear trend. |
| In the text | |
 |
Fig. 14 Weighted mean rms scatter around the best fits (top) and mean formal RV uncertainties (bottom) for HARPS, HIRES and CARMENES. The CARMENES data are more precise and have a lower scatter when compared to HIRES. The internal errors of HARPS are usually smaller than CARMENES, but comparable in terms of RV scatter. The rms scatter for GJ 15 A and GJ 1148 is averaged from the orbital solutions for these two targets given in Tables 7 and 4, respectively. |
| In the text | |
 |
Fig. A.1 Pre- and post- NZP correction RV scatter for three CARMENES targets that we consider as “RV-quiet” stars. The top two panels are for GJ 109, the middle two show GJ 172 and the bottom two GJ 4063. The NZP correction leads to lower rms scatter for almost all RV-quiet stars in the CARMENES sample (see Fig. A2). Note that the mean measurement error |
| In the text | |
 |
Fig. A.2 Improvement of the stellar rms due to NZP correction. For this plot we have selected a sample of 126 CARMENES RV-quiet stars, which have at least 10 RV measurements and an overall rms scatter less than 10 m s-1. On average the RV scatter for these stars is reduced when the NZP correction is applied. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.